Dynamics in a Chemotaxis Model with Periodic Source

Abstract

We consider a system of two differential equations modeling chemotaxis. The system consists of a parabolic equation describing the behavior of a biological species “u” coupled to an ODE patterning the concentration of a chemical substance “v”. The growth of the biological species is limited by a logistic-like term where the carrying capacity presents a time-periodic asymptotic behavior. The production of the chemical species is described in terms of a regular function h, which increases as “u” increases. Under suitable assumptions we prove that the solution is globally bounded in time by using an Alikakos-Moser iteration, and it fulfills a certain periodic asymptotic behavior. Besides, numerical simulations are performed to illustrate the behavior of the solutions of the system showing that the model considered here can provide very interesting and complex dynamics.

1. Introduction

Chemotaxis is the ability of some living organisms to direct their movement in response to the presence of a chemical gradient. This response can be either positive (chemoattractant) or negative (chemorepellent). Mathematical models for chemotaxis have been studied since 1970 when Keller and Segel proposed a system of two parabolic equations involving nonlinear second order terms in the form

$$-\nabla ·(\chi u\nabla v)$$

in the u-equation. Since the publication of the model, an extensive mathematical literature has treated the topic, see also [1]. To present an exhaustive literature review is not the aim of this article, therefore we refer to the reader to the survey works of Horstmann [2,3], and Bellomo et al. [4] for more details (see also [5]).

The mathematical model that we study in this article describes the behavior of a biological species “u” in terms of a PDE of parabolic type. The problem is posed in a bounded domain $\mathsf{\Omega }\subset {\mathbb{R}}^n$, with a regular boundary $\partial \mathsf{\Omega }$ as follows

$$\left\{\begin{array}{cc}{\displaystyle u_t=\mathsf{\Delta }u-\nabla ·(\chi u\nabla v)+\mu u(1-u+f(x,t)),}\hfill & x\in \mathsf{\Omega },t>0,\hfill \\ {\displaystyle v_t=h(u,v),}\hfill & x\in \mathsf{\Omega },t>0,\hfill \\ {\displaystyle u(x,0)=u_0\left(x\right),v(x,0)=v_0\left(x\right),}\hfill & x\in \mathsf{\Omega },\hfill \\ {\displaystyle \frac{\partial u}{\partial \overrightarrow{n}}-u\chi \frac{\partial v}{\partial \overrightarrow{n}}=0,}\hfill & x\in \partial \mathsf{\Omega },t>0.\hfill \end{array}\right.$$

(1)

The equation includes the linear diffusion of “u” which also moves following the direction of the chemical gradient of a non-diffusive substance “v”. The chemotactic coefficient $\chi$ is assumed to be constant and positive, i.e., the biological species moves to a higher concentration of “v”. The logistic term includes a carrying capacity that limits the growth of “u” and it presents a spatial and time dependence, $f(x,t)$. Then, the reaction part is given by the quadratic term $\mu u(1-u+f),$ where $\mu$ is a positive constant. The chemical substance “v” is considered non-diffusive, i.e., once it is secreted by the biological species “u”, it is maintained up to degradation. The evolution of “v” is given in terms of a general function “h” satisfying some technical assumptions presented in this section.

Function f, in the reaction term, is a smooth bounded given function, fulfilling

$$\parallel f(x,t)-f^{*}{\left(t\right)\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}\to 0,\mathrm{a}\mathrm{s}t\to \infty ,$$

with $f^{*}\left(t\right)$ being a time-periodic function independent of the space variable “x”.

In Ref. [6] the fully parabolic system is considered, i.e., the equation for the chemical includes a diffusive term and the equation for v reads

$$\tau v_t-\mathsf{\Delta }v+v=u,x\in \mathsf{\Omega },t>0.$$

The global existence of solutions for the fully parabolic system is achieved by employing an iterative method based on the Alikakos-Moser iteration. By using an energy method through a Lyapunov functional, the convergence of the solution to a homogeneous in space and periodic in time function $u^{*}$ is given. The parabolic-elliptic case, i.e., for v satisfying the equation

$$-\mathsf{\Delta }v+v=u,x\in \mathsf{\Omega },$$

has been studied in Negreanu, Tello and Vargas [7], where the global existence and similar asymptotic behavior are done. In that case, the proof follows a sub-super solutions method already featured in Pao [8], Tello and Winkler [9], Galakhov, Salieva and Tello [10] and Negreanu and Tello [11,12] among others. In [7], the problem is addressed for a non constant function f and $u^{*}$ satisfying the ODE

$$u_t^{*}=\mu u^{*}(1+f^{*}-u^{*}),$$

(2)

where $f^{*}$ is a periodic in time function such that

$$\underset{x\in \mathsf{\Omega }}{sup}|f(x,t)-f^{*}\left(t\right)|\to 0,\mathrm{a}\mathrm{s}t\to \infty .$$

In Issa and Shen [13] the logistic term is

$$u\left(a_1(x,t)-a_2(x,t)u-a_3(x,t){\int }_{\mathsf{\Omega }}udx\right)$$

and the authors got the existence of periodic solutions when the coefficients $a_i$ (for $i=1,2,3$) are periodic in time.

Parabolic-ODE systems with chemotactic terms have been considered from the last three decades, and after the pionering works of Levine and Sleeman [14] and Anderson and Chaplain [15] modeling tumor angiogenesis, a considerable number of authors have analyzed such models. In Othmer and Stevens [16] and Stevens [17], the authors address a Parabolic-ODE system of chemotaxis passing to the limit from a discrete to a continuous system of equations. Concerning angiogenesis, the model has been raised in Kubo and Suzuki [18], Suzuki [19] and Kubo, H. Hoshino and K. Kimura [20]. Mathematical analysis of these models with two equations can be found in Fontelos, Friedman and Hu [21], Friedman and Tello [22] and Negreanu and Tello [11] among others. Systems with three or more equations involving chemotaxis and diffusive or non-diffusive processes also appear in ecology and other biological applications (see [12,23]). In Ref. [24] the authors study a similar Parabolic-Parabolic-ODE system

$$\left\{\begin{array}{c}{\displaystyle u_t=\mathsf{\Delta }u-\nabla ·({\chi }_1\left(w\right)u\nabla w)+{\mu }_{1}u(1-u),x\in \mathsf{\Omega },t>0,}\hfill \\ {\displaystyle v_t=\mathsf{\Delta }v-\nabla ·({\chi }_2\left(w\right)v\nabla w)+{\mu }_{2}v(1-v),x\in \mathsf{\Omega },t>0,}\hfill \\ {\displaystyle w_t=h(u,v,w),x\in \mathsf{\Omega },t>0,}\hfill \end{array}\right.$$

where the chemosensitivities ${\chi }_1,{\chi }_2$ are non-constant. Global existence and convergence of the solution to a steady-state $(1,1,\tilde{w})$ satisfying $h(1,1,\tilde{w})=0$ are presented under suitable assumptions on the coefficients and the spatial dimension of the domain. The results in [24] have been improved in Mizukami and Yokota [25] for a larger range of parameters.

Also in the context of cancer dynamics, chemotactic systems with non-diffusive equations have been recently used to model cancer cell invasion in Stinner, Surulescu and Winkler [26] with a model consisting of six equations where the cancer cells behavior is described by a parabolic equation with chemotactic terms. Denoting by “u” the cancer cells density, by “v” the fibers of the extracellular matrix (ECM) and by “l”, “$y_1$” and “$y_2$” the concentration of chemoattractant, integrins bound to ECM fibers and integrins bound to proteolitic residuals then, their model is the following

$$\left\{\begin{array}{c}{\displaystyle c_t=\nabla ·(\frac{\kappa }{1+cv}\nabla c)-\nabla ·(\frac{\kappa vc}{1+v}\nabla v)-\nabla ·(\frac{c}{1+cl}\nabla l)+{\mu }_{c}c(1-u-{\eta }_{1}v),}\hfill \\ {\displaystyle v_t={\mu }_{v}c(1-u)-\lambda cv,}\hfill \\ {\displaystyle l_t=\mathsf{\Delta }l-l+cv,}\hfill \\ {\displaystyle {\left(y_1\right)}_t=k_1(1-y_1-y_2)v-k_{-1}{y}_1,}\hfill \\ {\displaystyle {\left(y_2\right)}_t=k_2(1-y_1-y_2)l-k_{-2}{y}_2,}\hfill \\ {\displaystyle {\kappa }_t=-\kappa +\frac{M{y}_1(·,t-\tau )}{1+y_2(·,t-\tau )}.}\hfill \end{array}\right.$$

The authors prove the existence of global weak solutions together with some boundedness properties. The proof is based on the properties of the functional

$${\int }_{\mathsf{\Omega }}clncdx+\frac{1}{2\lambda }{\int }_{\mathsf{\Omega }}\frac{{\kappa |\nabla v|}^2}{1+v}dx.$$

Notice that, in this case, three of the variables leading the movement satisfy ordinary differential equations (see also Stinner, Surulescu and Uatay [27], Tao and Winkler [28], Zhigun, Surulescu and Hunt [29] and Zhigun, Surulescu and Uatay [30] for similar models). Throughout the article we use the notation ${\mathsf{\Omega }}_t=\mathsf{\Omega }\times (0,t)$, for $t\in (0,\infty ]$, we assume, without loss of generality, that $\left|\mathsf{\Omega }\right|=1$ and we denote by g the function

$$g\left(v\right):=e^{\chi v}.$$

(3)

We work under the following hypotheses

• The positive initial data $(u_0,v_0)$ of (1) satisfy, $(u_0,v_0)\not\equiv (0,0)$ and

  $$(u_0,v_0)\in {\left(L^{\infty }\left(\mathsf{\Omega }\right)\cap W^{1,s}\left(\mathsf{\Omega }\right)\right)}^2,\underline{v}\le v_0\le \overline{v},$$

  (4)

  for some $s>max\{4,n\}$ and

  $$\frac{\partial u_0}{\partial \overrightarrow{n}}=\frac{\partial v_0}{\partial \overrightarrow{n}}=0,x\in \partial \mathsf{\Omega }.$$

  (5)
• There exists a periodic function $f^{*}$ verifying

  $$\parallel f(x,t)-f^{*}{\left(t\right)\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}\to 0,\mathrm{a}\mathrm{s}t\to \infty ,$$

  (6)

  $$\underset{x\in \mathsf{\Omega }}{inf}f(x,t)<f^{*}\left(t\right)<\underset{x\in \mathsf{\Omega }}{sup}f(x,t)$$

  and

  $$-1+\epsilon <f(x,t),\text{for}\text{some} \epsilon >0.$$

  (7)
• Function h fulfills

  $$h\in W_{loc}^{1,\infty }({\mathbb{R}}_{+}\times \mathbb{R})\cap C^2\left({\mathbb{R}}_{+}^2\right);$$

  (8)

  $$\frac{\partial h}{\partial u}>0,\frac{\partial h}{\partial v}\le -{ϵ}_v<0\mathrm{and}\frac{\partial h}{\partial v}+u\chi \frac{\partial h}{\partial u}<-{ϵ}_v/2<0,\mathrm{w}\mathrm{ith}{ϵ}_v>0;$$

  (9)
  Moreover, there exists a positive constant c such that

  $$-h(0,v)\le c{e}^{\chi v},0\le h(0,0)<\mu \epsilon /2\chi ,$$

  (10)

  with some $\epsilon$ as in (7).
• For a given constant $c_5:=c_5(u_0{,\parallel f\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)},\mu ,\chi ,c)$ (defined in Lemma 6) we have that

  $$\underset{s\to \infty }{lim\; sup}h\left(c_5{e}^{\chi s},s\right)\le -{ϵ}_0,{ϵ}_0>0.$$

  (11)

The functions given by $h(u,v)=(u{e}^{-\chi v}+v)/(1+v)-v$ and $h(u,v)=u{e}^{-\chi v}-av$, with $a>0$ verify the hypotheses.

2. Main Results

Our particular analysis will address the initial-boundary value problem (1) in a bounded open domain $\mathsf{\Omega }\subset {\mathbb{R}}^n$, where the initial data are as in (4). The issue of the global solvability is presented in the following theorem.

Theorem 1.

Let Ω be a bounded open domain with regular boundary of ${\mathbb{R}}^n$ and suppose that assumptions (4)–(11) hold. Then, there exists a unique pair of nonnegative functions u and v which forms a global solution

$$(u,v)\in C([0,\infty ),{\left(W^{1,s}\left(\mathsf{\Omega }\right)\right)}^2)\cap C^1((0,\infty ),{\left(W^{1,s}\left(\mathsf{\Omega }\right)\right)}^{\prime }\times W^{1,s}\left(\mathsf{\Omega }\right))$$

to the problem (1). In addition, $\left(u\right(x,t),v(x,t\left)\right)$ is uniformly bounded in $\mathsf{\Omega }\times (0,\infty )$, that is, there exists a constant $C:=C(u_0,v_0)>0$, such that

$${\parallel u(·,t)\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}+{\parallel v(·,t)\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}\le C<\infty .$$

Afterwards, we study the asymptotic properties of the solutions. We introduce the function $u^{*}$ as set out by

$${\displaystyle u^{*}\left(t\right)=\frac{{\displaystyle u_0^{*}{e}^{{\int }_0^t\mu (1+f^{*}\left(s\right))ds}}}{{\displaystyle 1+u_0^{*}{\int }_0^t{\displaystyle \mu e^{{\int }_0^{\tau }\mu (1+f^{*}\left(s\right))ds}}d\tau }},}$$

(12)

for $u_0^{*}$ defined by

$${\displaystyle u_0^{*}:=\frac{{\displaystyle e^{{\int }_0^T\mu (1+f^{*}\left(s\right))ds}-1}}{\mu {\int }_0^T{\displaystyle e^{{\int }_0^{\tau }\mu (1+f^{*}\left(s\right))ds}d\tau }}}$$

and $f^{*}$ as in (6). Notice that $u^{*}$ satisfies Equation (2) and it is an homogeneous in space and periodic in time function. We denote by $v^{*}\left(t\right)$, the solution of the ordinary differential equation

$$v_t^{*}=h(u^{*},v^{*}).$$

(13)

The following assertion is the main result on the asymptotic behavior of solutions of (1).

Theorem 2.

Assume (4)–(11) and let us denote by $(u,v)$ the corresponding solution of (1) from Theorem 1. Then, $(u,v)$ has the following asymptotic behavior

$$\parallel u(x,t)-u^{*}{\left(t\right)\parallel }_{L^p\left(\mathsf{\Omega }\right)}+{\parallel v(x,t)-v^{*}\left(t\right)\parallel }_{L^p\left(\mathsf{\Omega }\right)}\to 0,as t\to \infty ,$$

(14)

for any $p\in [1,\infty )$, where $u^{*}$ and $v^{*}$ are given by (12) and (13), respectively.

The paper is organized as follows: in Section 3 we proof the existence of a unique pair of classical solutions. A first key step consists in findining a maximal weak solution following [31], and we then get the boundedness of the solution. As a crucial ingredient in our derivation of a $L^{\infty }\left(\mathsf{\Omega }\right)$ bound for u, we employ a Alikakos-Moser-type iterative procedure [32]. By means of these and some further higher regularity properties will assert the statements on global existence and boundedness of u and v from Theorem 1. Our collection of estimates of Section 3 will moreover turn out to be sufficient to derive the stabilization result from Theorem 2 in Section 4 through an analysis into two steps. First, we prove that the solutions converge to their respective averages, i.e.,

$${\int }_{\mathsf{\Omega }}udx,{\int }_{\mathsf{\Omega }}vdx,$$

using energy estimates to conclude that these averages converge to the functions $u^{*}$ and $v^{*}$, respectively. Finally, in Section 5 we perform a brief numerical study of the system under consideration. Some of the results presented in this paper were announced in [33].

3. Global Existence of Solutions

The present section is devoted to the proof of Theorem 1. We study the local-in-time existence of classical solutions to (1) and we prove some preliminary technical facts. In order to prove the global existence of the solutions, we first obtain the local existence using classical results on partial differential equations and then we conclude the proof by constructing uniform bounds.

Lemma 1.

Let $\mathsf{\Omega }\subset {\mathbb{R}}^n$ be an open bounded set with smooth boundary, assume that the initial data, $(u_0,v_0)$, are as in (4) and hypotheses of Theorem 1 hold. Then, there exists a maximal existence time $T_{max}>0$ such that system (1) has an unique non-negative classical solution

$$(u(x,t),v(x,t))\in C([0,T_{max}),{(W^{1,s}(\mathsf{\Omega }))}^2)\cap C^1((0,T_{max}),{(W^{1,s}(\mathsf{\Omega }))}^{\prime }\times W^{1,s}(\mathsf{\Omega })),$$

as well as

$$\underset{t\to T_{max}}{lim\; sup}\left({\parallel u(x,t)\parallel }_{W^{1,s}\left(\mathsf{\Omega }\right)}+{\parallel v(x,t)\parallel }_{W^{1,s}\left(\mathsf{\Omega }\right)}+t\right)=\infty .$$

Proof. 

We consider the system (6.2) of [31] where

$$u_1=u,u_2=v,{\mathcal{A}}_{1}u=-\mathsf{\Delta }u,{\mathcal{A}}_2(u,v)v=\nabla ·(u\chi \nabla v),$$

$$f_1(·,t,u,v)=\mu u(1-u+f),f_2(·,t,u,v)=h(u,v)$$

and

$${\mathcal{B}}_{1}u=\frac{\partial u}{\partial n},{\mathcal{B}}_{2}v=-u\chi \frac{\partial v}{\partial n}.$$

We can rewrite then (1) as follows

$$\left\{\begin{array}{cc}{u}_t+{\mathcal{A}}_{1}u+{\mathcal{A}}_{2}v=f_1(·,t,u,v),\hfill & x\in \mathsf{\Omega },(0,T_{max}),\hfill \\ v_t=f_2(·,t,u,v),\hfill & x\in \mathsf{\Omega },(0,T_{max}),\hfill \\ {\mathcal{B}}_{1}u+{\mathcal{B}}_{2}v=0,\hfill & x\in \partial \mathsf{\Omega },(0,T_{max}),\hfill \end{array}\right.$$

with the same initial data as (1). We apply Theorem 6.4 in [31] and consider maximal interval of existence. So, the local-in-time existence for (1) is proved.

In order to see the non-negativity of u we introduce the following change of variables:

$$u=g\left(v\right)\tilde{u},\mathrm{for}g\left(v\right)=e^{\chi v}.$$

(15)

Then we can rewrite the first equation in (1) as

$$u_t={\tilde{u}}_{t}g\left(v\right)+\tilde{u}{g}^{\prime }\left(v\right)v_t={\tilde{u}}_{t}g\left(v\right)+\chi \tilde{u}g\left(v\right)h.$$

Now, deriving with respect to the spatial variable in the previous equation we get

$$\nabla u=g\left(v\right)\nabla \tilde{u}+\tilde{u}{g}^{\prime }\left(v\right)\nabla v=g\left(v\right)\nabla \tilde{u}+\chi \tilde{u}g\left(v\right)\nabla v,$$

$$\mathsf{\Delta }u=g\left(v\right)\mathsf{\Delta }\tilde{u}+2\chi g\left(v\right)\nabla \tilde{u}\nabla v+{\chi }^2\tilde{u}g\left(v\right){|\nabla v|}^2+\chi \tilde{u}g\left(v\right)\mathsf{\Delta }v,$$

and

$$\nabla (\chi u\nabla v)=\chi g\left(v\right)\nabla \tilde{u}\nabla v+{\chi }^2\tilde{u}g\left(v\right){|\nabla v|}^2+\chi \tilde{u}g\left(v\right)\mathsf{\Delta }v.$$

Then, the first equation of (1) becomes

$$g\left(v\right){\tilde{u}}_t=g\left(v\right)\mathsf{\Delta }\tilde{u}+\chi g\left(v\right)\nabla \tilde{u}\nabla v+\mu g\left(v\right)\tilde{u}(1-\tilde{u}g\left(v\right)+f)-\chi \tilde{u}g\left(v\right)h(\tilde{u}g\left(v\right),v),$$

we multiply by $e^{-\chi v}$ to get

$${\tilde{u}}_t=\mathsf{\Delta }\tilde{u}+\chi \nabla \tilde{u}\nabla v+\mu \tilde{u}(1-\tilde{u}g\left(v\right)+f)-\chi \tilde{u}h(\tilde{u}g\left(v\right),v).$$

(16)

Notice that the equation for v remains as an ordinary differential equation

$$v_t=h(\tilde{u}g\left(v\right),v).$$

(17)

So, the original system (1) becomes (16) and (17) together with the initial data

$$\tilde{u}(x,0)={\tilde{u}}_0\left(x\right)=\frac{u_0\left(x\right)}{g\left(v_0\left(x\right)\right)},v(x,0)=v_0\left(x\right),$$

and the Neumann boundary condition

$$\frac{\partial \tilde{u}}{\partial n}=0.$$

Finally, the Maximum Principle for parabolic equations and the regularity of h prove the non-negativity of u, taking into account that

$$[\mu \tilde{u}(1-\tilde{u}g\left(v\right)+f)-\chi \tilde{u}h(\tilde{u}g\left(v\right),v)]{\mid }_{\tilde{u}=0}=0.$$

Hypotheses (9) and (10) on h and the Maximum Principle applied to (17) prove

$$0\le v.$$

This completes the proof. □

Let us now collect some basic properties thereof which in our subsequent analysis will play important roles not only by providing some useful fundamental regularity features, but also by establishing the first quantitative information (18) on large time behavior. We remember that ${\mathsf{\Omega }}_{\infty }=\mathsf{\Omega }\times (0,\infty )$ for the next matches, and also, ${\parallel ·\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}={sup}_{t>0}{\parallel ·\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}$.

Lemma 2.

Under Hypotheses (4)–(11), the total mass of the component $u(x,t)$ of the solution to (1) is bounded:

$${\int }_{\mathsf{\Omega }}u(x,t)dx\le max\left\{{(1+\parallel f\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}),\parallel u_0{\parallel }_{L^1\left(\mathsf{\Omega }\right)}\right\}:=c_1.$$

(18)

Proof. 

We integrate the first equation of (1) directly over $\mathsf{\Omega }$ to get

$$\frac{d}{dt}{\int }_{\mathsf{\Omega }}udx\le {\mu (1+\parallel f(x,t)\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}){\int }_{\mathsf{\Omega }}udx-\mu {\int }_{\mathsf{\Omega }}{u}^{2}dx.$$

(19)

Applying the Cauchy-Schwarz inequality, since $\left|\mathsf{\Omega }\right|=1$,

$$|{\int }_{\mathsf{\Omega }}udx{|}^2\le {\int }_{\mathsf{\Omega }}{u}^{2}dx,$$

we directly obtain

$$\frac{d}{dt}{\int }_{\mathsf{\Omega }}udx\le {\mu (1+\parallel f(x,t)\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}){\int }_{\mathsf{\Omega }}udx-\mu |{\int }_{\mathsf{\Omega }}udx{|}^2.$$

(20)

Finally, (18) is a consequence of the Maximum Principle applied to (20), i.e.,

$${\int }_{\mathsf{\Omega }}udx\le max\left\{{(1+\parallel f\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}),\parallel u_0{\parallel }_{L^1\left(\mathsf{\Omega }\right)}\right\}.$$

□

Lemma 3.

Under the same assumptions of Lemma 2, the solution to (1) satisfies

$${\int }_t^{t+t_0}{\int }_{\mathsf{\Omega }}{u}^2(x,s)dxds\le c_2,$$

(21)

for all $t\in (0,T_{max}-t_0)$, where $t_0=min\{1,T_{max}/2\}$ and

$$c_2:=c_1\left(1+{\parallel f\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}+\frac{1}{\mu }\right).$$

Proof. 

We integrate (19) over the interval $(t,t+t_0)$ for $t_0=min\{1,T_{max}/2\}$ to obtain

$$\begin{array}{cc}\hfill {\int }_{\mathsf{\Omega }}u(·,t+t_0)dx& -{\int }_{\mathsf{\Omega }}u(·,t)dx\hfill \\ & \le {\mu (1+\parallel f\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}){\int }_t^{t+t_0}{\int }_{\mathsf{\Omega }}udxds-\mu {\int }_t^{t+t_0}{\int }_{\mathsf{\Omega }}{u}^{2}dxds,\hfill \end{array}$$

$\forall t\in (0,T_{max}-t_0)$, or, equivalently,

$${\int }_t^{t+t_0}{\int }_{\mathsf{\Omega }}{u}^{2}dxds\le \left(1+{\parallel f\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}\right){\int }_t^{t+t_0}{\int }_{\mathsf{\Omega }}udxds+\frac{1}{\mu }{\int }_{\mathsf{\Omega }}u(·,t)dx.$$

By the previous lemma it follows

$$\begin{array}{cc}{\displaystyle {\int }_t^{t+t_0}{\int }_{\mathsf{\Omega }}{u}^{2}dxds}\hfill & {\displaystyle \le {(1+\parallel f\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}){\int }_t^{t+t_0}{c}_{1}ds+\frac{c_1}{\mu }}\hfill \\ & {\displaystyle \le {(1+\parallel f\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)})c_1{t}_0+\frac{c_1}{\mu }}\hfill \\ \hfill & {\displaystyle \le c_1\left({(1+\parallel f\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)})t_0+\frac{1}{\mu }\right).}\hfill \end{array}$$

Finally, since $t_0\le 1$ we have

$${\int }_t^{t+t_0}{\int }_{\mathsf{\Omega }}{u}^{2}dxds\le c_1\left({(1+\parallel f\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)})+\frac{1}{\mu }\right):=c_2$$

thereby completes the proof. □

Lemma 4.

Under hypotheses of Theorem 1, the following assertion is verified: there exists a positive constant $c_3$ defined by

$$c_3:=\frac{c_2}{e^{t_0}-1},$$

for $t_0:=min\{1,T_{max}/2\}$ such that

$${\int }_0^t{e}^{s-t}{\int }_{\mathsf{\Omega }}{u}^{2}dxds\le c_3.$$

Proof. 

Notice that

$${\int }_0^t{e}^{s-t}{\int }_{\mathsf{\Omega }}{u}^{2}dxds\le \sum _{n=0}^{N-1}{\int }_{n{t}_0}^{(n+1)t_0}{e}^{s-N{t}_0}{\int }_{\mathsf{\Omega }}{u}^{2}dxds+{\int }_{N{t}_0}^t{\int }_{\mathsf{\Omega }}{u}^{2}dxds$$

for some $N\in \mathbb{N}$, such that $N{t}_0<t\le (N+1)t_0$. Then, we get

$$\begin{array}{cc}{\displaystyle {\int }_0^t{e}^{s-t}{\int }_{\mathsf{\Omega }}{u}^{2}dxds}\hfill & {\displaystyle \le \sum _{n=0}^{N-1}{e}^{(n-N+1)t_0}{\int }_{n{t}_0}^{(n+1)t_0}{\int }_{\mathsf{\Omega }}{u}^{2}dxds+{\int }_{N{t}_0}^t{\int }_{\mathsf{\Omega }}{u}^{2}dxds}\hfill \\ \hfill & {\displaystyle \le c_2\sum _{n=0}^N{e}^{(n-N+1)t_0}\le \frac{c_2}{e^{t_0}-1}.}\hfill \end{array}$$

□

We are now prepared to perform an iterative argument of Alikakos-Moser type in order to derive $L^{\infty }\left(\mathsf{\Omega }\right)$ bounds for u and v.

The proof starts with the following lemma.

Lemma 5.

Let $g\left(v\right)$ be defined by (15), then, for $p\ge 2$ the following estimate holds

$$\begin{array}{cc}{\displaystyle \frac{d}{dt}}\hfill & {\displaystyle {\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx}\hfill \\ & {\displaystyle \le -p(p-1){\int }_{\mathsf{\Omega }}\frac{u^{p-2}}{g^{p-3}}{\left|\nabla \frac{u}{g}\right|}^{2}dx+p\mu \left(1+{\parallel f\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}\right){\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx}\hfill \\ {\displaystyle }\hfill & {\displaystyle -p\mu {\int }_{\mathsf{\Omega }}{u}^{p+1}{g}^{1-p}dx+c(p-1)\chi {\int }_{\mathsf{\Omega }}{u}^p{g}^{2-p}dx,}\hfill \end{array}$$

(22)

where c is the constant given in assumption (10).

Proof. 

We proceed by induction in p, then, for $p\ge 2$ we have

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d}{dt}{\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx=p{\int }_{\mathsf{\Omega }}{u}^{p-1}{u}_t{g}^{1-p}dx+(1-p)\chi {\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}hdx}\hfill \\ \hfill & {\displaystyle =p{\int }_{\mathsf{\Omega }}{u}^{p-1}(\mathsf{\Delta }u-\chi \nabla (u\nabla v))g^{1-p}dx+p\mu {\int }_{\mathsf{\Omega }}{u}^p(1-u+f)g^{1-p}dx}\hfill \\ \hfill & {\displaystyle +(1-p)\chi {\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}hdx.}\hfill \end{array}$$

(23)

For the first integral in (23) we infer that

$$\begin{array}{cc}\hfill & {\displaystyle p{\int }_{\mathsf{\Omega }}{u}^{p-1}{g}^{1-p}(\mathsf{\Delta }u-\chi \nabla (u\nabla v))dx}\hfill \\ & =-p{\int }_{\mathsf{\Omega }}\nabla \left[u^{p-1}{g}^{1-p}\right](\nabla u-\chi u\nabla v)dx\hfill \\ \hfill & {\displaystyle =-p{\int }_{\mathsf{\Omega }}[(p-1)u^{p-2}{g}^{1-p}\nabla u+\chi (1-p)g^{1-p}{u}^{p-1}\nabla v](\nabla u-\chi u\nabla v)dx}\hfill \\ \hfill & {\displaystyle =-p(p-1){\int }_{\mathsf{\Omega }}{u}^{p-2}{g}^{1-p}{(\nabla u-\chi u\nabla v)}^{2}dx}\hfill \\ \hfill & {\displaystyle =-p(p-1){\int }_{\mathsf{\Omega }}{u}^{p-2}{g}^{1-p}{(e^{\chi v}\nabla \left(u{e}^{-\chi v}\right))}^{2}dx.}\hfill \end{array}$$

From the expression of the above identity, we deduce

$$p{\int }_{\mathsf{\Omega }}{u}^{p-1}(\mathsf{\Delta }u-\chi \nabla (u\nabla v))g^{1-p}dx\le 0.$$

(24)

We look now at the last term of (23). By the Mean Value Theorem and assumption (10) we have

$$h(u,v)={\left.\frac{\partial h}{\partial u}\right|}_{(\xi ,v)}u+h\left(0,v\right)\ge -cg\left(v\right),$$

then,

$$(1-p)\chi {\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}hdx\le (p-1)c\chi {\int }_{\mathsf{\Omega }}{u}^p{g}^{2-p}dx.$$

(25)

Moreover, for the restant term of (23), we have

$$\begin{array}{cc}\hfill p\mu & {\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}(1-u+f)dx\hfill \\ & \le {p\mu (1+\parallel f\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}){\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx-p\mu {\int }_{\mathsf{\Omega }}{u}^{p+1}{g}^{1-p}dx.\hfill \end{array}$$

(26)

We now replace (24)–(26) in (23) to get

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dt}{\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx}& {\displaystyle \le -p(p-1){\int }_{\mathsf{\Omega }}\frac{u^{p-2}}{g^{p-3}}{\left|\nabla \frac{u}{g}\right|}^{2}dx}\hfill \\ & +p\mu \left(1+{\parallel f\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}\right){\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx\hfill \\ \hfill & {\displaystyle -p\mu {\int }_{\mathsf{\Omega }}{u}^{p+1}{g}^{1-p}dx+c\chi (p-1){\int }_{\mathsf{\Omega }}{u}^p{g}^{2-p}dx,}\hfill \end{array}$$

which yields (22) and the proof ends. □

Lemma 6.

Let us consider $p\ge 1$ and $g\left(v\right)$ as in (15). Let ϵ be a positive constant defined by

$$ϵ:=\frac{\mu }{2\mu +{2\mu \parallel f\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}+2},$$

(27)

then, there exist $c_4>0$ and $c_5>0$ given by

$$c_4:=max\left\{\frac{6\parallel u_0{\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}}{min\{1,\mu \}},\frac{3}{{ϵ}^2},\frac{6c\chi }{\mu },c_3,1\right\}$$

and

$$c_5:=max\{3\parallel u_0{\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)},\frac{3\mu }{2{ϵ}^2},c\chi e{c}_4\},$$

for $c_3$ as in Lemma 4, such that

$${\int }_0^t{e}^{s-t}{\int }_{\mathsf{\Omega }}{u}^{p+1}{g}^{1-p}dxds\le c_4^p,$$

(28)

and

$${\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx\le c_5^p.$$

(29)

Proof. 

For $p=1$ the result is a consequence of Lemmas 2 and 3. For $p\ge 2$ we proceed by induction and assume the result for $p-1$, i.e.,

$${\int }_{\mathsf{\Omega }}{u}^{p-1}{g}^{2-p}dx\le c_5^{p-1},{\int }_0^t{e}^{s-t}{\int }_{\mathsf{\Omega }}{u}^p{g}^{2-p}dx\le c_4^{p-1}.$$

(30)

Taking $p\ge 2$, thanks to (22), we have

$$\begin{array}{cc}{\displaystyle \frac{d}{dt}{\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx}\hfill & {\displaystyle \le p\mu \left(1+{\parallel f\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}\right){\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx}\hfill \\ \hfill & {\displaystyle -p\mu {\int }_{\mathsf{\Omega }}{u}^{p+1}{g}^{1-p}dx+c\chi (p-1){\int }_{\mathsf{\Omega }}{u}^p{g}^{2-p}dx.}\hfill \end{array}$$

(31)

We first recall the Young’s inequality:

$$\frac{1}{ϵ}{u}^p\le \frac{p}{p+1}{u}^{p+1}+\frac{1}{(p+1){ϵ}^{p+1}};$$

multiplying it by $g^{1-p}$ we get

$$\frac{1}{ϵ}{u}^p{g}^{1-p}\le u^{p+1}{g}^{1-p}+\frac{1}{(p+1){ϵ}^{p+1}}{g}^{1-p},$$

which is equivalent to

$$-u^{p+1}{g}^{1-p}\le -\frac{1}{ϵ}{u}^p{g}^{1-p}+\frac{1}{(p+1){ϵ}^{p+1}}{g}^{1-p},$$

we integrate in space over $\mathsf{\Omega }$, and in view of $g^{1-p}\le 1$, we get

$$-\frac{p\mu }{2}{\int }_{\mathsf{\Omega }}{u}^{p+1}{g}^{1-p}dx\le -\frac{p\mu }{2ϵ}{\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}+\frac{p\mu }{2(p+1){ϵ}^{p+1}}.$$

(32)

Thanks to the definition (27) of $ϵ$, we have

$$p\mu \left(1+{\parallel f\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}\right)-\frac{p\mu }{2ϵ}\le -1.$$

We replace (32) into (31) to get

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dt}{\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx\le }& -{\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx+\frac{\mu }{2{ϵ}^{p+1}}-\frac{p\mu }{2}{\int }_{\mathsf{\Omega }}{u}^{p+1}{g}^{1-p}dx\hfill \\ & +c\chi (p-1){\int }_{\mathsf{\Omega }}{u}^p{g}^{2-p}dx.\hfill \end{array}$$

(33)

By solving the differential Equation (33) after integration in time, we obtain

$$\begin{array}{cc}\hfill {\displaystyle {\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx}& {\displaystyle \le e^{-t}{\int }_{\mathsf{\Omega }}{u}_0^p{g}^{1-p}\left(v_0\right)dx+\frac{\mu }{2{ϵ}^{p+1}}}\hfill \\ & -\frac{p\mu }{2}{\int }_0^t{e}^{s-t}{\int }_{\mathsf{\Omega }}{u}^{p+1}{g}^{1-p}dxds\hfill \\ \hfill & {\displaystyle +c\chi (p-1){\int }_0^t{e}^{s-t}{\int }_{\mathsf{\Omega }}{u}^p{g}^{2-p}dxds.}\hfill \end{array}$$

(34)

Dropping the nonpositive term and making use of a favorable cancellation, it yields

$${\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx\le {\parallel u_0\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}^p+\frac{\mu }{2{ϵ}^{p+1}}+c\chi (p-1)c_4^{p-1}$$

(35)

and

$${\int }_0^t{e}^{s-t}{\int }_{\mathsf{\Omega }}{u}^{p+1}{g}^{1-p}dx\le \frac{2}{p\mu }{\parallel u_0\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}^p+\frac{1}{p{ϵ}^{p+1}}+\frac{2c\chi }{\mu }{c}_4^{p-1}.$$

Then, it results

$$\begin{array}{cc}{\displaystyle {\int }_0^t{e}^{s-t}{\int }_{\mathsf{\Omega }}{u}^{p+1}{g}^{1-p}dx}\hfill & {\displaystyle \le 3max\left\{\frac{2}{p\mu }{\parallel u_0\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}^p,\frac{1}{p{ϵ}^{p+1}},\frac{2c\chi }{\mu }{c}_4^{p-1}\right\}}\hfill \\ \hfill & {\displaystyle \le max\left\{\frac{6}{\mu }{\parallel u_0\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}^p,\frac{3}{{ϵ}^{p+1}},\frac{6c\chi }{\mu }{c}_4^{p-1}\right\}}\hfill \\ & \le {\left[max\left\{\frac{6\parallel u_0{\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}}{min\{1,\mu \}},\frac{3}{{ϵ}^2},c_4,1\right\}\right]}^p.\hfill \end{array}$$

By definition of $c_4$ it follows

$${\int }_0^t{e}^{s-t}{\int }_{\mathsf{\Omega }}{u}^{p+1}{g}^{1-p}dx\le c_4^p$$

and due to (35), the following inequality holds

$$\begin{array}{cc}{\displaystyle {\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx}\hfill & {\displaystyle \le 3max\{\parallel u_0{\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}^p,\frac{\mu }{2{ϵ}^{p+1}},c\chi (p-1)c_4^{p-1}\}}\hfill \\ & {\displaystyle \le max\{3\parallel u_0{{\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)},\frac{3\mu }{2{ϵ}^2},c\chi e{c}_4\}}^p=c_5^p.}\hfill \end{array}$$

□

Lemma 7.

Under the assumptions of Theorem 1, we have

$${∥\frac{u}{g}∥}_{L^{\infty }\left(\mathsf{\Omega }\right)}\le c_5,$$

(36)

where $c_5$ has been defined in Lemma 6.

Proof. 

According to Lemma 6 we have that

$${\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx\le c_5^p$$

and therefore

$${\left[{\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx\right]}^{\frac{1}{p}}\le c_5.$$

Since

$${\left[{\int }_{\mathsf{\Omega }}{u}^p{g}^{-p}dx\right]}^{\frac{1}{p}}\le {\left[{\int }_{\mathsf{\Omega }}{u}^p{g}^{1-p}dx\right]}^{\frac{1}{p}},$$

we take limits when $p\to \infty$, to obtain (36). □

Lemma 8.

Suppose that (9)–(11) hold. Then there exists a positive constant $\overline{v}<\infty$ such that the solution v of (1) satisfies

$$v(x,t)<\overline{v}.$$

Proof. 

By contradiction, we assume that for any $\overline{v}>{\parallel v_0\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}$ there exists $t_0>0$ such that $v(x,t_0)=\overline{v}$ which is the first $t_0$ fulfilling this condition. Since by assumption (4) $v_0<\overline{v},$ v must be an increasing function in a neighborhood of $t_0$. Then, by applying (11), we obtain

$$v_t\left(t_0\right)=h(u,\overline{v})=h\left(\frac{u}{g\left(\overline{v}\right)}g\left(\overline{v}\right),\overline{v}\right)-h\left(c_{5}g\left(\overline{v}\right),\overline{v}\right)+h\left(c_{5}g\left(\overline{v}\right),\overline{v}\right)$$

then, since h is increasing in the first variable, we have

$$v_t\left(t_0\right)\le h\left(c_{5}g\left(\overline{v}\right),\overline{v}\right).$$

Thanks to assumption (11) we have that for $\overline{v}$ large enough

$$v_t\left(t_0\right)<0,$$

which is a contradiction and the proof ends. □

The above results entail the claimed qualitative properties of u:

Lemma 9.

Under assumptions of Theorem 1, the solution u is uniformly bounded by

$${\parallel u\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}\le e^{\chi \overline{v}}{c}_5.$$

Proof. 

The result is a consequence of Lemmas 7 and 8. □

Proof of Theorem 1.

The global existence of $(u,v)$ over $\mathsf{\Omega }\times (0,\infty )$ is a direct consequence of the local existence (Lemma 3.1, Theorem 6.4 in [31]) and the uniform boundedness of $(u,v)$ in $L^{\infty }\left(\mathsf{\Omega }\right)$ established in the previous Lemmas.□

4. Asymptotic Behavior

The main propose of this section is to demonstrate Theorem 2, i.e., to obtain the convergence of the solution $(u,v)$ to $(u^{*},v^{*})$. We proceed in two steps: first of all we get the convergence of the solution u to its average ${\int }_{\mathsf{\Omega }}u$, to get later the convergence of the average to the periodic function $u^{*}$ given by (12). For it, we need to prove the boundedness of $|\nabla v|$ in $L^2\left(\mathsf{\Omega }\right)$. The result is enclosed in the following lemma.

Lemma 10.

Suppose that the assumptions of Theorem 2 hold. Then, there exists $c_6>0$, independent of t, such that

$${\int }_{\mathsf{\Omega }}{|\nabla v|}^{2}dx\le c_6,$$

where v is the solution of (1).

Proof. 

We consider Equation (22), for $p=2$, and integrate over $(0,t)$ to obtain, after routinary computations and thanks to Lemmas 4, 6 and 7

$${\int }_0^t{e}^{ϵ(s-t)}{\int }_{\mathsf{\Omega }}g{\left|\nabla \frac{u}{g}\right|}^{2}dxds\le c_5,$$

(37)

for any $ϵ>0$. Recalling that v satisfies

$$v_t=h(u,v)=h\left(\frac{u}{g}g,v\right),$$

then taking gradients we get

$$\frac{d}{dt}\nabla v-[u\chi h_u+h_v]\nabla v=h_{u}g\nabla \frac{u}{g}.$$

(38)

Now, we multiply (38) by $\nabla v$ and integrate over $\mathsf{\Omega }$ to obtain, in view of assumptions (9)

$$\frac{d}{dt}\frac{1}{2}{\int }_{\mathsf{\Omega }}{|\nabla v|}^2+{ϵ}_v{\int }_{\mathsf{\Omega }}{|\nabla v|}^2\le {\int }_{\mathsf{\Omega }}g\nabla \frac{u}{g}\nabla v,$$

and therefore, by the Young’s inequality

$$\frac{d}{dt}\frac{1}{2}{\int }_{\mathsf{\Omega }}{|\nabla v|}^2+\frac{{ϵ}_v}{2}{\int }_{\mathsf{\Omega }}{|\nabla v|}^2\le \frac{c}{{ϵ}_v}{\int }_{\mathsf{\Omega }}g{\left|\nabla \frac{u}{g}\right|}^{2}dx.$$

After integration in time we get

$${\int }_{\mathsf{\Omega }}{|\nabla v|}^2\le e^{-{ϵ}_{v}t}{\int }_{\mathsf{\Omega }}{|\nabla v_0|}^2+\frac{2c}{{ϵ}_v}{\int }_0^t{e}^{{ϵ}_v(s-t)}{\int }_{\mathsf{\Omega }}g{\left|\nabla \frac{u}{g}\right|}^{2}dx.$$

and due to (37), we conclude the lemma. □

Lemma 11.

Under the assumptions of Theorem 2, there exists a positive constant ${\epsilon }_2>0$ such that

$${\int }_{\mathsf{\Omega }}udx\ge {\epsilon }_2.$$

Proof. 

We proceed as in Mizukami-Yokota [25] (Lemma 4.2.) and multiply the equation of u by $u^{-\beta }{e}^{\chi \beta v}$ for some $\beta \in (1,2)$, after integration by parts we obtain

$$\begin{array}{cc}& {\displaystyle \frac{d}{dt}{\int }_{\mathsf{\Omega }}{e}^{\chi \beta v}{u}^{1-\beta }dx=\chi \beta {\int }_{\mathsf{\Omega }}h(u,v)e^{\chi \beta v}{u}^{1-\beta }dx}\hfill \\ & {\displaystyle +(1-\beta )\beta {\int }_{\mathsf{\Omega }}{e}^{\chi \beta v}{u}^{1-\beta }{|\nabla u-\chi u\nabla v|}^{2}dx+\mu (1-\beta ){\int }_{\mathsf{\Omega }}{e}^{\chi \beta v}{u}^{1-\beta }(1+f-u).}\hfill \end{array}$$

Since $\beta \in (1,2)$, we have that

$$(1-\beta )\beta {\int }_{\mathsf{\Omega }}{e}^{\chi \beta v}{u}^{1-\beta }{|\nabla u-\chi u\nabla v|}^{2}dx\le 0.$$

Notice that, thanks to the Mean Value Theorem it yields $h(u,v)=h(0,0)+h_u({\xi }_1,0)u+h_v(u,{\xi }_2)v,$ for some $({\xi }_1,{\xi }_2)$. Assumptions (8)–(10) imply

$${\int }_{\mathsf{\Omega }}h(u,v)e^{\chi \beta v}{u}^{1-\beta }dx\le h(0,0){\int }_{\mathsf{\Omega }}{e}^{\chi \beta v}{u}^{1-\beta }dx+c_1{\int }_{\mathsf{\Omega }}{e}^{\chi \beta v}{u}^{2-\beta }dx,$$

with $0<c_1<\infty$. Therefore we have that

$$\begin{array}{cc}\hfill \frac{d}{dt}& {\int }_{\mathsf{\Omega }}{e}^{\chi \beta v}{u}^{1-\beta }dx\le \hfill \\ & \chi \beta h(0,0){\int }_{\mathsf{\Omega }}{e}^{\chi \beta v}{u}^{1-\beta }dx+\mu (1-\beta )\epsilon {\int }_{\mathsf{\Omega }}{e}^{\chi \beta v}{u}^{1-\beta }dx+[\mu (\beta -1)+c_1\chi \beta ]{\int }_{\mathsf{\Omega }}{e}^{\chi \beta v}{u}^{2-\beta }dx\hfill \end{array}$$

and then

$$\frac{d}{dt}{\int }_{\mathsf{\Omega }}{e}^{\chi \beta v}{u}^{1-\beta }dx\le [\chi \beta h(0,0)-\mu (\beta -1)\epsilon ]{\int }_{\mathsf{\Omega }}{e}^{\chi \beta v}{u}^{1-\beta }dx+c_2,c_2>0.$$

In view of assumption over h, for $\beta$ close enough to 2, we get, by the Maximum Principle that

$${\int }_{\mathsf{\Omega }}{e}^{\chi \beta v}{u}^{1-\beta }dx\le c$$

and the non-negativity of v implies

$${\int }_{\mathsf{\Omega }}{u}^{1-\beta }dx\le \tilde{c},$$

with positive constants c and $\tilde{c}$. Moreover, the Hölder inequality implies

$$\left|\mathsf{\Omega }\right|={\int }_{\mathsf{\Omega }}\frac{u^{\frac{\beta -1}{\beta }}}{u^{\frac{\beta -1}{\beta }}}dx\le {\left[{\int }_{\mathsf{\Omega }}udx\right]}^{\frac{\beta -1}{\beta }}{\left[{\int }_{\mathsf{\Omega }}\frac{1}{u^{\beta -1}}dx\right]}^{\frac{1}{\beta }}.$$

After some computations, the proof ends. □

Similar results can be found in Tao and Winkler [28] (Theorem 1.1) and [34] for parabolic-elliptic and fully parabolic systems.

Lemma 12.

Under assumption (6), the solution $u^{*}$ to (2) defined in (12) admits a lower bound

$$u^{*}\ge {\epsilon }_1,$$

for some ${\epsilon }_1>0$.

Proof. 

We divide by $u^{*}$ in (2) and integrate over $(0,t)$ to obtain the result. □

We now define the positive function

$$k_1\left(t\right):={\int }_{\mathsf{\Omega }}{\left(u-{\int }_{\mathsf{\Omega }}udx\right)}^{2}dx,$$

(39)

thus we achieve the following.

Lemma 13.

Under the assumptions of Theorem 2, there exists a positive constant $c_7$ independent of t such that the following estimate holds

$${\int }_0^{\infty }{k}_1\left(t\right)dt\le c_7<\infty .$$

(40)

Proof. 

We integrate the first equation of (1) over $\mathsf{\Omega }$ and in view of

$$\begin{array}{cc}\hfill {\int }_{\mathsf{\Omega }}& \left(u-{\int }_{\mathsf{\Omega }}udx\right)dx\hfill \\ & ={\int }_{\mathsf{\Omega }}\left(u-{\int }_{\mathsf{\Omega }}udx\right)f^{*}\left(t\right)dx={\int }_{\mathsf{\Omega }}\left({\int }_{\mathsf{\Omega }}udx\right)\left(u-{\int }_{\mathsf{\Omega }}udx\right)dx=0,\hfill \end{array}$$

we obtain

$$\begin{array}{cc}{\displaystyle }\hfill & {\displaystyle \frac{1}{\mu }\frac{d}{dt}{\int }_{\mathsf{\Omega }}udx={\int }_{\mathsf{\Omega }}u(1+f-u)dx}\hfill \\ \\ \hfill & {\displaystyle ={\int }_{\mathsf{\Omega }}\left(u-{\int }_{\mathsf{\Omega }}udx\right)(1+f-u)dx+{\int }_{\mathsf{\Omega }}udx\left(1+{\int }_{\mathsf{\Omega }}fdx-{\int }_{\mathsf{\Omega }}udx\right)}\hfill \\ \hfill & {\displaystyle ={\int }_{\mathsf{\Omega }}\left(u-{\int }_{\mathsf{\Omega }}udx\right)\left({\int }_{\mathsf{\Omega }}udx-u\right)dx+{\int }_{\mathsf{\Omega }}\left(u-{\int }_{\mathsf{\Omega }}udx\right)(f-f^{*})dx}\hfill \\ \hfill & {\displaystyle +{\int }_{\mathsf{\Omega }}u\left(1+f^{*}-{\int }_{\mathsf{\Omega }}udx\right)dx+{\int }_{\mathsf{\Omega }}u\left({\int }_{\mathsf{\Omega }}(f-f^{*})dx\right)dx.}\hfill \end{array}$$

Since f and $f^{*}$ are uniformly bounded, we have

$${\int }_{\mathsf{\Omega }}u(f-f^{*})dx={\int }_{\mathsf{\Omega }}\left(u-{\int }_{\mathsf{\Omega }}udx\right)(f-f^{*})dx+{\int }_{\mathsf{\Omega }}udx{\int }_{\mathsf{\Omega }}\left(f-f^{*}\right)dx,$$

and

$${\int }_{\mathsf{\Omega }}\left(u-{\int }_{\mathsf{\Omega }}udx\right)(f-f^{*})dx\le \delta k_1+c\left(\delta \right){\parallel f-f^{*}\parallel }_{L^1\left(\mathsf{\Omega }\right)},$$

for any $\delta >0$. We take $\delta =1/4$ and then

$$\frac{d}{dt}{\int }_{\mathsf{\Omega }}udx\le -\frac{\mu }{2}{k}_1\left(t\right)+\mu {\int }_{\mathsf{\Omega }}u\left(1+f^{*}-{\int }_{\mathsf{\Omega }}udx\right)dx+c{\parallel f-f^{*}\parallel }_{L^1\left(\mathsf{\Omega }\right)}.$$

We divide by ${\int }_{\mathsf{\Omega }}udx$ to get

$$\frac{d}{dt}ln\left({\int }_{\mathsf{\Omega }}udx\right)\le -\frac{\mu k_1}{2{\int }_{\mathsf{\Omega }}udx}+\mu \left(1+f^{*}-{\int }_{\mathsf{\Omega }}udx\right)+\frac{c}{{\int }_{\mathsf{\Omega }}udx}{\parallel f-f^{*}\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}.$$

Since $u^{*}$ satisfies

$$\frac{d}{dt}(ln{u}^{*})=\mu (1+f^{*}-u^{*}),$$

we have

$$\begin{array}{cc}\hfill \frac{d}{dt}\left(ln\left({\int }_{\mathsf{\Omega }}udx\right)-ln{u}^{*}\right)\le & -\frac{\mu k_1\left(t\right)}{2{\int }_{\mathsf{\Omega }}udx}+\mu \left(u^{*}-{\int }_{\mathsf{\Omega }}udx\right)\hfill \\ & +\frac{c}{{\int }_{\mathsf{\Omega }}udx}{\parallel f-f^{*}\parallel }_{L^1\left(\mathsf{\Omega }\right)}.\hfill \end{array}$$

(41)

Now, we consider the following functions

$$F_1:={\int }_{\mathsf{\Omega }}\frac{u}{u^{*}}dx-1+ln{u}^{*}-{\int }_{\mathsf{\Omega }}lnudx;F_2:=ln\left({\int }_{\mathsf{\Omega }}udx\right)-ln{u}^{*}.$$

(42)

Functionals of quite a similar form have previously been used in several works on related chemotaxis problems, e.g., in [35]. Notice that $F_1\ge 0$ and $F_2\ge c_0$. Let $c_1$ be defined in (18), then

$$\frac{d}{dt}{F}_2+\mu \left({\int }_{\mathsf{\Omega }}udx-u^{*}\right)\le -\frac{\mu }{2c_1}{k}_1\left(t\right)+\frac{c}{{\epsilon }_2}{\parallel f-f^{*}\parallel }_{L^1\left(\mathsf{\Omega }\right)},$$

(43)

and also

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dt}{F}_1}& {\displaystyle =\frac{d}{dt}\left(\frac{{\int }_{\mathsf{\Omega }}udx}{u^{*}}\right)+\mu (1+f^{*}-u^{*})-{\int }_{\mathsf{\Omega }}\frac{u_t}{u}dx}\hfill \\ & {\displaystyle =\frac{d}{dt}\left(\frac{{\int }_{\mathsf{\Omega }}udx}{u^{*}}\right)+\mu (1+f^{*}-u^{*})}\hfill \\ & +{\int }_{\mathsf{\Omega }}\left[-\frac{{|\nabla u|}^2}{u^2}+\chi \frac{\nabla u\nabla v}{u}-\mu (1+f-u)\right]dx.\hfill \end{array}$$

We take gradients in the equation of v, multiply the obtained equation by $\lambda \nabla v$ and integrate over $\mathsf{\Omega }$ to get

$$\frac{d}{dt}{\int }_{\mathsf{\Omega }}\frac{\lambda }{2}{|\nabla v|}^2-{\int }_{\mathsf{\Omega }}\lambda h_v{|\nabla v|}^2={\int }_{\mathsf{\Omega }}\lambda h_u\nabla u\nabla vdx.$$

Now we add both expressions to obtain

$$\begin{array}{c}{\displaystyle \frac{d}{dt}\left(F_1+{\int }_{\mathsf{\Omega }}\frac{\lambda }{2}{|\nabla v|}^2\right)-{\int }_{\mathsf{\Omega }}\lambda h_v{|\nabla v|}^2=\frac{d}{dt}\left(\frac{{\int }_{\mathsf{\Omega }}udx}{u^{*}}\right)+\mu (1+f^{*}-u^{*})}\hfill \\ {\displaystyle +{\int }_{\mathsf{\Omega }}\left[-\frac{{|\nabla u|}^2}{u^2}+\frac{\nabla v\nabla u}{u}\left[\chi +\lambda u{h}_u\right]-\mu (1+f-u)\right]dx.}\hfill \end{array}$$

We apply the Cauchy-Swartz inequality to the term $\nabla v\nabla u\left[\chi +\lambda u{h}_u\right]/u$

$$\frac{\nabla v\nabla u}{u}\left[\chi +\lambda u{h}_u\right]\le \frac{{|\nabla u|}^2}{u^2}+{|\nabla v|}^2\frac{1}{4}{\left[\chi +\lambda u{h}_u\right]}^2,$$

then, operating we achieve

$$\begin{array}{cc}{\displaystyle }\hfill & {\displaystyle \frac{d}{dt}\left(F_1+{\int }_{\mathsf{\Omega }}\frac{\lambda }{2}{|\nabla v|}^2\right)-{\int }_{\mathsf{\Omega }}\lambda h_v{|\nabla v|}^2\le \frac{d}{dt}\left(\frac{{\int }_{\mathsf{\Omega }}udx}{u^{*}}\right)+\mu (1+f^{*}-u^{*})+}\hfill \\ \hfill & {\displaystyle +{\int }_{\mathsf{\Omega }}\left[{|\nabla v|}^2\frac{1}{4}{\left[\chi +\lambda u{h}_u\right]}^2-\mu (1+f-u)\right]dx,}\hfill \end{array}$$

which is reduced to

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dt}}& \left(F_1+{\int }_{\mathsf{\Omega }}\frac{\lambda }{2}{|\nabla v|}^2\right)\hfill \\ & \le {\int }_{\mathsf{\Omega }}\frac{{|\nabla v|}^2}{4}\left({\lambda }^2{u}^2{h}_u^2+\lambda (4h_v+2\chi u{h}_u)+{\chi }^2\right)+\hfill \\ & {\displaystyle +\frac{d}{dt}\frac{{\displaystyle {\int }_{\mathsf{\Omega }}udx}}{u^{*}}+\mu (1+f^{*}-u^{*})-{\int }_{\mathsf{\Omega }}\mu (1+f-u)dx.}\hfill \end{array}$$

(44)

Due to the discriminant of the polynomial

$$p\left(\lambda \right)={\lambda }^2{u}^2{h}_u^2+\lambda (4h_v+2\chi u{h}_u)+{\chi }^2$$

(45)

is given by $16h_v(h_v+\chi u{h}_u)$, which is positive, we have two different roots ${\lambda }_{+}$ and ${\lambda }_{-}$ that are both positive. Since

$${\lambda }_{\pm }:=\frac{-2h_v-\chi u{h}_u\pm 2\sqrt{h_v(h_v+\chi u{h}_u)}}{u^2{h}_u^2}$$

we have that

$${\lambda }_{-}\ge 0.$$

Then, we take $\lambda ={\lambda }_{-}$ to obtain

$$\begin{array}{cc}{\displaystyle \frac{d}{dt}\left(F_1+{\int }_{\mathsf{\Omega }}\frac{{\lambda }_{-}}{2}{|\nabla v|}^2\right)}\hfill & {\displaystyle \le \frac{d}{dt}\frac{{\int }_{\mathsf{\Omega }}udx}{u^{*}}+\mu (1+f^{*}-u^{*})-{\int }_{\mathsf{\Omega }}\mu (1+f-u)dx}\hfill \\ {\displaystyle }\hfill & {\displaystyle \le \frac{d}{dt}\frac{{\int }_{\mathsf{\Omega }}udx}{u^{*}}+\mu {\parallel f^{*}-f\parallel }_{L^1\left(\mathsf{\Omega }\right)}+\mu \left({\int }_{\mathsf{\Omega }}udx-u^{*}\right).}\hfill \end{array}$$

Through the inequality (43) it results

$$\frac{d}{dt}\left(F_1+F_2+{\int }_{\mathsf{\Omega }}\frac{{\lambda }_{-}}{2}{|\nabla v|}^2\right)+k_1\le \frac{d}{dt}\frac{{\int }_{\mathsf{\Omega }}udx}{u^{*}}+\mu {\parallel f^{*}-f\parallel }_{L^1\left(\mathsf{\Omega }\right)}.$$

After integration over $(0,T)$ and taking limits when $T\to \infty$ we conclude the lemma. □

Lemma 14.

Under the assumptions of Theorem 2 the following estimate holds

$${\int }_{\mathsf{\Omega }}{|\nabla v|}^2+{\int }_0^{\infty }{\int }_{\mathsf{\Omega }}{|\nabla v|}^{2}dxdt\le c_8<\infty ,$$

(46)

with $c_8$ a positive constant.

Proof. 

We first notice that $p\left(\lambda \right)$ defined in (45) achieves its minimum at

$${\lambda }_0=\frac{-2h_v-\chi u{h}_u}{u^2{h}_u^2}$$

and

$$p\left({\lambda }_0\right)=-4\frac{h_v^2+\chi u{h}_u{h}_v}{u^2{h}_u^2}\le -\frac{4{ϵ}_v^2}{c_5^2{\parallel h_u\parallel }_{L^{\infty }\left(A\right)}^2}:=-p_0,$$

where $A={[0,\parallel u\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}{]\times [0,\parallel v\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}]$ is a compact set of ${\mathbb{R}}^2$. Due to (44) we get

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dt}}& {\displaystyle \left(F_1+{\int }_{\mathsf{\Omega }}\frac{{\lambda }_0}{2}{|\nabla v|}^2\right)+p_0{\int }_{\mathsf{\Omega }}\frac{{|\nabla v|}^2}{4}}\hfill \\ & {\displaystyle \le \frac{d}{dt}\frac{{\int }_{\mathsf{\Omega }}udx}{u^{*}}+\mu (1+f^{*}-u^{*})-{\int }_{\mathsf{\Omega }}\mu (1+f-u)dx.}\hfill \end{array}$$

We now proceed as in Lemma 13 and we obtain

$$\begin{array}{cc}\hfill \frac{d}{dt}& \left(F_1+F_2+{\int }_{\mathsf{\Omega }}\frac{{\lambda }_0}{2}{|\nabla v|}^2\right)+k_1+\frac{p_0}{4}{\int }_{\mathsf{\Omega }}\frac{{\lambda }_0}{2}{|\nabla v|}^2\hfill \\ & \le \frac{d}{dt}\frac{{\int }_{\mathsf{\Omega }}udx}{u^{*}}+\mu {\parallel f^{*}-f\parallel }_{L^1\left(\mathsf{\Omega }\right)}.\hfill \end{array}$$

After integration over $(0,\infty )$, in view of

$${\lambda }_0\ge \frac{-{ϵ}_v}{{\parallel u\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}{\parallel h_u\parallel }_{L^{\infty }\left(A\right)}}>0$$

we end the proof. □

We have the following boundedness

Lemma 15.

Under the assumptions of Theorem 2, there exists a positive constant $c_9$ such that the following inequality holds

$${\int }_0^{\infty }{\int }_{\mathsf{\Omega }}{|\nabla u|}^{2}dxdt\le c_9.$$

Proof. 

After integration in the time variable the expression

$$\begin{array}{cc}{\displaystyle \frac{d}{dt}(F_1+F_2)}\hfill & {\displaystyle \le \frac{d}{dt}\left(\frac{{\int }_{\mathsf{\Omega }}udx}{u^{*}}\right)+{\int }_{\mathsf{\Omega }}\left[-\frac{{|\nabla u|}^2}{u^2}+\chi \frac{\nabla u\nabla v}{u}\right]dx}\hfill \\ \hfill & {\displaystyle \le \frac{d}{dt}\left(\frac{{\int }_{\mathsf{\Omega }}udx}{u^{*}}\right)-\frac{1}{2}{\int }_{\mathsf{\Omega }}\frac{{|\nabla u|}^2}{u^2}dx+\frac{{\chi }^2}{2}{\int }_{\mathsf{\Omega }}{|\nabla v|}^{2}dx,}\hfill \end{array}$$

by Lemma 14, we obtain

$${\int }_0^{\infty }{\int }_{\mathsf{\Omega }}\frac{{|\nabla u|}^2}{u^2}dxdt\le c_{10}<\infty ,$$

with $c_{10}>0$. In view of the boundedness of u we have

$${\int }_0^{\infty }{\int }_{\mathsf{\Omega }}{|\nabla u|}^{2}dxdt\le {\parallel u\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}^2{\int }_0^{\infty }{\int }_{\mathsf{\Omega }}\frac{{|\nabla u|}^2}{u^2}dxdt\le c_9<\infty$$

and the proof ends. In Negreanu, Tello and Vargas [6], a similar problem is studied for the fully parabolic system. □

Lemma 16.

Under assumptions (2)–(9), there exists a positive constant $c_{12}<\infty$ independent of t such that

$$k_1^{\prime }\le c_{11},for t>0,$$

where $k_1$ is defined in (39).

Proof. 

The following relations hold:

$$\frac{d}{dt}\frac{1}{2}{\int }_{\mathsf{\Omega }}{\left(u-{\int }_{\mathsf{\Omega }}udx\right)}^{2}dx={\int }_{\mathsf{\Omega }}{u}_t\left(u-{\int }_{\mathsf{\Omega }}udx\right)dx$$

and

$$\begin{array}{c}\hfill {\displaystyle {\int }_{\mathsf{\Omega }}{u}_t\left(u-{\int }_{\mathsf{\Omega }}udx\right)dx=-{\int }_{\mathsf{\Omega }}{|\nabla u|}^{2}dx+\chi {\int }_{\mathsf{\Omega }}u\nabla u\nabla vdx}\\ \hfill {\displaystyle +\mu {\int }_{\mathsf{\Omega }}u(1+f-u)\left(u-{\int }_{\mathsf{\Omega }}udx\right)dx.}\end{array}$$

By applying the Young’s inequality we have

$$-{\int }_{\mathsf{\Omega }}{|\nabla u|}^{2}dx+\chi {\int }_{\mathsf{\Omega }}u\nabla u\nabla vdx\le c_{11}{\parallel u\parallel }_{L^{\infty }\left({\mathsf{\Omega }}_{\infty }\right)}^2{\int }_{\mathsf{\Omega }}{|\nabla v|}^{2}dx.$$

The boundedness of u and Lemma 14 imply the result. □

The following lemma is used to prove the behavior of the solution. The proof follows Lemma 5.1 in Friedman-Tello [22], where $k^{\prime }$ is uniformly bounded, i.e., $|k^{\prime }|<c$. Here, the boundedness of $k^{\prime }$ is replaced by a weaker assumption given in $\left(iii\right)$.

Lemma 17.

Let $k:{\mathbb{R}}_{+}\to \mathbb{R}$ a function satisfying

(i)

$k\left(t\right)\ge 0$ for any $t\ge 0,$

(ii)

${\displaystyle {\int }_0^{\infty }k\left(s\right)ds\le c<\infty ,}$

(iii)

$k^{\prime }\le c$ for any $t\ge 0$,

then, $k\left(t\right)\to 0$ as $t\to \infty$.

Proof. 

By contradiction, we assume that there exists a sequence $t_n$ such that $t_n\to \infty$ and ${lim\; sup}_{n\to \infty }k\left(t_n\right)\ge ϵ>0$. Then, there exist a subsequence $t_n^{\prime }$ such that $t_n^{\prime }\ge t_{n-1}^{\prime }+1$ and

$$k\left(t_n^{\prime }\right)\ge \frac{ϵ}{2}>0.$$

Then, $k\ge \frac{ϵ}{4}$ in the interval $[t_n^{\prime }-a,t_n^{\prime }]$ for $a:=min\{1,cϵ/4\}$. So

$${\int }_0^{t_n^{\prime }}k\left(s\right)ds\ge \frac{nϵ}{4},$$

and taking limits when $n\to \infty$ we reach the contradiction. □

Lemma 18.

Under assumptions of Theorem 2 we have

$$\parallel u-u^{*}{\parallel }_{L^2\left(\mathsf{\Omega }\right)}\to 0,ast\to \infty .$$

Proof. 

We consider $k_1$ defined in (39), then, thanks to Lemmas 13 and 16 we have

$${∥u-{\int }_{\mathsf{\Omega }}udx∥}_{L^2\left(\mathsf{\Omega }\right)}\to 0ast\to \infty .$$

(47)

Now, we define $k_2$ as follows

$$k_2\left(t\right):={\left({\int }_{\mathsf{\Omega }}udx-u^{*}\right)}^2.$$

By recalling the definition of $F_2\left(t\right)$ as in (42)

$$F_2\left(t\right)=ln{\int }_{\mathsf{\Omega }}udx-ln{u}^{*},$$

due to (39), we get

$$\frac{d}{dt}{F}_2+\mu \left({\int }_{\mathsf{\Omega }}udx-u^{*}\right)\le -k_1\left(t\right)+\mu {\parallel f-f^{*}\parallel }_{L^1\left(\mathsf{\Omega }\right)}.$$

We multiply by $F_2$ and due to the Mean Value Theorem we claim

$$\frac{d}{dt}{F}_2^2+2\mu \xi F_2^2\le |F_2|k_1\left(t\right)+\mu |F_2|\parallel f-f^{*}{\parallel }_{L^1\left(\mathsf{\Omega }\right)}\le 2c_5^2\left(k_1\left(t\right)+\mu {\parallel f-f^{*}\parallel }_{L^1\left(\mathsf{\Omega }\right)}\right),$$

for some $\xi \in \left[u^{*},{\int }_{\mathsf{\Omega }}udx\right]$ if $u^{*}<{\int }_{\mathsf{\Omega }}udx$ or $\xi \in \left[{\int }_{\mathsf{\Omega }}udx,u^{*}\right]$ otherwise. After integration it results

$${\int }_0^{\infty }{F}_2^{2}dt\le c_{12}<\infty .$$

Notice that Lemma 2 implies

$$k_2\le c_{13}{F}_2^2$$

for some positive constant $c_{13}$. Therefore, there exists $c_{14}>0$ such that

$${\int }_0^{\infty }{k}_{2}dt\le c_{14}<\infty .$$

(48)

In view of Lemma 2, assumption (6) and Lemma 9 it is easy to see that

$$|k_2^{\prime }|\le c_{15}<\infty .$$

(49)

Now, by Lemma 17, (48) and (49) we obtain

$$k_2\to 0ast\to \infty .$$

(50)

Since

$${\int }_{\mathsf{\Omega }}{|u-u^{*}|}^{2}dx\le k_1+k_2,$$

by taking into account (47) and (50), we get

$$\parallel u-u^{*}{\parallel }_{L^2\left(\mathsf{\Omega }\right)}\to 0,ast\to \infty$$

and the proof ends. □

In order to obtain

$$\parallel v-v^{*}{\parallel }_{L^2\left(\mathsf{\Omega }\right)}\to 0ast\to \infty ,$$

we proceed as before in the following lemma.

Lemma 19.

Under assumptions (4)–(8), the solution v fulfills

$$\parallel v(x,t)-v^{*}{\left(t\right)\parallel }_{L^2\left(\mathsf{\Omega }\right)}\to 0,as t\to \infty .$$

Proof. 

By the Mean Value Theorem, it follows

$$\begin{array}{cc}{v}_t-v_t^{*}\hfill & {\displaystyle =h(u,v)-h(u^{*},v^{*})=h(u,v)-h(u,v^{*})+h(u,v^{*})-h(u^{*},v^{*})}\hfill \\ \hfill & {\displaystyle ={\left.\frac{\partial h}{\partial v}\right|}_{(u,\eta )}(v-v^{*})+{\left.\frac{\partial h}{\partial u}\right|}_{(\xi ,v^{*})}(u-u^{*}).}\hfill \end{array}$$

We call $z=v-v^{*}$, by multiplying by z the above equation and after integrating over $\mathsf{\Omega }$, it yields

$$\begin{array}{cc}{\displaystyle \frac{1}{2}\frac{d}{dt}{\int }_{\mathsf{\Omega }}{z}^{2}dx}\hfill & {\displaystyle ={\int }_{\mathsf{\Omega }}{h}_v{z}^{2}dx+{\int }_{\mathsf{\Omega }}{h}_{u}z(u-u^{*})dx\le {\int }_{\mathsf{\Omega }}{h}_v{z}^{2}dx+}\hfill \\ & {\displaystyle +\parallel h_u{z\parallel }_{L^{\infty }\left(\mathsf{\Omega }\right)}{\int }_{\mathsf{\Omega }}{(u-u^{*})}^{2}dx,}\hfill \end{array}$$

where we have applied the Hölder inequality to the last term. Now, by assumption (9) it results

$$\frac{1}{2}\frac{d}{dt}{\int }_{\mathsf{\Omega }}{z}^{2}dx\le -{ϵ}_v{\int }_{\mathsf{\Omega }}{z}^{2}dx+\theta \left(t\right),$$

where $\theta \left(t\right)$ is uniformly bounded. We obtain the result by solving the differential inequality. □

Proof. 

(End of the proof of Theorem 2.) The asymptotic behavior (14) of $(u,v)$ is a direct consequence of Lemmas 18 and 19 and the uniform bounds of u and v established therein. □

5. Numerical Tests

Now we show some numerical results for the purpose of further clarifying that all conditions in the statement of the previous theorems play a relevant role in the behavior of the solution of (1). The suppression of some of the above conditions, together with the election of the initial data, may end up in the existence of blow-up of the solutions. We illustrate numerically the uniform boundedness and the convergence for the solution $(u,v)$ to obtain a numerical validation of Theorem 2. We use the Generalized Finite Differences Method for the space discretization and we performed several tests showing the explosion of solutions in the case that certain hypotheses of Theorem 2 are not verified as thus the asymptotic behavior of solutions.

5.1. Example 1: Uniform and Periodic Asymptotic Behavior

For our purpose, let us consider $\mu =1$ and $\chi =0.3$. The initial data used are

$$u_0(x,y)=e^{-10[{(x-0.1)}^2+{(y-0.1)}^2]},v_0(x,y)=0.7e^{-10[{(x-1.2)}^2+{(y-0.8)}^2]}$$

and the function f is

$$f(x,y,t)=\frac{cost}{4+sint}+\frac{x-y}{1+t^2},(x,y)\in \mathsf{\Omega }=[0,1]\times [0,1],t>0,$$

which fulfils assumptions (6) and (7). Direct calculations lead

$$f^{*}\left(t\right)=\frac{cost}{4+sint},u^{*}\left(t\right)=\frac{4+sin\left(t\right)}{4-\frac{cos\left(t\right)}{2}+\frac{sin\left(t\right)}{2}}.$$

The function $h(u,v)=u{e}^{-\chi v}-v$, as it is easy to check, is in accordance with the hypothesis of the theorem. We find the solution of the second ODE of (2) and (13) by numerical integration using the ode45 function of Matlab R2019a. In Figure 1, the $u,v—$solution is presented for 0, 0.5, 1 and 20 s. Table 1 shows the $l^{\infty }$ norm of the discrete $(u,v)—$solution and the value of $(u^{*}\left(t\right),v^{*}\left(t\right))$ for different times. In Figure 2 we illustrate the asymptotic solution $u^{*},v^{*}$ (solid line) and the value of the discrete solution for times in $[0,20]$.

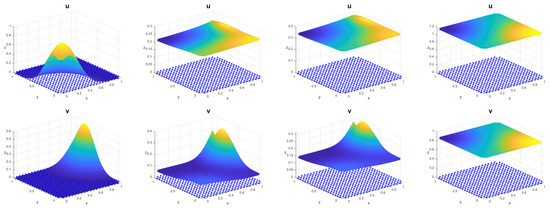
Figure 1. Approximate solution for 0, 0.5, 11 and 20 s.

Table 1. Values of the asymptotic solutions and $l^{\infty }$ norms of the numerical solutions.

t(s)	5	8	11	14	17	20
$u^{*}\left(t\right)$	0.9001	1.0924	0.8577	1.1273	0.8309	1.1553
${\parallel u\parallel }_{l^{\infty }}$	0.8609	1.0902	0.8583	1.1278	0.8312	1.1556
$v^{*}\left(t\right)$	0.7021	0.8644	0.6968	0.8740	0.7071	0.8729
${\parallel v\parallel }_{l^{\infty }}$	0.6331	0.8651	0.6969	0.8746	0.7010	0.8731

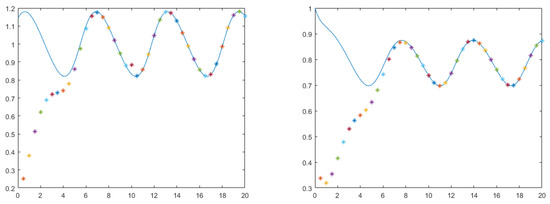
Figure 2. The solid lines correspond to $u^{*}$ and $v^{*}$, respectively, and the stars to the values of the approximate solutions.

Our simulations are in keeping with the theoretical results about global existence and boundedness of solutions to (1).

5.2. Example 2: Blow-Up Solutions

Next in order we present the results for the explosion of solutions in the case that certain hypotheses of Theorem 2 are not verified. We choose $\mu =1$ and $\chi =\pi$. The initial data used are

$$u_0(x,y)=8,v_0(x,y)=0.7e^{-10[{(x-1.2)}^2+{(y-0.8)}^2]}$$

and the same function f of the previous example. Now, we consider $h(u,v)=u-v,$ clearly it does not fulfil the assumptions. As we see from Table 2 and Figure 3, the solutions become unbounded before 0.40 s.

Table 2. Values of the asymptotic solutions and $l^{\infty }$ norms of the numerical solutions in the example 2.

t(s)	0.1	0.2	0.3	0.37	0.38
${\parallel u\parallel }_{l^{\infty }}$	16.5996	29.4849	187.6184	3.0630$\times {10}^5$	-
${\parallel v\parallel }_{l^{\infty }}$	0.5851	0.7902	1.3744	76.3346	-

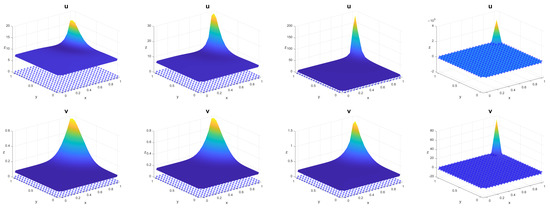
Figure 3. Approximate solution o in the example 2 for 0.1, 0.2, 0.3 and 0.37 s.

The formation of various patterns due to the effect of chemotaxis rate, domain size, initial data, the nature of the functions f and h or the complexity arisen in the solutions for large values of the chemotactic term are our goal for immediate studies.

6. Conclusions

We have obtained, under suitable assumptions, that the solution of a chemotaxis system is globally bounded in time by using an Alikakos-Moser iteration, and it fulfills a periodic asymptotic behavior. A possible future work is the consideration of the non-constant chemosensitivity, $\chi (u,v)$, as in [23,24,25,26,27,28,29,30,31,32,33,34,35,36], and to also consider biological systems with two species, two chemotactic terms and one chemical substance verifying a similar equation as in (1). Furthemore, a parabolic-parabolic-ordinary system with periodic terms serves as a model for some chemotaxis phenomena and appears naturally in the interaction of two biological species and a chemical. The presence of the periodic terms has a strong impact on the behavior of the solutions. We would find conditions on the system’s data that guarantee the global existence of solutions, the convergence to some periodical solutions of an associated ODE’s system. We got a similar result in [37] for a parabolic-parabolic-elliptic system.