Abstract
Wildfires are complex natural events that cause significant environmental and property damage, as well as human losses, every year throughout the world. In order to aid in their management and mitigate their impact, efforts have been directed towards developing decision support systems that can predict wildfire propagation. Most of the available tools for wildfire spread prediction are based on the Rothermel model that, apart from being relatively complex and computing demanding, depends on several input parameters concerning the local fuels, wind or topography, which are difficult to obtain with a minimum resolution and degree of accuracy. These factors are leading causes for the deviations between the predicted fire propagation and the real fire propagation. In this sense, this paper conducts a literature review on optimization methodologies for wildfire spread prediction based on the use of evolutionary algorithms for input parameter set calibration. In the present literature review, it was observed that the current literature on wildfire spread prediction calibration is mostly focused on methodologies based on genetic algorithms (GAs). Inline with this trend, this paper presents an application of genetic algorithms for the calibration of a set of the Rothermel model’s input parameters, namely: surface-area-to-volume ratio, fuel bed depth, fuel moisture, and midflame wind speed. The GA was validated on 37 real datasets obtained through experimental prescribed fires in controlled conditions.
1. Introduction
Wildfires are one of nature’s most dangerous hazards and, in the last few years, their impact has been increasing significantly, as reported by the European Commission’s 20th issue of the annual wildfire report [1,2,3]. This report, from 2019, shows a total burned area of 789,730 (ha) registered for 40 countries from Europe, the Middle East, and North Africa. This number is nearly four times larger than the records for the previous year (2018). Wildfires can impact ecosystems by destroying natural habitats, resources, and wildlife. Furthermore, they cause significant damage to society, being responsible for numerous fatalities, accidents, injuries, health problems, and the destruction of human infrastructures. These damages bear a significant economic impact, not only due to the fire damage but also the large investments in prevention, preparedness, fire suppression and recovery efforts [4]. It is essential to direct efforts towards understanding the behavior of wildfires and improving their management. In this sense, knowledge of how wildfires propagate is critical, allowing the prediction of where the fire will be and taking the appropriate measures to mitigate its impact.
Theoretical, empirical and semiempirical models have been developed to predict the wildfire behavior [5]. The semiempirical Rothermel model [6] is the most widely used model for wildfire spread prediction [5], particularly in Mediterranean European countries [7], being the core of some of the most cited fire simulators such as FARSITE [8] and FIRESTATION [9]. The Rothermel model uses several input parameters related to the available forest fuels, such as trees, grass or bushes (surface-area-to-volume ratio, height and moisture content), the terrain configuration (slope), and atmospheric conditions (wind speed and direction).
The quality of the fire spread prediction depends on the quality of the propagation model, and on the accuracy of the input parameters [10]. The present work focuses on the latter cause of uncertainty in wildfire spread predictions. As a matter of fact, while some variables remain constant throughout the whole fire event or can be obtained with a high degree of accuracy (e.g., terrain slope), other variables may change due to fire and cannot be obtained with enough temporal or spatial resolution (e.g., fuel characteristics and wind speed/direction). This uncertainty in the input parameters results in considerable deviations between the predicted and the real fire spread. In order to improve the fire spread simulations/predictions, it is essential to deal with this uncertainty in the Rothermel model input parameters. In an effort to find the accurate input parameters values for the wildfire prediction, some methodologies based on Evolutionary Algorithms (EAs) have been proposed to calibrate the Rothermel model [11]. EAs, such as genetic algorithms (GA), ant colony optimization (ACO), and particle swarm optimization (PSO), have proven their effectiveness for optimization/calibration problems [12,13,14].
In this paper, we present a review of genetic algorithm approaches for wildfire spread prediction calibration. The main contributions of the paper are:
- A literature review focused on wildfire spread prediction calibration using GAs is performed. The GA was chosen as a technique for the calibration due to its predominance in research works that used EAs to calibrate the wildfire spread prediction model;
- Based on the presented literature review, in a didactic way, wildfire spread calibration using genetic algorithm is described, in which a specific GA framework for Rothermel model calibration is presented. Moreover, the parameters to be calibrated are discussed, namely the surface-area-to-volume ratio (), fuel bed depth (), fuel moisture (), and midflame wind speed (U);
- The actual feasibility of using GAs for the calibration of the Rothermel model for wildfire spread prediction is explored/studied on 37 real datasets.
The results show a significant error reduction in the wildfire spread prediction, i.e., from to .
This paper is organized as follows. Section 2 contains a description of the Rothermel model, as well as an insight into the current state of the art regarding methods of wildfire spread prediction using genetic algorithms. In Section 3, GAs are revised, and the method used in this paper to calibrate the Rothermel model is presented. In Section 4, the results of the proposed calibration are presented and analyzed. Finally, Section 5 presents the final conclusions.
2. Literature Review of Wildfire Spread Prediction Calibration
Genetic algorithms are the most adopted technique for calibration of the Rothermel model’s input parameters. Due to the importance of this subject for wildfire spread prediction, and due to the number of latest developments in this particular field, a literature review of the most relevant work in this area is fundamental.
The search process for the presented literature review was performed by using the Science Direct and IEEE Xplore databases and defining the following search keywords: (“fire spread” OR “fire prediction” OR “fire rate of spread” OR “Rothermel model”) AND (“genetic algorithm” OR “evolutionary algorithm” OR “calibration” OR “tuning”). The years considered for the search were from 2000 until 2021. Additionally, the references of the selected papers were also analyzed and served as a source for finding new papers. The literature review rationale for article selection was based on the following criteria:
- Acceptance
- The article uses the Rothermel model or a Rothermel model-based simulator for fire propagation prediction/simulation;
- The article uses evolutionary algorithms for Rothermel model calibration;
- The article focuses on improving the prediction results or its execution time.
- Rejection
- The article’s method for fire propagation prediction is not based on the Rothermel model;
- The article implements calibration techniques other than evolutionary algorithms.
Based on this process, 15 papers were obtained.
2.1. Rothermel Model
The Rothermel model, proposed in [6], estimates a Rate Of Spread R of a fire front, given by
which is measured in units of distance per unit of time ([m/s] or [ft/min]), and it represents the linear velocity of a fire, in a given direction and set of conditions. The equations of the associated factors in (1) , , , , and depend on several input parameters and are given by:
where the description of the respective parameters is presented in Table 1.
The input parameters of the Rothermel model (1) can be separated into three categories: fuel properties, topography and wind properties. The fuel properties are heat content (h), mineral content ( (total) and (effective)), oven-dry particle density (), oven-dry fuel load (), surface-area-to-volume ratio (), fuel bed depth (), dead fuel moisture of extinction () and fuel moisture (). Topography is represented by slope steepness (tan), and wind properties correspond to the midflame wind speed (U). A deeper insight into the Rothermel model can be seen in [6,15].
2.2. The Need for a Fire Spread Model Calibration
Figure 1 presents a general illustration for wildfire spread prediction, which consists in feeding a fire simulator with a set of input parameters that aim to represent the initial real fire conditions, at . The result of the fire simulator, i.e., the simulated wildfire perimeter, at , should match the propagation of the real wildfire, i.e., the real wildfire perimeter [16]. However, the input parameters are related to the environmental conditions, e.g., fuel, weather, and terrain characteristics as described in Section 2.1, and obtaining them becomes a difficult task in order to provide an accurate prediction.
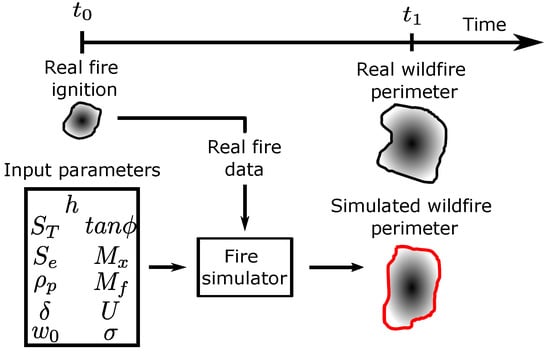
Figure 1.
Illustration of fire spread prediction using only one set of non-calibrated input parameters. Adapted from [17].
In more detail, some input parameters can be directly measured, such as terrain slope, which can also be obtained based on previous topographical information. However, other parameters, such as fuel-specific parameters, require detailed knowledge about the local vegetation, which might not be available. Some input parameters, such as fuel moisture, are calculated using models based on meteorological data [18], while wind field maps are estimated based on point observations from the available meteorological stations closer to the fire location. These estimations introduce a great amount of error in the prediction. In terms of behavior change, characteristics such as the terrain slope and the type of vegetation in a certain region are constant in time and space, while others, such as wind speed and direction, have very sudden variations during the wildfire [10]. Therefore, finding a set of input parameters that produces accurate results solely based on previous knowledge about the wildfire location and weather conditions is a challenging task. Due to the uncertainty and the consequent inaccuracy in wildfire spread simulation, there is a need to calibrate the input parameters.
2.3. Wildfire Spread Calibration Literature Overview
The Rothermel model is the most used and recognized fire spread prediction model, serving as the base for several fire simulators (FARSITE [8] and FIRESTATION [9]). Research works that deal with Rothermel model calibration and wildfire spread prediction mostly use genetic algorithms. Initially, works such as [19,20] have proved the performance of genetic algorithms by comparing them against other optimization techniques and with implementation in a parallel two-stage prediction framework. More recently, other works such as [17,21] aim to improve the calibration by merging the algorithms with other tools that complement their performance, such as the Statistical System for Forest Fire Management () and WildFire Analyst (WFA) (a component of the Tecnosylva Incident Management software suite designed to directly support multi-agency wild-fire incident management). Given that the quality of genetic algorithms was proven early, works evolved into directing efforts to improve their performance.
One of the areas explored to improve the performance of genetic algorithms is parallel computing. Several works used parallel implementations of genetic algorithms to reduce calibration time. In general, these strategies consisted of implementing a simulator’s intrinsic functions in parallel and allocating more processing cores to individuals (elements of a population that represent one possible solution for the problem) with longer predicted execution times.
In the following sections, the main works dealing with this topic are provided, providing a perspective of the philosophy currently being pursued in this research field.
2.4. Wildfire Spread Calibration Literature Using Genetic Algorithms
Genetic algorithms have been used to find the set of input parameters that better adjusts the wildfire spread model predictions to the real observations. In other words, optimizing the model using a framework for wildfire spread prediction tuning.
The authors in [20] introduced a framework, illustrated in Figure 2, that consists of two stages: a calibration stage and a prediction stage. After the ignition, the calibration stage starts, at . Sets of Rothermel’s input parameters are generated (using an optimization approach). Each set of input parameters is evaluated, at instant of time , by comparing the simulator prediction with the real observed fire data for that time instance. The optimal set of input parameters is the one that minimizes the deviation between the predicted and the real fire perimeter. This process is repeated several times or until a certain solution criterion is reached. In the prediction stage, assuming that environmental conditions remain constant, the resulting optimal set of parameters from the calibration stage is used as input for the fire simulator to predict the fire spread at every instant of time (). Here, the prediction stage is similar to the classical method/framework (Figure 1), except that now a tuned set of input parameters is used.
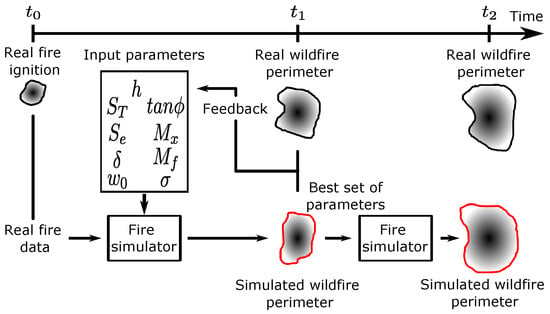
Figure 2.
Two-stage method for fire spread prediction, adapted from [17].
During the calibration stage, the goal is to find an optimal solution for the input parameters. In a generic way, the optimization problem can be defined as:
where represents the function to be minimized (by an optimization algorithm, such as GA), represents the input parameters vector, S is the respective search space, and represents the input parameters that minimize . A usual function to be optimized in wildfire spread calibration is the difference between the real wildfire rate of spread (measured from the real-time wildfire data) and the predicted rate of spread (obtained by the Rothermel model), or the difference between the real and the predicted burned area. The goal is to find the set of input parameters of (21) that most accurately predicts the real fire propagation.
The majority of the works from the current state of the art on wildfire spread prediction are based on the previously presented Two-Stage framework (Figure 2). Early works, such as [19,20], have proposed evolutionary algorithms as techniques that could be used to find an optimal set of input parameters for a fire simulator. Genetic algorithms are included in the group of evolutionary algorithms and they are the dominant optimization technique for input parameter calibration.
In [20], following the presentation of the two-stage framework, a sensitivity analysis was carried out in order to evaluate how the individual variation of each Rothermel input parameter across its range of possible values affects the model output: the bigger the sensitivity of one parameter, the more it affects the model’s output. Based on the sensitivity results, an experimental study was conducted to confirm that calibrating parameters with larger sensitivities and fixing the others reduces the GA’s search space and accelerates the optimization time. The results showed that, after 1000 generations, the scenarios in which only 6 input parameters were calibrated achieved an improvement in the objective function (XOR area between the real and simulated burned areas) of approximately (one third) in relation to the scenario in which 10 input parameters were calibrated. This reduction also matches the reduction in GA’s search space from one scenario to the other.
In [19], the genetic algorithm’s performance is tested against three other algorithms: Random Search, Tabu Search and Simulated Annealing. The tests were carried out by comparing the simulated fire line based on the sets of parameters generated by the algorithms against a fire line obtained by setting known values for all the inputs and running the ISStest simulator for 45 min. Each algorithm was executed 10 times up to 1000 iterations. The fire lines were compared using the Hausdorff distance H (22), which measures the degree of mismatch between two sets of points and , representing the fire line simulated based on the optimized parameters and the fire line generated with known input parameters for comparison. H (22) is given by
where and represents the Hausdorff distance between two sets of points and at a specific point in and , respectively (see [19] for more details). The results show that simulated annealing, tabu search and genetic algorithms presented similar results after the 500th generation.
In [16], a dynamic data-driven genetic algorithm was proposed to tune the fire simulator’s input parameters based on the real fire behavior. The simulator used was fireLib and, through reverse engineering, it was possible to obtain equations for wind values (wind speed and direction). These equations are fed with terrain slope with the position () of the fire front with the maximum rate of spread. The obtained wind speed and direction values were used to steer the search for an optimal input parameter set carried out by the genetic algorithm. Afterwards, in [22], the same research group proposed a new calibration steering method as an improvement to the previous strategy. Since this was highly dependent on the underlying simulator, the new approach consisted of generating a database with fire evolution information from both real and simulated (synthetic) fires. For the calibration stage, a dynamic data-driven genetic algorithm (DDDGA) was proposed to define the best wind direction and wind speed values, by searching the database of previous fires that were similar in terms of rate of spread, slope and fuel model to the real observed fire spread, and using wind values from those fires to steer the genetic algorithm’s search.
The authors in [17] introduced a system called SAPIFE (Spanish acronym for Adaptive System for Fire Prediction Based in Statistical-Evolutive Strategies) which is based on the two-stage fire spread prediction framework with a genetic algorithm implemented during the calibration stage. However, in SAPIFE, the genetic algorithm is coupled with another method called the Statistical System for Forest Fire Management () [23]. This new method receives a certain population from the GA and analyzes almost all possible input parameter combinations from all individuals in the population. From this analysis, evaluates the probability of each map cell to be burned or not and generates a probabilistic map. Then, based on these probabilities, the number of possible scenarios (parameter combinations between different individuals) is reduced, decreasing the calibration time required.
In [24], the two methods introduced in [16,22] were compared. The method introduced in [16] is named as the “analytical method” and, as was described above, is based on the inversion of a fire simulator. The method introduced in [22] is named as the “computational method” and relies on a database with information from past fires. Both of these methods use ongoing fire propagation data to obtain wind speed and direction values and use them to steer the genetic algorithm’s search. Two sets of tests were carried out: first, the two-stage framework was tested against the classical wildfire spread prediction method, which uses a single set of input parameters introduced in the fire simulator. This test used data from past fires and confirmed that the two-stage framework with a genetic algorithm provides better results than the classical prediction without input parameter calibration. Then, the second set of tests compared the use of a simple non-guided genetic algorithm against genetic algorithms with different configurations of the proposed steering strategies. The guided genetic algorithm with the computational and analytical methods obtained similar results and improved prediction quality over the non-guided genetic algorithm.
The work developed by [10] is also based on the two-stage prediction framework with a genetic algorithm and introduces an approach for reducing the prediction errors caused by the variability of wind parameters (wind speed and direction). During the calibration stage, wind parameters are not calibrated; instead, real wind measurements from the fire location are taken in periodic sub-intervals. These measurements are used as inputs for the fire simulator in the recurring simulations. Afterwards, during the prediction stage, a numerical weather prediction (NWP) model [25] is used to periodically estimate the wind parameters between sub-intervals of the prediction stage. The estimated wind parameters are introduced in the simulator and are updated at each sub-interval. The prediction result is obtained using the real wind measurements and the calibrated parameters, which are moisture contents and vegetation features. The test results showed that, when the wind conditions are stable, the basic two-stage framework with a genetic algorithm provides satisfactory results, in comparison with the new method of using measured and estimated wind values (prediction error of vs. , respectively). However, when the wind conditions are more dynamic, the results obtained by the introduced method are significantly better compared to the basic two-stage framework with a genetic algorithm (prediction error of vs. m, respectively).
In [26], a calibration of the fuel models within the Rothermel’s fire spread prediction model was carried out through the use of genetic algorithms. The GA’s individuals consisted of the following Rothermel fuel parameters: oven-dry fuel load (), surface-area-to-volume ratio (), fuel bed depth (), fuel moisture of extinction (), and heat content (h). Two tests were performed to evaluate the proposed GA method. The first test consisted of using GAs for the fuel model calibration method, with the support of two works [27,28] (grass and shrub fuels, respectively) that provided datasets of observed rate of spread R and other input parameters’ data (fuel moisture, wind speed and slope steepness). The GA was performed with 9999 maximum iterations, 100 individuals, mutation probability and elitism factor equal to and , respectively, and the fuel input parameters calibrated based on the parameter ranges given by the papers. Each individual was evaluated using the Root Mean Square Error (RMSE) between the observed and predicted rate of spread R. The second test consisted of implementing the GA for calibrating a fuel model for a type of vegetation (Calluna heath). Nine prescribed fire experiments were carried out in dry Calluna heathland vegetation and R, fire weather (1 h fuels moisture, live woody fuel moisture and wind speed) and terrain data (ignition line length, fire plot size and slope) were recorded from each experiment. From the nine fire experiments, four were considered for GA calibration and five were considered for validation. The calibration experiments data were used to run the GA and calibrate the fuel parameters, similarly to the first test. Then, predicted rate of spread R values were calculated using different fuel models: GA calibrated fuel parameters, the Standard Fuel Model which provided the smaller RMSE when comparing predicted vs. observed R, a custom fuel model for Calluna vegetation and a “custom fuel model parameterized with modal values from fuels inventoried in each fire experiment”. An additional prediction of the rate of spread R was obtained by a Rothermel model reformulation implemented in the Fuel Characteristics Classification System (FCCS) [29]. For the validation experiments data, the calibrated GA fuel parameters resulted in the lowest RMSE between predicted and observed rate of spread R, in comparison to the alternative models.
The study in [21] presents a dynamic data-driven genetic algorithm and introduces a new approach for predicting fire propagation based on Wildfire Analyst (WFA) [30]. The paper describes the two-stage prediction framework with a genetic algorithm, where the fire propagation is simulated using the FARSITE fire simulator [8], and the fitness function corresponds to the symmetric difference between predicted and burned areas obtained by:
where UnionCells represents the sum of the number of cells that were burned in the predicted area and the real area, IntersectionCells is the number of cells burned simultaneously in the predicted area and the real area, RealCells is the final number of cells burned in the real area, and InitCells is the starting number of cells burned in the real fire area. The newly introduced approach uses WildFire Analyst (WFA) and seeks the best R (Rate of Spread) adjustment factors, minimizing the error between simulated fire and the real fire data. Both the FARSITE fire simulator and Wildfire Analyst use the Rothermel model. Afterwards, the two-stage framework with the genetic algorithm and Wildfire Analyst are coupled together by overlapping their predicted fire spread maps. In order to test the two-stage framework and Wildfire Analyst, experiments were carried out with data from a real fire that occurred in Cardona, Catalonia, Spain in 2005. The results show that both methods adapt to drastic changes in the fire characteristics.
In [31], the two-stage framework was considered to reduce input parameter uncertainty and predict fire spread. However, when the wildfire is large, wind cannot be considered uniform throughout the whole wildfire area. So, this work introduced a wind field model (WindNinja), being represented by a cell map, to account for this variation. In essence, during the calibration phase, the obtained meteorological wind parameters are used to calculate the wind field for each scenario generated by the genetic algorithm. Then, having each individual’s wind field, the corresponding fire propagation map is calculated and the error function is evaluated.
Finally, in [32], a statistical study was carried out to characterize the genetic algorithm in the calibration phase of the two-stage prediction method. The characterization refers to estimating which GA parameter configuration results in a better calibration within the imposed time restrictions. A statistical study was conducted based on the results of a genetic algorithm calibration on a simulated five-hour fire obtained using FARSITE as the fire spread simulator. The results from this study were maximum adjustment errors which have different degrees of guarantee depending on the number of generations that the GA iterates. These results are important in understanding the compromise between the algorithm’s execution time (number of generations) and the adjustment error, which is larger when the algorithm iterates fewer generations.
2.5. Calibration through Parallel Computing
Throughout Section 2.4, several works regarding fire spread prediction using genetic algorithms were described. Despite their focus being on improving prediction accuracy, some works have proposed/adapted a Master/Worker paradigm (Figure 3) in order to reduce the calibration and prediction times.
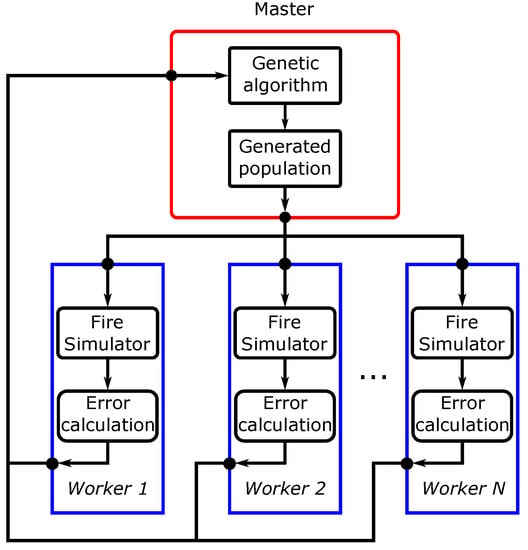
Figure 3.
Genetic algorithm using the Master/Worker paradigm, adapted from [33].
GAs, as with any evolutionary algorithm, require the execution of a set of individual simulations through several iterations, which can be very time-consuming, and given the urgency and need for accuracy associated with wildfire spread prediction in real-time, it is important to reduce the execution time of the calibration phase while maintaining appropriate accuracy. One way to achieve this is through the parallel implementation of the fire spread simulator used for the GA individuals’ simulation.
The authors in [34] presented a technique based on the parallelization of both the GA (used in the two-stage fire prediction framework) and the FARSITE fire simulator. For the first experiments, with fire simulations of 20 s, the results showed an improvement in GA execution time for reaching the same error (15%) when using more cores per individual. When replicating the experiments with longer fire simulations (120), the results showed that using more cores per individual still improved execution times for achieving the same error (approximately 14%). However, for the longer fire simulations, using more individuals (100) with one core per individual achieved the lowest error (approximately 8%).
Despite the strategy introduced in [34] improving the calibration time, there is still a drawback related to GA implementation. During the calibration phase, all of the GA individuals have to be simulated. The execution time of a fire simulation depends on the input parameters and, given the random nature of the generation of the population, some individuals will result in much longer simulation times than others. It would be possible to reduce the overall calibration time by dedicating more computing resources to the individuals with larger execution times and fewer resources to individuals that are executed faster. In order to achieve the said time reduction, it is necessary to predict each individual’s simulation time to provide more computing resources to those whose predicted execution time is larger. The prediction must be based only on the individuals’ genes—a set of input parameters. The study in [34] refers to [35], which introduces a method based on Decision Trees to characterize a fire simulator, allowing estimation of the execution time of one simulation, given a set of input parameters.
In [36], the method referenced in [34] is implemented and tested: Decision Trees are employed to classify each fire simulation according to its execution time so that the Decision Trees can label a new simulation. The core-allocation policy ensures that the individuals labeled with a longer execution time classification are simulated using more computing cores. The results showed that using the core-allocation policy reduced the execution time by , in relation to not using any policy. In [37], similarly to what was done in [36], GA individuals are labeled according to their estimated simulation time through the use of Decision Trees—A, B, C, D and E. Additionally, in this work, an additional restraint is imposed: each GA generation has a limited amount of time to be executed.
More recently, the study in [33] introduced a new strategy to deal with individuals with long execution times. An alternative approach is introduced, based on the monitoring of the fire spread prediction error that, in this particular work, corresponds to the symmetric difference between the real fire and the simulated fire areas, shown in Equation (23). During the execution of one individual, if the monitoring agent detects that the difference between the predicted and the simulated fires is larger than a predefined error threshold, the individual is interrupted. The fitness function is a weighted version of the symmetric difference, shown in Equation (24),
where PredictionTime represents the predicted time for the completion of the individual’s simulation, SimulationTime is the the time of simulation until the individual is terminated normally or early, and SymDifference represents the symmetric difference from (23). This fitness function penalizes individuals that have been terminated early due to a large prediction error: they are not removed from the population, which ensures diversification, but are ranked worst due to lower fitness. This method was tested using fire data from a real fire in La Jonquera, Spain and it reduced the overall execution time in relation to the Time Aware Core allocation technique from [34] by .
2.6. Literature Review Summary
The review presented above showed that the majority of the works are based on the two-stage framework formally introduced in [20] in conjunction with the use of genetic algorithms. Genetic algorithms show very good suitability for use as the optimization method in the referenced framework, not only based on their performance when compared to other optimization methods [19], but also because they have characteristics suited for being implemented in parallel. Implementing the two-stage framework with genetic algorithms and fire simulators in parallel is of great importance allowing the reduction of both calibration and prediction execution times [34].
Table 2 contains the above-cited works related to the literature review, organized by characteristics such as the focus of the paper, the source of the data used in experiments and tests and GA’s parameters (number of individuals per generation, number of generations, operators probabilities and fitness functions).

Table 2.
Review of the literature on wildfire spread prediction calibration using genetic algorithms. The Gens. column contains the number of GA’s generations. The Others column contains relevant information such as the GA’s operators probabilities and fitness functions.—represents no relevant or existing data. represents the percentage of the population’s individuals selected for the GA’s elitism operation. represents the number of individuals selected for the GA’s elitism operation. is the GA’s crossover operation probability. is the GA’s mutation operation probability. RMSE represents the Root Mean Square Error.
3. Wildfire Spread Calibration Using Genetic Algorithm
From the literature review we verified that, in some articles, there is a lack of details on how the genetic algorithm is implemented for the particular case of wildfire spread prediction calibration, which affects potential attempts for replicability. In this way, based on the presented literature review (Section 2), this section, in a didactic way, presents the use of a genetic algorithm for wildfire spread prediction calibration, where Section 3.1 summarily describes the genetic algorithm, and Section 3.2 presents the application of a genetic algorithm for wildfire spread prediction calibration.
3.1. Genetic Algorithms Overview
Genetic algorithms have proved to be useful in solving a variety of search and optimization problems [40]. In a general way, GAs are stochastic search methods introduced by [41] in 1975 inspired by natural selection and genetics. GAs work by processing a set of elements of a given search space, i.e., a large domain with several possible problem solutions. This set is named the population, and its elements are called individuals. Individuals, which represent the candidate solutions for the optimization problem, are also named chromosomes and are composed of genes. Genes are the primary parts of each solution. Individuals can have several representations depending on the problem: they can be binary sequences of zeros and ones, complex numbers, vectors, among others. The population is evolved/transformed during several generations in order to obtain a final population that contains individuals with the best possible quality for the problem at hand.
A GA generic structure is shown in Algorithm 1. After the encoding of the chromosomes (individuals), usually, a random initialization of the population is performed. Then, all of the individuals are evaluated according to a defined fitness function which measures the ability of a solution (individual) to optimize the fitness function that is specific to the problem being solved. Based on the fitness values of each individual, the selection process occurs where new individuals are chosen to be parents. The Crossover and Mutation reproduction operators and the Replacement operator are applied to the parents in order to breed the offspring and build the next generation. The above GA’s operators are repeated until a certain criterion is achieved.
| Algorithm 1 General genetic algorithm steps. |
|
3.2. Calibration Methodology Using Genetic Algorithms
In order to calibrate the Rothermel model (1), the genetic algorithm starts by randomly generating an initial population of N individuals. Each individual is composed of genes, which in this paper consist of Rothermel input parameters to be calibrated. In this paper, four input parameters were selected to be calibrated: (surface-area-to-volume ratio), (fuel bed depth), (fuel moisture) and U (midflame wind speed). Three main reasons motivated this parameter choice:
- (1)
- the fact that the first three parameters are related to fuel characteristics, which in simulations are approximated using fuel models. Fuel models assume constant and uniform fuel characteristics inside a cell, which is a fair approximation for small cell sizes, a large variety of fuel models and accurate fitting of the model to the existing fuels. However, available fuel maps can suffer from low resolution (large cell sizes), low variety of models (the most commonly used standard NFFL fuel models [42] includes only 13 different fuel models) and low accuracy, therefore increasing the probability of fuel models failing to accurately depict the average characteristics of existing fuels.
- (2)
- Furthermore, the fire dynamics are known to induce local changes in the fuel characteristics, as well as wind speed and direction, in the close vicinity of the fire front [43,44,45] (fuel moisture drastically decreases while wind speed increases). To some extent, such changes are intrinsic to the semi-empirical Rothermel model. However, local variations in such parameters should be expected.
- (3)
- These four input parameters are the ones that have the most influence on the final result (fire spread rate), so their small variations are highly significant [15,46].
For the parameters concerning the fuels, a specific search space was defined as the boundaries of the fuel class, assuming that fuel classes are well identified. For instance, grass-dominated fuels can be short grass (NFFL model 1), grass understory (NFFL model 2) or tall grass (NFFL model 3), each with their own parameters. The boundaries of the parameters for the grass-dominated fuel class were defined as the search space, in case the cell fuel is any of these three models. Concerning the midflame wind speed, we considered the search space to be within the interval ±25% of the dataset value, which is an average of the wind speed recordings during the fire drill, obtained with a weather station installed on-site.
In this way, an individual n () is represented by the chromosome presented in Figure 4, where , , , are the input parameters , , , U present on individual n, respectively.
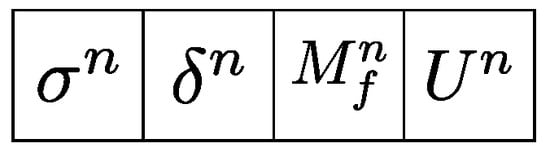
Figure 4.
Illustration of a chromosome.
To evaluate each n individual, the fitness function
was defined. The fitness function (25) consists on the relative error between , the rate of spread given by the Rothermel model (1) using the input parameters given by the individual n, and a real observed rate of spread value . The goal of GA is to minimize the fitness function.
The GA operators were chosen as follows.
- The selection operator is the tournament selection [47], which consists of randomly selecting a certain number of individuals of the current population, creating a tournament. The winner of the tournament is the individual with the best fitness and it is selected to be a parent for the next generation. This process is repeated a second time, and a pair of parent individuals is obtained.
- The crossover operator is the single point crossover technique [47]. It is executed on the parent pair by cutting the two chromosomes at corresponding points and exchanging the sections after the cuts. This generates a new offspring pair.
- The mutation operator is the uniform operator [48]. This operator consists of altering the value of a random gene in the offspring by a uniform random value which fits the gene’s respective search space, at a given probability of mutation , a parameter defined at the beginning of the GA implementation.
- The elitism is applied to the whole new population, i.e., a small percentage of the best individuals () of the previous generation replaces random individuals in the new population [48].
The new population is evaluated at each generation g () and the whole cycle is repeated until the maximum number of generations is reached. After the algorithm finishes, the final solution is the individual with the best fitness from the final population. This individual is the one that, when used as input for the Rothermel model (1), results in the closest rate of spread value to the real measured value provided from the experimental data. The used algorithm is represented in Algorithm 2.
| Algorithm 2 Genetic algorithm for wildfire spread calibration. |
|
4. Results
This section presents the validation and results of the calibration of the Rothermel model (1) using the Algorithm 2 on real datasets obtained through experimental prescribed fires in controlled conditions.
The datasets used for the calibration carried out in this work were obtained through experimental prescribed fires in controlled conditions—each dataset corresponds to a different controlled fire. There were 37 valid datasets, each one being a vector composed of the constant values for the fixed input parameters (, , , , , , h, U, ) (1), observed delta () and observed oven-dry fuel load (), and the measured values for the experimental rate of spread . According to Algorithm 2, four input parameters are calibrated: (surface-area-to-volume ratio), (fuel bed depth), (fuel moisture), and U (midflame wind speed). The remaining input parameters of Rothermel model (1) have fixed values which are the ones provided by the datasets. Despite (fuel moisture) and U (midflame wind speed) being parameters that are calibrated in this paper, they are provided on the dataset, and , respectively, based on the initial experimental conditions. However, these parameters can vary significantly during the fire itself, making it difficult for a single constant value to represent the real conditions. For each input parameter to be calibrated, there is a specific search space, i.e., a range of values that its respective gene could assume, according to the experts:
- ;
- ;
- ;
- .
The Algorithm 2 was configured in the following way: population size which were evolved for generations; tournament selection length ; crossover probability , mutation probability ; and elitism factor . The genetic algorithm was executed 30 times for each dataset and the final fitness for each dataset consisted of the average final error of the 30 GA runs:
where is given by (25).
Figure 5 shows the evolution of the 30 run average of the best fitness values, throughout the 100 generations, for each of the 37 datasets.
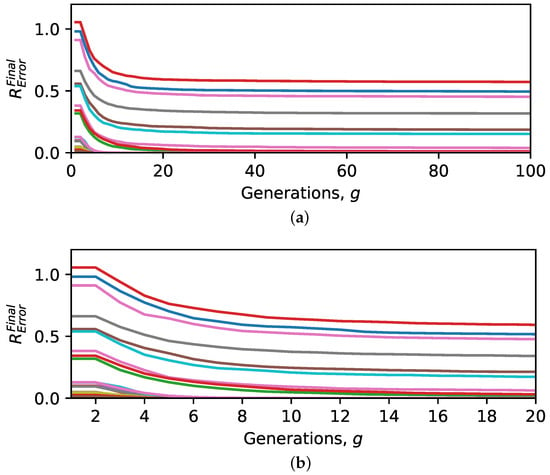
Figure 5.
Evolution of the 30-run average of the best fitness values for every calibrated dataset. (a) Evolution of the 30-run average of the best fitness values for 100 generations. (b) Evolution of the 30-run average of the best fitness values for 20 generations.
In order to compare the calibration method (Algorithm 2) to the prediction without calibration, a rate of spread was obtained for each dataset by running the Rothermel model (1) without calibration, i.e., the input parameters provided by the dataset were used, except for , whose value was not provided in the data set. The default value used was , which is the default value for NFFL fuel model no. 6 [42]. For the prediction without calibration, the relative error associated with the rate of spread for each dataset was obtained through:
Figure 6 shows two relative error values for each dataset, where represents the final fitness given by (26), and (27) represents the relative error between and the rate of spread value obtained without GA calibration , given by Equation (27). For 29 of the 37 datasets, the best rate of spread value obtained through GA calibration resulted in a null error. This means that, if a fire was to occur in the same conditions, the final individuals could serve as input for the Rothermel model and generate very good predictions. The mean prediction error from all of the datasets without GA calibration is (). With GA calibration, the mean error is (). This shows the importance of input parameters calibration, as seen in the literature.
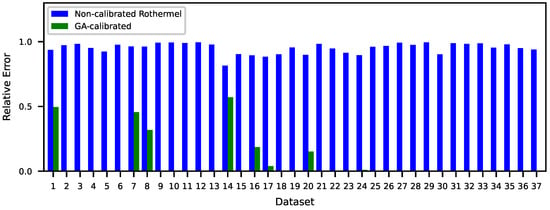
Figure 6.
Relative error between the predicted and observed rate of spread R for non calibrated vs. calibrated input parameters.
5. Conclusions
Due to the physical complexity of wildfires, their prediction models require the definition of several input parameters. However, some of them are very difficult to obtain accurately or, due to their nature, present significant variations over a short period of time, due to weather or fire-driven dynamics (e.g., fuel and wind properties). Therefore, the use of optimization methodologies—specifically, genetic algorithms—to calibrate the model and to overcome input parameter uncertainty has shown to be a valid strategy to obtain accurate prediction results. This strategy will pave the way to improved fire spread simulators, capable of adapting to the particular and constantly evolving conditions of each location, producing vital data for the decision makers and potentially mitigating the impact of wildfires.
In this work, a literature review of research works on fire spread prediction using genetic algorithms was presented, showing that genetic algorithms are the most well-accepted methodology for this application, being well-suited techniques for Rothermel model calibration. More recently, some works focused on coupling genetic algorithms with other methods to improve the prediction quality. However, due to the nature of genetic algorithms and the complexity of the model, the calibration process can be very computationally demanding. Therefore, other works also explore the possibility of reducing genetic algorithms’ execution time by using parallel computing and core-allocation techniques.
Furthermore, in this work, a calibration of the Rothermel model using a genetic algorithm implementation was carried out on real datasets. The calibration was performed on four input parameters: (surface-area-to-volume ratio), (fuel bed depth), (fuel moisture) and U (midflame wind speed). The results of the fire spread prediction using the calibrated model were compared to the fire spread prediction without calibration. The results showed that calibration improves prediction quality by .
As future work, based on the literature review, we intend to extend the prediction to the domain of a two-dimensional grid in order to improve the model’s applicability to real fire situations, where cells represent a squared area of the terrain through which fire propagates. This will result in the prediction of real fire behavior in the form of a map of burned cells over time. Furthermore, the parallel implementation of a genetic algorithm for the calibration of the two-dimensional Rothermel model based on the two-stage framework should be considered, which is validated by the review performed in this paper. Lastly, the framework should be tested and applied on data obtained through prescribed fires.
Author Contributions
Conceptualization, methodology, formal analysis: J.P. and J.M.; writing—original draft preparation: J.P., software, J.P. and J.S.S.J.; validation, writing—review and editing, J.M., C.V. and J.R.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was carried out under the project IMFire–Intelligent Management of Wildfires, ref. PCIF/SSI/0151/2018, and was fully funded by national funds through the Ministry of Science, Technology and Higher Education.
Conflicts of Interest
The authors declare no conflict of interest.
References
- San-Miguel-Ayanz, J.; Durrant, T.; Boca, R.; Maianti, P.; Libertà, G.; Vivancos, T.A.; Oom, D.J.F.; Branco, A.; Rigo, D.D.; Ferrari, D.; et al. Forest Fires in Europe, Middle East and North Africa 2019; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar]
- Júnior, J.S.S.; Paulo, J.; Mendes, J.; Alves, D.; Ribeiro, L.M. Automatic Calibration of Forest Fire Weather Index for Independent Customizable Regions Based on Historical Records. In Proceedings of the 2020 IEEE Third International Conference on Artificial Intelligence and Knowledge Engineering (AIKE), Laguna Hills, CA, USA, 9–13 December 2020; pp. 1–8. [Google Scholar]
- Júnior, J.S.; Paulo, J.R.; Mendes, J.; Alves, D.; Ribeiro, L.M.; Viegas, C. Automatic forest fire danger rating calibration: Exploring clustering techniques for regionally customizable fire danger classification. Expert Syst. Appl. 2022, 193, 116380. [Google Scholar] [CrossRef]
- Robinne, F.N. Impacts of Disasters on Forests, in Particular Forest Fires; Technical Report; United Nations Forum on Forests Secretariat: New York, NY, USA, 2021. [Google Scholar]
- Pastor, E.; Zárate, L.; Planas, E.; Arnaldos, J. Mathematical models and calculation systems for the study of wildland fire behaviour. Prog. Energy Combust. Sci. 2003, 29, 139–153. [Google Scholar] [CrossRef]
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; Forest Service, United States Department of Agriculture: Ogden, UT, USA, 1972.
- Sullivan, A. Wildland surface fire spread modelling, 1990–2007. 2: Empirical and quasi-empirical models. Int. J. Wildland Fire 2009, 18, 369–386. [Google Scholar] [CrossRef] [Green Version]
- Finney, M.A. FARSITE: Fire Area Simulator-Model Development and Evaluation; Technical Report; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Ogden, UT, USA, 1998.
- Lopes, A.G.; Cruz, M.; Viegas, D. FireStation—An integrated software system for the numerical simulation of fire spread on complex topography. Environ. Model. Softw. 2002, 17, 269–285. [Google Scholar] [CrossRef]
- Brun, C.; Artés, T.; Margalef, T.; Cortés, A. Coupling Wind Dynamics into a DDDAS Forest Fire Propagation Prediction System. In Proceedings of the 12th International Conference on Computational Science, Salvador, Bahia, Brazil, 18–21 June 2012; Volume 9, pp. 1110–1118. [Google Scholar]
- Jain, P.; Coogan, S.; Subramanian, S.G.; Crowley, M.; Taylor, S.; Flannigan, M. A review of machine learning applications in wildfire science and management. Environ. Rev. 2020, 28, 478–505. [Google Scholar] [CrossRef]
- Mendes, J.; Seco, R.; Araújo, R. Automatic Extraction of the Fuzzy Control System for Industrial Processes. In Proceedings of the 16th IEEE International Conference on Emerging Technologies and Factory Automation, Toulouse, France, 5–11 September 2011; pp. 1–8. [Google Scholar]
- Mendes, J.; Araújo, R.; Souza, F. Adaptive Fuzzy Identification and Predictive Control for Industrial Processes. Expert Syst. Appl. 2013, 40, 6964–6975. [Google Scholar] [CrossRef]
- Mendes, J.; Araújo, R.; Matias, T.; Seco, R.; Belchior, C. Evolutionary Learning of a Fuzzy Controller for Industrial Processes. In Proceedings of the 40th Annual Conference of the IEEE Industrial Electronics Society (IECON 2014), Dallas, TX, USA, 29 October–1 November 2014; IEEE: Dallas, TX, USA, 2014; pp. 139–145. [Google Scholar]
- Andrews, P.L. The Rothermel Surface Fire Spread Model and Associated Developments: A Comprehensive Explanation; Technical Report; Rocky Mountain Research Station, Forest Service: Fort Collins, CO, USA; United States Department of Agriculture: Fort Collins, CO, USA, 2018.
- Denham, M.; Cortés, A.; Margalef, T.; Luque, E. Applying a Dynamic Data Driven Genetic Algorithm to Improve Forest Fire Spread Prediction. In Proceedings of the 8th International Conference on Computational Science, Kraków, Poland, 23–25 June 2008; Volume 5103, pp. 36–45. [Google Scholar]
- Rodríguez, R.; Cortés, A.; Margalef, T. Injecting Dynamic Real-Time Data into a DDDAS for Forest Fire Behavior Prediction. In Proceedings of the 9th International Conference on Computational Science, Baton Rouge, LA, USA, 25–27 May 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 489–499. [Google Scholar]
- Chelli, S.; Maponi, P.; Campetella, G.; Monteverde, P.; Foglia, M.; Paris, E.; Lolis, A.; Panagopoulos, T. Adaptation of the Canadian Fire Weather Index to Mediterranean forests. Nat. Hazards 2014, 75, 1795–1810. [Google Scholar] [CrossRef]
- Abdalhaq, B.; Cortés, A.; Margalef, T.; Luque, E.; Viegas, D.X. Optimization of Parameters in Forest Fire Propagation Models. In Forest Fire Research Wildland Fire Safety; Springer: Berlin/Heidelberg, Germany, 2002; pp. 1–13. [Google Scholar]
- Abdalhaq, B.; Cortés, A.; Margalef, T.; Luque, E. Enhancing wildland fire prediction on cluster systems applying evolutionary optimization techniques. Future Gener. Comput. Syst. 2005, 21, 61–67. [Google Scholar] [CrossRef]
- Artès, T.; Cardil, A.; Cortés, A.; Margalef, T.; Molina, D.; Pelegrín, L.; Ramírez, J. Forest Fire Propagation Prediction Based on Overlapping DDDAS Forecasts. In Proceedings of the 15th International Conference on Computational Science, Banff, AB, Canada, 22–25 June 2015; Volume 51, pp. 1623–1632. [Google Scholar]
- Denham, M.; Cortés, A.; Margalef, T. Computational Steering Strategy to Calibrate Input Variables in a Dynamic Data Driven Genetic Algorithm for Forest Fire Spread Prediction. In Proceedings of the 9th International Conference on Computational Science, Baton Rouge, LA, USA, 25–27 May 2009; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5545, pp. 479–488. [Google Scholar]
- Bianchini, G.; Cortés, A.; Margalef, T.; Luque, E. S2F2M—Statistical System for Forest Fire Management. In Proceedings of the 5th International Conference on Computational Science, Atlanta, GA, USA, 22–25 May 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 427–434. [Google Scholar]
- Denham, M.; Wendt, K.; Bianchini, G.; Cortés, A.; Margalef, T. Dynamic Data-Driven Genetic Algorithm for forest fire spread prediction. J. Comput. Sci. 2012, 3, 398–404. [Google Scholar] [CrossRef]
- Group, W.W. Weather Research and Forecasting (WRF) Model; Technical Report, Director (INT-115); UCAR: Boulder, CO, USA, 2015. [Google Scholar]
- Ascoli, D.; Bovio, G.; Vacchiano, G. Calibrating Rothermel’s fuel models by genetic algorithms. In Advances in Forest Fire Research; Imprensa da Universidade de Coimbra: Coimbra, Portugal, 2014; pp. 102–106. [Google Scholar]
- Sneeuwjagt, R.; Frandsen, W. Behavior of experimental grass fires vs. predictions based on Rothermel’s fire model. Can. J. For. Res. 1977, 7, 357–367. [Google Scholar] [CrossRef]
- Wilgen, B.V.; Maitre, D.L.; Kruger, F. Fire behaviour in South African fynbos (macchia) vegetation and predictions from Rothermel’s fire model. J. Appl. Ecol. 1985, 22, 207–216. [Google Scholar] [CrossRef]
- Sandberg, D.; Riccardi, C.; Schaaf, M. Reformulation of Rothermel’s wildland fire behaviour model for heterogeneous fuelbeds. Can. J. For. Res. 2007, 37, 2438–2455. [Google Scholar] [CrossRef]
- Ramirez, J.; Monedero, S.; Buckley, D. New approaches in fire simulations analysis with Wildfire Analyst. In Proceedings of the 5th International Wildland Fire Conference, Sun City, South Africa, 9–13 May 2011. [Google Scholar]
- Artés, T.; Cortés, A.; Margalef, T. Large Forest Fire Spread Prediction: Data and Computational Science. In Proceedings of the 12th International Conference on Computational Science, Beijing, China, 4–7 July 2016; Volume 80, pp. 909–918. [Google Scholar]
- Cencerrado, A.; Cortés, A.; Margalef, T. Genetic Algorithm Characterization for the Quality Assessment of Forest Fire Spread Prediction. In Proceedings of the 12th International Conference on Computational Science, Salvador, Brazil, 18–21 June 2012; Volume 9, pp. 312–320. [Google Scholar]
- Fraga, E.; Cortés, A.; Cencerrado, A.; Hernández, P.; Margalef, T. Early Adaptive Evaluation Scheme for Data-Driven Calibration in Forest Fire Spread Prediction. In Proceedings of the 20th International Conference on Computational Science, Amsterdam, The Netherlands, 3–5 June 2020; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12142, pp. 17–30. [Google Scholar]
- Artés, T.; Cencerrado, A.; Cortés, A.; Margalef, T. Relieving the Effects of Uncertainty in Forest Fire Spread Prediction by Hybrid MPI-OpenMP Parallel Strategies. In Proceedings of the 13th International Conference on Computational Science, Ho Chi Minh City, Vietnam, 24–27 June 2013; Volume 18, pp. 2278–2287. [Google Scholar]
- Cencerrado, A.; Cortés, A.; Margalef, T. On the Way of Applying Urgent Computing Solutions to Forest Fire Propagation Prediction. In Proceedings of the 12th International Conference on Computational Science, Salvador, Bahia, Brazil, 18–21 June 2012; Elsevier: Amsterdam, The Netherlands, 2012; Volume 9, pp. 1657–1666. [Google Scholar]
- Cencerrado, A.; Artés, T.; Cortés, A.; Margalef, T. Relieving Uncertainty in Forest Fire Spread Prediction by Exploiting Multicore Architectures. In Proceedings of the 15th International Conference on Computational Science, Banff, AB, Canada, 22–25 June 2015; Volume 51, pp. 1752–1761. [Google Scholar]
- Artés, T.; Cencerrado, A.; Cortés, A.; Margalef, T. Time aware genetic algorithm for forest fire propagation prediction: Exploiting multi-core platforms. Concurr. Comput. Pract. Exp. 2016, 29, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Ascoli, D.; Lonati, M.; Marzano, R.; Bovio, G.; Cavallero, A.; Lombardi, G. Prescribed burning and browsing to control tree encroachment in southern European heathlands. For. Ecol. Manag. 2013, 289, 69–77. [Google Scholar] [CrossRef]
- Vacchiano, G.; Motta, R.; Bovio, G.; Ascoli, D. Calibrating and Testing the Forest Vegetation Simulator to Simulate Tree Encroachment and Control Measures for Heathland Restoration in Southern Europe. For. Sci. 2014, 60, 241–252. [Google Scholar] [CrossRef] [Green Version]
- Mendes, J.; Souza, F.; Araújo, R.; Gonçalves, N. Genetic Fuzzy System for Data-Driven Soft Sensors Design. Appl. Soft Comput. 2012, 12, 3237–3245. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Anderson, H. Aids to Determining Fuel Models for Estimating Fire Behavior; Technical Report; US Department of Agriculture, Forest Service, Intermountain Forest and Range: Fort Collins, CO, USA, 1982.
- Lopes, S.; Viegas, D.X.; de Lemos, L.T.; Viegas, M.T. Equilibrium moisture content and timelag of dead Pinus pinaster needles. Int. J. Wildland Fire 2014, 23, 721–732. [Google Scholar] [CrossRef]
- Rossa, C.G. A generic fuel moisture content attenuation factor for fire spread rate empirical models. For. Syst. 2018, 27, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Viegas, D.X.F.C.; Raposo, J.R.N.; Ribeiro, C.F.M.; Reis, L.C.D.; Abouali, A.; Viegas, C.X.P. On the non-monotonic behaviour of fire spread. Int. J. Wildland Fire 2021, 30, 702–719. [Google Scholar] [CrossRef]
- Fernandes, P.A.M. Fire spread prediction in shrub fuels in Portugal. For. Ecol. Manag. 2001, 144, 67–74. [Google Scholar] [CrossRef]
- Sivanandam, S.; Deepa, S.N. Introduction to Genetic Algorithms; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Gaspar-Cunha, A.; Takahashi, R.; Antunes, C.H. Manual de Computação Evolutiva e Metaheurística; Imprensa da Universidade de Coimbra, Coimbra University Press: Coimbra, Portugal, 2012. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).