On Global Offensive Alliance in Zero-Divisor Graphs

Abstract

Let $\Gamma (V,E)$ be a simple connected graph with more than one vertex, without loops or multiple edges. A nonempty subset $S\subseteq V$ is a global offensive alliance if every vertex $v\in V-S$ satisfies that ${\delta }_S\left(v\right)\ge {\delta }_{\overline{S}}\left(v\right)+1$. The global offensive alliance number ${\gamma }^o(\Gamma )$ is defined as the minimum cardinality among all global offensive alliances. Let R be a finite commutative ring with identity. In this paper, we study the global offensive alliance number of the zero-divisor graph $\Gamma \left(R\right)$.

1. Introduction

In this paper, $\Gamma =(V,E)$ denotes a simple connected graph of order $n>1$ and size m, where V is the vertex set and E the edge set. The subgraph induced by a set $S\subset V$ will be denoted by $⟨S⟩$. For a vertex $v\in V$, the open neighborhood of v is defined as $N\left(v\right):=\{u\in V:u$ is adjacent to $v\}$. The degree of the vertex $v\in V$, denoted by $\delta \left(v\right)$, is the cardinality of its open neighborhood. The minimum degree will be denoted by $\delta$, and the maximum degree by $\Delta$. For a non-empty subset $S\subset V$, and a vertex $v\in V$, the set of neighbors that v has in S is $N_S\left(v\right):=S\cap N\left(v\right)$. The degree of the vertex v over S is defined as ${\delta }_S\left(v\right)=\left|N_S\left(v\right)\right|$. The complement $V-S$ of any subset $S\subset V$ will be denoted with ${\overline{S}}_V$ or simply $\overline{S}$ when it is not necessary to specify V explicitly.

The mathematical properties of alliances in graphs were studied first by Kristiansen et al. [1]. They proposed different types of alliances, such as defensive alliances [2,3,4,5,6], offensive alliances [7,8,9] and dual alliances (also known as powerful alliances) [10].

Alliances in graphs serve as a mathematical model for several practical and theoretical problems that have been appearing in the literature of different areas of knowledge, such as data structure [11], web communities [12], bioinformatics (study of the proteome and genome) [13], as well as defense systems [14]. These types of alliances have been extensively studied in the last decade. In this paper, we are concerned with the study of a specific kind of alliance in a specific class of graphs, namely global offensive alliances on zero-divisor graphs.

The topic of global offensive alliances has been widely studied, for example, regarding the estimation of sharp bounds [7,8,15] and sharp bounds in planar graphs [16]. In [17], the authors consider sharp bounds for the global offensive alliance number of cubic graphs, their relationship with other graph-theoretic parameters such as the order, size and diameter [18] and the independence and domination numbers [19]. Offensive alliances have also been studied on graphs obtained as the result of an operation of graphs, e.g., the product of graphs [9].

Let S be a nonempty subset of the vertex set V, and S is a global offensive alliance of $\Gamma =(V,E)$ if it satisfies that

$${\delta }_S\left(v\right)\ge {\delta }_{\overline{S}}\left(v\right)+1forallv\in \overline{S}.$$

(1)

If, for a vertex $v\in \overline{S}$, relation (1) is verified, we will say that v satisfies the global offensive alliance condition in S. The global offensive alliance number ${\gamma }^o(\Gamma )$ is defined as the minimum cardinality among all global offensive alliances. For convenience, we will call ${\gamma }^o-$alliance a global offensive alliance of minimum cardinal.

In this work, R will denote a finite commutative ring with identity. The set of zero-divisors of R will be denoted by $Z\left(R\right)$. The zero-divisor graph is the simple graph $\Gamma \left(R\right)$, with the proper zero-divisors of R as the vertex set, i.e., $Z{\left(R\right)}^{*}=Z\left(R\right)-\left\{0\right\}$, and for different u, v $\in Z{\left(R\right)}^{*}$, the vertices u and v are adjacent if and only if $uv=0$. Examples of zero-divisor graphs can be found in [20]. We will denote with $U\left(R\right)$ the set of units of the ring R. If $Ann\left(v\right)$ denotes the annihilator of v (that is, the set of elements $u\in R$ such that $uv=0$), notice that $\delta \left(v\right)=\left|Ann\right(v\left)\right|-1$ if $v^2\ne 0$ or $\delta \left(v\right)=\left|Ann\right(v\left)\right|-2$ otherwise. The nilradical of the ring R is defined as $Nil\left(R\right)=\{r\in R:r^n=0,$ for some $n\}$. For more background on zero-divisor graphs, see [21].

I. Beck was the first to introduce the concept of a zero-divisor graph in 1988 for his study of the coloring of a commutative ring [22]. Beck considered all the elements of the ring as vertices of the graph, and an edge is obtained if two different elements u and v satisfy that $uv=0$. In 1999 [23], Anderson and Livingston introduced and studied the zero-divisor graph with a slight modification: the vertices of the graph are the proper zero-divisors.

Since then, the zero-divisor graph has become an important research topic, which is evidenced by the number of articles published on the subject. To cite a few examples, in [23], it is obtained that the diameter of $\Gamma \left(R\right)$ is at most three and the girth is at most four. In [24], the authors study and characterize those rings R for which $\Gamma \left(R\right)$ is a planar graph. In [25], Emad E. et. al. gave the dominance and independence number for $\Gamma \left({\mathbb{Z}}_n\right)$ for certain values of n. However, alliances had never been explored in this type of graph until recently, in 2020, when Muthana and Mamouni initiated the study of the global offensive alliance number in the zero-divisor graph [26]. The present work is motivated by the aforementioned study. Explicitly, we explore the global offensive alliance number in these graphs.

This paper is organized as follows: in Section 2.1, we give some results concerning the global offensive alliance number of the zero-divisor graph; for example, we give a characterization in terms of the global offensive alliance number for $\Gamma \left(R\right)$ to be a complete graph. We also give sharp bounds of ${\gamma }^o(\Gamma \left(R\right))$ for different kinds of rings R (local, co-local and certain direct products of rings). Finally, in Section 2.2, we give a complete characterization of rings with ${\gamma }^o(\Gamma \left(R\right))=1$ or 2.

2. Results

2.1. The Global Offensive Alliance Number of the Zero-Divisor Graph

In this section, our main goal is to calculate or provide sharp bounds to the global offensive alliance number of zero-divisor graphs for some kind of direct products of finite local rings with finite fields—in particular, to characterize when the global offensive alliance number over the ring formed by the direct product of ${\mathbb{Z}}_2$ with any ring R is ${|Z\left(R\right)}^{*}|+1$.

Recall that a commutative ring R is a local ring if it contains a unique maximal ideal M. Throughout this paper, we will use freely the well-known facts concerning this type of ring, listed in the following lemma (see [26]).

Lemma 1.

Let $(R,M)$ be a finite local ring that is not a field. Then, the following holds.

• (1) $M=Z\left(R\right)=Ann\left(x\right)$ for some $x\in Z{\left(R\right)}^{*}$.
• (2) $\left|R\right|=p^{nr}$, and $\left|M\right|=p^{(n-1)r}$ for some prime integer p, and some positive integers n and r.

Notice that if $\Gamma =(V,E)$ is a connected graph with more than one vertex, then, for each $x\in V$, the set $S=V-\left\{x\right\}$ is a global offensive alliance. Since $\Gamma \left(R\right)$ is a connected graph [23] (Theorem 2.3), the following remark arises naturally.

Remark 1.

Let R be a ring with $\left|Z\right(R\left)\right|\ge 3$, then

$${\gamma }^o(\Gamma \left(R\right))+2\le \left|Z\left(R\right)\right|.$$

Theorem 1.

If R is a local ring which is not a field, then

$${\gamma }^o(\Gamma \left(R\right))\le \left(\left|Z\left(R\right)\right|-{\gamma }^o(\Gamma \left(R\right))\right)({\gamma }^o(\Gamma \left(R\right))-1)+1.$$

Proof. 

Let $k={\gamma }^o(\Gamma \left(R\right))$; if any ${\gamma }^o-$alliance S contains some element $x\in Z{\left(R\right)}^{*}$ with $Z\left(R\right)=Ann\left(x\right)$, then

$$\begin{array}{ccc}\left|S\right|& =& 1+|S-\left\{x\right\}|=1+\left|(S-\left\{x\right\})\cap N\left(\overline{S}\right)\right|\hfill \\ & =& 1+\left|(S-\left\{x\right\})\cap \left({\displaystyle \bigcup _{v\in \overline{S}}N\left(v\right)}\right)\right|\hfill \\ & =& 1+\left|{\displaystyle \bigcup _{v\in \overline{S}}((S-\left\{x\right\})\cap N\left(v\right))}\right|\hfill \\ & \le & {\displaystyle 1+\sum _{v\in \overline{S}}\left|\right(S-\left\{x\right\})\cap N(v\left)\right|=1+\sum _{v\in \overline{S}}{\delta }_{S-\left\{x\right\}}\left(v\right)}\hfill \\ & =& {\displaystyle 1+\sum _{v\in \overline{S}}({\delta }_S\left(v\right)-1)}\hfill \\ & \le & {\displaystyle 1+\sum _{v\in \overline{S}}(k-1)}\hfill \\ & =& \left(\right|Z{\left(R\right)}^{*}|-k)(k-1)+1\hfill \\ & \le & \left(\right|Z\left(R\right)|-k)(k-1)+1.\hfill \end{array}$$

In the other case, if, for some x with $Ann\left(x\right)=Z\left(R\right)$, it occurs that $x\in \overline{S}$, then

$$k={\delta }_S\left(x\right)\ge {\delta }_{\overline{S}}\left(x\right)+1=\left|Z{\left(R\right)}^{*}\right|-k,$$

hence,

$$\left|Z\left(R\right)\right|=\left|S\right|+|\overline{S}|+1\le 2k+1\le (\left|Z\left(R\right)\right|-k)k+1,$$

consequently,

$$\begin{gathered} \left|S\right| \le \left(\right|Z\left(R\right)|-k)k+1-\left(\right|\overline{S}|+1) \\ =\left(\right|Z\left(R\right)|-k)k+1-\left(\right|Z\left(R\right)|-k) \\ =\left(\right|Z\left(R\right)|-k)(k-1)+1. \end{gathered}$$

□

Notice that the inequality of the preceding theorem becomes an equality for some rings; for example, if $R={\mathbb{Z}}_9$, then $\Gamma \left(R\right)$ ≅ $K_2$ and hence ${\gamma }^o(\Gamma \left(R\right))=1$.

In [9] (Remark 2.1), it is shown that ${\gamma }^o\left(K_{m,n}\right)=min\{m,n\}$. If F and L are fields then $\Gamma (F\times L)=K_{\left|F\right|-1,\left|L\right|-1}$ (see [23], Example 3.4). Hence, the next lemma follows at once.

Lemma 2.

If F and L are fields, then

$${\gamma }^o(\Gamma (F\times L))=min\left\{\right|F|-1,|L|-1\}.$$

Proposition 1.

If R is a ring, then

(i) 

The inequality ${\gamma }^o(\Gamma ({\mathbb{Z}}_2\times R))\le \left|Z\left(R\right)\right|$ holds.

(ii) 

If R has at least two units, then $(1,0)$ is an element of every ${\gamma }^o-$alliance of $\Gamma ({\mathbb{Z}}_2\times R)$.

Proof. 

(i) 

We claim that the set $S=\left\{(1,0)\right\}\cup (\left\{0\right\}\times Z{\left(R\right)}^{*})$ is a global offensive alliance. Take $(u,v)\in \overline{S}$; if $u=0$, then $v\in U\left(R\right)$ and ${\delta }_S(u,v)=1$ (since $(u,v)$ is adjacent to $(1,0)$), while ${\delta }_{\overline{S}}(u,v)=0$. On the other hand, if $u=1$, then $v\in Z{\left(R\right)}^{*}$; in this case, take $w\in Z{\left(R\right)}^{*}$ such that $vw=0$. This shows that ${\delta }_S(u,v)\ge 1$ (since $(u,v)$ is adjacent to $(0,w)$), while ${\delta }_{\overline{S}}(u,v)=0$.

(ii) 

Let S be a global offensive alliance that does not contain the element $(1,0)$. This implies that $\left\{0\right\}\times U\left(R\right)\subseteq S$. In this way, $(S-(\left\{0\right\}\times U\left(R\right)\left)\right)\cup \left\{\right(1,0\left)\right\}$ is a global offensive alliance with $\left|S\right|-\left|U\right(R\left)\right|+1\le \left|S\right|-1$ vertices.

□

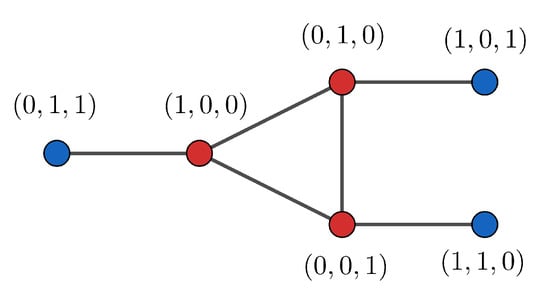
For an example of the above proposition, take R ≅ ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$; in this case, ${\gamma }^o(\Gamma ({\mathbb{Z}}_2\times R))=\left|Z\left(R\right)\right|=3$ (see Figure 1).

Figure 1. Diagram of the graph $\Gamma ({\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2$).

Theorem 2.

If R is a ring, then $\Gamma \left(R\right)=K_n$ if and only if ${\gamma }^o(\Gamma ({\mathbb{Z}}_2\times R))=n+1$ and exactly one of the following conditions hold:

• (i) $n\le 4$ and $R\ncong$${\mathbb{Z}}_3\times {\mathbb{Z}}_3$, or
• (ii) ${\delta }_{\Gamma \left(R\right)}\ge 4$.

Proof. 

⇒) In [23], it can be found that all zero-divisor graphs with at most four vertices, an easy computation shows the result and this establishes (i).

For (ii), if $n\ge 5$ by [23] (Theorem 2.8), R is a local ring such that, for each $x\in Z{\left(R\right)}^{*}$, $Ann\left(x\right)=Z\left(R\right)$.

Let S be a ${\gamma }^o-$alliance of $\Gamma ({\mathbb{Z}}_2\times R)$. If $x\in Z{\left(R\right)}^{*}$ is such that $(0,x)\notin S$, since the degree of this vertex in $\Gamma ({\mathbb{Z}}_2\times R)$ is ${2|Z\left(R\right)}^{*}|$, it must occur that $\left|S\right|\ge \left|Z\right(R\left)\right|=n+1$. The other inequality is Proposition 1 (i).

Suppose now that, for all element $x\in Z{\left(R\right)}^{*}$, $(0,x)\in S$. Since $n\ge 5$, Lemma 1 shows that R contains at least two units. According to Proposition 1 (ii), it follows that $(1,0)\in S$; hence, $\left\{(1,0)\right\}\cup (\left\{0\right\}\times Z{\left(R\right)}^{*})\subseteq S$ and again Proposition 1 (i) gives ${\gamma }^o(\Gamma ({\mathbb{Z}}_2\times R))=n+1$.

⇐) (i) If the zero-divisor graph $\Gamma \left(R\right)$ has at most four vertices and $R\ncong {\mathbb{Z}}_3\times {\mathbb{Z}}_3$, once again, an easy examination of all of these zero-divisor graphs shows that $\Gamma \left(R\right)$ must be complete.

(ii) The set $S=\left\{(0,1)\right\}\cup (\left\{0\right\}\times Z{\left(R\right)}^{*})$ is a global offensive alliance of $\Gamma ({\mathbb{Z}}_2\times R)$, which, by hypothesis, is in fact a ${\gamma }^o-$alliance. For each $x\in Z{\left(R\right)}^{*}$, since $S-\left\{\right(0,x\left)\right\}$ is not a global offensive alliance and ${\delta }_{\Gamma \left(R\right)}\ge 4$, it follows that $x^2=0$.

The above has several implications: the nilradical of R (i.e., the ideal of all those nilpotent elements $x\in R$) is equal to $Z\left(R\right)$ and therefore R is a local ring; each vertex of the form $(0,x)$ (and of the form $(1,x)$) with $x\in Z{\left(R\right)}^{*}$ has degree at least 5 and the set $X^{*}=\{x\in Z{\left(R\right)}^{*}|Ann\left(x\right)=Z\left(R\right)\}$ is nonempty.

The theorem is proven if we can see that $\overline{X^{*}}$ is empty. If this is not the case, there are different $x,y\in \overline{X^{*}}$ such that $xy\ne 0$. If $z\in X^{*}$, it can be verified that $(S-\{(0,x),(0,y)\left\}\right)\cup \left\{\right(1,z\left)\right\}$ is a global offensive alliance with n vertices, which is a contradiction. □

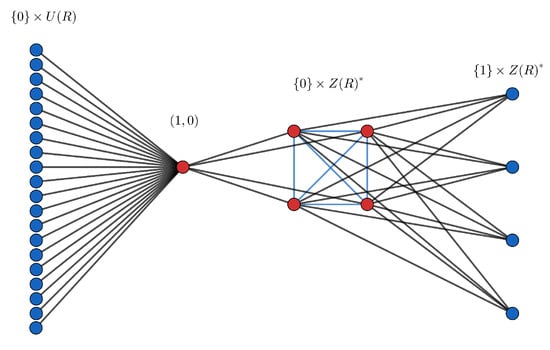
In Figure 2, we show an example of Theorem 2 where R ≅ ${\mathbb{Z}}_{25}$ and $\Gamma \left({\mathbb{Z}}_{25}\right)$ ≅ $K_4$. It can be seen that the vertices in red form a global offensive alliance of minimal size.

Figure 2. Diagram of the graph $\Gamma ({\mathbb{Z}}_2\times {\mathbb{Z}}_{25}$).

Recall that a ring R is co-local if it contains a non-trivial ideal contained in each non-trivial proper ideal.

Theorem 3.

If a finite ring R is co-local, then it is local.

Proof. 

If R is a field, the result is evident. If R is not a field, let N be the non-trivial ideal contained in each non-trivial proper ideal of R. Let $x\in N$ be with $x\ne 0$, and then x is contained in every non-trivial ideal of R. In particular, for each $y\in Z{\left(R\right)}^{*}$, $x\in Ann\left(y\right)$. Conversely, every $y\in Z{\left(R\right)}^{*}$ is such that $y\in Ann\left(x\right)$; in other words, $Ann\left(x\right)=Z\left(R\right)$; hence, R is local. □

Theorem 4.

Let R be a co-local ring that is not a field and N the non-trivial ideal contained in all proper non-trivial ideals of R. Then, ${\gamma }^o(\Gamma \left(R\right))\ge ⌈\frac{|N^{*}|}{2}⌉$. Furthermore, this bound is sharp.

Proof. 

By Theorem 3, R is a local ring with unique maximal ideal $Z\left(R\right)\ne \left\{0\right\}$. Moreover, $N\subseteq Z\left(R\right)$ and $\left|Z\left(R\right)\right|=p^n$ for some prime number p and for some positive integer number n and therefore $\left|N\right|=p^m$, with $m\le n$. If $NZ\left(R\right)$, then $\left|N\right|=p^m\le p^{n-1}=\frac{p^n}{p}\le \frac{p^n}{2}\le \frac{\left|Z\right(R\left)\right|}{2}$, and, from this, it follows that $|N^{*}|\le \frac{{|Z\left(R\right)}^{*}|}{2}$. Now, if S is a ${\gamma }^o-$alliance and some $x\in N^{*}$ does not belong to S, then x is adjacent to at least $⌈\frac{{|Z\left(R\right)}^{*}|}{2}⌉$ vertices in S.

On the other hand, if $N^{*}\subseteq S$, then $\left|S\right|\ge |N^{*}|\ge ⌈\frac{|N^{*}|}{2}⌉$.

Finally, if $N=Z\left(R\right)$, then $\Gamma \left(R\right)$ is a complete graph and it is well known that ${\gamma }^o(\Gamma \left(R\right))=⌈\frac{{|Z\left(R\right)}^{*}|}{2}⌉=⌈\frac{|N^{*}|}{2}⌉$.

It can be verified that the bound is attained for $R={\mathbb{Z}}_9$. □

Theorem 5.

Let R be a ring and r the minimum number of nilpotent elements of index 2 contained in the complement of a ${\gamma }^o-$alliance, then

$${\gamma }^o(\Gamma ({\mathbb{Z}}_2\times R))\le 1+r+2{\gamma }^o(\Gamma \left(R\right)).$$

Moreover, the bound is sharp.

Proof. 

Let $S^{\prime }$ be a ${\gamma }^o-$alliance of $\Gamma \left(R\right)$ that satisfies the conditions of the statement and let $P=\{x_1,x_2,\dots ,x_r\}$ be the nilpotent elements of index 2 contained in $\overline{S^{\prime }}$. Set $S=\left\{(1,0)\right\}\cup (\left\{0\right\}\times (S^{\prime }\cup P))$ and let us show that this set is a global offensive alliance of $\Gamma ({\mathbb{Z}}_2\times R)$. To this end, first observe that the elements of $\left\{0\right\}\times U\left(R\right)$ satisfy the global offensive alliance condition. For an element $x\in \overline{S^{\prime }\cup P}$, note that ${\delta }_{\overline{S^{\prime }}}\left(x\right)={\delta }_P\left(x\right)+{\delta }_{\overline{S^{\prime }}-P}\left(x\right)$ and ${\delta }_{\overline{S}}(0,x)={\delta }_{\overline{S^{\prime }}-P}\left(x\right)+{\delta }_{\overline{S^{\prime }}}\left(x\right)$; therefore,

$$\begin{array}{ccc}{\delta }_S(0,x)& =& 1+2{\delta }_{S^{\prime }}\left(x\right)+{\delta }_P\left(x\right)\hfill \\ & \ge & 1+2({\delta }_{\overline{S^{\prime }}}\left(x\right)+1)+{\delta }_P\left(x\right)\hfill \\ & =& 3+2{\delta }_{\overline{S^{\prime }}}\left(x\right)+{\delta }_P\left(x\right)\hfill \\ & =& 3+{\delta }_{\overline{S^{\prime }}}\left(x\right)+{\delta }_P\left(x\right)+{\delta }_{\overline{S^{\prime }}-P}\left(x\right)+{\delta }_P\left(x\right)\hfill \\ & =& 3+{\delta }_{\overline{S}}(0,x)+2{\delta }_P\left(x\right)\hfill \\ & \ge & {\delta }_{\overline{S}}(0,x)+1.\hfill \end{array}$$

Moreover, since ${\delta }_{\overline{S}}(1,x)={\delta }_{\overline{S^{\prime }\cup P}}\left(x\right)\le {\delta }_{\overline{S^{\prime }}}\left(x\right)$, we have

$$\begin{array}{ccc}{\delta }_S(1,x)& =& {\delta }_{S^{\prime }\cup P}\left(x\right)\hfill \\ & =& {\delta }_{S^{\prime }}\left(x\right)+{\delta }_P\left(x\right)\hfill \\ & \ge & {\delta }_{\overline{S^{\prime }}}\left(x\right)+1+{\delta }_P\left(x\right)\hfill \\ & \ge & {\delta }_{\overline{S}}(1,x)+1+{\delta }_P\left(x\right)\hfill \\ & \ge & {\delta }_{\overline{S}}(1,x)+1.\hfill \end{array}$$

A similar analysis to the previous one shows that if $x\in P$, then ${\delta }_S(1,x)\ge {\delta }_{\overline{S}}(1,x)+1$.

The bound is attained for $R={\mathbb{Z}}_8$. □

Proposition 2.

Let R be a ring, then

(1)

${\gamma }^o(\Gamma ({\mathbb{Z}}_2\times R))\ge {\gamma }^o(\Gamma \left(R\right))+1$;

(2)

and ${\gamma }^o(\Gamma ({\mathbb{Z}}_2\times R))\le 2{\gamma }^o(\Gamma \left(R\right))+1$ if R is a reduced ring (i.e., a ring not containing non-zero elements x such that $x^2=0$).

Proof. 

(1) Let $S\subset Z{({\mathbb{Z}}_2\times R)}^{*}$ be a dominating set; since $(1,0)$ is the unique neighbor of $(0,1)$, it must be $(1,0)\in S$ or $(0,1)\in S$. By cases.

Suppose $(1,0)\in S$ and consider ${\pi }_2:{\mathbb{Z}}_2\times Z{\left(R\right)}^{*}\to Z{\left(R\right)}^{*}$ the projection to the second factor, $S_1=\{(0,b):b\in Z{\left(R\right)}^{*}\}$ and $S_2=\{(1,b):b\in Z{\left(R\right)}^{*}\}$, then $|{\pi }_2\left(S_1\right)|+|{\pi }_2\left(S_2\right)|<{\gamma }^o(\Gamma \left(R\right))$; thus, $T={\pi }_2\left(S_1\right)\cup {\pi }_2\left(S_2\right)$ is not a global offensive alliance of $\Gamma \left(R\right)$, which implies the existence of $y\in \overline{{\pi }_2\left(S_1\right)\cup {\pi }_2\left(S_2\right)}$ such that

$${\delta }_T\left(y\right)<{\delta }_{\overline{T}}+1,$$

thus,

$${\delta }_S(1,y)<{\delta }_{\overline{S}}(1,y)+1,$$

so S is not a global offensive alliance of $\Gamma ({\mathbb{Z}}_2\times R)$.

Now, if $(0,1)\in S$ and $(1,0)\notin S$, we may observe that ${\left|S\right|\ge |Z\left(R\right)}^{*}|+|U\left(R\right)|$; then, ${\gamma }^o{(\Gamma \left(R\right))+1>|Z\left(R\right)}^{*}|+|U\left(R\right)|$; thus, ${\gamma }^o(\Gamma \left(R\right))>\left|R^{*}\right|+1$ a contradiction.

Hence, ${\gamma }^o(\Gamma ({\mathbb{Z}}_2\times R))\ge {\gamma }^o(\Gamma \left(R\right))+1$.

For the second statement, observe that if $T\subset Z{\left(R\right)}^{*}$ is a minimal global offensive alliance, then

$$S=\left\{\right(1,0\left)\right\}\cup \left(\right\{0\}\times T)\cup \left(\right\{1\}\times T)$$

is a global offensive alliance in $\Gamma ({\mathbb{Z}}_2\times R)$. Therefore,

$${\gamma }^o(\Gamma ({\mathbb{Z}}_2\times R))\le 2{\gamma }^o(\Gamma \left(R\right))+1.$$

□

Theorem 6.

If R is a ring such that $\Gamma \left(R\right)$ is a complete graph and F a field with $\left|F\right|\ge 3$, then

$${\gamma }^o(\Gamma (F\times R))=\left|Z{\left(R\right)}^{*}\right|+min\left\{\left|U\left(R\right)\right|,|F^{*}|,2+⌊\frac{{\left|U\left(R\right)\right|-|Z\left(R\right)}^{*}|}{2}⌋+⌊\frac{|F^{*}|}{2}⌋\right\}.$$

Proof. 

Consider the set

$$A=\left\{\left|U\left(R\right)\right|,|F^{*}|,2+⌊\frac{{\left|U\left(R\right)\right|-|Z\left(R\right)}^{*}|}{2}⌋+⌊\frac{|F^{*}|}{2}⌋\right\}.$$

If $R={\mathbb{Z}}_2\times {\mathbb{Z}}_2$, then $minA=\left|U\right(R\left)\right|=1$, ${|Z\left(R\right)}^{*}|=2$ and the set $S=\left\{\right(0,0,1),(0,1,0),$$(0,1,1)\}$ is a ${\gamma }^o-$alliance.

If $R\ne {\mathbb{Z}}_2\times {\mathbb{Z}}_2$, then R is a local ring in which $xy=0$ for any $x,y\in Z\left(R\right)$.

If R is a field, ${|Z\left(R\right)}^{*}|=0$, $minA=min\left\{\right|U\left(R\right)|,|F^{*}\left|\right\}$ and, in this case, the result is simply Lemma 2.

In another case, the proof is completed using the following steps.

Step 1. Any vertex of $\left\{0\right\}\times Z{\left(R\right)}^{*}$ must belong to each ${\gamma }^o-$alliance.

Indeed, if $S\subseteq Z{(F\times R)}^{*}$ is a global offensive alliance and for some $x\in Z{\left(R\right)}^{*}$, $(0,x)\notin S$, then S must contain at least $⌊\frac{{|Z\left(R\right)}^{*}\left|\right(|F^{*}|+1)+|F^{*}|-1}{2}⌋+1$ of the neighbors of $(0,x)$, which are distributed among the sets $F^{*}\times \left\{0\right\}$, $\left\{0\right\}\times Z{\left(R\right)}^{*}$ and $F^{*}\times Z{\left(R\right)}^{*}$.

If $|S\cap (F^{*}\times Z{\left(R\right)}^{*}){|>|Z\left(R\right)}^{*}|$, then $S-(S\cap (F^{*}\times Z{\left(R\right)}^{*}))\cup (\left\{0\right\}\times Z{\left(R\right)}^{*})$ is a global offensive alliance containing fewer vertices than S does. Now, if $|S\cap (F^{*}\times Z{\left(R\right)}^{*}){|\le |Z\left(R\right)}^{*}|$, some vertex of $F^{*}\times Z{\left(R\right)}^{*}$ not found in S and therefore it must be

$$|S\cap (\left\{0\right\}\times Z{\left(R\right)}^{*})|\ge ⌊\frac{{|Z\left(R\right)}^{*}|}{2}⌋+1.$$

(2)

Moreover, in order for the global offensive alliance condition to be satisfied at the vertex $(0,x)$, the following inequality must also be satisfied:

$$|S\cap (F^{*}\times Z{\left(R\right)}^{*})|\ge ⌊\frac{{|Z\left(R\right)}^{*}|}{2}⌋+1+|S\cap (F^{*}\times \left\{0\right\})|.$$

(3)

Thus, by inequalities (2) and (3), we obtain

$$|(\left\{0\right\}\times Z{\left(R\right)}^{*})-(S\cap (\left\{0\right\}\times Z{\left(R\right)}^{*}))|\le ⌈\frac{{|Z\left(R\right)}^{*}|}{2}⌉-1<⌊\frac{{|Z\left(R\right)}^{*}|}{2}⌋+1+|S\cap (F^{*}\times \left\{0\right\})|.$$

Therefore, $S_1=(S-(S\cap (F^{*}\times Z{\left(R\right)}^{*})))\cup ((\left\{0\right\}\times Z{\left(R\right)}^{*})-S)$ is a global offensive alliance and $|S_1|=|(S-(S\cap (F^{*}\times Z{\left(R\right)}^{*})))|+|(\left\{0\right\}\times Z{\left(R\right)}^{*})-S|=|S\cap (F^{*}\times \left\{0\right\}){|+|Z\left(R\right)}^{*}|=|S\cap (F^{*}\times \left\{0\right\})|+|S\cap (\left\{0\right\}\times Z{\left(R\right)}^{*}){|+|\left\{0\right\}\times Z\left(R\right)}^{*}-S|<2⌊\frac{{|Z\left(R\right)}^{*}|}{2}⌋+2|S\cap (F^{*}\times \left\{0\right\})|+2\le |S|.$

Step 2. The inequality ${\gamma }^o(\Gamma (F\times R))\le \left|Z{\left(R\right)}^{*}\right|+minA$ holds.

If $B\subseteq \left\{0\right\}\times U\left(R\right)$ and $C\subseteq F^{*}\times \left\{0\right\}$ are subsets whose cardinal numbers are $⌊\frac{{\left|U\left(R\right)\right|-|Z\left(R\right)}^{*}|}{2}⌋+1$ and $⌊\frac{|F^{*}|}{2}⌋+1$, respectively, then the subsets $\left(\left\{0\right\}\times Z{\left(R\right)}^{*}\right)$$\cup B\cup C$, $\left(\left\{0\right\}\times Z{\left(R\right)}^{*}\right)\cup \left(F^{*}\times \left\{0\right\}\right)$ and $\left(\left\{0\right\}\times Z{\left(R\right)}^{*}\right)\cup \left(U\left(R\right)\times \left\{0\right\}\right)$ are global offensive alliances, with what is certainly ${\gamma }^o(\Gamma (F\times R))\le \left|Z{\left(R\right)}^{*}\right|+minA$.

Finally, if S is a ${\gamma }^o-$alliance of $\Gamma (F\times R)$, by Step 1, we know that S has the form $\left\{0\right\}\times Z{\left(R\right)}^{*}\cup A_1$.

Now, if $A_1\ne \left\{0\right\}\times U\left(R\right)$, $F^{*}\times \left\{0\right\}$, we have $(0,x)\in \left\{0\right\}\times U\left(R\right)-S$ and $(y,0)\in F^{*}\times \left\{0\right\}-S$. In order for the global offensive alliance condition to be met in these two vertices, the set S is required to contain at least $⌊\frac{{\left|U\left(R\right)\right|-|Z\left(R\right)}^{*}|}{2}⌋+1$ vertices of $\left\{0\right\}\times U\left(R\right)$ and at least $⌊\frac{|F^{*}|}{2}⌋+1$ vertices of $F^{*}\times \left\{0\right\}$. In this way,

$${\gamma }^o{(\Gamma (F\times R))\ge |Z\left(R\right)}^{*}|+2+⌊\frac{{\left|U\left(R\right)\right|-|Z\left(R\right)}^{*}|}{2}⌋+⌊\frac{|F^{*}|}{2}⌋\ge \left|Z{\left(R\right)}^{*}\right|+minA.$$

□

Figure 3 shows an example of Theorem 6, where F ≅ ${\mathbb{Z}}_3$, R ≅ ${\mathbb{Z}}_9$ and $\Gamma \left({\mathbb{Z}}_9\right)$ ≅ $K_2$; in this case, ${\gamma }^o(\Gamma ({\mathbb{Z}}_3\times {\mathbb{Z}}_9))=2+min\left\{6,2,5\right\}=4$.

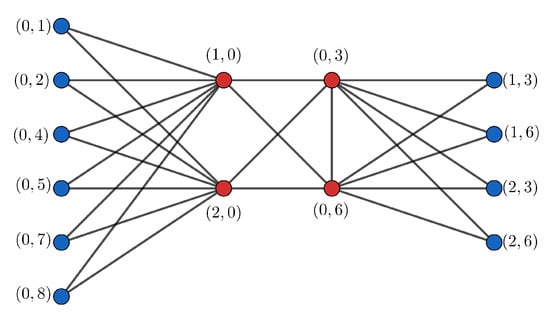
Figure 3. Diagram of the graph $\Gamma ({\mathbb{Z}}_3\times {\mathbb{Z}}_9$).

Theorem 7.

Let F and K be two fields with $\left|F\right|\ge 3$, then ${\gamma }^o(\Gamma ({\mathbb{Z}}_2\times K\times F))=1+$$min\left\{2|K^{*}|,2|F^{*}|,|F^{*}|+⌊\frac{|K^{*}|}{2}⌋+1,\left|K^{*}\right|+⌊\frac{|F^{*}|}{2}⌋+1\right\}$.

Proof. 

Since $|\left\{0\right\}\times K^{*}\times F^{*}|\ge 2$, the vertex $(1,0,0)$ is in each ${\gamma }^o-$alliance. In addition, if we consider the set

$$A=\left\{2|K^{*}|,2|F^{*}|,|F^{*}|+⌊\frac{|K^{*}|}{2}⌋+1,\left|K^{*}\right|+⌊\frac{|F^{*}|}{2}⌋+1\right\},$$

then there are global offensive alliances of cardinal $1+a$ for each $a\in A$. For example,

(i)

$\left\{(1,0,0)\right\}\cup (\left\{0\right\}\times K^{*}\times \left\{0\right\})\cup (\left\{1\right\}\times K^{*}\times \left\{0\right\})$,

(ii)

$\left\{(1,0,0)\right\}\cup (\left\{0\right\}\times \left\{0\right\}\times F^{*})\cup (\left\{1\right\}\times \left\{0\right\}\times F^{*})$,

(iii)

$\left\{(1,0,0)\right\}\cup (\left\{0\right\}\times \left\{0\right\}\times F^{*})\cup X$ (with $X\subseteq \left\{0\right\}\times K^{*}\times \left\{0\right\}$, $\left|X\right|=⌊\frac{|K^{*}|}{2}⌋+1$),

(iv)

$\left\{(1,0,0)\right\}\cup (\left\{0\right\}\times K^{*}\times \left\{0\right\})\cup Y$ (with $Y\subseteq \left\{0\right\}\times \left\{0\right\}\times F^{*}$, $\left|Y\right|=⌊\frac{|F^{*}|}{2}⌋+1$),

hence, ${\gamma }^o(\Gamma ({\mathbb{Z}}_2\times K\times F))\le 1+minA$.

Now, if S is a ${\gamma }^o-$alliance and there are vertices $(0,k,0)$, $(0,0,f)\notin S$ with $k\in K^{*}$ and $f\in F^{*}$, then $\left|S\right|\ge 1+|K^{*}|+|F^{*}|\ge 1+minA$ and we are done.

If $\left\{0\right\}\times K^{*}\times \left\{0\right\}\subseteq S$ y $(1,k,0)\notin S$ for some $k\in K^{*}$, then $\left|S\right|\ge 2+|K^{*}|+⌊\frac{|F^{*}|}{2}⌋\ge 1+minA$.Similarly, if $\left\{0\right\}\times \left\{0\right\}\times F^{*}\subseteq S$ and some $(1,0,f)\notin S$. □

Figure 4 shows an example of Theorem 7, where F ≅ ${\mathbb{F}}_4$ and K ≅ ${\mathbb{Z}}_3$; in this case, ${\gamma }^o(\Gamma ({\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{F}}_4))=1+min\left\{4,6,5,4\right\}=5$.

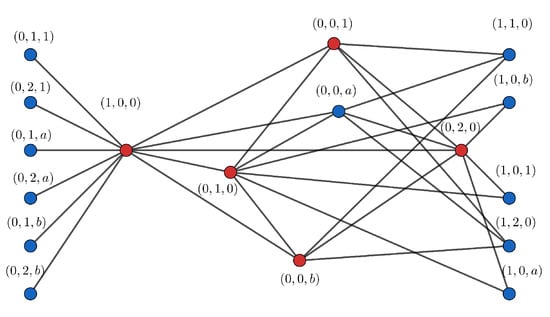
Figure 4. Diagram of the graph $\Gamma ({\mathbb{Z}}_2\times {\mathbb{Z}}_3\times {\mathbb{F}}_4$).

2.2. Rings with Small Global Offensive Alliance Number

Theorem 8.

Let R be a finite commutative ring, then ${\gamma }^o(\Gamma \left(R\right))=1$ if and only if R is isomorphic to any of the following rings ${\mathbb{Z}}_4$, ${\mathbb{Z}}_2\left[X\right]/\left(X^2\right)$, ${\mathbb{Z}}_9$, ${\mathbb{Z}}_3\left[X\right]/\left(X^2\right)$, ${\mathbb{Z}}_8$, ${\mathbb{Z}}_2\left[X\right]/\left(X^3\right),{\mathbb{Z}}_2\times F$ or ${\mathbb{Z}}_4\left[X\right]/(2X,X^2-2)$, where F is a field.

Proof. 

By [16] (Page 10), $\Gamma \left(R\right)$ is a star graph. Now, if $|\Gamma (R\left)\right|<4$, then $R\cong {\mathbb{Z}}_6$, ${\mathbb{Z}}_8$, ${\mathbb{Z}}_9$, ${\mathbb{Z}}_2\left[X\right]/\left(X^3\right)$, ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$ or ${\mathbb{Z}}_3\left[X\right]/\left(X^2\right)$ (see [23], Example 2.1). If $|\Gamma (R\left)\right|\ge 4$ by [23] (Theorem 2.13) $R\cong {\mathbb{Z}}_2\times F$, with F a finite field.

The converse is straightforward. □

A graph $\Gamma (V,E)$ is a 4-book if V is the union of subsets $X_1,X_2,\cdots ,X_r$ such that $3\le |X_i|\le 4$ and

• there exists $v_1,v_2\in V$, a pair of distinct vertices such that if $i\ne j$ then $X_i\cap X_j=\{v_1,v_2\}$,
• for $i\ne j$, there are no edges connecting vertices of $X_i-\{v_1,v_2\}$ with vertices of $X_j-\{v_1,v_2\}$,
• if $y\in V-\{v_1,v_2\}$, then it is adjacent to both $v_1$ and $v_2$.

Each one of these r-induced subgraphs $⟨X_i⟩$ is called a 4-book page of the $\Gamma$.

Proposition 3.

Let R be a finite commutative ring, then ${\gamma }^o(\Gamma \left(R\right))=2$ if and only if R is isomorphic to one of the following rings ${\mathbb{Z}}_3\times K$ (where K is a field), ${\mathbb{Z}}_2\times {\mathbb{Z}}_4$, ${\mathbb{Z}}_2\times {\mathbb{Z}}_2\left[X\right]/\left(X^2\right)$, ${\mathbb{Z}}_{16}$, ${\mathbb{Z}}_2\left[X\right]/\left(X^4\right)$, ${\mathbb{Z}}_4\left[X\right]/(2X,X^3-2)$, ${\mathbb{Z}}_4\left[X\right]/(X^2-2)$, ${\mathbb{Z}}_4\left[X\right]/(X^2+2X+2)$, ${\mathbb{F}}_4\left[X\right]/\left(X^2\right)$, ${\mathbb{Z}}_4\left[X\right]/(X^2+X+1)$, ${\mathbb{Z}}_2[X,Y]/{(X,Y)}^2$, ${\mathbb{Z}}_4\left[X\right]/{(2,X)}^2$, ${\mathbb{Z}}_{27}$, ${\mathbb{Z}}_3\left[X\right]/\left(X^3\right)$, ${\mathbb{Z}}_9\left[X\right]/(X^2-3,3X)$, ${\mathbb{Z}}_9\left[X\right]/(X^2-6,3X)$, ${\mathbb{Z}}_{25}$, ${\mathbb{Z}}_5\left[X\right]/\left(X^2\right)$.

Proof. 

By [16], ${\gamma }^o(\Gamma \left(R\right))=2$ if and only if $\Gamma \left(R\right)$ is a 4-book graph. However, such graphs are planar graphs; in [21] (Theorem 6.4), it is shown that there are only 44 types of rings whose zero-divisor graph is planar, of which the ones above are the only ones that meet the condition of being 4-book graphs. □

3. Conclusions

One of the main contributions of this work is to relate graph theory with commutative ring theory. In this paper, we propose the global offensive alliance number over the zero-divisor graph, which extends the study realized by Muthana and Mamouni in [26]. In the aforementioned work, the authors calculated the global defensive alliance number ${\gamma }_a(\Gamma \left(R\right))$ for some kinds of direct products of finite fields with finite local rings. In addition, they described a complete characterization of rings with ${\gamma }_a(\Gamma \left(R\right))=1$, or 2. In our work, we obtain similar results corresponding to the context of the global offensive alliances (see Theorems 6–8 and Proposition 3).

As far as other work is concerned, in [9,13,17], the authors studied global offensive alliances over specific families of graphs, such as cubic, trees, and Cartesian product graphs. Our work develops this subject within the family of zero-divisor graphs. The work [23] gave a characterization of the rings R in order for $\Gamma \left(R\right)$ to be a complete graph. In our work, Theorem 2 characterizes all those rings R with complete graph $\Gamma \left(R\right)$ in terms of the global offensive alliance number.

We conclude this paper by pointing out that the topic can be extended to the study of other types of alliances (e.g., strong global offensive alliances).