Incorporating Fuzziness in the Traditional Runge–Kutta Cash–Karp Method and Its Applications to Solve Autonomous and Non-Autonomous Fuzzy Differential Equations

Abstract

The study of the fuzzy differential equation is a topic that researchers are interested in these days. By modelling, this fuzzy differential equation can be used to resolve issues in the real world. However, finding an analytical solution to this fuzzy differential equation is challenging. Thus, this study aims to present the fuzziness in the traditional Runge–Kutta Cash–Karp of the fourth-order method to solve the first-order fuzzy differential equation. Later, this method is referred to as the fuzzy Runge–Kutta Cash–Karp of the fourth-order method. There are two types of fuzzy differential equations to be solved: autonomous and non-autonomous fuzzy differential equations. This fuzzy differential equation is divided into the (i) and (ii)–differentiability on the basis of the characterization theorem. The convergence analysis of the fuzzy Runge–Kutta Cash–Karp of the fourth-order method is also presented. By implementing the fuzzy Runge–Kutta Cash–Karp of the fourth-order method, the approximate solution is compared with the analytical and numerical solutions obtained from the fuzzy Runge–Kutta of the fourth-order method. The results demonstrated that the approximate solutions of the proposed method are accurate with an analytical solution, when compared with the solutions of the fuzzy Runge–Kutta of the fourth-order method.

1. Introduction

Physical models of real-world phenomena typically have considerable uncertainty and ambiguity, which can be attributed to a variety of causes. For the purpose of examining these issues, Zadeh introduced the fuzzy set theory in 1965 [1]. There are many disciplines in fuzzy sets, such as fuzzy topology, fuzzy arithmetic, fuzzy algebraic structures, fuzzy differential calculus, fuzzy geometry, fuzzy relational calculus, fuzzy databases, and fuzzy decision-making [2].

Many researchers attempted to apply the fuzzy set theory in the context of decision-making. A method of X fuzzy mathematics, also known as the analytical hierarchy process (AHP), was developed by Wang and Khadidos [3] and was applied in the basketball scoring strategy. The results showed that the proposed method is conceivable and credible in the scoring and analysis of basketball strategies. In [4], the authors used the fuzzy mathematics evaluation method to measure basketball players’ skill levels. The suggested approach can be used to assess basketball skill development and instruction, and it also serves as a general framework for enhancing players’ basketball skills. In 2021, a study was conducted on the usage of the eye movement method with the help of fractional order fuzzy differential equation (FDE) to maximise the effect of artistic images in artistic image migration [5]. The impact of the fuzzy mathematics simulation model on the growth of the martial arts industry in Wushu has been studied by Sun, Lv, Khadidos, and Kharabsheh [6]. According to the report, the martial arts market is still in its early stages of development, with a significant market potential and high benefits expectations. Based on the mathematical model of the fuzzy comprehensive evaluation of the differential equations, a study on the audio-visual family restoration of children with mental problems was undertaken [7].

In calculus, the study of the FDE is a topic that researchers are interested in these days [8]. For example, it produced a mathematical model for issues pertaining to hydraulic systems and population dynamics [9,10]. In 1972, Chang and Zadeh [11] pioneered the idea of fuzzy derivatives. The extension principle was then defined and developed by Dubois and Prade [12]. Next, Puri and Ralescu [13] applied the Hukuhara differentiability (H-differentiability) to the concept of fuzzy functions. Following that, Kaleva [14] and Seikkala [15] established some theorems for FDE using H-differentiability. Moreover, Friedman, Ma, and Kandel [16] presented the Friedman–Ming–Kandel derivative, a new approach to fuzzy derivatives, and compared it to previous approaches. Other than that, a historical survey of the FDE is carried out by Mazandarani and Xiu [17].

Research is now being carried out to find a solution to the fuzzy initial value problem (FIVP) and fuzzy boundary value problem (FBVP), both of which can be utilized to find solutions to real-world issues. However, due to the difficulty in finding their analytical solution, not all FIVP and FBVP could be solved precisely [18]. Therefore, reliable and efficient numerical techniques may be needed to handle the corresponding FDE.

The FDE has been studied and solved numerically using a variety of methods. Ma, Friedman, and Kandel [19] developed the Euler method to determine the pointwise convergence of approximate solutions to exact solutions. Meanwhile, Tapaswini, and Chakraverty [20] proposed a novel method, the improved Euler method (IEM). The authors considered two methods to solve both FIVP and FBVP in this study: max-min IEM and average IEM. The IEM performs better than the established approach and is discovered to be in good agreement. Moreover, Georgieva [21] presented the double fuzzy Sumudu transform to solve the partial Volterra fuzzy integro-differential equation with the convolution kernel under H-differentiability. In [22], You, Cheng, and Ma studied the stability of the fuzzy Euler method related to the FDE. The stabilities involved are the asymptotical stability, the mean square (MS) stability, the exponential stability and the A stability. The numerical examples were identified by comparing the effects of three fuzzy Euler schemes on the asymptotical and MS stabilities and examining the impact of $\alpha$ in a semi-implicit fuzzy Euler scheme on the MS stability.

Over the last few years, the Runge–Kutta (RK) method has received a lot of attention from researchers, and many researchers have proposed some RK modifications. By presenting new third and fourth-order numerical methods, Goeken and Johnson [23] proposed a higher derivative approximation of RK to solve the FDE. The RK of third and fourth-order methods were then introduced by Wu [24] by reducing the function of evaluations. Alternatively, Jayakumar, Maheskumar, and Kanagarajan [25] are interested in using the RK of the fifth-order method (RK5) to solve the FDE, and this method is compared with the IEM. It is evident that the RK5 performed better than the IEM because it has ordered five while the IEM only has ordered two. In addition, the fuzzy reduced Runge–Kutta of the fourth-order method (FRRK4) has been proposed to solve the hybrid FDE [26]. The hybrid FIVP is solved using the FRRK4 and, compared with the analytical solution, the RK of the fourth-order method (RK4), and the Euler method. The findings indicated that the FRRK4 method’s solution is quite close to an analytical solution. Moreover, the proposed method has undergone fewer function evaluations, demonstrating that it is more effective than the traditional RK method. Apart from that, Ramli, Ahmad, Din, and Salleh [27] proposed a developed Runge–Kutta of the fourth-order method (DRK4) to improve the solution of FDE. The authors presented the new approach and compared the results to the RK4. The discovery demonstrates that the proposed method is close to the analytical solution.

Likewise, Kanagarajan and Suresh [28] proposed the fuzzy Runge–Kutta of the fourth-order method (FRK4) to solve the FDE under a generalized differentiability. The proposed method provides a superior solution when compared to the Euler method. Ahmadian, Salahshour, Chan, and Baleanu [29] introduced an extended Runge–Kutta of the fourth-order method (ERK4), which the authors used to solve the autonomous and non-autonomous fuzzy systems. The method is compared to the RK4, showing that the ERK4 produces better results because it requires only three function evaluations, whereas the RK4 requires four function evaluations. In 2019, Rajkumar and Rubanraj [30] introduced a Runge–Kutta of the seventh-order method (RK7) to solve the FIVP. When this proposed method was compared to Euler’s and the RK4 methods, it was discovered that the RK7 provided a better solution. Majid, Rabiei, Hamid, and Ismail [31] proposed a new method, namely the fuzzy general linear method (FGL), to solve the fuzzy Volterra-integro differential equation (FVIDE). This method is combined with Simpson’s method and Lagrange’s interpolation polynomial, and the numerical examples are performed. To test the efficiency of the proposed method, the solutions of the FVIDE using the FGL are compared with the Homotopy perturbation method and the Runge–Kutta of the third-order method (RK3). It demonstrated that the proposed method provides an accurate result with an analytical solution.

Based on the earlier investigations, the proposed numerical methods to solve the FDE were discovered to be extensions of the traditional numerical methods. The researchers compared them to other numerical methods to demonstrate their efficacy. According to our observations, more researchers paid attention to the non-autonomous FDE than the autonomous FDE. In light of the current trend in this area, we concentrated on the creation of a novel numerical technique termed fuzzy Runge–Kutta Cash–Karp of the fourth-order method (FRKCK4) to solve both autonomous and non-autonomous FDEs. The major goal is to provide more precise instructions for creating sophisticated algorithms. To the best of our knowledge, this is the first time that the traditional Runge–Kutta Cash–Karp of the fourth-order method (RKCK4) is presented in a fuzzy setting. The goal of this paper is to solve the autonomous and non-autonomous FDEs using the FRKCK4. This paper is set up as follows: Section 2 goes over the definitions, and Section 3 goes over the methods, which consist of the characterization theorem for the FDEs and the traditional RKCK4. Furthermore, the proposed model and numerical simulations are discussed in Section 4 and Section 5. Tables and graphs will be used to present a brief summary of our findings. Meanwhile, Section 6 presents the advantages of the proposed model. We present our findings’ conclusions at the end of this paper, and future work is suggested.

2. Definitions

This section reviews a few definitions and theorems adopted from [32,33,34,35,36,37]. First, we denote the collection of all real numbers and fuzzy numbers as $ℝ$ and $F(ℝ),$ respectively.

Definition 1

[32]. A fuzzy number is a mapping $S:ℝ\to \left[0, 1\right]$ with the following properties:

(i)

$S$ is upper semi-continuous,

(ii)

$S$ is a fuzzy convex, i.e.,

$S\left(\lambda u+\left(1-\lambda \right)v\right)\ge \min \left\{S\left(u\right), S\left(v\right)\right\}$ for all $u, v\in ℝ, \lambda \in \left[0, 1\right]$,

(iii)

$S$ is normal, i.e., $\exists u_0\in ℝ$ for which $S\left(u_0\right)=1$,

(iv)

supp $S=\left\{\left.u\in ℝ \right| S\left(u\right)>0\right\}$ is the support of $S$, and its closure $\mathrm{cl}\left(\mathrm{supp} S\right)$ is compact.

Definition 2

[33]. A fuzzy number $S$ is completely determined by any pair $S=\left(\underset{¯}{s}, \overline{s}\right)$ of functions $\left[\underset{¯}{s}, \overline{s}\right]:\left[0, 1\right]\to ℝ$, which define the end–points of the $\alpha$- cuts and satisfy the following conditions:

• $\underset{¯}{s}:\alpha \to {\underset{¯}{s}}_{\alpha }\in ℝ$ is bounded monotonic increasing where the left–continuous $\forall \alpha \in (0,1]$ and right–continuous for $\alpha =0,$
• $\overline{s}:\alpha \to {\overline{s}}_{\alpha }\in ℝ$ is bounded monotonic decreasing where the left–continuous $\forall \alpha \in (0,1]$ and right–continuous for $\alpha =0,$
• ${\underset{¯}{s}}_{\alpha }\le {\overline{s}}_{\alpha }, \forall \alpha \in \left[0,1\right].$

Definition 3

[34]. The distance $D\left(S,T\right)$ between two fuzzy numbers $S$ and $T$ is defined as:

$$D\left(S,T\right)-\underset{\alpha \in \left[0,1\right]}{\sup } d_H\left({\left[S\right]}_{\alpha },{\left[T\right]}_{\alpha }\right),$$

where

$$d_H\left({\left[S\right]}_{\alpha },{\left[T\right]}_{\alpha }\right)=\max \left\{\left|s_1\left(\alpha \right)-t_1\left(\alpha \right)\right|,\left|s_2\left(\alpha \right)-t_2\left(\alpha \right)\right|\right\}$$

is the Hausdorff distance between ${\left[S\right]}_{\alpha }$ and ${\left[T\right]}_{\alpha }.$

Definition 4

[13]. Let $S,T\in F(ℝ).$ If there exits $U\in F(ℝ)$ such that $S=T+U,$ then $U$ is called the Hukuhara difference of $S$ and $T$ denoted by $S{-}_H T.$

Definition 5

[35]. A fuzzy function $G:\left[p,q\right]\to F\left(ℝ\right)$ is said to be continuous at $t_0\in \left[p,q\right]$ if for each $\epsilon >0,$ there is $\delta >0$ such that $D\left(G\left(t\right),G\left(t_0\right)\right)<\epsilon ,$ whenever $t\in \left[p,q\right]$ and $\left|t-t_0\right|<\delta .$ We say $G$ is continuous on $\left[p,q\right]$ if $G$ is continuous at each $t_0\in \left[p,q\right].$

Next, the fuzzy derivative of the fuzzy function is recalled.

Definition 6

[36]. Let $G:\left[p,q\right]\to F(ℝ)$ and fixed $t_0\in \left[p,q\right].$ It can be referred to as follows:

• $G$ is (i)-differentiable at $t_0$ if there exists an element $G^{\prime }\left(t_0\right)\in F(ℝ)$ such that, for all $\Delta t>0$ sufficiently near 0, there are $G \left(t_0+\Delta t\right){-}_H G \left(t_0\right) \mathrm{and} G \left(t_0\right){-}_H G \left(t_0-\Delta t\right)$ and the limit (in the metric $D$) is given by

  $$\underset{\Delta t\to 0^{+}}{\lim }\frac{G\left(t_0+\Delta t\right){-}_H G\left(t_0\right)}{\Delta t}=\underset{\Delta t\to 0^{+}}{\lim }\frac{G\left(t_0\right){-}_H G\left(t_0-\Delta t\right)}{\Delta t}=G^{\prime }\left(t_0\right)$$
• $G$ is (ii)-differentiable at $t_0$ if there exists an element $G^{\prime }\left(t_0\right)\in F(ℝ)$ such that, for all $\Delta t>0$ sufficiently near 0, there are $G \left(t_0\right){-}_H G \left(t_0+\Delta t\right) \mathrm{and} G \left(t_0-\Delta t\right){-}_H G \left(t_0\right)$ and the limit (in the metric $D$) is given by

  $$\underset{\Delta t\to 0^{+}}{\lim }\frac{G\left(t_0+\Delta t\right){-}_H G\left(t_0\right)}{-\Delta t}=\underset{\Delta t\to 0^{+}}{\lim }\frac{G\left(t_0\right){-}_H G\left(t_0-\Delta t\right)}{-\Delta t}= G^{\prime }\left(t_0\right)$$

From Definition 6, Chalco-Cano [37] obtained the following theorem.

Theorem 1.

Let $G:\left[p,q\right]\to F(ℝ)$be a fuzzy function, where $\left[G\left(t,\alpha \right)\right]= \left[\underset{¯}{g}\left(t,\alpha \right), \overline{g}\left(t,\alpha \right)\right]$for each $\alpha \in \left[0, 1\right]$.

• If $G$ is (i)-differentiable, then $\underset{¯}{g}\left(t,\alpha \right)$ and $\overline{g}\left(t,\alpha \right)$ are differentiable functions and $\left[G^{\prime }(t,\alpha )\right] = \left[{\underset{¯}{g}}^{\prime }\left(t,\alpha \right), {\overline{g}}^{\prime }\left(t,\alpha \right)\right]$.
• If $G$ is (ii)-differentiable, then $\underset{¯}{g}\left(t,\alpha \right)$ and $\overline{g}\left(t,\alpha \right)$ are differentiable functions and $\left[G^{\prime }(t,\alpha )\right] = \left[{\overline{g}}^{\prime }\left(t,\alpha \right), {\underset{¯}{g}}^{\prime }\left(t,\alpha \right)\right].$

3. Methods

This section starts with the characterization theorem for the FDE, followed by the steps to solve the autonomous and non-autonomous differential equations using the traditional RKCK4.

3.1. Characterization Theorem for the Fuzzy Differential Equations

Using Theorems 2 and 3 below, the authors in [35,36,37] have described a procedure for transforming an FDE into an ordinary differential equation (ODE) system.

Theorem 2

[38]. Let $G:\left(p,q\right)\to F(ℝ)$ be a Hukuhara differentiable and denote $\left[G\left(t, \alpha \right)\right] = \left[\underset{¯}{g}\left(t, \alpha \right), \overline{g}\left(t, \alpha \right)\right].$ Then, the boundary functions $\underset{¯}{g}\left(t, \alpha \right)$ and $\overline{g}\left(t, \alpha \right)$ are differentiable such that

$$\left[G^{\prime }\left(t, \alpha \right)\right] = \left[{\underset{¯}{g}}^{\prime }\left(t, \alpha \right), {\overline{g}}^{\prime }\left(t, \alpha \right)\right], \alpha \in \left[0, 1\right].$$

Let the FIVP as follows:

$$\left\{\begin{array}{l}{Y}^{\prime }\left(t\right) = G\left(t, Y\left(t\right)\right), t\in \left[p,q\right],\\ Y\left(t_0\right) = Y_0,\end{array}\right.$$

(1)

where $G:\left[p,q\right] \times F(ℝ)\to F(ℝ)$ and $Y_0 \in F(ℝ).$ Using Theorem 1, Equation (1) can be translated into systems of ODE as shown below.

• Type I

$$\left\{\begin{array}{l}{\underset{¯}{y}}^{\prime }\left(t, \alpha \right) = \underset{¯}{g}\left(t, \underset{¯}{y}\left(t, \alpha \right), \overline{y}\left(t, \alpha \right)\right), \underset{¯}{y}\left(t_0, \alpha \right) = {\underset{¯}{y}}_0, \\ {\overline{y}}^{\prime }\left(t, \alpha \right) = \overline{g}\left(t, \underset{¯}{y}\left(t, \alpha \right), \overline{y}\left(t, \alpha \right)\right), \overline{y}\left(t_0, \alpha \right) = {\overline{y}}_0. \end{array}\right.$$

(2)

• Type II

$$\left\{\begin{array}{l}{\underset{¯}{y}}^{\prime }\left(t, \alpha \right) = \overline{g}\left(t, \underset{¯}{y}\left(t, \alpha \right), \overline{y}\left(t, \alpha \right)\right), \underset{¯}{y}\left(t_0, \alpha \right) = {\underset{¯}{y}}_0, \\ {\overline{y}}^{\prime }\left(t, \alpha \right) = \underset{¯}{g}\left(t, \underset{¯}{y}\left(t, \alpha \right), \overline{y}\left(t, \alpha \right)\right), \overline{y}\left(t_0, \alpha \right) = {\overline{y}}_0, \end{array}\right.$$

(3)

where

$$\begin{array}{l}\underset{¯}{g} = \min \left\{\left.G\left(t,u\right)\right|u\in \left[\underset{¯}{y}\left(t,\alpha \right),\overline{y}\left(t,\alpha \right)\right]\right\},\\ \overline{g} = \max \left\{\left.G\left(t,u\right)\right|u\in \left[\underset{¯}{y}\left(t,\alpha \right),\overline{y}\left(t,\alpha \right)\right]\right\}.\end{array}$$

Theorem 3

[38]. Let’s consider the FIVP in Equation (1), where $G:\left[p,q\right]\times F(ℝ)\to F(ℝ)$ is such that

• ${\left[G \left(t,y\right)\right]}_{\alpha }=\left[{\underset{¯}{g}}_{\alpha }\left(t,\underset{¯}{y}\left(t,\alpha \right),\overline{y}\left(t,\alpha \right)\right),{\overline{g}}_{\alpha }\left(t,\underset{¯}{y}\left(t,\alpha \right), \overline{y}\left(t,\alpha \right)\right)\right],$
• ${\underset{¯}{g}}_{\alpha }$ and ${\overline{g}}_{\alpha }$ are equicontinuous (i.e., for any $\epsilon >0$ and for any $\left(t,x,y\right)\in \left[p,q\right]\times {ℝ}^2$, the $\left|G_{\alpha }\left(t,x,y\right)-G_{\alpha }\left(t_1,x_1,y_1\right)\right|<\epsilon ,\forall \alpha \in \left[0, 1\right],$ whenever $‖\left(t_1,x_1,y_1\right)-\left(t,x,y\right)‖<\delta$ and uniformly bounded on any bounded set),
• there exist $K > 0$ such that $\left|G_{\alpha }\left(t, x_1, y_1\right) - G_{\alpha }\left(t, x_2, y_2\right)\right| \le L \max$$\left\{\left|x - u\right|, \left|y - v\right|\right\}, \forall \alpha \in \left[0, 1\right].$

Then, the relationship between the FIVP in Equation (1) and the systems of the ODEs in Equations (2) and (3) for the (i) and (ii)–differentiability are equivalent.

3.2. The Traditional Runge–Kutta Cash–Karp of the Fourth-Order Method

This section described the traditional RKCK4 to solve the autonomous and non-autonomous differential equations. First, consider the following autonomous differential equation:

$$\left\{\begin{array}{l}{y}^{\prime }(t) = g\left(y\left(t\right)\right), t \in \left[p,q\right], \\ y\left(t_0\right) = y_0. \end{array}\right.$$

(4)

In order to approximate Equation (4), the traditional RKCK4 is suggested as follows:

$$y_{i+1} = y_i + \Delta t \left(\frac{2825}{27648} k_1 + \frac{18575}{48384}{k}_3 + \frac{13525}{55296} k_4 + \frac{277}{14336}{k}_5 + \frac{1}{4}{k}_6\right) ,$$

(5)

where

$$\begin{array}{l}{k}_1 = g \left(y_i\right),\\ k_2 = g \left(y_i + \frac{1}{5}\Delta t k_1\right),\\ k_3 = g \left(y_i + \frac{3}{40}\Delta t k_1 + \frac{9}{40}\Delta t k_2\right),\\ k_4 = g\left(y_i + \frac{3}{10}\Delta t k_1 - \frac{9}{10}\Delta t k_2 + \frac{6}{5}\Delta t k_3\right),\\ k_5 = g \left(y_i - \frac{11}{54}\Delta t k_1 + \frac{5}{2}\Delta t k_2 - \frac{70}{27}\Delta t k_3 + \frac{35}{27}\Delta t k_4\right),\\ k_6 = g\left(y_i + \frac{1631}{55296}\Delta t k_1 + \frac{175}{512}\Delta t k_2 + \frac{575}{13824}\Delta t k_3 + \frac{44275}{110592}\Delta t k_4 + \frac{253}{4096}\Delta t k_5\right).\end{array}$$

The local truncation error (LTE) of the RKCK4 for the autonomous differential equation is given by:

$$T\left(t,\Delta t\right) = \frac{{\left(\Delta t\right)}^5}{120}\left(11{(g_y)}^2{g}_{yy}{g}^2 + {(g_{yy})}^2{g}^3 + 7g_y{g}_{yyy}{g}^3 + {(g_y)}^{4}g + g_{yyyy}{g}^4\right).$$

Next, we consider the following non-autonomous differential equation:

$$\left\{\begin{array}{l}{y}^{\prime }\left(t\right) = g \left(t, y\left(t\right)\right), t \in \left[p,q\right],\\ y \left(t_0\right) = y_0.\end{array}\right.$$

(6)

The RKCK4 for Equation (6) is:

$$y_{i+1} = y_i + \Delta t \left(\frac{2825}{27648} k_1 + \frac{18575}{48384}{k}_3 + \frac{13525}{55296} k_4 + \frac{277}{14336}{k}_5 + \frac{1}{4}{k}_6\right) ,$$

(7)

where

$$\begin{array}{l}{k}_1 = g \left(t_i, y_i\right),\\ k_2 = g \left(t_i + \frac{1}{5}\Delta t, y_i + \frac{1}{5}\Delta t k_1\right),\\ k_3 = g \left(t_i + \frac{3}{10}\Delta t, y_i + \frac{3}{40}\Delta t{k}_1 + \frac{9}{40}\Delta t{k}_2\right),\\ k_4 = g\left(t_i + \frac{3}{5}\Delta t, y_i + \frac{3}{10}\Delta t{k}_1 - \frac{9}{10}\Delta t{k}_2 + \frac{6}{5}\Delta t{k}_3\right),\\ k_5 = g \left(t_i + \Delta t, y_i - \frac{11}{54}\Delta t{k}_1 + \frac{5}{2}\Delta t{k}_2 - \frac{70}{27}\Delta t{k}_3 + \frac{35}{27}\Delta t{k}_4\right),\\ k_6 = g(t_i + \frac{7}{8}\Delta t, y_i + \frac{1631}{55296}\Delta t{k}_1 + \frac{175}{512}\Delta t{k}_2 + \frac{575}{13824}\Delta t{k}_3 + \frac{44275}{110592}\Delta t{k}_4 +\\ \frac{253}{4096}\Delta t{k}_5).\end{array}$$

The LTE of RKCK4 for the non-autonomous differential equation is:

$$\begin{array}{l} T\left(t,\Delta t\right) = \frac{{\left(\Delta t\right)}^5}{120}(g_{tttt} + 4g_{ttty}g + 6g_t{g}_{tty} + 9g_y{g}_{tty}g + 6g_{ttyy}{g}^2 + 4g_{ty}{g}_{tt} + 8{(g_{ty})}^{2}g +\\ 12g_t{g}_{tyy}g + 7g_y{g}_t{g}_{ty} + 15g_y{g}_{tyy}{g}^2 + 9{(g_y)}^2{g}_{ty}g + 12g_{ty}{g}_{yy}{g}^2 + 3g_{tyyy}{g}^3 +\\ 13g_t{g}_y{g}_{yy}g + 11{(g_y)}^2{g}_{yy}{g}^2 + {(g_{yy})}^2{g}^3 + 7g_y{g}_{yyy}{g}^3 + 3{(g_t)}^2{g}_{yy} +\\ 4g_{tt}{g}_{yy}g + 6g_t{g}_{yyy}{g}^2 + g_y{g}_{ttt} + {(g_y)}^2{g}_{tt} + g_t{(g_y)}^3 + {(g_y)}^{4}g + g_{tyyy}{g}^3 +\\ g_{yyyy}{g}^4). \end{array}$$

The techniques discussed in this section are incorporated with the fuzzy set theory and explained in the following section.

4. Proposed Model

The fuzzification process of the traditional RKCK4 for the autonomous and non-autonomous fuzzy differential equations is discussed in the following subsections.

4.1. Autonomous Fuzzy Differential Equation

We consider the autonomous FDE as:

$$\left\{\begin{array}{l}{Y}^{\prime }\left(t\right) = G\left(Y\left(t\right)\right), t\in \left[p,q\right],\\ Y\left(t_0\right) = Y_0.\end{array}\right.$$

(8)

From Theorem 1, Equation (8) is transformed into the system of autonomous FDEs by splitting into Types 1 and 2, respectively.

(i)

Type 1

$$\left\{\begin{array}{l}{\underset{¯}{y}}^{\prime }\left(t, \alpha \right) = \underset{¯}{g}\left(\underset{¯}{y}\left(t, \alpha \right), \overline{y}\left(t, \alpha \right)\right), \underset{¯}{y}\left(t_0, \alpha \right) = {\underset{¯}{y}}_0, \\ {\overline{y}}^{\prime }\left(t, \alpha \right) = \overline{g}\left(\underset{¯}{y}\left(t, \alpha \right), \overline{y}\left(t, \alpha \right)\right), \overline{y}\left(t_0, \alpha \right) = {\overline{y}}_0. \end{array}\right.$$

(9)

Based on Equation (9), the approximate solution can be referred to as:

$$\begin{array}{l}\underset{\_}{y} \left(t_{i+1},\alpha \right) = \underset{\_}{y} \left(t_i,\alpha \right)+\Delta t (\frac{2825}{27648} {\underset{\_}{k}}_1 \left(t_i, \alpha \right)+\frac{18575}{48384} {\underset{\_}{k}}_3 \left(t_i, \alpha \right)+\frac{13525}{55296} {\underset{\_}{k}}_4 \left(t_i, \alpha \right)+\\ \frac{277}{14336} {\underset{\_}{k}}_5 \left(t_i, \alpha \right)+ \frac{1}{4} {\underset{\_}{k}}_6 \left(t_i, \alpha \right)) ,\\ \overline{y} \left(t_{i+1},\alpha \right) = \overline{y} \left(t_i,\alpha \right)+\Delta t (\frac{2825}{27648} {\overline{k}}_1 \left(t_i, \alpha \right)+\frac{18575}{48384} {\overline{k}}_3 \left(t_i, \alpha \right)+\frac{13525}{55296} {\overline{k}}_4 \left(t_i, \alpha \right)+\\ \frac{277}{14336} {\overline{k}}_5 \left(t_i, \alpha \right) +\frac{1}{4} {\overline{k}}_6 \left(t_i, \alpha \right)),\end{array}$$

where

$$\begin{array}{l}{\underset{¯}{k}}_1\left(t_i, \alpha \right) = \underset{¯}{g}\left(\underset{¯}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right),\\ {\overline{k}}_1\left(t_i, \alpha \right) = \overline{g}\left(\underset{¯}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right),\end{array}$$

$$\begin{array}{l}{\underset{\_}{k}}_2\left(t_i, \alpha \right) = \underset{\_}{g} \left(\underset{\_}{y}\left(t_i, \alpha \right) + \frac{1}{5}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \frac{1}{5}\Delta t{\overline{k}}_1\left(t_i, \alpha \right)\right),\\ {\overline{k}}_2\left(t_i, \alpha \right) = \overline{g} \left(\underset{\_}{y}\left(t_i, \alpha \right) + \frac{1}{5}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \frac{1}{5}\Delta t{\overline{k}}_1\left(t_i, \alpha \right)\right),\\ {\underset{\_}{k}}_3\left(t_i, \alpha \right) = \underset{\_}{g} (\underset{\_}{y}\left(t_i, \alpha \right) + \frac{3}{40}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{9}{40}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \frac{3}{40}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) +\\ \frac{9}{40}\Delta t{\overline{k}}_2\left(t_i, \alpha \right)),\\ {\overline{k}}_3\left(t_i, \alpha \right) = \overline{g} (\underset{\_}{y}\left(t_i, \alpha \right) + \frac{3}{40}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{9}{40}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \frac{3}{40}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) +\\ \frac{9}{40}\Delta t{\overline{k}}_2\left(t_i, \alpha \right)),\\ {\underset{\_}{k}}_4\left(t_i, \alpha \right) = \underset{\_}{g} (\underset{\_}{y}\left(t_i, \alpha \right) + \frac{3}{10}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) - \frac{9}{10}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) + \frac{6}{5}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) +\\ \frac{3}{10}\Delta t{\overline{\underset{\_}{k}}}_1\left(t_i, \alpha \right) - \frac{9}{10}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) + \frac{6}{5}\Delta t{\overline{k}}_3\left(t_i, \alpha \right)),\\ {\overline{k}}_4\left(t_i, \alpha \right) = \overline{g} (\underset{\_}{y}\left(t_i, \alpha \right) + \frac{3}{10}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) - \frac{9}{10}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) + \frac{6}{5}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) +\\ \frac{3}{10}\Delta t{\overline{\underset{\_}{k}}}_1\left(t_i, \alpha \right) - \frac{9}{10}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) + \frac{6}{5}\Delta t{\overline{k}}_3\left(t_i, \alpha \right)),\\ {\underset{\_}{k}}_5\left(t_i, \alpha \right) = \underset{\_}{g} (\underset{\_}{y}\left(t_i, \alpha \right) - \frac{11}{54}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{5}{2}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) - \frac{70}{27}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right) + \\ \frac{35}{27}\Delta t{\underset{\_}{k}}_4\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) - \frac{11}{54}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) + \frac{5}{2}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) - \\ \frac{70}{27}\Delta t{\overline{k}}_3\left(t_i, \alpha \right) + \frac{35}{27}\Delta t{\overline{k}}_4\left(t_i, \alpha \right)),\\ {\overline{k}}_5\left(t_i, \alpha \right) = \overline{g} (\underset{\_}{y}\left(t_i, \alpha \right) - \frac{11}{54}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{5}{2}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) - \frac{70}{27}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right) + \\ \frac{35}{27}\Delta t{\underset{\_}{k}}_4\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) - \frac{11}{54}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) + \frac{5}{2}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) - \\ \frac{70}{27}\Delta t{\overline{k}}_3\left(t_i, \alpha \right) + \frac{35}{27}\Delta t{\overline{k}}_4\left(t_i, \alpha \right)),\\ {\underset{\_}{k}}_6\left(t_i, \alpha \right) = \underset{\_}{g} (\underset{\_}{y}\left(t_i, \alpha \right) + \frac{1631}{55296}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{175}{512}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) + \frac{575}{13824}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right) +\\ \frac{44275}{110592}\Delta t{\underset{\_}{k}}_4\left(t_i, \alpha \right) + \frac{253}{4096}\Delta t{\underset{\_}{k}}_5\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \frac{1631}{55296}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) +\\ \frac{175}{512}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) + \frac{575}{13824}\Delta t{\overline{k}}_3\left(t_i, \alpha \right) + \frac{44275}{110592}\Delta t{\overline{k}}_4\left(t_i, \alpha \right) + \\ \frac{253}{4096}\Delta t{\overline{k}}_5\left(t_i, \alpha \right)),\\ {\overline{k}}_6\left(t_i, \alpha \right) = \overline{g} (\underset{\_}{y}\left(t_i, \alpha \right) + \frac{1631}{55296}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{175}{512}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) + \frac{575}{13824}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right) +\\ \frac{44275}{110592}\Delta t{\underset{\_}{k}}_4\left(t_i, \alpha \right) + \frac{253}{4096}\Delta t{\underset{\_}{k}}_5\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \frac{1631}{55296}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) +\\ \frac{175}{512}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) + \frac{575}{13824}\Delta t{\overline{k}}_3\left(t_i, \alpha \right) + \frac{44275}{110592}\Delta t{\overline{k}}_4\left(t_i, \alpha \right) + \\ \frac{253}{4096}\Delta t{\overline{k}}_5\left(t_i, \alpha \right)).\end{array}$$

(ii)

Type 2

$$\left\{\begin{array}{l}{\underset{¯}{y}}^{\prime }\left(t, \alpha \right) = \overline{g}\left(\underset{¯}{y}\left(t, \alpha \right), \overline{y}\left(t, \alpha \right)\right), \underset{¯}{y}\left(t_0, \alpha \right) = {\underset{¯}{y}}_0, \\ {\overline{y}}^{\prime }\left(t, \alpha \right) = \underset{¯}{g}\left(\underset{¯}{y}\left(t, \alpha \right), \overline{y}\left(t, \alpha \right)\right), \overline{y}\left(t_0, \alpha \right) = {\overline{y}}_0. \end{array}\right.$$

(10)

The approximate solution for Equation (10) is represented as:

$$\begin{array}{l}\underset{\_}{y} \left(t_{i+1},\alpha \right)=\underset{\_}{y} \left(t_i,\alpha \right)+\Delta t (\frac{2825}{27648} {\underset{\_}{k}}_1 \left(t_i, \alpha \right)+\frac{18575}{48384} {\underset{\_}{k}}_3 \left(t_i, \alpha \right)+\frac{13525}{55296} {\underset{\_}{k}}_4 \left(t_i, \alpha \right)+\\ \frac{277}{14336} {\underset{\_}{k}}_5 \left(t_i, \alpha \right)+ \frac{1}{4} {\underset{\_}{k}}_6 \left(t_i, \alpha \right)) ,\\ \overline{y} \left(t_{i+1},\alpha \right)=\overline{y} \left(t_i,\alpha \right)+\Delta t (\frac{2825}{27648} {\overline{k}}_1 \left(t_i, \alpha \right)+\frac{18575}{48384} {\overline{k}}_3 \left(t_i, \alpha \right)+\frac{13525}{55296} {\overline{k}}_4 \left(t_i, \alpha \right)+\\ \frac{277}{14336} {\overline{k}}_5 \left(t_i, \alpha \right) +\frac{1}{4} {\overline{k}}_6 \left(t_i, \alpha \right)),\end{array}$$

where

$$\begin{array}{l}{\underset{\_}{k}}_1\left(t_i, \alpha \right) = \overline{g}\left(\underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right),\\ {\overline{k}}_1\left(t_i, \alpha \right) = \underset{\_}{g}\left(\underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right),\\ {\underset{\_}{k}}_2\left(t_i, \alpha \right) = \overline{g} \left(\underset{\_}{y}\left(t_i, \alpha \right) + \frac{1}{5}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \frac{1}{5}\Delta t{\overline{k}}_1\left(t_i, \alpha \right)\right),\\ {\overline{k}}_2\left(t_i, \alpha \right) = \underset{\_}{g} \left(\underset{\_}{y}\left(t_i, \alpha \right) + \frac{1}{5}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \frac{1}{5}\Delta t{\overline{k}}_1\left(t_i, \alpha \right)\right),\\ {\underset{\_}{k}}_3\left(t_i, \alpha \right) = \overline{g} (\underset{\_}{y}\left(t_i, \alpha \right) + \frac{3}{40}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{9}{40}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \frac{3}{40}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) +\\ \frac{9}{40}\Delta t{\overline{k}}_2\left(t_i, \alpha \right)),\\ {\overline{k}}_3\left(t_i, \alpha \right) = \underset{\_}{g} (\underset{\_}{y}\left(t_i, \alpha \right) + \frac{3}{40}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{9}{40}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \frac{3}{40}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) +\\ \frac{9}{40}\Delta t{\overline{k}}_2\left(t_i, \alpha \right)),\\ {\underset{\_}{k}}_4\left(t_i, \alpha \right) = \overline{g} (\underset{\_}{y}\left(t_i, \alpha \right) + \frac{3}{10}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) - \frac{9}{10}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) + \frac{6}{5}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) +\\ \frac{3}{10}\Delta t{\overline{\underset{\_}{k}}}_1\left(t_i, \alpha \right) - \frac{9}{10}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) + \frac{6}{5}\Delta t{\overline{k}}_3\left(t_i, \alpha \right)),\\ {\overline{k}}_4\left(t_i, \alpha \right) = \underset{\_}{g} (\underset{\_}{y}\left(t_i, \alpha \right) + \frac{3}{10}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) - \frac{9}{10}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) + \frac{6}{5}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) +\\ \frac{3}{10}\Delta t{\overline{\underset{\_}{k}}}_1\left(t_i, \alpha \right) - \frac{9}{10}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) + \frac{6}{5}\Delta t{\overline{k}}_3\left(t_i, \alpha \right)),\\ {\underset{\_}{k}}_5\left(t_i, \alpha \right) = \overline{g} (\underset{\_}{y}\left(t_i, \alpha \right) - \frac{11}{54}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{5}{2}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) - \frac{70}{27}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right) + \\ \frac{35}{27}\Delta t{\underset{\_}{k}}_4\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) - \frac{11}{54}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) + \frac{5}{2}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) - \\ \frac{70}{27}\Delta t{\overline{k}}_3\left(t_i, \alpha \right) + \frac{35}{27}\Delta t{\overline{k}}_4\left(t_i, \alpha \right)),\end{array}$$

$$\begin{array}{l}{\overline{k}}_5\left(t_i, \alpha \right) = \underset{\_}{g} (\underset{\_}{y}\left(t_i, \alpha \right) - \frac{11}{54}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{5}{2}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) - \frac{70}{27}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right) + \\ \frac{35}{27}\Delta t{\underset{\_}{k}}_4\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) - \frac{11}{54}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) + \frac{5}{2}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) - \\ \frac{70}{27}\Delta t{\overline{k}}_3\left(t_i, \alpha \right) + \frac{35}{27}\Delta t{\overline{k}}_4\left(t_i, \alpha \right)),\\ {\underset{\_}{k}}_6\left(t_i, \alpha \right) = \overline{g} (\underset{\_}{y}\left(t_i, \alpha \right) + \frac{1631}{55296}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{175}{512}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) + \frac{575}{13824}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right) +\\ \frac{44275}{110592}\Delta t{\underset{\_}{k}}_4\left(t_i, \alpha \right) + \frac{253}{4096}\Delta t{\underset{\_}{k}}_5\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \frac{1631}{55296}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) +\\ \frac{175}{512}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) + \frac{575}{13824}\Delta t{\overline{k}}_3\left(t_i, \alpha \right) + \frac{44275}{110592}\Delta t{\overline{k}}_4\left(t_i, \alpha \right) + \\ \frac{253}{4096}\Delta t{\overline{k}}_5\left(t_i, \alpha \right)),\\ {\overline{k}}_6\left(t_i, \alpha \right) = \underset{\_}{g} (\underset{\_}{y}\left(t_i, \alpha \right) + \frac{1631}{55296}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{175}{512}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) + \frac{575}{13824}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right) +\\ \frac{44275}{110592}\Delta t{\underset{\_}{k}}_4\left(t_i, \alpha \right) + \frac{253}{4096}\Delta t{\underset{\_}{k}}_5\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \frac{1631}{55296}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) +\\ \frac{175}{512}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) + \frac{575}{13824}\Delta t{\overline{k}}_3\left(t_i, \alpha \right) + \frac{44275}{110592}\Delta t{\overline{k}}_4\left(t_i, \alpha \right) + \\ \frac{253}{4096}\Delta t{\overline{k}}_5\left(t_i, \alpha \right)).\end{array}$$

4.2. Non-Autonomous Fuzzy Differential Equation

Next, we consider the non-autonomous FDE given by:

$$\left\{\begin{array}{l}{Y}^{\prime }\left(t\right) = G\left(t, Y\left(t\right)\right), t\in \left[p,q\right],\\ Y\left(t_0\right) = Y_0.\end{array}\right.$$

(11)

The right-hand side of Equation (11) is explicitly dependent on time $t$. From Theorem 1, Equation (11) is translated into the system of the non-autonomous FDE.

(i)

Type 1

$$\left\{\begin{array}{l}{\underset{¯}{y}}^{\prime }\left(t, \alpha \right) = \underset{¯}{g}\left(t, \underset{¯}{y}\left(t, \alpha \right), \overline{y}\left(t, \alpha \right)\right), \underset{¯}{y}\left(t_0, \alpha \right) = {\underset{¯}{y}}_0, \\ {\overline{y}}^{\prime }\left(t, \alpha \right) = \overline{g}\left(t, \underset{¯}{y}\left(t, \alpha \right), \overline{y}\left(t, \alpha \right)\right), \overline{y}\left(t_0, \alpha \right) = {\overline{y}}_0. \end{array}\right.$$

(12)

Based on Equation (12), the approximate solution can be referred to as:

$$\begin{array}{l}\underset{\_}{y} \left(t_{i+1},\alpha \right)=\underset{\_}{y} \left(t_i,\alpha \right)+\Delta t (\frac{2825}{27648} {\underset{\_}{k}}_1 \left(t_i, \alpha \right)+\frac{18575}{48384} {\underset{\_}{k}}_3 \left(t_i, \alpha \right)+\frac{13525}{55296} {\underset{\_}{k}}_4 \left(t_i, \alpha \right)+\\ \frac{277}{14336} {\underset{\_}{k}}_5 \left(t_i, \alpha \right)+ \frac{1}{4} {\underset{\_}{k}}_6 \left(t_i, \alpha \right)) ,\\ \overline{y} \left(t_{i+1},\alpha \right)=\overline{y} \left(t_i,\alpha \right)+\Delta t (\frac{2825}{27648} {\overline{k}}_1 \left(t_i, \alpha \right)+\frac{18575}{48384} {\overline{k}}_3 \left(t_i, \alpha \right)+\frac{13525}{55296} {\overline{k}}_4 \left(t_i, \alpha \right)+\\ \frac{277}{14336} {\overline{k}}_5 \left(t_i, \alpha \right) +\frac{1}{4} {\overline{k}}_6 \left(t_i, \alpha \right)),\end{array}$$

where

$$\begin{array}{l}{\underset{\_}{k}}_1\left(t_i, \alpha \right) = \underset{\_}{g}\left(t_i,\underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right),\\ {\overline{k}}_1\left(t_i, \alpha \right) = \overline{g}\left(t_i,\underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right),\\ {\underset{\_}{k}}_2\left(t_i, \alpha \right) = \underset{\_}{g} \left(t_i + \frac{1}{5}\Delta t, \underset{\_}{y}\left(t_i, \alpha \right) + \frac{1}{5}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \frac{1}{5}\Delta t{\overline{k}}_1\left(t_i, \alpha \right)\right),\\ {\overline{k}}_2\left(t_i, \alpha \right) = \overline{g} \left(t_i + \frac{1}{5}\Delta t, \underset{\_}{y}\left(t_i, \alpha \right) + \frac{1}{5}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \frac{1}{5}\Delta t{\overline{k}}_1\left(t_i, \alpha \right)\right),\\ {\underset{\_}{k}}_3\left(t_i, \alpha \right) = \underset{\_}{g} (t_i + \frac{3}{10}\Delta t, \underset{\_}{y}\left(t_i, \alpha \right) + \frac{3}{40}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{9}{40}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \\ \frac{3}{40}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) + \frac{9}{40}\Delta t{\overline{k}}_2\left(t_i, \alpha \right)),\\ {\overline{k}}_3\left(t_i, \alpha \right) = \overline{g} (t_i + \frac{3}{10}\Delta t, \underset{\_}{y}\left(t_i, \alpha \right) + \frac{3}{40}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{9}{40}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \\ \frac{3}{40}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) + \frac{9}{40}\Delta t{\overline{k}}_2\left(t_i, \alpha \right)),\\ {\underset{\_}{k}}_4\left(t_i, \alpha \right) = \underset{\_}{g} (t_i + \frac{3}{5}\Delta t, \underset{\_}{y}\left(t_i, \alpha \right) + \frac{3}{10}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) - \frac{9}{10}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) + \frac{6}{5}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right), \\ \overline{y}\left(t_i, \alpha \right) + \frac{3}{10}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) - \frac{9}{10}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) + \frac{6}{5}\Delta t{\overline{k}}_3\left(t_i, \alpha \right)),\\ {\overline{k}}_4\left(t_i, \alpha \right) = \overline{g} (t_i + \frac{3}{5}\Delta t, \underset{\_}{y}\left(t_i, \alpha \right) + \frac{3}{10}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) - \frac{9}{10}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) + \frac{6}{5}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right), \\ \overline{y}\left(t_i, \alpha \right) + \frac{3}{10}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) - \frac{9}{10}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) + \frac{6}{5}\Delta t{\overline{k}}_3\left(t_i, \alpha \right)),\\ {\underset{\_}{k}}_5\left(t_i, \alpha \right) = \underset{\_}{g} (t_i + \Delta t, \underset{\_}{y}\left(t_i, \alpha \right) - \frac{11}{54}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{5}{2}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) - \frac{70}{27}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right) + \\ \frac{35}{27}\Delta t{\underset{\_}{k}}_4\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) - \frac{11}{54}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) + \frac{5}{2}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) - \\ \frac{70}{27}\Delta t{\overline{k}}_3\left(t_i, \alpha \right) + \frac{35}{27}\Delta t{\overline{k}}_4\left(t_i, \alpha \right)),\\ {\overline{k}}_5\left(t_i, \alpha \right) = \overline{g} (t_i + \Delta t, \underset{\_}{y}\left(t_i, \alpha \right) - \frac{11}{54}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{5}{2}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) - \frac{70}{27}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right) + \\ \frac{35}{27}\Delta t{\underset{\_}{k}}_4\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) - \frac{11}{54}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) + \frac{5}{2}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) - \\ \frac{70}{27}\Delta t{\overline{k}}_3\left(t_i, \alpha \right) +\frac{35}{27}\Delta t{\overline{k}}_4\left(t_i, \alpha \right)),\\ {\underset{\_}{k}}_6\left(t_i, \alpha \right) = \underset{\_}{g} (t_i + \frac{7}{8}\Delta t, \underset{\_}{y}\left(t_i, \alpha \right) + \frac{1631}{55296}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{175}{512}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) + \\ \frac{575}{13824}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right) + \frac{44275}{110592}\Delta t{\underset{\_}{k}}_4\left(t_i, \alpha \right) + \frac{253}{4096}\Delta t{\underset{\_}{k}}_5\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \\ \frac{1631}{55296}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) + \frac{175}{512}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) + \frac{575}{13824}\Delta t{\overline{k}}_3\left(t_i, \alpha \right) + \\ \frac{44275}{110592}\Delta t{\overline{k}}_4\left(t_i, \alpha \right) + \frac{253}{4096}\Delta t{\overline{k}}_5\left(t_i, \alpha \right)),\end{array}$$

$$\begin{array}{l}{\overline{k}}_6\left(t_i, \alpha \right) = \overline{g} (t_i + \frac{7}{8}\Delta t, \underset{\_}{y}\left(t_i, \alpha \right) + \frac{1631}{55296}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{175}{512}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) + \\ \frac{575}{13824}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right) + \frac{44275}{110592}\Delta t{\underset{\_}{k}}_4\left(t_i, \alpha \right) + \frac{253}{4096}\Delta t{\underset{\_}{k}}_5\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \\ \frac{1631}{55296}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) + \frac{175}{512}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) + \frac{575}{13824}\Delta t{\overline{k}}_3\left(t_i, \alpha \right) + \\ \frac{44275}{110592}\Delta t{\overline{k}}_4\left(t_i, \alpha \right) + \frac{253}{4096}\Delta t{\overline{k}}_5\left(t_i, \alpha \right)).\end{array}$$

(ii)

Type 2

$$\left\{\begin{array}{l}{\underset{¯}{y}}^{\prime }\left(t, \alpha \right) = \overline{g}\left(t, \underset{¯}{y}\left(t, \alpha \right), \overline{y}\left(t, \alpha \right)\right), \underset{¯}{y}\left(t_0, \alpha \right) = {\underset{¯}{y}}_0, \\ {\overline{y}}^{\prime }\left(t, \alpha \right) = \underset{¯}{g}\left(t, \underset{¯}{y}\left(t, \alpha \right), \overline{y}\left(t, \alpha \right)\right), \overline{y}\left(t_0, \alpha \right) = {\overline{y}}_0. \end{array}\right.$$

(13)

The approximate solution for Equation (13) is represented as:

$$\begin{array}{l}\underset{\_}{y} \left(t_{i+1},\alpha \right)=\underset{\_}{y} \left(t_i,\alpha \right)+\Delta t (\frac{2825}{27648} {\underset{\_}{k}}_1 \left(t_i, \alpha \right)+\frac{18575}{48384} {\underset{\_}{k}}_3 \left(t_i, \alpha \right)+\frac{13525}{55296} {\underset{\_}{k}}_4 \left(t_i, \alpha \right)+\\ \frac{277}{14336} {\underset{\_}{k}}_5 \left(t_i, \alpha \right)+ \frac{1}{4} {\underset{\_}{k}}_6 \left(t_i, \alpha \right)) ,\\ \overline{y} \left(t_{i+1},\alpha \right)=\overline{y} \left(t_i,\alpha \right)+\Delta t (\frac{2825}{27648} {\overline{k}}_1 \left(t_i, \alpha \right)+\frac{18575}{48384} {\overline{k}}_3 \left(t_i, \alpha \right)+\frac{13525}{55296} {\overline{k}}_4 \left(t_i, \alpha \right)+\\ \frac{277}{14336} {\overline{k}}_5 \left(t_i, \alpha \right) +\frac{1}{4} {\overline{k}}_6 \left(t_i, \alpha \right)),\end{array}$$

where

$$\begin{array}{l}{\underset{\_}{k}}_1\left(t_i, \alpha \right) = \overline{g}\left(t_i,\underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right),\\ {\overline{k}}_1\left(t_i, \alpha \right) = \underset{\_}{g}\left(t_i,\underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right),\\ {\underset{\_}{k}}_2\left(t_i, \alpha \right) = \overline{g} \left(t_i + \frac{1}{5}\Delta t, \underset{\_}{y}\left(t_i, \alpha \right) + \frac{1}{5}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \frac{1}{5}\Delta t{\overline{k}}_1\left(t_i, \alpha \right)\right),\\ {\overline{k}}_2\left(t_i, \alpha \right) = \underset{\_}{g} \left(t_i + \frac{1}{5}\Delta t, \underset{\_}{y}\left(t_i, \alpha \right) + \frac{1}{5}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \frac{1}{5}\Delta t{\overline{k}}_1\left(t_i, \alpha \right)\right),\\ {\underset{\_}{k}}_3\left(t_i, \alpha \right) = \overline{g} (t_i + \frac{3}{10}\Delta t, \underset{\_}{y}\left(t_i, \alpha \right) + \frac{3}{40}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{9}{40}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \\ \frac{3}{40}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) + \frac{9}{40}\Delta t{\overline{k}}_2\left(t_i, \alpha \right)),\\ {\overline{k}}_3\left(t_i, \alpha \right) = \underset{\_}{g} (t_i + \frac{3}{10}\Delta t, \underset{\_}{y}\left(t_i, \alpha \right) + \frac{3}{40}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{9}{40}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \\ \frac{3}{40}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) + \frac{9}{40}\Delta t{\overline{k}}_2\left(t_i, \alpha \right)),\\ {\underset{\_}{k}}_4\left(t_i, \alpha \right) = \overline{g} (t_i + \frac{3}{5}\Delta t, \underset{\_}{y}\left(t_i, \alpha \right) + \frac{3}{10}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) - \frac{9}{10}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) + \frac{6}{5}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right), \\ \overline{y}\left(t_i, \alpha \right) + \frac{3}{10}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) - \frac{9}{10}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) + \frac{6}{5}\Delta t{\overline{k}}_3\left(t_i, \alpha \right)),\end{array}$$

$$\begin{array}{l}{\overline{k}}_4\left(t_i, \alpha \right) = \underset{\_}{g} (t_i + \frac{3}{5}\Delta t, \underset{\_}{y}\left(t_i, \alpha \right) + \frac{3}{10}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) - \frac{9}{10}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) + \frac{6}{5}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right), \\ \overline{y}\left(t_i, \alpha \right) + \frac{3}{10}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) - \frac{9}{10}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) + \frac{6}{5}\Delta t{\overline{k}}_3\left(t_i, \alpha \right)),\\ {\underset{\_}{k}}_5\left(t_i, \alpha \right) = \overline{g} (t_i + \Delta t, \underset{\_}{y}\left(t_i, \alpha \right) - \frac{11}{54}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{5}{2}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) - \frac{70}{27}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right) + \\ \frac{35}{27}\Delta t{\underset{\_}{k}}_4\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) - \frac{11}{54}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) + \frac{5}{2}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) - \\ \frac{70}{27}\Delta t{\overline{k}}_3\left(t_i, \alpha \right) + \frac{35}{27}\Delta t{\overline{k}}_4\left(t_i, \alpha \right)),\\ {\overline{k}}_5\left(t_i, \alpha \right) = \underset{\_}{g} (t_i + \Delta t, \underset{\_}{y}\left(t_i, \alpha \right) - \frac{11}{54}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{5}{2}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) - \frac{70}{27}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right) + \\ \frac{35}{27}\Delta t{\underset{\_}{k}}_4\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) - \frac{11}{54}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) + \frac{5}{2}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) - \frac{70}{27}\Delta t{\overline{k}}_3\left(t_i, \alpha \right) + \\ \frac{35}{27}\Delta t{\overline{k}}_4\left(t_i, \alpha \right)),\\ {\underset{\_}{k}}_6\left(t_i, \alpha \right) = \overline{g} (t_i + \frac{7}{8}\Delta t, \underset{\_}{y}\left(t_i, \alpha \right) + \frac{1631}{55296}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{175}{512}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) + \\ \frac{575}{13824}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right) + \frac{44275}{110592}\Delta t{\underset{\_}{k}}_4\left(t_i, \alpha \right) + \frac{253}{4096}\Delta t{\underset{\_}{k}}_5\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \\ \frac{1631}{55296}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) + \frac{175}{512}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) + \frac{575}{13824}\Delta t{\overline{k}}_3\left(t_i, \alpha \right) + \\ \frac{44275}{110592}\Delta t{\overline{k}}_4\left(t_i, \alpha \right) + \frac{253}{4096}\Delta t{\overline{k}}_5\left(t_i, \alpha \right)),\\ {\overline{k}}_6\left(t_i, \alpha \right) = \underset{\_}{g} (t_i + \frac{7}{8}\Delta t, \underset{\_}{y}\left(t_i, \alpha \right) + \frac{1631}{55296}\Delta t{\underset{\_}{k}}_1\left(t_i, \alpha \right) + \frac{175}{512}\Delta t{\underset{\_}{k}}_2\left(t_i, \alpha \right) + \\ \frac{575}{13824}\Delta t{\underset{\_}{k}}_3\left(t_i, \alpha \right) + \frac{44275}{110592}\Delta t{\underset{\_}{k}}_4\left(t_i, \alpha \right) + \frac{253}{4096}\Delta t{\underset{\_}{k}}_5\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right) + \\ \frac{1631}{55296}\Delta t{\overline{k}}_1\left(t_i, \alpha \right) + \frac{175}{512}\Delta t{\overline{k}}_2\left(t_i, \alpha \right) + \frac{575}{13824}\Delta t{\overline{k}}_3\left(t_i, \alpha \right) + \\ \frac{44275}{110592}\Delta t{\overline{k}}_4\left(t_i, \alpha \right) + \frac{253}{4096}\Delta t{\overline{k}}_5\left(t_i, \alpha \right)).\end{array}$$

4.3. Theoretical Analysis

In this subsection, we discuss the theoretical convergence analysis of the FRKCK4.

First, we denote the analytical and approximate solutions of Equation (1) as $\tilde{Y} \left(t, \alpha \right) = [\underset{¯}{\tilde{y}} \left(t, \alpha \right), \tilde{\overline{y}} \left(t, \alpha \right)]$ and $Y \left(t, \alpha \right) = \left[\underset{¯}{y} \left(t, \alpha \right), \overline{y} \left(t, \alpha \right)\right],$ respectively. Then, from Taylor’s theorem, the analytical solution can be expressed as follows:

$$\begin{array}{l}\widetilde{\underset{\_}{y}}\left(t_{i+1}, \alpha \right) = \underset{\_}{\tilde{y}}\left(t_i, \alpha \right) + \Delta t\underset{\_}{g} \left(t_i, \underset{\_}{\tilde{y}}\left(t_i, \alpha \right), \tilde{\overline{y}}\left(t_i, \alpha \right)\right) + \frac{{\left(\Delta t\right)}^2}{2!}\underset{\_}{g} \left(t_i, \underset{\_}{\tilde{y}}\left(t_i, \alpha \right), \tilde{\overline{y}}\left(t_i, \alpha \right)\right) +\\ \frac{{\left(\Delta t\right)}^3}{3!}\underset{\_}{g} \left(t_i, \underset{\_}{\tilde{y}}\left(t_i, \alpha \right), \tilde{\overline{y}}\left(t_i, \alpha \right)\right) + \dots + \frac{{\left(\Delta t\right)}^N}{N!}\underset{\_}{g} \left(t_N, \underset{\_}{\tilde{y}}\left(t_N, \alpha \right), \tilde{\overline{y}}\left(t_N, \alpha \right)\right)+\\ \frac{{\left(\Delta t\right)}^{N+1}}{\left(N+1\right)!}\underset{\_}{g} \left(t_{N+1}, \underset{\_}{\tilde{y}}\left(t_{N+1}, \alpha \right), \tilde{\overline{y}}\left(t_{N+1}, \alpha \right)\right),\end{array}$$

$$\begin{array}{l}\tilde{\overline{y}}\left(t_{i+1}, \alpha \right) = \tilde{\overline{y}}\left(t_i, \alpha \right) + \Delta t\overline{g} \left(t_i, \underset{\_}{\tilde{y}}\left(t_i, \alpha \right), \tilde{\overline{y}}\left(t_i, \alpha \right)\right) + \frac{{\left(\Delta t\right)}^2}{2!}\overline{g} \left(t_i, \underset{\_}{\tilde{y}}\left(t_i, \alpha \right), \tilde{\overline{y}}\left(t_i, \alpha \right)\right)v +\\ \frac{{\left(\Delta t\right)}^3}{3!}\overline{g} \left(t_i, \underset{\_}{\tilde{y}}\left(t_i, \alpha \right), \tilde{\overline{y}}\left(t_i, \alpha \right)\right) + \dots + \frac{{\left(\Delta t\right)}^N}{N!}\overline{g} \left(t_N, \underset{\_}{\tilde{y}}\left(t_N, \alpha \right), \tilde{\overline{y}}\left(t_N, \alpha \right)\right)+\\ \frac{{\left(\Delta t\right)}^{N+1}}{\left(N+1\right)!}\overline{g} \left(t_{N+1}, \widetilde{\underset{\_}{y}}\left(t_{N+1}, \alpha \right), \tilde{\overline{y}}\left(t_{N+1}, \alpha \right)\right).\end{array}$$

The approximate solution of Equation (1) can then be expressed as follows:

$$\begin{array}{l}\underset{\_}{y}\left(t_{i+1}, \alpha \right) = \underset{\_}{y}\left(t_i, \alpha \right) + \Delta t\underset{\_}{g} \left(t_i, \underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right) + \frac{{\left(\Delta t\right)}^2}{2!}\underset{\_}{g} \left(t_i, \underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right) +\\ \frac{{\left(\Delta t\right)}^3}{3!}\underset{\_}{g} \left(t_i, \underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right) + \dots + \frac{{\left(\Delta t\right)}^N}{N!}\underset{\_}{g} \left(t_N, \underset{\_}{y}\left(t_N, \alpha \right), \overline{y}\left(t_N, \alpha \right)\right),\\ \overline{y}\left(t_{i+1}, \alpha \right) = \overline{y}\left(t_i, \alpha \right) + \Delta t\overline{g} \left(t_i, \underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right) + \frac{{\left(\Delta t\right)}^2}{2!}\overline{g} \left(t_i, \underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right) +\\ \frac{{\left(\Delta t\right)}^3}{3!}\overline{g} \left(t_i, \underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right) + \dots + \frac{{\left(\Delta t\right)}^N}{N!}\overline{g} \left(t_N, \underset{\_}{y}\left(t_N, \alpha \right), \overline{y}\left(t_N, \alpha \right)\right).\end{array}$$

The following lemmas are applied to show the convergence of the proposed method.

Lemma 1

[19]. Let a sequence of numbers ${\left\{P_i\right\}}_{i=o}^N$ satisfy,

$$\left|P_{i+1}\right| \le K_1 \left|P_i\right| + K_2, 0\le i\le N-1.$$

For some given positive constants $K_1 \mathrm{and} K_2,$ we then have

$$\left|P_i\right| \le K_1{}^N \left|P_0\right| + K_2 \frac{K_1^i - 1}{K_1 - 1}, 0 \le i \le N-1.$$

Lemma 2

[19]. Let a sequence of numbers ${\left\{P_i\right\}}_{i=o}^N, {\left\{Q_i\right\}}_{i=o}^N$ satisfy

$$\left\{\begin{array}{l}\left|P_{i+1}\right| \le \left|P_i\right| + K_1 \max \left\{\left|P_i\right|, \left|Q_i\right|\right\} + K_2,\\ \left|Q_{i+1}\right| \le \left|Q_i\right| + K_1 \max \left\{\left|P_i\right|, \left|Q_i\right|\right\} + K_2.\end{array}\right.$$

For some given positive constants $K_1 \mathrm{and} K_2$ and $U_i = \left|P_i\right| + \left|Q_i\right|, 0 \le i \le N,$ we have

$$U_i \le {\overline{K}}_1^i U_0 + K_2 \frac{{\overline{K}}_1^i - 1}{{\overline{K}}_1 - 1}, 1 \le i \le N,$$

where ${\overline{K}}_1 = 1 + 2K_1$ and ${\overline{K}}_2 = 2K_2.$

The following theorem is motivated by Theorem 1 in [19].

Theorem 4.

Let$\underset{¯}{g} \left(t, u, v\right)$and$\overline{g} \left(t, u, v\right)$belong to$C^4 \left(K\right)$and let the partial derivatives of$\underset{¯}{g}, \overline{g}$be bounded over$K.$Then, for the arbitrary fixed,$0 \le \alpha \le 1,$the FRKCK4 solutions converge to the exact solutions$\underset{¯}{\tilde{Y}} \left(t_N, \alpha \right)$and$\tilde{\overline{Y}} \left(t_N, \alpha \right)$uniformly in$t.$

Proof. 

As in Theorem 3, it is sufficient to show:

$$\underset{\Delta t\to 0}{\lim } {\underset{¯}{y}}_N \left(\alpha \right)=\underset{¯}{\tilde{y}} \left(t, \alpha \right), \underset{\Delta t\to 0}{\lim } {\overline{y}}_N \left(\alpha \right)=\tilde{\overline{y}} \left(t, \alpha \right).$$

By referring to Taylor’s theorem, we have

$$\begin{array}{l}\underset{\_}{\tilde{y}} \left(t_{i+1}, \alpha \right) = \underset{\_}{\tilde{y}} \left(t_i, \alpha \right) + \Delta t\underset{\_}{g} \left(t_i, \underset{\_}{\tilde{y}} \left(t_i, \alpha \right), \tilde{\overline{y}} \left(t_i, \alpha \right)\right) + \frac{{\left(\Delta t\right)}^2}{2}\underset{\_}{g} \left(t_i, \underset{\_}{\tilde{y}} \left(t_i, \alpha \right), \tilde{\overline{y}} \left(t_i, \alpha \right)\right) +\\ \frac{{\left(\Delta t\right)}^3}{3!}\underset{\_}{g} \left(t_i, \underset{\_}{\tilde{y}} \left(t_i, \alpha \right), \tilde{\overline{y}} \left(t_i, \alpha \right)\right) + \frac{{\left(\Delta t\right)}^4}{4!}\underset{\_}{g} \left(t_i, \underset{\_}{\tilde{y}} \left(t_i, \alpha \right), \tilde{\overline{y}} \left(t_i, \alpha \right)\right) +\\ \frac{{\left(\Delta t\right)}^5}{5!} {\underset{\_}{\tilde{y}}}^{\left(5\right)}\left({\underset{\_}{\xi }}_i\right),\\ \tilde{\overline{y}} \left(t_{i+1}, \alpha \right) = \tilde{\overline{y}} \left(t_i, \alpha \right) + \Delta t\overline{g} \left(t_i, \underset{\_}{\tilde{y}} \left(t_i, \alpha \right), \tilde{\overline{y}} \left(t_i, \alpha \right)\right) + \frac{{\left(\Delta t\right)}^2}{2}\overline{g} \left(t_i, \underset{\_}{\tilde{y}} \left(t_i, \alpha \right), \tilde{\overline{y}} \left(t_i, \alpha \right)\right) +\\ \frac{{\left(\Delta t\right)}^3}{3!}\overline{g} \left(t_i, \underset{\_}{\tilde{y}} \left(t_i, \alpha \right), \tilde{\overline{y}} \left(t_i, \alpha \right)\right) + \frac{{\left(\Delta t\right)}^4}{4!}\overline{g} \left(t_i, \underset{\_}{\tilde{y}} \left(t_i, \alpha \right), \tilde{\overline{y}} \left(t_i, \alpha \right)\right) +\\ \frac{{\left(\Delta t\right)}^5}{5!} {\tilde{\overline{y}}}^{\left(5\right)}\left({\underset{\_}{\xi }}_i\right),\end{array}$$

where $t_i < {\underset{\_}{\xi }}_i, {\overline{\xi }}_i < t_{i+1}.$ Consequently,

$$\begin{array}{l}\underset{\_}{\tilde{y}} \left(t_{i+1}, \alpha \right)-\underset{\_}{y}\left(t_{i+1}, \alpha \right)=(\underset{\_}{\tilde{y}} \left(t_i, \alpha \right) + \Delta t\underset{\_}{g} \left(t_i, \underset{\_}{\tilde{y}} \left(t_i, \alpha \right), \tilde{\overline{y}} \left(t_i, \alpha \right)\right) + \\ \frac{{\left(\Delta t\right)}^2}{2}\underset{\_}{g}\left(t_i, \underset{\_}{\tilde{y}} \left(t_i, \alpha \right), \tilde{\overline{y}} \left(t_i, \alpha \right)\right) +\frac{{\left(\Delta t\right)}^3}{3!}\underset{\_}{g} \left(t_i, \underset{\_}{\tilde{y}} \left(t_i, \alpha \right), \tilde{\overline{y}} \left(t_i, \alpha \right)\right) + \\ \frac{{\left(\Delta t\right)}^4}{4!}\underset{\_}{g} \left(t_i, \underset{\_}{\tilde{y}} \left(t_i, \alpha \right), \tilde{\overline{y}} \left(t_i, \alpha \right)\right)) - \\ (\overline{y}\left(t_i, \alpha \right) + \Delta t\underset{\_}{g} \left(t_i, \underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right) +\\ \frac{{\left(\Delta t\right)}^2}{2!}\underset{\_}{g} \left(t_i, \underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right) +\frac{{\left(\Delta t\right)}^3}{3!}\underset{\_}{g} \left(t_i, \underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right) +\\ \frac{{\left(\Delta t\right)}^4}{4!}\underset{\_}{g} \left(t_i, \underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right)) + \frac{{\left(\Delta t\right)}^5}{5!} {\underset{\_}{\tilde{y}}}^{\left(5\right)}\left({\underset{\_}{\xi }}_i\right),\\ \tilde{\overline{y}} \left(t_{i+1}, \alpha \right)-\overline{y}\left(t_{i+1}, \alpha \right)=(\tilde{\overline{y}} \left(t_i, \alpha \right) + \Delta t\overline{g} \left(t_i, \underset{\_}{\tilde{y}} \left(t_i, \alpha \right), \tilde{\overline{y}} \left(t_i, \alpha \right)\right) + \\ \frac{{\left(\Delta t\right)}^2}{2}\overline{g} \left(t_i, \underset{\_}{\tilde{y}} \left(t_i, \alpha \right), \tilde{\overline{y}} \left(t_i, \alpha \right)\right) +\frac{{\left(\Delta t\right)}^3}{3!}\overline{g} \left(t_i, \underset{\_}{\tilde{y}} \left(t_i, \alpha \right), \tilde{\overline{y}} \left(t_i, \alpha \right)\right) + \\ \frac{{\left(\Delta t\right)}^4}{4!}\overline{g} \left(t_i, \underset{\_}{\tilde{y}} \left(t_i, \alpha \right), \tilde{\overline{y}} \left(t_i, \alpha \right)\right)) - \\ (\overline{y}\left(t_i, \alpha \right) + \Delta t\overline{g} \left(t_i, \underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right) +\\ \frac{{\left(\Delta t\right)}^2}{2!}\overline{g} \left(t_i, \underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right) +\frac{{\left(\Delta t\right)}^3}{3!}\overline{g} \left(t_i, \underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right) +\\ \frac{{\left(\Delta t\right)}^4}{4!}\overline{g} \left(t_i, \underset{\_}{y}\left(t_i, \alpha \right), \overline{y}\left(t_i, \alpha \right)\right)) + \frac{{\left(\Delta t\right)}^5}{5!} {\tilde{\overline{y}}}^{\left(5\right)}\left({\overline{\xi }}_i\right).\end{array}$$

Denote $P_i = \underset{¯}{\tilde{y}} \left(t_i, \alpha \right) - \underset{¯}{y} \left(t_i, \alpha \right), Q_i = \tilde{\overline{y}} \left(t_i, \alpha \right) - \overline{y} \left(t_i, \alpha \right).$ Then,

$$\begin{array}{l}\left|P_{i+1}\right| \le \left|P_i\right| + 2K\Delta t\max \left\{\left|P_i\right|, \left|Q_i\right|\right\} + \frac{{\left(\Delta t\right)}^5}{120} \underset{¯}{M},\\ \left|Q_{i+1}\right| \le \left|Q_i\right| + 2K\Delta t \max \left\{\left|P_i\right|, \left|Q_i\right|\right\} + \frac{{\left(\Delta t\right)}^5}{120} \overline{M},\end{array}$$

where $\underset{¯}{M} = \underset{p \le t_i \le q}{\max } {\underset{¯}{\tilde{y}}}^{\left(5\right)} \left(t, \alpha \right)$ and $\overline{M} = \underset{p \le t_i \le q}{\max } {\tilde{\overline{y}}}^{\left(5\right)} \left(t, \alpha \right)$ while $K > 0$ is a bound for the partial derivative of $\underset{¯}{g}$ and $\overline{g}.$ Thus, using Lemma 2, we obtain

$$\begin{array}{l}\left|P_i\right| \le {\left(1 + 4K\Delta t\right)}^i \left|U_0\right| + \frac{{\left(\Delta t\right)}^5}{120} \underset{¯}{M} \left(\frac{{\left(1 + 4K\Delta t\right)}^i - 1}{4K\Delta t}\right),\\ \left|Q_i\right| \le {\left(1 + 4K\Delta t\right)}^i \left|U_0\right| + \frac{{\left(\Delta t\right)}^5}{120} \overline{M} \left(\frac{{\left(1 + 4K\Delta t\right)}^i - 1}{4K\Delta t}\right),\end{array}$$

where $\left|U_0\right| = \left|P_0\right| + \left|Q_0\right|.$ Particularly,

$$\begin{array}{l}\left|P_N\right| \le {\left(1 + 4K\Delta t\right)}^N \left|U_0\right| + \frac{{\left(\Delta t\right)}^5}{120} \underset{¯}{M} \left(\frac{{\left(1 + 4K\Delta t\right)}^{\left(p-q\right)/\Delta t} - 1}{4K}\right),\\ \left|Q_N\right| \le {\left(1 + 4K\Delta t\right)}^N \left|U_0\right| + \frac{{\left(\Delta t\right)}^5}{120} \overline{M} \left(\frac{{\left(1 + 4K\Delta t\right)}^{\left(p-q\right)/\Delta t} - 1}{4K}\right).\end{array}$$

Since $P_0 = Q_0 = 0,$ we have

$$\begin{array}{l}\left|P_N\right| \le \frac{{\left(\Delta t\right)}^5}{120} \underset{¯}{M} \left(\frac{e^{4K \left(p-q\right)} - 1}{4K}\right),\\ \left|Q_N\right| \le \frac{{\left(\Delta t\right)}^5}{120} \overline{M} \left(\frac{e^{4K \left(p-q\right)} - 1}{4K}\right),\end{array}$$

and if $\Delta t\to 0,$ then we conclude the proof since $P_N\to 0$ and $Q_N\to 0.$ □

5. Numerical Simulations

This section provides numerical simulations to demonstrate the capability of the proposed method. The proposed method is then compared to the analytical solutions, as well as the FRK4 for the (i) and (ii)–differentiability. In order to calculate the error, the absolute values of the analytical and approximate solutions are subtracted. The following sections discuss the examples of autonomous and non-autonomous fuzzy differential equations. The idea of Example 1 below is based on Example 5.1 in [25]. Some modification is made by changing the value of $t$ and $\alpha -\mathrm{cut}.$

Example 1. Let the autonomous FDE be given as follows:

$$\left\{\begin{array}{l}{Y}^{\prime }\left(t\right) = -Y\left(t\right), t\in \left[0, 4\right],\\ Y\left(0, \alpha \right) = \left(0.5 + 0.5\alpha , 1.5 - 0.5\alpha \right), 0\le \alpha \le 1. \end{array}\right.$$

(14)

Using the (i)–differentiability, we translate Equation (14) into the ODE system.

$$\left\{\begin{array}{l}{\underset{¯}{y}}^{\prime }\left(t\right) = -\overline{y}\left(t\right), t\in \left[0, 4\right],\\ {\overline{y}}^{\prime }\left(t\right) = -\underset{¯}{y}\left(t\right),\\ \underset{¯}{y}\left(0, \alpha \right)=0.5 + 0.5\alpha ,\\ \overline{y}\left(0, \alpha \right) = 1.5 - 0.5\alpha , 0\le \alpha \le 1. \end{array}\right.$$

(15)

In order to solve Equation (15), the following is proposed:

$$\begin{array}{l}{\underset{\_}{k}}_1 = -{\overline{y}}_i\left(\alpha \right),\\ {\overline{k}}_1 = -{\underset{\_}{y}}_i\left(\alpha \right),\\ {\underset{\_}{k}}_2 = -{\overline{y}}_i\left(\alpha \right) + \frac{1}{5}\Delta t{\underset{\_}{k}}_1,\\ {\overline{k}}_2 = -{\underset{\_}{y}}_i\left(\alpha \right) + \frac{1}{5}\Delta t{\overline{k}}_1,\\ {\underset{\_}{k}}_3 = -{\overline{y}}_i\left(\alpha \right) + \frac{3}{40}\Delta t{\underset{\_}{k}}_1 + \frac{9}{40}\Delta t{\underset{\_}{k}}_2,\\ {\overline{k}}_3 = -{\underset{\_}{y}}_i\left(\alpha \right) + \frac{3}{40}\Delta t{\overline{k}}_1 + \frac{9}{40}\Delta t{\overline{k}}_2,\\ {\underset{\_}{k}}_4 = -{\overline{y}}_i\left(\alpha \right) + \frac{3}{10}\Delta t{\underset{\_}{k}}_1 - \frac{9}{10}\Delta t{\underset{\_}{k}}_2 + \frac{6}{5}\Delta t{\underset{\_}{k}}_3,\\ {\overline{k}}_4 = -{\underset{\_}{y}}_i\left(\alpha \right) + \frac{3}{10}\Delta t{\overline{k}}_1 - \frac{9}{10}\Delta t{\overline{k}}_2 + \frac{6}{5}\Delta t{\overline{k}}_3,\\ {\underset{\_}{k}}_5 = -{\overline{y}}_i\left(\alpha \right) - \frac{11}{54}\Delta t{\underset{\_}{k}}_1 + \frac{5}{2}\Delta t{\underset{\_}{k}}_2 - \frac{70}{27}\Delta t{\underset{\_}{k}}_3 + \frac{35}{27}\Delta t{\underset{\_}{k}}_4,\\ {\overline{k}}_5 = -{\underset{\_}{y}}_i\left(\alpha \right) - \frac{11}{54}\Delta t{\overline{k}}_1 + \frac{5}{2}\Delta t{\overline{k}}_2 - \frac{70}{27}\Delta t{\overline{k}}_3 + \frac{35}{27}\Delta t{\overline{k}}_4,\\ {\underset{\_}{k}}_6 = -{\overline{y}}_i\left(\alpha \right) + \frac{1631}{55296}\Delta t{\underset{\_}{k}}_1 + \frac{175}{512}\Delta t{\underset{\_}{k}}_2 + \frac{575}{13824}\Delta t{\underset{\_}{k}}_3 + \frac{44275}{110592}\Delta t{\underset{\_}{k}}_4 + \frac{253}{4096}\Delta t{\underset{\_}{k}}_5,\\ {\overline{k}}_6 = -{\underset{\_}{y}}_i\left(\alpha \right) + \frac{1631}{55296}\Delta t{\overline{k}}_1 + \frac{175}{512}\Delta t{\overline{k}}_2 + \frac{575}{13824}\Delta t{\overline{k}}_3 + \frac{44275}{110592}\Delta t{\overline{k}}_4 + \frac{253}{4096}\Delta t{\overline{k}}_5.\end{array}$$

The analytical solution for the (i)–differentiability is:

$$\begin{array}{l}\underset{¯}{\tilde{y}}\left(t, \alpha \right) = e^{-t} - \frac{\left(1 - \alpha \right)}{2} e^t,\\ \tilde{\overline{y}}\left(t, \alpha \right) = e^{-t} + \frac{\left(1 - \alpha \right)}{2} e^t.\end{array}$$

Using the (ii)–differentiability, we translate Equation (14) into the ODE system.

$$\left\{\begin{array}{l}{\underset{¯}{y}}^{\prime }\left(t\right) = -\underset{¯}{y}\left(t\right), t\in \left[0, 4\right],\\ {\overline{y}}^{\prime }\left(t\right) = -\overline{y}\left(t\right),\\ \underset{¯}{y}\left(0, \alpha \right)=0.5 + 0.5\alpha ,\\ \overline{y}\left(0, \alpha \right) = 1.5 - 0.5\alpha , 0\le \alpha \le 1. \end{array}\right.$$

(16)

In order to solve Equation (16), the following is proposed:

$$\begin{array}{l}{\underset{\_}{k}}_1 = -{\underset{\_}{y}}_i\left(\alpha \right),\\ {\overline{k}}_1 = -{\overline{y}}_i\left(\alpha \right),\\ {\underset{\_}{k}}_2 = -{\underset{\_}{y}}_i\left(\alpha \right) + \frac{1}{5}\Delta t{\underset{\_}{k}}_1,\\ {\overline{k}}_2 = -{\overline{y}}_i\left(\alpha \right) + \frac{1}{5}\Delta t{\overline{k}}_1,\\ {\underset{\_}{k}}_3 = -{\underset{\_}{y}}_i\left(\alpha \right) + \frac{3}{40}\Delta t{\underset{\_}{k}}_1 + \frac{9}{40}\Delta t{\underset{\_}{k}}_2,\\ {\overline{k}}_3 = -{\overline{y}}_i\left(\alpha \right) + \frac{3}{40}\Delta t{\overline{k}}_1 + \frac{9}{40}\Delta t{\overline{k}}_2,\\ {\underset{\_}{k}}_4 = -{\underset{\_}{y}}_i\left(\alpha \right) + \frac{3}{10}\Delta t{\underset{\_}{k}}_1 - \frac{9}{10}\Delta t{\underset{\_}{k}}_2 + \frac{6}{5}\Delta t{\underset{\_}{k}}_3,\\ {\overline{k}}_4 = -{\overline{y}}_i\left(\alpha \right) + \frac{3}{10}\Delta t{\overline{k}}_1 - \frac{9}{10}\Delta t{\overline{k}}_2 + \frac{6}{5}\Delta t{\overline{k}}_3,\\ {\underset{\_}{k}}_5 = -{\underset{\_}{y}}_i\left(\alpha \right) - \frac{11}{54}\Delta t{\underset{\_}{k}}_1 + \frac{5}{2}\Delta t{\underset{\_}{k}}_2 - \frac{70}{27}\Delta t{\underset{\_}{k}}_3 + \frac{35}{27}\Delta t{\underset{\_}{k}}_4,\\ {\overline{k}}_5 = -{\overline{y}}_i\left(\alpha \right) - \frac{11}{54}\Delta t{\overline{k}}_1 + \frac{5}{2}\Delta t{\overline{k}}_2 - \frac{70}{27}\Delta t{\overline{k}}_3 + \frac{35}{27}\Delta t{\overline{k}}_4,\\ {\underset{\_}{k}}_6 = -{\underset{\_}{y}}_i\left(\alpha \right) + \frac{1631}{55296}\Delta t{\underset{\_}{k}}_1 + \frac{175}{512}\Delta t{\underset{\_}{k}}_2 + \frac{575}{13824}\Delta t{\underset{\_}{k}}_3 + \frac{44275}{110592}\Delta t{\underset{\_}{k}}_4 + \frac{253}{4096}\Delta t{\underset{\_}{k}}_5,\\ {\overline{k}}_6 = -{\overline{y}}_i\left(\alpha \right) + \frac{1631}{55296}\Delta t{\overline{k}}_1 + \frac{175}{512}\Delta t{\overline{k}}_2 + \frac{575}{13824}\Delta t{\overline{k}}_3 + \frac{44275}{110592}\Delta t{\overline{k}}_4 + \frac{253}{4096}\Delta t{\overline{k}}_5.\end{array}$$

The analytical solution for the (ii)–differentiability is:

$$\begin{array}{l}\underset{¯}{\tilde{y}}\left(t, \alpha \right) = \left(0.5 + 0.5 \alpha \right) e^{-t},\\ \tilde{\overline{y}}\left(t, \alpha \right) = \left(1.5 - 0.5 \alpha \right) e^{-t}.\end{array}$$

By implementing the proposed method, we tested Example 1 using the step size $\Delta t=0.04$, $N=100$ and the result was adjusted to 12 decimal places. The comparisons between the analytical and approximate solutions at $t=1$ for the (i)–differentiability are quantified and tabulated in Table 1, while the errors $\left(E(t,\alpha )=\left[\underset{¯}{e}(t,\alpha ),\overline{e}(t,\alpha )\right]\right)$ are listed in Table 2. For the (ii)–differentiability, the comparisons between the analytical and approximate solutions at $t=1$ are tabulated in Table 3, while the errors are listed in Table 4.

Table 1. The comparisons of the analytical and approximate solutions for the (i)–differentiability at t = 1.

$\mathit{\alpha }$	Analytical Solution		FRKCK4		FRK4
	$\underset{¯}{\tilde{\mathit{y}}}\left(1,\mathit{\alpha }\right)$	$\widetilde{\overline{\mathit{y}}}\left(1,\mathit{\alpha }\right)$	$\underset{¯}{\mathit{y}}\left(1,\mathit{\alpha }\right)$	$\overline{\mathit{y}}\left(1,\mathit{\alpha }\right)$	$\underset{¯}{\mathit{y}}\left(1,\mathit{\alpha }\right)$	$\overline{\mathit{y}}\left(1,\mathit{\alpha }\right)$
0	−0.991261473058	1.727020355401	−0.991261474002	1.727020355880	−0.991261436899	1.727020335470
0.1	−0.855347381635	1.591106263978	−0.855347382508	1.591106264385	−0.855347348280	1.591106246852
0.2	−0.719433290212	1.455192172555	−0.719433291014	1.455192172891	−0.719433259662	1.455192158233
0.3	−0.583519198789	1.319278081132	−0.583519199520	1.319278081397	−0.583519171044	1.319278069615
0.4	−0.447605107366	1.183363989709	−0.447605108026	1.183363989903	−0.447605082425	1.183363980996
0.5	−0.311691015943	1.047449898286	−0.311691016532	1.047449898409	−0.311690993807	1.047449892378
0.6	−0.175776924520	0.911535806863	−0.175776925038	0.911535806915	−0.175776905188	0.911535803760
0.7	−0.039862833097	0.775621715440	−0.039862833544	0.775621715421	−0.039862816570	0.775621715141
0.8	0.096051258326	0.639707624017	0.096051257951	0.639707623927	0.096051272049	0.639707626523
0.9	0.231965349748	0.503793532594	0.231965349445	0.503793532433	0.231965360667	0.503793537904
1.0	0.367879441171	0.367879441171	0.367879440939	0.367879440939	0.367879449286	0.367879449286

Table 2. The errors of the FRKCK4 and FRK4 for the (i)–differentiability at t = 1.

$\mathit{\alpha }$	Error Analysis of FRKCK4		Error Analysis of FRK4
	$\underset{¯}{\mathit{e}}\left(1,\mathit{\alpha }\right)$	$\overline{\mathit{e}}\left(1,\mathit{\alpha }\right)$	$\underset{¯}{\mathit{e}}\left(1,\mathit{\alpha }\right)$	$\overline{\mathit{e}}\left(1,\mathit{\alpha }\right)$
0	0.000000000944	0.000000000479	0.000000036159	0.000000019931
0.1	0.000000000873	0.000000000407	0.000000033355	0.000000017126
0.2	0.000000000802	0.000000000336	0.000000030550	0.000000014322
0.3	0.000000000731	0.000000000265	0.000000027746	0.000000011517
0.4	0.000000000660	0.000000000194	0.000000024941	0.000000008713
0.5	0.000000000588	0.000000000123	0.000000022137	0.000000005908
0.6	0.000000000517	0.000000000052	0.000000019332	0.000000003104
0.7	0.000000000446	0.000000000019	0.000000016528	0.000000000299
0.8	0.000000000375	0.000000000090	0.000000013723	0.000000002505
0.9	0.000000000304	0.000000000162	0.000000010919	0.000000005310
1.0	0.000000000233	0.000000000233	0.000000008114	0.000000008114

Table 3. The comparisons of the analytical and approximate solutions for the (ii)–differentiability at t = 1.

$\mathit{\alpha }$	Analytical Solution		FRKCK4		FRK4
	$\widetilde{\underset{¯}{\mathit{y}}}\left(1,\mathit{\alpha }\right)$	$\widetilde{\overline{\mathit{y}}}\left(1,\mathit{\alpha }\right)$	$\underset{¯}{\mathit{y}}\left(1,\mathit{\alpha }\right)$	$\overline{\mathit{y}}\left(1,\mathit{\alpha }\right)$	$\underset{¯}{\mathit{y}}\left(1,\mathit{\alpha }\right)$	$\overline{\mathit{y}}\left(1,\mathit{\alpha }\right)$
0	0.183939720586	0.551819161757	0.183939720469	0.551819161408	0.183939724643	0.551819173929
0.1	0.202333692644	0.533425189699	0.202333692516	0.533425189361	0.202333697107	0.533425201464
0.2	0.220727664703	0.515031217640	0.220727664563	0.515031217314	0.220727669571	0.515031229000
0.3	0.239121636761	0.496637245581	0.239121636610	0.496637245267	0.239121642036	0.496637256536
0.4	0.257515608820	0.478243273523	0.257515608657	0.478243273220	0.257515614500	0.478243284071
0.5	0.275909580879	0.459849301464	0.275909580704	0.459849301173	0.275909586964	0.459849311607
0.6	0.294303552937	0.441455329406	0.294303552751	0.441455329126	0.294303559429	0.441455339143
0.7	0.312697524996	0.423061357347	0.312697524798	0.423061357080	0.312697531893	0.423061366679
0.8	0.331091497054	0.404667385289	0.331091496845	0.404667385033	0.331091504357	0.404667394214
0.9	0.349485469113	0.386273413230	0.349485468892	0.386273412986	0.349485476821	0.386273421750
1.0	0.367879441171	0.367879441171	0.367879440939	0.367879440939	0.367879449286	0.367879449286

Table 4. The errors of the FRKCK4 and FRK4 for the (ii)–differentiability at t = 1.

$\mathit{\alpha }$	Error Analysis of FRKCK4		Error Analysis of FRK4
	$\underset{¯}{\mathit{e}}\left(1,\mathit{\alpha }\right)$	$\overline{\mathit{e}}\left(1,\mathit{\alpha }\right)$	$\underset{¯}{\mathit{e}}\left(1,\mathit{\alpha }\right)$	$\overline{\mathit{e}}\left(1,\mathit{\alpha }\right)$
0	0.000000000116	0.000000000349	0.000000004057	0.000000012171
0.1	0.000000000128	0.000000000337	0.000000004463	0.000000011766
0.2	0.000000000140	0.000000000326	0.000000004869	0.000000011360
0.3	0.000000000151	0.000000000314	0.000000005274	0.000000010954
0.4	0.000000000163	0.000000000303	0.000000005680	0.000000010549
0.5	0.000000000175	0.000000000291	0.000000006086	0.000000010143
0.6	0.000000000186	0.000000000279	0.000000006491	0.000000009737
0.7	0.000000000198	0.000000000268	0.000000006897	0.000000009331
0.8	0.000000000209	0.000000000256	0.000000007303	0.000000008926
0.9	0.000000000221	0.000000000244	0.000000007709	0.000000008520
1.0	0.000000000233	0.000000000233	0.000000008114	0.000000008114

Table 1 compared the analytical and numerical solutions for the (i)–differentiability produced by the FRKCK4 and FRK4 at time $t=1$. According to the table, the solution generated by the FRKCK4 is closer to the analytical solution than FRK4. This is obvious from error analysis, as shown in Table 2. Figure 1a–c presents the FRKCK4, FRK4, and analytical solutions, respectively, at the time intervals $t\in \left[0,4\right]$. The figures make it quite evident that the fuzzy solutions are expanding as $t$ increases. This is true under the property of the (i)–differentiability.

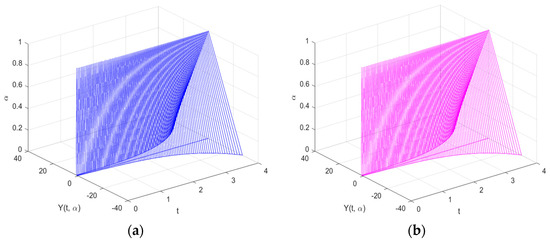
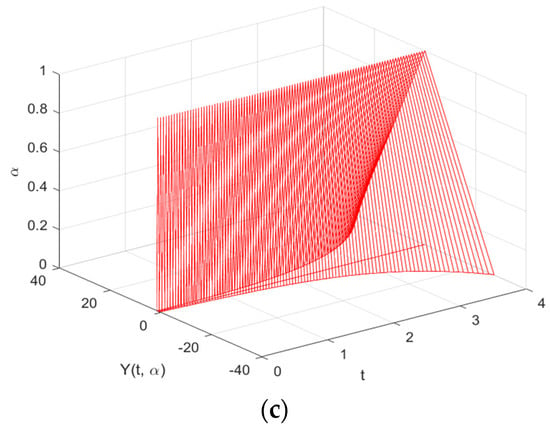
Figure 1. The approximate solutions of (a) the FRKCK4 and (b) the FRK4, and the (c) analytical solution of Example 1 for the (i)–differentiability.

The analytical and numerical solutions for the (ii)–differentiability generated by the FRKCK4 and FRK4 at time $t=1$ are presented in Table 3. From the table, it indicates that the solution produced by the FRKCK4 is closer to the analytical solution than the FRK4. This can be seen clearly from the error analysis, as demonstrated in Table 4. The FRKCK4, FRK4, and the analytical solutions at the time intervals $t\in \left[0,4\right]$ are shown in Figure 2a–c, respectively. The figures clearly demonstrate that as $t$ increases, the fuzzy solutions become contracted. This is true under the property of the (ii)–differentiability.

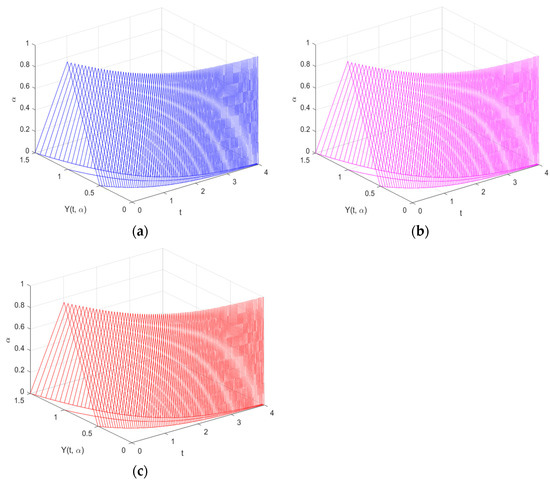
Figure 2. The approximate solutions of (a) the FRKCK4 and (b) the FRK4, and the (c) analytical solution of Example 1 for the (ii)–differentiability.

In the following example, we adopted Example 4.2 from [29].

Example 2 [29]. We consider the following non-autonomous FDE by implementing our proposed model:

$$\left\{\begin{array}{l}{Y}^{\prime }\left(t\right) = -\frac{R}{L} Y\left(t\right) + v\left(t\right), t\in \left[0, 1\right], \\ Y\left(0, \alpha \right) = (0.96 + 0.04\alpha , 1.01 - 0.01\alpha ), 0\le \alpha \le 1.\end{array}\right.$$

(17)

Equation (17) above refers to an electrical circuit with an alternating current (AC) source that contains a resistor (R) and inductor (L). Let $R=1 \Omega , L= 1 H$, and $v\left(t\right)=\sin \left(t\right).$ Therefore, Equation (17) may be written as follows:

$$\left\{\begin{array}{l}{Y}^{\prime }\left(t\right) = - Y\left(t\right) + \sin \left(t\right), t\in \left[0, 1\right], \\ Y\left(0, \alpha \right) = (0.96 + 0.04\alpha , 1.01 - 0.01\alpha ), 0\le \alpha \le 1.\end{array}\right.$$

(18)

Using the (i)–differentiability, we translate Equation (18) into the ODE system.

$$\left\{\begin{array}{l}{\underset{¯}{y}}^{\prime }\left(t\right) = -\overline{y}\left(t\right) + \sin \left(t\right), t\in \left[0, 1\right],\\ {\overline{y}}^{\prime }\left(t\right) = -\underset{¯}{y}\left(t\right) + \sin \left(t\right),\\ \underset{¯}{y}\left(0, \alpha \right)=0.96 + 0.04\alpha ,\\ \overline{y}\left(0, \alpha \right) = 1.01 - 0.01\alpha , 0\le \alpha \le 1. \end{array}\right.$$

(19)

In order to solve Equation (19), the following is proposed:

$$\begin{array}{l}{\underset{\_}{k}}_1 = -{\overline{y}}_i\left(\alpha \right) + \sin \left(t_i\right),\\ {\overline{k}}_1 = -{\underset{\_}{y}}_i\left(\alpha \right) + \sin \left(t_i\right),\\ {\underset{\_}{k}}_2 = -{\overline{y}}_i\left(\alpha \right) + \frac{1}{5}\Delta t{\underset{\_}{k}}_1 + \sin \left(t_i+\frac{1}{5}\Delta t\right),\\ {\overline{k}}_2 = -{\underset{\_}{y}}_i\left(\alpha \right) + \frac{1}{5}\Delta t{\overline{k}}_1 + \sin \left(t_i+\frac{1}{5}\Delta t\right),\\ {\underset{\_}{k}}_3 = -{\overline{y}}_i\left(\alpha \right) + \frac{3}{40}\Delta t{\underset{\_}{k}}_1 + \frac{9}{40}\Delta t{\underset{\_}{k}}_2 + \sin \left(t_i+\frac{3}{10}\Delta t\right),\\ {\overline{k}}_3 = -{\underset{\_}{y}}_i\left(\alpha \right) + \frac{3}{40}\Delta t{\overline{k}}_1 + \frac{9}{40}\Delta t{\overline{k}}_2 + \sin \left(t_i+\frac{3}{10}\Delta t\right),\\ {\underset{\_}{k}}_4 = -{\overline{y}}_i\left(\alpha \right) + \frac{3}{10}\Delta t{\underset{\_}{k}}_1 - \frac{9}{10}\Delta t{\underset{\_}{k}}_2 + \frac{6}{5}\Delta t{\underset{\_}{k}}_3 + \sin \left(t_i+\frac{3}{5}\Delta t\right),\\ {\overline{k}}_4 = -{\underset{\_}{y}}_i\left(\alpha \right) + \frac{3}{10}\Delta t{\overline{k}}_1 - \frac{9}{10}\Delta t{\overline{k}}_2 + \frac{6}{5}\Delta t{\overline{k}}_3 + \sin \left(t_i+\frac{3}{5}\Delta t\right),\\ {\underset{\_}{k}}_5 = -{\overline{y}}_i\left(\alpha \right) - \frac{11}{54}\Delta t{\underset{\_}{k}}_1 + \frac{5}{2}\Delta t{\underset{\_}{k}}_2 - \frac{70}{27}\Delta t{\underset{\_}{k}}_3 + \frac{35}{27}\Delta t{\underset{\_}{k}}_4 + \sin \left(t_i+\Delta t\right),\\ {\overline{k}}_5 = -{\underset{\_}{y}}_i\left(\alpha \right) - \frac{11}{54}\Delta t{\overline{k}}_1 + \frac{5}{2}\Delta t{\overline{k}}_2 - \frac{70}{27}\Delta t{\overline{k}}_3 + \frac{35}{27}\Delta t{\overline{k}}_4 + \sin \left(t_i+\Delta t\right),\\ {\underset{\_}{k}}_6 = -{\overline{y}}_i\left(\alpha \right) + \frac{1631}{55296}\Delta t{\underset{\_}{k}}_1 + \frac{175}{512}\Delta t{\underset{\_}{k}}_2 + \frac{575}{13824}\Delta t{\underset{\_}{k}}_3 + \frac{44275}{110592}\Delta t{\underset{\_}{k}}_4 + \\ \frac{253}{4096}\Delta t{\underset{\_}{k}}_5 + \sin \left(t_i+\frac{7}{8}\Delta t\right),\\ {\overline{k}}_6 = -{\underset{\_}{y}}_i\left(\alpha \right) + \frac{1631}{55296}\Delta t{\overline{k}}_1 + \frac{175}{512}\Delta t{\overline{k}}_2 + \frac{575}{13824}\Delta t{\overline{k}}_3 + \frac{44275}{110592}\Delta t{\overline{k}}_4 + \\ \frac{253}{4096}\Delta t{\overline{k}}_5 + \sin \left(t_i+\frac{7}{8}\Delta t\right).\end{array}$$

The analytical solution for the (i)–differentiability is:

$$\begin{array}{l}\widetilde{\underset{¯}{y}}\left(t, \alpha \right) = -\frac{1}{2} \left(0.05 - 0.05\alpha \right)e^t + \frac{1}{2} \left(2.97 + 0.03\alpha \right)e^{-t} + \frac{1}{2} \left(\sin \left(t\right) - \cos \left(t\right)\right),\\ \tilde{\overline{y}}\left(t, \alpha \right) = \frac{1}{2} \left(0.05 - 0.05\alpha \right)e^t + \frac{1}{2} \left(2.97 + 0.03\alpha \right)e^{-t} + \frac{1}{2} \left(\sin \left(t\right) - \cos \left(t\right)\right). \end{array}$$

Using the (ii)–differentiability, we translate Equation (18) into the ODE system below

$$\left\{\begin{array}{l}{\underset{¯}{y}}^{\prime }\left(t\right) = -\underset{¯}{y}\left(t\right) + \sin \left(t\right), t\in \left[0, 1\right],\\ {\overline{y}}^{\prime }\left(t\right) = -\overline{y}\left(t\right) + \sin \left(t\right),\\ \underset{¯}{y}\left(0, \alpha \right)=0.96 + 0.04\alpha ,\\ \overline{y}\left(0, \alpha \right) = 1.01 - 0.01\alpha , 0\le \alpha \le 1. \end{array}\right.$$

(20)

In order to solve Equation (20), the following is proposed:

$$\begin{array}{l}{\underset{\_}{k}}_1 = -{\underset{\_}{y}}_i\left(\alpha \right) + \sin \left(t_i\right),\\ {\overline{k}}_1 = -{\overline{y}}_i\left(\alpha \right) + \sin \left(t_i\right),\\ {\underset{\_}{k}}_2 = -{\underset{\_}{y}}_i\left(\alpha \right) + \frac{1}{5}\Delta t{\underset{\_}{k}}_1 + \sin \left(t_i+\frac{1}{5}\Delta t\right),\\ {\overline{k}}_2 = -{\overline{y}}_i\left(\alpha \right) + \frac{1}{5}\Delta t{\overline{k}}_1 + \sin \left(t_i+\frac{1}{5}\Delta t\right),\\ {\underset{\_}{k}}_3 = -{\underset{\_}{y}}_i\left(\alpha \right) + \frac{3}{40}\Delta t{\underset{\_}{k}}_1 + \frac{9}{40}\Delta t{\underset{\_}{k}}_2 + \sin \left(t_i+\frac{3}{10}\Delta t\right),\\ {\overline{k}}_3 = -{\overline{y}}_i\left(\alpha \right) + \frac{3}{40}\Delta t{\overline{k}}_1 + \frac{9}{40}\Delta t{\overline{k}}_2 + \sin \left(t_i+\frac{3}{10}\Delta t\right),\\ {\underset{\_}{k}}_4 = -{\underset{\_}{y}}_i\left(\alpha \right) + \frac{3}{10}\Delta t{\underset{\_}{k}}_1 - \frac{9}{10}\Delta t{\underset{\_}{k}}_2 + \frac{6}{5}\Delta t{\underset{\_}{k}}_3 + \sin \left(t_i+\frac{3}{5}\Delta t\right),\\ {\overline{k}}_4 = -{\overline{y}}_i\left(\alpha \right) + \frac{3}{10}\Delta t{\overline{k}}_1 - \frac{9}{10}\Delta t{\overline{k}}_2 + \frac{6}{5}\Delta t{\overline{k}}_3 + \sin \left(t_i+\frac{3}{5}\Delta t\right),\\ {\underset{\_}{k}}_5 = -{\underset{\_}{y}}_i\left(\alpha \right) - \frac{11}{54}\Delta t{\underset{\_}{k}}_1 + \frac{5}{2}\Delta t{\underset{\_}{k}}_2 - \frac{70}{27}\Delta t{\underset{\_}{k}}_3 + \frac{35}{27}\Delta t{\underset{\_}{k}}_4 + \sin \left(t_i+\Delta t\right),\\ {\overline{k}}_5 = -{\overline{y}}_i\left(\alpha \right) - \frac{11}{54}\Delta t{\overline{k}}_1 + \frac{5}{2}\Delta t{\overline{k}}_2 - \frac{70}{27}\Delta t{\overline{k}}_3 + \frac{35}{27}\Delta t{\overline{k}}_4 + \sin \left(t_i+\Delta t\right),\\ {\underset{\_}{k}}_6 = -{\underset{\_}{y}}_i\left(\alpha \right) + \frac{1631}{55296}\Delta t{\underset{\_}{k}}_1 + \frac{175}{512}\Delta t{\underset{\_}{k}}_2 + \frac{575}{13824}\Delta t{\underset{\_}{k}}_3 + \frac{44275}{110592}\Delta t{\underset{\_}{k}}_4 + \\ \frac{253}{4096}\Delta t{\underset{\_}{k}}_5 + \sin \left(t_i+\frac{7}{8}\Delta t\right),\\ {\overline{k}}_6 = -{\overline{y}}_i\left(\alpha \right) + \frac{1631}{55296}\Delta t{\overline{k}}_1 + \frac{175}{512}\Delta t{\overline{k}}_2 + \frac{575}{13824}\Delta t{\overline{k}}_3 + \frac{44275}{110592}\Delta t{\overline{k}}_4 + \\ \frac{253}{4096}\Delta t{\overline{k}}_5 + \sin \left(t_i+\frac{7}{8}\Delta t\right).\end{array}$$

The analytical solution for the (ii)–differentiability is:

$$\begin{array}{l}\widetilde{\underset{¯}{y}}\left(t, \alpha \right) = -\frac{1}{2} \left(\sin \left(t\right) - \cos \left(t\right)\right) + e^{-t} \left(1.46 + 0.04 \alpha \right),\\ \tilde{\overline{y}}\left(t, \alpha \right) = \frac{1}{2} \left(\sin \left(t\right) - \cos \left(t\right)\right) + e^{-t} \left(1.51 - 0.01 \alpha \right).\end{array}$$

By implementing the proposed method, we tested Example 2 using the step size $\Delta t=0.01,$ $N=100$, and the result was adjusted to 12 decimal places. The comparisons between the analytical and approximate solutions at $t=1$ for the (i)–differentiability is quantified and tabulated in Table 5, while the errors are listed in Table 6. For the (ii)–differentiability, the comparisons between the analytical and approximate solutions at $t=1$ is tabulated in Table 7, while the errors are listed in Table 8.

Table 5. The comparisons of the analytical and approximate solutions for the (i)–differentiability at t = 1.

$\mathit{\alpha }$	Analytical Solution		FRKCK4		FRK4
	$\widetilde{\underset{¯}{\mathit{y}}}\left(1,\mathit{\alpha }\right)$	$\widetilde{\overline{\mathit{y}}}\left(1,\mathit{\alpha }\right)$	$\underset{¯}{\mathit{y}}\left(1,\mathit{\alpha }\right)$	$\overline{\mathit{y}}\left(1,\mathit{\alpha }\right)$	$\underset{¯}{\mathit{y}}\left(1,\mathit{\alpha }\right)$	$\overline{\mathit{y}}\left(1,\mathit{\alpha }\right)$
0	0.628928263898	0.764842355321	0.628928263896	0.764842355320	0.628928263944	0.764842355356
0.1	0.636275787631	0.758598469912	0.636275787629	0.758598469910	0.636275787676	0.758598469947
0.2	0.643623311364	0.752354584502	0.643623311362	0.752354584501	0.643623311409	0.752354584538
0.3	0.650970835097	0.746110699093	0.650970835095	0.746110699091	0.650970835141	0.746110699129
0.4	0.658318358830	0.739866813683	0.658318358828	0.739866813682	0.658318358874	0.739866813721
0.5	0.665665882563	0.733622928274	0.665665882561	0.733622928272	0.665665882606	0.733622928312
0.6	0.673013406295	0.727379042865	0.673013406294	0.727379042863	0.673013406338	0.727379042903
0.7	0.680360930028	0.721135157455	0.680360930027	0.721135157454	0.680360930071	0.721135157494
0.8	0.687708453761	0.714891272046	0.687708453760	0.714891272044	0.687708453803	0.714891272085
0.9	0.695055977494	0.708647386636	0.695055977493	0.708647386635	0.695055977535	0.708647386677
1.0	0.702403501227	0.702403501227	0.702403501225	0.702403501225	0.702403501268	0.702403501268

Table 6. The errors of the FRKCK4 and FRK4 for the (ii)–differentiability at t = 1.

$\mathit{\alpha }$	Error Analysis of FRKCK4		Error Analysis of FRK4
	$\underset{¯}{\mathit{e}}\left(1,\mathit{\alpha }\right)$	$\overline{\mathit{e}}\left(1,\mathit{\alpha }\right)$	$\underset{¯}{\mathit{e}}\left(1,\mathit{\alpha }\right)$	$\overline{\mathit{e}}\left(1,\mathit{\alpha }\right)$
0	0.000000000002	0.000000000001	0.000000000046	0.000000000035
0.1	0.000000000002	0.000000000001	0.000000000045	0.000000000035
0.2	0.000000000002	0.000000000001	0.000000000045	0.000000000036
0.3	0.000000000002	0.000000000001	0.000000000044	0.000000000037
0.4	0.000000000002	0.000000000001	0.000000000044	0.000000000037
0.5	0.000000000002	0.000000000001	0.000000000043	0.000000000038
0.6	0.000000000002	0.000000000002	0.000000000043	0.000000000038
0.7	0.000000000002	0.000000000002	0.000000000042	0.000000000039
0.8	0.000000000002	0.000000000002	0.000000000042	0.000000000040
0.9	0.000000000002	0.000000000002	0.000000000041	0.000000000040
1.0	0.000000000002	0.000000000002	0.000000000041	0.000000000041

Table 7. The comparisons of the analytical and approximate solutions for the (ii)–differentiability at t = 1.

$\mathit{\alpha }$	Analytical Solution		FRKCK4		FRK4
	$\underset{¯}{\tilde{\mathit{y}}}\left(1,\mathit{\alpha }\right)$	$\widetilde{\overline{\mathit{y}}}\left(1,\mathit{\alpha }\right)$	$\underset{¯}{\mathit{y}}\left(1,\mathit{\alpha }\right)$	$\overline{\mathit{y}}\left(1,\mathit{\alpha }\right)$	$\underset{¯}{\mathit{y}}\left(1,\mathit{\alpha }\right)$	$\overline{\mathit{y}}\left(1,\mathit{\alpha }\right)$
0	0.687688323580	0.706082295639	0.687688323579	0.706082295637	0.687688323620	0.706082295680
0.1	0.689159841345	0.705714416198	0.689159841343	0.705714416196	0.689159841385	0.705714416239
0.2	0.690631359110	0.705346536756	0.690631359108	0.705346536755	0.690631359149	0.705346536797
0.3	0.692102876874	0.704978657315	0.692102876873	0.704978657314	0.692102876914	0.704978657356
0.4	0.693574394639	0.704610777874	0.693574394637	0.704610777872	0.693574394679	0.704610777915
0.5	0.695045912404	0.704242898433	0.695045912402	0.704242898431	0.695045912444	0.704242898474
0.6	0.696517430168	0.703875018992	0.696517430167	0.703875018990	0.696517430209	0.703875019033
0.7	0.697988947933	0.703507139551	0.697988947931	0.703507139549	0.697988947973	0.703507139591
0.8	0.699460465698	0.703139260109	0.699460465696	0.703139260108	0.699460465738	0.703139260150
0.9	0.700931983462	0.702771380668	0.700931983461	0.702771380667	0.700931983503	0.702771380709
1.0	0.702403501227	0.702403501227	0.702403501225	0.702403501225	0.702403501268	0.702403501268

Table 8. The errors of the FRKCK4 and FRK4 for the (ii)–differentiability at t = 1.

$\mathit{\alpha }$	Error Analysis of FRKCK4		Error Analysis of FRK4
	$\underset{¯}{\mathit{e}}\left(1,\mathit{\alpha }\right)$	$\overline{\mathit{e}}\left(1,\mathit{\alpha }\right)$	$\underset{¯}{\mathit{e}}\left(1,\mathit{\alpha }\right)$	$\overline{\mathit{e}}\left(1,\mathit{\alpha }\right)$
0	0.000000000002	0.000000000002	0.000000000040	0.000000000041
0.1	0.000000000002	0.000000000002	0.000000000040	0.000000000041
0.2	0.000000000002	0.000000000002	0.000000000040	0.000000000041
0.3	0.000000000002	0.000000000002	0.000000000040	0.000000000041
0.4	0.000000000002	0.000000000002	0.000000000040	0.000000000041
0.5	0.000000000002	0.000000000002	0.000000000040	0.000000000041
0.6	0.000000000002	0.000000000002	0.000000000040	0.000000000041
0.7	0.000000000002	0.000000000002	0.000000000040	0.000000000041
0.8	0.000000000002	0.000000000002	0.000000000041	0.000000000041
0.9	0.000000000002	0.000000000002	0.000000000041	0.000000000041
1.0	0.000000000002	0.000000000002	0.000000000041	0.000000000041

A comparison of the analytical and numerical solutions for the (i)–differentiability obtained by the FRKCK4 and FRK4 at time $t=1$ is shown in Table 5. The table shows that the solution produced by the FRKCK4 is closer to the analytical solution than the FRK4. This is clear through error analysis, which is presented in Table 6. The solutions of the FRKCK4, FRK4, and the analytical solutions at time intervals $t\in \left[0,4\right]$ are shown in Figure 3a–c. The figures clearly show that the fuzzy solutions are expanding as $t$ increases. This is true under the property of the (i)–differentiability.

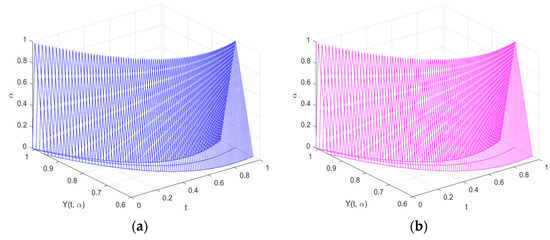
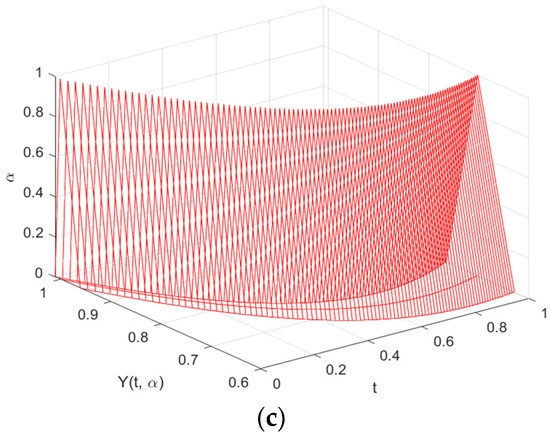
Figure 3. The approximate solutions of (a) the FRKCK4 and (b) the FRK4, and the (c) analytical solution of Example 2 for the (i)–differentiability.

Table 7 displays a comparison between the analytical and numerical solutions for the (ii)–differentiability obtained by the FRKCK4 and FRK4 at time $t=1$. The table demonstrates that the FRKCK4’s solution, as opposed to the FRK4, is closer to the analytical solution. The error analysis presented in Table 8 makes this very evident. Figure 4a–c displays the solutions of the FRKCK4 and FRK4 and the analytical solutions at time intervals $t\in \left[0,4\right]$. It is clear from the figures that as $t$ increases, the fuzzy solutions are contracting. This is true under the property of the (ii)–differentiability.

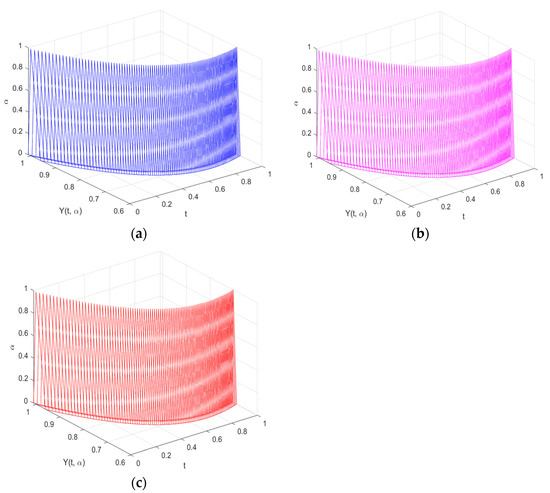
Figure 4. The approximate solutions of (a) the FRKCK4 and (b) the FRK4, and the (c) analytical solution of Example 2 for the (ii)–differentiability.

6. Advantages of the Proposed Model

Numerical methods are often used in science and engineering to solve real-world issues. Its ability to produce a result even without an analytical solution is one of its advantages. If an analytical solution is available, it may be possible to compare the analytical solution to an approximation using error analysis.

Based on the above study, a traditional RKCK4 has been proposed in the form of a fuzzy setting called the FRKCK4. Furthermore, the step-by-step procedures have been provided to help researchers to understand and develop algorithms in any programming language. Additionally, the theoretical convergence analysis of the FRKCK4 is presented and proved mathematically.

To demonstrate the effectiveness of the FRKCK4, two types of fuzzy differential equations, namely the autonomous and non-autonomous, have been considered. The results demonstrated that the FRKCK4 is superior to the FRK4 because the error obtained is smaller, when compared to the analytical solution. This can be seen clearly in Table 2, Table 4, Table 6 and Table 8.

Apart from that, the FRKCK4 is able to produce convex fuzzy solutions on each time domain $t$ (see Figure 1a, Figure 2a, Figure 3a and Figure 4a). This clearly showed that the fuzzy solution produced by the FRKCK4 satisfies Definition 1.

7. Conclusions

This study uses the characterization theorem to propose a traditional RKCK4 in a fuzzy setting. Under the interpretation of the (i) and (ii)–differentiability, the step-by-step procedures have been provided to solve the autonomous and non-autonomous fuzzy differential equations. Additionally, the theoretical convergence analysis is presented and proved mathematically.

To demonstrate the viability of the proposed method, numerical simulations of the autonomous and non-autonomous FDEs are then examined. The analytical solutions and the FRK4 were used to compare the results of the FRKCK4. The error analysis revealed that the FRKCK4 generates results that are more accurate than the FRK4. This is because the error produced by the FRKCK4 is smaller than the FRK4, when compared to the analytical solution.

Graphs are used to depict the study’s findings and demonstrate how the solutions to both FDEs behaved in the time domain $t$. It is discovered that both solutions are expanding as $t$ increases under the (i)-differentiability. However, this is not the case under the (ii)-differentiability, which is contracting. This is consistent under the (i) and (ii)–differentiability interpretations.

In general, the FRKCK4 can solve FDEs with a good agreement. Moreover, for a better approximation, it can be further extended to higher-order degrees.