Propose-Specific Information Related to Prediction Level at x and Mean Magnitude of Relative Error: A Case Study of Software Effort Estimation

Abstract

The prediction level at x ($PRED\left(x\right)$) and mean magnitude of relative error ($MMRE$) are measured based on the magnitude of relative error between real and predicted values. They are the standard metrics that evaluate accurate effort estimates. However, these values might not reveal the magnitude of over-/under-estimation. This study aims to define additional information associated with the $PRED\left(x\right)$ and $MMRE$ to help practitioners better interpret those values. We propose the formulas associated with the $PRED\left(x\right)$ and $MMRE$ to express the level of scatters of predictive values versus actual values on the left ($si{g}_{Left}$), on the right ($si{g}_{Right}$), and on the mean of the scatters ($sig$). We depict the benefit of the formulas with three use case points datasets. The proposed formulas might contribute to enriching the value of the $PRED\left(x\right)$ and $MMRE$ in validating the effort estimation.

1. Introduction

One of the essential aspects of developing software projects is software effort estimation (SEE) [1,2,3,4,5]. In the early stages of project development, resources or budgets must be measured. The estimation might assist software project managers in determining how much money from the budget is being spent on maintenance activities or project completion. The inaccurate estimate might lead to unrealistic resource allocation and project risk, leading to project failure [6]. The accuracy of effort estimation is, therefore, crucial. Scientists have always adopted evaluation criteria when comparing their proposal models to estimate software project efforts with others. The model that best meets the evaluation criteria is likely to be the most appropriate model chosen to be used to estimate subsequent projects [6,7].

The magnitude of relative error ($MRE$), prediction level at x ($PRED\left(x\right)$), and mean magnitude of relative error ($MMRE$) that were proposed by [8] are well-known evaluation criteria in SEE (see Equations (1)–(3) below). Although Myrtveit, Stensrud, and Shepperd stated that this criterion might have some disadvantages given the $MMRE$, it is still widely used in the validation of real effort estimation. As presented in Table 1, many researchers have used them for measuring the accurate predictive effort estimation:

$$MR{E}_i=\frac{|y_i-\widehat{y_i}|}{y_i}$$

(1)

$$MMRE=\frac{{\sum }_{i=1}^{N}MR{E}_i}{N}$$

(2)

$$PRED\left(x\right)=\frac{1}{N}\sum _{i=1}^N\left\{\begin{array}{cc}1\hfill & \mathrm{if}MR{E}_i\le x\hfill \\ 0\hfill & otherwise\hfill \end{array}\right.$$

(3)

where $\widehat{y_i}$ is the predicted and $y_i$ is the i-th observed value.

Table 1. Summary of reviewed related papers in recent years, where the MMRE was adopted.

Authors	Proposal Model	Compare With	Criteria
Mahmood et al. [3]	Machine-learning-based ensemble techniques	Machine-learning-based solo techniques	$MMRE,PRED\left(x\right)$
Praynlin [9]	Metacognitive neuro-fuzzy	Particle swarm optimization, genetic algorithm, and backpropagation network	$MMRE,PRED\left(x\right),$ and other evaluation criteria
Fadhil et al. [10]	DolBat	COCOMO II	$MMRE,PRED\left(x\right)$
Bilgaiyan, S. et al. [11]	Feedforward backpropagation NN	Cascade correlation NN, Elman NN	$MMRE,PRED\left(x\right)$, $MSE$
Mustapha et al. [12]	RF	Classical regression tree	$MMRE$, $PRED\left(x\right)$, $MdMRE$
Ullah et al. [13]	Flower pollination algorithm	COCOMO-II	$MMRE$
Sethy and Rani [14]	TLBO	Bailey, COCOMO 2, Halstead, SEL BCO	$MMRE$
Effendi et al. [15]	Optimization of COCOMO II constants	COCOMO II	$MMRE$
Khan et al. [16]	Optimization of COCOMO	COCOMO	$MMRE$
Desai and Mohanty [17]	ANN-COA	Other neural network-based techniques	$MMRE,RMSE$

As can be seen, Equations (2) and (3) only provide evaluation criteria for estimation, and they might not reveal the distribution of predicted values and observed values around a baseline. A baseline is a straight line where predictive and actual values are the same, i.e., a line with an equation $\widehat{y_i}=y_i$. Although such information might be determined by analyzing the prediction residuals, additional information associated with the $PRED\left(x\right)$ and $MMRE$ might be more interesting. The distribution of these values might be helpful information for researchers because it might bring additional information about the predictive model’s performance.

This article proposes the additional information related to the $PRED\left(x\right)$ and $MMRE$ by defining formulas, $si{g}_{Left}$, $si{g}_{Right}$, and $sig$, to determine how the predicted values in comparison with actual values are symmetric around the baseline. The $si{g}_{Left}$, $si{g}_{Right}$, and $sig$ values may reflect the proposed model’s trend. The closer the values reach 0, the better the proposed model distributes around the baseline. On the other hand, if they approach either –1 or +1, the proposed model is either under- or over-estimated. Hence, their value might contribute to the $PRED\left(x\right)$ and $MMRE$.

The sections of this article are organized as follows: Section 2 presents the related works; Section 3 proposes the three formulas $si{g}_{Left}$, $si{g}_{Right}$, and $sig$; the characteristics of the sig formula are presented in Section 4; Section 5 presents the research questions; Section 6 gives the result and discussion; Section 7 conveys the conclusion and future work.

2. Related Works

The $PRED\left(x\right)$ and $MMRE$ might be used in SEE situations because they interpret the absolute percentage error. Since the $PRED\left(x\right)$ and $MMRE$ do not scale, they might be used to aggregate estimated errors from software development projects of various sizes. According to Jørgensen et al., however, there is no top score constraint for overestimating in the $MMRE$; underestimating effort will never result in an $MMRE$ score more significant than one. In their publication [18], they investigated the requirements for the practical usage of the $MMRE$ in effort estimation contexts. As a result, they stated that this criterion was still helpful in effort estimation in most cases.

According to Conte et al., one of the advantages of the $MMRE$ is that its comparison might be adopted for all kinds of predicted models [8]. However, Foss et al. [19] concluded that it might not be correct when they simulated analysis using the model evaluation criteria $MMRE$. They realized that the $MMRE$ might be an untrustworthy or insufficient criterion when choosing suitable linear predicted models in terms of the $MMRE$. They stated that the $MMRE$ is likely to select a model that delivers an underestimation of a model. They advised employing a combination of the theoretical justification for the proposed models and additional criteria. A similar conclusion was also shown by Myrtveit et al. [20].

In addition, Kitchenham et al. [21] proposed the variable z (where z = predicted/actual) derived from the $MMRE$. They argued that the distribution of z was required to evaluate the accuracy of a predictive model. However, they also pointed out that the z variable had a limit regarding the summary statistics. The estimation may prefer prediction models that minimize overestimations over prediction systems rather than underestimates. Furthermore, several researchers used other criteria when evaluating the performance of effort estimation, such as the mean inverse balanced relative error ($MIBRE$), mean balanced relative error ($MBRE$), mean absolute error ($MAE$), and standardized accuracy (SA). They stated that the $MMRE$ might be unbalanced and yield an asymmetry distribution [22,23]. This means that this criterion might cause some problems identifying under-estimating or over-estimating.

Moreover, as mentioned in the reports [24,25], the $MMRE$ is possibly the most widely used measure of estimation error in research and industrial applications. There might be several advantages of the $MMRE$ that can boost its popularity, such as: (1) it is unaffected by the sizing unit used; it makes no difference whether SEE is measured in hours or months of workload [20]; (2) it might be not influenced by scale; this means that the accuracy of the $MMRE$ does not change with the sizing unit selected [26].

This section presents a literature overview of recent papers that used the $MMRE$ and $PRED\left(x\right)$ to validate the model’s accuracy in SEE. The search criteria are based on the most recently published articles with high citations. In addition, we will present some review studies in which the authors list the research articles related to SEE and the number of studies that use the $MMRE$ and $PRED\left(x\right)$.

In 2022, Mahmood et al. investigated the effectiveness of machine-learning-based effort estimation based on the $MMRE$ and $PRED\left(0.25\right)$ [3]. They concluded that ensemble effort estimation techniques might be better than solo techniques. Praynlin 2021 also used the $MMRE$ and other evaluation criteria to validate meta cognitive neuro fuzzy and other methods (particle swarm optimization, genetic algorithm, and backpropagation network) [9]. Furthermore, Fadhil et al. [10] proposed the DolBat model to predict effort estimation; this proposal was compared with the constructive cost model (COCOMO) based on the $MMRE$ and $PRED\left(x\right)$ [10]. As a result, they concluded that their model was better than COCOMO II. This criterion was also used by Hamid et al. [27] when they compared the IRDSS model with Delphi and Planning Poker [27].

Bilgaiyan, S. et al. [11] adopted the $MMRE$, $PRED\left(x\right)$, and mean-squared error ($MSE$) in comparison to the performance of the feedforward back-propagation neural network (NN), cascade correlation NN, and Elman NN in terms of effort estimation [11]. Mustapha et al. also used the $PRED\left(0.25\right)$, $MMRE$, and median of the magnitude of the relative error ($MdMRE$) to identify the accuracy of their approach when they investigated the use of random forest in software effort estimation [12]. The $MMRE$ was also adopted to validate the accurate effort estimation reported in the publication [13,14].

On the other hand, this criterion was employed by Desai and Mohanty [17]; Effendi, Sarno, and Prasetyo [15]; and Khan et al. [16]. Effendi et al. compared the Optimization of COCOMO with COCOMO [15]; Khan et al. used it and the $PRED\left(x\right)$ to compare their proposal and Delphi and Planning Poker [16], while Desai et al. applied the $MMRE$ and root-mean-squared error (RMSE) to validate ANN-COA with Other neural network-based techniques [17].

Last but not least, Asad Ali and Carmine Gravino (2019) studied the machine learning approaches employed in software effort prediction from 1991 to 2017 [28]. A total of 75 papers were selected after carefully evaluating the inclusion/exclusion and quality assessment filter. The $MMRE$, $PRED\left(0.25\right)$, and $MdMRE$ were studied in those papers. Out of the 75 papers chosen, 69 used the $MMRE$ as a measure of accuracy, accounting for 92% of the total. The following highest percentages were the $PRED\left(0.25\right)$ at 69% and 47% for the $MdMRE$. They claimed that the $MMRE$ and $PRED\left(0.25\right)$ are frequently employed as accuracy metrics in the papers they chose. In 2018, Gautam et al. examined software effort estimates published between 1981 and 2016 [29]. They provided a list of 56 publications that included the datasets used, validation techniques, performance metrics, statistical tests, and graphical analyses, where the $MMRE$ and $PRED\left(x\right)$ take into account 32 out of 56 observations (57%).

As presented above, there are several criteria that researchers might consider for their proposals, such as the $SA$, $MIBRE$, $MBRE$, $MAE$, and $RMSE$. However, the $MMRE$ and $PRED\left(x\right)$ are frequently used as evaluation criteria. Table 1 summarizes the several articles that adopted those criteria in validating SEE in recent years.

3. Sig Formula

This paper proposes a function $sign(y_i,\widehat{y_i})$ expressed below by Equation (4). “i” represents the i-th item in the survey dataset. If the predicted value of the i-th item, denoted as $\widehat{y_i}$, is greater than the actual value of the i-th item, denoted as $y_i$, the value of $sign(y_i,\widehat{y_i})$ is set to +1. If the predicted value is less than the actual one, the value of $sign(y_i,\widehat{y_i})$ is set to –1. If there is no difference between the predicted and actual values, then $sign(y_i,\widehat{y_i})$ is setto be equal to zero.

Three new $sig$ formulas ($si{g}_{Left}(y,\widehat{y})$, $si{g}_{Right}(y,\widehat{y})$, and $sig(y,\widehat{y})$) are introduced by Equations (5)–(7). The double sum in each of Equations (5) and (6) is the sum of $“cumulativesu{m}^{”}$ of $sign(y_i,\widehat{y_i})$ of the studied pairs. N is the number of all pairs.

$$sign(y_i,\widehat{y_i})=\left\{\begin{array}{cc}1\hfill & \mathrm{if}\widehat{y_i}>y_i\hfill \\ 0\hfill & \mathrm{if}\widehat{y_i}=y_i\hfill \\ -1\hfill & \widehat{y_i}<y_i\hfill \end{array}\right.$$

(4)

$$si{g}_{Left}(y,\widehat{y})=\frac{2}{N(N+1)}\sum _{k=1}^N\sum _{i=1}^{k}sign(y_i,\widehat{y_i})$$

(5)

$$si{g}_{Right}(y,\widehat{y})=\frac{2}{N(N+1)}\sum _{k=1}^N\sum _{i=1}^{k}sign(y_{N-i+1},{\widehat{y}}_{N-i+1})$$

(6)

$$sig(y,\widehat{y})=\frac{si{g}_{Left}(y,\widehat{y})+si{g}_{Right}(y,\widehat{y})}{2}$$

(7)

Suppose a coordinate system where actual values $y_i$ are on the horizontal axis and predicted values $\widehat{y_i}$ are on the vertical axis. In Figure 1, there is such a system with a dashed line of the equation $\widehat{y_i}=y_i$ (further, this line will be addressed as a “baseline’) and some dots. Each dot $(y_i,\widehat{y_i})$ represents a studied pair. Its first coordinate is the actual value, and its second coordinate is the predicted value.

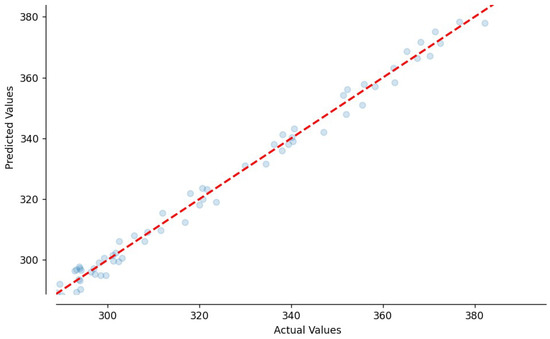
Figure 1. A sample of the distribution of predicted and actual values around the baseline.

Lemma 1.

Assume “$n$” is the number of dots above the baseline and “$m$” is the number of dots below the baseline; we have:

$$sig(y,\widehat{y})=\left\{\begin{array}{cc}>0\hfill & \mathrm{if}n>m,\hfill \\ <0\hfill & \mathrm{if}n<m,\hfill \\ =0\hfill & \mathrm{if}n=m,or “alldotslieonthebaselin{e}^{”}\hfill \end{array}\right.$$

(8)

Proof. 

Let us denote shortly $a_i=sign\left(y_i,\widehat{y_i}\right)$; Equations (5)–(7) will then be:

$$si{g}_{Left}(y,\widehat{y})=\frac{2}{N(N+1)}\sum _{k=1}^N\sum _{i=1}^{k}sign(y_i,{\widehat{y}}_i)=\frac{2}{N(N+1)}\sum _{k=1}^N\sum _{i=1}^k{a}_i$$

$$\Rightarrow si{g}_{Left}(y,\widehat{y})=\frac{2}{N(N+1)}\sum _{i=1}^N(N-i+1)a_i.$$

(9)

$$si{g}_{Right}(y,\widehat{y})=\frac{2}{N(N+1)}\sum _{k=1}^N\sum _{i=1}^{k}sign(y_{N-i+1},{\widehat{y}}_{N-i+1})$$

$$\Rightarrow si{g}_{Right}(y,\widehat{y})=\frac{2}{N(N+1)}\sum _{k=1}^N\sum _{i=1}^k{a}_{N-i+1}=\frac{2}{N(N+1)}\sum _{i=1}^N(N-i+1)a_{N-i+1}.$$

(10)

$$sig(y,\widehat{y})=\frac{si{g}_{Left}(y,\widehat{y})+si{g}_{Right}(y,\widehat{y})}{2},$$

$$\Rightarrow sig(y,\widehat{y})=\frac{1}{2}\frac{2}{N(N+1)}\sum _{i=1}^N(N+1)a_i=\frac{1}{N}\sum _{i=1}^N{a}_i.$$

(11)

The sum in Equation (11) is the sum of all signs. As the sign of each dot is +1 if the dot lies above the baseline, –1 if it lies below the baseline, and 0 if the dot lies on the baseline, it is obvious that the sum in Equation (11) is greater than zero if the number of dots above the baseline is greater than the number of dots below.

Similarly, the sum is less than zero if the number of dots above the baseline is less than the number of dots below the baseline.

Finally, the sum is equal to zero either if the number of dots above the baseline is the same as the number of dots below the baseline or if all dots lie on the baseline. □

Lemma 2.

Let us suppose a chart with N dots such that not all of them lie below the baseline. Changing the y-coordinate of any dot with a position below the baseline (with its x-coordinate unchanged) such that this change causes the dot to move to a position above the baseline will result in an increase of the values of both $si{g}_{Left}(y,\widehat{y})$ and $si{g}_{Right}(y,\widehat{y})$.

Proof. 

Let us denote shortly again $a_i=sign\left(y_i,\widehat{y_i}\right)$ and denote k $(1\le k\le N)$ as the position of the $k-th$ dot with the changed y-coordinate. The change means than that $a_k^{before}={sign(y}_k,{\widehat{y}}_k)=-1$ will change to $a_k^{after}={sign(y}_k,{\widehat{y}}_k)=+1$. Then, according to Equation (9):

$$si{g}_{Left}^{before}(y,\widehat{y})=\frac{2}{N(N+1)}[N{a}_1+(N-1)a_2+...+(N-k+1)a_k^{before}+...+1a_N)]$$

$$\Rightarrow si{g}_{Left}^{before}(y,\widehat{y})=\frac{2}{N(N+1)}[N{a}_1+(N-1)a_2+...+(N-k+1)\times (-1)+...+1a_N]$$

and

$$si{g}_{Left}^{after}(y,\widehat{y})=\frac{2}{N(N+1)}[N{a}_1+(N-1)a_2+...+(N-k+1)a_k^{after}+...+1a_N)]$$

$$\Rightarrow si{g}_{Left}^{after}(y,\widehat{y})=\frac{2}{N(N+1)}[N{a}_1+(N-1)a_2+...+(N-k+1)\times (+1)+...+1a_N]$$

Thus:

The values of $si{g}_{Left}^{before}(y,\widehat{y})$ and $si{g}_{Left}^{after}(y,\widehat{y})$ differ only in a term $(N-k+1)\times (-1)$, respectively $(N-k+1)\times (+1)$. It is obvious that $(N-k+1)\times (-1)<(N-k+1)\times (+1)$, because:

$-N+k-1<N-k+1,$

$\iff 2k<2N+2,$

$\iff k<N+1,$ as the assumption was $k\le N.$

Similarly, according to Equation (10),

$$si{g}_{Right}^{before}(y,\widehat{y})=\frac{2}{N(N+1)}[N{a}_N+(N-1)a_{N-1}+...+\left(k\right)a_k^{before}+...+1a_1)]$$

$$\Rightarrow si{g}_{Right}^{before}(y,\widehat{y})=\frac{2}{N(N+1)}[N{a}_N+(N-1)a_{N-1}+...+\left(k\right)\times (-1)+...+1a_1]$$

and

$$si{g}_{Right}^{after}(y,\widehat{y})=\frac{2}{N(N+1)}[N{a}_N+(N-1)a_{N-1}+...+\left(k\right)a_k^{after}+...+1a_1)]$$

$$\Rightarrow si{g}_{Right}^{after}(y,\widehat{y})=\frac{2}{N(N+1)}[N{a}_N+(N-1)a_{N-1}+...+\left(k\right)\times (+1)+...+1a_1]$$

The values of $si{g}_{Right}^{before}(y,\widehat{y})$ and $si{g}_{Right}^{after}(y,\widehat{y})$ differ only in a term $\left(k\right)\times (-1)$, respectively $\left(k\right)\times (+1)$. Again, it is obvious that $k\times (-1)<k\times (+1)$, because:

$-k<k\iff 0<2k\iff 0<k$, as the assumption was $1\le k.$

We conclude that if the number of consecutive dots above the baseline increases, the values of both $si{g}_{Left}(y,\widehat{y})$ and $si{g}_{Right}(y,\widehat{y})$ increase as well.

Remark: A similar lemma could be proven: If the number of consecutive dots below the baseline increases, the values of both $si{g}_{Left}(y,\widehat{y})$ and $si{g}_{Right}(y,\widehat{y})$ decrease. □

4. Characteristics of Sig Formula

Let us suppose a chart where the horizontal axis presents the actual values $y_i$ and the vertical axis stands for the expected values $\widehat{y_i}$. The baseline in such a chart would be a straight line with the equation $\widehat{y}=y$:

• If all predicted values are greater than all the respective actual values (i.e., all dots are above the baseline), then, according to Equation (11):

  $$sig(y,\widehat{y})=\frac{1}{N}\sum _{i=1}^N{a}_i=\frac{1}{N}\sum _{i=1}^N(+1)=1$$

  (12)

  which is the maximal possible value of $sig(y,\widehat{y})$.
• If all predicted values are smaller than all the respective actual values (i.e. all dots are below the baseline), then, according to Equation (11):

  $$sig(y,\widehat{y})=\frac{1}{N}\sum _{i=1}^N{a}_i=\frac{1}{N}\sum _{i=1}^N(-1)=-1$$

  (13)

  which is the minimal possible value of $sig(y,\widehat{y})$.
• If there is no difference between each predicted value and the respective actual value (i.e., all dots are on the baseline), then, according to Equation (11):

  $$sig(y,\widehat{y})=\frac{1}{N}\sum _{i=1}^N{a}_i=\frac{1}{N}\sum _{i=1}^N\left(0\right)=0$$

  (14)
• In general, the predicted and actual values fluctuate. Some predicted values might be greater than and others might be smaller than the respective actual ones. The dots in Figure 1 then form a cloudy distribution around the baseline. The value of $sig(y,\widehat{y})$ lies then between –1 and +1.
• Moreover, in the case of a uniform symmetry (named UniSym), i.e., if the values alternate around the baseline (one dot is above the baseline, the next one below, the next above, etc.), then with the increasing number N of the observations, the value of $sig(y,\widehat{y})$ approaches 0.

  $$\underset{N\to \infty }{lim}sig(y,\widehat{y})=\underset{N\to \infty }{lim}\frac{1}{N}\sum _{i=1}^N{a}_i=0$$

  (15)

5. Research Questions

These research questions (RQs) should be answered in this study:

• RQ1: What are the difference of the $si{g}_{Left}$, $si{g}_{Right}$, and $sig$ formulas?
• RQ2: What is the importance of additional information related to the $PRED\left(x\right)$ and $MMRE$ in measuring the performance of the predicted model?

6. Results and Discussion

In this section, we discuss the usefulness of additional information related to the $PRED\left(x\right)$ and $MMRE$ based on twenty-eight projects (Dataset-1) collected from [30,31,32,33] with eight different predicted assumptions as given in Table 2. The column “Real_P20” represents real efforts in terms of use case points (UCPs) [30,34]. The other columns (Model 1–Model 8) contain the corresponding estimated efforts. The UCPs were originally designed by Karner [35] as a simplification of the functional points method [36]. Size estimation is based on the UML use case model. The UCPs are used in industry or in research. Many studies map effort methods, including UCPs and UCP modification [7,37,38,39,40]. Use case points faced some design issues, which were discussed by Ouwerkerk and Abran [41]. The UCP design flaws are mainly based on scale transformation when the values of the UCP components are calculated [42].

Table 2. The twenty-eight projects and eight different predicted assumptions.

	EFFORT (Person-Hours)
No.		Estimation ($\widehat{\mathit{y}}$)
	Real_P20	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6	Model 7	Model 8
P1	151.85	157.2	135.9	108.4	157	148	149	133	145
P2	95.85	101	90	77.2	102	101	102	105.9	101.9
P3	58.65	64	48	51	60.3	55	53	39.8	49
P4	37.1	39	35	30	47	41	65.2	47	39.9
P5	30.7	54.6	24	28	34	17	25	18.2	20
P6	24.6	46	8	21	55	31.9	33	28	48
P7	13.85	15	5	6	15	8	9	8	8.2
P8	179.65	186	171	175.3	191.9	206	200	189	196
P9	84.05	83	82.3	68.2	103	78	74	72	76
P10	67.2	72	52	52	86	81	84	96	97
P11	61	80.5	41	46	64	64	49	58	44
P12	36	42	16	16	39.2	52	58	58	44.9
P13	25.7	31	13	8.7	34	22.6	24	18	17
P14	19.85	25	22.8	19	25	28	31	15.3	18
P15	184.2	193	182	197	170	157	176.3	181	179
P16	99	110	93	114	96	103	100	95	103
P17	197.5	203	180	207	183	192	169	193	178
P18	96.25	102	81.7	101	83	101	111	105	109
P19	108.75	115	93	109	93	72	78	93	93.1
P20	111.3	129	99.2	115	113.8	135.8	118	116	118
P21	132	145	118	145.9	113	105	103	109	113
P22	128.4	135.4	119	129	111	132	148.1	135.7	143
P23	152.1	172	151	155	138	123	151	137	149
P24	84.8	114	74	108.6	82	81	81	105.9	105
P25	183.5	195	177	230.2	171	193.2	200	157	167.2
P26	143	172	126	172	128.4	161	161	148	152
P27	137	156.1	121.6	154	117	148	148	123	132
P28	168	175	150	165	160	192	179	181	174

The presented models simulate the possible prediction model’s behavior based on real scenarios. The models’ behavior is configured as follows:

• Model 1: The predicted efforts are random guessing such that their values are mostly greater than the real values, and the $PRED\left(0.25\right)$ reaches the maximum compared with Models 5, 6, 7, and 8.
• Model 2: The predicted values are random guessing, as opposed to Model 1, where the $PRED\left(0.25\right)$ is equal to the $PRED\left(0.25\right)$ obtained from Model 1.
• Model 3: The predicted efforts are random guessing such that the first half of the predicted values is mostly less than the real values, but the remaining are mostly greater than the real values, where the $PRED\left(0.25\right)$ is assumed equal to the $PRED\left(0.25\right)$ obtained from Model 1.
• Model 4: It is assumed to be similar to Model 3 in the inverse sense. Furthermore, the predicted values in this model were purposefully chosen to minimize the $MMRE$.
• Models 5, 6, 7, and 8: The predicted efforts are based on the rule that one or more initial predicted values are greater/less than the actual values, and one or more subsequent predicted values are greater/less than the actual values. The following predicted values follow the same sequence as the previous ones. The rule is repeated until the testing dataset is exhausted. Furthermore, we assumed their $PRED\left(0.25\right)$ are the same; they are greater than 0.7, but less than $PRED\left(0.25\right)$, and their $MMRE$ is greater than or equal to Models 1, 2, 3, and 4.

As for the predictions (estimated values):

• The predicted values produced by Model 1 are mostly greater than the corresponding real values (all dots lie above the baseline), while Model 2 is the opposite.
• In Model 3, the dots in the first half mostly lie below and the dots in the second half mostly lie above the baseline, and vice versa in Model 4.
• The dots in Models 5 and 6 lie around the baseline, but the number of dots above the baseline is greater than the number of dots below the baseline (systematically overestimated). This is to demonstrate that the $sig$ value is positive.
• The dots in Model 7 also lie around the baseline, but the number of dots above the baseline is smaller than the number of dots below the baseline. This is to demonstrate that the $sig$ value is negative (systematically underestimated). Moreover, Model 8 is an approximately UniSym model. The $sig$ value then reaches zero.

Figure 2 illustrates the scatter of predicted efforts obtained from Models 1 and 2 vs. actual efforts around the baseline. These scatters are generated by using the “scatter” function from the “matplotlib” library of Python. By default, this function automatically re-orders the values from the minimum to maximum values. Figure 3, Figure 4 and Figure 5 below are used in the same manner. As seen in these figures, most of the dots (a pair of actual and predicted values) in Model 1 are above the baseline (where the predicted and actual values are the same, $\widehat{y_i}=y_i$), resulting in $si{g}_{Left}$, $si{g}_{Right}$, and $sig$ reaching +1.

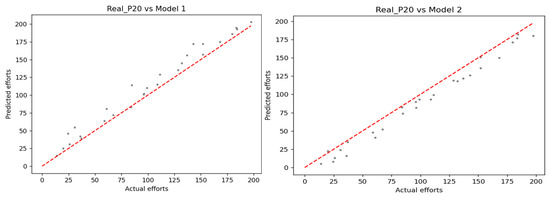
Figure 2. The scatter of predictive efforts vs. actual efforts: Model 1 vs. 2.

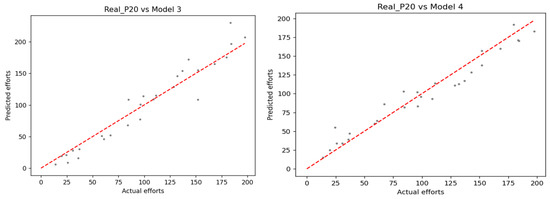
Figure 3. The scatter of predictive efforts vs. actual efforts: Model 3 vs. 4.

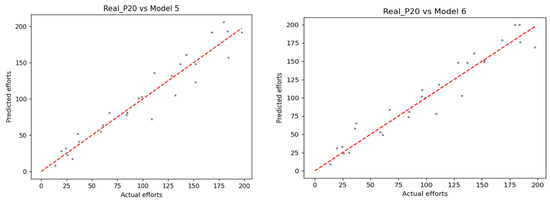
Figure 4. The scatter of predictive efforts vs. actual efforts: Model 5 vs. 6.

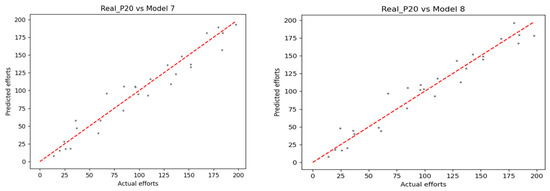
Figure 5. The scatter of predictive efforts vs. actual efforts: Model 7 vs. 8.

In a similar manner in Model 2, all of the dots are below the baseline; therefore, $si{g}_{Left}$, $si{g}_{Right}$, and $sig$ reach −1 (see Table 3). In practice, these assumptions are improbable because researchers are constantly looking for the most-efficient technique to obtain the best model. In some circumstances, the scatter between the real and predicted efforts might result in a case where the dots will lie around the baseline.

Table 3. The summary of the $sig$ values among the eight models.

Metrics	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6	Model 7	Model 8
$si{g}_{Left}$	0.901	−0.926	−0.488	0.527	0.059	−0.03	−0.172	−0.108
$si{g}_{Right}$	0.956	−0.931	0.345	−0.384	0.227	0.172	−0.113	−0.034
Sig	0.929	−0.929	−0.072	0.072	0.143	0.071	−0.143	−0.071
MMRE	0.163	0.179	0.175	0.156	0.163	0.186	0.175	0.175
PRED(0.25)	0.80	0.80	0.80	0.80	0.76	0.76	0.76	0.76

Another scenario is shown in Models 3 and 4 (see Figure 3). The $sig$ values calculated from both models reach zero. However, the scatter of the predicted and real values might not be realistic. In Model 3, the first half of the dots is mostly below the baseline, which results in $si{g}_{Left}=-0.488(<0)$, while the second half of dots is mostly above the baseline $si{g}_{Right}=0.345(>0)$ (see Table 3). This outcome is contrary to Model 4. Therefore, besides using only the $sig$ value, we might consider adding $si{g}_{Left}$ and $si{g}_{Right}$ to gain an insight. On the other hand, Figure 4 presents another case (Models 5 and 6) where the values of $si{g}_{Left}$ and $si{g}_{Right}$ are useful to be used together with $sig$, and the discussion below might be the answer for RQ1 regarding the difference of $si{g}_{Left}$, $si{g}_{Right}$, and $sig$. As can be seen, Models 5 and 6 are fairly random patterns around the baseline (see Table 4). Those scatters lead to a result that the absolute values of the $si{g}_{Right}$ obtained from Models 5 and 6 are larger than the absolute values of $si{g}_{Left}$ (see Table 3). Furthermore, Model 6 is more symmetrical than Model 5, and the predicted efforts obtained from the projects P10, P11, and P12 in Model 5 show the different positive/negative errors compared with Model 6 (see Table 4), which leads to the fact that the absolute value of the $si{g}_{Left}$ obtained from Model 5 is larger than that obtained from Model 6. Moreover, the $si{g}_{Right}$ obtained from Model 5 is greater than the $si{g}_{Right}$ obtained from Model 6, which might reveal that the number of dots on the same side of the baseline in the second half of Model 5 is greater than in the second half of Model 6 (see Lema 2). This information might be interesting because, if we use Model 5 as the predicted model, we should consider when we want to predict effort estimation with high values, as these may be overestimated.

Table 4. The difference between real efforts compared with predicted models.

No.	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6	Model 7	Model 8
P1	−5.35	15.95	43.45	−5.15	3.85	2.85	18.85	6.85
P2	−5.15	5.85	18.65	−6.15	−5.15	−6.15	−10.05	−6.05
P3	−5.35	10.65	7.65	−1.65	3.65	5.65	18.85	9.65
P4	−1.9	2.1	7.1	−9.9	−3.9	−28.1	−9.9	−2.8
P5	−23.9	6.7	2.7	−3.3	13.7	5.7	12.5	10.7
P6	−21.4	16.6	3.6	−30.4	−7.3	−8.4	−3.4	−23.4
P7	−1.15	8.85	7.85	−1.15	5.85	4.85	5.85	5.65
P8	−6.35	8.65	4.35	−12.25	−26.35	−20.35	−9.35	−16.35
P9	1.05	1.75	15.85	−18.95	6.05	10.05	12.05	8.05
P10	−4.8	15.2	15.2	−18.8	−13.8	−16.8	−28.8	−29.8
P11	−19.5	20	15	−3	−3	12	3	17
P12	−6	20	20	−3.2	−16	−22	−22	−8.9
P13	−5.3	12.7	17	−8.3	3.1	1.7	7.7	8.7
P14	−5.15	−2.95	0.85	−5.15	−8.15	−11.15	4.55	1.85
P15	−8.8	2.2	−12.8	14.2	27.2	7.9	3.2	5.2
P16	−11	6	−15	3	−4	−1	4	−4
P17	−5.5	17.5	−9.5	14.5	5.5	28.5	4.5	19.5
P18	−5.75	14.55	−4.75	13.25	−4.75	−14.75	−8.75	−12.75
P19	−6.25	15.75	−0.25	15.75	36.75	30.75	15.75	15.65
P20	−17.7	12.1	−3.7	−2.5	−24.5	−6.7	−4.7	−6.7
P21	−13	14	−13.9	19	27	29	23	19
P22	−7	9.4	−0.6	17.4	−3.6	−19.7	−7.3	−14.6
P23	−19.9	1.1	−2.9	14.1	29.1	1.1	15.1	3.1
P24	−29.2	10.8	−23.8	2.8	3.8	3.8	−21.1	−20.2
P25	−11.5	6.5	−46.7	12.5	−9.7	−16.5	26.5	16.3
P26	−29	17	−29	14.6	−18	−18	−5	−9
P27	−19.1	15.4	−17	20	−11	−11	14	5
P28	−7	18	3	8	−24	−11	−13	−6

Moreover, as shown in Figure 5, Models 7 and 8 randomly scatter between the predicted efforts against the actual efforts, whereas Model 8 is slightly more randomly scattered than Model 7. It is clear that the predicted efforts from P1 to P12 and P17 to P28 in both models have the same trend, but there are slight differences from P13 to P16 in Model 7 compared with Model 8 (see Table 4). The dots obtained from those efforts in Model 7 are below the baseline, which leads to the absolute value of $si{g}_{Left}$, $si{g}_{Right}$ attained from Model 7 being higher than those attained from Model 8. In addition, the number of dots above the baseline in both models is less than the number of dots below it. As a result, the calculated $sig$ values in both models are less than zero, while the absolute value of $sig$ obtained from Model 7 is less than that obtained from Model 8.

Table 3 summarizes the statistical metrics from the eight models, including $si{g}_{Left}$, $si{g}_{Right}$, $sig$, the $MMRE$, and the $PRED\left(0.25\right)$. As can be seen, the $MMRE$ and $PRED\left(0.25\right)$ obtained from Model 4 gain the best performance due to its $MMRE$ reaching the minimum and its $PRED\left(0.25\right)$ reaching the maximum compared with the other models. Based on these metrics, this model might be the most suitable among the remaining models. Unfortunately, its specific information $si{g}_{Left}$/$si{g}_{Right}$ values (obtained 0.527/−0.384) are farther from zero in comparison to the corresponding values obtained in Models 5 to 8 (see Lema 2). Thus, if we want to choose the suitable predictive model among the discussed eight models, we might consider choosing Model 5, 6, 7, or 8 due to the additional information related to the $MMRE$ and $PRED\left(0.25\right)$ obtained from those models being slightly closer to zero. This scenario might be a good example to answer RQ2; the values of $si{g}_{Left}$, $si{g}_{Right}$, and $sig$ might be the useful additional information related to the $MMRE$ and $PRED\left(0.25\right)$.

On the other hand, we suppose that we are considering two predictive models, namely Models 7 and 8, and we want to decide which one is better. We noticed that the $MMRE$ and $PRED\left(0.25\right)$ obtained from both are the same, 0.175 and 0.76, respectively. As discussed above, Model 8 has a fairly random scatter than Model 7 due to the $si{g}_{Left}$, $si{g}_{Right}$, and $sig$ values obtained from Model 8 being smaller than those obtained from Model 7. Based on these findings, we might conclude that Model 8 outperforms Model 7.

Last but not least, $si{g}_{Left}$, $si{g}_{Right}$, and $sig$ have a weakness, that is, if out of 28 predictions, 14 are underestimated by 1% and the remaining 14 are overestimated by 100%, the method proposed will indicate the prediction errors as symmetrical. This issue might raise confusion for software project practitioners. However, as mentioned in the purpose of these formulas, they are only additional information related to the $MMRE$ and $PRED\left(x\right)$, we still rely on the criteria of the $MMRE$ and $PRED\left(x\right)$ with more information obtained from these formulas as useful information. As discussed above, if we omit $si{g}_{Left}$, $si{g}_{Right}$, and $sig$, this might lead to the selection of an improper model.

Case study: To be more specific, we verified the benefit of the $si{g}_{Left}$, $si{g}_{Right}$, and $sig$ values based on the models obtained from XGBoost regression. XGBoost is a gradient-boosted decision tree development created for a highly efficient and accurate model. It is a Python open-source library, and it provides a framework such as the “fit” function to build a model based on the training dataset and the “predict” function to predict new values based on a new dataset [43]. In our scenario, we adopted XGBoost with a group of parameters. They include the learning rate (0.01), booster (“gblinear”), and n_estimators chosen by experimentation. We used Dataset-1 (twenty-eight projects) [30,31,32,33] and Dataset-2 (seventy-one projects) [31] as the historical datasets. Those datasets measure effort estimation in terms of use case points (UCPs) [30,34]. Both datasets are described by the unadjusted actor weight (UAW), unadjusted use case weight (UUCW), technical complexity factor (TCF), environmental complexity factor (ECF), and Real-P20. Real-P20 is considered as the dependent variable, and the UAW, UUCW, TCF, and ECF are considered as the independent variables.

Dataset-1/Dataset-2 is divided into two datasets, 80% of projects for training and the remaining projects for testing. As mentioned in Table 1, the $PRED\left(x\right)$ an $MMRE$ are used as the criteria to measure the accuracy of effort estimation in UCPs. In addition, the values of $si{g}_{Left}$, $si{g}_{Right}$, and $sig$ are shown.

Table 5 shows the evaluation criteria obtained from the XGBoost models. As can be seen, the $sig$ value obtained from the proposed models based on Dataset-1 and Dataset-2 is −0.556 and 0.286, respectively. Criterion $sig$ shows a model scatter (variance). If the variance reaches zero, that model is better. In those two datasets, we can see that model XGBoost has a tendency to underestimate Dataset-1 due to the values of $si{g}_{Left}$, $si{g}_{Right}$, and $sig$ being less than and so far from zero. The scatter of the model for Dataset-2 might be smaller than for Dataset-1 due to the absolute value of the $sig$ obtained from the model for Dataset-1 is larger than that obtained from the model for Dataset-2. As can be seen, the absolute values of $si{g}_{Left}$ are similar for Dataset-1 and Dataset-2. However, the |$si{g}_{Right}$| obtained from Dataset-2 is smaller than that obtained from Dataset-1, which demonstrates that the scatter of the model for Dataset-2 might be smaller than for Dataset-1. These findings reveal that the $si{g}_{Left}$, $si{g}_{Right}$, and $sig$ values might be used as reference criteria to consider choosing an appropriate predictive model. Compared to the $MMRE$ and $PRED\left(0.20\right)$, which is an absolute sig value, we might be confident to state that the XGBoost model for Dataset-2 outperforms that for Dataset-1.

Table 5. Evaluation criteria obtained from XGBoost.

	Dataset-1	Dataset-2
R-Squared	0.884	0.974
MMRE	0.318	0.136
PRED(0.20)	0.222	0.714
$si{g}_{Left}$	−0.422	0.429
$si{g}_{Right}$	−0.689	0.143
$sig$	−0.556	0.286

7. Conclusions and Future Work

$si{g}_{Left}$, $si{g}_{Right}$, and $sig$ refer to the sign of prediction error, not the magnitude. These values’ usefulness might be considered a contribution to the $MMRE$ and $PRED\left(x\right)$. Using the $MMRE$ and $PRED\left(x\right)$ together with them as performance indicators could be beneficial to validate the symmetry of the predictive model values around the baseline. On the other hand, since those values indicate under-/over-estimation in terms of effort estimation independent of the used sizing unit, these criteria might be useful when validating the accuracy of the predicted model along with the $PRED\left(x\right)$ and $MMRE$.

Moreover, as mentioned in Lemma 2, the lower the absolute value of $si{g}_{Left}$ and $si{g}_{Right}$, the more homogeneous the distribution of the predicted and actual values around the baseline. Using $si{g}_{Left}$, $si{g}_{Right}$, and $sig$ might detect whether the predictive model is under or over the baseline. Although this study proposes signals to identify the estimated model as under or over the baseline based on the limited dataset, based on the proof of Lemmas 1 and 2, the proposed formulas are completely adopted for the larger dataset. Last but not least, as discussed in Section 4, based on the adjusted values of $si{g}_{Left}$, $si{g}_{Right}$, and $sig$, the predictive model might be adjusted by increasing or decreasing the intercept, which might lead to a higher accuracy of the predictive model.

Limitations: Based on the $si{g}_{Left}$, $si{g}_{Right}$, and $sig$ values, we just stated whether the model is over or under the baseline. It may be more helpful when the quantification of this over-/under-estimation is discussed further in the future.