New Extensions of the Parameterized Inequalities Based on Riemann–Liouville Fractional Integrals

Abstract

In this article, we derive the above and below bounds for parameterized-type inequalities using the Riemann–Liouville fractional integral operators and limited second derivative mappings. These established inequalities generalized the midpoint-type, trapezoid-type, Simpson-type, and Bullen-type inequalities according to the specific choices of the parameter. Thus, a generalization of many inequalities and new results were obtained. Moreover, some examples of obtained inequalities are given for better understanding by the reader. Furthermore, the theoretical results are supported by graphs in order to illustrate the accuracy of each of the inequalities obtained according to the specific choices of the parameter.

1. Introduction

The theory of inequality, one of the cornerstones of mathematics, is used in many fields of science. Midpoint-type and Trapezoid-type inequalities formed by the right and left sides of Hermite–Hadamard-type inequality, Simpson-type inequalities, and Bullen-type inequalities have brought solutions to numerous important studies in the literature. In addition to these, fractional calculus is an important topic for explaining physical states as well as real-world problems. For more information about these topics, see [1,2,3,4] and references therein. One of the most famous types of fractional integrals is the Riemann–Liouville fractional integral. It has been the subject of many studies in the literature. The theory of inequality has been the focus of many researchers in the field.

Midpoint-type and trapezoid-type inequalities have been the focus of many researchers in recent years. Trapezoid-type inequalities for convex functions were given for the first time in [5]. On the other hand, midpoint inequalities were presented for the first time in [6]. Chen gave a refinement of the Hermite–Hadamard inequality via convex functions with the help of the Riemann–Liouville fractional integrals in [7]. In [8], the authors possessed the below and above bounds for the right and left-hand sides of fractional Hermite–Hadamard inequalities. In [9,10], Budak et al. derived two different versions of generalized fractional midpoint type and generalized fractional trapezoid-type inequalities for functions with second bounded derivatives. Barani et al. obtained inequalities involving twice differentiable convex mappings which are connected with Hadamard’s inequality in [11,12].

Since the convex theory is an efficient and useful way to obtain several problems from kind branches of science, many researchers have investigated Simpson-type inequalities in the case of a convex function. For instance, Alomari et al. [13] proved some inequalities of Simpson’s type with the aid of s-convex mappings via differentiable functions. Moreover, new variants of Simpson-type inequalities involving differentiable convex functions are presented in [14,15]. Sarıkaya et al. [16] obtained several Simpson-type inequalities for mappings whose second derivatives are convex. Some Simpson-type inequalities are investigated for functions whose absolute values are convex in [17]. The Simpson inequalities via differentiable mappings are extended to Riemann–Liouville fractional integrals in [18]. Furthermore, a large number of fractional Simpson-type inequalities for twice-differentiable mappings were given in [19].

In [20], Bullen introduced Bullen-type inequalities as one of the important inequalities in 1978. Sarikaya et al. [21] investigated generalized Bullen inequalities including a generalized convex function. Erden and Sarikaya obtained the generalized Bullen-type inequalities based on local fractional integrals in [22]. İşcan [23] proved some Hadamard-type and Bullen-type inequalities via Lipschitzian mappings based on Riemann–Liouville fractional integrals. Çakmak obtained a new identity via differentiable mappings and derived some new inequalities for differentiable mappings thought s-convexity based on Riemann–Liouville fractional integrals involving Gaussian hyper-geometric mapping in [24]. Moreover, Du et al. [25] investigated the generalized fractional integrals to possess Bullen-type inequalities. Furthermore, some generalizations of integral inequalities of Bullen-type for twice differentiable functions involving Riemann–Liouville fractional integrals were obtained in [26].

The main goal of this paper is to demonstrate that some parameterized type inequalities based on Riemann–Liouville fractional integrals on twice-differentiable functions are bounded. The general outline of the article consists of four sections including an introduction. In Section 2, after giving a general literature review and the definition of Riemann–Liouville fractional integral operators, we will build the main results of this research on three theorems that exist in the literature. These theorems about the above and below bounds of Hermite–Hadamard type inequalities for different versions based on Riemann–Liouville fractional integral operators are constructed using the second derivative bounded functions. Section 3 will consist of three subtitles. Different versions of the Riemann–Liouville fractional integral will be discussed in each other. It shows that these obtained inequalities generalize some studies in the literature with special choices of the parameter. Moreover, new results were obtained with some special choices of the parameter. Examples of the obtained inequalities are given in the graphs. In Section 4, comments and suggestions will make to the reader about the researched subject. Information will be given about future work for interested readers.

2. Preliminaries

Throughout this section, mathematical preliminaries about fractional calculus theory will be given as follows:

Definition 1

([27]). Let us consider a first-order integrable function f in the interval $[a,b]$ such that $f\in L_1[a,b]$. The Riemann–Liouville integrals $J_{a+}^{\alpha }f$ and $J_{b-}^{\alpha }f$ of order $\alpha >0$ are described by:

$$J_{a+}^{\alpha }f\left(x\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_a^x{\left(x-t\right)}^{\alpha -1}f\left(t\right)dt,x>a$$

and

$$J_{b-}^{\alpha }f\left(x\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_x^b{\left(t-x\right)}^{\alpha -1}f\left(t\right)dt,x<b,$$

respectively. Here, $\Gamma \left(\alpha \right)$ is the Gamma function, and it is described as follows:

$$\Gamma \left(\alpha \right)={\int }_0^{\infty }{e}^{-u}{u}^{\alpha -1}du.$$

Let us also note that $J_{a+}^{0}f\left(x\right)=J_{b-}^{0}f\left(x\right)=f\left(x\right).$

Theorem 1

([8]). Let $f:\left[a,b\right]\to \mathbb{R}$ denotes a twice differentiable positive mapping and $f\in L_1\left[a,b\right].$ If $f^{″}$ is bounded, i.e., $m\le f^{″}\left(t\right)\le M$, $t\in \left[a,b\right],$$m,M\in \mathbb{R},$ then we derived the following inequalities:

$$\begin{array}{cc}\hfill \frac{m{(b-a)}^2}{4(\alpha +1)(\alpha +2)}& \le \frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{\left(\frac{a+b}{2}\right)+}^{\alpha }f\left(b\right)+J_{\left(\frac{a+b}{2}\right)-}^{\alpha }f\left(a\right)\right]-f\left(\frac{a+b}{2}\right)\hfill \\ \hfill & \le \frac{M{(b-a)}^2}{4(\alpha +1)(\alpha +2)}\hfill \end{array}$$

(1)

and

$$\begin{array}{cc}\hfill \frac{m{(b-a)}^2\alpha (\alpha +3)}{8(\alpha +1)(\alpha +2)}& \le \frac{f\left(a\right)+f\left(b\right)}{2}-\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{\left(\frac{a+b}{2}\right)+}^{\alpha }f\left(b\right)+J_{\left(\frac{a+b}{2}\right)-}^{\alpha }f\left(a\right)\right]\hfill \\ \hfill & \le \frac{M{(b-a)}^2\alpha (\alpha +3)}{8(\alpha +1)(\alpha +2)}.\hfill \end{array}$$

(2)

Theorem 2

([8]). Suppose that the all conditions of Theorem 1 are valid. Then, it follows:

$$\frac{m{\left(b-a\right)}^2\alpha }{8(\alpha +2)}\le \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(\frac{a+b}{2}\right)+J_{b-}^{\alpha }f\left(\frac{a+b}{2}\right)\right]-f\left(\frac{a+b}{2}\right)\le \frac{M{\left(b-a\right)}^2\alpha }{8(\alpha +2)}$$

(3)

and

$$\frac{m{\left(b-a\right)}^2}{4(a+2)}\le \frac{f\left(a\right)+f\left(b\right)}{2}-\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(\frac{a+b}{2}\right)+J_{b-}^{\alpha }f\left(\frac{a+b}{2}\right)\right]\le \frac{M{\left(b-a\right)}^2}{4(a+2)}.$$

(4)

F. Chen proved the following inequalities:

Theorem 3

([7]). If all conditions of Theorem 1 hold, then it yields:

$$\begin{array}{c}\hfill \frac{{\left(b-a\right)}^2\left({\alpha }^2-\alpha +2\right)m}{8\left(\alpha +1\right)\left(\alpha +2\right)}\le \frac{\Gamma \left(\alpha +1\right)}{2{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(b\right)+J_{b-}^{\alpha }f\left(a\right)\right]-f\left(\frac{a+b}{2}\right)\le \frac{{\left(b-a\right)}^2\left({\alpha }^2-\alpha +2\right)M}{8\left(\alpha +1\right)\left(\alpha +2\right)}.\end{array}$$

(5)

and

$$\begin{array}{c}\hfill \frac{{\left(b-a\right)}^2\alpha m}{2\left(\alpha +1\right)\left(\alpha +2\right)}\le \frac{f\left(a\right)+f\left(b\right)}{2}-\frac{\Gamma \left(\alpha +1\right)}{2{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(b\right)+J_{b-}^{\alpha }f\left(a\right)\right]\le \frac{{\left(b-a\right)}^2\alpha M}{2\left(\alpha +1\right)\left(\alpha +2\right)}.\end{array}$$

(6)

for $\alpha >0.$ Here, $m={\displaystyle \underset{t\in \left[a,b\right]}{inf}}{f}^{″}\left(t\right),$$M={\displaystyle \underset{t\in \left[a,b\right]}{sup}}{f}^{″}\left(t\right).$

3. Main Results

In this section, new inequalities will be obtained by using the inequalities given in the preliminary section. Instead of using convexity, condition $m\le f^{″}\left(t\right)\le M$ is used in these inequalities for all $t\in \left[a,b\right]$. Each version has been examined in the form of three subtitles.

3.1. Parameterized Type Inequalities of the First Sense

Theorem 4.

Let us consider that all conditions of Theorem 1 hold and $\lambda \in \left[0,1\right].$ Then, we establish the following inequalities:

$$\begin{array}{cc}\hfill & \frac{{(b-a)}^2}{8(\alpha +1)(\alpha +2)}\left[\left(1-\lambda \right)\left(\alpha (\alpha +3)m\right)-2\lambda M\right]\hfill \\ \hfill \\ \hfill & \le \lambda f\left(\frac{a+b}{2}\right)+\left(1-\lambda \right)\frac{f\left(a\right)+f\left(b\right)}{2}-\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{\left(\frac{a+b}{2}\right)+}^{\alpha }f\left(b\right)+J_{\left(\frac{a+b}{2}\right)-}^{\alpha }f\left(a\right)\right]\hfill \\ \hfill \\ \hfill & \le \frac{{(b-a)}^2}{8(\alpha +1)(\alpha +2)}\left[\left(1-\lambda \right)\left(\alpha (\alpha +3)M\right)-2\lambda m\right].\hfill \end{array}$$

(7)

Proof. 

If we multiply the inequality (1) by $-\lambda$, then we obtain:

$$\begin{array}{cc}\hfill & \frac{-\lambda M{(b-a)}^2}{4(\alpha +1)(\alpha +2)}\hfill \\ \hfill & \le \lambda f\left(\frac{a+b}{2}\right)-\lambda \frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{\left(\frac{a+b}{2}\right)+}^{\alpha }f\left(b\right)+J_{\left(\frac{a+b}{2}\right)-}^{\alpha }f\left(a\right)\right]\hfill \\ \hfill & \le \frac{-\lambda m{(b-a)}^2}{4(\alpha +1)(\alpha +2)}.\hfill \end{array}$$

(8)

Let us multiply (2) by $\left(1-\lambda \right)$. Then, we have:

$$\begin{array}{cc}\hfill & \left(1-\lambda \right)\frac{m{(b-a)}^2\alpha (\alpha +3)}{8(\alpha +1)(\alpha +2)}\hfill \\ \hfill \\ \hfill & \le \left(1-\lambda \right)\frac{f\left(a\right)+f\left(b\right)}{2}-\left(1-\lambda \right)\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{\left(\frac{a+b}{2}\right)+}^{\alpha }f\left(b\right)+J_{\left(\frac{a+b}{2}\right)-}^{\alpha }f\left(a\right)\right]\hfill \\ \hfill \\ \hfill & \le \left(1-\lambda \right)\frac{M{(b-a)}^2\alpha (\alpha +3)}{8(\alpha +1)(\alpha +2)}.\hfill \end{array}$$

(9)

If we add (8) and (9), then the inequality is arranged as follows:

$$\begin{array}{cc}\hfill & \frac{{(b-a)}^2}{8(\alpha +1)(\alpha +2)}\left[\left(1-\lambda \right)\left(\alpha (\alpha +3)m\right)-2\lambda M\right]\hfill \\ \\ \hfill & \le \lambda f\left(\frac{a+b}{2}\right)+\left(1-\lambda \right)\frac{f\left(a\right)+f\left(b\right)}{2}-\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{\left(\frac{a+b}{2}\right)+}^{\alpha }f\left(b\right)+J_{\left(\frac{a+b}{2}\right)-}^{\alpha }f\left(a\right)\right]\hfill \\ \\ \hfill & \le \frac{{(b-a)}^2}{8(\alpha +1)(\alpha +2)}\left[\left(1-\lambda \right)\left(\alpha (\alpha +3)M\right)-2\lambda m\right].\hfill \end{array}$$

This completes the proof of Theorem 4. □

Remark 1.

If we take $\lambda =0$ in Theorem 4, then inequalities (7) reduce to inequalities (2).

Remark 2.

If we choose $\lambda =1$ in Theorem 4, the inequalities (7) turn into inequalities (1).

Remark 3.

Let us consider $\lambda =\frac{2}{3}$ in Theorem 4. Then, we possess fractional Simpson-type inequalities:

$$\begin{array}{cc}\hfill & \frac{{(b-a)}^2}{24(\alpha +1)(\alpha +2)}\left[4m-\alpha \left(\alpha +3\right)M\right]\hfill \\ \hfill \\ \hfill & \le \frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{\left(\frac{a+b}{2}\right)+}^{\alpha }f\left(b\right)+J_{\left(\frac{a+b}{2}\right)-}^{\alpha }f\left(a\right)\right]-\frac{1}{6}f\left[\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill \\ \hfill & \le \frac{{(b-a)}^2}{24(\alpha +1)(\alpha +2)}\left[4M-\alpha \left(\alpha +3\right)m\right],\hfill \end{array}$$

which is given by Budak et al. in [28].

Corollary 1.

If we assume that $\lambda =\frac{1}{2}$ in Theorem 4, then we have the following Bullen-type inequalities:

$$\begin{array}{cc}\hfill & \frac{{(b-a)}^2}{16(\alpha +1)(\alpha +2)}\left[\alpha (\alpha +3)m-2M\right]\hfill \\ \hfill & \\ \hfill & \le \frac{1}{2}\left[f\left(\frac{a+b}{2}\right)+\frac{f\left(a\right)+f\left(b\right)}{2}\right]-\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{\left(\frac{a+b}{2}\right)+}^{\alpha }f\left(b\right)+J_{\left(\frac{a+b}{2}\right)-}^{\alpha }f\left(a\right)\right]\hfill \\ \hfill & \\ \hfill & \le \frac{{(b-a)}^2}{16(\alpha +1)(\alpha +2)}\left[\alpha (\alpha +3)M-2m\right].\hfill \end{array}$$

Example 1.

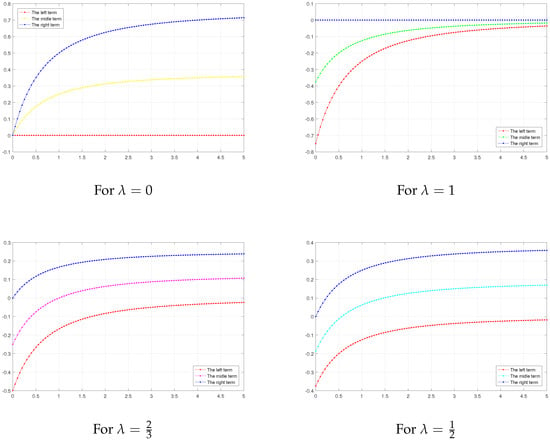
Let us define the function $f:[a,b]=[0,1]\to \mathbb{R}$ as $f\left(x\right)=x^3+4$ such that $m=0$ and $M=6$. Let us consider the left-hand side of the inequalities (7) as follows:

$$\frac{{(b-a)}^2}{8(\alpha +1)(\alpha +2)}\left[\left(1-\lambda \right)\left(\alpha (\alpha +3)m\right)-2\lambda M\right]=\frac{-3\lambda }{2(\alpha +1)(\alpha +2)}.$$

From the definitions of fractional integrals, the equalities

$$\begin{array}{cc}\hfill & \lambda f\left(\frac{1}{2}\right)+\left(1-\lambda \right)\frac{f\left(0\right)+f\left(1\right)}{2}-\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{\left(\frac{a+b}{2}\right)+}^{\alpha }f\left(b\right)+J_{\left(\frac{a+b}{2}\right)-}^{\alpha }f\left(a\right)\right]\hfill \\ \hfill & \\ \hfill & =\lambda \frac{33}{8}+\left(1-\lambda \right)\frac{9}{2}-2^{\alpha -1}\alpha \hfill \\ \hfill & \\ \hfill & \times \left[\frac{2^{-\alpha -3}\left(\alpha +4\right)\left({\alpha }^2+5\alpha +12\right)}{\left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)\alpha }+\frac{2^{2-\alpha }}{\alpha }+\frac{2^{-\alpha -3}}{\alpha +3}+\frac{2^{2-\alpha }}{\alpha }\right]\hfill \\ \hfill & \\ \hfill & =\frac{36-3\lambda }{8}-\frac{33{\alpha }^2+99\alpha +72}{8{\alpha }^2+24\alpha +16}\hfill \end{array}$$

are valid. Finally, the last expression of (7) is calculated as follows:

$$\frac{{(b-a)}^2}{8(\alpha +1)(\alpha +2)}\left[\left(1-\lambda \right)\left(\alpha (\alpha +3)M\right)-2\lambda m\right]=\frac{3\alpha (\alpha +3)\left(1-\lambda \right)}{4(\alpha +1)(\alpha +2)}.$$

Hence, we have the following double inequality:

$$\frac{-3\lambda }{2(\alpha +1)(\alpha +2)}\le \frac{36-3\lambda }{8}-\frac{33{\alpha }^2+99\alpha +72}{8{\alpha }^2+24\alpha +16}\le \frac{3\alpha (\alpha +3)\left(1-\lambda \right)}{4(\alpha +1)(\alpha +2)}.$$

(10)

As one can see in Figure 1, (10) in Example 1 shows the correctness of this inequality for all values of $\alpha \in (0,5]$ and special choices of λ.

Figure 1. Graph of both sides of (10) in Example 1, depending on $\alpha$ and $\lambda$, computed and plotted with MATLAB.

3.2. Parameterized-Type Inequalities of the Second Sense

Theorem 5.

Assume that the all conditions of Theorem 4 hold. Then, we obtain the following double inequality:

$$\begin{array}{cc}\hfill & \frac{{\left(b-a\right)}^2}{8(a+2)}\left(2m-\lambda \left(2m+M\alpha \right)\right)\hfill \\ \hfill \\ \hfill & \le \lambda f\left(\frac{a+b}{2}\right)+\left(1-\lambda \right)\frac{f\left(a\right)+f\left(b\right)}{2}-\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(\frac{a+b}{2}\right)+J_{b-}^{\alpha }f\left(\frac{a+b}{2}\right)\right]\hfill \\ \hfill \\ \hfill & \le \frac{{\left(b-a\right)}^2}{8(\alpha +2)}\left(2M-\lambda \left(2M+m\alpha \right)\right).\hfill \end{array}$$

(11)

Proof. 

Let us (3) and (4) are multiplied by $-\lambda$ and $\left(1-\lambda \right)$, respectively. If these two expressions are added, then the proof is completed. □

Remark 4.

If we assign $\lambda =0$ in Theorem 5, then inequalities (11) will be equal to inequalities (4).

Remark 5.

If we let $\lambda =1$ in Theorem 5, then the inequalities (11) are reduced to the inequalities (3) obtained by Budak et al. in [8].

Remark 6.

Consider $\lambda =\frac{2}{3}$ in Theorem 5. Then, the following fractional Simpson-type inequalities hold:

$$\begin{array}{cc}\hfill & \frac{{\left(b-a\right)}^2}{12(a+2)}\left(m-M\alpha \right)\hfill \\ \\ \hfill & \le \frac{2^{\alpha -1}\Gamma (\alpha +1)}{{\left(b-a\right)}^{\alpha }}\left[J_{a^{+}}^{\alpha }f\left(\frac{a+b}{2}\right)+J_{b^{-}}^{\alpha }f\left(\frac{a+b}{2}\right)\right]-\frac{1}{6}f\left[\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \\ \hfill & \le \frac{{\left(b-a\right)}^2}{12(\alpha +2)}\left(M-m\alpha \right).\hfill \end{array}$$

This double inequality is established by Budak et al. in [28].

Corollary 2.

If we assume λ equals to $\frac{1}{2}$ in Theorem 5, then the following inequalities hold:

$$\begin{array}{cc}\hfill & \frac{\left(2m-M\alpha \right){\left(b-a\right)}^2}{8(a+2)}\hfill \\ \hfill & \\ \hfill & \le \frac{1}{2}\left[f\left(\frac{a+b}{2}\right)+\frac{f\left(a\right)+f\left(b\right)}{2}\right]-\frac{2^{\alpha -1}\Gamma \left(\alpha +1\right)}{{\left(b-a\right)}^{\alpha }}\left[J_{\left(\frac{a+b}{2}\right)+}^{\alpha }f\left(b\right)+J_{\left(\frac{a+b}{2}\right)-}^{\alpha }f\left(a\right)\right]\hfill \\ \hfill & \\ \hfill & \le \frac{\left(2M-m\alpha \right){\left(b-a\right)}^2}{8(\alpha +2)}.\hfill \end{array}$$

Example 2.

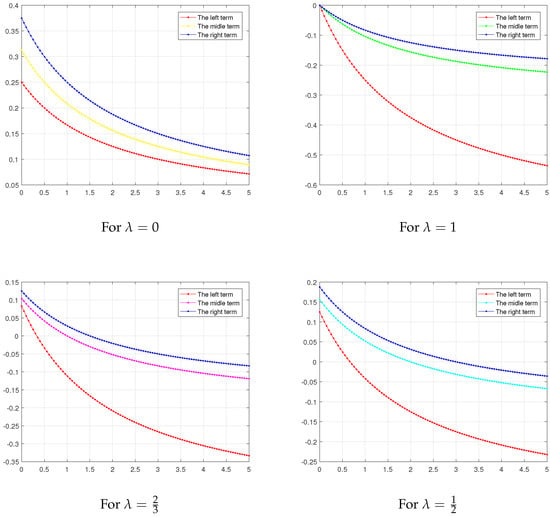
If we define a function $f:[a,b]=[0,1]\to \mathbb{R}$ by $f\left(x\right)=\frac{x^3}{6}+x^2$, then we obtain $m=2$ and $M=3$. Let us consider the left-hand side of the inequalities (11) as follows:

$$\frac{{\left(b-a\right)}^2}{8(a+2)}\left(2m-\lambda \left(2m+M\alpha \right)\right)=\frac{4-\lambda \left(4+6\alpha \right)}{8(a+2)}.$$

With the help of the Riemann–Liouville fractional integral operators, we obtain:

$$\begin{array}{cc}\hfill & \lambda f\left(\frac{a+b}{2}\right)+\left(1-\lambda \right)\frac{f\left(a\right)+f\left(b\right)}{2}\hfill \\ \hfill & \\ \hfill & -\frac{2^{\alpha -1}\Gamma (\alpha +1)}{{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(\frac{a+b}{2}\right)+J_{b-}^{\alpha }f\left(\frac{a+b}{2}\right)\right]\hfill \\ \hfill & \\ \hfill & =\frac{13\lambda }{48}+\frac{7\left(1-\lambda \right)}{12}-2^{\alpha -1}\alpha \left[\frac{4\alpha +13}{\alpha \left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)2^{\alpha +3}}+\frac{28{\alpha }^3+138{\alpha }^2+176\alpha +39}{3\alpha \left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)2^{\alpha +3}}\right]\hfill \\ \hfill & \\ \hfill & =\frac{28-15\lambda }{48}-\frac{28{\alpha }^3+138{\alpha }^2+188\alpha +78}{48\left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)}.\hfill \end{array}$$

Hence,

$$\frac{{\left(b-a\right)}^2}{8(\alpha +2)}\left(2M-\lambda \left(2M+m\alpha \right)\right)=\frac{6-\lambda \left(6+2\alpha \right)}{8(\alpha +2)}.$$

Consequently, we have the inequality:

$$\begin{array}{c}\hfill \frac{4-\lambda \left(4+6\alpha \right)}{8(a+2)}\le \frac{28-15\lambda }{48}-\frac{28{\alpha }^3+138{\alpha }^2+188\alpha +78}{48\left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)}\le \frac{6-\lambda \left(6+2\alpha \right)}{8(\alpha +2)}.\end{array}$$

(12)

As it can be seen in Figure 2, the accuracy of inequality (12) in Example 2 is obvious for all values of $\alpha \in (0,5]$ and for special choices of λ.

Figure 2. Graph of both sides of (12) in Example 2, depending on $\alpha$ and $\lambda$, evaluated and drawn with MATLAB.

3.3. Parameterized-Type Inequalities of the Third Sense

Theorem 6.

If all conditions of Theorem 4 hold, then we have the following inequalities:

$$\begin{array}{cc}\hfill & \frac{{\left(b-a\right)}^2\alpha }{2\left(\alpha +1\right)\left(\alpha +2\right)}\left[\left(1-\lambda \right)m-\lambda M\frac{\left({\alpha }^2-\alpha +2\right)}{4\alpha }\right]\hfill \\ \hfill & \hfill \\ \hfill & \le \lambda f\left(\frac{a+b}{2}\right)+\left(1-\lambda \right)\frac{f\left(a\right)+f\left(b\right)}{2}\hfill \\ \hfill & \hfill \\ \hfill & -\frac{\Gamma \left(\alpha +1\right)}{2{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(b\right)+J_{b-}^{\alpha }f\left(a\right)\right]\hfill \\ \hfill & \hfill \\ \hfill & \le \frac{{\left(b-a\right)}^2\alpha }{2\left(\alpha +1\right)\left(\alpha +2\right)}\left[\left(1-\lambda \right)M-\lambda m\frac{\left({\alpha }^2-\alpha +2\right)}{4\alpha }\right].\hfill \end{array}$$

(13)

Proof. 

Let us assume (5) and (6) are multiplied by $-\lambda$ and $\left(1-\lambda \right)$, respectively. If these two expressions are added, then the proof is completed. □

Remark 7.

When $\lambda =0$ is chosen in Theorem 6, the inequalities (13) is reduced to the inequalities (6).

Remark 8.

Let us consider $\lambda =1$ in Theorem 6. Then, the inequalities (13) leads to the inequalities (5) obtained by Chen in [7].

Remark 9.

Assume λ is equal to $\frac{2}{3}$ in Theorem 6. Then, the following fractional Simpson-type inequalities

$$\begin{array}{cc}\hfill & \frac{{(b-a)}^2\alpha }{6\left(\alpha +1\right)\left(\alpha +2\right)}\left[m\frac{{\alpha }^2-\alpha +2}{2\alpha }-M\right]\hfill \\ \hfill & \\ \hfill & \le \frac{\Gamma \left(\alpha +1\right)}{2{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(b\right)+J_{b-}^{\alpha }f\left(a\right)\right]-\frac{1}{6}\left[f\left(a\right)+4f\left(\frac{a+b}{2}\right)+f\left(b\right)\right]\hfill \\ \hfill & \\ \hfill & \le \frac{{(b-a)}^2\alpha }{6\left(\alpha +1\right)\left(\alpha +2\right)}\left[M\frac{{\alpha }^2-\alpha +2}{2\alpha }-m\right]\hfill \end{array}$$

are satisfied. This double inequality has been obtained by Budak et al. in [28].

Corollary 3.

If we let $\lambda =\frac{1}{2}$ in Theorem 6, then we obtain fractional Bullen-type inequalities:

$$\begin{array}{cc}\hfill & \frac{{\left(b-a\right)}^2\alpha }{4\left(\alpha +1\right)\left(\alpha +2\right)}\left[m-M\frac{{\alpha }^2-\alpha +2}{4\alpha }\right]\hfill \\ \hfill & \\ \hfill & \le \frac{1}{2}\left[f\left(\frac{a+b}{2}\right)+\frac{f\left(a\right)+f\left(b\right)}{2}\right]-\frac{\Gamma \left(\alpha +1\right)}{2{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(b\right)+J_{b-}^{\alpha }f\left(a\right)\right]\hfill \\ \hfill & \\ \hfill & \le \frac{{\left(b-a\right)}^2\alpha }{2\left(\alpha +1\right)\left(\alpha +2\right)}\left[M-m\frac{{\alpha }^2-\alpha +2}{4\alpha }\right].\hfill \end{array}$$

Example 3.

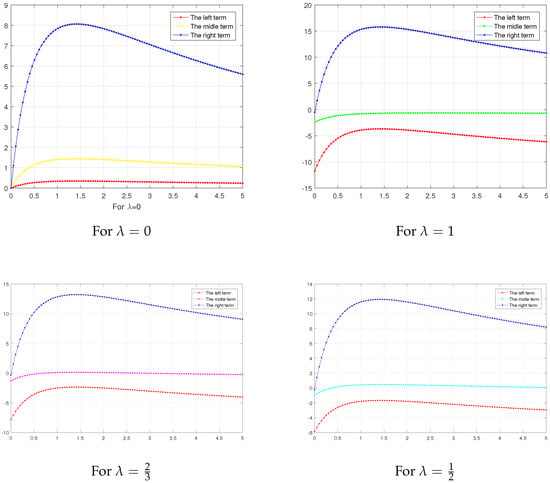
Let us note the function $f:[a,b]=[0,1]\to \mathbb{R}$ is $f\left(x\right)=3x^6+2x^2$. Then, it is clear that $m=4$ and $M=94$. Here, the first expression of the inequalities (13) is as follows:

$$\frac{{\left(b-a\right)}^2\alpha }{2\left(\alpha +1\right)\left(\alpha +2\right)}\left[\left(1-\lambda \right)m-\lambda M\frac{{\alpha }^2-\alpha +2}{4\alpha }\right]=\frac{8\alpha -\lambda \left(47{\alpha }^2-39\alpha +94\right)}{4\left(\alpha +1\right)\left(\alpha +2\right)}.$$

From the fact of the Definition 1, it will be calculated as follows:

$$\begin{array}{cc}\hfill & \lambda f\left(\frac{a+b}{2}\right)+\left(1-\lambda \right)\frac{f\left(a\right)+f\left(b\right)}{2}-\frac{\Gamma \left(\alpha +1\right)}{2{\left(b-a\right)}^{\alpha }}\left[J_{a+}^{\alpha }f\left(b\right)+J_{b-}^{\alpha }f\left(a\right)\right]\hfill \\ \hfill & \\ \hfill & =\lambda f\left(\frac{1}{2}\right)+\left(1-\lambda \right)\frac{f\left(0\right)+f\left(1\right)}{2}-\frac{\Gamma \left(\alpha +1\right)}{2}\left[J_{0+}^{\alpha }f\left(1\right)+J_{1-}^{\alpha }f\left(0\right)\right]\hfill \\ \hfill & \\ \hfill & =\frac{160-125\lambda }{64}-\frac{1080}{\left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)\left(\alpha +4\right)\left(\alpha +5\right)\left(\alpha +6\right)}\hfill \\ \hfill & \\ \hfill & -\frac{2}{\left(\alpha +1\right)\left(\alpha +2\right)}-\frac{6\alpha }{\alpha +6}-\frac{4\alpha }{\alpha +2}.\hfill \end{array}$$

Finally, the right-hand side of the inequality (13) is as follows:

$$\frac{{\left(b-a\right)}^2\alpha }{2\left(\alpha +1\right)\left(\alpha +2\right)}\left[\left(1-\lambda \right)M-\lambda m\frac{\left({\alpha }^2-\alpha +2\right)}{4\alpha }\right]=\frac{94\alpha -\lambda \left({\alpha }^2+93\alpha +2\right)}{2\left(\alpha +1\right)\left(\alpha +2\right)}.$$

Thus, we have the inequality:

$$\begin{array}{cc}\hfill & \frac{8\alpha -\lambda \left(47{\alpha }^2-39\alpha +94\right)}{4\left(\alpha +1\right)\left(\alpha +2\right)}\le \frac{160-125\lambda }{64}-\frac{1080}{\left(\alpha +1\right)\left(\alpha +2\right)\left(\alpha +3\right)\left(\alpha +4\right)\left(\alpha +5\right)\left(\alpha +6\right)}\hfill \\ \hfill & \hfill \\ \hfill & -\frac{2}{\left(\alpha +1\right)\left(\alpha +2\right)}-\frac{6\alpha }{\alpha +6}-\frac{4\alpha }{\alpha +2}\le \frac{94\alpha -\lambda \left({\alpha }^2+93\alpha +2\right)}{2\left(\alpha +1\right)\left(\alpha +2\right)}.\hfill \end{array}$$

(14)

Looking at Figure 3, the correctness of inequalities (14) in Example 3 are clear for all values of $\alpha \in (0,5]$ and special choices of λ.

Figure 3. Graph of both sides of (14) in Example 3, depending on $\alpha$ and $\lambda$, calculated and drawn with MATLAB.

4. Conclusions

In the present research, we investigated some Parameterized type inequalities including Riemann–Liouville fractional integral operators using the functions whose second derivatives are bounded. In addition, some examples with graphs are posses to demonstrate the main results. Interested readers can explore the other fractional types of the resulting inequalities. These given inequalities can be developed under the condition $m\le f^{″}\left(t\right)\le M$ for all $t\in \left[a,b\right]$ for different convexity types of mappings. With the motivation from this study, different types of inequalities can be developed in future studies.