The Properties of Harmonically cr-h-Convex Function and Its Applications

Abstract

In this paper, the definition of the harmonically $cr$-h-convex function is given, and its important properties are discussed. Jensen type inequality, Hermite–Hadamard type inequalities and Fejér type inequalities for harmonically $cr$-h-convex functions are also established. In addition, some numerical examples are given to verify the accuracy of the results.

1. Introduction

Interval analysis is a discipline that uses interval variables instead of point variables, and the calculation results are expressed as intervals, thus effectively avoiding errors that lead to invalid results, and it is also an effective tool for dealing with uncertainty problems. The importance of interval analysis is self-evident, both in theory and application. Interval analysis has a long history, but it was not until 1969 that Moore [1] first applied the interval analysis to automatic error analysis, which attracted the attention of many scholars and aroused their research interest. Thereby, there are many excellent results in the research of interval analysis, and interested readers can refer to Refs. [2,3,4].

On the other hand, convex analysis theory is widely used in optimization, economics, and other fields, and it has been concerned and studied by many scholars. The classical convex analysis has received many extensions and improvements, see Refs. [5,6,7]. Noor [8] introduced a new class of convex functions, called harmonically h-convex functions, which is an important generalization of convex functions. Regarding the properties and related research of harmonically h-convex functions, interested readers can refer to the Refs. [8,9]. It is worth noting that some integral inequalities have been extended to interval-valued functions, such as Wirtinger inequality, Ostrowski inequality, and Opial inequality, which have been well studied in the past decade, see Refs. [10,11,12,13]. As we all know, there is a close connection between convex functions and inequalities, so inspired by the literature, Jensen type inequality and Hermite–Hadamard type inequalities for convex interval-valued functions have been studied in recent years. However, it is worth noting that at present, interval-valued inequalities are obtained by using inclusion relations or $LU$-orders [14,15,16,17,18], and these relations are partial orders. In 2014, Bhunia and Samanta [19] defined the $cr$-order by using the midpoint and radius of the interval, which is a total order relation. In 2020, Rahman [20] gave the definition of $cr$-convex function and studied the nonlinear constrained optimization problem by using $cr$-order.

Inspired by Refs. [8,14,19,20], we introduce a new class of harmonically convex interval-valued functions by using $cr$-order, which is called harmonically $cr$-h-convex functions. By properly selecting the function h, some special harmonically convex functions can be obtained, such as harmonically $cr$-convex functions, harmonically $cr$-P-functions, harmonically $cr$-Godunova–Levin functions and harmonically $cr$-s-convex functions.

The main structure of this paper is as follows: Section 2 mainly presents some necessary preliminary knowledge. In Section 3, the definition of harmonically $cr$-h-convex function is introduced, some important basic properties of this kind of function are discussed, and we establish Jensen type inequality of harmonically $cr$-h-convex function. In Section 4, we prove Hermite–Hadamard type inequalities and Fejér type inequalities by using the definition and properties of harmonically $cr$-h-convex function. Some special cases are discussed and relevant numerical examples are given to verify the accuracy of our results. In Section 5, we summarize the main contents of this paper and the prospect of future research.

2. Preliminaries and Basic Results

Let us denote by ${\mathbb{R}}_{\mathcal{I}}$ the collection of all nonempty closed intervals of the real line $\mathbb{R}$. We call $\left[a\right]=[\underline{a},\overline{a}]$ positive if $\underline{a}>0$. We denote by ${\mathbb{R}}_{\mathcal{I}}^{+}$ and ${\mathbb{R}}^{+}$ the set of all positive intervals and the set of all positive numbers of $\mathbb{R}$, respectively. For $\lambda \in \mathbb{R}$, the Minkowski addition and scalar multiplication are defined by

$$a+b=[\underline{a},\overline{a}]+[\underline{b},\overline{b}]=[\underline{a}+\underline{b},\overline{a}+\overline{b}];$$

$$\lambda a=\lambda [\underline{a},\overline{a}]=\left\{\begin{array}{cc}\left[\lambda \underline{a},\lambda \overline{a}\right],\hfill & \lambda >0,\hfill \\ \left\{0\right\},\hfill & \lambda =0,\hfill \\ \left[\lambda \overline{a},\lambda \underline{a}\right],\hfill & \lambda <0,\hfill \end{array}\right.$$

respectively.

Let $a=[\underline{a},\overline{a}]\in {\mathbb{R}}_{\mathcal{I}},a_c=\frac{\overline{a}+\underline{a}}{2}$ is called the center of a, $a_r=\frac{\overline{a}-\underline{a}}{2}$ is called the radius of a. Then, $a=[\underline{a},\overline{a}]$ can also be presented in center-radius form as

$$a=⟨\frac{\overline{a}+\underline{a}}{2},\frac{\overline{a}-\underline{a}}{2}⟩=⟨a_c,a_r⟩.$$

The order relation by the center and radius of interval is defined in the following definition.

Definition 1

([19]). Let $a=[\underline{a},\overline{a}]=⟨a_c,a_r⟩,b=[\underline{b},\overline{b}]=⟨b_c,b_r⟩\in {\mathbb{R}}_{\mathcal{I}},$ then the center-radius order (for shortly, $cr$-order) relation defined as

$$a{⪯}_{cr}b\iff \left\{\begin{array}{cc}{a}_c<b_c,\hfill & if{a}_c\ne b_c,\hfill \\ \\ a_r\le b_r,\hfill & if{a}_c=b_c.\hfill \end{array}\right.$$

Obviously, for any two intervals $a,b\in {\mathbb{R}}_{\mathcal{I}},$ either $a{⪯}_{cr}b$ or $b{⪯}_{cr}a.$

The conception of thw Riemann integral for interval-valued function is introduced in Ref. [21]. Moreover, we have

Theorem 1

([21]). Let $f:[a,b]\to {\mathbb{R}}_{\mathcal{I}}$ be an interval-valued function given by $f=[\underline{f},\overline{f}]$. Then the f is Riemann integrable on $[a,b]$ iff $\underline{f}$ and $\overline{f}$ are Riemann integrable on $[a,b]$ and

$${\int }_a^{b}f\left(x\right)dx=\left[{\int }_a^b\underline{f}\left(x\right)dx,{\int }_a^b\overline{f}\left(x\right)dx\right].$$

The set of all Riemann integrable interval-valued functions on $[a,b]$ will be denoted by ${\mathcal{IR}}_{\left(\right[a,b\left]\right)}$.

Theorem 2

([22]). Let $f,g:[a,b]\to {\mathbb{R}}_{\mathcal{I}}^{+}$ given by $f=[\underline{f},\overline{f}]$, and $g=[\underline{g},\overline{g}]$. If $f,g\in {\mathcal{IR}}_{\left(\right[a,b\left]\right)}$, and $f\left(x\right){⪯}_{cr}g\left(x\right)$ for all $x\in [a,b],$ then

$${\int }_a^{b}f\left(x\right)dx{⪯}_{cr}{\int }_a^{b}g\left(x\right)dx.$$

For more basic notations with interval analysis, see Refs. [1,21]. Furthermore, we recall the following results in Ref. [8].

Definition 2

([8]). Let $f:[a,b]\to {\mathbb{R}}^{+}$ and $h:[0,1]\to {\mathbb{R}}^{+}$ be two non-negative functions. We say that f is harmonically h-convex function or that $f\in SHX(h,[a,b],{\mathbb{R}}^{+}),$ if for all $x,y\in [a,b]$ and $t\in [0,1],$ we have

$$\begin{array}{c}\hfill f\left(\frac{xy}{tx+(1-t)y}\right)\le h(1-t)f\left(x\right)+h\left(t\right)f\left(y\right).\end{array}$$

h is called supermultiplicative if

$$\begin{array}{c}\hfill h\left(\vartheta t\right)\ge h\left(\vartheta \right)h\left(t\right),\end{array}$$

(1)

for all $\vartheta ,t\in [0,1]$. If “≥" in (1) is replaced with “≤", then h is called submultiplicative.

3. Harmonically $\mathit{cr}$-$\mathit{h}$-Convex Function and Jensen Type Inequality

In this section, we first give the definition of harmonically $cr$-h-convex function.

Definition 3.

Let $f:[a,b]\to {\mathbb{R}}_{\mathcal{I}}^{+}$ be an interval-valued function given by $f=[\underline{f},\overline{f}].h:[0,1]\to {\mathbb{R}}^{+}$ be non-negative function. Then f is said to be harmonically $cr$-h-convex function over $[a,b]$ if

$$f\left(\frac{x_1{x}_2}{t{x}_1+(1-t)x_2}\right){⪯}_{cr}h(1-t)f\left(x_1\right)+h\left(t\right)f\left(x_2\right),$$

(2)

for each $t\in (0,1)$ and $\forall x_1,x_2\in [a,b].$

The set of all harmonically $cr$-h-convex function over $[a,b]$ is denoted by $SHX(cr$-$h,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+}).$

Remark 1.

If $\underline{f}\left(x\right)=\overline{f}\left(x\right),x\in [a,b]$, then Definition 3 reduces to Definition 2.

If $h\left(t\right)=t$, then Definition 3 reduces to harmonically $cr$-convex function:

$$f\left(\frac{x_1{x}_2}{t{x}_1+(1-t)x_2}\right){⪯}_{cr}(1-t)f\left(x_1\right)+tf\left(x_2\right).$$

If $h\left(t\right)=1$, then Definition 3 reduces to harmonically $cr$-P function:

$$f\left(\frac{x_1{x}_2}{t{x}_1+(1-t)x_2}\right){⪯}_{cr}f\left(x_1\right)+f\left(x_2\right).$$

If $h\left(t\right)=t^s,s\in (0,1]$, then Definition 3 reduces to harmonically $cr$-s-convex function:

$$f\left(\frac{x_1{x}_2}{t{x}_1+(1-t)x_2}\right){⪯}_{cr}{t}^{s}f\left(x_1\right)+{(1-t)}^{s}f\left(x_2\right).$$

Proposition 1.

Let $h_1,h_2:[0,1]\to {\mathbb{R}}^{+}$ be non-negative functions and

$$h_2\left(t\right)\le h_1\left(t\right),t\in [0,1].$$

If $f\in SHX(cr-h_2,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+})$, then $f\in SHX(cr-h_1,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+})$.

Proof. 

Since $f\in SHX(cr-h_2,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+})$, then for $\forall x_1,x_2\in [a,b],t\in [0,1]$, we have

$$\begin{array}{cc}\hfill f\left(\frac{x_1{x}_2}{t{x}_1+(1-t)x_2}\right)& {⪯}_{cr}{h}_2(1-t)f\left(x_1\right)+h_2\left(t\right)f\left(x_2\right)\hfill \\ & {⪯}_{cr}{h}_1(1-t)f\left(x_1\right)+h_1\left(t\right)f\left(x_2\right).\hfill \end{array}$$

Hence, $f\in SHX(cr-h_1,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+})$.

This completes the proof. □

Proposition 2.

Let $f:[a,b]\to {\mathbb{R}}_{\mathcal{I}}^{+}$ given by $f=[\underline{f},\overline{f}]=⟨f_c,f_r⟩$. If $f_c$ and $f_r$ are harmonically h-convex over $[a,b]$, then f is harmonically $cr$-h-convex function over $[a,b]$.

Proof. 

Since $f_c$ and $f_r$ are harmonically h-convex over $[a,b]$, then for each $t\in (0,1)$ and $\forall x_1,x_2\in [a,b],$ we have

$$f_c\left(\frac{x_1{x}_2}{t{x}_1+(1-t)x_2}\right)\le h(1-t)f_c\left(x_1\right)+h\left(t\right)f_c\left(x_2\right),$$

and

$$f_r\left(\frac{x_1{x}_2}{t{x}_1+(1-t)x_2}\right)\le h(1-t)f_r\left(x_1\right)+h\left(t\right)f_r\left(x_2\right).$$

Now, if $f_c\left(\frac{x_1{x}_2}{t{x}_1+(1-t)x_2}\right)\ne h(1-t)f_c\left(x_1\right)+h\left(t\right)f_c\left(x_2\right),$ then for each $t\in (0,1)$ and $\forall x_1,x_2\in [a,b],$

$$f_c\left(\frac{x_1{x}_2}{t{x}_1+(1-t)x_2}\right)<h(1-t)f_c\left(x_1\right)+h\left(t\right)f_c\left(x_2\right),$$

then

$$f\left(\frac{x_1{x}_2}{t{x}_1+(1-t)x_2}\right){⪯}_{cr}h(1-t)f\left(x_1\right)+h\left(t\right)f\left(x_2\right).$$

Otherwise, for each $t\in (0,1)$ and $\forall x_1,x_2\in [a,b],$

$$f_r\left(\frac{x_1{x}_2}{t{x}_1+(1-t)x_2}\right)\le h(1-t)f_r\left(x_1\right)+h\left(t\right)f_r\left(x_2\right),$$

that is,

$$f\left(\frac{x_1{x}_2}{t{x}_1+(1-t)x_2}\right){⪯}_{cr}h(1-t)f\left(x_1\right)+h\left(t\right)f\left(x_2\right).$$

Combining all the above, from the Definition 1, it can be written as

$$f\left(\frac{x_1{x}_2}{t{x}_1+(1-t)x_2}\right){⪯}_{cr}h(1-t)f\left(x_1\right)+h\left(t\right)f\left(x_2\right),$$

for each $t\in (0,1)$ and $\forall x_1,x_2\in [a,b].$

This completes the proof. □

Example 1.

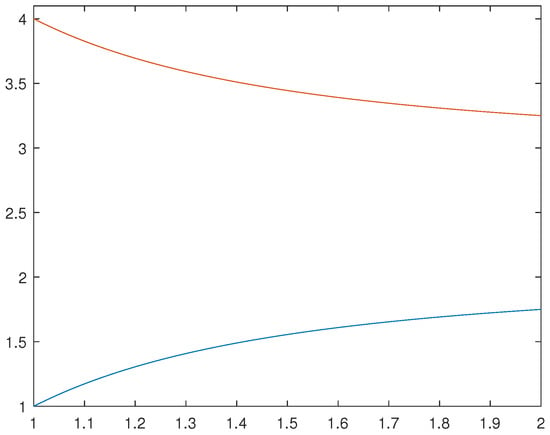
Let $[a,b]=[1,2],h\left(t\right)=t$ for all $t\in [0,1].f:[a,b]\to {\mathbb{R}}_{\mathcal{I}}^{+}$ be defined as

$$f\left(x\right)=\left[-\frac{1}{x^2}+2,\frac{1}{x^2}+3\right],x\in [1,2].$$

Then,

$$f_c\left(x\right)=\frac{5}{2},f_r\left(x\right)=\frac{1}{x^2}+\frac{1}{2},x\in [1,2].$$

Obviously, $f_c,f_r$ are harmonically h-convex functions on $[1,2].$ According to Proposition 2, f is harmonically $cr$-h-convex function over $[1,2]$ (See Figure 1).

Figure 1. Illustrationof Example 1: The function $\underline{f}$ is a blue line and the function $\overline{f}$ is a red line.

Next, we mainly establish Jensen type inequality about harmonically $cr$-h-convex function.

Theorem 3.

Let $f:[a,b]\to {\mathbb{R}}_{\mathcal{I}}^{+}$ be an interval-valued function such that $f=[\underline{f},\overline{f}]$. $h:[0,1]\to {\mathbb{R}}^{+}$ be a non-negative supermultiplicative function. If $f\in SHX(cr$-$h,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+})$, then

$$\begin{array}{c}\hfill f\left(\frac{{\mathcal{P}}_n}{{\displaystyle \sum _{i=1}^n}\frac{p_i}{x_i}}\right){⪯}_{cr}\sum _{i=1}^{n}h\left(\frac{p_i}{{\mathcal{P}}_n}\right)f\left(x_i\right),\end{array}$$

(3)

where ${\mathcal{P}}_n={\displaystyle \sum _{i=1}^n}{p}_i.$

Proof. 

We use mathematical induction to prove Theorem 3. If $n=2$, then inequality (3) is equivalent to inequality (2) with $t=\frac{p_1}{{\mathcal{P}}_2}$ and $1-t=\frac{p_2}{{\mathcal{P}}_2}$.

Suppose that inequality (3) holds for $n-1.$ Then for n-tuples $(x_1,x_2,\dots ,x_n)$ and $(p_1,p_2,\dots ,p_n)$, we have

$$\begin{array}{c}\hfill \begin{array}{cc}& f\left(\frac{{\mathcal{P}}_n}{{\displaystyle \sum _{i=1}^n}\frac{p_i}{x_i}}\right)=f\left(\frac{1}{\frac{p_n}{{\mathcal{P}}_n{x}_n}+\frac{1}{{\mathcal{P}}_n}{\displaystyle \sum _{i=1}^{n-1}}\frac{p_i}{x_i}}\right)\hfill \\ & =f\left(\frac{1}{\frac{p_n}{{\mathcal{P}}_n{x}_n}+\frac{{\mathcal{P}}_{n-1}}{{\mathcal{P}}_n}{\displaystyle \sum _{i=1}^{n-1}}\frac{p_i}{{\mathcal{P}}_{n-1}{x}_i}}\right)\hfill \\ & {⪯}_{cr}h\left(\frac{P_n}{{\mathcal{P}}_n}\right)f\left(x_n\right)+h\left(\frac{{\mathcal{P}}_{n-1}}{{\mathcal{P}}_n}\right)f\left(\frac{1}{{\displaystyle \sum _{i=1}^{n-1}}\frac{p_i}{{\mathcal{P}}_{n-1}{x}_i}}\right)\hfill \\ & {⪯}_{cr}h\left(\frac{P_n}{{\mathcal{P}}_n}\right)f\left(x_n\right)+h\left(\frac{{\mathcal{P}}_{n-1}}{{\mathcal{P}}_n}\right)\sum _{i=1}^{n-1}h\left(\frac{p_i}{{\mathcal{P}}_{n-1}}\right)f\left(x_i\right)\hfill \\ & {⪯}_{cr}h\left(\frac{P_n}{{\mathcal{P}}_n}\right)f\left(x_n\right)+\sum _{i=1}^{n-1}h\left(\frac{p_i}{{\mathcal{P}}_n}\right)f\left(x_i\right)\hfill \\ & =\sum _{i=1}^{n}h\left(\frac{p_i}{{\mathcal{P}}_n}\right)f\left(x_i\right).\hfill \end{array}\end{array}$$

(4)

This proof is completed. □

Remark 2.

It is clear that if $\underline{f}=\overline{f}$, then Theorem 3 reduces to Theorem 2.5 of [23].

If $h\left(t\right)=t$, then Theorem 3 reduces to the result for harmonically $cr$-convex function:

$$\begin{array}{c}\hfill f\left(\frac{{\mathcal{P}}_n}{{\displaystyle \sum _{i=1}^n}\frac{p_i}{x_i}}\right){⪯}_{cr}\sum _{i=1}^n\frac{p_i}{{\mathcal{P}}_n}f\left(x_i\right).\end{array}$$

If $h\left(t\right)=1$, then Theorem 3 reduces to the result for harmonically $cr$-P-function:

$$\begin{array}{c}\hfill f\left(\frac{{\mathcal{P}}_n}{{\displaystyle \sum _{i=1}^n}\frac{p_i}{x_i}}\right){⪯}_{cr}\sum _{i=1}^{n}f\left(x_i\right).\end{array}$$

If $h\left(t\right)=t^s,s\in (0,1]$, then Theorem 3 reduces to the result for the harmonically $cr$-s-convex function:

$$\begin{array}{c}\hfill f\left(\frac{{\mathcal{P}}_n}{{\displaystyle \sum _{i=1}^n}\frac{p_i}{x_i}}\right){⪯}_{cr}\sum _{i=1}^n{\left(\frac{p_i}{{\mathcal{P}}_n}\right)}^{s}f\left(x_i\right).\end{array}$$

4. Hermite-Hadamard Type Inequalities and Fejér Type Inequalities of Harmonically $\mathit{cr}$-$\mathit{h}$-Convex Functions

In this section, we mainly establish Hermite–Hadamard type inequalities and Fejér type inequalities about harmonically $cr$-h-convex functions.

Theorem 4.

Let $f:[a,b]\to {\mathbb{R}}_{\mathcal{I}}^{+}$ be an interval-valued function such that $f=[\underline{f},\overline{f}]$ and $f\in {\mathcal{IR}}_{\left(\right[a,b\left]\right)},h:[0,1]\to {\mathbb{R}}^{+}$ be a non-negative function and $h\left(\frac{1}{2}\right)\ne 0$. If $f\in SHX(cr$-$h,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+})$, then

$$\begin{array}{c}\hfill \frac{1}{2h\left(\frac{1}{2}\right)}f\left(\frac{2ab}{a+b}\right){⪯}_{cr}\frac{ab}{b-a}{\int }_a^b\frac{f\left(x\right)}{x^2}dx{⪯}_{cr}[f\left(a\right)+f\left(b\right)]{\int }_0^{1}h\left(t\right)dt.\end{array}$$

(5)

Proof. 

Since $f\in SHX(cr$-$h,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+})$, we have

$$\frac{1}{h\left(\frac{1}{2}\right)}f\left(\frac{2xy}{x+y}\right){⪯}_{cr}f\left(x\right)+f\left(y\right).$$

Let $x=\frac{ab}{ta+(1-t)b},y=\frac{ab}{(1-t)a+tb}$, $t\in [0,1]$, then

$$\frac{1}{h\left(\frac{1}{2}\right)}f\left(\frac{a+b}{2}\right){⪯}_{cr}f(ta+(1-t)b)+f((1-t)a+tb).$$

(6)

Integrating on $[0,1]$, we get

$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{1}{h\left(\frac{1}{2}\right)}f\left(\frac{2ab}{a+b}\right)\hfill \\ & {⪯}_{cr}\left[{\int }_0^{1}f\left(\frac{ab}{ta+(1-t)b}\right)dt+{\int }_0^{1}f\left(\frac{ab}{(1-t)a+tb}\right)dt\right]\hfill \\ & =\left[{\int }_0^1\left(\underline{f}\left(\frac{ab}{ta+(1-t)b}\right)+\underline{f}\left(\frac{ab}{(1-t)a+tb}\right)\right)dt,\right.\hfill \\ & \left.{\int }_0^1\left(\overline{f}\left(\frac{ab}{ta+(1-t)b}\right)+\overline{f}\left(\frac{ab}{(1-t)a+tb}\right)\right)dt\right]\hfill \\ & =\left[\frac{ab}{a-b}{\int }_b^a\frac{\underline{f}\left(x\right)}{x^2}dx+\frac{ab}{b-a}{\int }_a^b\frac{\underline{f}\left(x\right)}{x^2}dx,\frac{ab}{a-b}{\int }_b^a\frac{\overline{f}\left(x\right)}{x^2}dx+\frac{ab}{b-a}{\int }_a^b\frac{\overline{f}\left(x\right)}{x^2}dx\right]\hfill \\ & =\left[\frac{2ab}{b-a}{\int }_a^b\frac{\underline{f}\left(x\right)}{x^2}dx,\frac{2ab}{b-a}{\int }_a^b\frac{\overline{f}\left(x\right)}{x^2}dx\right]\hfill \\ & =\frac{2ab}{b-a}{\int }_a^b\frac{f\left(x\right)}{x^2}dx.\hfill \end{array}\end{array}$$

(7)

Similarly, since $f\in SHX(cr$-$h,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+})$,

$$f\left(\frac{ab}{ta+(1-t)b}\right)+f\left(\frac{ab}{(1-t)a+tb}\right){⪯}_{cr}\left[h\left(t\right)+h(1-t)\right]\left[f\left(a\right)+f\left(b\right)\right].$$

(8)

Integrating on $[0,1]$, we have

$$\frac{2ab}{b-a}{\int }_a^b\frac{f\left(x\right)}{x^2}dx{⪯}_{cr}[f\left(a\right)+f\left(b\right)]{\int }_0^1\left[h\left(t\right)+h(1-t)\right]dt.$$

(9)

By combining (7) with (9), the result follows.

This proof is completed. □

Remark 3.

It is clear that if $\underline{f}=\overline{f}$, then Theorem 4 reduces to Theorem 3.2 of [8].

If $h\left(t\right)=t$, then Theorem 4 reduces to the result for the harmonically $cr$-convex function:

$$\begin{array}{c}\hfill f\left(\frac{2ab}{a+b}\right){⪯}_{cr}\frac{ab}{b-a}{\int }_a^b\frac{f\left(x\right)}{x^2}dx{⪯}_{cr}\frac{f\left(a\right)+f\left(b\right)}{2}.\end{array}$$

If $h\left(t\right)=1$, then Theorem 4 reduces to the result for the harmonically $cr$-P-function:

$$\begin{array}{c}\hfill \frac{1}{2}f\left(\frac{2ab}{a+b}\right){⪯}_{cr}\frac{ab}{b-a}{\int }_a^b\frac{f\left(x\right)}{x^2}dx{⪯}_{cr}f\left(a\right)+f\left(b\right).\end{array}$$

If $h\left(t\right)=t^s,s\in (0,1]$, then Theorem 4 reduces to the result for the harmonically $cr$-s-convex function:

$$\begin{array}{c}\hfill 2^{s-1}f\left(\frac{a+b}{2}\right){⪯}_{cr}\frac{ab}{b-a}{\int }_a^b\frac{f\left(x\right)}{x^2}dx{⪯}_{cr}\frac{f\left(a\right)+f\left(b\right)}{s+1}.\end{array}$$

Example 2.

Further by Example 1, we have

$$\frac{1}{2h\left(\frac{1}{2}\right)}f\left(\frac{2ab}{a+b}\right)=\left[\frac{23}{16},\frac{57}{16}\right],$$

$$\frac{2ab}{b-a}{\int }_a^b\frac{f\left(x\right)}{x^2}dx=\left[\frac{17}{12},\frac{43}{12}\right],$$

$$[f\left(a\right)+f\left(b\right)]{\int }_0^{1}h\left(t\right)dt=\left[\frac{11}{8},\frac{29}{8}\right].$$

Since

$$\left[\frac{23}{16},\frac{57}{16}\right]{⪯}_{cr}\left[\frac{17}{12},\frac{43}{12}\right]{⪯}_{cr}\left[\frac{11}{8},\frac{29}{8}\right].$$

Consequently, Theorem 4 is verified.

Theorem 5.

Let $f:[a,b]\to {\mathbb{R}}_{\mathcal{I}}^{+}$ be an interval-valued function such that $f=[\underline{f},\overline{f}]$ and $f\in {\mathcal{IR}}_{\left(\right[a,b\left]\right)}.h:[0,1]\to {\mathbb{R}}^{+}$ be a non-negative function and $h\left(\frac{1}{2}\right)\ne 0$. If $f\in SHX(cr$-$h,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+})$, then

$$\begin{array}{cc}\hfill \frac{1}{4{\left[h\left(\frac{1}{2}\right)\right]}^2}f\left(\frac{2ab}{a+b}\right){⪯}_{cr}{\Delta }_1& {⪯}_{cr}\frac{ab}{b-a}{\int }_a^b\frac{f\left(x\right)}{x^2}dx\hfill \\ \hfill & {⪯}_{cr}{\Delta }_2{⪯}_{cr}\left[f\left(a\right)+f\left(b\right)\right]\left[\frac{1}{2}+h\left(\frac{1}{2}\right)\right]{\int }_0^{1}h\left(t\right)dt,\hfill \end{array}$$

(10)

where

$${\Delta }_1=\frac{1}{4h\left(\frac{1}{2}\right)}\left[f\left(\frac{4ab}{3a+b}\right)+f\left(\frac{4ab}{a+3b}\right)\right],$$

$${\Delta }_2=\left[\frac{f\left(a\right)+f\left(b\right)}{2}+f\left(\frac{2ab}{a+b}\right)\right]{\int }_0^{1}h\left(t\right)dt.$$

Proof. 

Since $f\in SHX(h,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+})$, on the $\left[a,\frac{a+b}{2}\right],$ we have

$$\begin{array}{cc}\hfill & f\left(\frac{4ab}{a+3b}\right)\hfill \\ \hfill & =f\left(\frac{\frac{a\frac{2ab}{a+b}}{ta+(1-t)\frac{2ab}{a+b}}}{2}+\frac{\frac{a\frac{2ab}{a+b}}{(1-t)a+t\frac{2ab}{a+b}}}{2}\right)\hfill \\ \hfill & {⪯}_{cr}h\left(\frac{1}{2}\right)\left[f\left(\frac{a\frac{2ab}{a+b}}{ta+(1-t)\frac{2ab}{a+b}}\right)+f\left(\frac{a\frac{2ab}{a+b}}{(1-t)a+t\frac{2ab}{a+b}}\right)\right].\hfill \end{array}$$

Integrating on $\left[0,1\right]$,

$$\frac{4abh\left(\frac{1}{2}\right)}{b-a}{\int }_a^{\frac{2ab}{a+b}}\frac{f\left(x\right)}{x^2}dx{⪯}_{cr}f\left(\frac{4ab}{a+3b}\right).$$

(11)

Similarly, on the $\left[\frac{a+b}{2},b\right]$, we get

$$\frac{4abh\left(\frac{1}{2}\right)}{b-a}{\int }_{\frac{2ab}{a+b}}^b\frac{f\left(x\right)}{x^2}dx{⪯}_{cr}f\left(\frac{4ab}{3a+b}\right).$$

(12)

Adding (11) and (12), then we obtain

$$\frac{ab}{b-a}{\int }_a^b\frac{f\left(x\right)}{x^2}dx{⪯}_{cr}\frac{1}{4h\left(\frac{1}{2}\right)}\left[f\left(\frac{4ab}{3a+b}\right)+f\left(\frac{4ab}{a+3b}\right)\right].$$

By Theorem 4,

$$\begin{array}{cc}\hfill & \frac{1}{4h^2\left(\frac{1}{2}\right)}f\left(\frac{2ab}{a+b}\right)\hfill \\ \hfill & =\frac{1}{4h^2\left(\frac{1}{2}\right)}f\left(\frac{1}{2}·\frac{4ab}{3a+b}+\frac{1}{2}·\frac{4ab}{a+3b}\right)\hfill \\ \hfill & {⪯}_{cr}\frac{1}{4h^2\left(\frac{1}{2}\right)}\left[h\left(\frac{1}{2}\right)f\left(\frac{4ab}{3a+b}\right)+h\left(\frac{1}{2}\right)f\left(\frac{4ab}{a+3b}\right)\right]\hfill \\ \hfill & {⪯}_{cr}{△}_1\hfill \\ \hfill & {⪯}_{cr}\frac{ab}{b-a}{\int }_a^b\frac{f\left(x\right)}{x^2}dx\hfill \\ \hfill & {⪯}_{cr}\frac{1}{2}\left[f\left(a\right)+f\left(b\right)+2f\left(\frac{2ab}{a+b}\right)\right]{\int }_0^{1}h\left(t\right)dt\hfill \\ \hfill & ={△}_2\hfill \\ \hfill & {⪯}_{cr}\left[\frac{f\left(a\right)+f\left(b\right)}{2}+h\left(\frac{1}{2}\right)\left[f\left(a\right)+f\left(b\right)\right]\right]{\int }_0^{1}h\left(t\right)dt\hfill \\ \hfill & {⪯}_{cr}\left[f\left(a\right)+f\left(b\right)\right]\left[\frac{1}{2}+h\left(\frac{1}{2}\right)\right]{\int }_0^{1}h\left(t\right)dt.\hfill \end{array}$$

Hence, we get (5).

This proof is completed. □

Remark 4.

As in Remark 3, from Theorem 5 we obtain particular results for harmonically $cr$-convex functions, harmonically $cr$-P-function, and harmonically $cr$-s-convex functions.

Example 3.

Further by Example 2, we have

$${\Delta }_1=\frac{1}{2}\left[f\left(\frac{8}{5}\right)+f\left(\frac{8}{7}\right)\right]=\left[\frac{91}{64},\frac{229}{64}\right],$$

$${\Delta }_2=\frac{1}{2}\left[\frac{f\left(1\right)+f\left(2\right)}{2}+f\left(\frac{4}{3}\right)\right]=\left[\frac{45}{32},\frac{115}{32}\right],$$

$$\left[f\left(a\right)+f\left(b\right)\right]\left[\frac{1}{2}+h\left(\frac{1}{2}\right)\right]{\int }_0^{1}h\left(t\right)dt=\left[\frac{11}{8},\frac{29}{8}\right].$$

Then, we have obtained that

$$\left[\frac{23}{16},\frac{57}{16}\right]{⪯}_{cr}\left[\frac{91}{64},\frac{229}{64}\right]{⪯}_{cr}\left[\frac{17}{12},\frac{43}{12}\right]{⪯}_{cr}\left[\frac{45}{32},\frac{115}{32}\right]{⪯}_{cr}\left[\frac{11}{8},\frac{29}{8}\right].$$

Consequently, Theorem 5 is verified.

Theorem 6.

Let $f,g:[a,b]\to {\mathbb{R}}_{\mathcal{I}}^{+}$ be two interval-valued functions given by $f=[\underline{f},\overline{f}],g=[\underline{g},\overline{g}]$ and $fg\in {\mathcal{IR}}_{\left(\right[a,b\left]\right)}.h_1,h_2:[0,1]\to {\mathbb{R}}^{+}$ be non-negative functions. If $f\in SHX(cr$-$h_1,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+}),g\in SHX(cr$-$h_2,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+})$, then

$$\frac{ab}{b-a}{\int }_a^b\frac{f\left(x\right)g\left(x\right)}{x^2}dx{⪯}_{cr}M(a,b){\int }_0^1{h}_1\left(t\right)h_2\left(t\right)dt+N(a,b){\int }_0^1{h}_1\left(t\right)h_2(1-t)dt,$$

(13)

where

$$\mathcal{M}(a,b)=f\left(a\right)g\left(a\right)+f\left(b\right)g\left(b\right),\mathcal{N}(a,b)=f\left(a\right)g\left(b\right)+f\left(b\right)g\left(a\right).$$

Proof. 

Since $f\in SHX(cr$-$h_1,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+}),g\in SHX(cr$-$h_2,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+})$, we have

$$f\left(\frac{ab}{ta+(1-t)b}\right){⪯}_{cr}{h}_1(1-t)f\left(a\right)+h_1\left(t\right)f\left(b\right),$$

$$g\left(\frac{ab}{ta+(1-t)b}\right){⪯}_{cr}{h}_2(1-t)g\left(a\right)+h_2\left(t\right)g\left(b\right).$$

Since $f,g\in {\mathbb{R}}_{\mathcal{I}}^{+}$, we obtain

$$\begin{array}{cc}\hfill & f\left(\frac{ab}{ta+(1-t)b}\right)g\left(\frac{ab}{ta+(1-t)b}\right)\hfill \\ \hfill & {⪯}_{cr}{h}_1(1-t)h_2(1-t)f\left(a\right)g\left(a\right)+h_1\left(t\right)h_2\left(t\right)f\left(b\right)g\left(b\right)\hfill \\ \hfill & +h_1(1-t)h_2\left(t\right)f\left(a\right)g\left(b\right)+h_1\left(t\right)h_2(1-t)f\left(b\right)g\left(a\right).\hfill \end{array}$$

(14)

In the same way as above, we have

$$\begin{array}{cc}\hfill & f\left(\frac{ab}{(1-t)a+tb}\right)g\left(\frac{ab}{(1-t)a+tb}\right)\hfill \\ \hfill & {⪯}_{cr}{h}_1\left(t\right)h_2\left(t\right)f\left(a\right)g\left(a\right)+h_1(1-t)h_2(1-t)f\left(b\right)g\left(b\right)\hfill \\ \hfill & +h_1\left(t\right)h_2(1-t)f\left(a\right)g\left(b\right)+h_1(1-t)h_2\left(t\right)f\left(b\right)g\left(a\right).\hfill \end{array}$$

(15)

By adding (14) and (15), we obtain

$$\begin{array}{cc}\hfill & f\left(\frac{ab}{ta+(1-t)b}\right)g\left(\frac{ab}{ta+(1-t)b}\right)+f\left(\frac{ab}{(1-t)a+tb}\right)g\left(\frac{ab}{(1-t)a+tb}\right)\hfill \\ \hfill & {⪯}_{cr}\left[h_1(1-t)f\left(a\right)+h_1\left(t\right)f\left(b\right)\right]\left[h_2(1-t)g\left(a\right)+h_2\left(t\right)g\left(b\right)\right]\hfill \\ \hfill & +\left[h_1\left(t\right)f\left(a\right)+h_1(1-t)f\left(b\right)\right]\left[h_2\left(t\right)g\left(a\right)+h_2(1-t)g\left(b\right)\right]\hfill \\ \hfill & =\mathcal{M}(a,b)\left[h_1(1-t)h_2(1-t)+h_1\left(t\right)h_2\left(t\right)\right]\hfill \\ \hfill & +\mathcal{N}(a,b)\left[h_1\left(t\right)h_2(1-t)+h_1(1-t)h_2\left(t\right)\right].\hfill \end{array}$$

(16)

Integrating on $[0,1]$, we have

$$\begin{array}{cc}\hfill & {\int }_0^{1}f\left(\frac{ab}{ta+(1-t)b}\right)g\left(\frac{ab}{ta+(1-t)b}\right)dt\hfill \\ \hfill & +{\int }_0^{1}f\left(\frac{ab}{(1-t)a+tb}\right)g\left(\frac{ab}{(1-t)a+tb}\right)dt\hfill \\ \hfill & {⪯}_{cr}\mathcal{M}(a,b){\int }_0^1\left[h_1\left(t\right)h_2\left(t\right)+h_1(1-t)h_2(1-t)\right]dt\hfill \\ \hfill & +\mathcal{N}(a,b){\int }_0^1\left[h_1(1-t)h_2\left(t\right)+h_1\left(t\right)h_2(1-t)\right]dt.\hfill \end{array}$$

(17)

Since

$$\begin{array}{cc}\hfill & {\int }_0^{1}f\left(\frac{ab}{ta+(1-t)b}\right)g\left(\frac{ab}{ta+(1-t)b}\right)dt\hfill \\ \hfill & +{\int }_0^{1}f\left(\frac{ab}{(1-t)a+tb}\right)g\left(\frac{ab}{(1-t)a+tb}\right)dt\hfill \\ \hfill & =\frac{2ab}{b-a}{\int }_a^b\frac{f\left(x\right)g\left(x\right)}{x^2}dx.\hfill \end{array}$$

(18)

By substituting the equalities (16) and (17), then we have inequality (13).

This proof is completed. □

Remark 5.

If $\underline{f}=\overline{f}$, then we get Theorem 3.6 of [8].

If $h_1\left(t\right)=h_2\left(t\right)=t$, then Theorem 6 reduces to the result for the harmonically $cr$-convex function:

$$\frac{ab}{b-a}{\int }_a^b\frac{f\left(x\right)g\left(x\right)}{x^2}dx{⪯}_{cr}\frac{\mathcal{M}(a,b)}{3}+\frac{\mathcal{N}(a,b)}{6}.$$

Example 4.

Let $[a,b]=[1,2],h_1\left(t\right)=h_2\left(t\right)=t$ for all $t\in [0,1].f,g:[a,b]\to {\mathbb{R}}_{\mathcal{I}}^{+}$ be defined as

$$f\left(x\right)=\left[-\frac{1}{x^2}+2,\frac{1}{x^2}+3\right],g\left(x\right)=\left[-\frac{1}{x}+1,\frac{1}{x}+2\right],x\in [1,2].$$

Then,

$$\begin{array}{cc}\hfill & \frac{ab}{b-a}{\int }_a^b\frac{f\left(x\right)g\left(x\right)}{x^2}dx=\left[\frac{37}{96},\frac{949}{96}\right],\hfill \\ \hfill & M(a,b){\int }_0^1{h}_1\left(t\right)h_2\left(t\right)dt+N(a,b){\int }_0^1{h}_1\left(t\right)h_2(1-t)dt=\left[\frac{3}{8},10\right].\hfill \end{array}$$

Since,

$$\left[\frac{37}{96},\frac{949}{96}\right]{⪯}_{cr}\left[\frac{3}{8},10\right].$$

So, the Theorem 6 is verified.

Theorem 7.

Let $f,g:[a,b]\to {\mathbb{R}}_{\mathcal{I}}^{+}$ be two interval-valued functions given by $f=[\underline{f},\overline{f}],g=[\underline{g},\overline{g}]$ and $fg\in {\mathcal{IR}}_{\left(\right[a,b\left]\right)}.h_1,h_2:[0,1]\to {\mathbb{R}}^{+}$ be non-negative functions and $h_1\left(\frac{1}{2}\right)h_2\left(\frac{1}{2}\right)\ne 0$. If $f\in SHX(cr$-$h_1,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+}),g\in SHX(cr$-$h_2,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+})$, then

$$\begin{array}{cc}\hfill & \frac{1}{2h_1\left(\frac{1}{2}\right)h_2\left(\frac{1}{2}\right)}f\left(\frac{2ab}{a+b}\right)g\left(\frac{2ab}{a+b}\right)\hfill \\ \hfill & {⪯}_{cr}\frac{ab}{b-a}{\int }_a^b\frac{f\left(x\right)g\left(x\right)}{x^2}dx+\mathcal{M}(a,b){\int }_0^1{h}_1\left(t\right)h_2(1-t)dt+\mathcal{N}(a,b){\int }_0^1{h}_1\left(t\right)h_2\left(t\right)dt.\hfill \end{array}$$

(19)

Proof. 

Since $f\in SHX(cr$-$h_1,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+}),g\in SHX(cr$-$h_2,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+})$, we get

$$f\left(\frac{2ab}{a+b}\right){⪯}_{cr}{h}_1\left(\frac{1}{2}\right)f\left(\frac{ab}{ta+(1-t)b}\right)+h_1\left(\frac{1}{2}\right)f\left(\frac{ab}{(1-t)a+tb}\right),$$

$$g\left(\frac{2ab}{a+b}\right){⪯}_{cr}{h}_2\left(\frac{1}{2}\right)g\left(\frac{ab}{ta+(1-t)b}\right)+h_2\left(\frac{1}{2}\right)g\left(\frac{ab}{(1-t)a+tb}\right).$$

Let $H\left(\frac{1}{2},\frac{1}{2}\right)=h_1\left(\frac{1}{2}\right)h_2\left(\frac{1}{2}\right)$, then

$$\begin{array}{cc}\hfill & f\left(\frac{2ab}{a+b}\right)g\left(\frac{2ab}{a+b}\right)\hfill \\ \hfill & {⪯}_{cr}H\left(\frac{1}{2},\frac{1}{2}\right)\left[\underline{f}\left(\frac{ab}{ta+(1-t)b}\right)\underline{g}\left(\frac{ab}{ta+(1-t)b}\right)+\underline{f}\left(\frac{ab}{ta+(1-t)b}\right)\underline{g}\left(\frac{ab}{(1-t)a+tb}\right)\right.\hfill \\ \hfill & +\underline{f}\left(\frac{ab}{(1-t)a+tb}\right)\underline{g}\left(\frac{ab}{ta+(1-t)b}\right)+\underline{f}\left(\frac{ab}{(1-t)a+tb}\right)\underline{g}\left(\frac{ab}{(1-t)a+tb}\right),\hfill \\ \hfill & \overline{f}\left(\frac{ab}{ta+(1-t)b}\right)\overline{g}\left(\frac{ab}{ta+(1-t)b}\right)+\overline{f}\left(\frac{ab}{ta+(1-t)b}\right)\overline{g}\left(\frac{ab}{(1-t)a+tb}\right)\hfill \\ \hfill & \left.+\overline{f}\left(\frac{ab}{(1-t)a+tb}\right)\overline{g}\left(\frac{ab}{ta+(1-t)b}\right)+\overline{f}\left(\frac{ab}{(1-t)a+tb}\right)\overline{g}\left(\frac{ab}{(1-t)a+tb}\right)\right]\hfill \\ \hfill & =H\left(\frac{1}{2},\frac{1}{2}\right)\left[\underline{f}\left(\frac{ab}{ta+(1-t)b}\right)\underline{g}\left(\frac{ab}{ta+(1-t)b}\right),\overline{f}\left(\frac{ab}{ta+(1-t)b}\right)\overline{g}\left(\frac{ab}{ta+(1-t)b}\right)\right]\hfill \\ \hfill & +H\left(\frac{1}{2},\frac{1}{2}\right)\left[\underline{f}\left(\frac{ab}{ta+(1-t)b}\right)\underline{g}\left(\frac{ab}{(1-t)a+tb}\right),\overline{f}\left(\frac{ab}{ta+(1-t)b}\right)\overline{g}\left(\frac{ab}{(1-t)a+tb}\right)\right]\hfill \\ \hfill & +H\left(\frac{1}{2},\frac{1}{2}\right)\left[\underline{f}\left(\frac{ab}{(1-t)a+tb}\right)\underline{g}\left(\frac{ab}{ta+(1-t)b}\right),\overline{f}\left(\frac{ab}{(1-t)a+tb}\right)\overline{g}\left(\frac{ab}{ta+(1-t)b}\right)\right]\hfill \\ \hfill & +H\left(\frac{1}{2},\frac{1}{2}\right)\left[\underline{f}\left(\frac{ab}{(1-t)a+tb}\right)\underline{g}\left(\frac{ab}{(1-t)a+tb}\right),\overline{f}\left(\frac{ab}{(1-t)a+tb}\right)\overline{g}\left(\frac{ab}{(1-t)a+tb}\right)\right]\hfill \\ \hfill & =H\left(\frac{1}{2},\frac{1}{2}\right)\left[f\left(\frac{ab}{ta+(1-t)b}\right)g\left(\frac{ab}{ta+(1-t)b}\right)+f\left(\frac{ab}{(1-t)a+tb}\right)g\left(\frac{ab}{(1-t)a+tb}\right)\right]\hfill \\ \hfill & +H\left(\frac{1}{2},\frac{1}{2}\right)\left[f\left(\frac{ab}{ta+(1-t)b}\right)g\left(\frac{ab}{(1-t)a+tb}\right)+f\left(\frac{ab}{(1-t)a+tb}\right)g\left(\frac{ab}{ta+(1-t)b}\right)\right]\hfill \\ \hfill & {⪯}_{cr}H\left(\frac{1}{2},\frac{1}{2}\right)\left[f\left(\frac{ab}{ta+(1-t)b}\right)g\left(\frac{ab}{ta+(1-t)b}\right)+f\left(\frac{ab}{(1-t)a+tb}\right)g\left(\frac{ab}{(1-t)a+tb}\right)\right]\hfill \\ \hfill & +H\left(\frac{1}{2},\frac{1}{2}\right)\left[\left(h_1\left(t\right)f\left(a\right)+h_1(1-t)f\left(b\right)\right)\left(h_2(1-t)g\left(a\right)+h_2\left(t\right)g\left(b\right)\right)\right.\hfill \\ \hfill & \left.+\left(h_1(1-t)f\left(a\right)+h_1\left(t\right)f\left(b\right)\right)\left(h_2\left(t\right)g\left(a\right)+h_2(1-t)g\left(b\right)\right)\right]\hfill \\ \hfill & =H\left(\frac{1}{2},\frac{1}{2}\right)\left[f\left(\frac{ab}{ta+(1-t)b}\right)g\left(\frac{ab}{ta+(1-t)b}\right)+f\left(\frac{ab}{(1-t)a+tb}\right)g\left(\frac{ab}{(1-t)a+tb}\right)\right]\hfill \\ \hfill & +H\left(\frac{1}{2},\frac{1}{2}\right)\left[\left(h_1\left(t\right)h_2(1-t)+h_1(1-t)h_2\left(t\right)\right)\mathcal{M}(a,b)\right.\hfill \\ \hfill & \left.+\left(h_1\left(t\right)h_2\left(t\right)+h_1(1-t)h_2(1-t)\right)\mathcal{N}(a,b)\right].\hfill \end{array}$$

Integrating on $[0,1]$,

$$\begin{array}{cc}\hfill & \frac{1}{2h_1\left(\frac{1}{2}\right)h_2\left(\frac{1}{2}\right)}f\left(\frac{2ab}{a+b}\right)g\left(\frac{2ab}{a+b}\right)\hfill \\ \hfill & {⪯}_{cr}\frac{ab}{b-a}{\int }_a^b\frac{f\left(x\right)g\left(x\right)}{x^2}dx+\mathcal{M}(a,b){\int }_0^1{h}_1\left(t\right)h_2(1-t)dt+\mathcal{N}(a,b){\int }_0^1{h}_1\left(t\right)h_2\left(t\right)dt.\hfill \end{array}$$

We have inequality (19).

This proof is completed. □

Remark 6.

If $h_1\left(t\right)=h_2\left(t\right)=t$, then Theorem 7 reduces to the result for harmonically $cr$-convex function:

$$\begin{array}{c}\hfill \frac{1}{2h_1\left(\frac{1}{2}\right)h_2\left(\frac{1}{2}\right)}f\left(\frac{2ab}{a+b}\right)g\left(\frac{2ab}{a+b}\right){⪯}_{cr}\frac{ab}{b-a}{\int }_a^b\frac{f\left(x\right)g\left(x\right)}{x^2}dx+\frac{\mathcal{M}(a,b)}{6}+\frac{\mathcal{N}(a,b)}{3}.\end{array}$$

Example 5.

Further, by Example 4, we have

$$\begin{array}{cc}\hfill & \frac{1}{2h_1\left(\frac{1}{2}\right)h_2\left(\frac{1}{2}\right)}f\left(\frac{2ab}{a+b}\right)g\left(\frac{2ab}{a+b}\right)=\left[\frac{23}{32},\frac{627}{32}\right],\hfill \\ \hfill & \frac{ab}{b-a}{\int }_a^b\frac{f\left(x\right)g\left(x\right)}{x^2}dx+\mathcal{M}(a,b){\int }_0^1{h}_1\left(t\right)h_2(1-t)dt+\mathcal{N}(a,b){\int }_0^1{h}_1\left(t\right)h_2\left(t\right)dt=\left[\frac{73}{96},\frac{1909}{96}\right].\hfill \end{array}$$

Since,

$$\left[\frac{23}{32},\frac{627}{32}\right]{⪯}_{cr}\left[\frac{73}{96},\frac{1909}{96}\right].$$

So, the Theorem 7 is verified.

Next, we establish Fejér type inequalities about harmonically $cr$-h-convex functions.

Theorem 8.

Let $f:[a,b]\to {\mathbb{R}}_{\mathcal{I}}^{+}$ be an interval-valued function such that $f=[\underline{f},\overline{f}]$ and $f\in {\mathcal{IR}}_{\left(\right[a,b\left]\right)},h:[0,1]\to {\mathbb{R}}^{+}$ be a non-negative function and $h\left(\frac{1}{2}\right)\ne 0$. If $f\in SHX(cr$-$h,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+})$, then

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{1}{2h\left(\frac{1}{2}\right)}f\left(\frac{2ab}{a+b}\right){\int }_a^b\frac{p\left(x\right)}{x^2}dx& {⪯}_{cr}{\int }_a^b\frac{f\left(x\right)}{x^2}p\left(x\right)dx\hfill \\ & {⪯}_{cr}\frac{(b-a)\left[f\left(a\right)+f\left(b\right)\right]}{2ab}{\int }_0^1\left[h\left(t\right)+h(1-t)\right]p\left(\frac{ab}{tb+(1-t)a}\right)dt,\hfill \end{array}\end{array}$$

(20)

where $p:[a,b]\to {\mathbb{R}}^{+}$ is non-negative, integrable, and satisfies

$$p\left(\frac{ab}{x}\right)=p\left(\frac{ab}{a+b-x}\right).$$

(21)

Proof. 

Since $f\in SHX(cr$-$h,[a,b],{\mathbb{R}}_{\mathcal{I}}^{+})$, we have

$$\frac{1}{h\left(\frac{1}{2}\right)}f\left(\frac{2xy}{x+y}\right){⪯}_{cr}f\left(x\right)+f\left(y\right).$$

Let $x=\frac{ab}{ta+(1-t)b},y=\frac{ab}{(1-t)a+tb}$, $t\in [0,1]$, then

$$\frac{1}{h\left(\frac{1}{2}\right)}f\left(\frac{a+b}{2}\right){⪯}_{cr}f\left(\frac{ab}{ta+(1-t)b}\right)+f\left(\frac{ab}{tb+(1-t)a}\right){⪯}_{cr}\left[h\left(t\right)+h(1-t)\right]\left[f\left(a\right)+f\left(b\right)\right].$$

(22)

Since p is non-negative and satisfies the condition (21), we obtain

$$\begin{array}{cc}\hfill & \frac{1}{h\left(\frac{1}{2}\right)}f\left(\frac{a+b}{2}\right)p\left(\frac{ab}{tb+(1-t)a}\right)\hfill \\ \hfill & {⪯}_{cr}f\left(\frac{ab}{ta+(1-t)b}\right)p\left(\frac{ab}{ta+(1-t)b}\right)+f\left(\frac{ab}{tb+(1-t)a}\right)p\left(\frac{ab}{tb+(1-t)a}\right)\hfill \\ \hfill & {⪯}_{cr}\left[h\left(t\right)+h(1-t)\right]\left[f\left(a\right)+f\left(b\right)\right]p\left(\frac{ab}{tb+(1-t)a}\right).\hfill \end{array}$$

(23)

Integrating on $[0,1]$, we get

$$\begin{array}{c}\hfill \begin{array}{cc}& \frac{ab}{h\left(\frac{1}{2}\right)(b-a)}f\left(\frac{2ab}{a+b}\right){\int }_a^b\frac{p\left(x\right)}{x^2}dx\hfill \\ & =\frac{1}{h\left(\frac{1}{2}\right)}f\left(\frac{2ab}{a+b}\right){\int }_0^{1}p\left(\frac{ab}{tb+(1-t)a}\right)dt\hfill \\ & {⪯}_{cr}{\int }_0^1\left[f\left(\frac{ab}{ta+(1-t)b}\right)p\left(\frac{ab}{ta+(1-t)b}\right)+f\left(\frac{ab}{tb+(1-t)a}\right)p\left(\frac{ab}{tb+(1-t)a}\right)\right]dt\hfill \\ & =\frac{2ab}{b-a}{\int }_a^b\frac{f\left(x\right)}{x^2}p\left(x\right)dx\hfill \\ & {⪯}_{cr}\left[f\left(a\right)+f\left(b\right)\right]{\int }_0^1\left[h\left(t\right)+h(1-t)\right]p\left(\frac{ab}{tb+(1-t)a}\right)dt.\hfill \end{array}\end{array}$$

(24)

This proof is completed. □

Remark 7.

It is clear that if $p\left(x\right)=1,x\in [a,b]$, then Theorem 8 reduces to Theorem 4.

If $h\left(t\right)=t$, then Theorem 8 reduces to the result for the harmonically $cr$-convex function:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill f\left(\frac{2ab}{a+b}\right){\int }_a^b\frac{p\left(x\right)}{x^2}dx{⪯}_{cr}{\int }_a^b\frac{f\left(x\right)}{x^2}p\left(x\right)dx{⪯}_{cr}\frac{\left[f\left(a\right)+f\left(b\right)\right]}{2}{\int }_a^b\frac{p\left(x\right)}{x^2}dx.\end{array}\end{array}$$

(25)

If $h\left(t\right)=1$, then Theorem 8 reduces to the result for the harmonically $cr$-P-function:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \frac{1}{2}f\left(\frac{2ab}{a+b}\right){\int }_a^b\frac{p\left(x\right)}{x^2}dx& {⪯}_{cr}{\int }_a^b\frac{f\left(x\right)}{x^2}p\left(x\right)dx\hfill \\ & {⪯}_{cr}\left[f\left(a\right)+f\left(b\right)\right]{\int }_a^b\frac{p\left(x\right)}{x^2}dx.\hfill \end{array}\end{array}$$

(26)

If $h\left(t\right)=t^s,s\in (0,1]$, then Theorem 8 reduces to the result for the harmonically $cr$-s-convex function:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill 2^{s-1}f\left(\frac{2ab}{a+b}\right){\int }_a^b\frac{p\left(x\right)}{x^2}dx& {⪯}_{cr}{\int }_a^b\frac{f\left(x\right)}{x^2}p\left(x\right)dx\hfill \\ & {⪯}_{cr}\frac{(b-a)\left[f\left(a\right)+f\left(b\right)\right]}{2ab}{\int }_0^1\left[t^s+{(1-t)}^s\right]p\left(\frac{ab}{tb+(1-t)a}\right)dt.\hfill \end{array}\end{array}$$

(27)

5. Conclusions

In this paper, we defined the harmonically $cr$-h-convex function by using the $cr$-order, and discuss its important basic properties. Based on the $cr$-order, we establish Jensen type inequality, Hermite–Hadamard type inequalities and Fejér type inequalities for harmonically $cr$-h-convex functions. $cr$-order is a kind of total order, and any two intervals can be compared by $cr$-order. Therefore, the results of this paper will provide a new research idea for other scholars. In the following research, we will try to use $cr$-order to study interval differential equations, and apply harmonically $cr$-h-convex functions to optimization problems.