Parity Properties of Configurations

Abstract

In the paper, the crossing number of the join product $G^{*}+D_n$ for the disconnected graph $G^{*}$ consisting of two components isomorphic to $K_2$ and $K_3$ is given, where $D_n$ consists of n isolated vertices. Presented proofs are completed with the help of the graph of configurations that is a graphical representation of minimum numbers of crossings between two different subgraphs whose edges do not cross the edges of $G^{*}$. For the first time, multiple symmetry between configurations are presented as parity properties. We also determine crossing numbers of join products of $G^{*}$ with paths $P_n$ and cycles $C_n$ on n vertices by adding new edges joining vertices of $D_n$.

1. Introduction

The issue of reducing the number of crossings on edges of simple graphs is interesting in a lot of areas. Probably one of the most popular areas is the implementation of the VLSI layout because it caused a significant revolution in circuit design and thus had a strong effect on parallel calculations. Crossing numbers have also been studied to improve the readability of hierarchical structures and automated graphs. The visualized graph should be easy to read and understand. For the sake of clarity of graphic drawings, some reduction of an edge crossing is probably the most important. Note that examining number of crossings of simple graphs is an NP-complete problem by Garey and Johnson [1].

The crossing number cr$\left(G\right)$ of a simple graph G with the vertex set $V\left(G\right)$ and the edge set $E\left(G\right)$ is the minimum possible number of edge crossings in a drawing of G in the plane (for the definition of a drawing see Klešč [2]). One can easily verify that a drawing with the minimum number of crossings (an optimal drawing) is always a good drawing, meaning that no two edges cross more than once, no edge crosses itself, and also no two edges incident with the same vertex cross. Let D be a good drawing of the graph G. We denote the number of crossings in D by cr${}_D\left(G\right)$. Let $G_i$ and $G_j$ be edge-disjoint subgraphs of G. We denote the number of crossings between edges of $G_i$ and edges of $G_j$ by cr${}_D(G_i,G_j)$, and the number of crossings among edges of $G_i$ in D by cr${}_D\left(G_i\right)$. For any three mutually edge-disjoint subgraphs $G_i$, $G_j$, and $G_k$ of G by [2], the following equations hold:

$${\mathrm{cr}}_D(G_i\cup G_j)={\mathrm{cr}}_D\left(G_i\right)+{\mathrm{cr}}_D\left(G_j\right)+{\mathrm{cr}}_D(G_i,G_j),$$

$${\mathrm{cr}}_D(G_i\cup G_j,G_k)={\mathrm{cr}}_D(G_i,G_k)+{\mathrm{cr}}_D(G_j,G_k).$$

Throughout this paper, some parts of proofs will be based on Kleitman’s result [3] on crossing numbers for some complete bipartite graphs $K_{m,n}$ on $m+n$ vertices with a partition $V\left(K_{m,n}\right)=V_1\cup V_2$ and $V_1\cap V_2=\varnothing$ containing an edge between every pair of vertices from $V_1$ and $V_2$ of sizes m and n, respectively. He showed that

$$\mathrm{cr}\left(K_{m,n}\right)=⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋,\mathrm{if}min\{m,n\}\le 6.$$

(1)

For an overview of several exact values of crossing numbers for specific graphs or some families of graphs, see Clancy [4]. The main goal of this survey is to summarize all such published results for crossing numbers along with references also in an effort to give priority to the author who published the first result. Chapter 4 is devoted to the issue of crossing numbers of join product with all simple graphs of order at most six mainly due to unknown values of $\mathrm{cr}\left(K_{m,n}\right)$ for both $m,n$ more than six in (1). The join product of two graphs $G_i$ and $G_j$, denoted $G_i+G_j$, is obtained from vertex-disjoint copies of $G_i$ and $G_j$ by adding all edges between $V\left(G_i\right)$ and $V\left(G_j\right)$. For $\left|V\right(G_i\left)\right|=m$ and $\left|V\right(G_j\left)\right|=n$, the edge set of $G_i+G_j$ is the union of the disjoint edge sets of the graphs $G_i$, $G_j$, and the complete bipartite graph $K_{m,n}$. Let $D_n$ denote the discrete graph (sometimes called empty graph) on n vertices, and let $K_n$ be the complete graph on n vertices. The exact values for crossing numbers of $G+D_n$ for all graphs G of order at most four are given by Klešč and Schrötter [5], and also for a lot of connected graphs G of order five and six [2,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Note that $\mathrm{cr}(G+D_n)$ are known only for some disconnected graphs G, and so the purpose of this paper is to extend known results concerning this topic to new disconnected graphs [25,26,27,28].

Let $G^{*}=(V\left(G^{*}\right),E\left(G^{*}\right))$ be the disconnected graph of order five consisting of two components isomorphic to the complete graphs $K_2$ and $K_3$, respectively, and let also $V\left(G^{*}\right)=\{v_1,v_2,\dots ,v_5\}$. We cannot determine the crossing number of the join product $G^{*}+D_n$ by a similar technique like in [2,18] because $|E\left(G^{*}\right)|<|V\left(G^{*}\right)|$. From the topological point of view, number of crossings of any drawing D of $G^{*}+D_n$ placed on surface of the sphere does not matter which of regions is unbounded, but on how many times edges of the graph $G^{*}$ could be crossed by a subgraph $T^i$ in D. This representation of $T^i$ best describes idea of a configuration utilizing some cyclic permutation on pre-numbered vertices of $G^{*}$.

Theorem 1.

$\mathrm{cr}(G^{*}+D_1)=0$ and $\mathrm{cr}(G^{*}+D_n)=n^2-2n+⌊\frac{n}{2}⌋$ for $n\ge 2$, i.e., $\mathrm{cr}(G^{*}+D_n)=4⌊\frac{n}{2}⌋\lfloor \frac{n-1}{2}\rfloor +⌊\frac{n}{2}⌋$ for n even and $\mathrm{cr}(G^{*}+D_n)=4⌊\frac{n}{2}⌋\lfloor \frac{n-1}{2}\rfloor +⌊\frac{n}{2}⌋-1$ for n odd at least 3.

All subcases of the proof of Theorem 2 will be clearer if a graph of configurations ${\mathcal{G}}_D$ is used as a graphical representation of minimum numbers of crossings between two different subgraphs. Moreover, in the case of our symmetric graph $G^{*}$, the graph ${\mathcal{G}}_D$ can be linked to parity properties of configurations. Our proof of the main Theorem 2 is therefore an inevitable combination of topological analysis of existing configurations with their parity properties. The color resolution of weighted edges in ${\mathcal{G}}_D$ will also serve us for a simpler description of existence of its possible subgraphs in the examined drawing D of $G^{*}+D_n$. Software COGA [29] should be also very helpful in certain parts of presented proofs mainly due to possibility of generating all cyclic permutations of five elements and counting of their subsequent interchanges of adjacent elements.

The obtained crossing number of the join product $G^{*}+D_n$ is in very special form which is caused by a completely different behavior for n even and odd number. The paper concludes by giving crossing numbers of $G^{*}+P_n$ and $G^{*}+C_n$ with same values in Corollaries 3 and 4, respectively, that is something unique in the crossing number theory.

2. Cyclic Permutations and Corresponding Configurations

The join product $G^{*}+D_n$ (sometimes used notation $G^{*}+n{K}_1$) consists of one copy of the graph $G^{*}$ and n vertices $t_1,\dots ,t_n$, and any vertex $t_i$ is adjacent to every vertex of the graph $G^{*}$. We denote the subgraph induced by five edges incident with the fixed vertex $t_i$ by $T^i$, which yields that

$$G^{*}+D_n=G^{*}\cup K_{5,n}=G^{*}\cup \left(\bigcup _{i=1}^n{T}^i\right).$$

(2)

We consider a good drawing D of $G^{*}+D_n$. By the rotation ${\mathrm{rot}}_D\left(t_i\right)$ of a vertex $t_i$ in D we understand the cyclic permutation that records the (cyclic) counterclockwise order in which edges leave $t_i$, as defined by Hernández-Vélez et al. [30] or Woodall [31]. We use the notation $\left(12345\right)$ if the counter-clockwise order of edges incident with the fixed vertex $t_i$ is $t_i{v}_1$, $t_i{v}_2$, $t_i{v}_3$, $t_i{v}_4$, and $t_i{v}_5$. We recall that rotation is a cyclic permutation. By ${\overline{\mathrm{rot}}}_D\left(t_i\right)$, we understand the inverse permutation of ${\mathrm{rot}}_D\left(t_i\right)$. In the given drawing D, it is highly desirable to separate n subgraphs $T^i$ into three mutually disjoint subsets depending on how many times edges of $G^{*}$ could be crossed by $T^i$ in D. Let us denote by $R_D$ and $S_D$ the set of subgraphs for which ${\mathrm{cr}}_D(G^{*},T^i)=0$ and ${\mathrm{cr}}_D(G^{*},T^i)=1$, respectively. Edges of $G^{*}$ are crossed by each remaining subgraph $T^i$ at least twice in D.

First, note that if D is a drawing of the join product $G^{*}+D_n$ with the empty set $R_D$, then ${\sum }_{i=1}^n{\mathrm{cr}}_D(G^{*},T^i)\ge n$ enforces at least $n^2-2n+⌊\frac{n}{2}⌋$ crossings in D provided by

$${\mathrm{cr}}_D(G^{*}+D_n)\ge {\mathrm{cr}}_D\left(K_{5,n}\right)+{\mathrm{cr}}_D(G^{*},K_{5,n})\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n\ge n^2-2n+⌊\frac{n}{2}⌋.$$

Based on this argument, we will only consider drawings of the graph $G^{*}$ for which there is a possibility to obtain a subgraph $T^i\in R_D$. Moreover, let $F^i$ denote the subgraph $G^{*}\cup T^i$ for any $T^i\in R_D$, which yields that each such subgraph $F^i$ is represented by its ${\mathrm{rot}}_D\left(t_i\right)$.

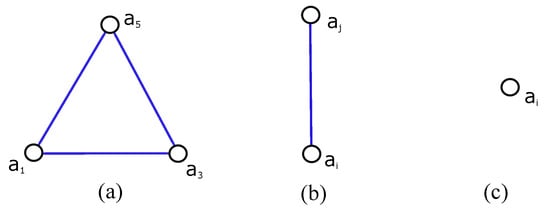
Let us discuss all possible subdrawings of $G^{*}$ induced by D. As edges of its subgraph isomorphic to $K_3$ do not cross each other, it is obvious there are only two such possible drawings of $G^{*}$ presented in Figure 1.

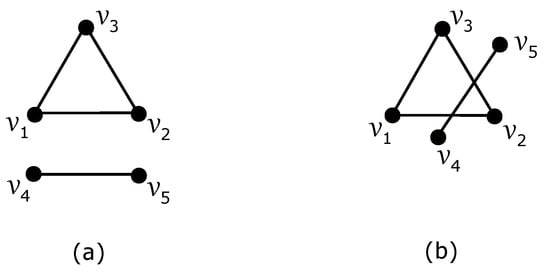
Figure 1. Two possible non isomorphic drawings of the graph $G^{*}$. (a): the planar drawing of $G^{*}$; (b): the drawing of $G^{*}$ with two crossings among edges.

Assume there is a good drawing D of $G^{*}+D_n$ with planar subdrawing of the graph $G^{*}$ induced by D and also the vertex notation of $G^{*}$ in such a way as shown in Figure 1a. Our aim is to list all possible rotations ${\mathrm{rot}}_D\left(t_i\right)$ which can appear in D if edges of $G^{*}$ are not crossed by $T^i$. Since there is only one subdrawing of $F^i\backslash \{v_4,v_5\}$ represented by the rotation $\left(132\right)$, there are three possibilities to obtain the subdrawing of $F^i$ without the edge $v_4{v}_5$ depending on in which region both edges $t_i{v}_4$ and $t_i{v}_5$ are placed. Of course, there are two next ways how to place the corresponding two edges together with the edge $v_4{v}_5$ for each mentioned case. These $3\times 2=6$ possibilities under our consideration can be denoted by ${\mathcal{A}}_k$, for $k=1,\dots ,6$. We will call them by the configurations of corresponding subdrawings of the subgraph $G^{*}\cup T^i$ in D and suppose their drawings as shown in Figure 2.

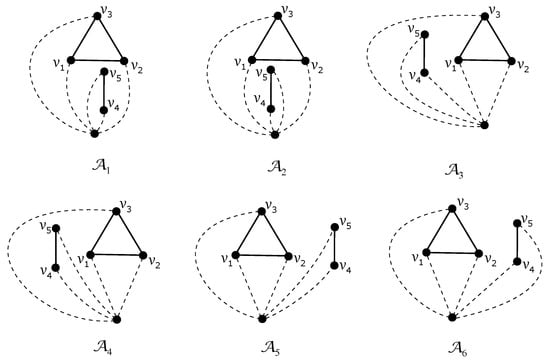
Figure 2. Drawings of six possible configurations ${\mathcal{A}}_k$ of subgraph $F^i=G^{*}\cup T^i$ for $T^i\in R_D$.

In the rest of the paper, we present a cyclic permutation by the permutation with 1 in the first position. Thus, the configurations ${\mathcal{A}}_1$, ${\mathcal{A}}_2$, ${\mathcal{A}}_3$, ${\mathcal{A}}_4$, ${\mathcal{A}}_5$, and ${\mathcal{A}}_6$ are represented by the cyclic permutations $\left(13245\right)$, $\left(13254\right)$, $\left(14532\right)$, $\left(15432\right)$, $\left(13452\right)$, and $\left(13542\right)$, respectively. Clearly, in a fixed drawing of the graph $G^{*}+D_n$, some configurations from $\mathcal{M}=\{{\mathcal{A}}_1,{\mathcal{A}}_2,{\mathcal{A}}_3,{\mathcal{A}}_4,{\mathcal{A}}_5,{\mathcal{A}}_6\}$ need not appear. We denote by ${\mathcal{M}}_D$ the set of all configurations that exist in the drawing D belonging to the set $\mathcal{M}$.

Let $\mathcal{X}$, $\mathcal{Y}$ be two configurations from ${\mathcal{M}}_D$ (not necessary distinct). We denote the number of edge crossings between two different subgraphs $T^i$ and $T^j$ with $\mathrm{conf}\left(F^i\right)=\mathcal{X}$ and $\mathrm{conf}\left(F^j\right)=\mathcal{Y}$ in D by ${\mathrm{cr}}_D(\mathcal{X},\mathcal{Y})$. Finally, let $\mathrm{cr}(\mathcal{X},\mathcal{Y})=min\left\{{\mathrm{cr}}_D(\mathcal{X},\mathcal{Y})\right\}$ among all good drawings of $G^{*}+D_n$ with the planar subdrawing of $G^{*}$ induced by D given in Figure 1a and with $\mathcal{X},\mathcal{Y}\in {\mathcal{M}}_D$. Our aim shall be to establish $\mathrm{cr}(\mathcal{X},\mathcal{Y})$ for all pairs $\mathcal{X},\mathcal{Y}\in \mathcal{M}$. In particular, the configurations ${\mathcal{A}}_1$ and ${\mathcal{A}}_4$ are represented by the cyclic permutations $\left(13245\right)$ and $\left(15432\right)$, respectively. Each subgraph $T^j$ with $\mathrm{conf}\left(F^j\right)={\mathcal{A}}_4$ crosses edges of each $T^i$ with $\mathrm{conf}\left(F^i\right)={\mathcal{A}}_1$ at least once provided by the minimum number of interchanges of adjacent elements of $\left(13245\right)$ required to produce $\overline{\left(15432\right)}=\left(12345\right)$ is one, i.e., $\mathrm{cr}({\mathcal{A}}_1,{\mathcal{A}}_4)\ge 1$. For more details see also Woodall [31]. The same reason gives $\mathrm{cr}({\mathcal{A}}_1,{\mathcal{A}}_2)\ge 3$, $\mathrm{cr}({\mathcal{A}}_1,{\mathcal{A}}_3)\ge 2$, $\mathrm{cr}({\mathcal{A}}_1,{\mathcal{A}}_5)\ge 2$, $\mathrm{cr}({\mathcal{A}}_1,{\mathcal{A}}_6)\ge 1$, $\mathrm{cr}({\mathcal{A}}_2,{\mathcal{A}}_3)\ge 1$, $\mathrm{cr}({\mathcal{A}}_2,{\mathcal{A}}_4)\ge 2$, $\mathrm{cr}({\mathcal{A}}_2,{\mathcal{A}}_5)\ge 1$, $\mathrm{cr}({\mathcal{A}}_2,{\mathcal{A}}_6)\ge 2$, $\mathrm{cr}({\mathcal{A}}_3,{\mathcal{A}}_4)\ge 3$, $\mathrm{cr}({\mathcal{A}}_3,{\mathcal{A}}_5)\ge 2$, $\mathrm{cr}({\mathcal{A}}_3,{\mathcal{A}}_6)\ge 1$, $\mathrm{cr}({\mathcal{A}}_4,{\mathcal{A}}_5)\ge 1$, $\mathrm{cr}({\mathcal{A}}_4,{\mathcal{A}}_6)\ge 2$, and $\mathrm{cr}({\mathcal{A}}_5,{\mathcal{A}}_6)\ge 3$. Clearly, also $\mathrm{cr}({\mathcal{A}}_k,{\mathcal{A}}_k)\ge 4$ for any $k=1,\dots ,6$. The lower bounds obtained for number of crossings between two configurations from $\mathcal{M}$ are summarized in the symmetric Table 1 (here, $\mathrm{conf}\left(F^i\right)={\mathcal{A}}_k$ and $\mathrm{conf}\left(F^j\right)={\mathcal{A}}_l$ with $k,l\in \{1,\dots ,6\}$). Note that these values cannot be increased, i.e., the lower bounds can be achieved in some subdrawings of $G^{*}\cup T^i\cup T^j$ for $T^i,T^j\in R_D$ with desired configurations.

Table 1. The minimum number of crossings between two different subgraphs $T^i$ and $T^j$ such that $\mathrm{conf}\left(F^i\right)={\mathcal{A}}_k$ and $\mathrm{conf}\left(F^j\right)={\mathcal{A}}_l$, where the achieved values are color-coded. Namely, the values 1, 2, 3, and 4 will correspond to green, blue, brown, and black, respectively.

-	${\mathcal{A}}_1$	${\mathcal{A}}_2$	${\mathcal{A}}_3$	${\mathcal{A}}_4$	${\mathcal{A}}_5$	${\mathcal{A}}_6$
${\mathcal{A}}_1$	4	3	2	1	2	1
${\mathcal{A}}_2$	3	4	1	2	1	2
${\mathcal{A}}_3$	2	1	4	3	2	1
${\mathcal{A}}_4$	1	2	3	4	1	2
${\mathcal{A}}_5$	2	1	2	1	4	3
${\mathcal{A}}_6$	1	2	1	2	3	4

Further, due to symmetry of mentioned configurations, let us define two functions

$${\pi }_1:\{1,2,3\}\to \{1,2,3\},\mathrm{with}{\pi }_1\left(1\right)=3,{\pi }_1\left(2\right)=1,\mathrm{and}{\pi }_1\left(3\right)=2,$$

$${\pi }_2:\{4,5\}\to \{4,5\},\mathrm{with}{\pi }_2\left(4\right)=5,\mathrm{and}{\pi }_2\left(5\right)=4.$$

Let ${\Pi }_1,{\Pi }_2:\mathcal{M}\to \mathcal{M}$ be the functions obtained by applying ${\pi }_1$ and ${\pi }_2$ on corresponding cyclic permutations of configurations in $\mathcal{M}$, respectively. Thus, we have

$${\Pi }_1\left({\mathcal{A}}_1\right)={\mathcal{A}}_3,{\Pi }_1\left({\mathcal{A}}_3\right)={\mathcal{A}}_5,{\Pi }_1\left({\mathcal{A}}_5\right)={\mathcal{A}}_1,{\Pi }_1\left({\mathcal{A}}_2\right)={\mathcal{A}}_4,$$

$${\Pi }_1\left({\mathcal{A}}_4\right)={\mathcal{A}}_6,{\Pi }_1\left({\mathcal{A}}_6\right)={\mathcal{A}}_2,{\Pi }_2\left({\mathcal{A}}_1\right)={\mathcal{A}}_2,{\Pi }_2\left({\mathcal{A}}_2\right)={\mathcal{A}}_1,$$

$${\Pi }_2\left({\mathcal{A}}_3\right)={\mathcal{A}}_4,{\Pi }_2\left({\mathcal{A}}_4\right)={\mathcal{A}}_3,{\Pi }_2\left({\mathcal{A}}_5\right)={\mathcal{A}}_6,{\Pi }_2\left({\mathcal{A}}_6\right)={\mathcal{A}}_5.$$

Therefore it is not difficult to show that values in rows of Table 1 can be obtained by successive application of the mentioned transformations ${\Pi }_1$ and ${\Pi }_2$.

3. The Graph of Configurations and Parity Properties

Low possible number of crossings between two different subgraphs from the nonempty set $R_D$ is one of main problems in determining $\mathrm{cr}(G^{*}+D_n)$, and graph of configurations as a graphical representation of Table 1 is going by useful tool in our research. This idea of representation was first introduced in [26].

Let D be a good drawing of $G^{*}+D_n$ with the planar subdrawing of $G^{*}$ induced by D given in Figure 1a, and let ${\mathcal{M}}_D$ be nonempty set of all configurations that exist in D belonging to $\mathcal{M}=\{{\mathcal{A}}_1,{\mathcal{A}}_2,{\mathcal{A}}_3,{\mathcal{A}}_4,{\mathcal{A}}_5,{\mathcal{A}}_6\}$. A graph of configurations ${\mathcal{G}}_D$ is an ordered triple $(V_D,E_D,w_D)$, where $V_D$ is the set of vertices, $E_D$ is the set of edges formed by all unordered pairs of two vertices (not necessary distinct), and a weight function $w:E_D\to \mathbb{N}$ that associates with each edge of $E_D$ an unordered pair of two vertices of $V_D$. The vertex $a_k\in V_D$ if the corresponding configuration ${\mathcal{A}}_k\in {\mathcal{M}}_D$ for some $k\in \{1,\dots ,6\}$. The edge $e=a_k{a}_l\in E_D$ if $a_k$ and $a_l$ are two vertices of ${\mathcal{G}}_D$. Finally, $w_D\left(e\right)=m\in \mathbb{N}$ for the edge $e=a_k{a}_l$, if m is associated lower bound between two configurations ${\mathcal{A}}_k$ and ${\mathcal{A}}_l$ in Table 1. Based on that ${\mathcal{G}}_D$ is an undirected edge-weighted graph without multiple edges uniquely determined by D and is also subgraph of $\mathcal{G}$ induced by $V_D$ if we define $\mathcal{G}=(V,E,w)$ in the same way over $\mathcal{M}$. The graph $\mathcal{G}=(V,E,w)$ corresponds to the edge-weighted complete graph $K_6$ in Figure 3, and thus will follow all subcases in the proof of the main Theorem 2 more clearly. In the rest of Figure 3, let any loop of the mentioned graph $\mathcal{G}$ be presented by circle around vertex with respect to weight 4.

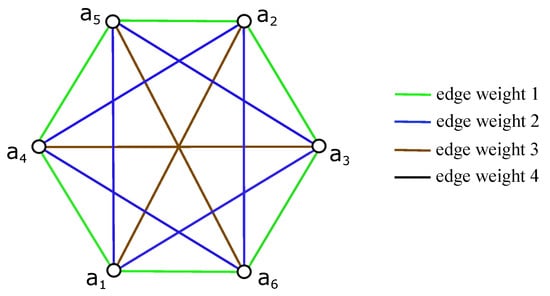
Figure 3. Representation of lower bounds of Table 1 by the graph $\mathcal{G}=(V,E,w)$.

Let ${\alpha }_i$ denote the number of all subgraphs $T^j\in R_D$ with the configuration ${\mathcal{A}}_i\in {\mathcal{M}}_D$ of $F^j=G^{*}\cup T^j$ for each $i=1,\dots ,6$. So, if we denote by $I_o=\{1,3,5\}$ and $I_e=\{2,4,6\}$, then ${\sum }_{i\in I_o\cup I_e}{\alpha }_i=\left|R_D\right|$. Moreover, for a better understanding, we get for all $i\in I_o\cup I_e$: ${\alpha }_i>0$ if and only if there is a subgraph $T^j\in R_D$ with the configuration ${\mathcal{A}}_i\in {\mathcal{M}}_D$ of $F^j=G^{*}\cup T^j$ if and only if $a_i\in V_D$ in the graph ${\mathcal{G}}_D$.

Now, let us assume the configurations ${\mathcal{A}}_1$ of $F^i$, ${\mathcal{A}}_4$ of $F^j$, and ${\mathcal{A}}_6$ of $F^k$. The reader can easily find a subdrawing of $G^{*}\cup T^i\cup T^j\cup T^k$ in which ${\mathrm{cr}}_D(T^i,T^j)=1$, ${\mathrm{cr}}_D(T^i,T^k)=1$, and ${\mathrm{cr}}_D(T^j,T^k)=2$, i.e., ${\mathrm{cr}}_D(T^i\cup T^j\cup T^k)=4=\mathrm{cr}\left(K_{5,3}\right)$. Further, there is a possibility to add another subgraph $T^l$ that crosses edges of the graph $T^i\cup T^j\cup T^k$ four times. We have to emphasize that the vertex $t_l$ must be placed in the triangular region with three vertices of $G^{*}$ on its boundary (in the subdrawing of $G^{*}\cup T^i\cup T^j\cup T^k$), i.e., $T^l\notin R_D\cup S_D$ and the subgraph $F^l=G^{*}\cup T^l$ is represented by ${\mathrm{rot}}_D\left(t_l\right)=\left(12435\right)$. Clearly, the number of adding crossings cannot be smaller than 4 according to the well-known fact that $\mathrm{cr}\left(K_{5,4}\right)=8$. This situation suggests one natural problem which requires the following definition of a new number ${\beta }_1$. If ${\alpha }_1>0$, ${\alpha }_4>0$, and ${\alpha }_6>0$, then let us denote by ${\beta }_1$ the number of subgraphs $T^l\notin R_D\cup S_D$ with ${\mathrm{rot}}_D\left(t_l\right)=\left(12435\right)$. It is obvious that any subgraph $T^l\notin R_D\cup S_D$ satisfies the condition ${\mathrm{cr}}_D(G^{*}\cup T^i\cup T^j\cup T^k,T^l)\ge 2+4=6$ with the configurations ${\mathcal{A}}_1$ of $F^i$, ${\mathcal{A}}_4$ of $F^j$, and ${\mathcal{A}}_6$ of $F^k$, and the number of $T^l\notin R_D\cup S_D$ that cross the graph $G^{*}\cup T^i\cup T^j\cup T^k$ exactly six times is at most ${\beta }_1$. Due to symmetry of some configurations, it is appropriate to use the transform functions ${\Pi }_1,{\Pi }_2$ defined above and by the similar way, we can also define the numbers ${\beta }_i$ for any $i=2,\dots ,6$. Thus, if ${\alpha }_2>0$, ${\alpha }_3>0$, and ${\alpha }_5>0$ or ${\alpha }_3>0$, ${\alpha }_2>0$, and ${\alpha }_6>0$ or ${\alpha }_4>0$, ${\alpha }_1>0$, and ${\alpha }_5>0$ or ${\alpha }_5>0$, ${\alpha }_2>0$, and ${\alpha }_4>0$ or ${\alpha }_6>0$, ${\alpha }_1>0$, and ${\alpha }_3>0$, then let us denote by ${\beta }_2$ or ${\beta }_3$ or ${\beta }_4$ or ${\beta }_5$ or ${\beta }_6$ the number of subgraphs $T^l\notin R_D\cup S_D$ represented by the rotation $\left(12534\right)$ or $\left(14253\right)$ or $\left(15243\right)$ or $\left(15234\right)$ or $\left(14235\right)$, respectively. The importance of the values ${\beta }_i$ will be presented in the proof of the main Theorem 2 as parity properties (6) and (7).

4. The Crossing Number of ${\mathit{G}}^{*}+{\mathit{D}}_{\mathit{n}}$

A drawing D of $G^{*}+D_n$ is said to be antipode-free if ${\mathrm{cr}}_D(T^i,T^j)\ge 1$ for any two different vertices $t_i$ and $t_j$. In the proof of Theorem 2, the following statements related to some restricted subdrawings of the graph $G^{*}+D_n$ are required.

Lemma 1.

Let D be a good and antipode-free drawing of $G^{*}+D_n$, $n>1$, with the vertex notation of the graph $G^{*}$ in such a way as shown in Figure 1a. For $T^i\in R_D$, let ${\mathcal{A}}_k\in {\mathcal{M}}_D$ be a configuration of the corresponding subgraph $F^i=G^{*}\cup T^i$ for some $k\in \{1,\dots ,6\}$. If there is a $T^j\in S_D$ such that ${\mathrm{cr}}_D(T^i,T^j)=1$, then all possible ${\mathrm{rot}}_D\left(t_j\right)$ are given in Table 2.

Table 2. The corresponding rotations of $t_j$, for $T^i\in R_D$, $F^i=G^{*}\cup T^i$ and $T^j\in S_D$ satisfying the restriction ${\mathrm{cr}}_D(T^i,T^j)=1$.

$\mathbf{conf}\left({\mathit{F}}^{\mathit{i}}\right)$	${\mathbf{rot}}_{\mathit{D}}\left({\mathit{t}}_{\mathit{j}}\right)$	$\mathbf{conf}\left({\mathit{F}}^{\mathit{i}}\right)$	${\mathbf{rot}}_{\mathit{D}}\left({\mathit{t}}_{\mathit{j}}\right)$	$\mathbf{conf}\left({\mathit{F}}^{\mathit{i}}\right)$	${\mathbf{rot}}_{\mathit{D}}\left({\mathit{t}}_{\mathit{j}}\right)$
${\mathcal{A}}_1$	$\left(14523\right)$	${\mathcal{A}}_3$	$\left(12345\right)$	${\mathcal{A}}_5$	$\left(12453\right)$
${\mathcal{A}}_2$	$\left(15423\right)$	${\mathcal{A}}_4$	$\left(12354\right)$	${\mathcal{A}}_6$	$\left(12543\right)$

Proof. 

Assume the configuration ${\mathcal{A}}_1$ of the subgraph $F^i=G^{*}\cup T^i$ for some $T^i\in R_D$, i.e., ${\mathrm{rot}}_D\left(t_i\right)=\left(13245\right)$. The subdrawing of $F^i$ induced by D contains just five regions with $t_i$ on their boundaries, see Figure 2. If there is a $T^j\in S_D$ such that ${\mathrm{cr}}_D(T^i,T^j)=1$, then the vertex $t_j$ must be placed in the region with the four vertices $v_1$, $v_2$, $v_4$, and $v_5$ of $G^{*}$ on its boundary. Besides that only the edge $v_1{v}_2$ of $G^{*}$ can be crossed by $t_j{v}_3$, and ${\mathrm{cr}}_D(T^i,T^j)=1$ is fulfilling for $T^j$ with ${\mathrm{rot}}_D\left(t_j\right)=\left(14523\right)$ if $t_j{v}_4$ crosses $t_i{v}_5$. The same idea also force that the rotations of the vertex $t_j$ are $\left(15423\right)$, $\left(12345\right)$, $\left(12354\right)$, $\left(12453\right)$, and $\left(12543\right)$ for the remaining configurations ${\mathcal{A}}_2$, ${\mathcal{A}}_3$, ${\mathcal{A}}_4$, ${\mathcal{A}}_5$, and ${\mathcal{A}}_6$ of $F^i$, respectively. □

Corollary 1.

Let D be a good and antipode-free drawing of $G^{*}+D_n$, for $n>3$, with the vertex notation of the graph $G^{*}$ in such a way as shown in Figure 1a. If $T^i,T^j$, and $T^k\in R_D$ are three different subgraphs with ${\mathrm{cr}}_D(T^i,T^j)=1$, ${\mathrm{cr}}_D(T^i,T^k)=1$ and such that $F^i$, $F^j$, and $F^k$ have three mutually different configurations from any of the sets $\{{\mathcal{A}}_1,{\mathcal{A}}_4,{\mathcal{A}}_6\}$, $\{{\mathcal{A}}_2,{\mathcal{A}}_3,{\mathcal{A}}_5\}$, $\{{\mathcal{A}}_3,{\mathcal{A}}_2,{\mathcal{A}}_6\}$, $\{{\mathcal{A}}_1,{\mathcal{A}}_4,{\mathcal{A}}_5\}$, $\{{\mathcal{A}}_2,{\mathcal{A}}_4,{\mathcal{A}}_5\}$, and $\{{\mathcal{A}}_1,{\mathcal{A}}_3,{\mathcal{A}}_6\}$, then

$${\mathrm{cr}}_D(T^i\cup T^j\cup T^k,T^l)\ge 6\mathit{for}\mathit{any}{T}^l\in S_D,$$

i.e.,

$${\mathrm{cr}}_D(G^{*}\cup T^i\cup T^j\cup T^k,T^l)\ge 7\mathit{for}\mathit{any}{T}^l\in S_D.$$

Proof. 

Let us assume the configurations ${\mathcal{A}}_1$ of $F^i$, ${\mathcal{A}}_4$ of $F^j$, and ${\mathcal{A}}_6$ of $F^k$ with respect to the restrictions ${\mathrm{cr}}_D(T^i,T^j)={\mathrm{cr}}_D(T^i,T^k)=1$ and recall that they are represented by the cyclic permutations ${\mathrm{rot}}_D\left(t_i\right)=\left(13245\right)$, ${\mathrm{rot}}_D\left(t_j\right)=\left(15432\right)$, and ${\mathrm{rot}}_D\left(t_k\right)=\left(13542\right)$. If there is a subgraph $T^l\in S_D$ with ${\mathrm{cr}}_D(T^i,T^l)=1$, then the subgraph $F^l$ can be represented only by ${\mathrm{rot}}_D\left(t_l\right)=\left(14523\right)$, where the edge $t_l{v}_3$ crosses $v_1{v}_2$ of $G^{*}$ and either $t_l{v}_4$ or $t_l{v}_5$ crosses corresponding edge of $T^i$. Any such subgraph $T^l$ must cross edges of both subgraphs $T^j$ and $T^k$ at least twice because the minimum number of interchanges of adjacent elements of $\left(14523\right)$ required to produce $\overline{\left(15432\right)}=\left(12345\right)$ and $\overline{\left(13542\right)}=\left(12453\right)$ is two. Clearly, if ${\mathrm{cr}}_D(T^j,T^l)>2$ or ${\mathrm{cr}}_D(T^k,T^l)>2$, we obtain the desired result ${\mathrm{cr}}_D(T^i\cup T^j\cup T^k,T^l)\ge 1+3+2=6$. Further, if ${\mathrm{cr}}_D(T^j,T^l)=2$ and ${\mathrm{cr}}_D(T^k,T^l)=2$, then the edge $t_i{v}_5$ is crossed by $t_l{v}_4$ in $D(T^i\cup T^j\cup T^l)$ and also $t_i{v}_4$ by $t_l{v}_5$ in $D(T^i\cup T^k\cup T^l)$, respectively. However, then ${\mathrm{cr}}_D(T^i,T^l)\ge 2$, which contradicts the fact that ${\mathrm{cr}}_D(T^i,T^l)=1$ in $D(T^i\cup T^j\cup T^k\cup T^l)$.

If there is a $T^l\in S_D$ with ${\mathrm{cr}}_D(T^j,T^l)=1$, then the subgraph $F^l$ is represented only by the cyclic permutation $\left(12354\right)$. Using same properties as in the previous subcase, we have ${\mathrm{cr}}_D(T^i,T^l)\ge 2$ and ${\mathrm{cr}}_D(T^k,T^l)\ge 3$. This in turn implies that ${\mathrm{cr}}_D(T^i\cup T^j\cup T^k,T^l)\ge 2+1+3=6$. Of course, we can apply the same idea for the case of ${\mathrm{cr}}_D(T^k,T^l)=1$.

To finish the proof, let us consider a subgraph $T^l\in S_D$ with ${\mathrm{cr}}_D(T^i,T^l)=2$, ${\mathrm{cr}}_D(T^j,T^l)=2$, and ${\mathrm{cr}}_D(T^k,T^l)=2$. This enforces that the minimum number of interchanges of adjacent elements of ${\mathrm{rot}}_D\left(t_l\right)$ required to produce $\overline{\left(13245\right)}=\left(15423\right)$, $\overline{\left(15432\right)}=\left(12345\right)$, and $\overline{\left(13542\right)}=\left(12453\right)$ must be exactly two. However, it is not difficult to show that such cyclic permutation does not exist. Similar arguments can be applied for remaining five cases (or using the transformations ${\Pi }_1$ and ${\Pi }_2$), and the proof is complete. □

Corollary 2.

Let D be a good and antipode-free drawing of $G^{*}+D_n$, for $n>3$, with the vertex notation of the graph $G^{*}$ in such a way as shown in Figure 1a. If $T^i,T^j$, and $T^k\in R_D$ are three different subgraphs such that $F^i$, $F^j$, and $F^k$ have three mutually different configurations from any of the sets $\{{\mathcal{A}}_1,{\mathcal{A}}_3,{\mathcal{A}}_5\}$ and $\{{\mathcal{A}}_2,{\mathcal{A}}_4,{\mathcal{A}}_6\}$, then

$${\mathrm{cr}}_D(T^i\cup T^j\cup T^k,T^l)\ge 5\mathit{for}\mathit{any}{T}^l\in S_D,$$

i.e.,

$${\mathrm{cr}}_D(G^{*}\cup T^i\cup T^j\cup T^k,T^l)\ge 6\mathit{for}\mathit{any}{T}^l\in S_D.$$

Proof. 

Let us assume the configurations ${\mathcal{A}}_1$ of $F^i$, ${\mathcal{A}}_3$ of $F^j$, and ${\mathcal{A}}_5$ of $F^k$. If there is a subgraph $T^l\in S_D$ with ${\mathrm{cr}}_D(T^i,T^l)=1$, then the subgraph $F^l$ can be represented only by the cyclic permutations $\left(14523\right)$. Uniqueness of all rotations in Table 2 confirms that ${\mathrm{cr}}_D(T^j,T^l)\ge 2$ and ${\mathrm{cr}}_D(T^k,T^l)\ge 2$. Hence, ${\mathrm{cr}}_D(T^i\cup T^j\cup T^k,T^l)\ge 1+2+2=5$, and the similar way can be applied for the case if ${\mathrm{cr}}_D(T^j,T^l)=1$ or ${\mathrm{cr}}_D(T^k,T^l)=1$ with $T^l\in S_D$. It remains to consider the case where ${\mathrm{cr}}_D(T^i,T^l)\ge 2$, ${\mathrm{cr}}_D(T^j,T^l)\ge 2$, and ${\mathrm{cr}}_D(T^k,T^l)\ge 2$, which yields that ${\mathrm{cr}}_D(T^i\cup T^j\cup T^k,T^l)\ge 2+2+2=6$ clearly holds for any such $T^l$, as claimed. The proof proceeds in the similar way for the second triple of configurations $\{{\mathcal{A}}_2,{\mathcal{A}}_4,{\mathcal{A}}_6\}$, and this completes the proof. □

Lemma 2.

$\mathrm{cr}(G^{*}+D_2)=1$.

Proof. 

If we consider the configurations ${\mathcal{A}}_2$ of $F^i$ and ${\mathcal{A}}_3$ of $F^j$, then one can easily find a subdrawing of $T^i\cup T^j$ in which ${\mathrm{cr}}_D(T^i,T^j)=1$, i.e., $\mathrm{cr}(G^{*}+D_2)\le 1$. The graph $G^{*}+D_2$ contains a subgraph that is a subdivision of the complete graph $K_5$ and it is well-known by Guy [32] that $\mathrm{cr}\left(K_5\right)=1$. As $\mathrm{cr}(G^{*}+D_2)\ge \mathrm{cr}\left(K_5\right)=1$, the proof of Lemma 2 is complete. □

Theorem 2.

$\mathrm{cr}(G^{*}+D_1)=0$ and $\mathrm{cr}(G^{*}+D_n)=n^2-2n+⌊\frac{n}{2}⌋$ for $n\ge 2$, i.e., $\mathrm{cr}(G^{*}+D_n)=4⌊\frac{n}{2}⌋\lfloor \frac{n-1}{2}\rfloor +⌊\frac{n}{2}⌋$ for n even and $\mathrm{cr}(G^{*}+D_n)=4⌊\frac{n}{2}⌋\lfloor \frac{n-1}{2}\rfloor +⌊\frac{n}{2}⌋-1$ for n odd at least 3.

Proof. 

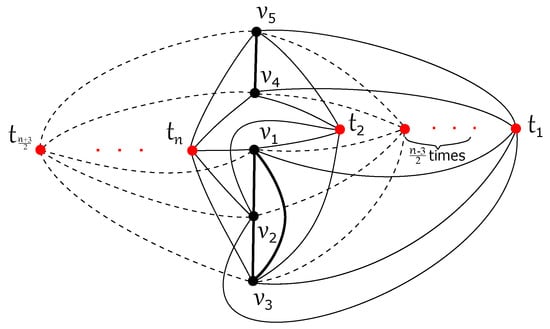
The graph $G^{*}+D_1$ is planar, hence $\mathrm{cr}(G^{*}+D_1)=0$. For $n\ge 2$, both special drawings in Figure 4 and Figure 5 produce $n^2-2n+⌊\frac{n}{2}⌋$ crossings, and so $\mathrm{cr}(G^{*}+D_n)\le n^2-2n+⌊\frac{n}{2}⌋$. The opposite inequality can be proved by induction on n, and the result holds for $n=2$ by Lemma 2. For some $n\ge 3$, suppose a drawing D of $G^{*}+D_n$ with

$${\mathrm{cr}}_D(G^{*}+D_n)<n^2-2n+⌊\frac{n}{2}⌋$$

(3)

and that

$$\mathrm{cr}(G^{*}+D_m)=m^2-2m+⌊\frac{m}{2}⌋\mathrm{for}\mathrm{any}\mathrm{integer}2\le m<n.$$

(4)

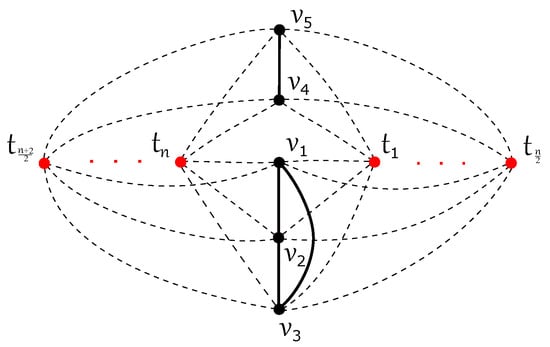
Figure 4. The good drawing of $G^{*}+D_n$ with $4⌊\frac{n}{2}⌋\lfloor \frac{n-1}{2}\rfloor +⌊\frac{n}{2}⌋$ crossings for n even, $n\ge 2$.

Figure 5. The good drawing of $G^{*}+D_n$ with $4⌊\frac{n}{2}⌋\lfloor \frac{n-1}{2}\rfloor +⌊\frac{n}{2}⌋-1$ crossings for n odd, $n\ge 3$, where three subgraphs $T^1$, $T^2$, and $T^n$ are fixed.

Let us first show that D must be antipode-free. Suppose that, without loss of generality, ${\mathrm{cr}}_D(T^{n-1},T^n)=0$. If at least one of $T^{n-1}$ and $T^n$, say $T^n$, does not cross $G^{*}$, it is not difficult to verify in Figure 1 that $\{T^{n-1},T^n\}⊈R_D$, i.e., ${\mathrm{cr}}_D(G^{*},T^{n-1}\cup T^n)\ge 1$. By (1), we already know that ${\mathrm{cr}}_D\left(K_{5,3}\right)\ge 4$, which yields that edges of the subgraph $T^{n-1}\cup T^n$ must be crossed at least four times by each other $T^k$. So, by fixing the subgraph $T^{n-1}\cup T^n$ in D, we have

$${\mathrm{cr}}_D(G^{*}+D_{n-2})+{\mathrm{cr}}_D(T^{n-1}\cup T^n)+{\mathrm{cr}}_D(K_{5,n-2},T^{n-1}\cup T^n)+{\mathrm{cr}}_D(G^{*},T^{n-1}\cup T^n)$$

$$\ge {(n-2)}^2-2(n-2)+⌊\frac{n-2}{2}⌋+0+4(n-2)+1=n^2-2n+⌊\frac{n}{2}⌋$$

The obtained crossing number contradicts the assumption (3) and confirms that the considered drawing D is antipode-free. For easier reading, if $r=|R_D|$ and $s=|S_D|$, then again (3) together with ${\mathrm{cr}}_D\left(K_{5,n}\right)\ge 4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋$ using (1) imply the following inequality with respect to possible edge crossings of $G^{*}$ in D:

$${\mathrm{cr}}_D\left(G^{*}\right)+s+2(n-r-s)<⌊\frac{n}{2}⌋.$$

(5)

The inequality (5) forces more than $⌈\frac{n}{2}⌉$ subgraphs $T^i$ by which edges of $G^{*}$ are not crossed, that is, $r\ge ⌈\frac{n}{2}⌉+1\ge 3$ and $s<⌊\frac{n}{2}⌋$. Of course, if n is odd then previous inequalities could be strengthened, but this is not necessary in the following process of obtaining a contradiction with number of crossings in D. Moreover, if $n=3$ then $r=3$, and ${\mathrm{cr}}_D(G^{*}+D_3)\ge \mathrm{cr}\left(K_{5,3}\right)=4$ with the assumption (3) enforce n at least four.

Case 1: ${\mathrm{cr}}_D\left(G^{*}\right)=0$ and choose the vertex notation of the graph $G^{*}$ in such a way as shown in Figure 1a. In this case, we deal with configurations from the nonempty set ${\mathcal{M}}_D$. As the set $R_D$ is nonempty, recall that

$${\displaystyle \sum _{i\in I_o}{\alpha }_i+\sum _{i\in I_e}{\alpha }_i=r\ge 3.}$$

Let us first suppose that either ${\alpha }_1+{\alpha }_3+{\alpha }_5=0$ or ${\alpha }_2+{\alpha }_4+{\alpha }_6=0$. For the rest of the proof we may therefore assume that ${\alpha }_2+{\alpha }_4+{\alpha }_6=0$, that is, ${\alpha }_1+{\alpha }_3+{\alpha }_5>0$. Since ${\mathcal{G}}_D$ is the subgraph of $\mathcal{G}$ induced by $V_D$ with respect to weights 2 of all its edges (without possible loops), three possible subcases presented in Figure 6 may occur:

Figure 6. Three possible components of the graph ${\mathcal{G}}_D$ if ${\alpha }_2={\alpha }_4={\alpha }_6=0$. (a): ${\alpha }_i>0$ for each $i\in I_o$; (b): ${\alpha }_i>0$ and ${\alpha }_j>0$ for exactly two different $i,j\in I_o$; (c): ${\alpha }_i>0$ for only one $i\in I_o$.

(a)

${\alpha }_i>0$ for each $i\in I_o$. Let us assume three subgraphs $T^{n-2},T^{n-1},T^n\in R_D$ such that $F^{n-2}$, $F^{n-1}$ and $F^n$ have three mutually different configurations from the set ${\mathcal{M}}_D=\{{\mathcal{A}}_1,{\mathcal{A}}_3,{\mathcal{A}}_5\}$. Then, ${\mathrm{cr}}_D(T^{n-2}\cup T^{n-1}\cup T^n,T^i)\ge 4+2+2=8$ holds for any other $T^i\in R_D$ by summing values in corresponding three rows of Table 1, and ${\mathrm{cr}}_D(G^{*}\cup T^{n-2}\cup T^{n-1}\cup T^n,T^i)\ge 6$ is true by Corollary 2 for any $T^i\in S_D$. Then, by fixing the graph $G^{*}\cup T^{n-2}\cup T^{n-1}\cup T^n$

$${\mathrm{cr}}_D(G^{*}+D_n)\ge 4⌊\frac{n-3}{2}⌋⌊\frac{n-4}{2}⌋+8(r-3)+6s+7(n-r-s)+6$$

$$=4⌊\frac{n-3}{2}⌋⌊\frac{n-4}{2}⌋+7n+r-s-18\ge 4⌊\frac{n-3}{2}⌋⌊\frac{n-4}{2}⌋$$

$$+7n+\left(⌈\frac{n}{2}⌉+1\right)+\left(1-⌊\frac{n}{2}⌋\right)-18\ge n^2-2n+⌊\frac{n}{2}⌋.$$

(b)

Assuming that ${\alpha }_i>0$ for exactly two $i\in I_o$, without lost of generality, let us consider two different subgraphs $T^{n-1},T^n\in R_D$ such that $F^{n-1}$ and $F^n$ have configurations ${\mathcal{A}}_1$ and ${\mathcal{A}}_3$, respectively. As ${\mathcal{M}}_D=\{{\mathcal{A}}_1,{\mathcal{A}}_3\}$, we have ${\mathrm{cr}}_D(T^{n-1}\cup T^n,T^i)\ge 4+2=6$ for any $T^i\in R_D$, $i\ne n-1,n$. Therewith, the antipode-free property of D forces that, ${\mathrm{cr}}_D(T^{n-1}\cup T^n,T^i)\ge 2$ trivially holds for any subgraph $T^i$ with $i\ne n-1,n$. Hence, by fixing the graph $G^{*}\cup T^{n-1}\cup T^n$

$${\mathrm{cr}}_D(G^{*}+D_n)\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+6(r-2)+3s+4(n-r-s)+2$$

$$=4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+4n+2r-s-10\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋$$

$$+4n+2\left(⌈\frac{n}{2}⌉+1\right)+\left(1-⌊\frac{n}{2}⌋\right)-10\ge n^2-2n+⌊\frac{n}{2}⌋.$$

(c)

${\alpha }_i>0$ for only one $i\in I_o$. As ${\mathcal{M}}_D=\left\{{\mathcal{A}}_i\right\}$, in the rest of the paper, we may consider $T^n\in R_D$ with the configuration ${\mathcal{A}}_1$ of $F^n$. Then edges of each other subgraph $T^j\in R_D$ cross at least four times edges of $T^n$ provided by ${\mathrm{rot}}_D\left(t_n\right)={\mathrm{rot}}_D\left(t_j\right)$. Thus, by fixing the graph $G^{*}\cup T^n$

$${\mathrm{cr}}_D(G^{*}+D_n)\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+4(r-1)+2s+3(n-r-s)+0$$

$$=4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+3n+r-s-4\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋$$

$$+3n+\left(⌈\frac{n}{2}⌉+1\right)+\left(1-⌊\frac{n}{2}⌋\right)-4\ge n^2-2n+⌊\frac{n}{2}⌋.$$

All three subcases contradict the assumption (3). In addition, let us suppose that ${\alpha }_1+{\alpha }_3+{\alpha }_5>0$ and ${\alpha }_2+{\alpha }_4+{\alpha }_6>0$. Remark that the subgraph ${\mathcal{G}}_D$ can be either connected (consisting of a single component) or also disconnected with several components. Now, we are able to discuss over remaining possible components of ${\mathcal{G}}_D$ in the following subcases:

• There are no two adjacent edges with weights 1 in the subgraph ${\mathcal{G}}_D$, that is, there are four possibilities presented in Figure 7.
  

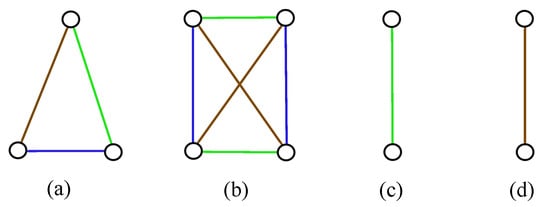  Figure 7. Four possible components of the subgraph ${\mathcal{G}}_D$ in which there are no two adjacent edges with weights 1. Green, blue, brown, and black correspond to the values 1, 2, 3, and 4, respectively. (a): the complete graph $K_3$ with edge weights 1, 2, and 3; (b): the complete graph $K_4$ with edge weights 1, 1, 2, 2, 3, and 3; (c): the complete graph $K_2$ with edge weight 1; (d): the complete graph $K_2$ with edge weight 3.
  • $w_D\left(a_i{a}_j\right)=1$ for some $i\in I_o$, $j\in I_e$, i.e., there are three cases mentioned in Figure 7a–c. Let us consider two subgraphs $T^{n-1},T^n\in R_D$ such that $F^{n-1},F^n$ have different configurations from $\{{\mathcal{A}}_i,{\mathcal{A}}_j\}$, where $i,j$ are associated indexes. Using weights of edges in the considered component of ${\mathcal{G}}_D$, one can easily verify that edges of the graph $T^{n-1}\cup T^n$ are crossed at least five times by edges of any another subgraph $T^k\in R_D$. Moreover, since the minimum number of interchanges of adjacent elements of ${\mathrm{rot}}_D\left(t_n\right)$ required to produce ${\mathrm{rot}}_D\left(t_{n-1}\right)$ is three, any subgraph $T^k$ with $k\ne n-1,n$ crosses edges of $T^{n-1}\cup T^n$ at least thrice. Thus, by fixing the graph $G^{*}\cup T^{n-1}\cup T^n$

    $${\mathrm{cr}}_D(G^{*}+D_n)\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+5(r-2)+4s+5(n-r-s)+1$$

    $$=4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+5n-s-9\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋$$

    $$+5n+\left(1-⌊\frac{n}{2}⌋\right)-9\ge n^2-2n+⌊\frac{n}{2}⌋.$$
  • $w_D\left(a_i{a}_j\right)>1$ for all $i\in I_o$, $j\in I_e$, i.e., there is only one case mentioned in Figure 7d. Let us again consider two subgraphs $T^{n-1},T^n\in R_D$ such that $F^{n-1},F^n$ have different configurations from $\{{\mathcal{A}}_i,{\mathcal{A}}_j\}$, where $i,j$ are associated indexes. Then, ${\mathrm{cr}}_D(T^{n-1}\cup T^n,T^k)\ge 7$ holds by summing edge-weights 4 and 3 for any other $T^k\in R_D$. Hence, by fixing the graph $G^{*}\cup T^{n-1}\cup T^n$

    $${\mathrm{cr}}_D(G^{*}+D_n)\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+7(r-2)+3s+4(n-r-s)+3$$

    $$=4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋+4n+3r-s-11\ge 4⌊\frac{n-2}{2}⌋⌊\frac{n-3}{2}⌋$$

    $$+4n+3\left(⌈\frac{n}{2}⌉+1\right)+1-⌊\frac{n}{2}⌋-11\ge n^2-2n+⌊\frac{n}{2}⌋.$$
  Both discussed cases again confirm a contradiction with (3) in D, and so, suppose that there are two adjacent edges with weights 1 in the subgraph ${\mathcal{G}}_D$. Further, only in the case if the number ${\beta }_j$ is defined, we claim that the following two properties (6) and (7) must be also fulfilled in D:

  $${\displaystyle {\beta }_j+\sum _{i\in I_o}{\alpha }_i>⌊\frac{n}{2}⌋\mathrm{for}\mathrm{some}j\in I_o,}$$

  (6)

  $${\displaystyle {\beta }_j+\sum _{i\in I_e}{\alpha }_i>⌊\frac{n}{2}⌋\mathrm{for}\mathrm{some}j\in I_e.}$$

  (7)
  For a contradiction, suppose, without loss of generality, that ${\beta }_1+{\alpha }_1+{\alpha }_3+{\alpha }_5\le ⌊\frac{n}{2}⌋$, that is, $-{\alpha }_1-{\alpha }_3-{\alpha }_5-{\beta }_1\ge -⌊\frac{n}{2}⌋$. In this case, from the definition of ${\beta }_1$, we have ${\alpha }_1>0$, ${\alpha }_4>0$, and ${\alpha }_6>0$. Thus, in the rest of the paper, let us consider three subgraphs $T^{n-2},T^{n-1},T^n\in R_D$ such that $F^{n-2}$, $F^{n-1}$, and $F^n$ have configurations ${\mathcal{A}}_1$, ${\mathcal{A}}_4$, and ${\mathcal{A}}_6$, respectively. Using values in Table 1, one can easily verify that edges of the graph $T^{n-2}\cup T^{n-1}\cup T^n$ are crossed at least six times and seven times by edges of any another subgraph $T^i\in R_D$ with the configuration ${\mathcal{A}}_1,{\mathcal{A}}_3,{\mathcal{A}}_5$ and ${\mathcal{A}}_2,{\mathcal{A}}_4,{\mathcal{A}}_6$ of $F^i$ (of course, if ${\mathcal{A}}_k\in {\mathcal{M}}_D$ for some $k\in I_o\cup I_e$ in D), respectively. However, from Corollary 1 we get that ${\mathrm{cr}}_D(G^{*}\cup T^{n-2}\cup T^{n-1}\cup T^n,T^i)\ge 7$ holds for any $T^i\in S_D$ provided by we can also assume that ${\mathrm{cr}}_D(T^{n-2},T^{n-1})=1$ and ${\mathrm{cr}}_D(T^{n-2},T^n)=1$ due to the congruence property (If ${\mathrm{rot}}_D\left(t_x\right)$ and ${\mathrm{rot}}_D\left(t_y\right)$ are two cyclic permutations of odd length, and $Q({\mathrm{rot}}_D\left(t_x\right),{\mathrm{rot}}_D\left(t_y\right))$ denotes the minimum number of interchanges of adjacent elements of ${\mathrm{rot}}_D\left(t_x\right)$ required to produce the inverse cyclic permutation of ${\mathrm{rot}}_D\left(t_y\right)$, then ${\mathrm{cr}}_D(T^x,T^y)=Q({\mathrm{rot}}_D\left(t_x\right),{\mathrm{rot}}_D\left(t_y\right))+2z$ for some nonnegative integer z, for more see Woodall [31]). Hence, by fixing the graph $G^{*}\cup T^{n-2}\cup T^{n-1}\cup T^n$

  $${\mathrm{cr}}_D(G^{*}+D_n)\ge 4⌊\frac{n-3}{2}⌋⌊\frac{n-4}{2}⌋+6({\alpha }_1+{\alpha }_3+{\alpha }_5-1)+7({\alpha }_2+{\alpha }_4+{\alpha }_6-2)+7s$$

  $$+6{\beta }_1+7(n-r-s-{\beta }_1)+4=4⌊\frac{n-3}{2}⌋⌊\frac{n-4}{2}⌋+7n-{\alpha }_1-{\alpha }_3-{\alpha }_5-{\beta }_1-16$$

  $$\ge 4⌊\frac{n-3}{2}⌋⌊\frac{n-4}{2}⌋+7n-⌊\frac{n}{2}⌋-16\ge n^2-2n+⌊\frac{n}{2}⌋.$$
  The obtained crossing number also contradicts the assumption (3) of D and confirms that both parity properties (6) and (7) must be fulfilled in D.
• There are two adjacent edges with weights 1 in the subgraph ${\mathcal{G}}_D$, that is, there are five possibilities presented in Figure 8.
  

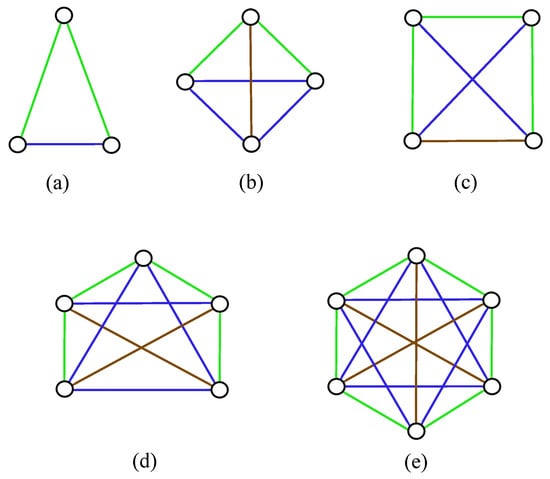  Figure 8. Five possible components of the subgraph ${\mathcal{G}}_D$ in which there are two adjacent edges with weights 1. Green, blue, brown, and black correspond to the values 1, 2, 3, and 4, respectively. (a): the complete graph $K_3$ with edge weights 1, 1, and 2; (b): the complete graph $K_4$ with edge weights 1, 1, 2, 2, 2, and 3; (c): the complete graph $K_4$ with edge weights 1, 1, 1, 2, 2, and 3; (d): the complete graph $K_5$; (e): the complete graph $K_6$.

  (a)

  Let the graph ${\mathcal{G}}_D$ consist of one component in such a way as shown in Figure 8a. Without lost of generality, let us assume that $a_2,a_3,a_6$ are vertices of the considered path on three vertices with weight 1 of both edges. In this case, it is obvious that ${\alpha }_2+{\alpha }_3+{\alpha }_6=r$. Since the number ${\beta }_3$ can be defined, the property (6) forces ${\beta }_3+{\alpha }_3>⌊\frac{n}{2}⌋$. Further, let us also assume that $T^n\in R_D$ with the configuration ${\mathcal{A}}_3$ of $F^n$. Then, by fixing the graph $G^{*}\cup T^n$

  $${\mathrm{cr}}_D(G^{*}+D_n)\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+4({\alpha }_3-1)+1({\alpha }_2+{\alpha }_6)+4{\beta }_3+2s$$

  $$+3(n-r-s-{\beta }_3)=4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+3n+({\alpha }_3+{\beta }_3-{\alpha }_2-{\alpha }_6)$$

  $$-(s+{\alpha }_2+{\alpha }_6)-4\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+3n+0-⌊\frac{n}{2}⌋-4\ge n^2-2n+⌊\frac{n}{2}⌋.$$

  (b)

  Let the graph ${\mathcal{G}}_D$ consist of one component in such a way as shown in Figure 8b. Without lost of generality, let us assume that $a_2,a_3,a_6$ are vertices of the considered path on three vertices with weight 1 of both edges and let $a_2,a_4,a_6$ be vertices of the 3-cycle with respect to weight 2 of all its edges. In this case, it is obvious that ${\alpha }_2+{\alpha }_3+{\alpha }_4+{\alpha }_6=r$. The property (6) enforces again ${\beta }_3+{\alpha }_3>⌊\frac{n}{2}⌋$ because the number ${\beta }_3$ can be defined. Further, if $T^n\in R_D$ is assumed with the configuration ${\mathcal{A}}_4$ of $F^n$, then by fixing the graph $G^{*}\cup T^n$

  $${\mathrm{cr}}_D(G^{*}+D_n)\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+3({\alpha }_3+{\beta }_3)+2(n-{\alpha }_3-{\beta }_3-1)$$

  $$\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+2n+\left(⌊\frac{n}{2}⌋+1\right)-2\ge n^2-2n+⌊\frac{n}{2}⌋.$$

  (c)

  Let the graph ${\mathcal{G}}_D$ consist of one component in such a way as shown in Figure 8c–e. Let us take a maximal path $P_k$ on k vertices as the subgraph of ${\mathcal{G}}_D$ with weights 1 on all its edges. If $a_i$ and $a_j$ are two inner vertices of $P_k$ with $i+1\equiv j\left(\mathrm{mod}2\right)$ for which the numbers ${\beta }_i$ and ${\beta }_j$ satisfy the parity properties (6) and (7), then addition of both inequalities thus obtained enforces a contradiction

  $$n\ge {\beta }_i+{\beta }_j+r\ge 2\left(⌊\frac{n}{2}⌋+1\right).$$

  The obtained contradictions in all three cases complete the proof for the planar subdrawing of $G^{*}$ induced by D given in Figure 1a.

Case 2. ${\mathrm{cr}}_D\left(G^{*}\right)=2$ and choose the vertex notation of the graph $G^{*}$ presented as in Figure 1b. Since the set $R_D$ is nonempty and there is only one subdrawing of a subgraph $F^i=G^{*}\cup T^i$ for all $T^i\in R_D$ represented by the rotation $\left(13524\right)$, the subgraph $T^i$ is crossed at least four times by edges of each subgraph $T^j\in R_D$ with $j\ne i$. Hence, by fixing the graph $G^{*}\cup T^i$

$${\mathrm{cr}}_D(G^{*}+D_n)\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+4(r-1)+2(n-r)+2=4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋$$

$$+2n+2r-2\ge 4⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋+2n+2\left(⌈\frac{n}{2}⌉+1\right)-2\ge n^2-2n+⌊\frac{n}{2}⌋.$$

For all these mentioned cases, it turned out that there is no drawing of the graph $G^{*}+D_n$ with fewer than $n^2-2n+⌊\frac{n}{2}⌋$ crossings, and the proof of Theorem 2 is complete. □

5. Conclusions

Into both drawings in Figure 4 and Figure 5, we could add $n-1$ or n edges forming paths $P_n$, $n\ge 2$ or cycles $C_n$, $n\ge 3$ on vertices of $D_n$ with no crossing, respectively. Thus, the following surprising results are obvious.

Corollary 3.

$\mathrm{cr}(G^{*}+P_n)=n^2-2n+⌊\frac{n}{2}⌋$ for $n\ge 2$, i.e., $\mathrm{cr}(G^{*}+P_n)=4⌊\frac{n}{2}⌋\lfloor \frac{n-1}{2}\rfloor +⌊\frac{n}{2}⌋$ for n even and $\mathrm{cr}(G^{*}+P_n)=4⌊\frac{n}{2}⌋\lfloor \frac{n-1}{2}\rfloor +⌊\frac{n}{2}⌋-1$ for n odd.

Corollary 4.

$\mathrm{cr}(G^{*}+C_n)=n^2-2n+⌊\frac{n}{2}⌋$ for $n\ge 3$, i.e., $\mathrm{cr}(G^{*}+C_n)=4⌊\frac{n}{2}⌋\lfloor \frac{n-1}{2}\rfloor +⌊\frac{n}{2}⌋$ for n even and $\mathrm{cr}(G^{*}+C_n)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋-1$ for n odd.

These results extend already known results of join products of graphs on at most six vertices with paths and cycles, see [2,5,18,20,26,33,34,35,36,37,38,39,40,41].