On Polynomials Orthogonal with Respect to an Inner Product Involving Higher-Order Differences: The Meixner Case

Abstract

In this contribution we consider sequences of monic polynomials orthogonal with respect to the Sobolev-type inner product ${\displaystyle ⟨f,g⟩=⟨{\mathbf{u}}^{\mathtt{M}},fg⟩+\lambda {\mathcal{T}}^{j}f\left(\alpha \right){\mathcal{T}}^{j}g\left(\alpha \right),}$ where ${\mathbf{u}}^{\mathtt{M}}$ is the Meixner linear operator, $\lambda \in {\mathbb{R}}_{+}$, $j\in \mathbb{N}$, $\alpha \le 0$, and $\mathcal{T}$ is the forward difference operator $\Delta$ or the backward difference operator ∇. Moreover, we derive an explicit representation for these polynomials. The ladder operators associated with these polynomials are obtained, and the linear difference equation of the second order is also given. In addition, for these polynomials, we derive a $(2j+3)$-term recurrence relation. Finally, we find the Mehler–Heine type formula for the particular case $\alpha =0$.

1. Introduction

Meixner orthogonal polynomials, usually denoted in the literature as $M_n(x;\beta ,c)$, constitute a family of classical orthogonal polynomials introduced by J. Meixner in 1934 in his seminal paper [1]. When $\beta >0$ and $0<c<1$, they are orthogonal with respect to the well-known negative binomial distribution of the probability theory, i.e., in such a case:

$$\sum _{x=0}^{\infty }\left(\genfrac{}{}{0pt}{}{x+\beta -1}{x}\right)c^x{M}_n(x;\beta ,c)M_m(x;\beta ,c)=0,m\ne n,m,n=0,1,\cdots ,$$

so the Meixner linear functional is

$${\mathbf{u}}^{\mathtt{M}}=\sum _{x=0}^{\infty }\left(\genfrac{}{}{0pt}{}{x+\beta -1}{x}\right)c^x{\delta }_x.$$

Therefore, they are orthogonal on the uniform lattice in the interval $[0,+\infty )$, and they satisfy a hypergeometric-type difference equation on the aforesaid uniform lattice. Due to its classical character, their finite differences also constitute an orthogonal polynomial family, their corresponding orthogonality weights satisfy a Pearson-type difference equation, and they even satisfy two different kinds of structure relations. A distinctive and interesting characteristic of this family is that they have certain dual character, that is, every formula one can derive for $M_n(x;\beta ,c)$ has a dual formula with x and n interchanged:

$$c^{m-n}n!{(1+\beta )}_{m-1}{M}_n(m;\beta ,c)=c^{n-m}m!{(1+\beta )}_{n-1}{M}_m(n;\beta ,c).$$

(See, for example [2,3,4] and the references therein).

On the other hand, since the first paper [5] on Sobolev’s orthogonal polynomials was published by Althammer, the results connected to these polynomials have attracted the attention of several mathematicians. The name of the Sobolev orthogonal polynomials is given to those families of polynomials orthogonal with respect to inner products involving positive Borel measures supported on infinite subsets of the real lines and also involving regular derivatives. Moreover, in the case that the derivatives appear only on function evaluations on a finite discrete set, the corresponding families are called Sobolev-type or discrete Sobolev orthogonal polynomial sequences. For a recent and comprehensive survey on the subject, see [6] and the references therein. In the last decade of the past century, H. Bavinck introduced the study of orthogonal polynomials with respect to the inner product involving differences instead of derivatives:

$${⟨f,g⟩}_{\lambda }={\int }_{\mathbb{R}}f\left(x\right)g\left(x\right)d\psi \left(x\right)+\lambda (\Delta f)\left(d\right)(\Delta g)\left(d\right),$$

(1)

where $\lambda \in {\mathbb{R}}^{+}$, $d\in \mathbb{R}$, and $\psi$ is a distribution function with infinite spectrum, see [7,8]. Moreover, in these works Bavinck obtained algebraic properties and some results connected to the location of the zeros of the orthogonal polynomials with respect to the inner product (1). On the other hand, in [8], he proved that the orthogonal polynomials with respect to inner product defined in Equation (1) satisfy a five-term recurrence relation. Furthermore, in [9], the authors considered the following inner product:

$$⟨f,g⟩={(1-c)}^{\beta }\sum _{x=0}^{\infty }f\left(x\right)g\left(x\right)\frac{c^x\Gamma (\beta +x)}{\Gamma \left(\beta \right)\Gamma (x+1)}+\lambda f\left(0\right)g\left(0\right),$$

(2)

where $\beta >0$, $0<c<1$, $\lambda >0$, and $\mathbb{P}$ denotes the linear space of all polynomials with real coefficients. Here, they obtained a second-order difference equation with polynomial coefficients, which the orthogonal polynomials with respect to (2) satisfy. Then, in [10], the authors showed that the Sobolev-type Meixner polynomials orthogonal with respect to the inner product are eigenfunctions of a difference operator:

$$⟨f,g⟩={(1-c)}^{\beta }\sum _{x=0}^{\infty }f\left(x\right)g\left(x\right)\frac{c^x\Gamma (\beta +x)}{\Gamma \left(\beta \right)\Gamma (x+1)}+Mf\left(0\right)g\left(0\right)+N(\Delta f)\left(0\right)(\Delta g)\left(0\right),$$

where $\beta >0$, $0<c<1$, and $M,N\ge 0$. Other slightly more recent results, connected with the Sobolev–Meixner polynomials, can be found in [11,12]. Note that our work is in someways connected to the paper [13], where the authors consider the Charlier case.

The structure of the paper is the following: In Section 2, we introduce some preliminary results about Meixner polynomials, which will be very useful in the analysis presented. In Section 3, we obtain the connection formula between the Meixner polynomials and the polynomials orthogonal with respect to the Sobolev-type inner product:

$$⟨f,g⟩=⟨{\mathbf{u}}^{\mathtt{M}},fg⟩+\lambda {\mathcal{T}}^{j}f\left(\alpha \right){\mathcal{T}}^{j}g\left(\alpha \right),$$

(3)

where ${\mathbf{u}}^{\mathtt{M}}$ is the Meixner linear operator, $\lambda \in {\mathbb{R}}_{+}$, $j\in \mathbb{N}$, $\alpha \le 0$, and $\mathcal{T}$ is the forward or the backward difference operator. In addition, we deduce the hypergeometric representation of such polynomials. In Section 4, we find the ladder (creation and annihilation) operators for the sequence of Sobolev-type orthogonal polynomials. As a consequence, the second-order linear difference equation associated with them is deduced. On the other hand, in Section 5, we determine the $(2j+3)$-term recurrence relation that these polynomials satisfy. Finally, in Section 6, we determine the Mehler–Heine-type formula for the special case of $\alpha =0$. Indeed, the techniques used in Section 3, Section 4 and Section 5 are based on those used in [3,14,15], respectively.

2. Preliminaries

We adopt the following set of notations: ${\mathbb{N}}_0:=\left\{0\right\}\cup \mathbb{N}=\{0,1,2,3,\dots \}$, and we use the sets $\mathbb{Z}$, $\mathbb{R}$, and $\mathbb{C}$, which represent the integers, real numbers, and complex numbers, respectively. $\mathbb{P}$ denotes the vector space of univariate, complex-valued polynomials, and let ${\mathbb{P}}^{\prime }$ denote its algebraic dual space.

We also adopt the following notation and conventions. We denote by $⟨\mathbf{u},p⟩$ the duality bracket for $\mathbf{u}\in {\mathbb{P}}^{\prime }$ and $p\in \mathbb{P}$.

Definition 1.

For $\mathbf{u}\in {\mathbb{P}}^{\prime }$, $\pi \in \mathbb{P}$, and $c\in \mathbb{C}$, let $\pi \mathbf{u}$, ${(x-c)}^{-1}\mathbf{u}$, $\nabla \mathbf{u}$, and $\Delta \mathbf{u}$ be the linear functionals defined by:

$$\begin{array}{ccc}\hfill ⟨\pi \mathbf{u},p⟩& :=& ⟨\mathbf{u},\pi p⟩,p\in \mathbb{P},\hfill \\ \hfill ⟨{(x-c)}^{-1}\mathbf{u},p⟩& :=& ⟨\mathbf{u},\frac{p\left(x\right)-p\left(c\right)}{x-c}⟩,p\in \mathbb{P},\hfill \\ \hfill ⟨\nabla \mathbf{u},p⟩& :=& -⟨\mathbf{u},\Delta p⟩,\hfill \end{array}$$

and thus: $⟨\Delta \mathbf{u},p⟩:=-⟨\mathbf{u},\nabla p⟩$, where ∇ and Δ are the backward and forward difference operators, defined as:

$$\Delta f\left(x\right):=f(x+1)-f\left(x\right),\nabla f\left(x\right):=f\left(x\right)-f(x-1).$$

The Dirac delta functional, ${\delta }_c$, is the functional defined by $⟨{\delta }_c,p⟩:=p\left(c\right)$, $p\in \mathbb{P}$.

In order to obtain our derived identities, we rely on properties of the Pochhammer symbol (shifted factorial). For any $n\in {\mathbb{N}}_0$, $a\in \mathbb{C}$, the Pochhammer symbol is defined as:

$${\left(a\right)}_n:=\left(a\right)(a+1)\cdots (a+n-1),n\in {\mathbb{N}}_0.$$

Furthermore, define for all $a,b\in \mathbb{C}$:

$${\left(a\right)}_b:={\displaystyle \frac{\Gamma (a+b)}{\Gamma \left(a\right)}},$$

where $a+b\notin -{\mathbb{N}}_0$, and we will also use the common notational product convention

$${(a_1,\dots ,a_k)}_b:={\left(a_1\right)}_b\cdots {\left(a_k\right)}_b.$$

The hypergeometric series, which we will use often, is defined for $z\in \mathbb{C}$ such that $\left|z\right|<1$, $s,r\in {\mathbb{N}}_0$, with $s\ge r-1$, as [16]:

$${}_r{F}_s\left(\begin{array}{c}{a}_1,\cdots ,a_r\\ b_1,\cdots ,b_s\end{array};z\right):=\sum _{k=0}^{\infty }\frac{{(a_1,\cdots ,a_r)}_k}{{(b_1,\cdots ,b_s)}_k}{\displaystyle \frac{z^k}{k!}},$$

(4)

wherethe parameters must be chosen such that the denominator factors in the terms of the series are never zero.

The Meixner Polynomials

Let $\beta$ and c be two complex numbers, such that $c\ne 0,1$ and $\beta$ is not a negative integer. We write ${\left\{M_n(x;\beta ,c)\right\}}_{n\ge 0}$ for the sequence of monic Meixner polynomials defined by [2]:

$$M_n(x;\beta ,c)=\frac{c^{n}n!}{{(1-c)}^n}\sum _{j=0}^n{c}^{-j}\left(\genfrac{}{}{0pt}{}{x}{j}\right)\left(\genfrac{}{}{0pt}{}{-x-\beta }{n-j}\right).$$

These polynomials are orthogonal with respect to the linear functional ${\mathbf{u}}^{\mathtt{M}}\in {\mathbb{P}}^{\prime }$, which is a classical functional since it fulfills the Pearson difference equation:

$$\Delta \left(x{\mathbf{u}}^{\mathtt{M}}\right)=\left(x(c-1)+\beta c\right){\mathbf{u}}^{\mathtt{M}},$$

(5)

which is equivalent to the Pearson difference equation:

$$\nabla \left(c(x+\beta ){\mathbf{u}}^{\mathtt{M}}\right)=\left(x(c-1)+\beta c\right){\mathbf{u}}^{\mathtt{M}}.$$

Remark 1.

Observe that when $\beta >0$ and $0<c<1$, then:

$$⟨{\mathbf{u}}^{\mathtt{M}},f⟩:=\sum _{x=0}^{\infty }\left(\genfrac{}{}{0pt}{}{x+\beta -1}{x}\right)c^{x}f\left(x\right),$$

which is a positive definite linear functional. Note that this definition can be extended to $\left|c\right|<1$, and $\beta \in \mathbb{C}$ is not a negative integer. Moreover, since

$$M_n(x;\beta ,c)={(-1)}^n{M}_n(-x-\beta ;\beta ,c^{-1}),$$

(6)

then one can extend the Meixner functional to $\left|c\right|>1$. In [17], the authors obtained an integral representation for this operator for $\beta ,c\in \mathbb{C}$, with $c\notin [0,+\infty )$ and $-\beta \notin \mathbb{N}$:

$$⟨{\mathbf{u}}^{\mathtt{M}},f⟩={\int }_{C}f\left(z\right)\Gamma (-z)\Gamma (\beta +z){(-c)}^{z}dz,$$

where C is a complex contour from $-\infty i$ to $\infty i$ separating the increasing poles $\{0,1,2,\cdots \}$ from the decreasing poles $\{-\beta ,-\beta -1,-\beta -2,\dots \}$.

When $c\ne 0,1$, they satisfy the following three-term recurrence formula:

$$x{M}_n(x;\beta ,c)=M_{n+1}(x;\beta ,c)+\frac{(c+1)n+\beta c}{1-c}{M}_n(x;\beta ,c)+{\gamma }_n{M}_{n-1}(x;\beta ,c),$$

(7)

where

$${\gamma }_n=\frac{cn(n+\beta -1)}{{(1-c)}^2},$$

which can be given explicitly in terms of hypergeometric series as [16]:

$$M_n(x;\beta ,c)={\displaystyle \frac{c^n{\left(\beta \right)}_n}{{(c-1)}^n}}{}_2{F}_1\left(\begin{array}{c}-n,-x\\ \beta \end{array};1-\frac{1}{c}\right).$$

(8)

Next, we summarize some basic properties of Meixner orthogonal polynomials to be used in the sequel.

Proposition 1

(cf. Proposition 2.1 in [18]). Let $\beta ,c\in \mathbb{C}$ such that $-\beta \notin \mathbb{N}$ and $\left|c\right|<1$. Then, the following identities hold true for the Meixner polynomials:

1. 

Second-order difference equation:

$$c(x+\beta )y_n(x+1)-(x(c+1)+\beta c)y_n\left(x\right)+x{y}_n(x-1)=n(c-1)y_n\left(x\right);$$

(9)

2. 

Structure relations. For every $n\in \mathbb{N}$:

$$\begin{array}{ccc}\hfill (x+\beta )\Delta M_n(x;\beta ,c)& =& n{M}_n(x;\beta ,c)+\frac{n(n+\beta -1)}{1-c}{M}_{n-1}(x;\beta ,c),\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill x\nabla M_n(x;\beta ,c)& =& n{M}_n(x;\beta ,c)+\frac{nc(n+\beta -1)}{1-c}{M}_{n-1}(x;\beta ,c);\hfill \end{array}$$

(11)

3. 

Squared norm. For every $n\in \mathbb{N}$:

$$d_n^2={\parallel M_n(x;\beta ,c)\parallel }^2=⟨{\mathbf{u}}^{\mathtt{M}},M_n^2(x;\beta ,c)⟩=\frac{{\left(\beta \right)}_n{c}^{n}n!}{{(1-c)}^{\beta +2n}};$$

(12)

4. 

The value at the left endpoint initial extreme:

$$M_n(0;\beta ,c)={\displaystyle \frac{{\left(\beta \right)}_n{c}^n}{{(c-1)}^n}};$$

(13)

5. 

Forward and backward difference operators. For every $n,k\in \mathbb{N}$:

$${\Delta }^k{M}_n(x;\beta ,c)={(m-k+1)}_k{M}_{n-k}(x;\beta +k,c),$$

(14)

where ${\Delta }^{k}f\left(x\right)={\Delta }^{k-1}\Delta f\left(x\right)$ for $k=1,2,\cdots$, and ${\Delta }^{0}f\left(x\right)=f\left(x\right)$;

6. 

Mehler–Heine type formula (Equation (35) in [19]):

$$\underset{n\to \infty }{lim}\frac{{(1-c)}^{n+\beta +z}{M}_n(z;\beta ,c)}{{(z-n+1)}_n}=1,z\in \mathbb{C}\setminus \mathbb{N}.$$

(15)

To complete this section, we present some useful results we will need throughout the paper.

Proposition 2

(Christoffel-Darboux formula). Let ${\left\{p_n\right\}}_{n\in {\mathbb{N}}_0}$ be a sequence of monic polynomials orthogonal with respect to the linear functional $\mathbf{u}$. If we denote the n-th reproducing kernel by

$$K_n(x,y):=\sum _{k=0}^{n-1}\frac{p_k\left(x\right)p_k\left(y\right)}{⟨\mathbf{u},p_k^2⟩},$$

(16)

then, for all $n\in \mathbb{N}$ and $x\ne y$:

$$K_n(x,y)=\frac{1}{⟨\mathbf{u},p_{n-1}^2⟩}\frac{p_n\left(x\right)p_{n-1}\left(y\right)-p_n\left(y\right)p_{n-1}\left(x\right)}{x-y}.$$

(17)

Taking into account the inner product we have considered, then it is natural to consider the partial derivatives of $K_n(x,y)$. We will use the following notation:

$${\mathcal{K}}_{n,1}^{(i,j)}(x,y):=\sum _{k=0}^{n-1}\frac{{\nabla }^i{p}_k\left(x\right){\nabla }^j{p}_k\left(y\right)}{⟨\mathbf{u},p_k^2⟩},$$

(18)

and

$${\mathcal{K}}_{n,2}^{(i,j)}(x,y):=\sum _{k=0}^{n-1}\frac{{\Delta }^i{p}_k\left(x\right){\Delta }^j{p}_k\left(y\right)}{⟨\mathbf{u},p_k^2⟩}.$$

(19)

Remark 2.

Since this work is related to the Meixner polynomials, we will have to substitute $p_k\left(x\right)$ (resp. $p_k\left(y\right)$) in (16) by $M_k(x;\beta ,c)$ (resp. $M_{k-1}(x;\beta ,c)$) and in all expressions that depend on it, such as (18) and (19).

Proposition 3.

The following identities hold:

$${\mathcal{K}}_{n,1}^{(0,j)}(x,y)=\frac{j!}{d_{n-1}^2}\sum _{k=0}^j\left({\displaystyle \frac{M_n(x;\beta ,c){\nabla }^k{M}_{n-1}(y;\beta ,c)-M_{n-1}(x;\beta ,c){\nabla }^k{M}_n(y;\beta ,c)}{k!{(x-y+k)}_{j+1-k}}}\right),$$

(20)

$${\mathcal{K}}_{n,2}^{(0,j)}(x,y)=\frac{j!}{d_{n-1}^2}\sum _{k=0}^j\left({\displaystyle \frac{M_n(x;\beta ,c){\Delta }^k{M}_{n-1}(y;\beta ,c)-M_{n-1}(x;\beta ,c){\Delta }^k{M}_n(y;\beta ,c)}{k!{(x-y-j)}_{j+1-k}}}\right),$$

(21)

where $d_{n-1}^2=⟨{\mathbf{u}}^{\mathtt{M}},M_{n-1}^2(x;\beta ,c)⟩$.

Proof. 

We are going to prove the first identity. After applying the difference operator ${\nabla }^j$ to (17) with respect to y, we obtain:

$${\mathcal{K}}_{n,1}^{(0,j)}(x,y)={\displaystyle \frac{1}{d_{n-1}^2}}\left(M_n(x;\beta ,c){\nabla }_y^j\left(\frac{M_{n-1}(x;\beta ,c)}{x-y}\right)-M_{n-1}(x;\beta ,c){\nabla }_y^j\left(\frac{M_n(y;\beta ,c)}{x-y}\right)\right).$$

(22)

Using an analogue of the Leibnitz’s rule

$${\nabla }^n\left(f\left(x\right)g\left(x\right)\right)=\sum _{k=0}^n\left(\genfrac{}{}{0pt}{}{n}{k}\right){\nabla }^{k}f\left(x\right){\nabla }^{n-k}g(x-k),$$

(23)

and since for any positive integer k we have

$${\nabla }_y^k\left(\frac{1}{x-y}\right)=\frac{k!}{{(x-y)}_{k+1}},$$

the result follows after a straightforward calculation. The proof of the second identity is analogous, and it will be omitted. Hence, the result follows. □

Proposition 4.

The following identity holds for the kernel associated with the Meixner polynomials:

$${\mathcal{K}}_{n,2}^{(j,j)}(0,0)={\displaystyle \frac{j!{(1-c)}^{\beta +2j}}{c^j{\left(\beta \right)}_j}}\sum _{k=0}^{n-j-1}{\displaystyle \frac{{(j+1)}_k{(\beta +j)}_k}{{\left(1\right)}_k}}{\displaystyle \frac{c^k}{k!}}.$$

Proof. 

Taking (13)–(16) into account, and, by definition, (18), we have:

$$\begin{array}{ccc}\hfill {\mathcal{K}}_{n,2}^{(j,j)}(0,0)& =& \sum _{k=0}^{n-1}\frac{{(k-j+1)}_j^2{(\beta +j)}_j^2{c}^{2k-2j}{(1-c)}^{\beta +2k}}{{(c-1)}^{2k-2j}{\left(\beta \right)}_j{c}^{k}k!}\hfill \\ & =& \frac{{(1-c)}^{2j+\beta }}{c^{2j}{\left(\beta \right)}_j^2}\sum _{k=0}^{n-1}\frac{{(k-j+1)}_j^2{\left(\beta \right)}_k{c}^k}{k!}.\hfill \end{array}$$

By using some identities of the Pochhammer symbols, we obtain:

$$\begin{array}{cc}\hfill {\mathcal{K}}_{n,2}^{(j,j)}(0,0)=& \frac{{(1-c)}^{2j+\beta }}{c^{2j}{\left(\beta \right)}_j^2}\sum _{k=0}^{n-1}\frac{{(k-j+1)}_j^2{\left(\beta \right)}_k{c}^k}{{\left(1\right)}_{k-j}^2}\hfill \\ \hfill =& \frac{{(1-c)}^{2j+\beta }}{c^{2j}{\left(\beta \right)}_j^2}\sum _{k=0}^{n-1-j}\frac{{\left(1\right)}_{k+j}{\left(\beta \right)}_{k+j}{c}^{k+j}}{{\left(1\right)}_k^2},\hfill \end{array}$$

from this expression, it is a direct calculation to obtain the desired expression. □

Corollary 1.

The following limit for the kernels associated to the Meixner polynomials holds:

$$\underset{n\to \infty }{lim}{\mathcal{K}}_{n,2}^{(j,j)}(0,0)={\displaystyle \frac{j!{(1-c)}^{\beta +2j}}{c^j{\left(\beta \right)}_j}}{}_2{F}_1\left(\begin{array}{c}1+j,\beta +j\\ 1\end{array};c\right).$$

3. The Sobolev-Type Meixner Polynomials

We start this section by introducing the Sobolev-type inner product (3):

$${⟨f,g⟩}_{\lambda ,j,\ell }=⟨{\mathbf{u}}^{\mathtt{M}},fg⟩+\lambda {\mathcal{T}}^{j}f\left(\alpha \right){\mathcal{T}}^{j}g\left(\alpha \right),$$

(24)

where ${\mathbf{u}}^{\mathtt{M}}$ is the Meixner linear operator, $j\in \mathbb{N}$, $\alpha \le 0$, and $\mathcal{T}$ is the operator ∇ when $\ell =1$, and it is the operator $\Delta$ when $\ell =2$.

We denote by ${\left\{{\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )\right\}}_{n\in {\mathbb{N}}_0}$ the sequence of monic polynomials, orthogonal with respect to the inner product (24). These polynomials are said to be Sobolev-type Meixner polynomials.

Connection Formula and Hypergeometric Representation

We first express the Sobolev-type Meixner polynomials in terms of the monic Meixner polynomials and the Kernel polynomials associated with the Meixner polynomials.

Taking into account the Fourier expansion and using the orthogonality conditions of $\left(M_n\left(x\right)\right)$ and $\left({\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )\right)$, we obtain (see cf. Equation (2.8) in [20]):

$${\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )=M_n(x;\beta ,c)-{\displaystyle \frac{\lambda {\mathcal{T}}^j{M}_n(\alpha ;\beta ,c)}{1+\lambda {\mathcal{K}}_{n,\ell }^{(j,j)}(\alpha ,\alpha )}}{\mathcal{K}}_{n,\ell }^{(0,j)}(x,\alpha ),\ell =1,2.$$

(25)

We can express the Sobolev-type Meixner polynomials in terms of the Meixner and their associated Kernel polynomials. Moreover, starting from (25) and by using the recurrence relation of the Meixner polynomials (7), we have:

$${\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )=A_{1,n}^{j,\ell }\left(x\right)M_n(x;\beta ,c)+B_{n,1}^{j,\ell }\left(x\right)M_{n-1}(x;\beta ,c),$$

(26)

where:

$$\begin{array}{cc}\hfill A_{1,n}^{j,1}\left(x\right)& =1-{\displaystyle \frac{\lambda {\mathcal{T}}^j{M}_n(\alpha ;\beta ,c)}{1+\lambda {\mathcal{K}}_{n,\ell }^{(j,j)}(\alpha ,\alpha )}}\frac{j!}{d_{n-1}^2}\sum _{k=0}^j{\displaystyle \frac{{\nabla }^k{M}_{n-1}(\alpha ;\beta ,c)}{k!{(x-\alpha +k)}_{j+1-k}}},\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill A_{1,n}^{j,2}\left(x\right)& =1-{\displaystyle \frac{\lambda {\mathcal{T}}^j{M}_n(\alpha ;\beta ,c)}{1+\lambda {\mathcal{K}}_{n,\ell }^{(j,j)}(\alpha ,\alpha )}}\frac{j!}{d_{n-1}^2}\sum _{k=0}^j{\displaystyle \frac{{\Delta }^k{M}_{n-1}(\alpha ;\beta ,c)}{k!{(x-\alpha -j)}_{j+1-k}}},\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill B_{1,n}^{j,1}\left(x\right)& ={\displaystyle \frac{\lambda {\mathcal{T}}^j{M}_n(\alpha ;\beta ,c)}{1+\lambda {\mathcal{K}}_{n,\ell }^{(j,j)}(\alpha ,\alpha )}}\frac{j!}{d_{n-1}^2}\sum _{k=0}^j\frac{{\nabla }^k{M}_n(\alpha ;\beta ,c)}{k!{(x-\alpha +k)}_{j+1-k}},\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill B_{1,n}^{j,2}\left(x\right)& ={\displaystyle \frac{\lambda {\mathcal{T}}^j{M}_n(\alpha ;\beta ,c)}{1+\lambda {\mathcal{K}}_{n,\ell }^{(j,j)}(\alpha ,\alpha )}}\frac{j!}{d_{n-1}^2}\sum _{k=0}^j\frac{{\Delta }^k{M}_n(\alpha ;\beta ,c)}{k!{(x-\alpha -j)}_{j+1-k}},\hfill \end{array}$$

(30)

where, in such a case, $\mathcal{T}f\left(\alpha \right)$ means

$$\mathcal{T}f\left(\alpha \right)=\mathcal{T}f\left(x\right){|}_{x=\alpha }.$$

From these identities, we can express the Sobolev-type Meixner polynomials in terms of hypergeometric series.

Theorem 1.

The monic Sobolev-type Meixner polynomial ${\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )$ has the following hypergeometric representation for $\ell =1,2$:

$${\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )={\displaystyle \frac{{\left(\beta \right)}_{n-1}{c}^{n-1}}{{(c-1)}^{n-1}}}{h}_n^{\ell }\left(x\right){}_3{F}_2\left(\begin{array}{c}-n,-x,-f_n^{\ell }\left(x\right)\\ \beta ,-f_n^{\ell }\left(x\right)-1\end{array};1-\frac{1}{c}\right),$$

(31)

where $f_n^{\ell }\left(x\right)$ is given in (33) and

$$h_n^{\ell }\left(x\right)=\frac{c(\beta +n-1)}{1-c}{A}_{1,n}^{j,\ell }\left(x\right)-B_{1,n}^{j,\ell }\left(x\right).$$

Proof. 

Taking into account ${(-x)}_k=0$ if $x<k$, as well as (8) and (26), we deduce:

$$\begin{array}{cc}\hfill {\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )& ={\displaystyle \frac{c^n{\left(\beta \right)}_n}{{(c-1)}^n}}{A}_{1,n}^{j,\ell }\left(x\right)\sum _{k=0}^n{\displaystyle \frac{{(-n)}_k{(-x)}_k}{{\left(\beta \right)}_{k}k!}}{\left(1-\frac{1}{c}\right)}^k\hfill \\ & +{\displaystyle \frac{c^{n-1}{\left(\beta \right)}_{n-1}}{{(c-1)}^{n-1}}}{B}_{1,n}^{j,\ell }\left(x\right)\sum _{k=0}^{n-1}{\displaystyle \frac{{(1-n)}_k{(-x)}_k}{{\left(\beta \right)}_{k}k!}}{\left(1-\frac{1}{c}\right)}^k.\hfill \end{array}$$

By using the identity:

$$(a+k){\left(a\right)}_k=a{(a+1)}_k,$$

(32)

we obtain:

$$\begin{array}{c}{\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )={\displaystyle \frac{c^n{\left(\beta \right)}_n}{{(c-1)}^n}}{A}_{1,n}^{j,\ell }\left(x\right)\sum _{k=0}^n\frac{{(-n)}_k{(-x)}_k}{{\left(\beta \right)}_{k}k!}{\left(1-\frac{1}{c}\right)}^k\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \frac{c^{n-1}{\left(\beta \right)}_{n-1}}{{(c-1)}^{n-1}}}\frac{B_{1,n}^{j,\ell }\left(x\right)}{n}\sum _{k=0}^n{\displaystyle \frac{(n-k){(-n)}_k{(-x)}_k}{{\left(\beta \right)}_{k}k!}}{\left(1-\frac{1}{c}\right)}^k.\end{array}$$

Thus, we have:

$${\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )={\displaystyle \frac{{\left(\beta \right)}_{n-1}{c}^{n-1}}{{(c-1)}^{n-1}}}\frac{B_{1,n}^{j,\ell }\left(x\right)}{n}\sum _{k=0}^n(f_n^{\ell }\left(x\right)-k+1)\frac{{(-n)}_k{(-x)}_k}{{\left(\beta \right)}_{k}k!}{\left(1-\frac{1}{c}\right)}^k,$$

where

$$f_n^{\ell }\left(x\right)=n-1-\frac{nc(\beta +n-1)A_{1,n}^{j,\ell }\left(x\right)}{(1-c)B_{1,n}^{j,\ell }\left(x\right)}.$$

(33)

In addition, after a straightforward calculation and by using (32) with $a\to -f_n^{\ell }\left(x\right)-1$, the identity (31) follows. This completes the proof. □

4. Second-Order Linear Difference Equation

In this section, we obtain a second-order linear difference equation that the sequence ${\left\{{\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )\right\}}_{n\ge 0}$ satisfies. In order to achieve this, we will find the ladder (creation and annihilation) operators, using the connection Formula (26), the three-term recurrence relation (7), and the structure relations (10) and (11) satisfied by them.

From (26) and the recurrence relation (7), we deduce the following result:

$${\mathcal{M}}_{n-1}^{j,\ell }(x;\beta ,c;\lambda )=A_{2,n}^{j,\ell }\left(x\right)M_n(x;\beta ,c)+B_{2,n}^{j,\ell }\left(x\right)M_{n-1}(x;\beta ,c),$$

(34)

where

$$A_{2,n}^{j,\ell }\left(x\right)=\frac{(c-1)B_{1,n-1}^{j,\ell }\left(x\right)}{(c+1)(n-1)+\beta c},\mathrm{and}{B}_{2,n}^{j,\ell }\left(x\right)=A_{1,n-1}^{j,\ell }\left(x\right)+A_{2,n}^{j,\ell }\left(x\right)(1-x).$$

Applying the operator $\mathcal{T}$ to (26) and by using (23), we have:

$$\begin{array}{cc}\hfill \mathcal{T}{\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda & )=M_n(x;\beta ,c)\mathcal{T}{A}_{1,n}^{j,\ell }\left(x\right)+A_{1,n}^{j,\ell }(x+{(-1)}^{\ell })\mathcal{T}{M}_n(x;\beta ,c)\hfill \\ \hfill +& M_{n-1}(x;\beta ,c)\mathcal{T}{B}_{1,n}^{j,\ell }\left(x\right)+A_{1,n}^{j,\ell }(x+{(-1)}^{\ell })\mathcal{T}{M}_{n-1}(x;\beta ,c).\hfill \end{array}$$

Then, multiplying the previous expression by x and using the structure relation (11) if $\ell =1$ and $x+\beta$, using the structure relation (10) if $\ell =2$, as well as using the recurrence relation (7), we deduce the following expressions:

$$x\nabla {\mathcal{M}}_n^{j,1}(x;\beta ,c;\lambda )=C_{1,n}^1\left(x\right)M_n(x;\beta ,c)+D_{1,n}^1\left(x\right)M_{n-1}(x;\beta ,c),$$

(35)

$$(x+\beta )\Delta {\mathcal{M}}_n^{j,2}(x;\beta ,c;\lambda )=C_{1,n}^2\left(x\right)M_n(x;\beta ,c)+D_{1,n}^2\left(x\right)M_{n-1}(x;\beta ,c),$$

(36)

$$x\nabla {\mathcal{M}}_{n-1}^{j,1}(x;\beta ,c;\lambda )=C_{2,n}^1\left(x\right)M_n(x;\beta ,c)+D_{2,n}^1\left(x\right)M_{n-1}(x;\beta ,c),$$

(37)

and

$$(x+\beta )\Delta {\mathcal{M}}_{n-1}^{j,2}(x;\beta ,c;\lambda )=C_{2,n}^2\left(x\right)M_n(x;\beta ,c)+D_{2,n}^2\left(x\right)M_{n-1}(x;\beta ,c),$$

(38)

respectively, where all the coefficients can be computed explicitly. Moreover, from (26)–(34), for $\ell =1,2$, we have:

$${\Theta }_n(x;\ell )M_n(x;\beta ,c)=B_{2,n}^{\ell }\left(x\right){\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )-B_{1,n}^{\ell }\left(x\right){\mathcal{M}}_{n-1}^{j,\ell }(x;\beta ,c;\lambda ),$$

and

$${\Theta }_n(x;\ell )M_{n-1}(x;\beta ,c)=A_{1,n}^{\ell }\left(x\right){\mathcal{M}}_{n-1}^{j,\ell }(x;\beta ,c;\lambda )-A_{2,n}^{\ell }\left(x\right){\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda ),$$

where

$${\Theta }_n(x;\ell )=det\left(\begin{array}{cc}{A}_{1,n}^{\ell }\left(x\right)& B_{1,n}^{\ell }\left(x\right)\\ A_{2,n}^{\ell }\left(x\right)& B_{2,n}^{\ell }\left(x\right)\end{array}\right),\ell =1,2.$$

After replacing the above in (35)–(38), we conclude:

$$\left({\tilde{\Theta }}_n(x;\ell )\mathcal{T}+{\Lambda }_{2,n}^{\left(1\right)}(x;\ell )\right)\left[{\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )\right]={\Lambda }_{1,n}^{\left(1\right)}(x;\ell ){\mathcal{M}}_{n-1}^{j,\ell }(x;\beta ,c;\lambda ).$$

and

$$\left({\tilde{\Theta }}_n(x;\ell )\mathcal{T}+{\Lambda }_{1,n}^{\left(2\right)}(x;\ell )\right)\left[{\mathcal{M}}_{n-1}^{j,\ell }(x;\beta ,c;\lambda )\right]={\Lambda }_{2,n}^{\left(2\right)}(x;\ell ){\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda ),$$

respectively, where

$${\tilde{\Theta }}_n(x;\ell )=\left\{\begin{array}{cc}\hfill x{\Theta }_n(x;\ell ),& \hfill \ell =1,\\ \hfill (x+\beta ){\Theta }_n(x;\ell ),& \hfill \ell =2,\end{array}\right.$$

(39)

and

$${\Lambda }_{j,n}^{\left(k\right)}(x;\ell )={(-1)}^{k}det\left(\begin{array}{cc}{C}_{k,n}^{\ell }\left(x\right)& A_{\nu ,n}^{j,\ell }\left(x\right)\\ D_{k,n}^{\ell }\left(x\right)& B_{\nu ,n}^{j,\ell }\left(x\right)\end{array}\right),\nu =1,2,k=1,2,\ell =1,2.$$

(40)

Proposition 5.

Let ${\left\{{\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )\right\}}_{n\in {\mathbb{N}}_0}$ be the sequence of monic Sobolev-type Meixner polynomials defined by (31) and let $\mathcal{I}$ be the identity operator. Then, the ladder (destruction and creation) operators $\mathfrak{a}$, ${\mathfrak{a}}^{†}$ are defined by:

$$\mathfrak{a}={\tilde{\Theta }}_n(x;\ell )\mathcal{T}+{\Lambda }_{2,n}^{\left(1\right)}(x;\ell ),$$

$${\mathfrak{a}}^{†}={\tilde{\Theta }}_n(x;\ell )\mathcal{T}+{\Lambda }_{1,n}^{\left(2\right)}(x;\ell ),$$

which verify

$$\mathfrak{a}\left({\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )\right)={\Lambda }_{1,n}^{\left(1\right)}(x;\ell ){\mathcal{M}}_{n-1}^{j,\ell }(x;\beta ,c;\lambda ),$$

(41)

$${\mathfrak{a}}^{†}\left({\mathcal{M}}_{n-1}^{j,\ell }(x;\beta ,c;\lambda )\right)={\Lambda }_{2,n}^{\left(2\right)}(x;\ell ){\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda ),$$

where ${\tilde{\Theta }}_n(x;\ell )$ and ${\Lambda }_{j,n}^{\left(k\right)}(x;\ell )$ with $j,k,\ell =1,2$ are given in (39) and (40).

Theorem 2.

The monic Sobolev-type Meixner polynomial sequence, which is orthogonal with respect to the inner product (24), fulfills the second-order difference equation:

$${\mathcal{F}}_n(x;\ell ){\mathcal{T}}^{2}y\left(x\right)+{\mathcal{G}}_n(x;\ell )\mathcal{T}y\left(x\right)+{\mathcal{H}}_n(x;\ell )y\left(x\right)=0,$$

(42)

where

$${\mathcal{F}}_n(x;\ell )=\frac{{\tilde{\Theta }}_n(x;\ell ){\tilde{\Theta }}_n(x+{(-1)}^{\ell };\ell )}{{\Lambda }_{1,n}^{\left(1\right)}(x+{(-1)}^{\ell };\ell )},$$

$$\begin{array}{cc}\hfill {\mathcal{G}}_n(x;\ell )=& \frac{{\tilde{\Theta }}_n(x;\ell )}{{\Lambda }_{1,n}^{\left(1\right)}(x+{(-1)}^{\ell };\ell )}\left(\mathcal{T}{\tilde{\Theta }}_n(x;\ell )-\frac{{\tilde{\Theta }}_n(x;\ell )\mathcal{T}{\Lambda }_{1,n}^{\left(1\right)}(x;\ell )}{{\Lambda }_{1,n}^{\left(1\right)}(x;\ell )}\right.\hfill \\ & +{\Lambda }_{2,n}^{\left(1\right)}(x+{(-1)}^{\ell };\ell ))+\frac{{\tilde{\Theta }}_n(x;\ell ){\Lambda }_{1,n}^{\left(2\right)}(x;\ell )}{{\Lambda }_{1,n}^{\left(1\right)}(x;\ell )},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\mathcal{H}}_n(x;\ell )=& \frac{{\tilde{\Theta }}_n(x;\ell )\mathcal{T}{\Lambda }_{2,n}^{\left(1\right)}(x;\ell )}{{\Lambda }_{1,n}^{\left(1\right)}(x+{(-1)}^{\ell };\ell )}-{\displaystyle \frac{{\tilde{\Theta }}_n(x;\ell ){\Lambda }_{2,n}^{\left(1\right)}(x;\ell )\mathcal{T}{\Lambda }_{1,n}^{\left(1\right)}(x;\ell )}{{\Lambda }_{1,n}^{\left(1\right)}(x;\ell ){\Lambda }_{1,n}^{\left(1\right)}(x+{(-1)}^{\ell };i)}}\hfill \\ & +{\displaystyle \frac{{\Lambda }_{1,n}^{\left(2\right)}(x;\ell ){\Lambda }_{2,n}^{\left(1\right)}(x;\ell )}{{\Lambda }_{1,n}^{\left(1\right)}(x;\ell )}}-{\Lambda }_{2,n}^{\left(2\right)}(x;\ell ),\hfill \end{array}$$

where ${\tilde{\Theta }}_n(x;\ell )$ and ${\Lambda }_{j,n}^{\left(k\right)}(x;\ell )$ with $j,k,\ell =1,2$ are given in (39) and (40).

Proof. 

From (41), we have:

$$\frac{1}{{\Lambda }_{1,n}^{\left(1\right)}(x;\ell )}\mathfrak{a}\left({\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )\right)={\mathcal{M}}_{n-1}^{j,\ell }(x;\beta ,c;\lambda ).$$

Next, applying the operator ${\mathfrak{a}}^{†}$ to both members of the previous expression, we obtain:

$${\mathfrak{a}}^{†}\left[\frac{1}{{\Lambda }_{1,n}^{\left(1\right)}(x;\ell )}\mathfrak{a}\left({\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )\right)\right]={\Lambda }_{2,n}^{\left(2\right)}(x;\ell ){\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda ).$$

Thus, by using the definitions of the operators $\mathfrak{a}$ and ${\mathfrak{a}}^{†}$, taking into account the identity:

$$\mathcal{T}\left\{{\displaystyle \frac{f\left(x\right)}{g\left(x\right)}}\right\}=\frac{g\left(x\right)\mathcal{T}f\left(x\right)-f\left(x\right)\mathcal{T}g\left(x\right)}{g\left(x\right)g(x+{(-1)}^{\ell })},$$

and after tedious calculations we obtain (42). Hence, the result follows. □

5. The $(\mathbf{2}\mathit{j}+\mathbf{3})$-Term Recurrence Relation

In this section, we find the $(2j+3)$-term recurrence relation that the sequence of monic Sobolev-type Meixner polynomials (31) fulfill. For this purpose, we use the fact, which is a straightforward consequence of (3), that the multiplication operator by ${\left(x-\alpha \right)}_{j+1}$ is a symmetric operator with respect to such a discrete Sobolev inner product. Indeed, for any $p,q\in \mathbb{P}$ and for $\ell =1$ we have the following:

$$\begin{array}{cc}\hfill {⟨{(x-\alpha )}_{j+1}p\left(x\right),q\left(x\right)⟩}_{\lambda ,j,\ell }=& ⟨{(x-\alpha )}_{j+1}{\mathbf{u}}^M,p\left(x\right)q\left(x\right)⟩\hfill \\ \hfill =& {⟨p\left(x\right),{(x-\alpha )}_{j+1}q\left(x\right)⟩}_{\lambda ,j,\ell },\hfill \end{array}$$

(43)

and for $\ell =2$:

$$\begin{array}{cc}\hfill {⟨{(x-\alpha -j)}_{j+1}p\left(x\right),q\left(x\right)⟩}_{\lambda ,j,\ell }=& ⟨{(x-\alpha -j)}_{j+1}{\mathbf{u}}^M,p\left(x\right)q\left(x\right)⟩\hfill \\ \hfill =& {⟨p\left(x\right),{(x-\alpha -j)}_{j+1}q\left(x\right)⟩}_{\lambda ,j,\ell }.\hfill \end{array}$$

(44)

Taking these identities into account and by using the three-term recurrence relation (7), we can state the following result.

Lemma 1.

The following identities related to the monic Sobolev-type Meixner polynomials hold:

$$\begin{array}{cc}\hfill {(x-\alpha )}_{j+1}{\mathcal{M}}_n^{j,1}(x;\beta ,c;\lambda )=& {\mathcal{A}}_n^1\left(x\right)M_n(x;\beta ,c)+{\mathcal{B}}_n^1\left(x\right)M_{n-1}(x;\beta ,c),\end{array}$$

(45)

$$\begin{array}{cc}\hfill {(x-\alpha -j)}_{j+1}{\mathcal{M}}_n^{j,2}(x;\beta ,c;\lambda )=& {\mathcal{A}}_n^2\left(x\right)M_n(x;\beta ,c)+{\mathcal{B}}_n^2\left(x\right)M_{n-1}(x;\beta ,c),\end{array}$$

(46)

where ${\mathcal{A}}_n^{\ell }\left(x\right)$, ${\mathcal{B}}_n^{\ell }\left(x\right)$ are polynomials which can be computed explicitly.

Theorem 3.

Let $\lambda \in {\mathbb{R}}_{+}$ and $j\in \mathbb{N}$, and let ${\left\{{\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )\right\}}_{n\in {\mathbb{N}}_0}$ be the sequence of monic Sobolev-type Meixner polynomials defined by (31).

Then, the norm of these polynomials fulfills the following identity:

$$\parallel {\mathcal{M}}_n^{j,\ell }{(x;\beta ,c;\lambda )\parallel }_{\lambda ,j,\ell }^2=\parallel M_n{(x;\beta ,c)\parallel }^2+b_n^{j,\ell }{\parallel M_{n-1}(x;\beta ,c)\parallel }^2,$$

(47)

where

$$b_n^{j,\ell }=\frac{\lambda }{\parallel M_{n-1}{(x;\beta ,c)\parallel }^2}\frac{{\mathcal{T}}^j{M}_n(\alpha ;\beta ,c){\mathcal{T}}^j{M}_n(\alpha ;\beta ,c)}{1+\lambda {\mathcal{K}}_{n,\ell }^{(j,j)}(\alpha ,\alpha )}\ge 0.$$

(48)

Proof. 

We will consider the $\ell =1$ case. The $\ell =2$ case is analogous.

By the property of orthogonality of Sobolev-type Meixner polynomials, we have:

$$\parallel {\mathcal{M}}_n^{j,\ell }{(x;\beta ,c;\lambda )\parallel }_{\lambda ,j,\ell }^2={⟨{\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda ),{(x-\alpha )}_{j+1}{\pi }_{n-j-1}\left(x\right)⟩}_{\lambda ,j,\ell },$$

for any monic polynomial $\pi$ of degree $n-j-1$. From (43), we have:

$${⟨{\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda ),{(x-\alpha )}_{j+1}\pi \left(x\right)⟩}_{\lambda ,j,\ell }={⟨{(x-\alpha )}_{j+1}{\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda ),\pi \left(x\right)⟩}_{\lambda ,j,\ell }.$$

By using the connection Formula (45) and taking into account that ${\mathcal{A}}_n^{\ell }\left(x\right)$ is a monic polynomial of degree $j+1$ and ${\mathcal{B}}_n^{\ell }\left(x\right)$ is a polynomial of degree j with the leading coefficient $b_n^{j,\ell }$, we deduce:

$$\begin{array}{cc}\hfill \parallel {\mathcal{M}}_n^{j,\ell }{(x;\beta ,c;\lambda )\parallel }_{\lambda ,j,\ell }^2=& {⟨{(x-\alpha )}_{j+1}{\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda ),\pi \left(x\right)⟩}_{\lambda ,j,\ell }\hfill \\ \hfill =& ⟨{\mathbf{u}}^{\mathtt{M}},{\mathcal{A}}_n^{\ell }\left(x\right)M_n(x;\beta ,c)\pi \left(x\right)⟩+⟨{\mathbf{u}}^{\mathtt{M}},{\mathcal{B}}_n^{\ell }\left(x\right)M_{n-1}(x;\beta ,c)\pi \left(x\right)⟩\hfill \\ \hfill =& ⟨{\mathbf{u}}^{\mathtt{M}},M_n(x;\beta ,c)x^n⟩+b_n^{j,\ell }⟨{\mathbf{u}}^{\mathtt{M}},M_{n-1}(x;\beta ,c)x^{n-1}⟩,\hfill \end{array}$$

which coincides with (47). □

Remark 3.

Observe that a direct consequence is the following:

$$\frac{\parallel {\mathcal{M}}_n^{j,\ell }{(x;\beta ,c;\lambda )\parallel }_{\lambda ,j,\ell }^2}{\parallel M_n{(x;\beta ,c)\parallel }^2}=\frac{1+\lambda {\mathcal{K}}_{n+1,\ell }^{(j,j)}(\alpha ,\alpha )}{1+\lambda {\mathcal{K}}_{n,\ell }^{(j,j)}(\alpha ,\alpha )}.$$

(49)

Theorem 4

($(2j+3)$-term recurrence relation). Let $\lambda \in {\mathbb{R}}_{+}$, $j\in {\mathbb{N}}_0$. Then, the monic Sobolev-type Meixner orthogonal polynomials sequence with respect to the inner product (24) satisfies the following $(2j+3)$-term recurrence relation:

$${(x-\alpha )}_{j+1}{\mathcal{M}}_n^{j,1}(x;\beta ,c;\lambda )={\mathcal{M}}_{n+j+1}^{j,1}(x;\beta ,c;\lambda )+\sum _{k=n-j-1}^{n+j}{c}_{n,k}^{j,1}{\mathcal{M}}_k^{j,1}(x;\beta ,c;\lambda ),$$

and

$${(x-\alpha -j)}_{j+1}{\mathcal{M}}_n^{j,2}(x;\beta ,c;\lambda )={\mathcal{M}}_{n+j+1}^{j,2}(x;\beta ,c;\lambda )+\sum _{k=n-j-1}^{n+j}{c}_{n,k}^{j,2}{\mathcal{M}}_k^{j,2}(x;\beta ,c;\lambda ),$$

where the constant coefficients $c_{n,k}^{j,\ell }$ can be explicitly computed for $\ell =1,2$.

Proof. 

In such a case, we will consider the $\ell =2$ case.

Since the Sobolev-type Meixner polynomials form a basis in $L_2\left({⟨·,·⟩}_{\lambda ,j,\ell }\right)$, if we consider the Fourier expansion of ${(x-\alpha -j)}_{j+1}{\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )$ in terms of the Sobolev-type Meixner polynomials, then:

$${(x-\alpha -j)}_{j+1}{\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )={\mathcal{M}}_{n+j+1}^{j,\ell }(x;\beta ,c;\lambda )+\sum _{k=0}^{n+j}{c}_{n,k}^{j,\ell }{\mathcal{M}}_k^{j,\ell }(x;\beta ,c;\lambda ).$$

Thus, by using the property of orthogonality of the sequence $\left\{{\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )\right\}$, we obtain:

$$c_{n,k}^{j,\ell }=\frac{{⟨{(x-\alpha -j)}_{j+1}{\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda ),{\mathcal{M}}_k^{j,\ell }(x;\beta ,c;\lambda )⟩}_{\lambda ,j,\ell }}{\parallel {\mathcal{M}}_k^{j,\ell }{(x;\beta ,c;\lambda )\parallel }_{\lambda ,j,\ell }^2},k=0,\cdots ,n+j.$$

Using (44) and the property of orthogonality of $\left\{{\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )\right\}$, we deduce that $c_{n,k}^{j,\ell }=0$ for $k=0,\dots ,n-j-2$. Observe that the rest of the coefficients can be computed by using again the same orthogonality conditions. The proof of the another identity is similar, and it will be omitted. □

6. Mehler–Heine-Type Formula

The main result of this section will be to establish a Mehler–Heine-type formula for the polynomial ${\mathcal{M}}_n^{j,\ell }(x;\beta ,c;\lambda )$ for the $\alpha \le 0$ case. The following results will allow us to prove such an expression.

Lemma 2.

Let $\beta ,c\in \mathbb{C}$, with $\left|c\right|<1$ and $-\beta \notin \mathbb{N}$, and let m be a positive integer. Then, the following limit holds:

$$\underset{n\to \infty }{lim}\frac{{\left(\beta \right)}_n{n}^m{c}^n}{(n-1)!}=0.$$

(50)

Proof. 

If we use the identity (p. 23) [21]

$$\Gamma \left(z\right)=\underset{n\to \infty }{lim}\frac{(n-1)!n^z}{{\left(z\right)}_n},$$

we deduce:

$$\underset{n\to \infty }{lim}\frac{{\left(\beta \right)}_n{n}^m{c}^n}{(n-1)!}=\frac{1}{\Gamma \left(\beta \right)}\underset{n\to \infty }{lim}{n}^{\beta +m}{c}^n.$$

(51)

Therefore, if Re$(\beta +m)>0$, then, applying to (51) the L’Hôpital’s rule several times, we obtain the desired result; otherwise, the limit is zero. Hence, the result holds. □

Lemma 3.

Let $\beta ,c\in \mathbb{R}$, with $\left|c\right|<1$, and β is not a negative integer, and let $k,j$ be integers, with $0\le k\le j$. If we set $\alpha =0$ in (25), then the following limits hold:

$$\underset{n\to \infty }{lim}{A}_{1,n}^{j,\ell }\left(x\right)=1and\underset{n\to \infty }{lim}{B}_{1,n}^{j,\ell }\left(x\right)=0,\ell =1,2.$$

(52)

Proof. 

By starting with (25) and using (21), we obtain:

$$A_{i,n}^{j,\ell }\left(x\right)=1-{\displaystyle \frac{\lambda {\mathcal{T}}^j{M}_n(\alpha ;\beta ,c)}{1+\lambda {\mathcal{K}}_{n,\ell }^{(j,j)}(\alpha ,\alpha )}}\frac{j!}{d_{n-1}^2}\sum _{k=0}^j\frac{{\mathcal{T}}^k{M}_{n-1}(\alpha ;\beta ,c)}{k!{(x-\alpha +k)}_{j+1-k}},$$

and

$$B_{i,n}^{j,\ell }\left(x\right)=\lambda {\displaystyle \frac{{\mathcal{T}}^j{M}_n(\alpha ;\beta ,c)}{1+\lambda {\mathcal{K}}_{n,\ell }^{(j,j)}(\alpha ,\alpha )}}\frac{j!}{d_{n-1}^2}\sum _{k=0}^j\frac{{\mathcal{T}}^k{M}_n(\alpha ;\beta ,c)}{k!{(x-\alpha +k)}_{j+1-k}}.$$

where $i=1,2$. Then, to prove this result, it is enough to check:

$$\underset{n\to \infty }{lim}{(1-c)}^n{a}_{k,n}^{j,\ell }=\underset{n\to \infty }{lim}{(1-c)}^n{b}_{k,n}^{j,\ell }=0,k=0,1,\cdots ,n,i=1,2,\ell =1,2,$$

where

$$a_{k,n}^{j,\ell }={\displaystyle \frac{\lambda j!{\mathcal{T}}^j{M}_n(\alpha ;\beta ,c){\mathcal{T}}^k{M}_{n-1}(\alpha ;\beta ,c)}{k!(1+\lambda {\mathcal{K}}_{n,\ell }^{(j,j)}(\alpha ,\alpha ))d_{n-1}^2}},$$

and

$$b_{k,n}^{j,\ell }={\displaystyle \frac{\lambda j!{\mathcal{T}}^j{M}_n(\alpha ;\beta ,c){\mathcal{T}}^k{M}_n(\alpha ;\beta ,c)}{k!(1+\lambda {\mathcal{K}}_{n,\ell }^{(j,j)}(\alpha ,\alpha ))d_{n-1}^2}}.$$

After a straightforward calculation, by using (15), we have that for any $0\le k\le j$

$${\mathcal{T}}^k{M}_n(\alpha ;\beta ,c)\approx {\mathcal{T}}^j{M}_n(\alpha ;\beta ,c),$$

for n large, and since $c-1<c$, then by using Lemma 2, it is clear that both limits related to such coefficients tend to zero. Hence, we deduce (52). □

Theorem 5.

Let $\beta ,c\in \mathbb{R}$, with $\left|c\right|<1$ and β is not a negative integer, and let m be a positive integer. Then, we have:

$$\underset{n\to \infty }{lim}\frac{{(1-c)}^{n+\beta +z}{\mathcal{M}}_n^{j,\ell }(z;\beta ,c;\lambda )}{{(z-n+1)}_n}=1,z\in \mathbb{C}\setminus \mathbb{N},$$

(53)

uniformly on compact subsets of the complex plane.

Proof. 

If we multiply (26) by ${(1-c)}^{n+\beta +z}/{(z-n+1)}_n$, we obtain:

$$\begin{array}{cc}\hfill \frac{{(1-c)}^{n+\beta +z}{\mathcal{M}}_n^{j,\ell }(z;\beta ,c;\lambda )}{{(z-n+1)}_n}=& A_{i,n}^{(j,\ell )}\left(z\right)\frac{{(1-c)}^{n+\beta +z}{M}_n(z;\beta ,c)}{{(z-n+1)}_n}\hfill \\ & +B_{1,n}^{(j,\ell )}\left(z\right)\frac{{(1-c)}^{n+\beta +z}{M}_{n-1}(z;\beta ,c)}{{(z-n+1)}_n}.\hfill \end{array}$$

Then, applying the previous Lemma as well as the (15), we arrive at the desired result. □

Remark 4.

Observe that we can extend some of the previous results even for $c\in \mathbb{C}$, so that $|c-1|<\left|c\right|<1$, or even into a wider region of the complex plane taking into account (6).

Finally, we show some graphical experiments of the limit function in (53) for several values of n using Mathematica software at the masspoint $\alpha =0$. Since

$${(z-n+1)}_n={(-1)}^n\frac{\Gamma (-z+n)}{\Gamma (-z)},$$

then (53) can be rewritten as:

$$\underset{n\to \infty }{lim}\frac{{(c-1)}^n{\mathcal{M}}_n^{j,\ell }(z;\beta ,c;\lambda )}{\Gamma (n-z)}=\frac{1}{{(1-c)}^{\beta +z}\Gamma (-z)},z\in \mathbb{C}\setminus \mathbb{N}.$$

(54)

The Figure 1, Figure 2 and Figure 3 show how such limit converges to the right value.

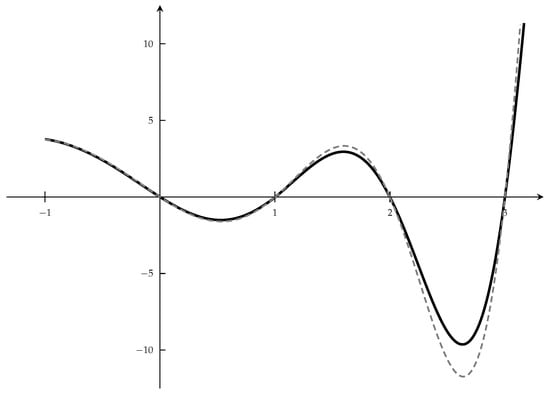
Figure 1. The gray-color curve represents the function in the left hand side in (54) for $n=50$, and the black curve is the limiting function. Data: $\beta =7$, $c=1/5$, $\lambda ={10}^{-21}$ and $j=2$.

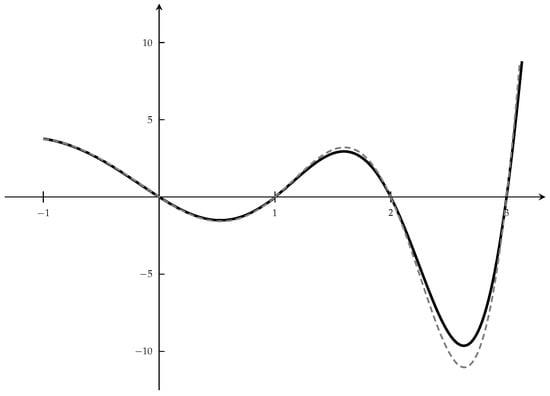
Figure 2. The gray-color curve represents the function in the left hand side in (54) for $n=70$, and the black curve is the limiting function. Data: $\beta =7$, $c=1/5$, $\lambda ={10}^{-21}$ and $j=2$.

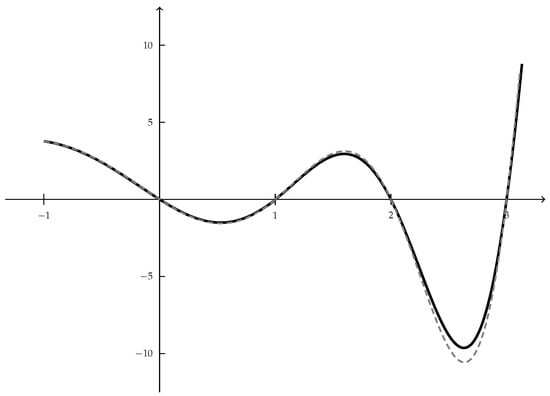
Figure 3. The gray-color curve represents the function in the left hand side in (54) for $n=100$, and the black curve is the limiting function. Data: $\beta =7$, $c=1/5$, $\lambda ={10}^{-21}$ and $j=2$.