Abstract
This research introduces three novel zeroing neural network (ZNN) models for addressing the time-varying Yang–Baxter-like matrix equation (TV-YBLME) with arbitrary (regular or singular) real time-varying (TV) input matrices in continuous time. One ZNN dynamic utilizes error matrices directly arising from the equation involved in the TV-YBLME. Moreover, two ZNN models are proposed using basic properties of the YBLME, such as the splitting of the YBLME and sufficient conditions for a matrix to solve the YBLME. The Tikhonov regularization principle enables addressing the TV-YBLME with an arbitrary input real TV matrix. Numerical experiments, including nonsingular and singular TV input matrices, show that the suggested models deal effectively with the TV-YBLME.
Keywords:
Yang–Baxter-like matrix equation (YBLME); zeroing neural network (ZNN); dynamical system; Tikhonov regularization MSC:
15A24; 65F20; 68T05
1. Introduction, Motivation, and Preliminaries
The Yang–Baxter equation [1,2] is a consistency equation that is frequently encountered in physics. The practice has shown that solving a Yang–Baxter equation is a central topic in braid groups [3], knot theory [4], statistical mechanics [5], and quantum theory [6]. Let be the input matrix and be the unknown matrix of interest in the following quadratic matrix equation:
which we refer to as a Yang–Baxter-like matrix equation (YBLME) since its form is similar to the classic parameter-free Yang–Baxter equation [1,2]. Notice that (1) has two apparent solutions, and , but its nonlinearity makes finding non-trivial solutions generally challenging. In the current research, the zeroing (or Zhang) neural network (ZNN) method was employed to solve the following time-varying YBLME (TV-YBLME):
for an arbitrary input real-valued time-varying (TV) matrix . More precisely, this research proposes and investigates one ZNN model based on an immediate solution to the TV-YBLME and two ZNN models based on indirect methods to solve the TV-YBLME, such as the model proposed in [7]. It is worth mentioning that the two models based on indirect methods arise from the splitting of the YBLME [8] and from sufficient conditions for a matrix to solve the YBLME [9]. Furthermore, unlike the models presented in [7], the three models proposed in this research solve the TV-YBLME for both nonsingular and singular square input matrices because they utilize the Tikhonov regularization procedure.
The ZNN method originated from the Hopfield neural network and was developed by Zhang et al. in [10] for producing online solutions to TV problems. Notice that the majority of ZNN-designed dynamical systems are classified as recurrent neural networks (RNNs) used to find the zeros of equations. The ZNN method, as a result of its in-depth examination, has been broadly utilized to solve a variety of TV problems; the main applications include problems of generalized inversions [11,12,13], matrix equations systems [14,15], problems of tensor and matrix inversions [16], problems of quadratic optimizations [17], linear equations systems [15,18], and various matrix function approximations [19,20].
The first step in creating the ZNN evolution is to create an appropriate error function (or Zhang function [21], or error matrix equation (EME)) that is suited to the underlying problem. The second step exploits the subsequent dynamical flow:
where denotes the time derivative, the scaling parameter is used to accelerate the convergence, whereas signifies element-wise usage of an increasing and odd activation function (AF) on . The time derivative of the time-varying matrix is the matrix . More precisely, the time derivative of represents the derivative of by the scalar t. Further, a matrix is differentiable if the derivative of each element exists at each point in its domain. Our research will explore the linear ZNN dynamics (3) that satisfy , which yield the following:
The following are the main points of this work:
- Two novel ZNN models (ZNN2 and ZNN3) are introduced based on principles to find indirect numerical solutions to the TV-YBLME for an arbitrary input real TV matrix.
- Application of the Tikhonov regularization enables usability of the proposed dynamical systems in solving the TV-YBLME with the arbitrary (regular or singular) input real TV matrix.
- In particular, the ZNN model from [7] (ZNN1), based on a straightforward error matrix corresponding to the TV-YBLME, is extended to an arbitrary input real TV matrix using the Tikhonov principle.
- Four numerical experiments, including nonsingular and singular input matrices, are presented to confirm the efficiency of the proposed dynamics in addressing the TV-YBLME solving.
Some of the generic notations are also worth mentioning: signifies the unit matrix with dimensions ; and signify the matrix consisting of zeros and ones, respectively, with dimensions ; signifies the vectorization procedure; ⊗ signifies the Kronecker product; signifies the matrix Frobenius norm; ⊙ signifies the Hadamard (or element-wise) product.
This paper is organized as follows. The ZNN1 model is defined and analyzed in Section 2. Further, ZNN2 and ZNN3 models are defined and analyzed in Section 3. The findings of four numerical experiments for solving the TV-YBLME with nonsingular and singular input matrices are presented and discussed in Section 4. Finally, Section 5 contains the final thoughts and conclusions.
2. ZNN Model Based on Direct Solution to the TV-YBLME
In this section, we introduce and analyze a ZNN model, called ZNN1, based on a direct numerical solution to the TV-YBLME for a random real TV matrix. Assuming a TV smooth matrix (2) is utilized in deploying the ZNN dynamics. That is, the ZNN1 model considers the EME used in [7]:
where is the desirable direct solution of the TV-YBLME. Additionally, the following is the time derivative of (5), i.e., :
After that, the following can be obtained by merging (5) and (6) with the ZNN method using the linear AF (4):
or equivalently:
As a result, setting:
the following ZNN model from [7] is derived:
It is observable that is a singular or nonsingular mass matrix when is singular or nonsingular, respectively. In order to extend the results from [7], the Tikhonov regularization [22] is employed to address the singularity problem in (11). If a constant diagonal matrix is chosen as the regularization matrix, (11) is changed into:
such that denotes the parameter of regularization. The ZNN model (12) is referred to as the ZNN1 model, and it may be handled effectively using a suitable ode MATLAB solver. Theorem 1 proves that the ZNN1 model exponentially converges to the theoretical solution of the TV-YBLME based on the input matrix .
Theorem 1.
Proof.
gives:
which guarantees the final negative-definiteness of . That is to say, for any , and for . In addition, as , . By the Lyapunov theory, the equilibrium point globally converges to zero for any . Therefore, we have as . So, if , then the neural state matrix is the exact solution to (2). If then and it will converge to the global asymptotic stable point; that is, we have or the neural state matrix will converge to .
We define the following Lyapunov energy function:
where refers to (5), to prove the global asymptotic convergence of the ZNN model (7). Considering the th element of , , we have the following:
Replacement of the ZNN rule (4) into the derivative of the energy function :
Furthermore, solving the linear first-order differential equation , yields readily . In other words, the matrix-valued error function is expressed explicitly as:
which indicates that exponentially converges to with the convergence rate . That is, starting from an initial state , the state matrix of (7) derived from (5) exponentially converges to .
3. ZNN Models Based on Indirect Methods for Solving the TV-YBLME
This section presents and analyzes ZNN models, ZNN2 and ZNN3, based on indirect numerical methods for solving the TV-YBLME for an arbitrary real TV matrix. It is worth mentioning that the utilized indirect numerical methods are based on splitting the YBLME [8] and the sufficient conditions for a matrix to solve the YBLME [9].
3.1. ZNN Model Based on Splitting the TV-YBLME
The YBLME splitting, as presented in [8] (Lemma 3.1), enables us to solve two matrix equations instead of one equation in (2). As a result, if is singular (in general) and is taken as , it gives a guarantee that W satisfies the conditions in [8] (Lemma 3.1). That is, a matrix W that is taken as and satisfies makes (1) consistent. More precisely, assuming a TV smooth matrix , we multiply (2) on the left by and then set , we obtain the following system of matrix equations:
where is the desirable solution to the problem. According to (13), the ZNN2 model assumes the next EME group for solving the TV-YBLME for an arbitrary :
Furthermore, the following are the time derivatives of EMEs included in (14):
Thereafter, the following can be obtained by merging (14) and (15) with the ZNN method based on the linear model (4):
The design (16) is equivalent to:
The dynamical systems involved in (17) are adjusted as follows using the Kronecker product and vectorization:
As a result, setting:
the following ZNN model is derived:
The mass matrix is singular or nonsingular if is singular or nonsingular, respectively. The Tikhonov regularization is employed to address the singularity problem, and (20) is changed into:
where denotes the parameter of regularization. The ZNN flow (21) is referred to as the ZNN2 model, and it may be handled effectively using a suitable ode MATLAB solver. Theorem 2 proves that the ZNN2 model exponentially converges to the theoretical solution of the TV-YBLME based on the input matrix .
Theorem 2.
Proof.
From [8] (Lemma 3.1), solving the matrix equation group defined in (13) results in a TV solution of the TV-YBLME. The EME is constructed as in (14), in keeping with the ZNN method and the matrix equation group (13), to produce the solution that correlates with the TV solution of the TV-YBLME based on the input matrix . Thereafter, the model (16) is derived by using the linear design formula for zeroing (14). Setting as the EME of (14) and following the same procedure as in Theorem 1, it is proved that the state matrix of (16), starting from any initial state , globally and exponentially converges to . Consequently, when , the solution of (16) converges to . Because of the derivation process, it is clear that (21) is just an equivalent vector form of (16), and it converges to . The proof has been completed. □
3.2. ZNN Model Based on Sufficient Conditions for a Solution
From [9] (Theorem 2.1), we know that if B is a matrix that satisfies , then B is a solution of (1). As a result, assuming a TV smooth matrix , we obtain the following system of matrix equations with respect to the unknown matrix :
According to (22), the ZNN3 model assumes the next EME group for solving the TV-YBLME for an arbitrary :
Furthermore, the following is the time derivative of EMEs involved in (23):
Thereafter, the following can be obtained by merging (23) and (24) with the ZNN method using the linear AF (4):
which is equivalent to:
Two dynamics involved in (26) are adjusted as follows using the Kronecker product and vectorization:
As a result, setting:
the following ZNN model is derived:
where is a singular or nonsingular mass matrix when is singular or nonsingular, respectively. The Tikhonov regularization is employed to address the singularity problem, and (29) is changed into:
where denotes the parameter of regularization. The ZNN model (30) is referred to as the ZNN3 model, and it may be handled effectively using a suitable ode MATLAB solver. Theorem 3 proves that the ZNN3 model exponentially converges to the theoretical solution of the TV-YBLME based on the input matrix .
Theorem 3.
Proof.
From [9] (Theorem 2.1), solving the matrix equation group defined in (22) results in a TV solution of the TV-YBLME. The EME is constructed as in (23), in keeping with the ZNN method and the matrix equation group (22), to produce the solution that correlates with the TV solution of the TV-YBLME based on the input matrix . After that, the model (25) is derived by using the linear design formula for zeroing (23). Setting as the EME of (23) and following the same procedure as Theorem 1, it is proved that the state matrix of (25), starting from an arbitrary initial state , globally and exponentially converges to . Consequently, when , the solution of (25) converges to the solution . In addition, we know that (30) is an equivalent form of (25) due to the derivation process, and converges to . The proof has been completed. □
4. Simulation Results
This section analyzes and compares the performance of the ZNN1 (12), ZNN2 (21), and ZNN3 (30) models in four numerical experiments, which solve the TV-YBLME with both nonsingular and singular input matrices . During the computation in all experiments, the time interval is limited to , with the ZNN gain parameter and with successive values of the Tikhonov regularization parameter equal to =1e-3, =1e-1, and =1e-8. Moreover, note that the symbols , , and in the legends in Figure 1 indicate the solutions generated by the ZNN1, ZNN2, and ZNN3 models, respectively. Finally, the MATLAB solver ode45 was employed, with the initial condition of in the ZNN2 model assigned to .
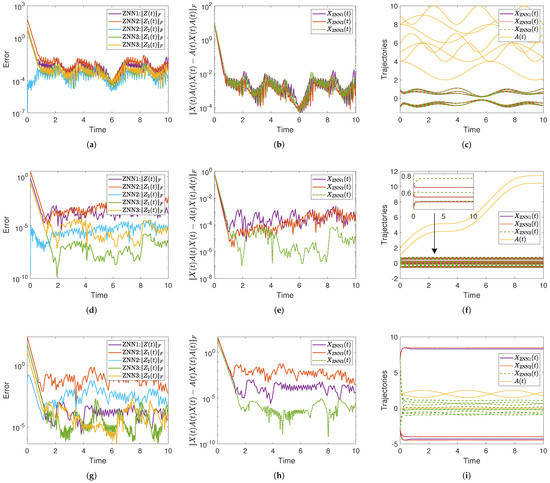
Figure 1.
The ZNN error tracking and the convergence and trajectories of the solutions in Section 4.1, Section 4.2 and Section 4.3. (a) Section 4.1: ZNN error tracking. (b) Section 4.1: Solutions convergence. (c) Section 4.1: Solutions trajectories. (d) Section 4.2: ZNN error tracking. (e) Section 4.2: Solutions convergence. (f) Section 4.2: Solutions trajectories. (g) Section 4.3: ZNN error tracking. (h) Section 4.3: Solutions convergence. (i) Section 4.3: Solutions trajectories.
4.1. Experiment 1
The TV-YBLME with the following nonsingular input matrix is solved in this simulation:
The initial condition of employed in all models tested in this example is:
4.2. Experiment 2
The input of the TV-YBLME in this experiment is the nonsingular matrix:
The initial condition for used in all models in this experiment is given by:
4.3. Experiment 3
The TV-YBLME, which involves the following singular input matrix of the rank , is solved in this simulation experiment:
The following is the initial condition of that is used in all models tested in this example:
4.4. Experiment 4
This experiment is concerned with the solution of the TV-YBLME with the singular input matrix of :
The initial conditions of (denoted by IC1: and IC2: ) equally utilized in all models compared in this example are:
4.5. Numerical Experiments Analysis—Findings and Comparison
The strengths of the ZNN1, ZNN2, and ZNN3 models for solving the TV-YBLME based on nonsingular and singular matrices are examined through four experiments presented in Section 4.1, Section 4.2, Section 4.3 and Section 4.4. The graphs generated by the ZNN1, ZNN2, and ZNN3 models are presented in Figure 1. Notice that the arrangement of Figure 1 and Figure 2 is as follows: the figures of the first column depict the tracking errors of the ZNN models, i.e., of the ZNN1 model and , of the ZNN2 and ZNN3 models; the figures of the second column depict the residual errors for solving the TV-YBLME, i.e., ; the figures in the third column depict the trajectories of solutions produced by the tested dynamical systems along with the obvious solution . Values marked with , and are appropriate to the solutions generated by ZNN1, ZNN2, and ZNN3, respectively.
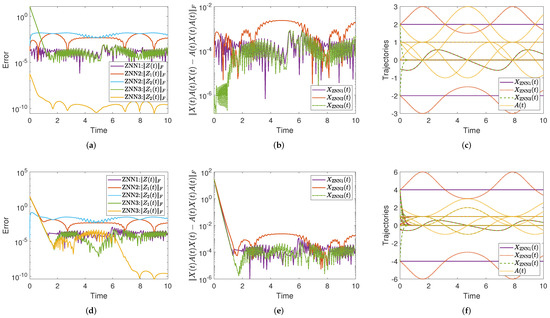
Figure 2.
The ZNN error tracking, convergence, and trajectories of the solutions in Section 4.4 under IC1 and IC2. (a) Section 4.4 under IC1: ZNN error tracking. (b) Section 4.4 under IC1: Solutions convergence. (c) Section 4.4 under IC1: Solutions trajectories. (d) Section 4.4 under IC2: ZNN error tracking. (e) Section 4.4 under IC2: Solutions convergence. (f) Section 4.4 under IC2: Solutions trajectories.
From the numerical experience of this section, the following observations may be noted. Overall, the ZNN3 model’s error functions have lower values than the ZNN1 and ZNN2 models’ error functions in all experiments, as depicted in Figure 1a,d,g and Figure 2a,d, while the ZNN2 model’s error function has the fastest convergence speed in Section 4.1, Section 4.2 and Section 4.3, as depicted in Figure 1a,d,g, respectively. The values of the residual norm show that the tested models have similar convergence speeds in Section 4.1, Section 4.2 and Section 4.3 as depicted in Figure 1b,e,h, respectively, while the ZNN3 model has the fastest convergence speed in Section 4.4, as depicted in Figure 2b. In addition, the residual errors of the ZNN3 model receive lower values than the ZNN1 and ZNN2 models in Section 4.2, Section 4.3 and Section 4.4, as depicted in Figure 1e and Figure 2b,e, respectively. For the initial conditions used, all the ZNN models produce the same solution in Section 4.1, the ZNN1 and ZNN2 models produce the same solution in Section 4.2, while all the ZNN models produce different solutions in Section 4.3 and Section 4.4. Furthermore, all the ZNN models produce different solutions in Section 4.4 under the initial conditions IC1 and IC2. The general conclusion is that the change of the initial value in the system dynamics initiates a different solution. This is conditioned by the fact that the closest solution can change with respect to different initial states. It is worth noting—in Figure 1c,f,i and Figure 2c,f—that all the solutions produced by the ZNN models are different from the obvious solution .
The following are some general conclusions based on the presented simulation experiments. The ZNN3 model, which is based on an indirect method for solving the TV-YBLME, performs better than the ZNN1 and ZNN2 models, based on direct and indirect methods for solving the TV-YBLME, respectively. Furthermore, the ZNN3 model provides the smallest Frobenius norm for both the residual errors and error functions. However, because all models usually produce different TV-YBLME solutions for the same initial conditions, we can conclude that all models are efficient for addressing the TV-YBLME. It is also worth noting that the bigger the value of the acceleration parameter , the quicker the models will converge.
5. Conclusions
This study addresses the problem of solving the TV-YBLME for a random real TV matrix by employing the ZNN neural design. As a result, three ZNN models were defined, analyzed, and compared. The first ZNN model, ZNN1, exploits an immediate method to solve the TV-YBLME from [7], whereas the other two, ZNN2 and ZNN3, utilize indirect methods to solve the TV-YBLME based on the fundamental properties of the Yang–Baxter matrix equation. According to four numerical experiments, all models efficiently address the TV-YBLME, including nonsingular and singular input matrices. However, the ZNN3 model converges to the TV-YBLME solution quicker than the ZNN1 and ZNN2 models. One interesting observation is that the dynamics based on the indirect approaches achieve a quicker convergence (ZNN2) and smallest residuals (ZNN3). Furthermore, because all three tested models usually produce different TV-YBLME solutions for the same initial conditions, we can conclude that all models are efficient and valuable for addressing the TV-YBLME.
The following are possible research topics:
- Research involving the fuzzy control parameters in the ZNN design. Corresponding results are presented in [23,24,25,26]. Future research could use cautiously selected fuzzy parameters to specify a certain rate of adaptation in the ZNN dynamics and corresponding improvements.
- Since all types of noise significantly impact the ZNN model accuracies, noise sensitivity is a shortcoming of the proposed ZNN1, ZNN2, and ZNN3 models. As a result, future studies might concentrate on adapting the ZNN1, ZNN2, and ZNN3 models to a noise-handling ZNN dynamical system class. Such research will be a continuation of [27] from the constant matrix case to the time-varying case and from the direct ZNN model to various ZNN models.
- One could expect that further developments of ZNN evolutions (arising from different properties of solutions to the Yang–Baxter equation) will be possible.
Author Contributions
W.J.: validation, investigation. C.-L.L.: formal analysis, investigation. V.N.K.: conceptualization, methodology, validation, formal analysis, investigation, writing—original draft. S.D.M.: conceptualization, methodology, validation, formal analysis, investigation, writing—original draft. P.S.S.: conceptualization, methodology, validation, formal analysis, investigation, writing—original draft. T.E.S.: methodology, formal analysis, investigation. All authors have read and agreed to the published version of the manuscript.
Funding
Predrag Stanimirović is supported by the Ministry of Education, Science, and Technological Development, Republic of Serbia, grant no. 451-03-68/2022-14/200124, and by the Science Fund of the Republic of Serbia, (no. 7750185, Quantitative Automata Models: Fundamental Problems and Applications—QUAM).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, C.N. Some exact results for the many-body problem in one dimension with repulsive delta-function interaction. Phys. Rev. Lett. 1967, 19, 1312–1315. [Google Scholar] [CrossRef]
- Baxter, R.J. Partition function of the eight-vertex lattice model. Ann. Phys. 1972, 70, 193–228. [Google Scholar] [CrossRef]
- Matsumoto, D.K.; Shibukawa, Y. Quantum Yang-Baxter equation, braided semigroups, and dynamical Yang-Baxter maps. Tokyo J. Math. 2015, 38, 227–237. [Google Scholar] [CrossRef]
- Przytycki, J.H. Knot theory: From Fox 3-colorings of links to Yang-Baxter homology and Khovanov homology. In Knots, Low-Dimensional Topology and Applications; Springer: Cham, Switzerland, 2019; Volume 284, pp. 115–145. [Google Scholar] [CrossRef] [Green Version]
- Vieira, R.S.; Lima-Santos, A. Solutions of the Yang-Baxter equation for (n + 1) (2n + 1)-vertex models using a differential approach. J. Stat. Mech. 2021, 2021, 053103. [Google Scholar] [CrossRef]
- Tsuboi, Z. Quantum groups, Yang-Baxter maps and quasi-determinants. Nucl. Phys. B 2018, 926, 200–238. [Google Scholar] [CrossRef]
- Zhang, H.; Wan, L. Zeroing neural network methods for solving the Yang-Baxter-like matrix equation. Neurocomputing 2020, 383, 409–418. [Google Scholar] [CrossRef]
- Kumar, A.; Cardoso, J.R.; Singh, G. Explicit solutions of the singular Yang-Baxter-like matrix equation and their numerical computation. Mediterr. J. Math. 2022, 19, 85. [Google Scholar] [CrossRef]
- Ding, J.; Zhang, C.; Rhee, N.H. Further solutions of a Yang-Baxter-like matrix equation. East Asian J. Appl. Math. 2013, 3, 352–362. [Google Scholar] [CrossRef]
- Zhang, Y.; Ge, S.S. Design and analysis of a general recurrent neural network model for time-varying matrix inversion. IEEE Trans. Neural Netw. 2005, 16, 1477–1490. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stanimirović, P.S.; Katsikis, V.N.; Zhang, Z.; Li, S.; Chen, J.; Zhou, M. Varying-parameter Zhang neural network for approximating some expressions involving outer inverses. Optim. Methods Softw. 2020, 35, 1304–1330. [Google Scholar] [CrossRef]
- Kornilova, M.; Kovalnogov, V.; Fedorov, R.; Zamaleev, M.; Katsikis, V.N.; Mourtas, S.D.; Simos, T.E. Zeroing neural network for pseudoinversion of an arbitrary time-varying matrix based on singular value decomposition. Mathematics 2022, 10, 1208. [Google Scholar] [CrossRef]
- Simos, T.E.; Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S.; Gerontitis, D. A higher-order zeroing neural network for pseudoinversion of an arbitrary time-varying matrix with applications to mobile object localization. Inf. Sci. 2022, 600, 226–238. [Google Scholar] [CrossRef]
- Stanimirović, P.S.; Katsikis, V.N.; Li, S. Integration enhanced and noise tolerant ZNN for computing various expressions involving outer inverses. Neurocomputing 2019, 329, 129–143. [Google Scholar] [CrossRef]
- Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S.; Zhang, Y. Solving complex-valued time-varying linear matrix equations via QR decomposition with applications to robotic motion tracking and on angle-of-arrival localization. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–10. [Google Scholar] [CrossRef]
- Ma, H.; Li, N.; Stanimirović, P.S.; Katsikis, V.N. Perturbation theory for Moore–Penrose inverse of tensor via Einstein product. Comput. Appl. Math. 2019, 38, 111. [Google Scholar] [CrossRef]
- Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S.; Li, S.; Cao, X. Time-varying mean-variance portfolio selection problem solving via LVI-PDNN. Comput. Oper. Res. 2022, 138, 105582. [Google Scholar] [CrossRef]
- Stanimirović, P.S.; Katsikis, V.N.; Li, S. Hybrid GNN-ZNN models for solving linear matrix equations. Neurocomputing 2018, 316, 124–134. [Google Scholar] [CrossRef]
- Katsikis, V.N.; Stanimirović, P.S.; Mourtas, S.D.; Li, S.; Cao, X. Generalized Inverses: Algorithms and Applications; Mathematics Research Developments; Chapter Towards Higher Order Dynamical Systems; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2021; pp. 207–239. [Google Scholar]
- Katsikis, V.N.; Mourtas, S.D.; Stanimirović, P.S.; Zhang, Y. Continuous-time varying complex QR decomposition via zeroing neural dynamics. Neural Process. Lett. 2021, 53, 3573–3590. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, D. Zhang Functions and Various Models; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Khalaf, G.; Shukur, G. Choosing ridge parameter for regression problems. Commun. Stat. Theory Methods 2005, 34, 1177–1182. [Google Scholar] [CrossRef]
- Dai, J.; Chen, Y.; Xiao, L.; Jia, L.; He, Y. Design and analysis of a hybrid GNN-ZNN model with a fuzzy adaptive factor for matrix inversion. IEEE Trans. Ind. Inform. 2022, 18, 2434–2442. [Google Scholar] [CrossRef]
- Jia, L.; Xiao, L.; Dai, J.; Cao, Y. A novel fuzzy-power zeroing neural network model for time-variant matrix Moore-Penrose inversion with guaranteed performance. IEEE Trans. Fuzzy Syst. 2021, 29, 2603–2611. [Google Scholar] [CrossRef]
- Jia, L.; Xiao, L.; Dai, J.; Qi, Z.; Zhang, Z.; Zhang, Y. Design and application of an adaptive fuzzy control strategy to zeroing neural network for solving time-variant QP problem. IEEE Trans. Fuzzy Syst. 2021, 29, 1544–1555. [Google Scholar] [CrossRef]
- Katsikis, V.N.; Stanimirović, P.S.; Mourtas, S.; Xiao, L.; Karabašević, D.; Stanujkić, D. Zeroing Neural Network with fuzzy parameter for computing pseudoinverse of arbitrary matrix. IEEE Trans. Fuzzy Syst. 2021, 1. [Google Scholar] [CrossRef]
- Shi, T.; Tian, Y.; Sun, Z.; Liu, K.; Jin, L.; Yu, J. Noise-tolerant neural algorithm for online solving Yang–Baxter-type matrix equation in the presence of noises: A control-based method. Neurocomputing 2021, 424, 84–96. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).