Abstract
Integrating digital technologies into mathematics teaching remains a complex task for teachers, despite its recognized potential to enhance learning. Research on teacher professional development (TPD) for integrating technology in the mathematics classroom is therefore essential to inform the design of effective TPD programs. This narrative review aims to support researchers by providing an overview of theoretical frameworks employed in the literature on TPD for teaching mathematics with technology. Specifically, we address the following research questions: what theoretical frameworks are employed in research that focuses on TPD for teaching mathematics with technology? In what ways are these theoretical frameworks used? Drawing from a set of studies identified in a recent systematic review, we identify ten theoretical frameworks and classify their use into three categories: design tools, analytical tools, and instructional tools. While most frameworks are used to inform TPD design and data analysis, their use as reflective tools with teachers is less common. This review contributes to clarifying the role of theoretical frameworks in the field and suggests future research directions, including the exploration of their metacognitive potential in TPD settings and the comparison of multiple frameworks through networking.
1. Introduction
Digital technologies have proven to be effective in supporting students’ learning in the mathematics classroom, for example by providing new kinds of representations of mathematical objects and enhancing active learning opportunities (Hegedus et al., 2017). However, the potential for technology use remains largely unexploited given that integrating technology in mathematics teaching is challenging and complex. (Drijvers, 2019). This complexity has led to an extensive body of literature on the topic, including a substantial number of review studies. For example, a search on Scopus using the keywords “digital technology,” “review,” and “mathematics education” yields 245 results. Some of these reviews focus on specific technologies used in mathematics teaching. For instance, Villa-Ochoa and Suárez-Téllez (2022) present a literature review spanning 8 years that explores the use of Computer Algebra Systems and Dynamic Geometry Environments, aiming to examine their role in mathematics teaching and student learning.
Other reviews address the broader impact of digital technology on student learning in mathematics. Hillmayr et al. (2020), for example, conducted a meta-analysis of studies published since 2000 that compare the learning outcomes of students using digital tools with those taught without them, specifically in secondary school mathematics and science. Their findings indicate an overall positive effect of digital tools on student learning. Notably, the impact is stronger when digital technologies are used in combination with other instruction methods. Furthermore, drawing on the classification of digital tools by Nattland and Kerres (2009), the review highlights that intelligent tutoring systems and simulations (such as dynamic mathematical tools) tend to produce more significant learning gains than hypermedia systems, that simply provide encyclopedic content via hyperlinks. Importantly, the review also underscores the role of teacher training in amplifying the benefits of digital technology on learning outcomes. This conclusion aligns with the findings of Clark-Wilson et al. (2014) and Drijvers (2019), who emphasize the central role of the teacher in successful technology integration in mathematics classrooms, thereby reinforcing the need for well-designed teacher professional development (TPD) programs.
In this direction, another strand of review literature focuses specifically on the preparation of mathematics teachers to integrate technology into their teaching. Dockendorff and Gomez Zaccarelli (2024), for instance, aim to systematize the core findings of studies that can inform the education of prospective mathematics teachers in relation to technology use. Through an inductive approach, the authors identify six categories that organize these findings, establishing new connections among previously isolated results. Still within the scope of teacher training for technology-enhanced mathematics teaching, a recent systematic review by Thurm et al. (2024) investigates the literature published between 2010 and 2021 on TPD programs in this domain. Their analysis focuses on the formats adopted, the design principles guiding effective TPD, and how policy, culture, and school context are taken into account. The authors conclude with several recommendations for future research, including the need for more design-based studies and for investigations into the classroom experiences of pre-service teachers.
In this work, which takes the form of a narrative review, we aim to guide, and support researchers interested in contributing to this field by providing an overview on the use of theoretical frameworks in research concerning TPD programs for teaching mathematics with technology. We decided to focus on theoretical frameworks because we share the value of theories in mathematics education research as “tools which help to produce knowledge about what, how and why […] things happen in a phenomenon of mathematics education.” (Prediger et al., 2008, p. 168). Furthermore, while Thurm et al. (2024) identify the TPACK model as the predominant theoretical framework in studies of TPD for teaching mathematics with technology, to the best of our knowledge, no existing review has specifically examined the use of theoretical frameworks in this area of research.
2. Methods
This work resorts the narrative review methodology. As outlined by Demiris et al. (2018), a narrative review represents an approach to synthesizing findings from multiple studies, aiming to generate conclusions informed also by the researchers’ own perspectives. Typically, the process of writing a narrative review follows four key phases:
- -
- Phase 1 involves performing a search of the literature contained in specific databases, explicitly excluding sources lacking clear identification.
- -
- Phase 2 entails selecting appropriate keywords to refine the search, ensuring alignment with the research question and facilitating the retrieval of additional relevant studies with respect to the research question.
- -
- Phase 3 encompasses the revision of the abstracts and full texts of the selected articles to determine their relevance to the research question, ultimately choosing those that most directly contribute to the topic.
- -
- Phase 4 involves integrating and interpreting the results of the chosen studies.
Despite the limitations of the narrative review methodology, such as the lack of a systematic approach and the absence of specific protocols for selecting the articles to be included, we chose to conduct a narrative review because of the qualitative nature of its results, which allow for the opportunity to gain in-depth information (Dochy et al., 2003). Furthermore, we resorted to this methodology, because, as highlighted in Sukhera (2022), it proved to be useful for exploring robustly researched fields using new perspectives, as is the focus on the use of theory in the thoroughly investigated topic of teacher training for technology-enhanced mathematics teaching.
Concerning phase 1, we considered the articles contained in the Appendix 3 of Thurm et al. (2024, pp. 910–915) as the database because it is particularly suited for the narrative synthesis we conduct for the following criteria: (i) it is recent; (ii) it is thematically focused; (iii) it is high-quality, since it considers high-ranking journals. Since we are interested in exploring the theoretical frameworks employed in the recent literature on TPD programs for teaching mathematics with technology, in phase 2, we began by analyzing the abstracts to identify keywords referring to a theoretical framework. We employed both general keywords (e.g., conceptual framework, theoretical framework, framework) and terms associated with specific theoretical models (e.g., TPACK, Pedagogical Technology Knowledge). In cases where the abstract did not include any explicit reference to the theoretical framework, we searched for such references within the main body of the article by locating a dedicated section discussing the framework. During phase 3 of the narrative review, we classified the articles based on the theoretical framework they employed. For each identified framework, we made explicit three dimensions: (i) whether each framework is specifically related to the use of technology (e.g., Technological Pedagogical Content Knowledge (TPACK)) or not (e.g., the Documentational Approach to Didactics); (ii) whether it was developed within the field of mathematics education research (e.g., Pedagogical Technology Knowledge (PTK)) or within the broader field of education (e.g., TPACK); and (iii) whether the framework supports the exploration of the cognitive domain (e.g., knowledge) or the affective domain (e.g., beliefs, emotions).
Focusing on phase 4 (integrating and interpreting the results of the chosen studies), it is important to clarify that this article does not aim to focus on the findings reported in the selected studies. Rather, the integration and discussion will center on the theoretical frameworks and the various ways in which they were employed in the literature. In particular, by examining the full texts of the articles through a holistic approach (Lieblich et al., 1998), we inductively identified possible uses for the theoretical framework. It is worth noting that the expression “use of theoretical framework” is intentionally employed here in a broad and exploratory sense, reflecting our goal of uncovering these uses from the data, rather than imposing pre-established categories. It is important to note that the association of a theoretical framework with a specific usage category is established even if only a single study within the database demonstrates that particular use. According to the methodology described in this section, we address the following research questions:
(RQ1) What theoretical frameworks are employed in research that focuses on TPD for teaching mathematics with technology?
(RQ2) In what ways are these theoretical frameworks used?
3. Data Analysis and Findings
We recall that the database for the narrative review identified in phase 1 is the Appendix 3 of Thurm et al. (2024, pp. 910–915), which contains 72 works. Phase 2 of the review, described in the previous section, allowed to include all the articles of the database in the subsequent phases since all of them appeared to be founded on a theoretical framework. Indeed, all the articles met the criteria outlined in the previous section: they either contained in the abstract keywords referring to a theoretical or conceptual framework or included a dedicated section in the body of the article. Phase 3 of the review allowed to identify ten theoretical frameworks, while phase 4 pointed out three distinct usage modes for these frameworks. In the following, we present our data analysis in detail. Each section includes a concise description of the framework, with particular attention to the three dimensions outlined in the previous section. We also provide one or more examples of articles that illustrate how the theoretical framework discussed in that section has been used in the literature.
3.1. Technological Pedagogical Content Knowledge (TPACK)
The Technological Pedagogical Content Knowledge (TPACK) model (Mishra & Koehler, 2006) was not proposed in the context of mathematics education but in a broader educational context. The model builds upon Shulman’s (1986) concept of Pedagogical Content Knowledge, extending it to describe how teachers integrate technology into their teaching practices. Mishra and Koehler (2006) emphasize the intricate relationships among three fundamental components of the learning environment: Content (C), Pedagogy (P), and Technology (T) (see Figure 1). Content Knowledge (CK) refers to teachers’ understanding of the subject matter they teach. It encompasses essential facts, theories, and procedures within a specific discipline.
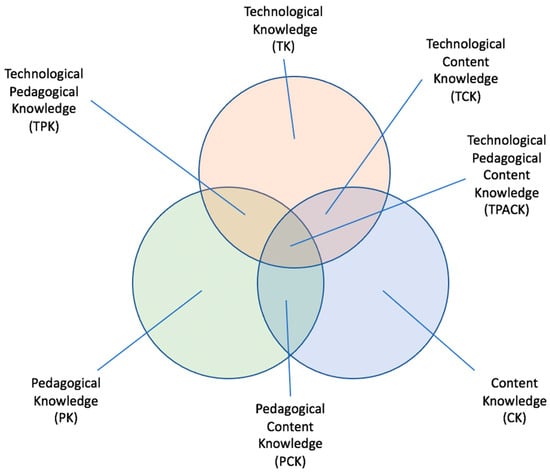
Figure 1.
The Technological Pedagogical Content Knowledge (TPACK) model (Mishra & Koehler, 2006).
Pedagogical knowledge (PK), on the other hand, pertains to a profound understanding of teaching methodologies, instructional strategies, and classroom management techniques. When CK and PK intersect, they form Pedagogical Content Knowledge (PCK), which involves knowing how to tailor teaching strategies to specific content areas, as well as structuring subject matter to optimize learning outcomes. PCK also encompasses an awareness of students’ beliefs—whether beneficial or obstructive to learning (Mishra & Koehler, 2006). Technological Knowledge (TK) involves familiarity with both traditional and digital tools. Given that technology is constantly evolving, TK is not static but requires ongoing learning. Technological Content Knowledge (TCK) explores the interplay between technology and subject matter, including how technological advancements reshape content and which digital tools best facilitate instruction in specific fields, such as mathematics. Meanwhile, Technological Pedagogical Knowledge (TPK) focuses on understanding how technology influences teaching and learning, as well as recognizing both its potential and its limitations in various pedagogical contexts. This aspect is especially significant since many digital tools are not originally designed for educational purposes. Teachers must therefore develop the ability to go beyond standard functionalities and adapt technologies to serve instructional goals. Ultimately, TPACK represents a distinct and integrated form of knowledge that transcends the three core components. As Koehler et al. (2013, p. 16) describe, “TPACK is the basis of effective teaching with technology, requiring an understanding of the representation of concepts using technologies, pedagogical techniques that use technologies in constructive ways to teach content [...].”
We now provide two examples of articles belonging to the database which allow us to highlight in what ways the TPACK framework has been used in the literature on TPD programs for teaching mathematics with technology.
Bowers and Stephens (2011) aimed at exploring how the TPACK framework can be used in a TPD program for prospective teachers for integrating technology in mathematics teaching, with “geometer’s sketchpad” as a technological tool. On the one hand, the authors proposed the TPACK framework as an instructional tool, for supporting teachers in integrating technology. On the other hand, TPACK was employed as a framework for analyzing the lesson plans teachers designed during the TPD program to investigate their progression toward the development of TPACK. As an instructional tool, the TPACK framework was explicitly presented to the teachers through literature results. Furthermore, teachers were involved in a whole classroom discussion in which they had to provide examples and descriptions of experiences that they thought they could fit in each of the components of TPACK. In a subsequent discussion, the teachers’ proposals were further shortened, clarified and classified to formulate criteria for the different components of TPACK. This shared operationalization of the different components of TPACK was used by the authors to analyze the lesson plans prepared by the teachers.
In Akkoç (2015), the TPACK framework was employed as a guiding tool for designing a TPD program aimed at enhancing pre-service teachers’ assessment skills, having the development of their skills to use formative questioning in computer-based learning environments as the main goal. The core focus of the study was thus on investigating the efficacy of the program in pursuing this goal. The TPACK framework strongly informed the design of the program, organized into three distinct workshops. The first, called the PCK workshop, provided an overview of assessment principles, offering examples of both summative and formative assessment. Additionally, it engaged teachers in lesson design activities centered on a specific mathematical topic. The second, named the TK workshop, involved teachers in hands-on group activities designed to familiarize them with educational software. Finally, the third workshop, the TPCK workshop, focused on pedagogical strategies for integrating technology, with a special emphasis on assessment. During this final workshop, pre-service teachers were encouraged to reflect on how technology and questioning techniques could be leveraged for both formative and summative assessment, aligning with the objectives set in the lesson designs created during the first workshop. While the TPACK framework was used to design the course, data analysis was informed by a different theoretical framework—Pierce and Stacey’s (2004) “technical and mathematical aspects of effective use of technology.” According to this framework, using technology for mathematics requires both traditional mathematical knowledge and knowledge of technology. These two domains of knowledge are interconnected through the technical aspects of effective use of technology, which refer to software-related skills rather than hardware operation (e.g., interpreting software outputs, effectively utilizing software syntax). Accordingly, in analyzing the questions posed by pre-service teachers in the lesson plans and teaching notes developed throughout the workshops, Akkoç (2015) categorized these questions as either “mathematical” or “technical.”
From the articles discussed above, we can identify three distinct usage modes for the TPACK framework: for providing direction for the design of the TPD program, for supporting the data analysis and as an instructional resource to support teachers in integrating technology.
3.2. Digital Content Evalutation (DCE) Competency
Digital Content Evaluation (DCE) competency is defined in Kim et al. (2017) as “a teacher’s capacity to use knowledge and skills in technology, pedagogy, content, and academic standards as well as affect-motivation to evaluate digital content.” The authors proposed a model for DCE that includes several components (see Figure 2). First, DCE appears to be closely tied to knowledge as conceptualized in the TPACK framework, described in the previous section. The authors argued that, since evaluation occupies the highest level in the hierarchical organization of cognitive building blocks according to the taxonomy proposed in Bloom (1956), it requires other thinking skills. For this reason, DCE draws upon prior knowledge, which the authors conceptualized through TPACK. Moreover, they highlighted how evaluation tasks involving digital content have the potential to enhance teachers’ awareness of the interaction between the different components of TPACK. Second, the authors presented DCE as being connected to teachers’ prior experience. In particular, they noted that previous studies had emphasized the influence of prior experience on TPACK development and on the implementation of technology. Given the role of TPACK in the development of DCE mentioned earlier, the authors emphasized how teachers’ previous experience with technology—especially professional development for technology integration and prior use of technology—affects DCE. Finally, the authors linked DCE competency to the construct of motivation, as understood within the expectancy–value framework (Eccles & Wigfield, 1995). Specifically, they argued that evaluation requires self-regulatory cognitive effort, and, thus, motivation is a fundamental enabler in the development of DCE competency. Furthermore, improvements in TPACK resulting from engagement in DCE tasks could in turn enhance teachers’ perception of their own progress, thereby boosting their motivation (Kim et al., 2017).
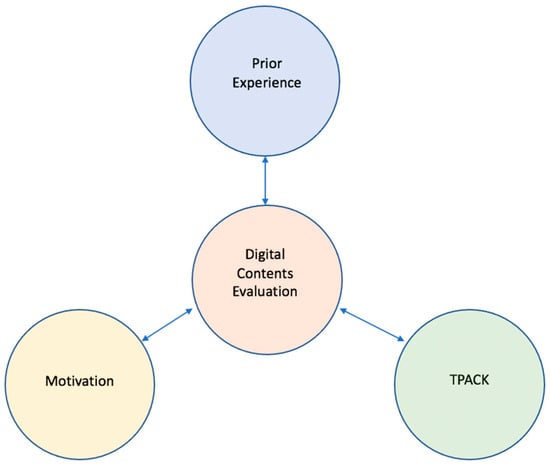
Figure 2.
The Digital Contents Evaluation competency model (Kim et al., 2017).
In Kim et al. (2017), the authors aimed to propose a model for DCE competency development within the context of a TPD program. It is important to note that the study was not limited to mathematics teachers. However, a significant portion of the sample (23.5%) consisted of mathematics teachers. The DCE competency framework informed both the design of the TPD program and the data analysis. Regarding the design, the course included face-to-face workshops and blended learning modules on TPACK—a key component of DCE competency—as well as hands-on activities involving the evaluation of existing digital content, supported by content specialists, over an eight-month period.
As for the data analysis, the authors collected various types of data: on the one hand, interviews and self-reflections were analyzed qualitatively through thematic analysis; on the other hand, structured questionnaires—analyzed quantitatively using cluster analysis—were administered. These questionnaires included scales to measure TPACK and motivation: the TPACK scale by Schmidt et al. (2009) and the expectancy–value scale (Eccles & Wigfield, 1995). The thematic analysis allowed to identify four distinct levels in the development of DCE competency, which the authors termed “familiarization”, “utilization”, “integration”, and “reorientation”. These levels were subsequently confirmed by the cluster analysis. Each level has distinct characteristics in terms of the components of DCE competency. For instance, the “familiarization” level is characterized by a low level of TPACK—partly due to limited experience in prior TPD programs—and a low perceived utility of the evaluation activity. In contrast, teachers at the “integration” level possess advanced TPACK, which they had either developed through previous TPD programs or improved through the evaluation activities during the TPD program. At this level, the perceived utility of the evaluation activity is also higher, as is the teachers’ expectancy for success in such tasks.
We can summarize that the DCE competency model has been used both as a tool for the design of the TPD program and for the data analysis.
3.3. Pedagogical Technology Knowledge (PTK)
Pedagogical Technology Knowledge (PTK) is a framework introduced by Thomas and Hong (2005) to describe teachers’ progress in integrating technology within the mathematics classroom. The framework was constructed by considering various factors that influence mathematics teachers’ use of technology, as identified by previous research in mathematics education. In particular, three key factors shape teachers’ PTK. The first is Mathematical Knowledge for Teaching (MKT) (Ball et al., 2005), which builds upon Shulman’s (1986) framework of Pedagogical Content Knowledge. The second factor is teachers’ instrumental genesis (Rabardel, 1995) in relation to digital technologies, with particular emphasis on the process through which technological tools are transformed into instruments that enhance students’ conceptual understanding of mathematics. The third factor corresponds to teachers’ orientations, as defined in the Resources, Orientations, and Goals (ROG) framework proposed by Schoenfeld (2011). In the ROG framework, teaching is conceived as a goal-oriented practice, where decision-making is shaped by the interplay between resources, goals, and orientations. Within PTK, the focus is placed on orientations, understood as teachers’ dispositions, beliefs, values, tastes, and preferences. These orientations contribute to goal setting and resource selection—such as knowledge—to support teaching goals. Among orientations specifically related to technology use, Thomas and Palmer (2014) highlighted teachers’ confidence in using technology and the value they assign to it.
In Thurm and Barzel (2020), the PTK framework is applied as an analytical lens in a quasi-experimental quantitative study aimed at evaluating the effectiveness of a teacher professional development (TPD) program. Given the centrality of orientations—particularly beliefs—within the PTK framework, the authors assessed the program’s effectiveness by measuring changes in specific teacher beliefs: beliefs about teaching mathematics with technology, self-efficacy beliefs, and epistemological beliefs. In particular, beliefs about teaching with technology were examined using a dedicated questionnaire, which was administered to both an experimental group and a control group. The PTK framework and the aforementioned categories of beliefs also informed the design of the TPD program. To foster positive beliefs about teaching mathematics with technology, participating teachers were engaged in activities showcasing the potential of technology to support student learning. The program also included try-out phases, allowing teachers to observe these benefits with their own students. To enhance teachers’ self-efficacy, teachers were provided with opportunities to solve tasks and design lessons incorporating technology. The try-out phases were also intended to facilitate mastery experiences, which are known to promote a stronger sense of self-efficacy. Lastly, with respect to epistemological beliefs, the program was designed to encourage constructivist beliefs and a dynamic view of mathematics—both commonly associated in the literature with the effective use of technology in the mathematics classroom.
In summary, two different usage modes for the PTK framework have been identified: as a support for the design phase and as a basis for data analysis.
3.4. Documentational Approach to Didactics (DAD)
The Documentational Approach to Didactics framework does not specifically deal with technology. In fact, it focuses, more in general, on explaining the interaction between teachers and resources, where resources can comprise, for example, textbooks, a piece of software, a discussion with a colleague (Gueudet & Trouche, 2009). The teacher is viewed as a designer who is involved in the documentational work, defined as the process of searching for resources, adapting them, enacting and reviewing them. During the documentational work, the teacher produces documents, which are a combination of resources and professional knowledge (Gueudet & Trouche, 2009). This process of producing documents is central in TPD and it is called documentational genesis. Thus, in this perspective, supporting and fostering teachers’ documentational genesis is a key factor for TPD. Among the different ways to support documentational genesis, there is the design of meta-resources, where a meta-resource is defined as “a resource that helps to design other resources by creating a reflective posture on the documentation work to be conducted, or on its effects” (Prieur, 2016, p. 75).
In Gueudet et al. (2021), using a Design Research approach, the authors aimed at fostering teachers’ documentational genesis aligned with two goals of a new curriculum in France related to Digital Technologies and students’ autonomy. In particular, the object of the research was the design and evaluation of a meta-resource for supporting teachers in evaluating the quality of existing lesson plans and in designing lesson plans from scratch. Both the aim and the object of the research were strongly informed by the Documentational Approach to Didactics, since both of them were formulated in terms of construct and processes characteristic of this framework. The research was carried out in two cycles. At the beginning of the first cycle, a first version of the meta-resource, composed of 5 categories, was proposed by mathematics education researchers. For each category a list of criteria was developed. The authors, in particular, affirmed that “the documentational approach was the central inspiration for category 2”, namely “The lesson plan is easy to adapt for the specific context of the user and to implement”. Even if in the article it is not made explicit how the DAD theoretical framework was operationalized to get to the formulation of the criteria, we can argue that DAD was employed as a design tool.
3.5. Pedagogical Design Capacity (PDC)
The framework of Pedagogical Design Capacity (PDC) was introduced by Brown (2009) as a theoretical construct referring to a teacher’s capacity to effectively use and transform curricular resources, as well as to design new ones, in order to teach mathematics. Brown (2009) identified a spectrum of ways in which teachers engage with curricular materials, ranging from “offloading”, to “adapting”, and finally to “improvising”. In the first mode, teachers remain closely aligned with the curricular material. In the second, they modify the material to meet specific instructional goals. In the third mode, teachers design instructions without specific guidance from the materials. In their theoretical work, Pepin et al. (2017) aimed to deepen the understanding of the PDC. Drawing on the literature, they proposed three dimensions to study this construct with a focus on teachers’ use of digital curricular resources, where the term “resources” was used by the authors in the sense of the Documentational Approach to Didactics (DAD) described in the previous section. The first dimension, which Pepin et al. (2017) referred to as the goal and points of reference for the design, implies that the teacher must know the students’ starting point (e.g., their misconceptions) and define a target learning outcome for the design. This dimension also involves situating the specific design within a broader context—such as the national curriculum—and identifying how it fits both in the short term (e.g., within a lesson sequence) and the long term (e.g., across different grades and topics). The second dimension involves a set of design principles, which must be evidence-informed, robust, and flexible, allowing the teacher to be guided across diverse teaching contexts. Finally, the third dimension, reflection in action, refers to the teacher’s real-time understanding and the associated potential lines of action developed during instruction.
To illustrate the PDC framework and its dimensions, Pepin et al. (2017) presented two studies focusing on teachers’ interaction with digital curriculum materials. One of these studies took place within a TPD program aimed at supporting mathematics and science teachers in implementing Inquiry-Based Learning pedagogies. The teacher in focus played the role of a multiplier, meaning she was expected to participate in the program and, in turn, collaborate with her colleagues. The authors analyzed the three dimensions of PDC and their development during the TPD program, using various data sources (lesson designs, video observations and interviews, and a Schematic Representation of a Teacher’s Resource System (Gueudet et al., 2013)). Examples of the first dimension (points of reference) include the Norwegian curriculum guidelines and materials provided during the TPD program. An example of the second dimension (robust design principles) is the emphasis on designing lessons around students’ thinking. Thus, in Pepin et al. (2017) the PDC framework was used as a basis for the data analysis to investigate the progression of a teacher involved in a TPD program. As a future work, the authors also proposed using the same framework to guide the design of TPD programs specifically aimed at developing teachers’ PDC.
3.6. Pedagogical Opportunities Map
The Pedagogical Opportunities Map, proposed in Pierce and Stacey (2010), is a theoretical framework associated with a specific type of technology: mathematics analysis software. In particular, it provides a taxonomy of the pedagogical opportunities supported by this particular piece of technology. As shown in Figure 3, the pedagogical opportunities enabled by the technology are made possible by underlying functional opportunities, such as the ability to execute algorithms quickly and efficiently. Specifically, the Pedagogical Opportunities Map identifies ten ways in which technology can be used to enhance learning. These are organized into three levels. At the first level, we find pedagogical opportunities that the teacher might exploit during the task design phase, such as the opportunity to link different representations of the same mathematical object through their simultaneous visualization. The second level includes pedagogical opportunities useful for fostering classroom interactions, for example by supporting social dynamics that encourage active student participation. Finally, at the third level, the pedagogical opportunities focus on shaping students’ views of mathematics, such as supporting conceptual understanding.
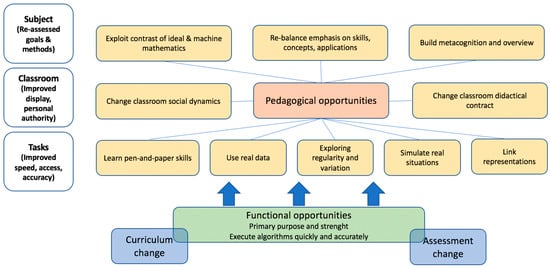
Figure 3.
Pedagogical Opportunities Map (Pierce & Stacey, 2010).
The theoretical tool of the Pedagogical Opportunities Map was used in Pierce and Stacey (2013) for the sake of data analysis. The authors presented a set of four descriptive case studies, developed within a TPD program, aimed at supporting teachers in introducing a CAS in their classrooms. They designed a questionnaire, called the P-Map Survey, which allowed them to monitor the teachers’ perceptions and exploitation of the pedagogical opportunities offered by the technological tool (CAS) at both the beginning and the end of the TPD program. In addition to using the Pedagogical Opportunities Map for data analysis, the authors framed the study within the theory of Diffusion of Innovations (Rogers, 1995), which played a significant role in both the choice of the research object and the design of the TPD program. From the perspective of the research object, the authors concentrated on teachers belonging to the early majority, who, according to the theory of Diffusion of Innovations, follow the innovators and early adopters in the implementation of an innovation. The authors emphasized the importance of studying this group because it is larger than the first two groups, and because it may provide insights into some of the integration issues that could be encountered by the ‘late majority’. From a design perspective, the authors pointed out that an important component of the TPD program—structured according to the lesson study methodology—is represented by research lessons, mainly developed by the researchers, but in which school mathematics leadership played a significant role in the design. The decision to involve school mathematics leadership was made in order to increase the compatibility of the innovation with the current practice, a factor identified by Rogers (1995) as crucial for the successful implementation of an innovation.
3.7. Zone Theory Framework
The zone theory of child development is a framework proposed in Valsiner (1997) as an extension of the Vygotsky’s (1978) concept of zone of proximal development to include also the social context, goals and actions of the learner. In particular, together with the Zone of Proximal Development (ZPD), Valsiner (1997) introduced two additional zones: the zone of promoted action (ZPA) and the zone of free movement (ZFM). The former refers to the actions of a more experienced person to promote learning, while the latter refers to the learner’s interactions in the learning environment. In Goos (2008), an adaptation of the Valsiner’s zone theory was proposed for investigating teachers’ professional learning. In such a context, the author interpreted each of the zones described using a set of key elements. In particular, the ZFM is reframed in terms of access to resources (e.g., software, time), support from colleagues, institutional culture, curriculum and assessment requirements, and students’ characteristics in terms of perceived abilities, motivation and behavior. The ZPD is considered as a set of possibilities for teachers’ development influenced by knowledge and beliefs. Knowledge is intended as skills in working in technology, general pedagogical knowledge and the knowledge necessary for using technology to promote mathematics learning, conceptualized as the PTK (Thomas & Hong, 2005) presented in Section 3.3. Beliefs correspond to pedagogical beliefs related to technology and mathematics. Finally, the ZPA corresponds to learning opportunities, such as preservice education, in-service TPD programs and the exchange with colleagues in school.
The zone theory framework as adapted by Goos (2008) for teachers’ development, was used in Benninson and Goos (2010) to analyze the relationship between participation in TPD programs for technology integration, a key element of the ZPA, and teachers’ confidence in their skills and their pedagogical beliefs about employing technology for teaching mathematics, elements belonging to the ZPD. To this end, the authors developed a questionnaire, referred to as the Teacher Technology Survey, which comprised several sections: use, access, experience, attitudes, and professional development. Participation in a previous TPD program was investigated through an item which asked whether teachers had previously had any professional development on the use of computers/graphics calculators/the Internet in teaching mathematics. The item which investigated confidence in technology skills asked teachers how confident they felt in using such technologies in teaching mathematics. This item was associated with a 3-point Likert scale answer. Finally, an example of item investigating pedagogical belief is “technology helps students to understand concepts”, associated with a 3-point Likert scale (disagree, undecided, agree). The zone theory framework thus served the purpose of analyzing the data.
3.8. Dimensions of Mathematics Related Affect: Belief, Motivation, Emotions
In Hannula (2012), a model for affective variables influencing the teaching and learning of mathematics was proposed. This model was developed within the field of mathematics education but is not specifically related to the use of technology. The model identifies three types of affective variables: (i) cognitive (e.g., beliefs), (ii) motivational (e.g., values), and (iii) emotional (e.g., feelings). In Reinhold et al. (2021), the authors aimed to apply this model to investigate the evolution of certain affective variables related to the use of digital tools in the mathematics classroom, focusing on a group of in-service teachers participating in a TPD program. Specifically, among the cognitive variables, the authors focused on teachers’ self-efficacy beliefs toward teaching mathematics with digital tools, defined as “beliefs in [their] capabilities to organize and execute the course of action required to produce” (Bandura, 1997, p. 3) adequate learning scenarios using technology-enriched classroom practices. Regarding motivational and emotional aspects, the focus was placed on teachers’ perceived values of digital tools in the mathematics classroom and on anxiety toward teaching mathematics with digital tools. Concerning anxiety, the authors referred to Zeidner’s (2014) definition of anxiety as “a loosely coupled ensemble of cognitive, affective, somatic arousal, and behavioral components, evoked in response to mental representations” (p. 266) of teaching mathematics with digital tools.
This theoretical framework, along with promising practices suggested in the literature for changing teachers’ motivational and emotional orientations related to teaching with digital technologies, informed the design of the TPD program. Specifically, the authors proposed introducing teachers to suitable theoretical models that justify why and how digital technologies can support learning, aiming to positively impact their perceived value of teaching mathematics with digital tools. Furthermore, to increase teachers perceived self-efficacy, they involved them in hands-on activities to allow them to live successful experiences using digital technologies and designing technology-enriched lessons. Finally, the program included group activities, designed to enhance teachers’ perceived values and self-efficacy through collaboration with more experienced peers.
Regarding data analysis, the framework was operationalized by assessing perceived value, perceived self-efficacy, and perceived anxiety before and after the TPD program. To assess these constructs, the authors employed four-point Likert scales adapted from existing instruments used in the Programme for International Student Assessment (PISA) student and teacher surveys.
Thus, we can conclude that the model for affective variables discussed in this section has been used as a reference framework for both the design and the data analysis.
3.9. Pivotal Teaching Moments (PTM)
A Pivotal Teaching Moment (PTM) is defined by Stockero and Van Zoest (2013) as “an instance in a classroom lesson in which an interruption in the flow of the lesson provides the teacher an opportunity to modify instruction in order to extend or change the nature of students’ mathematical understanding” (p. 127). In the same study, the authors categorized PTMs into several types, which they named Extending, Incorrect Mathematics, Sense Making, Mathematical Contradiction, and Mathematical Confusion. Later, Hollebrands et al. (2013) identified two additional categories specific to technology-intensive secondary mathematics classrooms: Incorrect Use of Technology and Technology confusion. The former refers to situations in which students experience difficulty navigating the technological tools using these tools incorrectly, while the latter involves instances where the technology is applied inappropriately or ineffectively for mathematical exploration.
Both Stockero and Van Zoest (2013) and Hollebrands et al. (2013) also identified five specific types of teacher responses to PTMs. Among them, we find for example Pursuing Student Thinking where the teacher seeks to further investigate and unpack the ideas expressed by the student that initially triggered the PTM. Hollebrands et al. (2013) identified an additional teachers’ action, specific to technology-rich environments: Repeat Technology Directions. This action is characterized by the teacher reiterating previously given instructions related to the use of technology.
The construct of PTMs is employed in Cayton et al. (2017) to analyze how teachers respond to such moments within technology-rich mathematics classrooms. The study focuses on teacher–student interactions—such as actions, statements, and questions—during PTMs, in order to explore how these moments may reflect the teacher’s relationship with digital tools (Zbiek et al., 2007). The study involved three high school mathematics teachers who participated in a TPD program centered on geometry. During the program, participants engaged with dynamic geometry tasks as learners, then reflected on those same tasks from a teaching perspective. They also analyzed classroom video recordings with a focus on task implementation and teacher questioning. As a culminating activity, teachers designed and presented a dynamic geometry task intended for use in their own classrooms and were encouraged to implement it in practice.
Importantly, the PTM framework was not explicitly used to design the TPD program. Instead, PTMs—along with the typologies of PTMs and teacher responses provided by Stockero and Van Zoest (2013) and Hollebrands et al. (2013)—served as analytical tools in the study, with the purpose of identifying patterns in the types of questions associated with particular teachers’ responses to PTMs. The data consisted of video recordings of classroom lessons delivered by the participating teachers. PTMs were independently identified by multiple authors of the study based on the aforementioned definition. Once identified, each PTM was classified by type and by the nature of the teacher’s response. The video data were then transcribed, and for each PTM, the type of teacher question was coded.
3.10. Lesson Hiccups
The construct of lesson hiccups was introduced in the context of mathematics education research by Clark-Wilson (2010) and defined as “the perturbation experienced by a teacher during teaching that has been triggered by the use of mathematical technology.” Thus, the construct is specifically related to the implementation of technology in the mathematics classroom. In Clark-Wilson and Noss (2015), the authors further emphasize the unanticipated and unplanned nature of such events, highlighting how technology-enhanced classrooms are particularly conducive to their occurrence. Indeed, in these settings, students are often able to engage with mathematical tasks in ways that differ significantly from traditional, non-technological environments. As a result, teachers are required to make real-time sense of these unexpected students’ actions. A key aspect of the lesson hiccup construct lies in the central role teachers play in recognizing these unanticipated events during their own teaching. These events are not externally identified, but rather directly perceived by the teachers themselves. In particular, such events have been shown to prompt teachers to reflect on their task design decisions. As noted by the authors, hiccups can thus serve as catalysts for epistemological development by exposing discontinuities in teachers’ knowledge. We can thus argue that hiccups are related to the cognitive domain. The identification of hiccups by the teachers notably distinguishes the construct from PTMs as defined by Stockero and Van Zoest (2013) and discussed in the previous section. In both Stockero and Van Zoest (2013) and Cayton et al. (2017), the recognition and classification of unanticipated classroom events are primarily conducted by researchers rather than by the teachers. Given the active role of teachers in noticing and interpreting hiccups, Clark-Wilson and Noss (2015) suggest that these moments offer valuable opportunities for the development of teachers’ strategic knowledge (Shulman, 1986).
In their study, Clark-Wilson and Noss (2015) used the hiccup construct as an analytical lens. Data collected from lessons—specifically teacher audio recordings and synchronized student software activity—were used to generate a coding framework for identifying lesson hiccups. This process led to the identification of seven distinct types. For instance, Type 6, labeled “Instrumentation issues experienced by teachers whilst actively engaging with the technology,” includes cases such as a teacher forgetting how to display a specific representation during whole-class instruction. In addition to categorizing the hiccups themselves, the authors also analyzed the ways in which teachers responded to them. They identified three types of response repertoires: no immediate response repertoire, a developing response repertoire, and a well-rehearsed response repertoire, reflecting increasing levels of preparedness.
Importantly, Clark-Wilson and Noss (2015) also offered a preliminary proposal for using the hiccup construct as an instructional tool for TPD. They argue that teachers should be placed in situations where they can encounter, recognize, and respond productively to hiccups during TPD activities. To this end, they propose the use of known hiccups embedded in pre-designed PD tasks with teachers who may not have personally experienced those specific hiccups in their own classrooms. These tasks are intended to allow teachers to experience the phenomenon, interpret it from an epistemological standpoint, and collaboratively discuss and rehearse possible response strategies for similar classroom situations. The ultimate goal is to foster the development of teachers’ strategic knowledge in the context of technology-enhanced mathematics instruction.
Summarizing, the hiccup construct has been used as an analytical tool, as an instructional tool and as a guide for design.
4. Discussion
In this narrative review, we examined the set of studies included in Thurm et al. (2024), focusing specifically on the theoretical frameworks underpinning research into TPD programs for teaching mathematics with technology. Our investigation allows us to address two research questions: (RQ1) What theoretical frameworks are employed in research that focuses on TPD for teaching mathematics with technology? (RQ2) In what ways are these theoretical frameworks used?
In phase 3 of the narrative review, our analysis, summarized in Table 1, led to the identification of ten theoretical frameworks, some developed within mathematics education and others originating from broader educational research domains. Several of the identified frameworks were specifically developed in relation to teaching with digital technologies. Others—such as the Documentational Approach to Didactics—address digital technologies as part of a broader range of educational resources. Most of the frameworks included in this review support the exploration of the cognitive domain, while only a few also account for the affective one. This is noteworthy, as the importance of affective variables—such as beliefs, emotions, and motivation—in the successful integration of digital technology has been increasingly emphasized in recent literature (e.g., Thomas & Palmer, 2014).

Table 1.
Summary of the findings.
One of the main contributions of this study lies in highlighting and summarizing the different theoretical uses in research on TPD programs for teaching mathematics with technology. In phase 4 of the narrative review, we inductively identified three distinct modes: (i) informing data analysis; (ii) guiding the design of TPD programs; and (iii) acting as instructional tools for teachers. The third usage mode, although potentially powerful for promoting teachers’ reflection on a metacognitive level, appears to be rare. Only in the cases of TPACK and lesson hiccups, we find examples where these frameworks were explicitly presented to teachers and used as a basis for shared reflection (Bowers & Stephens, 2011; Clark-Wilson & Noss, 2015).
While Thurm et al. (2024) primarily focus on program formats, policy aspects, and design principles, the present study offers a complementary perspective by emphasizing theoretical considerations. In particular, it sheds light on the role of conceptual frameworks in shaping both the understanding and the implementation of TPD for teaching mathematics with technology. To that end, rather than merely providing a list of frameworks, we aimed to offer a structured and informative overview. Specifically, for each framework identified in the selected literature, we provided a detailed account that includes: (i) its disciplinary origin—distinguishing between those rooted in mathematics education and those from general educational research; (ii) its connection to digital technologies, as not all frameworks were originally conceived with technology in mind; (iii) the type of domains—cognitive, affective, or both—that each framework enables researchers to investigate; and (iv) the specific usage modes in the context of the reviewed studies. As mentioned above, these modes include informing data analysis, guiding the design of TPD programs, and, in some cases, serving as instructional tools.
We note that the usage modes inductively identified in this study, regarding the context of professional development for teaching mathematics with technology, can be meaningfully discussed in light of the roles of theory proposed by Silver and Herbst (2007) in the broader domain of mathematics education research. These authors emphasize the central function of theory in mediating the relationships among research, problems, and practice. Specifically, for each of the pairs—research–problems, problems–practice, and practice–research—they illustrate, through various examples, how theory serves as a mediating construct. The category we identified as “theory for informing data analysis” closely aligns with one of the roles of theory that Silver and Herbst (2007) associate with the mediation between research and problems, namely theory “as a lens to look at data gathered or coded and to proceed with the analysis” (p. 47). Similarly, the category “theory for guiding the design of TPD programs” can be interpreted as corresponding to the function of theory as a mediator between practice and research, where theory is conceived as a system of “best practices” derived from empirical investigation. In the context of professional development for teaching mathematics with technology such a best practice could corresponds, for example, to the choice of designing group activities to enhance teachers’ self-efficacy thanks to the collaboration with more expert peers (Reinhold et al., 2021). Finally, the category “theory as instructional tool” may also be situated within the theory–practice–research relationship, albeit with a slightly different nuance: it aligns with the role of theory “as an organization of by-products of the research that practitioners might use” (Silver & Herbst, 2007, p. 56). For example, in the context of lesson hiccups, such a by-product corresponds to pre-designed tasks, with embedded known hiccups, which teachers’ educators might use to allow teachers to experience the hiccup phenomenon (Clark-Wilson & Noss, 2015).
5. Conclusions
This narrative review explored the theoretical frameworks used in research on teacher professional development (TPD) for teaching mathematics with technology, and the ways in which these frameworks are employed. Through the analysis of a set of 72 studies, we identified ten theoretical frameworks and classified their use into three inductively derived categories: informing data analysis, guiding the design of TPD programs, and serving as instructional tools for teachers. We highlight that, as a narrative review, this study does not claim to exhaustively cover all theoretical frameworks. Despite this limitation, the identification of the usage modes, as well as the discussion of these modes in relationship with the roles of theory identified in Silver and Herbst (2007), provides support in understanding how the theories are used in the reviewed studies. Since, as highlighted in Prediger et al. (2008), p. 171, “understanding a theory means to understand their articulation in research practices”, we maintain that the present study could contribute to “making understandable” the theoretical frameworks employed in the context of TPD programs for teaching mathematics with technology, thus providing guidance for researchers interested in conducting studies in this field. From a practical point of view, our findings may offer insights for TPD designers. For example, a program focused on changing teachers’ beliefs might benefit from being guided by frameworks that explicitly address affective variables, such as the PTK model or Hannula’s model of affect.
Our findings point to several possible directions for future research that may be worth exploring. Concerning empirical research, one of them could involve investigating whether and how the explicit use of theoretical frameworks as reflective tools within TPD programs might support teachers in technology integration in the mathematics classroom. Furthermore, strategies might be investigated for integrating such frameworks in ways that are accessible and meaningful for teachers. From a more theoretical research perspective, one possible area of exploration could be to engage in networking between different theoretical frameworks—more specifically, by “comparing” them, for example, through the joint analysis of a shared dataset using the criteria proposed by Prediger et al. (2008, p. 172).
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article.
Acknowledgments
The author acknowledges the use of ChatGPT (OpenAI, GPT-5) for assistance in refining the English phrasing of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Akkoç, H. (2015). Formative questioning in computer learning environments: A course for pre-service mathematics teachers. International Journal of Mathematics Education in Science and Technology, 46(8), 1096–1115. [Google Scholar] [CrossRef]
- Ball, D. L., Hill, H. C., & Bass, H. (2005). Who knows mathematics well enough to teach third grade, and how can we decide? American Educator, 29(1), 14–17, 20–22, 43–46. Available online: http://hdl.handle.net/2027.42/65072 (accessed on 26 May 2025).
- Bandura, A. (1997). Self-efficacy: The exercise of control. Freeman. [Google Scholar]
- Benninson, A., & Goos, M. (2010). Learning to teach mathematics with technology: A survey of professional development needs, experiences and impacts. Mathematics Education Research Journal, 22(1), 31–56. [Google Scholar] [CrossRef]
- Bloom, B. S. (1956). Taxonomy of educational objectives: Handbook 1, cognitive domain. David McKay. [Google Scholar]
- Bowers, J. S., & Stephens, B. (2011). Using technology to explore mathematical relationships: A framework for orienting mathematics courses for prospective teachers. Journal of Mathematics Teacher Education, 14(4), 285–304. [Google Scholar] [CrossRef]
- Brown, M. V. (2009). The teacher-tool relationship: Theorizing the design and use of curriculum materials. In J. T. Remillard, B. A. Herbel-Eisenmann, & G. M. Lloyd (Eds.), Mathematics teachers at work: Connecting curriculum materials and classroom instruction (pp. 17–36). Routledge. [Google Scholar]
- Cayton, C., Hollebrands, K., Okumus, S., & Boehm, E. (2017). Pivotal teching moments in technology-intensive secondary geometry classrooms. Journal of Mathematics Teacher Education, 20, 75–100. [Google Scholar] [CrossRef]
- Clark-Wilson, A. (2010). Connecting mathematics in the connected classroom: TI-NspireTM NavigatorTM. University of Chichester. [Google Scholar]
- Clark-Wilson, A., Aldon, G., Cusi, A., Goos, M., Haspekian, M., Robutti, O., & Thomas, M. (2014). The challenges of teaching mathematics with digital technologies—The evolving role of the teacher. In P. Liljedahl, C. Nichol, S. Oesterle, & D. Allan (Eds.), Proceedings of the joint meeting of PME38 and PME-NA (Vol. 36, pp. 87–116). University of British Columbia. [Google Scholar]
- Clark-Wilson, A., & Noss, R. (2015). Hiccups within technology mediated lessons: A catalyst for mathematics teachers’ epistemological development. Research in Mathematics Education, 17(2), 92–109. [Google Scholar] [CrossRef]
- Demiris, G., Oliver, D. P., & Washington, K. T. (2018). Behavioral intervention research in hospice and palliative care: Building an evidence base. Academic Press. [Google Scholar]
- Dochy, F., Segers, M., Van den Bossche, P., & Gijbels, D. (2003). Effects of problem-based learning: A meta-analysis. Learning and Instruction, 13(5), 533–568. [Google Scholar] [CrossRef]
- Dockendorff, M., & Gomez Zaccarelli, F. (2024). Successfully preparing future mathematics teachers for digital technology integration: A literature review. International Journal of Mathematical Education in Science and Technology, 56, 948–979. [Google Scholar] [CrossRef]
- Drijvers, P. (2019). Head in the clouds, feet on the ground—A realistic view on using digital tools in mathematics education. In A. Büchter, M. Glade, R. Herold-Blasius, M. Klinger, F. Schacht, & P. Scherer (Eds.), Vielfältige Zugänge zum Mathematikunterricht (pp. 163–176). Springer. [Google Scholar] [CrossRef]
- Eccles, J. S., & Wigfield, A. (1995). In the mid of the actor: The structure of adolescents’ achievement task values and expectancy-related beliefs. Personality and Social Psychology Bullettin, 21(3), 215–225. [Google Scholar] [CrossRef]
- Goos, M. (2008). Sociocultural perspectives on learning to teach mathematics. In B. Jaworski, & T. Wood (Eds.), International handbook of mathematics teacher education (Vol. 4, pp. 75–91). Sense Publishers. [Google Scholar]
- Gueudet, G., Pepin, B., & Lebaud, M. P. (2021). Designing meta-resources for mathematics teachers in the context of curriculum reforms: The case of digital technology use and student autonomy in France. ZDM, 53(6), 1359–1372. [Google Scholar] [CrossRef]
- Gueudet, G., Pepin, B., & Trouche, L. (2013). Collective work with resources: An essential dimension for teacher documentation. ZDM, 45(7), 1003–1016. [Google Scholar] [CrossRef]
- Gueudet, G., & Trouche, L. (2009). Towards new documentation systems for mathematics teachers? Educational Studies in Mathematics, 71, 199–2018. [Google Scholar] [CrossRef]
- Hannula, M. S. (2012). Exploring new dimensions of mathematics-related affect: Embodied and social theories. Research in Mathematics Education, 14(2), 137–161. [Google Scholar] [CrossRef]
- Hegedus, S., Laborde, C., Brady, C., Dalton, S., Siller, H. S., Tabach, M., Trgalova, J., & Moreno-Armella, L. (2017). Uses of technology in upper secondary mathematics education. Springer. [Google Scholar] [CrossRef]
- Hillmayr, D., Ziernwald, L., Reinhold, F., Hofer, S. I., & Reiss, K. M. (2020). The potential of digital tools to enhance mathematics and science learning in secondary schools: A context-specific meta-analysis. Computers & Education, 153, 103897. [Google Scholar] [CrossRef]
- Hollebrands, K., Cayton, C., & Boehm, E. (2013, July 28–August 2). Pivotal teaching moments in a technology-intensive secondary geometry classroom. Proceedings of the 37th International Group for the Psychology of Mathematics Education (Vol. 3, pp. 73–80), Kiel, Germany. [Google Scholar]
- Kim, M. K., Xie, K., & Cheng, S. L. (2017). Building teacher competency for digital content evaluation. Teaching and Teacher Education, 66, 309–324. [Google Scholar] [CrossRef]
- Koehler, M., Mishra, P., & Cain, W. (2013). What is technological pedagogical content knowledge (TPACK)? Journal of Education, 193(3), 13–19. [Google Scholar] [CrossRef]
- Lieblich, A., Tuval-Mashiach, R., & Zilber, T. (1998). Narrative research. Reading, analysis and interpretation (Vol. 47). Sage. [Google Scholar] [CrossRef]
- Mishra, P., & Koehler, M. J. (2006). Technological pedagogical content knowledge: A framework for integrating technology in teachers’ knowledge. Teachers College Record, 108(6), 1017–1054. [Google Scholar] [CrossRef]
- Nattland, A., & Kerres, M. (2009). Computerbasierte Methoden im Unterricht [Computer-based Methods in Class]. In K.-H. Arnold, U. Sandfuch, & J. Wiechmann (Eds.), Handbuch Unterricht (2nd ed., pp. 317–324). Julius Klinkhardt. [Google Scholar]
- Pepin, B., Gueudet, G., & Trouche, L. (2017). Refining teacher design capacity: Mathematics teachers’ interactions with digital curriculum resources. ZDM, 49, 799–812. [Google Scholar] [CrossRef]
- Pierce, R., & Stacey, K. (2004). A framework for monitoring progress and planning teaching towards the effective use of computer algebra systems. International Journal of Computers for Mathematical Learning, 9(1), 59–93. [Google Scholar] [CrossRef]
- Pierce, R., & Stacey, K. (2010). Mapping pedagogical opportunities provided by mathematics analysis software. International Journal of Computers for Mathematical Learning, 15(1), 1–20. [Google Scholar] [CrossRef]
- Pierce, R., & Stacey, K. (2013). Teaching with new technology: Four ‘early majority’ teachers. Journal of Mathematics Teacher Education, 16, 323–347. [Google Scholar] [CrossRef]
- Prediger, S., Bikner-Ahsbahs, A., & Arzarello, F. (2008). Networking strategies and methods for connecting theoretical approaches: First steps towards a conceptual framework. ZDM, 40, 165–178. [Google Scholar] [CrossRef]
- Prieur, M. (2016). La conception co-disciplinaire de méta-ressources comme appui à l’évolution des connaissances des professeurs de sciences [Ph.D. Thesis, l’Université Lyon 1]. [Google Scholar]
- Rabardel, P. (1995). Les hommes et les technologies, approche cognitive des instruments contemporains. Armand Colin. [Google Scholar]
- Reinhold, F., Strohmaier, A., Finger-Collazos, Z., & Reiss, K. (2021). Considering teachers’ beliefs, motivation, and emotions regarding teaching mathematics with digital tools: The effect of an in-service teacher training. Frontiers in Education, 6, 723869. [Google Scholar] [CrossRef]
- Rogers, E. (1995). Diffusion of innovations. The Free Press. [Google Scholar]
- Schmidt, D. A., Baran, E., Thompson, A. D., Mishra, P., Koehler, M. J., & Shin, T. S. (2009). Technological pedagogical content knowledge (TPACK) the development and validation of an assessment instrument for preservice teachers. Journal of Research on Technology in Education, 42(2), 123–149. [Google Scholar] [CrossRef]
- Schoenfeld, A. H. (2011). Toward professional development for teachers grounded in a theory of decision making. ZDM, 43, 457–469. [Google Scholar] [CrossRef]
- Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4–14. [Google Scholar] [CrossRef]
- Silver, E. A., & Herbst, P. G. (2007). Theory in Mathematics Education Scholarship. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 39–68). NCTM. [Google Scholar]
- Stockero, S. L., & Van Zoest, L. R. (2013). Characterizing pivotal teaching moments in beginning mathematics teachers’ practice. Journal of Mathematics Teacher Education, 16(2), 125–147. [Google Scholar] [CrossRef]
- Sukhera, J. (2022). Narrative Reviews: Flexible, Rigorous, and Practical. Journal of Graduate Medical Education, 14(4), 414–417. [Google Scholar] [CrossRef]
- Thomas, M. O. J., & Hong, Y. Y. (2005, July 10–15). Teacher factors in integration of graphic calculators into mathematics learning. Proceedings of the 29th conference of the international group for the psychology of mathematics education (pp. 257–264), Melbourne, Australia. [Google Scholar]
- Thomas, M. O. J., & Palmer, J. (2014). Teaching with digital technology: Obstacles and opportunities. In A. Clark-Wilson, O. Robutti, & N. Sinclair (Eds.), The mathematics teacher in the digital era: An international perspective on technology focused professional development (pp. 71–89). Springer. [Google Scholar] [CrossRef]
- Thurm, D., & Barzel, B. (2020). Effects of a professional development program for teaching mathematics with technology on teachers’ beliefs, self-efficacy and practices. ZDM, 52, 1411–1422. [Google Scholar] [CrossRef]
- Thurm, D., Bozkurt, G., Barzel, B., Sacristán, A. I., & Ball, L. (2024). A review of research on professional development for teaching mathematics with digital technology. In B. Pepin, G. Gueudet, & J. Choppin (Eds.), Handbook of Digital Resources in Mathematics Education (pp. 883–921). Springer. [Google Scholar]
- Valsiner, J. (1997). Culture and the development of children’s action: A theory of human development (2nd ed.). John Wiley & Sons. [Google Scholar]
- Villa-Ochoa, J. A., & Suárez-Téllez, L. (2022). Computer algebra systems and dynamic geometry for mathematical thinking. In M. Danesi (Ed.), Handbook of cognitive mathematics (pp. 843–868). Springer. [Google Scholar] [CrossRef]
- Vygotsky, L. (1978). Mind in society. Harvard University Press. [Google Scholar]
- Zbiek, R. M., Heid, M. K., Blume, G. W., & Dick, T. P. (2007). Research on technology in mathematics education: A perspective of constructs. In F. K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (Vol. 2, pp. 1169–1207). Information Age. [Google Scholar]
- Zeidner, M. (2014). Anxiety in Education. In R. Pekrun, & L. Linnenbrink-Garcia (Eds.), International handbook of emotions in education (pp. 120–141). Routledge. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).