Abstract
Smartphones are currently proposed as potential portable laboratories to perform a wide variety of physical experiments for teaching purpose. However, the frequent lack of clarity about the ease of replication of the experiments and on their accuracy often limits their effective use. In this work we deeply compare several smartphone-based experiments to determine the gravity acceleration g by only using cheap materials easily available at home. The experiment and the data analysis complexity are progressively increased, starting from fast and easy to replicate methods. The advantages and possible limits of all the methods are deeply discussed in order to allow an evaluation of the most suitable method for any particular teaching scenario.
1. Introduction
The possibility of performing experiments is a fundamental aspect of physics learning. Unfortunately, the necessity of a suitably equipped didactic laboratory often strongly limits, or even prevents, the inclusion of practical activities not only at high school level, but often also in university courses with a too high number of students. For this reason, the development of experimental techniques able to avoid the use of a standard laboratory is extremely important.
In this frame, the recent demonstration of the possibility to exploit the camera or the internal sensors of common smartphones for a wide variety of physical experiments can potentially be a real revolution [1,2,3]. For example, it has been shown that a smartphone camera can be used as light sensor in homemade spectrometers [4], or as indirect position sensors in mechanics experiments based on video analysis [5]. Another extremely interesting possibility is the use of the data coming from the internal sensors, like the accelerometer, the light meter, the microphone, the magnetometer and so on, to perform experiments of mechanics [5,6], magnetism [7], acoustic [8,9] and optics [10,11]. Access to the sensors data is nowadays made straightforward by the development of specific free apps, like Physics Toolbox Sensor Suite or Phyphox [12], really allowing anybody to easily transform their smartphone into a potentially extremely versatile portable laboratory. This possibility is amazing, as it potentially paves the way for the execution of quantitative physics experiments in a classroom in which each student has his/her own instrument, or even to experiments performed individually at home.
For these reasons, smartphone-based physics teaching is currently receiving huge attention, also documented by editorials in journals from American Physical Society [13] and Springer Nature [14], and proposals of smartphone base experiments can be found not only in professional journals, but also on web-pages and video sharing platforms.
Among the different proofs of concepts of smartphone-based physical experiments, the possibility to measure gravity acceleration g is one of the most important for high school and university students, as the vertical free fall motion is typically proposed as an example of uniformly accelerated linear motion.
When a body is left to fall with initial vertical velocity, assuming negligible drag viscous air resistance and a constant gravitational attraction force, it is well known that the motion temporal law is given by:
where is the body height at time t measured along a vertical axis, oriented upwards, and with origin on the ground level, h is the initial height, is the vertical component of the initial velocity, g is the modulus of the gravity acceleration and is the initial instant. We remember that is not necessarily the time instant in which the motion starts, but can also simply be the instant in which the height is h and the velocity vertical component is . Assuming that is the instant in which the motion starts and that the body starts to fall from rest, it is immediate to show that Equation (1) reduces to:
Starting from this equation, it is straightforward to demonstrate that the time needed to reach the ground () is related to g value and the initial height h by the equation:
and, just reversing the previous Equation, the g value can be obtained as:
Unfortunately, a direct experimental investigation of the free fall motion is absolutely not trivial because the velocity of a falling object is too high to allow the manual measurement of the position as a function time, preventing the determination of the motion temporal law and the experimental proof of Equation (2).
In a similar way, Equation (4) potentially allows to determine g by simply measuring the time needed to reach the ground from a known starting height of any object in free fall, but this experiment is complicated by the small values of when the starting height is within the range simply accessible at home ( s if m, assuming ms). This prevents to manually measure the falling time, as it is of the same order of magnitude of the error related to the reaction time.
For these reasons the measurement of g from the free fall analysis typically requires experimental set-up too complex to be replicated by a student [15,16,17,18,19,20], limiting the determination of the gravity acceleration with easy techniques to indirect measurements based, for example, on the periodicity of the simple pendulum oscillation or of bodies attached to elastic springs.
These problems were well known already at the beginning of modern science and, for example, led Galileo Galilei to use inclined planes to slow down the motion of rolling spheres, or to investigate (or guess as it is not sure that the experiment was really done) the dependence of the falling time on the mass for objects falling by high buildings, like the Pisa Tower.
A potential breakthrough in the g measurements from the free fall analysis is the demonstration, in the last few years, of several smartphone-based techniques to perform the measurement.
The most widely used method is based on the determination of the falling time from a known initial height, measuring the falling time by the internal accelerometer [6], from the video of the motion filmed by the smartphone camera [21] or with the Phyphox acoustic stopwatch [22].
Even more interesting is the possibility to determine the motion temporal law from the video of the motion combined with video analysis [23] with free Software such as Tracker [24].
However, a general problem of all these proof of concept demonstrations of smartphone-based physical measurements is the frequent lack of clarity on their real ease and on the possible accuracy that the proposed methods allow to reach, often limiting their real application to the physics education world.
In this paper, which aims to address these issues and to allow a conscious choice of the best smartphone-based method to determine g at home from free fall analysis, we quantitatively compared several different methods and experimental procedures.
We focused our attention on both the accuracy of obtained g values and the complexity of the technique.
The complexity of the experiment and of the data analysis was increased in steps, starting from a single measurement of the falling time from a single starting height, and finishing to the determination of the motion temporal law.
Furthermore, the data analysis was performed at different complexity levels, starting from a trivial use of a common calculator, moving to a spreadsheet software (Microsoft Excel) and finishing with a best-fit analysis with a professional software (Origin Lab Corporation Origin 8), to be intended as an upper limit benchmark.
In all the cases, great care has been devoted to the evaluation not only of the eventual benefits of the more complex procedures, in terms of relative accuracy (RA) of the g value, but also of the costs, in terms both of time needed and overall complexity.
We demonstrate that the measurement of the falling time from a single starting height allows to determine, in the best case, g with a RA above 99% and a statistical uncertainty of only 0.1 ms.
We also demonstrate that the nature of the motion, i.e., uniformly accelerated, can be verified by determining the falling time dependence on the starting height, reaching a maximum RA up to 99% and statistical uncertainty down to 0.040 ms.
Finally, we show that the combination of the video of the falling motion and video analysis allows to determine the motion temporal law, obtaining a g estimate with a RA of 98.2% and an uncertainty of 0.07 ms, but only after careful image distortion correction and with best fit analysis with professional software. Overall, our results demonstrate that the proper choice of the experimental method allows smartphone-based experiments to reach RA very close to the one obtained with a professional didactic set-up, but by exploiting much simpler experimental procedures and low cost materials.
2. Materials and Methods
In this paper, we used, as a benchmark for the smartphone-based methods, a set-up from 3B-Scientific, made by a free-fall apparatus (U8400830) and a digital time counter (U8533341-230) (see Figure 1a). The set-up allows the measurement of the falling time of a steel sphere with 16 mm diameter with a temporal sensitivity of 0.1 ms in a height range between 2 cm and 96 cm in steps of 1.0 cm. The falling time was determined for 40 different values of the starting height in the range 2.0 ÷ 95.0 cm. The reading error on the starting height was estimated at 0.5 mm, coinciding to one half of the thickness of the lines on the ruler. In order to determine the uncertainty on the falling time we measured it 5 times, both for h = 95.0 cm and h = 47.0 cm. In both cases, the standard deviation of the obtained values was found to be 0.5 ms, which was taken as the statistical error bar for all the measured falling time values.

Figure 1.
(a) Picture of the 3B-Scientific set-up. On the left there is the vertical guide, with the steel ball release system on top and the ball arrival sensor (red circle) on the bottom. The time counter is on the right. (b) Picture of the material used to exploit the Phyphox acoustic stopwatch. (c) Picture of the material used to make the video of a falling tennis ball. The smartphone is fixed on a mini-tripod on a chair. On the back, and in the smartphone screen, the bookshelf with the folding meter is visible. (d) Picture of the sofa used for the experiment with the smartphone accelerometer, also showing the vertical meter used to control the smartphone release height.
The determination of g from Equation (4) was also performed with smartphone-based experiments, using a Huawei Y6 2019 and different methods.
The first method exploits the acoustic stopwatch of the app Phyphox, that determines the time interval between two sounds, with a nominal temporal resolution of 1 ms (see Figure 1b). The falling body was a steel sphere with a 1.3 cm diameter, taken from a famous magnetic construction toy, initially at rest on a metallic ruler protruding from the shelf of a bookshelf. The initial height was measured with a wooden folding meter rule, while the starting sound was generated by suddenly hitting the ruler with a pen, in order to make it move along the horizontal direction. The stopping sound was instead generated by the sphere impact with a metal box on the floor [22].
For the second method, we determined the falling time starting from the video of the motion, made with the smartphone internal camera with the smartphone fixed to a mini-tripod (see Figure 1c). The video (originally in 3gp format) was converted to mp4 by using the free software Video to Video converter, from Media Converters, and opened with the free software Tracker [24]. The necessity to easily see the falling object in the movie lead us to use a tennis ball rather than the steel sphere which was too small. The ball was held in hands, taking care to leave it falling without giving it any initial velocity and in the fastest possible way. The determination of the falling time in this case is a bit tricky, as the temporal sensitivity is limited by the video frame rate (30 Hz), leading to one frame every 33.3 ms. For this reason, the movie typically contains neither a frame showing the release instant nor the instant in which the ball hits the ground . The ball release instant was determined by carefully looking at the video frame by frame, focusing the attention on the few frames across the ball release (see Figure 2). We thus determined as the average value between the time of the last frame showing the ball being held by the hand (Frame 0 in Figure 2) and the time of the first frame showing the movement of the fingers to release the ball (Frame 1 in Figure 2) .
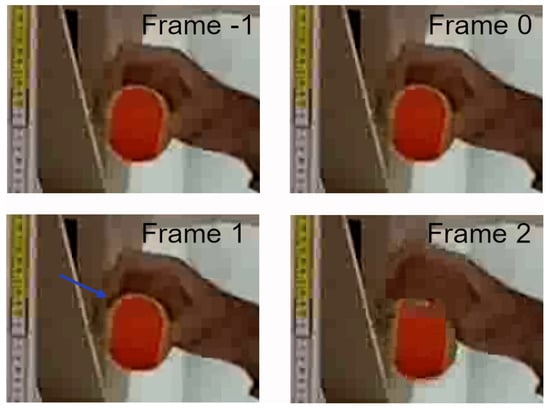
Figure 2.
Picture of the frames across the ball release. Frame −1 and Frame 0 are the last two frames showing the ball held in the hand. Frame 1 show a space, evidenced by the blue arrow, between the hand and the ball, indicating the hand opening and Frame 2 clearly show that the ball has been fully released and is already moving.
In a similar way was determined as the average between the time of the last frame of the falling motion and the following frame (already showing the ball after the bounce on the ground). Both values lie in a time interval 33 ms wide, thus have a maximum uncertainty of 16.5 ms, leading to a maximum error of 33 ms on their difference. A statistical error on and was instead determined by dividing the maximum uncertainty by , as expected for a uniformly distributed variable, and on by adding the statistical errors in quadrature, obtaining 13.5 ms.
As a third method, we instead exploited the smartphone’s internal accelerometer, again using Phyphox, which allows to measure the acceleration in the smartphone reference system. In this experiment, the falling object is the smartphone itself, which is left to fall on a soft body (a sofa in our case, see Figure 1d), starting from rest. When the smartphone is in equilibrium (for example when it is held by the hand) the accelerometer basically measures the force necessary to compensate its weight, thus providing an acceleration measurement equal to g (if it is properly calibrated). When the smartphone is in free fall, both the accelerometer and the smartphone experience the same acceleration, thus their relative acceleration is zero. Thus, during the free fall, the acceleration measured by the accelerometer suddenly reaches values close to 0 m/s. Finally, when the smartphone reaches the sofa, a sharp acceleration increase is observed, followed by some peaks, due to the acceleration given by the force exerted by the sofa (see Figure 3). The acquisition rate of the accelerometer data is 200 Hz, leading to a nominal temporal resolution of 5.0 ms.
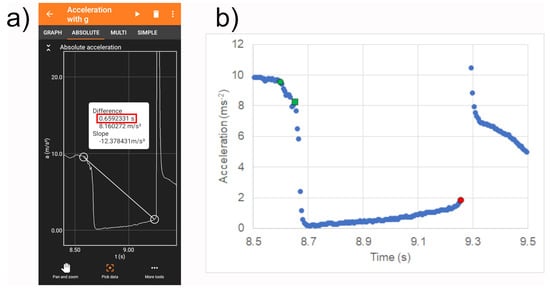
Figure 3.
(a) Screenshot of the Phyphox accelerometer option, evidencing the acceleration decrease after the smartphone release, followed by a quick acceleration increase after the impact with the sofa. The first line of the white rectangle (evidenced by the red rectangle) contains the time differences between and as determined on the smartphone screen with the “Pick data” option. (b) The same data plotted with Microsoft Excel. The green circle is the point corresponding to as the time of beginning of acceleration decrease, the green square is the point corresponding to the time of slope increase of the acceleration decrease and the red circle is the point corresponding to .
Phyphox allows to save the accelerometer data to visualize them on the smartphone’s screen and then to export them in ASCII. The falling time can be determined as the time difference between the instant of acceleration increase due to the impact with the sofa (first point showing a sudden acceleration increase) and the smartphone release instant.
The falling time was determined both by visually selecting the beginning and final instant of the motion from the Phyphox app from the smartphone screen (see Figure 3a) and, for an accuracy test, with Microsoft Excel, after transfer of the saved ASCII file to a notebook by email (see Figure 3b).
For all these three methods, we determined the falling time for 5 different values of the initial height, given by the height of 5 different shelves of the used bookshelf.
For the two methods with the highest nominal temporal resolution (acoustic stopwatch and accelerometer) we also estimated the uncertainty on by repeating the measurement 3 times.
The acceleration of gravity was determined with different experimental procedures of progressively increasing complexity:
- From Equation (4) by using a single value of the falling time for each starting height. In this case the g estimation is very easy but the uncertainty level of the obtained value cannot be estimated (for all the three methods).
- From Equation (4) by using the average value of the falling time obtained, for each starting height, by repeating the measurements three times (for acoustic stopwatch and accelerometer methods). In this case g can be determined for each starting height with an estimate of the error bar.
- From the best fit with Excel of the dependence on h, that is expected to be linear with a slope . In this case the linearity of the dependence allows to evidence the validity of Equation (4), thus demonstrating that the falling motion is uniformly accelerated, but no error bar on the g value can be obtained [25](for all the three methods when using single measurements of and, only for acoustic stopwatch and accelerometer methods, when using the average values).
- From the best fit with a professional software (Origin 8) with Equation (4), fully including the data error bars and thus obtaining the statistically correct uncertainty on the g values (again for all the three methods when using single measurements of and only for acoustic stopwatch and accelerometer methods when using the average values).
As a final approach we exploited the video of the falling motion of the tennis ball (acquired and processed as already described above) to extract the time dependence of its position, thus determining the temporal law of the motion, exploiting the presence of the side of the book shelf of a folding meter rule fixed with tape, used for the pixel–cm conversion. The position of the ball in the different frames was extracted with Tracker.
We observed that the exposure time during the video results in a poorly defined ball image when the velocity exceeds about 2 m/s, opening to possible errors of the automatic object tracking option of the software (see Figure 4). We thus determined the position of the ball during the free fall by manually selecting the central pixel of the frame region containing the ball image. The presence of the meter in the filmed frames allows to perform a pixel-length calibration with Tracker, thus converting the position in pixel in height in meters. The ball radius (3.2 cm) was then subtracted in order to determine the height of the bottom point. The uncertainty of each position is limited by the size of the pixels and is about 0.5 cm.

Figure 4.
Pictures of four frames after the ball release evidencing the progressively less defined ball image as the velocity increases. The time is measured by considering t = 0 s for Frame 1 of Figure 2, while the velocity is determined by Tracker.
Furthermore, in this case the data analysis has been performed at two different complexity levels. The simplest one is based on a linear regression with Microsoft Excel of the lost height dependence on :
The second one is instead based on a best fit of the original data with Equation (2) and Origin.
In order to quantify the relative accuracy of the obtained g values we define the following quantity:
where is the experimentally determined value and the expected one.
3. Results
3.1. Professional Set-Up
As a first step we present the results obtained by the 3B-Scientific set-up, in order to have a benchmark for the simpler smartphone-based methods. In this case the system counts the time starting from the release instant, thus = 0 s and .
The dependence of the falling time on the initial height shows (see Figure 5) a smooth increase, visually consistent with the expected square root dependence. The qualitative agreement between the experimental data and the expected increase is even more striking when looking at the height dependence of the squared falling time (see inset of Figure 5), that shows a very clear linear increase.
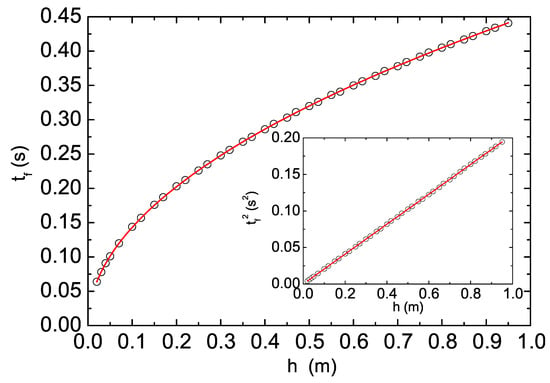
Figure 5.
Falling time dependence on the starting height for the steel ball used in the 3B-Scientific set-up. The red line is the best fit curve with Equation (4). Inset: the same data re-plotted with on the vertical axis, evidencing a nice linear increase, expected for a uniformly accelerated fall.
The g value has been determined by a best-fit with Equation (4) performed with Origin, that allows to obtain an excellent fit for g = (9.7660 ± 0.0045) ms. This value is very close to the expected value (9.8020 ms) calculated by the International Gravity Equation [26], for a latitude = 40.334 °N:
The relative accuracy is thus very high ( = 99.6%), but the extremely small statistical uncertainty on g (relative statistical uncertainty of only 0.046 %) allows to observe that the best fit value is not consistent with the expected value within 3 standard deviations. A possible explanation of this result is a slight, but systematic overestimation of the falling time. We observe that an underestimation of the g value of 0.4%, as in the current case, can be obtained for an overestimation of of just 0.2%, thus below 1 ms in the investigated height range. Overall, the capability of the professional system to determine g and to verify that the falling motion is uniformly accelerated is excellent and the small lack of accuracy can only be observed due to the excellent reproducibility of the falling time values.
Similar very high accuracy and small statistical errors can be typically obtained with other set-up often used in teaching laboratories, like for example spark timer-based systems [20].
3.2. Smartphone Based Falling Time vs. Starting Height Dependence
3.2.1. Single Measurement
As the initial step in the evaluation of the smartphone-based methods we started by performing a single measurement of the falling time for each of the five starting heights.
The values obtained from the motion video and the acoustic stopwatch are reported in the second and third column of Table 1, while the values obtained with the accelerometer are reported in the fourth and fifth column.

Table 1.
Values of the falling time obtained from a single measurement with acoustic stopwatch, accelerometer and video analysis techniques for 5 different values of the starting height h. The expected value of is also reported for comparison.
Concerning the falling time determined from the accelerometer data we observe that (see Figure 3 and Figure 6a) the final impact always determined a sudden acceleration increase, thus making easy the determination of the final instant in correspondence of the last point before the acceleration increase. On the contrary, the initial acceleration decrease is much smoother (see Figure 3b and Figure 6b) and it is thus not obvious which is the instant corresponding to the free fall beginning. We thus initially assumed that the smartphone release instant coincides with the instant of beginning of the acceleration decrease (green dot in Figure 3b and Figure 6b, corresponding to the last point before the initial acceleration decrease), but we observed that this choice leads to systematically overestimate the falling time of about 30–50 ms (with respect to the value calculated from Equation (2) with g = 9.8020 ms).
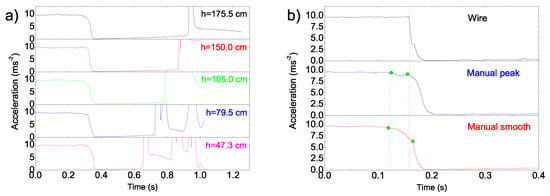
Figure 6.
(a) Accelerometer data for different starting height, evidencing the progressive increase of the falling time. The signals are horizontally aligned to the release instant. (b) Comparison of the acceleration signals obtained for h = 175.5 cm for manual release, with smooth decrease (red line) and for decrease followed by a peak (blue line), and for release by cutting a suspension wire (black line). The signals have been aligned to the final instant. The dotted green line demonstrates the good correspondence between the time of beginning of acceleration decrease for manual release (green dot), while the red dotted line demonstrates the correspondence between the release time when cutting the wire and the time of acceleration peak or slope increase (green square).
Moreover, we observed that if the smartphone is released by suspending it with a wire and cutting the wire with scissors [6], the acceleration decrease is much faster and the falling time is very close to the expected one (see black line in Figure 6a). Finally we show that, in the case of a manual smartphone release, the initial acceleration decrease is gradual in the first 30–50 ms, and then a clear slope increase is observed. In some cases, after a gradual decrease, a small peak is observed after 30–50 ms, followed by a fast decrease. Moreover, the release instant for the cutting wire method almost coincides with the instant of the slope increase or of the peak (see Figure 6a).
Overall, we concluded that the initial gradual acceleration decrease, or the decrease followed by a peak, is relative to the time interval in which the smartphone starts to move, but it is still in contact with the hand. The real free fall starts in correspondence of the slope increase of the acceleration decrease, that was thus considered as the starting instant (green square in Figure 3b and Figure 6b, corresponding to the last point before the slope increase of the acceleration decrease).
Even if the signal is obtained by suspending the smartphone and cutting the wire is easier to analyze, we find this advantage smaller than the complexity increase due to the creation of a suspension system that allows a good alignment with the meter and an easy repetition of the measurements. We thus preferred to use the straightforward manual release procedure, making care in the falling time extraction.
As already noticed the difficult part of an accurate determination of g starting from the falling time values is given by the requirement of determining the small values of with a small error. As increases with h it is reasonable to expect that a good strategy to minimize the relative error on will be the increase of h. For this reason, we start the presentation and discussion from the results based on the values obtained for the maximum available height (h = 1.755 m).
We initially observe that the two values obtained by the acoustic stopwatch and the accelerometer (extracted from the smartphone screen) are almost identical, with just 1 ms of difference. On the contrary the value extracted from the accelerometer and Excel is slightly smaller, even if the difference is of only about 10 ms, corresponding to just two measurement steps. The value extracted from the video, that can change only for multiples of 33 ms, is instead consistent with all the previous 3 values.
Despite this promising similarity between different methods, we observe that the obtained values are higher than the expected value, with differences between 2 ms and 16 ms. Even if this difference looks small, providing a relative error below 2.7%, the inverse proportionality between g and the squared falling time leads to very evident differences between the obtained values (see Figure 7a), spanning from 9.33 ms (acoustic stopwatch) to 9.75 ms (video).
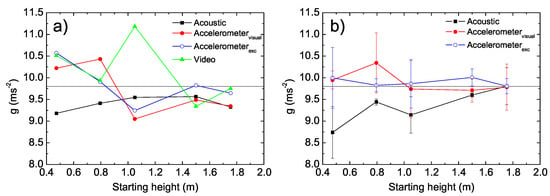
Figure 7.
(a) Values of g obtained from a single measurement of the falling time for 5 different starting heights determined with the Phyphox acoustic stopwatch, with the accelerometer and from the motion video. The horizontal line demonstrates the expected value. (b) Values of g obtained from the average value of 3 measurements of for 5 different starting heights, with the Phyphox acoustic stopwatch and with the accelerometer. The horizontal line demonstrates the expected value.
This first set of measurements suggests a general tendency of all the methods of overestimating the falling time value and, concerning the accelerometer data, a further overestimation of the values directly extracted with Phyphox from the smartphone screen with respect to the one determined from Excel.
In order to probe the generality of this result, we repeated the measurement for four further values of the starting height (see Table 1). The obtained results allow to observe that the values obtained with the acoustic stopwatch are again always slightly overestimated (between 6 ms and 10 ms), with a relative error between 1.2% for h = 1.50 ms and about 3% for h = 0.473 m. Moreover the values obtained with the internal accelerometer and directly extracted form the smartphone screen are again always slightly larger (between 5 ms and 9 ms) than the values extracted with Excel. As a consequence, the g values obtained from the values measured by the acoustic stopwatch are systematically lower than the expected value, with values between 9.18 ms and 9.57 ms (see Figure 7a). The point to point variation of the values extracted with the accelerometer data is instead higher, even if in a couple of cases (data extracted with Excel for h ≥ 1.50 m) the g value is very close to the expected one.
Overall, these further data confirm that the acoustic stopwatch has a systematic tendency to overestimate the falling time, thus underestimating g. On the contrary, the data obtained from the accelerometer, even if a bit more scattered, seems to sometimes allow a good evaluation of the g value.
Anyway, for both methods, the presence of a single value of does not allow to estimate its error bar and thus an error bar for g, preventing any conclusion about the consistency between the obtained values and the expected ones beyond a qualitative comparison of the two values.
Concerning the g values obtained from the video of the free fall (see Figure 7a) we observe that the potentialities of this technique are clearly limited by the coarse time scale, that is intrinsically limited to variations in steps of 33 ms. This results in a coarse determination of and, as a direct consequence, in highly scattered values of g that vary in the range between 9.34 ms and 11.1 ms without any regular dependence on h. A unique relevant advantage of this technique is that its poor temporal sensitivity allows to use the time step as uncertainty on the values, thus allowing to estimate an error bar for g even with a single measurement.
The maximum error bar on is fixed to 33 ms, thus the relative error on decreases from about 10% for h = 0.473 m to about 5% for h = 1.755 m, leading to a maximum (statistical) error on g decreasing from 2.4 ms (0.8 ms) to 1.1 ms (0.4 ms). The best g estimate is thus obtained for the maximum value of h and it is g = 9.8 ± 1.1 ms (g = 9.8 ± 0.4 ms if the statistical error is considered). We observe anyway that this best performance is positively affected by a casualty of the almost perfect coincidence of the measured with the expected one. In other cases, the interplay between an increasing relative error on and less lucky correspondence of the expected time with the possible ones results in much higher uncertainty bar. For example, for h = 1.05 m the obtained value is g = 11.2 ± 1.7 ms (g = 11.2 ± 0.6 ms if the statistical error is considered) that is neither accurate nor precise.
3.2.2. Average of Many Measurements
As a next step we decided to explore in further detail the potentiality of the two methods with the better nominal sensitivity on , thus the acoustic stopwatch and the accelerometer ones, focusing our attention on the estimation of a reasonable error bar on the values while preserving the overall simplicity of the experiment.
We thus repeated all the measurements two more times for each starting height, determining the best estimate of as average and of the maximum uncertainty as the semi-dispersion of the three measured values. The obtained values (see Table 2) allow to observe a generally good reproducibility of the values obtained with the acoustic stopwatch, with semidispersion between 1.0 ms and about 10 ms, even if the values are again overestimated for four of the five investigated values of h. As a consequence, with the only exception of the value obtained for h = 1.755 m, the obtained g values (see Figure 7b) are systematically lower than the expected value and, more importantly, not compatible with it within the error bar. The average value of g for m is g = 9.5 ± 0.2 ms when maximum errors are considered (g = 9.50 ± 0.07 ms for statistical errors).

Table 2.
Average values and corresponding maximum error bar of for both acoustic stopwatch and accelerometer techniques, obtained by performing 3 independent measurements of for each value of h. The expected value of is also reported for comparison.
On the contrary, the data obtained from the accelerometer and directly determined from the smartphone screen show a slightly larger semidispersion of about 15 ms, but the average values of is consistent within the error with the expected one for all the h values. As a consequence, also the corresponding g values are comparable with each other, with an average value of g = 9.9 ± 0.3 ms, and compatible with the expected one within the error bar (see Figure 7b). When statistical errors are used, rather than the maximum errors, we find g = 9.91 ± 0.10 ms, that is compatible with the correct value within one standard deviation.
The data obtained from the accelerometer and Excel shows a semidispersion between 3 ms and 13 ms and are again consistent with the expected value for all the investigated heights. As a consequence also the corresponding g values are consistent within the error bar with the expected value (see Figure 7b). By estimating the average value of all the obtained g values we find g = 9.9 ± 0.1 ms, that becomes g = 9.90 ± 0.03 ms when statistical errors are considered (compatible with the expected value within 3 standard deviations).
3.2.3. Comparison of the Methods
Coming to a comparison of the cost/result balance of the three methods we observe that the potentiality of use of the video is clearly limited by the coarse determination of , leading to a rather unpredictable accuracy and a large error bar on g. In the best case we obtained a relative accuracy as high as 99.5%, but with a relative error bar of 11%. In the worst case the relative accuracy was only 86%, with a relative error above 17%. Overall, this technique is in general not very precise, potentially not particularly accurate and, in addition, it is not immediate, as it requires several steps (making the video, transfer to the computer, file format conversion, extraction with Traker and paying attention to determine the starting and finish frame of the motion). The only reasonable use of a similar experiment is to provide an example of unconventional use of a video made by a smartphone for the determination of a reasonable value of a physical quantity, but certainly it is not the best choice as easy and accurate method for the g determination.
Concerning the acoustic stopwatch, it has the enormous quality of being the only method that allows to directly measure the falling time, without requiring any additional step after the measurement. The required set-up is very simple and the time needed for the measure on the scale of few minutes.
However, the method has a systematic tendency to overestimate the falling time values [27], thus underestimating g. The reproducibility of the values is instead generally very good, thus allowing a very precise measurement (average statistical error as low as 0.7%), but unfortunately the technique is not the most accurate, with typical 95%. Overall, if this accuracy level is considered acceptable, this method with a single measurement is certainly the best choice.
We also observe that the time cost of repeating the measurements in order to allow the addition of the error bar is extremely limited, and the accuracy of the technique seems to increase with increasing h, thus suggesting to use the average of many measurements approach for 1.50 m as the best cost/results option, allowing to reach .
Concerning the method exploiting the internal accelerometer, used with single measurement and data extraction from the smartphone screen, we found a relative accuracy similar to the acoustic stopwatch one for 1.50 m, and a comparable complexity. However in this case the accuracy is limited by the small errors on (typically below 10 ms if care is taken in selecting the start and finish points on the screen) due to the use of direct extraction from the smartphone screen. The addition of the data export step and extraction with Excel is rewarded by an accuracy increase above 98.4 % for 1.50 m.
When the repetition of measurements is added, the technique allows to obtain g values compatible within the error to the expected one for any h value. It is interesting to observe that, even when directly extracting the data from the smartphone screen, very high 99% can be obtained for 1.05 m. No advantages are observed instead when extracting the data with Excel, showing that the errors induced by direct extraction of from the screen average out when repeating the measurements just three times.
Overall the average of many measurements option with direct data extraction is the best choice in terms of costs/results ratio, demonstrating amazingly high relative accuracy and overall simple and fast execution.
3.3. Investigation of the Nature of the Motion
After the establishment of the potentiality of the acoustic stopwatch, accelerometer and video analysis methods to determine g starting from Equation (4), a limited number of measurements and a simple error analysis, we investigated how far these methods can go in the physical analysis of the free fall.
Even if these further experiments can probably go beyond the level expected for high school students, they could be suitable for experiments at university level, or for hybrid courses organized by universities for high school students.
A very instructive aspect would be the experimental test of the validity of Equation (3), that would allow to directly probe the validity of the assumptions on which the solution is based (negligible viscous friction and constant gravity acceleration) and to show to the students how a theoretical prediction can be experimentally validated.
In order to obtain this result, we analyzed, for each technique, the falling time dependence on the starting height, basically reproducing the experiment performed with the 3B-Scientific set-up.
Again we followed two experimental procedures, measuring just once for each starting height (thus performing five measurements of in total, one for each of the five different investigated heights), or measuring it three times for each height and using the average values (requiring three measurements of for each height, thus 15 measurements overall).
In both cases we performed two different analysis, starting from a simple one based on Excel and then moving to a professional best fit performed with Origin.
The simple analysis is performed by plotting with Excel the squared values as a function of h that, according to Equation (3), should show a linear dependence with slope 2/g. We first analyzed the data obtained by a single measure for each h, observing (see Figure 8), for all the investigated methods, a visually good linear increase, thus qualitatively confirming the motion with uniform acceleration. A simple linear regression allows to determine the best value of the slope and, thus, the best estimate of g. Even if Excel does not estimate any error bar for the best fit parameters, the regression on five points allows to compensate the effects of scattered values of on the value of g, thus leading to best g estimates most of the time quite close to the expected values. In particular, the relative accuracy of the g value obtained from the video (see Figure 8a) is = 99.5%, and also the values obtained by using the accelerometer differ from the expected value of less than 4% ( = 96.4% for the values directly extracted from the screen and = 99.8% when the extracted with Excel are used). On the contrary the systematic, and rather regular, overestimation of with the acoustic chronometer leads in this case to an underestimated g value (9.43 ms, thus = 96.2%).
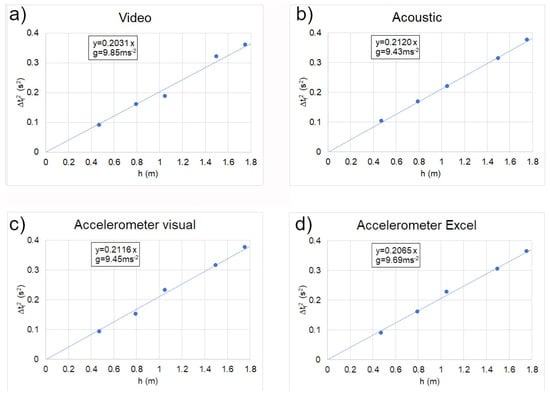
Figure 8.
Starting height dependence of the squared falling time obtained from a single measurement with the video (a), acoustic stopwatch (b), accelerometer and direct extraction from the screen (c) and with Excel (d). The dotted lines are the best regression line determined by Excel.
When the average values are used, the additional averaging of the point to point fluctuations further improves the accuracy for the accelerometer methods above 99% (g = 9.80 ms for the visual method, and g = 9.85 ms with Excel method). The value obtained with the acoustic stopwatch data is instead still underestimated, even if with slightly improved accuracy (g = 9.57 ms, thus = 97.6%).
The absence of an error bar of course technically prevents to evaluate the real compatibility between the obtained values and the expected one but, at an introductory level, such a good accuracy easily allows to qualitatively agree that the values are very close to the expected one.
In order to add a proper error bar to the obtained g values, the data have been re-analyzed with Origin and directly fitting them to the following equation:
The obtained best fit values of g coincide with the ones obtained by Excel, thus allowing to limit the discussion to the differences in the g error bars.
The data scattering from the video leads to a maximum (statistical) error on g of 0.9 ms (0.31 ms) confirming the lack of precision of the method. On the contrary the acoustic stopwatch is confirmed as the method with higher precision, evidenced by a maximum (statistical) error on g of only 0.2 ms (0.066 ms) when the single measurements are used and 0.13 ms (0.044 ms) when average values are used. Finally the data from the accelerometer and extracted from the screen lead to a maximum (statistical) error on g of 0.6 ms (0.22 ms) when the single measurements are used and 0.2 ms (0.070 ms) when average values are used. When the step of data extraction with Excel is added the data quality is slightly improved, reducing the maximum (statistical) error on g of 0.5 ms (0.17 ms) when the single measurement is used and 0.12 ms (0.040 ms) when average values are used.
Comparison of the Methods
All the four methods allow to evidence the expected square root dependence of on h, basically confirming the differences in terms of accuracy and precision already found in Section 3.2.3.
Concerning the video method, the averaging effect of a single fit on many points allows to reach a good accuracy, but the starting high data scattering makes it the one with the worst precision.
The acoustic stopwatch method turns out to have the worst accuracy due to the systematic overestimation of the falling times, but is the most precise. This makes it again competitive with the accelerometer with visual data extraction when single measurements of are made in terms of final accuracy and overall suitable for easily demonstrate the validity of Equation (3).
When high accuracy is desired, the average of more is required and the most powerful methods are without any doubt the ones exploiting the accelerometer, allowing to reach accuracy above 99% with relative maximum (statistical) error bar down to only 1.2% (0.4 %).
3.4. Motion Temporal Law
In this last section we discuss the possibility to use the video of the falling motion of the tennis ball to extract the temporal dependence of its height, thus directly determining the position-time dependence.
The time dependence of the ball position extracted with Tracker clearly shows (see Figure 9a) the progressive increase of the covered distance between consecutive frames (thus for a fixed time interval), fully consistent with an accelerated motion. It is also evident that the picture is very similar to the ones typically shown on text books but determined with typically inaccessible instrumentation (like the photographs under stroboscopic flash light). Even if only qualitative, this first result is extremely interesting, because it demonstrates that the combination between a smartphone, a free software and a bit of time can allow anybody curious and patient enough to reproduce the results typically requiring professional instrumentation.
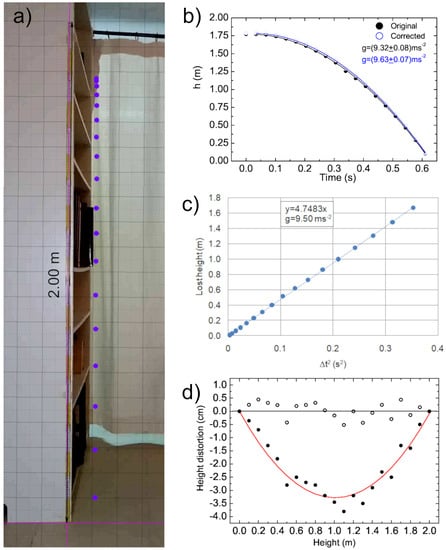
Figure 9.
(a) Picture of the library used to extract the motion temporal law from the video. The pink lines are the axis of the reference system, while the black line is the calibration stick built exploiting the folding meter on the side of the library. The full blue dots represent the positions of the ball extracted from the different frames of the video between the ball release and the bounce on the floor. (b) Time dependence of the tennis ball height extracted from the motion video for both the data originally extracted with Tracker (full black dots) and the data with distortion correction (open blue dots). The lines are the best-fit curves with Equation (2). (c) Lost height dependence on the squared time, evidencing the expected linear increase. The line is a linear regression line obtained with Excel. (d) Difference between the ball height extracted with Tracker and the ones measured from the meter image in the video (full black dots) and best-fit curve (red line). The open black dots represent the difference between the distortion corrected heights and the best-fit ones.
The time dependence of the ball height is shown in Figure 9b and demonstrates a downward convex curved dependence, qualitatively consistent with the expected parabolic dependence of Equation (2) (in this set of data the t = 0 s point is relative to the last frame in which the hand holds the ball, thus Frame 0 in Figure 2).
In order to better visualize the qualitative agreement between the expected dependence and the experimental data, we also plotted the lost height at any time as a function of (see Figure 9c), which shows a smooth increase, qualitatively consistent with the linear dependence expected from Equation (5).
In order to quantitatively analyze the data we started again from an Excel-based analysis of the linearized dependence of the lost height, providing in this case a slope . By performing a linear regression fixing the intercept at 0 and = 16.5 ms (average between t = 0 s of Frame 0 and t = 33 ms of Frame 1) we obtained g = 9.50 ms. We also investigated the importance of a correct knowledge of , that is not directly measured but only estimated as average value between the two extreme values t = 0 s and t = 33 ms, by repeating the analysis for the two extreme values. By fixing = 0 s we find g = 8.87 ms, that is macroscopically underestimated, while for = 33 ms we find g = 10.19 ms, that is on the contrary overestimated. This result demonstrates that the g value is strongly affected by the value of , that unfortunately cannot be directly measured, leading to potentially widely scattered g values despite the availability of a data set with 19 measured points, by far the richest one among all the investigated techniques, and the use of great care to determine in the best possible way the two frames across the ball release, the position of the ball at each frame and the pixel-length calibration. Differences between the estimated and the real value can determine g variations up to 0.7 ms resulting in a rather unpredictable accuracy (down to 90% even without making any error).
In addition, we also simulated a situation in which an error of just one frame is made in determining the last frame in which the ball is at rest, obtaining g = 8.29 ms when is placed one frame back and g = 10.94 ms when it is placed one frame forward, further reducing the accuracy down to about 84%. This result clearly demonstrates that the careful determination of the correct frames across the ball release is fundamental in order to have chances to adequately quantify g.
We thus decided to investigate in further detail the g dependence on , leaving the Excel-based data analysis and moving to a professional analysis with Origin. In this case we directly used the original data and we adapted them, in the sense of minimum Chi squared, with Equation (2).
The best fit was initially obtained by fixing to 16.5 ms, the initial height to the measured one, and the initial velocity to 0 and allowed to obtain g = 9.47 ± 0.03 ms. The best g estimate almost coincides with the one determined with Excel, but the addition of the error bar demonstrates that this value is clearly not consistent with the expected value.
A slightly improved fit is obtained by allowing the variation of (best fit value = 12 ± 2 ms, thus actually between Frame 0 and Frame 1, as expected) but for g = 9.32 ± 0.08 ms, that is even farther from the correct value. This disagreement thus demonstrates that something else is still preventing a good agreement between the data and the model.
As a last step we thus checked the correctness of the frame-time and the pixel-length correspondence.
The video frame rate has been checked by making a video of a running chronometer and observing that actually 30 frames are always present in 1 second. Thus, each frame is effectively recorded every 33 ms, as assumed.
The pixel-length calibration has been instead checked by exploiting the presence of the meter in the video and determining the pixels corresponding to the meter change of color (from yellow to white and viceversa, every 10 cm). We thus compared the height values obtained from the pixel-position calibration () with the corresponding values read on the meter (), observing (see Figure 9d) a clear systematic difference down to about −4 cm for 1 m (the two values at h = 2.000 m and h = 0.000 m are the same by construction of the calibration stick).
We thus adapted the dependence of the measured height on the real one with a quadratic function, and we then used the best fit curve to calculate the correct height values for each frame of the video. The differences between the corrected heights and the ones calculated from the best fit are always below 0.5 cm, and are correctly randomly distributed around 0 (see Figure 9d).
By performing a best fit with Equation (2) of the temporal dependence of the corrected heigth we finally obtained g = 9.63 ± 0.07 ms.
This last g value is finally compatible within three standard deviations with the expected value, and demonstrates a relative accuracy = 98.2% with a relative statistical uncertainty of 0.7%.
Basically the same result ( ms) can be obtained by performing a best fit with Equation (1), fixing ms and leaving as free parameter (best fit value ms).
We can thus conclude that the extraction of the motion temporal law starting from the frames of the video is surely possible. However, it cannot be expected to extract quantitatively correct values of g without the image spatial distortion correction and the possibility to perform a best fit more complex than a regression of the linearized data.
Overall, also this approach is potentially very interesting, as it is the only one that directly gives access to the possibility to fully analyze the motion (i.e., the variation with time of the position) but the complexity of the whole procedure is likely above the level accessible to students/curious individually working at home without a professional supervision.
4. Conclusions
In conclusion, we quantitatively compared several different methods to determine g with smartphone-based experiments.
We demonstrated that the determination of g from the falling time measurement from a single known height, that just needs one measurement and a standard calculator, is in general possible with all the tested methods.
Anyway, the falling time extraction from the video of the motion was evaluated too complex for the results that it allows to obtain, with low precision and rather unpredictable accuracy.
On the contrary, reasonable accuracy ( 95%) was obtained when using the Phyphox acoustic stopwatch and the internal accelerometer with direct data export, for starting height of at least 1.50 m.
For the accelerometer method, the addition of data export to Excel allows better accuracy with single measurement (above 98%) for starting height of at least 1.50 m, but of course increased complexity.
With the addition of two further measurements, allowing to determine the average falling time, an accuracy increase is observed for the acoustic stopwatch (98%) and h ≥ 1.50 m, while the use of the accelerometer with direct data extraction allows to reach higher accuracy (above 99 %) for every starting height, and can thus be suggested as best compromise between high accuracy and easy operation. The use of average measurement and data extraction with Excel provides the same accuracy, but it is more complex, thus it is not recommended.
Moving to methods requiring spreadsheet software for data analysis, to verify the actual nature of the motion, i.e., uniformly accelerated, again all the methods provide visually good data. When accuracy is considered, the best compromise between accuracy and complexity is provided by the use of the accelerometer with direct data extraction and average of many measurements.
Finally, we demonstrated that the combination of the video of the free fall motion and video analysis with Tracker allows to determine the motion temporal law with a qualitative agreement with the expected one. However, beyond the general complexity of the procedure for the determination properly calibrated ball position as a function of time, the method was demonstrated not reliable to quantitatively obtain the g value without professional data analysis techniques. The g value extracted from an Excel data analysis strongly depends on the initial instant value, leading to a rather poor accuracy (down to about 90%) even without making any error. In addition, if an error of just one frame is made in the determination of the release time the accuracy can decrease down to 85 %.
A proper correction of the image distortion and the use of professional fitting program allows to reach accuracy of about 98%, that remains lower than the much simpler techniques based on the falling time dependence on the starting height.
Among all the methods and experimental procedures, the best choice is given by the g determination from the falling time measurement from a known starting height, the use of the internal accelerometer with direct data extraction and average of three falling time measurements. This technique is overall simple, fast, and does not require any external software of data processing, except a standard calculator. The only aspect that requires care is the fast release of the smartphone and a bit of attention in correctly determining the starting and final times from the acceleration temporal dependence. While the 3B-Scientific set-up is unbeatable in terms of absolute accuracy and versatility in performing many falling time measurements easily and quickly, it is interesting to observe that the best smartphone-based method allows to obtain overall similar performances in terms of relative accuracy (99% against 99.6%) with a relative statistical uncertainty of just 1% (20 times higher than the 3B-Scientific one).
Funding
This research received no external funding.
Data Availability Statement
The data in this manuscript can be shared with interested people by directly contacting the author.
Acknowledgments
Maria Luisa De Giorgi is acknowledged for useful discussions along all the paper preparation, my two sons Raimondo (12 years old) and Filippo (8 years old) are acknowledged for repeating part of the measurements to check the suitability of the different methods to be reproduced.
Conflicts of Interest
The author declares no conflict of interest.
References and Notes
- Sukariasih, L.; Erniwati.; Sahara, L.; Hariroh, L.; Fayanto, S. Studies The Use Of Smartphone Sensor For Physics Learning. Int. J. Sci. Technol. Res. 2019, 8, 862–870. [Google Scholar]
- Lincoln, J. Five smartphone experiments that do not need apps. Phys. Teach. 2018, 56, 652–653. [Google Scholar] [CrossRef]
- Countryman, C.L. Familiarizing Students with the Basics of a Smartphone’s Internal Sensors. Phys. Teach. 2014, 52, 557–559. [Google Scholar] [CrossRef]
- Onorato, P.; Malgieri, M.; Ambrosis, A.D. Quantitative analysis of transmittance and photoluminescence using a low cost apparatus. Eur. J. Phys. 2015, 37, 015301. [Google Scholar] [CrossRef]
- Listiaji, P.; Salma Darmawan, M.; Daeni, F.; Karmuji. Comparison between the use of acceleration sensor and video tracker on smartphone for spring oscillation experiment. Phys. Educ. 2020, 56, 013001. [Google Scholar]
- Vogt, P.; Kuhn, J. Analyzing free fall with a smartphone acceleration sensor. Phys. Teach. 2012, 50, 182–183. [Google Scholar] [CrossRef] [Green Version]
- Ogawara, Y.; Bhari, S.; Mahrley, S. Observation of the magnetic field using a smartphone. Phys. Teach. 2017, 55, 184–185. [Google Scholar] [CrossRef]
- Hawley, S.H.; McClain, R.E. Visualizing Sound Directivity via Smartphone Sensors. Phys. Teach. 2018, 56, 72–74. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, J.; Vogt, P. Analyzing acoustic phenomena with a smartphone microphone. Phys. Teach. 2013, 51, 118–119. [Google Scholar] [CrossRef]
- Girot, A.; Goy, N.A.; Vilquin, A.; Delabre, U. Studying Ray Optics with a Smartphone. Phys. Teach. 2020, 58, 133–135. [Google Scholar] [CrossRef]
- Pons, A.; García-Martínez, P.; Barreiro, J.C.; Moreno, I. Learning Optics using a smart-phone. In Proceedings of the ETOP 2013 Proceedings, Optical Society of America, Porto, Portugal, 23–26 July 2013; p. EWP13. [Google Scholar]
- Staacks, S.; Hütz, S.; Heinke, H.; Stampfer, C. Advanced tools for smartphone-based experiments: Phyphox. Phys. Educ. 2018, 53, 045009. [Google Scholar] [CrossRef] [Green Version]
- Wright, K. Smartphone Physics on the Rise. Physics 2020, 13, 68. [Google Scholar]
- Stampfer, C.; Heinke, H.; Staacks, S. A lab in the pocket. Nat. Rev. Mater. 2020, 5, 169–170. [Google Scholar] [CrossRef]
- Oliver, W.R.; Pirie, J. Measurement of g by free fall. Phys. Educ. 1969, 4, 49–51. [Google Scholar] [CrossRef]
- Lindemuth, J. The Effect of Air Resistance on Falling Balls. Am. J. Phys. 1971, 39, 757–759. [Google Scholar] [CrossRef]
- Walton, D.S. A simple apparatus for the determination of g by free fall. Phys. Educ. 1974, 9, 80–81. [Google Scholar] [CrossRef]
- Bunker, K. A new free-fall experiment to determine the acceleration due to gravity. Phys. Educ. 1991, 26, 386–390. [Google Scholar] [CrossRef]
- Rueckner, W.; Titcomb, P. An accurate determination of the acceleration of gravity for lecture hall demonstration. Am. J. Phys. 1987, 55, 324–330. [Google Scholar] [CrossRef]
- Krieger, M.E.; Stith, J.H. Spreadsheets in the physics laboratory. Phys. Teach. 1990, 28, 378–384. [Google Scholar] [CrossRef]
- See for Example Anderson, M. “How to Measure Gravity with a Pencil, Paper and a Smartphone”. Available online: https://www.youtube.com/watch?v=q_fh8WKqVCw (accessed on 15 July 2021).
- See for Example “Smartphone Experiment: Free Fall”. Available online: https://www.youtube.com/watch?v=zRGh9_a1J7s (accessed on 15 July 2021).
- Brown, D.; Cox, A.J. Innovative Uses of Video Analysis. Phys. Teach. 2009, 47, 145–150. [Google Scholar] [CrossRef] [Green Version]
- Tracker can be Freely Downloaded at the Link. Available online: https://physlets.org/tracker/ (accessed on 15 July 2021).
- Even it Excel does not directly provide the error bar on the best fit parameters an estimate of the slope uncertainty can be obtained with the LINEST option.
- Moritz, H. Geodetic Reference System 1980. J. Geod. 2000, 74, 128–133. [Google Scholar] [CrossRef]
- Actually the possible problems in accurately determining the falling time are clearly written in the app and could be exploited for teaching the importance of a properly calibrated instrument in order to correctly quantify a physical quantity (it would be for example very easy to simultaneously use all the smartphones of the students in the classroom in order to compare the results as a function of the smartphone brand, model and so on).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).