Unsupervised Real-Time Anomaly Detection in Hydropower Systems via Time Series Clustering and Autoencoders

Abstract

Hydropower plants generate large volumes of data with high-dimensional time series, making early anomaly detection essential for monitoring, preventive maintenance and cost reduction. This study addresses the challenge of detecting anomalies in real time without labeled failure data by proposing an unsupervised approach that combines time series clustering, autoencoder-based models, and an adaptative anomaly thresholding. Initially, a clustering process is applied to historical time series data from multiple sensors in a hydroelectric power plant to identify groups of variables with similar temporal dynamics. Subsequently, for each cluster, various unsupervised models are trained to learn the normal behavior of the variables, including ARIMA, Autoencoders, Variational Autoencoders, Long Short-Term Memory networks, Sliding-window Autoencoders and Sliding-window Variational Autoencoders. Among these, the Autoencoder model demonstrated superior performance and was selected for real-time deployment. Finally, anomalies were detected by comparing predicted and actual values, using an adaptative threshold based on prediction errors. The system was tested on a real hydropower plant with over 150 time-dependent variables. The results show that 97% of the variables achieved an R² score above 0.8, with low MAE values indicating high reconstruction accuracy. The proposed approach, deployed in a real-time system integrated with Grafana dashboards, demonstrates the system’s capability to detect anomalies.

1. Introduction

Hydroelectric power plants play an essential role in the global transition toward sustainable energy. Their operation, however, involves complex processes and critical infrastructure that demand reliable monitoring and control strategies to maintain efficiency, safety, and compliance with environmental standards [1].

Within these facilities, control devices regulate the flow of water and the generation of electricity, ensuring stable and secure performance. Malfunctions in these systems can lead not only to costly interruptions but also to significant environmental disturbances in nearby ecosystems [2]. It may also significantly affect the operation and supply of electricity and could even lead to legal or regulatory sanctions. For these reasons, control systems for turbine speed, frequency, and excitation, among others, are of critical importance.

Despite their advantages, the operation of hydroelectric power plants involves numerous technical challenges due to the dynamic behavior of water flow, mechanical components, and electrical systems. Any malfunction or deviation in these subsystems can result in efficiency losses, costly downtime, or even hazardous situations with environmental, penalization, and regulatory consequences. Therefore, monitoring key variables such as water flow rate, turbine speed, active power and excitation levels is essential for early detection of abnormal conditions. Traditional threshold-based monitoring systems, however, may fall short in identifying complex patterns or subtle deviations, especially in large-scale systems with high variability. In this context, the integration of unsupervised machine learning techniques for anomaly detection offers a promising approach to enhance situational awareness and support timely decision-making [3].

This study proposes an artificial intelligence system for anomaly detection in the monitoring variables of a hydroelectric power generation unit, leveraging unsupervised machine learning techniques. The approach is designed to identify deviations from normal operating behavior without the need for labeled fault data, which is often unavailable in industrial contexts.

Anomaly detection techniques are useful for identifying deviations from standard operating conditions in industrial equipment, systems, or infrastructure. By continuously analyzing sensor data, vibration patterns, active power, temperature variations, or other relevant indicators, early signs of abnormal behavior can be detected [4,5]. This enables timely maintenance interventions, reduces unexpected downtime, and enhances operational efficiency.

Anomalies, understood as unexpected or irregular events, can generally be classified into three types: point, contextual and dynamic anomalies [6,7]:

• Static or point anomalies refer to isolated data points that differ significantly from expected behavior, such as a sudden spike in energy consumption, an abrupt rise in pipeline pressure, a malfunctioning sensor, or an unexpected drop in water level.
• Contextual refers to data points that are only considered anomalous within a specific context, such as time, location, or operational conditions—for example, a high temperature that is normal in summer but abnormal in winter.
• Dynamic anomalies, also called temporal or collective anomalies, involve a sequence of data points that together form an anomalous pattern over time. An example is the gradual deterioration of a turbine, where multiple variables slowly drift from normal ranges until failure occurs.

Given the context of this study, focused on time series data and the continuous monitoring of system behavior over time, we chose to concentrate exclusively on the detection of temporal anomalies. These types of anomalies are particularly relevant in industrial settings where early signs of failure or performance degradation often manifest gradually through subtle changes in trends or patterns. While point and contextual anomalies can provide useful alerts for isolated events, our goal was to identify evolving abnormal behaviors that may indicate underlying issues requiring preventive action.

One of the key challenges in anomaly detection is the identification of suspicious patterns in datasets that contain no prior examples of failures. Although this is a long-standing problem, recent advancements have introduced a variety of approaches based on statistical methods and machine learning techniques.

Machine learning techniques offer powerful tools for detecting complex and non-linear patterns in data. Within the context of the Fourth Industrial Revolution and the ongoing digital transformation of industry, artificial intelligence (AI) has emerged as a key driver of technological innovation, enabling systems that replicate aspects of human reasoning and perception [8]. Among its main fields, AI encompasses machine learning, natural language processing, and computer vision. Machine learning, in particular, allows systems to identify patterns and improve their performance based on historical data. It is commonly categorized into supervised and unsupervised approaches. The former relies on labeled datasets to train predictive models, while the latter is used to reveal underlying structures or relationships in unlabeled data.

Given the critical need to ensure the reliable and efficient operation of hydroelectric plants, this study examines the use of unsupervised machine learning methods to detect anomalies in key monitoring variables, focusing specifically on hydroelectric generation units. By leveraging real-world operational data, the proposed approach aims to improve anomaly detection capabilities without relying on historical failure labels. The results of this study contribute to the development of more robust and intelligent monitoring systems, supporting preventive maintenance strategies and ultimately enhancing the reliability and sustainability of hydroelectric power generation.

To address this challenge, this study introduces an unsupervised anomaly detection framework that integrates time series clustering and autoencoder-based reconstruction models. The clustering process autonomously groups variables according to their temporal dynamics, enabling the training of specialized detection models for each behavioral category. The framework operates in real time, leveraging adaptive thresholds to identify deviations from the normal operational patterns of each cluster.

Unlike traditional supervised approaches, the proposed method does not require labeled data and can generalize across heterogeneous sensors by learning representative temporal embeddings. Furthermore, the system is fully integrated into an industrial monitoring environment through Grafana and Microsoft Azure, demonstrating its applicability for online detection and visualization.

1.1. Related Works

The literature on anomaly detection in industrial systems spans a wide range of approaches, from model-based and statistical techniques to modern unsupervised learning and deep neural architectures. In the specific context of hydropower systems, these methods have been explored to enhance reliability and enable early fault detection in key operational variables. This section reviews the most relevant contributions in three main areas: (1) the application of unsupervised anomaly detection in hydropower systems, (2) general unsupervised techniques for time series anomaly detection, and (3) modeling strategies for multivariate systems, including the proposed cluster-based approach that balances scalability and accuracy.

1.1.1. Anomaly Detection in Hydropower Systems

Several studies have applied unsupervised anomaly detection techniques to hydroelectric and hydropower systems. For instance, De Santis and Costa [9] evaluated the use of the Extended Isolation Forest model for fault detection in small hydroelectric power plants, comparing it with PCA-based models. Using one year of operational data, the model demonstrated good performance and lower variability, standing out as a suitable option for online monitoring applications in the hydroelectric sector.

On the other hand, Rai [10] presented a comparative study of unsupervised anomaly detection techniques in time series, such as One-Class SVM and Isolation Forest, applied to the monitoring of machines in hydropower plants using sensor data. These techniques allowed the identification of abnormal behaviors that may indicate potential failures, contributing to more efficient monitoring.

Similarly, Guan et al. [11] proposed a new anomaly detection algorithm for multivariate time series (VSAD), designed to monitor complex physical equipment. VSAD combines spatial–temporal graph networks with variational autoencoders to capture temporal and spatial dependencies in sensor data, operating in an unsupervised manner. It also uses an automatic strategy for threshold selection.

Yang et al. [12] proposed a real-time anomaly detection system for small hydropower plant clusters, based on a single multivariate model that simultaneously analyzes multiple variables; the system integrates multivariate time series analysis with a combination of Z-score and multivariate Dynamic Time Warping (DTW). These works demonstrate that unsupervised learning approaches are effective in capturing abnormal events in hydropower operations, even in the absence of labeled failure data.

1.1.2. Unsupervised Anomaly Detection Techniques

In unsupervised machine learning, anomaly detection has been widely studied due to the scarcity of labeled failure data in real-world systems. Detection of point and contextual anomalies commonly includes methods such as K-nearest neighbors [13], Isolation Forest [14], One-Class SVM [15], K-means [16] and DBSCAN [17]. Contextual anomalies extend point anomaly detection by incorporating additional contextual variables, such as time, location, or operational conditions, into the analysis [18]. In contrast, dynamic or temporal anomalies, which involve sequences or patterns over time, are typically addressed using time series models such as ARIMA, Autoencoders, Variational Autoencoders and Long Short-Term Memory (LSTM) networks [19]. These methods are especially effective in identifying gradual deviations or collective behaviors that would not be detectable through single-point analysis. This study addresses the challenge of unsupervised detection of dynamic or temporal anomalies.

A traditional approach is the ARIMA model (AutoRegressive Integrated Moving Average), which has been used to predict future values from historical data to identify anomalies when the observed values deviate significantly from the model’s predictions. ARIMA remains effective for univariate time series that show autocorrelation and non-stationary trends by combining three components to capture temporal dependencies in the data such as autoregression (AR), integration (I), and moving average (MA) [20].

However, in many industrial applications, variables have nonlinear interactions. In these cases, Autoencoders, which are artificial neural networks used for unsupervised learning, include an architecture with an encoder that compresses high-dimensional inputs into a latent representation and a decoder that reconstructs the original input. Training aims to minimize the difference between the original and reconstructed data, often using a loss function such as the Mean Squared Error [21]. When the reconstruction error exceeds a defined threshold, the instance is flagged as an anomaly, indicating that it differs from the learned patterns of normal operation.

The Variational Autoencoder (VAE) extends the standard autoencoder by incorporating probabilistic modeling. Instead of generating a single latent representation, the VAE learns a distribution, typically a multivariate Gaussian, characterized by mean and variance parameters. During training, the model uses variational inference to approximate the posterior distribution of latent variables. The encoder maps the input into this latent distribution, samples are drawn, and the decoder reconstructs the original input. The objective function includes both a reconstruction loss, which measures fidelity, and a regularization term based on the Kullback–Leibler divergence, encouraging the learned distributions to remain close to a prior, usually a standard normal [22].

Recurrent Neural Networks (RNNs), particularly the Long Short-Term Memory (LSTM) architecture, are specifically designed to model sequential data such as time series. LSTMs address the limitations of traditional RNNs by effectively learning long-term dependencies and mitigating the vanishing gradient problem. Their capacity to capture complex temporal dynamics makes them particularly suitable for detecting subtle or evolving anomalies over time. The construction of a sequential LSTM model is carried out progressively by adding layers one after another, each based on the LSTM architecture. Every LSTM layer in the model consists of a specific number of units (or nodes) that process information in a step-by-step manner [23]. This sequential structure allows the network to learn patterns and dependencies over time, making it particularly effective for tasks such as time series forecasting, natural language processing (NLP), and other applications involving sequentially organized data.

A variation of autoencoders known as sliding-window models processes time series data by applying a fixed-length window of size L that slides step by step along the temporal axis. Each window captures a local segment of the data, preserving temporal dependencies [24]. These overlapping segments are used to train the autoencoder to reconstruct normal patterns within each window.

The literature review reveals that unsupervised methods have become increasingly important in the field of time series anomaly detection, primarily due to the scarcity of labeled data in real-world applications. In particular, dynamic anomalies demand models capable of capturing sequential dependencies, multivariate relationships, and subtle changes in temporal patterns. Table 1 summarizes some of the most widely used unsupervised methods for dynamic anomaly detection, providing a brief description of each technique along with scientific references that demonstrate their successful application in this domain.

Table 1. Unsupervised machine learning methods for dynamic anomaly detection.

Reference	ML Technique	Description
[25,26]	ARIMA	Captures temporal patterns using autoregressive and moving average components
[27,28,29,30]	Autoencoders	Neural network trained to reconstruct input data; anomalies are inferred from reconstruction error.
[22,31]	Variational Autoencoder (VAE)	Learns latent representations and reconstructs input; high reconstruction error suggests anomalies
[32,33,34]	LSTM	Recurrent neural network that learns long-term dependencies in time series.

1.1.3. Unsupervised Anomaly Detection in Multivariate Systems

The traditional approach for multivariate systems involves training a separate model for each variable or sensor. Techniques such as ARIMA, Isolation Forest, and Autoencoders are typically applied to individual time series, identifying anomalies based on deviations from their expected behavior [35,36]. This strategy makes it possible to capture the specific dynamics and error characteristics of each variable; however, it tends to be computationally demanding and scales poorly when monitoring large numbers of signals simultaneously.

In contrast, some researchers have explored alternative strategies that use a single multivariate model to analyze all variables jointly [37,38]. These methods take advantage of the relationships between variables through architectures such as multivariate Autoencoders, Long Short-Term Memory (LSTM) networks, and Graph Neural Networks, allowing for a more integrated view of system behavior. Although they can capture cross-variable relationships, their performance may degrade when variables have heterogeneous behaviors or operate on different scales.

An intermediate and scalable alternative followed in this study involves grouping variables with similar temporal dynamics through time series clustering and then training specialized anomaly detection models for each cluster [39]. This hybrid approach combines the interpretability and adaptability of variable-specific models with the generalization capabilities of multivariate models. It enables the detection of dynamic anomalies across similar operating patterns while significantly reducing computational complexity.

Time series clustering has been widely used to group variables that exhibit similar temporal dynamics, supporting pattern discovery, anomaly detection, and forecasting in complex systems. Several clustering algorithms can be applied depending on the structure and objectives of the analysis.

Traditional partition-based methods, such as K-Means [16] and K-Medoids [40], group time series according to similarity measures like Euclidean distance or Dynamic Time Warping (DTW) [41]. Hierarchical clustering builds nested partitions that are useful when the number of clusters is unknown or when multilevel aggregation is needed [42]. Density-based approaches, such as DBSCAN, identify arbitrarily shaped clusters and are effective in detecting noise and outliers [43]. More recently, dynamic clustering techniques have been introduced to adapt cluster structures over time as data distributions evolve [44,45].

Comparative evaluations of clustering techniques for time series highlight that no single method universally outperforms others; the optimal choice depends on data characteristics and computational constraints. However, several reviews highlight K-means as the most frequently adopted clustering algorithm due to its simplicity, stability, and suitability for high-frequency operational data [16,46,47]. These findings support its selection in this study as an effective balance between interpretability, clustering quality, and computational efficiency for grouping variables by temporal dynamics prior to model training.

1.1.4. Comparative Analysis

The reviewed literature shows that unsupervised learning techniques have been widely applied to hydropower systems, mainly through models such as Isolation Forest, One-Class SVM, and PCA-based methods. These approaches effectively detect abnormal behavior but are typically limited to small-scale or single-variable implementations.

Time-series-based methods such as Autoencoders, Variational Autoencoders, and LSTM networks have proven more suitable for detecting dynamic anomalies, as they capture gradual temporal deviations that point-based techniques cannot. However, their complexity and computational cost highlight the need for approaches that maintain both accuracy and efficiency.

In multivariate contexts, traditional per-variable models offer interpretability but poor scalability, while fully multivariate architectures capture dependencies at the expense of transparency. The cluster-based strategy adopted in this study provides a balanced alternative—grouping variables with similar dynamics to enable scalable, interpretable, and accurate anomaly detection in complex industrial environments.

1.2. Research Significance

The increasing complexity and scale of monitoring systems in hydroelectric power plants pose significant challenges for ensuring operational reliability and early fault detection. Traditional rule-based or supervised anomaly detection approaches often require extensive labeled datasets and expert-defined thresholds, which are not scalable across diverse systems or adaptable to dynamic operational conditions. This research addresses these limitations by proposing a framework for real-time anomaly detection in hydropower systems using (1) time series clustering, (2) unsupervised anomaly detection models, and (3) an adaptative anomaly thresholding.

The time series clustering allows the autonomous characterization of different types of variables based on their temporal behavior and definition of tailored anomaly detection models accordingly. The use of unsupervised anomaly detection models enables the system to learn latent representations of normal patterns without requiring labeled anomalies, which is particularly valuable in industrial settings where annotated data is scarce or unreliable. The models use historical power data and cluster representatives to capture typical variable behavior, distinguishing between normal fluctuations during startup/shutdown and potential anomalies when power remains stable. Moreover, the adaptive anomaly thresholding mechanism based on prediction error variance enhances the robustness of the detection process, reducing false positives and negatives.

This work provides a scalable and generalizable solution that can be extended to other hydropower units or similar industrial environments. By integrating the models into a real-time visualization dashboard, the system supports operational decision-making and proactive maintenance strategies. Overall, the proposed approach contributes to advancing intelligent monitoring frameworks for critical infrastructure.

2. Materials and Methods

2.1. Problem Statement

Hydroelectric power plants rely on the continuous monitoring of hundreds of operational variables to ensure efficient and safe energy production. Each of these variables generates time-series data, which must be analyzed to detect potential anomalies that could indicate equipment failure, deviations from optimal performance, or safety risks. Given the volume and complexity of the data, manual inspection is infeasible, and traditional one-model-per-variable anomaly detection is computationally intensive and difficult to maintain and monitor.

Let X ∈ ℝ^n×T represent the dataset, where n is the number of sensor variables and T is the number of time steps (e.g., minute-level data over two months). The objective is to detect anomalies for each time series x_i = [x_i1, x_i2, …, x_it], where i ∈ {1, 2, …, n}. The main challenges include:

• Scalability: Designing and maintaining separate anomaly detection models is inefficient.
• Temporal behavior: Anomalies can be either point anomalies (sharp outliers) or temporal anomalies (gradual drift), requiring distinct detection strategies.
• Similarity among variables: Some variables may exhibit similar patterns, suggesting potential for grouping and shared modeling.

2.2. Proposed System Architecture

To address the problem of identifying deviations in the monitoring variables of a hydroelectric generation unit, we propose an anomaly detection architecture based on time series clustering, autoencoders models and an adaptive anomaly thresholding. Time series clustering enables grouping of variables with similar temporal behavior [48], autoencoders learn the normal patterns within each group to detect deviations, and adaptive thresholding dynamically adjusts the sensitivity of anomaly detection based on the characteristics of each variable. This solution is designed to operate on real-time data streams, enabling continuous and proactive monitoring of system behavior.

The proposed architecture consists of two core processes. First, a set of unsupervised anomaly detection models is developed using historical data that is labeled as anomaly-free. These models are designed to detect deviations in the temporal patterns of the monitored variables. Second, the trained models are then applied to incoming real-time data to detect unusual events that could affect the operation of the generation unit.

2.2.1. Anomaly Detection Models Creation

The construction of the anomaly detection models followed a systematic process starting with exploratory analysis of historical datasets confirmed to be free of anomalies. Next, the time series were segmented based on the monitored variable or system component and then grouped using the k-means clustering technique. For each resulting cluster, we built unsupervised detection models, which were constructed and trained exclusively on normal data so that, once deployed, they could detect significant deviations from the learned behavior. The complete architecture of this process is illustrated in Figure 1, showing the sequential steps from raw data input to the final model generation.

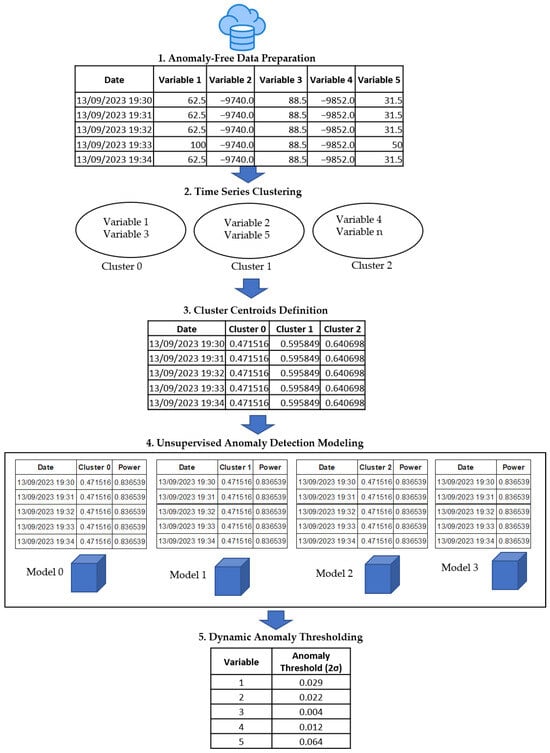
Figure 1. Anomaly detection model creation.

The creation of anomaly detection models follows these stages:

• Anomaly-Free Data Preparation: To develop reliable anomaly detection models, it is essential to start with a dataset that is free of anomalies. This phase included data preprocessing steps such as anomalies cleaning, handling of missing values, and variable standardization. This ensures that the models learn the normal behavior patterns without being biased by abnormal conditions.
• Time Series Clustering: Detecting anomalies for each variable independently would require developing a large number of individual models. To mitigate this, we propose a time series clustering approach that groups variables exhibiting similar temporal behavior. The dataset was transposed so that each row represents a variable and each column a timestamp. The K-Means algorithm was applied to identify clusters of variables with similar time series patterns, enabling the development of a single detection model per cluster. This step allowed the identification of common behavioral patterns and the development of specialized models for each cluster. K-means was chosen for its simplicity and efficiency in partitioning large datasets.
• Cluster Centroids Definition: For each cluster obtained, a centroid was calculated to represent the average time series behavior of the variables within the group. The centroids were then transposed, so that each cluster was represented as a column and each row corresponds to a time point, forming the basis for model training.
• Unsupervised Anomaly Detection Modeling: Each cluster centroid was used to train unsupervised anomaly detection models, including ARIMA, Autoencoder, VAE, LSTM, Sliding-window Autoencoders and Sliding-window VAE. These models were trained using the historical power data and the cluster representative, capturing the typical behavior of the associated variables. Power must be considered because it directly reflects the system’s energy consumption, and anomalous changes in its behavior may indicate operational failures, inefficiencies, or atypical process conditions. Furthermore, variable behavior may vary significantly during system startup or shutdown; in such scenarios, fluctuations should not be flagged as anomalies. However, if fluctuations arise while power remains stable, they may indeed signal anomalous behavior.
• Adaptive Anomaly Thresholding: Anomalies were identified by comparing the predicted value of a variable with its actual value. If the discrepancy exceeds a defined threshold, it is flagged as an anomaly. However, determining an appropriate threshold is nontrivial. A fixed threshold may result in false positives or missed anomalies. To address this, we defined the anomaly threshold based on the predictive reliability of the model. When the model exhibits low prediction error, even small differences may indicate anomalies. In contrast, models with higher error require more tolerant thresholds to avoid misclassification.

2.2.2. Real-Time Anomaly Detection

The real-time anomaly detection phase is designed to identify deviations in sensor data streams during the continuous operation of the hydroelectric power plant. The complete workflow described above is illustrated in Figure 2.

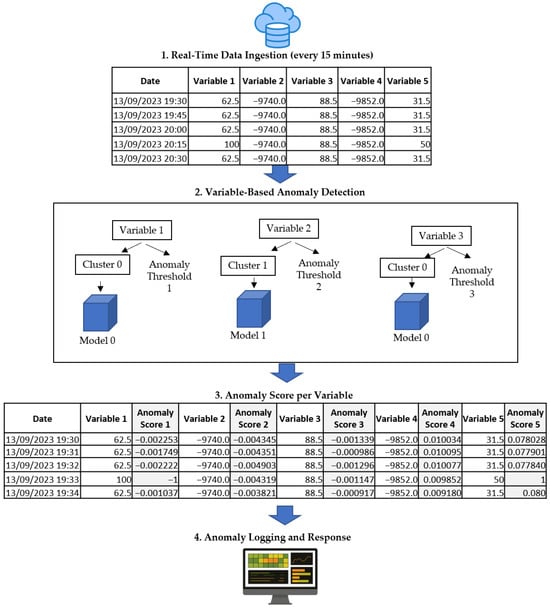
Figure 2. Real-time anomaly detection.

This stage involves the following steps:

• Real-Time Data Ingestion: During the real-time operation of the hydroelectric power plant, sensor data is continuously collected and stored in the cloud. A scheduled process reads data in fixed time windows (e.g., every 15 min) from the database. Once a time window is retrieved, the anomaly detection routine is executed, with each task placed into a processing queue. This queuing mechanism ensures that results are written back to the database in a sequential and controlled manner.
• Variable-Based Anomaly Detection: Anomalies are detected for each variable individually, using the reconstruction error produced by the autoencoder model corresponding to the assigned cluster. For example, if Variable 1 is assigned to Cluster 0, it will be evaluated using the detection model specifically trained for that cluster. Importantly, each variable uses a specific anomaly threshold, calculated as twice the standard deviation of its own prediction error. This ensures that the detection process is tailored to the behavior and variability of each variable, rather than applying a common threshold across all variables. By combining cluster-specific models with variable-specific thresholds, the method enhances the precision of anomaly detection while reducing false positives.
• Anomaly Score per Variable: For each variable, a new column is added containing the anomaly score. This score quantifies the degree of deviation from normal behavior, as learned by the corresponding model.
• Anomaly Logging and Response: Anomaly scores are stored in the database for future analysis and visualization. Depending on the severity of the detected anomalies, automated responses could be triggered, such as pausing or adjusting operational processes, notifying plant operators, or activating contingency systems.

2.3. Methodology

The development of this project followed a hybrid methodological approach that combines the CRISP-DM (Cross-Industry Standard Process for Data Mining) framework with agile principles inspired by Scrum, as proposed in the Team Data Science Process (TDSP) by Microsoft [49]. This approach enabled a structured yet flexible workflow suitable for iterative development and continuous refinement based on stakeholder feedback.

The project was organized into the following phases:

• Business Understanding: A detailed understanding of the operational context of the power generation systems was developed in collaboration with domain experts. The main objective was defined as the detection of anomalies in high-dimensional sensor data from power plants.
• Data Acquisition and Understanding: Historical datasets from a power generation unit were explored to assess data quality, completeness, and relevance. Particular attention was given to selecting the main operational variables and understanding their typical behavior under normal operating conditions.
• Data Preparation: The time series data were preprocessed to address missing values, outliers, and synchronization issues. Feature engineering was also performed to derive meaningful attributes for the subsequent modeling phase.
• Modeling: The proposed approach involved three main components such as (1) Time series clustering and centroid definition, used to group variables with similar temporal behavior. This step enabled contextual analysis while reducing the total number of models required; (2) Unsupervised anomaly detection models, developed to identify unusual patterns without relying on labeled data; and (3) Adaptive anomaly thresholding, designed to adjust decision boundaries dynamically according to the statistical characteristics of each cluster. This modular structure allowed for flexible experimentation and model calibration, ensuring the proposed solution could generalize across multiple operating scenario.
• Evaluation: Model outputs were evaluated using historical anomalies data and expert judgment. Iterative feedback loops enabled the refinement of model parameters.
• Deployment and Monitoring: A real-time anomaly detection system was implemented using a four-phase architecture: (1) Real-Time Data Ingestion, where streaming data from monitored assets was collected and pre-processed; (2) Variable-Based Anomaly Detection, in which each variable was evaluated independently using the trained models to compute anomaly scores; (3) Anomaly Score per Variable, allowing fine-grained detection and interpretation of abnormal behavior; and (4) An additional module, Anomaly Logging and Response, was used to store alerts and support timely operational response. A real-time dashboard was developed to support continuous monitoring, displaying key operational metrics and detected anomalies.

The implementation followed agile principles inspired by Scrum, using short, iterative development cycles (sprints), periodic review meetings with stakeholders, and a dynamic product backlog to prioritize tasks. This approach enabled the continuous delivery of intermediate results and helped maintain alignment with business objectives throughout the project lifecycle.

2.4. Technical Implementation Specifications

The Table 2 outlines the technical specifications for implementing the proposed solution. For each activity, the applicable methods, quality measures to validate performance, and success criteria are provided. The process is divided into two main stages: Anomaly Detection Model Creation and Real-Time Anomaly Detection.

Table 2. Technical implementation specifications.

Process	Activity	Methods	Quality Measure	Success Criteria
Anomaly Detection Model Creation	Anomaly-Free Data Preparation	Direct query from the database	Number of records retrieved	Records retrieved = Records in the database
	Time series clustering	- K-Means - Elbow method to identify optimal number of clusters	- Inertia - Silhouette score	- Low inertia values - Silhouette score greater than 0.5
	Cluster Centroids Definition	- Averaging the variables in each cluster	- Compare the centroid with a representative variable to verify similar behavior	Cluster centroid should be similar to the variables within its cluster
	Unsupervised Anomaly Detection Modeling	- ARIMA - Autoencoders - VAE - LSTM - Sliding-window Autoencoders - Sliding-window VAE.	- MAE - MAPE - R2	Prediction error < 10% of true values R2 > 0.8
	Adaptive Anomaly Thresholding	Based on statistical analysis of model error distribution	Threshold per variable or cluster	Thresholds defined and validated for all monitored variables
Real-Time Anomaly Detection	Real-time data acquisition	Direct reading from database	Number of records retrieved	Records retrieved = Records in the database
	Anomaly detection per variable	Apply pre-trained models per variable	Not applicable	One anomaly detection model applied to each variable
	Anomaly score per variable	Anomaly identification based on thresholding	Not applicable	Anomaly score generated for each variable
	Anomaly logging in a database	Direct write to database; update if score already exists	Number of correctly inserted records	One score per variable successfully stored in the database

The proposed solution was validated using a modular architecture. The core anomaly detection algorithms were developed in Python 3.10.12. Operational data from the hydroelectric plant is retrieved from a cloud-based Azure platform, ensuring secure and scalable access to real-time data. Detected anomalies are stored in a MySQL database, serving as a centralized repository for historical and current alerts. Finally, a real-time dashboard was built using Grafana to visualize the anomaly alerts across different systems of the plant, enabling continuous monitoring and timely decision-making.

2.5. Use of Generative AI Tools

This study was conducted using real-world data. All figures and tables were produced by the authors. The study design, proposed methodology, and validation of results were entirely conceived and executed by the research team. Generative AI tools, specifically ChatGPT-4 and Gemini 1.5 Pro, were used to assist in drafting certain code segments; however, all code was thoroughly reviewed, tested, and validated by the authors. These tools were also employed to support language editing and the refinement of selected text sections. The authors assume full responsibility for the accuracy, integrity, and originality of the manuscript.

3. Results

To address the problem of identifying deviations in the monitoring variables of a hydroelectric generation unit, this study leverages real-time operational data from ISAGEN S.A. E.S.P., one of Colombia’s leading electricity generation companies. ISAGEN (https://www.isagen.com.co/es/home) operates several hydroelectric, solar and wind power plants across the country.

The plants are equipped with a multi-level monitoring and control architecture. Data is collected from real-time measurements of the control systems of the generation units and is used to feed a model for anomaly detection. Generation unit control systems integrate various controls over main equipment, such as unit control, speed and voltage regulators, transformer control, among others. A system installed at the plants collects and stores 228 operational variables in one power plant. These variables are continuously monitored and provide a comprehensive, real-time view of plant operations. All data is stored in a centralized storage, making it accessible for further analysis and integration into machine learning models.

By analyzing this data, the proposed anomaly detection model aims to identify abnormal patterns that may indicate potential faults or performance deviations in the generation unit, enhancing operational reliability and preventive maintenance strategies.

3.1. Anomaly Detection Models Results

The process of building the anomaly detection models is described below, detailing the main steps involved in data preparation, clustering, model training, and adaptive thresholding.

3.1.1. Anomaly-Free Data Preparation

The dataset used in this study was collected over a three-month period from the monitoring systems of a power plant operated by ISAGEN (Medellín, Colombia). After an initial inspection, a total of 149 variables were selected, corresponding to a one unit of generation in a power plant, based on one-minute frequency measurements. Furthermore, a classification of the variables was conducted according to the control systems to which they belong within the power generation unit (see Figure 3).

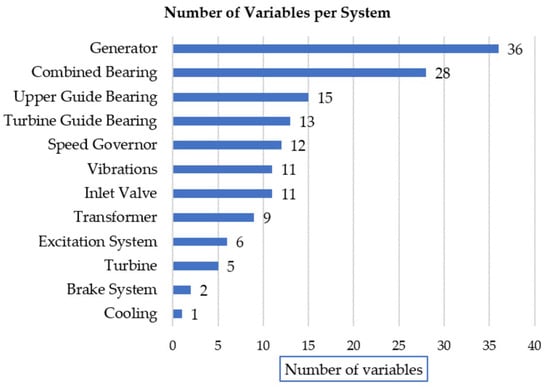
Figure 3. Distribution of variables across systems.

The dataset was split into two subsets:

• Training Set: This subset was used to train machine learning models for anomaly detection based on two-months historical operational behavior. The training set undergoes a cleaning process to ensure that the models were trained on data free from anomalies.
• Testing Set: This one-month subset was reserved for evaluating the performance of the models and validating the error thresholds used to differentiate between normal and anomalous behavior. The test set is divided into two subsets: one clean and another containing known anomalies.

As part of the data cleaning process, outliers were removed, missing values were handled, time series were verified to be complete at one-minute intervals, and all variables were standardized to ensure consistency across the dataset.

3.1.2. Time Series Clustering

The time series clustering process aims to autonomously characterize groups of variables that share similar temporal behavior, allowing the definition of tailored anomaly detection models for each type of dynamic pattern. Instead of training a separate model for each of the 149 monitored variables, clustering enables grouping them into representative categories of operational behavior, thus improving scalability and model generalization.

Several clustering algorithms can be applied to time series data, including K-Means, K-Medoids, hierarchical clustering, density-based methods such as DBSCAN, and dynamic clustering methods. Among them, K-Means offers a robust trade-off between interpretability, computational efficiency, and scalability, particularly in applications involving large sets of synchronized time series such as hydroelectric monitoring systems [46,47,50].

While alternative methods like DTW-based, density-based, or dynamic clustering can better capture local misalignments or non-stationary behaviors, their higher computational cost and complexity make them less practical for real-time industrial implementations.

Therefore, the use of K-Means in this study aligns with prior evidence and domain-specific literature, ensuring both methodological consistency and computational feasibility. On the other hand, the elbow method is a visual technique used to determine the optimal number of clusters [51]. It involves running the algorithm for a range of cluster numbers and plotting the resulting inertia (a measure of how internally compact the clusters are). As the number of clusters (k) increases, the inertia decreases. The goal is to identify the point where adding more clusters yields diminishing returns, this point forms an “elbow” in the graph.

As seen in Figure 4, the decrease in inertia begins to level off progressively after k = 16, indicating that adding more clusters beyond this point yields only marginal improvements in the model’s performance.

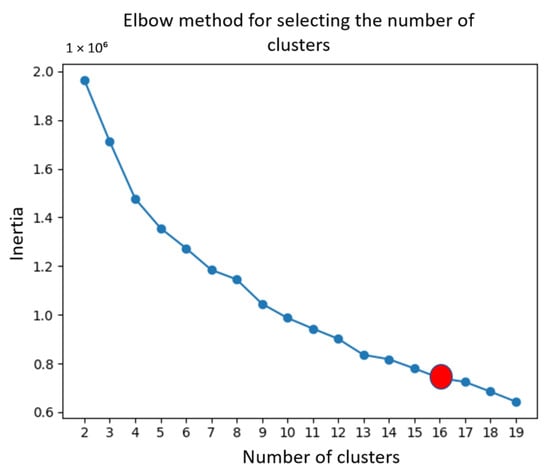
Figure 4. Elbow curve used to determine the optimal number of clusters, where the x-axis represents the number of clusters and the y-axis shows the inertia. The red dot indicates the selected number of clusters.

We selected k = 16 clusters based on the following considerations:

• The inertia continues to decrease meaningfully up to k = 16, suggesting that additional clusters do not contribute valuable segmentation without overfitting the data.
• The distribution of variables across clusters shows a balanced and interpretable structure, with some clusters capturing dominant patterns and others revealing more specialized behaviors.

Therefore, the choice of 16 clusters reflects a well-founded balance between model simplicity and clustering quality.

The Figure 5 shows the proportion of variables assigned to each of the 16 clusters generated. Cluster 11 contains the largest group of variables (34%), followed by Cluster 0 (16%) and Cluster 15 (15%). The remaining clusters represent smaller portions, with each accounting for between 1% and 6% of the total number of variables. This distribution reflects the similarity patterns among the variables based on their behavior, and it serves as the basis for building specialized anomaly detection models for each group.

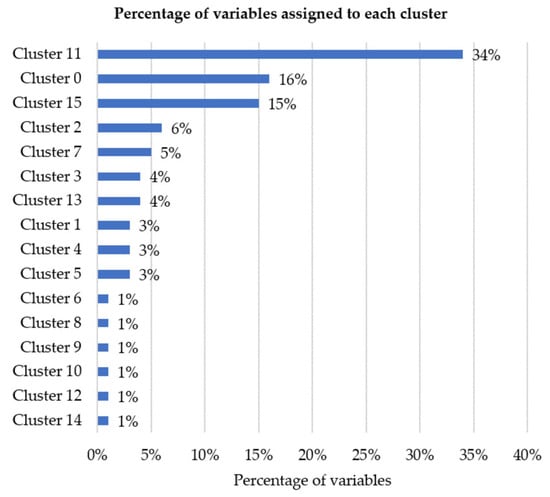
Figure 5. Distribution of variables across the 16 clusters.

3.1.3. Cluster Centroids Definition

The cluster centroids represent distinct patterns of variable behavior observed over time. Figure 6 presents some of the behavior patterns identified in the cluster centroids.

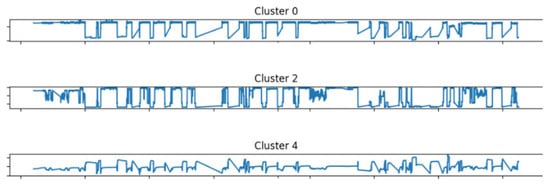
Figure 6. Variable behavior as represented by the cluster centroids, where the x-axis corresponds to time, while the y-axis displays the average values of the clusters.

3.1.4. Unsupervised Anomaly Detection Modeling

Several machine learning techniques were explored to detect temporal anomalies using the training set. It is important to note that this study focused on the detection of dynamic or temporal anomalies, as these are the most representative in hydroelectric power systems, where deviations usually evolve gradually over time. Consequently, classical unsupervised algorithms such as K-nearest neighbors, Isolation Forest, One-Class SVM, K-means, and DBSCAN were intentionally excluded from the modeling experiments because they primarily target point or contextual anomalies.

The selected models belong to the family of time-series-based anomaly detection methods, which are better suited to capture sequential dependencies and evolving operational patterns. The models evaluated were ARIMA, Autoencoder, Variational Autoencoder (VAE), LSTM, Sliding-Window Autoencoder, and Sliding-Window VAE.

This methodological decision ensures that the comparison focuses on approaches capable of handling the temporal nature of industrial process data. The selected models were trained on the historical power behavior and on the centroid of each cluster, which characterizes the overall behavior of the variables. Table 3 presents a sample of the data used to train an anomaly detection model for Cluster 1.

Table 3. Sample of the training dataset for the anomaly detection model of Cluster 1.

Date	Cluster 1	Power
13 September 2023 19:30	0.471516	0.836539
13 September 2023 19:31	0.471516	0.836539
13 September 2023 19:32	0.471516	0.836539
13 September 2023 19:33	0.471516	0.836539
13 September 2023 19:34	0.471516	0.836539

In addition to the 16 models associated with the clusters, an independent anomaly detection model was built for power. By training machine learning models on historical data under normal operating conditions, it is possible to learn the relationships between power output and sensor variables. Using power as a key variable offers several advantages: it synthesizes the operational state into a single metric; it is highly reliable, given the accuracy and stability of power measurements; and it allows for the indirect detection of anomalies, even when no specific sensor shows an explicit fault. In this context, generated power serves as an aggregate indicator of plant functionality. Comparing its behavior with individual sensor signals helps identify inconsistencies that may reveal sensor faults, measurement errors, or abnormal operating conditions. In this way, 17 anomaly detection models were created.

The performance of each model was evaluated on the clean test set using two complementary metrics: the Mean Absolute Percentage Error (MAPE) and the coefficient of determination (R²). The MAPE measures the average relative difference between the observed and reconstructed values as a percentage, where a lower MAPE values indicate smaller differences between the actual and predicted signals.

The R² metric was also used to quantify how well the reconstructed signal fits the original data [38]; values close to 1 suggest that the model successfully explains most of the data variability, values near 0 indicate a poor fit, and negative values reveal that the model performs worse than simply predicting the mean of the observations.

Figure 7 compares the reconstruction performance of the evaluated models, showing the average MAPE and R² across the clusters.

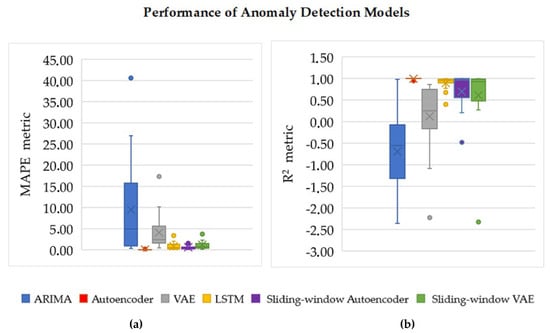
Figure 7. Boxplot comparison of reconstruction performance for six unsupervised models. (a) Mean Absolute Percentage Error (MAPE). (b) Coefficient of Determination (R²). Lower MAPE and higher R² values indicate better reconstruction accuracy.

Given these results, Autoencoder is selected as the most appropriate model for the anomaly detection process due to its consistently high performance across clusters with the higher R² and the lowest MAPE. Although the selected Autoencoder models were trained on cluster centroids, their application requires processing the full set of 149 sensor variables. This discrepancy between the training and inference contexts introduces a significant challenge.

The Autoencoder model architecture was composed of two input features: the cluster centroid and the power. The model architecture followed a symmetric encoder–decoder structure. The encoder consisted of two hidden layers with 60 and 20 neurons, using ‘tanh’ and ‘linear’ activation functions respectively, followed by a latent layer of dimension 2 with a linear activation. The decoder mirrored this structure, reconstructing the input from the latent representation. The latent dimension was set to 2, which is suitable for capturing non-linear dependencies between the input variables while maintaining a compact representation. This configuration is used when the goal is to perform non-linear reconstruction and detect deviations (anomalies) in the relationship between sensor values and power output.

3.1.5. Adaptive Anomaly Thresholding

The anomaly threshold is defined as two times the standard deviation of the prediction error for each variable. Using a threshold of two standard deviations allows for more sensitive anomaly detection compared to the traditional three-standard-deviation rule [52]. In the context of real-time monitoring for early fault detection, this trade-off favors the identification of subtle deviations that may precede critical failures. This adaptive strategy ensures tighter thresholds for more accurate models and more flexible ones for less accurate models.

This adaptive strategy aligns with common statistical practices, where values beyond two standard deviations from the mean are considered outliers:

• For models with low prediction error, the threshold becomes narrower, enabling the detection of even minor anomalies.
• For models with higher variability, the threshold becomes wider, reducing the likelihood of false positives.

This method allows each variable to have a customized threshold based on the distribution of its own reconstruction error, rather than a fixed or arbitrary limit. Table 4 presents the mean and standard deviation of the prediction error for a sample of variables. These values were used to compute the anomaly thresholds as twice the standard deviation, in accordance with the adaptive logic described.

Table 4. Mean and standard deviation of prediction error for some variables.

Variable	Mean Error (μ)	Std. Deviation (σ)	Anomaly Threshold (2σ)
1	0.006	0.014	0.029
2	0.005	0.011	0.022
3	0.030	0.002	0.004
4	0.004	0.006	0.012
5	0.023	0.032	0.064

3.2. Evaluation

To assess the performance of the anomaly detection system, two test subsets were used: the clean test set and the test set containing anomalies.

Initially, the Autoencoder models were evaluated on the clean test set by applying them to all 149 sensor variables, using the cluster assignment of each variable as a reference. The R² evaluation results are summarized in Table 5.

Table 5. Autoencoder models performance by variable on the clean test set.

R2 Value	Number of Variables	Variables
R2 between 0.8–1.0	145	-
R2 between 0.4–0.7	1	37
R2 < 0.4	3	7, 32 and 44

The R² results indicated that 145 variables achieved a good prediction performance, 1 variable had intermediate prediction quality, and 3 variables showed very poor prediction quality. Since 97% of the variables achieved an R² score between 0.8 and 1.0, indicating excellent predictive performance.

In addition to the R² coefficient, the Mean Absolute Error (MAE) was computed to complement the evaluation of reconstruction quality. While R² measures the proportion of variance explained by the model, MAE provides a direct quantification of the average reconstruction deviation in the same scale as the input data. Across the 149 standardized variables, the average MAE was 0.006, with most values below 0.02, indicating that the reconstruction errors were very small relative to the data range. These results are consistent with the R² analysis, where 97% of the variables achieved values above 0.8, confirming that the proposed clustering-based Autoencoder models effectively capture the temporal dynamics of the monitored signals.

Subsequently, the adaptive anomaly detection thresholds were applied to the test set containing anomalous data. As a result, anomalies were detected in nine variables of the hydroelectric system. Figure 8 shows the number of anomalies detected per variable in the test data. The y-axis represents the number of one-minute measurements flagged as anomalous for each variable.

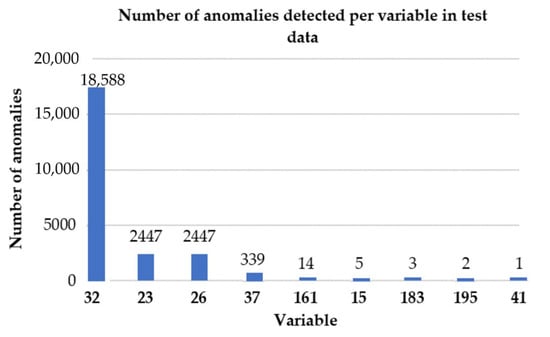
Figure 8. Detected anomalies per variable using the unsupervised detection system on the test set.

3.3. Real-Time Implementation and Monitoring

A real-time anomaly detection system was implemented through a four-phase architecture: (1) Real-Time Data Ingestion, where streaming data from monitored assets is collected and pre-processed; (2) Variable-Based Anomaly Detection, where each variable is independently evaluated using trained models to compute anomaly scores; (3) Anomaly Score per Variable, enabling fine-grained detection and interpretation of abnormal behavior; and (4) Anomaly Logging and Response, a module that stores alerts and supports timely operational responses

The real-time results are visualized through a Grafana dashboard. Grafana is a data visualization tool designed primarily for real-time monitoring and analysis. A customized dashboard was developed to allow users to select a plant, a unit, and two systems, which can then be visualized as heatmaps. The interface allows users to choose a specific subsystem (e.g., Turbine, Admission Valve), and upon selection, it displays time series data of the associated variables. Each variable’s minimum and maximum values are summarized at the top of the dashboard. Additionally, when a variable is selected, a heat map expands to visualize its behavior over time in greater detail, facilitating anomaly detection and operational monitoring.

This development is currently in the implementation phase, aiming to operate as close to real-time as possible. The proof of concept (PoC) incorporates the entire pipeline: data acquisition, machine learning processing, model retraining, and result presentation (including variable deviations) on the Azure platform.

Figure 9 illustrates the architecture of the Azure-based implementation. The system integrates several services to ensure scalability, automation, and real-time operation. Data are collected and stored in Azure Database, transferred to Blob Storage for staging, and processed through Azure Data Factory, which orchestrates ETL and scheduling tasks. Azure Machine Learning executes model training and inference, while the results are visualized in Grafana, allowing operators to monitor system behavior and anomalies continuously.

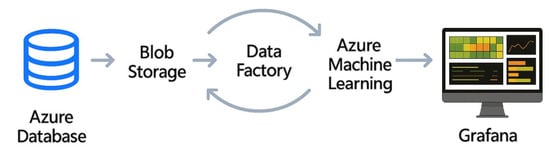
Figure 9. Azure-based implementation architecture integrating data ingestion, processing, modeling, and visualization components.

4. Discussion

The obtained results confirm that combining time series clustering, autoencoder-based models, and adaptive anomaly thresholding provides a scalable and robust solution for real-time anomaly detection in hydropower systems. Grouping variables by temporal similarity enables the definition of specialized models while maintaining computational efficiency and interpretability.

4.1. Discussion on Anomaly Detection Models Creation

The process of model creation demonstrated the advantages of combining time series clustering with unsupervised learning models for dynamic anomaly detection. The application of K-Means clustering effectively reduced the complexity of the system by grouping 149 variables into 16 representative clusters, each capturing similar temporal behaviors. This approach improved scalability and model generalization while preserving the interpretability of the results.

Several unsupervised machine learning techniques were implemented to detect temporal anomalies, based on the results:

• The ARIMA model showed the weakest performance, with a wide range of R² values, including negative scores, indicating poor fit and limited ability to capture the non-linear dynamics of the data. Its high MAPE values also reveal large reconstruction errors, confirming its inadequacy for modeling temporal dependencies in complex signals.
• Autoencoder and LSTM models achieved consistently high R² scores, with the Autoencoder exhibiting the lowest variability, indicating strong and stable reconstruction capabilities. Correspondingly, the Autoencoder obtained the lowest MAPE values across all clusters, confirming its superior reconstruction accuracy and robustness against dynamic variations in the data.
• VAE demonstrated high variability in both R² and MAPE, with some clusters showing poor reconstruction performance. This suggests sensitivity to the complexity of local patterns.
• The sliding-window variants exhibited mixed results, while some samples achieving high R² and low MAPE values, others showed the opposite behavior. This indicates that their performance is sensitive to the selected window length and local fluctuations in the data.

Finally, the Autoencoder was selected as it achieved the highest R² and the lowest MAPE among all evaluated models across the clusters.

The centroid of each cluster represents the dominant temporal behavior, ensuring scalability while acknowledging some loss of local variability. To mitigate this, the autoencoders were applied to all original variables to compute individual reconstruction errors. The results indicated that 145 variables achieved good predictive performance (R² > 0.8), one showed intermediate accuracy, and three displayed poor prediction quality. In addition, the MAE across standardized variables was approximately 0.006, corroborating the high reconstruction accuracy observed through R² and confirming the overall robustness of the proposed framework. These outcomes confirm that the clustering-based modeling approach achieved high consistency across most variables. A future suggestion is to train specific autoencoder models for those four variables, instead of applying the models associated with the clusters.

4.2. Discussion on Evaluation

During the system evaluation using the test dataset containing known abnormal events, anomalies were successfully detected in nine monitored variables (see Figure 8).

An internal review with plant personnel confirmed that these anomalies corresponded to real issues in the measurement data. None of the cases were false positives caused by system start-up or shutdown events. Notably, variable 32 presented 18,558 anomalous measurements, which corresponds to nearly 13 consecutive days of sensor malfunction. This suggests that the sensor associated with variable 32 may have been consistently faulty during that period.

The Figure 10 displays the measurements of the variables in which anomalies were detected. The first column displays the prediction error over time. When the error exceeds two standard deviations from the expected value, it is flagged as an anomaly. The second column displays the actual values (in blue) together with the model predictions (in yellow), allowing a direct visual comparison of the model’s performance. The third column provides a consolidated view that includes the actual variable values (in blue), the detected anomalies (in red), and the system’s power output (in purple).

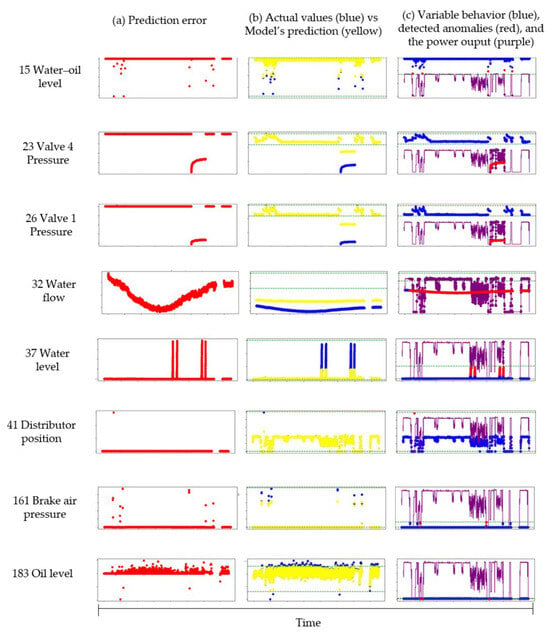
Figure 10. Occurrence of anomalies with fluctuations in system power. Each row of images represents a variable from the hydroelectric system. In each image, the x-axis indicates the date, while the y-axis shows the corresponding measurements of that variable. (a) prediction error over time. (b) Actual values alongside the model’s predictions. (c) Actual variable values, the detected anomalies and the power output.

This visualization helps correlate the occurrence of anomalies with fluctuations in system power, providing useful context for interpretation and potential root-cause analysis:

• First column: Displays the prediction error over time. Anomalies are flagged when the error exceeds two standard deviations from the mean. This statistical threshold highlights instances where the model’s predictions deviate notably from the observed data, suggesting possible abnormal system behavior.
• Second column: The blue points represent the actual measured values of the variable, while the yellow points correspond to the model’s predicted values. When there is a strong alignment, the model is considered accurate. In several cases, the yellow and blue curves diverge clearly around detected anomaly points, reinforcing the validity of the flags.
• Third column: Overlays the actual values (blue), anomalies (red), and power output (purple). The inclusion of power output provides critical operational context. For several variables, anomalies coincide with fluctuations or drops in power, which suggests a possible causal relationship. For example, rows 1, 3, and 6 exhibit clear anomaly peaks in red that align temporally with power dips, hinting at a connection between operational instability and variable behavior.

These results demonstrate the model’s capability to detect sustained anomalies and differentiate them from normal operational fluctuations, confirming its applicability for real-world monitoring scenarios.

4.3. Anomaly Detection Models Limitations

Two of the detected anomalies are associated with variables that exhibited poor predictive performance in the Autoencoder models. This suggests a potential weakness in the system’s ability to accurately model and detect anomalies in certain variables, possibly due to data quality issues, sensor malfunctions, or the inherent complexity of those signals. Specifically, the presence of poorly performing models introduces uncertainty when interpreting anomaly results for those variables, as it becomes difficult to distinguish between genuine anomalies and model inaccuracies.

4.4. Operational Validation and Expert Assessment

The system was monitored using historical data from the same power plant and two additional plants, with datasets covering up to three months of history. During validation, the results closely matched the test outcomes. Only three variables—representing 2% of the total—showed predictions below the average reference levels. A notable false positive occurred in a generating unit that had undergone modernization; the model flagged the change as anomalous because it had been trained on data from the prior configuration, although the new behavior reflected improved operating conditions.

Additionally, a confirmed true positive case was detected in a system involving a cylindrical valve. The algorithm successfully issued an alert approximately four hours before the failure occurred, demonstrating its predictive capabilities.

4.5. Inference and Retraining Time

In the laboratory configuration, the system performs anomaly inference every 15 min to update the Grafana dashboard in near real time, enabling continuous monitoring of hydropower operation variables. The prediction of the most recent 15 min of data requires approximately 0.03 s, confirming that the inference process is almost instantaneous relative to the data sampling interval. Retraining 17 autoencoder models (one per cluster and one for active power) using 22 days of minute-level operational data requires approximately 26 min. The reported retraining time corresponds to execution using a standard configuration with 2 CPU cores; this duration may vary depending on the available computational resources, as multi-core or GPU configurations can substantially reduce training time.

In a Proof of Concept (PoC) deployed at the industrial partner, the anomaly-detection script is executed hourly to analyze the previous 60 min of data. Using a virtual machine with 2 CPUs and 14–28 GB RAM (Microsoft Azure, Redmond, WA, USA), each execution takes approximately 6 min 27 s.

5. Conclusions and Future Work

This study addressed the problem of identifying anomalies in the operation of power generation systems by analyzing high-dimensional sensor data, where each unit contains hundreds of time series variables.

The proposed solution involves developing unsupervised models, particularly autoencoders, to forecast the behavior of key operational variables in energy generation systems. Anomalies are detected by comparing real-time values with model predictions, using an adaptive threshold based on the standard deviation of prediction errors. The system was deployed to operate in real time, enabling early detection of anomalies, which are visualized through an interactive Grafana dashboard. This allows operators to efficiently monitor system performance using heatmaps and customizable filters. The following conclusions are drawn from this work:

• Anomaly detection with unlabeled data: the concept of using process variable data to identify changes in condition and equipment deterioration without the need to label data with specific faults opens up a huge range of applications for effective machine condition monitoring for hundreds of industries that do not have sufficient fault-related data with which to train supervised models. Anomalies detected with unsupervised monitoring systems are a source of information for labeling data and complementing monitoring with supervised systems.
• Effective modeling using cluster centroids: The anomaly detection models were trained on cluster centroids derived from historical operational data, rather than the full dataset. This strategy significantly reduced the training complexity while preserving the essential patterns of system behavior. Despite this abstraction, the models achieved high predictive performance, showing that the centroids captured the main behaviors of the variables without losing relevant operational details.
• Autoencoder as the best-performing model: Among the evaluated techniques, the Autoencoder achieved the highest predictive performance and was selected for the anomaly detection stage. The model learns the typical behavior of each cluster under normal operating conditions by minimizing reconstruction error during training; when applied in operation, deviations between the actual and reconstructed values are interpreted as anomalies. This approach allows the autoencoder to be effectively used for anomaly detection by anticipating deviations from expected behavior before they escalate into failures.
• High performance of unsupervised models: The robustness of the proposed framework was confirmed by the R² and MAE metrics, which showed that the models accurately reconstructed the signals.
• Real-time anomaly detection: The implementation of the real-time system allows for the identification of significant deviations between predicted and actual values, facilitating the timely generation of alerts that can be viewed through a Grafana control panel.
• Intuitive visualization for monitoring: the way the results are presented is crucial to achieving the operator’s level of awareness and focus when working with a large number of variables. Grafana is a platform that achieves this goal by presenting the status of systems that associate groups of variables, allowing the operator to identify the status of an entire machine in a single display in a matter of seconds. Additionally, the operator has the ability to drill down to view the variable that affects the status of a system and the machine.
• The proposed system is scalable and can be extended to other power plants, systems, or industries with similar characteristics, allowing for adaptation to various industrial or energy monitoring contexts.

Future work will focus on enhancing the anomaly detection framework by incorporating Transformer-based architectures to better capture complex temporal and multivariate dependencies. Integration of Transformer-based models could enhance anomaly detection robustness, reduce sensitivity to local noise, and enable a more accurate distinction between transient fluctuations and persistent abnormal trends. Transformers employ self-attention mechanisms that dynamically weigh the relevance of all-time steps across multiple variables, allowing them to capture long-range dependencies, cross-variable correlations, and contextual patterns without relying on predefined sequence lengths. This capability makes them particularly suitable for hydropower systems, where sensor interactions and delayed effects often span extended temporal horizons.

The integration of contextual and maintenance data, such as environmental and operational conditions, will be explored to improve the interpretability and usefulness of detected anomalies for predictive maintenance.