On Transaction-Cost Models in Continuous-Time Markets

Abstract

Transaction-cost models in continuous-time markets are considered. Given that investors decide to buy or sell at certain time instants, we study the existence of trading strategies that reach a certain final wealth level in continuous-time markets, under the assumption that transaction costs, built in certain recommended ways, have to be paid. Markets prove to behave in manners that resemble those of complete ones for a wide variety of transaction-cost types. The results are important, but not exclusively, for the pricing of options with transaction costs.

1. Introduction

Our source of inspiration is the attempt to price options in a continuous-time environment. Black and Scholes developed a model with no transaction costs, under the hypothesis that there are no market imperfections, such as transaction costs, taxes, etc. Since then, there have been numerous different approaches, deviating from their original work, both on the initial assumptions used as well as the existence of transaction costs.

When transaction costs are paid, the arbitrage arguments, as well as the completeness of markets assumptions are not necessarily valid any more. Therefore, one needs to study first how transaction costs are incorporated, then investigate their properties, such as type of cost, time of occurrence, number of payments, etc., and finally explore/address the consequences of the existence of costs to the continuous-time market environment.

Since the Black-Scholes approach, several attempts have been made to improve their result as well as to bring it closer to reality, which was related in part to the inclusion of transaction costs. Initially, proportional costs were added, and later costs that had a fixed and a proportional part (still linear though) were considered. In relation to the addition of proportional costs, we can find among others the work initially of Merton [1] and later of Monoyios [2]. Whalley and Willmot [3] included small transaction costs, while Damgaard [4,5] and Kocinski [6], followed a more global approach. On the other hand, the addition of fixed and proportional costs has been studied by Zakamouline [7] and Amster [8], among others.

With regards to the literature on transaction costs globally, Kabanov and Safarian [9] present a mathematical approach of financial markets with proportional transaction costs. They include a variety of results, focusing on a series of topics, such as approximative hedging, arbitrage theory and consumption-investment problems. Safarian [10] continues to study a hedging problem for European options with transaction costs in incomplete markets, using the concept of risk minimization.

Our contribution mainly lies in the way transaction costs are incorporated. We assume that transaction costs are built as an expression of the form

$$\beta ={\alpha }_0(\Delta Y)+\lambda {(\Delta Y)}^{\Gamma },$$

(1)

where $\Delta Y$ is the total change in the risky asset position since the last payment of transaction costs, for $\lambda$ and $\Gamma$ constants in $[0,1]$ and ${\alpha }_0(x)$ a step function that becomes equal to a constant ${\alpha }_0$ if $x$ is not 0 and equals to 0 if $x$ is 0. The above transaction costs have a fixed and a proportional part but are not necessarily linear.

The time instants at which transaction costs are paid are the points of time at which the investor decides to adjust the portfolio as a result of a significant change in the price of the risky asset. The change in price is monitored with respect to the maximum and minimum price achieved since the last transaction took place. When the price deviates by a preset quantity or proportion, then the investor adjusts/rebalances his or her portfolio by performing a transaction on the (specific risky) asset.

In our setting, the change in the position is made purely for the purpose of paying the transaction costs that behave similarly to management or commission fees. This means that whenever the risky asset price deviates from the minimum or maximum price since the last payment of management fees, then management or commission fees need to be paid again.

The properties of the time instants where the management or commission fees are paid have been studied in Poufinas [11]. More precisely, it has been proved that in a time interval $[0,T]$ there are finitely many such time instants and they are stopping times.

The existence of a trading strategy on the risky asset that pays for the management or commission fees and simultaneously reaches a desired wealth level at time $T$ is investigated. We derive conditions for which such a strategy exists and we prove that when $\Gamma <1$, then such a strategy always exists.

To the best of the author’s knowledge, there has not been a similar approach, either to the way the transaction costs are modeled as well as the way their properties are built or to their effect on the existence of trading strategies that allow the investor to reach a certain final level of wealth.

In Section 2, we describe the environment in which we derive our results. The differences from the Black-Scholes approach are stressed so that the derived results are better interpreted. In Section 3, we present our models for the time instants at which transaction costs or management fees have to be paid as developed in Poufinas [12]. In Section 4, the cost functions are modeled and our main findings about the existence of trading strategies, which pay for the costs incurred and reach a desired final wealth, are examined. In Section 5, certain special cases with respect to the parameters involved are presented. In Section 6, we make a short comment about the applicability of our findings to the pricing of European Options on the risky asset. In Section 7, we describe some further steps and extensions that could be followed towards the inclusion of transaction costs. If achieved, then a more general result would be in place that would allow for the improvement of the modeling of transaction costs when looking for trading strategies that reach a certain final wealth level or pricing options. In Section 8, we conclude with the findings of the main body of the paper. From an organizational perspective, we present the proofs of the propositions, corollaries and theorems as an appendix at the end of the manuscript.

2. Description of the Mathematical Setting

In the following we consider continuously trading markets with transaction costs (commission fees). Our mathematical setting comprises of a filtered complete probability space $(\Omega ,F,\mathrm{Pr},{(F_t)}_{0\le t\le \infty })$. Filtered means that ${(F_t)}_{0\le t\le +\infty }$ is an increasing family of σ-algebras (called a filtration), i.e., $F_s\subseteq F_t$ for $s\le t$ (see Protter [13] p. 3). We assume that all the stochastic processes that appear are adapted, unless otherwise mentioned. This means that if ${(X_t)}_{0\le t\le \infty }$ is a stochastic process, then $X_t\in F_t$, for all $t$. In other words $X_t$ is $F_t$ measurable (see Protter [13] (pp. 3–4)). Furthermore, all the functions and stochastic processes are continuous, unless otherwise stated. (In)equalities that involve random variables are understood to hold almost surely. We assume the existence of a risky asset such that its prices are generated by an Itô process (see Merton [1] (pp.122–124) or Duffie [14] (pp. 80–84)), and its stochastic differential satisfies

$$\frac{dP}{P}=\alpha (P,t)dt+\sigma (P,t)dW.$$

(2)

$\alpha$ is the instantaneous conditional expected change in price per unit time, ${\sigma }^2$ is the instantaneous conditional variance per unit time and $W$ is a Brownian Motion. Moreover we assume the existence of a riskless asset that has a rate of return $r(B,t).$ If $B_t$ denotes the dollar amount invested in the riskless security at time t, then

$$\frac{dB}{B}=r(B,t)dt.$$

(3)

For the rest of our discussion we assume that $\alpha$, $\sigma$ do not depend on P, t and r does not depend on B, t. $V_t$ denotes the portfolio value at time t. $N_t$ denotes the number of shares of stock that the individual holds at time t. For our models we assume the existence of only one risky and only one riskless asset. Then $V_t$ is given by

$$V_t:=N_t{P}_t+B_t.$$

(4)

We define

$$Y_t:=N_t{P}_t$$

(5)

to be the market value of the risky asset. Continuing in line with the problem that stimulated our theme, there is also a third security—an option—that receives no payments at time $t\in [0,T)$ and its value at time T is given by

$$O_T:=\max (0,P_T-E).$$

(6)

where E is the exercise or strike price. T is the agreed-upon date at which the buyer has to exercise the option. This date is called the expiration or maturity date. Such an option is also known as a European Call Option, since it can be exercised only on the expiration date (see Merton [1] (pp. 256–257, p. 280)).

Given the payment to the individual at expiration, the problem is to find the price of the option at any other time instant and in particular at t = 0. This is the price that the intermediary would charge the buyer for the option. To develop option pricing models (option valuation techniques) one needs to determine the production cost of the option by deriving a portfolio strategy that mixes the stock with the riskless security and exactly replicates the payoff to the option. By following this strategy the intermediary that intends to sell the call option to the customer (buyer) completely hedges the risk (perfect hedge), i.e., he or she eliminates the possibility of future gain or loss (see Downes and Goodman [15] (pp. 184–185)). The ask price for the call option is the value of the portfolio at t = 0, i.e., $V_0$. The question is whether we can find such a portfolio (trading) strategy.

Two concepts are needed in such an analysis: those of arbitrage and complete markets. A trading strategy is said to be an arbitrage if either $V_0<0$ and $V_T\ge 0$ or $V_0\le 0$ and $V_T>0$ holds (see Duffie [14] (p. 107)). We say that markets are complete if for any random variable X (with finite variance) there exists an adapted, self-financing portfolio strategy such that X is obtained as the terminal value of the portfolio, i.e., $V_T=X$ (see Duffie [14] (pp. 103–104)).

Returning to the search of a portfolio strategy that replicates the payoff to the option, it is required that the individual’s portfolio is not an arbitrage. To rule out the possibility of arbitrage at any time instant $t\in [0,T]$, $V_t=O_t$ must hold in a Black-Scholes environment.

In the following discussion we assume that commission fees as described in the Introduction have to be paid. Different ways of incorporating transaction costs are given in Section 4 below. In our models we get to choose the time instants at which the aforementioned payments are made. These time instants (and their properties) are presented first in Section 3 that follows. However, the addition of such transaction costs modifies the Black-Scholes working environment. As a consequence, markets are not necessarily complete, arbitrage may be possible and it is not necessary that a self-financing portfolio that has any given X (with finite variance) as terminal value does exist. We therefore need the following definitions:

Definition 1: Markets are said to be weakly complete when for each random variable X with finite variance there exists an $F_T$—measurable portfolio strategy on the stock (risky asset) and the bond (riskless asset) such that X is obtained as the final value of the strategy, i.e., $V_T=X$.

Definition 2: We say that a strategy N on the risky asset finances the security X at time T if

$$N_T{P}_T+B_T=X$$

(7.1)

and

$$N_t{P}_t=N_0{P}_0+{\displaystyle {\int }_0^t{N}_s}d{P}_s-{\displaystyle {\int }_0^{t}c(s)ds,\forall t\in [0,T]},$$

(7.2)

where $c(s)$ is the cost paid for the transaction at time s.

The trigger—intuition behind this approach is that we still want to investigate if we can construct a portfolio that allows us to reach a desired final wealth level, realizing that when transaction costs have to be paid markets are not frictionless, thus not necessarily complete. This means that a complete set of possible outcomes on future states-of-the-world may not be constructed with existing assets as was the case without friction. In this manuscript we examine the conditions (for different cost functions) under which we can find a portfolio strategy on a risky and a riskless asset (let us say stock and bond, respectively), which is rebalanced every time transaction costs have to be paid to cover for these costs, which matches a final value. We defined the markets for which this can be achieved as “weakly complete”. These are markets in which the volume and availability of securities ensures that there are no constraints on investment outcomes. Attention needs to be paid on the fact that even weak completeness is not always secured when transaction costs have to be paid. The type of the cost function may lead to specific conditions under which markets are weakly complete. We comment more on the economic meaning of this (as well as on the measurability) when we define cost more explicitly, in Section 4 (in the text following Equation (18)).

In the case that $\alpha (P,t)=\alpha (t)$ and $\sigma (P,t)=\sigma (t)$, i.e., they are functions of time only and not the risky asset, then the solution of Equation (2) becomes

$$P_t=P_0{e}^{\gamma (t)},$$

(8.1)

where

$$\gamma (t)={\displaystyle {\int }_0^t\mu (s)ds+{\displaystyle {\int }_0^s\sigma (s)d{W}_s}}$$

(8.2)

and

$$\mu (t)=\alpha (t)-\frac{1}{2}{\sigma }^2(t).$$

(8.3)

For the rest of our discussion we assume that μ and σ are continuous or even fixed, hence in any case they are bounded.

3. The Time Instants at Which Payments Have to Be Made

We assume that payment of transaction costs takes place on the time instants ${\tau }_i$, $i=1\dots N^{*}$, which are determined in the following way (see Poufinas [12] (pp.374–375, p. 392)); first let J be a fixed positive real number and ${\tau }_0:=0$. Assume that ${\tau }_i$ has already been defined and let

$$M_t:=\max \{P_s:s\in [{\tau }_i,t]\}$$

(9.1)

and

$$m_t:=\min \{P_s:s\in [{\tau }_i,t]\}$$

(9.2)

for $t\in [0,T]$. Let

$$\phi (t):=\max (M_t-P_t,P_t-m_t)$$

(10.1)

and for $\omega \in \Omega$, let

$$\phi (t,\omega )=\max (M_t(\omega )-P_t(\omega ),P_t(\omega )-m_t(\omega )).$$

(10.2)

Then define ${\tau }_{i+1}$ by

$${\tau }_{i+1}(\omega ):=\inf \{t\ge {\tau }_i(\omega ):\phi (t,\omega )=J\}.$$

(11)

${\tau }_i$ denotes the time instant on which the payment of the transaction cost takes place. In other words, after the transaction cost is paid at time ${\tau }_i$ the next payment is done at time ${\tau }_{i+1}$. This is the time instant at which the price has deviated from its maximum or minimum since ${\tau }_i$ by a preset amount J.

The rationale behind using such a choice for the time of the transaction lies in the fact that the investor chooses to adjust the risky asset part of the portfolio when the price of the risky asset has departed from the maximum or minimum price by a certain amount.

One could recommend using both the risky and the riskless asset to cover for the transaction costs. This would yield an alternative strategy with a different cost function or level of total cost incurred for the investor. The question then would be how to choose one of the two (or more) potential approaches. As a matter of fact a similar question can be raised when we have a portfolio of more than one risky asset and a riskless asset. We have identified this problem for future research, as mentioned in the relevant Section 7 below. We recommend addressing the problem with the use of the utility function of the investor, which allows us to find the optimal solution (strategy) from his or her perspective (as reflected through the utility function).

A different way to define ${\tau }_i$ is given if $J_{i+1}:=\nu \left|P_{{\tau }_i}\right|$, where ν is a fixed positive number. Set ${\tau }_0:=0$. If ${\tau }_i$ is given we define ${\tau }_{i+1}$ by

$${\tau }_{i+1}(\omega ):=\inf \{t\ge {\tau }_i(\omega ):\phi (t,\omega )=J_{i+1}(\omega )\},\omega \in \Omega .$$

(12)

The reasoning behind such a choice is that the investor chooses to perform a transaction and adjust the portfolio when the stock price has increased or decreased compared to its maximum or minimum by a certain multiple of the price at the time of the previous transaction, thus reflecting a “percentage change”.

A further elaboration of the choice of such a criterion to transact—for both ways as defined above—can be given as follows:

• The investor buys or sells shares of stock when the price increases or decreases vs. the min or max by a certain amount.
• This is based on the rationale that the investor monitors the price move, e.g., through a price chart and, as soon as the price deviates from the minimum (maximum) recorded since the previous transaction, he or she transacts again by, e.g., selling (buying) shares of stock, respectively.
• This seems to be a reasonable direction/choice, not far removed from the technical analysis approach. In the model described minimum and maximum prices from the last transaction price are used, whereas in technical analysis relative maxima and minima are observed.
• This amount is absolute (J) in the case of Equations (9.1)–(11), but it becomes relative to the previous transaction price in Equation (12). In the latter, $J_{i+1}:=\nu \left|P_{{\tau }_i}\right|$, where ν is a proportion of the last transaction price.
• However, instead of transacting when the price has deviated from the last transaction price by more than a specific amount, the aforementioned criterion is used. Such a choice seems appropriate as it considers not only the price shift from the last transaction, but rather its shift from the max or the min posted since the last transaction.
• The latter somehow seems to be a “more secure” signal to transact.

The above is illustrated in Figure 1 below, where we have taken $P_0=1$ and $J=0,5$. The choice has been made simply to elaborate, as $J=0,5$ is quite big compared to the price (the graph is more an indicative sketch as opposed to an accurate price chart). Only the first seven time instants at which the investor transacts have been mapped.

As one can see from the graph, the investor buys the share at time 0 for $P_0=1$ and then transacts when the price has departed by $J=0,5$ from the minimum, which coincides with $P_0=1$. At that time, ${\tau }_1$, he or she sells. Consequently, he or she incurs transaction costs.

Then he or she transacts again at the time instant ${\tau }_2$, when the price has parted from the maximum by $J=0,5$; he or she buys. There has not been a previous time instant at which the price has moved from the maximum or the minimum by $J=0,5$. He or she has to pay transaction costs again.

This continues for the entire time horizon of the investor, and the relevant time instants are shown on the sketch.

The purchase or sale of shares of stock when the difference of the current (at the time) price and the max or min has reached $J=0,5$ can be explained by the fact that the investor exits as soon as a targeted profit has been made and he or she re-enters when the price has reached a level he or she considers as reasonable to give him or her an upside potential. One can see that this is the case in the relative lows (e.g., at time instants ${\tau }_2$, ${\tau }_4$) as well as in upward moves (e.g., at time instant ${\tau }_6$).

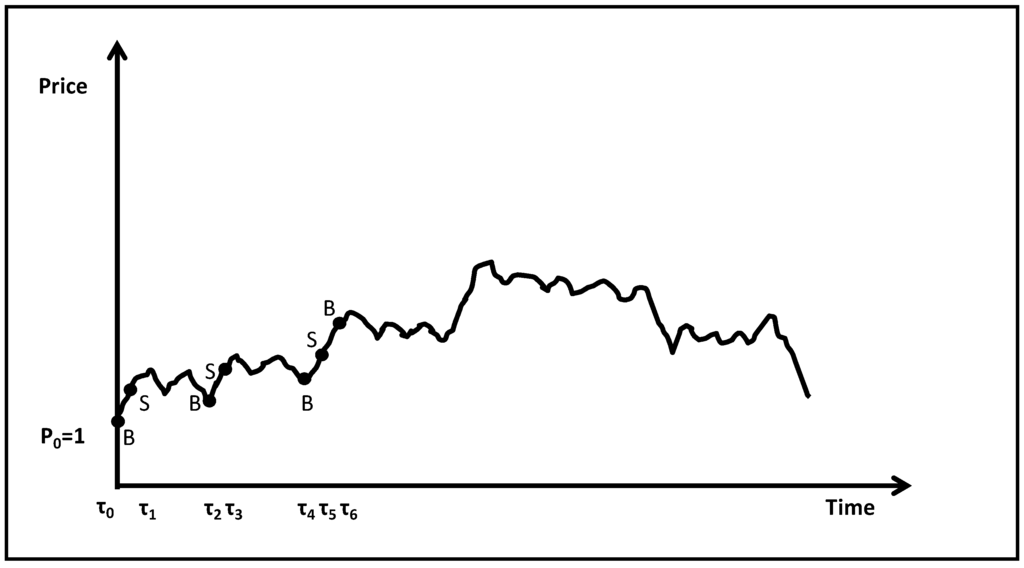
Figure 1. Times of transaction cost occurrence.

Figure 1. Times of transaction cost occurrence.

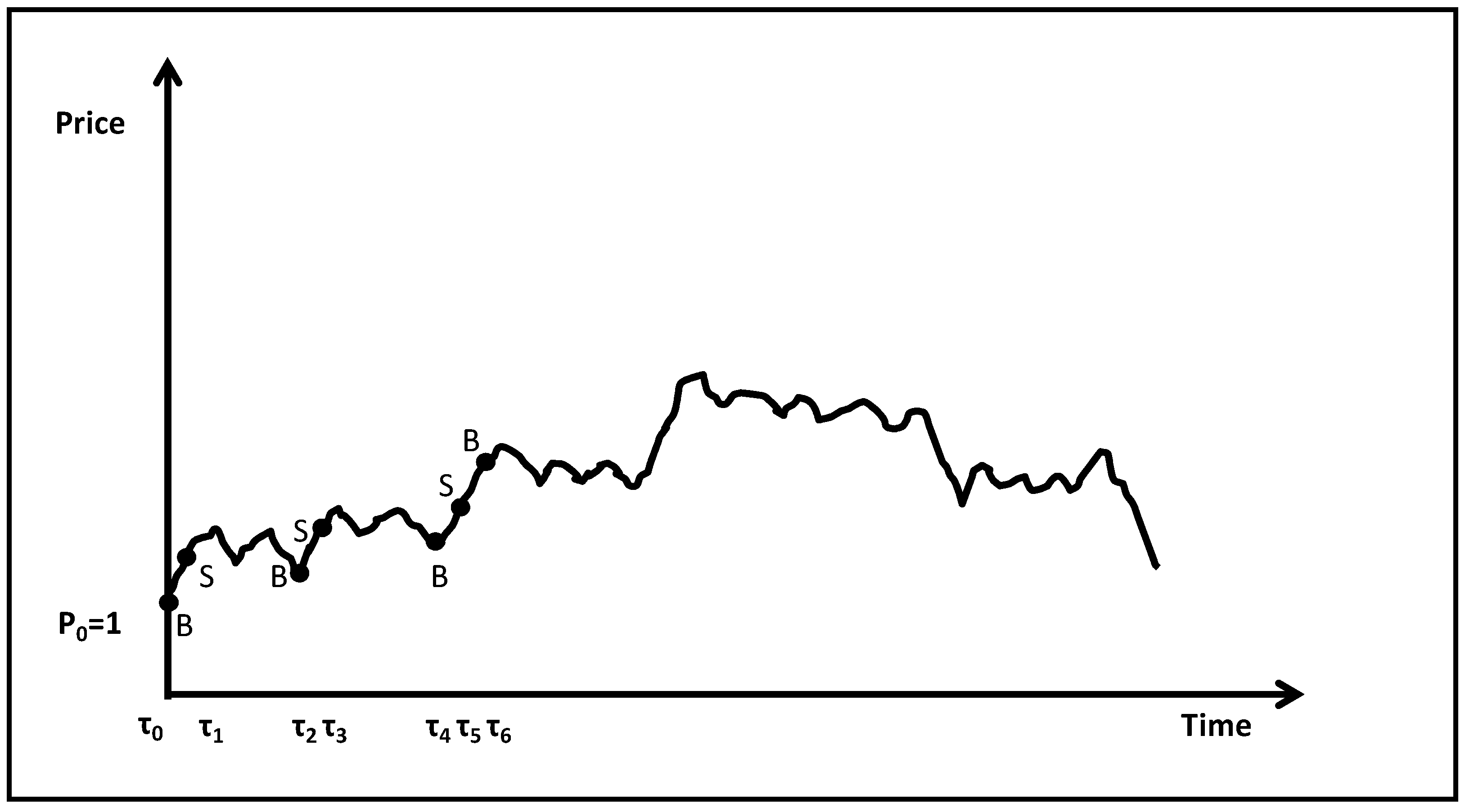
One can note that when the price goes up (increasing pieces of the chart), then $M_t=P_t$, hence $\max (M_t-P_t,P_t-m_t)=P_t-m_t$. This is due to the fact that when the price goes up there is always a new maximum.

On the other hand, when the price goes down (decreasing pieces of the chart), then $m_t=P_t$, hence $\max (M_t-P_t,P_t-m_t)=M_t-P_t$. This is due to the fact that when the price goes down there is always a new minimum.

As can be seen from Figure 1, and inferred from the definition of the time instants ${\tau }_i$, if J is too small, then there will be many transactions hence the investor will incur higher transaction costs. For example, as $J\to 0$, almost every time instant will be an instant suitable for transaction. In such a case, the transaction costs will be very high and will most likely make the strategy worthless to follow.

Let $I_{\omega }$ be the index set for the ${\tau }_i(\omega )$’s. In Poufinas [11] it has been proved that for almost every ω, $I_{\omega }$ is finite and that for each i, ${\tau }_i$ is a stopping time (see Protter [13] (pp. 3–5)).

4. The Cost Functions

The amount that the individual has to pay at ${\tau }_i$, $i=1\dots N^{*}$ may be given by different cost functions. If ${\beta }_i$ is this amount and c(t) denotes the cost function, then

$$c(t)dt={\displaystyle \sum _{i=1}^{N^{*}}{\beta }_i{\delta }_0({\tau }_{\iota }-\tau )dt}$$

(13)

where ${\delta }_0(x)$ denotes the Dirac delta function. This function has the properties that ${\delta }_0(x)=0$ for $x\ne 0$ and ${\delta }_0(0)=+\infty$ in such a way that ${\displaystyle {\int }_a^b{\delta }_0}(x)dx=1$ for any $a<0<b$ (Merton [1]). There are no functions, in the usual sense of the world, with such properties, and, this is thus referred to as generalized function.

c(t) is essentially the individual’s “consumption” at time t, since his or her expenses are only the commission fees. On the other hand the individual’s consumption in terms of his or her shares of stock is given by $dN(dP+P)$. We conclude that

$$-c(t)dt=PdN+dNdP.$$

(14)

This is where our fist deviation from the Black-Scholes environment occurs. The portfolio cannot be self-financing in the standard sense, as self-financing portfolios assume that there is no “inflow” or “outflow”. In our model, there is an outflow when transaction costs are paid. The “consumption” of the investor equals the transaction costs. Moreover, we assume that the transaction costs are only paid from the risky asset, i.e., the investor does not liquidate part of the riskless asset to pay for the transaction costs incurred when he or she performs a transaction on the risky asset. This means that such costs are paid by trading on the risky asset (stock), and the riskless asset (bond) position does not change.

We apply Itô’s Lemma to differentiate Equation (4) to see that

$$dV=NdP+PdN+dNdP+dB.$$

(15)

Equations (13)–(15) yield that

$$dV=NdP+dB-{\displaystyle \sum _{i=1}^{N^{*}}{\beta }_i}{\delta }_0({\tau }_i-t)dt.$$

(16)

Use Equation (2) to realize (see Merton [1] (pp. 124–126)) that

$$dV=NP\alpha dt+NP\sigma dW+dB-{\displaystyle \sum _{i=1}^{N^{*}}{\beta }_i}{\delta }_0({\tau }_i-t)dt.$$

(17)

Recall that $NP=V-B=Y$. Hence $dV=dB+dY$ and thus

$$dY=\alpha Ydt+\sigma YdW-{\displaystyle \sum _{i=1}^{N^{*}}{\beta }_i}{\delta }_0({\tau }_i-t)dt.$$

(18)

In the following we will prove that, with our model assumptions, markets are weakly complete and the strategy chosen is $F_T$-measurable. The strategy constructed is piecewise constant (step function) with respect to time. Our approach focuses more on the explicit construction or proof of existence of the strategy rather than on the measurability, as we would like to be able to point out the exact number of shares of stock (units of the risky asset) that the investor should hold.

Moreover, in today’s markets the time period between 0 and T may not result in a significant difference on the information available, thus $F_0,\dots ,F_T$ may reflect the same information for trading the security. This can be partially attributed to the insider information that traders have. This is particularly true when the time interval $[0,T]$ is small, especially when pricing stock options.

Given a desired final wealth level/outcome at time T, the time horizon of the investor (or maturity of the option when applicable), we try to construct a strategy on the risky and the riskless asset that gives as outcome the aforementioned wealth level. This strategy is affected by the fee payment, whenever it takes place, and the rebalancing performed by the investor occurs only at the fee payment times. This mimics a mutual fund or a portfolio holding where fees are paid when there is a given deviation from its share price.

No other assumption about the change in the holding of shares of the risky asset can be made, since each investor increases or decreases his or her number of shares (even at the time instants of Section 3) based on his or her individual choices. Consequently, in our analysis we study the existence of portfolio strategies that finance any given outcome, allow for the payment of the management fees (as modeled in each of the section below) and are adjusted purely for the payment of the management fees.

Due to the previous relaxation of the measurability requirement, Itô integration may not work. The fact that the strategy chosen is piecewise constant (step function of time) allows us to proceed with the same notation. This is because the investor does not change his or her position at any other point of time except for the ones described in this paper. Moreover, we examine the change in the units of the risky asset held to cover the transaction costs. Therefore, there is a very tight relationship between the units of the risky asset held before and after costs are paid.

The problem of pricing a European Option on the risky asset—if we wanted to follow the Black-Scholes approach—is then reduced to solving the Stochastic Differential Equation (18) subject to the boundary condition

$$Y_T=W_T-B_T=O_T-B_T,$$

(19)

which becomes

$$Y_T=\max (0,P_T-E)-B_T.$$

(20)

As a result, we are looking for a solution of Equation (18) subject to Equation (20). Our approach—as mentioned above—cannot use the standard arbitrage arguments, and lacks the measurability of the trading strategy. However, it still gives a financing strategy for the terminal price of the option.

As a remark, one can see that as ${\beta }_i\to 0$, then the cost goes to zero, hence Equation (18) reduces to the equation followed in the Black and Scholes approach, thus leading to the Black-Scholes formula/solution.

4.1. Constant Cost Function

The first case we consider is

$${\beta }_i:=\beta ,i=1\cdots N^{*}$$

(21)

i.e., the individual pays a fixed amount. Then the following proposition holds:

Proposition 1: If the amount ${\beta }_i$, paid at time instant ${\tau }_i$, for $i=1\dots N^{*}$ is given by Equation (21), then markets are weakly complete.

The natural question here is whether the previous integrals, as well as the ones to follow, make sense, since the strategy followed is only $F_T$-measurable. The answer is provided by the fact that within each interval $[{\tau }_{i-1},{\tau }_i)$ the number of shares of the risky asset held is unchanged with respect to time. Therefore one can readily see that for $s_1$ and $s_2$ in $[{\tau }_{i-1},{\tau }_i)$.

$$\begin{array}{l}{Y}_{s_2}=Y_{s_1}+{\displaystyle {\int }_{s_1}^{s_2}\alpha (s)Y_{s}ds}+{\displaystyle {\int }_{s_1}^{s_2}\sigma (s)Y_s}d{W}_s\\ \iff Y_{s_2}=N_{s_1}{P}_{s_1}+{\displaystyle {\int }_{s_1}^{s_2}\alpha (s)N_s{P}_{s}ds}+{\displaystyle {\int }_{s_1}^{s_2}\sigma (s)N_s{P}_s}d{W}_s\\ \iff Y_{s_2}=N_{s_1}{P}_{s_1}+N_{s_1}{\displaystyle {\int }_{s_1}^{s_2}\alpha (s)P_{s}ds}+N_{s_1}{\displaystyle {\int }_{s_1}^{s_2}\sigma (s)P_s}d{W}_s\\ \iff Y_{s_2}=N_{s_1}{P}_{s_1}{e}^{\gamma (s_2)-\gamma (s_1)}=Y_{s_1}{e}^{\gamma (s_2)-\gamma (s_1)}.\end{array}$$

(22)

The aforementioned result is the basis of our algebraic calculation and allows for the integral notation used in our proofs. It appears that we do not need to use such a notation; instead we can proceed simply with producing $N_t$ backwards for each point of time. Care is necessary at the time instants ${\tau }_i$, where costs are paid.

In the discussion below, as well as in the proofs, we denote by $Y_{{\tau }_i}^{-}$ the value of $Y$ at time ${\tau }_i$ immediately before the payment of the transaction costs and by $Y_{{\tau }_i}^{+}$ the value of $Y$ at time ${\tau }_i$ immediately after the payment of the transaction costs.

4.2. Linear Cost Function

This time the individual pays a proportion of the amount of the transaction at ${\tau }_i$, i.e.,

$${\beta }_i=\lambda (\left|Y_{{\tau }_t}^{+}-Y_{{\tau }_t}^{-}\right|+\left|Y_{{\tau }_t}^{-}-Y_{{\tau }_{t-1}}^{+}\right|).$$

(23)

The reasoning behind such a choice of the transaction cost is that the investor pays a proportion λ of the total change of the portfolio value since the last portfolio adjustment due to the risky asset only. This consists of two parts; one due to the passage of time and another due to the occurrence of transaction costs. In this sense λ is the proportion of the change in the value of the portfolio paid in transaction costs. Set $\theta ({\tau }_0)=1$ and for $i=1\dots N^{*}$ let (see Poufinas [12] (pp. 397–398, p. 401))

$$\theta ({\tau }_i):=\theta ({\tau }_{i-1})e^{\gamma ({\tau }_i)-\gamma ({\tau }_{i-1})}-\frac{\lambda }{1-\lambda }\left|\theta ({\tau }_{i-1})\right|\left|e^{\gamma ({\tau }_i)-\gamma ({\tau }_{i-1})}-1\right|,$$

(24)

$${\theta }_0({\tau }_i):=e^{\gamma ({\tau }_i)-\gamma ({\tau }_{i-1})}-\frac{\lambda }{1-\lambda }\left|e^{\gamma ({\tau }_i)-\gamma ({\tau }_{i-1})}-1\right|,$$

(25)

$$\tilde{\theta }({\tau }_i):=\tilde{\theta }({\tau }_{i-1})e^{\gamma ({\tau }_i)-\gamma ({\tau }_{i-1})}+\frac{\lambda }{1-\lambda }\left|\tilde{\theta }({\tau }_{i-1})\right|\left|e^{\gamma ({\tau }_i)-\gamma ({\tau }_{i-1})}-1\right|,$$

(26)

$${\tilde{\theta }}_0({\tau }_i):=e^{\gamma ({\tau }_i)-\gamma ({\tau }_{i-1})}+\frac{\lambda }{1-\lambda }\left|e^{\gamma ({\tau }_i)-\gamma ({\tau }_{i-1})}-1\right|.$$

(27)

We observe that $\tilde{\theta }({\tau }_i)>0$ and ${\tilde{\theta }}_0({\tau }_i)>0$ for all i. Two necessary and sufficient conditions for the weak completeness of markets are given in the following proposition.

Proposition 2: If the amount paid at time ${\tau }_i$ is given by Equation (23) markets are weakly complete if and only if $\theta ({\tau }_i)>0$ for all $i=1\dots N^{*}$. In addition, markets are weakly complete if and only if ${\theta }_0({\tau }_i)>0$ for all $i=1\dots N^{*}$.

4.3. Concave Cost Function

A third way to incorporate costs is given if we assume that the individual pays a proportion of a power of the dollar amount of the transaction in fees, i.e.,

$${\beta }_i=\lambda {(\left|Y_{{\tau }_t}^{+}-Y_{{\tau }_t}^{-}\right|+\left|Y_{{\tau }_t}^{-}-Y_{{\tau }_{t-1}}^{+}\right|)}^{\Gamma },where0\le \Gamma <1.$$

(28)

The introduction of concave functions is justified by the fact that as the traded amount becomes bigger due to the price difference or size of shares of stock traded, then the cost charged increases at a lower pace and not at the same constant pace. In other words, the cost paid is reflected by a concave function.

The case Γ = 0 is equivalent to the one we examined when ${\beta }_i=\beta$. Observe that if Γ = 1, then Equation (28) is identical to Equation (23). We assume that $\lambda \in (0,1)$ since if $\lambda =0$ then ${\beta }_i=0=\beta$.

Proposition 3: With costs incorporated as in Equation (28), markets are weakly complete.

4.4. Affine Cost Function

Next we generalize the cost function given by Equation (23). We add to it a “fixed” cost. This additional cost is zero if there is no transaction and is strictly positive otherwise. It is given by

$${\beta }_i={\alpha }_0(\left|Y_{{\tau }_t}^{+}-Y_{{\tau }_t}^{-}\right|+\left|Y_{{\tau }_t}^{-}-Y_{{\tau }_{t-1}}^{+}\right|)+\lambda (\left|Y_{{\tau }_t}^{+}-Y_{{\tau }_t}^{-}\right|+\left|Y_{{\tau }_t}^{-}-Y_{{\tau }_{t-1}}^{+}\right|).$$

(29)

${\alpha }_0$ is defined by

$${\alpha }_0(x):=\{\begin{array}{c}{\alpha }_{0}x\ne 0\\ 0x=0\end{array},$$

(30)

where ${\alpha }_0$ is a strictly positive number. If we allow ${\alpha }_0$ to be zero, then we have the case discussed in Proposition 2.

Such a choice of the transaction costs is justified by the fact that costs may also have a fixed part besides the variable part. The latter is of course paid only when the transaction leads to a change in value. As far as the weak completeness of the markets is concerned, the following theorem holds.

Theorem 1: If the fees that have to be paid at time instant ${\tau }_i$ are given by (30), then markets are weakly complete if and only if ${\theta }_0({\tau }_i)>0$.

4.5. Affine-Concave Cost Function

Finally, we generalize the cost function of Equation (28) by adding a “fixed’’ cost as given by (30). Our cost function becomes

$${\beta }_i={\alpha }_0(\left|Y_{{\tau }_t}^{+}-Y_{{\tau }_t}^{-}\right|+\left|Y_{{\tau }_t}^{-}-Y_{{\tau }_{t-1}}^{+}\right|)+\lambda {(\left|Y_{{\tau }_t}^{+}-Y_{{\tau }_t}^{-}\right|+\left|Y_{{\tau }_t}^{-}-Y_{{\tau }_{t-1}}^{+}\right|)}^{\Gamma },$$

(31)

where $0\le \Gamma <1$.

The introduction of affine-concave functions is justified by the fact that as the traded amount becomes bigger due to the price difference or size of shares of stock traded, then the cost charged increases at a lower pace and not at the same constant pace. In other words, the cost paid is reflected by a concave function but there is also a fixed part. The following theorem now holds:

Theorem 2: If the transaction costs that the individual has to pay at time instant ${\tau }_i$ are given by Equation (31), then markets are weakly complete.

5. Some Special Cases

5.1. $\Gamma =0$, $\lambda \in (0,1)$

A particular case of the model we have been examining appears when $\lambda \in (0,1)$ and $\Gamma =0$. It follows that

$${\beta }_i={\alpha }_0(\left|Y_{{\tau }_t}^{+}-Y_{{\tau }_t}^{-}\right|+\left|Y_{{\tau }_t}^{-}-Y_{{\tau }_{t-1}}^{+}\right|)+\lambda .$$

(32)

As before, let $x:=\left|Y_{{\tau }_i}^{+}-Y_{{\tau }_i}^{-}\right|=Y_{{\tau }_i}^{-}-Y_{{\tau }_i}^{+}\ge 0$ and $C:=\left|Y_{{\tau }_i}^{-}-Y_{{\tau }_{i-1}}^{+}\right|$ to see that Equation (32) is equivalent to

$$x={\alpha }_0(x+C)+\lambda .$$

(33)

Recall that $\lambda >0$ and thus x > 0. This implies that $a_0(x+C)={\alpha }_0$ and

$$x=a_0+\lambda .$$

(34)

Conclude that for each $i=1\dots N^{*}$

$${\beta }_i={\alpha }_0+\lambda =:\beta$$

(35)

i.e., ${\beta }_i$ is constant and does not depend on $Y_{{\tau }_i}$. As a result, our analysis is identical to the one we gave when ${\beta }_i$ is given by Equation (21), with $\beta ={\alpha }_0+\lambda$, and therefore a solution (replicating strategy) $Y_t$ always exists, and is given by Equation (60).

5.2. $\lambda =0$, $\Gamma \in [0,1]$

Theorem 1 covers the case $\Gamma =1$ and $\lambda \in (0,1)$. Theorem 2 discusses the case $\Gamma \in (0,1)$ and $\lambda \in (0,1)$. Finally in the previous paragraph we examined the case $\Gamma =0$, $\lambda \in (0,1)$. The obvious question is what happens when $\lambda =0$ and ${\alpha }_0$ is as before. Observe that, no matter what $\Gamma$ is, the term that is multiplied by $\lambda$ is annihilated since $\lambda =0$. Therefore,

$${\beta }_i={\alpha }_0(\left|Y_{{\tau }_t}^{+}-Y_{{\tau }_t}^{-}\right|+\left|Y_{{\tau }_t}^{-}-Y_{{\tau }_{t-1}}^{+}\right|).$$

(36)

Set once more $x:=Y_{{\tau }_i}^{-}-Y_{{\tau }_i}^{+}\ge 0$ and $C:=\left|Y_{{\tau }_i}^{-}-Y_{{\tau }_{i-1}}^{+}\right|$ to see that Equation (36) becomes

$$x={\alpha }_0(x+C).$$

(37)

Observe that if x = 0, then ${\alpha }_0(x+C)=0$ and thus x + C = 0, which implies that C = 0. If C = 0 though it does not necessarily follow that x = 0. x might be positive, in which case $x={\alpha }_0$. If C > 0, then ${\alpha }_0(x+C)={\alpha }_0$, since x + C > 0. Hence, $x={\alpha }_0$. To preserve a uniform notation with the rest of the cases we set

$$x=:R({\alpha }_0;\left|Y_{{\tau }_i}^{-}-Y_{{\tau }_{i-1}}^{+}\right|),$$

(38)

which also shows the dependence of x on the value of ${\alpha }_0$. $R({\alpha }_0;\cdot )$ is a well defined function on $(0,+\infty )$ and

$$R({\alpha }_0;\cdot )={\alpha }_0$$

(39)

on that interval. On the other hand, if C = 0, $R({\alpha }_0;C)$ may be 0 or ${\alpha }_0$. If we keep the positive solution when C = 0, then $R({\alpha }_0;\cdot )$ becomes a well defined function on $[0,+\infty )$ and Equation (39) holds on $[0,+\infty )$ as well. The solution $Y_t$ is now given by

$$Y_t=[Y_0-{\displaystyle \sum _{i=1}^{N^{*}}R({\alpha }_0};\left|Y_{{\tau }_{i-1}}^{+}\right|\left|e^{\gamma ({\tau }_i)-\gamma ({\tau }_{i-1})}-1\right|)H_{\tau i}(t)e^{-\gamma ({\tau }_i)}]e^{\gamma (t)}.$$

(40)

There are two ways to choose the value of ${\beta }_i$. The first is exactly like the one we followed for the case $\lambda \in (0,1)$. The details of the corresponding analysis will be presented later. There is a second way though we can choose ${\beta }_i$. We observed that ${\beta }_i=x={\alpha }_0$ if C > 0. Moreover, if C = 0, then $x={\alpha }_0$ is one of the two possible solutions for ${\beta }_i$. As a consequence, we may take

$${\beta }_i={\alpha }_0=\beta .$$

(41)

to see that our problem becomes equivalent to the one we considered when ${\beta }_i$ was given by Equation (21). The weak completeness of markets is guaranteed by Proposition3.

Going back to the traditional way of proving the weak completeness of markets, for fixed $i=1\dots N^{*}$ we define

$$\tilde{y}:=\left|Y_{{\tau }_{\iota -1}}^{+}\right|\ge 0,$$

(42.1)

$$c:=\left|e^{\gamma ({\tau }_i)-\gamma ({\tau }_{i-1})}-1\right|,$$

(42.2)

$$y:=Y_{{\tau }_{i-1}}^{+},$$

(42.3)

to see that Equation (37) can be written as

$$x={\alpha }_0(x+c\left|y\right|),$$

(43)

$$\iff x={\alpha }_0(x+c\tilde{y}).$$

(44)

The question of the completeness of markets is answered by the following corollary.

Corollary 1: For $\Gamma \in [0,1]$ and ${\beta }_i$ given by Equation (36) markets are weakly complete.

6. Application to the Pricing of European Options

The methodology presented could be used for the pricing of European Options on the risky asset. More precisely, recall that for any given X we were able construct a portfolio strategy that satisfies

$$X=N_T{P}_T+B_T.$$

(45)

Take now $X=O_T$, i.e., the value of the option at maturity, to see that such a portfolio strategy ($F_T$-measurable) can be built. We can set

$$O_t=N_t{P}_t+B_t\forall t\in [0,T]$$

(46)

as the price of the option. It is of further research interest to examine the properties of such a choice and how it compares with the actual option price. Unfortunately, such a proposed solution does not meet the measurability requirements of the Black-Scholes environment. Therefore, the conditions under which the $F_t$-measurability is established are to be investigated.

7. Future Research

A natural generalization would be to consider any nonnegative function f as our cost function. This means that the cost would be given as

$${\beta }_i=f(\left|Y_{{\tau }_t}^{+}-Y_{{\tau }_t}^{-}\right|+\left|Y_{{\tau }_t}^{-}-Y_{{\tau }_{t-1}}^{+}\right|).$$

(47)

The properties that f must satisfy can be derived by the conditions that are necessary to guarantee the existence of the solution of the resulting equations if we try to mimic the steps that we followed for our cost functions. A reasonable assumption is that f is concave, as is indicated by the functions we considered in our models.

Moving in another direction, we could try to retrieve what conditions on our fee functions would allow for our results to be readily used for the pricing of (European) options. Such a result appears to be very interesting as it would incorporate transactions only when the risky asset price moves from its maximum or minimum within a certain time interval by a certain amount or percentage. The number of shares of the risky asset transacted would not have to be the ones that the investor needs to transact so that only the fees are paid but could be of any number. This means that the $F_T$-measurability may not be sufficient and we would need to strengthen our result by producing a strategy that is adapted. The completeness or weak completeness of the markets would have to be examined as well.

Another next step in our analysis is the study of portfolios with more than one risky asset. Such portfolios allow for the trading of more than one risky asset and give more choices. This means that there is not only one strategy that can be followed, but the investor would have to choose among the available ones. This hints that we need to move towards the use of utility functions and control theory so as to derive the strategy that is optimal for the investor.

In a different direction, the models presented above could be used for the valuation of hedge funds that include high-water mark features as a compensation scheme (or valuation of high-water mark contracts embedded in hedge funds)—as recommended by one of the anonymous referees, whom we sincerely thank. Indeed, such funds include high-water mark contracts, which “… have the appealing feature of paying the manager a bonus only when the investor makes a profit, and in addition, requiring that the manager make up any earlier losses before becoming eligible for the bonus payment. On the other hand, their option-like characteristics clearly induce risk-taking behavior when the manager is below the high-watermark, and the large bonus above the benchmark clearly reduces long-run asset growth.”, as per Goetzmann, Ingersoll and Ross [16]. “…high water mark provisions condition the payment of the incentive upon exceeding the maximum achieved share value”.The problem is relevant, as not only has the maximum share value been utilized (which is somehow common with our approach), but also because “The payoff at any point in time depends on the high-water mark which is related to the maximum asset value achieved. As such the contract can be valued using option-pricing methods”. We trust that such a problem could be tackled as part of finding the global properties of a function that would map transaction costs and is thus considered for future research.

Last but not least, of interest would be to examine the validity or not of such results in a discrete-time framework. This means that we would have to examine the changes of the Cox-Ross-Rubinstein environment as a result of the introduction of transaction costs, modeled in a way similar to the one presented in this paper. Buss and Dumas [17] have recently published a paper in this area. We thank one of the anonymous reviewers for bringing this to our attention.

Computer programs could be built for the findings of this paper as well as the recommended future research so as to compare the results with empirical evidence. When it comes to option pricing, this could be used as a lead to show how to proceed in incorporating the proposed transaction-cost models in option pricing techniques.

8. Conclusions

We modeled costs in a way dependent on the change of the risky part of the portfolio. Transaction costs incur at time instants where the price of the risky asset departs from its maximum or minimum either by a certain amount or a certain percentage. We established that markets are weakly complete or found conditions so that the latter occurs under the fee models we studied; namely the ones with fixed, linear, affine, concave and affine-concave costs.