Dynamic Analysis of Variable-Stiffness Laminated Composite Plates with an Arbitrary Damaged Area in Supersonic Airflow
Abstract
1. Introduction
2. Theoretical Formulations
2.1. Model of Damaged VSCL Plate
2.2. Energy Functional Calculation
2.3. Damage Modeling
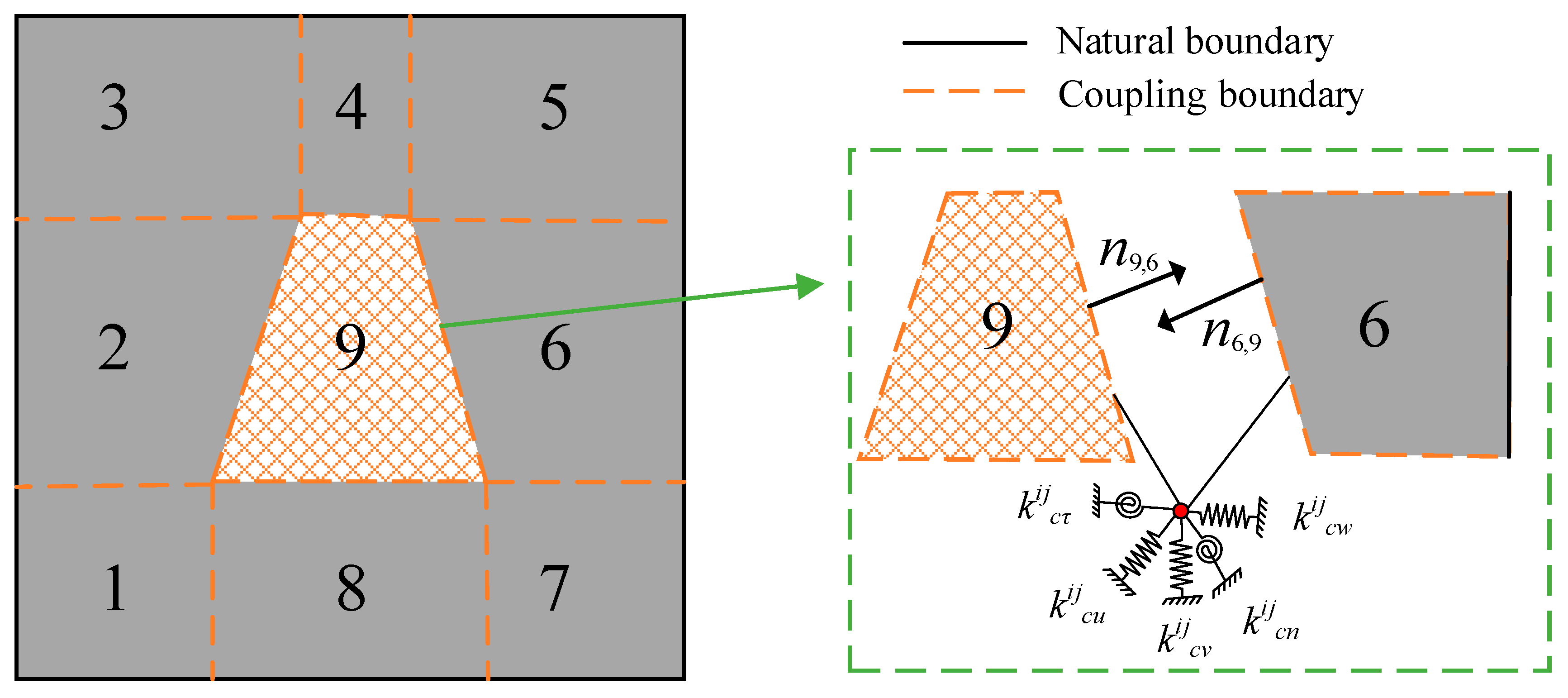
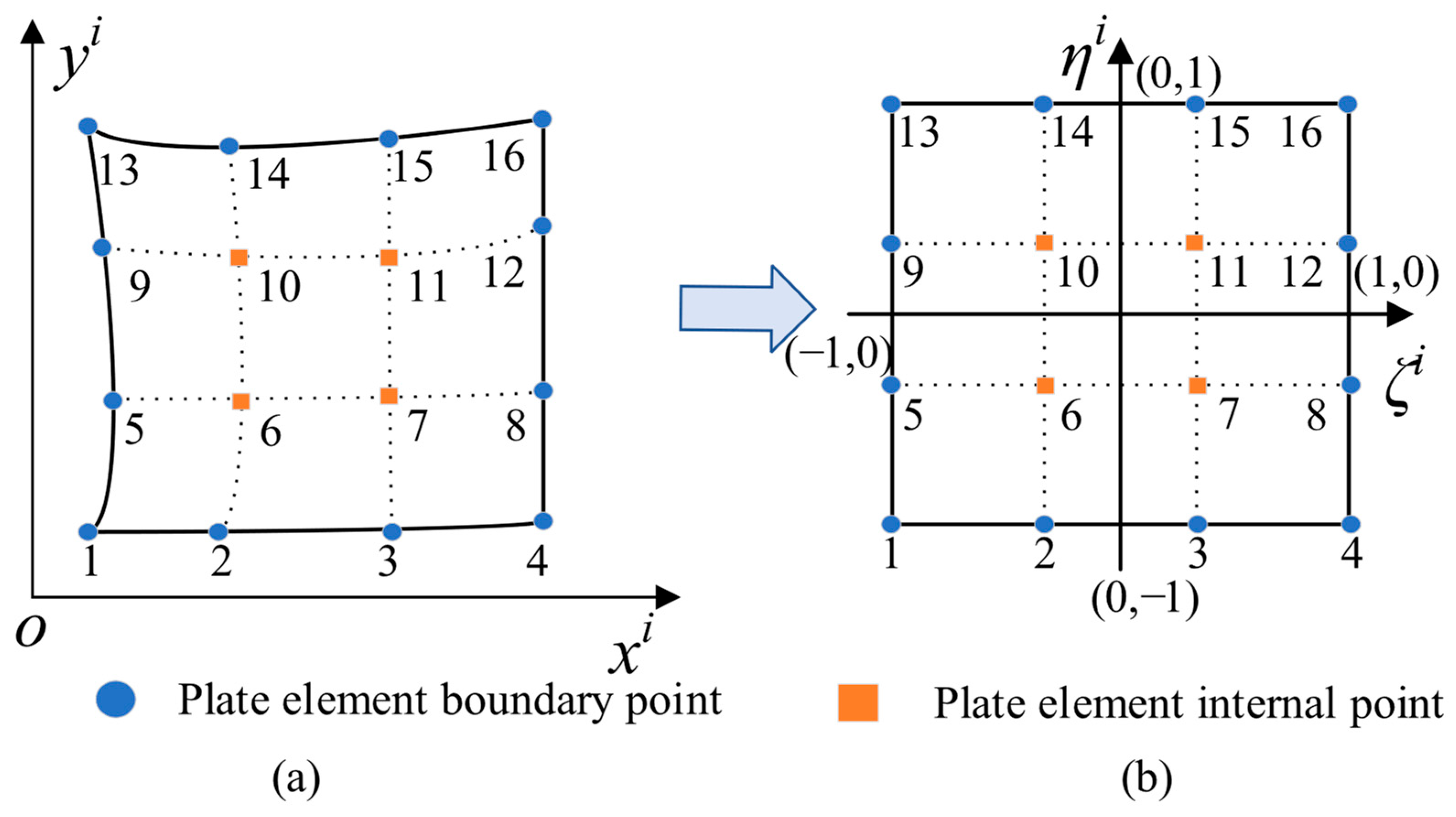
2.4. Irregular Domain Coupling Technology
2.5. Forced Vibration
2.6. Flutter Solution
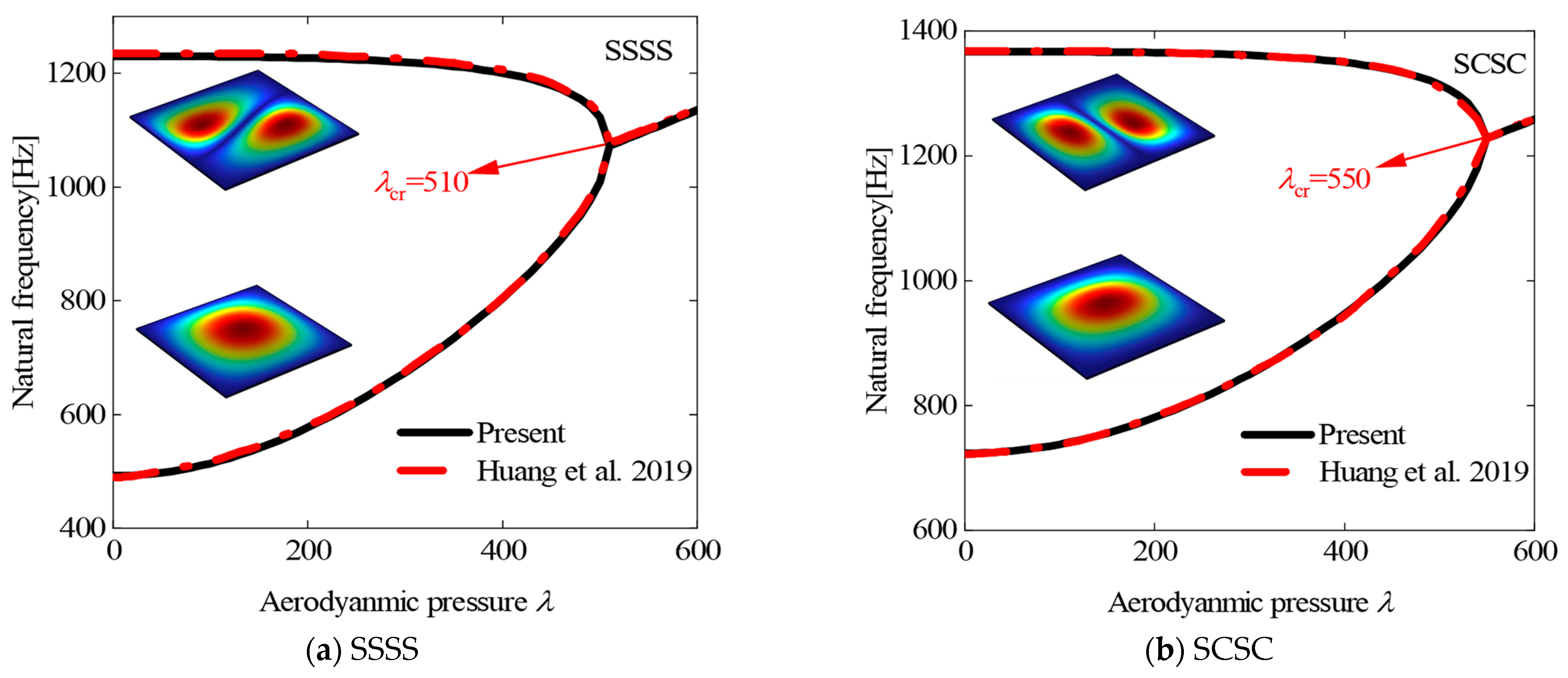
3. Result Verification
4. Parametric Cases and Discussion
4.1. Analysis of Free Vibration
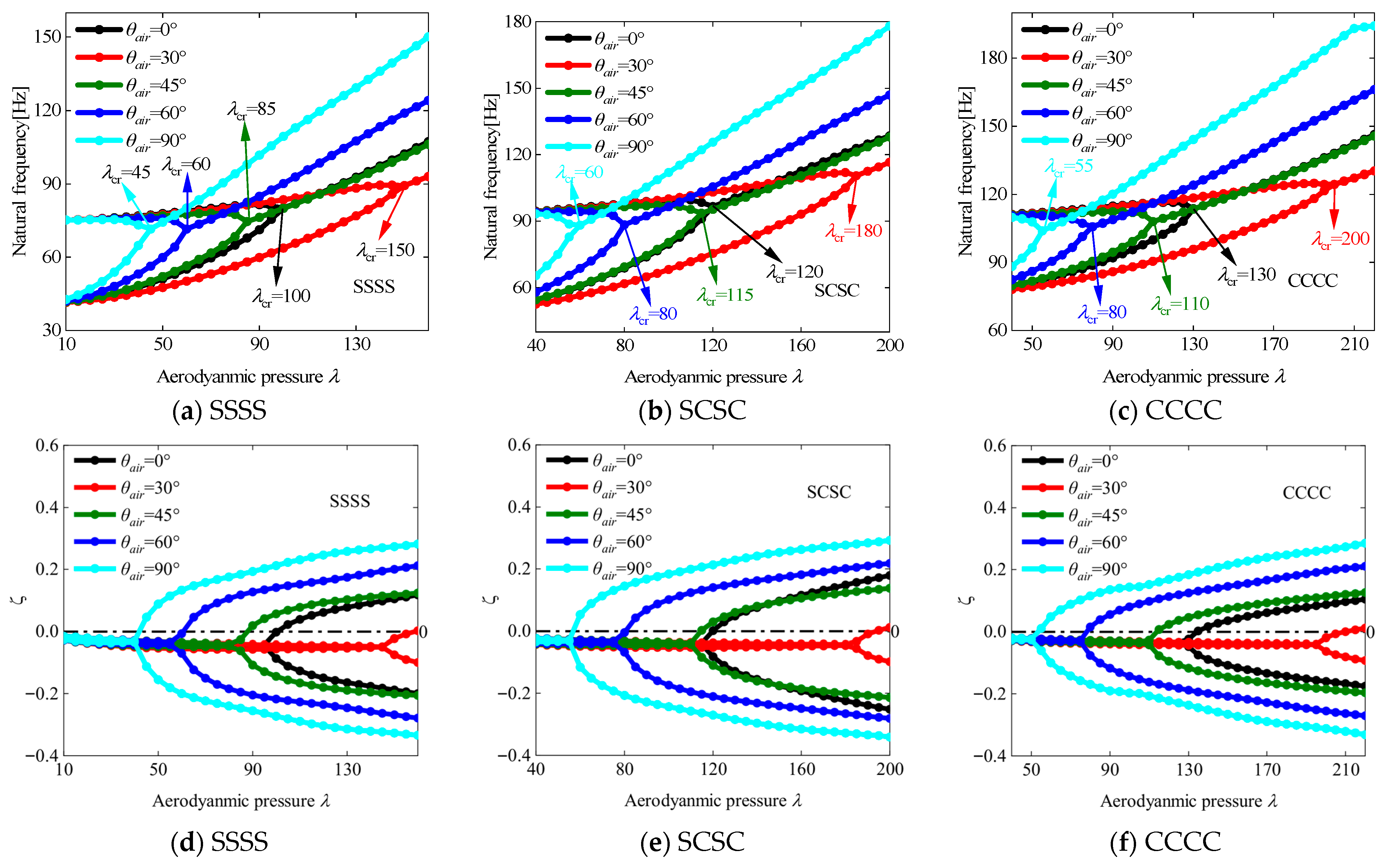
4.2. Analysis of Flutter Boundary
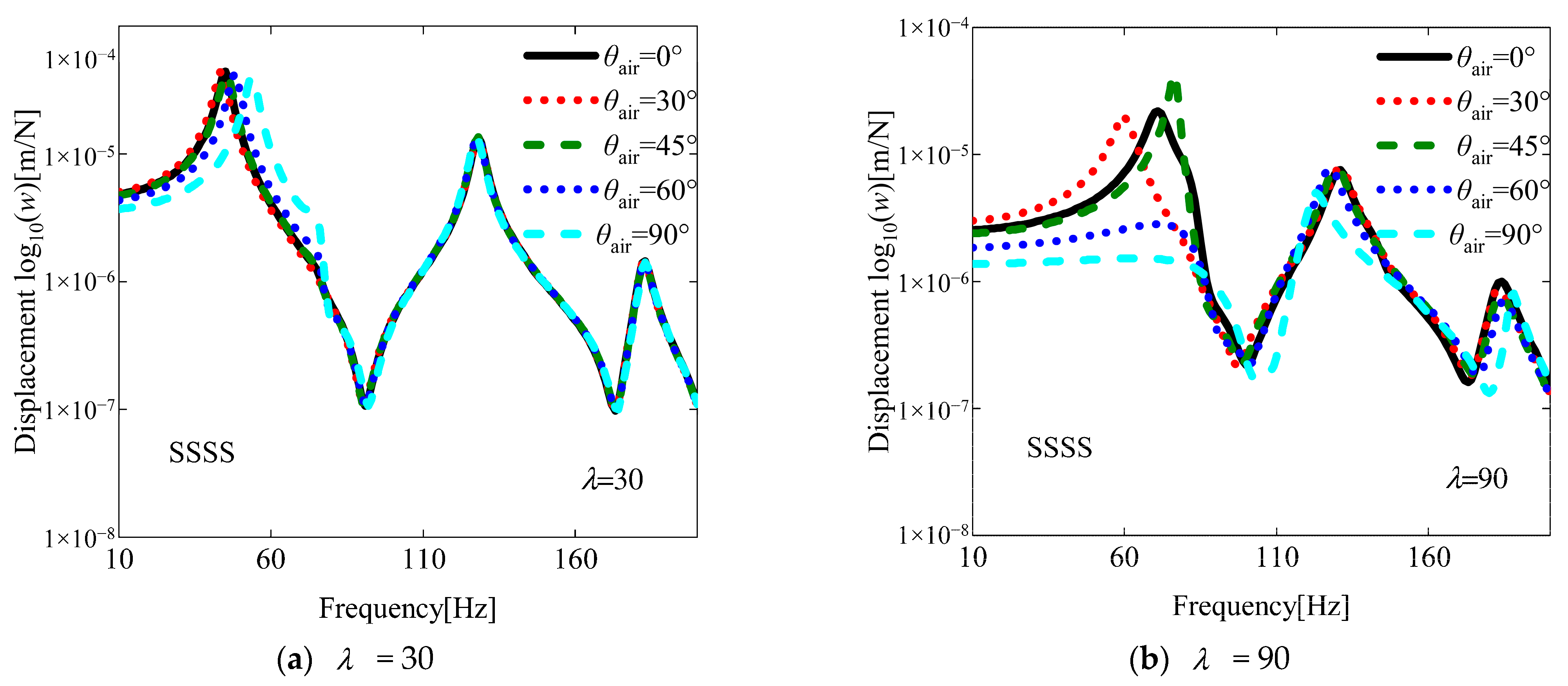
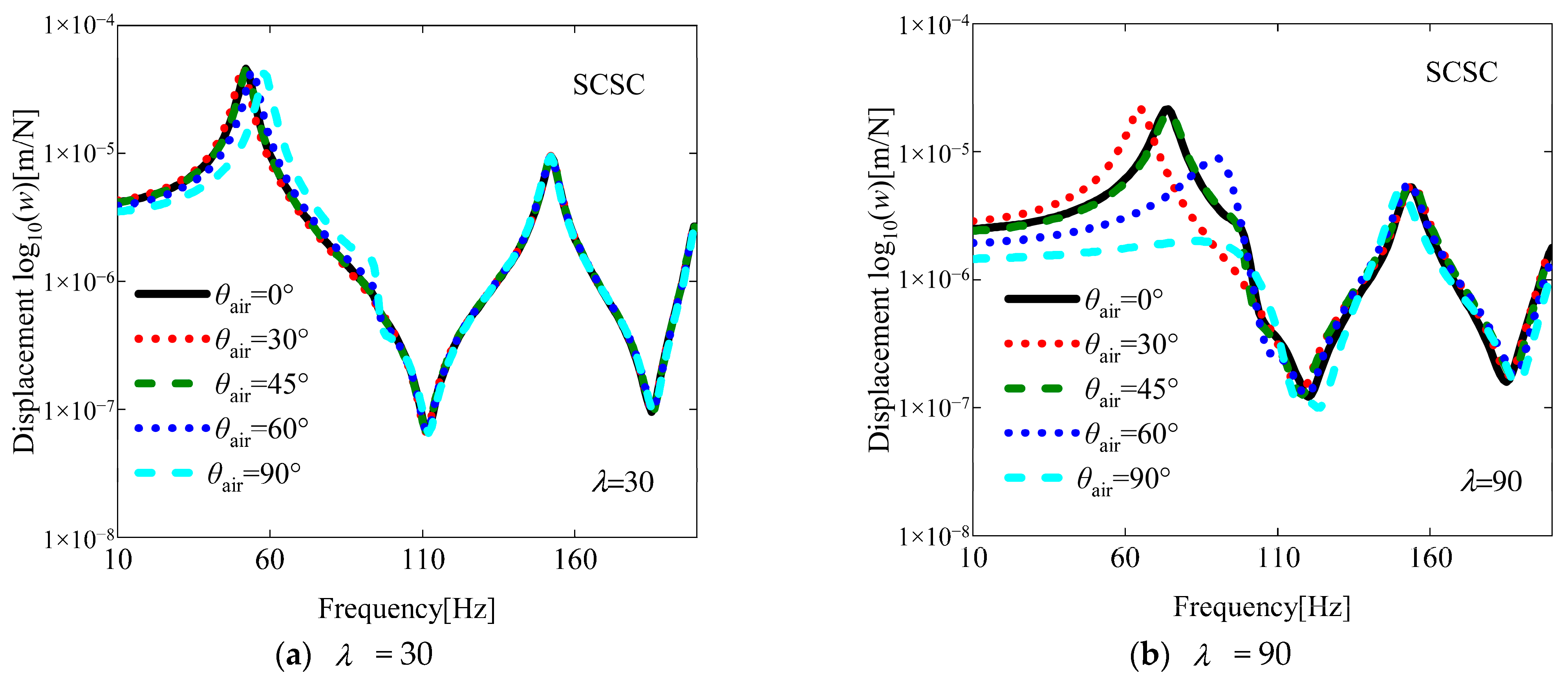
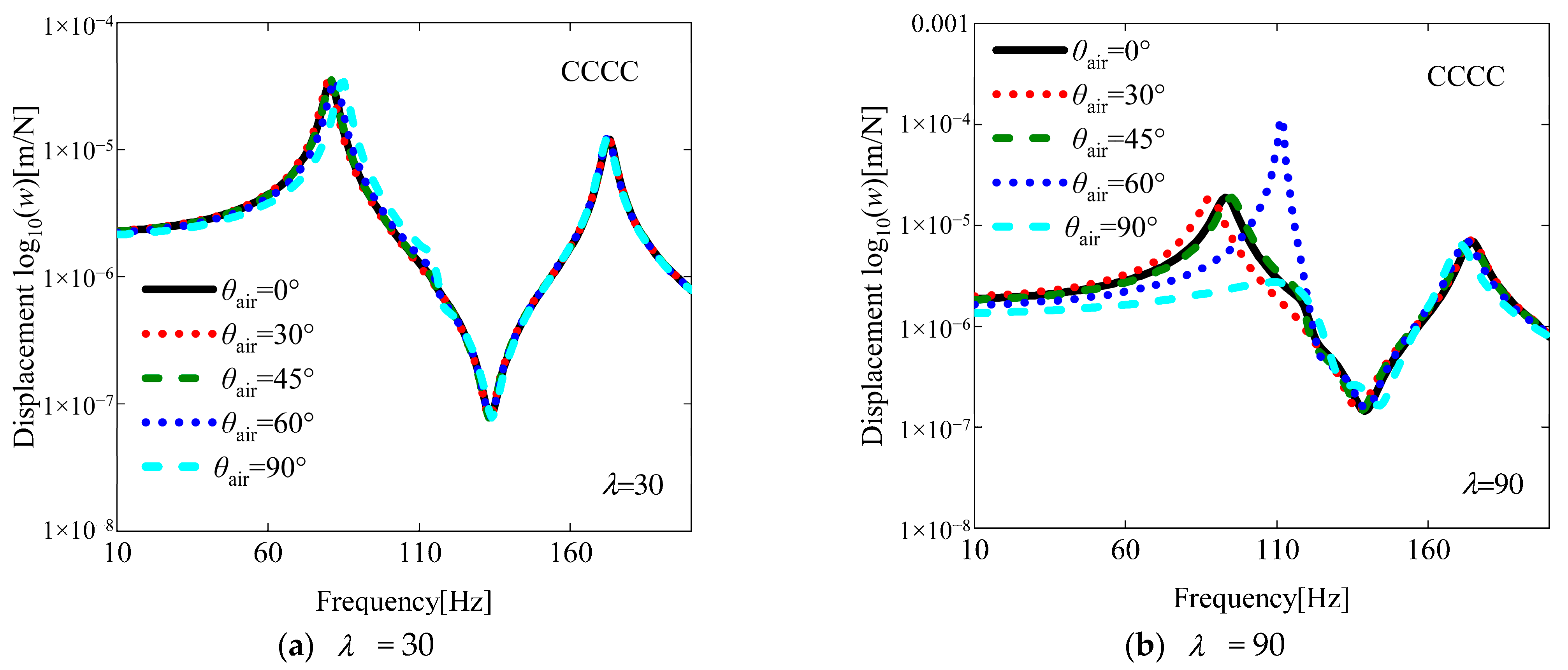
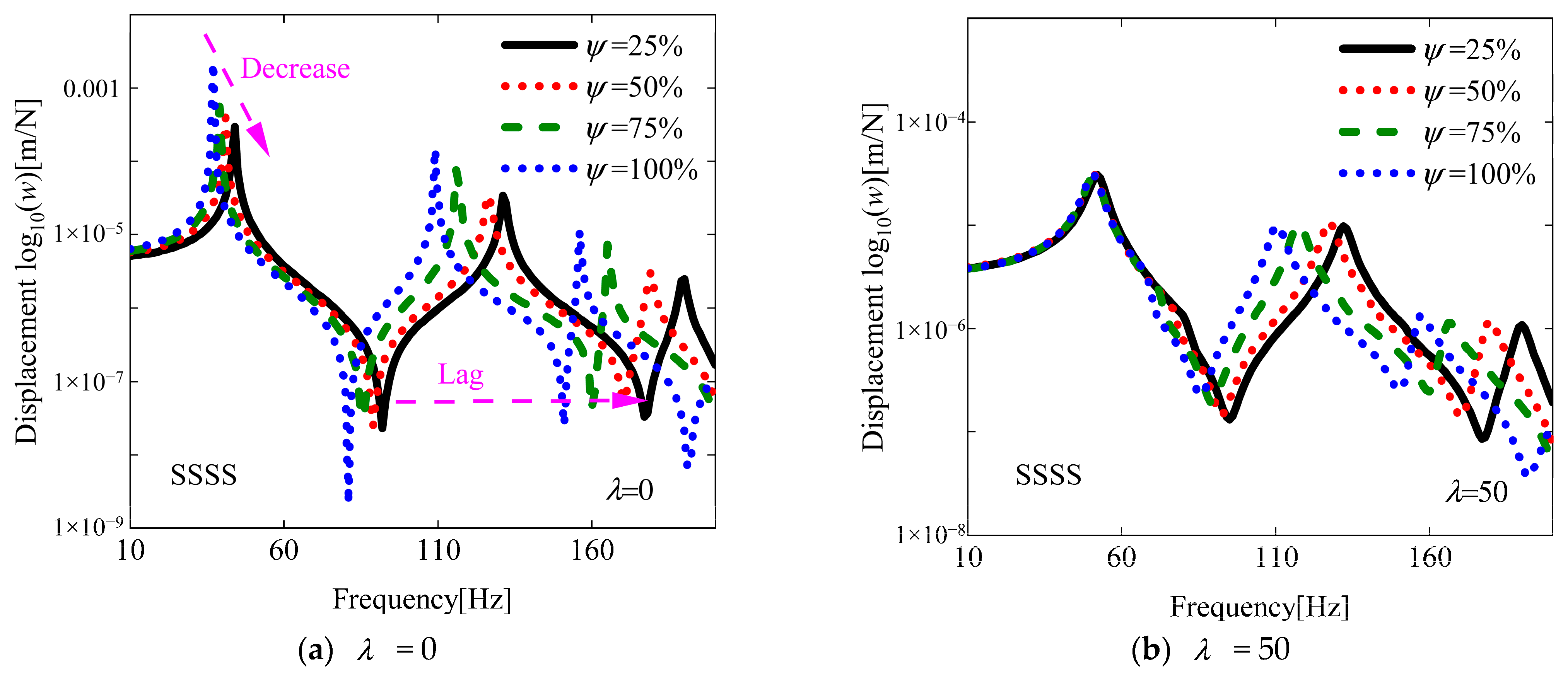
4.3. Analysis of Aeroelastic Response
5. Conclusions
- (1)
- A pronounced inverse relationship is observed between damage severity parameters (a1 and a2) and structural stability, manifesting as coordinated degradation of vibrational characteristics (natural frequencies) and aeroelastic performance (flutter boundaries) with increasing damage magnitude. Damage orientation relative to fiber direction critically influences vibration response, with damage parallel to fiber orientation exhibiting better stability compared to perpendicular damage cases;
- (2)
- Boundary conditions substantially affect damage tolerance, with the fully clamped (CCCC) configuration showing superior stability preservation due to enhanced constraint stiffness;
- (3)
- Optimal flutter dynamic pressure is achieved at the yaw angle θair = 30°, while minimum flutter dynamic pressure occurs at θair = 90°, indicating significant directional sensitivity. Fiber orientation angle θ plays a crucial role in modifying flutter boundaries through its influence on stiffness redistribution within the laminate structure;
- (4)
- The damage area ratio Ψ exhibits an inverse correlation with flutter stability, indicating that an increase in the damage area results in a substantial decrease in critical flutter conditions. The effects of aerodynamic damping become increasingly pronounced when the applied aerodynamic pressure significantly surpasses the critical flutter pressure. Maximum displacement amplitudes consistently manifest at the onset of flutter and exhibit characteristic variations depending on different boundary constraint configurations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Ω | damage region | B | partial differential matrix |
| Lx | length | off-axis stiffness coefficient | |
| Ly | width | density of the plate | |
| h | thickness | air density | |
| θair | yaw angle | Mach number | |
| U∞ | airflow velocity | natural boundary | |
| F | excitation force | coupling boundary | |
| generalized mass matrix | generalized stiffness matrix | ||
| damping matrix |
Appendix A
References
- Morangueira, Y.L.A.; Pereira, J.C.D. Energy harvesting assessment with a coupled full car and piezoelectric model. Energy 2020, 210, 118668. [Google Scholar] [CrossRef]
- Zhao, T.; Xu, M.; Xiao, X.; Ma, Y.; Li, Z.; Wang, Z.L. Recent progress in blue energy harvesting for powering distributed sensors in ocean. Nano Energy 2021, 88, 106199. [Google Scholar] [CrossRef]
- Dudem, B.; Kim, D.H.; Bharat, L.K.; Yu, J.S. Highly-flexible piezoelectric nanogenerators with silver nanowires and barium titanate embedded composite films for mechanical energy harvesting. Appl. Energy 2018, 230, 865–874. [Google Scholar] [CrossRef]
- Eugeni, M.; Elahi, H.; Fune, F.; Lampani, L.; Mastroddi, F.; Romano, G.P.; Gaudenzi, P. Numerical and experimental investigation of piezoelectric energy harvester based on flag-flutter. Aerosp. Sci. Technol. 2020, 97, 105634. [Google Scholar] [CrossRef]
- Elahi, H. The investigation on structural health monitoring of aerospace structures via piezoelectric aeroelastic energy harvesting. Microsyst. Technol. 2020, 27, 2605–2613. [Google Scholar] [CrossRef]
- Ucar, H. Patch-based piezoelectric energy harvesting on a marine boat exposed to wave-induced loads. Ocean. Eng. 2021, 236, 109568. [Google Scholar] [CrossRef]
- Ribeiro, P.; Akhavan, H.; Teter, A.; Warminski, J. A review on the mechanical behaviour of curvilinear fibre composite laminated panels. J. Compos. Mater. 2014, 48, 2761–2777. [Google Scholar] [CrossRef]
- Punera, D.; Mukherjee, P. Recent developments in manufacturing, mechanics, and design optimization of variable stiffness composites. J. Reinf. Plast. Comp. 2022, 41, 917–945. [Google Scholar] [CrossRef]
- Kim, B.C.; Potter, K.; Weaver, P.M. Continuous tow shearing for manufacturing variable angle tow composites. Compos. Part A Appl. Sci. Manuf. 2012, 43, 1347–1356. [Google Scholar] [CrossRef]
- Sharma, N.; Swain, P.K.; Maiti, D.K.; Singh, B.N. Vibration and Uncertainty Analysis of Functionally Graded Sandwich Plate Using Layerwise Theory. Aiaa J. 2022, 60, 3402–3423. [Google Scholar] [CrossRef]
- Salehi, M.; Gholami, R.; Ansari, R. Analytical solution approach for nonlinear vibration of shear deformable imperfect FG-GPLR porous nanocomposite cylindrical shells. Mech. Based Des. Struct. Mach. 2023, 51, 2177–2199. [Google Scholar] [CrossRef]
- Sharma, N.; Tiwari, P.; Maiti, D.K.; Maity, D. Free vibration analysis of functionally graded porous plate using 3-D degenerated shell element. Compos. Part C Open Access 2021, 6, 100208. [Google Scholar] [CrossRef]
- Jing, Z.; Duan, L.; Wang, S.Q.; Li, B. Buckling optimization of variable-stiffness composite plates via variable stiffness optimization algorithm. Compos. Struct. 2024, 327, 117657. [Google Scholar] [CrossRef]
- Sharma, N.; Swain, P.K.; Maiti, D.K.; Singh, B.N. Stochastic frequency analysis of laminated composite plate with curvilinear fiber. Mech. Adv. Mater. Struct. 2022, 29, 933–948. [Google Scholar] [CrossRef]
- Gao, Y.H.; Duan, J.B.; Lei, Y.J.; Xu, B.Q. Aerothermoelastic analysis of curvilinear fiber variable stiffness laminated panels in supersonic flow. Acta Mech. 2022, 233, 4327–4345. [Google Scholar] [CrossRef]
- Kumar, P.; Arya, R.; Sharma, N.; Hirwani, C.K.; Panda, S.K. Curved Fiber-Reinforced Laminated Composite Panel and Variable Stiffness Influence on Eigenfrequency Responses: A Higher-Order FE Approach. J. Vib. Eng. Technol. 2023, 11, 2349–2359. [Google Scholar] [CrossRef]
- Guo, Q.; Hang, J.T.; Wang, S.A.; Hui, W.Z.; Xie, Z.H. Design optimization of variable stiffness composites by using multi-fidelity surrogate models. Struct. Multidiscip. Optim. 2021, 63, 439–461. [Google Scholar] [CrossRef]
- Hu, S.W.; Zhong, R.; Wang, Q.S.; Qin, B.; Shao, W. A strong-form Chebyshev-RPIM meshless solution for free vibration of conical shell panels with variable thickness and fiber curvature. Compos. Struct. 2022, 296, 115884. [Google Scholar] [CrossRef]
- Karimi, M.; Khorshidi, K.; Rezaeisaray, M.; Moutsanidis, G. Vibration of variable stiffness composite laminate and hybrid composite laminate plates coupled to sloshing fluid. Compos. Struct. 2022, 292, 115630. [Google Scholar] [CrossRef]
- Milazzo, A.; Oliveri, V. Investigation of buckling characteristics of cracked variable stiffness composite plates by an eXtended Ritz approach. Thin Wall Struct. 2021, 163, 107750. [Google Scholar] [CrossRef]
- Nie, G.J.; Chen, X.D. Analytical solution for buckling of VAT composite laminates with elastic restraints on two opposite edges. Meccanica 2022, 57, 2085–2099. [Google Scholar] [CrossRef]
- Honda, S.; Oonishi, Y.; Narita, Y.; Sasaki, K. Vibration Analysis of Composite Rectangular Plates Reinforced along Curved Lines. J. Syst. Des. Dyn. 2008, 2, 76–86. [Google Scholar] [CrossRef]
- Honda, S.; Narita, Y. Natural frequencies and vibration modes of laminated composite plates reinforced with arbitrary curvilinear fiber shape paths. J. Sound. Vib. 2012, 331, 180–191. [Google Scholar] [CrossRef]
- Houmat, A. Nonlinear free vibration of laminated composite rectangular plates with curvilinear fibers. Compos. Struct. 2013, 106, 211–224. [Google Scholar] [CrossRef]
- Houmat, A. Optimal lay-up design of variable stiffness laminated composite plates by a layer-wise optimization technique. Eng. Optim. 2018, 50, 205–217. [Google Scholar] [CrossRef]
- Yan, Y.; Liu, B.; Xing, Y.F.; Carrera, E.; Pagani, A. Free vibration analysis of variable stiffness composite laminated beams and plates by novel hierarchical differential quadrature finite elements. Compos. Struct. 2021, 274, 114364. [Google Scholar] [CrossRef]
- Akhavan, H.; Ribeiro, P. Natural modes of vibration of variable stiffness composite laminates with curvilinear fibers. Compos. Struct. 2011, 93, 3040–3047. [Google Scholar] [CrossRef]
- Venkatachari, A.; Natarajan, S.; Ramajeyathilagam, K.; Ganapathi, M. Assessment of certain higher-order structural models based on global approach for bending analysis of curvilinear composite laminates. Compos. Struct. 2014, 118, 548–559. [Google Scholar] [CrossRef]
- Talreja, R. A Continuum-Mechanics Characterization of Damage in Composite-Materials. P Roy Soc. Lond. A Mat. 1985, 399, 195–216. [Google Scholar] [CrossRef]
- Valliappan, S.; Murti, V.; Wohua, Z. Finite-Element Analysis of Anisotropic Damage Mechanics Problems. Eng. Fract. Mech. 1990, 35, 1061–1071. [Google Scholar] [CrossRef]
- Sreehari, V.M.; George, L.J.; Maiti, D.K. Bending and buckling analysis of smart composite plates with and without internal flaw using an inverse hyperbolic shear deformation theory. Compos. Struct. 2016, 138, 64–74. [Google Scholar] [CrossRef]
- Hirwani, C.K.; Panda, S.K.; Mahapatra, T.R. Nonlinear Finite Element Analysis of Transient Behavior of Delaminated Composite Plate. J. Vib. Acoust. 2018, 140, 021001. [Google Scholar] [CrossRef]
- Swain, P.K.; Adhikari, B.; Maiti, D.K.; Singh, B.N. Aeroelastic analysis of CNT reinforced functionally graded laminated composite plates with damage under subsonic regime. Compos. Struct. 2019, 222, 110916. [Google Scholar] [CrossRef]
- Patera, A.T. A Spectral Element Method for Fluid-Dynamics - Laminar-Flow in a Channel Expansion. J. Comput. Phys. 1984, 54, 468–488. [Google Scholar] [CrossRef]
- Motlagh, P.L.; Bediz, B.; Alan, S.; Kefal, A. Analysis of smart laminated composites integrated with piezoelectric patches using spectral element method and lamination parameters. J. Sound. Vib. 2023, 567, 118063. [Google Scholar] [CrossRef]
- Zhong, R.; Wang, Q.S.; Hu, S.W.; Qin, B.; Shuai, C.J. Spectral element modeling and experimental investigations on vibration behaviors of imperfect plate considering irregular hole and curved crack. J. Sound. Vib. 2022, 529, 116924. [Google Scholar] [CrossRef]
- Choe, K.; Tang, J.Y.; Shui, C.J.; Wang, A.L.; Wang, Q.S. Free vibration analysis of coupled functionally graded (FG) doubly-curved revolution shell structures with general boundary conditions. Compos. Struct. 2018, 194, 413–432. [Google Scholar] [CrossRef]
- Shao, D.; Zou, P.G.; Wu, D.T.; Wu, H.R. Electro-mechanical responses analysis of composite trapezoidal plate with conformal piezoelectric arrays in supersonic airflow. Thin Wall Struct. 2025, 216, 113631. [Google Scholar] [CrossRef]
- Ma, Y.B.; Zhang, Y.H.; Kennedy, D. A hybrid wave propagation and statistical energy analysis on the mid-frequency vibration of built-up plate systems. J. Sound. Vib. 2015, 352, 63–79. [Google Scholar] [CrossRef]
- Shao, D.; Wang, Q.S.; Shuai, C.J.; Gu, J.Y. Investigation on dynamic performances of a set of composite laminated plate system under the influences of boundary and coupling conditions. Mech. Syst. Signal Pr. 2019, 132, 721–747. [Google Scholar] [CrossRef]
- Kuo, S.Y. Flutter of rectangular composite plates with variable fiber pacing. Compos. Struct. 2011, 93, 2533–2540. [Google Scholar] [CrossRef]
- Sharma, N.; Swain, P.K.; Maiti, D.K.; Singh, B.N. Stochastic aeroelastic analysis of laminated composite plate with variable fiber spacing. J. Compos. Mater. 2021, 55, 4527–4547. [Google Scholar] [CrossRef]
- Rahmanian, M.; Farsadi, T.; Kurtaran, H. Nonlinear flutter of tapered and skewed cantilevered plates with curvilinear fiber paths. J. Sound. Vib. 2021, 500, 116021. [Google Scholar] [CrossRef]
- Rasool, M.; Singha, M.K. Aeroelastic analysis of pre-stressed variable stiffness composite panels. J. Vib. Control 2020, 26, 724–734. [Google Scholar] [CrossRef]
- Fazilati, J.; Khalafi, V. Aeroelastic panel flutter optimization of tow-steered variable stiffness composite laminated plates using isogeometric analysis. J. Reinf. Plast. Comp. 2019, 38, 885–895. [Google Scholar] [CrossRef]
- Filippi, M.; Carrera, E. Aerodynamic and mechanical hierarchical aeroelastic analysis of composite wings. Mech. Adv. Mater. Struct. 2016, 23, 997–1004. [Google Scholar] [CrossRef]
- Vindigni, C.R.; Mantegna, G.; Esposito, A.; Orlando, C.; Alaimo, A. An aeroelastic beam finite element for time domain preliminary aeroelastic analysis. Mech. Adv. Mater. Struct. 2023, 30, 1064–1072. [Google Scholar] [CrossRef]
- Xue, Y.Q.; Jin, G.Y.; Ma, X.L.; Chen, H.L.; Ye, T.G.; Chen, M.F.; Zhang, Y.T. Free vibration analysis of porous plates with porosity distributions in the thickness and in-plane directions using isogeometric approach. Int. J. Mech. Sci. 2019, 152, 346–362. [Google Scholar] [CrossRef]
- Li, F.M.; Song, Z.G. Flutter and thermal buckling control for composite laminated panels in supersonic flow. J. Sound. Vib. 2013, 332, 5678–5695. [Google Scholar] [CrossRef]
- Gao, X.S.; Zhong, R.; Wang, Q.S.; Bin, Q.; Xu, H.L. Spectral-Tchebychev technique for the free and stochastic vibration analysis of functionally graded plates with piezoelectric patches. Eng. Anal. Bound. Elem. 2023, 152, 688–703. [Google Scholar] [CrossRef]
- Huang, Y.X.; Zhao, Y.; Wang, T.; Tian, H. A new Chebyshev spectral approach for vibration of in-plane functionally graded Mindlin plates with variable thickness. Appl. Math. Model. 2019, 74, 21–42. [Google Scholar] [CrossRef]
- Shao, D.; Zhang, Y.L.; Tao, Y.Q.; Zhao, Y.H.; Cao, Y. Theoretical and experimental investigations on free vibration characteristics of arbitrary spatially closed-coupled plates. J. Sound. Vib. 2024, 570, 118007. [Google Scholar] [CrossRef]
- Viglietti, A.; Zappino, E.; Carrera, E. Analysis of variable angle tow composites structures using variable kinematic models. Compos. Part B-Eng. 2019, 171, 272–283. [Google Scholar] [CrossRef]
- Zhou, K. Nonlinear dynamic analysis and vibration suppression on the composite laminated plates with general boundary conditions in supersonic airflow. Thin Wall Struct. 2023, 190, 110956. [Google Scholar] [CrossRef]
- Dinulovic, M.; Benign, A.; Rasuo, B. Composite Fins Subsonic Flutter Prediction Based on Machine Learning. Aerospace 2024, 11, 26. [Google Scholar] [CrossRef]






| Mode | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| [<0°, 45°>, <−45°, −60°>, <0°, 45°>] | ||||||||
| Ref. [27] | 92.26 | 130.82 | 195.19 | 237.86 | 274.99 | 282.67 | 340.09 | 389.10 |
| Ref. [53] | 92.65 | 131.50 | 196.86 | 239.23 | 276.76 | 286.34 | 342.84 | 395.43 |
| Present | 92.20 | 130.80 | 195.21 | 237.44 | 274.49 | 282.70 | 339.21 | 388.79 |
| Error [27] | −0.07% | −0.02% | 0.01% | −0.18% | −0.18% | 0.01% | −0.26% | −0.08% |
| Error [53] | −0.49% | −0.53% | −0.84% | −0.75% | −0.82% | −1.27% | −1.06% | −1.68% |
| [<90°, 45°>, <60°, 30°>, <90°, 45°>] | ||||||||
| Ref. [27] | 113.18 | 145.25 | 212.66 | 269.06 | 292.47 | 316.49 | 362.78 | 392.79 |
| Ref. [53] | 113.02 | 145.21 | 212.99 | 269.67 | 292.70 | 315.84 | 358.88 | 393.29 |
| Present | 112.86 | 145.33 | 212.52 | 267.40 | 291.42 | 315.91 | 356.85 | 390.42 |
| Error [27] | −0.28% | 0.06% | −0.07% | −0.62% | −0.36% | −0.18% | −1.63% | −0.60% |
| Error [53] | −0.14% | 0.08% | −0.22% | −0.84% | −0.44% | 0.02% | −0.57% | −0.73% |
| Mode | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| [<0°, 45°>, <−45°, −60°>, <0°, 45°>] | ||||||||
| Ref. [27] | 22.44 | 27.10 | 54.87 | 76.05 | 94.35 | 114.01 | 114.47 | 138.89 |
| Ref. [53] | 22.26 | 27.04 | 54.39 | 75.73 | 93.65 | 113.60 | 112.99 | 159.39 |
| Present | 22.30 | 27.06 | 54.56 | 75.83 | 94.17 | 112.92 | 113.70 | 137.69 |
| Error [27] | −0.62% | −0.15% | −0.56% | −0.29% | −0.19% | −0.96% | −0.67% | −0.86% |
| Error [53] | 0.18% | 0.07% | 0.31% | 0.13% | 0.56% | −0.60% | 0.63% | −13.61% |
| [<90°, 45°>, <60°, 30°>, <90°, 45°>] | ||||||||
| Ref. [27] | 19.61 | 24.10 | 44.19 | 62.03 | 64.41 | 91.98 | 99.10 | 110.45 |
| Ref. [53] | 19.54 | 24.09 | 44.12 | 62.11 | 64.35 | 91.76 | 99.11 | 110.19 |
| Present | 19.78 | 24.10 | 44.12 | 61.97 | 64.00 | 91.46 | 99.28 | 109.53 |
| Error [27] | 0.87% | 0.00% | −0.16% | −0.10% | −0.64% | −0.57% | 0.18% | −0.83% |
| Error [53] | 1.23% | 0.04% | 0.00% | −0.23% | −0.54% | −0.33% | 0.17% | −0.60% |
| Mode | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| SFSF | undamaged | FEM | 47.15 | 49.64 | 64.75 | 107.70 | 182.07 | 187.43 | 189.91 | 200.28 |
| Present | 47.15 | 49.63 | 64.77 | 107.74 | 182.12 | 187.38 | 189.86 | 200.25 | ||
| Error | 0.00% | −0.02% | 0.03% | 0.04% | 0.03% | −0.03% | −0.03% | −0.01% | ||
| damaged | FEM | 43.37 | 48.69 | 60.70 | 98.97 | 170.14 | 177.65 | 187.32 | 195.35 | |
| Present | 43.37 | 48.68 | 60.71 | 98.99 | 170.14 | 177.61 | 187.25 | 195.30 | ||
| Error | 0.00% | −0.02% | 0.02% | 0.02% | 0.00% | −0.02% | −0.04% | −0.03% | ||
| SSSS | undamaged | FEM | 51.57 | 78.10 | 137.57 | 190.62 | 204.99 | 227.30 | 242.02 | 310.63 |
| Present | 51.57 | 78.10 | 137.58 | 190.57 | 204.94 | 227.37 | 241.97 | 310.61 | ||
| Error | 0.00% | 0.00% | 0.01% | −0.03% | −0.02% | 0.03% | −0.02% | −0.01% | ||
| damaged | FEM | 45.69 | 72.72 | 129.91 | 178.13 | 196.98 | 212.02 | 234.25 | 299.27 | |
| Present | 45.68 | 72.71 | 129.92 | 178.08 | 196.92 | 212.35 | 234.21 | 299.44 | ||
| Error | −0.02% | −0.01% | 0.01% | −0.03% | −0.03% | 0.16% | −0.02% | 0.06% | ||
| Mode | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| SFSF | undamaged | FEM | 19.78 | 27.75 | 56.41 | 83.81 | 107.10 | 112.83 | 147.46 | 173.00 |
| Present | 19.78 | 27.76 | 56.41 | 83.83 | 107.08 | 112.86 | 147.44 | 173.01 | ||
| Error | 0.00% | 0.04% | 0.00% | 0.02% | −0.02% | 0.03% | −0.01% | 0.01% | ||
| damaged | FEM | 18.39 | 27.27 | 53.49 | 81.22 | 100.95 | 108.36 | 141.51 | 165.57 | |
| Present | 18.40 | 27.26 | 53.48 | 81.20 | 100.92 | 108.33 | 141.46 | 165.53 | ||
| Error | 0.05% | −0.04% | −0.02% | −0.02% | −0.03% | −0.03% | −0.04% | −0.02% | ||
| SSSS | undamaged | FEM | 51.87 | 95.28 | 149.25 | 150.84 | 213.55 | 228.55 | 284.19 | 302.99 |
| Present | 51.94 | 95.30 | 149.30 | 150.96 | 213.59 | 228.49 | 284.27 | 302.93 | ||
| Error | 0.13% | 0.02% | 0.03% | 0.08% | 0.02% | −0.03% | 0.03% | −0.02% | ||
| damaged | FEM | 47.50 | 89.57 | 141.22 | 142.04 | 202.76 | 219.00 | 270.38 | 281.09 | |
| Present | 47.56 | 89.60 | 141.29 | 142.10 | 202.83 | 218.99 | 270.59 | 281.27 | ||
| Error | 0.13% | 0.03% | 0.05% | 0.04% | 0.03% | 0.00% | 0.08% | 0.06% | ||
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | Mode 6 |
|---|---|---|---|---|---|
 |  | 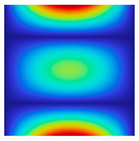 |  | 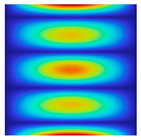 | 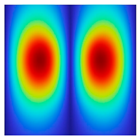 |
| fFEM = 43.37 Hz | fFEM = 48.69 Hz | fFEM = 60.70 Hz | fFEM = 98.97 Hz | fFEM = 170.14 Hz | fFEM = 177.65 Hz |
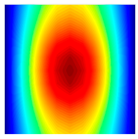 | 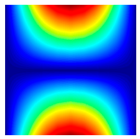 |  | 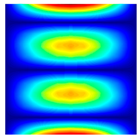 | 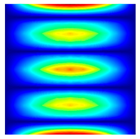 | 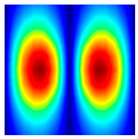 |
| fPresent = 43.37 Hz 0.00% | fPresent = 48.68 Hz −0.02% | fPresent = 60.71 Hz 0.02% | fPresent = 98.99 Hz 0.02% | fPresent = 170.14 Hz 0.00% | fPresent = 177.61 Hz −0.02% |
| Mode 1 | Mode 2 | Mode 3 | Mode 4 | Mode 5 | Mode 6 |
|---|---|---|---|---|---|
 | 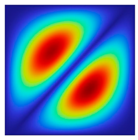 |  | 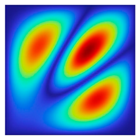 | 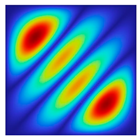 | 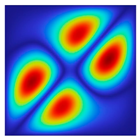 |
| fFEM = 47.50 Hz | fFEM = 89.57 Hz | fFEM = 141.22 Hz | fFEM = 142.04 Hz | fFEM = 202.76 Hz | fFEM = 219.00 Hz |
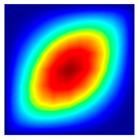 | 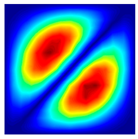 | 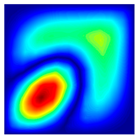 |  | 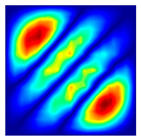 |  |
| fPresent = 47.56 Hz 0.13% | fPresent = 89.60 Hz 0.03% | fPresent = 141.29 Hz 0.05% | fPresent = 142.10 Hz 0.04% | fPresent = 202.83 Hz 0.03% | fPresent = 218.99 Hz 0.00% |
| Boundary | SSSS | SCSC | CCCC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [<0°, 45°>, <−45°, −60°>, <0°, 45°>] | ||||||||||||
| a1 = a2 | 0 | 0.1 | 0.3 | 0.5 | 0 | 0.1 | 0.3 | 0.5 | 0 | 0.1 | 0.3 | 0.5 |
| Mode 1 | 56.68 | 54.34 | 49.01 | 43.02 | 64.73 | 62.22 | 56.59 | 50.36 | 92.14 | 88.62 | 81.01 | 73.03 |
| Mode 2 | 93.43 | 91.17 | 85.81 | 79.43 | 112.92 | 109.80 | 102.56 | 94.21 | 130.62 | 126.73 | 117.84 | 107.75 |
| Mode 3 | 152.50 | 149.12 | 141.14 | 130.80 | 175.94 | 171.90 | 160.09 | 140.35 | 195.30 | 190.21 | 177.95 | 162.07 |
| Mode 4 | 170.57 | 166.84 | 155.75 | 136.78 | 180.29 | 175.98 | 165.56 | 151.88 | 237.63 | 230.93 | 211.89 | 182.44 |
| Mode 5 | 210.24 | 206.92 | 197.91 | 183.52 | 230.05 | 225.62 | 213.77 | 195.69 | 275.24 | 269.23 | 248.80 | 221.37 |
| Mode 6 | 231.49 | 224.38 | 208.62 | 189.31 | 264.09 | 256.45 | 238.43 | 214.10 | 278.99 | 269.87 | 253.32 | 228.93 |
| [<90°, 45°>, <60°, 30°>, <90°, 45°>] | ||||||||||||
| Mode 1 | 52.09 | 49.18 | 42.98 | 36.62 | 103.30 | 100.18 | 93.73 | 86.88 | 113.09 | 109.29 | 101.58 | 93.50 |
| Mode 2 | 84.73 | 81.93 | 75.22 | 67.11 | 117.01 | 114.04 | 107.06 | 98.56 | 144.96 | 140.18 | 129.36 | 117.01 |
| Mode 3 | 140.58 | 136.95 | 128.47 | 117.19 | 167.96 | 163.47 | 153.17 | 139.35 | 212.84 | 206.64 | 191.50 | 170.80 |
| Mode 4 | 173.20 | 166.78 | 149.77 | 125.27 | 230.25 | 223.49 | 208.07 | 188.73 | 269.17 | 259.79 | 236.02 | 204.28 |
| Mode 5 | 201.39 | 196.23 | 182.79 | 163.30 | 262.52 | 256.80 | 241.51 | 211.98 | 292.97 | 284.44 | 262.57 | 232.99 |
| Mode 6 | 219.57 | 212.28 | 195.98 | 177.87 | 283.45 | 272.91 | 246.54 | 220.40 | 312.40 | 300.35 | 274.27 | 244.33 |
| Boundary | SSSS | SCSC | CCCC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [<0°, 45°>, <−45°, −60°>, <0°, 45°>] | ||||||||||||
| a2 | 0.1 | 0.2 | 0.4 | 0.6 | 0.1 | 0.2 | 0.4 | 0.6 | 0.1 | 0.2 | 0.4 | 0.6 |
| Mode 1 | 54.34 | 54.17 | 53.86 | 53.59 | 62.22 | 61.95 | 61.46 | 61.05 | 88.62 | 88.37 | 87.91 | 87.52 |
| Mode 2 | 91.17 | 90.36 | 88.78 | 87.37 | 109.80 | 108.51 | 106.06 | 103.94 | 126.73 | 125.39 | 122.82 | 120.58 |
| Mode 3 | 149.12 | 147.36 | 143.83 | 140.48 | 171.90 | 171.67 | 168.61 | 163.82 | 190.21 | 187.43 | 181.70 | 176.17 |
| Mode 4 | 166.84 | 166.70 | 166.42 | 166.11 | 175.98 | 173.59 | 171.26 | 170.79 | 230.93 | 230.66 | 230.03 | 229.15 |
| Mode 5 | 206.92 | 206.43 | 205.38 | 204.31 | 225.62 | 224.66 | 222.69 | 220.79 | 269.23 | 264.66 | 254.26 | 244.32 |
| Mode 6 | 224.38 | 220.48 | 212.98 | 206.17 | 256.45 | 252.21 | 243.43 | 234.68 | 269.87 | 268.46 | 266.80 | 265.14 |
| [<90°,45°>, <60°,30°>, <90°,45°>] | ||||||||||||
| Mode 1 | 49.18 | 48.84 | 48.21 | 47.63 | 100.18 | 100.05 | 99.76 | 99.45 | 109.29 | 108.91 | 108.19 | 107.53 |
| Mode 2 | 81.93 | 80.38 | 77.00 | 73.44 | 114.04 | 112.91 | 110.43 | 107.83 | 140.18 | 137.70 | 132.47 | 127.26 |
| Mode 3 | 136.95 | 134.19 | 128.14 | 121.08 | 163.47 | 160.50 | 154.03 | 146.56 | 206.64 | 201.89 | 191.00 | 177.95 |
| Mode 4 | 166.78 | 165.57 | 162.45 | 158.31 | 223.49 | 218.51 | 207.63 | 196.25 | 259.79 | 257.16 | 249.50 | 238.22 |
| Mode 5 | 196.23 | 194.62 | 190.86 | 186.25 | 256.80 | 254.93 | 249.73 | 241.69 | 284.44 | 282.48 | 277.82 | 272.27 |
| Mode 6 | 212.28 | 208.79 | 201.93 | 195.90 | 272.91 | 271.08 | 267.92 | 265.13 | 300.35 | 295.49 | 287.34 | 281.92 |
| Boundary | SSSS | SCSC | CCCC | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [<0°, 45°>, <−45°, −60°>, <0°, 45°>] | ||||||||||||
| a1 | 0.1 | 0.2 | 0.4 | 0.6 | 0.1 | 0.2 | 0.4 | 0.6 | 0.1 | 0.2 | 0.4 | 0.6 |
| Mode 1 | 54.34 | 51.97 | 46.78 | 41.37 | 62.22 | 59.81 | 54.56 | 49.18 | 88.62 | 85.17 | 77.99 | 70.93 |
| Mode 2 | 91.17 | 89.54 | 86.09 | 82.65 | 109.80 | 107.75 | 103.44 | 99.09 | 126.73 | 123.94 | 118.17 | 112.44 |
| Mode 3 | 149.12 | 147.28 | 143.51 | 124.82 | 171.90 | 166.98 | 152.41 | 128.37 | 190.21 | 187.54 | 182.09 | 165.68 |
| Mode 4 | 166.84 | 162.17 | 148.23 | 139.80 | 175.98 | 173.72 | 169.04 | 164.11 | 230.93 | 222.78 | 199.75 | 176.80 |
| Mode 5 | 206.92 | 203.44 | 193.83 | 178.76 | 225.62 | 221.34 | 209.74 | 192.39 | 269.23 | 262.87 | 245.80 | 220.51 |
| Mode 6 | 224.38 | 220.94 | 213.97 | 206.89 | 256.45 | 252.55 | 244.43 | 235.74 | 269.87 | 265.58 | 256.96 | 248.36 |
| [<90°, 45°>, <60°, 30°>, <90°, 45°>] | ||||||||||||
| Mode 1 | 49.18 | 46.49 | 41.05 | 35.89 | 100.18 | 97.15 | 90.93 | 84.02 | 109.29 | 105.85 | 98.92 | 91.33 |
| Mode 2 | 81.93 | 80.41 | 77.24 | 74.04 | 114.04 | 111.96 | 107.62 | 102.99 | 140.18 | 137.58 | 132.21 | 126.59 |
| Mode 3 | 136.95 | 135.81 | 133.17 | 113.16 | 163.47 | 161.70 | 158.04 | 153.98 | 206.64 | 204.56 | 200.00 | 189.43 |
| Mode 4 | 166.78 | 160.05 | 140.79 | 130.17 | 223.49 | 220.92 | 211.32 | 185.98 | 259.79 | 250.65 | 224.08 | 194.98 |
| Mode 5 | 196.23 | 191.82 | 180.60 | 166.04 | 256.80 | 251.75 | 237.28 | 218.81 | 284.44 | 276.50 | 257.08 | 233.22 |
| Mode 6 | 212.28 | 208.18 | 200.60 | 194.15 | 272.91 | 262.52 | 240.06 | 225.46 | 300.35 | 293.35 | 282.19 | 273.24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, P.; Shao, D.; Sun, N.; Liang, W. Dynamic Analysis of Variable-Stiffness Laminated Composite Plates with an Arbitrary Damaged Area in Supersonic Airflow. Aerospace 2025, 12, 802. https://doi.org/10.3390/aerospace12090802
Zou P, Shao D, Sun N, Liang W. Dynamic Analysis of Variable-Stiffness Laminated Composite Plates with an Arbitrary Damaged Area in Supersonic Airflow. Aerospace. 2025; 12(9):802. https://doi.org/10.3390/aerospace12090802
Chicago/Turabian StyleZou, Pingan, Dong Shao, Ningze Sun, and Weige Liang. 2025. "Dynamic Analysis of Variable-Stiffness Laminated Composite Plates with an Arbitrary Damaged Area in Supersonic Airflow" Aerospace 12, no. 9: 802. https://doi.org/10.3390/aerospace12090802
APA StyleZou, P., Shao, D., Sun, N., & Liang, W. (2025). Dynamic Analysis of Variable-Stiffness Laminated Composite Plates with an Arbitrary Damaged Area in Supersonic Airflow. Aerospace, 12(9), 802. https://doi.org/10.3390/aerospace12090802






