Generating Large-Scale Datasets for Spacecraft Pose Estimation via a High-Resolution Synthetic Image Renderer

Abstract

The trend toward conducting vision-based spacecraft pose estimation using deep neural networks, which necessitates accurately labeled datasets for training, is addressed in this paper. A method for generating an image regression-labeled dataset for spacecraft pose estimation through simulations involving Unreal Engine 5 is proposed herein. This work provides detailed algorithms for pose sampling and image generation, making it easy to reproduce the employed dataset. The dataset consists of images obtained under harsh lighting conditions and high-resolution backgrounds, featuring spacecraft models including Dragon, Soyuz, Tianzhou, and the ascent vehicle of Chang’E-6. The dataset comprises 40,000 high-resolution images, which are evenly distributed, with 10,000 images for each spacecraft model in scenes with both the Earth and the Moon. Each image is labeled with multivariate pose vectors that represent the relative position and attitude of the corresponding spacecraft with respect to the camera. This work emphasizes the critical role of realistic simulations in creating cost-effective synthetic datasets for training neural network-based pose estimators and publicly available for further study.

1. Introduction

The increasing number of space missions, such as on-orbit servicing, is vital for ensuring the stable operations of spacecraft in serious space environments. In such a scenario, a precise estimate of the pose of a noncooperative spacecraft is crucial for contributing to close proximity operations, which include target tracking, debris removal, and monitoring. Precise pose estimation can help not only save time but also enable relevant operations to obtain pose data in a timely manner. Moreover, the use of a precise pose estimation model is crucial for research involving subsequent tasks, including docking, determining the orbital decay of on-orbit spacecraft, performing maintenance operations, calculating flight pose angles, and measuring the angle between solar panels and two hulls. It is also important as a prerequisite for computing aerodynamics during the reentry processes of large spacecraft from rails involved in subsequent operations [1].

On-orbit noncooperative spacecraft cannot directly utilize sensors to obtain attitude data. This approach lacks cooperation information. The notion of performing vision-based pose estimation for a noncooperative target has been extensively researched with different kinds of space photography. For example, synthetic thermal images [2] can be implemented for close proximity spacecraft operations, and synthetic RGB images [3,4,5] can be used to construct artificial intelligence models for spacecraft pose estimation. To overcome the limitations of public datasets for spacecraft pose estimation, one reason is to improve the accuracy and robustness of the models by providing more diverse and high-quality data. Public datasets often have constraints like limited variety in spacecraft angles, environmental conditions, and imaging sources, which can lead to biased or less generalizable models. By creating specialized datasets or augmenting existing ones, more representative and challenging scenarios can be addressed, ultimately enhancing the performance of pose estimation systems in real-world applications. A method proposed in this paper for generating symmetric datasets by using graphical software and publicly sharing these data contributes to advanced studies and research in this field. The main contributions of this work are as follows:

(1)

A method for creating a labeled spacecraft pose estimation dataset is presented.

(2)

The proposed generated dataset method is based on RGB images, which tend to be used in vision-based spacecraft navigation operations.

(3)

The datasets generated from the four spacecraft, namely Dragon, Soyuz, Tianzhou, and ChangE-6, are publicly accessible.

The rest of the paper is organized as follows. In Section 2, the related works briefly explain the spacecraft that were used in the experiment. Section 3 describes the proposed method. The results are illustrated in Section 4. Conclusions and suggestions for future work are presented in Section 5 and Section 6, respectively.

2. Related Works

Some publications have addressed methods for generating datasets for spacecraft pose estimation, and only several of them have been made public for further research. The next-generation spacecraft pose estimation dataset (SPEED+) [6] includes 60,000 synthetic images for training and 9531 simulated images acquired from a spacecraft mockup model or the Testbed for Rendezvous and Optical Navigation (TRON) facility. TRON is a first-of-its-kind robotic testbed that is capable of capturing target images with accurate and maximally diverse pose labels and high-fidelity spaceborne illumination conditions. Furthermore, SPEED+ was used as a dataset for the International Satellite Pose Estimation Challenge (SPEC) 2021, which was hosted by the European Space Agency and the Space Rendezvous Laboratory (SLAB) of Stanford University. SPEED+ consists of an image of the Tango spacecraft that was used in the PRecursore IperSpettrale della Missione Applicativa (PRISMA) mission. The OpenGL-based optical simulator camera emulation software of the Stanford SLAB was used to generate the first synthetic images. TRON is a hardware-in-the-loop (HIL) facility that separates two different sources of illumination, namely a lightbox and a sunlamp. The lightbox constructs realistic illumination conditions with diffuser plates for albedo simulation, whereas the sunlamp mimics direct high-intensity homogeneous light from the sun. The lightbox and sunlamp domains are unlabeled since their capture corner cases, stray lights, shadowing effects, and visual effects, in general, are not easy to obtain, which is akin to computer graphics. Therefore, it is intended mainly for use as testing datasets. The SPEED [7], which was introduced for SPEC 2019, features images and poses of the Tango spacecraft (from the PRISMA mission) and consists of almost 15,000 synthetic and 300 real images separated into training and testing sets. Both images were generated using the same camera specifications. The real images were captured using the Point Gray Grasshopper3 camera with a Xenoplan 1.9/17 mm lens, whereas the synthetic images were created using the same camera properties. The ground-truth pose labels are contained in vectors and unit quaternions, which describe the relative orientation of the Tango spacecraft with respect to the camera. A synthetic version of the SPEED was created by using the camera emulation software of an optical simulator [8,9]. The software used the OpenGL-based image rendering pipeline to generate photorealistic images. Random Earth images captured by the Himawari-8 geostationary weather satellite were inserted into the backgrounds of half of the synthetic images. The illumination conditions of the synthetic images were processed with Gaussian blurring ($\mathsf{\sigma }=1$) and zero-mean Gaussian white noise (${\mathsf{\sigma }}^2=0.0022$) using MATLAB software. The TRON facility was applied to create real images. Several datasets for spacecraft pose estimation tasks have also been published [10]. For example, Ref. [11] implement the VBN camera for the RemoveDEBRIS mission, which is the first mission to successfully demonstrate this technology. Ref. [3] presented the Unreal Rendered Spacecraft on-Orbit (URSO) dataset generated by Unreal Engine 4 to render synthetic images of the Soyuz and Dragon spacecraft. Synthetic images of the Cygnus spacecraft generated from Blender and its cycle rendering engine were presented in [12]. Approximately 3000 synthetic images of different satellites were also rendered for various tasks, such as bounding box prediction and satellite foreground and part segmentation [13]. The Envisat spacecraft was rendered for pose estimation with 4D cinema, as presented in [14], whereas the Swisscube dataset was rendered by using Mitsuba 2 [15]. The SPARK [16] dataset consists of synthetic images of 11 different spacecraft rendered by using Unity 3D, and synthetic-Minerva-II2 [17], which rendered images of the Minerva-II2 rover from the Hayabusa2 mission [18] via the Photoview 360 renderer of SolidWorks. SEENIC [19] was first introduced as an event-based satellite pose estimation technique. It was trained purely on synthetic event data with a basic augmentation scheme to enhance its robustness against practical noise event sensors. Researchers have conducted experiments involving the Hubble Space Telescope (HST) with the aim of reducing the gap between simulated and target environments. Unlike its counterpart, SEENIC emphasizes the need for image sequences rather than independent and uniformly distributed scenes. [20] The SPAcecraft Pose Estimation Dataset using Event Sensing (SPADES) was introduced by employing the Proba-2 satellite of the PROBA-2 mission [21] as a target. The dataset was generated on the basis of simulated real-event data collected using a realistic satellite mockup and the SnT Zero-G testbed facility [22]. Another synthetic dataset [23] that attempted to overcome the gap between real-world data and synthetic data suffered from effects such as sun power and spectra, the albedo of the Earth, and atmospheric absence effects, which are costly to replicate on the ground. A fine statistical balance was applied in the associated experiment to ensure that the data were appropriate for training and assessing pose estimation solutions. A physically based camera that contributes to realistic light flux, radiometric properties, and texture scattering is available. The produced dataset has 120,000 images with masks, distance maps, celestial body positions, and precise camera parameters. Another dataset was generated under the framework of a project called RAPTOR: Robotic and Artificial Intelligence Processing Test in Representative Target [24]. The researchers collected a large-scale dataset for training and a testing dataset. They performed imaging simulations on spacecraft using Blender software based on 126 satellite CAD models. They used an optical camera and light detection and ranging (LIDAR) with a model replica derived from the specification parameters of a real product and obtained 6336, 576, and 1152 points of data for training, validation, and testing, respectively [25]. Researchers have presented a new dataset called the “Multi-Illumination Angles Spacecraft Image Dataset” (MIAS dataset), which uses Unreal Engine 4 with 3D spacecraft models collected from online resources such as the NASA open-source 3D satellite model website [26]; illumination and other properties were set. The MIAS dataset has been used in an image fusion model for removing shadows from spacecraft images; this is the method that was proposed in [27,28]. Stereovision-based solutions have been introduced to implement the proximity operation for noncooperative space objects and conduct pose estimation on uncooperative space debris. The stereoscopic imaging system in the associated experiment consisted of hardware and software parts. Two cameras were separated into left and right cameras. The images taken from those two cameras were next processed by stereo feature matching software implemented by the scale-invariant feature transform (SIFT) feature detector, which is a brute-force matching algorithm [27]. In contrast, the SURF algorithm was used to extract the descriptors from the image pairs derived from both cameras, and then the fast library for approximate nearest neighbors (FLANN) was used to calculate the Euclidean distances of the feature vectors and match the features between image pairs. The random sample consensus algorithm (RANSAC) was applied to remove or filter inaccurate feature pairs [28]. Another method for generating spacecraft pose estimation datasets is based on open-source ray-tracing software [29]. Ray tracing is a rendering technique that relies on evaluating and simulating view line paths that begin from an observer camera and interact with generic virtual objects in the target scene. A physical-based ray tracer (PBRT), which simulates the physics of light, enables the generation of synthetic images with high accuracy [30]. Ref. [31] showed the different characteristics or properties of real and rendered images. With respect to real images, the researchers set up an experimental room to take photos of microsatellite physical models, while microsatellite rendering models were created for synthetic images. The researchers analyzed the domain gap between the synthetically rendered and real images in the context of image RGB values. Then, physics- and sensor-based noise were included to help shrink the domain gap and render the target model, which was the H2A second-stage rocket body from the JAXA CRD2 project. A pipeline for conducting vision-based on-orbit proximity operations using deep learning and synthetic imagery involved two custom software tools that integrated the working process [32]. The first tool is a plugin-based framework for effectively performing dataset curation and model training. The second tool is Blender, which is an open-source 3D graphic toolset that generates and labels synthetic training data, lighting conditions, backgrounds, and commonly observed in-space image aberrations. The proposed system has an on-cloud base architecture, and the public article provides an example of a Cygnus spacecraft model that was implemented in the system. The system was used in the Texas Spacecraft Laboratory at the University of Texas, Austin, with development benefits in terms of speed and quality. Synthetic thermal images of close proximity spacecraft operations have been studied [2]. Given the scarcity of readily available thermal infrared (TIR) images captured in orbit, these new rendering processes were implemented to generate physically accurate thermal images that were relevant to close proximity operations, which ranged from 15 m to 50 m. Another article presents a novel spacecraft trajectory estimation method that leverages three cross-domain datasets [33]. Different datasets were generated with different distance ranges [34] related to the observer camera, as presented in Table 1.

Table 1. Summary of the recently proposed spacecraft pose estimation datasets based on their distance ranges [34].

Satellite Model	Spacecraft	Range	Resolution	Tools
URSO	Dragon, Soyuz	10 m–40 m	1080 × 960	Unreal Engine 4
SPEED	Tango	3 m–40.5 m	1920 × 1200	OpenGL
SPEED+	Tango	$\le$10 m	1920 × 1200	OpenGL
SwissCube	SwissCube	0.1 m–1 m	1024 × 1024	Mitsuba 2

3. Methods

Three-dimensional models of four spacecraft, namely Dragon, Soyuz, Tianzhou, and ChangE-6, are created on the basis of the available data [35,36,37,38,39,40,41,42,43]. For ChangE-6, only the ascent vehicle that will dock with the Chang’e-6 orbiter in lunar orbit is used to construct the corresponding 3D model. All 3D models are built by using the Unreal Engine 5 software. The large-scale dataset generation procedure for conducting spacecraft pose estimation via a high-resolution synthetic image renderer is composed of three processes: (1) raw data generation, (2) background image generation, and (3) dataset generation. The raw data generation process randomly generates the position and orientation of the spacecraft. The background generation process implements high-dynamic-range imaging (HDRI) backdrop technology [44] in Unreal Engine [45] to randomly create background images to be used during the dataset generation process. Finally, the dataset generation process randomly selects the generated background image and combines it with the generated raw satellite pose data to generate a dataset.

3.1. Raw Data Generation

To generate a robust dataset for spacecraft pose estimation, randomized spatial data are produced within the Unreal Engine environment, simulating diverse and realistic spacecraft configurations. The raw data include spacecraft positions in 3D coordinates $(\mathrm{x},\mathrm{y},\mathrm{z}$), which are dynamically constrained to maintain alignment with the perspective of the camera; orientations are represented in both quaternion $({\mathrm{q}}_1,{\mathrm{q}}_2,{\mathrm{q}}_3,{\mathrm{q}}_4)$ and Euler angles $({\mathrm{r}}_{\mathrm{x}},{\mathrm{r}}_{\mathrm{y}},{\mathrm{r}}_{\mathrm{z}})$. Quaternions are provided for training, offering smooth interpolation and avoiding gimbal lock, whereas Euler angles are used during the dataset generation process in Unreal Engine rotations. Figure 1 shows the spacecraft models rendered with the background presented via predefined axes, including the x-axis, which is defined as a red arrow, the y-axis, which is represented by a green arrow, and the z-axis, which is identified with a blue arrow.

Figure 1. (a) Generated dataset for the Dragon spacecraft model and its predefined axes; (b) generated dataset for the Soyuz spacecraft model and its predefined axes; (c) generated dataset for the Tianzhou spacecraft model and its predefined axes; (d) generated dataset for the ChangE-6 spacecraft model and its predefined axes.

3.1.1. Position Generation

The field of view of the camera at a specific distance $\left(\mathrm{z}\right)$ is determined by the parameters ${\mathrm{f}}_{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{x}}$ and ${\mathrm{f}}_{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{y}}$, which represent the maximum visible horizontal and vertical positions, respectively, when the object is at the nearest allowable distance (${\mathrm{z}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$) from the camera. The perspective projection dictates that the visible bounds scale linearly with distance, maintaining the proportionality defined at ${\mathrm{z}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$.

Under an arbitrary distance $\mathrm{z}$, the maximum allowable horizontal (${\mathrm{f}}_{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{x}}$) and vertical (${\mathrm{f}}_{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{y}}$) positions are calculated as follows:

$${\mathrm{x}}_{\max }={\displaystyle \frac{{\mathrm{f}}_{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{x}}}{{\mathrm{z}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}}\cdot \mathrm{z},\hspace{1em}{\mathrm{y}}_{\max }={\displaystyle \frac{{\mathrm{f}}_{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{y}}}{{\mathrm{z}}_{\mathrm{m}\mathrm{i}\mathrm{n}}}}\cdot \mathrm{z}$$

(1)

where $\mathrm{z}$ is randomly sampled within the range $\left[{\mathrm{z}}_{\mathrm{m}\mathrm{i}\mathrm{n}},{\mathrm{z}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right]$, ensuring that the object is positioned at a valid distance from the camera.

The $\mathrm{x}$ and $\mathrm{y}$ coordinates of the object are then sampled uniformly within their corresponding ranges:

$$\mathrm{x}\in \left[-{\mathrm{x}}_{\max },{\mathrm{x}}_{\max }\right],\hspace{1em}\mathrm{y}\in \left[-{\mathrm{y}}_{\max },{\mathrm{y}}_{\max }\right]$$

(2)

3.1.2. Orientation Generation

In addition to positional variations, the rotation of the satellite is randomized to simulate realistic coverage in all scenarios, ensuring that the dataset captures a wide range of operationally relevant orientations. The pitch $\left({\mathrm{r}}_{\mathrm{x}}\right)$ and yaw angles $\left({\mathrm{r}}_{\mathrm{y}}\right)$ reflect the angular adjustments that are typically performed during docking operations. Both angles can vary within the range $\left[-{360}^{\circ },{360}^{\circ }\right]$. The roll angle $\left({\mathrm{r}}_{\mathrm{z}}\right)$ is also allowed to vary within the full range of $\left[-{360}^{\circ },{360}^{\circ }\right]$, accommodating the potential for full rotational freedom around the principal axis of the satellite.

Euler angles $\left({\mathrm{r}}_{\mathrm{x}},{\mathrm{r}}_{\mathrm{y}},{\mathrm{r}}_{\mathrm{z}}\right)$ are initially used to define these rotations for the Unreal Engine-based object rotation process. However, to overcome computational challenges such as gimbal lock [46] and provide a more robust, singularity-free orientation representation, these angles are converted into quaternions $({\mathrm{q}}_1,{\mathrm{q}}_2,{\mathrm{q}}_3,{\mathrm{q}}_4)$, which are included in the metadata of the generated dataset. The conversion step is performed using the following equations:

$${\mathrm{q}}_1=\cos \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{x}}}{2}}\right)\cos \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{y}}}{2}}\right)\cos \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{z}}}{2}}\right)+\sin \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{x}}}{2}}\right)\sin \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{y}}}{2}}\right)\sin \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{z}}}{2}}\right)$$

(3)

$${\mathrm{q}}_2=\sin \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{x}}}{2}}\right)\cos \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{y}}}{2}}\right)\cos \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{z}}}{2}}\right)-\cos \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{x}}}{2}}\right)\sin \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{y}}}{2}}\right)\sin \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{z}}}{2}}\right)$$

(4)

$${\mathrm{q}}_3=\cos \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{x}}}{2}}\right)\sin \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{y}}}{2}}\right)\cos \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{z}}}{2}}\right)+\sin \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{x}}}{2}}\right)\cos \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{y}}}{2}}\right)\sin \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{z}}}{2}}\right)$$

(5)

$${\mathrm{q}}_4=\cos \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{x}}}{2}}\right)\cos \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{y}}}{2}}\right)\sin \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{z}}}{2}}\right)-\sin \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{x}}}{2}}\right)\sin \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{y}}}{2}}\right)\cos \left({\displaystyle \frac{{\mathrm{r}}_{\mathrm{z}}}{2}}\right)$$

(6)

where ${\mathrm{q}}_1$, ${\mathrm{q}}_2$, ${\mathrm{q}}_3$, and ${\mathrm{q}}_4$ are the quaternion components that efficiently encode the orientation of the satellite.

Algorithm 1 outlines a systematic approach for generating raw data for the dataset preparation process, ensuring efficiency and consistency during the creation of diverse data points. The generation procedure begins by initializing an empty list (L) for storing the results. n is the number of images to be generated. For each data point, its z-coordinate is uniformly sampled from the range $\left[{\mathrm{z}}_{\mathrm{m}\mathrm{i}\mathrm{n}},{\mathrm{z}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right]$, while the bounds for x and y are calculated using Equation (1). Random values for $\mathrm{x}$ and $\mathrm{y}$ are then selected within these bounds. The rotational values ${\mathrm{r}}_{\mathrm{x}}$,${\mathrm{r}}_{\mathrm{y}}$, and ${\mathrm{r}}_{\mathrm{z}}$ are independently sampled using separate uniform random functions across $\left[-{360}^{\circ },{360}^{\circ }\right]$. Since the objective of this experiment is to generate a dataset for close-range spacecraft operations, the camera frame—shown in Figure 2—is implemented as the reference frame. This differs from the approach in [47], which uses a stationary world frame as the reference for 3D rigid body path planning.

Algorithm 1: Pseudocode for the Raw Data Generation Process
Input: $\mathrm{n}$$,\mathbf{ }{\mathrm{f}}_{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{x}}$$,{\mathrm{f}}_{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{y}}$$,{\mathrm{z}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$$,{\mathrm{z}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$ Output: $\mathrm{n}$$\mathrm{list}\mathrm{of}\left[\mathrm{x},\mathrm{y},\mathrm{z},{\mathrm{r}}_{\mathrm{x}},{\mathrm{r}}_{\mathrm{y}},{\mathrm{r}}_{\mathrm{z}},{\mathrm{q}}_1,{\mathrm{q}}_2,{\mathrm{q}}_3,{\mathrm{q}}_4\right]$
1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: 14: 15: 16:	$\mathrm{L}$= empty list for $\mathrm{i}=1,\dots ,\mathrm{n}$ do $\hspace{1em}\mathrm{z}$$=\mathrm{uniform}\mathrm{random}\mathrm{number}\mathrm{within}\mathrm{the}\mathrm{range}\left[{\mathrm{z}}_{\mathrm{m}\mathrm{i}\mathrm{n}},{\mathrm{z}}_{\mathrm{m}\mathrm{a}\mathrm{x}}\right]$ ${\hspace{1em}\mathrm{x}}_{\max }$= calculated from Equation (1) ${\hspace{1em}\mathrm{y}}_{\max }$= calculated from Equation (1) $\hspace{1em}\mathrm{x}$$=\mathrm{uniform}\mathrm{random}\mathrm{number}\mathrm{within}\mathrm{the}\mathrm{range}\left[-{\mathrm{x}}_{\max },{\mathrm{x}}_{\max }\right]$ $\hspace{1em}\mathrm{y}$$=\mathrm{uniform}\mathrm{random}\mathrm{number}\mathrm{within}\mathrm{the}\mathrm{range}\left[-{\mathrm{y}}_{\max },{\mathrm{y}}_{\max }\right]$ ${\hspace{1em}\mathrm{r}}_{\mathrm{x}}$$=\mathrm{uniform}\mathrm{random}\mathrm{numbers}\mathrm{within}\mathrm{the}\mathrm{range}\left[-{360}^{\circ },{360}^{\circ }\right]$ ${\hspace{1em}\mathrm{r}}_{\mathrm{y}}$$=\mathrm{uniform}\mathrm{random}\mathrm{numbers}\mathrm{within}\mathrm{the}\mathrm{range}\left[-{360}^{\circ },{360}^{\circ }\right]$ ${\hspace{1em}r}_z$$=\mathrm{uniform}\mathrm{random}\mathrm{numbers}\mathrm{within}\mathrm{the}\mathrm{range}\left[-{360}^{\circ },{360}^{\circ }\right]$ $\hspace{1em}{\mathrm{q}}_1$= calculated from Equation (3) $\hspace{1em}{\mathrm{q}}_2$= calculated from Equation (4) ${\hspace{1em}\mathrm{q}}_3$= calculated from Equation (5) $\hspace{1em}{\mathrm{q}}_4$= calculated from Equation (6) $\hspace{1em}\mathrm{L}$$\text{<}=\mathrm{insert}\left[\mathrm{x},\mathrm{y},\mathrm{z},{\mathrm{r}}_{\mathrm{x}},{\mathrm{r}}_{\mathrm{y}},{\mathrm{r}}_{\mathrm{z}},{\mathrm{q}}_1,{\mathrm{q}}_2,{\mathrm{q}}_3,{\mathrm{q}}_4\right]$ as last element end for $\mathrm{write}\mathrm{csv}\mathrm{file}\mathrm{from}\mathrm{L}$ list

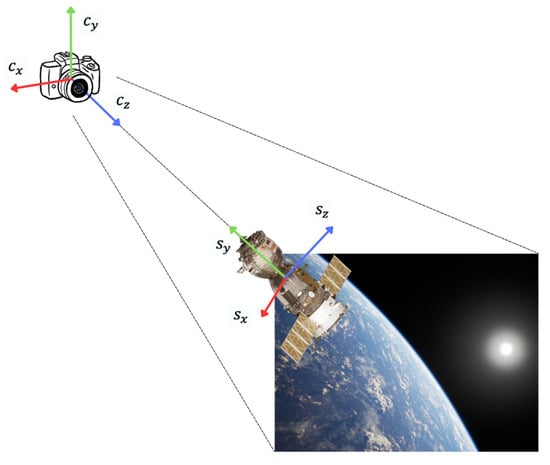
Figure 2. Demonstration of camera reference frame and the integrated scene acquisition system.

The quaternion components $\left[{\mathrm{q}}_1,{\mathrm{q}}_2,{\mathrm{q}}_3,{\mathrm{q}}_4\right]$ are calculated via Equations (3)–(6), ensuring accurate rotational representations. Each data point is appended to the list (L). Finally, the script writes the completed list to a CSV file for the next process.

3.2. Background Image Generation

Realistic and diverse backgrounds are essential for enhancing the quality of satellite pose estimation datasets. The HDRI backdrop method of Unreal Engine is applied to simulate visually accurate environments featuring 3D backdrops of the Earth and Moon. By leveraging HDRI, this approach produces photorealistic backgrounds that closely resemble orbital scenarios.

To introduce variability, the camera is placed at the center of the Unreal Engine environment and randomly rotated to capture a wide range of perspectives. Each rotation results in a unique background image, ensuring diverse environmental conditions. These backgrounds are captured and stored, forming a repository of high-quality images for dataset integration purposes. Figure 3 illustrates examples of the generated backgrounds, presenting the visual realism achieved through HDRI technology.

Figure 3. Examples of generated background images: (a) Earth scene and (b) Moon scene.

The process for generating background images, described in Algorithm 2, uses Python 3.11 scripting within the Unreal Engine environment to produce diverse and high-quality visuals. $n_b$ is the total number of backgrounds created. In this workflow, the camera actor is identified and initialized at the origin (x: 0, y: 0, z: 0). The camera orientation is then systematically varied by assigning random rotational values within a range of $\left[-{360}^{\circ },{360}^{\circ }\right]$ for each axis, ensuring a comprehensive range of perspectives in the generated images. For each of the required background images, the camera is rotated to the specified random orientation, and a high-resolution screenshot is captured. The seamless integration of Python scripting within Unreal Engine enables programmatic control over in-world objects, enabling the efficient automation of this process.

Algorithm 2: Pseudocode for the Background Image Generation Process
Input: $n_b$, camera actor label Output: background image files
1: 2: 3: 4: 5: 6: 7: 8: 9:	Obtain camera actor from the label Initialize the camera position to (x: 0, y: 0, z: 0) for $\mathrm{i}=1,\dots ,n_b$ do $\hspace{1em}{\mathrm{r}}_{\mathrm{c}\mathrm{x}}$$=\mathrm{uniform}\mathrm{random}\mathrm{number}\mathrm{within}\mathrm{the}\mathrm{range}\left[-\mathrm{360,360}\right]$ $\hspace{1em}{\mathrm{r}}_{\mathrm{c}\mathrm{y}}$$=\mathrm{uniform}\mathrm{random}\mathrm{number}\mathrm{within}\mathrm{the}\mathrm{range}\left[-\mathrm{360,360}\right]$ $\hspace{1em}{\mathrm{r}}_{\mathrm{c}\mathrm{z}}$$=\mathrm{uniform}\mathrm{random}\mathrm{number}\mathrm{within}\mathrm{the}\mathrm{range}\left[-\mathrm{360,360}\right]$ $\hspace{1em}\mathrm{Set}\mathrm{camera}\mathrm{rotation}\mathrm{to}(\mathrm{x}\text{: }{\mathrm{r}}_{\mathrm{c}\mathrm{x}}$$,\mathrm{y}\text{: }{\mathrm{r}}_{\mathrm{c}\mathrm{y}}$$,\mathrm{z}\text{: }{\mathrm{r}}_{\mathrm{c}\mathrm{z}}$) Take high-resolution screenshot from the camera view end for

3.3. Dataset Generation

The dataset generation process, as detailed in Algorithm 3, integrates raw positional and rotational data with pregenerated background images to construct a robust and comprehensive training dataset. This method ensures a precise and realistic simulation setup when implemented within the Unreal Engine environment. The scene is anchored by a fixed camera located at the center of the world, while a satellite object is dynamically positioned and oriented on the basis of the raw data. A randomly selected background image is placed behind the satellite, emphasizing the satellite as the focal point while maintaining accurate spatial relationships within the environment. The dataset images are systematically captured from the camera view, providing a reliable foundation for machine learning applications and enhancing the realism and diversity of the training dataset.

By rendering the high-resolution images produced from this setup, the dataset encapsulates diverse satellite poses with various backgrounds. Each image is paired with generated raw data, including 3D coordinates, Euler orientations, and background identifiers. The integrated scene acquisition system is shown in Figure 2, highlighting how the satellite is positioned with its orientations and realistic backdrops alongside the axes of the camera model (${\mathrm{c}}_{\mathrm{x}},{\mathrm{c}}_{\mathrm{y}},{\mathrm{c}}_{\mathrm{z}}$), which are positioned at the center of the world, and those of the satellite model (${\mathrm{s}}_{\mathrm{x}},{\mathrm{s}}_{\mathrm{y}},{\mathrm{s}}_{\mathrm{z}}$). This ensures that the dataset captures the intricacies of satellite motion and perspectives, providing a reliable foundation for training advanced pose estimation models.

Algorithm 3: Pseudocode for the Dataset Generation Process
Input: Output of Algorithm 1, output of Algorithm 2, camera actor label, satellite actor label, background image plate actor label Output: Dataset image files
1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11:	Obtain camera actor from its label Obtain satellite actor from its label Obtain background image plate actor from its label Initial camera position and orientation for $\left[\mathrm{x},\mathrm{y},\mathrm{z},{\mathrm{r}}_{\mathrm{x}},{\mathrm{r}}_{\mathrm{y}},{\mathrm{r}}_{\mathrm{z}}\right]$ in raw data list do $\hspace{1em}\mathrm{Set}\mathrm{position}\mathrm{of}\mathrm{satellite}\mathrm{actor}\mathrm{to}(\mathrm{x}\text{: }\mathrm{x}$$,\mathrm{y}\text{: }\mathrm{y}$$,\mathrm{z}\text{: }\mathrm{z}$) $\hspace{1em}\mathrm{Set}\mathrm{rotation}\mathrm{of}\mathrm{satellite}\mathrm{actor}\mathrm{to}(\mathrm{x}\text{: }{\mathrm{r}}_{\mathrm{x}}$$,\mathrm{y}\text{: }{\mathrm{r}}_{\mathrm{y}}$$,\mathrm{z}\text{: }{\mathrm{r}}_{\mathrm{z}}$)  Uniformly and randomly select the generated background image from Section 3.2  Set the selected background image to the image plate actor  Take a high-resolution screenshot from the camera view end for

4. Results

A comprehensive dataset is generated using the methodology outlined above; this dataset consists of 40,000 high-resolution images designed for satellite pose estimation with 3000 pregenerated Earth scene backgrounds and 3000 pregenerated Moon scene backgrounds. Figure 4 shows the generated sample data derived from four kinds of concentrated spacecraft. This dataset is publicly available at https://huggingface.co/datasets/ascom/spacecraft-close-proximity-pose (accessed on 3 March 2025), and it encompasses four distinct satellite models—Dragon, Soyuz, Tianzhou, and the ascent vehicle of the ChangE-6 spacecraft—captured against Earth and Moon backgrounds. The camera used for dataset generation purposes is a Cine Camera Actor in Unreal Engine, which is configured with a position at the origin (x: 0, y: 0, z: 0), a rotation of x: 0, y: 90, z: -90, and a uniform scale of 1 along all axes. The camera settings include a cropped aspect ratio of 1.33 (4:3), a resolution of 1280 × 960 pixels, a focal length of 8.9, and an aperture of 2.8. These consistent settings ensure uniformity across all generated images. All parameters are provided in Table 2, with depths $\left(\mathrm{z}\right)$ ranging from 5.0 m to 40.0 m and minimum horizontal and vertical bounds $\left({\mathrm{f}}_{\min \mathrm{x}},{\mathrm{f}}_{\min \mathrm{y}}\right)$ ranging from 0.8 m to 2.0 m. Each satellite model is represented by 10,000 images, capturing diverse poses and orientations. The dataset is generated using high-performance hardware, including an AMD Ryzen Threadripper 3970X 32-Core processor (3.69 GHz), 128 GB of RAM, and an NVIDIA GeForce RTX 4070 GPU. Metadata accompany the settings of the Unreal Engine environment, including the parameters used during the generation process, the camera settings, and the model positioning settings, which are provided along with each dataset. This dataset provides a robust foundation for training and validating satellite pose estimation models for satellite docking operations, simulating diverse orbital scenarios with photorealistic accuracy.

Figure 4. Examples of generated datasets for the (a) Dragon spacecraft, (b) Soyuz spacecraft, (c) Tianzhou spacecraft, and (d) ascent vehicle of the ChangE-6 spacecraft.

Table 2. Summary of the generated satellite pose estimation datasets, including their background scenes, spatial parameters, and image counts for each satellite model.

Satellite Model	Background Scene	${\mathbf{f}}_{\mathbf{min}\mathbf{x}}$ (m)	${\mathbf{f}}_{\mathbf{min}\mathbf{y}}$ (m)	${\mathbf{z}}_{\mathbf{min}}$ (m)	${\mathbf{z}}_{\mathbf{max}}$ (m)	Number of Images
Dragon	Earth	2.0	1.0	5.0	40.0	10,000
Soyuz	Earth	1.0	0.8	5.0	40.0	10,000
Tianzhou	Earth	2.0	1.0	7.0	40.0	10,000
ChangE-6	Moon	2.0	1.0	5.0	40.0	10,000

Table 3 expresses the performance of the proposed four generated datasets when tested with UrsoNet [3], a simple architecture developed for object pose estimation, which uses Resnet as a backbone and is applied in several studies [4,5,48] to obtain the mean position estimation error and mean orientation estimation error; these values are compared with the results obtained for the state-of-the-art dataset when running the pre-trained model by implementing the COCO weight. The Soyuz spacecraft dataset derived from the URSO dataset is presented together with the proposed generated datasets to confirm that the overall performance of the proposed datasets aligns with that of the conventional dataset. The URSO dataset is the only one used for comparison with the proposed dataset because it shares common characteristics, such as the use of RGB images and a similar generation method. The mean position estimation error and mean orientation estimation error results produced for each dataset and shown in Table 3 demonstrate that the proposed data synthesis method can perform well with the widely used pose estimation architecture. Differences in the mean location error and mean orientation error metrics arise due to the distinct characteristics of the corresponding datasets, including variations in image sizes and the total number of images across the datasets.

Table 3. The mean position estimation errors and the mean orientation estimation errors induced by each dataset.

Dataset	Location Error (Meters)	Orientation Errors (Degrees)	Best Epoch (Out of 100)
Soyuz hard (URSO dataset)	1.4701	21.1169	96
Soyuz proposed dataset	1.0671	11.3927	100
Dragon proposed dataset	0.9905	12.3303	91
Tianzhou proposed dataset	1.3729	15.7545	97
ChangE-6 proposed dataset	0.8886	11.9321	99

5. Conclusions

Large-scale datasets, which include datasets for the Dragon spacecraft, Soyuz spacecraft, Tianzhou spacecraft, and Change’ spacecraft, are created with 10,000 images each, and they are separated into training, testing, and validation datasets with 8000 images, 1000 images, and 1000 images, respectively. The presented generation method consists of three processes. The first step is raw data generation. This process randomly draws 3D coordinates (x, y, z), with orientations represented in both quaternion (${\mathrm{q}}_1,{\mathrm{q}}_2,{\mathrm{q}}_3,{\mathrm{q}}_4$) and Euler angles (${\mathrm{r}}_{\mathrm{x}},{\mathrm{r}}_{\mathrm{y}},{\mathrm{r}}_{\mathrm{z}}$). These quaternions are applied during the training process, offering smooth interpolation and avoiding gimbal lock. The Euler angles are used for dataset generation via an implementation with the Unreal Engine. The second process involves background image generation. The HDRI backdrop mechanism of Unreal Engine is applied to simulate visually accurate environments featuring 3D backdrops of the Earth and Moon. The final process concerns dataset generation. The raw data obtained from the first step and the background image acquired from the second step are input into a robust environment in Unreal Engine, and a dataset is generated. The dataset is tested with UrsoNet [3], which is a simple architecture developed for object pose estimation that uses ResNet as its backbone. The overall results demonstrate that the proposed datasets perform well. Differences in both the mean location error and mean orientation error metrics occur because of the different properties of the corresponding datasets, such as the different sizes and numbers of total images in various datasets.

6. Future Work

This research concentrates on the processes used to generate spacecraft datasets for performing pose estimation while sharing datasets with the community. In future work, we will expand these datasets to build artificial intelligence models for pose estimation to predict the movements of objects in space via the alternative state estimation method and some relative orbital motion. This simplified system would keep the spacecraft pose estimation model as its state estimation mechanism and implement a relative orbit motion as the system model. In such scenarios, the research will cover areas from dataset generation to space object attitude prediction, which could contribute to the estimation of noncooperative on-orbit targets.