Abstract
This paper presents a stability analysis of single-channel, slow-rolling, Semi-Automatic Command to Line of Sight (SACLOS) missiles using a comparison of the Routh–Hurwitz and the Frank–Wall stability criteria and a nonlinear analysis. Beginning with a six-degree-of-freedom (6-DOF) model in the Resal frame, a linearized model for the commanded motion is developed. This linearized model, which features complex coefficients due to the coupling of longitudinal channels in rolling missiles, is used to define the structural scheme of the commanded object and its flight quality parameters. The guidance kinematic relations, guidance device equations, and actuator relations, incorporating a switching function specific to slow-rolling, single-channel missiles, are also defined and linearized within the Resal frame to construct a comprehensive structural diagram of the SACLOS missile. From this, the characteristic polynomial with complex coefficients is derived and analyzed by comparing the Routh–Hurwitz and the Frank–Wall stability criteria. This analysis determines a stability domain for the guidance gain and establishes a minimum limit for the guidance time. The stability domain defined through the linear model is then validated using a nonlinear model in the body frame.
Keywords:
SACLOS missile; slow-rolling missile; single–channel command missile; characteristic polynomial with complex coefficients; stability criterion; mathematical model; Routh–Hurwitz stability criterion; Frank–Wall stability criterion; flight dynamics; guidance and control; Resal frame; thrust vector control 1. Introduction
In modern anti-armor warfare, guided missiles are a primary tool, often employing “three-point guidance” methods that rely on the alignment of the carrier, missile, and target. These systems can be categorized by their guidance mechanism, with wire-guided missiles typically using angular error control, while laser- or radio-beam-guided missiles utilize linear error control. This paper focuses on the former, specifically on wire-guided missiles that require a direct hit on heavily armored targets. This is achieved through a Semi-Automatic Command to Line of Sight (SACLOS) guidance method, where an operator tracks the target, and a guidance signal is automatically generated and transmitted to the missile via a wire.
For subsonic flight regimes, where aerodynamic control surfaces have limited effectiveness, these missiles often rely on jet controls, such as thrust vector control, to perform necessary maneuvers. The use of slow-rolling missiles in engaging heavily armored targets has become increasingly prevalent in modern weaponry. This design offers several advantages, including a reduction in the missile’s size and mass. The rolling motion also serves to cancel out disturbing forces and torques that arise from aerodynamic or gas-dynamic asymmetries. Furthermore, the roll allows for control to be executed on a single channel with a single pair of mobile nozzles, simplifying the control system and reducing energy requirements, which is conducive to the development of portable missile systems.
Although these systems are well known and technically developed, they represent a special aircraft class, for which, due to the specifics of their movement, theoretical models necessary to clarify certain aspects regarding the improvement of their functionality are still in development.
The guidance and control of rolling missiles have been extensively studied. Research has addressed two-channel rolling missiles [1,2], including dual-spin projectiles with high-velocity rotating bodies for gyroscopic stability and lower-velocity rotating tips with canards for trajectory control [3]. Other studies have focused on single-channel missiles with time-modulated commands [4,5,6,7,8]. Recent work on two-channel missiles has explored autopilot design with double [9] or triple [10] feedback loops, the stability of precession motion (conical) [1,2], and the influence of signal errors from the target tracking system [9,11]. Another area of research has been the development of sensors to determine the missile’s attitude, particularly the roll angle, which is crucial for command signal generation [12,13]. For instance, some have proposed a new combination of silicon micro-gyroscopes to demodulate yaw, pitch, and spin angular velocities. Another strategy suggested in the literature is the application of a two-step, adaptive, augmented, unscented Kalman filter (TS-AAUKF) [13], which serves to calibrate the magnetometer for accurate roll angle estimation.
To address what was done in the specific case of the single-channel missile, the following section analyzes the results from previous research [4,5,6,7,8,14] in detail.
Reference [4] proposes a digital controller as an alternative to the conventional analogue time-modulation controller. The authors demonstrate that by substituting the analogue phase control with a digital amplitude control system, it is possible to achieve decoupling of the yaw and pitch channels. This method effectively mitigates errors arising from actuator delay and sensor noise. However, the primary limitation of this solution (at the time of proposal) was the increased complexity of the missile control system, which consequently led to a higher overall cost.
The stability of a rolling rocket with single-channel control is examined in [5] through the development of closed-form analytical solutions from linearized dynamics. This analysis uses a mixed reference frame: the control command is processed in the body frame, while the system dynamics is modelled in the non-rolling Resal frame. Furthermore, the command signal is generated via a series expansion, facilitating a comparative analysis between an idealized rectangular command and a practical implementation that accounts for actuator delays.
In reference [6], a linear model for the commanded motion of a slow-rotating rocket is developed from the equations of motion in the Resal frame. This model employs complex coefficients to account for the coupling between channels caused by gyroscopic and Magnus terms, enabling the characterization of both nutation and precession motion, as well as the definition of flight quality parameters. This linear analysis concludes in a structural scheme of the commanded object that is specific to slow-rolling missiles with complex coefficients. Unlike the serial development approach in [5], the proposed solution in [6] generates the switch command by considering the sign of a trigonometric expression that depends on the roll angle, as detailed in [15].
This paper analyzes two types of single-channel, slow-rolling guided missiles: a portable anti-aircraft homing missile and a portable anti-tank wire-guided missile. In contrast to [5], which formulates the command in the body frame, [6] derives an equivalent command in the Resal frame from the time-modulated command. This equivalent command is then used to construct structural diagrams for both the homing and wire-guided missile types. Due to the complexity introduced by the structural schemes’ complex coefficients, the scope was limited to determining the characteristic polynomial’s roots and the phase–frequency/amplitude–frequency diagrams for the wire-guided rocket, emphasizing the differences from a non-rolling rocket.
The feasibility of controlling an autonomous rolling rocket via a single-channel reactive command is explored in [7]. The work contrasts a simplified two-nozzle Reaction Control System (RCS) with a conventional six-nozzle configuration. While the traditional system ensures complete three-axis attitude control, the proposed two-nozzle alternative provides actuation for only the pitch and yaw channels. This latter approach leaves the roll angle uncontrolled, thus allowing for free roll rotation of the vehicle.
In [8], starting from the results in paper [6], the case of the anti-aircraft rolling homing missile was analyzed, performing a stability analysis with the Frank–Wall criterion.
Reference [14] addresses the optimal control problem for the minimum-time attitude maneuvering of a rolling missile. In this formulation, a single reaction jet is used to generate the necessary transverse control moments. The problem considers a rocket with an arbitrary initial transverse angular velocity. The objective is to steer the missile to a specified final attitude in the shortest possible time, while simultaneously nullifying the final transverse angular velocity.
The current paper builds upon previous work on single-channel missiles, particularly the findings in [6], by analyzing the stability of a single-channel, slow-rolling SACLOS missile using the Frank–Wall stability criterion [16]. A key distinction between two-channel and single-channel missiles lies in the command formation. While two-channel systems use proportional deflection of both canards, single-channel missiles employ a time-modulated maximum deflection of one canard, managed by a switching function. We will also consider the influence of the guidance gain () and time guidance () of the guided device system, leading to a fifth-order characteristic polynomial, which introduces additional stability conditions that will be analyzed in detail. The effect of phase shift, introduced by actuator delay and inaccuracies in roll angle determination, will also be examined.
Since this paper represents an alternative development of paper [8], for the case of single-channel slow-rolling missiles with thrust vector control and SACLOS guidance, we will present only the specific elements that appear in this new case, for the common aspects referring to paper [8].
Contributions of This Paper
This paper presents several key contributions to the study of single-channel, slow-rolling missiles. The primary novelty lies in the comprehensive stability analysis of a SACLOS missile using both Routh–Hurwitz (R-H) and Frank–Wall (F-W) stability criteria and nonlinear analysis. This analysis examines the influence of key guidance system parameters, leading to the definition of specific restrictions and stability domains. To support this analysis, the paper establishes a method for determining the F-W stability parameters for the resulting fifth-order characteristic polynomial, with detailed calculation procedures provided in Appendix E. A detailed structural scheme for a single-channel, slow-rolling SACLOS missile is also developed and presented. Furthermore, this work includes a thorough analysis of the stability and command derivative magnitudes derived from the linearized model, as well as the flight quality parameters. Finally, the stability domains identified through the linear analysis using the R-H and F-W criteria are validated against a nonlinear 6-DOF model, confirming the accuracy and applicability of the results.
The novelty of the paper consists of the following:
- Comparative analysis between the exact solution and the approximate solution for the equilibrium flight parameters (Section 2).
- The detailed structural scheme for the SACLOS slow-rolling missile with a single channel.
- The stability analysis for slowly rolling, single-channel SACLOS missiles, employing the Frank–Wall stability criterion. The investigation examines the influence of key guidance system parameters on stability, utilizing a comprehensive model that incorporates higher-order dynamic terms. Based on this analysis, operational constraints are identified, and stability domains are defined for several of these critical parameters (Section 7.2).
- The validation of linear analysis with R-H and F-W stability criteria using a nonlinear model (Section 7.3).
2. Basic Movement
Since the general equations of motion in the body frame and the Resal frame were presented in paper [8], to linearize the equations of motion, we will now analyze the basic motion in the Resal frame, because in this case, unlike in [8], we have jet control.
We will consider a symmetrical evolution in the vertical plane as basic motion. The lateral movement elements are set to zero:
. From Figure 1, we can write the equilibrium equations in the vertical plane:
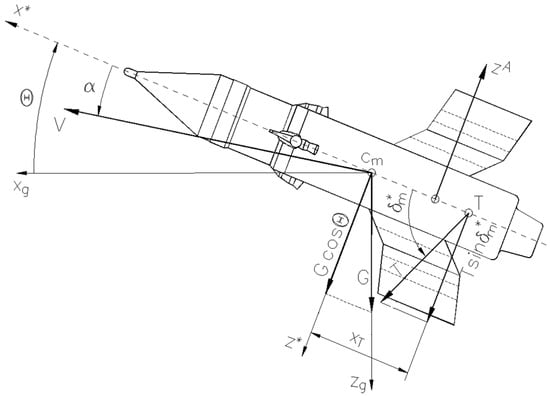
Figure 1.
Vertical plane motion elements with thrust vector control.
If we detail the lateral accelerations,
and
, the relations become
If the terms of jet damping [17] are neglected and it is noted that
and
the thrust components become
where, as shown in [6,18], the equivalent jet deflection to the pitch axis of the Resal frame can be taken for twin-channel missiles approximately equal to the deflection in a control plane, and for single-channel missiles it is obtained by integrating the projection of the deflection from the control plane over a period of rotation along the direction of the pitch axis of the quasi-linked frame.
Note: Since in the body frame the position of application of the jet command is behind the center of mass, it follows
.
The aerodynamic coefficients are developed in this way:
For analyzing the magnitude terms in these expressions, and those that will be elaborated later, we will use, according to [19,20], the following parameters:
Small values:
—reference time;
—reduced gravitational acceleration.
Large values:
—the reduced mass of the aircraft;
—the reduced moment of inertia in pitch.
Introducing these parameters into relations (2), we obtain
where we noted
and
, while
is the dimensionless angular rate of precession, and
is the flight-path inclination angle.
If we impose angular velocities
,
and the angle of inclination of the trajectory
, system (5) can be solved numerically with a Newton algorithm [21] in relation to the sizes
,
,
, and
, which represent the flight parameters for the basic motion under consideration.
If we impose a translational motion with zero angular velocity of pitch and yaw (, and neglecting the aerodynamic terms of higher order (, the system decouples and becomes
One can notice that for lateral motion, the last two homogeneous equations lead to the trivial solution
,
while the first two equations, corresponding to longitudinal motion, for the given
lead to a transcendent equation in the angle
and a calculus relation for the equivalent thrust deflection in pitch
.
Thus, eliminating the incidence between the equations of longitudinal motion, we obtain
where the static stability reserve was noted:
.
If the terms of the thrust are eliminated, the following is obtained:
Imposing the value of the climb angle
, implicitly for the particular case of horizontal flight
, the system is reduced to relation (8), which becomes a transcendent equation that is solved iteratively in relation to the incidence to which is added the explicit relation (7), which allows the determination of the equivalent thrust angular deflection. Figure 2 and Figure 3 compare the exact solution (5) with the approximate solution (7) and (8) for the equilibrium command.
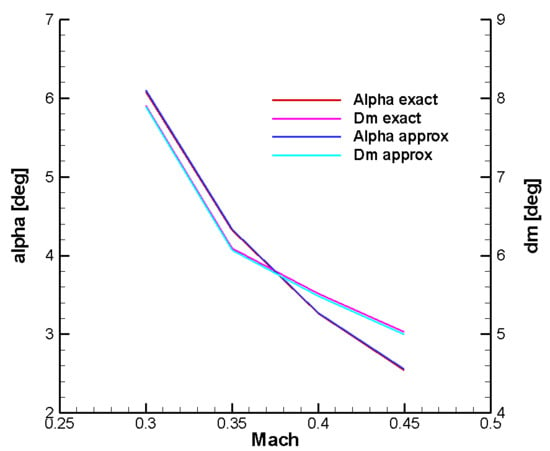
Figure 2.
Equilibrium command and incidence for initial mass value.
Figure 3.
Equilibrium command and incidence for final mass value.
These parameters (represent the basic movement of the rolling missile, presented in Appendix B.
From Figure A12, it can be seen that the equilibrium incidence in the lateral plane (β) is negative, which will lead to a deviation of the trajectory to the left of the firing plane, a phenomenon specific to aerodynamically stabilized rolling missiles.
3. The Linear Equations
To obtain the linear equations, we will consider the hypotheses from reference [8].
Also, for the symmetry, for the gas-dynamic commands, we will consider the small angular deflections so that
Linearizing translational equations in the Resal frame [8], we obtain
On the other hand, linearizing rotational equations in the Resal frame [8], we obtain
Following ref. [8], we use the following dual notation for the coupled equations:
These parameters represent the stability and command derivatives that are presented in Appendix B.
Next, we will rewrite the coefficients of the equations of motion, in which we will include the previously defined parameters for the basic movement, obtaining the following:
Also, we define the complex quantities:
with
.
In this case, Equations (10) and (11) are
Applying the Laplace transform, the homogeneous form is
with the characteristic polynomial:
Separating complex terms, we obtain
With the approximations in (13), the characteristic polynomial becomes
where
will be explained later.
We verify the correctness of relations (13) by comparing the exact and approximate roots of the characteristic polynomials in Figure 4 and Figure 5; they match closely. The diagrams are obtained for a range of Mach numbers: 0.3 to 0.45.
Figure 4.
The roots of the characteristic polynomial—initial.
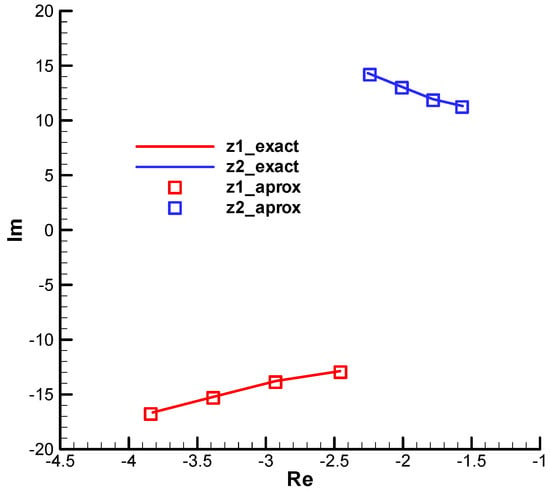
Figure 5.
The roots of the characteristic polynomial—final.
Based on these results, the approximate relations (13) will be used to obtain the simplified structural scheme for the commanded object.
4. The Flight Quality Parameters
Following [8], we use the following notation:
where
is the angular rate of precession, with dimensionless form
, and
represents static stability (Figure A27).
In this case, the characteristic polynomial (19) has the following form:
with natural pulsation
and damping factor
having the following expressions:
Sometimes, the inverse of natural pulsation is used:
—time constant of nutation movement.
In Figure A28, Figure A29 and Figure A31 from Appendix B, the natural pulsation, damping factor and time constant according to the Mach number are presented.
The roots of the characteristic polynomial (21) are
Developing this, we obtain
where ;
;
To obtain the command parameter, we put the relation (15) in matrix form:
with the inverse matrix:
where
is the characteristic polynomial.
Based on this relation, as shown in [11], after processing, the following transfer function is obtained:
where the input
is the complex form of gas-dynamic deflection in the Resal frame, and the output
represents the complex form of the angular velocity of the velocity vector.
With the notation
the transfer function, due to the large value of the parameter
, becomes
where the following notation was used:
- —the command factor and the parameter;
- —the advance time on command or the aircraft’s time constant [22], and is a Magnus term.
Dropping the secondary terms for the reaction commanded missile, the parameters from relations (28) become
where we recall that it was noted that
, where
represents the distance between the point of application of the jet control and the center of mass, in the body frame, having a negative value.
We can also evaluate the complex acceleration in the Resal frame:
with
Based on these relations, we can build the structural scheme of the commanded movement for slow-rolling missiles, with reaction command, shown in Figure 6.
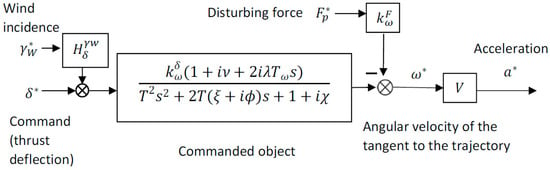
Figure 6.
Structural scheme of commanded movement for a slow-rolling missile.
5. The Guided Flight Model
5.1. The Guidance Relations
As shown in [18,23,24], the guidance kinematic relations will be constructed into a frame linked to the carrier-target line of sight called the guiding frame (Figure 7). The guiding frame
originates at point (, which represents the position of the carrier; the axis
points towards the target
; the axis
is in a vertical plane facing downwards; and the axis
is positioned horizontally; it follows from the condition of the right frame. The guiding frame is non-inertial.
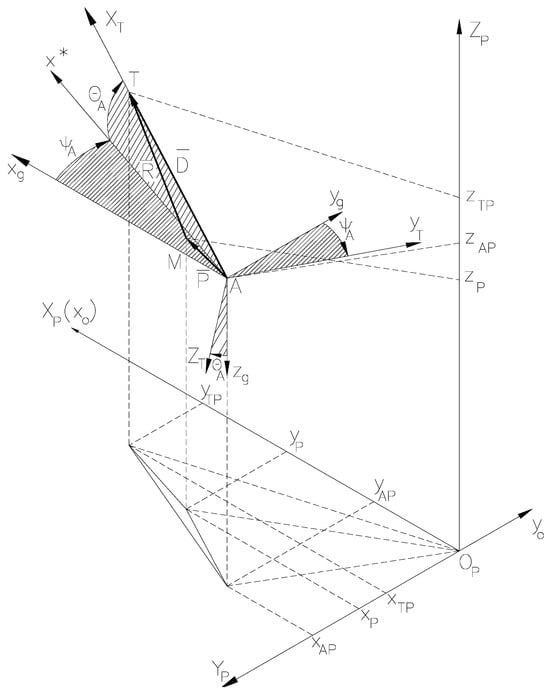
Figure 7.
Orientation of the guiding frame with respect to the local frame [23].
The angles defining the orientation of the guiding frame with respect to the local frame are given by the following relations:
where
, and
are the coordinates of the carrier in the local frame, respectively, and
,
, and
are the target coordinates in the local frame.
In Figure 8 and Figure 9, the following are marked: A—the position of the carrier; M—the position of the missile; and T—the position of the target. The two figures also show the position vector of the target D, the position vector of the missile P, the position vector of the target relative to the missile R, and the angles
that the target line of sight and the missile line of sight make with a fixed direction in space.
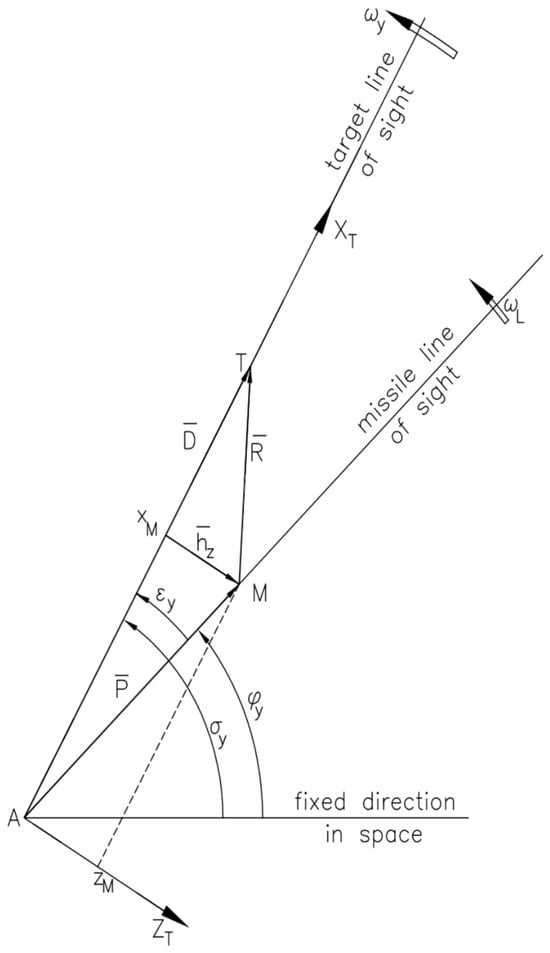
Figure 8.
Kinematics of three-point guidance method—first guiding plane (vertical).
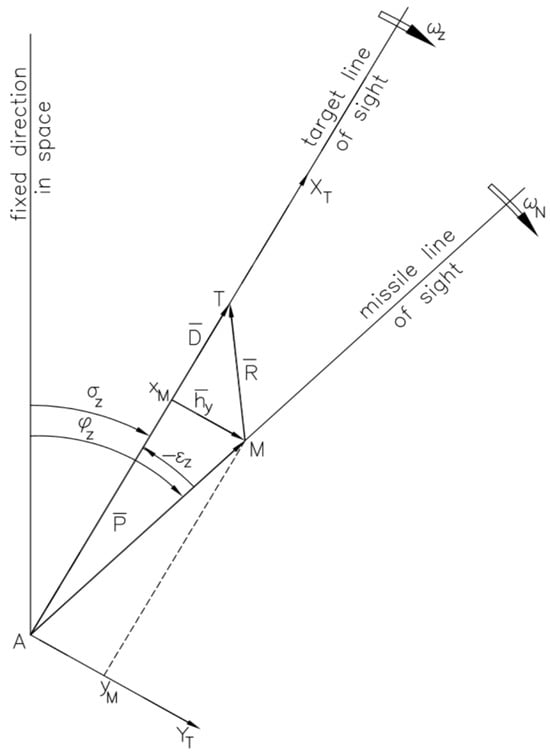
Figure 9.
Kinematics of three-point guidance method—second guiding plane (inclined).
In the case of angular deviation control, the guidance parameters are
, for determining which relations are used:
From Figure 8 and Figure 9, it is observed that the angular error in the two guidance planes can be expressed as follows:
Assuming that the target, the carrier, and the mobile evolve independently in the two planes, the geometric connection between the angles can be derived, obtaining the following:
where the angular velocities were noted:
5.2. Linear Form of Kinematic Guidance Relations
In the case of semiautomatic command to line of sight (SACLOS), which is based on angular error control, the collinearity of the three points (A-M-T) is achieved by cancelling the angular deviation in the two guidance planes:
Considering the geometric connections between angles in the guiding planes (35), one can write
which represents the collinearity of the position vectors for target
and missile
(Figure 7).
If the condition of cancelling the rate of the deviations is also imposed,
relation (36) shows
which is the condition that the vectors
and
rotate with the same angular velocity.
To construct a model of guidance with angular deviation control, we start from the observation that the linear shape of the guide controls is decoupled for the case of a general movement.
Thus, if the definition relation of the angular errors (34) is linearized, under the conditions of the basic movement, the following is obtained:
Developing the expression of the linear deviation, we obtain
On the other hand,
In this case, the deviation of the angular errors becomes
From whence,
Considering the particularity of the basic movement adopted, in which the velocity vector of the mobile is collinear with the target’s line of sight, namely
and noting the input functions of order “0” due to the carrier’s position deviations,
the deviation of the angular error can be put in the following form:
thus obtaining the cinematic block.
From this relation, it can be seen that for the case of the fixed carrier, the deviation of the absolute angle of the line of sight of the missile is given by
On the other hand, the guidance commands in the guidance planes are
where
By applying the Laplace transform, the guidance command can be put in the following form:
For the linearization of the guidance command, a particular basic motion is considered where the target, the mobile, and the carrier are collinear, and the velocity vector of the missile is oriented along this line.
In this case, the angle of lateral inclination of the missile must be zero; the head angle of the missile is equal to the angle of rotation in the horizontal plane of the guidance frame
, which overlaps the pitch plane of the missile with the vertical plane of guidance.
The axis of the rocket is above the velocity vector, with which it forms a positive incidence that balances the force of weight.
For the simplification of the structural scheme, in the case of the fixed carrier, the zero-order input functions
can be considered cumulated with the inputs due to the target through the angles
, obtaining in this case a simplified transfer function with a single input.
5.3. The Guidance Command
As shown in paper [8], neglecting the angle of incidence in the vertical plane and assuming that the pitch angle of the rocket
overlaps the angle of the guiding frame
, the command can be put in the following form:
where the following notation was used:
being the direct rotation matrix with roll angle.
Next, we will seek to transform matrix expressions into a complex form using a polar coordinate system that highlights the module and phase of the guidance command. Thus, if the commands are put in the complex form
where
is the command in body frame and
is the command in the guiding frame/Resal frame.In this case, relation (54) becomes
Based on Figure 10, the guidance command can be put in polar coordinates:
where
is the command module and
is the command phase.
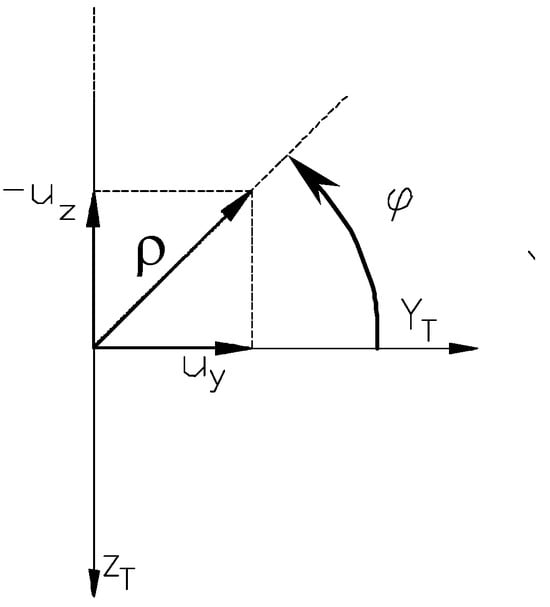
Figure 10.
The guidance command in polar coordinates.
In this case, the command for the two channels (pitch and yaw) in the body frame becomes
where
is the phase shift, the significance of this angular error being detailed in reference [8].
As we showed in papers [6,8], for the single-channel case we can give up one component of the command in the body frame, obtaining in the guiding frame a command oriented in both directions due to the roll rotation.
To obtain the time modulation of the command for a single-channel missile, it is necessary to use a switching function of the form indicated in work [15]:
where
, called the fill factor, is given by the following relation:
in which
is the command module,
is the maximum guidance command, and the argument
, called the relative roll angle, is given by
where
represents the command phase (Figure 10),
is the roll angle, and
is the phase shift.
The switching function (60) is applied instantaneously through a nonlinear element, relay-type, the pitch canard deflection angle being
As shown in [15] for the expression of the equivalent command, the weight compensation command is also entered. This is achieved by the equilibrium fill factor for a horizontal base motion, which is a function of the ratio of the weight compensation control component to the maximum order value:
Unlike the roll-stabilized missile, where the balance command can be achieved directly by changing the zero position of the command surfaces (canard and elevator), in the case of rolling missiles, the equivalent balance command is introduced by the guidance term; in this case, the balance control is non-zero. In summary, the linear relation established in works [6,8] can be written as
which expresses the connection in deviations between the command and the thrust equivalent deflection.
5.4. The Structural Scheme
Next, to build the structural scheme of the SACLOS, it is necessary to define the complex shape of certain pairs of kinematic parameters in the guiding planes.
Thus, for the absolute angles of the rocket’s line of sight, the complex size can be defined:
Similarly, for the absolute angles of the target’s line of sight, the quantity is defined:
and from the angular deviations in the guiding planes, the following are obtained:
where
Between the three complex quantities defined above, there is the following relationship:
Finally, it is also possible to define the complex form of the zero-order entry function in the system due exclusively to the operator or the sighting device:
a function that will be cumulated with the absolute angle of the target’s line of sight (
).
Processing of the error signal and formation of the guidance control signal is performed using a P.D. (derivative proportional) type element that has the following known structure:
where
and
are guidance gains, and
is a time constant that eliminates high frequencies.
Note: In the case of Manual Command to Line of Sight (MCLOS), the control is performed manually by a human operator, as indicated in paper [15], and the signal can be shaped by a transfer function:
an expression which, as indicated in the same paper, can be approximated with
Based on the relations thus obtained, the structural scheme for the SACLOS single-channel rolling missile controlling the angular deviation in the case of the fixed carrier is presented in Figure 11.
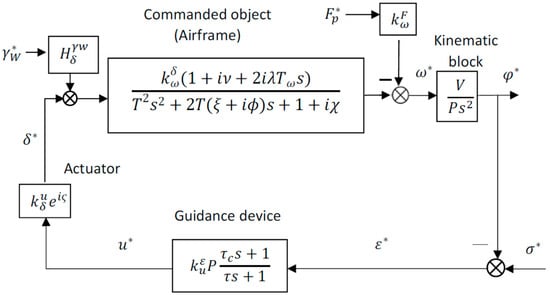
Figure 11.
Structural scheme for the rolling single-channel SACLOS missile.
5.5. Determination of the Characteristic Polynomial
For the analysis of the stability, the transfer function of the open system is first determined:
where we considered null the phase shift introduced by the actuator
, and we noted the guidance gain:
and the guidance time:
In this case, the transfer function of the closed system becomes
where
represents the pulsation.
For the stability check, we develop the characteristic polynomial from the denominator of the transfer function.
The characteristic polynomial, after ordering, becomes
For the stability analysis, we put the polynomial in the following form:
where
5.6. The Guidance System Synthesis
At this point, we aim to determine the three parameters of the guidance system:
.
To begin with, we will neglect the complex coefficients, considering a regular missile without roll rotation. In this case, the transfer function of the closed system (78) becomes
Next, we will use an allocation of poly-zeros according to the methodology “Standard coefficient method”, following reference [25]. This analysis can give us indicative information on the main control parameters of the system.
According to the methodology, for the transfer function obtained (83), with a characteristic fifth-order polynomial, the recommended transfer function is of the following form:
where
, with
being the desired system response time.
By identifying the coefficients of the characteristic polynomial of the two transfer functions, the following relations are obtained:
The main quantities that intervene in these relations and that are related to the dynamics of the missile are as follows:
—pulsation;
—damping factor; and
—amplification factor that intervenes in the gain
.
The values of these quantities are presented graphically according to the Mach number in the initial phase (with fuel) and in the final phase (without fuel) in Annex B of this work.
From the diagrams (Annex B), for the analyzed velocity range
, the parameters have the following values:
;
;
.
From the last two relations of (84), we obtain
Eliminating
, the equation is as follows:
with the positive solution:
For the range of values of pulsation
and damping factor
, the solution has the following values:
…3.85.
From
, the response time can be estimated:
Since the response time of the system must be low enough to combat close targets, we choose
, from which it follows that
.
From the third relation (84) we obtain
which, for the pulsation value range
, has values in the range of
Combining the second relation of (84) with the relation (88) yields
for which an estimate of the gain
is needed.
Considering approximate relations (30) we obtain
The parameters that intervene in the expression of gain are
;
;
;
;
, from which it follows that
.
For this range of variation of the gain
from (89) we obtain
Based on the results obtained, the values adopted are as follows:
At the end of this section, we will conduct a brief frequency analysis to assess the system’s stability. In paper [6], the frequency analysis was developed comparatively, for the case with and without coupling terms, presenting the Bode and Nyquist diagrams and determining the gain margin and phase margin for the value of the guidance gain corresponding to the operating point.
In the context of the present work, we will develop the results obtained in [6], analyzing gain margin (GM) and phase margin (PM) as a function of the guidance gain.
Figure 12 and Figure 13 show dependence of the gain margin and phase margin as a function of the guidance gain for fixed time constants. Figure 12 shows the case without coupling, and Figure 13 the case with coupling terms. From the comparative analysis of the diagrams, a decrease in the stability range for the guidance gain is observed in the initial phase, from k = 7.5 to k = 5.1, and in the final phase, from k= 16 to k = 9, due to the coupling.
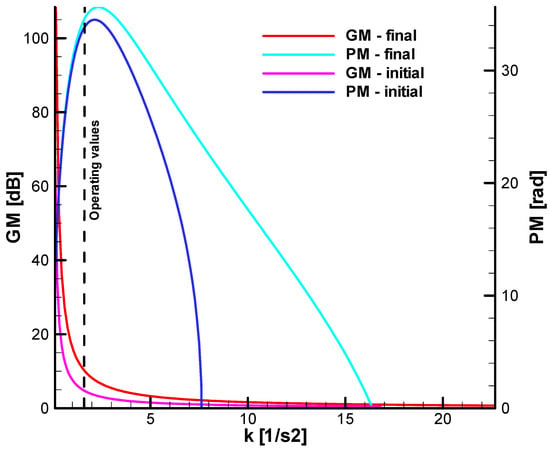
Figure 12.
The system gain margin (GM) and phase margin (PM) without coupling terms.
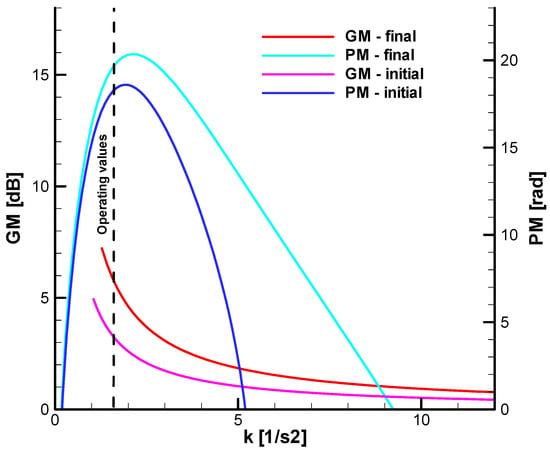
Figure 13.
The system gain margin (GM) and phase margin (PM) with coupling terms.
;
This decrease in the stability domain will be evident in the comparative analysis with the Routh–Hurwitz and Frank–Wall criteria presented in the following sections of the paper, as well as in the analysis using the nonlinear model.
6. Calculus Model
To obtain numerical results, we will further specify the data of the calculus model.
6.1. Aerodynamic Characteristics
The aerodynamic characteristics were determined using the configuration from Figure 14.
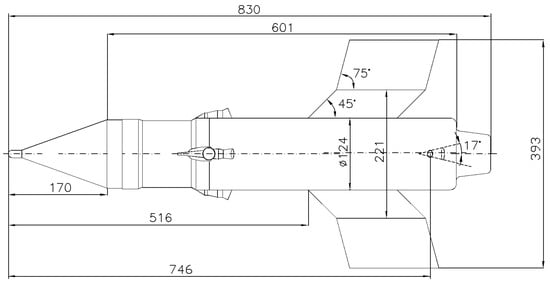
Figure 14.
Rolling missiles with reaction jet controls.
Considering the specifics of the configuration and the flight regimes, starting from the regular aerodynamic coefficients indicated in [26,27], and in accordance with [28], we introduce additional terms that account for the influence of rotational and non-stationary motion, as well as combinations with incidences.
Thus, the development of aerodynamic coefficients in the body frame for the slow-rolling airframe from Figure 14 is given by
where the rotational velocities and non-stationary translational variables that are considered dimensionless, according to the standards [19,29], are as follows:
The terms of development of aerodynamic coefficients are presented against the Mach number in Appendix A.
6.2. Mechanical and Reference Characteristics
The mechanical characteristics of the model are indicated in Table 1.

Table 1.
Mechanical characteristics.
For the considered configuration, the reference length is
reference surface is
, and the maximum angular thrust deflection is
.
6.3. Thrust Characteristic
The thrust characteristic of the model is shown in Figure 15.
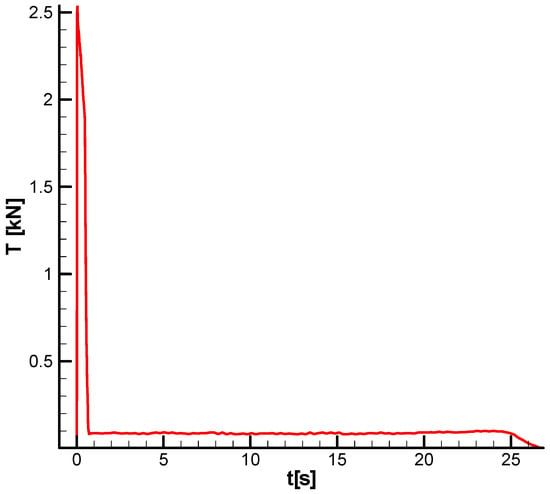
Figure 15.
Thrust diagram.
Given the thrust diagram and the table of mechanical characteristics, the missile will have two flight phases: a first phase of acceleration (boosting) and a second phase of marching flight, with approximately constant velocity, as shown in the velocity diagram in Section 7.3.
6.4. Time Constants and Controller Gains
As basic data for the linear model, the following parameters were considered:
- Guidance gain indicated as the optimal value in the previous analysis;
- The guidance time constant for the derivative term of the guidance law, ;
- The time constant for guidance control, ;
- Rolling rotational velocity close to that indicated in Section 7.3, ;
- Calculation altitude ;
- Phase shift .
7. Stability Analysis of the Single-Channel SACLOS Slow-Rolling Missile
7.1. Stability Analysis with the Routh–Hurwitz Criterion
Further, neglecting complex terms, we will perform a stability analysis with the Routh–Hurwitz criterion to highlight restrictions on the guidance and control parameters.
The Routh–Hurwitz conditions for the fifth-order polynomial with real coefficients are obtained from the matrix of coefficients constructed as follows:
From the condition
the following is successively obtained:
From condition
, the following is successively obtained:
For stabile missile, with
and
, relation (96) is always satisfied, being quadratic equations in
with complex conjugate roots.
From the condition
, the following is successively obtained:
Since
is linear in
, condition (97) becomes
a relation that allows obtaining the stability domain related to
for a fixed
.
From the condition
, the following is successively obtained:
Since
is quadratic in
, the second condition (99) becomes
The relations (98) and (100) allow the stability domains related to
and
to be obtained.
Figure 16 and Figure 17 show the corresponding stability domains
for
and
, obtained with relations (98) and (100), for
fixed at the operating point (, in the initial and final part of the second phase.
Figure 16.
Stability R-H domains, Mach = 0.3,
—initial.
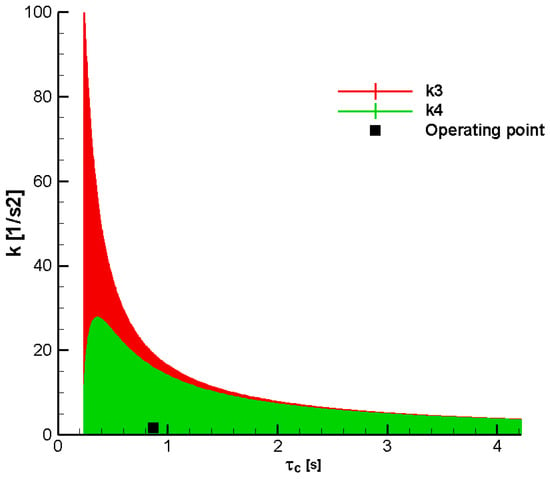
Figure 17.
Stability R-H domains, Mach = 0.45,
—final.
It can be seen from the two diagrams that the stability domain for
is more restrictive than that for
, and hence only the domain corresponding to
will be taken into consideration.
In addition, the domain
highlights the inner limit of
:
where the gain
becomes zero.
Applying relations (98) and (100) over the entire Mach number range, the diagrams from Figure 18 and Figure 19 are obtained. It can be seen from these diagrams that the
limit is always more restrictive than
and that the current value of the gains
falls within the stability domain over the entire Mach number range.
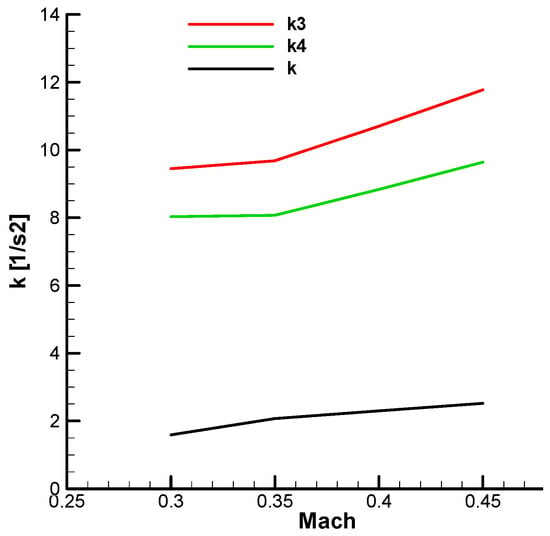
Figure 18.
Upper limits ( and
) and gain (k)—initial;
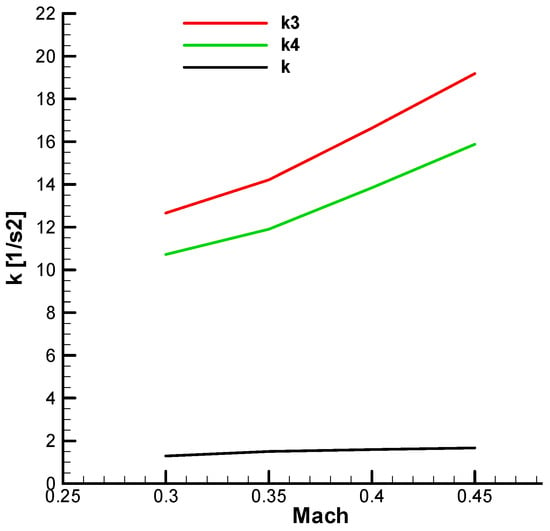
Figure 19.
Upper limits ( and ) and gain (k)—final;
Finally, the condition , because we have already imposed the condition
leads to
, i.e.,
.
To summarize, for a regular system with a subunitary damping factor (0
) and a positive time constant of nutation
, the only constraints that remain active are those given by
, which limits the guidance gain
and lower-limits the guidance time
and
which lower-limits the time constant (
).
The result obtained is equivalent to the criterion Liénard–Chipart, which for the fifth-order polynomial with real coefficients imposes the following conditions [30]:
As an additional check, in Figure A45 and Figure A46, the roots of the characteristic polynomial with real coefficients at the operating point, analyzed by the R-H conditions, are presented. It is observed that the polynomial has four conjugate complex roots with negative real parts and a negative real root, which confirms the stability of the analyzed system.
Next, we will analyze the characteristic polynomial of the system, considering the complex part of its terms using the Frank–Wall stability criterion.
7.2. Stability Analysis with the Frank–Wall Criterion
Based on the relations (A5)–(A7) and the characteristic polynomial coefficients, the Frank–Wall parameters ( were determined and graphically shown in Appendix C. For the basic input data considered, the stability criterion F-W is met:
, as we can see from Figure A41, Figure A42, Figure A43 and Figure A44. It is observed that they are positive over the entire domain, which means that the roots of the characteristic polynomial will have real negative parts.
Next, we will analyze the root locus of the characteristic polynomial (Appendix D) To begin, we shall consider the basic test case set out in Section 7.3, Table 1, for the second phase of flight at two points, at the beginning () and the end of the phase (). The analysis is performed on the range of Mach numbers corresponding to phase 2 () at ground level. A first observation of a general nature is that the roots do not have a symmetrical distribution with respect to the real axis, as in the case of stabilized roll rockets, where the characteristic polynomial has real coefficients. There are five roots of the polynomial, thus:
- -
- Roots 2 and 4 are close to those of the characteristic polynomial of the commanded object (23) or (24), which has a negative real part and large complex parts that are almost conjugate.
- -
- Root 3 is large in module, with a negative real part and a small complex part, due to guidance control.
- -
- Roots 1 and 5 are small in module, with negative real parts and small complex parts due to the guidance loop.
Figure A47 and Figure A48 present the roots of the characteristic polynomial with complex coefficients for the initial point of the second phase, without phase shift
) and with phase shift (.
Figure A49 and Figure A50 present the roots of the characteristic polynomial with complex coefficients for the final point of the second phase, without phase shift () and with phase shift
. In this case, unlike the case with real coefficients previously analyzed (Figure A45 and Figure A46), we have five complex roots arranged non-symmetrically related to the real axis; that is, we no longer have complex conjugate roots. However, it is observed that the real part of the roots is negative in all cases, which ensures the stability of the analyzed system.
It is of interest to verify whether, in the case of the missile with rolling rotation (polynomial with complex coefficients), we obtain the same stability domains as in the case of the R-H analysis for a missile without rolling (polynomial with real coefficients).
Unfortunately, because the F-W calculation relations are complicated, we cannot find an analytic solution like in the R-H case. Therefore, we will summarize some numerical results for verification.
Thus, in Figure 20, Figure 21, Figure 22 and Figure 23, the variation of the F-W parameters is presented depending on the guidance gain
. It is observed that the cancellation of these parameters (), that is, the limit of the stability domain, is achieved by a jump from a positive to a negative value. The jump is explained by the fact that these points are close to the points of cancellation of the R-H determinants and by relation (A8), between the determinants R-H and the parameters F-W, in which the determinant R-H is in the denominator of the parameter F-W. Due to the jump at the point of cancellation, determining an exact numerical solution for these points is challenging.
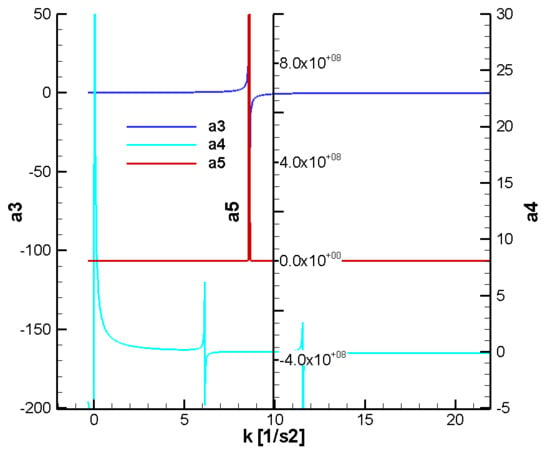
Figure 20.
Variation of the F-W parameters as a function of the guidance gain—initial;
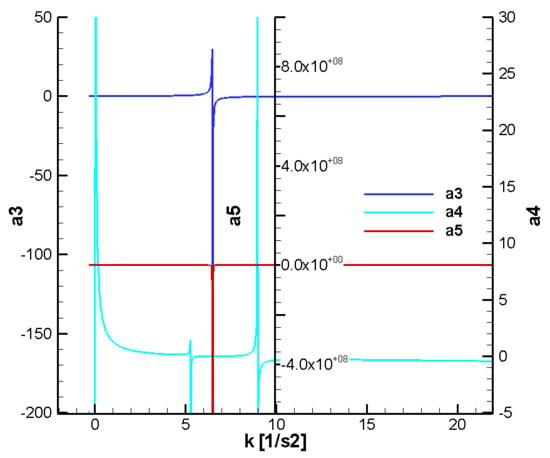
Figure 21.
Variation of the F-W parameters as a function of the guidance gain—initial;
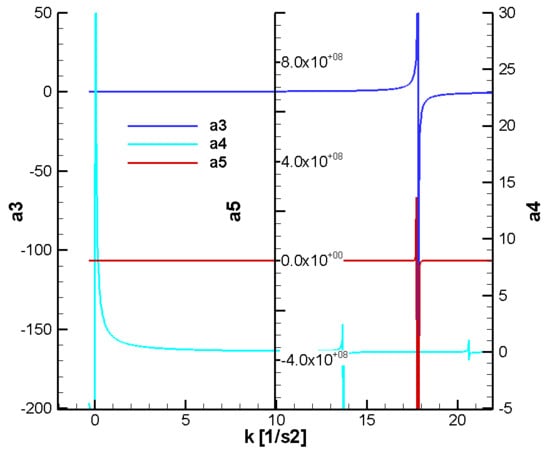
Figure 22.
Variation of the F-W parameters as a function of the guidance gain—final;
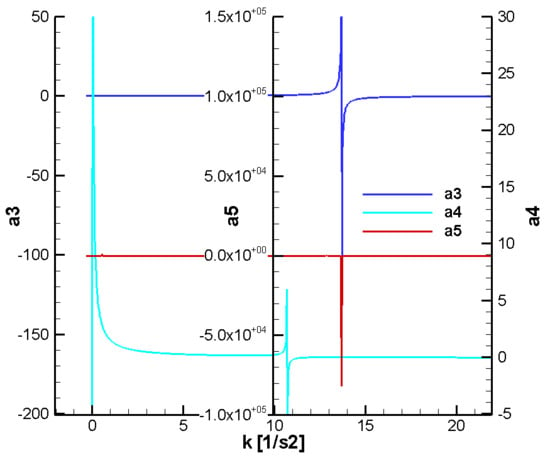
Figure 23.
Variation of the F-W parameters as a function of the guidance gain—final;
From the analysis of the diagrams, it is observed that for
a condition similar to
is found, i.e.,
, and for
stability conditions similar to
are found, i.e., we have a domain for
between
and
. The condition
is also found, i.e., the stability condition for
is more restrictive than
. As for
, this introduces a condition similar to
. Regarding
and
, these parameters were not analyzed because they do not depend on the gain
.
It can be seen from the figures that in the initial phase (Figure 20 and Figure 21) the cancellation values
are smaller and in the final phase (Figure 22 and Figure 23), which means that the domain of stability is more restricted in the initial phase. Also, in the initial phase, a third cancellation point
is observed, which is not found in the final phase nor in the R-H analysis. Regarding the phase shift, it is observed that this leads to a decrease in the upper cancellation point
; therefore, there is a slight decrease in the stability domain.
Figure 24, Figure 25, Figure 26 and Figure 27 present the stability domains
for
and
with
fixed at the operating point (in the initial and final of the second phase.
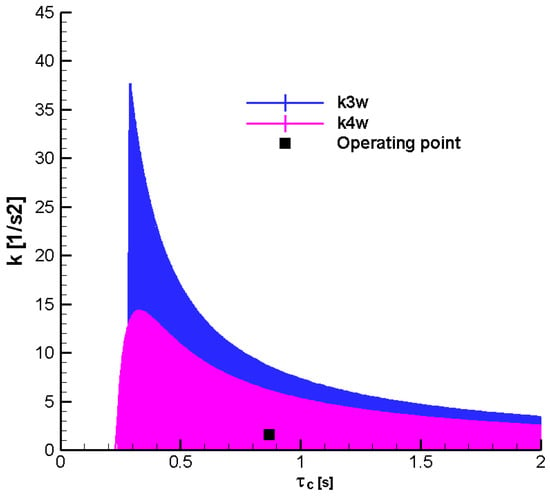
Figure 24.
Stability F-W domains; Mach = 0.3;
—initial.
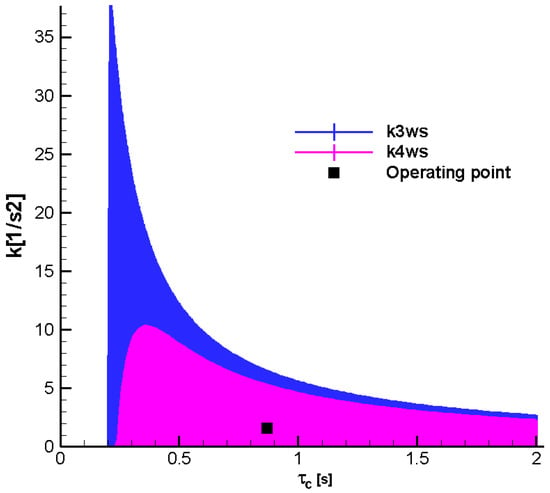
Figure 25.
Stability F-W domains; Mach = 0.3;
—initial.
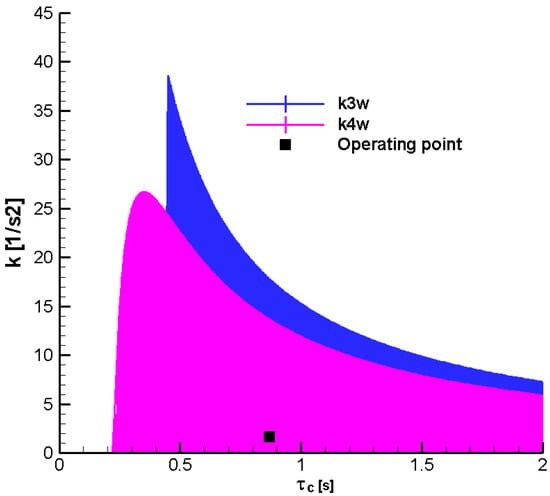
Figure 26.
Stability F-W domains; Mach = 0.45
;
—final.
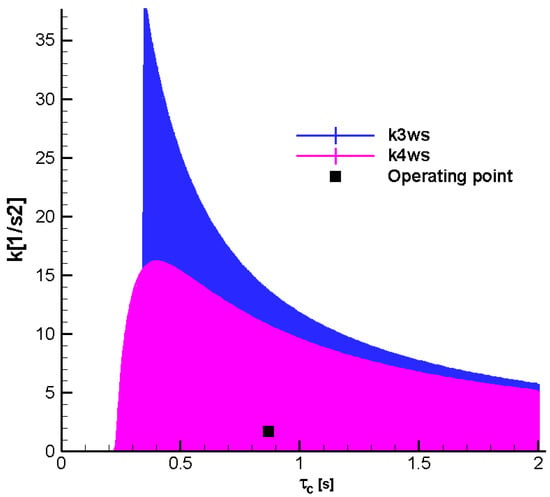
Figure 27.
Stability F-W domains; Mach = 0.45
;
—final.
It can be seen from the diagrams that the stability domain for
is more restrictive than that for
, and hence only the domain corresponding to
will be taken into consideration.
In addition, the domain
highlights the inner limit of
from relation (101).
The stability domains are presented for the initial moment (Mach = 0.3) and the final moment (Mach = 0.45). Similar to the R-H analysis, it is observed that in the case of the F-W analysis, the stability domain is smaller in the initial phase than in the final phase of the guided flight. It is also observed that the phase shift leads to a decrease in the stability range.
From the previous analysis, it follows that the most restrictive stability domain F-W, which must be considered, depends on the first point of cancellation of
, namely
To have a comparative picture, in Figure 28 and Figure 29, the stability range
obtained with the R-H criterion and the stability range
obtained with the F-W criterion are presented together.
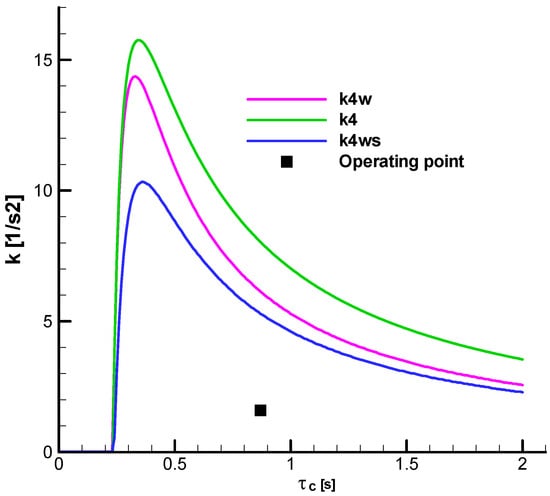
Figure 28.
Stability domains; Mach = 0.3
;
—initial.
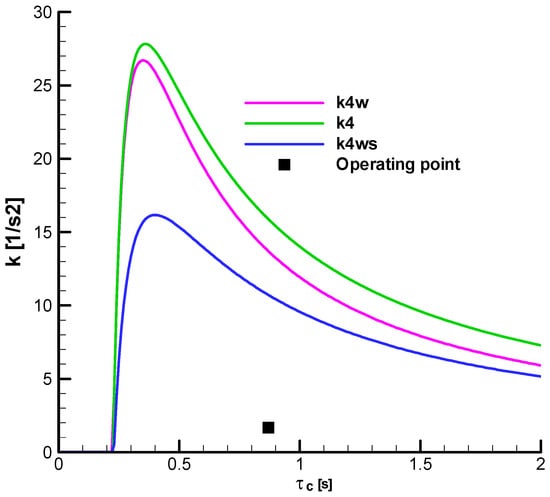
Figure 29.
Stability domains; Mach = 0.45;
;
—final.
Thus, in these diagrams, the stability range of the gain
as a function of the guiding time
for a fixed time constant
is presented. It is also observed from all the diagrams that for the considered operating range, the F-W stability domain (k4w) is reduced compared to the R-H domain (k4), which represents an important result in the comparative analysis performed. Additionally, in the case of F-W stability, it is observed that the stability domain considering the phase shift (k4ws) is smaller than that with a zero phase shift (k4w).
To exemplify the result of the previous analysis, we will start from the operating point and increase the gain
until we obtain instability on the F-W criterion. Then, we will check whether stability is maintained for the R-H criterion at that new operating point.
Thus, if we increase
from
to
, and the other parameters remain unchanged (
,
), the F-W parameter that will become negative will be
, as can be seen from Figure 30.
Figure 30.
Stability parameters F-W—initial;
;
At the same time, one root of the characteristic polynomial with complex coefficients has a positive real part, as seen in Figure 31. The diagram is obtained for a range of Mach numbers from 0.3 to 0.45.
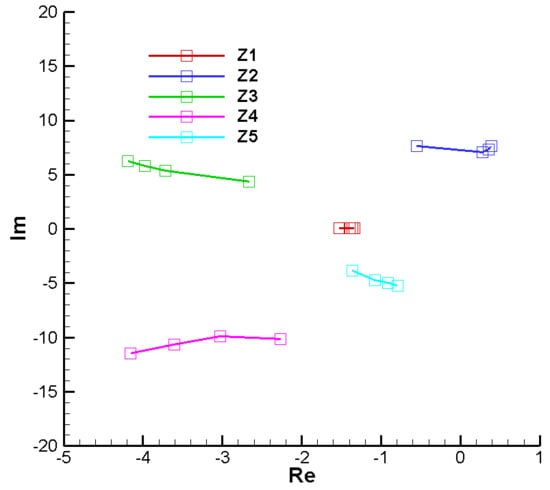
Figure 31.
Roots of the characteristic polynomial with complex coefficients—initial;
On the other hand, from Figure 32, it can be seen that for
, the gain k value is maintained within the stability range (R-H) determined by the polynomial with real coefficients, but it is outside the stability range (F-W) determined by the polynomial with complex coefficients.
Figure 32.
Upper limits ( and ) and gain (k)—initial;
Moreover, for this case, the roots of the characteristic polynomial with real coefficients have a negative real part, as can be seen from Figure 33. The diagram is obtained for a range of Mach numbers: 0.3 to 0.45.
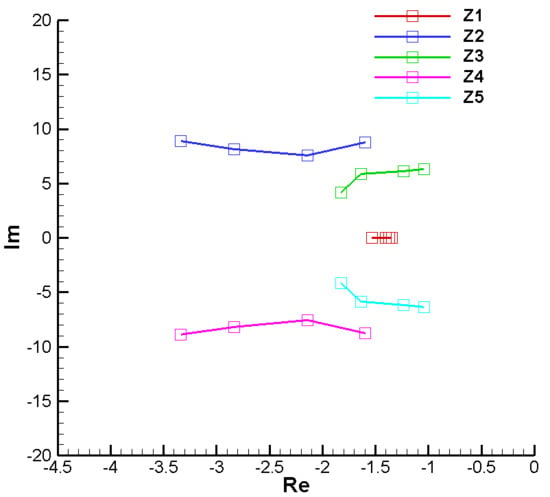
Figure 33.
Roots of the characteristic polynomial with real coefficients—initial.
This means that for the case of a rolling missile, the stability analysis on the polynomial with real coefficients, in this case R-H, is insufficient, requiring an additional analysis on the polynomial with complex coefficients of the F-W type and an evaluation of the nonlinear model, as we will proceed further.
7.3. Stability Analysis Based on the Nonlinear Model
Based on equations of motion in the body frame [8] and kinematic guidance relations (34), as well as guidance control equations (72), switching function (60), with the relative roll angle definition relation (62), and expression of pitch canard deflection angle (63), the nonlinear model of guided flight of the single-channel, slow-rolling, SACLOS missile is obtained.
A nonlinear model in the Resal frame, based on relations from paper [8], would be much easier to build and use, but we would lose essential information related to command formation, such as the fill factor or the command phase, which are parameters useful in the analysis, as will be seen below.
The objective of the nonlinear model analysis is to verify the limits of the guidance gain ( set out in the previous point, such as the guidance time
We will consider parameters similar to linear analysis,
and a tactical situation with a fixed target placed at a distance of 3 km and a height of 10 m. For the gain, we will use relation (90):
From this relation, only the first factor
can be imposed because it is related to the constructive solution guidance device. At the same time, the second factor is constant
, and the third factor
depends on the dynamics of the missile, being difficult to control. In this case, we will choose
so that, when multiplied by the other two gains and velocity, a value close to the desired
is obtained. Given the objectives of this section of the paper, we will seek to obtain three gains, the first less than the operating value
, the second close to the operating value
, considerate optimal, and used in linear analysis, and the third bigger than the operating value, at the limit of the stability F-W range, as can be seen from Figure 32, namely
. As previously stated, these values will be determined as a function of time, simultaneously with the integration of nonlinear equations of motion, which will be performed in the body frame. Obviously, due to the variation in the third factor
and the velocity
, the guidance gain will vary over time, as can be seen in Figure 34 and Figure 35, where the phase shift was
. The analysis is performed considering three identical missiles but with different guidance gains, the first, M1, below the optimal value (the under-gain case), the second, M2, close to the optimal value defined in the linear analysis (the optimal-gain case), and the third, M3, bigger than the optimal (the over-gain case).
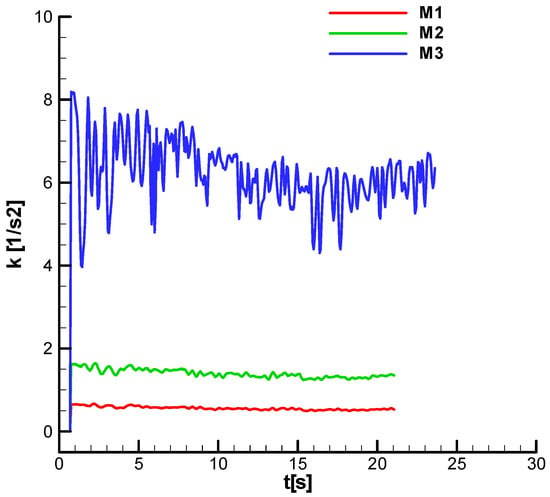
Figure 34.
Guidance gain;
;
;
Figure 35.
Guidance gain;
;
;
For the three rocket models defined above, Figure 36 and Figure 37 show the velocity diagram that was previously used to define the analysis range on the linear model,
, which corresponds to the second phase of flight. There are no significant differences between M1 and M2. For M3 (over-gain case), a loss of velocity is observed. This phenomenon occurs regardless of the phase shift, as evident from the two diagrams.
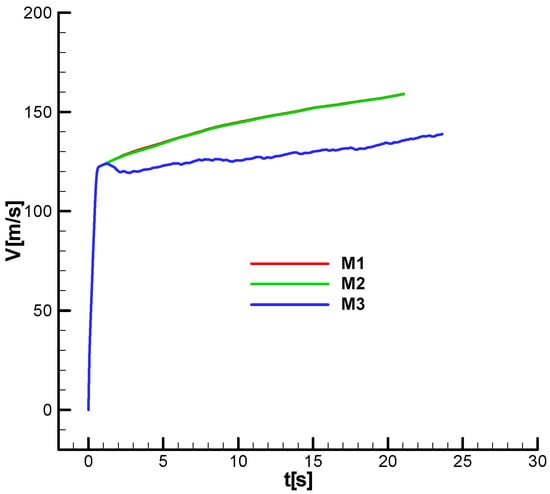
Figure 36.
Velocity diagram;
;
;
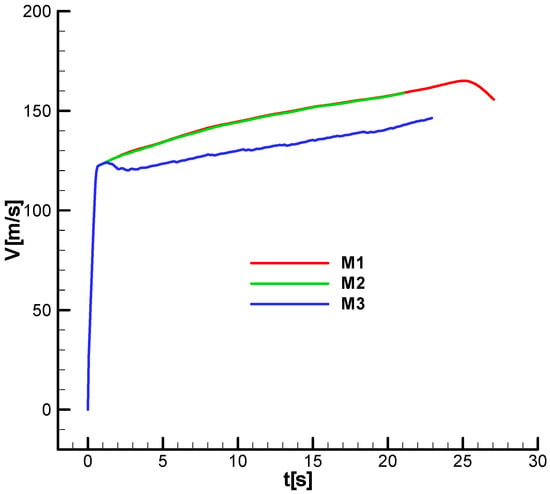
Figure 37.
Velocity diagram;
;
;
To analyze the cause of the loss of speed for M3, the incidence in the body frame is presented in Figure 38 and Figure 39. In the case of M3, large-amplitude oscillations are observed, which lead to an increase in the drag force and, consequently, a loss of speed.
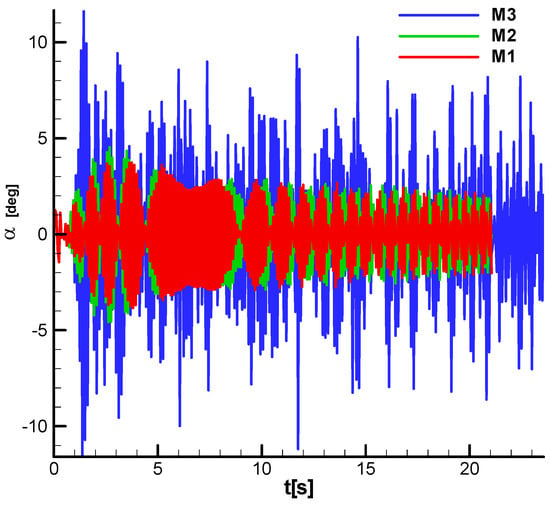
Figure 38.
Incidence diagram;
;
;
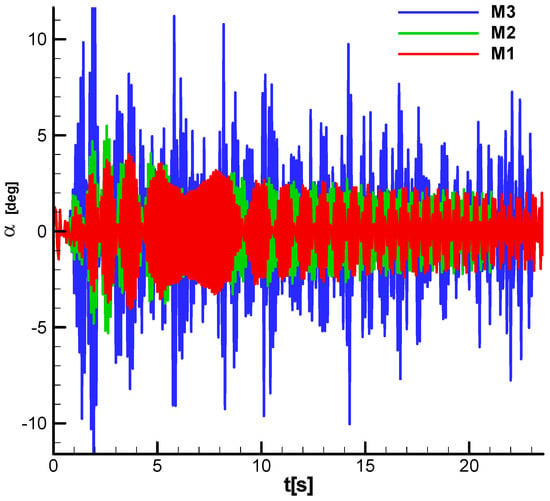
Figure 39.
Incidence diagram;
;
;
Figure 40 and Figure 41 show the angular roll velocity diagram based on which the rotational velocity of
, corresponding to the second phase of flight, used in linear analysis, was chosen. It is observed that the roll velocity follows the velocity profile and does not differ substantially between M1 and M2. For M3 (over-gain case) a loss of roll velocity is observed due to loss of speed. Similarly, for roll velocity, the phase shift has no significant influence.
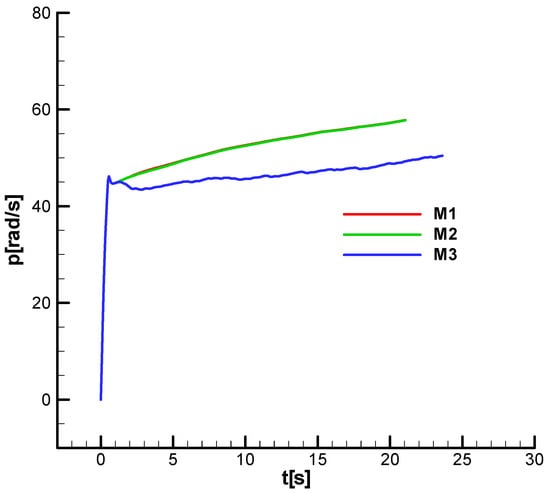
Figure 40.
Roll velocity diagram;
;
;
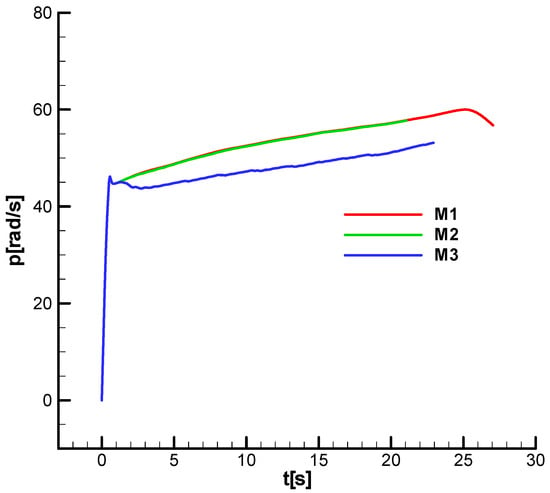
Figure 41.
Roll velocity diagram;
;
;
Figure 42 and Figure 43 show the vertical and horizontal projections of the trajectories for the three analyzed cases without phase shift.
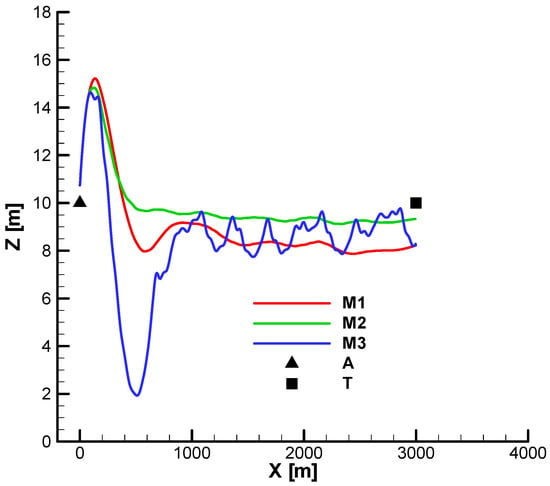
Figure 42.
Target hitting—vertical view;
;
;
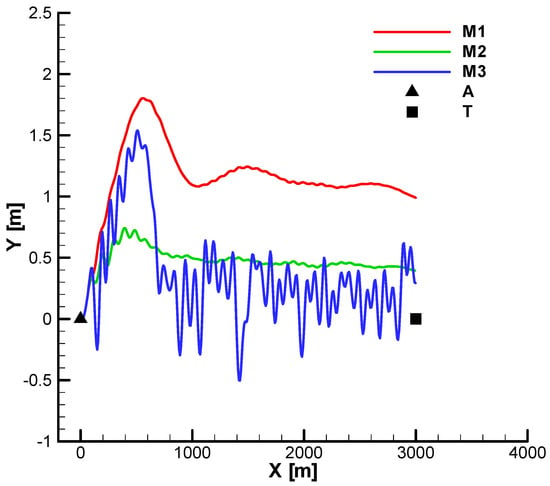
Figure 43.
Target hitting—horizontal view;
;
Observation: In the trajectory diagrams, the following were noted, according to [23]: A—carrier; T—target; M—missile.
Although all missiles hit the target, for M3 (the over-gain case), from vertical projection (Figure 42), an overshoot can be seen at the entry into the second phase which caused the loss of velocity and roll velocity observed in the previous diagrams.
From the horizontal projection (Figure 43), pronounced oscillations are observed for M3 (the over-gain), which can also lead to loss of velocity. Also, from both diagrams (the vertical and horizontal projection), it is observed that for M1, a greater final distance from the target is obtained but still within the imposed final distance of 3 m.
Figure 44 and Figure 45 show the vertical and horizontal projection of the trajectories for the three analyzed cases with phase shift (). Unlike the previously analyzed cases, if the phase shift is considered M1, with under-gain, it no longer reaches the target. The other features of the movement are preserved. For M3, overshoots and oscillations along the trajectory are observed, leading to a loss of velocity and a decrease in the performance of combating distant targets (over 3 km).
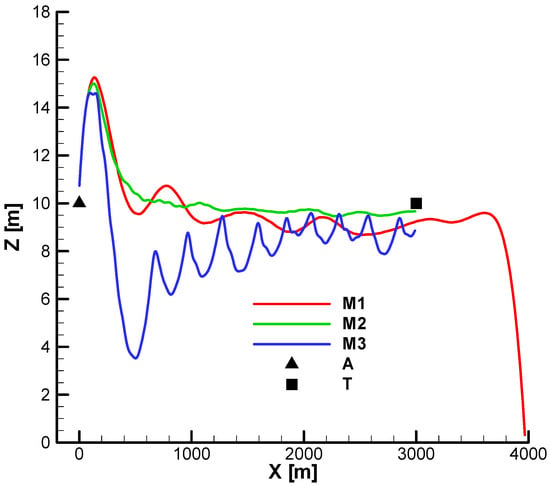
Figure 44.
Target hitting—vertical view;
;
;
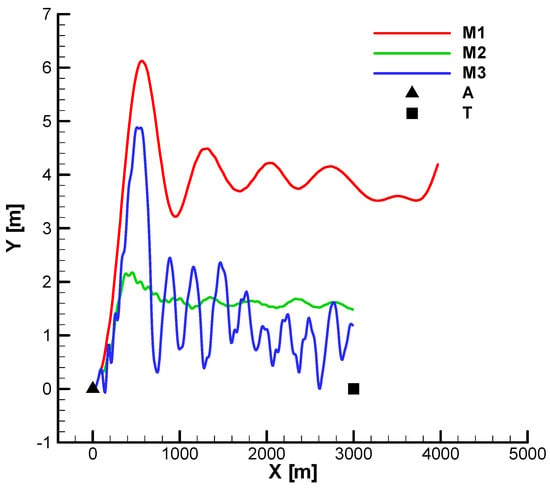
Figure 45.
Target hitting—horizontal view;
;
;
From the vertical projection (Figure 44), it can be seen that M1, after missing the target, continues to fly until it hits the ground.
From Figure 43 and Figure 45, a deviation of the trajectory to the left of the firing plane can be observed, a phenomenon specific to aerodynamically stabilized rolling missiles.
Figure 46 and Figure 47 show the command fill factor without and with phase shift. It is observed that in both situations, for all missiles, the filling factor stabilizes at the equilibrium value, which achieves weight compensation. For both cases (Figure 46 and Figure 47), for M3, the filling factor saturates over a longer period, resulting in a decrease in the missile’s maneuverability and, consequently, a decrease in performance, including against close targets. Additionally, for M3, strong oscillations are observed during the trajectory, resulting in a loss of velocity and, consequently, a decrease in performance for distant targets. As for M1, it shows pronounced long-period oscillations of the filling factor, especially under phase shift conditions (Figure 47).
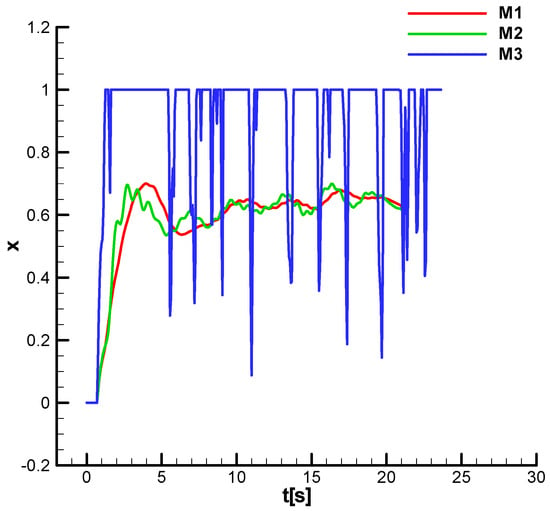
Figure 46.
Command fill factor;
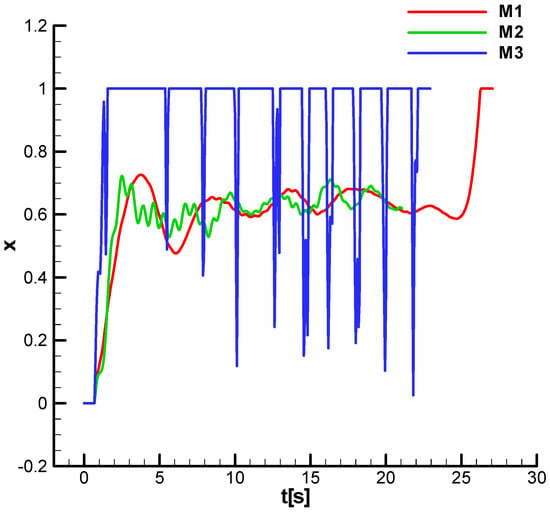
Figure 47.
Command fill factor;
;
;
Figure 48 and Figure 49 show the command phase without and with phase shift. It is observed that in both situations, for all missiles, the phases stabilize at a small negative equilibrium value, which compensates for the Magnus and gyroscopic effects in the lateral plane.
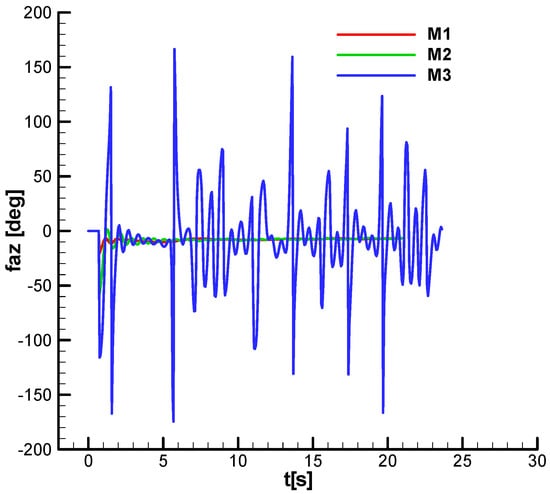
Figure 48.
Command phase;
;
;
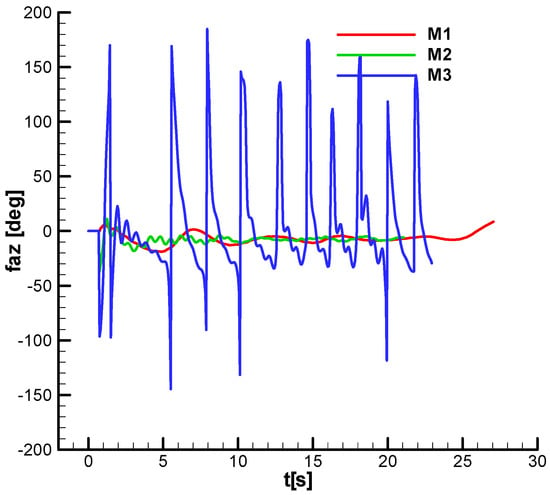
Figure 49.
Command phase;
;
For both cases, the phase of M3 exhibits strong oscillations at all times, resulting in a loss of velocity and, consequently, a decrease in performance for distant targets.
Figure 50, Figure 51, Figure 52 and Figure 53 show the influence of the guidance time
. Unlike the cases previously analyzed, in these last situations, the three gain cases will be resumed, but with a reduced value of the guidance time
.
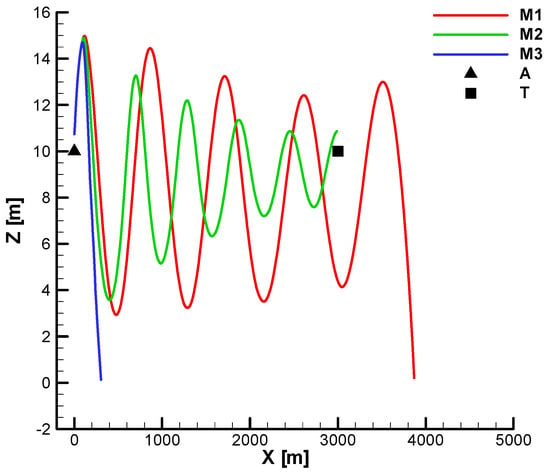
Figure 50.
Target hitting—vertical view;
;
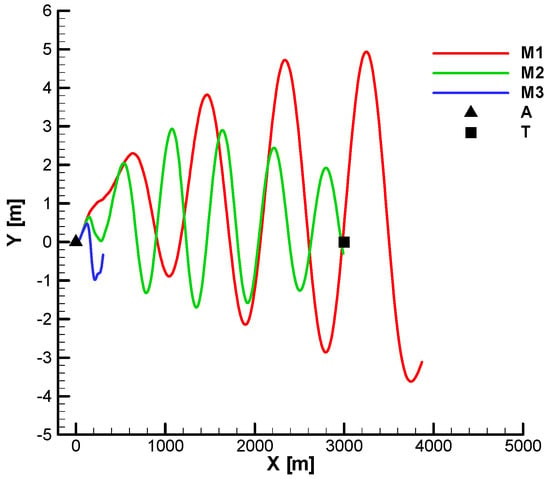
Figure 51.
Target hitting—horizontal view;
;
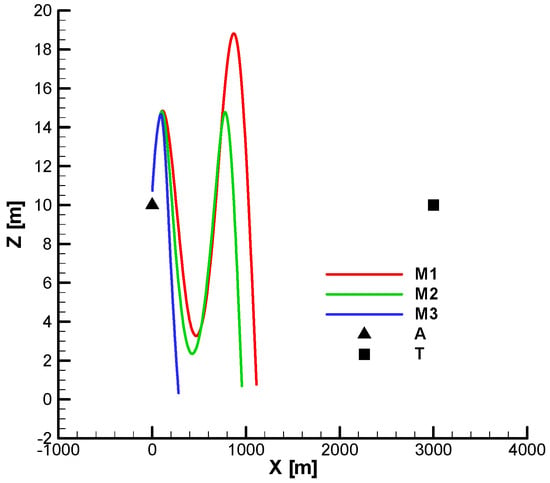
Figure 52.
Target missing—vertical view;
;
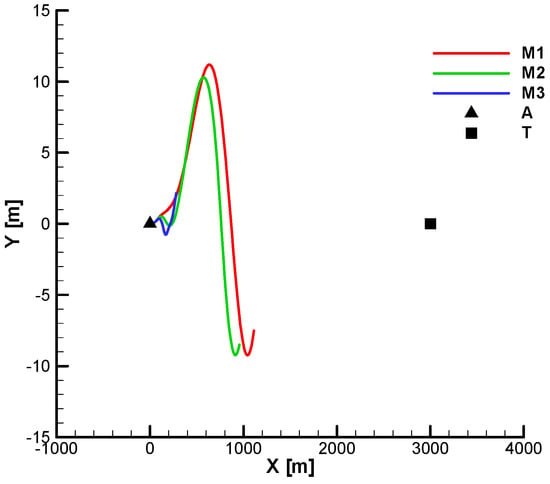
Figure 53.
Target missing—horizontal view;
;
Thus, in Figure 50 and Figure 51, the vertical and horizontal projection of the trajectories for the case without phase shift and
is presented. Let us compare it with the corresponding diagrams in Figure 36 and Figure 37 (with ta). We can see that the decrease to
leads to strong oscillations in the trajectory, indicating a tendency to destabilize the system. In cases without phase shift, M2 hit the target, while M1 and M3 missed the target. In contrast, for the cases with phase shift (Figure 52 and Figure 53), with
, all three missiles miss the target, which shows the importance of a correct choice of guidance parameters.
8. Organization of Results from the Appendix
Appendix A illustrates the variation of the primary aerodynamic coefficients as a function of the Mach number.
Appendix B tabulates the thrust incidence, equilibrium thrust deflection angle, and key flight quality parameters for the start and end of the flight’s second phase (marching mode), based on the mechanical data in Table 1. The analysis domain, selected with reference to the velocity profiles in Figure 36 and Figure 37, covers Mach numbers from 0.34 to 0.45 within the operational flight altitude.
The characteristic polynomial coefficients were determined for the start and end of the second flight phase using relation (81) and the flight parameters from Appendix B. From these coefficients and relations (A5)–(A7), the Frank–Wall (F-W) parameters ( were calculated as a function of the Mach number. As shown graphically in Appendix C, the results confirm the F-W stability criterion.
is met, with the positivity of the parameters demonstrated in Figure A41, Figure A42, Figure A43 and Figure A44.
Appendix D contains the root locus of the characteristic polynomial in both cases with real coefficients and complex coefficients.
Appendix E contains the algorithm details for the Frank–Wall stability criterion for fifth-order polynomials.
9. Conclusions
After the preliminary Section 1, Section 2, Section 3, Section 4, Section 5 and Section 6, in which the SACLOS missile model was developed, Section 7, which is the main section of the paper, performs the stability analysis. It contains three parts. First, it is dedicated to a simplified analysis using the R-H criterion for the characteristic polynomial with real coefficients. The second is the complex analysis using the F-W stability criterion for the characteristic polynomial with complex coefficients, and the third is for a realistic 6-DOF model. The results obtained were compared among the three models, revealing significant similarity between the linear model with complex coefficients and the nonlinear model. The presence of complex-valued elements in the system’s structural scheme results in a characteristic polynomial with complex coefficients. Consequently, stability was assessed using the Frank–Wall (F-W) criterion, a generalization of the Routh–Hurwitz (R-H) criterion applicable to such polynomials. For the resulting fifth-order characteristic polynomial, the F-W criterion requires five distinct parameters to be positive to ensure system stability. Due to the analytical complexity of these F-W parameters, a simplified case was initially considered in which the missile’s roll was neglected. This simplification enabled the use of the standard R-H criterion, yielding determinants with much simpler expressions. The subsequent analysis of these five R-H parameters resulted in the definition of five corresponding system constraints. Thus, from the first condition, R-H resulted in the first lower limitation for the time constant
, the second condition for regular case with damping factor subunitary (, and the time constant of nutation positive
is always fulfilled. The third condition resulted in an upper limitation for the guidance gain
, and the fourth condition imposed a lower and the upper limit of the guidance gain
) more restrictive than the third condition. Also, a fifth condition imposes a lower limit for the guidance time
.
The simplified Routh–Hurwitz (R-H) analysis yielded a fifth, more restrictive constraint on the time constant (τ > 0). While the R-H parameters were treated analytically, the more complex Frank–Wall (F-W) parameters required numerical evaluation (Section 7). This numerical study included evaluating the F-W stability parameters and the influence of key parameters on the system’s characteristic roots. A key finding from comparing the R-H (non-rolling) and F-W (rolling) results is that roll motion contracts the stable range for the guidance gain, particularly at the upper boundary. Finally, the linear F-W stability predictions were verified through nonlinear simulations of a tactical scenario. Three cases were tested: under-gained (M1), optimal-gained (M2), and an over-gained case (M3) set at the predicted stability limit.
The results of the nonlinear model confirmed the limitations obtained with the F-W stability criterion. In the first and last cases, the system performance is degraded; for the first case (the under-gain case), a greater final distance from the target is obtained, with the possibility of missing the target, and for the third case, there are large oscillations of the guidance parameters (phase and fill factor) during the flight. Moreover, for the third case, a significant overshoot is observed in the initial phase, which, along with the oscillations, leads to a loss of velocity and an inability to combat targets at long distances. Instead, in the second case, with the guidance gain close to the operating value, the missile hit the target, with the guidance parameters having an asymptotic behavior during the trajectory. In parallel with the guidance gain, the behavior of the missile in the conditions of decreasing the guidance time from
0.87 [s] to
0.3 [s], for the three cases that were analyzed, revealed that
decrease leads to strong oscillations in the trajectory, which denotes a tendency to destabilize the system. In cases without phase shift, M2 hit the target, while M1 and M3 missed the target. In contrast, for the cases with a phase shift with
, all three missiles miss the target, which shows the importance of a correct choice of guidance parameters.
In summary, this paper develops a comprehensive stability analysis for a slowly rolling, single-channel SACLOS missile, starting from a nonlinear 6-DOF model formulated in the Resal frame. This model is first linearized to derive a structural scheme for the commanded motion, which yields flight quality parameters with a complex-valued form due to channel coupling. Subsequently, the guidance loop components, including the kinematic relations, guidance device, and a single-channel actuator with a specific switching function, are defined and linearized. These elements are then integrated into a complete, closed-loop linear model of the SACLOS system. From this linear model, the system’s characteristic polynomial is determined. The presence of complex coefficients necessitates the use of the Frank–Wall (F-W) stability criterion, which is compared against the simpler Routh–Hurwitz (R-H) criterion for the non-rolling case. This analysis establishes a stability domain for the guidance gain and lower limits for the guidance time constant. A key finding is that the stability domain predicted by the F-W criterion (with roll) is more restrictive than that obtained with the R-H criterion. Finally, the results of the linear stability analysis are verified through simulation with the original nonlinear 6-DOF model. The nonlinear system’s behavior shows strong agreement with the predictions of the more accurate F-W criterion, thus validating the derived stability boundaries for the guidance gain and time constant.
The paper contains five appendices, as follows: Appendix A graphically presents the main terms of development of aerodynamics coefficients; Appendix B graphically presents the linear model flight quality parameters used for the characteristic polynomial of the transfer function; Appendix C graphically presents the real and imaginary part of the characteristic polynomial coefficients as well as the five F-W stability parameters; Appendix D contains the root locus of the characteristic polynomial; and Appendix E details the calculation of F-W stability parameters.
Author Contributions
Conceptualization, T.-V.C.; Methodology, T.-V.C.; Software, T.-V.C.; Validation, T.-V.C. and C.E.C.; Formal analysis, C.E.C., V.P. and C.E.; Investigation, C.E.C. and V.P.; Resources, T.-V.C.; Writing—original draft, T.-V.C.; Writing—review & editing, C.E.C., V.P. and C.E.; Visualization, V.P. and C.E.; Supervision, T.-V.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Aerodynamics terms |
| ; —term of development of axial force coefficient; |
| ; —terms of development of coefficients for normal forces; |
| ; —terms of development of the torque coefficients in pitch and yaw; |
| —terms of development of the roll torque coefficient. |
| The flight quality parameters |
| —the natural pulsation of nutation; |
| —the damping factor of nutation; |
| —the time constant of nutation; |
| —the command factor; |
| —the advance time on command; |
| —the angular rate of precession; |
| —the static stability; |
| —the reference time; |
| —the reduced mass of the aircraft or relative density; |
| —the reduced moment of inertia in pitch; |
| —the reduced gravitational acceleration; |
| —the maximum load factor. |
| The guidance parameters |
| A—the carrier; |
| M—the missile; |
| T—the target; |
| —carrier–target line of sight; |
| AM—carrier–missile line of sight; |
| —range of the target in relation to the carrier; |
| —range of the missile in relation to the carrier; |
| —range of the target in relation to the missile; |
| —the attitude angles for the guiding frame orientation; |
| , —absolute angles of the carrier–target line of sight; |
| , —absolute angles of the carrier–missile line of sight; |
| —the angular deviations in guiding planes; |
| —the rate of angular deviations in guiding planes; |
| —the linear deviations in guiding planes; |
| —missile velocity; |
| —target velocity; |
| , —angular rate of carrier–target LOS; |
| , —angular rate of carrier–missile LOS; |
| —missile angular rates of the velocity vector; |
| —the guidance gain; |
| —the guidance time; |
| —the time constant; |
| —the guidance command in the body frame; |
| —the guidance command in the Resal frame; |
| —the command module; |
| —the command phase; |
| —the phase shift error; |
| —the fill factor; |
| the relative roll angle; |
| —the pitch command; |
| —the average equivalent command; |
| —the guidance device gain; |
| —the actuator gain. |
| The stability parameters |
| —Routh–Hurwitz determinants; |
| —Frank–Wall stability parameters. |
Appendix A. Aerodynamics
The reference system for all aerodynamic coefficients is the body frame.
The reference area and the reference length for all aerodynamic coefficients are, respectively, the fuselage cross-section and the fuselage length.
For torque coefficients, the reference point is the final center of mass of the rocket.
For the translational development terms, work [26] with experimental corrections was used.
For rotational and non-stationary terms, including Magnus terms, paper [28] was used.
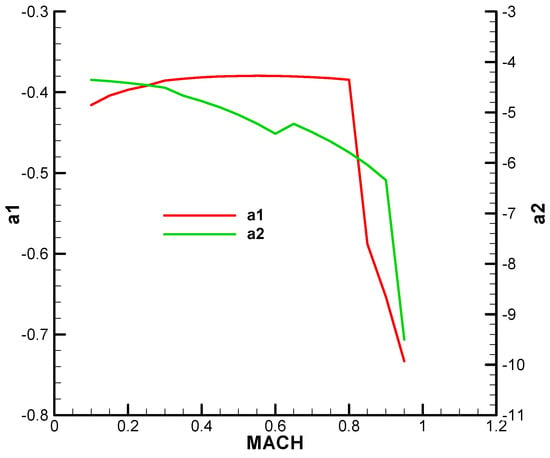
Figure A1.
Term of axial force coefficient at zero incidence (a1). Term of development of the coefficient of axial force with the squares of incidences (a2).
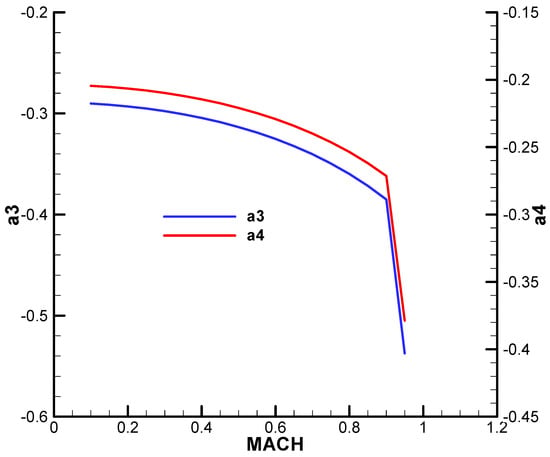
Figure A2.
Term of development of the coefficient of axial force with the incidence of the 4th power (a3). Term of development of the coefficient of axial force with the product of quadrat incidences (a4).
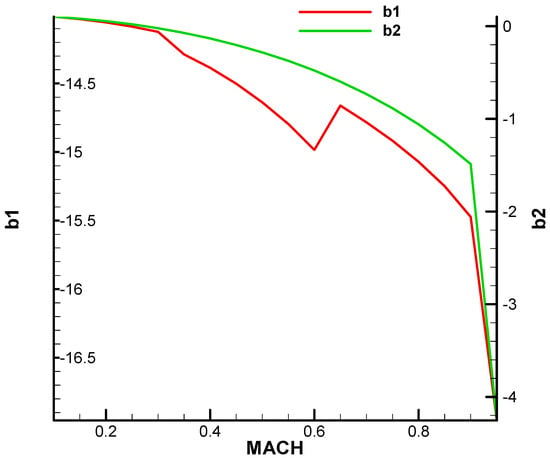
Figure A3.
Terms of development of coefficients for the normal forces with incidences.
Figure A4.
Magnus terms of the development of coefficients for the normal forces.
Figure A5.
Terms of development of coefficients of normal forces with rate of incidence (b9) and angular velocity (b4).
Figure A6.
Terms of development of the torque coefficients in pitch and yaw with incidences.
Figure A7.
Magnus terms of the development of pitch and yaw torque coefficients.
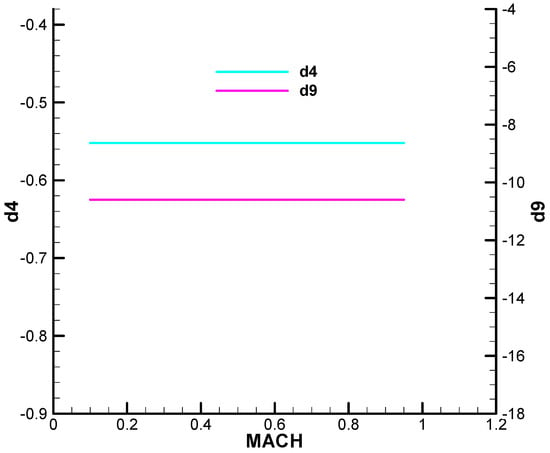
Figure A8.
Terms of development of the torque coefficient in pitch with rate of incidence (d9) and angular velocity (d4).
Figure A9.
Terms of development of the roll torque coefficient.
Appendix B. Parameters of the Linear Model
In this appendix, we use the following notation: i—initial mechanical characteristics; f—final mechanical characteristics (according to Table 1).
Appendix B.1. Basic Movement
Appendix B.1 presents the equilibrium flight parameters obtained in Section 2 of the paper.
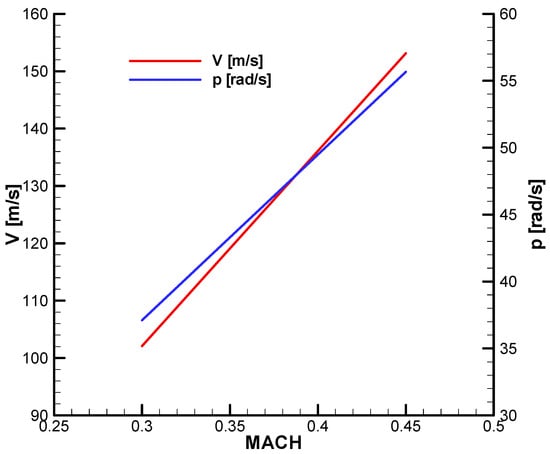
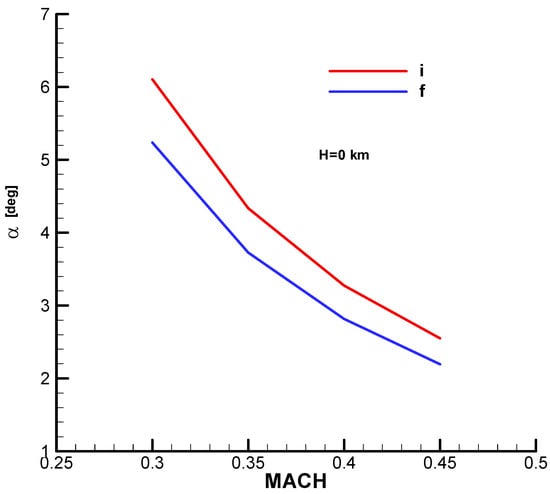
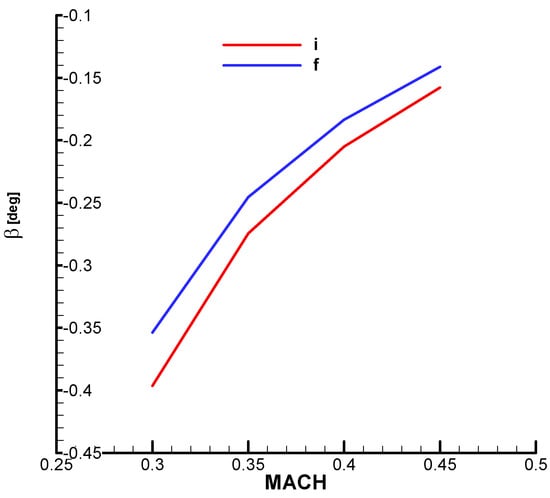
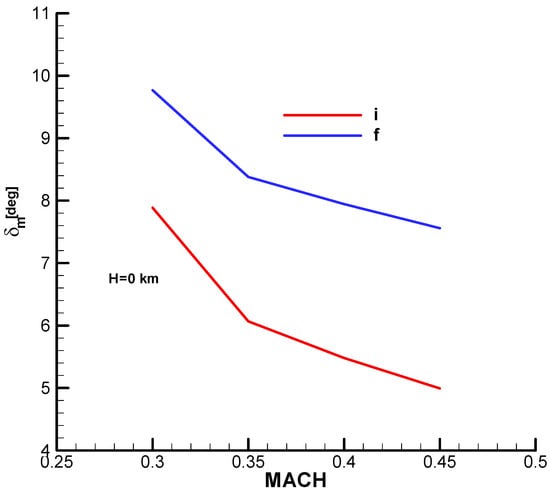
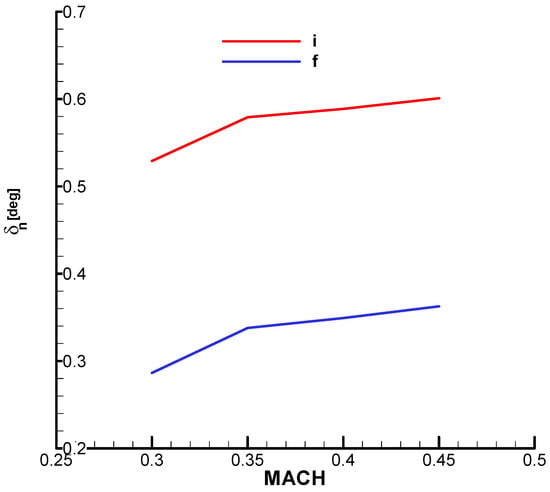

Figure A10.
Velocity (V) and roll angular rate (p) corresponding to velocity.

Figure A11.
Equilibrium incidence in the vertical plane (i—initial; f—final).

Figure A12.
Equilibrium incidence in the lateral plane (i—initial; f—final).

Figure A13.
Equilibrium pitch thrust deflection (i—initial; f—final).

Figure A14.
Equilibrium yaw thrust deflection (i—initial; f—final).
Appendix B.2. Stability Matrix
Appendix B.2 presents the stability derivatives obtained in Section 3 of the paper.
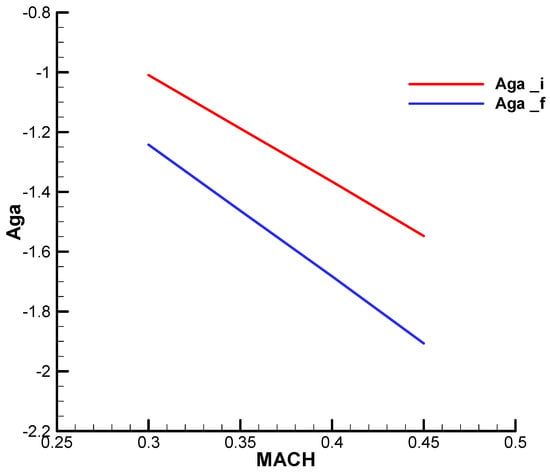
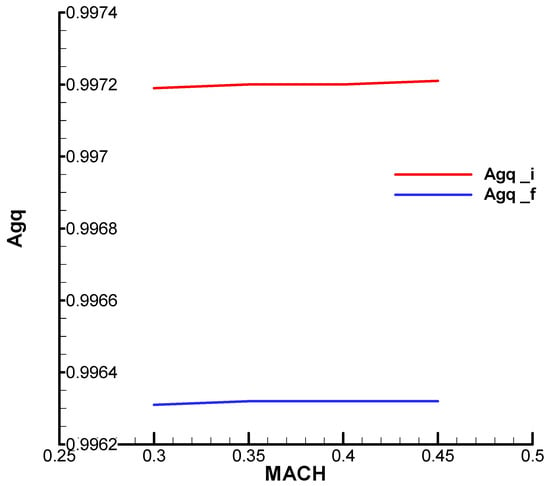
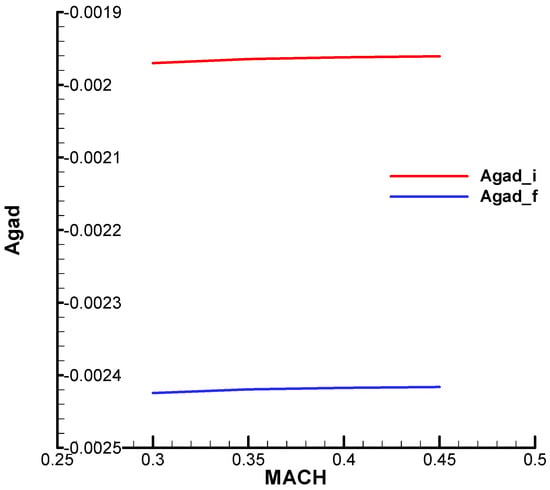
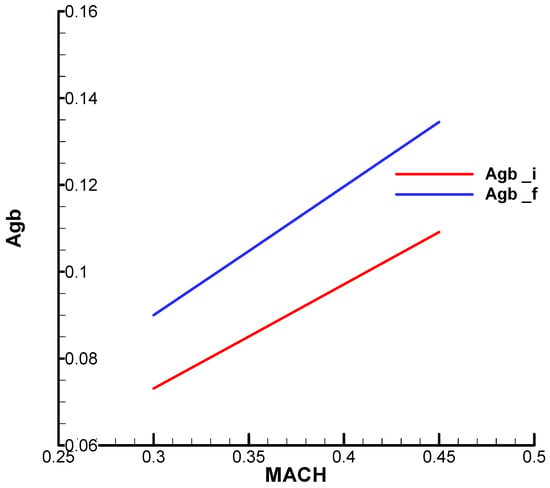
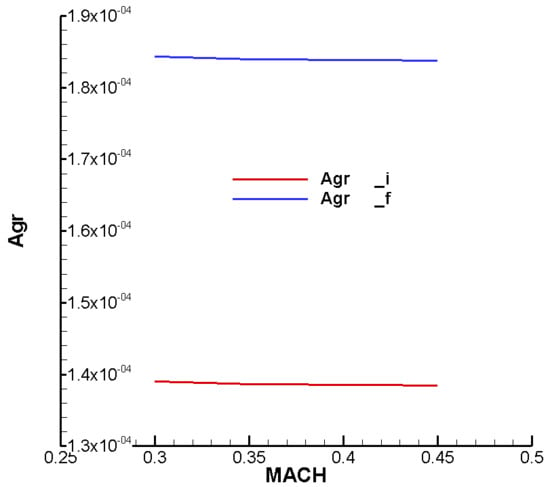
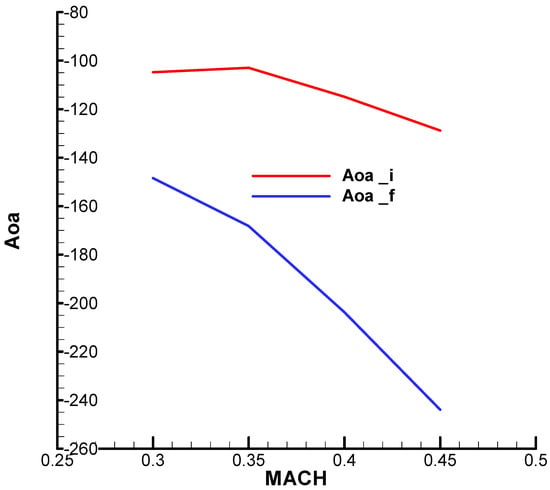
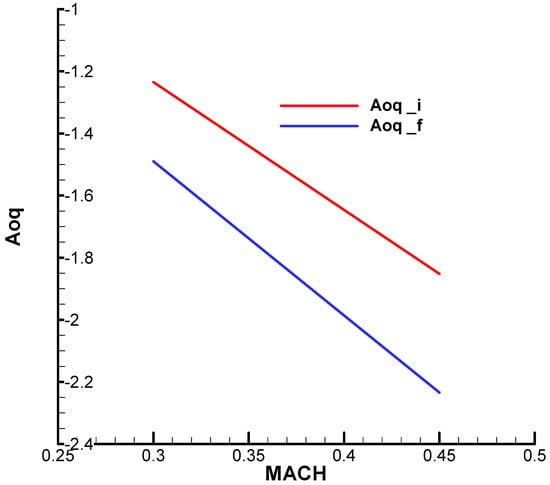
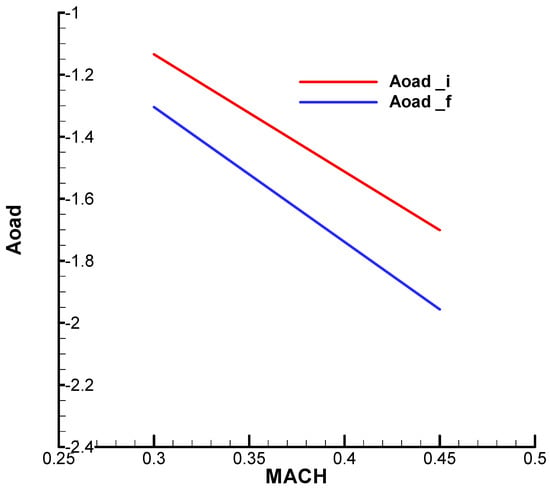
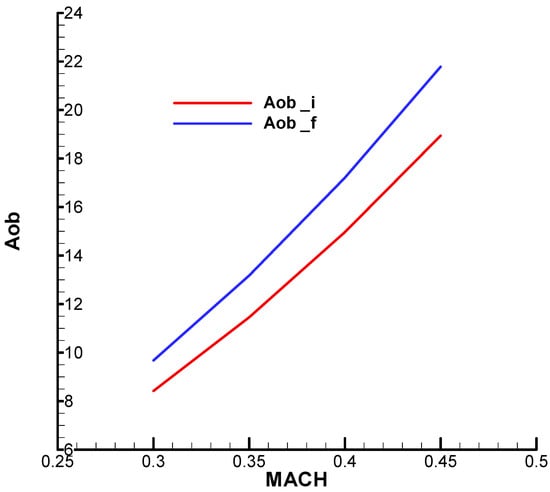
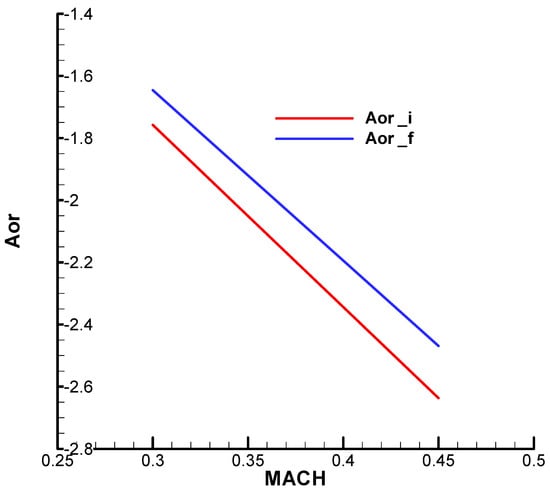

Figure A15.
Derivative term of the incidence equation against incidence (i—initial; f—final).

Figure A16.
Derivative term of the incidence equation against angular velocity (i—initial; f—final).

Figure A17.
Derivative term of the incidence equation against unsteady incidence (i—initial; f—final).

Figure A18.
Derivative term of the incidence equation against the cross incidence—Magnus term (i—initial; f—final).

Figure A19.
Derivative term of the incidence equation against the cross angular velocity—Magnus term (i—initial; f—final).

Figure A20.
Derivative term of the angular velocity equation against the incidence (i—initial; f—final).

Figure A21.
Derivative term of the angular velocity equation with respect to angular velocity (i—initial; f—final).

Figure A22.
Derivative term of the angular velocity equation against unsteady incidence (i—initial; f—final).

Figure A23.
Derivative term of the angular velocity equation against cross incidence—Magnus term (i—initial; f—final).

Figure A24.
Derivative term of the angular velocity equation against the cross angular velocity—Magnus and gyroscopic term (i—initial; f—final).
Appendix B.3. Command Matrix
Appendix B.3 presents the command derivatives obtained in Section 3 of the paper.

Figure A25.
Derivative term of the incidence equation against thrust deflection (i—initial; f—final).

Figure A26.
Derivative term of the angular velocity equation against thrust deflection (i—initial; f—final).
Appendix B.4. Flight Quality Parameters
Appendix B.4 presents the flight quality parameters obtained in Section 3 of the paper.
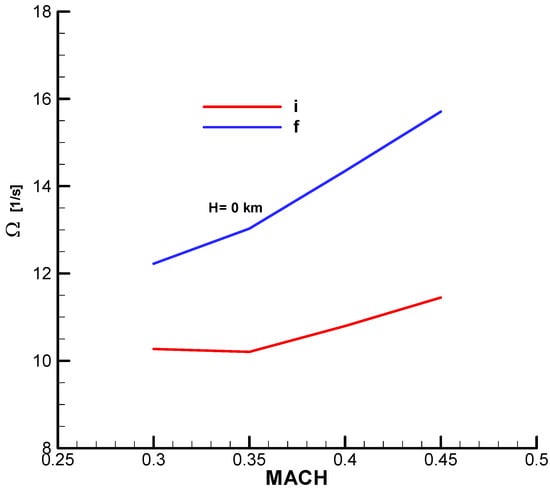
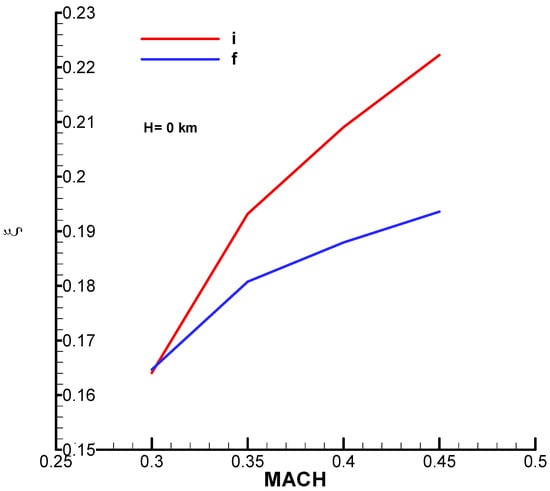
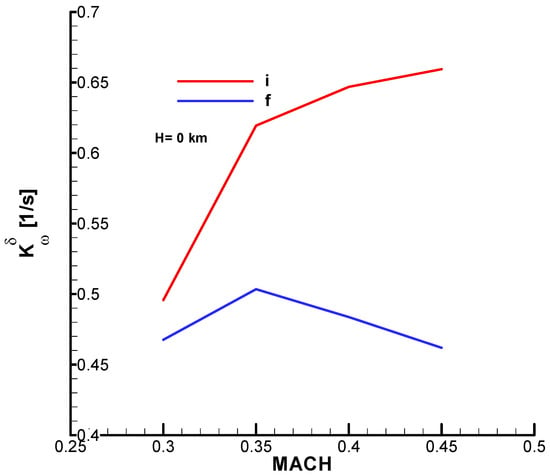
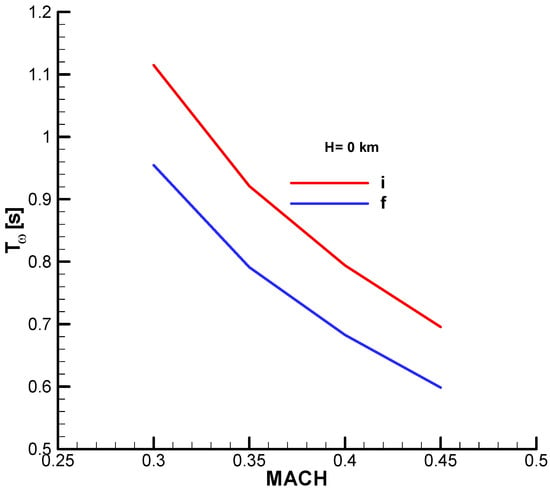
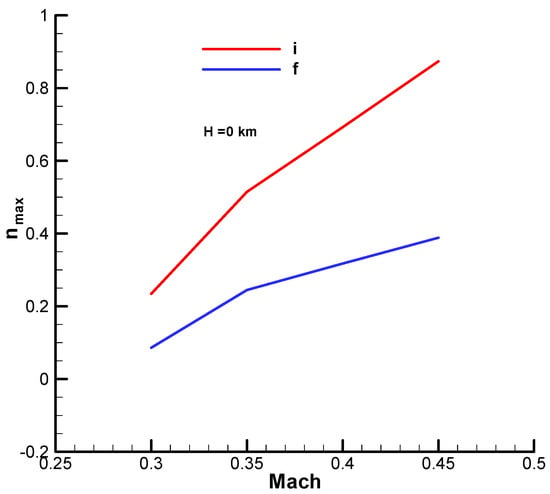

Figure A27.
Static stability (i—initial; f—final).

Figure A28.
Natural pulsation of nutation (i—initial; f—final).

Figure A29.
Nutation damping factor (i—initial; f—final).

Figure A30.
Command factor (i—initial; f—final).

Figure A31.
The time constant of the missile (i—initial; f—final).

Figure A32.
Maximum overload factor (i—initial; f—final).
Appendix C. Frank–Wall Analysis Results
Appendix C.1. Coefficients of the Characteristic Polynomial
Appendix C.1 presents the coefficients of the characteristic polynomial obtained in Section 5.5 of the paper.
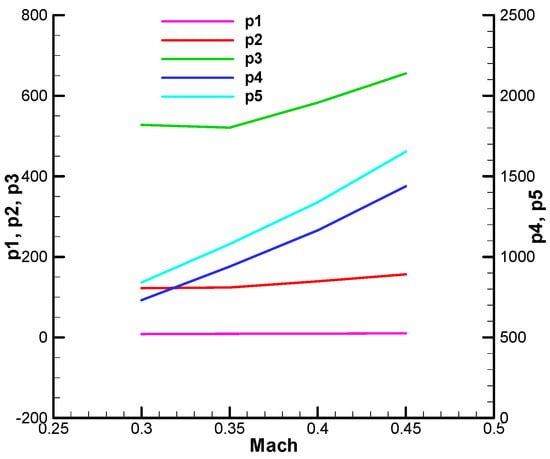
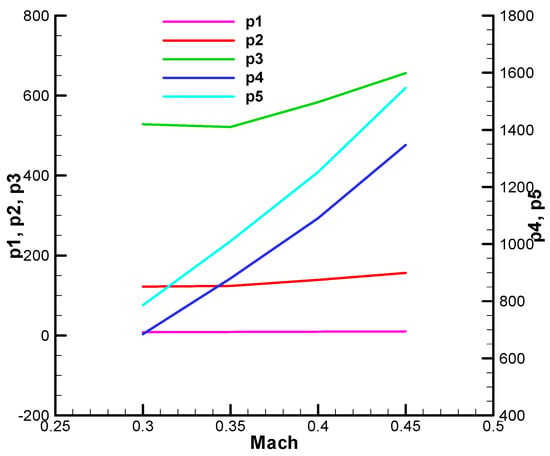
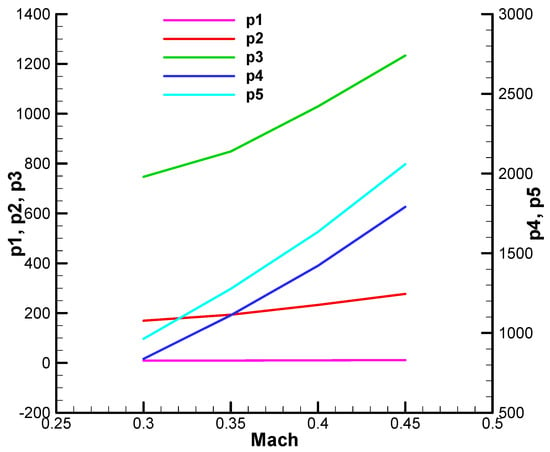
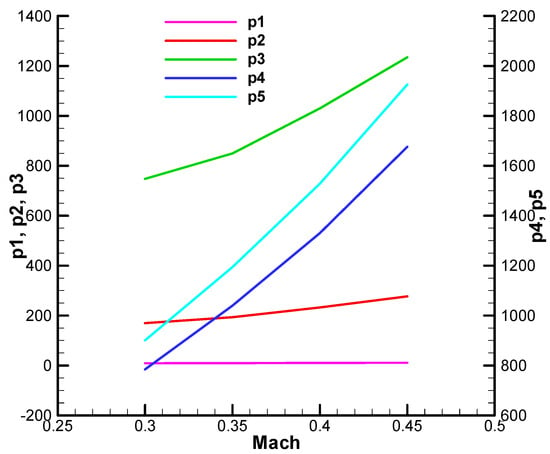
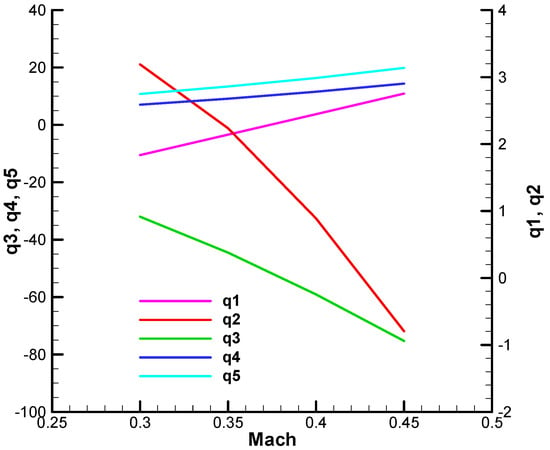
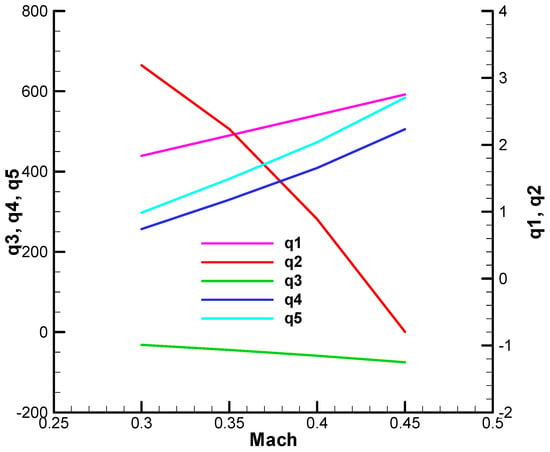
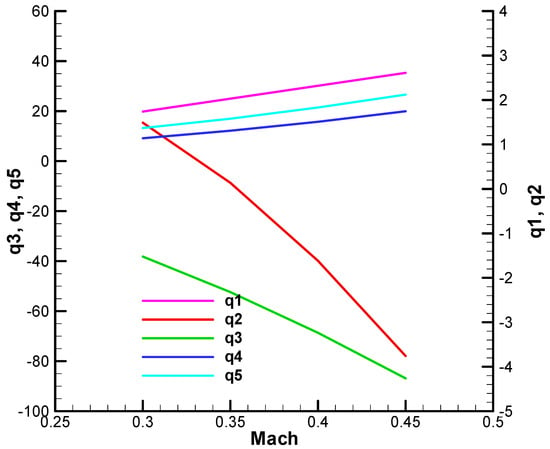
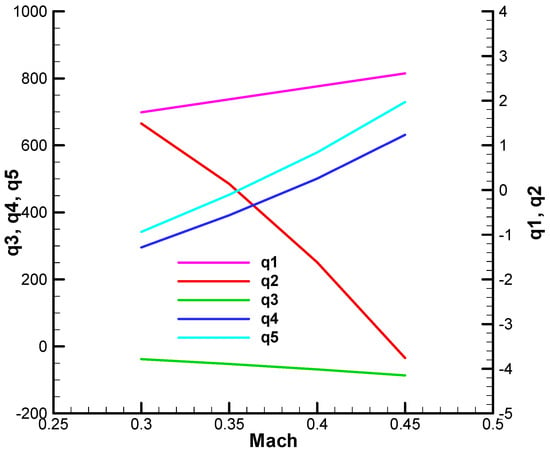

Figure A33.
Coefficient of the characteristic polynomial—the real part, initial;

Figure A34.
Coefficient of the characteristic polynomial—the real part, initial;

Figure A35.
Coefficient of the characteristic polynomial—the real part, final;

Figure A36.
Coefficient of the characteristic polynomial—the real part, final;

Figure A37.
Coefficient of the characteristic polynomial—the imaginary part, initial;

Figure A38.
Coefficient of the characteristic polynomial—the imaginary part, initial;

Figure A39.
Coefficient of the characteristic polynomial—the imaginary part, final;

Figure A40.
Coefficient of the characteristic polynomial—the imaginary part, final;
Appendix C.2. Stability Parameters F-W
Appendix C.2 presents the F-W stability parameters obtained in Section 7.2 of the paper.
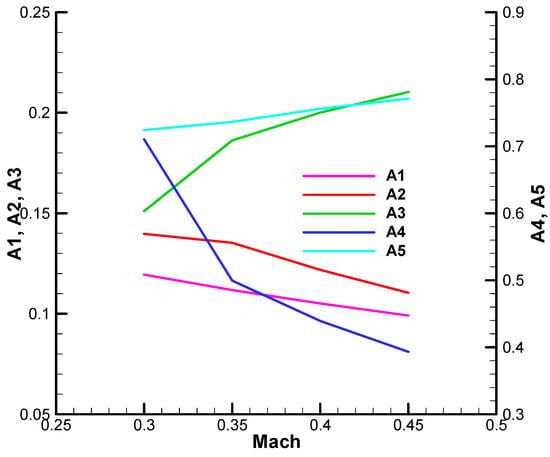
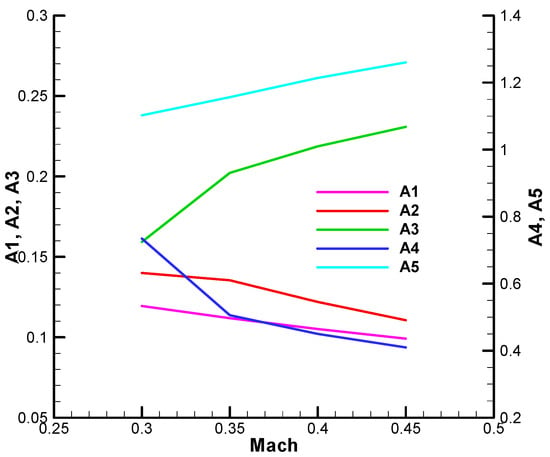
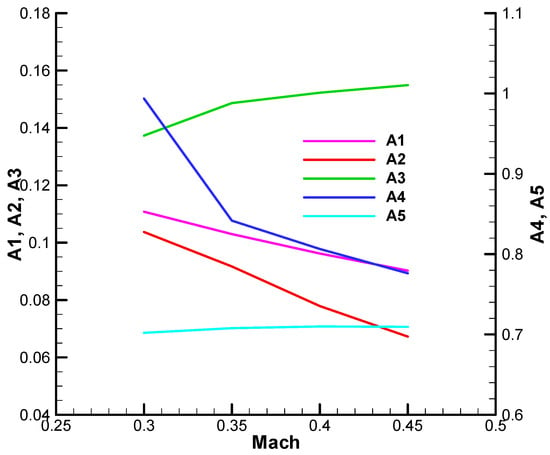
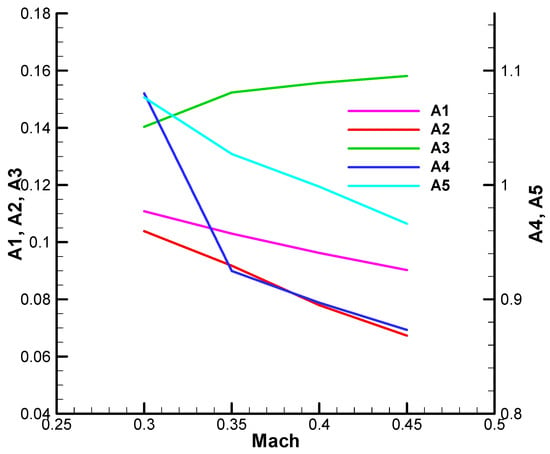

Figure A41.
Stability parameters F-W—initial;

Figure A42.
Stability parameters F-W—initial;

Figure A43.
Stability parameters F-W—final;

Figure A44.
Stability parameters F-W—final;
Appendix D. The Roots Locus of the Characteristic Polynomial
The diagrams are obtained for a range of Mach numbers: 0.3–0.45.
Appendix D.1. The Roots Locus of the Characteristic Polynomial with Real Coefficients
Appendix D.1 presents the roots locus of the characteristic polynomial with real coefficients obtained in Section 7.1 of the paper.
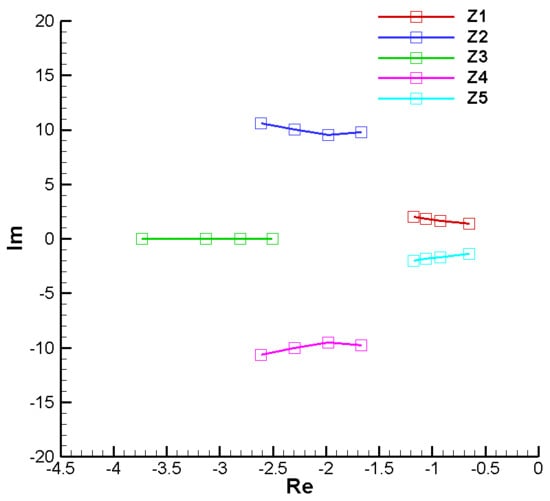
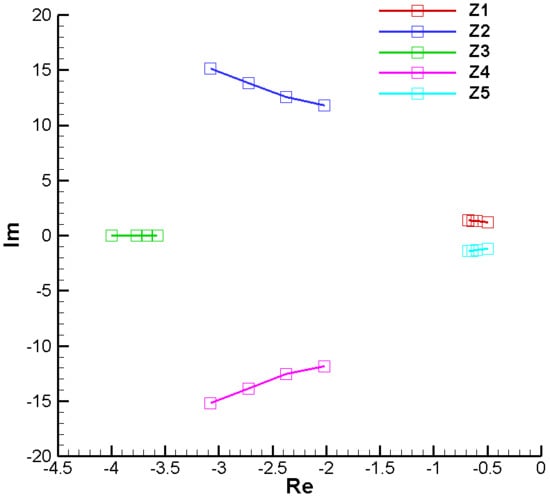

Figure A45.
Roots of the characteristic polynomial with real coefficients—initial.

Figure A46.
Roots of the characteristic polynomial with real coefficients—final.
Appendix D.2. The Roots Locus of the Characteristic Polynomial with Complex Coefficients
Appendix D.2 presents the roots of the characteristic polynomial with complex coefficients obtained in Section 7.2 of the paper.
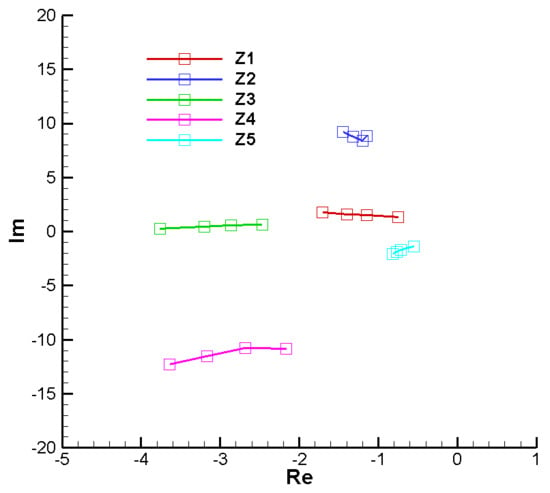
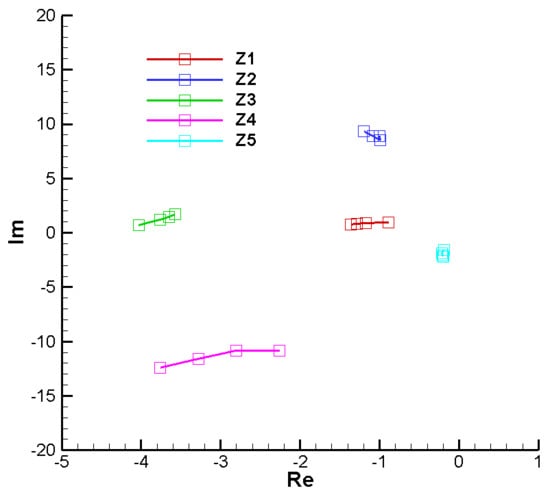
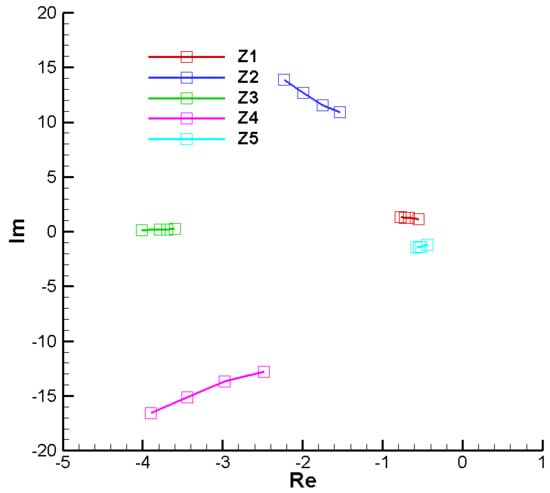
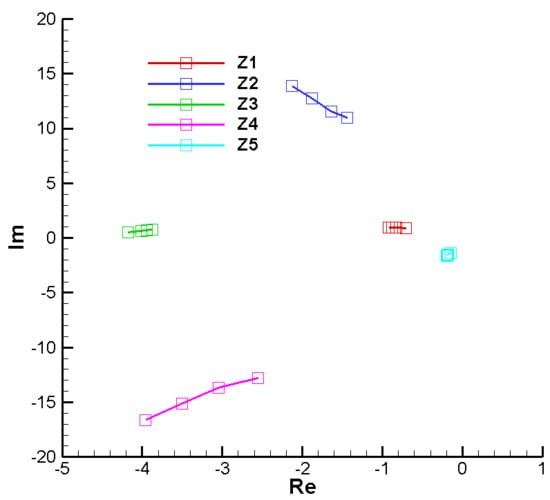

Figure A47.
Roots of the characteristic polynomial with complex coefficients—initial;

Figure A48.
Roots of the characteristic polynomial with complex coefficients—initial;

Figure A49.
Roots of the characteristic polynomial with complex coefficients—final;

Figure A50.
Roots of the characteristic polynomial with complex coefficients—final;
Appendix E. Frank–Wall Stability Criterion for the Fifth-Order Polynomial
Considering a fifth-order polynomial with complex coefficients,
to check if the real part of the roots is negative, first an associated polynomial is constructed:
after which the ratio of the polynomials is put in the following form:
According to the F-W stability theory [16], the necessary and sufficient condition for all roots of the polynomial (E1) to have the negative real part is that
and that
be pure complex numbers or null.
In the same paper [16], the algorithm for calculating the F-W stability parameters is presented, which we detail below for a fifth-order polynomial.
After which, for the fifth-order polynomial, the following is obtained successively:
Based on these relations, the stability parameters can be determined, respectively:
and
Check for non-rolling case
For the case without rotation, the five parameters become
where
are the R-H determinants for the fifth-order polynomial with real coefficients. It is observed that in this case the two conditions are equivalent:
References
- Hu, X.; Yang, S.X. Coning motion instability of spinning missiles induced by the delay of strap-down seeker. Chin. J. Aeronaut. 2021, 33, 3360–3368. [Google Scholar] [CrossRef]
- Hu, S.; Wang, J.; Wang, Y.; Tian, S. Stability Limits for the Velocity Orientation Autopilot of Rolling Missiles. IEEE Access 2021, 9, 110940–110951. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhou, Z. Flight Stability of Canard-Guided Dual-Spin Projectiles with Angular Rate Loops. Int. J. Aerosp. Eng. 2020, 2020, 2705175. [Google Scholar] [CrossRef]
- Suiçmez, E.C.; Kutay, A.T. Single channel digital controller design for a high spinning rate rolling airframe missile. Aeronaut. J. 2022, 126, 1815–1833. [Google Scholar] [CrossRef]
- Karimi, J. A new closed form solution for dynamic stability analysis of rolling airframes having one pair on-off actuator. Aviat. Open Access 2021, 25, 92–103. [Google Scholar] [CrossRef]
- Botez, R.M.; Chelaru, V.; Parvu, P.; Gheorghe, C. Calculus model for a rolling guided missile. J. Vib. Control 2001, 7, 863–889. [Google Scholar] [CrossRef]
- Chelaru, T.-V.; Constantinescu, C.E. Theoretical and experimental solutions for multistage quasi-guided rocket. In Proceedings of the International Astronautical Congress, IAC, Washington, DC, USA, 21–25 October 2019. [Google Scholar]
- Chelaru, T.V.; Constantinescu, C.E.; Pana, V.; Ene, C.; Chelaru, A. Stability of single channel homing rolling aerospace vehicle. Aerospace 2024, 11, 660. [Google Scholar] [CrossRef]
- Zheng, D.; Lin, D.; Wang, J.; Xu, X. Dynamic stability of rolling missiles employing a two-loop autopilot with consideration for the radome aberration parasitic feedback loop. Aerosp. Sci. Technol. 2017, 61, 1–10. [Google Scholar] [CrossRef]
- Tian, S.; Lin, D.; Wang, J.; Li, B. Dynamic stability of rolling missiles with angle-of-attack feedback three-loop autopilot considering parasitic effect. Aerosp. Sci. Technol. 2017, 71, 592–602. [Google Scholar] [CrossRef]
- Zheng, D.; Lin, D.; Xu, X.; Tian, S. Dynamic stability of rolling missile with proportional navigation & PI autopilot considering parasitic radome loop. Aerosp. Sci. Technol. 2017, 67, 41–48. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, F. A Combination of Silicon Micro-gyroscope that Application Rotary Missile Attitude Control System. In Proceedings of the 2011 International Conference on Physics Science and Technology (ICPST), Hong Kong, China, 12–13 December 2011. [Google Scholar]
- Yan, X.; Chen, G.; Tian, X. Two-Step Adaptive Augmented Unscented Kalman Filter for Roll Angles of Spinning Missiles Based on Magnetometer Measurements. Meas. Control. 2018, 51, 73–82. [Google Scholar] [CrossRef]
- Jahangir, E.; Howe, R.M. Time-Optimal Attitude Control Scheme for a Spinning Missile. J. Guid. Control. Dyn. 1993, 16, 346–353. [Google Scholar] [CrossRef][Green Version]
- Kocetkov, V.T.; Polovko, A.M.; Ponomarev, B.M. Theory of Self-Guided and Remote-Controlled Missile Systems; Nauka: Moskva, Russia, 1964. [Google Scholar][Green Version]
- Frank, E. On the zeros of polynomials with complex coefficients. Bull. Amer. Math. Soc. 1946, 52, 144–157. [Google Scholar] [CrossRef]
- Niţă, M.M.; Andreescu, D.Ş.T. Rocket Flight; Militara: Bucharest, Romania, 1964. [Google Scholar]
- Chelaru, T.V. Dynamics of Flight—Guided Missile, Revised and Added, 2nd ed.; Printech: Bucharest, Romania, 2004; p. 434. [Google Scholar]
- ISO 1151-1:1988; Flight Dynamics—Concepts, Quantities and Symbols—Part 1: Aircraft Motion Relative to the Air. ISO: Geneva, Switzerland, 1988.
- Hacker, T. Stability and Control in Flight Theory; Romanian Academy: Bucharest, Romania, 1968. [Google Scholar]
- Brown, K.M. A Quadratically convergent Newton-like method based upon Gaussian elimination. Siam J. Num. Anal. 1969, 6, 560–569. [Google Scholar] [CrossRef]
- Belea, C.; Lungu, R.; Cismaru, C. Gyroscopic Systems and Their Applications; Scrisul Romanesc: Craiova, Romania, 1986. [Google Scholar]
- Nita, M.M.; Chelaru, T.V. STP M 40455-99 the Guided Missile System—Terminology and Symbols; Ministry of Defence: Bucharest, Romania, 1998. [Google Scholar]
- Carpantier, R. Guidance des avions et des missiles aerodynamiques. Tom I II III Lit. ENSAE 1989, 112, ISSN 2840881241/9782840881247. Available online: https://books.google.com.au/books/about/Guidage_des_avions_et_des_missiles_a%C3%A9ro.html?id=4UX0GAAACAAJ&redir_esc=y (accessed on 9 October 2025).
- Kuzovkov, N.T. Flight Stabilization Systems, Ballistic Missile and Anti-Aircraft Missile; Visaia Skola: Moskva, Russia, 1976. [Google Scholar]
- Niţă, M.M.; Moraru, F.L.; Patraulea, R. Airplanes and Missiles, Design Concepts; Militară: Bucharest, Romania, 1985. [Google Scholar]
- Sviatoduh, V. Dynamics of Spatial Motion of Guided Missiles; Masinostroenie: Moskva, Russia, 1969. [Google Scholar]
- Nielsen, J. Missile Aerodynamics; McGraw-Hill Book Company, Inc.: New-York, NY, USA; Toronto, ON, Canada; London, UK, 1960. [Google Scholar]
- Nita, M.M.; Chelaru, T.V. STP M 40406-99 the Commanded Missile System—Terminology and Symbols; Ministry of Defence: Bucharest, Romania, 1998. [Google Scholar]
- Daud, A.A.M. A Note on Lienard-Chipart Criteria and its Application. Math. Stat. 2021, 9, 41–45. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).