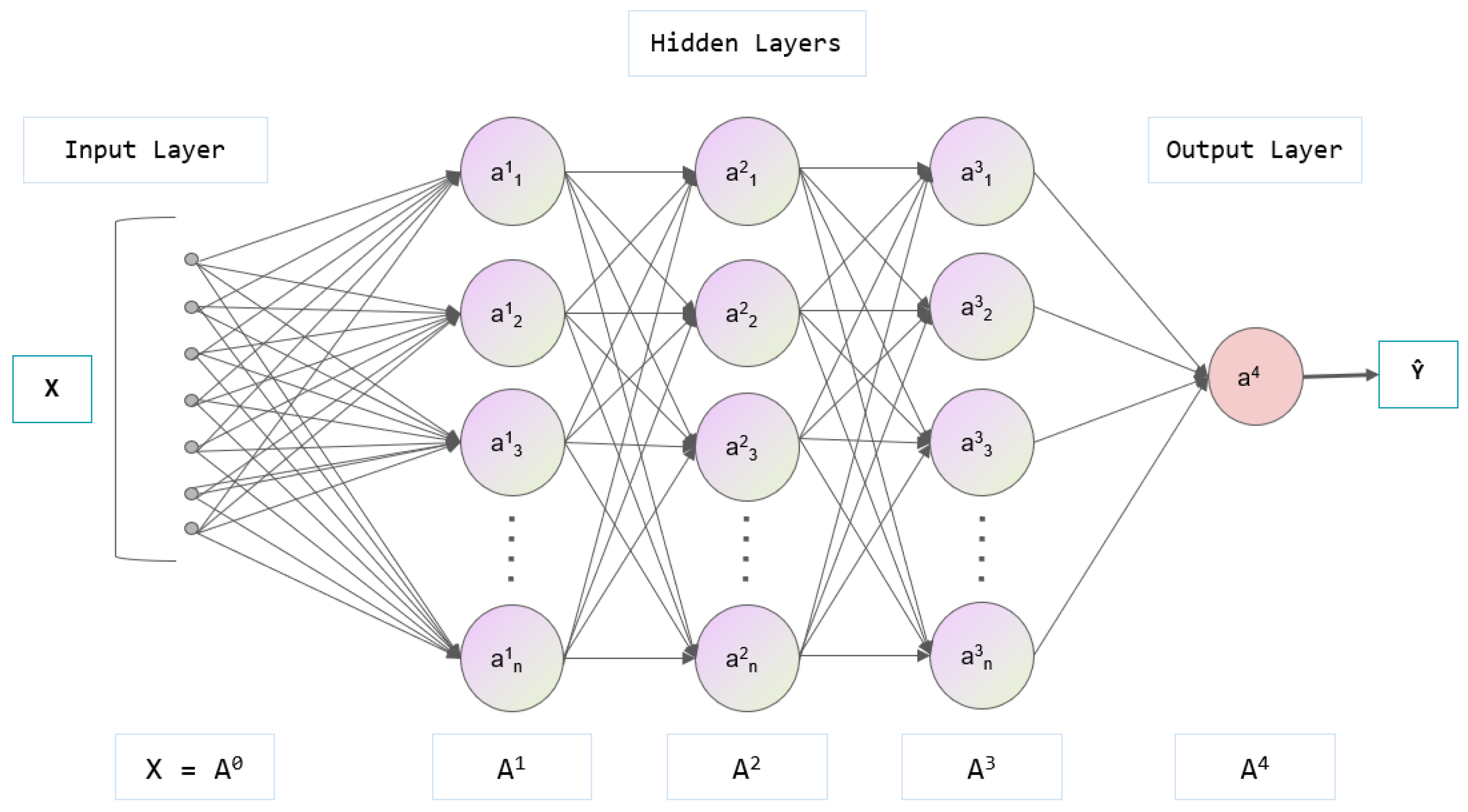
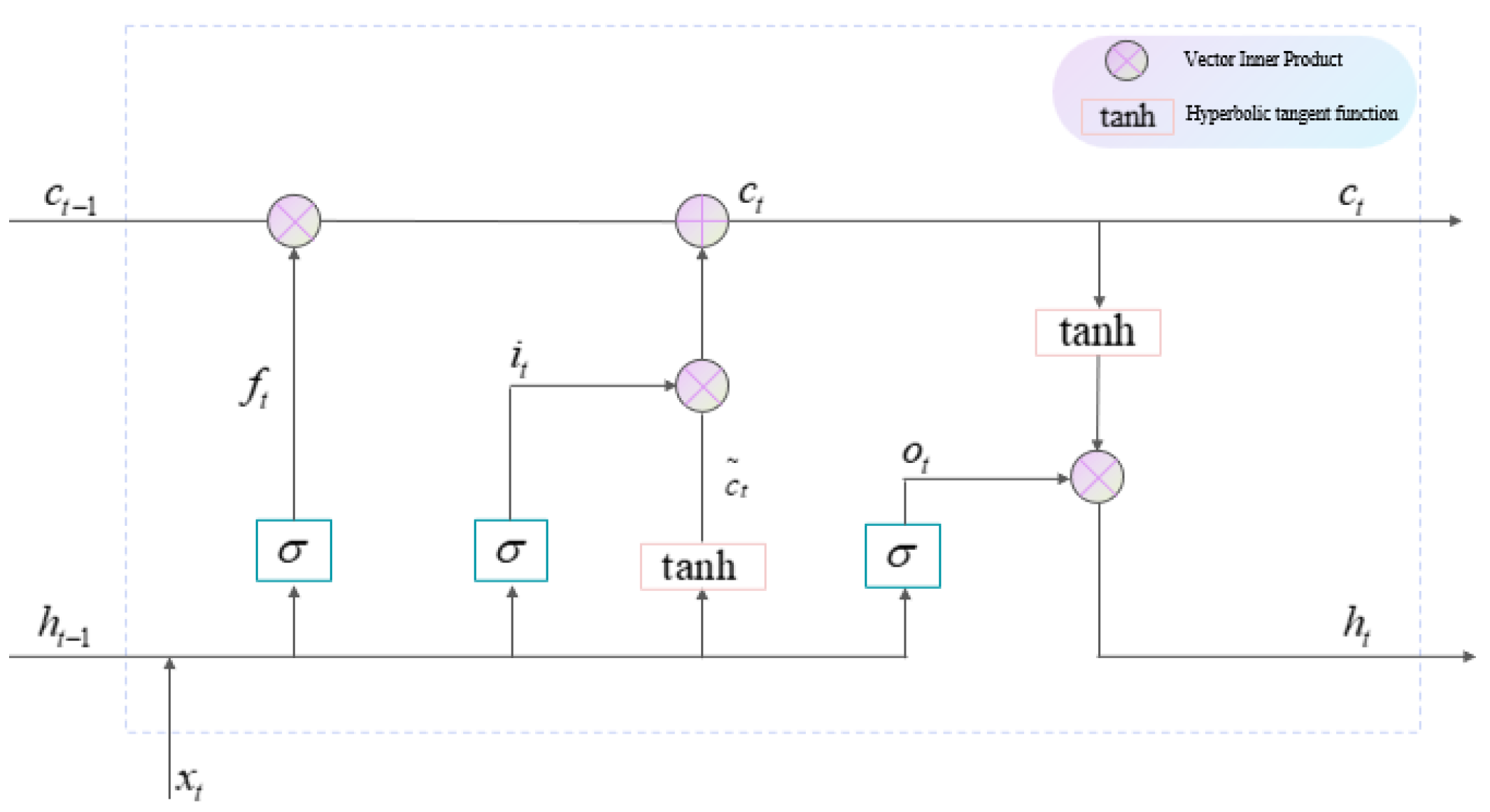
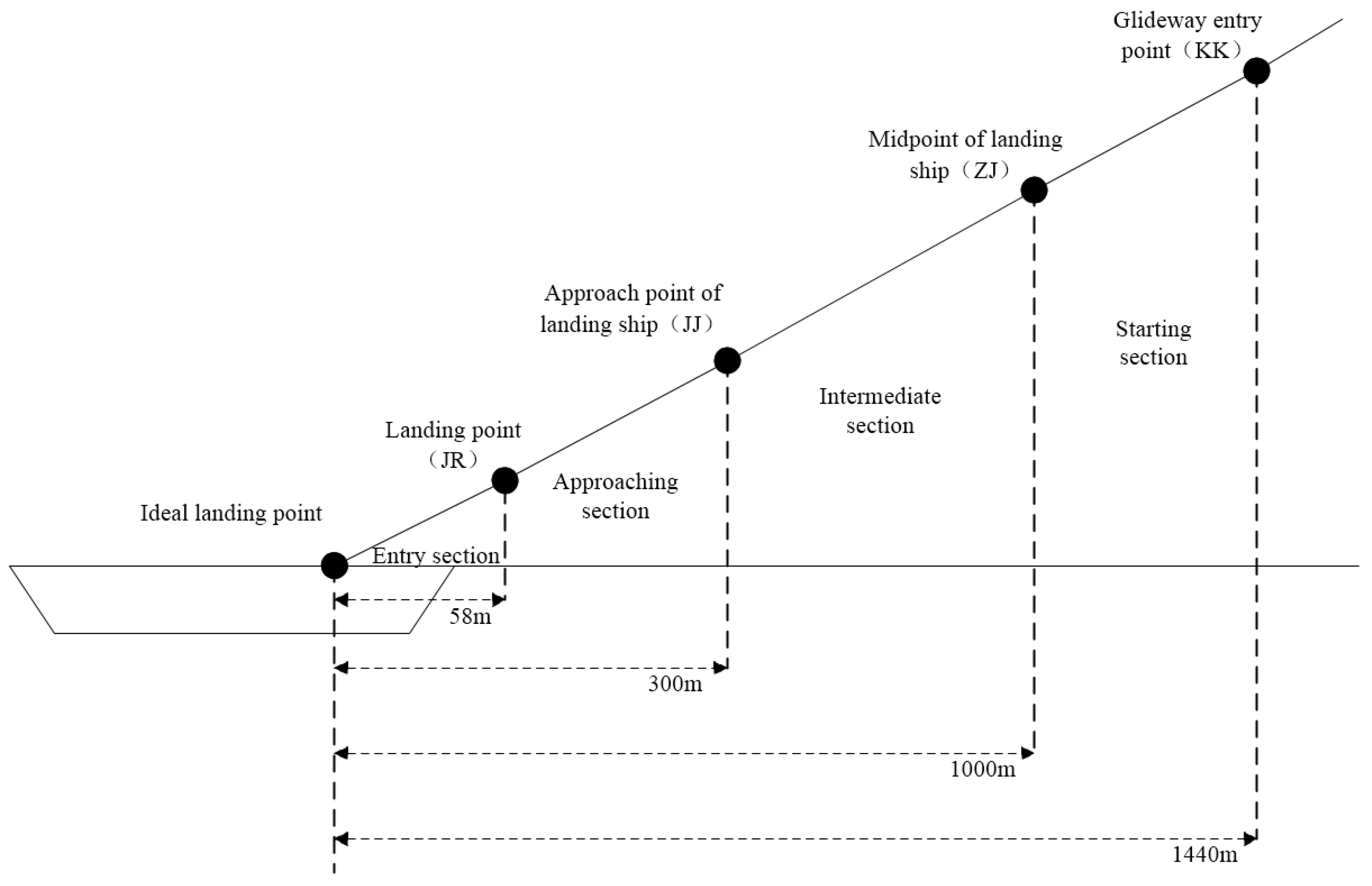
1. Introduction
Shipborne aircraft are a vital component of naval infrastructure. Compared with other operational tools, they possess the unique ability to rapidly enter and exit battlefields and execute efficient strikes against air, surface, underwater, and ground combat targets. The primary distinguishing feature of shipborne aircraft that sets them apart from land-based aircraft is their landing platform, the aircraft carrier deck. This uniqueness poses considerable challenges, and among all the operational phases of shipborne aircraft, the landing stage has the highest hazard coefficient and is the most accident-prone. According to empirical data, 80% of shipborne aircraft accidents occur during landing [
1]. Therefore, investigating the safety of the landing process has substantial theoretical and practical importance.
Extensive studies have been conducted to address this issue. Bobylev et al. [
2] studied the effects of airflow fields and weather on aircraft safety across four dimensions: ship wake-simulation devices, multi-aircraft interaction effects, airflow disturbance effects, and the decomposition and analysis of airflow disturbances. The results, validated through wind tunnel and real-aircraft testing, revealed key airflow disturbance characteristics and identified critical safety distance thresholds during landing. Bayen et al. [
3] applied optimal control theory and the level set method to investigate the automatic landing safety of high-dimensional aircraft models. They proposed a numerical method to calculate the reachable set of hybrid systems and derived both the maximum controllable invariant set and a corresponding control law to ensure that the ship remains within a safe state space, thereby guaranteeing aircraft safety.
In recent years, with the advancement of aircraft carrier capabilities in China, studies in the country have focused on shipborne aircraft landing safety. Tian and Zhao [
4] introduced a safety-oriented multidimensional state-space modeling approach for shipborne aircraft landing missions. They established nonlinear relationships between system state representation data and landing safety features. Moreover, they employed multivariate statistical techniques to reduce dimensionality, and ultimately constructed a numerical model linking independent variables to landing safety. Wang et al. [
5] focused on the adaptability of shipborne aircraft, analyzed the influence of both aircraft and environmental factors on safety, and quantitatively determined the minimum deck length for safe escape. Li and Zhao [
6] developed a safety model for shipborne aircraft approach and landing by integrating human, machine, and system loop factors using a fuzzy control approach. They evaluated the influence of safety factors through simulation. Yang et al. [
7] extended the multidimensional state-space model for landing by incorporating actual landing data from F-18 shipborne aircraft. They further analyzed the data using Bayesian methods and proposed a method to assess the landing status of shipborne aircraft.
Ship-landing safety control strategies are generally categorized into two types: Landing Signal Officer (LSO)-assisted decision-making and automatic landing systems. In recent years, several studies on fully automatic shipborne aircraft landing have been conducted in China. Zhu et al. [
8,
9,
10] and Jiang et al. [
11] explored the design of longitudinal and transverse guidance laws, compensation of deck-motion compensation, and suppression of ship wake disturbances using predictive control and sliding mode variable structure approaches [
12,
13,
14,
15]. Additionally, combinations of sliding mode variable structures with fuzzy proportional–integral–derivative control and intelligent control algorithms have been employed to improve control performance [
16,
17,
18]. However, research on automatic landing systems in China has been largely theoretical, and practical implementation is yet to progress.
At present, shipborne aircraft landings primarily rely on LSOs to provide auxiliary guidance to pilots to enhance safety. With ongoing technological advancements, the equipment used by LSOs has become increasingly diverse. Anti-jamming radios and video-based head-up displays (HUDs) offer more accurate information to support LSO decision-making. Several tools and their operational principles, such as optical aid systems and video HUDs, as well as shore-based landing-aid and manually operated visual assistance systems have also been adopted. Although these tools enhance decision-making efficiency, the final judgment still relies heavily on the subjective assessment of the LSO. Furthermore, there remains substantial potential for improving timeliness and accuracy beyond the general outline of present and future risks provided by existing systems.
Owing to technological advancements, aircraft recording equipment now provide more comprehensive and accurate flight data. Simultaneously, improvements in computer performance have enabled the application of Machine Learning (ML) methods [
19] to process these data; uncover hidden information; and identify, reduce, and prevent flight risks, thereby enhancing operational safety. Considerable progress has been made in the control and risk-prediction of land-based aircraft during landing. Puranik et al. [
20] utilized a Random Forest (RF) algorithm to predict vacuum and ground velocities during aircraft landing based on flight parameters from the approach phase. Compared with existing methods, their approach offered greater accuracy and faster processing, enabling sufficient time for flight decision-making. The model demonstrated robustness across different aircraft types and airports.
To evaluate the structural performance of aircraft landing gear, Xu [
21] developed a neural network model to predict the vertical load on the landing gear at the 100% limit sinking speed. The approach enhanced test-point accuracy and offered a novel method for studying landing gear strength. Given that flight data are sequential, Wang et al. [
5] employed a Long Short-Term Memory (LSTM) network to model long-term dependencies and predict vertical landing velocity. They used Bayesian inference to convert network outputs into probabilistic distributions. Experimental results confirmed the robustness of the model across different aircraft types and airport environments. Although most studies predominantly use numerical predictors, ML is also applicable to classification tasks. Zhang et al. [
22] examined the proportional relationship between offset center distance and lateral landing risk. They further constructed a transformation function using a Back Propagation (BP) neural network, and defined risk levels based on threshold values. Ni et al. [
23] used an ensemble learning approach, combining deep neural networks and Support Vector Machine (SVM) to process both numerical and textual variables in imbalanced flight data (e.g., aviation summaries). They classified events into five risk levels and built a decision support system to assist analysts in examining incidents, thereby helping risk managers quantify landing risks, prioritize actions, allocate resources, and implement proactive safety strategies [
22].
As with land-based aircraft, shipborne flight data comprise numerous parameters recorded at high frequency. Effectively mining the hidden information within these data can enable the identification of risks and their influencing factors, thereby shifting risk management from passive response to proactive prevention [
24]. Conventional flight data analysis techniques primarily focus on collecting data from onboard recorders, retrospectively analyzing flight data records, identifying anomalies, designing and implementing corrective measures, and evaluating their effectiveness. Although this approach contributes to flight safety management, it relies on prior knowledge from past flights and lacks adequate timeliness, as it cannot provide real-time analysis of current flight conditions.
Compared with conventional data analysis methods, ML techniques, particularly Deep Learning (DL), offer substantial advantages in terms of prediction accuracy and processing speed. They effectively manage large-sample multivariable flight data, predict ship-performance indicators, identify factors affecting safety, and support risk management. Studies worldwide have applied these techniques to shipboard landing risk management. Li [
25] used neural networks to predict the risk of shipborne aircraft landings and analyze related factors affecting ship safety, thereby establishing a control model for landing operations. Experimental results indicated that variables such as velocity and disturbance sinking rate significantly influence LSO decision-making, and risk areas during return flights can be classified based on decision-making time frames.
ML methods have also been applied to establish a nonlinear mathematical relationship between time-related factors and landing safety. Studies have explained the principle of minimizing risk during the landing process using event tree models, where the target is defined as the tree root and events as branch leaves, enabling detailed analysis of event risk levels [
4,
26]. Brindisi and Concilio [
27] employed probabilistic and regression neural networks to develop a comfort model for pilots during shipboard operations, emphasizing the subjective nature of comfort.
However, in China, research in this area remain relatively limited. Xiao et al. [
28] performed dimensionality reduction through principal component analysis of helicopter landing data, eliminating variable correlations, and subsequently entered the reduced data into a BP neural network to predict helicopter landing loads. Experimental results revealed that their method could technically support the evaluation of landing loads at the edge of the flight envelope and in envelope extension conditions [
29]. Tang et al. [
30] applied a BP neural network to combine positional elevation deviations obtained from electronic and optical landing systems. Their findings demonstrated the improvement in accuracy of deviation angle signals.
The descent phase of landing usually lasts 20–30 s, and the pilot/LSO needs to make a decision within 3–5 s [
15]. So timely and appropriate decision-making is crucial during the landing phase. ML-based data-driven quantitative methods reliably predict future risks associated with shipboard landings, offering valuable tools for real-time monitoring and supporting LSO decisions [
31,
32]. Therefore, this study employs both conventional machine learning and deep learning algorithms to model and predict the status parameters of shipborne aircraft during the landing phase. Furthermore, while deep learning methods are chosen for their superior capability in capturing complex temporal dependencies in sequential data [
33,
34], conventional methods such as Gradient Boosting are included as strong baselines to provide a comprehensive performance benchmark and to assess the relative value of more complex models for this specific application.
The remainder of this paper is organized as follows.
Section 2 presents the dataset and preprocessing methods, describes the data sources, and explains relevant shipborne indices and modeling theory. It also outlines the structure of each model and the evaluation metrics used.
Section 3 presents the experimental results obtained from applying the models to the dataset.
Section 4 discusses the findings, and
Section 5 summarizes the experimental outcomes and offers scope for future work.
3. Experiments
3.1. Data Preprocessing
The data were cleaned and preprocessed to ensure their format aligned with the model’s input requirements. First, the flight landing stage data were extracted based on specific indicators. Second, the independent and dependent variables used in the model were identified, following which the input feature and prediction vectors were constructed. Finally, the data were cleaned by removing irrelevant variables and addressing missing or abnormal values through manual techniques and ML methods.
The sensors started recording data immediately from system start-up. The data captured included the entire simulated flight training process. This study focused specifically on the sliding phase of shipboard landing, which necessitated isolating the relevant segment based on appropriate discrete indicators. The key evaluation criteria for shipboard landing were identified based on existing literature. Among the three recognized aircraft landing mode classes (I–III), the simulator recorded Class I data. The landing path was not a straight descent; rather, it followed a “spiral progressive” trajectory. Specifically, it was described as “three legs, four turns,” where the aircraft began a turn approximately 30 s after crossing the ship’s island, aligning with the ship’s heading.
During the landing process, the aircraft maintained an attack angle of approximately 11°, calculated from the attitude angle. In the sliding phase, pilots adhered to the strategy of “looking at the light, aligning, and maintaining angle.” The ideal sliding trajectory was a straight line relative to the aircraft carrier deck. Using time, altitude, angle of attack, and vertical velocity data, the flight data were segmented to extract the portion corresponding to the sliding phase.
Owing to variability in landing times across different sorties and the use of fixed-interval sensor sampling, variations existed in the data length for each flight. To address this and ensure uniform vector length for model input, the sliding phase was standardized based on the relative distance between the aircraft and key ship positions. Four characteristic points were selected as landmarks for segmenting the landing trajectory: the entry point of the sliding track (KK), the midpoint of the landing path (ZJ), a mid-to-late phase marker (JJ), and the actual touchdown point (JR). These four key assessment points for shipboard landing are illustrated in
Figure 5.
The dataset originally contained 18 variables, resulting in high dimensionality that increased computational resource consumption during model training. Additionally, the variable set included independent variables such as aircraft shelf number and pilot code. Some samples exhibited missing or abnormal values owing to equipment testing errors or early termination of recordings. Therefore, data cleaning was necessary.
The cleaning process began with manual inspection to identify and eliminate irrelevant variables, reducing the number of variables from 18 to 13. In handling outliers and missing values, samples with more than 30% anomalous data were discarded. When the proportion of missing or abnormal values was below 30%, interpolation was performed using the average of the two adjacent recorded points. After preprocessing, there were 436 valid samples.
For the four characteristic points identified in the previous section, the 13 variables obtained after dimension reduction were used as the key feature parameters for predicting ship landing risks. Additionally, four variables related to the moment the aircraft’s tail hook engaged the arresting gear were selected. Among them, ZX and ZY represent the positions of the carrier-based aircraft’s tail hook on the aircraft carrier’s deck arrestor wire, reflecting the lateral and longitudinal deviations of the landing position; ZAS and ZRFR represent the speed inertia of the carrier-based aircraft during landing, reflecting the sinking rate deviation at the time of landing. They all have a significant impact on landing risks. For example, when the lateral deviation ZX during landing is too large, it indicates that the carrier-based aircraft’s touchdown point is too far to the right/left (the standard landing should be aligned with the center-line of the carrier’s deck), which may cause the aircraft to overshoot the deck during landing; also, if the sink rate of the carrier-based aircraft is too high, it will greatly increase the risk of the aircraft’s tail striking the front deck of the carrier. Details of each feature are presented in
Table 2.
The RF algorithm was employed to rank the importance of the 13 variables retained after manual screening. RF is an ensemble learning method that uses the bagging approach to combine decision trees for improved prediction performance. It involves randomly sampling data to train each tree and randomly selecting features at each node to determine the optimal split. One key application of RF is ranking the importance of input variables. Feature importance is assessed by calculating the average reduction in Gini purity across all tree nodes where the feature is used.
There were four prediction targets (
Table 2). A separate RF model was trained for each target. The number of decision trees was set to 100, and each tree was trained on a maximum of 128 samples.
Table 3 presents the significance scores of each characteristic variable with respect to each prediction index. The final column in the table presents the average importance score of each variable across all four targets. The variables were ranked in descending order based on these average scores. The top nine variables, highlighted in bold in
Table 3, were selected for further analysis.
Through further screening of characteristic variables using the RF algorithm, nine flight parameters at four feature points were selected as the input data for the subsequent models. These inputs were represented by matrix A, and the prediction vectors were denoted as B, as shown in Equation (5). Considering that the scales of the four predictor variables are different, where ZX and ZY are 10
−1, and ZAS and ZRFR are 10
1, the scales will be unified when calculating MAE, as detailed in Equation (6). In addition, to more intuitively reflect the difference between the model’s predicted values and the actual values, the Mean Absolute Error Proportion (MAEP) is used, which allows for a better vertical comparison between the predicted values and the actual values, as detailed in Equation (7).
3.2. Model Training and Reasoning
This section presents the results of model training and prediction. The hardware specifications used for the experiments are listed in
Table 4. Python (v 3.10.4) was used as the programming language, with PyTorch (v 12.6) selected as the DL framework.
The preprocessed dataset was divided into training, validation, and test sets in a 7:2:1 ratio. The relevant hyperparameter settings used during model training are listed in
Table 5. The model was trained for 200 epochs, with a batch size of 64. The initial learning rate was set to 0.01, and the Adam optimizer was used to update the training parameters during the BP phase.
It is reasonable to assume that the closer a point is to the landing point, the more accurate the prediction will be. However, at closer distances, pilots have less time to make necessary adjustments. Hence, this study compared models using combined input modes—for example, a model trained with input from point KK alone versus one trained with combined inputs from points KK and ZJ.
Table 6 lists all the input combinations, where combinations 1–4 correspond to individual inputs from each key point, and combinations 5–10 represent combined inputs. For the ANN, ten separate models were trained corresponding to the ten input combinations. As LSTM and Transformer networks account for the temporal nature of the input data, only six combined input configurations were used for training them.
Table 7 presents the architecture of the ANN constructed in this study (using single feature point input as an example). The network comprised three hidden layers. The number of neurons in the input layer was determined by the dimensionality of the input variables. The three hidden layers were fully connected, containing 128, 64, and 32 neurons. The output layer contained four neurons, corresponding to the number of predicted variables. Notably, dropout was applied to the first two fully connected layers, at a rate of 0.2. This means that 20% of the neurons in these layers were randomly deactivated during training—a regularization technique that prevented overfitting.
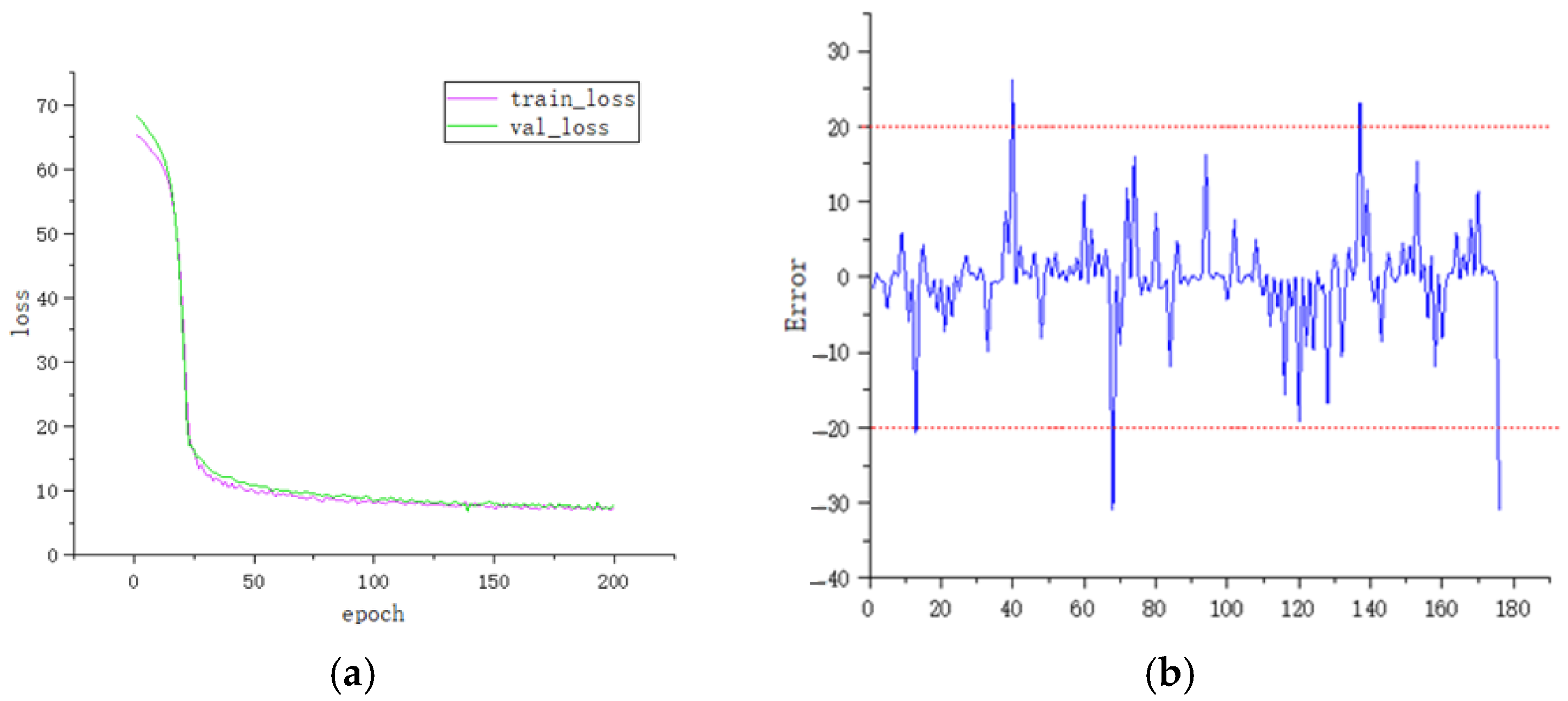
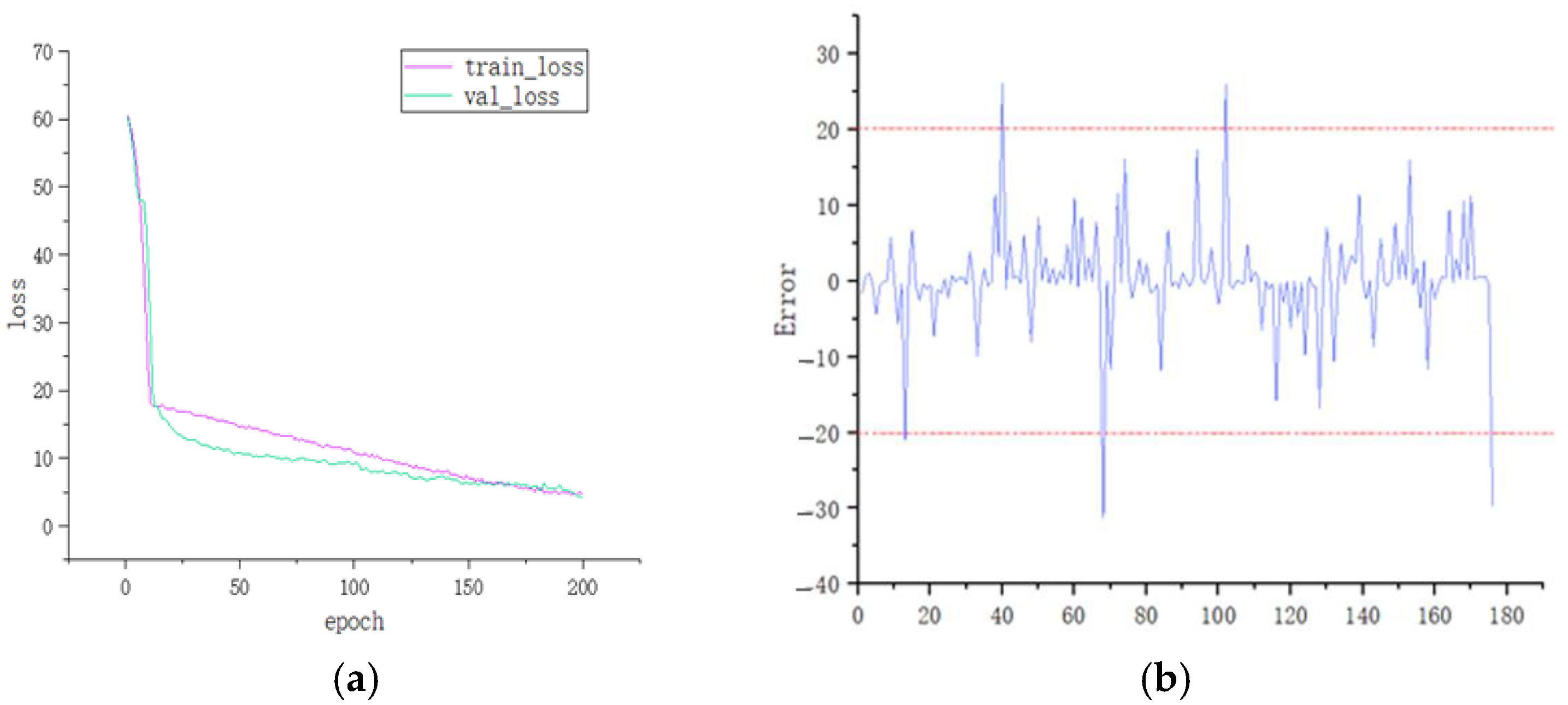
Figure 6 illustrates the loss curves for the training and validation sets during model training using KK as input, as well as the prediction results on the test set after training completion. The training loss curve exhibited a significant drop within the first 25 epochs, and both the training and validation losses stabilized after approximately 100 epochs. Regarding prediction accuracy, 89.78% of the test samples had an error within the range of 10, whereas only 2.84% of the samples exhibited an error exceeding 20. Detailed results for the remaining nine input combinations are provided in
Table 8. Among them, the model using JJ + JR as input achieved the best performance in both the training and test phases, with a test set MAE of 4.2039.
The input format supported by LSTM is defined in Equation (8), where
represents the sample size of the input data,
denotes the number of time steps per input sample, and
indicates the number of features at each time step. To fit this structure, the input data were remodeled accordingly. Using two key points as an example, each containing nine features, the time step was set to 2. The input features were divided into two segments, with each time step including nine features. Consequently, the sample feature size was set to 9. This approach was applied similarly to other input configurations.
The structure of the LSTM model is detailed in
Table 9. The first layer comprised 64 LSTM units, with each unit following the architecture illustrated in
Figure 4. To mitigate overfitting, a dropout layer with a rate of 0.2 was applied. The output layer was a fully connected layer with four neurons, corresponding to the four prediction targets.
The training and test results of the LSTM model, using KK + ZJ as the input, are shown in
Figure 7. During the training phase, the model loss decreased rapidly within the first 20 epochs, with the rate of decline gradually slowing thereafter. By approximately the 175th epoch, the loss stabilized. In terms of prediction accuracy, 90.9% of the LSTM model’s prediction errors fell within a range of 10. Only 2.27% of the sample errors exceeded 20, indicating slightly better performance than the ANN model. The results for all six input combinations are summarized in
Table 10. Among them, the KK + ZJ + JJ + JR input yielded the lowest loss on the training set, and ZJ + JJ + JR achieved the lowest loss on the validation set and the best overall performance on the test set.
The structure of the Transformer model is presented in
Table 11, which outlines the output vector dimensions and parameter counts for each layer of the model when two key points are used as input. As the Transformer supports sequential data input, the input format was the same as that used for the LSTM model. Based on the number of key points involved in the ship landing phase, the data were divided into corresponding time steps, with each time step containing nine variables.
The input data first passed two modules: the embedding layer and positional encoding layer (pos_encoder). These layers inserted positional information into the sequence, thus enabling the attention mechanism of the model to recognize the order of the input elements. The embedding layer sets the hyperparameter
to 64, mapping each feature in each time step into 64-dimensional vectors. Position indices were generated sequentially using natural numbers. Finally, the positional encoding was applied as follows. The even- and odd-numbered dimensions used sine and cosine functions, respectively, as defined in Equation (9), where
represents the position index,
represents the dimension index, and
is fixed at 64.
Transformer models were trained and tested using the same six input combinations as the LSTM models.
Figure 8 presents the training and test results for the model using KK + ZJ as input. According to the loss curve, the model shows a relatively rapid and balanced decline in loss during the first 140 epochs, after which the loss stabilized. Compared with the ANN and LSTM models, the Transformer converged more slowly; however, it ultimately achieved a lower loss value.
Based on the model’s prediction results, 92.7% of the sample errors fell within a range of 10, whereas only 1.7% exceeded an error of 20. Furthermore, the maximum error was significantly lower than those observed in the ANN and LSTM models. All results are summarized in
Table 12. Among all the input configurations, KK + ZJ + JJ + JR yielded the best performance across the training, validation, and test sets.
5. Discussion
This study applied DL methods to predict the landing risk of shipborne aircraft. The study comprised two major components. First, data of F/A-18 shipborne aircraft were preprocessed. As the initial step, the sliding phase data of the landing process was extracted. Then, four key landing points—KK, ZJ, JJ, and JR—were identified. During data cleaning, missing and abnormal values were either removed or interpolated. Variables were manually screened, and their importance was ranked using the RF algorithm. Ultimately, nine key flight parameters were retained as characteristic variables.
Second, three DL models—ANN, LSTM, and Transformer—were employed. Up to ten combinations of key input points were used to model aircraft landing risk. Based on the MAE, the results indicate that all three models effectively capture the nonlinear relationships between characteristic and predicted variables. The LSTM and Transformer models’ ability to process temporal data enabled them to better exploit the time-dependent structure of the landing data. For each model, prediction accuracy improved with an increase in the number of input variables. However, more inputs also increased model complexity and demand for computational resources. Additionally, inputs closer to the landing point reduce the time available for LSOs and pilots to make corrective decisions, necessitating a trade-off when selecting input points.
Among the three models, the Transformer model achieved the highest prediction accuracy, but at the cost of significantly greater computational demand. The ANN model, while less accurate, required the fewest parameters and was more resource-efficient. Model selection should balance prediction performance and deployment cost based on practical needs. Furthermore, we compare the accuracy of DL models and three traditional machine learning models. DL models perform better in handling multivariable nonlinear relationships, while traditional machine learning models have the advantage of lower hardware computing power requirements and are easier to deploy in practical applications.
Practical Implications and Usage: This article evaluates the accuracy of the model by predicting four key landing parameters and using the MAE of these four parameters. The experimental results show that the overall prediction error of the model for these landing parameters is within an acceptable range. Therefore, in practical applications, during the descent of carrier-based aircraft, the related flight parameters can be input into the model to obtain predicted landing indicators, thus providing auxiliary decision-making support for LSO.
Limitations and Critical Reflection: While the results are promising, several limitations must be acknowledged. Firstly, the study relies entirely on simulated data. Although the simulator is high-fidelity, it cannot perfectly replicate all nuances of real-world operations, such as extreme atmospheric turbulence, sudden mechanical failures, or the full psychological stress experienced by pilots. Secondly, limited by prior knowledge, this article does not further convert the landing indicators into landing risk values. Therefore, the LSO needs to refer to the predicted values and use prior knowledge to assess the levels of risk and whether to attempt a go-around; for instance, if the predicted lateral deviation exceeds 10 m or the descent rate is above 6 m/s, the system could issue a high-risk warning, suggesting a go-around. Thirdly, the current study predicts parameters, and the translation into a holistic risk assessment, while proposed, requires further validation with operational experts to define robust and accepted threshold values for different risk levels. Finally, the computational complexity of the best-performing model (Transformer) poses a challenge for real-time embedded applications aboard carriers or aircraft, necessitating future work on model optimization and distillation.
Future Work: Future research should focus on several areas: (1) Validating the models using real flight data from shipborne aircraft operations. (2) Further research could combine the expertise of professionals to quantitatively model landing risks, and directly output risk levels based on operational guidelines and expert knowledge, rather than just predicting parameters. (3) By consulting expert opinions, set corresponding weights based on the importance of each indicator, thereby providing a more detailed basis for the overall risk assessment. (4) Implementing a real-time predictive system interface and conducting human-in-the-loop evaluations with experienced LSOs to assess its practical utility and integration into existing workflows.