Two Hierarchical Guidance Laws of Pursuer in Orbital Pursuit–Evasion–Defense Game

Abstract

In this study, differential game theory was applied to propose two guidance laws of a pursuer in an orbit pursuit–evasion–defense game. One was a conservative guidance law of maneuvering to absolute safety before pursuing the evader, and the other was a radical guidance law of playing with the defender only when necessary. Both guidance laws enable the pursuer to avoid the defender while pursuing the evader, but the radical guidance law reduces the pursuit time by moving the pursuer closer to the defender. The pursuer, defender, and evader are all spacecraft carrying three-axis thrusters that can provide independent thrust in three directions. The proximity dynamics processes of the participants were described by the Clohessy–Wiltshire equations. A method for solving the time-to-go analytically was proposed by simplifying the dynamics model to meet real-time requirements. The effectiveness of the two guidance laws was verified by numerical simulations, and the differences between the two laws were analyzed.

1. Introduction

With the continuous development of human space technology, various control theories and methods have been applied in space exploration in recent years [1,2,3]. However, with the gradual increase of assets in space, the issue of space security has been emphasized by various countries. Orbit pursuit–evasion problem has received increasing attention as a key technology in the field of space security. The orbit pursuit–evasion problem can be formulated as a differential game, which was first be introduced by Isaacs [4] to solve the missile interception problem. Thereafter, differential game theory was subsequently applied to the orbital pursuit–evasion problem. Wong [5] solved the problem of the pursuit of a maneuvering fleeing target in a constant gravitational field. Anderson and Grazier [6] investigated the pursuit–evasion problem for low-orbiting spacecraft and presented an analytical solution of the barrier for the planar fugitive problem with a linear dynamics model. Linear quadratic differential games are widely used in orbit pursuit–evasion problems. Ho and Bryson [7] used a variational method to solve the differential game problem and showed that a proportional navigation law was the optimal interception strategy. The final optimal policy obtained for linear quadratic differential games was a state-dependent linear policy. However, linear quadratic differential games do not guarantee a definite miss distance because there are no constraints imposed by the end states.

The solutions of differential games with terminal state constraints that guarantee the determination of miss distances usually involve solving high-dimensional two-point boundary value problems. These types of problems can usually be solved only by numerical methods. Pontani and Conway [8] proposed a numerical calculation method for solving for open-loop trajectories. The pre-solution was first obtained by the genetic algorithm, and then the exact open-loop trajectory was obtained by substituting this solution into a semi-analytic method as the initial guess. Sun [9] proposed a semi-direct parametric method combined with the multiple shooting method to obtain a saddle point solution. Hafer [10] proposed a sensitivity method aimed at obtaining a saddle point solution under a nonlinear orbital dynamics model, locating the barrier trajectory to determine the region where interception was guaranteed and speeding up the computational efficiency to meet real-time requirements. The open-loop solution methods for game strategies often face problems such as large computational efforts and long solution times, and therefore, they are not effective in real-time game scenarios.

Obtaining the closed-loop solutions of differential games is a much more difficult task. Ghosh and Conway [11] proposed an extremal field approach to synthesize an approximate optimal strategy for a nonlinear two-player game. The open-loop extremal field was first solved for offline, and then real-time feedback control was obtained by interpolating the open-loop extremal field. Jagat and Sinclair [12] proposed a linear control law for a finite horizon based on linear quadratic differential game theory. A nonlinear control law was then obtained by solving the state-dependent Riccati differential equation. However, since in an actual problem a rational evader is unlikely to accept such an evaluation function but will instead flee with all its might at the last moment, the practical significance of this solution is worth discussing. Tartaglia and Innocenti [13] solved the infinite-horizon spacecraft rendezvous problem by solving the state-dependent Riccati differential equation, but this approach did not take into account the thrust limitations of the spacecraft. Gutman and Rubinsky [14] proposed a nonlinear guidance law for the extra-atmospheric interception problem. The time-to-go was treated as a solution of a quartic polynomial equation. In that study, the objects of the game were long-range missiles, so the gap between the gravitational fields was neglected because it was small compared to the control magnitude. Ye [15] obtained the optimal pursuit strategy for a closed loop by proposing an online method to solve for the time-to-go. That paper pointed out that there are four cases in which the terminal moment distance varies with the terminal moment, and an online numerical method was designed to solve for the time-to-go for these four cases. Closed-loop strategies for pursuit-evasion games are often only available in problems with simple dynamical models or special evaluation functions. The reason is that it is difficult to guarantee the real-time requirement for numerically solving the optimal strategy. With the development of intelligent control, many data-based control algorithms with low dependence on models provide new solutions for autonomous decision making. Yusuf Kartal et al. [16] proposed an on-policy reinforcement learning method for real-time online solution of the HJI equations, thus solving a non-quadratic value function pursuit-evasion problem under an arbitrary order nonlinear model. In the orbital game, if the evader relies only on its own ability to play with the pursuer, then it needs to carry more fuel, and the evasive maneuver will take it out of its original orbit. This would have a significant impact on its original mission, and even if it evades the pursuer, it would be disabled by running out of fuel.

Li and Cruz [17] examined the issue of asset protection as distinct from the pursuit–evasion game. In such a problem, there are the intruder, protector, and asset. They studied three scenarios: the asset fixation scenario, the asset moving in an arbitrary trajectory scenario, and the asset escape scenario. Rusnak [18] likened the target–missile–defender problem to a two-team linear differential game problem, with the target and defender as a team and the missile as a team. It was also pointed out that the game-theory-based guidance law outperformed the conventional guidance law in terms of the miss distance and the sum of maneuvers. In terms of the orbital three-player game, Liu et al. [19] proposed a combined semi-direct method and nonlinear programming approach to determine the strategy and used the NSGA-II algorithm to provide the initial guess. Liu et al. [20] proposed a combination of a particle swarm algorithm and Newton interpolation to solve the orbital defense problem, in which the pursuer and defender had only one maneuver opportunity and the pursuer could not sense the presence of the defender. The study used an impulsive thrust model, which was less applicable in the close-range orbital defense problem. Zhou et al. [21] expressed the pursuer’s evaluation function by a fuzzy algorithm and solved the orbit pursuit–evasion–defense problem under continuous thrust conditions by an indirect method. However, this method did not guarantee a definite miss distance, and the game end time was not accurately obtained by the genetic algorithm. Furthermore, this was an offline algorithm and could not be used in online scenarios. Gutman et al. [22] proposed a pursuer online guidance law enabling the pursuer to avoid the defender while chasing the evader, and the time-to-go was obtained by solving a quartic polynomial equation. The current work was inspired by this to design a conservative guidance law. However, this guidance law may produce many redundant maneuvers throughout the pursuit process and therefore wastes fuel and time, so a radical guidance law was designed to solve this problem. Pursuit-evasion-defense games are the simplest form of multiagent games, and there are also related studies of multiple pursuers chasing a single evader. Xiaoqian Wei [23] investigated the problem of multiple pursuers encircling a single evader, centering on the notion of detection distance to categorize pursuers into trackers and interceptors, where trackers drive the evader into the circle of the interceptor to complete the capture of the evader. Haomiao Huang et al. [24] proposed a pursuer cooperative strategy based on Voronoi can ensure that the capture of the evader is accomplished in a limited space. Most of the previous studies on orbital games considered only the magnitude of the thrust constraint but not directional constraints. Satellites performing orbital maneuvering missions in orbit are more often configured with a three-axis thrust, i.e., three engines operating independently in the orthogonal direction. This thrust configuration has been widely applied in formation flights [25], position holding [26], and spacecraft rendezvous [27]. Ye et al. [28] studied the problem of a pursuer with a three-axis thrust configuration launching a pursuit against an evader with a single-axis thrust configuration and showed that the indirect method did not always yield a solution in this case.

In this paper, we consider the orbital pursuit–evasion–defense game, where the goal of the pursuer is to capture the evader while avoiding interception by the defender, the goal of the evader is to move away from the pursuer, and the goal of the defender is to intercept the pursuer before the evader is captured by the pursuer. Obviously for the pursuer this is a multi-objective mission, chasing down evader and evading defender. There may be a conflict between these two goals, i.e., the importance of the two tasks must be weighed for the pursuer. The main contributions of this paper are as follows: (1) Unlike the traditional multi-objective optimization problem that converts multi-objective into a single-objective optimization problem by weighting them, we design two hierarchical guidance algorithms for the pursuer to deal with the contradiction between objectives. (2) Compared to the model with single-axis thrust in any direction in previous studies, a three-axis orthogonal thrust configuration that is closer to the actual situation is considered in this paper. (3) In order to avoid solving the differential equation two point boundary value problem(TPBVP), this paper proposes an analytical solution to approximate the saddle-point solution by transforming the problem and combining the characteristics of the three-axis thrust to meet the real-time requirements for the calculation of the guidance law.

The remaining parts of this paper are organized as follows. The mathematical model of the orbit pursuit–evasion–defense game is presented in Section 2. The problem solution is simplified by introducing a zero-effort miss. Section 3 focuses on the design of the guidance law in a one-to-one pursuit–evasion scenario. Based on differential game theory, the optimal form of the guidance law for the pursuer and the evader is given, and the solution of the time-to-go of the game is simplified to the solution of quadratic equations and logical judgments by simplifying the dynamics model according to the characteristics of the three-axis thrust configuration. Section 4 introduces two guidance laws that deal with both the evader and the defender. By introducing the concept of a safety function, a conservative guidance law is designed to first make the pursuer escape to a safe state and then launch a pursuit against the evader. Subsequently, a radical guidance law is designed based on the optimal distance curve between the pursuer and the defender, which allows the pursuer to fly over the defender at a closer position to reduce redundant maneuvers and conserve fuel and time. In Section 5, simulation tests of the two proposed pursuer guidance laws are presented, and the characteristics and differences between the two laws are analyzed and discussed. Section 6 summarizes the article.

2. Mathematical Modeling of Spacecraft Pursuit–Evasion–Defense Game

The spacecraft pursuit–evasion–defense game studied in this paper occurs in the final stage of the game, where the relative distance between the spacecraft is small compared to the orbital radius. The geometry is described in Figure 1. In the figure, P, D, and E represent the pursuer, defender, and evader, respectively. A circular orbit virtual satellite near the three spacecraft is chosen, and the center of mass of the satellite is the origin. The geocentric vector of the satellite is the X-axis, the Z-axis points to the orbital plane normal, and the Y-axis is in the orbital plane and points to the forward direction to form a right-handed coordinate system with the other two axes. Since the spacecraft are close together, the Clohessy–Wiltshire equations can be used to describe the relative motion of each spacecraft in this coordinate system:

$$\left\{\begin{array}{c}{\ddot{x}}_i=3{\omega }^2{x}_i+2\omega {\dot{y}}_i+u_x\hfill \\ {\ddot{y}}_i=-2\omega {\dot{x}}_i+u_y\hfill \\ {\ddot{z}}_i=-{\omega }^2{z}_i+u_z\hfill \end{array}\right.,$$

(1)

where the subscripts $i=P,E,D$ represent the pursuer, evader, and defender, respectively.

Define the state vector ${\mathit{X}}_i={\left[x_i,y_i,z_i,{\dot{x}}_i,{\dot{y}}_i,{\dot{z}}_i\right]}^T$. The relative dynamics equations are written in matrix form as follows:

$${\dot{\mathit{X}}}_i=\mathit{A}{\mathit{X}}_i+\mathit{B}{\mathit{U}}_i,$$

(2)

$$\mathit{A}=\left[\begin{array}{cccccc}0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\\ 3{\omega }^2& 0& 0& 0& 2\omega & 0\\ 0& 0& 0& -2\omega & 0& 0\\ 0& 0& -{\omega }^2& 0& 0& 0\end{array}\right],\mathit{B}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right],$$

(3)

$${\mathit{U}}_i={\left[\begin{array}{ccc}{u}_{xi}& u_{yi}& u_{zi}\end{array}\right]}^T,$$

(4)

where $\omega$ represents the orbital angular velocity of the virtual satellite, and $\left[u_{xi}\right.$ ${\left.u_{yi}{u}_{zi}\right]}^T$ denotes the acceleration projection of the spacecraft in the directions of the three axes in the coordinate system. Since a three-axis orthogonal thrust configuration is used in this paper, the control variables satisfy the following constraints:

$$\left\{\begin{array}{c}\left|u_{xi}\right|\le {\rho }_i\\ \left|u_{yi}\right|\le {\rho }_i\\ \left|u_{zi}\right|\le {\rho }_i\end{array}\right.,i=P,E,D,$$

(5)

where ${\rho }_i$ denotes the maximum thrust that can be provided by each spacecraft.

The relative states ${\mathit{X}}_{PE}$ and ${\mathit{X}}_{DP}$ are introduced, which are defined as follows:

$$\begin{array}{cc}\hfill & {\mathit{X}}_{PE}={\mathit{X}}_P-{\mathit{X}}_E,\hfill \\ \hfill & {\mathit{X}}_{DP}={\mathit{X}}_D-{\mathit{X}}_P.\hfill \end{array}$$

(6)

The dynamics equations are obtained as follows:

$$\left\{\begin{array}{c}{\dot{\mathit{X}}}_{PE}=\mathit{A}{\mathit{X}}_{PE}+\mathit{B}{\mathit{U}}_P-\mathit{B}{\mathit{U}}_E\\ {\dot{\mathit{X}}}_{DP}=\mathit{A}{\mathit{X}}_{DP}+\mathit{B}{\mathit{U}}_D-\mathit{B}{\mathit{U}}_P\end{array}\right..$$

(7)

These relative dynamics equations differ from those in [22]. The coordinate system describing the motion process is a non-inertial coordinate system, and thus, the motions along the X- and Y-axes are coupled and related to $\omega$. Therefore, the zero-effort miss is solved for slightly differently:

$$\left\{\begin{array}{c}{\mathit{y}}_{PE}\left(t_f,t\right)=\mathit{D}\mathbf{\Phi }\left(t_f,t\right){\mathit{X}}_{PE}\left(t\right)\\ {\mathit{y}}_{DP}\left(t_f,t\right)=\mathit{D}\mathbf{\Phi }\left(t_f,t\right){\mathit{X}}_{DP}\left(t\right)\end{array}\right.,$$

(8)

$$\mathit{D}=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\end{array}\right].$$

(9)

$\mathbf{\Phi }\left(t_f,t\right)$ is the state transfer matrix for the state transfer from t to $t_f$. The following relationships hold:

$$\left\{\begin{array}{c}\dot{\mathbf{\Phi }}\left(t_f,t\right)=-\mathbf{\Phi }\left(t_f,t\right)\mathit{A}\hfill \\ \mathbf{\Phi }\left(t_f,t_f\right)={\mathit{I}}_{6\times 6}\hfill \end{array}\right..$$

(10)

The value of $\mathbf{\Phi }\left(t_f,t\right)$ is related to $t_f-t$, which is exactly related to the time-to-go. The time-to-go is defined as $\tau =t_f-t$, and $\mathbf{\Phi }\left(t_f,t\right)$ is defined as

$$\mathbf{\Phi }\left(t_f,t\right)=\left[\begin{array}{cc}{\mathbf{\Phi }}_{11}\left(t_f,t\right)& {\mathbf{\Phi }}_{12}\left(t_f,t\right)\\ {\mathbf{\Phi }}_{21}\left(t_f,t\right)& {\mathbf{\Phi }}_{22}\left(t_f,t\right)\end{array}\right],$$

(11)

$$\begin{array}{cc}\hfill & {\mathbf{\Phi }}_{11}\left(t_f,t\right)=\left[\begin{array}{ccc}4-3cos\left(\omega \tau \right)& 0& 0\\ 6(sin(\omega \tau )-\omega \tau )& 1& 0\\ 0& 0& cos\left(\omega \tau \right)\end{array}\right],\hfill \\ \hfill & {\mathbf{\Phi }}_{12}\left(t_f,t\right)=\left[\begin{array}{ccc}\frac{sin\left(\omega \tau \right)}{\omega }& \frac{2\left(1-cos\left(\omega \tau \right)\right)}{\omega }& 0\\ \frac{2(cos(\omega \tau )-1)}{\omega }& \frac{4sin\left(\omega \tau \right)-3\omega \tau }{\omega }& 0\\ 0& 0& \frac{sin\left(\omega \tau \right)}{\omega }\end{array}\right],\hfill \\ \hfill & {\mathbf{\Phi }}_{21}\left(t_f,t\right)=\left[\begin{array}{ccc}3\omega sin\left(\omega \tau \right)& 0& 0\\ 6\omega \left(cos\left(\omega \tau \right)-1\right)& 0& 0\\ 0& 0& -\omega sin\left(\omega \tau \right)\end{array}\right],\hfill \\ \hfill & {\mathbf{\Phi }}_{22}\left(t_f,t\right)=\left[\begin{array}{ccc}cos\left(\omega \tau \right)& 2sin\left(\omega \tau \right)& 0\\ -2sin\left(\omega \tau \right)& 4cos\left(\omega \tau \right)-3& 0\\ 0& 0& cos\left(\omega \tau \right)\end{array}\right].\hfill \end{array}$$

(12)

The zero-effort miss is the relative position vector from the moment t, without any control applied, to the moment $t_f$. From Equation (8), we obtain

$$\left\{\begin{array}{c}{\mathit{y}}_{PE}={\mathbf{\Phi }}_{11}{\mathit{r}}_{PE}+{\mathbf{\Phi }}_{12}{\mathit{v}}_{PE}\\ {\mathit{y}}_{DP}={\mathbf{\Phi }}_{11}{\mathit{r}}_{DP}+{\mathbf{\Phi }}_{12}{\mathit{v}}_{DP}\end{array}\right.,$$

(13)

where ${\mathit{r}}_i$ and ${\mathit{v}}_i$ ($i=PE,DP$) are the relative position and relative velocity, respectively. The derivatives of the equations in Equation (8) are as follows:

$$\left\{\begin{array}{c}{\dot{\mathit{y}}}_{PE}=\mathit{D}\mathbf{\Phi }\mathit{B}{\mathit{U}}_P-\mathit{D}\mathbf{\Phi }\mathit{B}{\mathit{U}}_E\\ {\dot{\mathit{y}}}_{DP}=\mathit{D}\mathbf{\Phi }\mathit{B}{\mathit{U}}_D-\mathit{D}\mathbf{\Phi }\mathit{B}{\mathit{U}}_P\end{array}\right.,$$

(14)

where $\mathit{D}\mathbf{\Phi }\mathit{B}={\mathbf{\Phi }}_{12}$. Thus,

$$\left\{\begin{array}{c}{\dot{\mathit{y}}}_{PE}={\mathbf{\Phi }}_{12}{\mathit{U}}_P-{\mathbf{\Phi }}_{12}{\mathit{U}}_E\hfill \\ {\dot{\mathit{y}}}_{DP}={\mathbf{\Phi }}_{12}{\mathit{U}}_D-{\mathbf{\Phi }}_{12}{\mathit{U}}_P\hfill \end{array}\right..$$

(15)

In the orbital pursuit–evasion–defense game, two one-on-one games are involved, i.e., the game between the pursuer and the evader and the game between the pursuer and the defender. Two quantitative differential game problems can be defined as follows:

Quantitative Differential Game Problem 1: An one-on-one game between the pursuer and the evader. The equation of states is Equation (7). The evaluation function is shown below:

$$J_{PE}=∥{\mathit{y}}_{PE}\left(t_f^{PE}\right)∥.$$

(16)

where $t_f^{PE}$ is the terminal moment of the game between the pursuer and the evader, which will be defined in the subsequent sections. The pursuer wants Equation (16) to be extremely small through its own control, and the evader wants Equation (16) to be extremely large, finally forming the saddle point strategy $\left(U_P^{*},U_E^{*}\right)$. The saddle point strategy satisfies the following relationship:

$$J_{PE}\left(U_P^{*},U_E\right)<J_{PE}\left(U_P^{*},U_E^{*}\right)<J_{PE}\left(U_P,U_E^{*}\right).$$

(17)

Quantitative Differential Game Problem 2: An one-on-one game between the pursuer and the defender. The equation of states is Equation (7). The evaluation function is shown below:

$$J_{DP}=∥{\mathit{y}}_{DP}\left(t_f^{DP}\right)∥.$$

(18)

where $t_f^{DP}$ represents the terminal moment of the game between the pursuer and the defender, which will be defined in the subsequent sections. Equation (18) represents the distance between the pursuer and the defender at the terminal moment. The pursuer wants to make Equation (18) extremely large through its own control, and the defender wants Equation (18) to be extremely small. The saddle point strategy for the quantitative differential game problem 2 satisfies the following relation:

$$J_{DP}\left(U_P,U_D^{*}\right)<J_{DP}\left(U_P^{*},U_D^{*}\right)<J_{DP}\left(U_P^{*},U_D\right).$$

(19)

It is clear that the orbital pursuit–evasion–defense game is difficult to be described and guide the strategy of the pursuer with a single quantitative differential game problem. We define the saddle point strategy of the pursuer in the quantitative differential game problem 1 as $U_{PE}^{*}$ and the saddle point strategy of the pursuer in the quantitative differential game problem 2 as $U_{DP}^{*}$. Since the focus of this paper is to design strategies for the pursuer in the orbital pursuit–evasion–defense game, it is considered that the evader and the defender each play the game with the pursuer individually, and the synergy between the two is reflected in their joint influence on the pursuer. The strategy of the evader is the saddle point strategy $U_E^{*}$ in the quantitative differential game problem 1, and the strategy of the defender is the saddle point strategy $U_D^{*}$ in the quantitative differential game problem 2.

Issues to be addressed in this paper:

(1)

How does the pursuer weigh the two goals of pursuing the evader and evading the defender in the orbital pursuit–evasion–defense game?

(2)

When the pursuer determines the object of the game at this moment, how exactly to design the pursuer’s guidance law.

3. Simple Pursuit–Evasion Problem Guidance Law Design

3.1. Form of Optimal Guidance Law

In the pursuit–evasion problem, the purpose of the pursuer is to minimize the terminal moment distance by its own control, while the purpose of the evader is to maximize the terminal moment distance by its own control. First, an ending time $t_f^{PE}$ is prescribed. Therefore, the evaluation function is Equation (16). Both sides of the pursuer and evader will compete around this evaluation function. The pursuer wants to minimize this evaluation function while the evader tries to maximize it. Differentiating $J_{PE}$ with respect to t yields

$$\frac{d}{dt}{J}_{PE}=\frac{d}{dt}∥{\mathit{y}}_{PE}∥=\frac{{\mathit{y}}_{PE}^T}{∥{\mathit{y}}_{PE}∥}{\dot{\mathit{y}}}_{PE}={\mathit{\xi }}_{PE}^T\left({\mathbf{\Phi }}_{12}{\mathit{U}}_P-{\mathbf{\Phi }}_{12}{\mathit{U}}_E\right),$$

(20)

where ${\mathit{\xi }}_{PE}=\frac{{\mathit{y}}_{PE}}{∥{\mathit{y}}_{PE}∥}$. The pursuer wants Equation (16) to take the minimum at time $t_f^{PE}$, while the evader wants Equation (16) to take the maximum at time $t_f^{PE}$. Since the time of the whole game is determined, the pursuer wants Equation (16) to fall at the fastest rate while the evader wants Equation (16) to rise at the fastest rate. Thus, the optimal control strategy satisfies the following equation:

$$\left\{\begin{array}{c}{\mathit{U}}_P^{*}=argmin\frac{d}{dt}{J}_{PE}\hfill \\ {\mathit{U}}_E^{*}=argmax\frac{d}{dt}{J}_{PE}\hfill \end{array}\right..$$

(21)

The constraints of the three-axis thrust configuration are taken into account. Thus, the optimal control takes the following form:

$$\left\{\begin{array}{c}{\mathit{U}}_P^{*}=-{\rho }_{P}sign\left({\mathbf{\Phi }}_{12}^T{\mathit{\xi }}_{PE}\right)\hfill \\ {\mathit{U}}_E^{*}=-{\rho }_{E}sign\left({\mathbf{\Phi }}_{12}^T{\mathit{\xi }}_{PE}\right)\hfill \end{array}\right..$$

(22)

Performing a sign operation on a vector here means performing a sign operation on each element of the vector separately. Bilateral optimal control is the saddle point solution, which satisfies $J_{PE}\left({\mathit{U}}_P^{*},{\mathit{U}}_E\right)\le J_{PE}\left({\mathit{U}}_P^{*},{\mathit{U}}_E^{*}\right)\le J_{PE}\left({\mathit{U}}_P,{\mathit{U}}_E^{*}\right)$.

3.2. Solving for Time-to-Go

Since the form of the optimal strategy has been obtained in Equation (22), it is still necessary to solve for the time-to-go to obtain the final control strategy. By substituting Equation (22) into Equation (20), we can obtain the rate of change of the evaluation function for the optimal control:

$$\frac{d}{dt}{J}_{PE}=-\left({\rho }_P-{\rho }_E\right){∥{\mathbf{\Phi }}_{12}^T{\mathit{\xi }}_{PE}∥}_1.$$

(23)

The ${\parallel •\parallel }_1$ represents the first order norm.

To facilitate this study, we define the variable $\theta =\omega \tau$, where $\tau$ is the time-to-go. Because $\frac{d\theta }{dt}=-\omega$, Equation (23) can be rewritten as follows:

$$\frac{d{J}_{PE}}{d\theta }=\frac{{\rho }_P-{\rho }_E}{\omega }{∥{\mathbf{\Phi }}_{12}^T{\mathit{\xi }}_{PE}∥}_1.$$

(24)

Let ${\theta }^{*}=\omega \ast t_f$ and $\Delta \rho ={\rho }_P-{\rho }_E$. Then, the evaluation function at the initial moment is $J_{PE}\left({\theta }^{*}\right)$. The relative distance at the terminal moment is obtained by integrating Equation (24):

$$J_{PE}\left(0\right)=J_{PE}\left({\theta }^{*}\right)-\frac{\Delta \rho }{\omega }{\int }_0^{{\theta }^{*}}{∥{\mathbf{\Phi }}_{12}^T\left(s\right){\mathit{\xi }}_{PE}\left(s\right)∥}_{1}ds.$$

(25)

It is worth noting that in the case where the state of the pursuer and the evader are determined at the initial moment and the maximum maneuvering capacity of the pursuer and the evader and the rotational angular velocity of the coordinate system are fixed, $J_{PE}\left(0\right)$ is only a function of ${\theta }^{*}$. Therefore, the function is defined as follows:

$$f\left({\theta }^{*}\mid X_P\left(0\right),X_E\left(0\right),{\rho }_P,{\rho }_E,\omega \right)=f\left({\theta }^{*}\right)=J_{PE}\left({\theta }^{*}\right)-\frac{\Delta \rho }{\omega }{\int }_0^{{\theta }^{*}}{∥{\mathbf{\Phi }}_{12}^T\left(s\right){\mathit{\xi }}_{PE}\left(s\right)∥}_{1}ds.$$

(26)

The limits of $f\left({\theta }^{*}\right)$ are

$$\begin{array}{c}\underset{{\theta }^{*}\to 0}{\lim }f\left({\theta }^{*}\right)=J_{PE}\left(0\right)=∥{\mathit{r}}_{PE}\left(0\right)∥>0,\hfill \\ \underset{{\theta }^{*}\to \infty }{\lim }f\left({\theta }^{*}\right)=-\infty <0.\hfill \end{array}$$

(27)

Thus, in the case where ${\rho }_P$ is greater than ${\rho }_E$, it is always possible to find a $\widehat{\theta }$ such that $f\left(\widehat{\theta }\right)=0$. This means that the strategy ensures a guaranteed miss-distance. Selecting the proper $t_f$ always ensures that the final miss-distance is zero. Thus, the entire game changes from fighting for the last distance to fighting for the end moment of the game. That means $t_f\left({\mathit{U}}_P^{*},{\mathit{U}}_E\right)\le t_f\left({\mathit{U}}_P^{*},{\mathit{U}}_E^{*}\right)\le t_f\left({\mathit{U}}_P,{\mathit{U}}_E^{*}\right)$. That is, if the pursuing party deviates from the optimal control, the game end moment will be lagged; if the evader party deviates from the optimal control, the game end moment will be advanced.

Solving for the roots of the equation $f\left({\theta }^{*}\right)=0$ yields a time-to-go that ensures the guaranteed miss-distance. However, Equation (26) is a nonlinear equation containing an integral term, and it is difficult to find its analytical solution. Thus, we need to try a numerical solution method.

First, we present an approach that takes a long time to calculate but finds the solution exactly. Let ${\theta }^{*}$ start from 0 and increase in a very small step $d\theta$ until $f\left(\theta \right)$ is less than 0. Then, a more exact solution is obtained by the dichotomy. By this method, it is also guaranteed that we obtain the first positive root of Equation (26). This is exactly the answer we expect.

However, the small-step search method will make the solution time quite long, which cannot meet the real-time requirements. Therefore, the results obtained by this method are only used for reference, and we propose an approximate fast-solving method below.

Considering that the orbital angular rate of the satellite is small, the following relationship is obtained:

$$\left\{\begin{array}{c}\underset{\omega \to 0}{\lim }{\mathbf{\Phi }}_{11}=\left[\begin{array}{ccc}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & 1\hfill & 0\hfill \\ 0\hfill & 0\hfill & 1\hfill \end{array}\right]\hfill \\ \underset{\omega \to 0}{\lim }{\mathbf{\Phi }}_{12}=\left[\begin{array}{ccc}\tau \hfill & 0\hfill & 0\hfill \\ 0\hfill & \tau \hfill & 0\hfill \\ 0\hfill & 0\hfill & \tau \hfill \end{array}\right]\hfill \end{array}\right..$$

(28)

Equation (28) is substituted into Equation (22), yielding

$$\left\{\begin{array}{c}{\mathit{U}}_P^{*}=-{\rho }_{P}sign\left({\mathbf{\Phi }}_{12}^T{\mathit{\xi }}_{PE}\right)=-{\rho }_{P}sign\left(\tau {\mathit{\xi }}_{PE}\right)\hfill \\ =-{\rho }_{P}sign\left({\mathit{y}}_{PE}\right)\hfill \\ {\mathit{U}}_E^{*}=-{\rho }_{E}sign\left({\mathbf{\Phi }}_{12}^T{\mathit{\xi }}_{PE}\right)=-{\rho }_{E}sign\left(\tau {\mathit{\xi }}_{PE}\right)\hfill \\ =-{\rho }_{E}sign\left({\mathit{y}}_{PE}\right)\hfill \end{array}\right..$$

(29)

The derivative of the zero-effort miss (ZEM) can be obtained by substituting Equation (29) into Equation (15):

$${\dot{\mathit{y}}}_{PE}={\mathbf{\Phi }}_{12}{\mathit{U}}_P^{*}-{\mathbf{\Phi }}_{12}{\mathit{U}}_E^{*}=-\tau \left({\rho }_P-{\rho }_E\right)sign\left({\mathit{y}}_{PE}\right).$$

(30)

From Equation (30), it can be seen that the absolute values of each component of the ZEM converge to zero at the same rate, as shown in Figure 2. This is a different phenomenon from that in the uniaxial thrust case. Therefore, when solving for the time for the ZEM to converge to zero under optimal control, it is only necessary to focus on the component of the ZEM with the largest absolute value. However, the ZEM contains the variable time-to-go we require, and at the beginning of the solution we do not know exactly which component of the ZEM is the largest in absolute value. Thus, we first have to use the hypothesis method, assuming that the absolute value of each component of the ZEM on each axis is likely to be the largest, and then we use the exclusion method to find the final result. By substituting Equation (28) into Equation (13), we obtain an expression of the ZEM containing the time-to-go:

$${\mathit{y}}_{PE}={\mathit{r}}_{PE}+\tau {\mathit{v}}_{PE}.$$

(31)

Since the absolute values of the components on each axis of the ZEM change at the same rate, the following equation is applicable:

$$\left|{\mathit{r}}_{PE,i}+t_{f,i}{\mathit{v}}_{PE,i}\right|-{\int }_0^{t_{f,i}}\tau \left[{\rho }_P-{\rho }_E\right]d\tau =0.$$

(32)

Furthermore,

$$\left|{\mathit{r}}_{PE,i}+t_{f,i}{\mathit{v}}_{PE,i}\right|=\frac{1}{2}{t}_{f,i}^2\left({\rho }_P-{\rho }_E\right),$$

(33)

where $i=x,y,z$ are the components of the ZEM. Removing the absolute value sign yields two quadratic equations and up to four solutions of the resolution:

$$\left\{\begin{array}{c}{r}_{PE,i}+t_{f,i}{v}_{PE,i}=\frac{1}{2}\left({\rho }_P-{\rho }_E\right)t_{f,i}^2,\mathrm{if}\left(r_{PE,i}+t_{f,i}{v}_{PE,i}>0\right)\hfill \\ -r_{PE,i}-t_{f,i}{v}_{PE,i}=\frac{1}{2}\left({\rho }_P-{\rho }_E\right)t_{f,i}^2,\mathrm{if}\left(r_{PE,i}+t_{f,i}{v}_{PE,i}<0\right)\hfill \end{array}\right..$$

(34)

Equation (34) can be solved analytically and subsequently judged to be reasonable based on the positive or negative value of ${\mathit{r}}_{PE,i}+t_{f,i}{\mathit{v}}_{PE,i}$. The obtained ${\mathit{T}}_{0f,i}$ corresponds to the time it takes for the components to converge to zero on that axis. ${\mathit{T}}_{0f,i}$ is a set that may have more than one element. However, the convergence of this axis to zero does not mean that the other two axes have also converged to zero, and so a comparison with the other two axes is needed to determine if this solution is the time that allows the entire ZEM to converge to zero. The X-axis is selected as an example. The final candidate solution ${\mathit{T}}_{1f,x}$ is

$$\begin{array}{c}\hfill {\mathit{T}}_{1f,x}=\left\{t_f\in {\mathit{T}}_{0f,x}:\left|{\mathit{r}}_{PE,x}+t_f{\mathit{v}}_{PE,x}\right|=\right.\\ \hfill \left.max\left(\left|{\mathit{r}}_{PE,i}+t_f{\mathit{v}}_{PE,i}\right|\right),i=x,y,z\right\}.\end{array}$$

(35)

In this way, the candidate solutions ${\mathit{T}}_{1f,x}$, ${\mathit{T}}_{1f,y}$, and ${\mathit{T}}_{1f,z}$ for each of the three axes were calculated. Considering the physical nature of the orbit pursuit–evasion game, the entire game process ends when the evader is captured for the first time. Thus, the final solution is

$$t_f=\min \left\{{\mathit{T}}_{1f,x}\cup {\mathit{T}}_{1f,y}\cup {\mathit{T}}_{1f,z}\right\}.$$

(36)

The final optimal control policy is obtained by substituting the obtained $t_f$ into Equation (22). The closed-loop guidance can be achieved by calculating $t_f$ at each step of the game process. The entire process of solving for $t_f$ involves only simple quadratic equations and logical judgments, thus satisfying the real-time requirement.

It was mentioned in [15] that in the case of a single-axis thrust configuration, the control rate does not chatter. However, in the three-axis thrust configuration, the remaining two components converge to zero first before the last component of the ZEM converges to zero. This causes the control rate in those two directions to chatter. When both the pursuer and the evader adopt the saddle point strategy, the computed time-to-go decreases linearly in real time. This conclusion is the same as that in [15] and will not be repeated here.

The entire solution process is simplified by ignoring the small-angle rotation of the coordinate system. Therefore, it is necessary to analyze the magnitude of the error caused by this method. For demonstration purposes, we assume that the initial relative velocities of the pursuer and evader are zero and that they are in the same orbital plane. The initial relative positions on the X- and Y-axes were taken to be in the range of $-10,000$ to $10,000$ m. The error distribution was analyzed by the fast calculation method and the exact small-step search method mentioned above. Figure 3 and Figure 4 show the relative errors of the time-to-go calculated by the fast algorithm in high- and low-orbit conditions, respectively. The geocentric distance is 42,878.165 km under high-orbit conditions and 6878.165 km under low-orbit conditions. It can be seen that the distributions of both were roughly similar, and the method performed better close to the axis and worse far from it. The error distribution was not symmetric about the X- and Y-axes, which was caused by the rotation of the reference coordinate system. The performance was better under the high-orbit conditions, where the maximum relative error did not exceed 1%, but the maximum relative error in the low-orbit condition was roughly 18%. This indicated that the fast calculation method can only handle the low-orbit close-range game problem and the high-orbit game problem.

4. Pursuit–Evasion–Defense Problem Guidance Law Design

The pursuit–evasion–defense problem is different from the simple pursuit–evasion problem in that there is a role of the defender. Thus, the pursuer in the pursuit at the same time needs to consider the avoidance of the defender. There may be a contradiction between these two purposes, and the pursuit–evasion–defense problem in the pursuer guidance law design need to considers the trade-off between these two purposes, which is complex.

The game between the pursuer and the defender is now analyzed, and the evaluation function is as follows:

$$J_{DP}=∥{\mathit{y}}_{DP}\left(t_f\right)∥.$$

(37)

In the same way as the analysis of the pursuit–evasion problem, the optimal strategy for the pursuer and the defender is

$$\left\{\begin{array}{c}{\mathit{U}}_P^{*}=-{\rho }_{P}sign\left({\mathbf{\Phi }}_{12}^T\mathit{\xi }\right)\hfill \\ {\mathit{U}}_D^{*}=-{\rho }_{D}sign\left({\mathbf{\Phi }}_{12}^T\mathit{\xi }\right)\hfill \end{array}\right..$$

(38)

Substituting the optimal control of the pursuer and defender into the derivative of the evaluation function yields:

$$\frac{d{J}_{DP}}{d\theta }=\frac{{\rho }_D-{\rho }_P}{\omega }{∥{\mathbf{\Phi }}_{12}^T{\mathit{\xi }}_{DP}∥}_1.$$

(39)

This leads to

$$J_{DP}\left(0\right)=J_{DP}\left({\theta }^{*}\right)-\frac{\Delta \rho }{\omega }{\int }_0^{{\theta }^{*}}{∥{\mathbf{\Phi }}_{12}^T\left(s\right){\mathit{\xi }}_{DP}\left(s\right)∥}_{1}ds.$$

(40)

Equation (40) is the relative distance between the pursuer and the defender at the end moments under the action of optimal control in the case of a determined game time $t_f=\frac{{\theta }^{*}}{\omega }$. Let

$$f\left({\theta }^{*}\right)=J_{DP}\left({\theta }^{*}\right)-\frac{\Delta \rho }{\omega }{\int }_0^{{\theta }^{*}}{∥{\mathbf{\Phi }}_{12}^T\left(s\right){\mathit{\xi }}_{DP}\left(s\right)∥}_{1}ds.$$

(41)

Considering that the pursuer has a stronger maneuvering ability than the defender, it is different from the game between the pursuer and the evader. The derivative of $f\left({\theta }^{*}\right)$ at ${\theta }^{*}=0$ is as follows:

$$\begin{array}{c}\underset{{\theta }^{*}\to 0}{\lim }\dot{f}\left({\theta }^{*}\right)={\left.\frac{d}{d{\theta }^{*}}{J}_{DP}\left({\theta }^{*}\right)\right|}_{{\theta }^{*}=0}=\frac{{\mathit{y}}_{DP}^T}{∥{\mathit{y}}_{DP}∥}\frac{d}{d{\theta }^{*}}{\mathit{y}}_{DP}\hfill \\ =\frac{{\mathit{r}}_{DP}^T}{∥{\mathit{r}}_{DP}^T∥}·\frac{{\mathit{v}}_{DP}}{\omega }.\hfill \end{array}$$

(42)

According to the analysis, the $f\left({\theta }^{*}\right)$ curve changes with ${\theta }^{*}$ in two cases. From Figure 5, it can be seen that $f\left({\theta }^{*}\right)$ increases with increasing ${\theta }^{*}$ in case 1, and in case 2, $f\left({\theta }^{*}\right)$ decreases and then increases with increasing ${\theta }^{*}$, and there is one minimal value point. A detailed analysis of case 2 is given in [22]. Equation (42) shows that whether the true curve is that of case 1 or 2 depends only on the angle between the initial relative position and the initial relative velocity. If the angle is an acute angle, then the curve is like that of case 1; otherwise, it is like that of case 2.

In case 1, when the pursuer adopts the optimal strategy, the pursuer will never be captured as long as the relative distance at the initial moment is greater than the capture radius of the defender, and in case 2, when the pursuer and the defender adopt the optimal strategy, there exists a minimum distance q, as shown in Figure 6. Let the moment when the minimum distance appears be $t_f^{DP}$. Then, ${\theta }_{fDP}=\omega t_f^{DP}$. Finally, the optimal strategy of the defender is also obtained.

4.1. Conservative Guidance Law

Let the optimal control be ${\mathit{U}}_{DP}^{*}$ when the pursuer is playing with the defender, and let the optimal strategy be ${\mathit{U}}_{PE}^{*}$ when the pursuer is playing with the evader. The pursuer has to finish evading the defender while pursuing the evader. The best case is ${\mathit{U}}_{DP}^{*}={\mathit{U}}_{PE}^{*}$, which means evading the defender while pursuing the evader at the same time. The worst case is ${\mathit{U}}_{DP}^{*}=-{\mathit{U}}_{PE}^{*}$, which means that the evader is being pursued while the defender is approaching the pursuer at the fastest speed. Inspired by previous work [22], we consider the worst case scenario when the pursuer plays with the defender:

$${\mathit{U}}_P={\mathit{U}}_{PE}^{*}=-{\mathit{U}}_{DP}^{*},$$

(43)

$$\left\{\begin{array}{c}{\mathit{U}}_P={\rho }_{P}sign\left({\mathbf{\Phi }}_{12}^T\mathit{\xi }\right)\hfill \\ {\mathit{U}}_D=-{\rho }_{D}sign\left({\mathbf{\Phi }}_{12}^T\mathit{\xi }\right)\hfill \end{array}\right..$$

(44)

Substituting in the derivative of the evaluation function yields

$$\frac{d{J}_{DP}}{d\theta }=\frac{{\rho }_D+{\rho }_P}{\omega }{∥{\mathbf{\Phi }}_{12}^T{\mathit{\xi }}_{PE}∥}_1.$$

(45)

The modal length of the zero-effort miss at the terminal moment when the game time is $t_f=\frac{{\theta }^{*}}{\omega }$ can be calculated as follows:

$$J_{DP}\left(0\right)=J_{DP}\left({\theta }^{*}\right)-\frac{{\rho }_D+{\rho }_P}{\omega }{\int }_0^{{\theta }^{*}}{∥{\mathbf{\Phi }}_{12}^T\left(s\right){\mathit{\xi }}_{PE}\left(s\right)∥}_{1}ds.$$

(46)

Let $J\left(0\right)=m$, where m is the capture radius of the defender. A lower bound for the modal length of the zero-effort miss can be obtained:

$$L\left(\theta \right)=m+\frac{{\rho }_D+{\rho }_P}{\omega }{\int }_0^{\theta }{∥{\mathbf{\Phi }}_{12}^T\left(s\right){\mathit{\xi }}_{PE}\left(s\right)∥}_{1}ds,$$

(47)

where $\theta \in \left(0,{\theta }^{*}\right)$. The implication of this lower bound is that when $∥\mathit{y}\left(\theta \right)∥\ge L\left(\theta \right)$, even if the pursuer takes the worst control, it can ensure that $J_{DP}\left(0\right)>m$ at $\theta =0$ so that it will not be intercepted by the defender. Define the function $L\left(\theta \right)$ as a safety function, as shown in Figure 7. Therefore, the design idea of the pursuer’s guidance law is to first adopt strategy $U_{DP}^{*}$ to play with the defender and then switch to strategy $U_{PE}^{*}$ to play with the evader at the safety limit. In this way, the defender can be overcome even in the worst case scenario. That is, the strategy of the pursuer is

$${\mathit{U}}_{PCGL}^{*}=\left\{\begin{array}{c}{\mathit{U}}_{DP}^{*},\parallel \mathit{y}\left(\theta \right)\parallel <L\left(\theta \right)\hfill \\ {\mathit{U}}_{PE}^{*},\parallel \mathit{y}\left(\theta \right)\parallel \ge L\left(\theta \right)\hfill \end{array}\right..$$

(48)

4.2. Radical Guidance Law

The conservative guidance law (CGL) first evades the defender and switches to pursuing the evader when $∥\mathit{y}\left(\theta \right)∥\ge L\left(\theta \right)$. In the worst case, ${\mathit{U}}_{PE}^{*}=-{\mathit{U}}_{DP}^{*}$, the pursuer will fly over the defender at a distance of m, and when ${\mathit{U}}_{PE}^{*}\ne -{\mathit{U}}_{DP}^{*}$, the pursuer will brush the defender at a distance of $l(l>m)$, as shown in Figure 8. Since the vast majority of cases belong to the latter case, the pursuer may brush against the defender at a distance much greater than m. Therefore, it can be assumed that the pursuer undergoes many redundant maneuvers, resulting in a waste of time and fuel, and to solve this problem, a second guidance law is designed. We call this the radical guidance law (RGL).

For the game between the pursuer and the defender, Figure 5 shows the curves for the optimal strategy adopted by both the pursuer and the defender. When the pursuer deviated from the optimal control, the curves changed as shown in Figure 9. Case 1 will gradually shift to case 2, and the minimum value in case 2 will continue moving down. In fact, case 2 is the only case that requires the attention of the pursuer. Recall that Equation (41) specifies the relative distance at the terminal moment as a function of the terminal moment when both the pursuer and the defender adopt the optimal strategy. This means that as long as the minimum value q of Equation (41) is greater than m, the pursuer can escape by adopting the optimal strategy. Therefore, the pursuer can ignore the defender to start the pursuit of the evader. When the value of q keeps moving down to be tangent to m, the pursuer takes the optimal strategy to avoid the defender, and it can be guaranteed to escape at a distance of m from the defender. The expression of the radical guidance law is as follows:

$$U_{PRGL}^{*}=\left\{\begin{array}{c}{U}_{PE}^{*},(q>m)\parallel \left({\left.\left(df/d{\theta }^{*}\right)\right|}_{{\theta }^{*}=0}>0\right)\hfill \\ U_{DP}^{*},q=m\hfill \end{array}\right..$$

(49)

The method of calculating q in real time for each step has been mentioned in [15] and will not be repeated here.

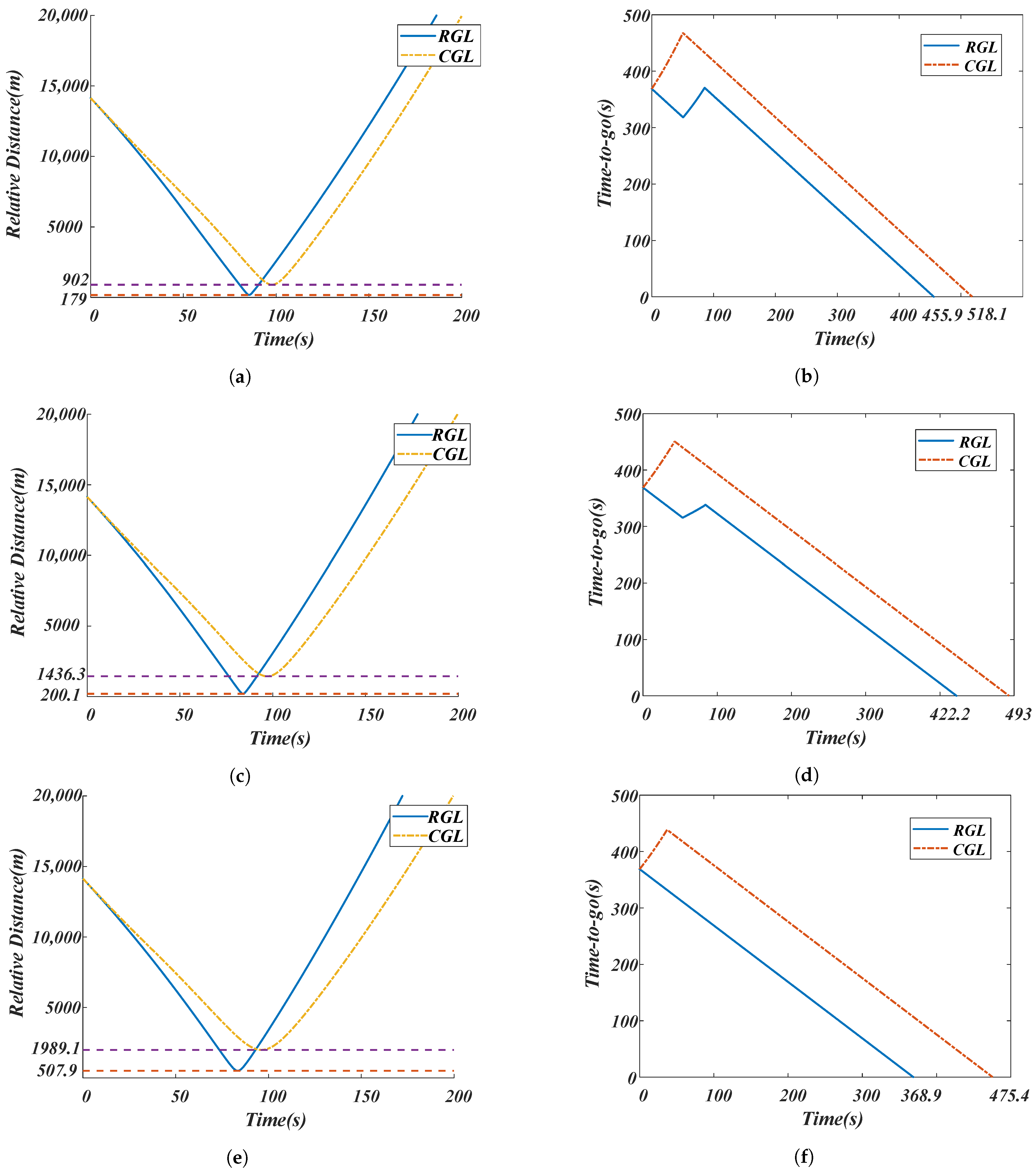
5. Simulations and Discussions

In this section, we discuss the proposed two guidance laws for the pursuer through numerical simulations. Since many high-value space assets are in synchronous orbits, the gaming scenario was set to high-orbit conditions. The orbital radius of the virtual satellite was $r=42,378.165\mathrm{km}$, and the pursuer, evader, and defender were in its vicinity. The initial state was as follows:

$$\left\{\begin{array}{c}{x}_P={(0,0,20,000,0,0,0)}^T\hfill \\ x_E={(12,000,16,000,0,0,0,0)}^T\hfill \\ x_D={(6000,8000,10000,-60,-80,100)}^T\hfill \end{array}\right..$$

(50)

The maximum thrust acceleration that can be generated on a single axis of the pursuer, evader, and defender were ${\rho }_P=0.392\mathrm{m}/{\mathrm{s}}^2$, ${\rho }_E=0.098\mathrm{m}/{\mathrm{s}}^2$, and ${\rho }_D=0.196\mathrm{m}/{\mathrm{s}}^2$, respectively. The orbital angular rate $\omega$ of the virtual satellite was $7.272\times {10}^{-5}\mathrm{rad}/\mathrm{s}$.

For all the examples, the capture radius of the defender was set to 100 m, while the pursuer was required to overlap exactly with the evader. The simulation step size was set to $0.1$ s. Considering the accuracy of the numerical calculation, a redundant distance $\delta m=100$ m was added to the defender’s capture radius. When q in Equation (49) was less than $m+\delta m$, the pursuer started playing with the defender.

The first example was a test of both the CGL and RGL assuming that the pursuer, defender, and evader all used the optimal strategy. It can be seen in Figure 10 that both guidance laws successfully bypassed the defender and completed the interception of the evader. The CGL and RGL bypassed the defender at distances of 902 and 179 m, respectively. From Figure 10e,f, we can see that the CGL had one policy switching point and the RGL had two policy switching points. The times for the two guidance laws to complete the game were $518.1$ and $455.9$ s, respectively. The RGL achieved an earlier interception of the evader by flying over the defender at a closer distance. Both guidance laws delayed the interception of the evader due to the interference of the defender, but the RGL saved $62.2$ s.

The next example is the case where the defender deviated from optimal control (which is more common in real-world problems). We assumed that the defender could only provide half of the thrust. From Figure 11c, it can be seen that despite the defender’s deviation from the optimal control, the pursuer still played with it in the most conservative way. Thus, bypassing of the defender, at $1436.3$ m, occurred at a greater distance than that in example 1. In the current example, the RGL saved 70.8 s, which was more than that in example 1.

Finally, we assumed that the defender failed completely, i.e., ${\mathit{U}}_D={\theta }_{3\times 1}$. From Figure 12c,e, it can be seen that the CGL chose to maneuver to a safe state first, even in the case of defender failure, which reflected the conservative nature of the CGL. From Figure 12f, it can be seen that the RGL ignored the defender throughout and only played with the evader, reflecting its characteristic of playing with the defender only when necessary, thus saving 106.5 s compared to the CGL.

Based on several sets of simulation experiments, the RGL reduced the interception times compared to those of the CGL. Because the RGL adopted an aggressive approach in avoiding the defender to play with it only when necessary, there were fewer redundant actions in avoidance. As can be seen in Figure 13, the more severely the defender’s strategy deviated from the optimal strategy, the greater the advantage gained by the RGL was.

6. Conclusions

In this paper, we studied the problem of designing guidance laws to complete the pursuit of an evader in the presence of a defender. Two guidance laws were designed for the pursuer considering a three-axis orthogonal thrust configuration model that was consistent with real scenarios. The conservative guidance law was designed by using the safety function allowed the pursuer to first play with the defender to reach the safety region and then switch its strategy to play with the evader. The radical guidance law used the optimal distance profile of the pursuer and defender game to predict the minimum distance to the defender and played with the defender only when necessary, and it played with the evader most of the time to reduce redundant actions and lower fuel consumption. The solution of the time-to-go of the game was simplified by using the characteristics of the three-axis thrust configuration to avoid the time-consuming numerical solution process. The simulations showed that both designed guidance laws enabled the pursuer to complete the evasion of the defender and the capture of the evader at the same time. The radical guidance law saved more time than the conservative law, and in some cases, the radical law allowed the pursuer to completely ignore the defender, while the conservative law still required the pursuer to move to a safe area and waste fuel. In this study, the defender and the evader accomplished their tasks without good coordination, thus actually reducing the difficulty of the pursuer to accomplish its task. Subsequent research work will design a more reasonable cooperative defense strategy for the defender and the evader and analyze the respective winning conditions of the attacker and defender under such conditions.