E-Sail Optimal Trajectories to Heliostationary Points

Abstract

The aim of this paper is to investigate the performance of a robotic spacecraft, whose primary propulsion system is an electric solar wind sail (E-sail), in a mission to a heliostationary point (HP)—that is, a static equilibrium point in a heliocentric and inertial reference frame. A spacecraft placed at a given HP with zero inertial velocity maintains that heliocentric position provided the on-board thrust is able to counterbalance the Sun’s gravitational force. Due to the finite amount of storable propellant mass, a prolonged mission toward an HP may be considered as a typical application of a propellantless propulsion system. In this respect, previous research has been concentrated on the capability of high-performance (photonic) solar sails to reach and maintain such a static equilibrium condition. However, in the case of a solar-sail-based spacecraft, an HP mission requires a sail design with propulsive characteristics that are well beyond the capability of current or near-future technology. This paper shows that a medium-performance E-sail is able to offer a viable alternative to the use of photonic solar sails. To that end, we discuss a typical HP mission from an optimal viewpoint, by looking for the minimum time trajectory necessary for a spacecraft to reach a given HP. In particular, both two- and three-dimensional scenarios are considered, and the time-optimal mission performance is analyzed parametrically as a function of the HP heliocentric position. The paper also illustrates a potential mission application involving the observation of the Sun’s poles from such a static inertial position.

1. Introduction

A heliostationary point (HP) is a static equilibrium point in an inertial (heliostationary) reference frame and is characterized by a single design parameter—its distance from the Sun. In this sense, an HP is a type of application of Robert Forward’s “statite” concept [1], originally proposed to operate a spacecraft in near-Earth space for scientific observation and telecommunication purposes [2,3], extended to the more general case of a heliocentric mission case.

An HP is initially reached by steering the propulsive acceleration vector so that the spacecraft inertial velocity goes to zero at that particular point [4] and is then maintained there by balancing the Sun’s gravitational pull with the aid of a continuous-thrust system [5]. For this reason, a prolonged robotic mission toward an HP may be seen as a natural application of a propellantless propulsion system and, indeed, the scientific literature reports elegant studies involving photonic solar sails, starting from the pioneering works by Forward [1] and McInnes et al. [6].

It is known, however, that the maintenance of an HP requires a very high-performance solar sail [7,8]—that is, a sail with a reference propulsive acceleration well beyond the current or near-future technology [9,10]. The need for a high-performance solar sail is due to the fact that the solar radiation pressure, which is responsible for the sail thrust, varies with the solar distance in the same manner as the Sun’s gravitational acceleration.

As a result, an HP can only be maintained provided that the solar sail has a lightness number, defined as the ratio of the maximum sail-induced thrust to the local Sun’s gravitational pull, equal to one. In other terms, when the Sun–HP distance is one astronomical unit, a solar sail with no degradation [11] must be able to produce a propulsive acceleration slightly below $6\mathrm{mm}/{\mathrm{s}}^2$. To give an idea on how large this value is, the design of the CubeSat solar sail used in the NASA’s Near-Earth Asteroid Scout mission (which is currently considered as lost after its deployment failure in mid November 2022) had a lightness number of $0.0106$, while NASA’s Solar Cruiser, to be launched in 2025, will have a lightness number of about $0.0287$ [12].

Fortunately enough, there exist other propellantless thruster concepts that do not employ the solar radiation pressure for producing a propulsive acceleration [13,14] and which allow an HP to be reached and maintained for a theoretically indefinite time interval by means of a medium-performance propulsion system. This is the case of the electric solar wind sail (E-sail) [15], an innovative propulsion concept proposed by Pekka Janhunen [16] in 2004, which converts the momentum from the solar wind charged particles into deep space thrust [17] through a grid of long charged tethers [18].

In a typical design, the thrust magnitude and the attitude of the reference plane of a spin-stabilized E-sail can be controlled by suitably varying the electric voltage of each tether [19,20]. According to the latest E-sail thrust model [21], the maximum propulsive acceleration magnitude varies with the inverse spacecraft distance from the Sun, so that an HP with a solar distance greater than one astronomical unit can be theoretically maintained with a sail lightness number below one.

The aim of this paper is to investigate the E-sail performance in a representative HP mission from an optimal viewpoint. In particular, both two- and three-dimensional mission scenarios are studied to analyze the minimum-time transfer of an E-sail-based spacecraft toward a given HP as a function of its position in a heliocentric reference frame. The paper also discusses a set of mission applications that involve observation of the Sun’s poles from a static inertial position. The proposed analysis allows the minimum flight time to be obtained in a parametric way as a function of the mission design parameters. In this sense, the numerical results presented in this paper extend the recent study of Ref. [22], which only focuses on the stability and control problem of an E-sail already placed at a prescribed HP.

The remainder of the paper is organized as follows. Section 2 describes the HP mission and introduces the mathematical model, including a brief discussion on the approach used in the trajectory optimization. Section 3 shows the numerical results obtained in a set of E-sail-based missions, with a focus on the special case of equilibrium points that are useful for the scientific observation of the Sun’s poles. Finally, the last section contains our concluding remarks.

2. Mission Description and Mathematical Problem Statement

Consider a spacecraft that initially (time $t=t_0\triangleq 0$) traces a heliocentric circular orbit in the ecliptic plane. Let $r_{\oplus }\triangleq 1\mathrm{au}$ be the orbital radius and introduce a spherical reference frame $\mathcal{T}(O;r,\theta ,\varphi )$ with its origin O coinciding with the Sun’s center-of-mass, where r is the Sun–spacecraft distance, $\theta$ is the ecliptic longitude, and $\varphi$ is the ecliptic latitude; see Figure 1. In the same figure, ${\widehat{\mathit{i}}}_r$ is the radial unit vector, ${\widehat{\mathit{i}}}_{\theta }$ is the trasverse unit vector, and ${\widehat{\mathit{i}}}_{\varphi }$ is the azimuthal unit vector.

The ecliptic longitude $\theta$ is measured, in the ecliptic plane counterclockwise from the x-axis of a heliocentric-ecliptic [23] reference frame ${\mathcal{T}}_S(O;x,y,z)$, while the ecliptic latitude $\varphi$ gives the inclination of the Sun–spacecraft line relative to the $(x,y)$ plane—that is, the ecliptic; see Figure 1. The initial condition describes a simplified Earth’s heliocentric trajectory, whose orbital eccentricity is neglected, and a spacecraft that leaves the Earth’s sphere of influence with zero hyperbolic excess velocity relative to the starting planet.

The primary propulsion system of the spacecraft is an E-sail that, according to the latest thrust model [21], gives a propulsive acceleration vector

$$\mathit{a}=\tau \frac{a_c}{2}\left(\frac{r_{\oplus }}{r}\right)\left[{\widehat{\mathit{i}}}_r+\left(\widehat{\mathit{n}}·{\widehat{\mathit{i}}}_r\right)\widehat{\mathit{n}}\right]$$

(1)

where $\tau \in \{0,1\}$ is a switching (dimensionless) parameter that models the thruster operating mode: either on (when $\tau =1$) or off (i.e., $\tau =0$). These two modes are obtained by switching on or off the onboard electron gun powered by the solar panels [24,25]. In Equation (1), $a_c$ is the characteristic acceleration [26], which is defined as the maximum propulsive acceleration magnitude $\parallel \mathit{a}\parallel$ at a solar distance $r=r_{\oplus }$, and $\widehat{\mathit{n}}$ is the unit vector normal to the sail nominal plane (the plane that ideally contains the charged tethers) in the direction opposite to the Sun. Note that the maximum propulsive acceleration is obtained when $\widehat{\mathit{n}}\equiv {\widehat{\mathit{i}}}_r$, that is, when the E-sail is in a Sun-facing condition [27,28], and the propulsion system gives a purely radial thrust. In that particular case, the spacecraft heliocentric trajectory may be described with a semi-analytical approach as thoroughly discussed in Refs. [29,30].

2.1. E-Sail Performance Requirements

The HP to be reached and maintained by the spacecraft is characterized by a given distance $r_{\mathrm{HP}}$ from the Sun and a prescribed ecliptic latitude ${\varphi }_{\mathrm{HP}}$. The ecliptic longitude, instead, is left free, so that the pair $\{r_{\mathrm{HP}},{\varphi }_{\mathrm{HP}}\}$ locates a sort of “ring” of possible static equilibrium points placed at a distance $h_{\mathrm{HP}}=r_{\mathrm{HP}}sin{\varphi }_{\mathrm{HP}}$ from the ecliptic, as sketched in Figure 2. The special case when ${\varphi }_{\mathrm{HP}}=0\mathrm{deg}$ coincides with an HP that lies on the ecliptic at a distance $r_{\mathrm{HP}}$ from the star.

As soon as the spacecraft reaches the design HP with zero inertial velocity, it immediately assumes a Sun-facing orientation to fully exploit the available propulsive acceleration magnitude and balance the gravitational acceleration from the Sun. The latter is in the radial direction and has a magnitude ${\mu }_{\odot }/r_{\mathrm{HP}}^2$, where ${\mu }_{\odot }$ is the Sun’s gravitational parameter. Bearing in mind Equation (1), the assigned HP may be maintained with a Sun-facing attitude (i.e., $\widehat{\mathit{n}}={\widehat{\mathit{i}}}_r$) if

$$a_c\left(\frac{r_{\oplus }}{r_{\mathrm{HP}}}\right)=\frac{{\mu }_{\odot }}{r_{\mathrm{HP}}^2}$$

(2)

from which the required value $a_c^{★}$ of the characteristic acceleration is

$$a_c=a_c^{★}\triangleq \left(\frac{r_{\oplus }}{r_{\mathrm{HP}}}\right)\left(\frac{{\mu }_{\odot }}{r_{\oplus }^2}\right)$$

(3)

Note that the ratio ${\mu }_{\odot }/r_{\oplus }^2\simeq 5.93\mathrm{mm}/{\mathrm{s}}^2$ coincides with the characteristic acceleration necessary for a solar-sail-based spacecraft [8] to maintain a generic HP. Therefore, according to Equation (3), a spacecraft propelled by an E-sail is potentially able to maintain a static equilibrium condition with a characteristic acceleration smaller than that required by a photonic solar sail. This aspect is better appreciated by looking at Figure 3, which shows the variation of $a_c^{★}$ with the solar distance $r_{\mathrm{HP}}$ as modeled by Equation (3).

According to Figure 3, a medium-performance E-sail with a characteristic acceleration of $1\mathrm{mm}/{\mathrm{s}}^2$ can maintain an HP at a distance from the Sun of roughly $6\mathrm{au}$, while a high-performance E-sail with $a_c=a_c^{★}=3\mathrm{mm}/{\mathrm{s}}^2$ is able to perform an HP scientific mission at a solar distance of about $2\mathrm{au}$. In both cases, the required characteristic acceleration is only a fraction of the value required by a solar sail (roughly $17\%$ and $50\%$, respectively). For a given value of $a_c$, the characteristics of the E-sail propulsion system depend on the payload mass as discussed in Ref. [31]. For example, assuming a value of $a_c=1\mathrm{mm}/{\mathrm{s}}^2$ and a payload mass of $100\mathrm{kg}$, the typical mass budget model [31] gives an E-sail with 44 tethers of $15\mathrm{km}$ each, a required electric power of about $500\mathrm{W}$, and a total mass of slightly less than $400\mathrm{kg}$.

Unfortunately, a higher value of the Sun–HP distance $r_{\mathrm{HP}}$ poses a number of technical issues, such as those related to the actual capability of the solar panels to provide the electric power necessary for the spacecraft (including the E-sail propulsion system) and for the regular working of the scientific payload. In the remainder of this section, we quantify the effect of the Sun–HP distance on the flight time necessary for the spacecraft to reach the given equilibrium point starting from the parking orbit. To this end, the spacecraft dynamics are described in the spherical reference frame $\mathcal{T}$, and the transfer trajectory is obtained with an indirect approach as discussed in the next section.

2.2. Spacecraft Dynamics and Trajectory Optimization

The orientation of the normal and radial unit vectors ($\widehat{\mathit{n}}$ and ${\widehat{\mathit{i}}}_r$, respectively) may be written as a function of the sail cone angle $\alpha \in [0,\pi /2]\mathrm{rad}$ and the sail clock angle $\delta \in [0,2\pi ]\mathrm{rad}$, which are illustrated in Figure 4.

According to Figure 4, the components of these unit vectors in $\mathcal{T}(O;{\widehat{\mathit{i}}}_r,{\widehat{\mathit{i}}}_{\theta },{\widehat{\mathit{i}}}_{\varphi })$ are

$${\left[\widehat{\mathit{n}}\right]}_{\mathcal{T}}=\left[\begin{array}{c}cos\alpha \\ sin\alpha cos\delta \\ sin\alpha sin\delta \end{array}\right],{\left[{\widehat{\mathit{i}}}_r\right]}_{\mathcal{T}}=\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$$

(4)

so that, from Equation (1), the components of the propulsive acceleration vector $\mathit{a}$ in the spherical reference frame $\mathcal{T}$ can be written as

$${\left[\mathit{a}\right]}_{\mathcal{T}}=\left[\begin{array}{c}{a}_r\\ a_{\theta }\\ a_{\varphi }\end{array}\right]\triangleq \tau \frac{a_c}{2}\left(\frac{r_{\oplus }}{r}\right)\left[\begin{array}{c}1+cos{\alpha }^2\\ cos\alpha sin\alpha cos\delta \\ cos\alpha sin\alpha sin\delta \end{array}\right]$$

(5)

From the preceding equation, the three control (scalar) variables are, therefore, $\{\tau ,\alpha ,\delta \}$, and the E-sail-based spacecraft equations of motion in $\mathcal{T}$ are given by [32,33]

$$\begin{array}{cc}\hfill \dot{r}& =v_r\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \dot{\theta }& =\frac{v_{\theta }}{rcos\varphi }\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill \dot{\varphi }& =\frac{v_{\varphi }}{r}\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\dot{v}}_r& =\frac{v_{\theta }^2+v_{\varphi }^2}{r}-\frac{{\mu }_{\odot }}{r^2}+a_r\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill {\dot{v}}_{\theta }& =\frac{v_{\theta }{v}_{\varphi }tan\varphi -v_r{v}_{\theta }}{r}+a_{\theta }\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\dot{v}}_{\varphi }& =-\frac{v_{\theta }^{2}tan\varphi +v_r{v}_{\varphi }}{r}+a_{\varphi }\hfill \end{array}$$

(11)

where $\{a_r,a_{\theta },a_{\varphi }\}$ are obtained from Equation (5) as a function of the control variables, while $\{v_r,v_{\theta },v_{\varphi }\}$ are the three components of the spacecraft (inertial) velocity vector. Without loss of generality, we assume that, at time $t=t_0$, the spacecraft lies along the x-axis of the ${\mathcal{T}}_S(O;x,y,z)$ frame (see Figure 1) so that the initial spacecraft state variables are

$$r\left(t_0\right)=r_{\oplus },\theta \left(t_0\right)=0,\varphi \left(t_0\right)=0,v_r\left(t_0\right)=0,v_{\theta }\left(t_0\right)=\sqrt{\frac{{\mu }_{\odot }}{r_{\oplus }}},v_{\varphi }\left(t_0\right)=0$$

(12)

while the final conditions (at time $t=t_f$) are

$$r\left(t_f\right)=r_{\mathrm{HP}},\varphi \left(t_f\right)={\varphi }_{\mathrm{HP}},v_r\left(t_f\right)=0,v_{\theta }\left(t_f\right)=0,v_{\varphi }\left(t_f\right)=0$$

(13)

The time variation of the three control variables $\tau =\tau \left(t\right)$, $\alpha =\alpha \left(t\right)$, and $\delta =\delta \left(t\right)$ are obtained by minimizing the flight time $\mathsf{\Delta }t=t_f-t_0\equiv t_f$ necessary for the spacecraft to move from the (ecliptic) circular parking orbit of radius $r=r_{\oplus }$ to the HP of given geometric characteristics $\{r_{\mathrm{HP}},{\varphi }_{\mathrm{HP}}\}$. Note that, according to Equation (13), the final value of the ecliptic longitude is left free, so that both $t_f$ and $\theta \left(t_f\right)$ are two outputs of the optimization process briefly described below.

The minimum time trajectories are sought by imposing the constraint that, along the transfer trajectory, the Sun–spacecraft distance cannot be smaller than a minimum allowable perihelion radius $r_p>0$ or

$$r\ge r_p\mathrm{for}t\in [t_0,t_f]$$

(14)

The value of $r_p$ essentially depends on the characteristics of the E-sail structure. For example, using the data reported in Ref. [34], in the rest of the paper, we assume $r_p\triangleq 0.33\mathrm{au}$, a value consistent with the copper tethers employed in the E-sail structural design. The optimization process uses an indirect approach, whose main features are discussed in the classical textbook by Bryson and Ho [35]. The presence of Equation (14) implies that we are dealing with a minimum time problem with inequality (path) constraints on one of the state variables—that is, the Sun–spacecraft distance r.

In this case, the Hamiltonian function, the Euler–Lagrange equations, and the set of additional constraints required to complete the (associated) two-point boundary value problem are obtained paralleling the procedure used in Ref. [34]. In particular, the optimal control law of the switching parameter $\tau$ and that for the sail attitude angles $\{\alpha ,\delta \}$ were derived from the general results of Huo et al. [21]. The mathematical model used in the optimization process is summarized in the Appendix A.

3. Numerical Simulations and Parametric Analysis

With the aid of Figure 3, which gives the required characteristic acceleration for a desired Sun–HP distance, a set of interplanetary trajectories are optimized to estimate the transfer performance of an E-sail-based spacecraft in a mission to a stationary point placed at a distance $r_{\mathrm{HP}}\in [2,8]\mathrm{au}$ from the Sun. The range of variation of the target HP distance allows the designer to appreciate how the E-sail propulsive performance influences the optimal transfer trajectory characteristics. The chosen interval of $r_{\mathrm{HP}}$ approximately corresponds to a characteristic acceleration $a_c^{★}\in [3,0.9]\mathrm{mm}/{\mathrm{s}}^2$, thus, including the cases of high- and medium-performance E-sails.

A preliminary trajectory analysis shows that the topology of the generic optimal transfer trajectory falls into one of the following three cases, which are illustrated in Figure 5 assuming a simplified two-dimensional scenario to facilitate the figure’s readability.

The notation of Figure 5, below described, was adapted from that introduced by the authors in Ref. [34].

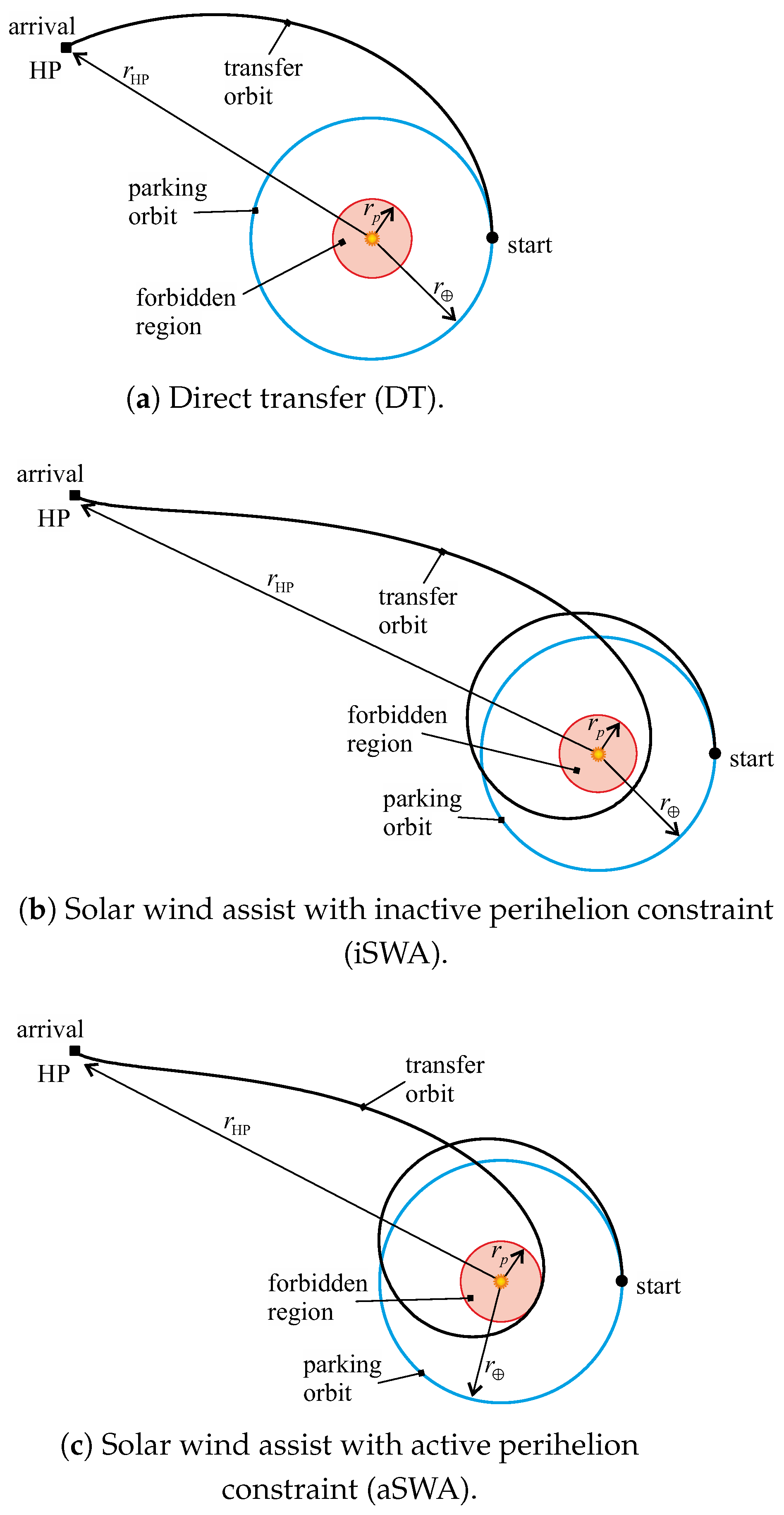
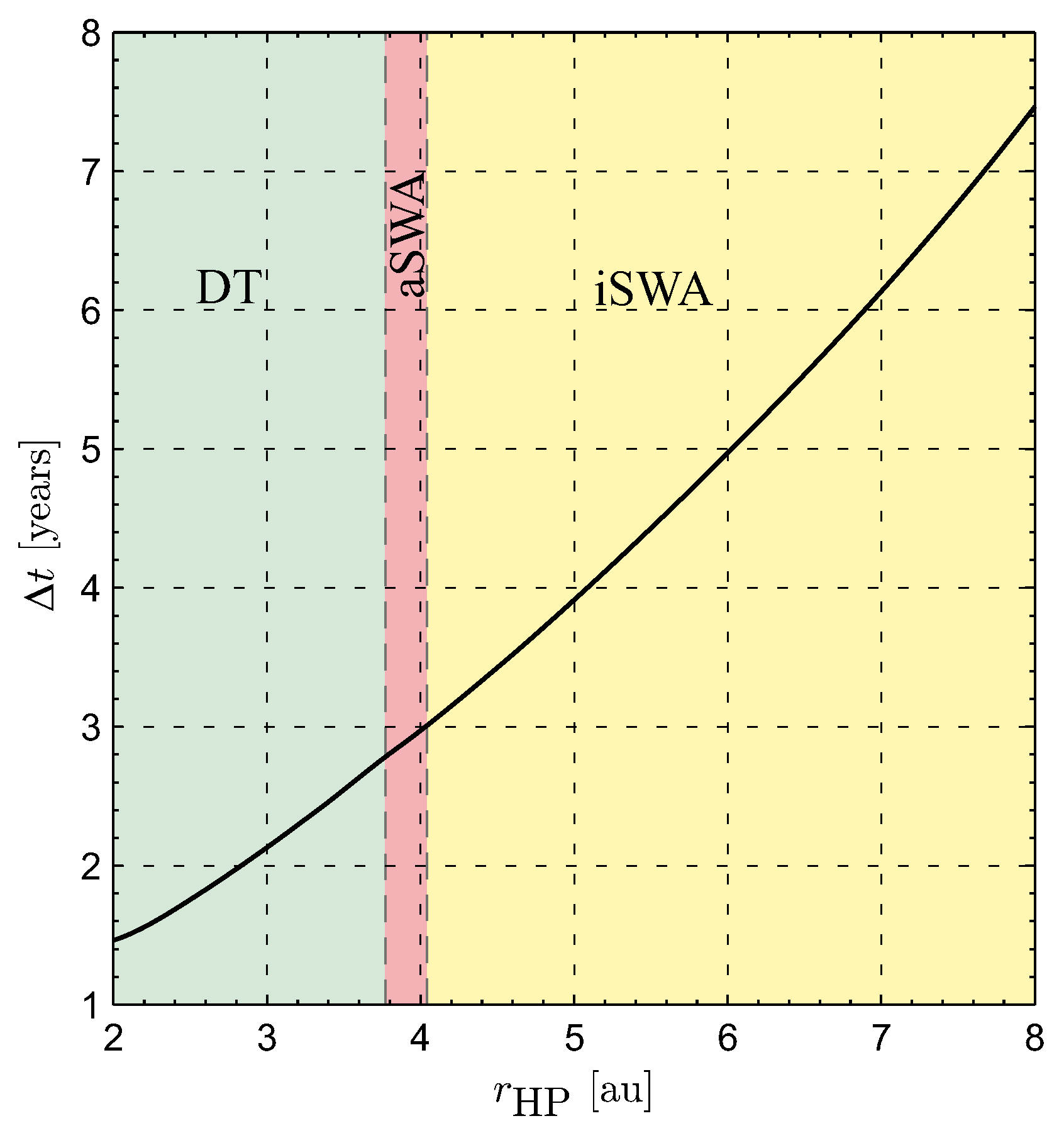
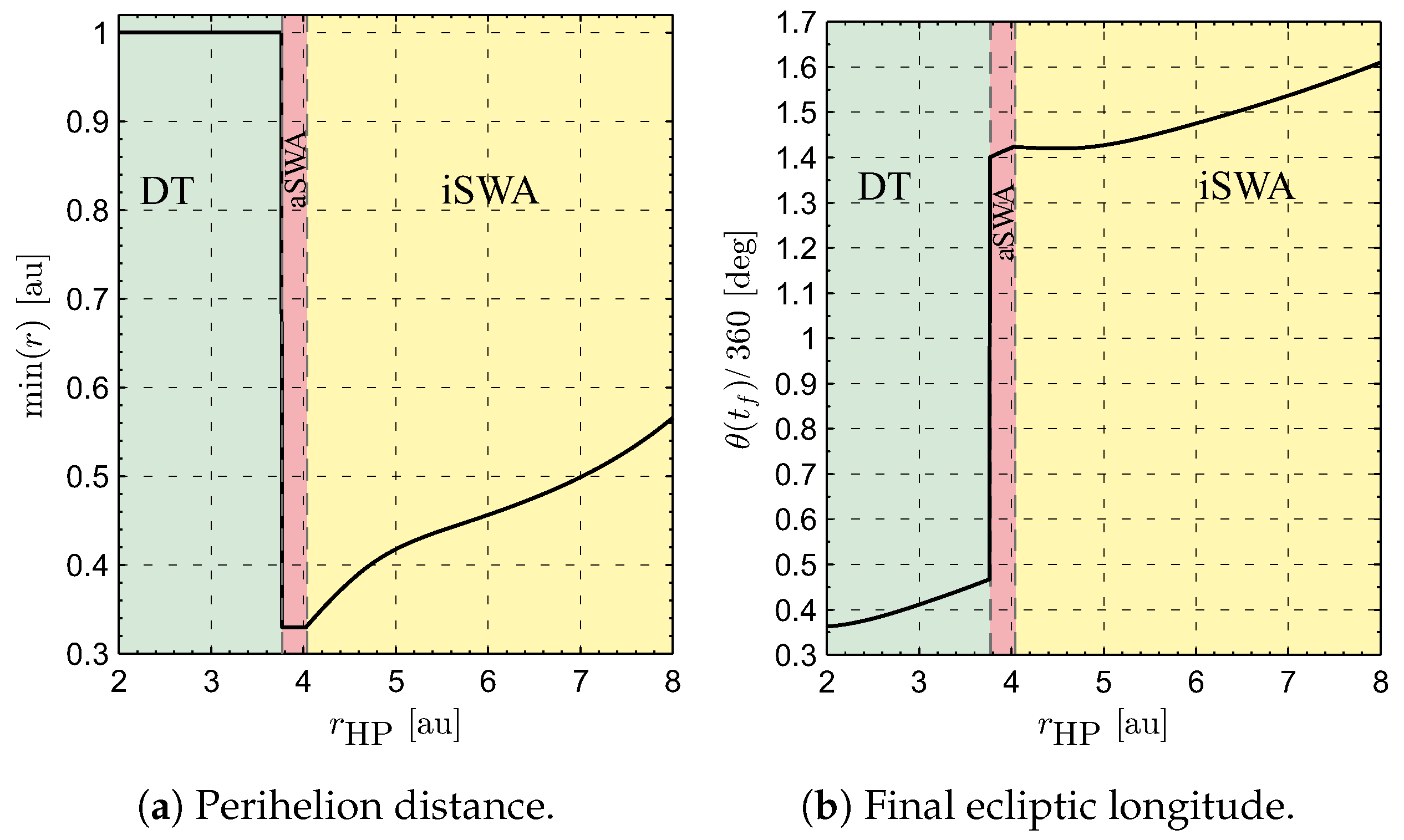
• Direct transfer (DT). During the optimal transfer, the Sun–spacecraft distance r continuously increases with time until the vehicle reaches the target HP, so that the perihelion distance of the optimal transfer coincides with the radius $r_{\oplus }$ of the circular parking orbit; see Figure 5a.
• Solar wind assist with inactive perihelion constraint (iSWA). In this case, the minimum-time transfer trajectory contains a phase where the spacecraft approaches the Sun to increase its propulsive acceleration magnitude according to the thrust model of Equation (1). Paralleling the nomenclature used for a solar sail mission case [36], this behavior can be seen as a sort of solar wind assist (SWA) because of the thrust increase due to the variation of solar wind plasma density. The approaching phase ends when the spacecraft reaches a perihelion distance $min\left(r\right)$ that, in this case, is greater than the minimum admissible value $r_p=0.33\mathrm{au}$, so that the inequality constraint (14) is naturally satisfied (case of inactive constraint); see Figure 5b.
• Solar wind assist with active perihelion constraint (aSWA). This case is similar to the preceding one, with the only difference that the perihelion distance of the transfer trajectory is equal to $r_p=0.33\mathrm{au}$ as sketched in Figure 5c. In other terms, $min\left(r\right)=r_p$, and thus the constraint (14) on the solar distance becomes active at the perihelion.

3.1. Two-Dimensional Trajectory

The transfer performance is initially estimated by simulating a two-dimensional mission case in which the HP lies on the ecliptic (i.e., $h_{\mathrm{HP}}\equiv 0\mathrm{au}$), and the ecliptic latitude of the target equilibrium point is ${\varphi }_{\mathrm{HP}}=0\mathrm{deg}$. In this simplified case, the design parameter reduces to the target solar distance, which was selected to be in the range $r_{\mathrm{HP}}\in [2,8]\mathrm{au}$. The numerical results—that is, the minimum flight time as a function of the Sun–HP distance—are sketched in Figure 6.

The simulations show that an interplanetary transfer toward a HP with a medium-performance propulsion system (i.e., an E-sail with $a_c=a_c^{★}=1\mathrm{mm}/{\mathrm{s}}^2$) requires a flight time of about $5\mathrm{years}$, while a high-performance E-sail with $a_c=a_c^{★}=3\mathrm{mm}/{\mathrm{s}}^2$ needs a flight time of about $1.5\mathrm{years}$.

Figure 6 also shows that a DT is obtained when the Sun–HP distance is below $3.77\mathrm{au}$, that is, when the spacecraft characteristic acceleration is above $1.57\mathrm{mm}/{\mathrm{s}}^2$; see also Figure 3. On the other hand, a SWA appears in the optimal trajectory when a medium-performance E-sail is considered with an active constraint (that is, an aSWA) in the range of $a_c=a_c^{★}\in [1.47,1.57]\mathrm{mm}/{\mathrm{s}}^2$, that is, when $r_{\mathrm{HP}}\in [3.77,4]\mathrm{au}$. This behavior is consistent with the curve of Figure 7a, which shows the variation of the perihelion distance of the transfer trajectory with $r_{\mathrm{HP}}$ and with the optimal transfer trajectories sketched in Figure 8. Finally, the lines shown in Figure 7b, which report the final value of the ecliptic longitude $\theta \left(t_f\right)$, define the position of the HP on the ecliptic.

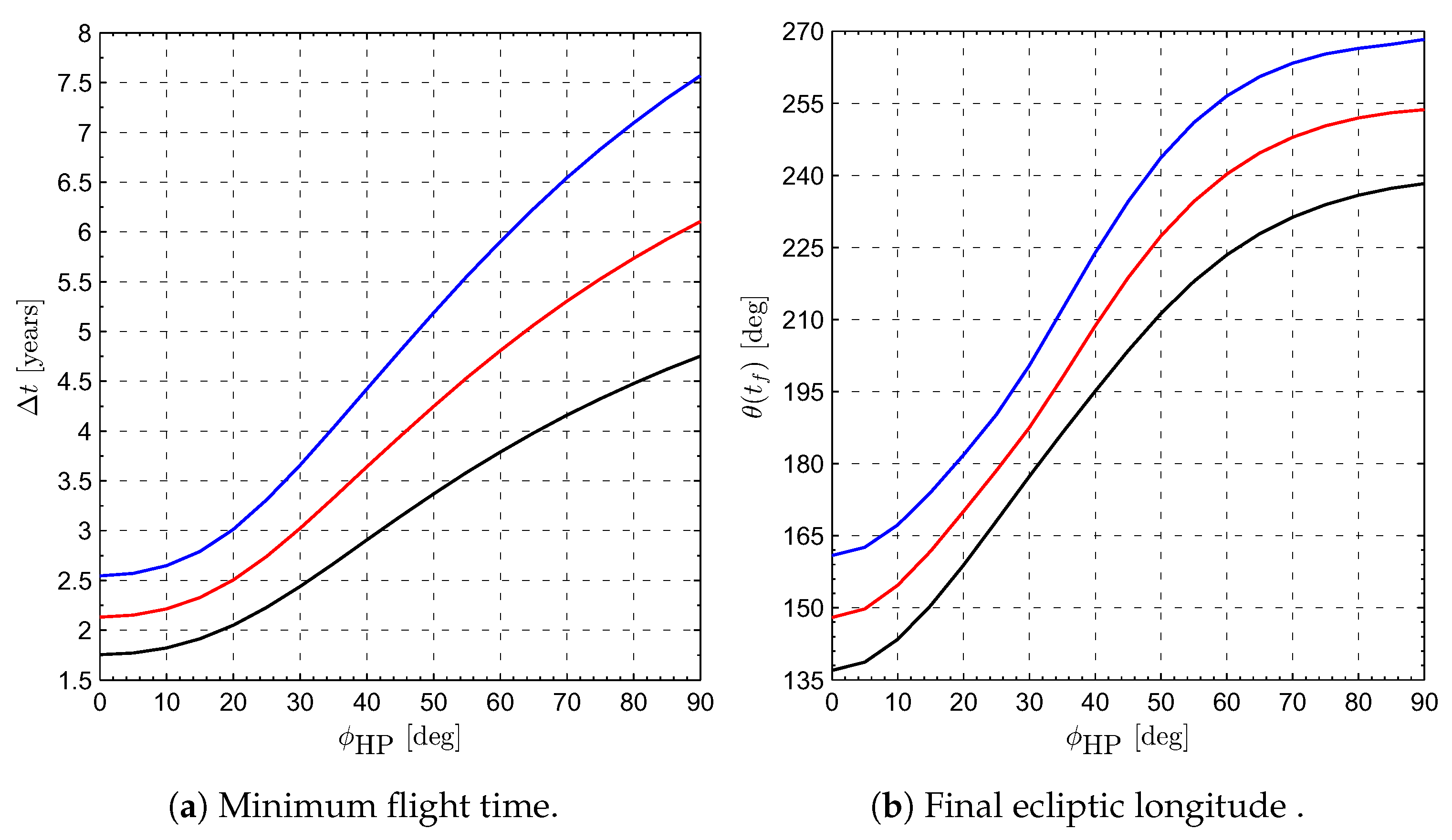
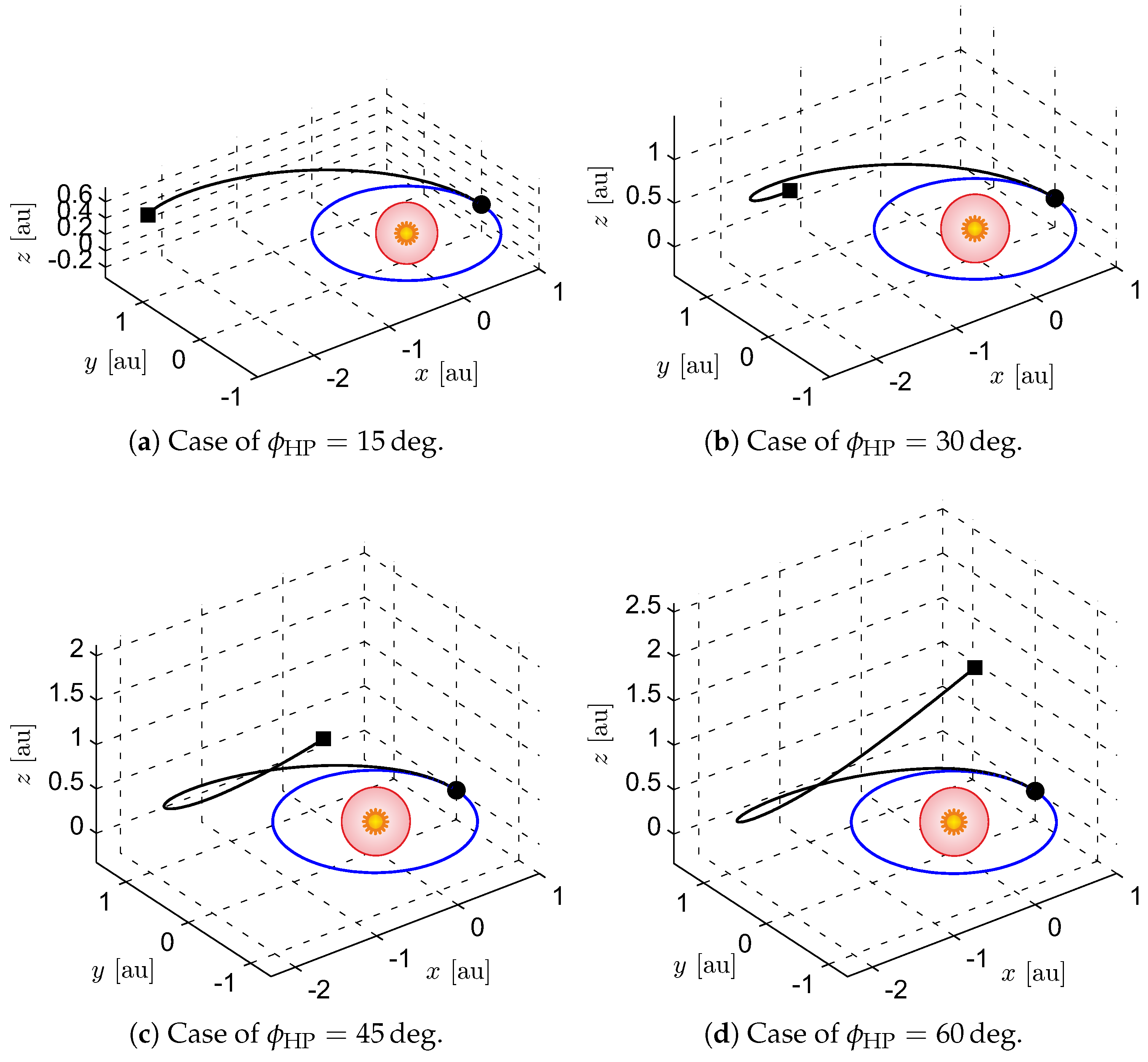
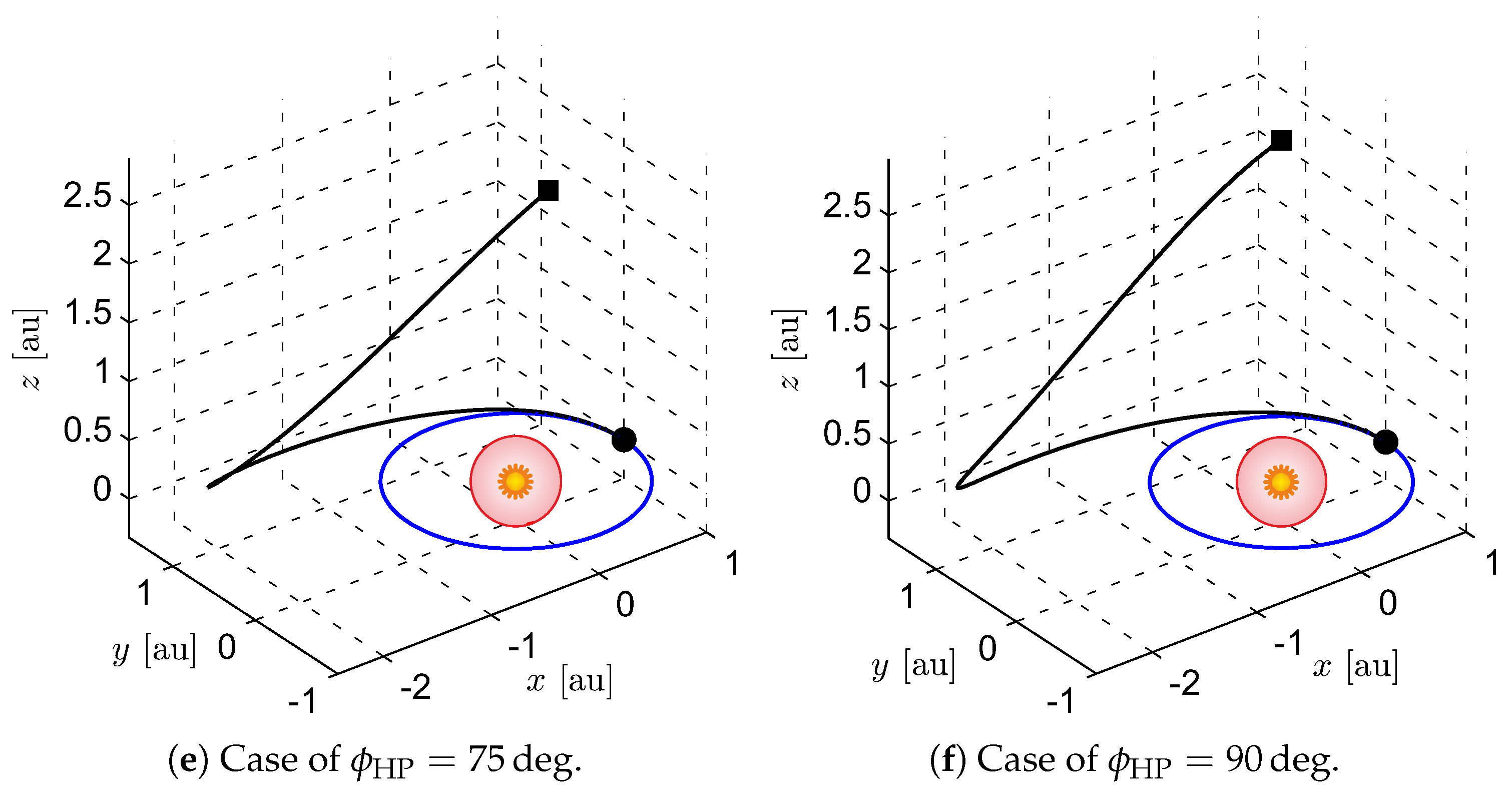
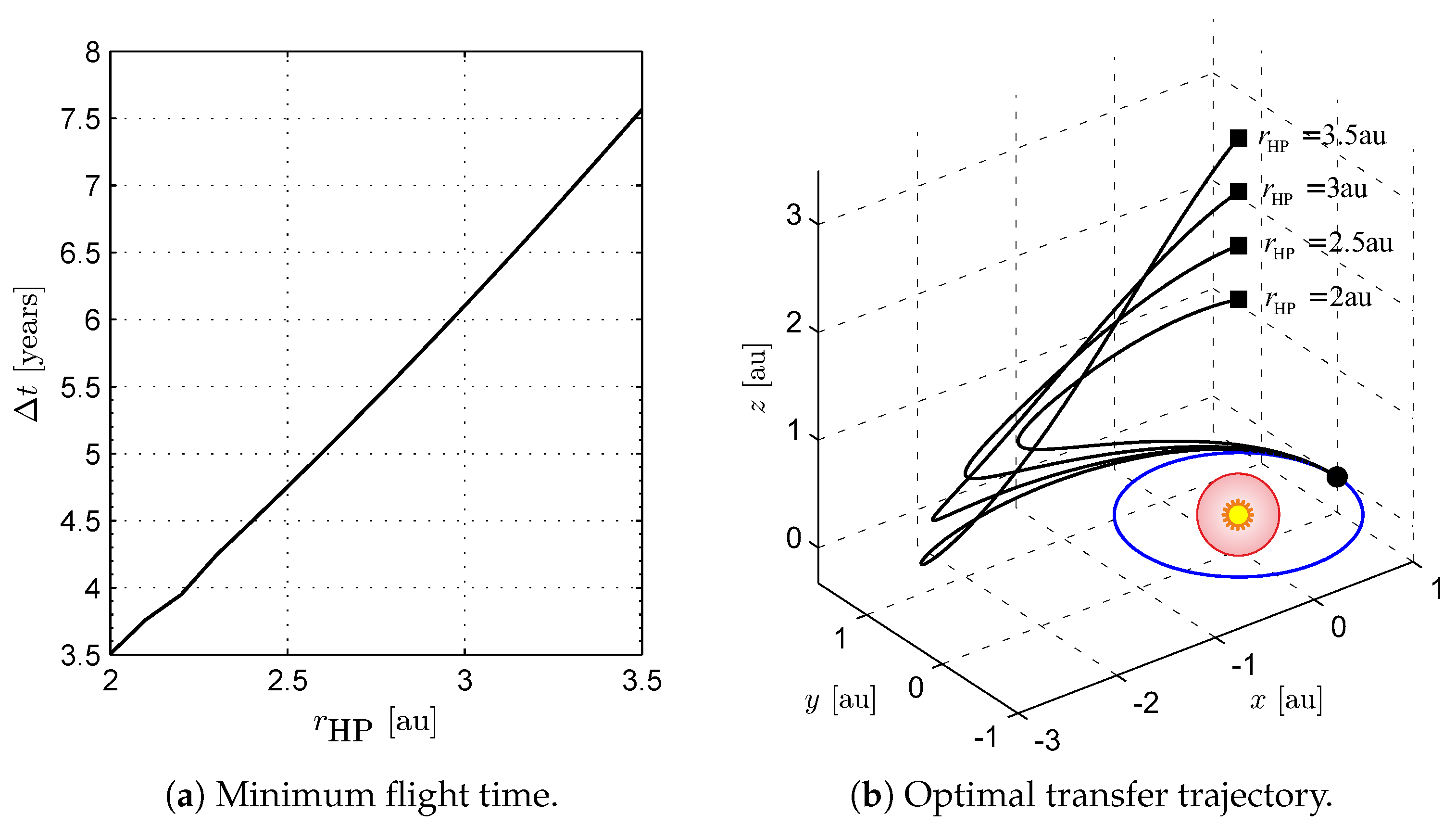
3.2. Three-Dimensional Scenario

In a more general three-dimensional case, the position of the HP target is identified by the pair $\{r_{\mathrm{HP}},{\varphi }_{\mathrm{HP}}\}$, so that the minimum flight time $\mathsf{\Delta }t$ is now a function of two independent design parameters—that is, $\{r_{\mathrm{HP}},{\varphi }_{\mathrm{HP}}\}$. Due to the problem symmetry with respect to the ecliptic (see Figure 2) without loss of generality, we assume ${\varphi }_{\mathrm{HP}}\in [0,90]\mathrm{deg}$, where the special case of ${\varphi }_{\mathrm{HP}}=0\mathrm{deg}$ (or ${\varphi }_{\mathrm{HP}}=90\mathrm{deg}$) corresponds to a target HP point on the ecliptic (or exactly above the Sun’s north pole).

To reduce the number of simulations, three different values of the Sun–HP distance are considered, i.e., $r_{\mathrm{HP}}\in \{2.5,3,3.5\}\mathrm{au}$, with a required characteristic acceleration of $a_c=a_c^{★}\in \{2.37,1.97,1.69\}\mathrm{mm}/{\mathrm{s}}^2$, respectively. In the selected range of $a_c^{★}$, a DT is first simulated to facilitate the numerical convergence of the optimization procedure. Figure 9a,b show the flight time and the final ecliptic longitude as a function of the HP ecliptic latitude. Note, in particular, that the values of $\{\mathsf{\Delta }t,\theta \left(t_f\right)\}$ when ${\varphi }_{\mathrm{HP}}=0\mathrm{deg}$ are consistent with those obtained in the two-dimensional mission case; see Figure 6 and Figure 7b.

The transfer trajectories when $r_{\mathrm{HP}}=3\mathrm{au}$ are sketched in Figure 10 for a set of values of ${\varphi }_{\mathrm{HP}}$ to better emphasize the change in the transfer trajectory shape with ${\varphi }_{\mathrm{HP}}$. The special trajectory reported in Figure 10f shows the transfer toward a polar HP—a stationary point exactly above the Sun’s north pole. A potential mission application that requires the transfer toward such a vantage point for solar observation purposes is discussed in the next section.

3.3. Mission Application

Consider a three-dimensional mission scenario in which the E-sail-based spacecraft reaches a polar HP (a point with ${\varphi }_{\mathrm{HP}}=90\mathrm{deg}$) placed at a distance $r_{\mathrm{HP}}\in [2,3.5]\mathrm{au}$. In that case, the numerical simulations give the variation of the optimal flight time $\mathsf{\Delta }t$ with the final solar distance $r_{\mathrm{HP}}$ as shown in Figure 11a. The mission time increases nearly linearly with the target distance $r_{\mathrm{HP}}$. The optimal transfer trajectories are illustrated in Figure 11b. From the simulation results, we found that a polar HP at a solar distance of $3\mathrm{au}$ can be reached within about $6\mathrm{years}$, while a distance of $2.5\mathrm{au}$ is reached in less than $5\mathrm{years}$. In the latter case, that is, when $r_{\mathrm{HP}}=2.5\mathrm{au}$, the time variations of the three control variables $\{\tau ,\alpha ,\delta \}$ are sketched in Figure 12.

4. Conclusions

In this paper, we analyzed the performance of an E-sail-based spacecraft in an interplanetary transfer toward a heliocentric equilibrium point. The peculiarity of the E-sail thrust concept allows for a heliostationary point to be reached by a probe propelled by a medium-performance propulsion system. This is particularly true when the heliostationary point is sufficiently far from the Sun. For example, a spacecraft with a propulsive acceleration equal to $1\mathrm{mm}/{\mathrm{s}}^2$ is able to maintain a static equilibrium point placed on the Ecliptic at about 6 astronomical units from the Sun and to reach it within a transfer time of about 5 years.

The required E-sail performance increases as the equilibrium point heliocentric distance reduces. Even though a heliostationary point at a solar distance of 2 astronomical units needs a high performance E-sail, the required characteristic acceleration, equal to about $3\mathrm{mm}/{\mathrm{s}}^2$, is well below the value (roughly equal to $6\mathrm{mm}/{\mathrm{s}}^2$) needed to maintain the same point by means of a photonic solar sail. Nevertheless, a fair comparison between these two propulsion concepts in such an advanced mission scenario is not so simple and requires a more accurate mission analysis, which is beyond the scope of this paper. In particular, the comparison should include a mass breakdown scheme and a mathematical model able to quantify the interactions between the main trajectory characteristics (perihelion distance and flight time) and the mission design parameters, such as the heliostationary point position and the spacecraft subsystem masses, including the payload.