Abstract
Rainfall disaggregation is a key challenge in hydrology, especially in regions with limited high-resolution records. This study applies the Random Bartlett–Lewis Rectangular Pulse Model to four regions of Hellas to generate hourly rainfall from daily totals. The work is novel in evaluating the model under data-scarce Mediterranean conditions, incorporating a two-tiered uncertainty analysis, testing alternative pulse intensity distributions (Gamma and Exponential), and comparing its performance with a deterministic machine learning (ML) approach. Results show that the RBLRPM reproduces essential rainfall properties such as variance, autocorrelation, skewness, and dry spell probabilities, even when calibrated with as little as three years of data. The ML approach ensures perfect conservation of daily totals and computational efficiency, but it smooths temporal variability and underestimates extremes. By contrast, the stochastic RBLRPM captures clustering, intermittency, and heavy tails more realistically, which is crucial for hydrological design and flood risk analysis. The Gamma distribution consistently outperforms the Exponential form, though both remain applicable. Overall, the Gamma-based RBLRPM offers a robust and transferable method for rainfall disaggregation in data-limited contexts, highlighting the importance of stochastic approaches for water resource management, infrastructure resilience, and climate adaptation.
1. Introduction and Background
1.1. Background and Research Motivation
High-resolution and high-quality precipitation data are vital for hydrological modeling and the sustainable management of water resources. These data serve as critical input for designing stormwater infrastructure, managing urban floods, and studying climate change impacts []. However, fine-scale precipitation data are often unavailable, particularly in regions with sparse meteorological networks. This limitation significantly hinders the detection and analysis of high-intensity, short-duration rainfall events. Rainfall disaggregation—the process of converting coarser-scale precipitation data into finer temporal resolutions—addresses this gap by enabling synthetic reconstruction of high-resolution rainfall dynamics [].
Despite advancements in rainfall disaggregation, existing models often rely on extensive observational records for calibration and validation, making them less effective in data-scarce regions. In these cases, the need for models that can generate realistic rainfall time series from minimal data inputs is particularly pressing. The availability of data calls for developing resilient and adaptive models that could effectively generate synthetic rainfall information from very minimal initial data, imitating the temporal dynamics and precipitation intensities at every high resolution level []. Among the available modeling approaches, the Bartlett-Lewis Rectangular Pulse Model (BLRPM) has shown significant promise due to its stochastic nature and ability to reproduce realistic rainfall patterns, especially at the hourly scale.
Several studies have explored variants of the Bartlett–Lewis model under different climatic conditions. Kossieris et al. [] examined the model’s performance in Athens; Ritschel et al. [] applied it for IDF curve derivation in Germany; Onof and Wheater [] introduced the Random-Parameter extension for British rainfall; and Cowpertwait et al. [] validated stochastic point-process versions across the UK. Despite these efforts, no study has systematically evaluated the Random BLRPM under data-scarce Mediterranean conditions or compared it against deterministic ML disaggregation. This gap defines the rationale and novelty of the present work.
Nonetheless, few research rigorously examine such models under Mediterranean, data-scarce situations, or compare them directly to machine learning (ML) standards. Furthermore, no research has been conducted to study the effect of alternate pulse intensity distributions, such as the Gamma and Exponential forms, or to clearly quantify parameter uncertainty. This work fills these gaps by using the Random Bartlett-Lewis Rectangular Pulse Model (RBLRPM) as a stochastic benchmark versus ML and includes distributional and uncertainty estimates.
1.2. Study Area Challenges and Data Limitations
Hellas is a region characterized by complex and variable precipitation patterns influenced by its Mediterranean climate. While certain areas may experience frequent high-intensity storms, others remain relatively dry for prolonged periods. Unfortunately, most regions in Hellas suffer from insufficient temporal resolution in rainfall records, with available data often containing gaps or lacking continuity. These data limitations present serious challenges for flood risk modeling, hydrological forecasting, and infrastructure design in the face of increasing climate variability. Advanced stochastic rainfall disaggregation, particularly using models like the BLRPM, can help overcome these challenges by generating synthetic, yet realistic, rainfall time series that replicate key statistical properties. High-resolution synthetic data can assist in enhancing hydrological models, as well as influence infrastructure development and flood mitigation efforts [,].
This study explicitly tests whether such stochastic approaches remain robust under short and incomplete rainfall records, reflecting the realistic data conditions of Mediterranean environments. In doing so, it highlights the practical implications of rainfall disaggregation for regions where long-term, high-resolution observations are not available.
1.3. Stochastic Modeling Framework
The simulation of high-resolution rainfall time series is especially challenging because of the intermittent and clustered nature of precipitation events, particularly at sub-daily timescales []. These challenges are compounded in data-poor settings, where the paucity of observational records makes the use of conventional, data-hungry approaches problematic. Rainfall usually falls in uneven bursts, punctuated by dry periods, with pronounced diurnal and interdiurnal variability. Simulating these processes realistically is crucial for hydrological prediction, flood risk assessment, and water infrastructure design.
Rainfall disaggregation methods try to downscale coarser precipitation records (e.g., daily) to finer resolutions (e.g., hourly), and can generally be classified into deterministic and stochastic schemes [,]. Deterministic approaches—like wavelet or Fourier-based methods—are computationally simple but tend to miss important characteristics of rainfall like temporal autocorrelation, intermittency, and clustering [,,,]. Stochastic models, by contrast, are more likely to capture the probabilistic character of rainfall through the preservation of statistical measures like variance, autocorrelation, and the probability of dry periods [,,,].
Stochastic disaggregation models can be subclassified as empirical/statistical, random cascade, and cluster-based models []. Empirical models (e.g., regression-based and autoregressive methods) depend strongly on historical relationships, and tend to perform poorly under extreme or anomalous conditions [,,]. Random cascade models use multifractal theory to generate intermittency on time scales, but their use in fine-resolution applications is restricted by high data demands and decreased capability to model temporal clustering [,,,,]. Cluster-based models view rainfall as a sequence of pulses within storms, with more realistic portrayals of event-based precipitation [,,].
Among cluster models, the Bartlett-Lewis Rectangular Pulse Model (BLRPM) has been the focus of significant attention because of its capability to recreate both the inner structure and the statistical properties of rainfall events [,,,,,,]. The BLRPM generates storms as Poisson-distributed clusters of rectangular pulses, defined by parameters that include storm arrival rate, pulse frequency, duration, and intensity [,,,]. Its merits include its ability to duplicate essential statistical measures, such as skewness, autocorrelation, and intermittency, even without detailed high-resolution data [,,]. Further, its flexibility renders it suitable for application under varied climates, such as Mediterranean climates like Hellas [,].
In spite of these strengths, the standard BLRPM has limitations—most notably its assumption of constant pulse duration for all storms. This may cause overestimation of dry spell probability and poor representation of rainfall variability at finer time scales, especially []. To rectify these weaknesses, the RBLRPM extends the baseline formulation by making the pulse duration a storm-dependent random variable, instead of a parameter. This refinement enhances the model’s ability to reproduce the heterogeneity of natural rainfall, without sacrificing applicability to data-poor environments.
Widespread uses of the Bartlett–Lewis Rectangular Pulse Model (BLRPM) and its extensions have demonstrated the model’s robustness and adaptability across diverse hydrological conditions. For instance, Onof and Wheater employed a Random Parameter BLRPM to model British rainfall, showcasing the model’s ability to capture variability across multiple time scales []. Similarly, Cowpertwait et al. implemented a stochastic point process version of the BLRPM to simulate UK rainfall and validated its performance under single-site configurations []. Smithers et al. applied the BLRPM for design rainfall estimation in South Africa, highlighting its practical utility in engineering contexts []. Ritschel et al. extended the BLRPM to evaluate precipitation extremes and derive intensity–duration–frequency curves in Germany []. Further developments have been proposed by Park et al., who introduced a simplified scheme to enhance the model’s sub-hourly simulation performance, broadening its applicability to finer temporal resolutions []. Collectively, these studies affirm the BLRPM’s effectiveness for stochastic rainfall modeling, particularly in data-scarce environments and design-focused applications.
In this study, the RBLRPM is applied with additional considerations, including the use of alternative pulse intensity distributions (Gamma and Exponential) and an uncertainty analysis to assess calibration robustness under short observational records.
1.4. Objectives
This study applies the RBLRPM to generate high-resolution synthetic rainfall series from daily observations in four Hellenic regions. The model is implemented through the HYETOS-R package, a free tool developed in R-4.5.0 by Kossieris et al. [], and its performance is systematically evaluated against observed hourly data.
The specific objectives of this research are:
- 1.
- To evaluate the performance of the RBLRPM for rainfall disaggregation in data-scarce Mediterranean regions.
- 2.
- To compare the stochastic RBLRPM with a deterministic machine learning (ML) benchmark method, highlighting their respective strengths and limitations.
- 3.
- To assess the influence of alternative pulse intensity distributions (Gamma and Exponential) on the model’s ability to reproduce rainfall statistics.
- 4.
- To quantify parameter uncertainty through a two-tier sensitivity and record-length analysis, testing the robustness of calibration under short datasets.
- 5.
- To identify the implications of these findings for hydrological modeling, flood risk assessment, and infrastructure design in regions with limited rainfall data.
This study is novel in that it combines a stochastic rainfall generator with a deterministic ML benchmark, tests alternative pulse intensity distributions systematically, and incorporates a two-tier uncertainty analysis in data-scarce Mediterranean settings—a combination not previously reported in the rainfall disaggregation literature. The study addresses the gap in previous BLRPM applications by evaluating the Random BLRPM in Mediterranean data-scarce settings and by introducing a comparative ML benchmark to assess its stochastic realism versus computational simplicity.
2. Methodology
2.1. Study Area and Data
The analysis focuses on four regions in Greece: Corfu, Rhodes, Alexandroupolis, and Herakleion (Figure 1). These sites were selected to represent diverse hydroclimatic conditions across the Mediterranean. Corfu, located in the northwestern Ionian Sea, is among the wettest parts of Greece, while Rhodes in the southeastern Aegean is considerably drier. Alexandroupolis in northeastern Greece exhibits a continental–Mediterranean climate, and Herakleion on Crete represents a semi-arid Mediterranean setting. Together, these regions capture the strong spatial and seasonal gradients that characterize rainfall regimes in the area.
Figure 1.
Location of the four study areas in Greece: Corfu, Rhodes, Alexandroupolis, and Herakleion.
Daily precipitation records spanning 1995–2004 are available for all sites, while hourly data covering 2000–2004 are used for validation. Specifically, the RBLRPM is calibrated using daily precipitation data from 1995 to 1999, while independent hourly records from 2000 to 2004 are employed for model validation to ensure an unbiased performance evaluation. These datasets reflect the constraints commonly faced in data-scarce environments, including limited record length and temporal resolution, making them suitable test cases for rainfall disaggregation. A summary of the main precipitation characteristics is provided in Table 1, while detailed monthly statistics are included in Appendix A.

Table 1.
Summary of study areas, precipitation characteristics, and climatic setting.
In many Mediterranean regions, and especially in remote areas and islands, long and high-resolution rainfall records are often unavailable. This study, therefore, evaluates whether stochastic and deterministic disaggregation methods remain robust under such short and incomplete observational datasets, reflecting the realities of data-scarce environments.
2.2. Random Bartlett-Lewis Rectangular Pulse Model (RBLRPM)
The RBLRPM is an alteration of the traditional BLRPM and generates synthetic rainfall time series by simulating rainfall events as clusters of independent rectangular pulses. The model is structured to reflect the stochastic (random) nature of natural rainfall, where intensity, duration, and frequency of rainfall vary. The traditional BLRPM model has a main disadvantage of the general model is the overestimation of the probability of no precipitation for a specific period of time, where it is a fairly significant quantity. This fact makes it difficult for the model to produce accurate time series, which are input data in antiflood studies. This weakness is covered by the Bartlett-Lewis rectangular pulse random model (RBLRPM), which differs in the way it models the random variable of the pulse duration []. RBLRPM models this random variable assuming that it follows an exponential distribution function with a different parameter (i) for each storm i, as opposed to the general model, which assumes that the parameter is common to all storms.
More specifically, RBLRPM consists of the following statistical parameters [], as Figure 2 shows:
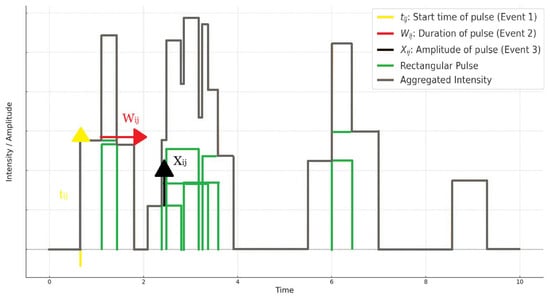
Figure 2.
Temporal representation of the elements that characterize the rectangular intensity pulses of rain events.
i. The parameter of the initial Poisson evolution refers to the starting time points of event i and characterizes the overall stochastic modeling process.
ii. The parameter of the second Poisson evolution, which refers to the starting time points of the pulses of each event i, since the arrival time of the first pulse is identical to the arrival time of the corresponding storm.
iii. The parameter of the exponential distribution, which is linked to the random variable of the time interval , which includes the starting time points of the pulses of each event i.
iv. The parameter of the exponential distribution, describing the random variable of the time duration of the pulses of event i.
v. The parameter of the exponential distribution, where it is related to the random variable of the rain height of the pulses of the event i, the Random BLRPM introduces randomness in key parameters, allowing each storm and pulse to have variable properties, thereby capturing natural rainfall variability.
In more detail, the computational process used in the BLRPM is described by the following equations:
- 1.
- Storm Arrival Process: Modeled as a Poisson process with rate , the number of storms in a time interval t is given by:where k is the number of storms, and t is the time interval (e.g., one day). Following standard BLRPM practice [], a minimum inter-storm interval of six hours is adopted to distinguish independent storm events.
- 2.
- Storm Duration : The duration D of each storm is modeled as:with mean storm duration , allowing for the representation of typical storm lengths in the region.
- 3.
- Pulse Intensity and Duration: The intensity I and duration of each pulse within a storm are defined by:where and shape the Gamma distribution of pulse intensities. The exponential distribution with parameter ensures that pulse duration varies naturally, reflecting the random nature of rainfall events.
- 4.
- Cumulative Rainfall Generation: Total rainfall for each time interval is the sum of all pulses within storms during that interval:
2.3. Calibration and Parameter Estimation
Evolutionary annealing-simplex (EAS) optimization, by Efstratiadis and Koutsoyiannis [,], is a hybrid optimization method that recombines evolutionary algorithms, simulated annealing, and the simplex method. It combines the global search capabilities of evolutionary algorithms with the convergence control of simulated annealing and the precision of the simplex method, enabling efficient refinement of solutions []. This embedding allows the algorithm to perform searches in high-dimensional spaces and handle nonlinear and stochastic problems, which is important in complex modeling tasks.
The BLRPM is one of the major stochastic models applied to disaggregating rainfall data. This approach is critical in calibrating crucial parameters such as storm arrival rates, storm duration, and intensity; these parameters are integral in ensuring that the model produces simulated statistical and temporal characteristics that closely resemble the actual recorded rainfall occurrences. The EAS reduces discrepancies between simulated precipitation and observed patterns, increasing the accuracy and applicability of the BLRPM in hydrological modeling.
The hybrid nature of the algorithm is a substantial reason for its success in searching non-convex and multidimensional parameter spaces. Traditional approaches are often hindered by limitations, notably when dealing with conflicting objectives such as satisfying temporal details versus statistical accuracy. The EAS avoids local minima and identifies globally optimal solutions, producing reliable rainfall simulations. These features have made it a must in several applications, including flood forecasting, water resource management, and detailed hydrological studies, thereby showing the strength and flexibility of the algorithm in solving complex stochastic modeling problems.
As shown in Figure 3, the first step of the algorithm is to initialize a population of candidate solutions representative of possible parameter combinations. Populations can be generated at random or informed by prior knowledge to ensure broad exploration of the search space—steps critical in dealing with nonlinear systems with many parameters. Then, an objective function is applied to each candidate solution to measure its fitness. In the case of BLRPM, the evaluation compares simulated rainfall data and observed characteristics in relation to intensity, duration, and autocorrelation structures. Objective functions act as benchmarks that guide optimization toward parameter sets that best mimic observed hydrological behaviors [].
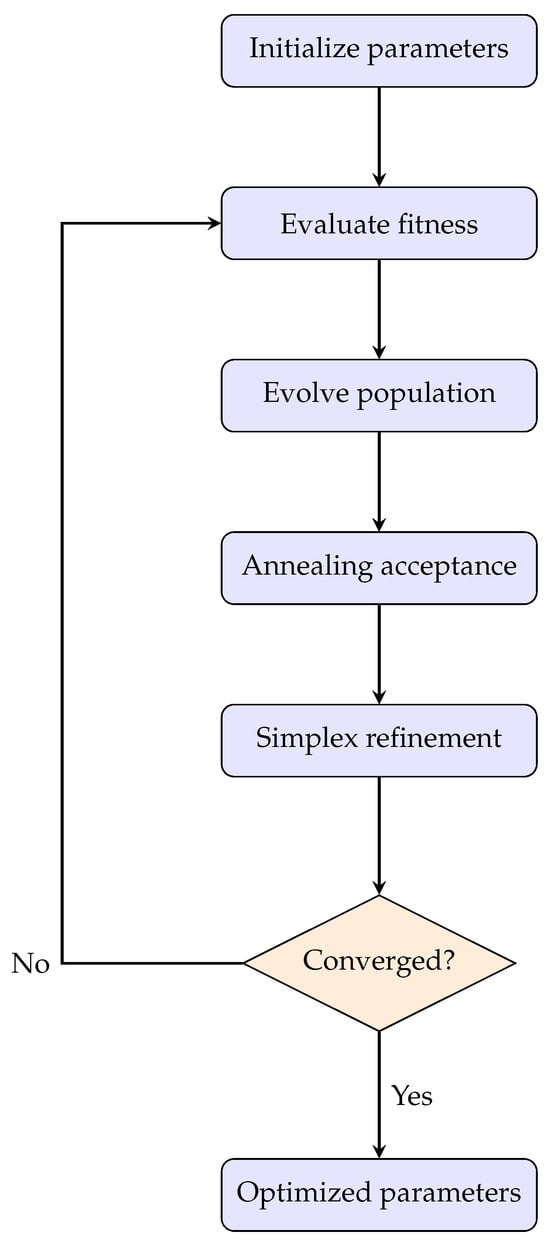
Figure 3.
Simplified flowchart of the EAS calibration process for BLRPM.
Evolutionary algorithm techniques enable global exploration, developing fresh solutions through mutation and crossover, which provides diversity and allows the algorithm to escape local minima. It is augmented by simulated annealing, which includes a “temperature” parameter in determining whether to accept new solutions. Higher temperatures accept worse answers, which permits exploration, while lower temperatures focus on refining attractive areas of the search space []. This dynamic cooling schedule offers a balance between exploration and exploitation. Once promising solutions have been found, these are refined using the simplex method.
Since it is a deterministic local optimization algorithm, the simplex method gradually adjusts the parameters to maximize the objective function to arrive at a high-precision final solution. The algorithm iterates through these three steps—evaluation, exploration, and refinement—until convergence requirements are met, which could either be a minimum error threshold or a predetermined number of iterations. The final outcome is the optimized set of parameters that meet the requirements of the model. In the case of the BLRPM, this results in parameters that allow for the disaggregation of rainfall data to serve applications in hydrology for flood risk assessment and water resource management. The combination of global and local search strategies is particularly valuable for calibrating the RBLRPM in Mediterranean regions with short observational records, ensuring robustness under data-scarce conditions.
To complement the calibration procedure, an uncertainty assessment is incorporated to examine the reliability of the estimated parameters under limited and variable data conditions. Rather than focusing only on best-fit values, the analysis investigates how small perturbations in input statistics or variations in record length influence parameter stability. Two complementary experiments are therefore introduced: (i) perturbing rainfall statistics with controlled noise to test sensitivity, and (ii) varying the available years of data to test the effect of record length.
2.4. Disaggregation Algorithm
The Koutsoyiannis and Onof [] algorithm is a HYETOS-R package-based approach for disaggregating daily rainfall data into finer temporal scales, such as hourly data. This approach combines the BLRPM for continuous rainfall simulation with a correction procedure to ensure that the statistical features of the synthetic data closely match those of the real data. The methodology includes an iterative generation of synthetic time series, adjusted with defined thresholds, together with extra steps to improve computational efficiency. The algorithm essentially works around the disaggregation of the rainfall series into independent rainy events modeled as clusters of storms. Storms are generated by a Poisson process, assuming a realistic temporal distribution of rainfall events. Within each storm, pulses are generated with varying intensities and durations, each representing the stochastic nature of the rainfall. The method proceeds through multiple iterative steps. For clarity, the complete disaggregation and calibration workflow is summarized in Figure 4, which provides a step-by-step overview of the data processing, storm generation, optimization, and validation stages.
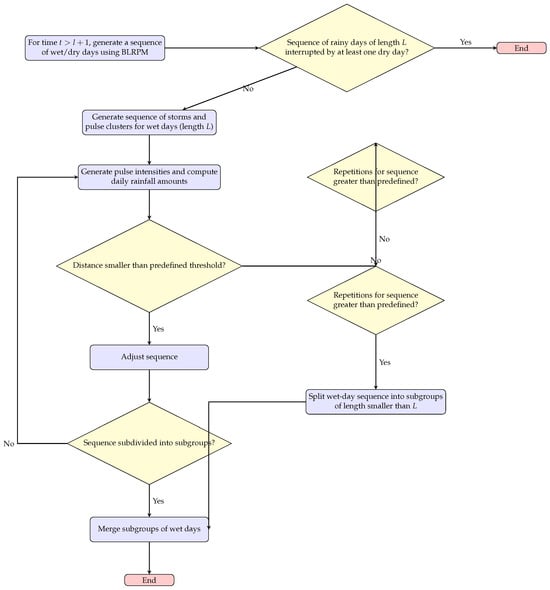
Figure 4.
Flowchart of the iterative process for rainfall sequence generation using the BLRPM.
As shown in Figure 4, the first step is to break down the daily rainfall time series into sequences of consecutive days with non-zero rain. Then, for each sequence detected, BLRPM produces synthetic rainfall pulses and subsequently sums up these pulses to calculate the associated daily rainfall. A deviation check is performed to ensure that the synthetic data generated does not significantly deviate from the observed data. This check is made by using a previously defined threshold, , and this process is carried out until the deviation is less than the threshold or the maximum number of iterations is reached. The deviation is calculated according to Equation (5):
where d is the deviation between the observed and synthetic rainfall, L the number of rainy days in the group being analyzed, the observed value of the i-th day, the corresponding synthetic rainfall value and c a small constant equal to 0.1 mm added to avoid division by zero and ensure numerical stability. Should the resulting sequence fail to meet these requirements, the algorithm splits the group into smaller groups and performs the simulation and repair procedures iteratively. When all subgroups reach the criteria, they are merged to create the final synthetic rainfall series. This hierarchical strategy preserves the statistical features of the observed data in the synthetic series while reducing computational complexity.
In this study, the disaggregation algorithm is applied to short Mediterranean rainfall records, providing a test of whether the method can preserve realistic rainfall statistics under conditions of limited data availability.
2.5. Machine Learning Disaggregation Method
In addition to the stochastic disaggregation technique provided by the RBLRPM, a machine learning (ML)-based approach is also employed to disaggregate total daily precipitation into hourly totals using linear regression []. This method is attractive in data-sparse conditions due to its minimal computational cost, interpretability, and ease of deployment [].
The ML model is intended to learn the diurnal distribution pattern of rainfall using past hourly data. The objective variable is the proportion of daily rainfall seen at each hour, which is calculated by normalizing the hourly value by the daily total. The model’s only predictor variable is time of day, allowing it to capture ordinary everyday activity without overfitting to specific storm occurrences. The estimate method used is ordinary least squares linear regression.
Hourly rainfall observations are preprocessed to eliminate days with zero total rainfall and rows containing missing values before training. Once trained, the model predicts the hourly fractions for each hour (0–23). The predicted fractions are multiplied by the observed daily precipitation sum to reconstruct a full hourly time series that exactly preserves daily totals.
This deterministic technique reflects the average structure of daily rainfall but does not account for intra-day fluctuation or unpredictability. It is most suited for scenarios requiring rapid disaggregation while maintaining daily totals, such as hydrological modeling or operational decision support. In this work, the ML model is used as a deterministic benchmark to assess the stochastic RBLRPM, shedding light on the trade-offs between efficiency and statistical realism.
3. Results and Discussion
This section presents the outcomes of applying the RBLRPM and the ML benchmark method to the four Mediterranean case study regions. Results are organized into four parts: (i) performance evaluation of the RBLRPM across regions, (ii) analysis of uncertainty in parameter estimation under limited data, (iii) comparative assessment between the stochastic RBLRPM and deterministic ML disaggregation, and (iv) discussion of model limitations and applicability. This structure reflects both the technical performance of the methods and their practical relevance for hydrological applications.
Exponential and Gamma distributions are both tested for pulse intensity, and their suitability is found to be region- and month-dependent. These outcomes help establish the model’s strengths and limitations, as well as its usability in data-scarce and hydrologically sensitive environments.
The novelty of this study lies in testing the RBLRPM under short observational records in Mediterranean environments while, at the same time, benchmarking its performance against a simple machine learning method. This dual perspective highlights the trade-offs between stochastic realism and computational efficiency, and underlines the suitability of each approach under different hydrological contexts.
3.1. Performance Evaluation
The performance of the RBLRPM is assessed by comparing synthetic hourly rainfall series with observed data across the four study regions. Evaluation focuses on statistical properties relevant to hydrological modeling, including variance, skewness, lag-1 autocorrelation, and dry/wet spell persistence. These metrics capture both the distributional characteristics of rainfall and its temporal organization, which are essential for applications such as flood estimation and infrastructure design.
Rather than restating the model formulation, the analysis here emphasizes how well the RBLRPM reproduces observed rainfall behavior in data-scarce Mediterranean settings. The results are presented region by region (Corfu, Rhodes, Alexandroupolis, and Herakleion), followed by additional aggregated findings. This structure allows both site-specific features and broader model tendencies to be highlighted.
Overall, the evaluation demonstrates that the RBLRPM is capable of capturing key rainfall dynamics even when calibrated on short records, while differences across regions underline the influence of local climatic variability. The detailed results are discussed in the following subsections.
The monthly results for all four regions are available in Appendix B. Here, the discussion focuses on seasonal contrasts and overall model performance. A month-by-month calibration approach was retained because it captures the strong intra-seasonal variability characteristic of Mediterranean climates. In Greece, months within the same meteorological “season” may differ drastically—some nearly dry (e.g., July) and others very wet (e.g., December). Seasonal aggregation would therefore mask this variability and degrade performance. In contrast, a seasonal approach may be more suitable for climates with smoother intra-seasonal behavior, such as those in northern Europe.
3.1.1. Corfu
The outcomes of the study in Corfu, the westernmost understudied area of Hellas, are reported first. Based on historical data, the wettest and driest months are December and July, with average daily precipitation of 6.305 mm and 0.442 mm, respectively. However, all months are simulated. Based on the precipitation data in Table 1, the EAS is used to estimate the parameters of the Bartlett–Lewis rectangular pulse random model (RBLRPM) for the known alternative variants, which are shown in Table 2. The logarithmic distance is set to 0.1. Moreover, the minimum number of iterations for level 1 is set to 50, the parameter F to 20, and the maximum number of iterations for levels 1 and 2 to 5000.

Table 2.
RBLRPM parameters for Corfu.
Table 2 summarizes the calibrated parameters for the RBLRPM. Here represents the storm arrival frequency (storms h−1), the mean pulse count per storm, the mean pulse depth, and the pulse intensity variance. Lower and higher and values under the Gamma formulation imply fewer but more clustered and variable storms, consistent with observed rainfall intermittency. Both formulations reproduce the winter storm regime, yet the Gamma distribution more effectively captures rainfall clustering and variance. In January and February, both distributions capture the winter storm regime, but Gamma produces more realistic clustering and higher variance. March and April show the transition into spring; here, Exponential tends to smooth variability, while Gamma better reflects skewness and intermittency. May still retains notable variance, though reduced compared to winter. During June, July, and August, rainfall nearly vanishes. July in particular demonstrates unstable parameterization, with extreme values of under both formulations, highlighting the scarcity of rainfall and the difficulty in representing very dry conditions.
The parameter in Table 2 refers to the mean pulse depth parameter used internally by HYETOS-R, not the mean daily rainfall. The seemingly large values arise because scales pulse intensities to match total rainfall depths based on storm and pulse frequencies. Together with (storm frequency), (mean pulse count), and (pulse intensity variance), these parameters control rainfall clustering and variability. Both distributions capture the winter storm regime, with the Gamma formulation reproducing stronger clustering and higher variance consistent with observations. By September and October, rainfall gradually returns, with Gamma capturing temporal persistence more effectively. November resembles early winter conditions, while December strongly reflects the wettest conditions, where Gamma again provides higher fidelity in representing storm bursts compared to Exponential. This interpretation is supported by the parameter values in Table 2, where the Gamma formulation yields a smaller (0.025 h−1 vs. 0.031 h−1) and higher (2.9 vs. 2.4) and (0.45 vs. 0.33) compared to the Exponential case. These numerical differences indicate that the Gamma distribution produces storms that are less frequent but contain more pulses of greater variability, thereby reproducing the observed clustering and higher variance characteristic of Corfu’s winter rainfall.
Corfu represents the rainiest of the four study areas and exhibits a distinctly maritime Mediterranean climate with intense rainfall events in winter and long dry intervals in summer. This pronounced seasonal contrast provides a valuable test case for evaluating the RBLRPM’s performance across highly variable rainfall regimes.
During the wettest month (December), as shown in Figure 5, both pulse–intensity formulations reproduce the observed rainfall characteristics effectively. The exponential formulation performs better in capturing short-term persistence and reproduces the rapid fluctuations observed in hourly rainfall. This outcome reflects the tendency of the exponential model to generate more intense, short rainfall pulses, consistent with the convective dynamics typical of Corfu’s winter storms. The gamma formulation, by contrast, produces a smoother autocorrelation decay, offering a slightly more conservative representation of persistence. Nevertheless, both distributions maintain realistic rainfall structure and clustering.
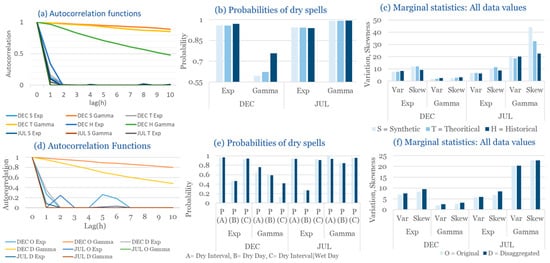
Figure 5.
Statistical Characteristics of Corfu, with the intensity of the pulses following both distributions (December and July combined): (a) autocorrelation functions, (b) probabilities of dry spells, (c) variance and skewness. Panels (a–c) include: H = historical (observed data), T = theoretical (analytical RBLRPM expectation from fitted parameters), and S = synthetic (simulated hourly series) and panels (d–f) include: O = Original and D = Disaggregated. Separate curves correspond to Gamma and Exponential pulse-intensity formulations.
The model successfully reproduces the probability of dry spells and overall intermittency of rainfall in December. The exponential formulation tends to slightly underestimate the frequency of short dry intervals due to denser pulse generation, while the gamma variant maintains more balanced rainfall sequences. Variance and skewness analysis show that the exponential model yields higher variability and a closer match to the observed right-skewed distribution of hourly rainfall. These findings indicate that the exponential distribution better reproduces the intensity dynamics of winter precipitation, whereas the gamma distribution emphasizes stability and smoother temporal transitions.
In the driest month (July), the climatic regime shifts dramatically toward long dry periods interrupted by isolated convective events. Under these highly intermittent conditions, both formulations perform reasonably well in reproducing the dryness probability and low rainfall variability observed. However, the exponential model slightly overestimates the occurrence of minor rainfall events, whereas the gamma formulation better captures the dominance of dry spells and the sporadic nature of precipitation. Despite the scarcity of data for July, both models remain stable and produce physically consistent simulations that mirror observed dryness patterns.
Across both months, the RBLRPM demonstrates its flexibility and robustness in simulating rainfall under contrasting climatic conditions. The exponential pulse–intensity formulation better reproduces the high-frequency variability and intensity peaks characteristic of Corfu’s wet season, while the gamma formulation excels under dry conditions, offering greater stability and coherence in low-rainfall environments. These results confirm that the RBLRPM, when properly calibrated through the EAS optimization framework, effectively represents rainfall intermittency and intensity across diverse Mediterranean settings.
As a result, Corfu illustrates how the RBLRPM successfully adapts to a wet Mediterranean climate. Gamma offers superior reproduction of rainfall clustering, skewness, and variance across the full seasonal cycle, while Exponential provides smoother outcomes with more stable calibration under dry conditions.
3.1.2. Rhodes
Rhodes, positioned in the southeastern Aegean, represents the driest boundary of the Hellenic rainfall regime. Its precipitation regime is shaped by sharp seasonality, with intense winter storms contrasting against nearly rainless summers. December records an average daily precipitation of 4.120 mm, while September—the driest month—averages only 0.112 mm. This pronounced gradient makes Rhodes a valuable testbed for assessing the ability of the RBLRPM to reproduce both high-frequency winter rainfall and prolonged summer droughts. Simulations are therefore performed for all months, and the calibrated parameter values are presented in Table 3.

Table 3.
RBLRPM parameters for Rhodes.
As shown in Table 3, the parameter sets vary widely across the year, underscoring the pronounced rainfall intermittency of Rhodes. In the wettest months (November–January), both distributions calibrate reasonably well, with indicating high storm arrival frequency. In contrast, during the summer months (June–August), the model struggles with sparse data, leading to unstable or missing parameter estimates. Transitional months such as April and October show intermediate performance, where the Exponential model frequently overestimates dry spell probabilities, while the Gamma distribution better preserves variance and clustering.
Rhodes presents markedly different rainfall behavior compared to the western regions of Greece, being drier and more irregular throughout the year. Its semi-arid conditions offer a rigorous test of the RBLRPM’s ability to simulate rainfall under limited moisture availability and sparse storm activity.
During the wettest month (December), as shown in Figure 6, both model variants reproduce the observed rainfall structure with high reliability. The autocorrelation behavior is consistent with the observed data, particularly at short lags, confirming the model’s ability to preserve temporal dependence even under a less humid regime. The gamma formulation performs marginally better in reproducing long-term persistence and smoother rainfall evolution, while the exponential formulation emphasizes short, intense bursts that characterize occasional convective storms. This difference illustrates the flexibility of the RBLRPM in balancing storm intensity against temporal coherence.
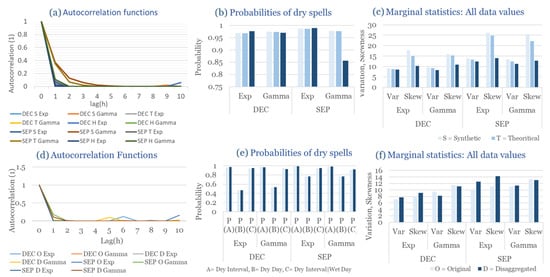
Figure 6.
Statistical Characteristics of Rhodes, with the intensity of the pulses following both distributions (December and September combined): (a) autocorrelation functions, (b) probabilities of dry spells, (c) variance and skewness. Panels (a–c) include: H = historical (observed data), T = theoretical (analytical RBLRPM expectation from fitted parameters), and S = synthetic (simulated hourly series) and panels (d–f) include: O = Original and D = Disaggregated. Separate curves correspond to Gamma and Exponential pulse-intensity formulations.
Dry-spell probabilities and rainfall variability during December are well represented in both formulations, though the exponential distribution tends to slightly overestimate the frequency of very short dry intervals. The gamma distribution, conversely, captures longer inter-event periods and yields more stable statistical behavior. Variance and skewness analyses confirm that the exponential model enhances high-frequency variability, while the gamma distribution results in more moderate fluctuations. These tendencies reflect Rhodes’ intermediate climatic character—between the humid west and the arid southeast of Greece.
In the driest month (September), rainfall is scarce and dominated by isolated, low-intensity events. Under these conditions, the model successfully reproduces the rarity of rainfall and the extended dry-spell probabilities observed. The exponential formulation produces slightly more frequent but weaker rainfall pulses, while the gamma variant aligns more closely with the observed intermittency. Despite the scarcity of rainfall data, both distributions yield coherent outputs without instability in the generated series, indicating robustness of the calibration and parameter estimation process.
Overall, for Rhodes, the RBLRPM captures the essential features of rainfall variability and persistence despite the semi-arid context. The gamma pulse–intensity distribution proves more suitable for representing the island’s smoother rainfall evolution and prolonged dry intervals, while the exponential formulation better reproduces the intensity peaks during rare convective storms. These results demonstrate the adaptability of the RBLRPM framework and its ability to handle diverse rainfall regimes within the Mediterranean domain.
As in the case of Corfu, the expanded analysis in Rhodes confirms that the RBLRPM performs reliably when parameterized through the EAS optimization approach. The model accurately captures both stochastic and temporal rainfall characteristics under constrained data conditions, reinforcing its potential for hydrological simulation and rainfall disaggregation in semi-arid Mediterranean environments.
3.1.3. Alexandroupolis
Located in northeastern Hellas, Alexandroupolis lies at the interface of continental and Mediterranean climatic regimes, which creates distinctive precipitation behavior. Winters are dominated by frequent frontal systems bringing moderate rainfall, while summers are relatively dry but less extreme than in the southern Aegean. December registers the highest daily average precipitation at 3.882 mm, whereas July and August mark the driest conditions, with averages of 0.160 mm and 0.142 mm, respectively. To fully evaluate model performance across these diverse regimes, simulations are carried out for all months. The calibrated parameter values are summarized in Table 4, estimated using the EAS optimization procedure.

Table 4.
RBLRPM parameters for Alexandroupolis.
The parameter sets in Table 4 reveal several features. Winter months (December–February) are characterized by high storm arrival rates and relatively stable variance, consistent with the region’s exposure to frontal systems. By contrast, late spring and summer show parameter instability, with Exponential tending to overestimate dry spell persistence. Gamma parameters indicate greater flexibility in these months, capturing limited but intense events more reliably. Transitional months such as April and October highlight the competing influences of continental and Mediterranean processes, producing wider variability in and .
Alexandroupolis is an interesting transition zone between maritime and continental rainfall regimes. Its mixed climatic character makes it a critical case for testing the RBLRPM’s ability to capture both short-duration, convective rainfall events and longer, stratiform precipitation events.
According to Figure 7, both model formulations simulate the temporal structure and statistical features of rainfall in the wettest month, December, reasonably well. The exponential pulse-intensity distribution captures better high-frequency fluctuations and rapid succession of storms, reflecting its strength for simulating convective events. In contrast, smoother rainfall variability generated by the gamma distribution is closer to longer-duration storm sequences typical of regional maritime influence. The results of the autocorrelation indicate that both formulations retain the observed persistence at different time scales, with a slightly more stable decay for longer lags when using the gamma variant.
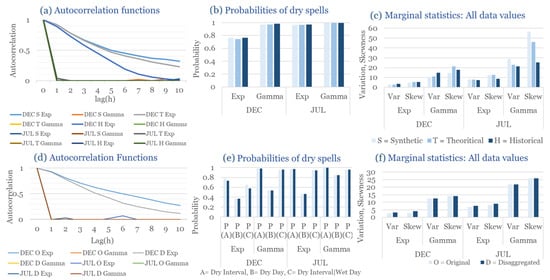
Figure 7.
Statistical Characteristics of Alexandroupolis, with the intensity of the pulses following both distributions (December and July combined): (a) autocorrelation functions, (b) probabilities of dry spells, (c) variance and skewness. Panels (a–c) include: H = historical (observed data), T = theoretical (analytical RBLRPM expectation from fitted parameters), and S = synthetic (simulated hourly series) and panels (d–f) include: O = Original and D = Disaggregated. Separate curves correspond to Gamma and Exponential pulse-intensity formulations.
Dry-spell probabilities and statistical moments (variance and skewness) confirm this pattern. The exponential formulation gives higher variance and more pronounced right-skewness, indicating stronger intensity contrasts, while in the case of the gamma distribution, variability remains balanced, with smoother rainfall evolution. Such differences evidence the fact that Alexandroupolis, due to its intermediate climatic position, benefits from a model capable of blending the characteristics of both humid and semi-arid conditions.
In the driest month (July), rainfall events are scarce and mostly of a convective nature. Isolated storms disrupt prolonged dry periods. Within this regime, the RBLRPM is stable in both formulations. The exponential variant overestimates the occurrence of light rainfall events, while the gamma formulation represents the observed intermittency reasonably well. Both models reproduce the dominant dryness and low rainfall variability despite the limited availability of data.
Overall, the RBLRPM demonstrates consistent skill in capturing seasonal contrasts and the dual influence of maritime and continental weather systems for Alexandroupolis. The exponential distribution performs a little better when it comes to representing short-duration rainfall peaks, while the gamma formulation captures persistence and long dry periods more accurately. These findings support the model’s applicability in regions where rainfall regimes exhibit transitional characteristics between humid and semi-arid climates.
In other words, the findings from Alexandroupolis confirm that the EAS-calibrated RBLRPM retains high adaptability, yielding reliable stochastic rainfall representations in various seasonal and climatic conditions of the wider Mediterranean region.
3.1.4. Herakleion
Herakleion, located on the northern coast of Crete, represents the semi-arid end of the Hellenic rainfall spectrum. Annual precipitation is considerably lower than in the other study sites, and the seasonal cycle is dominated by short, intense winter storms alternating with long, dry summers. December is the wettest month, averaging 2.882 mm of daily rainfall, while July receives only 0.081 mm. These conditions make Herakleion a critical case for testing the robustness of the RBLRPM in data-scarce and low-rainfall environments. Model calibration is performed for all months, with parameter estimates presented in Table 5.

Table 5.
RBLRPM parameters for Herakleion.
As seen in Table 5, parameter estimates vary considerably, reflecting the site’s low but irregular rainfall regime. Winter months (November–January) show higher storm arrival rates, while spring and summer parameters are more erratic due to the paucity of events. The Exponential distribution often inflates dry spell probabilities, while Gamma produces more balanced estimates of clustering and variance. Transitional months, such as October, display the widest uncertainty, consistent with the onset of autumn storms.
Herakleion exhibits one of the most pronounced seasonal contrasts among the examined study areas, with abundant winter rainfall and extended dry summers. This extreme variability makes it an excellent case for testing the stability and adaptability of the RBLRPM under highly contrasting hydrological regimes.
During the wettest month (December), both formulations reproduce the statistical properties of rainfall effectively, as presented in Figure 8. The exponential pulse–intensity formulation captures short-term persistence and event clustering with high fidelity, reflecting the influence of frequent synoptic systems that bring heavy rainfall to Crete during winter. The gamma formulation provides a smoother autocorrelation pattern, indicating longer but less intense storms. Both versions simulate realistic probabilities of dry spells, closely matching the observed values.
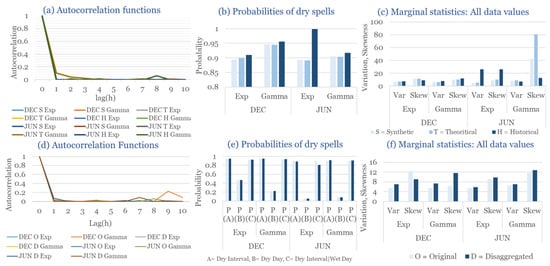
Figure 8.
Statistical Characteristics of Herakleion, with the intensity of the pulses following both distributions (December and July combined): (a) autocorrelation functions, (b) probabilities of dry spells, (c) variance and skewness. Panels (a–c) include: H = historical (observed data), T = theoretical (analytical RBLRPM expectation from fitted parameters), and S = synthetic (simulated hourly series) and panels (d–f) include: O = Original and D = Disaggregated. Separate curves correspond to Gamma and Exponential pulse-intensity formulations.
Comparisons of variance and skewness show that the gamma formulation retains more moderate variability and a slightly lower bias at longer aggregation scales, whereas the exponential formulation more accurately depicts the variability and right-skewed intensity distribution typical of heavy rainfall events. As a result, the RBLRPM effectively captures the temporal and stochastic aspects of rainfall, with the gamma variant offering more overall stability and the exponential variant offering a more dynamic response.
On the other hand, July, the driest month, has almost no precipitation and only sporadic convective storms. The model retains coherence and statistical consistency in both formulations, even though there are not many recorded rainfall events. The exponential distribution produces a slightly higher frequency of weak rainfall events than observed, while the gamma formulation better captures the dominance of extended dry periods. This outcome highlights the model’s ability to remain robust even under extreme intermittency and low data availability.
The strong climatic contrast in Herakleion underlines the importance of model flexibility in handling both persistent and intermittent rainfall structures. The RBLRPM achieves this through its capacity to adjust pulse generation and cluster parameters across distinct regimes. The exponential pulse–intensity distribution is more responsive to high-intensity events, while the gamma distribution excels in smoother representation and persistence.
Overall, Herakleion demonstrates the RBLRPM’s robustness across the Mediterranean spectrum, from intense winter rainfall to prolonged summer droughts. Both formulations perform reliably, with the exponential capturing event-scale variability and the gamma providing stable long-term statistics. These results confirm that the EAS-calibrated RBLRPM framework can be effectively applied in regions with extreme hydrological seasonality, enhancing rainfall disaggregation and modeling accuracy for water resource and flood risk management in southern Mediterranean environments.
3.1.5. Additional Results
In the last subsection of the results, the statistical characteristics of the synthetic partitioned time series are compared with those of the historical ones, for the four study areas. Specifically, the following are examined: (Figure 9a) the probability of rain over the entire time series, (Figure 9b) the first-order autocorrelation coefficient and (Figure 9c) the variability coefficient, at the time scales of 1, 6, 12 and 24 h. Indicatively, the statistical characteristics of each region for the wettest and driest month are presented, due to the plurality of results. The results presented for each month consider that the intensity of the rectangular pulses follows each time the most appropriate distribution for the region, which results from the previous subchapters. As shown in Figure 9, the model satisfactorily maintains the statistical characteristics under study in the various time scales presented. The model performance is similar for all study areas, with the deviations slightly increasing in the drier months.
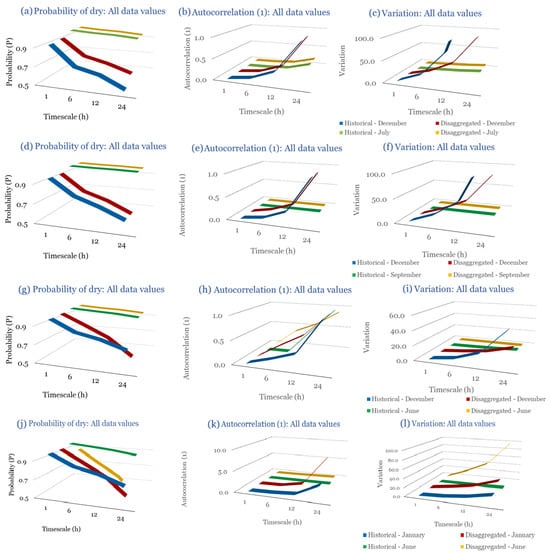
Figure 9.
Comparison of statistical characteristics of the synthetic and historical time series at various aggregation scales, for Corfu, Rhodes, Alexandroupolis and Herakleion, for the driest and rainiest month of each area, where: (a,d,g,j) the diagram of the probability of dry, (b,e,h,k) the diagram of the 1st order autocorrelation coefficient, (c,f,i,l) the diagram of the coefficient of variation.
As presented in Figure 9, at different time scales, the model successfully preserves the statistical properties of the situations under examination.
In Figure 9, the term Probability of Dry refers to the fraction of time intervals with zero rainfall depth, which quantifies rainfall intermittency. The labels D and H at the end of the x-axis correspond to statistics calculated from the disaggregated and historical datasets, respectively, allowing a direct comparison between modelled and observed rainfall behaviour across different aggregation scales.
Notably, deviations increase slightly during the drier months, based on a comparison of the likelihood of rain across the full-time series, the coefficient of variability, and the asymmetry coefficient. These parameters are assessed at several time frames, spanning from 1 to 24 h. The model maintains the statistical integrity of the parameters under control, highlighting the resilience found across time scales.
It should be noted that Figure 9 is not intended as a comprehensive benchmark against all existing disaggregation techniques, but rather as a consistency check of the model’s ability to preserve key rainfall properties. The RBLRPM successfully reproduces rainfall intermittency, variance, and temporal persistence across aggregation scales, demonstrating a level of performance comparable to or better than cascade-based and scaling approaches commonly used for temporal disaggregation [,,]. These methods often struggle to maintain both the intermittency and autocorrelation structure observed in real rainfall data, while the RBLRPM achieves this balance within a physically based stochastic framework suited for data-scarce Mediterranean conditions.
The results shown in Figure 9 provide quantitative support for the model’s ability to reproduce observed rainfall structure. The RBLRPM accurately maintains rainfall intermittency across scales, as evidenced by the disaggregated series’ probability of dry intervals closely matching that of the historical data. It is also confirmed that the temporal persistence of rainfall is maintained because the autocorrelation curves do not change between the two datasets. This consensus supports the claim that the RBLRPM operates consistently across a range of temporal scales by showing that the disaggregation process preserves the key statistical characteristics of the observed rainfall.
However, even if the model maintains the basic statistical properties of the historical data across time scales, any model of natural processes must analyze whether the resulting time series looks to be realistic across time. In all research areas, synthetic hourly time series exhibit satisfactory and realistic behavior. As illustrated in Figure 10, the model appears to create more clustered rain events when the likelihood of dry is high (for the driest months), but rain events appear to be more evenly distributed during the wettest months. More in Appendix C.
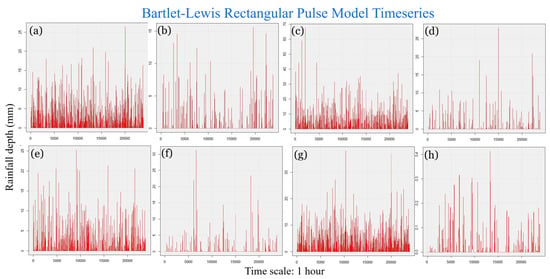
Figure 10.
Diagram of the produced synthetic hourly time series for Corfu (a,b), Rhodes (c,d), Alexandroupolis (e,f) and Herakleion (g,h) for the rainiest and driest month respectively.
Beyond the statistical evaluation, illustrative comparisons between observed and disaggregated hourly rainfall events are provided in Appendix C. These figures show representative wettest- and driest-month events for each study area, generated using the distribution (Exponential or Gamma) identified as most appropriate in Section 3.
BLRPM has indeed shown very good flexibility for the generation of high-resolution rainfall time series at hourly disaggregation for quite a wide range of climatic regimes and data availability. A stochastic process-based parameterization facilitates the capability to reproduce the crucial properties of rainfall, which include intermittency, time-scale-dependent autocorrelation, and clustering. This makes it a very useful tool for applications that require fine temporal resolution, such as urban hydrology and flash flood modeling. On the other hand, important limitations still affect the model, mainly its capacity to simulate extreme rainfall events, which is crucial for risk assessment in high-intensity storms. Consequently, reliance on simple distributions such as Gamma or Exponential for pulse duration and intensity is likely to be inadequate in capturing the tail behavior of rainfall distributions, leading to underestimation of extremes. Moreover, this model does not easily accommodate diurnal variability-one of the most important features in regions with strong solar-driven precipitation cycles especially when it is calibrated based on daily data, which inherently masks sub-daily patterns. These findings might suggest that the BLRPM is suitable for broad disaggregation applications, but that it requires hybrid methodologies or perhaps additional data source integrations to simulate extreme events or diurnal cycles with more accuracy and realism. To better represent extreme rainfall events, distributions such as the Generalized Pareto Distribution (GPD) could be a good approach, as suggested by Park et al. []. Also, the development of machine learning-based hybrid models that incorporate GPD for tail estimation alongside temporal clustering techniques could enhance the accuracy and realism of extreme rainfall predictions.
While the selected datasets provide a representative sample of seasonal variability and rainfall intensity, we acknowledge that the relatively short duration of the hourly records (five years) may limit the model’s capacity to capture rare extreme events or longer-term climatic shifts fully. This is a known challenge in regions with sparse high-resolution data, such as Hellas. Despite this limitation, the validation results suggest that the RBLRPM is able to replicate the main temporal and statistical characteristics of observed hourly rainfall.
A comparative analysis of the four study regions—Corfu, Rhodes, Alexandroupolis, and Herakleion—yields significant insights regarding the geographical and climatic applicability of the RBLRPM. Corfu and Alexandroupolis depict wetter and more continental climates, respectively, with larger temporal autocorrelation and lower intermittency, which the model adequately captures. In contrast, the drier and more dry circumstances of Herakleion, as well as Rhodes’ transitional Mediterranean climate, pose a bigger difficulty due to increased rainfall irregularity and scarce event frequency throughout the summer months. Nonetheless, the RBLRPM shows flexibility across these disparate climates, particularly when pulse intensity distributions are locally adjusted (i.e., exponential vs. gamma). The model performs best at capturing temporal structure in wetter places and during months with more frequent rainfall, while still giving convincing findings in drier environments. These findings indicate that RBLRPM is reliable across a variety of hydrometeorological regimes, making it especially useful in varied, data-scarce Mediterranean contexts.
3.1.6. Uncertainty Analysis
A two-tiered uncertainty analysis is performed to evaluate the robustness of the RBLRPM parameter estimation process. The first component assesses the sensitivity of calibrated parameters to small perturbations in input rainfall statistics. The second investigates the influence of sample size—specifically, the length of the historical time series—on parameter stability.
Sensitivity to Statistical Perturbations
To simulate realistic uncertainty in monthly rainfall statistics, Gaussian noise is added at a 5% level to the mean, variance, lag-1 autocorrelation, and probability of dry. For each scenario, the model is recalibrated using the Evolutionary Annealing-Simplex (EAS) algorithm. A total of 100 independent simulations are run per month, region, and distribution type (Gamma and Exponential), and 95% confidence intervals (CIs) are derived from the resulting parameter distributions.
The analysis revealed notable variability among parameters. For example, in January (Herakleion, Gamma distribution), the 95% CI width for is approximately 40.4, indicating substantial sensitivity to perturbations in rainfall intensity. In contrast, , which controls storm arrival frequency, had a much narrower CI width of 0.0195, reflecting strong stability. Parameters related to storm structure, such as and , showed wider CI widths of 26.8 and 49.9, respectively, emphasizing their sensitivity to event timing and clustering. On the other hand, and / had moderate to narrow CI widths (approximately 4.99 and 4.77, respectively), indicating a more consistent calibration across perturbations.
These results demonstrate that while the RBLRPM is generally robust, parameters controlling rainfall structure rather than magnitude are more susceptible to uncertainty induced by small changes in input statistics.
Influence of Historical Sample Size
To quantify the role of the length of observational records in model uncertainty, the uncertainty analysis is executed with 3, 4, and 5 years of data. Confidence interval widths are computed for each configuration, and trends are graphed over sample sizes and months.
Results confirmed that longer records moderately increased parameter stability for key variables. For example, the CI range for was decreased by approximately 2.3% using 5 vs. 3 years of data, which was reflective of better storm frequency characterization. Parameters and featured near-zero change, which was indicative of high intrinsic stability. Conversely, mean pulse depth () and cluster structure parameter featured small increases in CI range, which were reflective of potential overfitting or seasonal interaction effects in shorter records.
Temporal patterns also highlighted seasonal influences on uncertainty. CI widths would frequently be widest for transition months (e.g., May, October), but narrowest for stable dry-season months (e.g., August), particularly for parameters like . These findings emphasize the interaction between seasonal rainfall processes and parameter sensitivity.
Implications for Data-Scarce Regions
While greater stability is obtained with longer data records, total uncertainty magnitudes were within acceptable limits for all sample sizes. This favorably indicates the usability of the RBLRPM calibration technique in sparse-data conditions. With just three years of data, parameter estimates are sufficiently constrained to facilitate effective rainfall disaggregation and subsequent hydrological modeling. The double distribution technique (Gamma and Exponential) provides flexibility, although the Gamma form generally proves more robust.
Overall, despite only modest gains from additional data, the model remains effective under realistic constraints, offering a valuable tool for rainfall modeling in regions without long-term records.
3.2. Model Limitations and Applicability
RBLRPM has demonstrated good promise in generating major statistical properties of rainfall time series, such as autocorrelation, coefficient of variation, and dry spell probabilities. However, some limitations need to be explicitly accepted whenever its outputs are utilized or the model is applied practically. The rationale for applying the RBLRPM is consistent with previous stochastic rainfall modeling efforts [,,,], which demonstrated the model’s reliability under diverse climatic regimes. The present study extends this body of work by testing the Random version under Mediterranean data-scarce conditions and by integrating an ML benchmark for direct performance comparison.
It also needs to be explained that the fundamental distinction between forecasting models and stochastic rainfall generators like RBLRPM needs to be described. Forecast models are normally intended to forecast the evolution of specific rainfall events with physical or numerical schemes and often on the basis of statistical inputs in real time. Stochastic models, on the other hand, generate statistically representative rainfall sequences for long-term behavior but are not designed to fit specific observed events. In this sense, the RBLRPM provides realistic inputs to hydrological simulation and planning in situations involving uncertainty, where detailed event-level records are either lacking or unavailable.
Most notably, the RBLRPM does not replicate the precise timing or quantity of individual rainfall occurrences. Instead, it produces synthetic time series that retain the average statistical features of the historical data. This makes it unsuitable for operational uses that require event-level detail, such as real-time flooding prediction, early warning systems, or stormwater planning based on observed maxima.
The model also supports temporal stationarity across the calibration period, i.e., free from trends or non-stationarities caused by long-term climatic changes. This limits its future stability in the face of climate change, particularly for long-term forecasting. In places with significant seasonal fluctuations or tough topography, the hypothesis of statistical homogeneity of storm features may not be valid.
Here the model is calibrated to five years of hourly rain gauge data for each region. While short by some measures, such records are a standard data situation for many regions with reduced observational coverage. Far from a limitation, the model’s ability to operate reliably with reduced data constitutes its practical utility, especially in data-limited contexts like most of Hellas.
Finally, the model’s performance depends heavily on the supposed pulse intensity distributions. While both the Exponential and Gamma forms are examined in this study, these may not describe all the tails or skewness for extreme rainfall. In such cases, other or more general distributions could improve performance.
Overall, the RBLRPM is ideally suited for application in hydrological modeling, infrastructure design, and climate resilience planning for regions with limited rainfall data, where it is more crucial to mimic the statistical behavior of rainfall than the individual events. In cases that require higher temporal resolution or physical information, connection with event-based or physically based models could be necessary.
The results align with earlier findings on stochastic rainfall models [,,,] confirming the BLRPM’s capacity to reproduce temporal rainfall structure. However, unlike prior studies, the present work quantifies parameter uncertainty, evaluates two pulse-intensity distributions, and benchmarks against a deterministic ML model. These combined analyses highlight both the stochastic realism of the Random BLRPM and its complementary role alongside ML for rainfall disaggregation in data-scarce Mediterranean contexts.
4. Conclusions and Future Research
This study evaluates the performance of the Random Bartlett–Lewis Rectangular Pulse Model (RBLRPM) for rainfall disaggregation in four regions of Hellas under data-scarce conditions. The novelty of this work lies in testing and validating the RBLRPM in a Mediterranean setting with limited records, where such models are rarely applied, and in contrasting its performance with a machine learning benchmark. By generating high-resolution synthetic series from daily observations, the model reproduces essential rainfall properties such as autocorrelation, variability, and intermittency, even when calibration data are sparse.
To enhance clarity and presentation, two flowcharts were incorporated in the revised version—one outlining the overall RBLRPM algorithm and another describing the calibration and validation process through the EAS optimization framework. In addition, the results and discussion were expanded for each study area, followed by a comparative synthesis across regions to strengthen interpretation and regional context.
The comparison with a machine learning (ML)-based linear regression approach provides valuable insight into the trade-offs between stochastic and deterministic methods. The ML model preserves daily totals effectively and offers a quick, low-cost solution for generating hourly data, but it smooths extremes and underrepresents temporal clustering. By contrast, the RBLRPM reproduces the dynamic structure of rainfall more faithfully, including wet–dry persistence and asymmetry. These differences underline that method selection depends on the application: ML is adequate for preliminary analyses or real-time decision support, whereas RBLRPM is better suited for design and risk assessment.
Another important aspect of this work concerns the choice of pulse intensity distribution within the RBLRPM. Results indicate that the Gamma distribution generally provides a closer match to observed rainfall statistics, especially in terms of autocorrelation and variability. The Exponential distribution, while computationally simpler, is less robust overall but remains useful in specific months and locations, such as December in Corfu. This finding suggests that model performance benefits from flexibility, with distribution choice tailored to local conditions.
The broader implication of this study is that stochastic approaches remain essential in rainfall disaggregation under data scarcity. The RBLRPM, particularly when coupled with the Gamma distribution, demonstrates strong capacity to capture the statistical and temporal dynamics of Mediterranean rainfall. This ability is crucial for hydrological design, stormwater management, and flood risk assessment, where realistic representation of extremes and persistence patterns matters.
At the same time, the inclusion of ML highlights a complementary path forward. The novelty here lies in directly contrasting a traditional stochastic framework with a deterministic ML approach within the same experimental design, offering clear guidance for practitioners. While stochastic methods excel in realism, ML provides efficiency, transparency, and rapid deployability. A promising direction for future research lies in hybrid frameworks that combine the computational simplicity of ML with the statistical fidelity of stochastic models. Such integration strengthens the package available for rainfall disaggregation, supporting both scientific analysis and practical water management in data-scarce environments. Lastly, future work will explore the integration of remotely sensed rainfall datasets (e.g., ERA5, IMERG) to validate gauge records and extend temporal coverage beyond 2004.
Author Contributions
Conceptualization, S.S. and E.B.; methodology, S.S.; software, S.S.; validation, S.S.; formal analysis, S.S.; investigation, S.S.; resources, S.S. and E.B.; data curation, E.B.; writing—original draft preparation, S.S.; writing—review and editing, S.S. and E.B.; visualization, S.S.; supervision, E.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is unavailable due to privacy or ethical restrictions.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BLRPM | Bartlett-Lewis Rectangular Pulse Model |
| NSRPM | Neyman-Scott Rectangular Pulse Model |
| EAS | Evolutionary Annealing-Simplex Algorithm |
| HNMS | Hellenic National Meteorological Service |
| RBLRPM | Random Bartlett-Lewis Rectangular Pulse Model |
Appendix A. Detailed Study Area and Data Analysis
The first research area is Corfu, a Hellenic island located in the northwestern region of Hellas, along the border of Albania and mainland Hellas, at the entrance of the Adriatic Sea and the second-largest Ionian island. Corfu is one of Hellas’s rainiest places, with average annual precipitation ranging between 1000 and 2000 mm, which contributes greatly to the island’s lush vegetation. Seasonal rainfall feeds streams and recharges groundwater, although heavy rains can cause flash flooding in particular locations. As an island, it has heavy rains in winter and very dry summers. The wettest month is December, while the driest is July, as seen in Table A1, along with the statistical characteristics of the rest of the months.

Table A1.
Historical statistical precipitation characteristics of Corfu [].
Table A1.
Historical statistical precipitation characteristics of Corfu [].
| Scale (h) | Months | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| Average | 1 | 0.192 | 0.101 | 0.081 | 0.104 | 0.033 | 0.021 | 0.018 | 0.055 | 0.134 | 0.209 | 0.244 | 0.263 |
| 6 | 1.153 | 0.608 | 0.483 | 0.625 | 0.198 | 0.124 | 0.110 | 0.330 | 0.805 | 1.254 | 1.462 | 1.576 | |
| 12 | 2.306 | 1.216 | 0.966 | 1.250 | 0.396 | 0.249 | 0.221 | 0.659 | 1.611 | 2.507 | 2.924 | 3.152 | |
| 24 | 4.612 | 2.432 | 1.932 | 2.501 | 0.792 | 0.497 | 0.442 | 1.318 | 3.221 | 5.015 | 5.848 | 6.305 | |
| Standard deviation | 1 | 1.920 | 0.860 | 0.518 | 1.050 | 0.366 | 0.147 | 0.194 | 3.234 | 2.364 | 3.537 | 5.455 | 2.727 |
| 6 | 14.240 | 7.309 | 4.411 | 7.769 | 2.344 | 1.216 | 1.883 | 19.712 | 18.840 | 30.526 | 37.100 | 21.878 | |
| 12 | 38.329 | 23.872 | 12.631 | 17.366 | 5.115 | 2.972 | 4.146 | 39.488 | 45.071 | 77.456 | 119.384 | 75.092 | |
| 24 | 101.085 | 56.450 | 31.799 | 46.337 | 10.511 | 6.102 | 8.226 | 107.467 | 102.035 | 197.137 | 319.837 | 216.277 | |
| Covariance | 1 | 0.037 | 0.010 | 0.006 | 0.011 | 0.001 | 0.000 | 0.000 | 0.003 | 0.018 | 0.044 | 0.072 | 0.069 |
| 6 | 1.329 | 0.370 | 0.233 | 0.391 | 0.039 | 0.015 | 0.012 | 0.109 | 0.649 | 1.572 | 2.694 | 2.484 | |
| 12 | 5.317 | 1.478 | 0.933 | 1.563 | 0.157 | 0.062 | 0.049 | 0.434 | 2.594 | 6.287 | 9.978 | 9.937 | |
| 24 | 21.267 | 5.913 | 3.734 | 6.253 | 0.627 | 0.247 | 0.195 | 1.737 | 10.377 | 18.629 | 40.740 | 35.334 | |
| Probability of Dry | 1 | 0.941 | 0.962 | 0.968 | 0.964 | 0.983 | 0.991 | 0.995 | 0.995 | 0.973 | 0.959 | 0.946 | 0.925 |
| 6 | 0.758 | 0.835 | 0.861 | 0.850 | 0.919 | 0.955 | 0.976 | 0.977 | 0.877 | 0.829 | 0.787 | 0.705 | |
| 12 | 0.697 | 0.787 | 0.832 | 0.800 | 0.884 | 0.942 | 0.965 | 0.968 | 0.823 | 0.787 | 0.716 | 0.645 | |
| 24 | 0.613 | 0.677 | 0.774 | 0.697 | 0.819 | 0.916 | 0.942 | 0.955 | 0.735 | 0.710 | 0.606 | 0.523 | |
Consequently, the second study area is Rhodes, the fourth largest Hellenic island, located in the southeastern Aegean Sea, close to the coast of Turkey. Rhodes has a Mediterranean climate characterized by hot, dry summers and warm, rainy winters. It is noted for having one of the longest yearly sunlight periods in Europe. Annual rainfall is between 600 and 700 mm, which is less than on northern Hellenic islands such as Corfu, but sufficient to maintain agricultural activity and winter water demands. Intense winter rains combined with rapid runoff from steep terrain may lead to localized floods. The island’s wettest month is once again December, while after zero months, the driest month is September. Rhodes’ essential historical statistical precipitation characteristics are shown in Table A2.

Table A2.
Historical statistical precipitation characteristics of Rhodes [].
Table A2.
Historical statistical precipitation characteristics of Rhodes [].
| Scale (h) | Months | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| Average | 1 | 0.176 | 0.098 | 0.061 | 0.065 | 0.010 | 0.000 | 0.000 | 0.000 | 0.003 | 0.011 | 0.098 | 0.203 |
| 6 | 1.056 | 0.586 | 0.364 | 0.387 | 0.059 | 0.000 | 0.000 | 0.001 | 0.015 | 0.064 | 0.587 | 1.220 | |
| 12 | 2.111 | 1.173 | 0.728 | 0.775 | 0.118 | 0.000 | 0.000 | 0.002 | 0.030 | 0.129 | 1.174 | 2.439 | |
| 24 | 4.223 | 2.345 | 1.455 | 1.549 | 0.237 | 0.000 | 0.000 | 0.003 | 0.060 | 0.257 | 2.347 | 4.879 | |
| Standard deviation | 1 | 2.177 | 0.901 | 0.827 | 1.354 | 0.062 | 0.000 | 0.000 | 0.000 | 0.009 | 0.071 | 1.308 | 2.491 |
| 6 | 18.310 | 7.854 | 5.417 | 9.216 | 0.398 | 0.000 | 0.000 | 0.000 | 0.052 | 0.424 | 9.904 | 20.247 | |
| 12 | 39.812 | 25.996 | 13.767 | 18.274 | 0.871 | 0.000 | 0.000 | 0.001 | 0.110 | 0.902 | 21.591 | 51.132 | |
| 24 | 94.932 | 68.621 | 35.394 | 36.173 | 1.981 | 0.000 | 0.000 | 0.002 | 0.293 | 1.816 | 50.011 | 143.790 | |
| Covariance | 1 | 0.031 | 0.010 | 0.004 | 0.004 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.010 | 0.041 |
| 6 | 2.580 | 0.344 | 0.132 | 0.150 | 0.004 | 0.000 | 0.000 | 0.000 | 0.000 | 0.004 | 0.344 | 1.488 | |
| 12 | 2.376 | 1.375 | 0.530 | 0.600 | 0.014 | 0.000 | 0.000 | 0.000 | 0.001 | 0.017 | 1.377 | 5.950 | |
| 24 | 3.452 | 5.500 | 2.118 | 2.400 | 0.056 | 0.000 | 0.000 | 0.000 | 0.004 | 0.066 | 5.509 | 23.802 | |
| Probability of Dry | 1 | 0.951 | 0.970 | 0.984 | 0.981 | 0.996 | 1.000 | 1.000 | 1.000 | 0.998 | 0.995 | 0.976 | 0.951 |
| 6 | 0.779 | 0.866 | 0.924 | 0.905 | 0.981 | 1.000 | 1.000 | 0.998 | 0.989 | 0.973 | 0.890 | 0.787 | |
| 12 | 0.700 | 0.797 | 0.890 | 0.842 | 0.965 | 1.000 | 1.000 | 0.997 | 0.984 | 0.958 | 0.832 | 0.703 | |
| 24 | 0.587 | 0.716 | 0.832 | 0.735 | 0.942 | 1.000 | 1.000 | 0.994 | 0.974 | 0.935 | 0.735 | 0.600 | |
The third case study region is Alexandroupolis. The city is located in northeast Hellas near the Aegean Sea and enjoys a Mediterranean continental climate with harsh winters and mild summers. As shown in Table A3, the region receives the majority of its precipitation during the winter months, with December receiving the most rain. The summer months, particularly July and August, are the driest.

Table A3.
Historical statistical precipitation characteristics of Alexandoupolis [].
Table A3.
Historical statistical precipitation characteristics of Alexandoupolis [].
| Scale (h) | Months | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| Average (mm) | 1 | 0.065 | 0.028 | 0.041 | 0.034 | 0.028 | 0.014 | 0.016 | 0.026 | 0.030 | 0.042 | 0.051 | 0.090 |
| 6 | 0.391 | 0.166 | 0.249 | 0.202 | 0.171 | 0.081 | 0.094 | 0.156 | 0.179 | 0.251 | 0.306 | 0.540 | |
| 12 | 0.783 | 0.333 | 0.497 | 0.405 | 0.342 | 0.162 | 0.187 | 0.312 | 0.358 | 0.502 | 0.612 | 1.079 | |
| 24 | 1.566 | 0.665 | 0.995 | 0.809 | 0.683 | 0.325 | 0.374 | 0.624 | 0.716 | 1.004 | 1.224 | 2.158 | |
| Standard deviation (mm) | 1 | 0.582 | 0.192 | 0.237 | 0.129 | 0.181 | 0.097 | 0.124 | 0.901 | 0.177 | 0.440 | 0.510 | 0.512 |
| 6 | 4.122 | 1.438 | 1.827 | 0.935 | 1.288 | 0.631 | 0.741 | 5.715 | 1.214 | 2.911 | 4.862 | 4.560 | |
| 12 | 9.195 | 3.767 | 5.381 | 2.682 | 3.101 | 1.379 | 1.482 | 11.399 | 3.095 | 6.860 | 16.424 | 15.395 | |
| 24 | 20.876 | 9.047 | 18.414 | 5.871 | 7.586 | 2.973 | 3.322 | 22.732 | 10.238 | 13.423 | 43.758 | 47.004 | |
| Covariance (mm2) (lag-1) | 1 | 0.004 | 0.001 | 0.002 | 0.001 | 0.001 | 0.000 | 0.000 | 0.001 | 0.001 | 0.002 | 0.003 | 0.008 |
| 6 | 0.153 | 0.028 | 0.062 | 0.041 | 0.029 | 0.007 | 0.009 | 0.024 | 0.032 | 0.063 | 0.094 | 0.141 | |
| 12 | 0.613 | 0.111 | 0.247 | 0.164 | 0.117 | 0.509 | 0.035 | 0.097 | 0.128 | 0.252 | 0.374 | 0.301 | |
| 24 | 2.452 | 0.442 | 0.990 | 0.655 | 0.194 | 2.621 | 0.140 | 0.389 | 0.513 | 1.008 | 1.498 | 2.931 | |
| Probability of Dry (%) | 1 | 0.974 | 0.985 | 0.983 | 0.978 | 0.989 | 0.996 | 0.996 | 0.997 | 0.990 | 0.988 | 0.984 | 0.963 |
| 6 | 0.884 | 0.932 | 0.916 | 0.895 | 0.947 | 0.977 | 0.979 | 0.982 | 0.948 | 0.940 | 0.924 | 0.840 | |
| 12 | 0.842 | 0.906 | 0.877 | 0.845 | 0.916 | 0.961 | 0.961 | 0.965 | 0.919 | 0.913 | 0.884 | 0.787 | |
| 24 | 0.774 | 0.858 | 0.800 | 0.768 | 0.865 | 0.935 | 0.929 | 0.935 | 0.877 | 0.858 | 0.832 | 0.703 | |
The last study is Herakleion, which is on the northern coast of Crete in southern Hellas, and experiences a hot-summer Mediterranean climate. Winters are mild with moderate rainfall and warm to hot and dry with clear skies during the summer. The city averages around 464 mm of precipitation per year, with the majority occurring between October and May, as shown in Table A4.

Table A4.
Historical statistical precipitation characteristics of Herakleion [].
Table A4.
Historical statistical precipitation characteristics of Herakleion [].
| Scale (h) | Months | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| Average | 1 | 0.059 | 0.015 | 0.023 | 0.053 | 0.046 | 0.009 | 0.021 | 0.012 | 0.025 | 0.047 | 0.027 | 0.069 |
| 6 | 0.355 | 0.091 | 0.137 | 0.320 | 0.275 | 0.051 | 0.125 | 0.072 | 0.151 | 0.281 | 0.159 | 0.413 | |
| 12 | 0.710 | 0.181 | 0.275 | 0.640 | 0.549 | 0.103 | 0.251 | 0.145 | 0.302 | 0.563 | 0.318 | 0.826 | |
| 24 | 1.420 | 0.363 | 0.550 | 1.281 | 1.099 | 0.206 | 0.501 | 0.289 | 0.603 | 1.125 | 0.636 | 1.652 | |
| Standard deviation | 1 | 0.395 | 0.037 | 0.113 | 0.294 | 0.322 | 0.031 | 0.136 | 0.134 | 0.212 | 0.284 | 0.114 | 0.228 |
| 6 | 2.889 | 0.242 | 1.099 | 2.105 | 2.108 | 0.185 | 1.368 | 0.805 | 1.288 | 2.791 | 0.912 | 1.816 | |
| 12 | 8.718 | 0.632 | 3.482 | 5.069 | 4.465 | 0.497 | 3.260 | 1.602 | 2.759 | 6.385 | 2.567 | 5.366 | |
| 24 | 18.904 | 1.299 | 13.154 | 12.853 | 9.780 | 1.162 | 8.741 | 3.201 | 5.420 | 15.675 | 6.806 | 13.052 | |
| Covariance | 1 | 0.004 | 0.000 | 0.001 | 0.003 | 0.002 | 0.000 | 0.000 | 0.000 | 0.001 | 0.002 | 0.001 | 0.005 |
| 6 | 0.126 | 0.008 | 0.019 | 0.103 | 0.075 | 0.003 | 0.016 | 0.005 | 0.023 | 0.079 | 0.025 | 1.605 | |
| 12 | 0.504 | 0.033 | 0.076 | 0.410 | 0.302 | 0.011 | 0.063 | 0.021 | 0.091 | 0.316 | 0.101 | 3.199 | |
| 24 | 3.238 | 0.131 | 0.302 | 1.640 | 1.207 | 0.042 | 0.251 | 0.084 | 0.364 | 1.266 | 0.405 | 9.494 | |
| Probability of Dry | 1 | 0.967 | 0.982 | 0.986 | 0.971 | 0.980 | 0.994 | 0.991 | 0.994 | 0.990 | 0.978 | 0.984 | 0.958 |
| 6 | 0.847 | 0.918 | 0.934 | 0.873 | 0.911 | 0.969 | 0.955 | 0.971 | 0.948 | 0.902 | 0.919 | 0.813 | |
| 12 | 0.790 | 0.884 | 0.894 | 0.826 | 0.858 | 0.942 | 0.923 | 0.942 | 0.913 | 0.865 | 0.877 | 0.752 | |
| 24 | 0.697 | 0.819 | 0.832 | 0.735 | 0.800 | 0.903 | 0.890 | 0.897 | 0.845 | 0.806 | 0.806 | 0.665 | |
Appendix B. Full Monthly Disaggregation Results by Region
This section contains the complete set of monthly disaggregation results for all four study regions—Corfu, Rhodes, Alexandroupolis, and Herakleion—using both exponential and gamma pulse intensity distributions. While the main manuscript presents results only for the wettest and driest months of each region to emphasize key contrasts, the full twelve-month comparisons are provided here to ensure transparency and reproducibility. The figures include statistical comparisons between observed and synthetic rainfall series, supporting the evaluation of the RBLRPM’s performance across different climatic conditions and seasonal regimes.
Figure A1.
Statistical Characteristics of Corfu for January, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
Figure A2.
Statistical Characteristics of Corfu for February, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
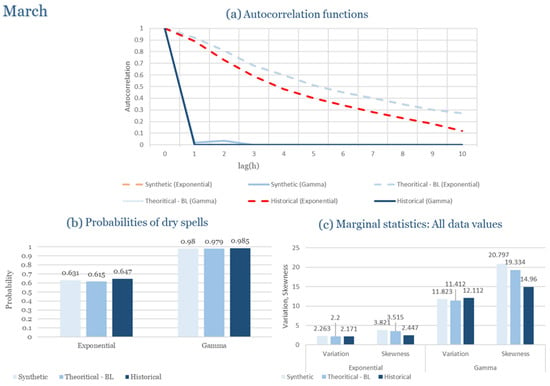
Figure A3.
Statistical Characteristics of Corfu for March, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
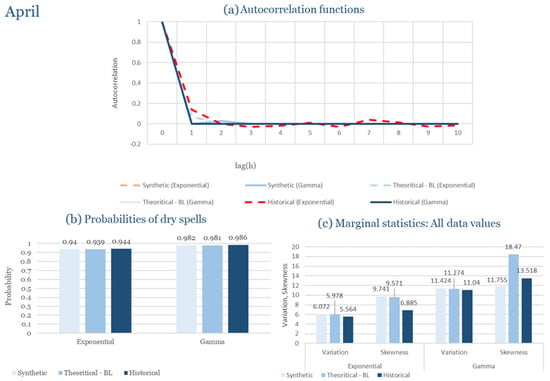
Figure A4.
Statistical Characteristics of Corfu for April, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
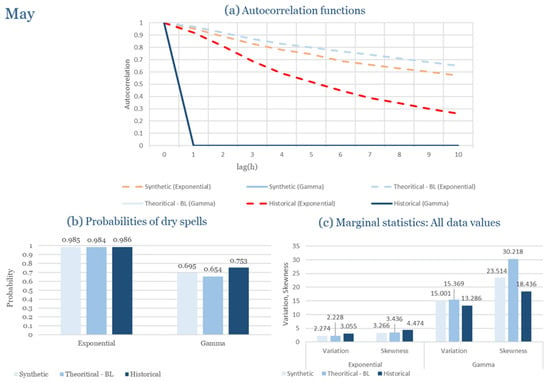
Figure A5.
Statistical Characteristics of Corfu for May, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
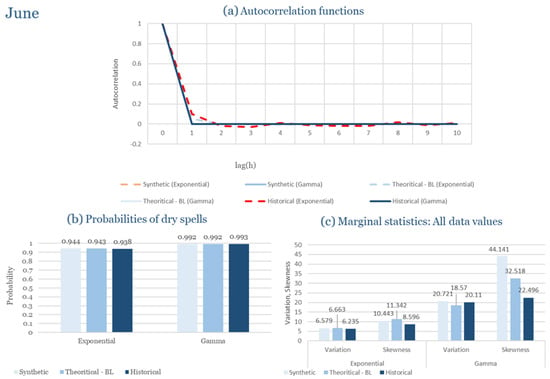
Figure A6.
Statistical Characteristics of Corfu for June, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
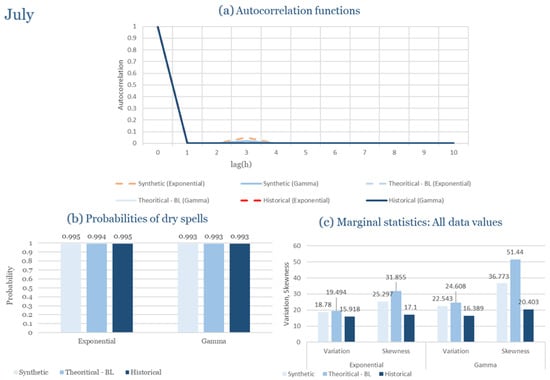
Figure A7.
Statistical Characteristics of Corfu for July, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
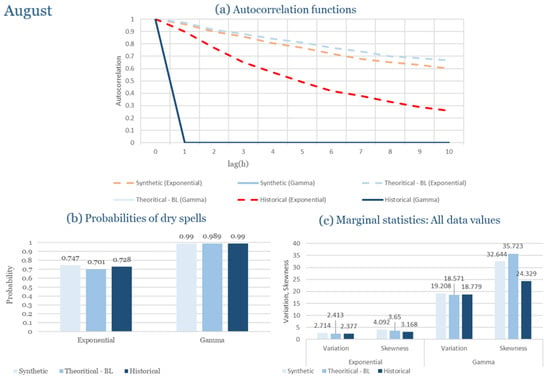
Figure A8.
Statistical Characteristics of Corfu for August, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
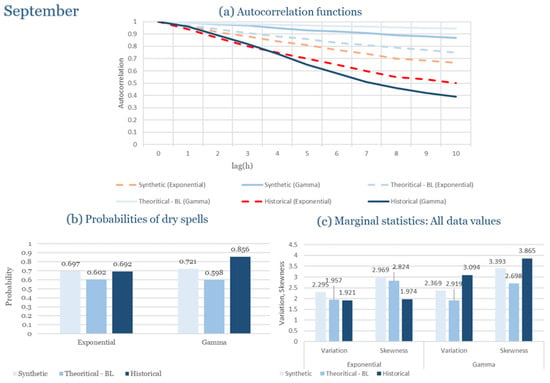
Figure A9.
Statistical Characteristics of Corfu for September, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
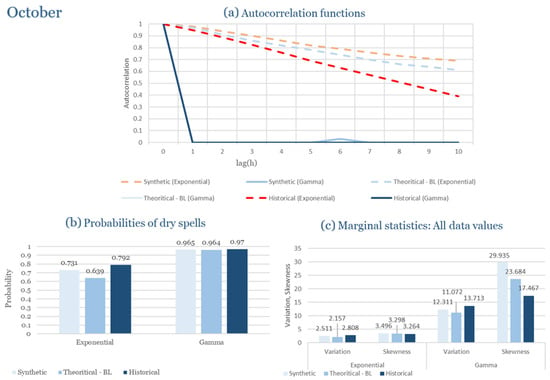
Figure A10.
Statistical Characteristics of Corfu for October, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
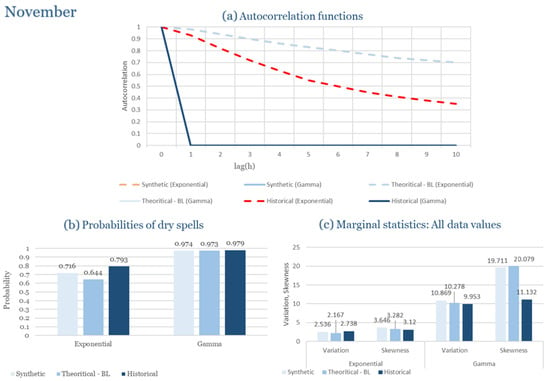
Figure A11.
Statistical Characteristics of Corfu for November, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
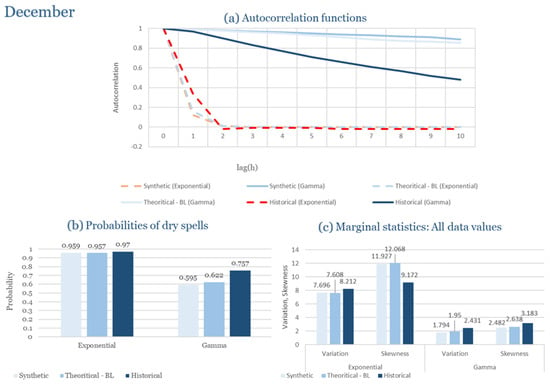
Figure A12.
Statistical Characteristics of Corfu for December, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
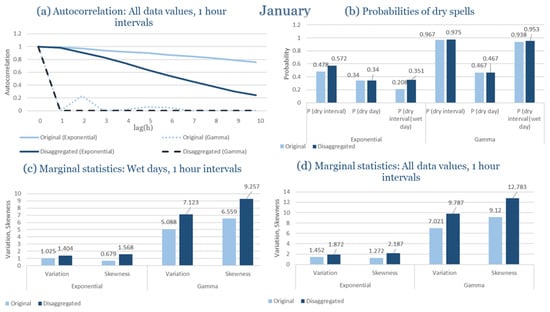
Figure A13.
Statistical Characteristics of Corfu for January, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
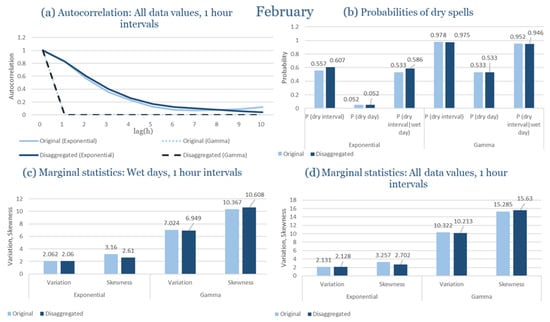
Figure A14.
Statistical Characteristics of Corfu for February, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
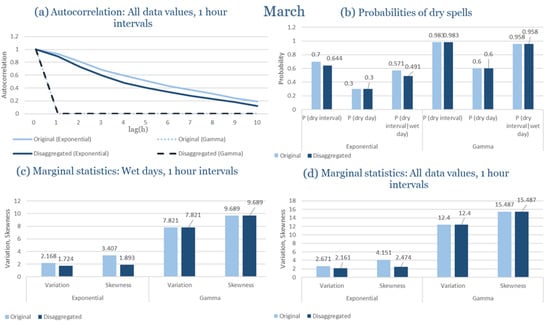
Figure A15.
Statistical Characteristics of Corfu for March, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
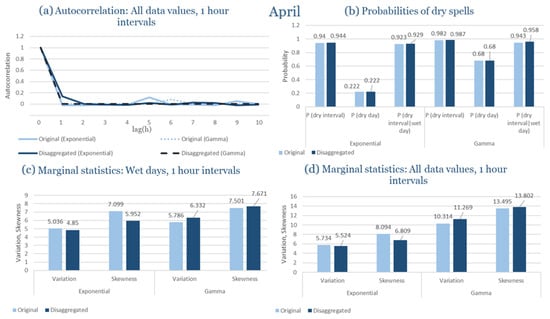
Figure A16.
Statistical Characteristics of Corfu for April, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
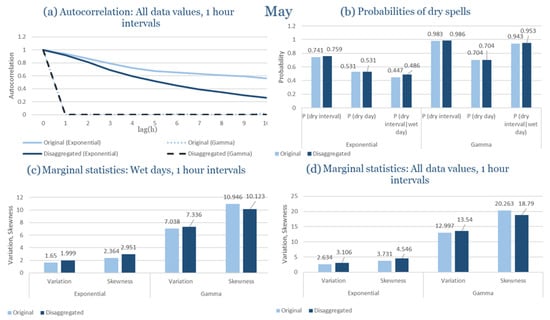
Figure A17.
Statistical Characteristics of Corfu for May, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
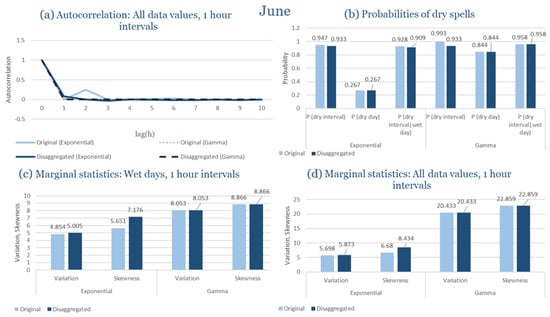
Figure A18.
Statistical Characteristics of Corfu for June, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
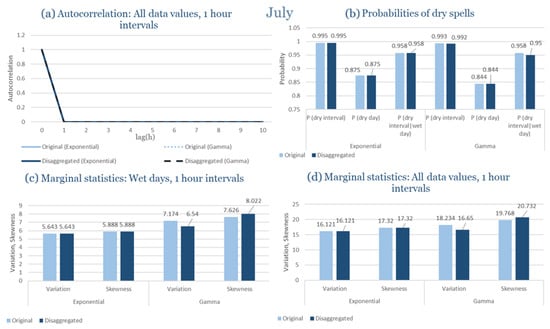
Figure A19.
Statistical Characteristics of Corfu for July, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
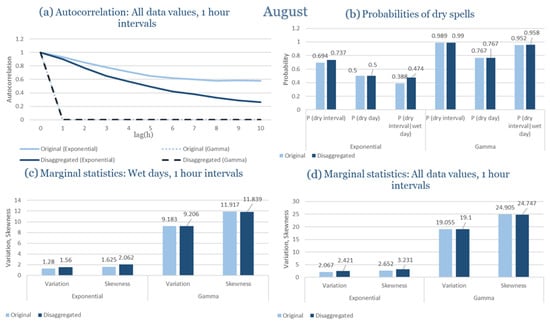
Figure A20.
Statistical Characteristics of Corfu for August, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
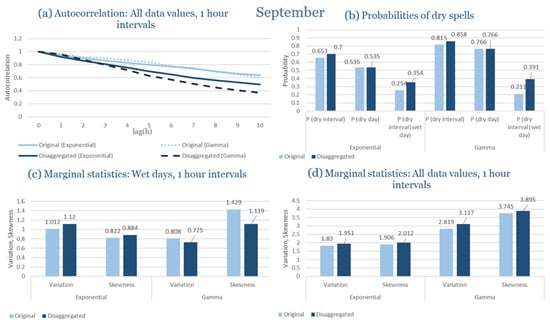
Figure A21.
Statistical Characteristics of Corfu for September, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
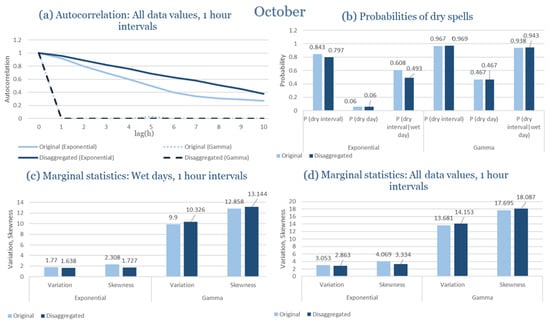
Figure A22.
Statistical Characteristics of Corfu for October, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
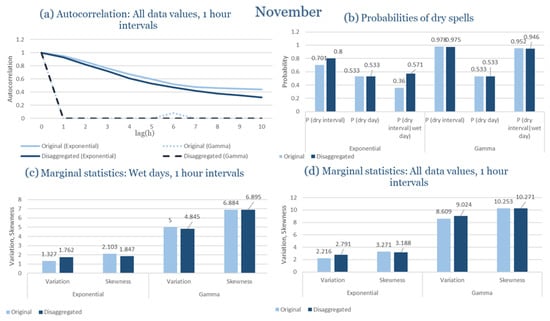
Figure A23.
Statistical Characteristics of Corfu for November, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
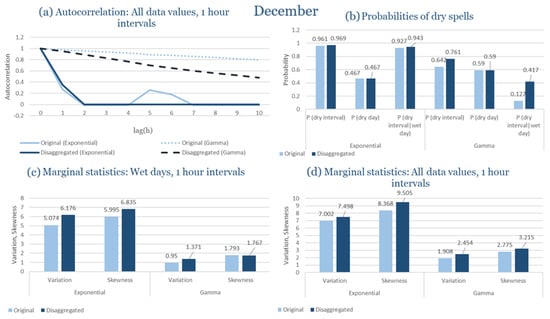
Figure A24.
Statistical Characteristics of Corfu for December, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
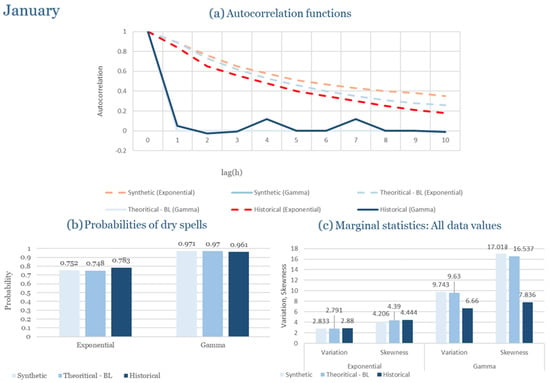
Figure A25.
Statistical Characteristics of Rhodes for January, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
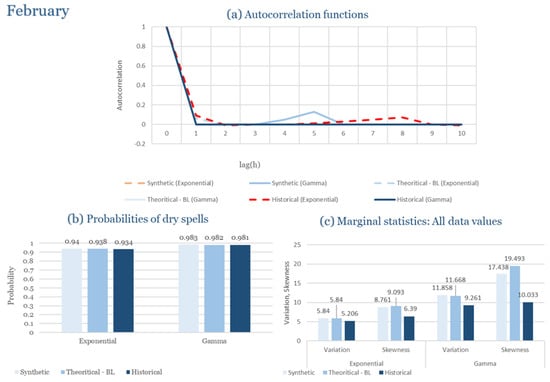
Figure A26.
Statistical Characteristics of Rhodes for February, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
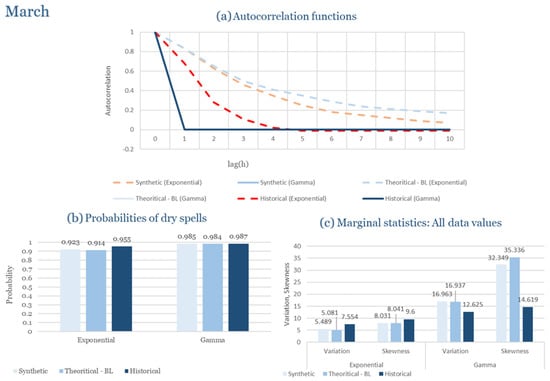
Figure A27.
Statistical Characteristics of Rhodes for March, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
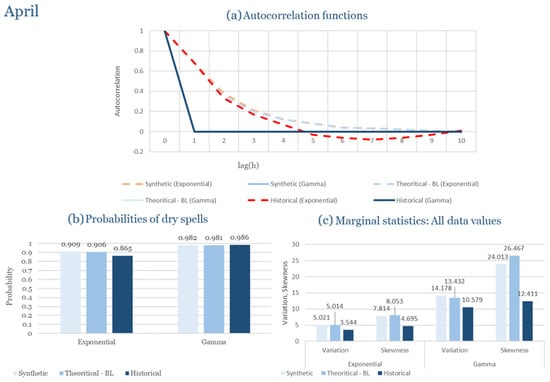
Figure A28.
Statistical Characteristics of Rhodes for April, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
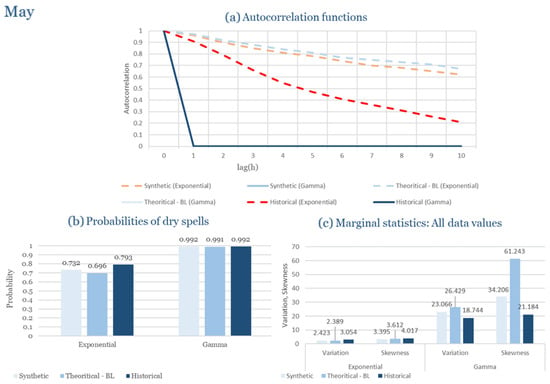
Figure A29.
Statistical Characteristics of Rhodes for May, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
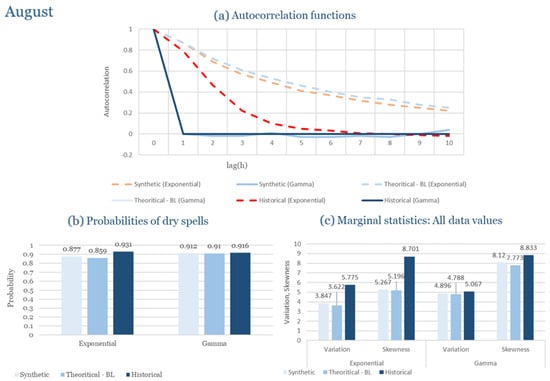
Figure A30.
Statistical Characteristics of Rhodes for August, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
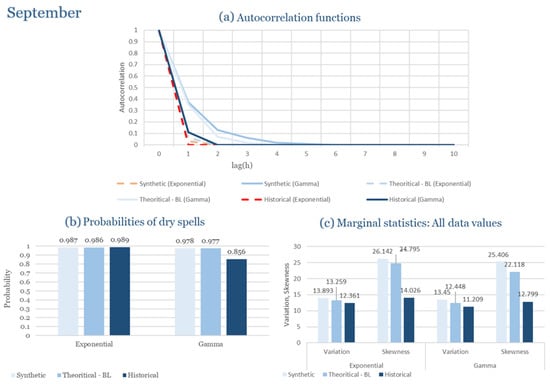
Figure A31.
Statistical Characteristics of Rhodes for Septemebr, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
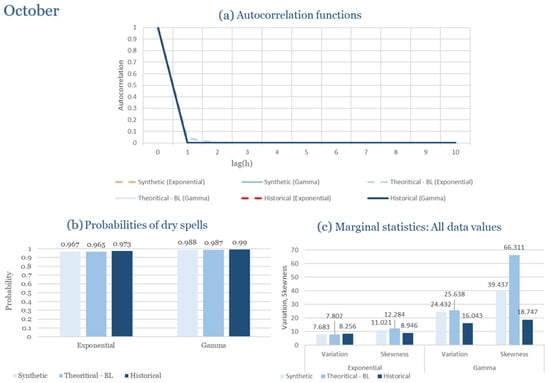
Figure A32.
Statistical Characteristics of Rhodes for October, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
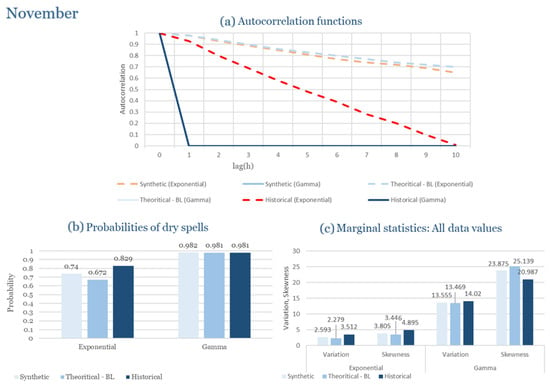
Figure A33.
Statistical Characteristics of Rhodes for November, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
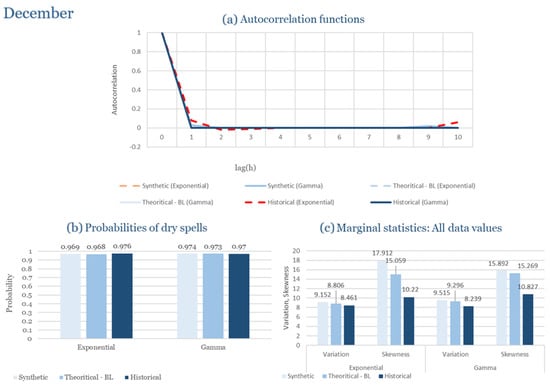
Figure A34.
Statistical Characteristics of Rhodes for December, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
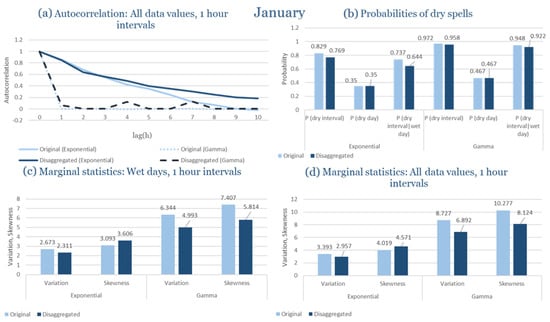
Figure A35.
Statistical Characteristics of Rhodes for January, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
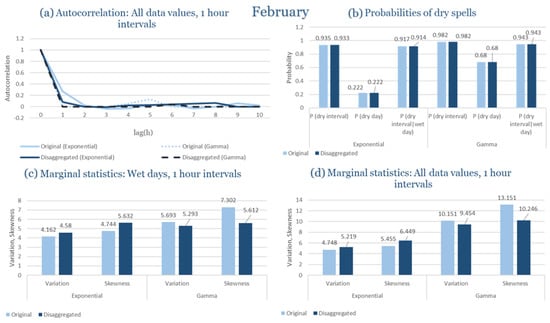
Figure A36.
Statistical Characteristics of Rhodes for February, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
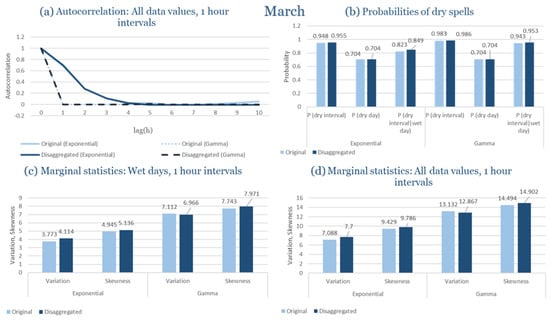
Figure A37.
Statistical Characteristics of Rhodes for March, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
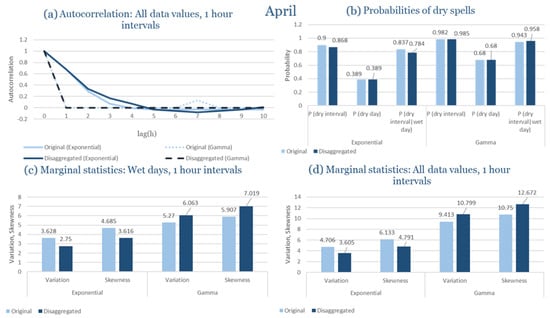
Figure A38.
Statistical Characteristics of Rhodes for April, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
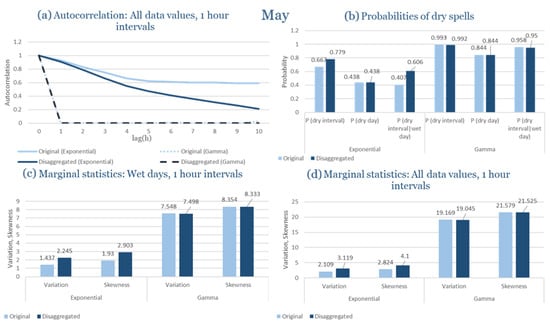
Figure A39.
Statistical Characteristics of Rhodes for May, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
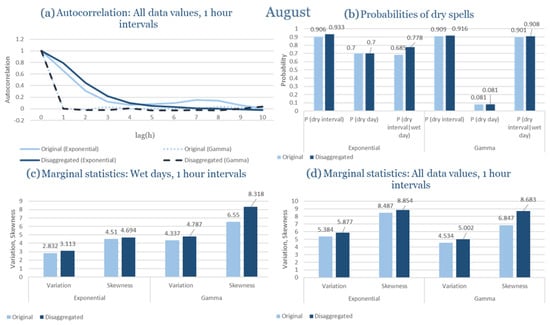
Figure A40.
Statistical Characteristics of Rhodes for August, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
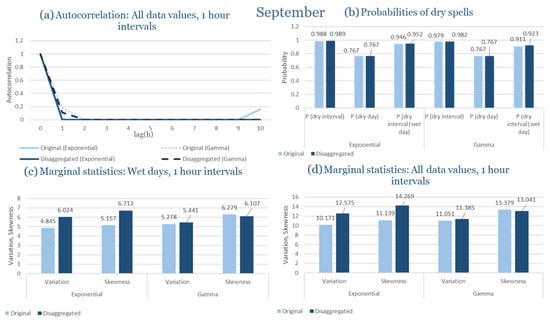
Figure A41.
Statistical Characteristics of Rhodes for September, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
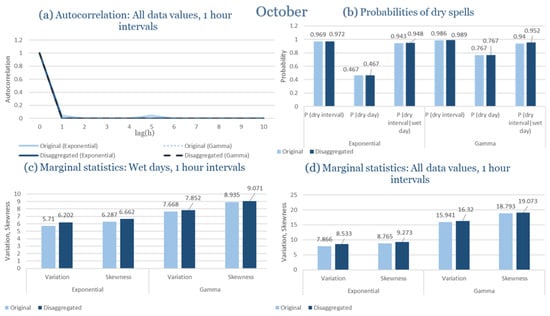
Figure A42.
Statistical Characteristics of Rhodes for October, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
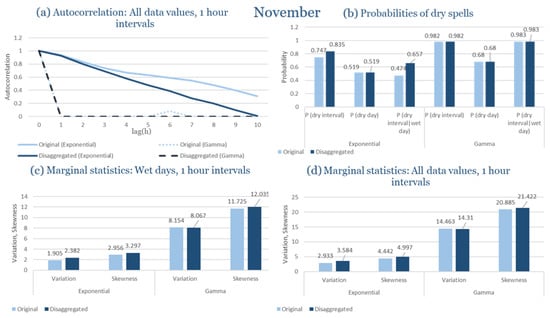
Figure A43.
Statistical Characteristics of Rhodes for Novemebr, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
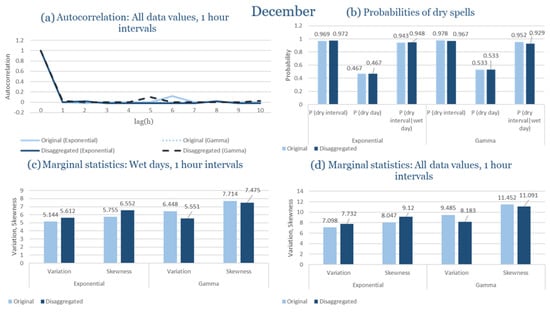
Figure A44.
Statistical Characteristics of Rhodes for December, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
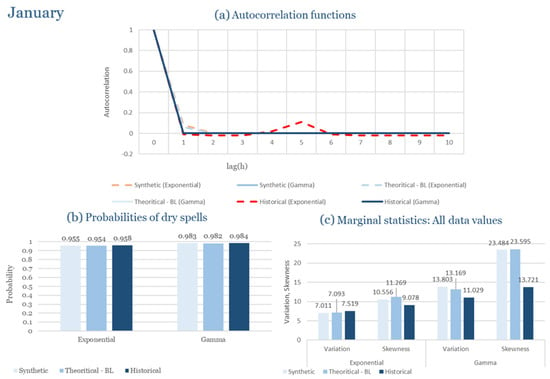
Figure A45.
Statistical Characteristics of Alexandroupolis for January, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
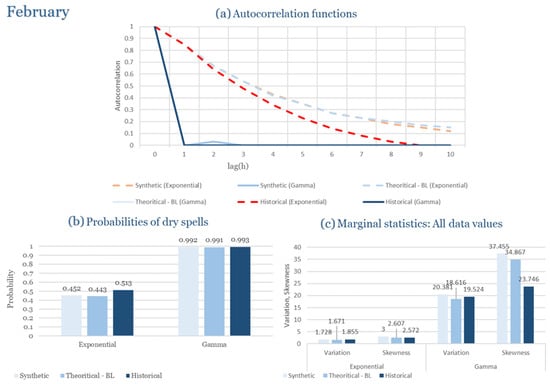
Figure A46.
Statistical Characteristics of Alexandroupolis for February, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
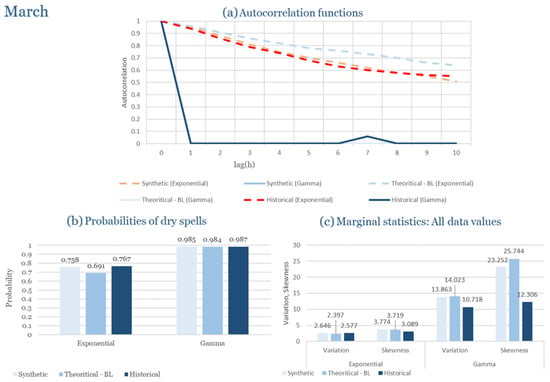
Figure A47.
Statistical Characteristics of Alexandroupolis for March, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
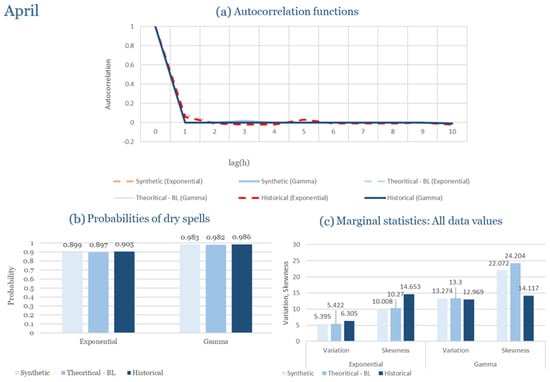
Figure A48.
Statistical Characteristics of Alexandroupolis for April, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
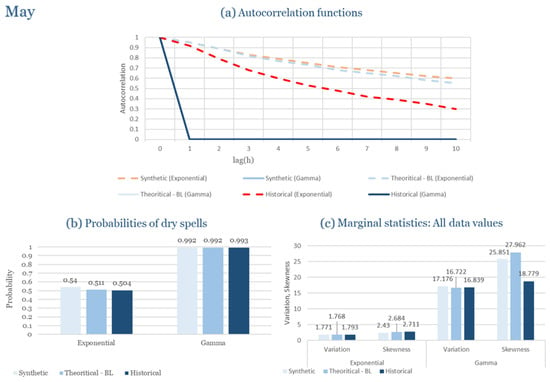
Figure A49.
Statistical Characteristics of Alexandroupolis for May, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
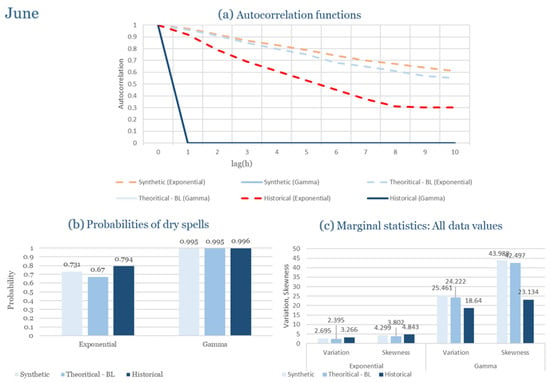
Figure A50.
Statistical Characteristics of Alexandroupolis for June, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
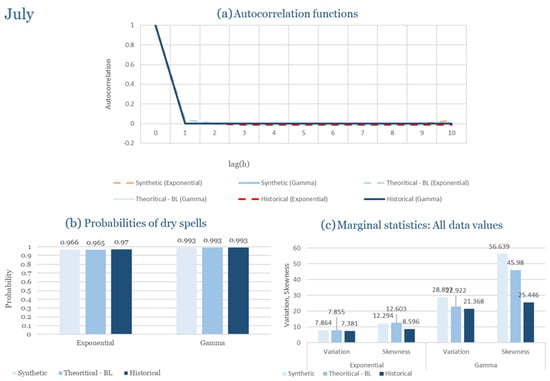
Figure A51.
Statistical Characteristics of Alexandroupolis for July, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
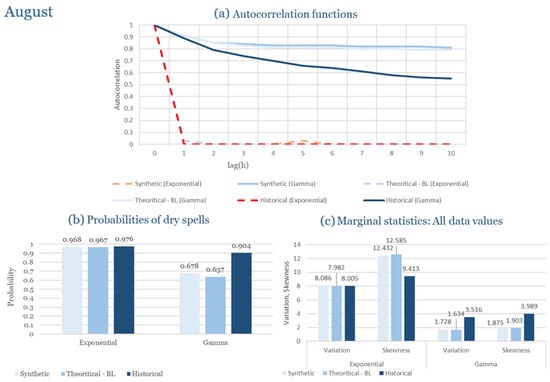
Figure A52.
Statistical Characteristics of Alexandroupolis for August, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
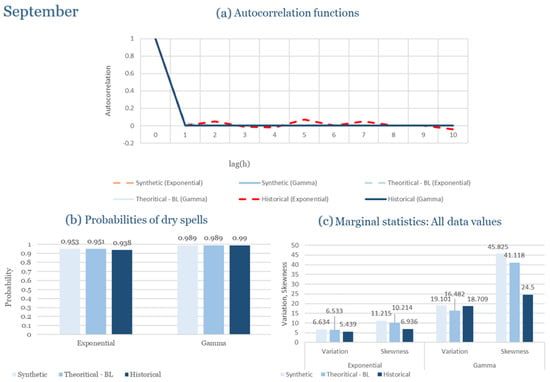
Figure A53.
Statistical Characteristics of Alexandroupolis for September, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
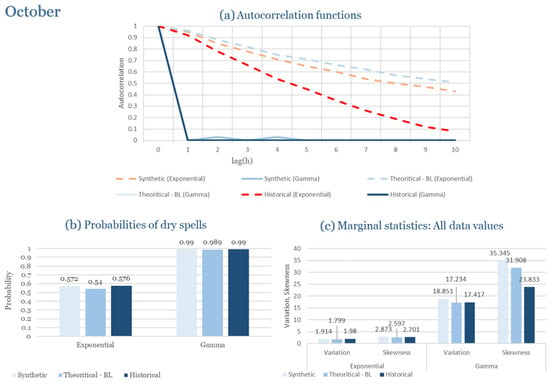
Figure A54.
Statistical Characteristics of Alexandroupolis for October, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
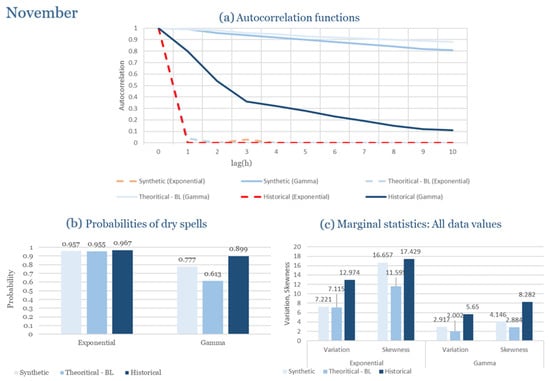
Figure A55.
Statistical Characteristics of Alexandroupolis for November, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
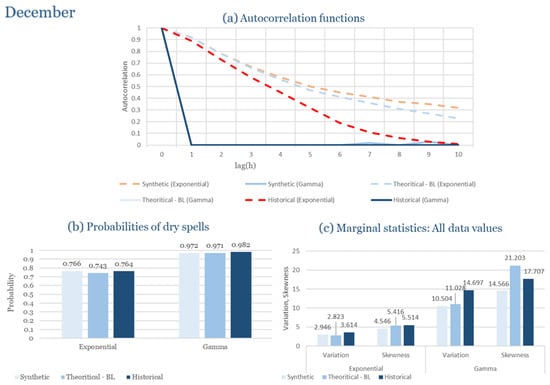
Figure A56.
Statistical Characteristics of Alexandroupolis for December, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
Figure A57.
Statistical Characteristics of Alexandroupolis for January, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
Figure A58.
Statistical Characteristics of Alexandroupolis for February, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
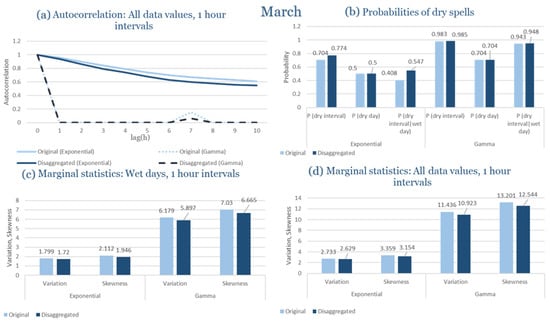
Figure A59.
Statistical Characteristics of Alexandroupolis for March, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
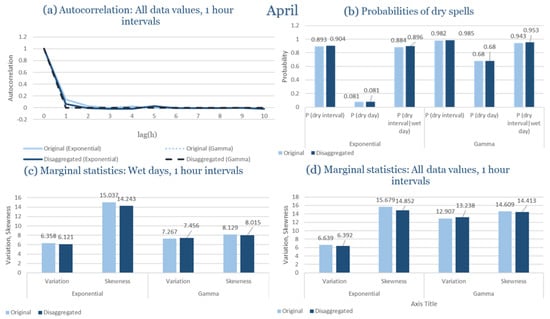
Figure A60.
Statistical Characteristics of Alexandroupolis for April, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
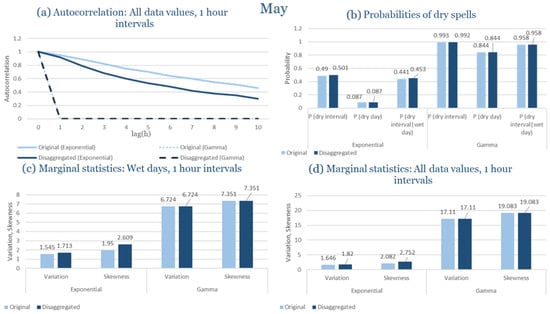
Figure A61.
Statistical Characteristics of Alexandroupolis for May, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
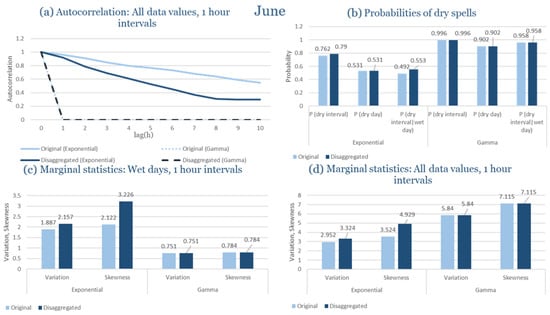
Figure A62.
Statistical Characteristics of Alexandroupolis for June, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
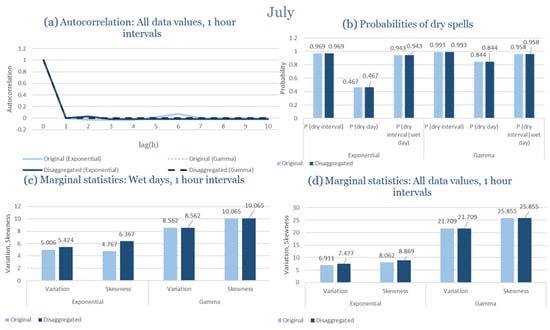
Figure A63.
Statistical Characteristics of Alexandroupolis for July, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
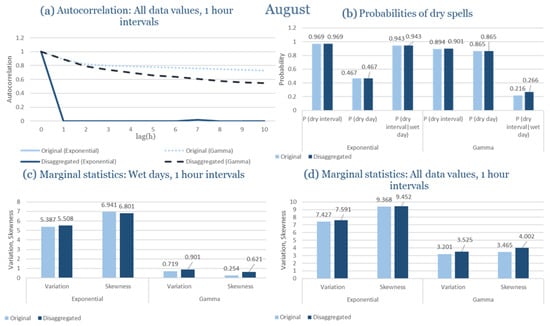
Figure A64.
Statistical Characteristics of Alexandroupolis for August, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
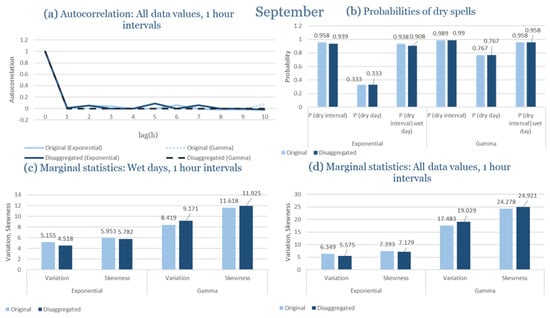
Figure A65.
Statistical Characteristics of Alexandroupolis for September, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
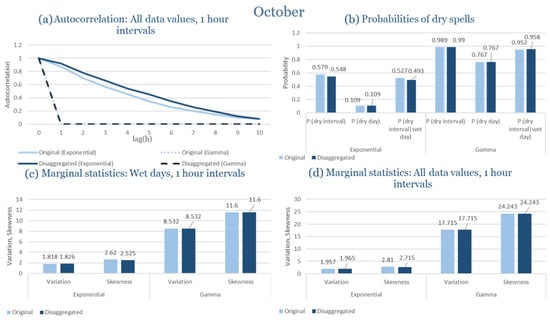
Figure A66.
Statistical Characteristics of Alexandroupolis for October, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
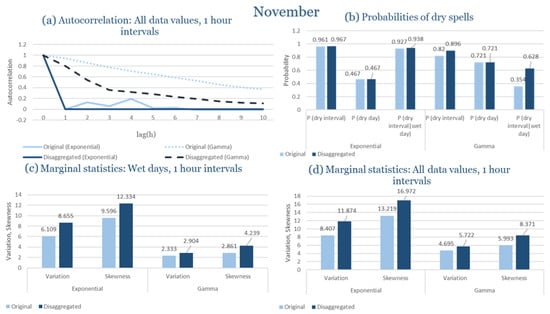
Figure A67.
Statistical Characteristics of Alexandroupolis for November, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
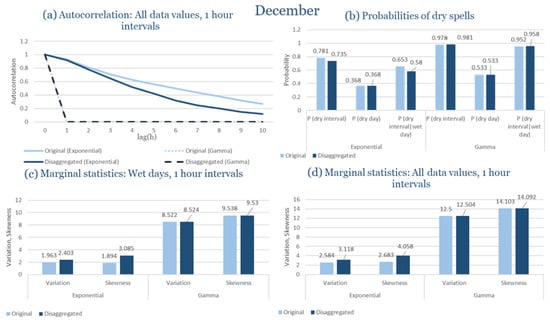
Figure A68.
Statistical Characteristics of Alexandroupolis for December, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
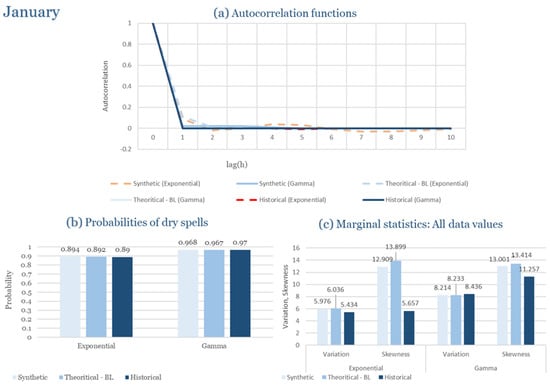
Figure A69.
Statistical Characteristics of Herakleion for January, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
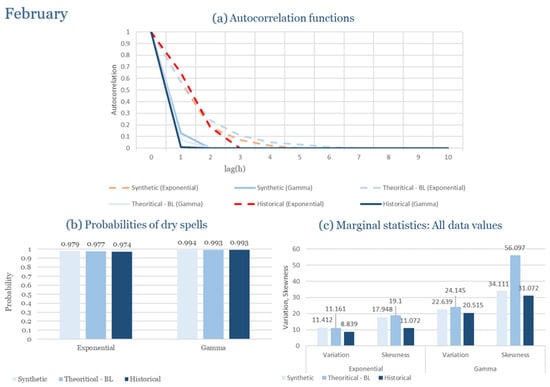
Figure A70.
Statistical Characteristics of Herakleion for February, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
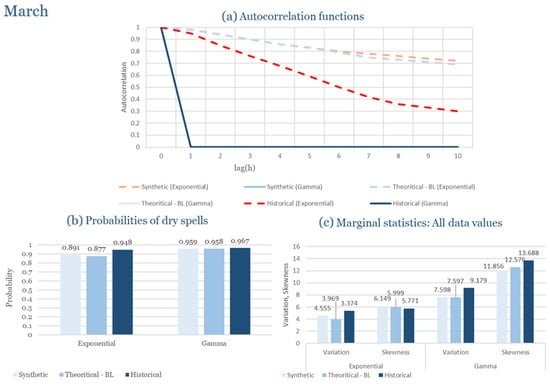
Figure A71.
Statistical Characteristics of Herakleion for March, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
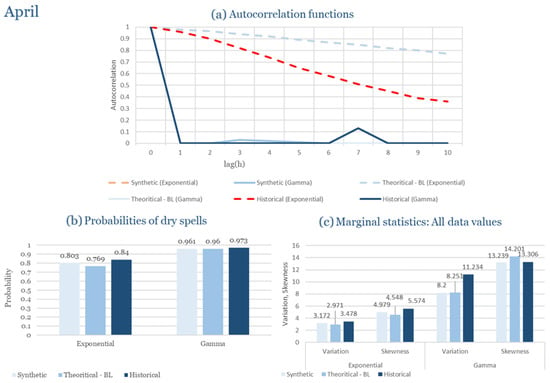
Figure A72.
Statistical Characteristics of Herakleion for April, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
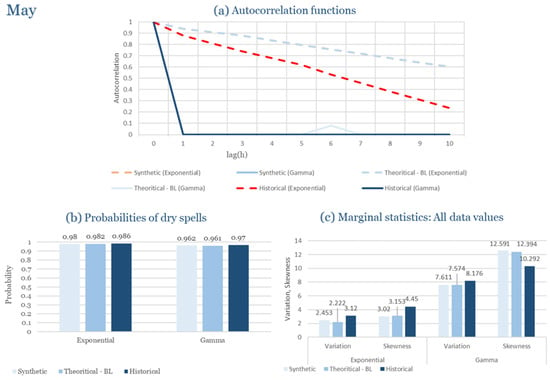
Figure A73.
Statistical Characteristics of Herakleion for May, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
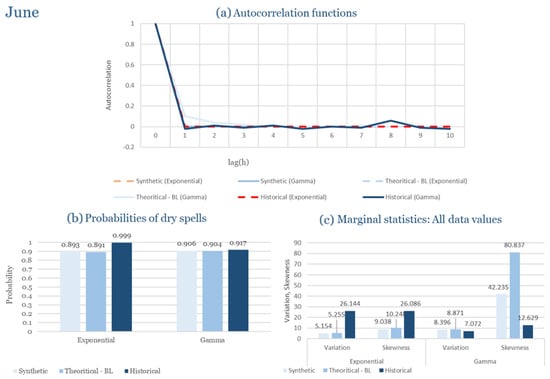
Figure A74.
Statistical Characteristics of Herakleion for June, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
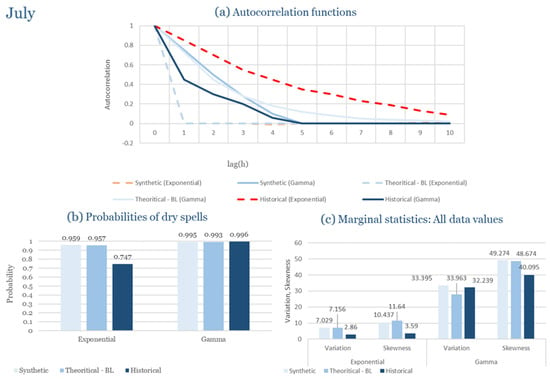
Figure A75.
Statistical Characteristics of Herakleion for July, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
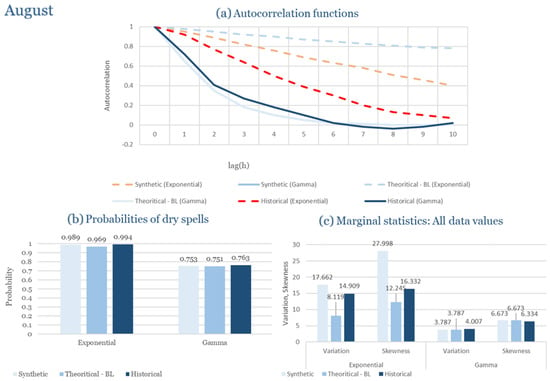
Figure A76.
Statistical Characteristics of Herakleion for August, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
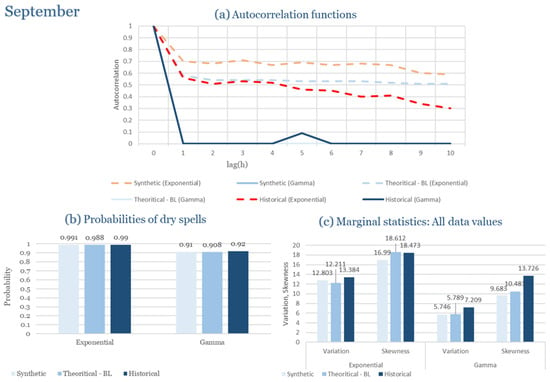
Figure A77.
Statistical Characteristics of Herakleion for September, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
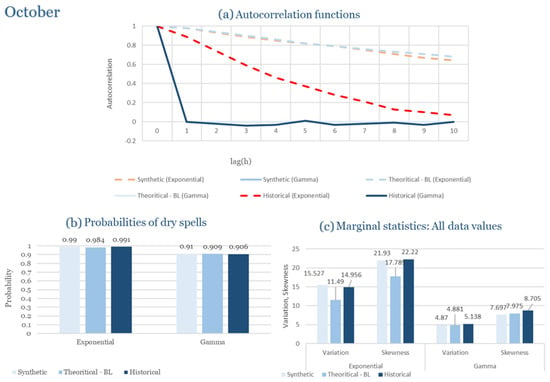
Figure A78.
Statistical Characteristics of Herakleion for October, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
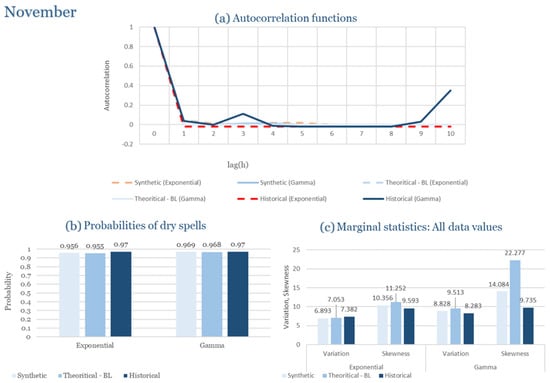
Figure A79.
Statistical Characteristics of Herakleion for November, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
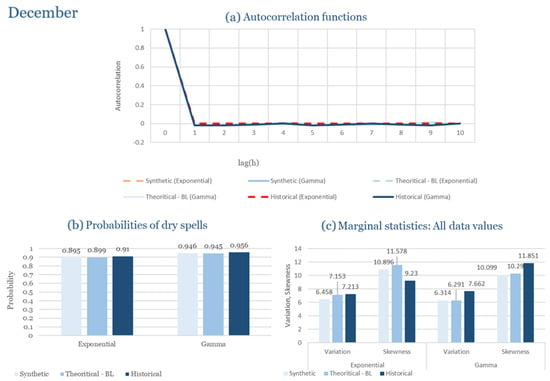
Figure A80.
Statistical Characteristics of Herakleion for December, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagram of the probability of dry and (c) the diagrams for the coefficient of variation and skewness of the historical and synthetic timeseries.
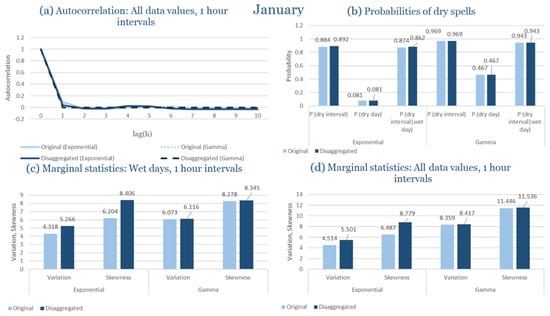
Figure A81.
Statistical Characteristics of Herakleion for January, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
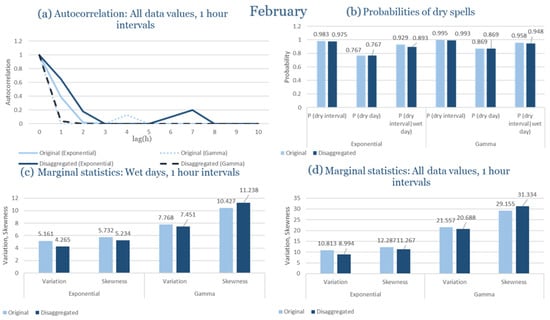
Figure A82.
Statistical Characteristics of Herakleion for February, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
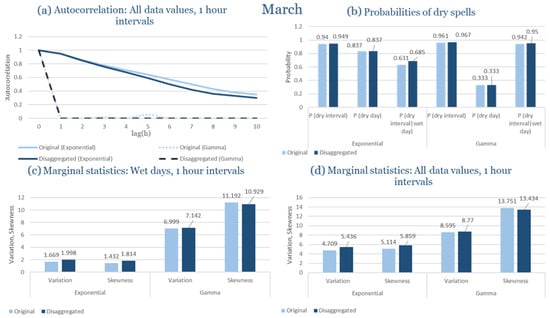
Figure A83.
Statistical Characteristics of Herakleion for March, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
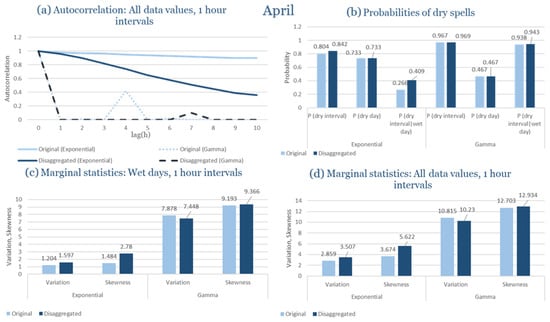
Figure A84.
Statistical Characteristics of Herakleion for April, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
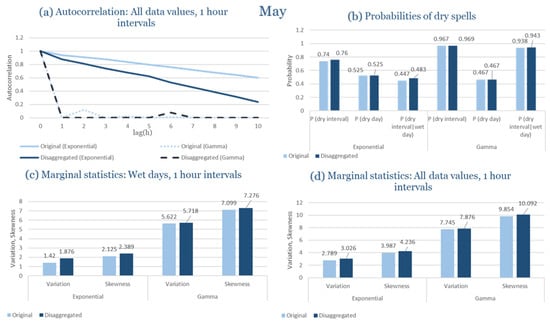
Figure A85.
Statistical Characteristics of Herakleion for May, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
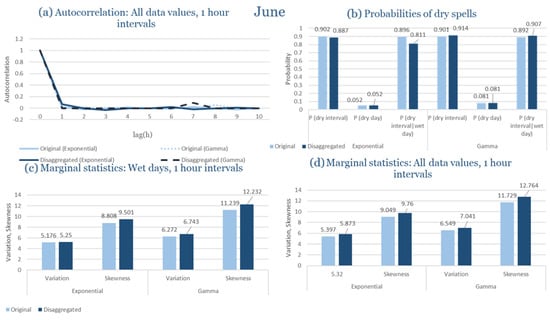
Figure A86.
Statistical Characteristics of Herakleion for June, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
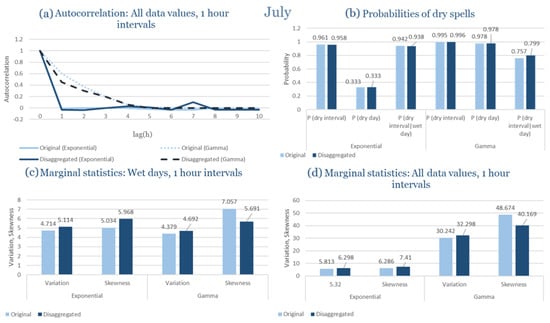
Figure A87.
Statistical Characteristics of Herakleion for July, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
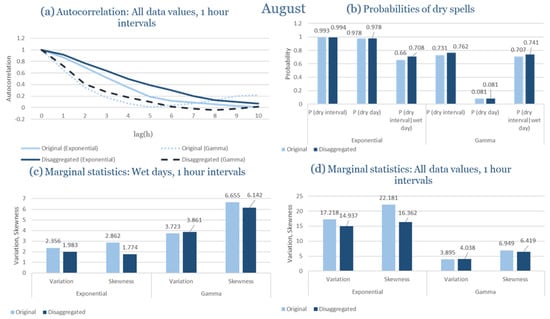
Figure A88.
Statistical Characteristics of Herakleion for August, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
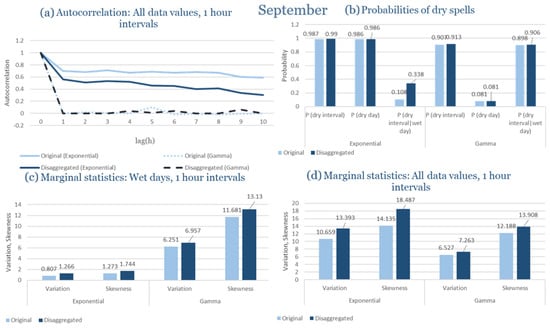
Figure A89.
Statistical Characteristics of Herakleion for September, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
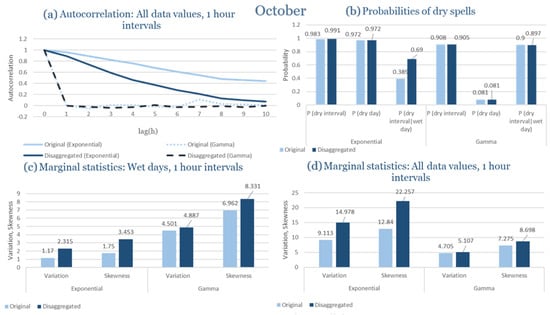
Figure A90.
Statistical Characteristics of Herakleion for October, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
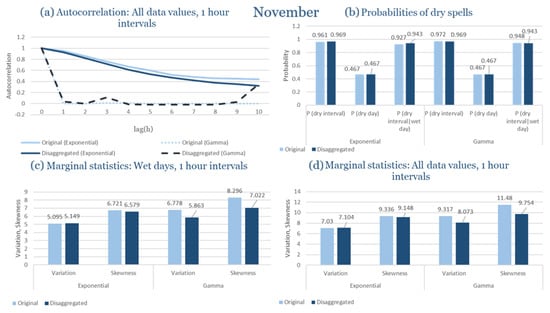
Figure A91.
Statistical Characteristics of Herakleion for November, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
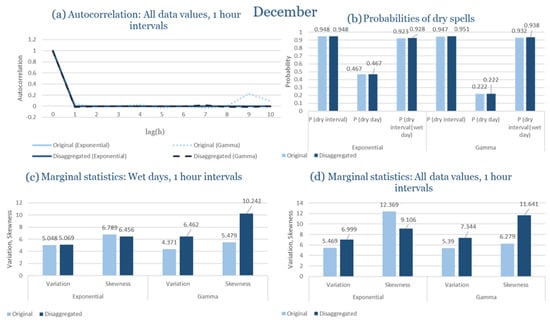
Figure A92.
Statistical Characteristics of Herakleion for December, with the intensity of the pulses following both distributions, where: (a) the diagram of the autocorrelation coefficient, (b) the diagrams of the probability of dry during a dry hour, a dry day and a dry hour||rainy day respectively, (c) the plots for the coefficient of variation and the coefficient of skewness of rainy days and (d) the plots for the coefficient of variation and the coefficient skewness for all data of the respective disagreggated time series.
Appendix C. Comparison of Observed and Disaggregated Rainfall
This section provides visual comparisons between the observed and disaggregated hourly rainfall time series for each study area, for the wettest and driest month. The results reflect the most appropriate distribution—Exponential or Gamma—for each region, as determined through statistical evaluation in prior sections of the paper.
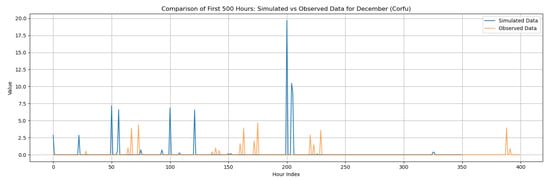
Figure A93.
Observed vs. disaggregated rainfall for December, Corfu.
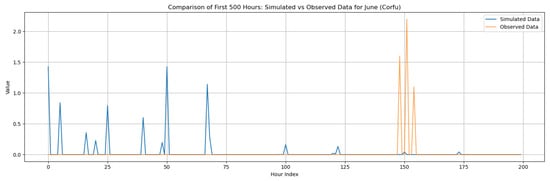
Figure A94.
Observed vs. disaggregated rainfall for June, Corfu.
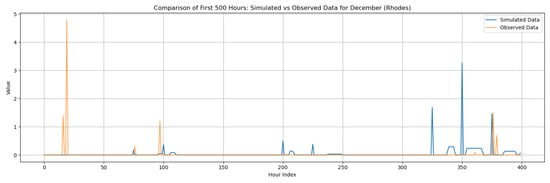
Figure A95.
Observed vs. disaggregated rainfall for December, Rhodes.
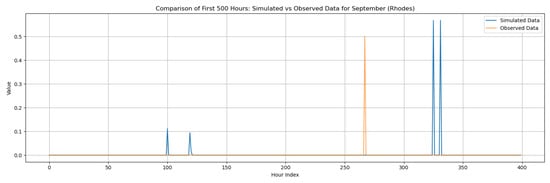
Figure A96.
Observed vs. disaggregated rainfall for September, Rhodes.
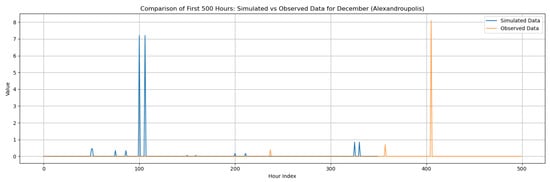
Figure A97.
Observed vs. disaggregated rainfall for December, Alexandroupolis.
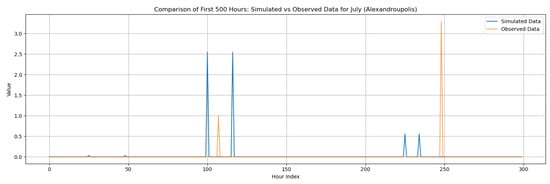
Figure A98.
Observed vs. disaggregated rainfall for July, Alexandroupolis.
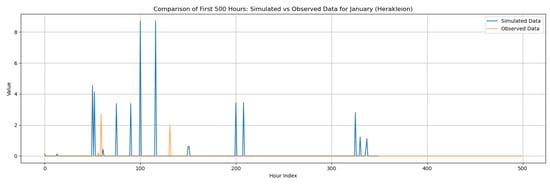
Figure A99.
Observed vs. disaggregated rainfall for January, Heraklion.
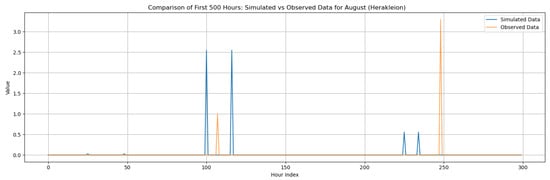
Figure A100.
Observed vs. disaggregated rainfall for June, Heraklion.
References
- Magallanes-Quintanar, R.; Galván-Tejada, C.E.; Galván-Tejada, J.I.; Gamboa-Rosales, H.; Méndez-Gallegos, S.D.J.; García-Domínguez, A. Auto-Machine-Learning Models for Standardized Precipitation Index Prediction in North–Central Mexico. Climate 2024, 12, 102. [Google Scholar] [CrossRef]
- Kim, S.; Kisi, O.; Seo, Y.; Singh, V.P.; Lee, C.J. Assessment of rainfall aggregation and disaggregation using data-driven models and wavelet decomposition. Hydrol. Res. 2016, 48, 99–116. [Google Scholar] [CrossRef]
- Monteiro, L.A.F.; do Nascimento, F.I.C.; de Oliveira-Júnior, J.F.; Nunes, D.D.; Mendes, D.; de Gois, G.; Gobo, J.P.A. Rainfall Projections for the Brazilian Legal Amazon: An Artificial Neural Networks First Approach. Climate 2024, 12, 187. [Google Scholar] [CrossRef]
- Kossieris, P.; Tyralis, H.; Koutsoyiannis, D.; Makropoulos, C.; Efstratiadis, A. HyetosMinute: A Package for Temporal Stochastic Simulation of Rainfall at Fine Time Scales. R Package Version 2. 2016. Available online: https://www.itia.ntua.gr/en/docinfo/1200/ (accessed on 20 October 2025).
- Ritschel, C.; Ulbrich, U.; Névir, P.; Rust, H.W. Precipitation extremes on multiple timescales – Bartlett–Lewis rectangular pulse model and intensity–duration–frequency curves. Hydrol. Earth Syst. Sci. 2017, 21, 6501–6517. [Google Scholar] [CrossRef]
- Onof, C.; Wheater, H.S. Modelling of British rainfall using a Random Parameter Bartlett-Lewis Rectangular Pulse Model. J. Hydrol. 1993, 149, 67–95. [Google Scholar] [CrossRef]
- Cowpertwait, P.S.P.; O’Connell, P.E.; Metcalfe, A.V.; Mawdsley, J.A. Stochastic point process modelling of rainfall. I. Single-site fitting and validation. J. Hydrol. 1996, 175, 17–46. [Google Scholar] [CrossRef]
- Lagouvardos, K.; Dafis, S.; Giannaros, C.; Karagiannidis, A.; Kotroni, V. Investigating the role of extreme synoptic patterns and complex topography during two heavy rainfall events in Crete in February 2019. Climate 2020, 8, 87. [Google Scholar] [CrossRef]
- Evelpidou, N.; Cartalis, C.; Karkani, A.; Saitis, G.; Philippopoulos, K.; Spyrou, E. A GIS-Based Assessment of Flood Hazard through Track Records over the 1886–2022 Period in Hellas. Climate 2023, 11, 226. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Manetas, A. Simple disaggregation by accurate adjusting procedures. Water Resour. Res. 1996, 32, 2105–2117. [Google Scholar] [CrossRef]
- Harris, D.; Seed, A.; Menabde, M.; Austin, G. Factors affecting multiscaling analysis of rainfall time series. Nonlinear Processes Geophys. 1997, 4, 137–156. [Google Scholar] [CrossRef]
- Gupta, V.K.; Waymire, E. Multiscaling properties of spatial rainfall and river flow distributions. J. Geophys. Res. 1990, 95, 1999–2009. [Google Scholar] [CrossRef]
- Kavvas, M.L.; Delleur, J.W. A stochastic cluster model of daily rainfall sequences. Water Resour. Res. 1981, 17, 1151–1160. [Google Scholar] [CrossRef]
- Duong, S.; Song, L.; Chhin, R. Precipitation Projection in Cambodia Using Statistically Downscaled CMIP6 Models. Climate 2023, 11, 245. [Google Scholar] [CrossRef]
- Rodríguez-Iturbe, I.; Gupta, V.K.; Waymire, E. Scale Considerations in the Modeling of Temporal Rainfall. Water Resour. Res. 1984, 20, 1611–1619. [Google Scholar] [CrossRef]
- Todorovic, P.; Yevjevich, V. Stochastic Process of Precipitation; Hydrol. Pap. Ser., No. 35; Colorado State University: Fort Collins, CO, USA, 1969. [Google Scholar]
- Olsson, J.; Burlando, P. Reproduction of temporal scaling by a rectangular pulses rainfall model. Hydrol. Processes 2002, 16, 611–630. [Google Scholar] [CrossRef]
- Sivapalan, M.; Blöschl, G. Transformation of point rainfall to areal rainfall: Intensity-duration-frequency curves. J. Hydrol. 1998, 204, 150–167. [Google Scholar] [CrossRef]
- Over, T.M.; Gupta, V.K. A space-time theory of mesoscale rainfall using random cascades. J. Geophys. Res. Atmos. 1996, 101, 26319–26331. [Google Scholar] [CrossRef]
- Gyasi-Agyei, Y.; Willgoose, G.R. A hybrid model for point rainfall modeling. Water Resour. Res. 1997, 33, 1699–1706. [Google Scholar] [CrossRef]
- Bras, R.L.; Rodriguez-Iturbe, I. Random Functions and Hydrology; Dover Publications: Garden City, NY, USA, 1993. [Google Scholar]
- Koutsoyiannis, D. A generalized mathematical framework for stochastic simulation and forecast of hydrologic time series. Water Resour. Res. 2000, 36, 1519–1533. [Google Scholar] [CrossRef]
- Tabari, H. Statistical analysis and stochastic modelling of hydrological extremes. Water 2019, 11, 1861. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale issues in hydrological modelling: A review. Hydrol. Processes 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Yu, P.S.; Yang, T.C.; Lin, C.S. Regional rainfall intensity formulas based on scaling property of rainfall. J. Hydrol. 2004, 295, 108–123. [Google Scholar] [CrossRef]
- Ly, S.; Charles, C.; Degré, A. Different methods for spatial interpolation of rainfall data for operational hydrology and hydrological modeling at watershed scale: A review. Biotechnol. Agron. Soc. Environ. 2013, 17, 392–406. [Google Scholar]
- Northrop, P.J. Stochastic Models of Rainfall. Annu. Rev. Stat. Its Appl. 2024, 11, 51–74. [Google Scholar] [CrossRef]
- Waymire, E.; Gupta, V.K. The Mathematical Structure of Rainfall Representations: 1. A review of the Stochastic Rainfall Models. Water Resour. Res. 1981, 17, 1261–1272. [Google Scholar] [CrossRef]
- Rodríguez-Iturbe, I.; Power, B.F.D.; Valdes, J.B. Rectangular pulses point process models for rainfall: Analysis of empirical data. J. Geophys. Res. 1987, 92, 9645–9656. [Google Scholar] [CrossRef]
- Palmer, T.N.; Buizza, R.; Doblas-Reyes, F.; Jung, T.; Leutbecher, M.; Shutts, G.J.; Weisheimer, A. Stochastic Parametrization and Model Uncertainty; European Centre for Medium-Range Weather Forecasts: Reading, UK, 2009. [Google Scholar]
- Cho, H.; Yu, J.U.; Moon, J.; Kwon, H.H. Evaluation of Characteristics of Simulated Extreme Rainfall Obtained from NSRP model under Different Object Functions. In Proceedings of the Korea Water Resources Association Conference, Daegu, Republic of Korea, 29 November–3 December 2021; p. 363. [Google Scholar]
- Smithers, J.C.; Pegram, G.G.S.; Schulze, R.E. Design rainfall estimation in South Africa using Bartlett–Lewis rectangular pulse rainfall models. J. Hydrol. 2002, 258, 83–99. [Google Scholar] [CrossRef]
- Dotse, S.Q.; Larbi, I.; Limantol, A.M.; De Silva, L.C. A review of the application of hybrid machine learning models to improve rainfall prediction. Model. Earth Syst. Environ. 2024, 10, 19–44. [Google Scholar] [CrossRef]
- Bhattacharyya, D.; Saha, U. Deep learning application for disaggregation of rainfall with emphasis on preservation of extreme rainfall characteristics for Indian monsoon conditions. Stoch. Environ. Res. Risk Assess. 2023, 37, 1021–1038. [Google Scholar] [CrossRef]
- Nourani, V.; Farboudfam, N. Rainfall time series disaggregation in mountainous regions using hybrid wavelet-artificial intelligence methods. Environ. Res. 2019, 168, 306–318. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Cox, D.R.; Isham, V. Some models for rainfall based on stochastic point processes. Proc. R. Soc. Lond. A Math. Phys. Sci. 1987, 410, 269–288. [Google Scholar]
- Olsson, J. Evaluation of a cascade model for temporal rainfall disaggregation. Hydrol. Earth Syst. Sci. 1998, 2, 19–30. [Google Scholar] [CrossRef]
- Kumar, P.; Foufoula-Georgiou, E. Wavelet analysis in geophysics: Applications to rainfall. Rev. Geophys. 1997, 35, 385–412. [Google Scholar] [CrossRef]
- McIntyre, N.; Shi, M.; Onof, C. Incorporating parameter dependencies into temporal downscaling of extreme rainfall using a random cascade approach. J. Hydrol. 2016, 542, 896–912. [Google Scholar] [CrossRef]
- Sharior, S.; McDonald, W.; Parolari, A.J. Improved reliability of stormwater detention basin performance through water quality data-informed real-time control. J. Hydrol. 2019, 573, 422–431. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Rainfall disaggregation methods: Theory and applications. In Proceedings of the Workshop on Statistical and Mathematical Methods for Hydrological Analysis, Rome, Italy, May 2003; Volume 5270, pp. 1–23. [Google Scholar]
- Cowpertwait, P.; Isham, V.; Onof, C. Point process models of rainfall: Developments for fine-scale structure. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 2569–2587. [Google Scholar] [CrossRef]
- Cowpertwait, P.S. A Poisson-cluster model of rainfall: Some high-order moments and extreme values. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 885–898. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. A Point Rainfall Disaggregation Model. Ph.D. Thesis, National Technical University of Athens, Athens, Greece, 1988. [Google Scholar]
- Dubrovský, M.; Buchtele, J.; Žalud, Z. High-frequency and low-frequency variability in stochastic daily weather generator and its effect on agricultural and hydrologic modelling. Clim. Change 2004, 63, 145–179. [Google Scholar] [CrossRef]
- Onof, C.; Wheater, H.S. Improvements to the modelling of British rainfall using a modified random parameter Bartlett-Lewis rectangular pulse model. J. Hydrol. 1994, 157, 177–195. [Google Scholar] [CrossRef]
- Park, J.; Cross, D.; Onof, C.; Chen, Y.; Kim, D. A simple scheme to adjust Poisson cluster rectangular pulse rainfall models for improved performance at sub-hourly timescales. J. Hydrol. 2021, 598, 126296. [Google Scholar] [CrossRef]
- Solomatine, D.P. Two strategies of adaptive cluster covering with descent and their comparison to other algorithms. J. Glob. Optim. 1999, 14, 55–78. [Google Scholar] [CrossRef]
- Efstratiadis, A.; Koutsoyiannis, D. An evolutionary annealing-simplex algorithm for global optimisation of water resource systems. In Proceedings of the Fifth International Conference on Hydroinformatics, Cardiff, UK, 1–5 July 2002; Volume 11, pp. 431–441. [Google Scholar]
- Efstratiadis, A. Investigation of Global Optimum Seeking Methods in Water Resources Problems. Master’s Thesis, Department of Water Resources, Hydraulic and Maritime Engineering, National Technical University of Athens, Athens, Greece, 2001. [Google Scholar]
- Rozos, E.; Efstratiadis, A.; Nalbantis, I.; Koutsoyiannis, D. Calibration of a semi-distributed model for conjunctive simulation of surface and groundwater flows. Hydrol. Sci. J. 2004, 49, 819–842. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Onof, C. Rainfall disaggregation using adjusting procedures on a Poisson cluster model. J. Hydrol. 2001, 246, 109–122. [Google Scholar] [CrossRef]
- Sachindra, D.A.; Ahmed, K.; Rashid, M.M.; Shahid, S.; Perera, B.J.C. Statistical downscaling of precipitation using machine learning techniques. Atmos. Res. 2018, 212, 240–258. [Google Scholar] [CrossRef]
- Frost, A.J.; Charles, S.P.; Timbal, B.; Chiew, F.H.; Mehrotra, R.; Nguyen, K.C.; Kent, D.M. A comparison of multi-site daily rainfall downscaling techniques under Australian conditions. J. Hydrol. 2011, 408, 1–18. [Google Scholar] [CrossRef]
- Hellenic National Meteorological Service. 2022. Available online: https://emy.gr/en (accessed on 10 May 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).