Abstract
As the amount of collected spatial information (2D/3D) increases, the real-time processing of these massive data is among the urgent issues that need to be dealt with. Discretizing the physical earth into a digital gridded earth and assigning an integral computable code to each grid has become an effective way to accelerate real-time processing. Researchers have proposed optimization algorithms for spatial calculations in specific scenarios. However, a complete set of algorithms for real-time processing using grid coding is still lacking. To address this issue, a carefully designed, integral grid-coding algebraic operation framework for GeoSOT-3D (a multilayer latitude and longitude grid model) is proposed. By converting traditional floating-point calculations based on latitude and longitude into binary operations, the complexity of the algorithm is greatly reduced. We then present the detailed algorithms that were designed, including basic operations, vector operations, code conversion operations, spatial operations, metric operations, topological relation operations, and set operations. To verify the feasibility and efficiency of the above algorithms, we developed an experimental platform using C++ language (including major algorithms, and more algorithms may be expanded in the future). Then, we generated random data and conducted experiments. The experimental results show that the computing framework is feasible and can significantly improve the efficiency of spatial processing. The algebraic operation framework is expected to support large geospatial data retrieval and analysis, and experience a revival, on top of parallel and distributed computing, in an era of large geospatial data.
1. Introduction
With the rapid development of three-dimensional (3D) space exploration abilities and urban spatial technology, the ability of humans to obtain spatial data has been significantly improved [1,2,3]. The data volume of multidimensional spatial information, such as ocean, environment, space exploration, or urban building information modeling (BIM) and various types of point-of-interest (POI) data, is growing exponentially [4,5]. In today’s era of big geospatial data, the processing and application of this massive spatial information has created higher requirements for real-time spatial computing abilities. However, when the traditional spatial data model is used for spatial calculation, it is mainly based on the floating point calculation of latitude and longitude, and the algorithm is complicated and needs to be improved [6]. As mathematics is an abstraction of the essence of objective things, discrete grid abstraction can essentially reflect the spatial position and spatial relationship [2,4]. As a discrete abstraction of geographic space, discretizing the physical Earth into a digital discrete Earth and assigning an integral computable code to each grid has become an effective way to accelerate real-time processing (shown in Figure 1).

Figure 1.
From the planet Earth to digital discrete Earth: (a) planet Earth; (b) digital discrete Earth.
For an Earth subdivision model to be complete and scientific, it should contain the following two parts: the Earth subdivision method and an encoding method [7,8]. The former stipulates how the 3D Earth divides into multiscale subdivision units, with similar shapes and regular sizes. The latter mainly determines the rules for assigning a unique identification code to each unit. The grid code establishes the connection between geographic space and computer space [9]. Meanwhile, the efficient association and operation of spatial information included in the subdivision system require the corresponding code’s algebraic operation rules to be defined. Thus, the code’s algebra is an essential part of the geospatial subdivision theory, and also an indispensable tool when using the subdivision theory to solve a series of practical problems.
The geospatial grid model has been gradually accepted and widely studied by industry and academia, becoming an important solution to effective organization, integration, sharing, retrieval, distribution, and the application of massive multisource spatial data [10]. The researchers also proposed a discrete grid data model and corresponding spatial calculation algorithms according to the needs of different scenarios, such as the retrieval of massive remote-sensing data, anti-collision calculations for drone swarms, routing planning for satellite constellations, trajectory prediction of POI points in cities, emergency response ability calculations for urban safety management, etc. [11,12,13,14]. Based on the grid model, filling curves are often used to assign values to the grid. A space-filling curve is filled with the whole space via a curve, to map from high-dimensional data to a low-dimensional storage space. It calculates the index value of the curve corresponding to the space object, and it represents an object or a unit. Each filling curve has its own calculation method. The Hilbert Z-order curves and Peano’s and Gray codes are the main spatial filling curves [15,16]. However, previous studies are aimed at specific application algorithms, and they lack systemicity and versatility [17,18,19]. Therefore, a complete set of algorithms that use grid codes for real-time processing is still lacking, which would tell us how spatial information is converted into discrete grid codes and the specific processes of spatial measurements, spatial calculations, and spatial analysis using codes.
Among the 3D grid models proposed in previous studies, a geographical coordinate subdivision grid with one-dimension integral coding on 2n-tree 3D (GeoSOT-3D) is a standardized, multiscale, latitude and longitude grid data model [6]. It has the advantages of intuitive expression of the latitude and longitude grid, an effective octree index, and efficient calculation using grid codes [20]. This grid model has 2n grids in each layer (n is the grid layer), and can use integral multiples of “2” to replace the calculations of floating-point numbers based on longitude and latitude (making it convenient for the computer to conduct binary operations) [11,13,14,19]. Therefore, it is necessary to make full use of the advantages of the binary integer of GeoSOT-3D codes, as the computer’s integer operation efficiency is much better than the floating-point operation. In our study, an integral grid-coding algebraic operation framework based on binary bit operations was developed to support large geospatial data analysis. We developed major algorithms.
2. Algebraic Operation Framework for GeoSOT-3D
2.1. GeoSOT-3D Grid Model
The Open Geospatial Consortium (OGC) has published relevant standards for the discrete grid, the first of which is to define the method of subdivision [21]. In our study, GeoSOT-3D is selected as the discrete grid framework. It is developed by subdividing the height dimension on the basis of the geographical coordinates subdivision grid with one-dimension integral coding on 2n-tree (GeoSOT) spherical 2D model.
The GeoSOT model is a subdivision and coding method that subdivides the Earth’s surface into grids [13]. Through dividing the Earth three times (expand the earth (180° × 360°) into 512° × 512°, then each 1° expand into 64′, and each 1′ expand into 64″), oct-tree subdivisions at the degree, minute, and second layers are obtained. The GeoSOT is congruent and aligned. The largest subdivision grid in the highest layer (Layer 0) can cover the whole earth’s surface, while the smallest subdivision grid in the lowest layer (Layer 32) can represent centimeter scales.
The GeoSOT-3D model (Figure 2) is a multilayer 3D grid model. It expands the height dimension of the GeoSOT grid model, and divides the three dimensions of longitude, latitude, and elevation continuously through octree division [6]. Finally, we obtain the multilayer grid model of integer degrees, integer minutes, and integer seconds, and form an Earth grid 3D model with a space of 50,000 km up to the outer periphery of the earth and down to the center of the earth, with 32 layers. Then, each grid is given a code to uniquely identify the spatial area. Codes in the same layer are sorted according to the Z-order space-filling curve [12]. Finally, the high-dimensional spatial information is converted into one-dimensional grid code, which is convenient for the identification, storage, and calculation of spatial information.
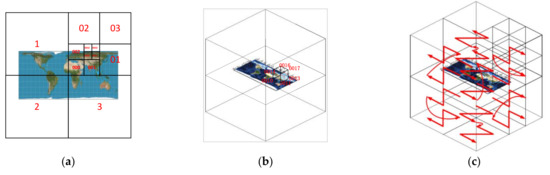
Figure 2.
GeoSOT-3D model: (a) GeoSOT subdivision; (b) GeoSOT-3D subdivision; (c) Z-order filling curve.
GeoSOT-3D is based on a binary one-dimensional code, and has a designed corresponding octal one-dimensional code and binary three-dimensional code, which can be quickly converted according to different applications:
- (1)
- Octal one-dimensional code. The code is coded with octal values (0, 1, 2, 3, 4, 5, 6, 7) up to 32 digits long. The length of the code identifies the layer of the grid. When writing the code, it starts with G; the codes for degrees, minutes, and seconds are separated by “-”, and the codes below seconds are separated by “.”. The form is Gddddddddd-mmmmmm-ssssss.uuuuuuuuuuu, where d, m, s, and u are octal numbers with values of 0, 1, 2, 3, 4, 5, 6, 7. The code of each layer of grid is based on the previous layer of the grid code, and the Z-order encoding direction is related to the same layer grid where the grid is located. The octal one-dimensional code is mainly used for index establishment and domain name identification.
- (2)
- Binary one-dimensional code (Figure 3a). The code is composed of 96-bit binary values (0,1), and each three-bit code represents an octal value, so the binary one-dimensional code corresponds exactly to the octal one-dimensional code. The binary one-dimensional code is mainly used for calculation, and is generally stored in the form of a structure. It is impossible to use a variable-length code to express the hierarchical layer of the section, such as an octal one-dimensional code. Therefore, the binary one-dimensional code generally needs the addition of a layer code with a length of 5-bit to represent the layer, and the total length of the code is 96 + 5 = 101 bits.
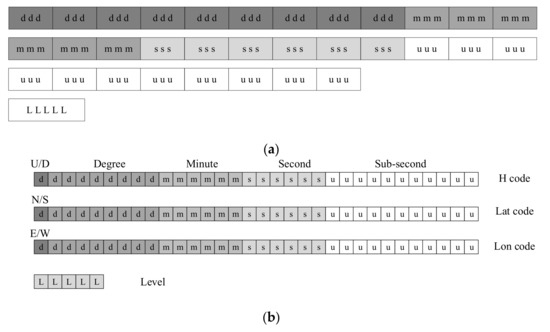 Figure 3. The composition of the binary code: (a) binary 1D code; (b) binary 3D code.
Figure 3. The composition of the binary code: (a) binary 1D code; (b) binary 3D code. - (3)
- Binary three-dimensional code (Figure 3b). In the 96-bit binary one-dimensional code of GeoSOT-3D grid, every three-bit binary number represents the code of a grid in a layer. These three digits are disassembled and stored separately to form a GeoSOT-3D binary three-dimensional code. The GeoSOT-3D binary three-dimensional code has an obvious geographic meaning, and 32-bit binary values are used to represent altitude, latitude, and longitude. The first bit of the code indicates the interval in which the grid is located.
2.2. Algebraic Operation Framework Design
The ideal subdivision theory should be complete. A closed coordinate calculation system can be defined, and spatial data can be identified, correlated, calculated, and analyzed in the system. The system has a complete framework, identification, and algorithm rules. Most of the current research focuses on the research on the frame (subdivision frame) and the label (subdivision code). It does not involve the code algebraic operation under the subdivision system. The current spatial operation mode of the subdivision data is shown in Figure 4. The subdivision data are first converted into latitude and longitude elevation data, and then the corresponding calculation and analysis are performed based on the geographic spatial coordinates. Finally, the result is mapped back to the subdivision space. This will reduce the accuracy and efficiency, while losing the advantages of the subdivision frame.
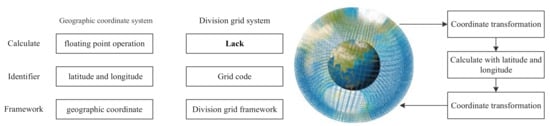
Figure 4.
The current spatial operation mode of the subdivision data.
In the GeoSOT-3D model, each grid is given a unique and hierarchical code to identify the spatial area. The code value implies the spatial location and scale of the area. Points, lines, polygons, volumes, and spatial fields are all composed of grid sets, and their spatial information can be defined by grid-code sets. Based on this rule, we designed the integral grid-coding algebraic operation framework for GeoSOT-3D. In our framework, the attributes of grids and the relationship between grids are obtained through binary operations between integral codes, and complex spatial analyses can be converted into binary-coding operations.
The framework of grid-coding algebraic operations is shown in Figure 5, including previous work, basic definitions, operations, and applications.
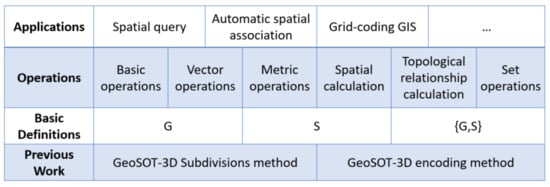
Figure 5.
The design of the algebraic operation framework.
Firstly, the three basic definitions mentioned above are as follows:
Definition 1.
G is all the grid codes in GeoSOT-3D (with a total number of 232∗3).
Definition 2.
S is all grid-coding algebra operations defined in GeoSOT-3D.
Definition 3.
{G, S} is the grid-coding algebraic space, which is the group formed by the grid code set and algebraic operation set.
Then, according to the function, we classify the operations, including:
- Basic operations.
This means the basic operation for the code itself, which mainly provides functional support for other operations. The basic operation only manipulates the code, and does not involve the spatial information contained in the code. In our study, the basic operations include bitwise operation, layer operation, code prefix operation, and code suffix operation.
- Vector operations.
The code contains the location information of the grid, which can be regarded as a vector pointing from the origin of the Earth’s three-dimensional space to this grid. We construct the vector operations of code, including “+” and “−“.
- Metric operations.
Metric operation calculates the actual geographic attributes of an area through code, including area measurement, distance measurement, projection area measurement, and orientation measurement.
- Spatial calculation.
Spatial operation is the calculation of regional grids and geographic attributes between grids through binary bit operations, which mainly include the acquisition of neighborhood codes, and the acquisition of parent–child codes.
- Topological relationship operations.
The topological relationship operation is mainly used to determine the spatial position relationship between grids.
- Set operations.
In practical applications, grid sets are often used to identify the location of spatial objects. Therefore, operations based on code set are urgently required, including code set merging, code set intersection, code set difference, code set relationship judgment and other operations.
Based on the proposed operations, applications such as spatial query, automatic spatial association, and even new grid-coding GIS can be developed. As can be seen, the most important part is algebraic operations. In Section 3, we describe the operations of each category.
3. Algebraic Operations
Along with the proposed framework, we have further summarized the operations above, as shown in Figure 6. We further discuss them in detail.
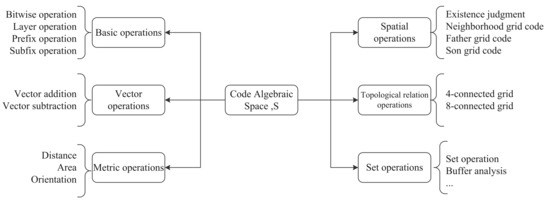
Figure 6.
Algebraic operation framework for GeoSOT-3D.
3.1. Basic Operations
The basic operation is mainly used to provide basic operational support to other operations. It only acts on the GeoSOT-3D code and does not involve the spatial information contained in the code. Its basic operations include bitwise operation, layer operation, code prefix operation, and code suffix operation.
3.1.1. Bitwise Operations
GeoSOT-3D code algebraic operations are mainly based on the following basic binary bit operations, including &, |, ^, ~, <<, >>. The bitwise operation rule is the same as corresponding programming languages, such as C.
- Bitwise andOperator:&
- Bitwise OROperator:|
- Bitwise XOROperator:^
- Inverted by bitOperator~
- Shift leftOperator:<<
- Shift rightOperator:>>
3.1.2. Get the Layer of Layer
CodeLayer is the operation used to obtain the layer of the code. Since the code length is related to the times the Earth model is subdivided, the code length is the code layer. For example, CodeLayer(100101) = 6.
3.1.3. Code Prefix Operation
The code content of the specified length is obtained from the beginning of the split code, and recorded as CodePre.
CodePre = Code >> (96 − n); (n is the prefix digits)
3.1.4. Code Suffix Operation
The code content of the specified length is obtained from the ending of the split code, and recorded as CodeLast.
CodeLast = Code << (96 − n); (n is the suffix digits)
3.2. Vector Operation
The GeoSOT-3D code contains the location information of the grid, which can be regarded as a vector pointing from the origin of the earth’s three-dimensional space to this grid. Therefore, the code can be regarded as a vector. We construct the arithmetic operations of the code, including “+” and “−“.
When regarding GeoSOT-3D code as a vector, the first thing that needs to be defined is the “+” and “−” of the vector. The GeoSOT-3D code addition operation can be defined as the “+” between two vectors, so the “+” of CodeA and CodeB is the code of the area pointed to by the new vector, as shown in Figure 7.
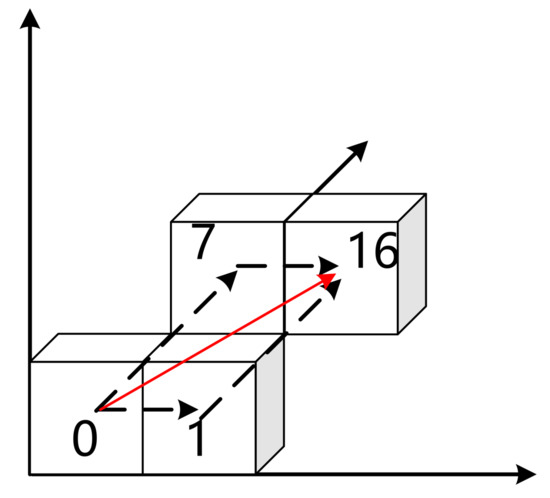
Figure 7.
The “+” operation of GeoSOT-3D code.
The “−” operation is the inverse operation of “+”, and the code that needs to be added must be replaced with its inverse element.
The pseudocode of the operation is attached in Appendix A.
3.3. Metric Operation
The metric operation calculates the actual geographic attributes through the GeoSOT-3D code, including distance measurement, projection area measurement, and orientation measurement.
Distance, area, and orientation are the primary attributes of spatial and other entities. In the GeoSOT-3D subdivision framework, a unique subdivision code is formulated for each region in the Earth’s space. Its code system is equivalent to the set of a coordinate system. Therefore, the use of GeoSOT-3D code can support spatial measurement operations at multiple scales.
3.3.1. Distance
The calculation of the distance between the two grids C1 (CodeLon, CodeLat, CodeHei) and C2 (CodeLon, CodeLat, CodeHei) in the three-dimensional space of the Earth is as follows:
where Span1, Span2, Span3 are the spans of C1 and C2 in three dimensions, and satisfy Span1 > Span2 > Span3. The distance calculation method here is close to the Euclidean distance on the GeoSOT-3D grid. It is important to note that when calculating the distance of a small span, the spherical distance can be approximately equal to the Euclidean distance. If users need to calculate an accurate and large-span distance, they need to convert it back to an ellipsoid. We recommend that the grid distance is only used to indicate the approximate range rather than the precise range, for example, calculations such as fast estimation of length.
3.3.2. Projection Area
The projection of the three-dimensional grid on the reference ellipsoid is a GeoSOT 2D grid, which can be expressed by a spherical trapezoid: the latitude range is B1~B2, and the longitude range is L1~L2. The formula for calculating the area of any trapezoid on the ellipsoid is as follows:
where A, B, C, D, and E are constants, and can be calculated as follows:
3.3.3. Orientation
The grids’ orientation relationship refers to the directional relationship of the two grids in space, such as up and down, left and right, east and west, south and north, etc. Up, down, left, and right are a set of relative azimuth relationships, and they generally appear in pairs. Unlike these orientation relationships, the east, west, north, and south imply an absolute reference direction.
Figure 8a shows the definition of the relative orientation of the grid. In its local coordinate system, “up” is defined as north. Figure 8b shows the definition of the absolute orientation of the grid. The difference from top, bottom, left, and right is that east, west, south, and north imply absolute reference directions. The spatial orientation relationship of the grid can be obtained through a coding comparison in three dimensions. Any two grids are chosen, C1 (CodeE1, CodeB1, CodeL1), C2 (CodeE2, CodeB2, CodeL2), where C1 is the reference grid, C2 is the pointing grid, and the grid spatial orientation relationship is calculated as Figure 9.
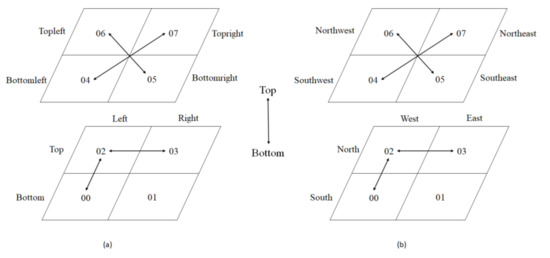
Figure 8.
Spatial orientation. (a) shows the definition of the relative orientation of the grid. (b) shows the definition of the absolute orientation of the grid.
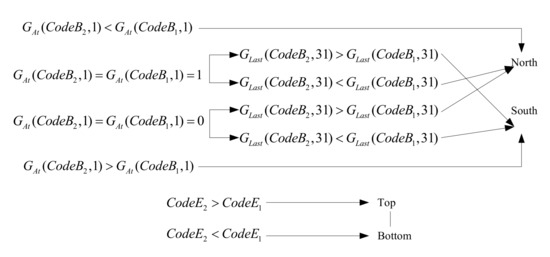
Figure 9.
The calculation of grid spatial orientation relationship.
3.4. Spatial Calculation
Spatial operation refers to the calculation of regional grids and geographic attributes between grids through bitwise operations, which mainly include the acquisition of neighborhood codes, and the acquisition of parent–child codes.
3.4.1. Neighborhood Operation
The neighborhood operation obtains the adjacent grid code of the area (Figure 10a). For the GeoSOT subdivision framework, the neighboring relationship between a region and the surrounding region is divided into surface neighboring, edge neighboring, and corner neighboring. In short, starting from the given area, one grid is moved along the longitude/latitude/height direction to obtain the neighborhood code set.
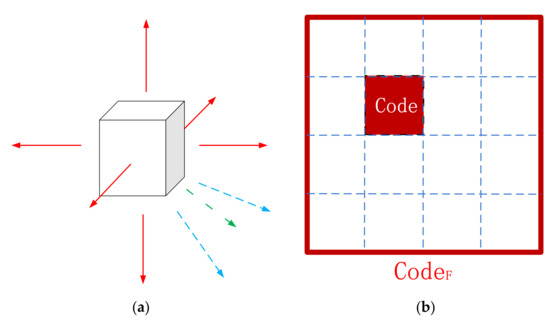
Figure 10.
Spatial calculation: (a) neighboring directions; (b) geometry meaning graph for parent grid operation (in 2D).
Grid neighborhood calculation is based on binary 3D code (other codes can be converted to binary 3D coding first), and then the neighborhood calculation is performed. For a grid coded as (CodeLon, CodeLat, CodeHei), a displacement combination of its code in the height dimension, longitude dimension, and latitude dimension represents a certain neighborhood grid of the grid. For a certain dimension Code in the binary 3D code, the code displacement can be performed as follows:
- (1)
- Move a grid forward:
- (2)
- Move a grid in the negative direction:
3.4.2. Parent Grid Operation
We define a higher-level grid that contains the grid as the parent grid of this grid (Figure 10b). Since the grid code in GeoSOT-3D model directly reflects the inheritance between grids, the parent grid coding calculation can be directly carried out by prefixing the codes. Code is the octal one-dimensional code of a certain grid, and its parent grid code is the prefix of the Code (length is Layer−1 layer), where Layer is the grid code layer of Code. The calculation formula is shown as follows:
where GP is the calculation operation of the parent grid code; the calculation input is the grid code; the output is the parent grid code of the grid.
3.4.3. Child Grid Operation
In the same way, after the inheritance of the grid model, the child grid code can be combined with the parent code and the code of the child grid in the parent grid. The calculation formula is shown as follows:
where GS is the calculation operation of the parent grid code; the calculation input is the grid code; the output is the parent grid code of the grid.
3.5. Topological Relationship Calculation
The topological relationship operation is mainly used to determine the spatial position relationship between grids. The topological relationship between entities can be described by a nine-intersection model [22,23]. In the nine-intersection model for GeoSOT, we define A0 as the grids with a distance of 1 in the Voronoi diagram (Figure 11).
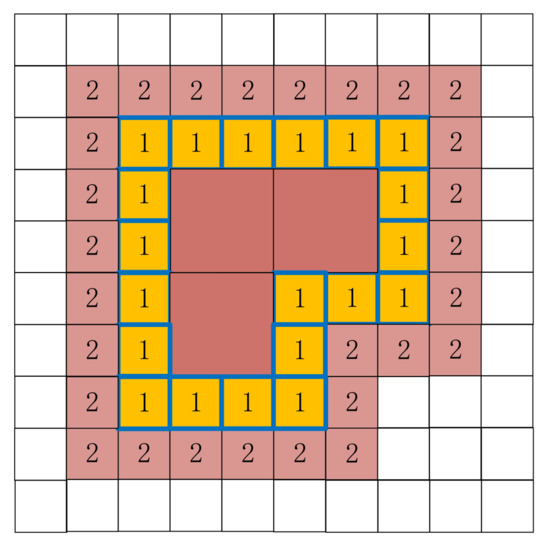
Figure 11.
Voronoi diagram.
There is no way for one grid cell to “intersect” another, since two grid cells cannot overlap at the same grid, they can only be neighbors (which is covered by the touches relation). Only a containment relationship may exist between grids of different layers (Figure 12a). Therefore, we can obtain six relationships: contains(T*****FF*), cover(T*****FF*,*T****FF*,***T**FF*,****T*FF*), covered by(T*F**F***,*TF**F***,**FT*F***,**F*TF***), disjoint(FF*FF****,), equal(T*F*FFF*), and touch(FT*******, F**T*****,F***T****). Then, we expand this into eight topological relationships by distinguishing the adjacent edges and adjacent corners (Figure 12).
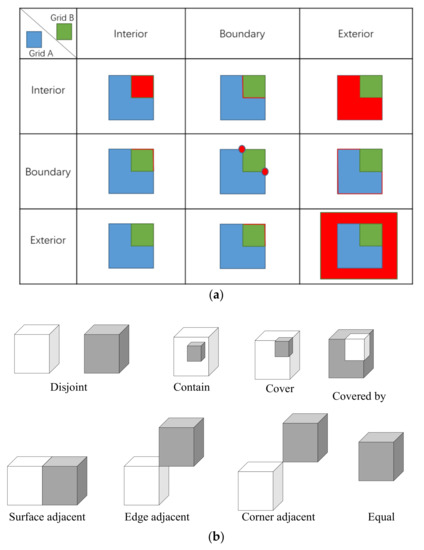
Figure 12.
Spatial topological relationship between grids. (a) Correspondence with DE-9IM; (b) spatial topological relationship between grids (3D).
In our method, we calculate the topological relationship by judging the magnitude of the codes. Firstly, the topological relationship between the grids is calculated in 3D. Then, the 2D topological relationship and the high-dimensional topological relationship are calculated, and finally the spatial topological relationship of the grids is obtained.
CA and CB are the binary codes of grid A and B on dimension D, respectively, and the code length is LA, LB. The calculation process of the topological relationship between grid A and grid B in dimension D is as follows.
For the same code layer (LA = LB), it is judged whether CA = CB, meaning that the topological relationship RD of grid A and B in dimension D is equal; otherwise, the real grid span between LA and LB is calculated. If the span is 1, then RD is adjacent; if the span is larger than 1, then RD is disjointed.
For different code layers, without loss of generality, it is assumed that LA > LB, and the prefix CA′, whose CA length is LB, is taken. If CA′ = CB, then B contains A; if CA′ > CB, LA-LB is added after CB, and then the topological relationship is calculated according to the same-layer code; if CA′ < CB, LA-LB 0s is added after CB, and then the topological relationship is calculated according to the same-layer code. According to the proposed method, the topological relations RE, RB, and RL of grid A and grid B in three dimensions can eventually be calculated.
3.6. Set Operations
After explaining the basic operations between grids, it is also necessary to analyze the operations of grid sets. Grid set operation is a computing algorithm oriented to spatial objects. Spatial objects can be abstracted into point entities, linear entities, surface entities, volume entities, and space fields (when the boundaries and attributes of the space field are defined, they can be regarded as volume entities in a large area). These spatial objects are identified by one or a set of grids and are uniquely determined by the grid codes. Therefore, the object-oriented spatial calculation method is transformed into the calculation grid collection method.
The algorithm of the grid coding set operation is based on the basic operation algorithm of code, including the displacement operation of the object, the operation of the set attribute of the object, the operation of the orientation relationship of the object, and the operation of the topological relationship of the object. We then use overlay analysis as an example.
Overlay analysis is one of the main functions of spatial analysis. It belongs to the spatial operation of the superposition of two entities or objects, such as intersection, union, difference, etc. Overlay analysis is used to overlay two or more spatial objects and update the attribute information at the same time. In the grid model, spatial objects are composed of grids or grid collections, so the superposition of spatial objects is transformed into a superposition analysis of grid collections. When discussing the overlay analysis of grid sets, the overlay analysis between grids is first discussed.
To find the union of two given grids, it is necessary to calculate the inclusion relationship between the grids. The algorithm flowchart is shown in Figure 13a. Then, the union operation between grid sets is based on the union operation between grids (Figure 13b).
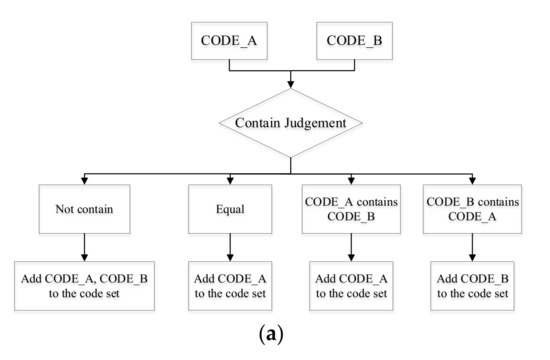
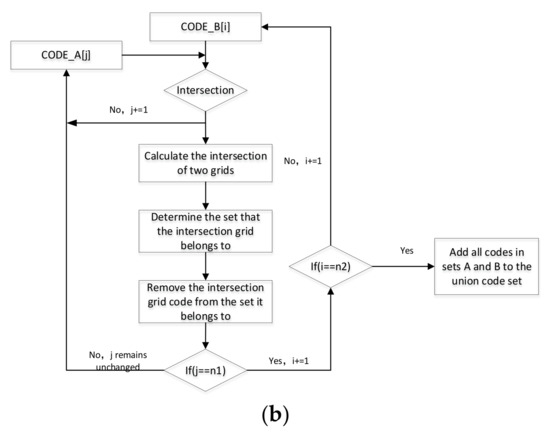
Figure 13.
Union operation: (a) for two grids; (b) for two sets of grids.
4. Experimental Results
4.1. Experimental Platform and Experiment Design
Based on the framework we proposed, we developed an experimental platform, using C++. In this experimental platform, we can visualize the grid through the given layer and area range and carry out the corresponding spatial measurement and analysis on the basis of this (major algorithms are shown in the Appendix A). The memory required to use our platform is 8 GB. Figure 14 show the division of the sphere by selecting the spatial region under a given layer. Among these, the overground and underground subdivisions are all selected as the 9th subdivision layer, and the latitude and longitude range is 120° E~150° E, 20° N~50° N.
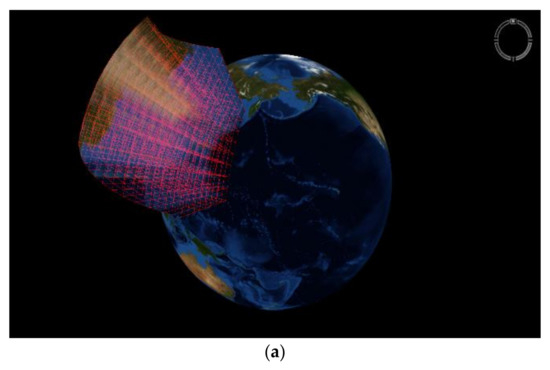
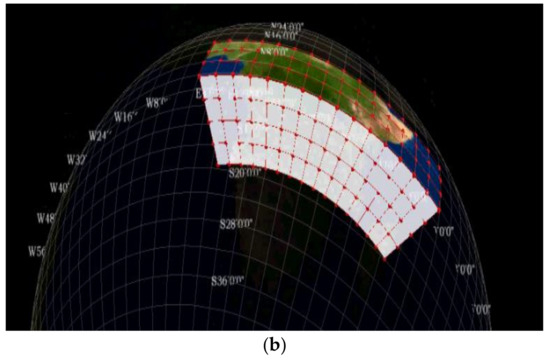
Figure 14.
Experimental platform: (a) overground; (b) underground.
Then, we generated randomly simulated data and performed our metric operation experiments and topological relationship calculation, and then analyzed the efficiency of algebraic operations. This work verifies the feasibility and efficiency of the integral grid-coding algebraic operation framework.
The experimental environment: Win7 Ultimate 64-bit, Intel Core i5-2400 @ 3.10 GHz, RAM 8 GB, hard disk 512 GB, Visual Studio 2010.
4.2. Comparison of Vector Operation Efficiency
The Hilbert space-filling curve is a continuous, fractal space-filling curve (Figure 15). The key to Hilbert is the basic curve and flip of the coordinate system. Studies have shown that, among the many space-filling curves, the Hilbert curve has the best data aggregation [24]. Therefore, the Hilbert curve is mostly used in spatial indexing.
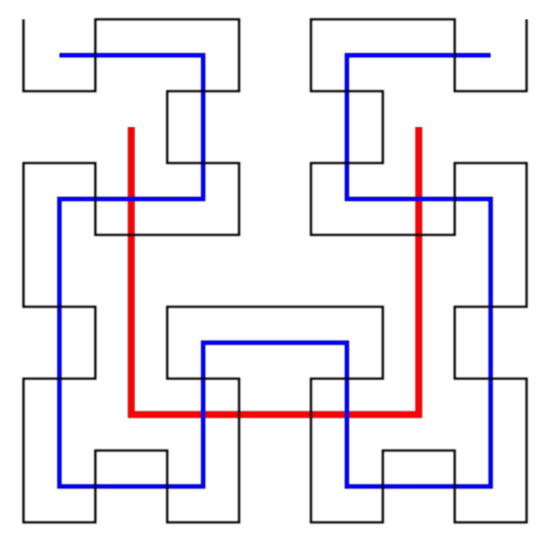
Figure 15.
Hilbert curve.
We compared the calculation efficiency of the Hilbert curve and Z-order curve with the basic displacement calculation in two-dimensional space and set average time as a gold standard. For the Hilbert curve, since the coordinate system is constantly rotating, we must determine its (x, y) before we can calculate the grid code after displacement. We randomly generated 300,000 grid codes and calculated the grid codes on their east side. Table 1 shows the average time taken to convert the Hilbert curve code to (x,y) is 180 ms. Under the same conditions, it takes only 11 ms to complete the displacement calculation under the Z-order. We believe that the z-order retains the spatial coordinate properties to a greater extent than the Hilbert curve, and is more suitable for spatial calculations. However, for spatial calculations, the Hilbert curve cannot perform efficient calculations. Therefore, we are conducting research on space calculations based on z-order.

Table 1.
Comparing studies of the two curves for displacement calculations.
4.3. Comparison of Metric Operation Efficiency
Firstly, we compared the metric operations of the grid (algorithm in Section 3.3) with the geometric measurements of the latitude, longitude, and height (LLH) of the coordinate system (including distance and orientation). We also set average time as a gold standard.
We randomly generated 1,000,000 point entities around the world, calculated the 1~32-layer GeoSOT-3D code of each points, and then performed the following operations:
Step 1.1: For any two points, the Euclidean distance between them is calculated, and the average calculation time is recorded.
Step 1.2: For any two points (same as Step 1.1), their corresponding codes (from layer 1 to layer 32) are used to calculate the grid distance between the grids (algorithm in Section 3.3.1), and the calculation time is recorded.
Step 2.1: For any two points, the spatial orientation between them is calculated, and the calculation time is recorded.
Step 2.2: For any two points (same as Step 2.1), their corresponding codes (from layer 1 to layer 32) are used to calculate the orientation between the grids (algorithm in Section 3.3.3), and the calculation time is recorded.
Figure 16 shows the average time taken for spatial distance measurement. The efficiency of the grid-coding algebraic operation is much better than that of the latitude, longitude, and height coordinate system. The average time spent using LLH is about 0.5 μs, while the calculation time of the grid is stable at 0.07 μs. The main reason for this is that the longitude and latitude calculation distance requires polar coordinate conversion and square calculation. The grid operation avoids a large number of trigonometric functions and square root operations.
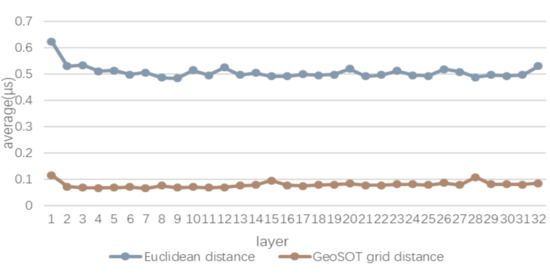
Figure 16.
Average time for spatial distance measurement.
Figure 17 shows the average time taken to calculate the spatial orientation. The average time used to calculate the spatial orientation between two points using latitude and longitude takes 0.6 μs, and the grid-coding algebraic operation is around 0.1 μs. The latter uses bit arithmetic to calculate the spatial orientation, so it is more efficient. Similarly, the algebraic operations provide a qualitative orientation relationship between two grids, which is suitable for application scenarios that require a rough orientation relationship.
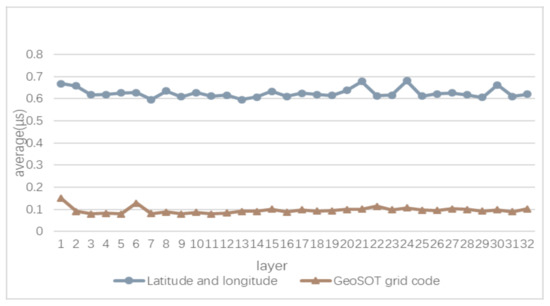
Figure 17.
Average time for spatial orientation measurement.
4.4. Comparison of Topological Operation Efficiency
Overlay analysis is one of the most important topological relationship calculations. Currently, computer graphics are used in almost all fields, including games, entertainment, education, CAD/CAM, etc. One of the most important operations in computer graphics is overlay. Overlay analysis can be applied to VLSI CAD, GIS, the clothing industry, etc. There are many algorithms, but the intersection calculation will incur huge costs. In this experiment, we compared the overlay operation of the grid (algorithm in Section 3.5) with the overlay analysis of the latitude, longitude, and height (LLH) coordinate system.
The overlaying process needs two or more layers. The layers used in this experiment are divided into two types: one is a layer with only one area object (Figure 18a,b and Table 2), and the other is a layer with multiple area objects (Figure 19 and Table 3).
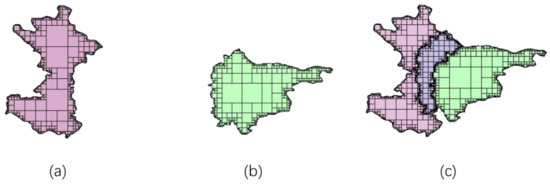
Figure 18.
Experiments of overlay: layer (a) and layer (b) are the layers to be overlaid that have only one area object; layer (c) is the result of the overlay. The pink and green areas are the original areas. The purple area is the overlaid area.

Table 2.
Comparing a study of the two algorithms for the layer with a single area.
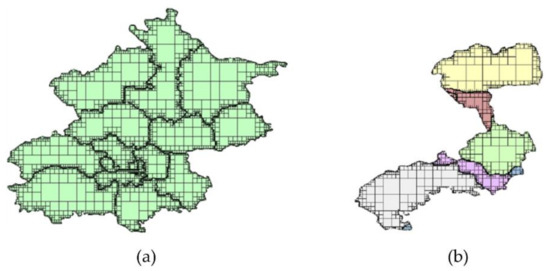
Figure 19.
Experiments of overlay: layer (a) is a layer with multiple area objects. We moved (a) along the x-axis and formed a new layer, which was overlaid with the old layer (a). Layer (b) is the result of the overlay.

Table 3.
Comparing study of the two algorithms for a layer with multiple area objects.
We use multilayer grids to represent a geographic object. For a geographic entity, we need its boundary grid data and an internal point, and then use the seed filling algorithm to calculate its corresponding grid set. Finally, we aggregate the grids set according to the grid octree division rule as shown in the Figure 18a.
This experiment is divided into two parts, layer overlay with only one area object and layer overlay with multiple area objects, to analyze the influence of the number of objects. Meanwhile, we used Weiler–Atherton clipping algorithm (Weiler–Atherton is a classic polygon clipping algorithm based on the latitude and longitude system, and the algorithm complexity is positively correlated with the geometric complexity of the elements and the number of polygon intersections [25]) to conduct overlay analysis. Finally, we compared the results with the computational efficiency of the algebraic operation (Table 2 and Table 3).
Based on the results, the following two points can be drawn:
- (1)
- For the overlay calculation of layers containing a single area object, the algebraic operation’s efficiency is slightly higher than that of the Weiler–Atherton algorithm. Under the experimental conditions in this article, the algebraic operation’s efficiency is increased by about 1.32 times. For the overlapping calculation of two surface objects, the most time-consuming part of the overlay algorithm lies in judgment of the nesting relationship between the two grid sets. This operation is the most basic kind of bit operation. It is related to the number of grids covered by each area object. In comparison, the Weiler–Atherton algorithm’s largest time consumption lies in the judgment of the intersection between two objects. The number of judgments is related to the number of line segments expressing the two surface objects: the number of intersection points.
- (2)
- For the overlay calculation of layers containing multiple area objects, the algebraic operation ‘s efficiency is much higher than that of the Weiler–Atherton algorithm. Under the experimental conditions of this article, the efficiency of the algebraic operation is improved by about 6.44 times. For the overlay calculation between two area object sets, the time consumption of the algebraic operation is related to the size of the overall coverage area of the grid set and the data accuracy. It is associated with the total number of associated grids. It has a weak correlation with the number of objects involved in the calculation. However, the time consumed by the Weiler–Atherton algorithm is related to the number of objects in the reference calculation. The more objects there are, the more intersection points there are that express the spatial information of the objects, and the more times the intersection relationship is judged and the longer this process takes.
4.5. Analysis Efficiency of Algebraic Operation
We begin with the problem of the intersection of lines and lines in 3D space, and the intersection of entities, and compare algebraic operations with the spatial relationship judgment method under the traditional latitude, longitude, and height (LLH) system to demonstrate the superiority of our method regarding the spatial relationship.
We take the intersection calculation of 3D space curves as an example to analyze the calculation assuming of the 3D space line–line intersection algorithm (Figure 20). Curves in three-dimensional space widely exist, such as the flight trajectory of a missile. The two curves in the three-dimensional space are defined as follows:
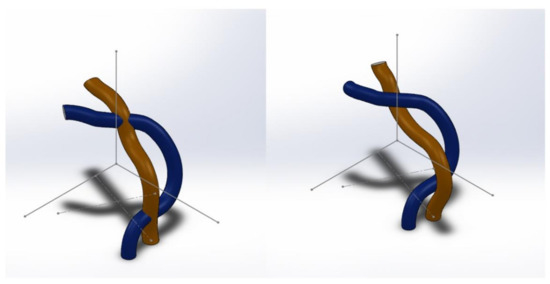
Figure 20.
Intersection of two lines in three-dimensional space.
If the two curves need to have a focus, the four equations of curve 1 and curve 2 need to be solved simultaneously. If curve 1 and curve 2 degenerate to the simplest straight line, it is relatively easy to solve the focal point. Then, for the equations corresponding to higher-order surfaces, the process of solving them will have a higher complexity. In practical applications, the requirements for collision detection are more complicated than simply finding the intersection of curves. This is because, for collision detection in the track, it is not only necessary to consider whether the track curve has an intersection, but also whether there will be an intersection in a certain radius of space around the two tracks. Therefore, the collision detection of the track changed from the intersection of two curves to the intersection of two spatial pipes.
This problem can be attributed to the objective function optimization problem based on equality constraints. The constraint condition is the expression equation of the two curves, and the optimization goal is the distance between the two points. To solve the minimum distance, the method used in practice is the Lagrange multiplier method (Lagrange multiplier). That is, the equation constraint is written as a formula with a coefficient and an objective function, which is called a Lagrangian function, and the coefficient is called a Lagrangian multiplier. The Lagrangian function is used to derive each variable and set it to zero to obtain a set of candidate values, and then verify that the optimal value is obtained.
Through the above analysis, it can be seen that the traditional 3D spatial relationship calculation algorithm is complicated. However, under our framework, the abovementioned complex spatial calculations can be converted into 3D spatial calculations of spatial entities, which can then be realized using algebraic operations. The method is based on the multiscale nature of the code. With the support of algebraic operations, the intersection of the inner lines in the space can be detected and coarse positioning can be performed. Then, the algebraic operations have nothing to do with the geometric shape of the space entity (line) and the number of space entities. The algorithm for the judgment of multiple space line entities is the same as the algorithm for the intersection operation of two space line entities. Therefore, the complexity of this calculation can be reduced to O(nlogn), where n is the number of elements in the grid set, and the algorithm has high stability.
5. Conclusions
As the amount of collected spatial information (2D/3D) increases, the real-time processing of these massive data is one of the urgent issues that require answers. Discretizing the physical Earth into a digital gridded Earth and assigning an integral computable code to each grid has become an effective way to accelerate real-time processing. Based on the GeoSOT-3D grid model, we established an integral grid-coding algebraic operation framework for GeoSOT-3D. By converting traditional floating-point calculations based on latitude and longitude into binary operations, the complexity of the algorithm is greatly reduced. Then, various operations within the framework were discussed, including basic operations, vector operations, code conversion operations, spatial operations, metric operations, and topological relation operations. To verify the feasibility and efficiency of the above algorithms, we developed an experimental platform using the C++ language (including major algorithms, and more algorithms may be expanded on in the future). Then, we generated random data and conducted experiments. The experiments proved that this is better than calculations in the latitude, longitude, and height system, which provides a more direct calculation method for the GeoSOT-3D model.
However, there are still some limitations. For example, if the spatial granularity is too fine, the encoding will occupy a large storage resource, and encoding compression design should be carried out. The special case where the codes are arranged very far apart at the inflection point of the filling curve (at the edge of the adjacent grid) should be discussed further. In future, we will continue to improve our method for both algorithms and applications, using Voronoi diagram generation, buffer analysis, cellular automata, etc. The algebraic operation framework is expected to support big geospatial data retrieval and analysis, and experience a revival, on top of parallel and distributed computing in the era of large geospatial data.
Author Contributions
Conceptualization, Kaihua Hou and Shuang Li; methodology, Kaihua Hou and Shuang Li; software, Kaihua Hou and Chi Zhang; validation, Kaihua Hou, Shuang Li, and Bo Chen.; formal analysis, Shuang Li; investigation, Shuang Li and Liesong He; writing—original draft preparation, Kaihua Hou; writing—review and editing, Shuang Li and Li Meng; visualization, Kaihua Hou; supervision, Chengqi Cheng; project administration, Chengqi Cheng and Bo Chen; funding acquisition, Chengqi Cheng All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by National Key Research and Development Plan (Grant No. 2018YFB0505300) and the National Natural Science Foundation of China (No. 42001184).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The algorithms presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
1. Hilbert curve decode vs. Z-order displacement code
| void rot (int n, int* x, int* y, int rx, int ry){ |
| if (ry == 0){ |
| if (rx == 1){ |
| *x = n − 1 − *x; |
| *y = n − 1 − *y; |
| } |
| int t = *x; |
| *x = *y; |
| *y = t; |
| } |
| } |
| void d2xy (int n, int d, int* x, int* y){ |
| int rx, ry, s, t = d; |
| *x = *y = 0; |
| for (s = 1; s < n; s *= 2){ |
| rx = 1 & (t / 2); |
| ry = 1 & (t ^ rx); |
| rot(s, x, y, rx, ry); |
| *x += s * rx; |
| *y += s * ry; |
| t /= 4; |
| } |
| } |
| unsigned int moveR(int n, unsigned code) { |
| if (code % 2 == 0) |
| return (code + 1); |
| n -= 2; |
| for (int i = 4; i < n; i = i * 4) { |
| if ((code & i) == 0) |
| return code & n|i; |
| n −= i; |
| } |
| return 0; |
| } |
2. Encode function pseudocode
| Function 2: encode: |
| Input: longitude, Latitude, Height, Layer Output: GeoSOT-3D Code |
3. Decode function pseudocode:
| Function 3: decode: |
| Input: GeoSOT-3D Code Output: longitude, Latitude, Height, Layer |
4. Vector +
| Function 4: vector + |
| Input: GeoSOT-3D Code1, GeoSOT-3D Code2 Output: GeoSOT-3D Code |
References
- Chen, S. Geo-spatial/temporal Analysis in Geo-processing. J. Remote Sens. 1997, 161–171. [Google Scholar] [CrossRef]
- Song, J.C.; Zhao, C.L.; Zhong, S.P.; Nielsen, T.A.S.; Prishchepov, A.V. Mapping spatio-temporal patterns and detecting the factors of traffic congestion with multi-source data fusion and mining techniques. Comput. Environ. Urban Syst. 2019, 77. [Google Scholar] [CrossRef]
- Xiong, X.; Qiao, S.J.; Li, Y.Y.; Han, N.; Yuan, G.; Zhang, Y.Q. A point-of-interest suggestion algorithm in Multi-source geo-social networks. Eng. Appl. Artif. Intell. 2020, 88. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, H.; Zhang, S.; Li, J.; Gao, H. Efficient quality-driven source selection from massive data sources. J. Syst. Softw. 2016, 118, 221–233. [Google Scholar] [CrossRef]
- Song, S.; Cheng, C.; Pu, G.; An, F.; Luo, X. Global Remote Sensing Data Subdivision Organization Based on GeoSOT. Acta Geod. Cartogr. Sin. 2014, 43, 869–876. [Google Scholar]
- Cheng, C.; Tong, X.; Chen, B.; Zhai, W. A Subdivision Method to Unify the Existing Latitude and Longitude Grids. ISPRS Int. J. Geo-Inf. 2016, 5, 161. [Google Scholar] [CrossRef]
- Wang, R.; Ben, J.; Du, L.; Zhou, J.; Li, Z. Encoding and Operation for the Planar Aperture 4Hexagon Grid System. Acta Geod. Cartogr. Sin. 2018, 47, 1018–1025. [Google Scholar]
- Xiaochong, T.; Jin, B.E.N.; Zhiyuan, Q.I.N.; Yongsheng, Z. The Subdivision of Partial Grid Based on Discrete Global Grid Systems. Acta Geod. Cartogr. Sin. 2009, 38, 506–513. [Google Scholar]
- Xiaochong, T.; Jin, B.E.N.; Yongsheng, Z. The Subdivision of Global Multi-resolution Hexagonal Grid and the Rules of Address Coding. Acta Geod. Cartogr. Sin. 2007, 36, 428–435. [Google Scholar]
- Goodchild, M.F.; Shiren, Y. A hierarchical spatial data structure for global geographic information systems. CVGIP Graph. Models Image Process. 1992, 54, 31–44. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Cheng, C.; Pu, G. QRA-Grid: Quantitative Risk Analysis and Grid-based Pre-warning Model for Urban Natural Gas Pipeline. ISPRS Int. J. Geo-Inf. 2019, 8, 122. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Hou, K.; Cheng, C.; Li, S.; Chen, B. A Space-Interconnection Algorithm for Satellite Constellation Based on Spatial Grid Model. Remote Sens. 2020, 12, 2131. [Google Scholar] [CrossRef]
- Miao, S.; Cheng, C.; Zhai, W.; Ren, F.; Zhang, B.; Li, S.; Zhang, J.; Zhang, H. A Low-Altitude Flight Conflict Detection Algorithm Based on a Multilayer Grid Spatiotemporal Index. ISPRS Int. J. Geo-Inf. 2019, 8, 289. [Google Scholar] [CrossRef] [Green Version]
- Yang, M.; Cheng, C.; Chen, B. Mining Individual Similarity by Assessing Interactions with Personally Significant Places from GPS Trajectories. ISPRS Int. J. Geo-Inf. 2018, 7, 126. [Google Scholar] [CrossRef] [Green Version]
- Bradley, P.E.; Jahn, M.W. On the Behaviour of p-Adic Scaled Space Filling Curve Indices for High-Dimensional Data. Comput. J. 2020. [Google Scholar] [CrossRef]
- Laurini, R.; Thompson, D. Fundamentals of Spatial Information Systems; Academic press: Cambridge, MA, USA, 1992; Volume 37. [Google Scholar]
- Jin, A.; Cheng, C. Spatial Data Coding Method Based on Global Subdivision Grid. J. Geomat. Sci. Technol. 2013, 30, 284–287. [Google Scholar]
- Tong, X.; Ben, J.; Wang, Y.; Zhang, Y.; Pei, T. Efficient encoding and spatial operation scheme for aperture 4 hexagonal discrete global grid system. Int. J. Geogr. Inf. Sci. 2013, 27, 898–921. [Google Scholar] [CrossRef]
- Zhou, X.; Tang, D.; Hao, L.; Song, Y. Application of earth partition gird theory in image processing. Sci. Surv. Mapp. 2019, 44, 84–89. [Google Scholar]
- Li, S.; Pu, G.; Cheng, C.; Chen, B. Method for managing and querying geo-spatial data using a grid-code-array spatial index. Earth Sci. Inform. 2019, 12, 173–181. [Google Scholar] [CrossRef]
- Open Geospatial Consortium Topic 21: Discrete Global Grid Systems Abstract Specification. Available online: https://docs.opengeospatial.org/as/15-104r5/15-104r5.html (accessed on 18 July 2021).
- Chen, J.; Li, C.M.; Li, Z.L.; Gold, C. A Voronoi-based 9-intersection model for spatial relations. Int. J. Geogr. Inf. Sci. 2001, 15, 201–220. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, S.; Guan, Y. An Efficient Parallel Algorithm for Polygons Overlay Analysis. Appl. Sci. 2019, 9, 4857. [Google Scholar] [CrossRef] [Green Version]
- Moon, B.; Jagadish, H.V.; Faloutsos, C.; Saltz, J.H. Analysis of the clustering properties of the hilbert space-filling curve. IEEE Trans. Knowl. Data Eng. 2001, 13, 124–141. [Google Scholar] [CrossRef] [Green Version]
- Weiler, K.; Atherton, P. Hidden surface removal using polygon area sorting. ACM SIGGRAPH Comput. Graph. 1977, 11, 214–222. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).