Abstract
Single electron capture in collisions involving neutral hydrogen atoms impacted by highly charged dressed projectiles is theoretically investigated using the distorted wave formalism. A series of continuum distorted wave approximations is employed to investigate the electron capture from neutral hydrogen atom impact by boron and carbon projectiles. The projectile potential is described using a two-parameter analytical Green–Sellin–Zachor (GSZ) model potential. The theoretical prediction of total cross sections are compared against other theories and experiments. We looked at a very broad range of collision energies, from 10 keV/u up to 10 MeV/u. In addition, the state-selective cross sections for boron ions are presented.
1. Introduction
Research into electronic reactions from ion–molecule collisions is very relevant to several fields, including plasma physics, astrophysics, medical physics, and radiobiology. The electron capture process induced by bare projectiles has been extensively studied over the years [1,2]. In the literature, numerous theoretical studies have computed total cross sections (TCSs) for charge transfer between highly charged bare ions and neutral atoms. However, interactions involving dressed projectiles and neutral atoms have received considerably less attention. In the framework of the perturbative method, Das et al. [3], within the boundary-corrected continuum intermediate state (BCCIS) approximation, calculated charge transfer cross sections for dressed projectiles with varying charge states interacting with atomic hydrogen [3,4]. In the context of the classical trajectory Monte Carlo (CTMC) method, Olson and Salop calculated the charge transfer cross sections for collisions between multiply charged projectiles (q charged ions) and atomic hydrogen over a range of intermediate to high energies [5]. Schultz et al. computed all inelastic cross sections for collisions of Beq+ (with ) with atomic and molecular hydrogen across a range of energies [6]. Das et al. employed the CTMC method to calculate total electron capture cross sections, including subshell distributions, for collisions between Bq+ ions () and atomic hydrogen in the energy range of 10−200 keV/u [7]. Hansen and Dubois employed a two-center atomic-state expansion method—specifically, the atomic orbital close-coupling (AOCC) approach—to study charge transfer cross sections in collisions of Bq+ with hydrogen and helium atoms for charge states over the energy range from 0.1 to 100 keV/u [8]. Their calculations provide charge transfer cross sections into specific subshells of the projectile ions. Within the framework of the distorted wave (DW) approximation, the electron capture process was first investigated by Cheshire to describe charge transfer in the H+−H system [9]. Over the following years, the CDW method and its variants were widely used to model electron capture processes [10]. Subsequently, Martinez et al. proposed the Continuum Distorted Wave-Eikonal Initial State (CDW-EIS) approximation to address the overestimation of TCS at intermediate impact energies predicted by the CDW model [11]. To provide a more accurate theoretical description for processes in which the projectile–electron interaction exerts a stronger influence on the initial bound state than the target nucleus–electron interaction does on the final bound state, Busnengo et al. introduced the Continuum Distorted Wave-Eikonal Final State (CDW-EFS) approximation [12]. They found that the CDW-EFS approximation is particularly well-suited for describing electron capture in asymmetric collisions [12]. In recent decades, several non-perturbative theoretical approaches have been developed to compute electron capture cross sections at low-to-intermediate energies. For both fully and partially stripped projectiles in the impact energy range of 1–100 keV/u, Leung and Kirchner employed the two-center basis generator method (TC-BGM) to calculate cross sections for Li3+, C3+, and O3+ colliding with neutral hydrogen. Their results showed good agreement between theoretical predictions and experimental data for electron capture [13]. Antonio et al. extended the two-center wave-packet convergent close-coupling (WP-CCC) approach to model dressed, i.e., partially stripped-carbon ions (C2+ and C3+), incorporating residual bound electrons via an effective three-body potential. Their study revealed a noticeable phenomenon: above 100 keV/u, dressed C2+ and C3+ ions exhibit larger total electron capture cross sections than their bare counterparts (e.g., He2+ and Li3+). As stated by the authors, this enhancement is attributed to the softened projectile–target interaction potential induced by the presence of bound electrons on the projectile. Furthermore, very good agreement was found between theory and experiment for electron capture across the entire energy range from 1 keV/u to 1 MeV/u [14]. Hill et al. presented a comprehensive review and comparison of several non-perturbative methods—including the TC-BGM, WP-CCC, CTMC, and the AOCC method—for computing ionization, excitation, and charge-exchange cross sections relevant to fusion plasma applications [15].
The present work aims to investigate single electron capture processes at intermediate and high collision energies where perturbative methods such as the CDW approximation are often more suitable than non-perturbative approaches, which can require significant computational resources, particularly when large basis sets are needed to ensure the result is consistent. Moreover, the accuracy of non-perturbative methods may be limited in high-energy collisions, where cross sections span several orders of magnitude. To address these challenges, we study the electron capture processes within the distorted wave formalism, employing the CDW, CDW-EIS, and CDW-EFS approximations for Bq+ (with ) and Cq+ (with ) projectiles colliding with neutral hydrogen atoms. The investigated projectiles—boron and carbon ions—have significant practical applications: boron ions have recently been explored as potential candidates for interface materials in plasma technology [16], while carbon ions play a key role in radiobiology, particularly in therapeutic applications such as carbon-ion beam therapy [17]. Following the approach of Monti et al. [18] for target ionization induced by dressed projectiles, we describe the interaction between the projectile and the captured electron using the Green–Sellin–Zachor (GSZ) analytical potential model. For bare projectiles such as B5+ and C6+, the final excited state is represented by a hydrogenic-like wavefunction [19]. In contrast, for partially stripped ions, the final excited state is described by Slater-type wavefunctions. Unless otherwise stated, atomic units (a.u.) are used throughout this work.
2. Theory
We consider the problem of atomic collisions as a system consisting of a dressed projectile and a hydrogen-like target with nuclear charge . We consider that the projectile electrons remain in their original states throughout the interaction. The projectile nuclear charge is screened by its bound electrons, resulting in a net charge q. The independent electron model (IEM) is employed, along with the straight-line version of the impact parameter approximation. We find that
where is the vector between the nuclei, is the impact parameter, is the velocity of the collision, and t is the time. The target electron Hamiltonian is as follows:
where is the electron position relative to the target nucleus and is its position relative to the projectile nucleus. The potential describes the interaction between the target electron and its own nucleus. The term represents the interaction of the target electron with the projectile. Finally, accounts for the static interaction between the screened projectile nucleus and the target nucleus.
The target under consideration is a neutral hydrogen atom, whose potential is a pure Coulomb potential given by the following:
Also, extending the analysis given in Refs. [11,12] for dressed projectiles, the potential can be written as follows:
represents the initial state wavefunctions of the N projectile electrons, where is the position vector of the jth electron relative to the projectile nucleus. Given its dependence on the internuclear distance , the potential introduces a phase factor that affects only the projectile differential cross sections as a function of its scattering angle. Consequently, this phase does not influence the total capture cross section when calculated as functions of the projectile velocity, as demonstrated in Ref. [10].
The first-order term of the scattering transition amplitude (in its prior form) yields a function of the impact parameter :
Consequently, represents the transition amplitude from the initial to the final electronic state. As previously noted, the potential does not influence the electronic transition and can therefore be neglected in the Hamiltonian :
where
The functions and represent the distorted wavefunctions that solve the time-dependent Schrödinger equation for the initial and final states, respectively [12,19]. The represents the hydrogenic ground state, i.e., , and denotes the final projectile wavefunction, characterized by the quantum numbers . Also, and denote the initial and final channel distortion functions, respectively.
The potential represents the interaction between the active electron and the projectile, accounting for both the nucleus and its bound electrons. It is defined as follows:
In the case of ionization induced by dressed projectiles, Monti et al. [18] modeled the potential in Equation (9) using a non-Coulombic form. Specifically, it was represented by the two-parameter Green–Sellin–Zachor (GSZ) analytic potential [20]. In this model, we can express the projectile potential as the combination of a long-range Coulomb term and a short-range screening term:
where Ω accounts for screening effects due to bound projectile electrons. The GSZ potential parameters H and d are functions of the projectile nuclear charge and its net ionization state q. See Ref. [20] for a table of these values.
Within this framework, the scattering amplitude is composed of two contributions: a long-range term from the Coulomb potential and a short-range term from the potential screening effects. The scattering amplitude can be obtained from Equation (6), and it can be written as
where represents the contribution from the long-range Coulombic potential, and is the part that comes from the short-range term. In collisions involving bare projectiles, the short-range term is zero () because the transition amplitude is determined solely by the Coulomb interaction. However, for dressed projectiles, both terms must be included in the calculation.
Within the CDW framework, the initial and final channel distortion functions are defined as follows:
Here, v denotes the projectile velocity, with and . The term (with being the Euler Gamma function) represents the normalization factor of the hypergeometric function 1F1. The initial distortion function is replaced by a eikonal function in the CDW-EIS approximation, it is expressed by the following:
The CDW-EFS approximation, on the other hand, replaces the final distortion function by the following:
The final projectile excited bound state, , is expressed by a linear combination of Slater-type functions. is expressed as follows:
where are the corresponding expansion coefficients. The Slater-type orbital is given by the following:
with
being the normalization factor of each Slater function. denotes the normalized spherical harmonics in complex form. The parameters , , and the quantum numbers (with ) for various atoms and ions are tabulated in Ref. [21]. In the case of a bare projectile, the final excited state is described by a hydrogen-like wavefunction, as reported in Ref. [19].
The transition amplitude in Equation (11) can be expressed in terms of the transverse momentum transfer by applying the Fourier transform:
The cross sections can be computed analytically using Equation (19) [22]. The theoretical formula for electronic capture cross sections from a hydrogen ground state to a projectile final state is calculated as a function of the projectile velocity and is given by the following:
The total electron capture cross section is the sum of all contributions from every possible final state:
3. Results
In this section, we report the TCS for single electron capture from H atom impacted by Bq+ and Cq+ obtained within the prior version of the CDW, CDW-EIS, and CDW-EFS approximations. As stated above, for bare projectiles, namely B5+ and C6+, the final excited state is represented by a hydrogenic wavefunction [19]. In the present results, we have considered the final states up to . Whereas for dressed projectiles, Bq+ with and Cq+ with , in the first step, the final states are limited to the Slater-type wavefunction reported by Novikov [21], where the final excited state is consolidated up to d-type orbitals ().
3.1. Total Cross Sections
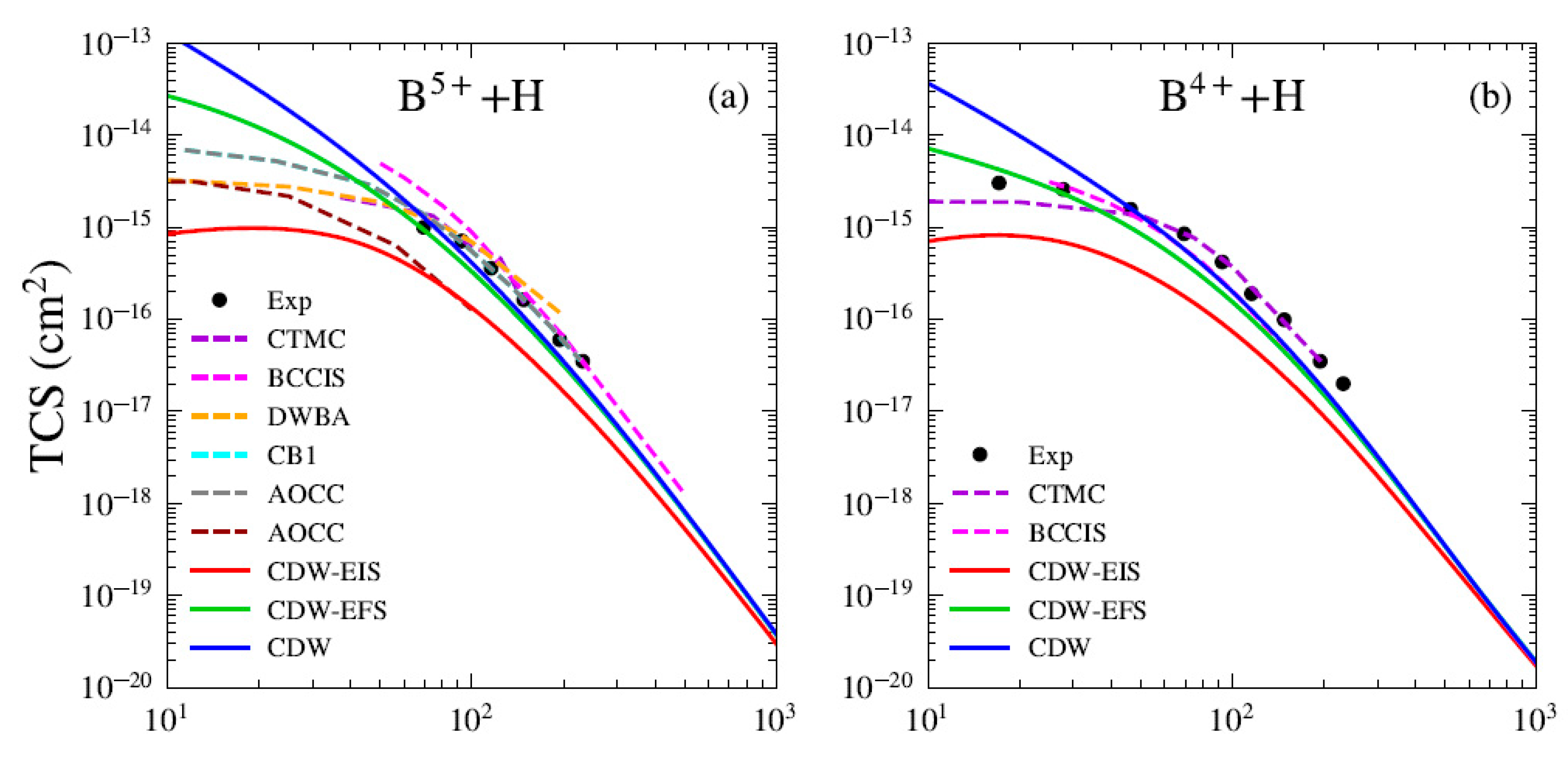
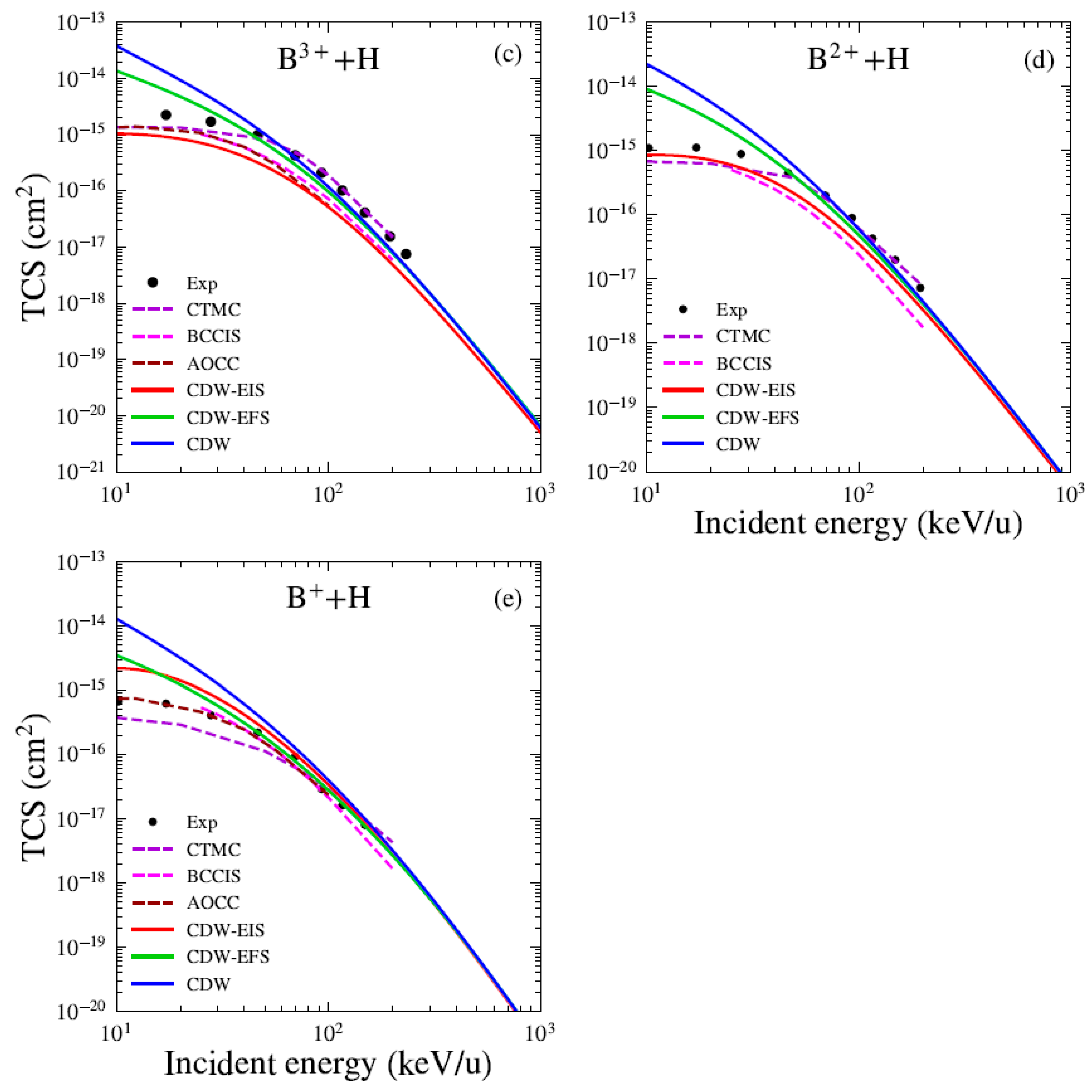
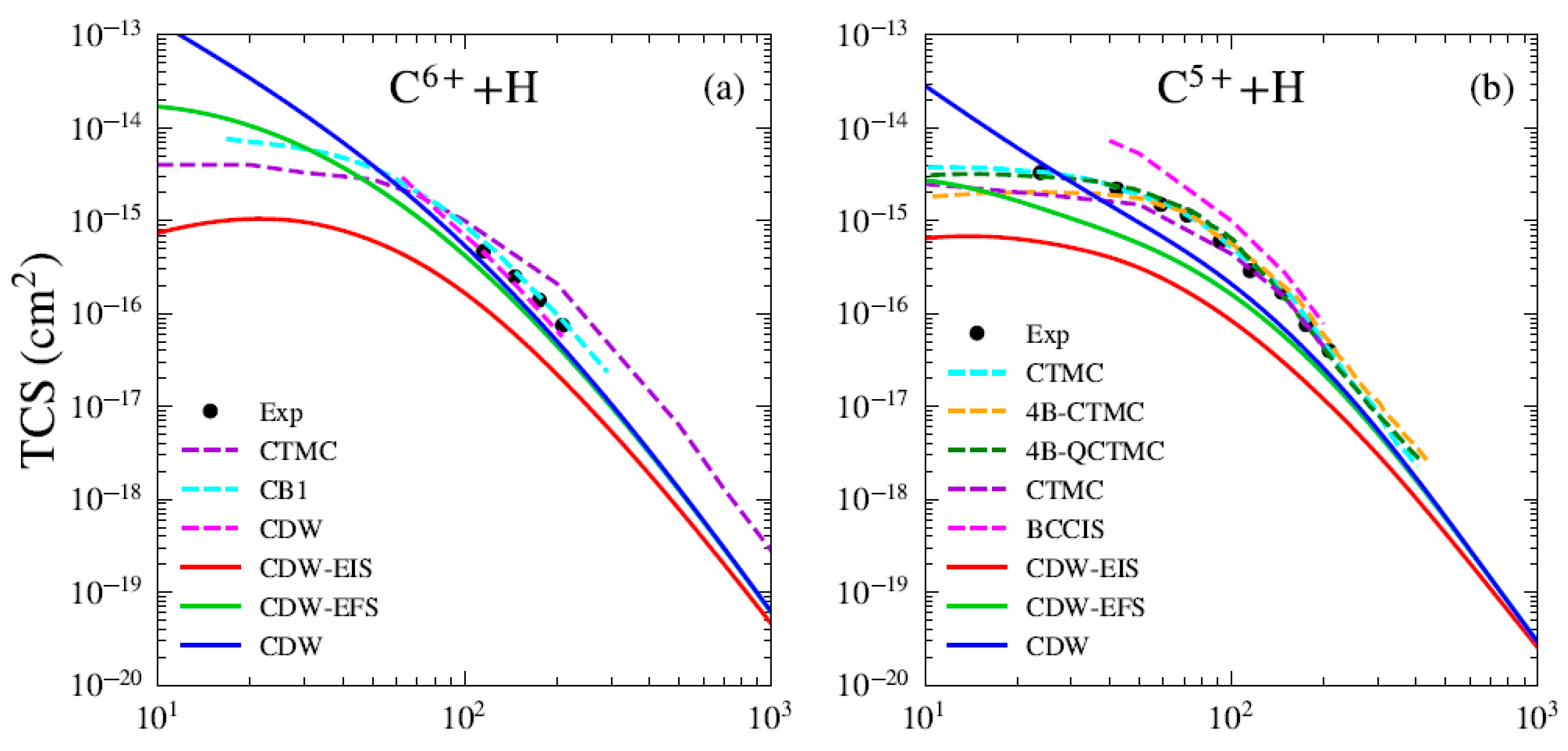
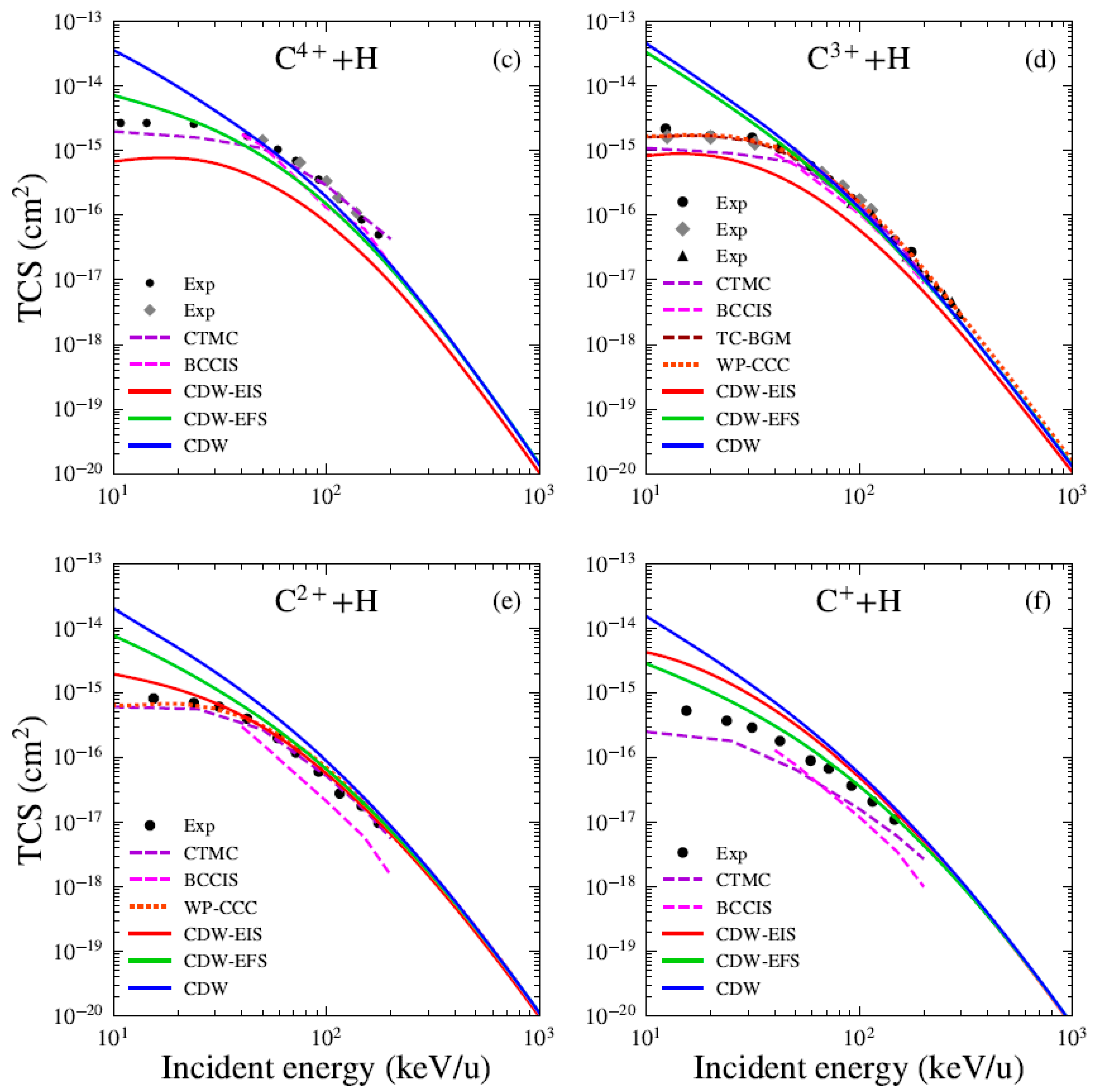
Figure 1 presents the total cross sections (TCSs) for electron capture in the Bq+ + H systems. For all considered charge states, our theoretical results are compared with the CTMC predictions of Olson and Salop [5] and with the BCCIS perturbative approach of Das et al. [7]. Here, we compare our results with the BCCIS calculations, which were computed using a model potential to describe the interaction between the target electron and the projectile ion. Similar to the CDW method, BCCIS is a high-order approximation in which the projectile–active electron interaction is included only in the final state [7]. The main difference resides in the fact that in BCCIS the asymptotic boundary condition associated with projectile–target interaction is considered in the entry channel, depending on the internuclear vector between the aggregates of the collision, whereas in the CDW models this interaction is taken to depend on the position vector of the target electron with respect to the projectile framework. In this sense, the initial distorted wavefunctions in the CDW models are two-center ones because they depend simultaneously on the electronic coordinates with respect to the target and projectile frameworks, while BCCIS uses a one center wavefunction [23]. A comparison with the experimental data reported by Goffe et al. [24] is also presented. We observe good agreement between our results and other available data for impact energies greater than 40 keV/u. For the B5+ projectile (see Figure 1a), we compare our results with several theoretical models available in the literature. The present CDW and CDW-EFS approximations show good agreement with the unitarized distorted wave approximation (UDWA) of Ryufuku and Watanabe [25] and the corrected first Born (CB1) method of Belkić et al. [26] and the AOCC of Toshima [27] for impact energies greater than 40 keV/u. We also observe that the results reported by the UDWA theory [25], AOCC method by Toshima [27], and the CTMC model [5] show excellent agreement and are nearly indistinguishable in Figure 1a. For charge states , (see Figure 1a,c,e), a comparison with the AOCC theory of Hansen and Dubois is also included. For B2+ (see Figure 1d), the CDW-EIS results show good agreement with the experimental measurements, as well as with the CTMC and BCCIS models. In Figure 2, we present the total cross sections (TCSs) for electron capture in the Cq+ + H systems. For all charge states, we compare our theoretical results with CTMC calculations by Schmidt [28] and BCCIS and CTMC predictions by et al. [4,29]. The experimental data reported by Goffe et al. are also used for comparison. Good agreement is found between the present results and existing data for impact energies greater than 40 keV/u. For the C6+ projectile (see Figure 2a), the CB1 results of Belkić et al. [26] are included and show good agreement with the present CDW-EFS TCS. Furthermore, our CDW results align well with those reported by Mandal et al. [30]. We also include a comparison with the AOCC model of Toshima [27]. The results from the UDWA, AOCC, and CTMC models exhibit the same trend observed previously for the B5+ projectile. For C5+ (see Figure 2b), our theories slightly underestimate the experimental data and other theoretical results. We observe that the CTMC results of Janev and McDowell [31] are in agreement with the four-body quasi-CTMC (4B-QCTMC) of Atawneh [32]. Whereas the CTMC results of [29] are in close agreement with those of 4B-CTMC given by [32]. For C4+ and C3+ (see Figure 2c,d), the measurements of Phaneuf et al. [33] are included for comparison. Additionally, the experimental measurements reported by Sant’Anna et al. [34] for the C3+ projectile are depicted. For C3+ and C2+ (see Figure 2d,e), we compare our results with those from the TC-BGM [13] and WP-CCC [14] theories. Remarkably, both non-perturbative methods show excellent agreement with experimental data in the low-energy regime below 40 keV/u. For C3+, the TC-BGM and WP-CCC results are in very close agreement with each other and are nearly indistinguishable in Figure 2d. Furthermore, we observe good convergence between these models and our present calculations for energies greater than 40 keV/u. For C+ (see Figure 2f), the present results slightly overestimate the experimental and other theoretical predictions, although they converge toward the asymptotic energy limit. Overall, the CDW and CDW-EFS models show good qualitative agreement with both experimental measurements and theoretical results across the energy range of 40 keV/u to 10 MeV/u, for all considered projectiles and their respective charge states. In contrast, the CDW-EIS theory consistently underestimates both the experimental and theoretical predictions. Furthermore, for all investigated systems, the three theoretical models converge at high impact energies. For projectiles with a high charge state q, the CDW-EFS approximation provides better agreement with experimental or reference data compared to CDW-EIS, as previously observed by Busnengo et al. [12]. In the low-energy range, the CDW theory consistently overestimates both the experimental measurements and other theoretical TCSs. In the case of B4+ and C5+ projectiles (see Figure 1b and Figure 2b), the present theoretical models underestimate the experimental and CTMC results for impact energies below 200 keV/u. This discrepancy may arise from limitations in the maximum principal quantum number of the excited states considered. Including higher final excited states with could improve the agreement.
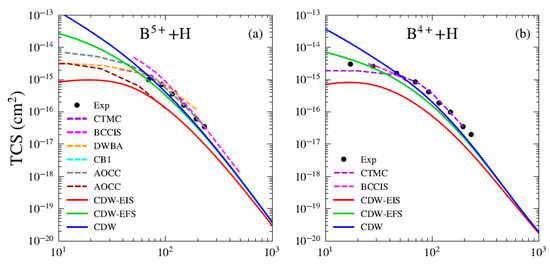
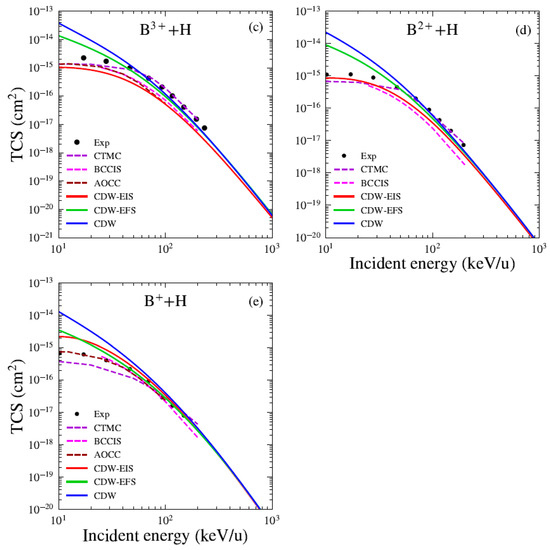
Figure 1.
TCS for electron capture by (a) B5+, (b) B4+, (c) B3+, (d) B2+, and (e) B+ from H atom as a function of impact energy. Present theoretical calculations (solid lines): CDW-EIS (red), CDW-EFS (green), and CDW (blue). Others theories (dashed lines): CTMC (violet) [5], BCCIS (magenta) [3], CB1 (cyan) [26], DWBA (orange) [25], AOCC (brown) [8], and AOCC (gray) [27]. Experimental data from [24].
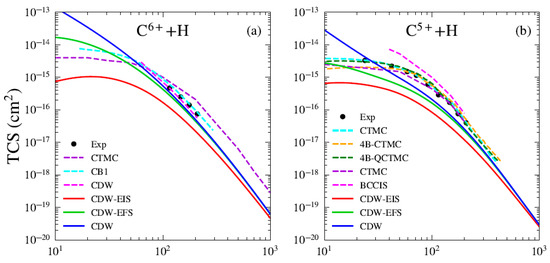
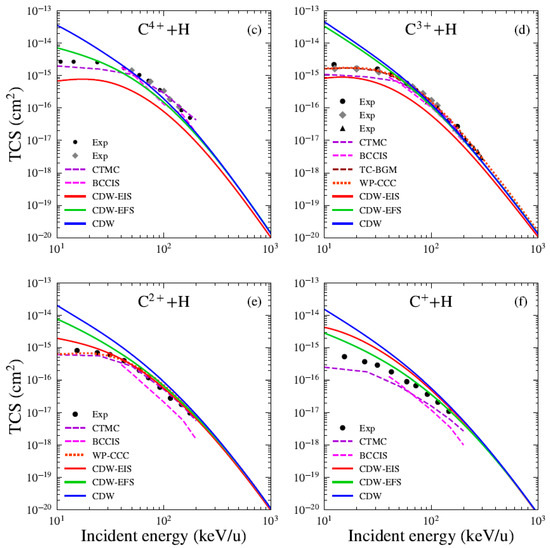
Figure 2.
TCS for electron capture by (a) C6+, (b) C5+, (c) C4+, (d) C3+, (e) C2+, and (f) C+ projectiles form H atom as a function of impact energy. Present theoretical calculations (solid lines): CDW-EIS (red), CDW-EFS (green), and CDW (blue). Others theories (dashed lines): (a) CTMC (violet) [28] CB1 (cyan) [26], DWBA (orange) [25], CDW (magenta) [30], and AOCC (gray) [27]; (b) CTMC (cyan) [31], 4B-CTMC (orange), and 4B-QCTMC (green) [32]; (b–f) CTMC (violet) [29], and BCCIS (magenta) [4]; (d) TC-BGM (brown) [13]; (d,e) WP-CCC (orange) [14]. Experimental data: (a–f) black circles [24], (c,d) gray diamonds [33], and (d) black triangles [34].
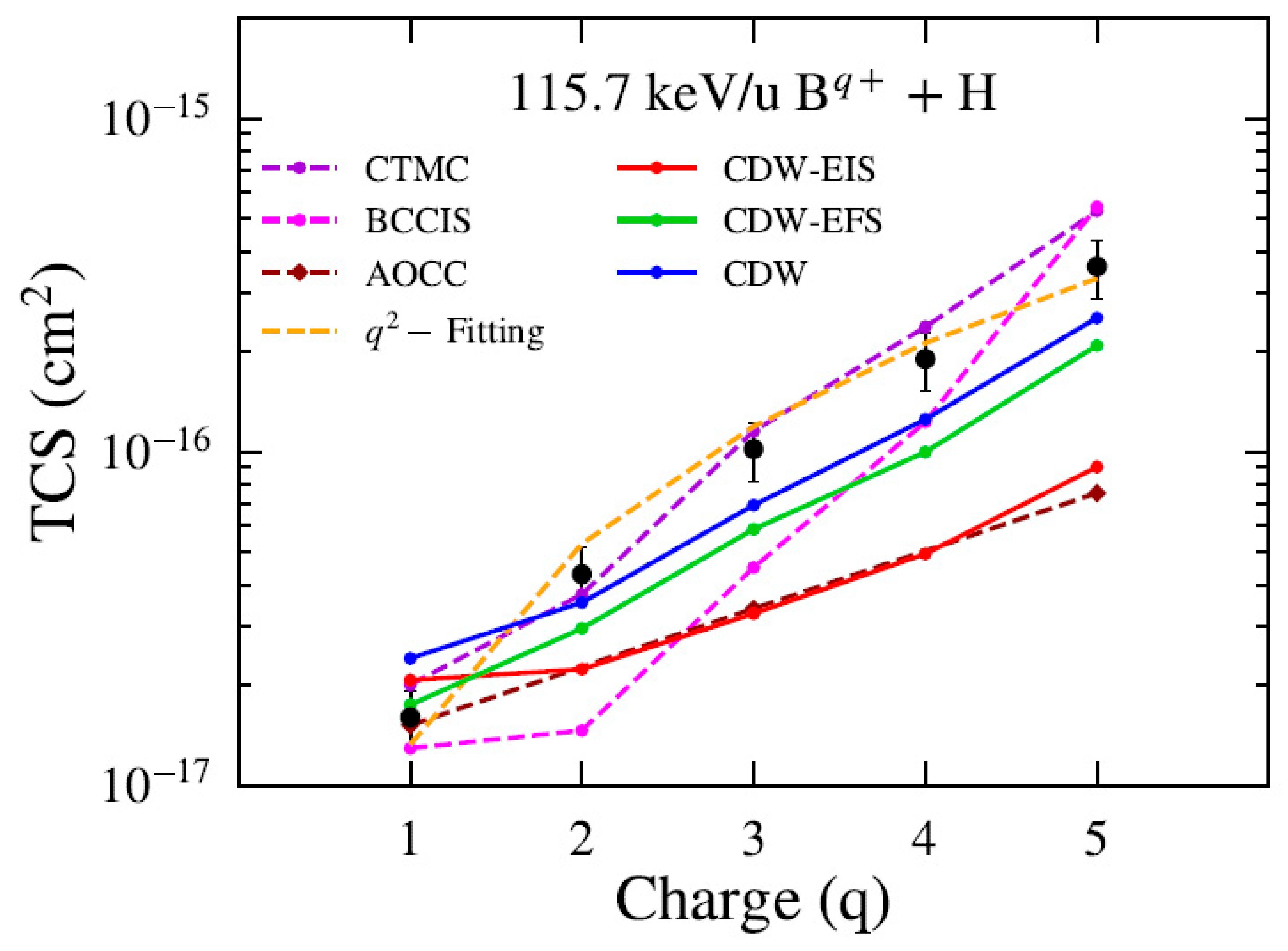
3.2. q-Charge Dependency
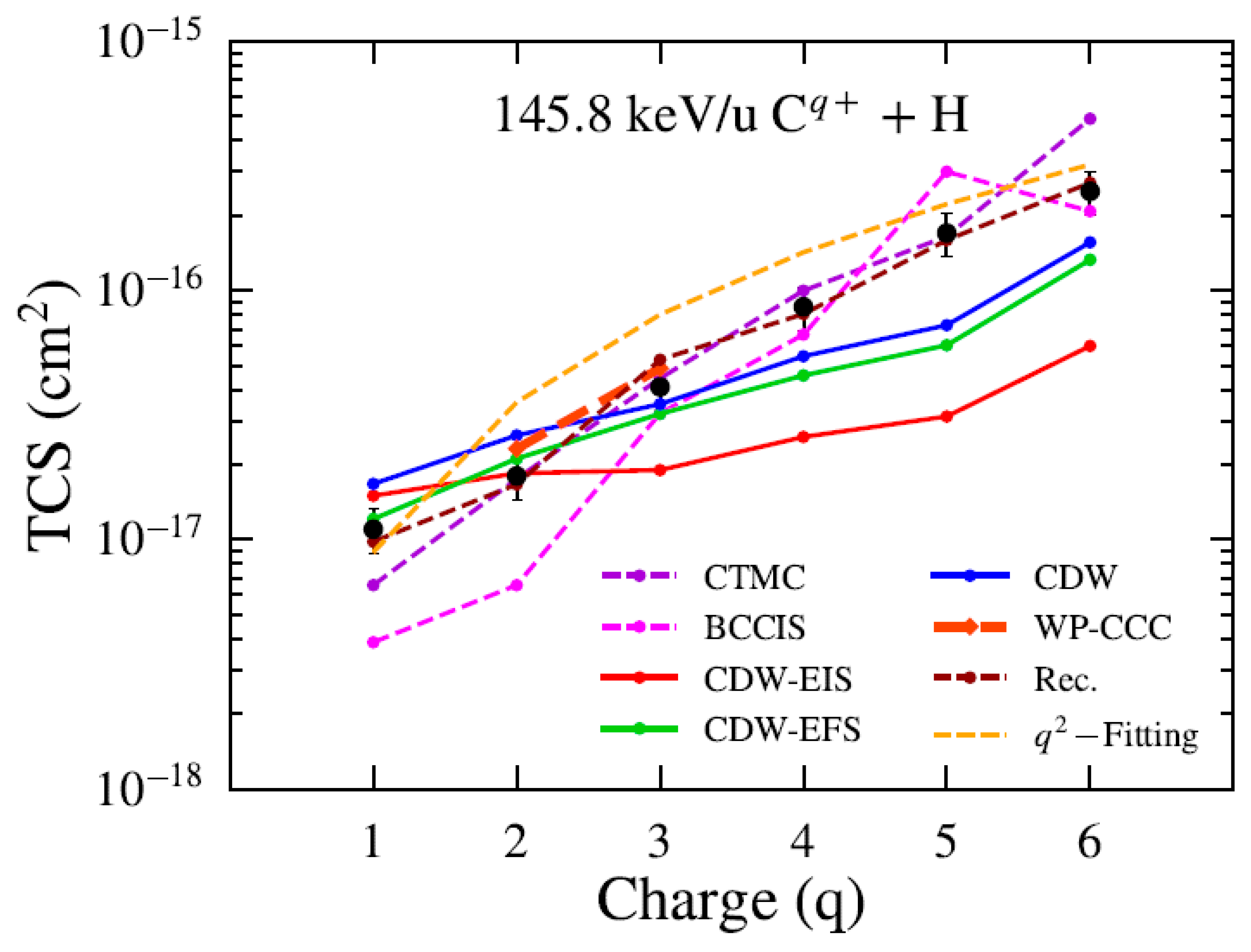
Figure 3 shows the TCS as a function of charge state for boron ions at a fixed impact energy of 115.7 keV/u. The present CDW and CDW-EFS results show good qualitative agreement with the experimental data and CTMC calculations. In contrast, the CDW-EIS approximation underestimates the TCS values by a factor of approximately five for charge states , yielding results close to those predicted by the AOCC theory. The BCCIS results show a slight discrepancy with respect to our theoretical predictions and the experimental data at intermediate charge states . Also, we include the -law (dashed orange line) proposed by Phaneuf et al. [33] to model the charge-state dependence of the cross sections. Figure 4 presents the same TCS analysis for carbon ions at a fixed impact energy of 145.8 keV/u. The present theoretical predictions follow the same trend as observed for the Bq+ case. For completeness, we compare our results with those from the CTMC and BCCIS methods, alongside the recommended data reported by Janev and McDowell [31] and the WP-CCC results from Antonio et al. [14]. Close agreement is observed at low charge states (q).
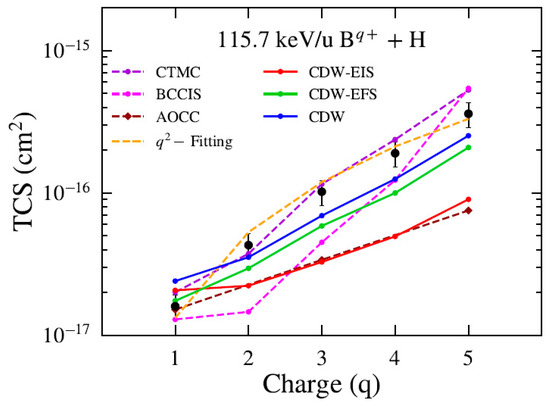
Figure 3.
TCS for electron capture by Bq+ from H atom as a function of the projectile charge. Present theoretical calculations (solid lines): CDW-EIS (red), CDW-EFS (green) and CDW (blue). Other theories: CTMC (violet) [5], BCCIS (magenta) [3], and AOCC (brown) [8]. Experimental data black circles from [24].
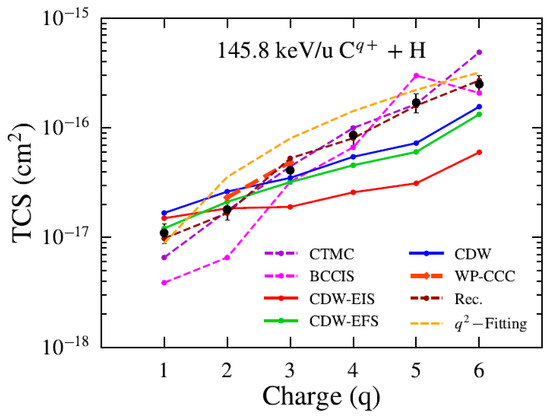
Figure 4.
TCS for electron capture by Cq+ from H atom as a function of the projectile charge. Present theoretical calculations (solid lines): CDW-EIS (red), CDW-EFS (green), and CDW (blue). Other theories: CTMC (violet) [5,29], BCCIS (magenta) [3,7], WP-CCC (orange), and recommended data (brown) [31]. Experimental data black circles from [24].
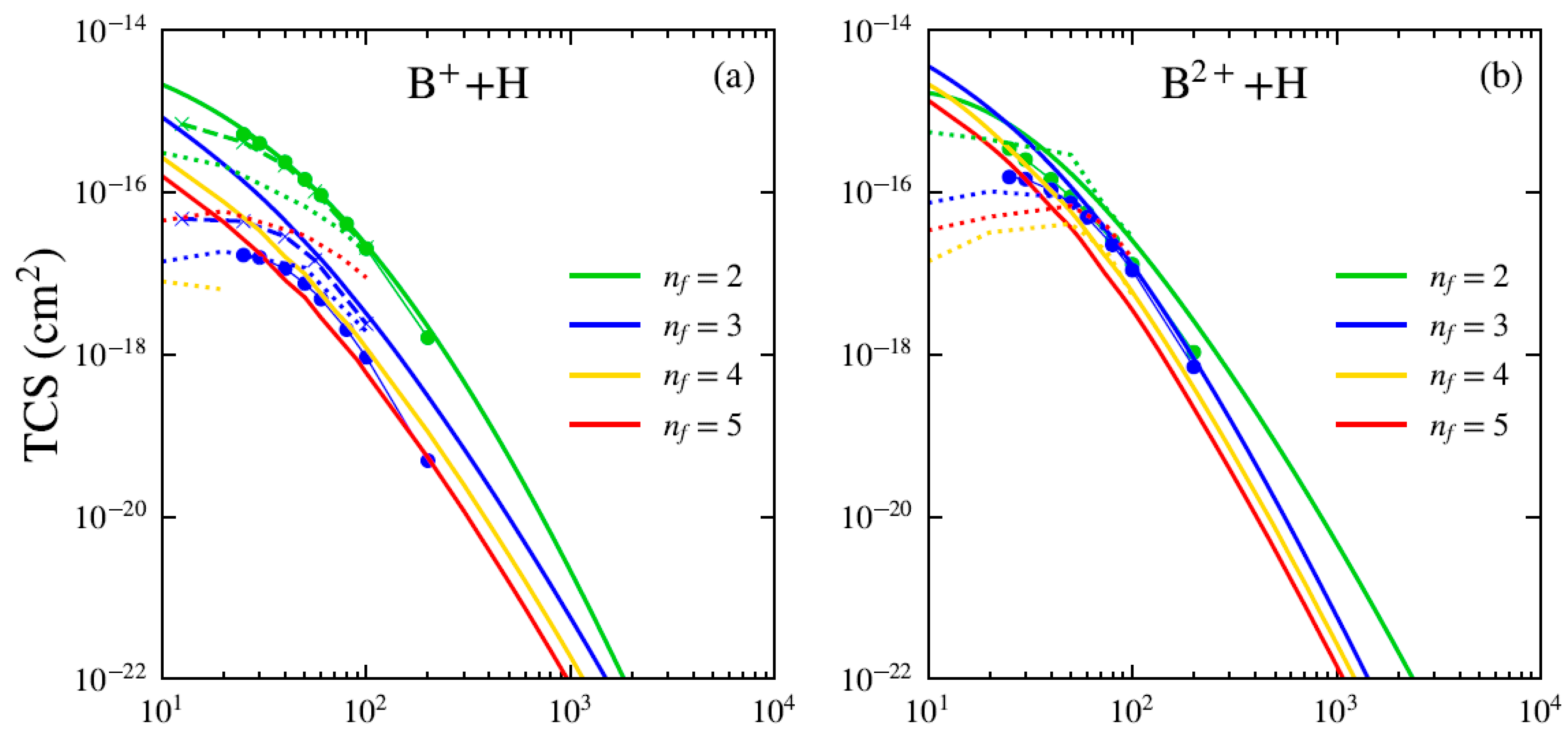
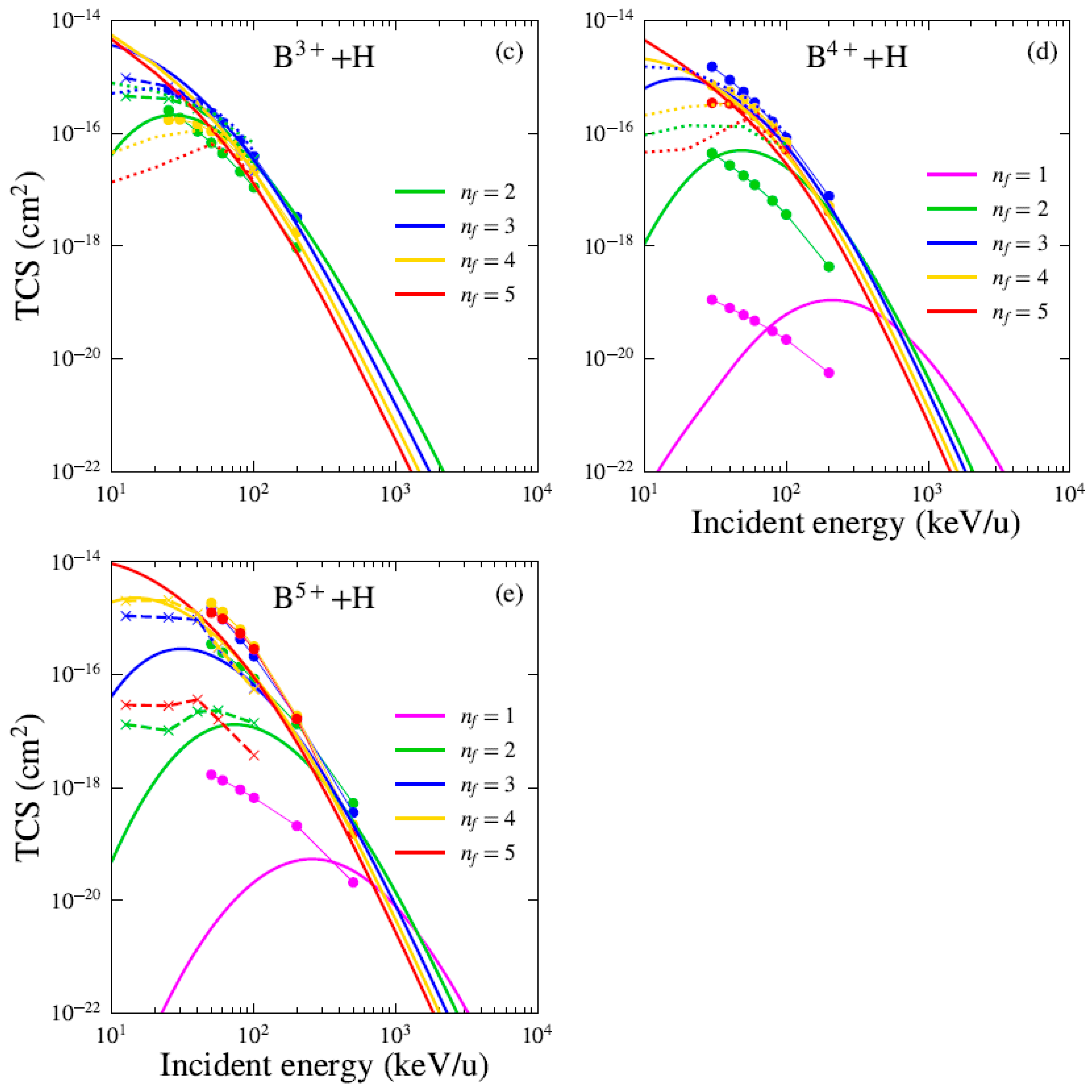
3.3. State-Selective Cross Sections
We show in Figure 5 the state-selective cross sections for the cases of Bq+ (with ) projectiles. As previously shown, the CDW-EFS approximation provides a better description compared to the other DW models presented. Accordingly, the comparison is restricted to the CDW-EFS model and the theoretical results from the BCCIS approximation [3], the CTMC model of Das et al. [7] and the AOCC model of Hansen and DuBois [8]. For low-charge-state projectiles like B+, electron capture predominantly populates the state over the full range of impact energies. For this projectile, the 1s and 2s orbitals are fully occupied, making the 2p and 3s orbitals the first accessible final states for electron capture. Their Hartree–Fock binding energies are (2p) and (3s) [21]. The 2p state is favored due to its binding energy being closer to the initial state energy of hydrogen (), enhancing the likelihood of resonant capture. Higher excited states contribute negligibly, with cross sections at least an order of magnitude below those for . For this state, the three models show excellent agreement over the full energy range. However, for , the CDW-EFS results exceed the AOCC predictions by a significant margin at energies below 40 keV/u. The BCCIS model reproduces the qualitative behavior of the AOCC results, though the cross sections are scaled down by a factor of about two. For the B2+ ion, the state dominates the electron capture cross section for impact energies greater than 20 keV/u within the CDW-EFS framework. Below this energy, the state becomes dominant. In contrast, for both BCCIS and CTMC results, the contribution of final states decreases with increasing quantum number across the entire energy range considered. For Bq+ ions with , electron capture predominantly populates the final state at intermediate energy range, from a few keV/u up to several hundred keV/u. This preference arises because the binding energy of the orbital closely matches that of the hydrogenic ground state (1s). For example, the binding energies of the 3d-orbital in B3+ () and the 4d-orbital in B4+ () are nearly resonant with . resulting in a significant enhancement of the electron capture cross section. For B5+, the final-state binding energy () coincides exactly with the hydrogenic eigenvalue , which matches precisely the binding energy of the target hydrogen atom (1s). This near-resonant condition strongly enhances the capture cross section into compared to all other final states. For highly charged projectiles such as B4+ and B5+, capture into high- excited states dominates at low impact energies (below 1 MeV/u), whereas population of the ground state becomes dominant at higher energies. For Bq+ ions with , the CDW-EFS and BCCIS models show improved agreement for highly excited final states; however, significant discrepancies remain for the states at low collision energies—specifically below a few hundred keV/u. In general, for B+, B3+, and B5+ ions, we observe a close agreement between the CDW-EFS model and the AOCC results for suggests that these capture channels are well described by perturbative approaches. However, for , significant deviations appear—consistent with the known limitations of the AOCC method in treating highly excited states [8]. The CTMC selective-state cross sections for Bq+ ions with , reported by Das et al., [7], show good agreement with CDW-EFS theory for projectile charge states at impact energies greater than 40 keV/u. However, a significant discrepancy is observed for the B+ projectile.
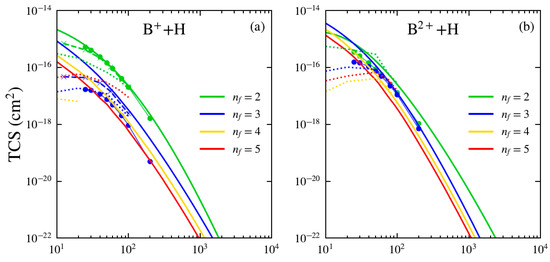
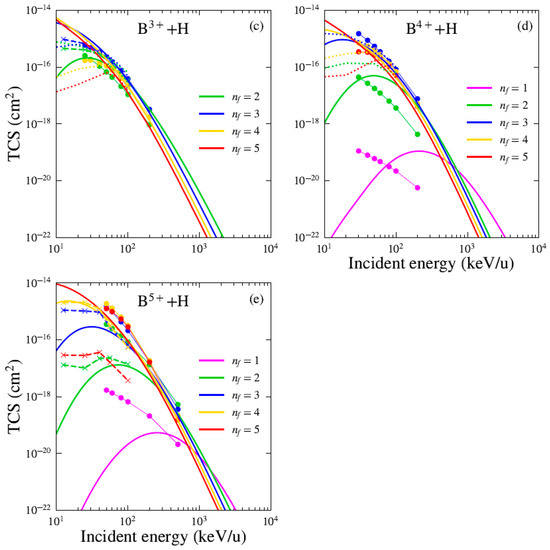
Figure 5.
State-selective cross section for electron capture by (a) B+, (b) B2+, (c) B3+, (d) B4+, and (e) B5+ from H atom as a function of impact energy. Present theoretical calculations: CDW-EFS (solid lines), BCCIS (symbols with lines) [3], CTMC (dotted lines) [7] and AOCC (symbols with dashed lines) [8].
4. Conclusions
In this work, we have theoretically investigated the electron capture process in collisions between boron and carbon-dressed projectiles and hydrogen atoms using the distorted wave formalism. In particular, three perturbative approximations were employed: the CDW, CDW-EIS, and CDW-EFS models. The GSZ potential model was employed to describe the effective projectile potential, which accounts for the screening effect arising from its bound electrons. For the investigated systems, the CDW approximation was found to systematically overestimate both experimental data and other theoretical predictions for TCSs in the low-energy range. In contrast, the CDW-EIS model consistently underestimates the TCS values, particularly for high projectile charge states. The improved agreement of the CDW-EFS approximation with experimental data and other theoretical models supports its reliability in describing asymmetric collision systems. The observed asymmetry is associated with projectile ion charges that are higher than the nuclear charge of hydrogen. It is important to note that the CDW-EIS model provides an improved description of experimental results as the collision system becomes more symmetric, which occurs when the charge of the projectile is reduced. While a qualitative agreement with published data is found for impact energies above 40 keV/u, the theoretical models tend to overestimate the cross sections at lower energies compared to non-perturbative methods such as CTMC and AOCC. As a result, we conclude that the CDW-based approaches presented here are valid for the energy range greater than 40 keV/u.
State-selective cross sections for boron ions reveal distinct capture patterns depending on the projectile charge state. For low-charge-state ions, capture is predominantly into low- states. In contrast, for fully stripped projectiles, high- states dominate at low and intermediate energies, while low- capture prevails at high impact energies. In future studies, the current framework will be extended to multielectronic atomic and molecular targets, with a focus on state-selected cross sections. The description of the final excited state will also be expanded to include higher principal quantum numbers () for dressed projectiles using hydrogenic-like wavefunctions.
Author Contributions
Conceptualization, M.A.Q., J.M.M. and R.D.R.; methodology, M.A.Q., J.M.M. and R.D.R.; software, M.A.Q.; validation, M.A.Q., J.M.M. and R.D.R.; formal analysis, M.A.Q., J.M.M. and R.D.R.; investigation, M.A.Q., J.M.M. and R.D.R.; writing—original draft preparation, M.A.Q.; writing—review and editing, M.A.Q., J.M.M. and R.D.R.; visualization, M.A.Q.; supervision, J.M.M. and R.D.R.; funding acquisition, R.D.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this article are not publicly available. The data are available from the authors upon reasonable request.
Acknowledgments
The authors acknowledge support from the Consejo Nacional de Investigaciones Científicas y Técnicas de la República Argentina, through Project PIP 2021–3245. The results presented in this work have been obtained using the facilities of the CCT–Rosario Computational Center, a member of the High–Performance Computing National System (SNCAD, Secretaría de Innovación, Ciencia y Tecnología, Argentina).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AOCC | Atomic Orbital Close-Coupling |
| BCCIS | Boundary-Corrected Continuum Intermediate State |
| CB1 | Corrected First Born Approximation |
| CDW | Continuum Distorted Wave |
| CDW-EIS | Continuum Distorted Wave - Eikonal Initial State |
| CDW-EFS | Continuum Distorted Wave - Eikonal Final State |
| CTMC | Classical Trajectory Monte Carlo |
| DW | Distorted Wave |
| 4B-CTMC | Four-Body Classical Trajectory Monte Carlo |
| 4B-QCTMC | Four-Body Quasi Classical Trajectory Monte Carlo |
| GSZ | Green–Sellin–Zachor |
| TCS | Total Cross Section |
| TC-BGM | Two-Center Basis Generator Method |
| UDWA | Unitarized Distorted Wave Approximation |
| WP-CCC | Wave-Packet Convergent Close-Coupling |
References
- Bransden, B.H.; McDowell, M.R.C. Charge Exchange and the Theory of Ion-Atom Collisions; Oxford University Press: Oxford, UK, 1992. [Google Scholar] [CrossRef]
- Belkić, D. Quantum Theory of High-Energy Ion-Atom Collisions, 1st ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar] [CrossRef]
- Das, M.; Purkait, M.; Mandal, C.R. Charge-transfer cross sections in collisions of Beq+(q = 1 − 4) and Bq+(q = 1 − 5) with ground-state atomic hydrogen. Phys. Rev. A 1998, 57, 3573–3582. [Google Scholar] [CrossRef]
- Purkait, M.; Das, M.; Mandal, C.R. State-selective electron capture by multicharged ions of carbon, nitrogen, and oxygen from ground-state atomic hydrogen. Phys. Rev. A 1999, 60, 3025–3028. [Google Scholar] [CrossRef]
- Olson, R.E.; Salop, A. Charge-transfer and impact-ionization cross sections for fully and partially stripped positive ions colliding with atomic hydrogen. Phys. Rev. A 1977, 16, 531–541. [Google Scholar] [CrossRef]
- Schultz, D.R.; Krstić, P.S.; Reinhold, C.O. Inelastic processes in 1–1000 keV/u collisions of Beq+ (q = 2 − 4) ions with atomic and molecular hydrogen. Phys. Scr. 1996, 1996, 69. [Google Scholar] [CrossRef]
- Das, M.; Purkait, M.; Mandal, C.R. Sub-shell distributions of total electron capture and ionization cross-sections in Bq+ (q = 1 − 4) + H collisions. Eur. Phys. J. D 2000, 8, 13–18. [Google Scholar] [CrossRef]
- Hansen, J.P.; Dubois, A. Cross sections for electron capture in H–Bq+ and He–Bq+ (q = 1, 3, 5) collisions. Phys. Scr. 1996, 1996, 55. [Google Scholar] [CrossRef]
- Cheshire, I.M. Continuum distorted wave approximation; resonant charge transfer by fast protons in atomic hydrogen. Proc. Phys. Soc. 1964, 84, 89. [Google Scholar] [CrossRef]
- Belkić, D.; Gayet, R.; Salin, A. Electron capture in high-energy ion-atom collisions. Phys. Rep. 1979, 56, 279. [Google Scholar] [CrossRef]
- Martínez, A.E.; Deco, G.R.; Rivarola, R.D.; Fainstein, P.D. K-Shell vacancy production in asymmetric collisions. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms 1988, 34, 32–36. [Google Scholar] [CrossRef]
- Busnengo, H.F.; Corchs, S.E.; Martínez, A.E.; Rivarola, R.D. Single electron capture by impact of multicharged ions. Phys. Scr. 1997, 1997, 242. [Google Scholar] [CrossRef]
- Leung, A.C.K.; Kirchner, T. Two-Center Basis Generator Method Calculations for Li3+, C3+ and O3+ Ion Impact on Ground State Hydrogen. Atoms 2022, 10, 11. [Google Scholar] [CrossRef]
- Antonio, N.W.; Plowman, C.T.; Abdurakhmanov, I.B.; Kadyrov, A.S. Calculations of the integrated cross sections in dressed carbon-ion collisions with atomic hydrogen. Phys. Rev. A 2024, 109, 012817. [Google Scholar] [CrossRef]
- Hill, C.; Heinola, K.; Dubois, A.; Sisourat, N.; Taoutioui, A.; Agueny, H.; Tőkési, K.; Ziaeian, I.; Illescas, C.; Jorge, A.; et al. Atomic collisional data for neutral beam modeling in fusion plasmas. Nucl. Fusion 2023, 63, 125001. [Google Scholar] [CrossRef]
- Janev, R.K. Atomic and Molecular Processes in Fusion Edge Plasmas, 1st ed.; Springer: New York, NY, USA, 1995. [Google Scholar] [CrossRef]
- Liamsuwan, T.; Nikjoo, H. A Monte Carlo track structure simulation code for the full-slowing-down carbon projectiles of energies 1 keVu−1 –10 MeV−1 in water. Phys. Med. Biol. 2013, 58, 673. [Google Scholar] [CrossRef]
- Monti, J.M.; Rivarola, R.D.; Fainstein, P.D. Distorted wave theories for dressed-ion-atom collisions with GSZ projectile potentials. J. Phys. B: At. Mol. Opt. Phys. 2011, 44, 195206. [Google Scholar] [CrossRef]
- Quinto, M.A.; Montenegro, P.R.; Monti, J.M.; Fojón, O.A.; Rivarola, R.D. Electron capture by swift ions from molecules of biological interest. J. Phys. At. Mol. Opt. Phys. 2018, 51, 165201. [Google Scholar] [CrossRef]
- Szydlik, P.P.; Green, A.E.S. Independent-particle-model potentials for ions and neutral atoms with Z < 18. Phys. Rev. A 1974, 99, 1885–1894. [Google Scholar] [CrossRef]
- Novikov, N. New Method of the Approximation of Hartree-Fock Wave Functions. Int. J. Math. Comput. Sci. 2015, 1, 55–58. [Google Scholar]
- Gravielle, M.S.; Miraglia, J.E. Some Nordsieck integral of interest in radiation and atomic collision theories. Comput. Phys. Commun. 1992, 69, 53–58. [Google Scholar] [CrossRef]
- Stolterfoht, N.; Schneider, D.; Tanis, J.; Altevogt, H.; Salin, A.; Fainstein, P.D.; Rivarola, R.; Grandin, J.P.; Scheurer, J.N.; Andriamonje, S.; et al. Evidence for Two-Centre Effects in the Electron Emission from 25 MeV/u Mo40+ + He Collisions: Theory and Experiment. Europhys. Lett. 1987, 4, 899. [Google Scholar] [CrossRef]
- Goffe, T.V.; Shah, M.B.; Gilbody, H.B. One-electron capture and loss by fast multiply charged boron and carbon ions in H and H2. J. Phys. B: At. Mol. Phys. 1979, 12, 3763. [Google Scholar] [CrossRef]
- Ryufuku, H.; Watanabe, T. Charge transfer cross sections for collisions of Li3+, Be4+, B5+, and C6+ ions with atomic hydrogen. Phys. Rev. A 1979, 19, 1538–1549. [Google Scholar] [CrossRef]
- Belkić, D.; Saini, S.; Taylor, H.S. Critical test of first-order theories for electron transfer in collisions between multicharged ions and atomic hydrogen: The boundary condition problem. Phys. Rev. A 1987, 36, 1601–1617. [Google Scholar] [CrossRef]
- Toshima, N. Ionization and charge transfer of atomic hydrogen in collision with multiply charged ions. Phys. Rev. A 1994, 50, 3940–3947. [Google Scholar] [CrossRef]
- Schmidt, A.; Horbatsch, M.; Dreizler, R.M. Semiclassical phase space description of ionisation and capture for ions colliding with hydrogen-like targets. J. Phys. At. Mol. Opt. Phys. 1990, 23, 2327S. [Google Scholar] [CrossRef]
- Purkait, M.; Dhara, A.; Sounda, S.; Mandal, C.R. Inelastic processes in the interactions of partially stripped ions of carbon, nitrogen and oxygen with atomic hydrogen at intermediate and high energies. J. Phys. At. Mol. Opt. Phys. 2001, 34, 755. [Google Scholar] [CrossRef]
- Mandal, C.R.; Datta, S.; Mukherjee, S.C. Charge-transfer cross sections by high-velocity, completely stripped boron and carbon ions from atomic hydrogen. Phys. Rev. A 1983, 28, 1144–1146. [Google Scholar] [CrossRef]
- Janev, R.; McDowell, M. Electron removal from H and He atoms in collisions with Cq+, Oq+ ions. Phys. Lett. A 1984, 102, 405–408. [Google Scholar] [CrossRef]
- Al Atawneh, S.J.; Tőkési, K. Target electron removal in C5+ + H collision. Nucl. Fusion 2021, 62, 026009. [Google Scholar] [CrossRef]
- Phaneuf, R.A.; Meyer, F.W.; McKnight, R.H. Single-electron capture by multiply charged ions of carbon, nitrogen, and oxygen in atomic and molecular hydrogen. Phys. Rev. A 1978, 17, 534–545. [Google Scholar] [CrossRef]
- Sant’Anna, M.M.; Melo, W.S.; Santos, A.C.F.; Shah, M.B.; Sigaud, G.M.; Montenegro, E.C. Absolute measurements of electron capture cross sections of C3+ from atomic and molecular hydrogen. J. Phys. At. Mol. Opt. Phys. 2000, 33, 353. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).