Abstract
We consider a scenario of large-scale modification of gravity that does not invoke extra degrees of freedom, but includes coupling between baryonic matter and dark matter in the Einstein frame. The total matter energy density follows the standard conservation, and evolution has the character of deceleration in this frame. The model exhibits interesting features in the Jordan frame realised by virtue of a disformal transformation where individual matter components adhere to standard conservation but gravity is modified. A generic parametrization of disformal transformation leaves thermal history intact and gives rise to late time acceleration in the Jordan frame, which necessarily includes phantom crossing, which, in the standard framework, can be realised using at least two scalar fields. This scenario is embodied by two distinguished features, namely, acceleration in the Jordan frame and deceleration in the Einstein frame, and the possibility of resolution of the Hubble tension thanks to the emergence of the phantom phase at late times.
1. Introduction
The hot Big Bang model has several remarkable successes to its credit, including prediction of the expanding universe, microwave background radiation, synthesis of light elements in the early universe, and growth of structure via gravitational instability. The model, however, suffers from inbuilt inconsistencies related to early times—for instance, the flatness problem, horizon problem, and late stages of evolution—an age puzzle. Because the matter-dominated era contributes the most to the age of the Universe, the late time slow-down of Hubble expansion must be invoked, allowing the Universe to spend more time before reaching and thus improving the age of the Universe. The only way to accomplish the Hubble slowdown at late stages of evolution is to introduce a late time acceleration [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22].
The inconsistencies of the hot Big Bang are successfully resolved by complementing the model with early and late time-phases of accelerated expansion. Inflation not only addresses the early time inconsistencies of the model, but also provides a mechanism for the generation of primordial density perturbations responsible for structure in the universe [23,24,25,26,27,28,29]. Inflation can be achieved using scalar field(s) or gravity modification at small scales, as in the Starobinsky model [30]. As for late-time cosmic acceleration, it may either be caused by an exotic fluid of large negative pressure dubbed “dark energy” (quintessence) or by a large-scale modification of gravity [10,11,12,13,14,15,16,31,32,33,34,35,36,37]. As mentioned before, late time acceleration is the only known remedy for the age puzzle in the hot Big Bang scenario. Age considerations, however, do not accurately constrain the equation-of-state of dark energy and its contribution to the total energy budget of the Universe; the necessary steps are performed by Ia supernovae [38,39,40,41] and other indirect observations [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56].
Different schemes of large-scale modifications of gravity have been investigated in the literature [57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78]. Most of these schemes reduce to Einstein’s gravity plus extra degrees of freedom, which are non-minimally coupled. One extra scalar degree of freedom exists in gravity; massive gravity has three extra degrees of freedom (two vector and one scalar) [58,59]. The scalar degree of freedom, to comply with the requirement of late time acceleration, should be light, with a mass of the order of eV. These extra degrees of freedom are directly coupled to matter through universal coupling similar to graviton, resulting in an effective doubling of the Newton constant G in the case of gravity, wreaking havoc locally where Einstein gravity complies with the observation to one part in [2]. In massive gravity, only mass-less scalar degrees of freedom survive in the decoupling limit relevant to local physics, and is beautifully screened due to an inbuilt arrangement known as the Vainstein mechanism [68,69]. Unfortunately, massive gravity fails for other reasons [60,61]. The chameleon mechanism is used in the theory, where the extra degree of freedom becomes heavy locally and escapes dynamics, but remains light over large distances and causes late time acceleration [67,70,71]. Surprisingly, at the onset, it turns out that accurate local screening leaves no scope for late time acceleration in chameleon theories [66,67,70,71,72,73,74]. In fact, in this case, acceleration cannot be distinguished from the one caused by a cosmological constant or quintessence. It sounds quite strange that screening at the level of a solar system with a size of the order of cm influences physics at the horizon scale ( cm). However, it might not be that strange if we think in terms of relative matter densities, namely, gm/cc in the solar system versus the critical density, gm/cc, with a difference of five orders of magnitude; ironically, Einstein gravity is accurate to one part in in the solar system. Thus, the purpose of large-scale modification due to extra degrees of freedom invoked to mimic late time acceleration is grossly defeated. A generic large-scale modification of gravity should have the following distinguished property: Acceleration in the Jordan frame and no acceleration in the Einstein frame. In that case, acceleration can be attributed to the modification of gravity.
In theories, for instance, matter follows standard conservation in the Jordan frame, and gravity is modified—its action differs from Einstein–Hilbert; in the Einstein frame, the Lagrangian is diagonalized, and gravity is standard, but there is a scalar field with direct coupling to matter. Acceleration in the Einstein frame is not removed by proper screening of the scalar degree of freedom, and the theory fails to meet the criterion of generic modification (see the Ref. [57], and references therein). A novel scheme of large-scale modification of gravity was proposed in the Ref. [62] (see also the Refs. [63,64]) where one assumes coupling between baryonic and dark matter in the Einstein frame, such that baryonic and dark matter follows the standard conservation in the Einstein frame and there is no acceleration there. On the other hand, one can remove the said coupling by going to the Jordan frame via disformal transformation, where baryonic and dark matter individually follow standard conservation, but gravity action is different from Einstein–Hilbert. In this case, disformal coupling can be parameterised to yield late time acceleration in the Jordan frame which should naturally be attributed to modification of gravity. Obviously, the criterion of generic modification is satisfied and necessarily manifests in this case in a generic way. It was demonstrated in the Ref. [79] that the Hubble tension gets resolved in this case. It should be noted that the phantom phase naturally appears here and does not require the presence of a phantom field. In the model under consideration, deviations from CDM take place only at late stages of evolution around the present epoch where the phantom phase appears automatically. It should be noted that one needs at least two scalar fields to realise phantom crossing, which is naturally mimicked here by assuming coupling between baryonic and dark matter components in the Einstein frame.
In this article, we briefly describe the aforementioned modification of gravity and Hubble tension between the Planck and local measurements of the Hubble parameter. We present details as to how the tension gets naturally resolved in the framework under consideration.
2. Hubble Tension Overview
The fact that the present-day cosmic expansion rate km/s/Mpc [80] predicted by the CDM model from the cosmic microwave background (CMB) radiation observations by the Planck satellite does not agree with the low-redshift observations on the Hubble constant gives rise to the “Hubble Tension” problem [45,81,82,83,84,85,86,87,88,89]. Specifically, the Supernovae for the equation-of-state (SH0ES) collaboration estimates a substantially higher value of the Hubble constant, that is, km/s/Mpc (which amounts to a level discrepancy with Planck) using Cepheid calibrated supernovae Type Ia [45]. The same level of discrepancies on have also been observed in various other low-z measurements, including H0LiCOW’s km/s/Mpc [50] and Megamaser Cosmology Project’s km/s/Mpc [90,91,92,93] results. We have shown the Figure 1.
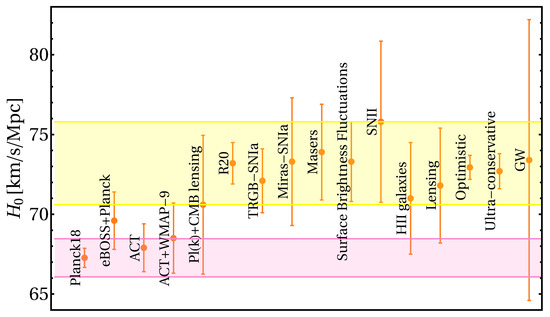
Figure 1.
Whisker plot (following the Ref. [54]) with confidence limit constraints of the Hubble constant through several direct and indirect measurements. The yellow horizontal band corresponds to the value from the Team ( km/s/Mpc at confidence limit), ref. [45] and the pink vertical band corresponds to the value, as reported by Planck (2018) [80] within a vanilla CDM scenario.
Despite the observable disparity, several theoretical solutions have been proposed to deal with this problem. These solutions may be divided into three main types:
- Early-Time Modifications: In cosmology, the positions of the acoustic peaks in the CMB temperature and anisotropy spectra are among the most accurately measured quantities [80]. These acoustic peaks help in determining the size of the sound horizon at the recombination epoch. In order to attempt to modify the sound horizon, one needs to introduce new physics during the pre-recombination epoch that deform at [94,95,96,97,98,99,100,101,102,103,104]. One such modification was motivated by some string–axiverse-inspired scenarios for dark energy, in which dark energy density at early times behaves like the cosmological constant but then decays quickly. However, in this approach, the Hubble constant can, at most, shift to km/s/Mpc at redshift [94]. Other approaches, such as modifying the standard model neutrino sector [105,106], additional radiation [107], primordial magnetic fields [108], or adjusting basic constants with the goal of lowering the sound horizon at recombination [109], are insufficient to properly answer the Hubble Tension problem. Additionally, they expect large growth of matter perturbations than reported by redshift space distortion (RSD) and weak lensing (WL) data, worsening the tension [110].
- Late-Time Modifications: In this approach, one considers late-time alternative forms of DE [1], unified dark fluid models [2,5] where the Dark Matter (DM) and DE behave as a single fluid, alternative gravitational theories including either modified versions of GR or new gravitational theories beyond GR [57], and interacting DE models [1,2] in which DM and the DE interact with each other in a non-gravitational way [111,112], (for more, please see the Refs. [113,114,115,116,117,118]). In the latter scenario, the DE–DM interaction provides a possible solution to the cosmic coincidence problem, and can also explain the phantom DE regime without any scalar fields having a negative kinetic term. It is argued that some of these models are also not able to fully resolve the Hubble Tension problem [119].
- Late-Time Transition of SnIa absolute magnitude M: The shifting of M to a lower value by at redshift is also a possible approach to address the Hubble Tension problem. Such a reduction in M at may be caused, for example, by a comparable transition of the effective gravitational constant , which would result in a rise in the SnIa intrinsic brightness at . This class of models has the potential to solve the Hubble Tension problem entirely while also addressing the growth tension by slowing the growth rate of matter perturbations [89,120,121].
In this paper, we will show a proposition to solve the Hubble Tension issue which relies entirely on dark matter and baryonic matter. The mechanism depends on the coupling of dark matter and baryonic matter via an effective metric. We will demonstrate that this model may well fit cosmological observables under the assumption of a set of parametrizations of the effective metric.
3. Coupling between Baryonic and Dark Matter Components in the Einstein Frame
In what follows, we shall discuss a scenario which assumes coupling between Baryonic and dark matter in the Einstein frame such that the total sum of matter components adheres to standard conservations in this frame. One can then imagine going back to the physical frame, namely, the Jordan frame via a disformal coupling where the matter components individually satisfy the standard conservation but the Einstein–Hilbert action is modified. A suitable parametrization that conforms to CDM in the past might give rise to late time acceleration which has the characteristic of supper-acceleration dubbed phantom behaviour.
3.1. Disformal Coupling between Matter Components
In this sub-section, we discuss a framework which operates through a mechanism that assumes an interaction between BM and DM in the Einstein frame. The latter can be realized by assuming the following action in the Einstein frame [62]:
where and denote the Jordan and Einstein frame metric, respectively1. The action (1) gives rise to coupling between DM and BM in the Einstein frame where evolution would have a decelerating character. We should then construct the Jordan frame metric, from and parameters that define the dark matter. To this effect, we shall make use of “disformal transformation” between the two frames. Disformal transformation, in general, relates the space-time geometries between two frames. These transformations relate two space-time geometries through a conformal factor (a scalar field) and also through the first-order derivatives of the scalar field, with the coefficient of the latter known as the disformal factor. In a perfect fluid representation, the dark matter can then be described by a scalar field,
and by varying Equation (2) with the Einstein frame metric () we get the energy momentum tensor of dark matter, as
where denotes the action for dark matter. The energy momentum tensor can be cast in the perfect fluid form,
which when compared with the above expression (3), we get
Moreover, by using the constraint: , in Equation (2), we get the following relation:
which determines that the DM fluid velocity components are sourced by the rate of change of the DM field with the corresponding spacetime coordinates. By using Equation (7) back in (6), we get
The energy momentum tensor for Baryonic matter is given by:
where denotes the action for the Baryonic matter.
3.2. Equations of Motion for DM Field
Since the Baryonic matter and DM follow geodesics corresponding to and , respectively, a disformal relation between these metrics will eventually be translated to the coupling between these two forms of matter. Hence, their equations of motion in the Einstein frame will now be dependent on each other. It is also worth noting that in the Jordan frame, the matter components are not connected to one other; while the dynamics may appear cumbersome, the energy momentum tensors of each components are preserved individually, that is,
Though it is a common perception that Einstein and Jordan frame metrics are related to each other by conformal transformations, that has its own limitations when taking into account the interaction(s) between the two. In particular, BM being pressureless results in vanishing sound speed; similarly, DM in the absence of any interaction with BM also gives rise to a vanishing sound speed. However, in the presence of a BM–DM interaction, the DM sound speed can give rise to relativistic sound speed. As a consequence, DM will behave as a relativistic fluid, which is undesirable as it can give rise to oscillatory perturbations. This problem is inevitable when the Jordan and Einstein frame metrics are conformally related to each other. Interestingly, this problem can be avoidable in presence of disformal coupling (see [62]).
A general form of disformal coupling can be written as:
with Q and Y being arbitrary functions of X. Thus, it is evident that
Now, by varying the action (1) with respect to , we get
where by using Equation (11), one can write
Since
one can re-express Equation (14) as follows:
The first term on the r.h.s. of the above expression can be further expressed as
similarly, the second term can be expressed as
and the third term as
Putting Equations (17)–(20) back in (13), we finally get the equations of motion of the DM field in the Einstein frame, that is,
Additionally, note that the variations of two metrices are related with each other as follows:
by use of which one can write the Einstein equation as:
where is the Einstein tensor. This indicates that the energy momentum tensor reduces to the sum of the energy momentum tensors of the individual components in the absence of coupling, that is, .
3.3. Dynamics in FRW Universe
For our analysis, we resort to the Einstein frame metric that satisfies the spatially homogeneous and isotropic background, given by
due to which coupling functions Q and R depend only upon the scale factor. Consequently, the Jordan frame metric is given by
By using Equation (23), Friedmann and Raychaudhuri equations are respectively given as
where the superscript ”eq” denotes the reference point at the matter–radiation equality epoch. Additionally, P() designates the pressure of DM(BM) in the Einstein frame, such that . Assuming both DM and BM to be pressureless, it implies that and ).
Due to the fact that BM is pressureless in the Jordan frame, one finds
Since the dynamics of the Universe governed by only depend on the pressureless BM in the Einstein frame (see Equation (27)), it is easy to find that . From Equation (26), the total matter density in the Einstein frame can be expressed as
which implies that the quantity in the parentheses is constant for an arbitrary function . It was demonstrated in the Ref. [62] that the system is plagued with instability in the case where (conformal coupling), and one should therefore focus on disformal transformation. For the sake of simplicity, we shall assume that (maximally disformal case). In that case, we are left with one function, Y, to deal with. In what follows, without the loss of generality, we shall adhere to the maximally disformal case, namely, , leaving us with a single function Y to deal with. Let us recall that we wish to have acceleration in the Jordan frame, () and deceleration in the Einstein frame (). The function, , needs to be parametrized in such a way that the thermal history is respected, followed by accelerated expansion at late times—that is, with regard to the physical scale factor, for the entire history and only at late stages of evolution, it should grow sufficiently fast such that experiences acceleration at late times. Indeed, assuming Y to concave upward, its growth at late times might compensate for the effect of deceleration in , making positive,
where by assumption. If is large or Y increases fast at late times, it might compensate for the last term in (30) which has a decelerating character. In the sub-section to follow, we shall use convenient representations for the scale factor that would conform to the mentioned phenomenological consideration.
3.4. Polynomial Parametrization
We now choose function in accordance to the aforementioned requirement. We shall use the following polynomial parametrization,
where and are constants. In respective frames, the scale factor and redshift have the following relationships:
Since we are working in a spatially flat space-time, the physical scale factor can be normalized to one, that is, ; and as a result, the Einstein frame scale factor gets re-scaled by some factors. For instance, (for ).
By using (31) and (32), one may express the Hubble parameter in terms of in the Jordan frame as
which can be used to obtain the effective equation-of-state parameter,
In order to extract the dark energy (DE) equation-of-state , from (34), we need to define the dimensionless fractional density parameters for cold matter and dark energy, and . This can be accomplished by expressing (33) in the standard form by isolating the term proportional to , that is,
where
Casting the Friedmann equation into the Jordan frame in terms of fractional energy density parameters, we have
where , , and . By using Equation (38), the equation-of-state parameter for (effective) dark energy is then obtained in the Jordan frame as
where and are the effective matter (dust-like) and DE density parameters, respectively. It is also important to mention that for and , the equation-of-state parameter for these parametrization approaches is the CDM limit, that is, at the present epoch.
Let us take notice of the fact that the dark-energy equation-of-state parameter might, at some point, take on a super-negative value (<) with a general behaviour reflected by phantom-crossing. It is important to note that phenomena such as this cannot be replicated by a quintessence field; at least two scalar fields are required to simulate phantom-crossing. It is intriguing that the aforementioned behaviour may result from the presence of disformal coupling between DM and BM. It should also be emphasized that the Einstein–Hilbert action gets modified at the expense of decoupling of DM and BM in the Jordan frame. However, the modification of gravity under consideration does not result in any more degrees of freedom—it can still enable the realisation of acceleration at later times. Last but not least, acceleration in this framework is generically caused by modification of gravity in the manner of acceleration in the Jordan frame and deceleration in the Einstein frame.
3.5. Exponential Parametrization
Let us now consider the exponential parametrization that is given below:
such that the Hubble parameter and effective equation-of-state parameter are given by
Here, it should be noted that, in contrast to the situation in (31), the Friedman equation derived for the exponential parametrization (41) is not given in a standard form that is useful for carrying out the parametric estimation. In order to do this, we cast (42) in the form corresponding to (35), for which we apply the following ansatz:
where A, B and C are constants. It is then natural to identify with the effective matter density, that is, and B with the effective dark-energy density parameters at the present epoch. The condition yields a constraint on constants, namely, , leaving us with two unknowns, say, A and C to fit with (44).
Let us now implement the fitting in such a way that at the present epoch. Using non-linear model fitting, we find: and . It is then straightforward to express the equation-of-state parameter for dark energy () as
where the fitted values of B and C have been used for . Let us note that the exponential parametrization mimics CDM for .
4. Observational Datasets
In this section, we demonstrate the parametric estimations for both (31) and (41) parametrizations from the late-time background level observational data. Three sets of data were specifically used in the analysis: the distance modulus measurements of type Ia supernovae (SNIa), observational Hubble data (OHD), and angular diameter distances obtained with water megamasers. A brief description of these datasets is given below:
- Pantheon + MCT SnIa data:
The Hubble rate data points, that is, , reported in the Ref. [122] for six distinct redshifts in the range of , are used in this study which efficiently compress the information of SnIa at that are utilized in the Pantheon compilation, and the 15 SnIa at of the CLASH Multi-Cycle Treasury (MCT) and CANDELS programs provided by the HST. The raw SnIa data were transformed into [122,123] by parametrizing at those six redshifts. The dimensionless Hubble rate is defined as , and hence, for the supernova data is calculated as
where is the correlation matrix between the data points.
- Observational Hubble Data (OHD):
These correspond to the measurements of the expansion rate of the universe, , in the redshift range [124,125,126]. These data points can be retrieved using two strategies:
- 1
- Differential age technique: In this technique, the data points are calculated using the relation between the redshift z and the rate of change of the galaxy’s age.
- 2
- Galaxy clustering technique: The data points are obtained by utilising galaxy or quasar clustering that provides direct measurements of from the radial peaks of baryon acoustic oscillations (BAO) [76,127].The for the Hubble parameter measurements is
- Masers Data:
The Megamaser Cosmology Project measures the angular diameter distances. Its is defined as
such that
where is the angular diameter distance.
5. Parametric Estimations
The Bayesian inference approach, which is frequently employed for parameter estimation in cosmological models, is used here to carry out the statistical analysis. These statistics state that the posterior probability distribution function of model parameters is directly proportional to the prior probability of the model parameters and their likelihood function. The likelihoods used to estimate the parameters are multivariate Gaussian likelihoods, and are given by
where belongs to a set of parameters. The posterior probability is proportional to . Consequently, a minimum will guarantee a maximum likelihood. In our analysis, the Gaussian likelihood is given by
where . This formulation will be the same for both parametrizations. For the polynomial parametrization, the parameters that need to be constrained are: , and , whereas for the exponential parametrization, we have and . In our analysis, we employed uniform priors. For the estimations, the technique used was Markov Chain Monte Carlo (MCMC). The obtained MCMC chains were then studied using the GetDist program [128].
6. Constraints on Hubble Parameter and Dark-Energy Equation-of-State Parameter: Phantom-Crossing and Hubble Tension
This was from the obtained chains of parameters , and , from our MCMC simulation, up to (shown in Figure 2). In Figure 2, we have plotted the obtained parametric dependence between , and using OHD and its combination with Pantheon and Masers. From this Figure, one can note that the combination of all data sets significantly reduces the error bars on as compared to the only-OHD data set. The obtained results are given in Table 1 where we show that the only-OHD data set gives , which is significantly larger than the combined data set. In particular, we did not find any significant Hubble tension for OHD, even for the combined data set, where the tension reduced to a level of . The reduction of this tension can be attributed to phantom-crossing taking place in the case of the polynomial parametrization.
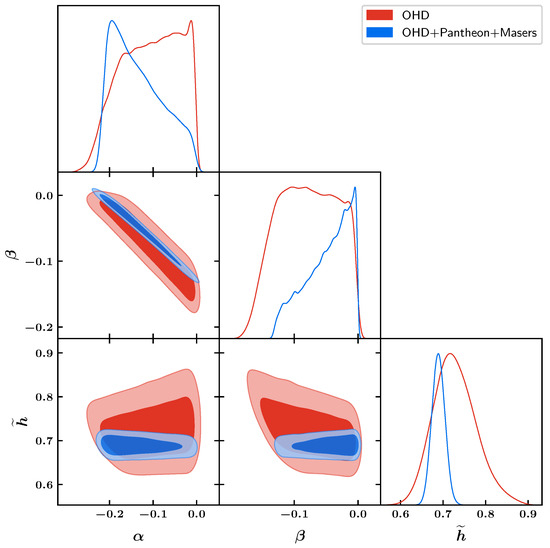
Figure 2.
Polynomial: contour levels between , and for OHD and its combinations with Pantheon + Masers [79].

Table 1.
Best fits with their levels for polynomial and exponential parametrizations, and for the CDM model from the OHD and OHD + Pantheon + Masers datasets [79].
The corresponding evolution of and up to is shown in Figure 3 and Figure 4, respectively. In Figure 3, it can be seen that because of the large deviations, the OHD data set alone does not show tension with Riess et al. [129] and BOSSLy- [130]. However, the combined data set exhibits a substantial tension with the findings of Riess et al. by yielding a comparably smaller (Figure 3). Additionally, we demonstrate in Figure 4 that both data sets result in phantom-crossing near the current epoch. It is noteworthy that this property arises exclusively as a result of the coupling between two matter components (BM + DM), and with no additional degrees of freedom.
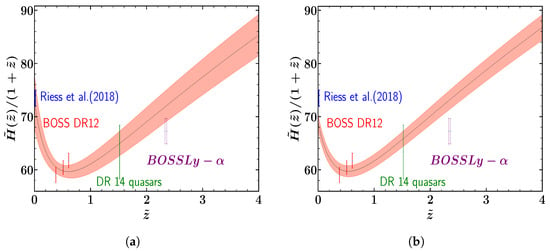
Figure 3.
Polynomial: Figures (a,b) depict the evolution of with for the datasets OHD and OHD + Pantheon + Masers, respectively [129,130]. The dark line represents the best fit and the shaded region corresponds to the limit [79].
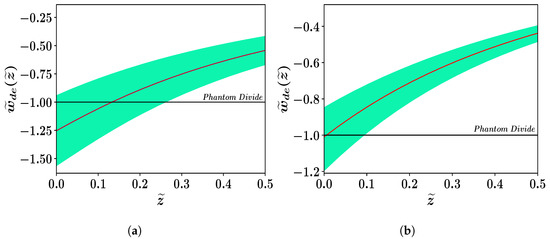
Figure 4.
Polynomial: Figures (a,b) depict the evolution of with for the datasets OHD and OHD + Pantheon + Masers, respectively. The dark line represents the best fit and the shaded region corresponds to the limit [79].
A similar analysis was also carried out for the second parametrization, and in this instance, we demonstrate the parametric dependency between and for two sets of data in Figure 5, and the resulting constraints are shown in Table 1. Here, the value of the Hubble constant is consistent with the combined data up to the 1- level (see Table 2 and Equation (45) of [80]). As a result, the tension does not significantly decrease. This was expected because the exponential parametrization model mimics the CDM, since there is no phantom crossover (prior to the current epoch).
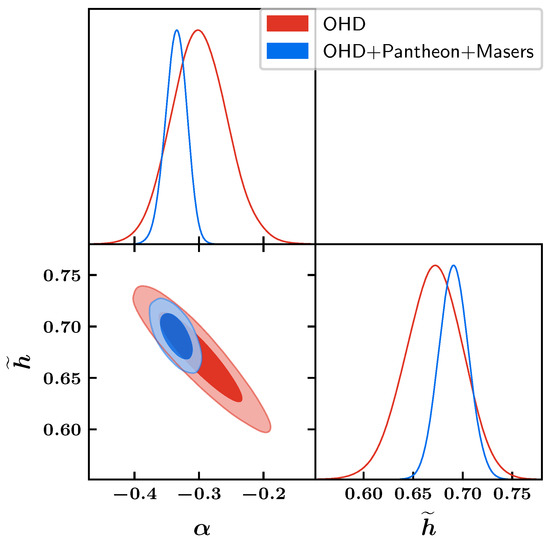
Figure 5.
Exponential: contour levels between and for OHD and its combinations with Pantheon + Masers [79].
In contrast to the polynomial scenario, the combined data set agrees with Riess et al. and BOSSLy-, which is not the case when simply utilising the OHD data set, as can be shown in Figure 6. Additionally, it can be seen from Figure 7 that the phantom crossing of does not occur.
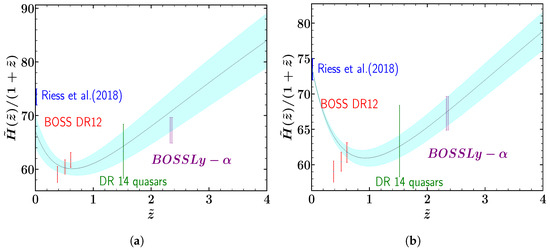
Figure 6.
Exponential: Figures (a,b) depict the evolution of with for the datasets OHD and OHD + Pantheon + Masers, respectively [129,130]. The dark line represents the best fit and the shaded region corresponds to the limit [79].
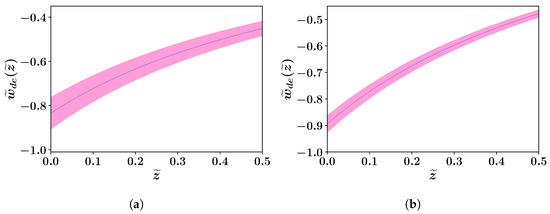
Figure 7.
Exponential: Figures (a,b) depict the evolution of with for the datasets OHD and OHD + Pantheon + Masers, respectively. The dark line represents the best fit and the shaded region corresponds to the limit [79].
Moreover, from Figure 7, one can notice that the phantom crossing of does not happen. In Figure 8, we explicitly show the dependence of model parameters on the . In Figure 8a, we demonstrate that both and must be negative in order to produce phantom crossing. Similarly, for the exponential case, Figure 7 illustrates the dependency of on parameter .
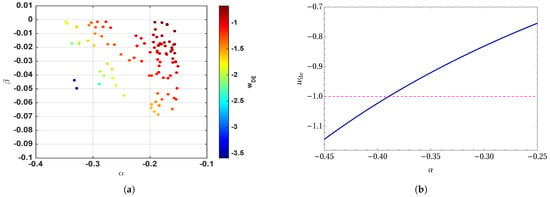
Figure 8.
Exponential: Figures (a,b) show the variation of the two model parameters with the equation-of-state of the dark energy () [79].
7. Comparison with CDM
Let us first note that while comparing the two parametrizations, polynomial (31) and exponential (41), with the CDM model, the inclusion of the additional parameters in comparison to the standard model must be taken into consideration.
To compare the two parametrizations, polynomial (31) and exponential (41) with the vanilla CDM model, one needs to take care of the introduction of the extra parameters with respect to the standard model. We have two extra parameters for the polynomial and one extra parameter for the exponential. In order to handle it, a thorough Bayesian Information Criterion (BIC) was calculated. In the BIC analysis, a model with more parameters gets penalised more. Under the assumption that the model errors are independent and obey a normal distribution, then the BIC can be rewritten in terms of as
where is the number of free parameters in the test and n is the number of points in the observed data. In Table 2, we provide details about our findings. The polynomial parametrization has good evidence, as can be shown from Table 2, when compared to the typical CDM case. Any indication that indicates extremely strong support for the novel model proposed in comparison to the conventional one. Even while the exponential scenario has strong support when the data are combined, it has no such support when the OHD data are the only ones taken into account. We find compelling support for the polynomial parametrization for both OHD and combined data.

Table 2.
The evidence in support of polynomial and exponential parametrizations for OHD and OHD + Pantheon + Masers datasets with respect to the standard CDM scenario [79].
8. Conclusions and Future Perspectives
In this paper, we have shown the observable validity and wider implications of the dark matter and baryonic matter interaction in the Einstein frame, which is produced by a general disformal transformation between the Jordan and the Einstein frames. The idea behind the phenomena is that dark matter adheres to Einstein frame geodesics, whereas baryonic matter follows Jordan frame trajectories. Since both matter components are coupled together under the usual disformal transformation, their respective energy conservation in the Einstein frame is lost.
We employed two distinct parametrizations to relate the scale factors of both frames in the conventional FRW space-time since the geodesics of the two frames are not identical (as a result of the disformal transformation between them). To obtain the constraints on the model parameters in the Jordan frame, which we assumed to be the physical frame, we specifically used the polynomial and exponential parametrizations (the Jordan frame was used for all observations because the underlying mechanism predicts that baryonic matter will follow its path in this frame). The best-fit Hubble parameter values for two distinct data combinations are such that they significantly lessen the so-called “Hubble tension” in the case of the polynomial parametrization Equation (31). In the case of polynomial parametrization, the tension for OHD data is negligible, with a computed value of consistent with Riess et al. However, with the combined OHD + Pantheon + Masers data, the tension is lowered to a level. We would like to emphasize that this is associated to the fact that, in this specific parametrization, the dark energy equation-of-state passes from quintessence to the phantom regime. Thus, when doing the BIC analysis, which is shown in Table 2, we noticed substantial evidence in favour of this parametrization.
As for the exponential parametrization in Equation (41), we did not notice any appreciable Hubble-tension reduction (see, Figure 5) with both the data combinations, which was understood by the model’s quintessence-like behaviour with around the current epoch. In the exponential case, we only found a little amount of positive evidence in the combined data scenario, which is not substantial enough when simply taking OHD data into account (see Table 2).
Let us again emphasise that the scenario under consideration which is based on the interaction between DM and BM enables late-time cosmic acceleration without including any exotic fluid, and is also consistent with other observations. The occurrence of phantom crossover, which is currently supported by the majority of observations, is one of the most significant and general implications of the DM–BM interaction. Last but not least, given the existence of disformal coupling between DM and BM, it would be intriguing to consider a different kind of parametrization, such as or its variants, which can also be helpful to alleviate the Hubble tension (see the Ref. [88] for more details) or take perturbations into account and examine the matter power spectrum, which we will attempt to report on soon.
Author Contributions
All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Note
| 1 | Note that the Baryonic sector only couples to the metric , and not to g. |
References
- Amendola, L.; Tsujikawa, S. Dark Energy. Theory and Observations; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1935. [Google Scholar] [CrossRef]
- Sami, M. Why is Universe so dark? New Adv. Phys. 2016, 10, 77. [Google Scholar]
- Sami, M. A Primer on problems and prospects of dark energy. Curr. Sci. 2009, 97, 887. [Google Scholar]
- Sami, M. Models of dark energy. Lect. Notes Phys. 2007, 720, 219. [Google Scholar]
- Jaman, N.; Sami, M. What Is Needed of a Scalar Field If It Is to Unify Inflation and Late Time Acceleration? Galaxies 2022, 10, 51. [Google Scholar] [CrossRef]
- Sami, M.; Myrzakulov, R. Cosmological relevance of scaling solutions: A recipe for quintessential inflation. Gen. Rel. Grav. 2022, 54, 86. [Google Scholar] [CrossRef]
- Sami, M.; Pravabati, C. Aspects of tachyonic inflation with an exponential potential. Phys. Rev. D 2002, 66, 043530. [Google Scholar] [CrossRef]
- Silvestri, A.; Trodden, M. Approaches to Understanding Cosmic Acceleration. Rep. Prog. Phys. 2009, 72, 096901. [Google Scholar] [CrossRef]
- Sahni, V.; Starobinsky, A.A. The Case for a positive cosmological Lambda term. Int. J. Mod. Phys. D 2000, 9, 373. [Google Scholar] [CrossRef]
- Frieman, J.; Turner, M.; Huterer, D. Dark Energy and the Accelerating Universe. Ann. Rev. Astron. Astrophys. 2008, 46, 385. [Google Scholar] [CrossRef]
- Caldwell, R.R.; Kamionkowski, M. The Physics of Cosmic Acceleration. Ann. Rev. Nucl. Part. Sci. 2009, 59, 397. [Google Scholar] [CrossRef]
- Perivolaropoulos, L. Accelerating universe: Observational status and theoretical implications. AIP Conf. Proc. 2006, 848, 698. [Google Scholar]
- Frieman, J.A. Lectures on dark energy and cosmic acceleration. AIP Conf. Proc. 2008, 1057, 87. [Google Scholar]
- Carroll, S.M. The Cosmological constant. Living Rev. Rel. 2001, 4, 1. [Google Scholar] [CrossRef] [PubMed]
- Padmanabhan, T. Cosmological constant: The Weight of the vacuum. Phys. Rep. 2003, 380, 235–320. [Google Scholar] [CrossRef]
- Spergel, D.N.; Bolte, M.; Freedman, W. The age of the universe. Proc. Natl. Acad. Sci. USA 1997, 94, 6579–6584. [Google Scholar] [CrossRef]
- Dunlop, J.; Peacock, J.; Spinrad, H.; Dey, A.; Jimenez, R.; Stern, D.; Windhorst, R. A 3.5-Gyr-old galaxy at redshift 1.55. Nature 1996, 381, 581–584. [Google Scholar] [CrossRef]
- Damjanov, I.; McCarthy, P.J.; Abraham, R.G.; Glazebrook, K.; Yan, H.; Mentuch, E.; Le Borgne, D.; Savaglio, S.; Crampton, D.; Murowinski, R.; et al. Red Nuggets at z∼1.5: Compact passive galaxies and the formation of the Kormendy Relation. Astrophys. J. 2009, 101, 695. [Google Scholar] [CrossRef]
- Salaris, M.; Degl’Innocenti, S.; Weiss, A. The Age of the Oldest Globular Clusters. Astrophys. J. 1997, 479, 665–672. [Google Scholar] [CrossRef]
- López-Corredoira, M.; Vazdekis, A.; Gutiérrez, C.M.; Castro-Rodríguez, N. Stellar content of extremely red quiescent galaxies at z > 2. Astron. Astrophys. 2017, 600, A91. [Google Scholar] [CrossRef]
- López-Corredoira, M.; Vazdekis, A. Impact of young stellar components on quiescent galaxies: Deconstructing cosmic chronometers. arXiv 2018, arXiv:1802.09473. [Google Scholar] [CrossRef]
- Linde, A.D. Chaotic Inflation. Phys. Lett. B 1983, 129, 177–181. [Google Scholar] [CrossRef]
- Kolb, E.W.; Turner, M.S. The Early Universe. Front. Phys. 1990, 69, 1–547. [Google Scholar]
- Mathews, G.J.; Gangopadhyay, M.R.; Ichiki, K.; Kajino, T. Possible Evidence for Planck-Scale Resonant Particle Production during Inflation from the CMB Power Spectrum. Phys. Rev. D 2015, 92, 123519. [Google Scholar] [CrossRef]
- Bastero-Gil, M.; Bhattacharya, S.; Dutta, K.; Gangopadhyay, M.R. Constraining Warm Inflation with CMB data. JCAP 2018, 02, 054. [Google Scholar] [CrossRef]
- Gangopadhyay, M.R.; Myrzakul, S.; Sami, M.; Sharma, M.K. Paradigm of warm quintessential inflation and production of relic gravity waves. Phys. Rev. D 2021, 103, 043505. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Gangopadhyay, M.R. Study in the noncanonical domain of Goldstone inflation. Phys. Rev. D 2020, 101, 023509. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Das, S.; Dutta, K.; Gangopadhyay, M.R.; Mahanta, R.; Maharana, A. Nonthermal hot dark matter from inflaton or moduli decay: Momentum distribution and relaxation of the cosmological mass bound. Phys. Rev. D 2021, 103, 063503. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The Cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559. [Google Scholar] [CrossRef]
- Wetterich, C. Cosmology and the Fate of Dilatation Symmetry. Nucl. Phys. B 1988, 302, 668. [Google Scholar] [CrossRef]
- Ratra, B.; Peebles, P.J.E. Cosmological Consequences of a Rolling Homogeneous Scalar Field. Phys. Rev. D 1988, 37, 3406. [Google Scholar] [CrossRef] [PubMed]
- Caldwell, R.R.; Dave, R.; Steinhardt, P.J. Cosmological imprint of an energy component with general equation-of-state. Phys. Rev. Lett. 1998, 80, 1582. [Google Scholar] [CrossRef]
- Sami, M. Modified Theories of Gravity and Constraints Imposed by Recent GW Observations. IJMPD 2019, 28, 5. [Google Scholar]
- Bamba, K.; Hossain, M.W.; Myrzakulov, R.; Nojiri, S.; Sami, M. Cosmological investigations of (extended) nonlinear massive gravity schemes with nonminimal coupling. Phys. Rev. D 2014, 89, 083518. [Google Scholar] [CrossRef]
- Sami, M.; Myrzakulov, R. Late-time cosmic acceleration: ABCD of dark energy and modified theories of gravity. Int. J. Mod. Phys. D 2016, 25, 1630031. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. [Supernova Cosmology Project Collaboration]. Measurements of Omega and Lambda from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Betoule, M.E.A.; Kessler, R.; Guy, J.; Mosher, J.; Hardin, D.; Biswas, R.; Astier, P.; El-Hage, P.; Konig, M.; Kuhlmann, S.; et al. Improved cosmological constraints from a joint analysis of the SDSS-II and SNLS supernova samples. Astron. Astrophys. 2014, 568, A22. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The Complete Light-curve Sample of Spectroscopically Confirmed Type Ia Supernovae from Pan-STARRS1 and Cosmological Constraints from The Combined Pantheon Sample. arXiv 2017, arXiv:1710.00845. [Google Scholar]
- Seljak, U.; Makarov, A.; McDonald, P.; Anderson, S.F.; Bahcall, N.A.; Brinkmann, J.; Burles, S.; Cen, R.; Doi, M.; Gunn, J.E.; et al. [SDSS Collaboration]. Cosmological parameter analysis including SDSS Ly-alpha forest and galaxy bias: Constraints on the primordial spectrum of fluctuations, neutrino mass, and dark energy. Phys. Rev. D 2005, 71, 103515. [Google Scholar] [CrossRef]
- Fernández Arenas, D.; Terlevich, E.; Terlevich, R.; Melnick, J.; Chávez, R.; Bresolin, F.; Telles, E.; Plionis, M.; Basilakos, S. An independent determination of the local Hubble constant. Mont. Not. R. Astron. Soc. 2018, 474, 1250–1276. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics beyond ΛCDM. ApJ 2019, 876, 85. [Google Scholar] [CrossRef]
- Riess, A.G.; Casertano, S.; Yuan, W.; Bowers, J.B.; Macri, L.; Zinn, J.C.; Scolnic, D. Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with ΛCDM. ApJL 2021, 908, L6. [Google Scholar] [CrossRef]
- Blakeslee, J.P.; Jensen, J.B.; Ma, C.P.; Milne, P.A.; Greene, J.E. The Hubble Constant from Infrared Surface Brightness Fluctuation Distances. ApJ 2021, 911, 65. [Google Scholar] [CrossRef]
- Freedman, W.L.; Madore, B.F.; Hatt, D.; Hoyt, T.J.; Jang, I.S.; Beaton, R.L.; Burns, C.R.; Lee, M.G.; Monson, A.J.; Neeley, J.R.; et al. The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch. ApJ 2019, 882, 34. [Google Scholar] [CrossRef]
- Birrer, S.; Treu, T.; Rusu, C.E.; Bonvin, V.; Fassnacht, C.D.; Chan, J.H.H.; Agnello, A.; Shajib, A.J.; Chen, G.C.-F.; Auger, M.; et al. H0LiCOW-IX. Cosmographic analysis of the doubly imaged quasar SDSS 1206+4332 and a new measurement of the Hubble constant. Mon. Not. R. Astron. Soc. 2019, 484, 4726–4753. [Google Scholar] [CrossRef]
- Chen, G.C.-F.; Fassnacht, C.D.; Suyu, S.H.; Rusu, C.E.; Chan, J.H.; Wong, K.C.; Auger, M.W.; Hilbert, S.; Bonvin, V.; Birrer, S.; et al. A SHARP view of H0LiCOW: H0 from three time-delay gravitational lens systems with adaptive optics imaging. Mon. Not. R. Astron. Soc. 2019, 490, 1743–1773. [Google Scholar] [CrossRef]
- Wong, K.C.; Suyu, S.H.; Chen, G.C.; Rusu, C.E.; Millon, M.; Sluse, D.; Bonvin, V.; Fassnacht, C.D.; Taubenberger, S.; Auger, M.W.; et al. H0LiCOW XIII. A 2.4% measurement of H0 from lensed quasars: 5.3σ tension between early and late-Universe probes. Mon. Not. R. Astron. Soc. 2020, 498, 1420–1439. [Google Scholar] [CrossRef]
- Huang, C.D.; Riess, A.G.; Yuan, W.; Macri, L.M.; Zakamska, N.L.; Casertano, S.; Whitelock, P.A.; Hoffmann, S.L.; Filippenko, A.V.; Scolnic, D. Hubble Space Telescope Observations of Mira Variables in the Type Ia Supernova Host NGC 1559: An Alternative Candle to Measure the Hubble Constant. ApJ 2020, 889, 5. [Google Scholar] [CrossRef]
- de Jaeger, T.; Stahl, B.E.; Zheng, W.; Filippenko, A.V.; Riess, A.G.; Galbany, L. A measurement of the Hubble constant from Type II supernovae. Mon. Not. R. Astron. Soc. 2020, 496, 3402–3411. [Google Scholar] [CrossRef]
- Schombert, J.; McGaugh, S.; Lelli, F. Using The Baryonic Tully-Fisher Relation to Measure H0. Astron. J. 2020, 160, 71. [Google Scholar] [CrossRef]
- Valentino, E.D.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the Realm of the Hubble tension—A Review of Solutions. arXiv 2021, arXiv:2103.01183. [Google Scholar] [CrossRef]
- Efstathiou, G. H0 revisited. Mont. Not. R. Astron. Soc. 2014, 440, 1138. [Google Scholar] [CrossRef]
- Nunes, R.C. Structure formation in f(T) gravity and a solution for H0 tension. JCAP 2018, 05, 052. [Google Scholar] [CrossRef]
- Felice, A.D.; Tsujikawa, S. f(R) theories. Living Rev. Rel. 2010, 13, 1–161. [Google Scholar] [CrossRef]
- Rham, C.d.; Gabadadze, G.; Tolley, A.J. Resummation of Massive Gravity. Phys. Rev. Lett. 2011, 106, 231101. [Google Scholar] [CrossRef]
- Hinterbichler, K. Theoretical Aspects of Massive Gravity. Rev. Mod. Phys. 2012, 84, 671–710. [Google Scholar] [CrossRef]
- Deser, S.; Izumi, K.; Ong, Y.C.; Waldron, A. Problems of Massive Gravities. Mod. Phys. Lett. A 2015, 30, 1540006. [Google Scholar] [CrossRef]
- Deser, S.; Waldron, A. Acausality of Massive Gravity. Phys. Rev. Lett. 2013, 110, 111101. [Google Scholar] [CrossRef] [PubMed]
- Berezhiani, L.; Khoury, J.; Wang, J. Universe without dark energy: Cosmic acceleration from dark matter-baryon interactions. Phys. Rev. D 2017, 95, 123530. [Google Scholar] [CrossRef]
- Agarwal, A.; Myrzakulov, R.; Pacif, S.K.J.; Sami, M.; Wang, A. Cosmic acceleration sourced by modification of gravity without extra degrees of freedom. Int. J. Geom. Meth. Mod. Phys. 2019, 16, 1950128. [Google Scholar] [CrossRef]
- Agarwal, A.; Myrzakulov, R.; Pacif, S.K.J.; Shahalam, M. Cosmic acceleration from coupling of baryonic and dark matter components: Analysis and diagnostics. Int. J. Mod. Phys. D 2019, 28, 1950083. [Google Scholar] [CrossRef]
- Wang, J.; Hui, L.; Khoury, J. No-Go Theorems for Generalized Chameleon Field Theories. Phys. Rev. Lett. 2012, 109, 241301. [Google Scholar] [CrossRef] [PubMed]
- Bamba, K.; Gannouji, R.; Kamijo, M.; Nojiri, S.; Sami, M. Spontaneous symmetry breaking in cosmos: The hybrid symmetron as a dark energy switching device. JCAP 2013, 1307, 017. [Google Scholar] [CrossRef]
- Upadhye, A.; Hu, W.; Khoury, J. Quantum Stability of Chameleon Field Theories. Phys. Rev. Lett. 2012, 109, 041301. [Google Scholar] [CrossRef] [PubMed]
- Joyce, A.; Jain, B.; Khoury, J.; Trodden, M. Beyond the Cosmological Standard Model. Phys. Rep. 2015, 568, 1–98. [Google Scholar] [CrossRef]
- Babichev, E.; Deffayet, C. An introduction to the Vainshtein mechanism. Class. Quant. Grav. 2013, 30, 184001. [Google Scholar] [CrossRef]
- Mota, D.F.; Barrow, J.D. Varying alpha in a more realistic Universe. Phys. Lett. B 2004, 581, 141. [Google Scholar] [CrossRef]
- Khoury, J.; Weltman, A. Chameleon fields: Awaiting surprises for tests of gravity in space. Phys. Rev. Lett. 2004, 93, 171104. [Google Scholar] [CrossRef]
- Brax, P.; Bruck, C.v.; Davis, A.C.; Khoury, J.; Weltman, A. Detecting dark energy in orbit—The Cosmological chameleon. Phys. Rev. D 2004, 70, 123518. [Google Scholar] [CrossRef]
- Capozziello, S.; D’Agostino, R.; Luongo, O. Extended Gravity Cosmography. arXiv 2019, arXiv:1904.01427. [Google Scholar] [CrossRef]
- Capozziello, S.; Nojiri, S.; Odintsov, S.D.; Troisi, A. Cosmological viability of f (R)-gravity as an ideal fluid and its compatibility with a matter dominated phase. Phys. Lett. B 2006, 639, 135–143. [Google Scholar] [CrossRef]
- Ballardini, M.; Braglia, M.; Finelli, F.; Paoletti, D.; Starobinsky, A.A.; Umiltà, C. Scalar-tensor theories of gravity, neutrino physics, and the H0 tension. JCAP 2020, 10, 044. [Google Scholar] [CrossRef]
- Umiltà, C.; Ballardini, M.; Finelli, F.; Paoletti, D. CMB and BAO constraints for an induced gravity dark energy model with a quartic potential. JCAP 2015, 08, 017. [Google Scholar] [CrossRef]
- Braglia, M.; Ballardini, M.; Finelli, F.; Koyama, K. Early modified gravity in light of the H0 tension and LSS data. Phys. Rev. D 2021, 103, 043528. [Google Scholar] [CrossRef]
- Ballardini, M.; Finelli, F.; Umilta, C.; Paoletti, D. Cosmological constraints on induced gravity dark energy models. JCAP 2016, 05, 067. [Google Scholar] [CrossRef]
- Adil, S.A.; Gangopadhyay, M.R.; Sami, M.; Sharma, M.K. Late time acceleration due to generic modification of gravity and Hubble tension. Phys. Rev. D 2021, 104, 10353. [Google Scholar] [CrossRef]
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.; Anderson, J.; MacKenty, J.W.; Bowers, J.B.; Clubb, K.I.; Filippenko, A.V.; Jones, D.O.; et al. New Parallaxes of Galactic Cepheids from Spatially Scanning the Hubble Space Telescope: Implications for the Hubble Constant. arXiv 2018, arXiv:1801.01120. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.; Casertano, S.; Lampeitl, H.; Ferguson, H.C.; Filippenko, A.V.; Jha, S.W.; Li, W.; Chornock, R. A 3% Solution: Determination of the Hubble Constant with the Hubble Space Telescope and Wide Field Camera 3. Astrophys. J. 2011, 730, 119, Erratum in ibid 2011, 732, 129. [Google Scholar] [CrossRef]
- Riess, A.G.; Macri, L.M.; Hoffmann, S.L.; Scolnic, D.; Casertano, S.; Filippenko, A.V.; Tucker, B.E.; Reid, M.J.; Jones, D.O.; Silverman, J.M.; et al. A 2.4% Determination of the Local Value of the Hubble Constant. Astrophys. J. 2016, 826, 56. [Google Scholar] [CrossRef]
- Anderson, R.I.; Riess, A.G. On Cepheid distance scale bias due to stellar companions and cluster populations. arXiv 2017, arXiv:1712.01065. [Google Scholar] [CrossRef]
- Valentino, E.D.; Melchiorri, A.; Silk, J. Reconciling Planck with the local value of H0 in extended parameter space. Phys. Lett. B 2016, 761, 242–246. [Google Scholar] [CrossRef]
- Evslin, J.; Sen, A.A. Ruchika, The Price of Shifting the Hubble Constant. Phys. Rev. D 2018, 97, 103511. [Google Scholar] [CrossRef]
- Feeney, S.M.; Peiris, H.V.; Williamson, A.R.; Nissanke, S.M.; Mortlock, D.J.; Alsing, J.; Scolnic, D. Prospects for resolving the Hubble constant tension with standard sirens. arXiv 2018, arXiv:1802.03404. [Google Scholar] [CrossRef]
- Dainotti, M.G.; De Simone, B.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G.; Bogdan, M.; Ugale, S. On the Evolution of the Hubble Constant with the SNe Ia Pantheon Sample and Baryon Acoustic Oscillations: A Feasibility Study for GRB-Cosmology in 2030. Galaxies 2022, 10, 24. [Google Scholar] [CrossRef]
- Dainotti, M.G.; De Simone, B.; Schiavone, T.; Montani, G.; Rinaldi, E.; Lambiase, G. On the Hubble constant tension in the SNe Ia Pantheon sample. ApJ 2021, 912, 150. [Google Scholar] [CrossRef]
- Pesce, D.W.; Braatz, J.A.; Reid, M.J.; Riess, A.G.; Scolnic, D.; Condon, J.J.; Gao, F.; Henkel, C.; Impellizzeri, C.M.V.; Kuo, C.Y.; et al. The megamaser cosmology project. XIII. Combined Hubble constant constraints. Astrophys. J. 2020, 891, L1. [Google Scholar] [CrossRef]
- Reid, M.J.; Braatz, J.A.; Condon, J.J.; Lo, K.Y.; Kuo, C.Y.; Impellizzeri, C.M.V.; Henkel, C. The Megamaser Cosmology Project: IV. A Direct Measurement of the Hubble Constant from UGC 3789. Astrophys. J. 2013, 767, 154. [Google Scholar] [CrossRef]
- Kuo, C.; Braatz, J.A.; Reid, M.J.; Lo, F.K.Y.; Condon, J.J.; Impellizzeri, C.M.V.; Henkel, C. The Megamaser Cosmology Project. V. An Angular Diameter Dis- tance to NGC 6264 at 140 Mpc. Astrophys. J. 2013, 767, 155. [Google Scholar] [CrossRef]
- Gao, F.; Braatz, J.A.; Reid, M.J.; Lo, K.Y.; Condon, J.J.; Henkel, C.; Kuo, C.Y.; Impellizzeri, C.M.V.; Pesce, D.W.; Zhao, W. The Megamaser Cosmology Project VIII. A Geometric Distance to NGC 5765b. Astrophys. J. 2016, 817, 128. [Google Scholar] [CrossRef]
- Karwal, T.; Kamionkowski, M. Dark energy at early times, the Hubble parameter, and the string axiverse. Phys. Rev. D 2016, 94, 103523. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Karwal, T.; Kamionkowski, M. Early dark energy can resolve the Hubble tension. Phys. Rev. Lett. 2019, 122, 221301. [Google Scholar] [CrossRef] [PubMed]
- Caldwell, R.R.; Doran, M.; Mueller, C.M.; Schafer, G.; Wetterich, C. Early Quintessence in Light of WMAP. Astrophys. J. Lett. 2003, 591, L75–L78. [Google Scholar] [CrossRef]
- Karwal, T.; Kamionkowski, M. Early dark energy, the Hubble-parameter tension, and the string axiverse. arXiv 2016, arXiv:1608.01309. [Google Scholar]
- Pettorino, V.; Amendola, L.; Wetterich, C. How early is early dark energy? Phys. Rev. D 2013, 87, 083009. [Google Scholar] [CrossRef]
- Kamionkowski, M.; Pradler, J.; Walker, D.G.E. Dark energy from the string axiverse. Phys. Rev. Lett. 2014, 113, 251302. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Grin, D.; Karwal, T.; Kamionkowski, M. Cosmological implications of ultra-light axion-like fields. Phys. Rev. D 2018, 98, 083525. [Google Scholar] [CrossRef]
- Banerjee, A.; Cai, H.; Heisenberg, L.; Colgáin, E.O.; Sheikh-Jabbari, M.M.; Yang, T. Hubble Sinks In The Low-Redshift Swampland. arXiv 2021, arXiv:2006.00244. [Google Scholar] [CrossRef]
- Alam, U.; Bag, S.; Sahni, V. Constraining the Cosmology of the Phantom Brane using Distance Measures. Phys. Rev. D 2017, 95, 023524. [Google Scholar] [CrossRef]
- Valentino, E.D.; Linder, V.E.; Melchiorri, A. A Vacuum Phase Transition Solves H0 Tension. Phys. Rev. D 2018, 97, 043528. [Google Scholar] [CrossRef]
- Pandey, K.L.; Karwal, T.; Das, S. Alleviating the H0 and σ8 anomalies with a decaying dark matter model. JCAP 2020, 07, 026. [Google Scholar] [CrossRef]
- Sakstein, J.; Trodden, M. Early dark energy from massive neutrinos as a natural resolution of the Hubble tension. Phys. Rev. Lett. 2020, 124, 161301. [Google Scholar] [CrossRef]
- Gogoi, A.; Sharma, R.K.; Chanda, P.; Das, S. Early mass varying neutrino dark energy: Nugget formation and Hubble anomaly. arXiv 2021, arXiv:2005.11889. [Google Scholar] [CrossRef]
- Barenboim, G.; Kinney, W.H.; Park, W.I. Flavor versus mass eigenstates in neutrino asymmetries: Implications for cosmology. Eur. Phys. J. C 2017, 77, 590. [Google Scholar] [CrossRef]
- Jedamzik, K.; Pogosian, L. Relieving the Hubble tension with primordial magnetic fields. Phys. Rev. Lett. 2020, 125, 181302. [Google Scholar] [CrossRef]
- Jedamzik, K.; Pogosian, L.; Zhao, G.B. Why reducing the cosmic sound horizon alone can not fully resolve the Hubble tension. Commun. Phys. 2021, 4, 123. [Google Scholar] [CrossRef]
- Alestas, G.; Perivolaropoulos, L. Late-time approaches to the Hubble tension deforming H(z), worsen the growth tension. Mon. Not. R. Astron.Soc. 2021, 504, 3956–3962. [Google Scholar] [CrossRef]
- Kumar, S.; Nunes, R.C.; Yadav, S.K. Dark sector interaction: A remedy of the tensions between CMB and LSS data. Eur. Phys. J. C 2019, 79, 576. [Google Scholar] [CrossRef]
- Valentino, E.D.; Melchiorri, A.; Mena, O. Can interacting dark energy solve the H0 tension? Phys. Rev. D 2017, 96, 043503. [Google Scholar] [CrossRef]
- Solà, J.; Gómez-Valent, A.; Pérez, J.d. The H0 tension in light of vacuum dynamics in the Universe. Phys. Lett. B 2017, 774, 317. [Google Scholar] [CrossRef]
- Solà, J.; Gómez-Valent, A.; de Pérez, J. Hints of dynamical vacuum energy in the expanding Universe. Astrophys. J. 2015, 811, L14. [Google Scholar] [CrossRef]
- Solà, J.; Gómez-Valent, A.; Pérez, J. First evidence of running cosmic vacuum: Challenging the concordance model. Astrophys. J. 2017, 836, 43. [Google Scholar] [CrossRef]
- Solà, J.; de Pérez, J.; Gómez-Valent, A. Dynamical dark energy versus Λ=const. in light of observations. Europhys. Lett. 2018, 121, 39001. [Google Scholar] [CrossRef]
- Chen, G.; Ratra, B. Median statistics and the Hubble constant. Publ. Astron. Soc. Pac. 2011, 123, 1127. [Google Scholar] [CrossRef]
- Guidorzi, C.; Margutti, R.; Brout, D.; Scolnic, D.; Fong, W.; Alexander, K.D.; Cowperthwaite, P.S.; Annis, J.; Berger, E.; Blanchard, P.K.; et al. Improved constraints on H0 from a combined analysis of gravitational-wave and electromagnetic emission from GW170817. Astrophys. J. 2017, 851, L36. [Google Scholar] [CrossRef]
- Benevento, G.; Hu, W.; Raveri, M. Can late dark energy transitions raise the Hubble constant? Phys. Rev. D 2020, 101, 103517. [Google Scholar] [CrossRef]
- Tammann, G.A.; Reindl, B. The luminosity of supernovae of type Ia from TRGB distances and the value of H0. Astron. Astrophys. 2013, 549, A136. [Google Scholar] [CrossRef][Green Version]
- Jang, S.; Lee, M.G. The Tip of the Red Giant Branch Distances to Type Ia Supernova Host Galaxies. V. NGC 3021, NGC 3370, and NGC 1309 and the Value of the Hubble Constant. Astrophys. J. 2017, 836, 74. [Google Scholar] [CrossRef]
- Riess, A.G.; Rodney, S.A.; Scolnic, D.M.; Shafer, D.L.; Strolger, L.G.; Ferguson, H.C.; Postman, M.; Graur, O.; Maoz, D.; Jha, S.W.; et al. Type Ia Supernova distances at redshift > 1.5 from the Hubble Space Telescope Multy-Cycle Treasury programs: The early expansion rate. Astrophys. J. 2018, 853, 126. [Google Scholar] [CrossRef]
- Gomez-Valent, A.; Amendola, L. H0 from cosmic chronometers and Type Ia supernovae, with Gaussian Processes and the novel Weighted Polynomial Regression method. J. Cosmol. Astropart. Phys. 2018, 1804, 051. [Google Scholar]
- Moresco, M.; Cimatti, A.; Jimenez, R.; Pozzetti, L.; Zamorani, G.; Bolzonella, M.; Dunlop, J.; Lamareille, F.; Mignoli, M.; Pearce, H.; et al. Improved constraints on the expansion rate of the Universe up to z ∼ 1.1 from the spectroscopic evolution of cosmic chronometers. JCAP 2012, 2012, 006. [Google Scholar] [CrossRef]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6% measurement of the Hubble parameter at z∼0.45: Direct evidence of the epoch of cosmic re-acceleration. JCAP 2016, 05, 014. [Google Scholar] [CrossRef]
- Moresco, M. Raising the bar: New constraints on the Hubble parameter with cosmic chronometers at z ∼ 2. Mon. Not. R. Astron. Soc. Lett. 2015, 450, L16. [Google Scholar] [CrossRef]
- Blake, C.; Kazin, E.A.; Beutler, F.; Davis, T.M.; Parkinson, D.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; et al. The WiggleZ Dark Energy Survey: Mapping the distance-redshift relation with baryon acoustic oscillations. Mon. Not. R. Astron. Soc. 2011, 418, 1707–1724. [Google Scholar] [CrossRef]
- Lewis, A. GetDist: A Python package for analysing Monte Carlo samples. arXiv 2019, arXiv:1910.13970. [Google Scholar]
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.; Bucciarelli, B.; Lattanzi, M.G.; MacKenty, J.W.; Bowers, J.B.; Zheng, W.; Filippenko, A.V.; et al. Milky Way Cepheid Standards for Measuring Cosmic Distances and Application to Gaia DR2: Implications for the Hubble Constant. ApJ 2018, 861, 126. [Google Scholar] [CrossRef]
- Delubac, T.; Bautista, J.E.; Rich, J.; Kirkby, D.; Bailey, S.; Font-Ribera, A.; Slosar, A.; Lee, K.-G.; Pieri, M.M.; Hamilton, J.-C.; et al. Baryon Acoustic Oscillations in the Lyα forest of BOSS DR11 quasars. Astron. Astrophys. 2015, 574, A59. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).