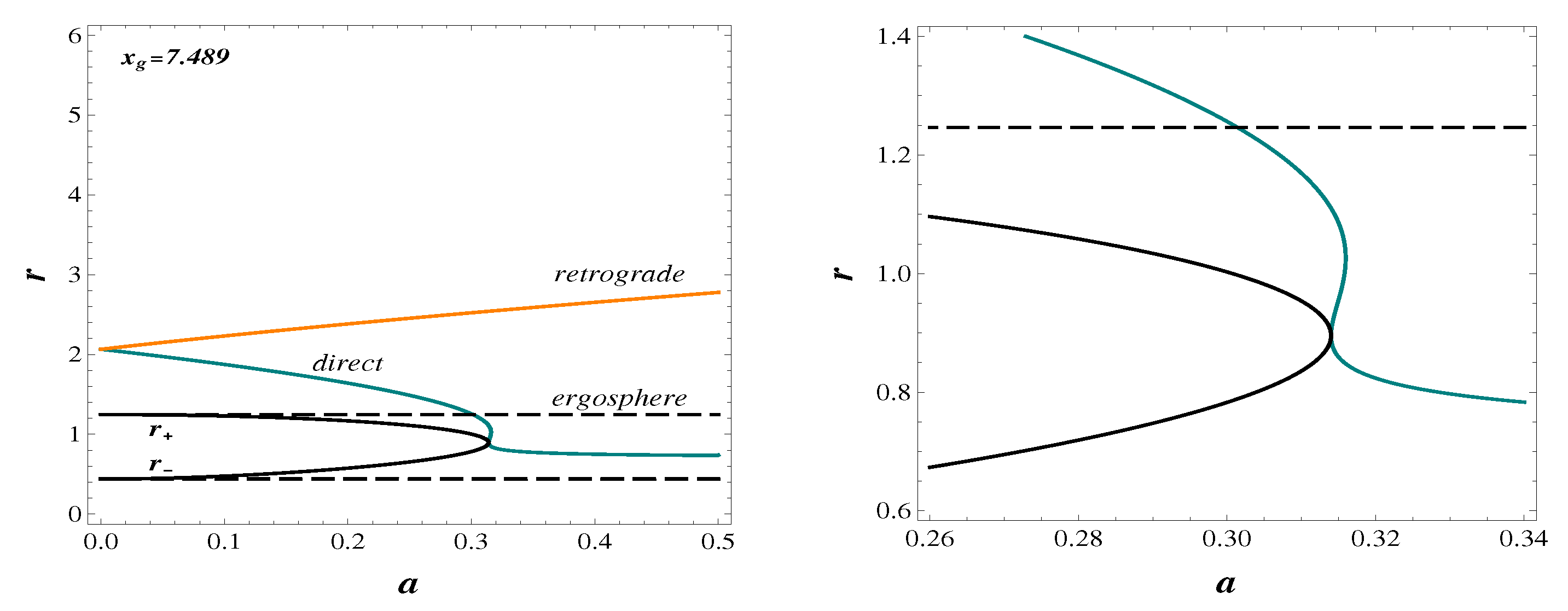Abstract
We study the basic properties of the circular equatorial orbits for the regular axially symmetric solutions, obtained with using the Gürses–Gürsey formalism which includes the Newman–Janis algorithm, from regular spherically symmetric metrics of the Kerr–Schild class specified by . Solutions of this class describe regular rotating black holes and spinning solitons replacing naked singularities. All these objects have the interior de Sitter equatorial disk, and can have two kinds of interiors determined by the energy conditions. One of them contains an additional interior de Sitter vacuum -surface with the de Sitter disk as a bridge, whose internal cavities are filled with a phantom fluid. We study in detail the innermost equatorial circular orbits and show that in the field of spinning solitons, the innermost orbits exist within ergoregions related to phantom regions. We show also that around spinning solitons there can exist four corotating light rings and around a regular black hole, one corotating light ring, which is stable for a certain class of black holes. For all objects there exists one counterrotating light ring.
1. Introduction
Presented in the current literature, regular solutions for rotating black holes [1,2,3,4,5,6,7,8,9,10] (for a review [11]) are typically obtained from regular spherical solutions with using the Newman–Janis complex translation [12]. As was shown by Gürses and Gürsey [13], the Newman–Janis algorithm works for the metrics:
which belong to the Kerr–Schild class [14] (for extension and applications of the Kerr-Shild formalism see [15]) and can be presented as , where is the Minkowski metric and are the principle null congruences. This is a special class of the algebraically degenerated solutions to the Einstein equations [14]. A general approach using properties of the Kerr–Schild metrics has been applied for obtaining axially symmetric solutions in the non-commutative geometry [16,17,18].
The regular spherical metrics of the Kerr–Schild class (1) are generated by source terms that satisfy:
and present anisotropic vacuum dark fluid , [19]. They are transformed by the Gürses–Gürsey formalism [13], which includes the Newman–Janis algorithm, into regular axially symmetric solutions that satisfy the condition (2) in the co-rotating reference frame [20,21], and describe regular rotating compact objects with de Sitter interiors, asymptotically Kerr for a distant observer [22].
The key point is that the stress-energy tensors responsible for the spherical metrics (1) have the algebraic structure (2); as a result regular spherical solutions satisfying WEC (the weak energy condition that requires a non-negativity of density as measured by any local observer), have the de Sitter center [23,24,25,26]. Rotation transforms the de Sitter center into the interior de Sitter disk , which is the obligatory constituent of all compact objects described by regular solutions specified by (2). They include regular de Sitter–Kerr black holes and spinning solitons, replacing naked singularities and defined as physical solitons in the spirit of the Coleman lumps—nonsingular, non-dissipative compact objects bound by their self-interaction [27]—in the considered case, the de Sitter-Kerr spinning solitons [22]. The mass of objects is generically related to the interior de Sitter vacuum and breaking of space-time symmetry from the de Sitter group [25]. In this paper, we show that they can be identified as the ultracompact objects defined as the self-gravitating systems confined by the light rings, formed by the bound null orbits ([28,29] and references therein).
In the paper [20] it was noted that rotation inevitably leads to the violation of WEC in the interior regions of regular objects. Violation of WEC was found for several particular regular solutions obtained with the Newman–Janis algorithm [3,4,5,6,10]. In our papers [22] we studied the question of WEC violation on a general setting and found the existence of two kinds of regular interiors—one preserving and the other violating WEC beyond an additional de Sitter vacuum -surface () incorporating the de Sitter disk as a bridge. In cavities between the -surface and disk, violation of WEC leads to the appearance of a phantom fluid [22], typically defined as [30,31]. Phantom substance, which inevitably has a negative energy density for a certain class of observers was introduced [30] in searching for a reason for the observed accelerated expansion of our universe (“desperate times evidently call for desperate measures” [32]). In the interiors of the regular rotating objects violating WEC, the phantom fluid is essentially anisotropic, ([33] and references therein).
In this paper we study the basic properties and classification of circular equatorial orbits in the field of the regular de Sitter–Kerr black holes and spinning solitons. These orbits play the essential role in the geodesic structure of a spacetime and provide a diagnostic tool for an investigation of generic features and typical behavior of considered objects. The most important is the case of the innermost orbits existing in the interior regions of rotating objects where the physical processes can occur leading to the extraction of their rotational energy. Inside ergospheres of rotating black holes, there exist trajectories of particles with negative energy [34,35] which powers the processes of energy extraction in particles collisions [36,37,38,39,40]. This mechanism was found also for naked singularities [41,42,43,44], and we expect that it works for spining solitons involving an additional vacuum and phantom energy [22].
Circular equatorial orbits for particles in the Kerr geometry were studied in [45]; in the Kerr–Newman geometry [46] they were studied in [47] for both black hole and naked singularity, and for an extreme black hole in [48]. Circular geodesics, including photon orbits, around a Kerr–Newman–Kasuya black hole are presented in [49]. The innermost circular particle orbits are presented in [50] for regular rotating solution related to the particular spherical solution [51], and in [52] in the weak field approximation for two regular black hole solutions with electric or magnetic charge. For the Hayward black hole timelike and null geodesics are studied in [53], and the difference of particle orbits from those for the Kerr black hole is analyzed in [54]. Photon orbits for the Kerr and Kerr-like black holes are examined in [55], and for the extreme asymptotically Kerr–Newman-AdS black holes in [56]. Stable photon orbits in the stationary axisymmetric electrovacuum spacetimes are considered in [57]. Stability of light rings around spherical ultracompact objects is studied in [58,59], and for the axisymmetric case in [29,60,61,62].
The present paper is devoted to the general analysis and classification of equatorial circular orbits in the field of regular de Sitter–Kerr black holes and spinning solitons, with special attention to the innermost orbits and their location with respect to ergospheres.
The paper is organized as follows. In Section 2, we briefly outline the basic general features of the internal structure of regular rotating compact objects specified by the condition , typical for most solutions presented in the literature (for details [11,22,63]), and study location of the boundary of the de Sitter/phantom interior with respect to the ergoregion.1 Section 3 contains derivation and analysis of general equations for circular orbits. In Section 4, we present a detailed analysis and classification of the photon orbits, as well as of the marginally stable and marginally bound particle orbits, illustrated by the pictures of orbits calculated for the exact solution with the phenomenologically regularized Newtonian profile. In Section 5, we summarize and discuss the results.
2. Structure of the de Sitter–Kerr Compact Objects
Spherically symmetric solutions satisfying (2) are described by the Kerr–Shild metrics (1) with:
where is a density profile. Regular spherical metrics (1) are asymptotically Schwarzschild at , and asymptotically de Sitter at provided that their source terms satisfy WEC [23,24,25]. The mass M is generically related to breaking of space-time symmetry from the de Sitter group [25]. In terms of the dimensionless variable , the mass function, normalized to M, reads:
where , and is normalized to . It follows:
where is the transversal pressure, .
Regular spherical metrics (3) belong to the Kerr–Schild class and are transformed to the axially symmetric metrics by using the Gürses–Gürsey formalism [13]. In the Boyer–Lindquist coordinates related to the Cartesian coordinates by:
and in the geometrical units , the Gürses–Gürsey metrics read [13]:
A metric from class (7) is thus determined by the mass function , which originated from a spherical solution (3). For , it tends to the mass M, which gives , and the metic (7) asymptotically tends to the Kerr metric [13]. The parameter a in (7) is the specific angular momentum, .
In geometry with metric (7), the surfaces of constant r are the confocal ellipsoids [65] (for specifics in regular geometry [66]):
which degenerate, for , to the equatorial disk:
bounded by the ring .
The de Sitter–Kerr spacetime is asymptotically flat and can have at most two horizons and two ergospheres for spinning solitons [22]. Horizons are defined by the equation:
where is the event horizon and is the internal horizon. An extreme black hole with the double horizon is defined by . Since a represents the source of geometry, we fix its rotation direction as . Ergospheres are defined by:
A black hole has one ergosphere and ergoregion around the event horizon. A spinning soliton can have, dependently on the density profile , two ergospheres and ergoregion between them, one ergosphere which confines the whole interior as the ergoregion, or no ergosphere [22].
The stress-energy tensor responsible for the metric (7) can be written in the form [13]:
in the orthonormal tetrad:
The sign plus refers to the R-regions outside the event horizon and inside the internal horizon where the vector is time-like. The sign minus refers to the regions between the horizons where the vector is time-like. The vectors and are space-like in all regions.
The eigenvalues of the stress-energy tensor (13) in the co-rotating frame with the angular velocity , satisfy the relations [22]:
These relations correspond to the equation of state:
which represents a generically anisotropic fluid [67].
On the equatorial disk (10), and , the equation of state takes the form and describes the rotating de Sitter vacuum disk in the co-rotating frame [21,22].
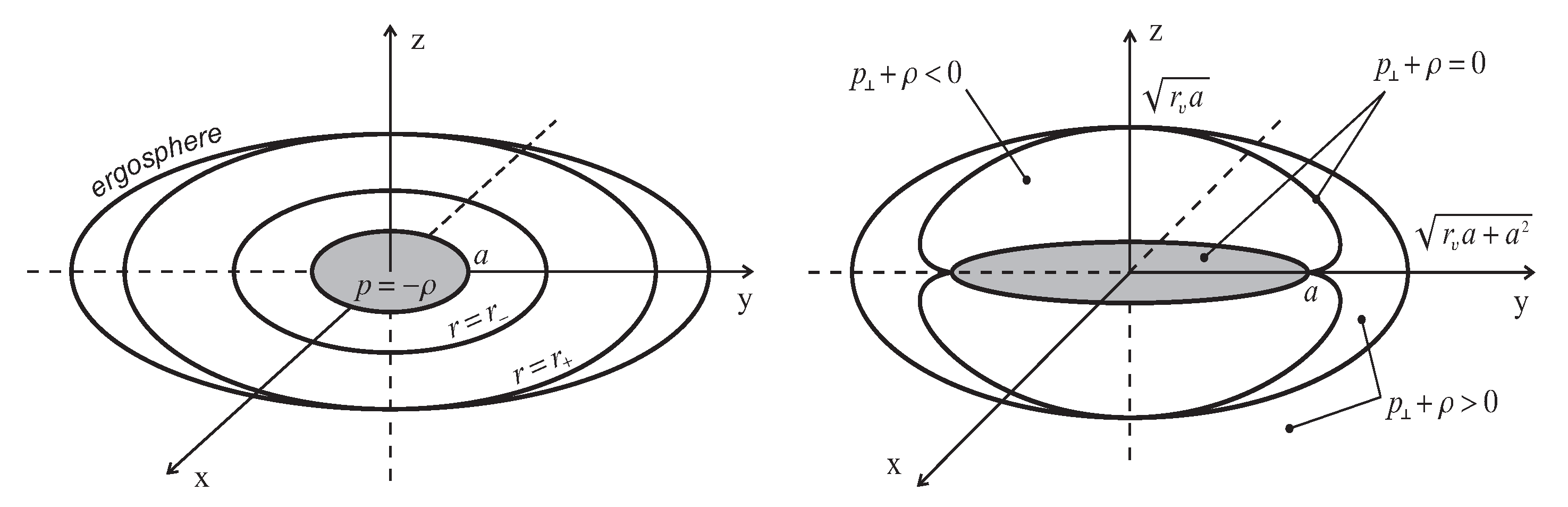
Behavior outside of the disk (10) is governed by energy conditions. When a related spherical solution violates the dominant energy condition (DEC), in (15), then the function vanishes only at disk . In this case, WEC is satisfied and Equation (16) represents an anisotropic quintessence [67]. This type of interior is shown in Figure 1 Left [22] together with the horizons and the ergosphere.
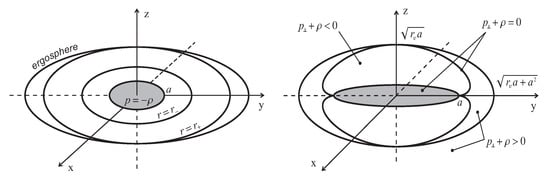
Figure 1.
(Left) Horizons, ergosphere, and de Sitter vacuum disk for the first type of interior. (Right) Vacuum -surface incorporating the de Sitter disk in the second type interior.
When the spherical solution satisfies DEC, , there can exist -surface with the de Sitter disk as a bridge. In the cavities between the upper and down boundaries of the -surface and the de Sitter bridge , WEC is violated, in the equation of state (16), and cavities are filled with a generically anisotropic phantom fluid [22]. It is the second type of interior shown in Figure 1 Right [22].
The existence of two types of interior and the form of the -surface are generic [11,22]. Ergoregions are defined by the condition , which makes possible extraction of energy from interior high density regions; they are confined by ergospheres which coincide with the event horizons on the z-axis. Therefore a condition suggesting favorable location of the -surface with respect to the event horizon and ergosphere is the same on the z-axis.
The double horizon is described by two equations:
The function evolves from as to as with one minimum where , and for the case of the double horizon:
From , it follows that:
and satisfaction of DEC constrains the function as:
The -surface exists, by virtue of (15), if , which results in the condition on z-axis . With taking into account that and [25] for spherical solutions satisfying WEC, the condition for a favorable mutual location of an upper boundary of the double horizon (ergosphere) and -surface reads on the z-axis:
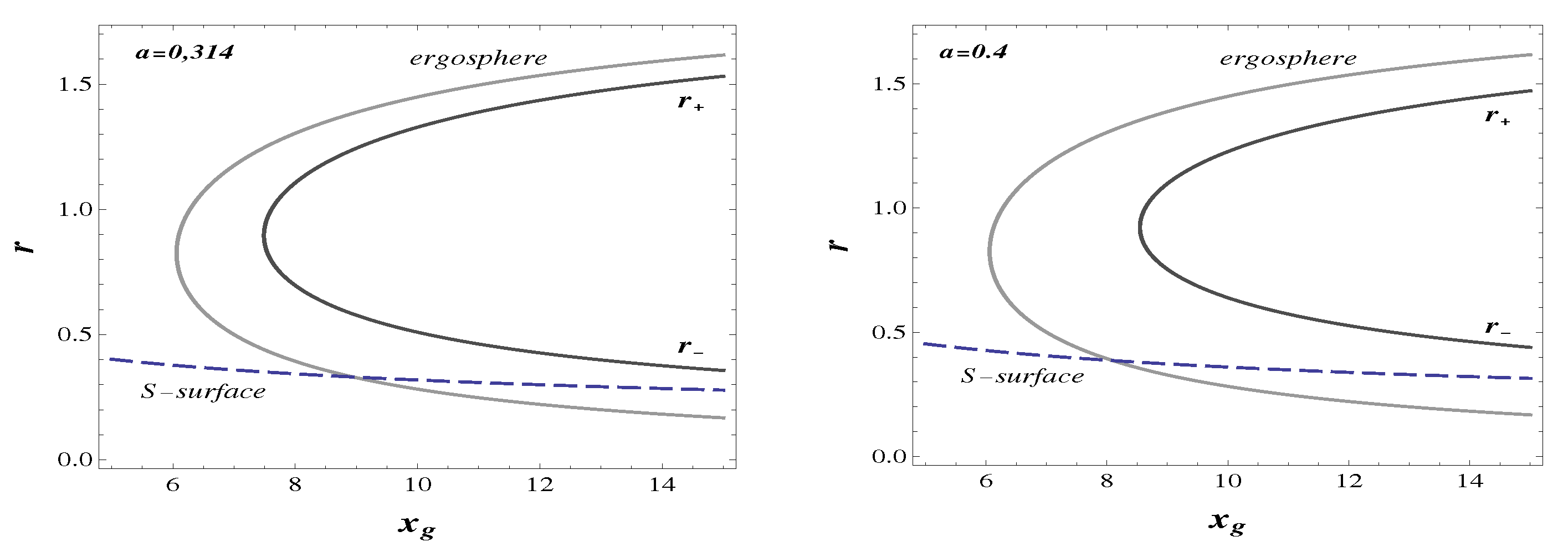
In Figure 2, we show the location of the -surface with respect to the ergoregion for two values of the angular momentum a.
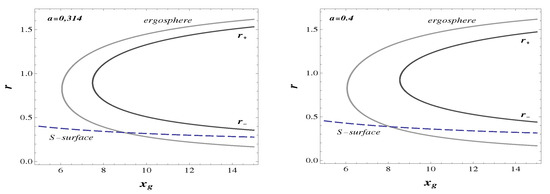
Figure 2.
-surface, horizons and ergospheres for (Left) and (Right).
As follows from Equation (15), the height of the -surface decreases when increases, while the event horizon increases with increasing , so that for the case of a black hole -surface, its located in the ergoregion beyond the internal horizon in the interior R-region, which is unavailable for an outside observer. The case of a soliton -surface is located beyond the ergosphere, its height increases with increasing a, i.e., the phantom region fits within the ergoregion, and the processes of energy extraction involve the phantom energy and are facilitated by the absence of the event horizon.
Pictures illustrating generic behavior of -surface are plotted for the particular exact axially symmetric solution [22], originating from the spherical symmetric solution with the phenomenologically-regularized Newtonian profile [68]:
For the density profile (22) the metric function and the function are:
The cut-off length scale is characteristic for the de Sitter–Schwarzschild geometry matching directly [69] or continuously [23,24] the Schwarzschild exterior to the de Sitter interior. For geometry with the metric function (23), it corresponds to the zero gravity surface at which the strong energy condition is violated and the gravitational acceleration changes its sign, .
Relation of the cut-off scale with parameter in (22) gives which corresponds to related to the de Sitter center, in accordance with the underlying idea to associate a cosmological constant with the energy density of self-interaction ([22] and references therein). For gravitationally-bound structures, the scale of the interior de Sitter vacuum can be the Planck scale in the frame of the hypothesis of the arising de Sitter vacuum due to self-regulation of geometry [69] and for the hypothesis of an existing limiting curvature [70], either the GUT scale due to symmetry restoration in a gravitational collapse [71,72]. Appearance of the de Sitter core replacing the Schwarzschild singularity was found in the frame of “renormalization group improving” [73], of a noncommutative geometry approach [16], and in an ultraviolet quantum gravity [74]. In the estimates for pictures, we apply the GUT scale GeV which gives cm.
3. Basic Equations
The equation for timelike geodesics reads [65]:
where E is the energy on the orbit, and is the projection of the angular momentum on the z-axis, related to the Killing vector in the axially symmetric geometry (7).
The potential differs crucially from that in the Kerr geometry where the potential increases from at , the first extremum is the maximum and the innermost orbits are unstable. In the regular geometry potential decreases from at , the first extremum is the minimum and the innermost orbits are stable.
Introducing the variable , typically used for studying orbits, we obtain the equations:
Determinant of Equation (29) is given by:
The universal formula for reads:
where
This gives:
and the integrals of motion on the orbits:
An upper sign applies to the retrograde orbits, and a lower sign to the direct orbits. For , these integrals of motion coincide with those in the Kerr geometry [65].
The equation for null geodesics which describes the motion of photons with the wavelength being much less than the characteristic scale of geometry, reads:
Introducing the parameter , we obtain for the potential:
where we denoted by the potential normalized to . The basic constraint on the photon orbital moment follows directly from (39) and reads:
The radii of orbits are determined by zeros of the potential derivative,
Here and in what follows, the prime denotes differentiation with respect to u or to r in formulae expressed in u or r variable, respectively.
Equation (41) yields the radius of the orbit related to the integral of motion as:
which for coincides with the relevant relation for the Kerr metric [65].
These relations lead to the constraints on the mass function on the orbits:
Introducing the variable in Equation (42), we obtain the relation:
and putting it into (39) we derive the equation for the integral of motion y on the orbits:
which for coincides with the relevant equation in the Kerr geometry [65]. For an extreme black hole, its double horizon, presents the lower boundary of a manifold for an outside observer. For , the involved functions are fixed, and we can apply the standard procedure relating the roots of Equation (46) with the function which gives:
On the double horizon, we obtain , and the appropriate value of y is given by the double root of Equation (46):
Expressing the mass function and its derivative in terms of the function and its derivatives:
we get on the double horizon:
the equation for (45) takes the form and is satisfied for on the double horizon where . The direct orbit:
coincides for with the unstable orbit in the Kerr geometry [65].
4. Generic Properties of Orbits
4.1. Photon Orbits
For analysis of photon orbits we apply the general Equation (36) in the limit (), which gives:
and in terms of the variable r:
where an upper sign applies to a retrograde orbit and a lower sign to a direct orbit.
The type of an orbit satisfying the orbit Equations (39) and (41), is defined by the second derivative of the potential given by:
For each value of the parameter , there exists such a value of the parameter a, , which defines an extreme black hole with the double horizon ; it presents a lower boundary of the manifold for an outside observer for a given value of . The case corresponds to a rotating black hole with two horizons, and to a spinning soliton without horizons. To study behavior and character of orbits dependently on a, we consider the curve defined parametrically by the orbit Equation (53). For the direct orbits:
Differentiating , we obtain the equation:
which transforms to the form:
For , the function is the increasing function, and .
Starting from the Kerr limit, and , for which the derivative (57) is known and negative, what is easy to check from Equation (53) for , the curve with follows the asymptotically Kerr branch with decreasing r and increasing a, until it meets a branching point where:
As a result , the derivative changes its sign, and an additional branch appears, with , at which the curve is directed towards decreasing r and decreasing a unless it meets the next branching point on the double horizon, corresponding to the orbit (51). In this point, according to (49), , and . Derivative changes its sign, originating the innermost branch with , at which the curve is directed towards decreasing r and increasing a in the field of a soliton.
Looking at this picture from a soliton region with , we can learn more about type of orbits on the curve . For a soliton, the whole manifold is available, the potential (38) decreases from as , its first extremum is the minimum and the innermost direct orbit is stable and represents the stable light ring around a spinning soliton. The branch of these orbits approaches the branching point from a soliton region with . The type of orbit depends on given by (54). On the double horizon , while by virtue of (49). As a result . For regular solutions satisfying DEC, according to (20), it follows .
The innermost orbits in the field of a soliton have radii , and hence exist inside the ergoregion, since its upper boundary goes on the level .
The unstable orbit corresponds to the maximum of , and originates from the additional branch with directed to increasing r with increasing a. Further along the way to the asymptotically Kerr branch with , the curve meets the branching point for . Dependently on the density profile, the third, asymptotically Kerr branch can be a continuation of the second branch of unstable orbits. Another option corresponds to existence of the next minimum in the potential, then the orbit degenerates (), and orbits of third branch are stable and include, for , stable light rings around black holes. The next extremum of is a maximum, which should exist since a potential decreases to as . This branch of orbits contains the unstable retrograde orbits.
For retrograde orbits the curve , determined by the equation:
which differs from (57) by the sign of , and by the sign in the denominator, denoted below as , which can be transformed as:
This function is positive on the unstable orbit according to the behavior of given by (54), negative for unstable orbits. As a result everywhere, the curve never changes its direction and achieves the Kerr limit for . For an extreme black hole, , the retrograde orbit is given by:
and for coincides with the relevant orbit in the Kerr geometry [65].
This behavior is illustrated by Figure 3 plotted for the density profile (22). Direct orbits are shown in the blue color, and retrograde orbits in the orange color.
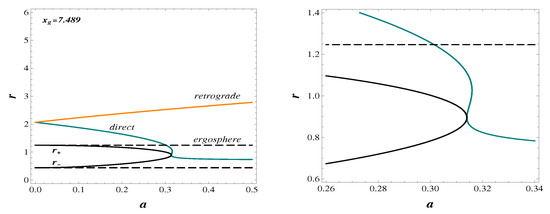
Figure 3.
Photon orbits, horizons, and ergospheres dependently on a (left) and the enlarged image near the double horizon (right).
The double horizon of the extreme black hole with is . Two ergospheres exist at and ; the surface confines the ergoregion around a black hole; both surfaces confine the ergoregion in the field of a spinning soliton. In this region we see, within the range , three branches of direct orbits due to the appearance of the branching point . At , we see two direct orbits, and , and the retrograde orbit . For , there exists one branch of the innermost direct orbits, and one branch of the retrograde orbits. All innermost orbits go inside the ergoregion.
In the field of a black hole with , we see one branch of the direct orbits and one branch of the retrograde orbits. In the field of the extreme black hole, , we see the direct orbit on the horizon , the direct orbit , and the retrograde orbit .
The curve has two branching points for direct orbits, on the double horizon , and on . In the field of a black hole, , there exists one branch of unstable retrograde orbits, and one branch of direct orbits, stable or unstable depending on the density profile. In the field of a spinning soliton, for , there are three branches of direct orbits, and one branch of retrograde orbits. For , there are two direct orbits and one retrograde orbit. For , there are the innermost stable direct orbits and unstable retrograde orbits. All the innermost orbits are located within the ergoregion. The photon orbits around solitons and black holes present the light rings defined as bound null orbits ([29] and references therein). The existence of light rings around these objects allows one to identify them as the ultracompact objects in accordance with their definition as the self-gravitating systems with the light rings [28]. The innermost light rings around solitons and a certain class of black holes are stable.
4.2. Particle Orbits
In the regular de Sitter–Kerr geometry, there are two types of the limiting particles orbits: The marginally bound orbits () and the marginally stable orbits ().
Marginally bound orbits, defined by the condition , present the inner boundary of the manifold for the particles closed orbits.
Applying the condition in (28) and taking into account (33) and (34) we obtain the equation for the marginally bound orbits:
which for coincides with the relevant equation in the Kerr geometry [65]. Transition to the variable r transforms Equation (62) to the form:
where an upper sign applies to the retrograde orbits, while a lower sign applies to the direct orbits. In Kerr geometry this equation gives in agreement with [65].
Expressing the mass function and its derivative via and its derivatives,
we find that Equation (63) is satisfied on the double horizon () for the direct orbit .
Treating the orbit Equation (63) as the equation for a curve defined by and differentiating with respect to r and a we find:
The coefficient in front of vanishes at the double horizon which results in the existence of the branching point at where at . The curve approaches this point from the soliton region where the potential (24), written as:
decreases from for as . In its minimum, there exists the innermost stable direct orbit for each value of . These orbits form the branch of stable orbits with . After crossing the branching point , the curve changes its direction to and must meet another branching point to arrive at the asymptotically Kerr branch with according to [65].
For the marginally bound orbit can be obtained directly from (28) with which gives:
Stability of the marginally bound orbits depends on behavior of which can be written, accounting for on the orbit, in the form:
for any particle orbit. Applying Equations (67) and (68) we obtain for marginally bound orbits:
and ultimately, after some algebra:
For , written as a polynomial with the positively defined coefficients:
the Cartesius rule, which states that the number of positive roots equals to the number of sign changes, suggests the existence of one positive root which defines the degenerate (marginally (un)stable) orbit . For the orbit on the double horizon satisfies:
Applying Equation (19), we obtain , which results in the constraint:
Dependently on the form of the density profile, can have any sign or vanish. On the other hand, according to the Cartesius rule for Equation (72), potential can vanish only once, so that two options are possible. Approaching the point along the branch of stable orbits for in the soliton region, can vanish at , then the branch between and the next branching point , and the asymptotically Kerr branch with contains unstable orbits. Another option is that vanishes at the second branching point for , then an additional branch between two branching points continues the preceding branch of stable orbits, while the asymptotically Kerr branch contains unstable orbits. The choice between two above options comes from the analysis of the mutual location of the branching points and . The intuitive idea , suggested by the mutual location of the photon and limiting particle orbits in the Kerr limit, can be justified by investigation of the potentials and in the branching point .
Behavior of photon orbits requires, for both options for photons, . In expression (54) for this requirement leads to . Applying this constraint in (71), we find , while the behavior of marginally bound orbits requires at . The derivative cannot vanish at since in this point according to (54). We can thus conclude that which results in . It follows that the point belongs to the branch of the stable orbits , and hence the constraint distinguishes from the two above options for marginally bound orbits the branch of stable orbits in the range , followed by the asymptotically Kerr branch of unstable orbits .
For the retrograde orbits, Equation (63) is written as a polynomial, which takes the form:
and the Cartesius rule testifies for one positive root and hence one branch of the retrograde orbits, asymptotically Kerr for . Marginally bound orbits are shown in Figure 4 Left.
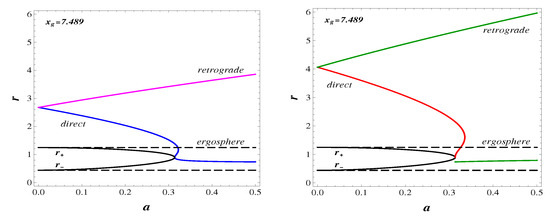
Figure 4.
Dependence of radii on a for the marginally bound orbits (left), and for the marginally stable orbits (right).
Marginally stable orbits correspond to in the potential (24) for each value of the angular momentum a. In terms of the variable u orbits are defined by the orbit equations , and by the condition which reads:
For , this equation gives the proper equation for the Kerr geometry [65].
Behavior of the marginally stable orbits on the double horizon of an extreme black hole and in the field of a spinning soliton can be studied by applying Equation (78) in terms of the related metric function , which gives:
An upper sign in Equation (79) applies to the retrograde orbits, while the lower sign applies to the direct orbits. Applying Formula (64), we obtain on the double horizon:
and find that for a given value of the direct orbit satisfies Equation (79).
The number or orbits can be estimated by presenting the orbit Equation (78) as a polynomial:
with an upper sign for direct orbits and a lower for the retrograde orbits. In the polynomial (81), there are two changes of the sign, independently on the sign of . The Cartesius rule predicts the existence of two retrograde marginally stable orbits, one for , in the soliton region where and , the other for the asymptotically Kerr branch with , where and .
Four changes of signs for the direct orbits in the polynomial (81) suggest the existence of four or two direct orbits. On the double horizon , according to (49), , and Equation (78) reduces to . Calculating in the closest vicinity of the double horizon we obtain:
which for tends to . As a result there is no direct orbit with in this region. The curve starts at and is directed towards increasing r with increasing a in the soliton region, then it must meet a branching point at to change its direction to on the way to the asymptotically Kerr branch with [65].
In the field of a black hole, within the range , we see one branch of the direct orbits and one branch of the retrograde orbits for both types of marginal orbits.
For , there exist the direct marginally bound stable orbit and the marginally stable orbit on the double horizon . In the field of the extreme black hole, there are the direct marginally bound orbit , the direct marginally stable orbit , the retrograde marginally bound orbit , and the retrograde marginally stable orbit .
At corresponding to the branching point of marginally bound orbits, there exist two direct orbits, and , and one retrograde orbit . At corresponding to the branching point of the marginally stable orbits, there are two retrograde orbits, and , and the direct orbit . For there is no direct marginally stable orbits.
Two ergospheres, and , confine the ergoregion around the spinning soliton. Within its ergoregion, there exists the stable marginally bound orbit in the range , and the retrograde marginally stable orbit whose radius is slowly increasing from at a close to , to at .
Both types of particle limiting orbits suffer branching. There exist three branches of direct marginally bound orbits and one branch of unstable retrograde orbits. Stable marginally bound orbits exist around both black holes and as the innermost orbits around solitons.
For marginally stable orbits there are two branches of retrograde orbits, one of the innermost orbits, two branches of direct orbits for , and no direct orbits for .
The innermost stable direct marginally bound orbit and the innermost retrograde marginally stable orbit exists within the ergoregion of a spinning soliton.
5. Summary and Discussion
In the Kerr geometry, the potentials increase from to their maxima. The innermost photon orbits are unstable and followed by the marginally bound orbits with , followed by the marginally stable orbits which [65].
In a regular geometry, the potentials decrease from to their minima, and as a result the situation is essentially different. There exists the innermost stable photon and particle orbits. In addition, all orbits suffer branching on the way to the asymptotically Kerr region .
The innnermost stable direct photon orbits in the field of a soliton, for where corresponds to the double horizon , with , meets the branching point at the unstable orbit . It is followed by an additional branch of unstable orbits directed towards increasing r at increasing a which meets the branching point to arrive at the asymptotically Kerr orbits with increasing r at decreasing a, which present the light rings around the black hole for . The existence of the light rings around spinning solitons and regular rotating black holes allows one to identify them as the ultracompact objects. Stability of the asymptotically Kerr light rings depends on the density profile. They can be a continuation of the preceding additional branch of unstable orbits if does not change a sign at the orbit . However, if on the orbit , the next branch presents the stable asymptotically Kerr light rings around a soliton for and the innermost stable light rings around a black hole for . In this case, the orbit represents a degenerate light ring around a spinning soliton. This confirms the prediciton of the existence of degenerate light rings for a certain class of spherical ultracompact objects [58] and extends it to the case of spinning solitons.
The innermost direct photon orbits around black holes form the corotating light rings around them, while the retrograde photon orbits represent the counterrotating light rings extended to the soliton region for . The cases of two light rings, direct and retrograde, around a black hole and around a soliton for , agree in a sense with the results presented in [61] that corotating and counterrotating light rings “always appear in pairs”, although the dynamics of direct (corotating) light rings around a spinning soliton are more diverse. Around a spinning soliton, there can exist four sets of corotating light rings: Tthe innermost stable light rings for and ; the unstable light rings for and ; the degenerate light ring for a certain class of objects at and ; and the light rings for and for all objects.
All three limiting orbits exist as the direct orbits on the double horizon , which is the branching point for the marginally bound orbits where their innermost stable orbits change direction from to , then meet the branching points, , change their direction to and arrive at the asymptotically Kerr branch of unstable orbits.
Marginally stable direct orbits start from the double horizon, then meet their branching point and follow the asymptotically Kerr branch. As a result, they exist only for and there is no marginally stable orbits for . Instead in the soliton region , there exist retrograde marginally stable orbits.
In the field of a spinning soliton, an upper boundary of the ergroregion goes on the level while the innermost orbits exist at . Therefore all the innermost orbits move close to each other within the ergoregion.
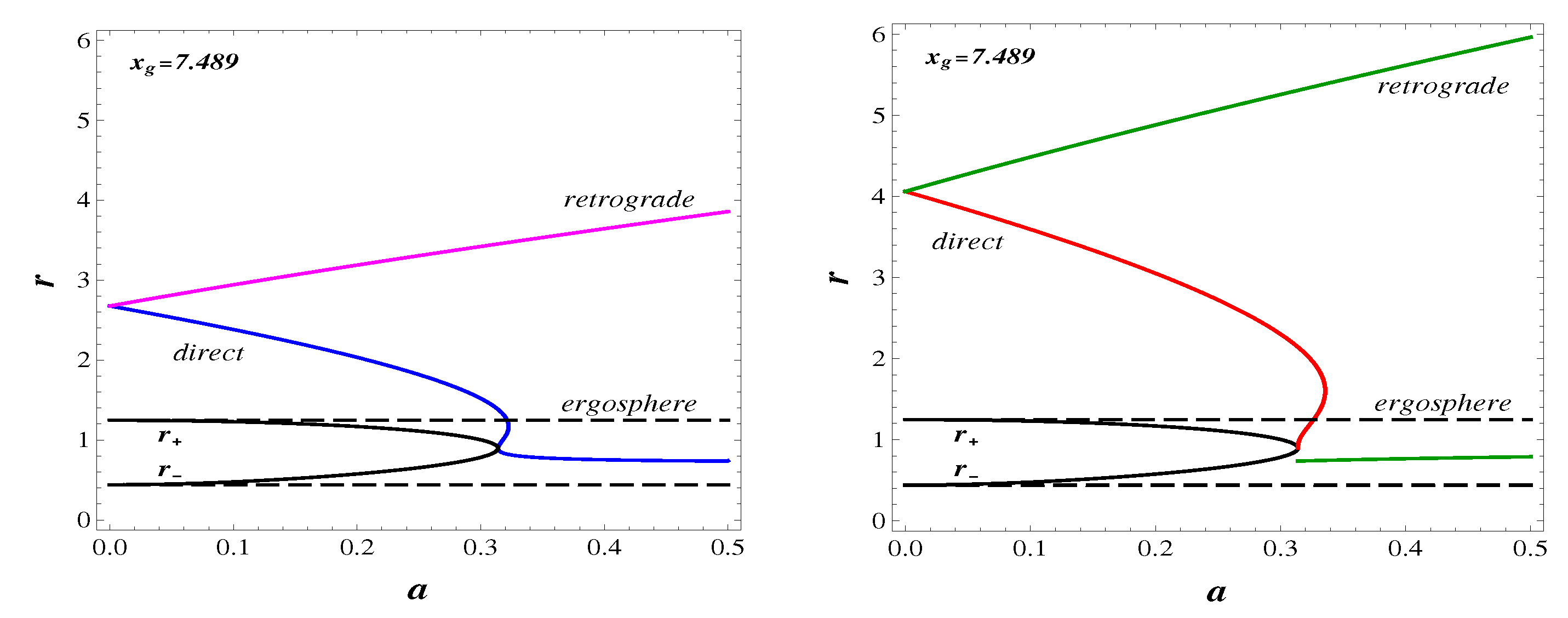
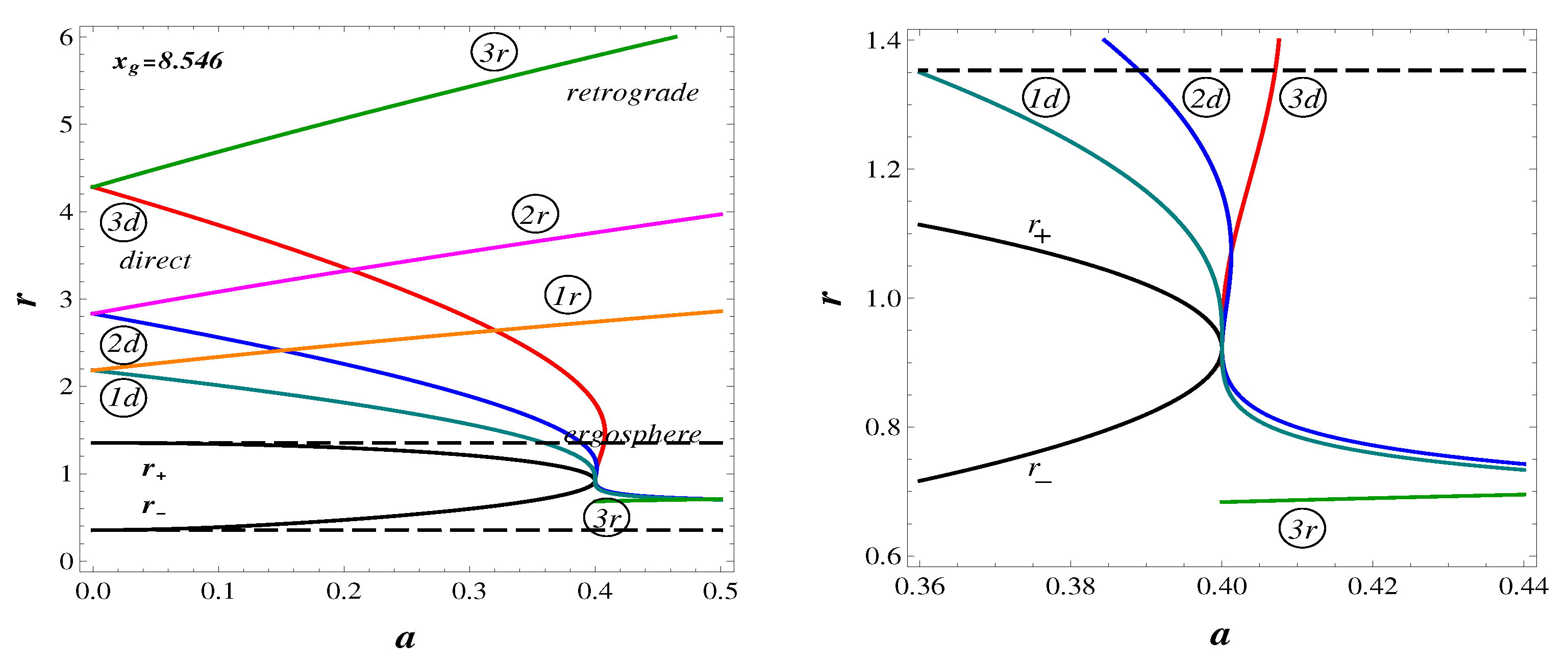
In Figure 5, we show all limiting orbits. Ergospheres are plotted by the intermittent lines.
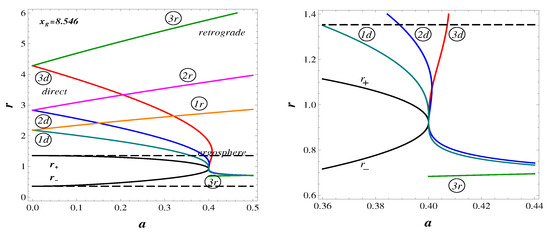
Figure 5.
Limiting orbits in the de Sitter–Kerr geometry dependently on a (Left), and the enlarged image near the double horizon (Right).
In the field of a black hole we see the direct photon orbits denoted by “ and the retrograde orbits denoted by “; the marginally bound direct orbits denoted by “ and the retrograde orbits denoted by “; and the direct marginally stable orbits denoted by “ and the retrograde marginally stable orbits denoted by “. In the field of a spinning soliton there are three branches of the direct photon orbits and one branch of the retrograde orbits within the range , two direct and one retrograde photon orbit at , and two branches of the photon orbits, direct and retrograde, for .
Two innermost direct photon orbits and marginally bound orbits approach the horizon from very close to each other within the ergoregion. The situation is essentially different for the marginally stable direct orbits, which start at the double horizon. Inside the ergoregion there exist the retrograde marginally stable orbits.
Regular rotating black holes and spinning solitons specified by have an obligatory de Sitter vacuum disk in their deep interiors. In the case of a spinning soliton, the region of a very strong field around the de Sitter vacuum disk is open for an outside observer. In addition, the -surface is located beyond the ergosphere, and the ergoregion contains the phantom region. Particles and photons on the innermost orbits within ergoregion can participate in collisions with particles following unbound orbits that can cross the phantom region, which increases the energy output in collisions. As a result, the processes of energy extraction, facilitated by the absence of the event horizon, involve the rotation energy from ergoregions and can involve the phantom energy in collisions.
Information about the physical properties of a black hole interiors can be obtained from an observation of its shadow whose boundary is determined by photons captured on the innermost orbits, which give the image of the black hole imposed on the image of the distant bright source of radiation. Nowadays, the study of black hole shadows has become the subject of direct astronomical interest [75] due to the observational possibilities of the Event Horizon Telescope Collaboration manifested by the first observation of the black hole shadow in M87 [76] (for a recent review see [77]).
The shadows of de Sitter–Kerr black holes visibly differ from the shadow of the Kerr black hole, and the differences depend essentially on the properties of their interior regions and especially on the pace of a density decreasing [63]. The detailed numerical analysis of difference between the shadows of the Kerr black hole and the regular black hole with the relatively slow decreasing density (22) has shown that this difference can be significant [63]. A decreasing shadow has been also found in the Kerr–Newman–Kasuya (KNK) spacetime for a rotating dyon black hole with extra dyon charge [78].
Currently, we plan the detailed analysis of the observed black hole shadow by fitting its boundary by the photon gravitational capture cross-section using theoretical results on the description of shadows for regular black holes.
Author Contributions
All authors contributed equally to this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Note
| 1 | Non-singular compact Kerr–Newman–de Sitter instantons are presented and comprehensively studied in [64]. |
References
- Iso, S.; Umetsu, H.; Wilczek, F. Anomalies, Hawking radiations, and regularity in rotating black holes. Phys. Rev. D 2006, 74, 044017. [Google Scholar] [CrossRef]
- Caravelli, F.; Modesto, L. Spinning loop black holes. Class. Quant. Grav. 2010, 27, 245022. [Google Scholar] [CrossRef]
- Bambi, C.; Modesto, L. Rotating regular black holes. Phys. Lett. B 2013, 721, 329–334. [Google Scholar] [CrossRef]
- Balart, L.; Vagenas, E.C. Regular black hole metrics and the weak energy condition. Phys. Lett. B 2014, 730, 14–17. [Google Scholar] [CrossRef]
- Toshmatov, B.; Ahmedov, B.; Abdujabbarov, A.; Stuchlik, Z. Rotating regular black hole solution. Phys. Rev. D 2014, 89, 104017. [Google Scholar] [CrossRef]
- Neves, J.C.S.; Saa, A. Regular rotating black holes and the weak energy condition. Phys. Lett. B 2014, 734, 44–48. [Google Scholar] [CrossRef]
- Ghosh, S.G. A nonsingular rotating black hole. Eur. Phys. J. C 2015, 75, 532. [Google Scholar] [CrossRef]
- Takeuchi, S. Hawking fluxes and Anomalies in Rotating Regular Black Holes with a Time-Delay. Class. Quant. Grav. 2016, 33, 225016. [Google Scholar] [CrossRef][Green Version]
- de Lorenzo, T.; Giusti, A.; Speziale, S. Non-singular rotating black hole with a time delay in the center. Gen. Rel. Grav. 2016, 48, 31. [Google Scholar] [CrossRef]
- Torres, R.; Fayos, F. On regular rotating black holes. Gen. Rel. Grav. 2017, 49, 2. [Google Scholar] [CrossRef]
- Dymnikova, I.; Galaktionov, E. Basic Generic Properties of Regular Rotating Black Holes and Solitons. Adv. Math. Phys. 2017, 2017, 1035381. [Google Scholar] [CrossRef]
- Newman, E.T.; Janis, A.J. Note on the Kerr Spinning Particle Metric. J. Math. Phys. 1965, 6, 915–917. [Google Scholar] [CrossRef]
- Gürses, M.; Gürsey, F. Lorentz covariant treatment of the Kerr-Schild geometry. J. Math. Phys. 1975, 16, 2385–2390. [Google Scholar] [CrossRef]
- Kerr, R.P.; Schild, A. Some algebraically degenerate solutions of Einstein’s gravitational field equations. Proc. Symp. Appl. Math. 1965, 17, 199. [Google Scholar]
- Burinskii, A. The Kerr theorem, Kerr-Schild formalism and multi-particle Kerr-Schild solutions. Grav. Cosmol. 2006, 12, 119–125. [Google Scholar]
- Nicolini, P.; Smailagic, A.; Spalucci, E. Noncommutative geometry inspired Schwarzschild black hole. Phys. Lett. B 2006, 632, 547–551. [Google Scholar] [CrossRef]
- Ansoldi, S.; Nicolini, P.; Smailagic, A. Noncommutative geometry inspired charged black holes. Phys. Lett. B 2007, 645, 261–266. [Google Scholar] [CrossRef]
- Modesto, L.; Nicolini, P. Charged rotating noncommutative black holes. Phys. Rev. D 2010, 82, 104035. [Google Scholar] [CrossRef]
- Dymnikova, I.; Galaktionov, E. Vacuum dark fluid. Phys. Lett. B 2007, 645, 358–364. [Google Scholar] [CrossRef]
- Burinskii, A.; Elizalde, E.; Hildebrandt, S.R.; Magli, G. Regular sources of the Kerr-Schild class for rotating and nonrotating black hole solutions. Phys. Rev. D 2002, 65, 064039. [Google Scholar] [CrossRef]
- Dymnikova, I. Spinning self-gravitating electrovacuum soliton. Phys. Lett. B 2006, 639, 368–372. [Google Scholar] [CrossRef]
- Dymnikova, I.; Galaktionov, E. Regular rotating de Sitter-Kerr black holes and solitons. Class. Quant. Grav. 2016, 33, 145010. [Google Scholar] [CrossRef]
- Dymnikova, I. Vacuum nonsingular black hole. Gen. Rel. Grav. 1992, 24, 235–242. [Google Scholar] [CrossRef]
- Dymnikova, I. The algebraic structure of a cosmological term in spherically symmetric solutions. Phys. Lett. B 2000, 472, 33–38. [Google Scholar] [CrossRef]
- Dymnikova, I. The cosmological term as a source of mass. Class. Quant. Grav. 2002, 19, 725–740. [Google Scholar] [CrossRef]
- Dymnikova, I. Spherically symmetric space-time with the regular de Sitter center. Int. J. Mod. Phys. D 2003, 12, 1015–1034. [Google Scholar] [CrossRef]
- Coleman, S. Classical lumps and their quantum descendants. In New Phenomena in Subnuclear Physics; Zichichi, A., Ed.; Plenum: New York, NY, USA, 1977; p. 297. [Google Scholar]
- Cardoso, V.; Crispino, L.C.B.; Macedo, C.F.B.; Okawa, H.; Pani, P. Light rings as observational evidence for event horizons: Long-lived modes, ergoregions and nonlinear instabilities of ultracompact objects. Phys. Rev. D 2014, 90, 044069. [Google Scholar] [CrossRef]
- Cunha, P.V.P.; Herdeiro, C.A.R. Stationary Black Holes and Light Rings. Phys. Rev. Lett. 2020, 124, 181101. [Google Scholar] [CrossRef]
- Caldwell, R.R. A phantom menace? Cosmological consequences of a dark energy component with super-negative equation of state. Phys. Lett. B 2002, 545, 23–29. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Rubin, S.G. Black Holes, Cosmology and Extra Dimensions; World Scientific: Singapore, 2013. [Google Scholar]
- Gibbons, G.W. Phantom Matter and the Cosmological Constant; DAMTP-2003-19; Cambridge University: Cambridge, UK, 2003. [Google Scholar]
- Dymnikova, I. Mass, Spacetime Symmetry, de Sitter Vacuum, and the Higgs Mechanism. Symmetry 2020, 12, 634. [Google Scholar] [CrossRef]
- Grib, A.A.; Pavlov, Y.V.; Piattella, O.F. On collisions with unlimited energies in the vicinity of Kerr and Schwarzschild black hole horizons. Grav. Cosmol. 2012, 18, 70–75. [Google Scholar] [CrossRef][Green Version]
- Grib, A.A.; Pavlov, Y.V.; Vertogradov, V.D. Geodesics with negative energy in the ergosphere of rotating black holes. Mod. Phys. Lett. A 2014, 29, 1450110. [Google Scholar] [CrossRef]
- Banados, M.; Silk, J.; West, S.M. Kerr Black Holes as Particle Accelerators to Arbitrarily High Energy. Phys. Rev. Lett. 2009, 103, 111102. [Google Scholar] [CrossRef]
- Jacobson, T.; Sotiriou, T.P. Spinning Black Holes as Particle Accelerators. Phys. Rev. Lett. 2010, 104, 021101. [Google Scholar] [CrossRef]
- Zaslawski, O.B. Energy extraction from extremal charged black holes due to the Banados-Silk-West effect. Phys. Rev. D 2012, 86, 124039. [Google Scholar] [CrossRef]
- Harada, T.; Kimura, M. Black holes as particle accelerators: A brief review. Class. Quant. Grav. 2014, 31, 243001. [Google Scholar] [CrossRef]
- Ghosh, S.G.; Sheoran, P.; Amir, M. Rotating Ayón-Beato-García black hole as a particle accelerator. Phys. Rev. D 2014, 90, 103006. [Google Scholar] [CrossRef]
- Patil, M.; Joshi, P.S. Naked singularities as particle accelerators. Phys. Rev. D 2010, 82, 104049. [Google Scholar] [CrossRef]
- Patil, M.; Joshi, P.S. Kerr Naked Singularities as Particle Accelerators. Class. Quant. Grav. 2011, 28, 235012. [Google Scholar] [CrossRef]
- Patil, M.; Joshi, P.S.; Malafaria, D. Naked singularities as particle accelerators. II. Phys. Rev. D 2011, 83, 064007. [Google Scholar] [CrossRef]
- Patil, M.; Joshi, P.S.; Kimura, M.; Nakao, K.I. Acceleration of particles and shells by Reissner-Nordström naked singularities. Phys. Rev. D 2012, 86, 084023. [Google Scholar] [CrossRef]
- Pugliese, D.; Quevedo, H.; Ruffini, R. Equatorial circular motion in Kerr spacetime. Phys. Rev. D 2011, 84, 044030. [Google Scholar] [CrossRef]
- Newman, E.T.; Cough, E.; Chinnapared, K.; Exton, A.; Prakash, A.; Torrence, R. Metric of a Rotating, Charged Mass. J. Math. Phys. 1965, 6, 918. [Google Scholar] [CrossRef]
- Pugliese, D.; Quevedo, H.; Ruffini, R. Equatorial circular orbits of neutral test particles in the Kerr-Newman spacetime. Phys. Rev. D 2013, 88, 024042. [Google Scholar] [CrossRef]
- Ulbricht, S.; Meinel, R. A note on circular geodesics in the equatorial plane of an extreme Kerr-Newman black hole. Class. Quant. Grav. 2015, 32, 147001. [Google Scholar] [CrossRef]
- Khan, S.U.; Ren, J. Circular geodesics in Kerr-Newman-Kasuya black hole. AIP Conf. Proc. 2021, 2319, 040005. [Google Scholar]
- Toshmatov, B.; Abdujabbarov, A.; Ahmedov, B.; Stuchlik, Z. Particle motion and Penrose processes around rotating regular black hole. Astroph. Space Sci. 2015, 357, 41. [Google Scholar] [CrossRef]
- Ayon-Beato, E.; Garcia, A. Regular Black Hole in General Relativity Coupled to Nonlinear Electrodynamics. Phys. Rev. Lett. 1998, 80, 5056. [Google Scholar] [CrossRef]
- Toshmatov, B.; Stuchlik, Z.; Ahmedov, B. Generic rotating regular black holes in general relativity coupled to nonlinear electrodynamics. Phys. Rev. D 2017, 95, 084037. [Google Scholar] [CrossRef]
- Chiba, T.; Kimura, M. A note on geodesics in the Hayward metric. Prog. Theor. Exp. Phys. 2017, 2017, 043E01. [Google Scholar] [CrossRef]
- Bautista-Olvera, B.; Degollado, J.C.; German, G. Geodesic structure of a rotating regular black hole. arXiv 2019, arXiv:1908.01886. [Google Scholar]
- Johannsen, T. Photon rings around Kerr and Kerr-like black holes. Astrophys. J. 2013, 777, 170. [Google Scholar] [CrossRef]
- Mokdad, M. Reissner-Nordstrøm-de Sitter Manifold: Photon Sphere and Maximal Analytic Extension. arXiv 2017, arXiv:1701.06982. [Google Scholar] [CrossRef]
- Dolan, S.R.; Shipley, J.O. Stable photon orbits in stationary axisymmetric electrovacuum spacetimes. Phys. Rev. D 2016, 94, 044038. [Google Scholar] [CrossRef]
- Hod, S. On the number of light rings in curved spacetimes of ultra-compact objects. Phys. Lett. B 2018, 776, 1–4. [Google Scholar] [CrossRef]
- Hod, S. Analytic study of self-gravitating polytropic spheres with light rings. Eur. Phys. J. C 2018, 78, 417. [Google Scholar] [CrossRef]
- Cunha, P.V.P.; Berti, E.; Herdeiro, C.A.R. Light-Ring Stability for Ultracompact Objects. Phys. Rev. Lett. 2017, 119, 251102. [Google Scholar] [CrossRef]
- Guo, M.; Gao, S. Universal properties of light rings for stationary axisymmetric spacetimes. Phys. Rev. D 2021, 103, 104031. [Google Scholar] [CrossRef]
- Ghosh, R.; Sarkar, S. Light rings of stationary spacetimes. Phys. Rev. D 2021, 104, 044019. [Google Scholar] [CrossRef]
- Dymnikova, I.; Kraav, K. Identification of a regular black hole by its shadow. Universe 2019, 5, 163. [Google Scholar] [CrossRef]
- Chrusciel, P.T.; Hörzinger, M. Compact singularity-free Kerr–Newman–de Sitter instantons. Phys. Rev. D 2017, 95, 086012. [Google Scholar]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Clarendon Press: Oxford, UK, 1983. [Google Scholar]
- Dymnikova, I.; Galaktionov, E. Regular rotating electrically charged black holes and solitons in nonlinear electrodynamics minimally coupled to gravity. Class. Quant. Grav. 2015, 32, 165015. [Google Scholar] [CrossRef]
- Dymnikova, I. The Fundamental Roles of the de Sitter Vacuum. Universe 2020, 6, 101. [Google Scholar] [CrossRef]
- Dymnikova, I. Regular electrically charged vacuum structures with de Sitter center in nonlinear electrodynamics coupled to general relativity. Class. Quant. Grav. 2004, 21, 4417. [Google Scholar] [CrossRef]
- Poisson, E.; Israel, W. Structure of the black hole nucleus. Class. Quant. Grav. 1988, 5, L201–L205. [Google Scholar] [CrossRef]
- Frolov, V.P.; Markov, M.A.; Mukhanov, V.F. Black holes as possible sources of closed and semiclosed worlds. Phys. Rev. D 1990, 41, 383–394. [Google Scholar] [CrossRef]
- Dymnikova, I. De Sitter-Schwarzschild black hole: Its particlelike core and thermodynamical properties. Int. J. Mod. Phys. D 1996, 5, 529–540. [Google Scholar] [CrossRef]
- Dymnikova, I. Internal structure of nonsingular spherical black holes. In Internal Sructure of Black Holes and Spacetime Singularities; Burko, M., Ori, A., Eds.; Bristol In-t of Physics Pulishing: Bristol, TN, USA; Philadelphia, PA, USA; Annals of the Israel Physical Society 13: Jerusalem, Israel, 1997; pp. 422–440. [Google Scholar]
- Bonanno, A.; Reuter, M. Spacetime structure of an evaporating black hole in quantum gravity. Phys. Rev. D 2006, 73, 083005. [Google Scholar] [CrossRef]
- Modesto, L.; Moffat, J.W.; Nicolini, P. Black holes in an ultraviolet complete quantum gravity. Phys. Lett. B 2011, 695, 397–400. [Google Scholar] [CrossRef]
- Falcke, H.; Melia, F.; Agol, E. Viewing the shadow of the black hole at the Galactic Center. Astrophys. J. Lett. bf 2000, 528, L13–L16. [Google Scholar] [CrossRef] [PubMed]
- Alberdi, A.; Gómez Fernández, J.L.; The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole. Astrophys. J. Lett. 2019, 875, L1. [Google Scholar]
- The Event Horizon Telescope Collaboration. First M87 Event Horizon Telescope Results. VIII. Magnetic Field Structure near the Event Horizon. Astrophys. J. Lett. 2021, 910, L13. [Google Scholar] [CrossRef]
- Övgün, A.; Sakallı, İ.; Saavedra, J. Shadow cast and deflection angle of Kerr-Newman-Kasuya spacetime. J. Cosmol. Astropart. Phys. 2018, 10, 041. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).