Periodic Orbits of the Restricted Three-Body Problem Based on the Mass Distribution of Saturn’s Regular Moons
Abstract
1. Introduction
2. Best-Fitting Distribution of the Regular Moons’ Mass
3. Dynamic Equations and Approximate Periodic Orbits
3.1. Dynamic Model with Variable Mass
3.2. Periodic Orbits near the Lagrangian Point
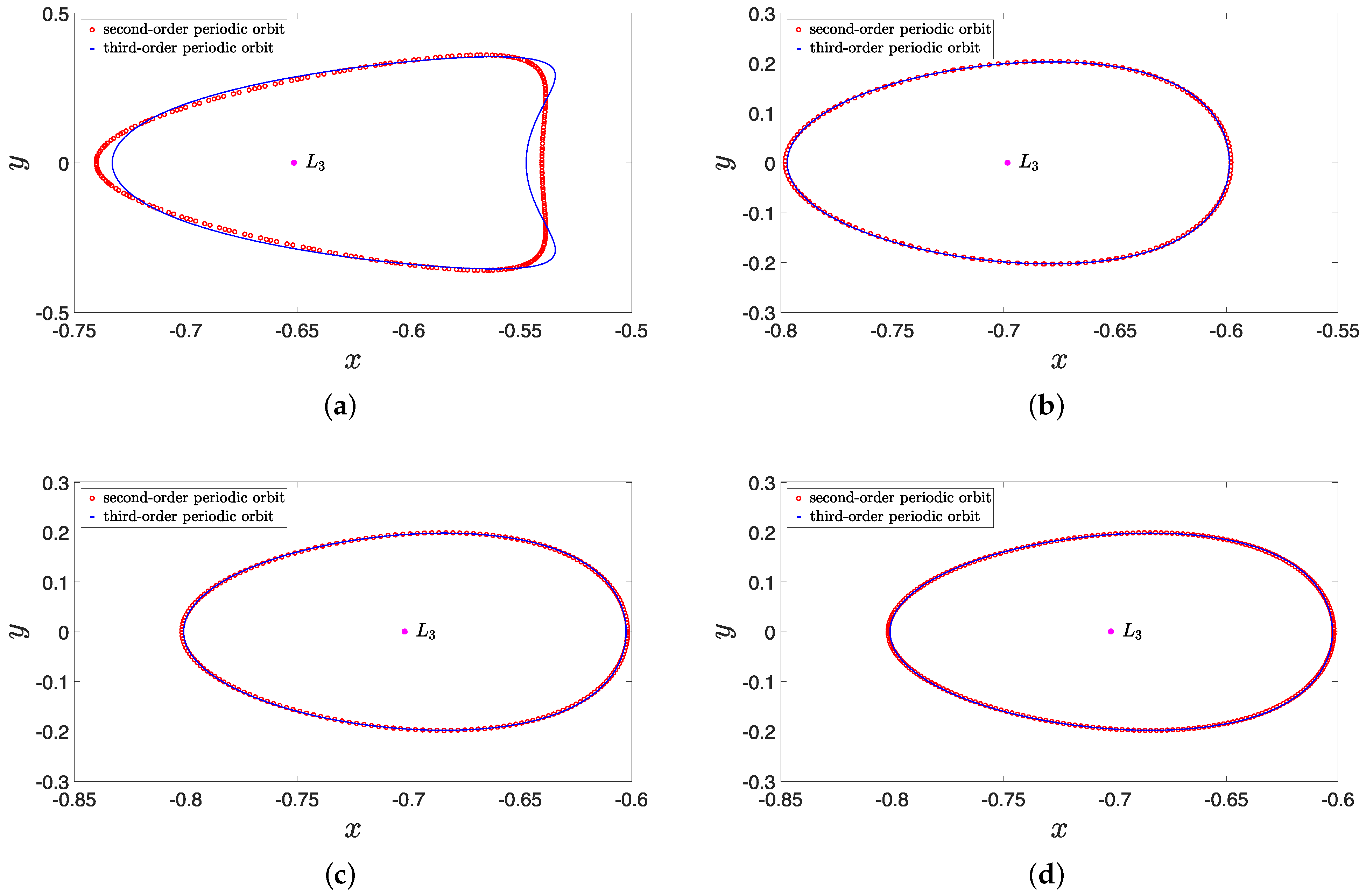
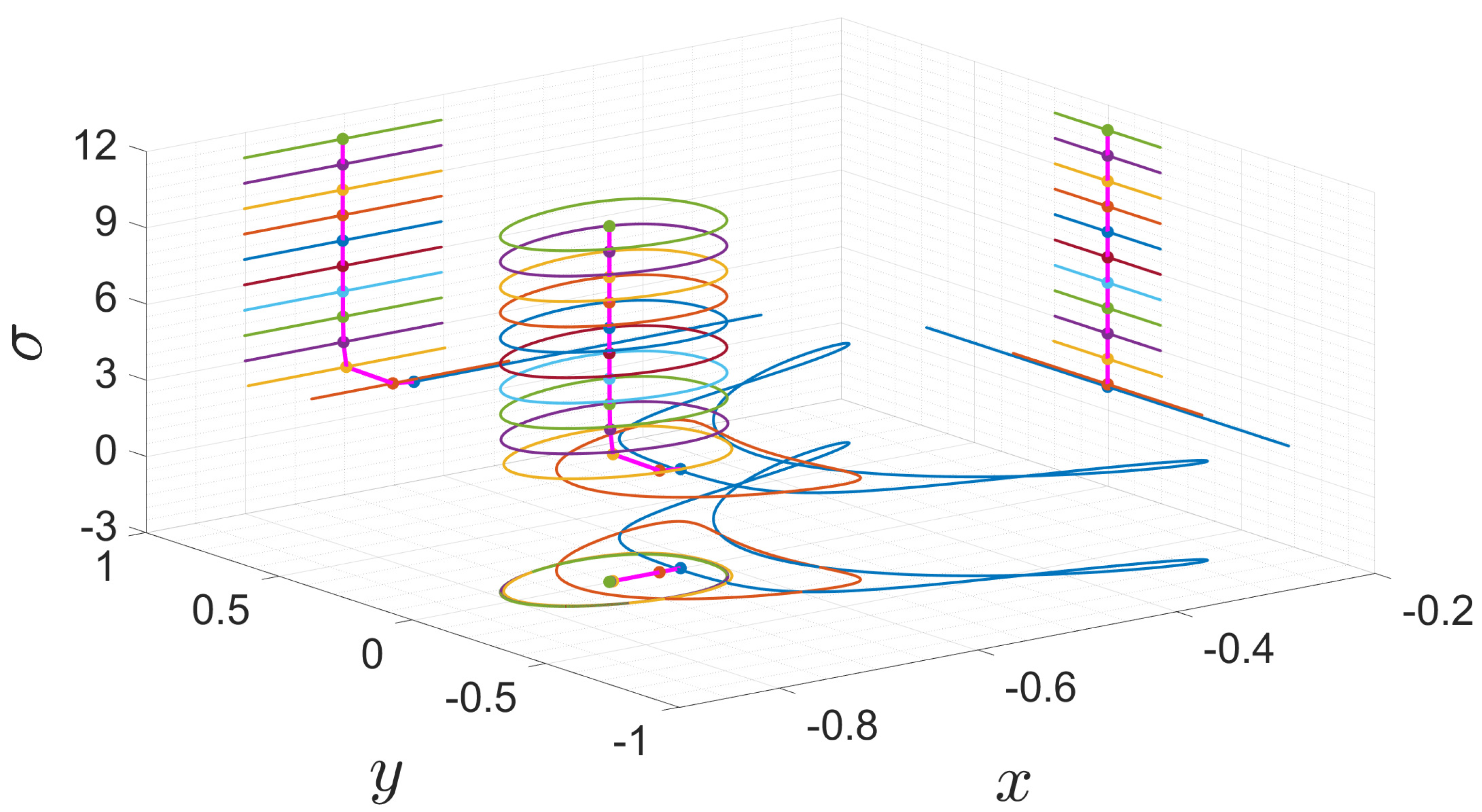
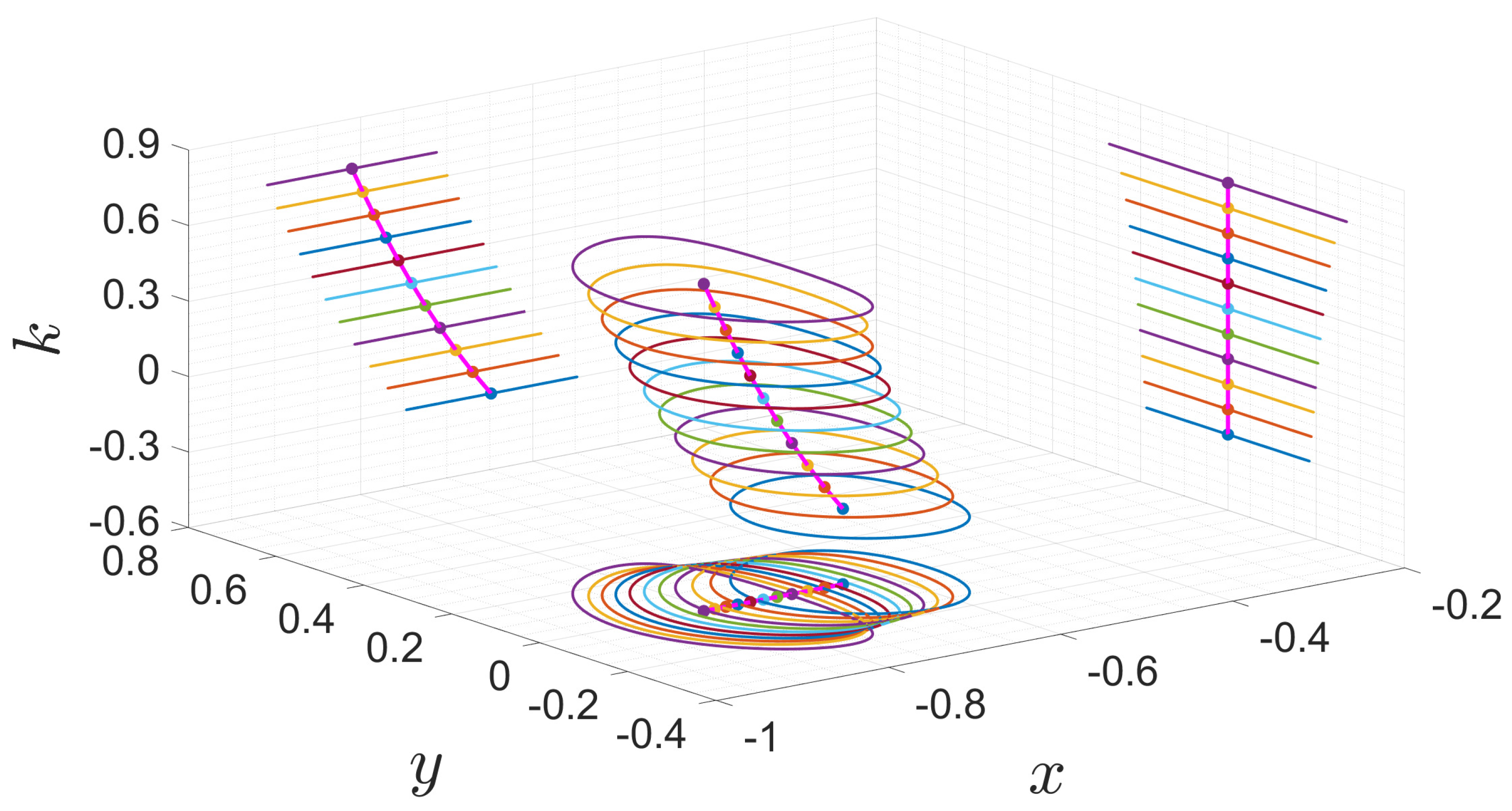
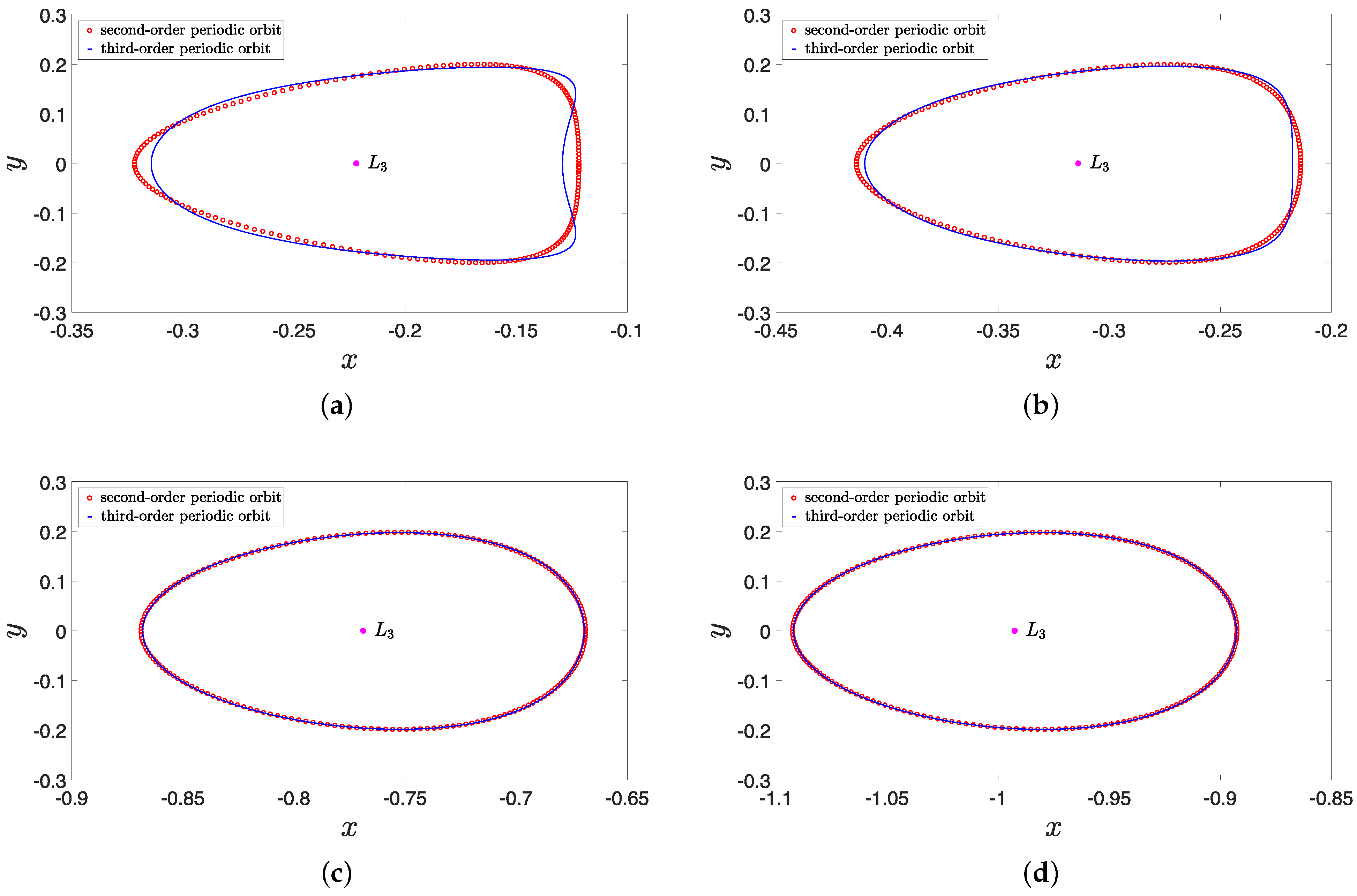
4. Numerical Simulation
4.1. Influence of the Scale Parameter
4.2. Influence of the Three-Body Interaction Parameter k
4.3. Influence of the Variable-Mass Parameter
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sheppard, S.S. New Saturn Moons. Available online: https://sites.google.com/carnegiescience.edu/sheppard/home/newsaturnmoons2019 (accessed on 8 October 2021).
- Sheppard, S.S. Saturn Moons. Available online: https://sites.google.com/carnegiescience.edu/sheppard/moons/saturnmoons (accessed on 8 October 2021).
- Dones, L.; Chapman, C.R.; McKinnon, W.B.; Melosh, H.J.; Kirchoff, M.R.; Neukum, G.; Zahnle, K.J. Icy satellites of Saturn: Impact cratering and age determination. In Saturn from Cassini-Huygens; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Hirata, N. Differential impact cratering of Saturn’s satellites by heliocentric impactors. J. Geophys. Res. Planets 2016, 121, 111–117. [Google Scholar] [CrossRef]
- Dorofeeva, V.A. Genesis of volatile components at Saturn’s regular satellites. Origin of Titan’s atmosphere. Geochem. Int. 2016, 54, 7–26. [Google Scholar] [CrossRef]
- Castillo-Rogez, J.; Vernazza, P.; Walsh, K. Geophysical evidence that Saturn’s moon Phoebe originated from a C-type asteroid reservoir. Mon. Not. R. Astron. Soc. 2019, 486, 538–543. [Google Scholar] [CrossRef]
- Gao, F.B.; Zhu, X.H.; Liu, X.; Wang, R.F. Distribution inference for physical and orbital properties of Jupiter’s moons. Adv. Astron. 2018, 2018, 1894850. [Google Scholar] [CrossRef]
- Gao, F.B.; Liu, X. Revisiting the distributions of Jupiter’s irregular moons: I. physical characteristics. Bulg. Astron. J. 2021, 34, 113–135. [Google Scholar]
- Wang, R.F.; Wang, Y.Q.; Gao, F.B. Bifurcation analysis and approximate analytical periodic solution of ER3BP with radiation and albedo effects. Astrophys. Space Sci. 2021, 366, 29. [Google Scholar] [CrossRef]
- Gao, F.B.; Wang, R.F. Bifurcation analysis and periodic solutions of the HD 191408 system with triaxial and radiative perturbations. Universe 2020, 6, 35. [Google Scholar] [CrossRef]
- Gao, F.B.; Wang, Y.Q. Approximate analytical periodic solutions to the restricted three-body problem with perturbation, oblateness, radiation and varying mass. Universe 2020, 6, 110. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Selim, H.H.; Minglibayev, M.Z.; Kushekbay, A.K. A new model emerged from the three-body problem within frame of variable mass. Astron. Rep. 2021, 65, 1170–1178. [Google Scholar] [CrossRef]
- Suraj, M.S.; Aggarwal, R.; Asique, M.C.; Mittal, A. On the modified circular restricted three-body problem with variable mass. New Astron. 2021, 84, 101510. [Google Scholar] [CrossRef]
- Letelier, P.S.; da Silva, T.A. Solutions to the restricted three-body problem with variable mass. Astrophys. Space Sci. 2011, 332, 325–329. [Google Scholar] [CrossRef]
- Zhang, M.J.; Zhao, C.Y.; Xiong, Y.Q. On the triangular libration points in photogravitational restricted three-body problem with variable mass. Astrophys. Space Sci. 2012, 337, 107–113. [Google Scholar] [CrossRef]
- Shrivastava, A.K.; Ishwar, B. Equations of motion of the restricted problem of three bodies with variable mass. Celest. Mech. 1983, 30, 323–328. [Google Scholar] [CrossRef]
- Ansari, A.A.; Alhussain, Z.A.; Prasad, S.N. Circular restricted three-body problem when both the primaries are heterogeneous spheroid of three layers and infinitesimal body varies its mass. J. Astrophys. Astron. 2018, 39, 1–20. [Google Scholar] [CrossRef]
- Singh, J. Nonlinear stability of equilibrium points in the restricted three-body problem with variable mass. Astrophys. Space Sci. 2008, 314, 281–289. [Google Scholar] [CrossRef]
- Singh, J.; Richard, T.K. A study on the positions and velocity sensitivities in the restricted three-body problem with radiating and oblate primaries. New Astron. 2022, 91, 101704. [Google Scholar] [CrossRef]
- Yang, H.; Bai, X.; Li, S. Artificial equilibrium points near irregular-shaped asteroids with continuous thrust. J. Guid. Control Dyn. 2018, 41, 1308–1319. [Google Scholar] [CrossRef]
- Ershkov, S.; Leshchenko, D.; Abouelmagd, E.I. About influence of differential rotation in convection zone of gaseous or fluid giant planet (Uranus) onto the parameters of orbits of satellites. Eur. Phys. J. Plus 2021, 136, 1–9. [Google Scholar] [CrossRef]
- Zotos, E.E.; Chen, W.; Abouelmagd, E.I.; Han, H. Basins of convergence of equilibrium points in the restricted three-body problem with modified gravitational potential. Chaos Solitons Fractals 2020, 134, 109704. [Google Scholar] [CrossRef]
- Bosanac, N.; Howell, K.C.; Fischbach, E. A natural autonomous force added in the restricted problem and explored via stability analysis and discrete variational mechanics. Astrophys. Space Sci. 2016, 361, 49. [Google Scholar] [CrossRef]
- Suraj, M.S.; Aggarwal, R.; Asique, M.C.; Mittal, A.; Jain, M.; Paliwal, V.K. Effect of three-body interaction on the topology of basins of convergence linked to the libration points in the R3BP. Planet. Space Sci. 2021, 205, 105281. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Guirao, J.L.G. On the perturbed restricted three-body problem. Appl. Math. Nonlinear Sci. 2016, 1, 123–144. [Google Scholar] [CrossRef]
- Poddar, A.K.; Sharma, D. Periodic orbits in the restricted problem of three bodies in a three-dimensional coordinate system when the smaller primary is a triaxial rigid body. Appl. Math. Nonlinear Sci. 2021, 6, 429–438. [Google Scholar] [CrossRef]
- Abouelmagd, E.I.; Alzahrani, F.; Guirao, J.L.G.; Hobiny, A. Periodic orbits around the collinear libration points. J. Nonlinear Sci. Appl. 2016, 9, 1716–1727. [Google Scholar] [CrossRef]
- Qian, Y.J.; Zhai, G.Q.; Zhang, W. Planar periodic orbit construction around the triangular libration points based on polynomial constraints. Chin. J. Theor. Appl. Mech. 2017, 49, 154. (In Chinese) [Google Scholar]
- Šuvakov, M.; Dmitrašinović, V. Three classes of Newtonian three-body planar periodic orbits. Phys. Rev. Lett. 2013, 110, 114301. [Google Scholar] [CrossRef] [PubMed]
- Li, X.M.; Liao, S.J. On the stability of the three classes of Newtonian three-body planar periodic orbits. Sci. China Phys. Mech. Astron. 2014, 57, 2121–2126. [Google Scholar] [CrossRef][Green Version]
- Li, X.M.; Jing, Y.P.; Liao, S.J. Over a thousand new periodic orbits of a planar three-body system with unequal masses. Publ. Astron. Soc. Jpn. 2018, 70, 64. [Google Scholar] [CrossRef]
- Pathak, N.; Elshaboury, S.M. On the triangular points within frame of the restricted three–body problem when both primaries are triaxial rigid bodies. Appl. Math. Nonlinear Sci. 2017, 2, 495–508. [Google Scholar] [CrossRef]
- Yang, H.; Yan, J.; Li, S. Fast computation of the Jovian-moon three-body flyby map based on artificial neural networks. Acta Astronaut. 2021. [Google Scholar] [CrossRef]
- Hu, H.Y. Applied Nonlinear Dynamics; China Aeronautical Industry Press: Beijing, China, 2000. (In Chinese) [Google Scholar]
- Zheng, X.T.; Tu, L.Z. Photogravitationally restricted three-body problem and coplanar libration point. Chin. Phys. Lett. 1993, 10, 61. [Google Scholar] [CrossRef]



| Names of Saturn’s Regular Moons | Mass (kg) | Names of Saturn’s Regular Moons | Mass (kg) |
|---|---|---|---|
| Aegaeon | 59,946,737,324 | Methone | 8,992,010,598,583 |
| Anthe | 1,498,668,433,097 | Mimas | 37,505,676,206,690,400,000 |
| Atlas | 6,594,141,105,627,650 | Pallene | 32,970,705,528,138 |
| Calypso | 2,547,736,336,265,230 | Pan | 4,945,605,829,220,740 |
| Daphnis | 77,930,758,521,054 | Pandora | 138,476,963,218,181,000 |
| Dione | 1,095,745,430,185,280,000,000 | Polydeuces | 4,496,005,299,292 |
| Enceladus | 107,944,591,230,692,000,000 | Prometheus | 160,956,989,714,639,000 |
| Epimetheus | 526,032,620,017,115,000 | Rhea | 2,307,089,151,289,080,000,000 |
| Helene | 11,389,880,091,538,700 | S/2009 S1 | —— |
| Hyperion | 5,585,537,250,153,240,000 | Telesto | 4,046,404,769,362,420 |
| Iapetus | 1,805,952,411,282,580,000,000 | Tethys | 617,551,805,221,061,000,000 |
| Janus | 1,892,818,231,001,750,000 | Titan | 134,552,523,083,241,000,000,000 |
| Beta | Birnbaum– Saunders | Burr | Exponential | Extreme Value | Gamma | Generalized Extreme Value | Generalized Pareto | Half Normal | Inverse Gaussian | Logistic | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mass () | h | null | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| p | 0.0345 | 0.8643 | 0.0000 | 0.0000 | 0.3145 | 0.0000 | 0.1723 | 0.0000 | 0.0000 | 0.0000 | ||
| parameter | = 8.9038 × = 370.466 | = 3.76388 × c = 0.170255 k = 2.83657 | = 6.11012 × | = 2.40706 × = 4.92323 × | a = 0.0760157 b = 8.03796 × | k = 0.569397 = 1.32889 × = 7.07519 × | k = 11.3686 = 1.55618 × = 0 | = 0 = 2.8064 × | = 6.11012 × = 1.29748 × | = 6.11012 × = 1.54407 × | ||
| confidence interval | ∈ [3.5716 × , 1.4236 × ] ∈ [263.409, 477.524] | ∈ [664.59, 2.13166 × ] c ∈ [0.0739575, 0.39194] k ∈ [0.0204874, 392.734] | ∈ [4.21915 × , 9.63871 × ] | ∈ [2.54927 × , 4.5592 × ] ∈ [3.85631 × , 6.28534 × ] | a∈ [0.049786, 0.116065] b ∈ [1.72057 × , 3.75508 × ] | k∈ [0.494556, 0.644238] ∈ [7.47124 × , 2.36367 × ] ∈ [1.14168 × , 1.30087 × ] | k∈ [6.12161, 16.6156] ∈ [1.31349 × , 1.84372 × ] = 0 | = 0 ∈ [2.18117 × , 3.93671 × ] | ∈ [−Inf,Inf] ∈ [−Inf,Inf] | ∈ [−Inf,Inf] ∈ [−Inf,Inf] | ||
| Log-logistic | Lognormal | Nakagami | Negative Binomial | Normal | Poisson | Rayleigh | Rician | t Location- Scale | Weibull | Stable | ||
| Mass() | h | 0 | 0 | 0 | null | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| p | 0.9759 | 0.9889 | 0.2574 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.7818 | 0.0000 | ||
| parameter | = 39.1312 = 4.58867 | = 39.1272 = 7.82406 | = 0.0357998 = 7.8759 × | = 6.11012 × = 2.80064 × | = 6.11012 × | B = 1.98443 × | s = 1 = 2.71315 × | = −1.54662 × = 1.81001 × = 0.177628 | A = 4.42076 × B = 0.142598 | = 0.4 = 0.987279 c = 3.62044 × = 2.24553 × | ||
| confidence interval | ∈ [35.7976, 42.4648] ∈ [3.29169, 6.39669 | ∈ [35.7438, 42.5106] ∈ [6.05109, 11.0738] | ∈ [0.0236219, 0.0542557] ∈ [9.08296 × , 6.82924 × ] | ∈ [−6.00076 × , 1.8221 × ] ∈ [2.166 × , 3.96389 × ] | ∈ [6.11012 × , 6.11012 × ] | B∈ [1.64901 × , 2.49241 × ] | s = 1 ∈ [2.71315 × , 2.71315 × ] | ∈ [−Inf,Inf] ∈ [−Inf,Inf] ∈ [−Inf,Inf] | A∈ [2.12356 × , 9.20299 × ] B ∈ [0.104361, 0.194845] | ∈ [0,2] ∈ [−1,1] c ∈ [0,Inf] ∈ [−Inf,Inf] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, H.; Gao, F. Periodic Orbits of the Restricted Three-Body Problem Based on the Mass Distribution of Saturn’s Regular Moons. Universe 2022, 8, 63. https://doi.org/10.3390/universe8020063
Cheng H, Gao F. Periodic Orbits of the Restricted Three-Body Problem Based on the Mass Distribution of Saturn’s Regular Moons. Universe. 2022; 8(2):63. https://doi.org/10.3390/universe8020063
Chicago/Turabian StyleCheng, Huan, and Fabao Gao. 2022. "Periodic Orbits of the Restricted Three-Body Problem Based on the Mass Distribution of Saturn’s Regular Moons" Universe 8, no. 2: 63. https://doi.org/10.3390/universe8020063
APA StyleCheng, H., & Gao, F. (2022). Periodic Orbits of the Restricted Three-Body Problem Based on the Mass Distribution of Saturn’s Regular Moons. Universe, 8(2), 63. https://doi.org/10.3390/universe8020063






