Abstract
In this paper, we have explored non-gravitational interaction dark energy model between dark energy and cold dark matter (CDM). The main purpose of this work is to explore the deviations from and to distinguish the evolution trajectory of the interaction dark energy model with different parameters. Six forms of interaction were focused on. We have analyzed the deceleration parameters of the coupled model and explored the theoretical models through and the diagnostic. We have considered that the Equation of State (EoS) parameter w and parameter take different values on the interaction dark energy model respectively and keep another parameter unchanged. It was found that is the worst of the four diagnoses. , and are good tools to distinguish the interaction dark energy model from . is a better diagnostic tool when the state parameter w changes and the coupling parameter is fixed, while works better when the coupling parameter changes and the state parameter w is fixed.
1. Introduction
Cosmology is one of the most active research areas. It is well known that modern cosmology was established and developed with the birth of general relativity [1,2]. Therefore, general relativity plays a very important role in the study of gravity and cosmology, and so far can be verified by many experiments without adding special case assumptions. Even so, there is evidence that the theory is incomplete—the search for quantum gravity and the reality of space-time singularities remain to be solved; the results of experimental observations supporting the existence of dark matter and dark energy imply a desire for new physics. However, general relativity is still full of possibilities that deserve deep exploration—mathematical relativists are seeking to understand the nature of singularities and the basic properties of the Einstein field equation; and, after the first direct observation of gravitational waves in 2016, subsequent contests and development applications are continuing, human beings hope to be able to create more opportunities to test the theory’s validity in a field of gravity that is much stronger than it has ever been. So today, a hundred years after Einstein published his theory, general relativity is still a highly active research field.
After the establishment of modern cosmology with the advent of general relativity, scientists became interested in the causes of the universe’s accelerating expansion. In recent years, astronomical observations have shown that our universe is undergoing accelerated expansion [3,4,5,6,7]. Many people are trying to find a perfect explanation for the accelerating expansion of the universe. The most likely explanation is that the universe is currently being dominated by an exotic component with negative pressure, named dark energy (DE). According to Planck 2015 observational results [8], the universe is spatially flat, and it consists of about 68.4 percent dark energy, 26.7 percent dark matter, 4.9 percent baryon matter.
As scientists study the accelerating expansion of the universe, various theoretical models have been proposed. Among them, the cosmological constant model ( model) is the simplest and most idealized of the many models that explain today’s accelerating expansion of the universe [9,10,11,12,13,14], its state parameter is . This cosmological constant was originally introduced by Einstein into a static cosmological model. From 1915 to 1917, Einstein explained our universe with the general relativity gravitational field equation, trying to build a new cosmological model. At that time, the scientific community still thought that the universe was still and did not change with time, so Einstein added the cosmological constant to get a stable solution. The function of this constant in Einstein’s equation was repulsion, so one possibility of dark energy was the cosmological constant. Einstein gave up the constant and thought it was a mistake after Hubble discovered that the universe accelerated expansion in 1929. However, the cosmological constant was reintroduced in 1998 after the discovery of the accelerating expansion of the universe by the observed type 1a supernova. One finds that the cosmological constant model ( model)is just enough to explain that the expansion of the universe is due to repulsion of a component. This model is very consistent with astronomical observations, there are still some problems with the model, such as fine-tuning and cosmic coincidence.
To alleviate these problems, people have proposed dynamic dark energy model one after another: quintessence [15,16], phantom [17], quintom [18,19], holographic dark energy model [20,21,22,23,24], Chaplygin gas (CG) model [25,26,27], Dirac-Born-Infeld (DBI) dark energy [28,29], and so forth.
In this paper, we have studied the non-gravitational interaction dark energy model between dark energy and cold dark matter in which the equation of state (EoS) parameter w is a constant, this kind of interacting dark energy model have been widely studied [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55], and in this paper the coupled dark energy model is called model. It can also explain the accelerated expansion of the large scale universe [56,57,58,59,60,61,62,63,64,65]. Meanwhile, the existence of non-gravitational interaction not only lead to an alleviation of the coincidence problem, but also make theoretical models work better. Compared to or its extended model , the the interacting dark energy model make dark energy and dark matter with energy exchange from the background evolution, in this way in the early time of expanding universe, the less dark energy will implicitly affect the evolution of dark matter, it will slightly influence the matter structure growth, meanwhile in the late time of expanding universe, the dark matter will exchange the energy with dark energy, the interaction will affect the universe acceleration. In this paper, we will focus on the background evolution of interacting dark energy model. In addition, we also have explored the deviation of the interaction dark energy model from and the behavior of evolution trajectory when the interaction dark energy model takes different parameter values through the [56,66,67,68,69,70,71,72,73,74] and [75,76,77] diagnostic. The is a sensitive diagnostic of DE, which uses the higher-order derivatives of and can break the degeneracy of the model very well. However, the advantage of the diagnostic is its less dependency on the matter density. That means the diagnostic is much easier than the .
In the spatially homogeneous and isotropic Friedmann-Robertson-Walker () universe filled with DE (de), CDM (c), baryons (b), and radiation (r). The continuity equation for each component can be written as follows:
where the dot denotes a derivative with respect to time t, is the Hubble parameter, is the energy density of each component, for , and r respectively, and Q is the energy transfer rate between DE and CDM. In this paper, six interacting forms were considered: , , , , , , where is the dimensionless coupling parameter. For these six interaction terms, there are some relations, such as and , and , and , here we show the evolutional trajectories of dimensionless density parameter in Figure 1.
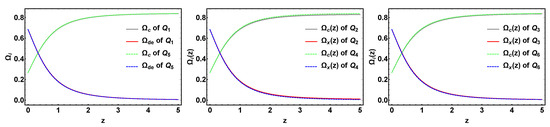
Figure 1.
The evolution trajectories of versus red shift z of interacting dark energy models, to compare and , and , and , here we fixed and , the other related parameters was fixed as the results of Planck 2015, , , , .
The paper is organized as follows. In Section 2, two diagnostic methods were briefly introduced—the and the diagnostic. In Section 3, we have explored the evolutionary behavior of the interacting dark energy model through the diagnostic tools—the deceleration parameter q, the , the diagnostic, and compared them [9,10,72,78]. Section 4 is the summary of this paper.
2. Statefinder Hierarchy and Om Diagnostic
Since many dark energy models are pretty good explanations for the accelerating expansion of the universe, in order to distinguish between them, we need to use some distinguishing tools. So various tools have been developed to distinguish dark energy models. In this section, we adopted the diagnostic and diagnostic.
2.1. The Statefinder Hierarchy
The scale factor of the Universe can be Taylor expanded around the present epoch as follows [66]
where , , is the nth derivative of the scale factor with respect to time, and is the deceleration parameter. For ,
where , is transformed to , , which can be defined as [66]:
obviously, of the model is a fixed value during the cosmic expansion, . However, the value of other DE models is not fixed, so we can easily distinguish the model from other DE models through this diagnostic method. Now, we consider a spatially FRW universe containing DE, CDM, baryons, and radiation, is no longer a fixed value, but changes slowly over time during the expansion of the universe. However, can also be regarded as a reference model.
In this paper, we have discussed the interaction DE model, so and can be represented as follows [56]:
where the prime denotes the derivative with respect to and . Equations (13) and (14) can be applied to all the interaction DE models. When we take different forms of interaction, the corresponding physical quantities can be substituted into the above formulas respectively, also the corresponding value can be obtained.
2.2. The Diagnostic
In this section, another commonly used method to distinguish dark energy models will be introduced, namely diagnosis. The diagnostic is based on Hubble parameters, it can provide a null diagnostic of the concordance cosmology () and distinguish between models without reference to the density of matter. The diagnostic can be defined as [75]:
where and . is the Hubble parameter and is the value of the Hubble parameter at . For , we have found that .
3. Exploration of Interacting Dark Energy with Statefinder Hierarchy and Om Diagnostic
In this section, we shall discuss the deviations from and distinguish the evolution trajectory of the interaction dark energy model with different parameters by using the diagnostics of and the diagnostic. Here, we only consider the influence of EoS parameter w and coupling parameter . In addition, for all models, the present-day fractional density parameters of DE, Cold Dark Matter (CDM), baryons, and radiation are fixed to be, according to Planck 2015 observational results [8], , , , . Firstly, we shall consider the influence of the EoS parameter w on model and keep the coupling parameter unchanged. Then, we will discuss the influence of the coupling parameter on model, and the EoS parameter w will be kept unchanged.
3.1. Consider the Change of w and Keep the Parameter Constant
In this subsection we only consider the EoS parameter w to take different values on the interaction dark energy model, and keep the parameter unchanged. Here we have chosen , and let the parameters of w be equal to −0.9, −1.1, and −1.2, respectively.
First, the models with (denoted as ) has been diagnosed according to the deceleration parameter q, the parameter , and the diagnostic respectively. We have plotted the function , , q and versus red shift z for the IwCDM1 model in Figure 2. Here we have chosen = 0.02, w = −0.9, −1.1 and −1.2.
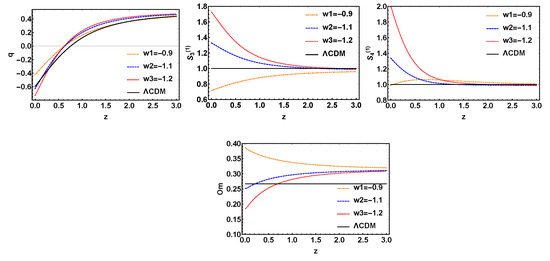
Figure 2.
The evolution trajectories of q, , and , respectively, versus red shift z for the model with variable w and fixed . The evolution curve of is also shown in these sets of figures.
In Figure 2, we have seen that for , the change of parameter w has little effect on the transition red shift, and in the high red shift region, there is a high degree of degeneracy between the evolution trajectories of the model with different parameter values and even including . However, in the low red shift region the degeneracy is destroyed to some extent. But these evolutionary trajectories, including , are very close to each other. Therefore, it can be concluded that the deceleration parameter q does not distinguish the model very well. And from the image of the deceleration parameters, we can see that the evolution of the universe is from deceleration expansion to accelerated expansion. For , the degeneracy is perfectly broken in the low red shift region, and because the parameters w are different, the curve shows the trend of symmetry. In the high red shift region, the curve of the model is somewhat degeneracy. But it doesn’t matter, because the observations are mainly concentrated in the low red shift range (). Also, it is easy to separate from . For , we have seen that in the high red shift region, the evolution trajectory of different parameters is highly degenerate, and it’s hard to distinguish between and . In the low red shift region, the evolution curves of different parameters w are hugely separate from each other, yet there is a bit of degeneracy between the lines of w = −0.9 and . We still think is a good tool to distinguish between from , but works better. For , interestingly, the evolution trend of the model is similar to that in the , the three curves in the low red-shift region are all separated from each other and can be well distinguished from the , except that the distance between them is obviously not far from the . Overall, the evolution trajectories corresponding to different parameters are separated further in the , and can better distinguish from , in the low red shift region. From this point of view, the diagnostic effect of is the best.
In Figure 3, we have been discussed the model with interaction (denoted as ), as well as made a comparison with the model and explored degeneracy between the evolution trajectories of the model with different parameter values. We have seen that the four diagnostic curves of model are similar to those of , and , , also can distinguish between and . Similarly among them, performs better.
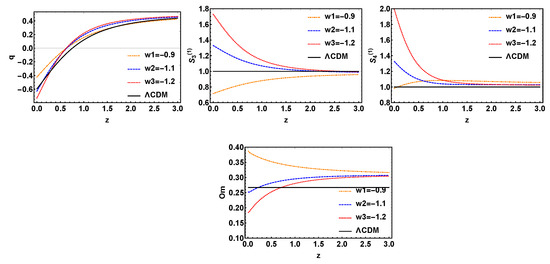
Figure 3.
The evolution trajectories of q, , and , respectively, versus red shift z for the model with variable w and fixed . The evolution curve of is also shown in these sets of figures.
In Figure 4, the evolutionary trajectories are similar to those of the first two models, and will not be elaborated on here. From the images of the above three interaction models, it can be concluded that has a better effect on distinguishing the curves with different parameters of the model itself, and is also better in distinguishing and .
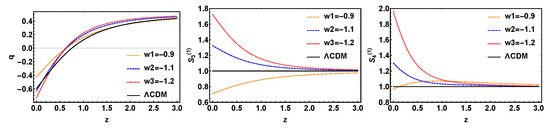
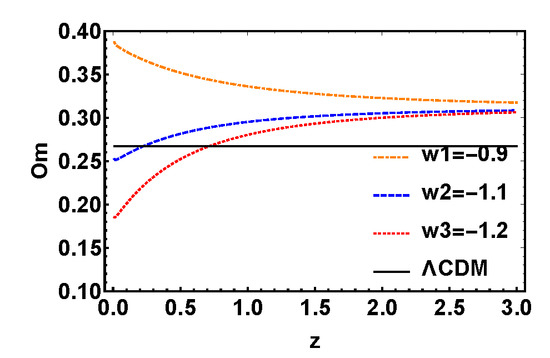
Figure 4.
The evolution trajectories of q, , and , respectively, versus red shift z for the model with variable w and fixed . The evolution curve of is also shown in these sets of figures.
Next, we will discuss the three models with interaction terms , and , which are called , , . The interactions of these three models are actually multiplied by on the basis of , and , other rules are similar to the first three models. We have draw a conclusion from Figure 5, Figure 6 and Figure 7, , and diagnostic methods all can distinguish different model well in the low red shift region. For , the curve has a large degeneracy in the low red shift region. In the same light, is the best of the four diagnostic tools. From the above discussion, we has been found that is the worst of the four diagnoses, with the change of state parameters, the evolution trajectory in q is not greatly affected. , and are all good diagnostic tools to distinguish different dark energy models. By comparison, is the best tool for diagnostic results for these interactive dark energy models.
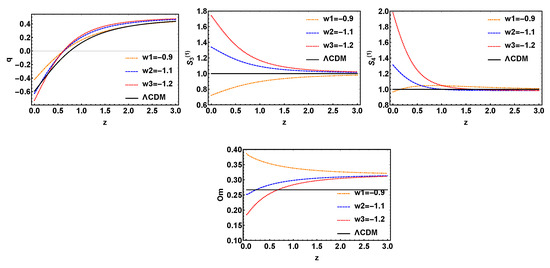
Figure 5.
The evolution trajectories of q, , and , respectively, versus red shift z for the model with variable w and fixed . The evolution curve of is also shown in these sets of figures.
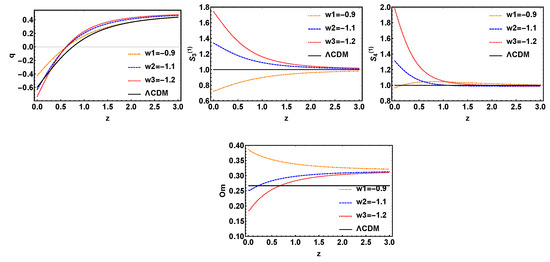
Figure 6.
The evolution trajectories of q, , and , respectively, versus red shift z for the model with variable w and fixed . The evolution curve of is also shown in these sets of figures.
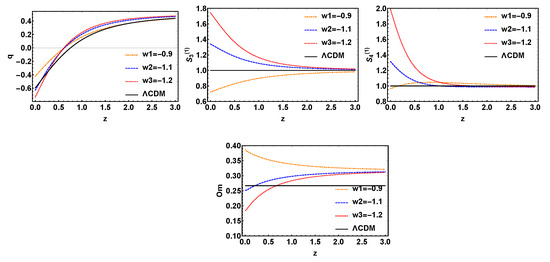
Figure 7.
The evolution trajectories of q, , and , respectively, versus red shift z for the model with variable w and fixed . The evolution curve of is also shown in these sets of figures.
3.2. Consider the Change of and Keep the Parameter w Constant
In this subsection, it is only considered that the parameter to take different values on the interaction dark energy model, and keeps the EoS parameter w unchanged.
First of all, we have plotted four diagnostic images of q, , and for the model in Figure 8. It can be seen that the evolution trajectories in q are not affected by the change of the coupling parameter . For , the evolution trajectories are highly coincident in the high red shift region, and in the low red shift region, although the curves are separated from each other, there is still a high degeneracy. However, diagnosis can distinguish from model well in the low red shift region. For , the evolution is also highly degenerate in the high red shift region, but in the low red shift zone, this degeneracy is destroyed well. In the same way, diagnosis can similarly distinguish from model well in the low red shift region. On the contrary, For the , the evolution trajectories is highly coincident in the low red shift region, but separated from each other in the high red shift region. In addition, the observations are mainly concentrated in the low red shift range (), so we usually only consider the situation in the low red shift region. In other word, that diagnostic effect of is not good at low red shift region. To sum up, , and can all be used to distinguish from model in the low red shift region. However, only can distinguish the different evolutionary curves of the model with different coupling parameter well.
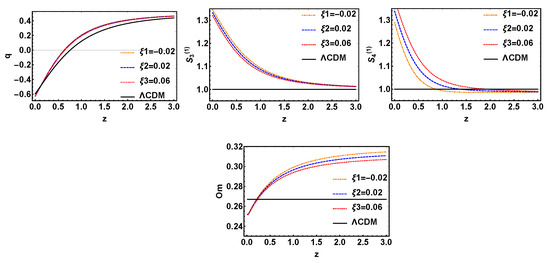
Figure 8.
The evolution trajectories of q, , and , respectively, versus red shift z for the model with variable and fixed , where is taken separately −0.02, 0.02, 0.06. The evolution curve of is also shown in these sets of figures.
Then, the model should be discussed now. For Figure 9, it can be found that the evolution curves of q are less affected when the parameter is changed, also it can not be distinguished from . And the evolution curves of , and for model have some degeneracy in the low red shift region. But in the high red shift region, they are more separated from each other. However, this is not helpful because of the observations are mainly concentrated in the low red shift range. By comparing these three kinds of diagnosis, we have seen that variable have a greater effect on the evolution curves of . In other words, the diagnostic effect of on the model is better.
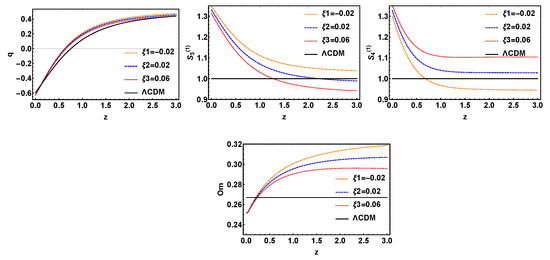
Figure 9.
The evolution trajectories of q, , and , respectively, versus red shift z for the model with variable and fixed , where is taken separately −0.02, 0.02, 0.06. The evolution curve of is also shown in these sets of figures.
Next we discuss the model. In Figure 10, it can be seen that the evolution curves of q coincide with each other, and the evolution curves of and have high degeneracy in the low red shift. Interestingly, the evolutionary trajectory in is completely coincident within , but when the red shift , the degeneracy of the curves in is broken well, the evolution curves also can be distinguished easily from each other. In general, has better diagnostic behavior.
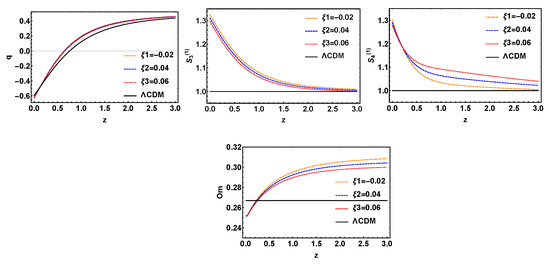
Figure 10.
The evolution trajectories of q, , and , respectively, versus red shift z for the model with variable and fixed , where is taken separately 0.02, 0.04, 0.06. The evolution curve of is also shown in these sets of figures.
Then, the three models with interaction terms , and will be discussed, which are called , , . From Figure 11, Figure 12 and Figure 13, we can see that the evolutionary trajectory of this three models are almost unaffected by the change of parameter . So for , and , they can only distinguish from the model, but cannot distinguish the evolution curves of variable .
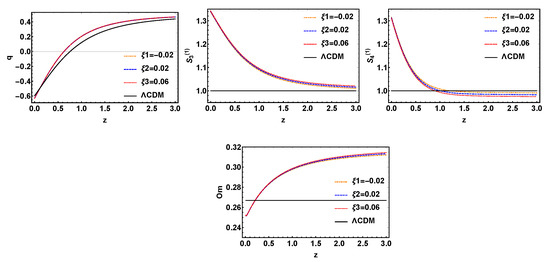
Figure 11.
The evolution trajectories of q, , and , respectively, versus red shift z for the model with variable and fixed , where is taken separately −0.02, 0.02, 0.06. The evolution curve of is also shown in these sets of figures.
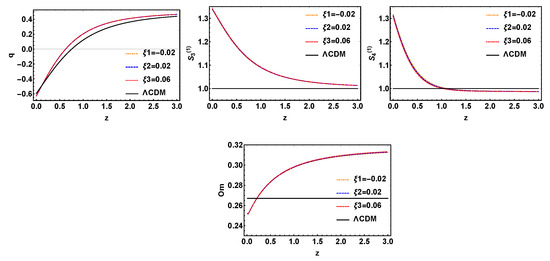
Figure 12.
The evolution trajectories of q, , and , respectively, versus red shift z for the model with variable and fixed , where is taken separately −0.02, 0.02, 0.06. The evolution curve of is also shown in these sets of figures.
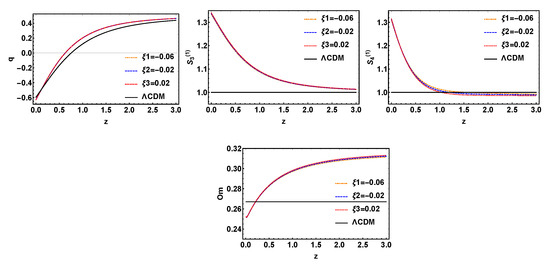
Figure 13.
The evolution trajectories of q, , and , respectively, versus red shift z for the model with variable and fixed , where is taken separately −0.02, 0.02, −0.06. The evolution curve of is also shown in these sets of figures.
In summary, the influence of the state parameter w on the model is much greater than that of the coupling parameter on the model. is a better diagnostic tool when the state parameter w changes and the coupling parameter is fixed, while works better when the coupling parameter changes and the state parameter w is unchanged.
4. Conclusions
In this paper, we have studied the interaction of dark energy models with deceleration parameter q, and the diagnostic. We hope to explore the deviations from and to distinguish the evolution trajectory of the interaction dark energy model with different parameters. First, we only take the EoS parameter w with different values on the interaction dark energy model, and kept the coupling parameter constant. We have found that for , the evolution trajectories of different parameters in the high red shift region, is highly degenerate. In the low red shift region, the degeneracy is destroyed to some extent. From q, we have seen that the universe is indeed a process from decelerated expansion to accelerated expansion, and no matter how the state parameter w changes, it will not affect the transition red shift. In addition, , and are good diagnostic methods to distinguish from the model, and to separate the evolution curves of variable parameter w especially in the low red shift region. We just need to consider the low red shift region because of the observational data are mainly within it. Through the above research, we have found that the evolution curve of the model with different values of state parameter w is more separated in . That is to say, is a better tool for diagnostic models. Next, we have only considered the impact of the coupling parameter to the interaction dark energy model, and kept w unchanged. It can be seen that the law of q is similar to that of the previous one. Compared with , and , the evolution curves in are more separated from each other. So the diagnosis of is better. It should be noted that the change of state parameter w has a greater influence on the model than the coupling parameter .
As a consequence of all that studied above, we have found that the higher-order statefinder does not diagnose the model as well. We need to make a specific analysis of the specific model.
Since we still know little about the microscopic nature of dark energy and dark matter, it is difficult to calculate a very clear interaction term from a theoretical point of view. Therefore, we can only construct some reasonable interaction terms by phenomenological description, and then make further analysis on this basis. Nowadays, the most widely studied interaction phenomenological model is divided into three main categories, namely, assuming that Q is proportional to dark energy density, Q to dark matter density and Q to the density sum of dark energy and dark matter. The novelty of this paper is that in the construction of the interaction term, we also assume that the Q is proportional to the , proportional to the , and so on. The study of interaction models is more advantageous than , and the introduction of interaction between dark matter and dark energy can help us to alleviate or solve some theoretical problems in cosmology, such as the problem of cosmic coincidence, the problem of cosmic “great tear” caused by ghost dark energy, and the problem of cosmic age caused by ancient quasars.
Author Contributions
Y.J.: search the references, plot the figures, write the manuscript; Z.H.: plot the figures, design the research plan, data analysis; Q.Z.: data collection, data analysis, edit the manuscript; W.Y.: design the research plan, numerical simulation, revise the manuscript; Y.W.: corresponding author, review the manuscript; revise the manuscript; J.L.: explain the data, data analysis, numerical simulation; H.L.: plot the figures, search the references, edit the manuscript; C.Z.: search the references, arrange the references, design the research plan; Y.W.: explain the data, data analysis, revise the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
NSFC No. 11575075, 11705079, 11647153.
Acknowledgments
Y. Wu has been supported by the National Natural Science Foundation of China under Grant No. 11575075. W. Yang has been supported by the National Natural Science Foundation of China under Grants No. 11705079 and No. 11647153.
Conflicts of Interest
There is no conflict of interest.
References
- Iorio, L. Editorial for the Special Issue 100 Years of Chronogeometrodynamics: The Status of the Einstein’s Theory of Gravitation in Its Centennial Year. Universe 2015, 1, 38–81. [Google Scholar] [CrossRef]
- Debono, I.; Smoot, G.F. General Relativity and Cosmology: Unsolved Questions and Future Directions. Universe 2016, 2, 23. [Google Scholar] [CrossRef]
- Riess, A.G. Supernova search team collaboration. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S. Supernova cosmology project collaboration. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Spergel, D.N.; Bean, R.; Dore, O.; Nolta, M.R.; Bennett, C.L.; Dunkley, J.; Hinshaw, G.; Jarosik, N.; Komatsu, E.; Page, L.; et al. WMAP collaboration. Astrophys. J. Suppl. 2007, 170, 377. [Google Scholar] [CrossRef]
- Adelman-McCarthy, J.K.; Agueros, M.A.; Allam, S.S.; Prieto, C.A.; Anderson, K.S.J.; Anderson, S.F.; Annis, J.; Bahcall, N.A.; Bailer-Jones, C.A.L.; Baldry, I.K.; et al. SDSS collaboration. Astrophys. J. Suppl. 2008, 175, 297. [Google Scholar]
- Tegmark, M.; Strauss, M.; Blanton, M.; Abazajian, K.; Dodelson, S.; Sandvik, H.; Wang, X.; Weinberg, D.; Zehavi, I.; Bahcall, N.; et al. Cosmological parameters from SDSS and WMAP. Phys. Rev. D 2004, 69, 103501. [Google Scholar] [CrossRef]
- Ade, P.A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck Collaboration. Planck 2015 results—XIII. Cosmological parameters. A&A 2016, 594, A13. [Google Scholar]
- Singh, C.P.; Kumar, A. Ricci dark energy model with bulk viscosity. Eur. Phys. J. Plus 2018, 133, 312. [Google Scholar] [CrossRef]
- Wang, F.Y.; Dai, Z.G.; Qi, S. Probing the cosmographic parameters to distinguish between dark energy and modified gravity models. Astron. Astrophys. 2009, 507, 53–59. [Google Scholar] [CrossRef]
- Batista, C.E.; Daouda, M.H.; Fabris, J.C.; Piattella, O.F.; Rodrigues, D.C. Rastall Cosmology and the ΛCDM Model. Phys. Rev. D 2012, 85, 084008. [Google Scholar] [CrossRef]
- Cao, S.L.; Duan, X.W.; Meng, X.L.; Zhang, T.J. Cosmological model-independent test of ΛCDM with two-point diagnostic by the observational Hubble parameter data. Eur. Phys. J. C 2018, 78, 313. [Google Scholar] [CrossRef]
- Yang, R.-J.; Zhang, S.-N. The age problem in the ΛCDM model. Mon. Not. R. Astron. Soc. 2010, 407, 1835. [Google Scholar] [CrossRef]
- Popolo, A.D.; Delliou, M.L. Small Scale Problems of the ΛCDM Model: A Short Review. Galaxies 2017, 5, 17. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Vilenkin, A. Quintessential inflation. Phys. Rev. D 1999, 59, 063505. [Google Scholar] [CrossRef]
- Wang, L.; Steinhardt, P.J. Cluster Abundance Constraints on Quintessence Models. Astrophys. J. 1998, 508, 483. [Google Scholar] [CrossRef]
- Caldwell, R.R. A Phantom Menace, Cosmological consequences of a dark energy component with super-negative equation of state. Phys. Lett. B 2002, 545, 23–29. [Google Scholar] [CrossRef]
- Guo, Z.K.; Piao, Y.S.; Zhang, X.; Zhang, Y.Z. Cosmological Evolution of a Quintom Model of Dark Energy. Phys. Lett. B 2005, 608, 177–182. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Liu, H. Reconstructing generalized ghost condensate model with dynamical dark energy parametrizations and observational datasets. Mod. Phys. Lett. A 2008, 23, 139–152. [Google Scholar] [CrossRef]
- Li, M. A Model of Holographic Dark Energy. Phys. Lett. B 2004, 603, 1–5. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, F.-Q. Constraints on holographic dark energy from type Ia supernova observations. Phys. Rev. D 2005, 72, 043524. [Google Scholar] [CrossRef]
- Zhang, X. Statefinder diagnostic for holographic dark energy model. Int. J. Mod. Phys. D 2005, 14, 1597–1606. [Google Scholar] [CrossRef]
- Yu, F.; Zhang, J.-F. Statefinder diagnosis for the extended holographic Ricci dark energy model without and with interaction. Commun. Theor. Phys. 2013, 59, 243. [Google Scholar]
- Cui, J.L.; Zhang, J.F. Comparing holographic dark energy models with statefinder. Eur. Phys. J. C 2014, 74, 2849. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Generalized Chaplygin gas, accelerated expansion, and dark-energy-matter unification. Phys. Rev. D 2002, 66, 043507. [Google Scholar] [CrossRef]
- Bento, M.C.; Bertolami, O.; Sen, A.A. Revival of the unified dark energy—Dark matter model? Phys. Rev. D 2004, 70, 083519. [Google Scholar] [CrossRef]
- Kamenshchik, A.; Moschella, U.; Pasquier, V. An alternative to quintessence. Phys. Lett. B 2001, 511, 265–268. [Google Scholar] [CrossRef]
- Garousi, M.R.; Sami, M.; Tsujikawa, S. Constraints on Dirac-Born-Infeld type dark energy models from varying alpha. Phys. Rev. D 2005, 71, 083005. [Google Scholar] [CrossRef]
- Cai, R.G.; Wang, S.J. Dark matter superfluid and DBI dark energy. Phys. Rev. D 2016, 93, 023515. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Nunes, R.C.; Mota, D.F. Dark calling Dark: Interaction in the dark sector in presence of neutrino properties after Planck CMB final release. arXiv 2019, arXiv:1910.08821. [Google Scholar]
- Pan, S.; Yang, W.; Valentino, E.D.; Saridakis, E.N.; Chakraborty, S. Interacting scenarios with dynamical dark energy: Observational constraints and alleviation of the H0 tension. Phys. Rev. D 2019, 100, 103520. [Google Scholar] [CrossRef]
- Yang, W.; Mena, O.; Pan, S.; Valentino, E.D. Dark sectors with dynamical coupling. Phys. Rev. D 2019, 100, 083509. [Google Scholar] [CrossRef]
- Yang, W.; Vagnozzi, S.; Valentino, E.D.; Nunes, R.C.; Pan, S.; Mota, D.F. Listening to the sound of dark sector interactions with gravitational wave standard sirens. JCAP 2019, 1907, 037. [Google Scholar] [CrossRef]
- Pan, S.; Yang, W.; Singha, C.; Saridakis, E.N. Observational constraints on sign-changeable interaction models and alleviation of the H0 tension. Phys. Rev. D 2019, 100, 083539. [Google Scholar] [CrossRef]
- Yang, W.; Banerjee, N.; Paliathanasis, A.; Pan, S. Reconstructing the dark matter and dark energy interaction scenarios from observations. Phys. Dark Univ. 2019, 26, 100383. [Google Scholar] [CrossRef]
- Yang, W.; Mukherjee, A.; Valentino, E.D.; Pan, S. Interacting dark energy with time varying equation of state and the H0 tension. Phys. Rev. D 2018, 98, 123527. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Herrera, R.; Chakraborty, S. Large-scale (in) stability analysis of an exactly solved coupled dark-energy model. Phys. Rev. D 2018, 98, 043517. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Valentino, E.D.; Nunes, R.C.; Vagnozzi, S.; Mota, D.F. Tale of stable interacting dark energy, observational signatures, and the H0 tension. JCAP 2018, 1809, 019. [Google Scholar] [CrossRef]
- Yang, W.; Pan, S.; Barrow, J.D. Large-scale Stability and Astronomical Constraints for Coupled Dark-Energy Models. Phys. Rev. D 2018, 97, 043529. [Google Scholar] [CrossRef]
- Yang, W.; Xu, L. Cosmological constraints on interacting dark energy with redshift-space distortion after Planck data. Phys. Rev. D 2014, 89, 083517. [Google Scholar] [CrossRef]
- Yang, W.; Xu, L. Testing coupled dark energy with large scale structure observation. JCAP 2014, 1408, 034. [Google Scholar] [CrossRef]
- Nunes, R.C.; Pan, S.; Saridakis, E.N. New constraints on interacting dark energy from cosmic chronometers. Phys. Rev. D 2016, 94, 023508. [Google Scholar] [CrossRef]
- Sharov, G.S.; Bhattacharya, S.; Pan, S.; Nunes, R.C.; Chakraborty, S. A new interacting two fluid model and its consequences. Mon. Not. R. Astron. Soc. 2017, 466, 3497–3506. [Google Scholar] [CrossRef]
- Pan, S.; Mukherjee, A.; Banerjee, N. Astronomical bounds on a cosmological model allowing a general interaction in the dark sector. Mon. Not. R. Astron. Soc. 2018, 477, 1189–1205. [Google Scholar] [CrossRef]
- Pan, S.; Bhattacharya, S.; Chakraborty, S. An analytic model for interacting dark energy and its observational constraints. Mon. Not. R. Astron. Soc. 2015, 452, 3038–3046. [Google Scholar] [CrossRef]
- Feng, L.; Li, H.L.; Zhang, J.F.; Zhang, X. Exploring neutrino mass and mass hierarchy in interacting dark energy models. Sci. China Phys. Mech. Astron. 2020, 63, 220401. [Google Scholar] [CrossRef]
- Guo, R.Y.; Zhang, J.F.; Zhang, X. Exploring neutrino mass and mass hierarchy in the scenario of vacuum energy interacting with cold dark matte. Chin. Phys. C 2018, 42, 095103. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, J.F.; Zhang, X. Search for sterile neutrinos in a universe of vacuum energy interacting with cold dark matter. Phys. Dark Univ. 2019, 23, 100261. [Google Scholar] [CrossRef]
- Zhang, J.; An, R.; Luo, W.; Li, Z.; Liao, S.; Wang, B. The First Constraint from SDSS Galaxy-Galaxy Weak Lensing Measurements on Interacting Dark Energy Models. Astrophys. J. 2019, 875, L11. [Google Scholar] [CrossRef]
- Zhang, J.; An, R.; Liao, S.; Luo, W.; Li, Z.; Wang, B. Fully self-consistent cosmological simulation pipeline for interacting dark energy models. Phys. Rev. D 2018, 98, 103530. [Google Scholar] [CrossRef]
- Shenavar, H.; Javidan, K. A Modified Dynamical Model of Cosmology I Theory. Universe 2020, 6, 1. [Google Scholar] [CrossRef]
- Dymnikova, I.; Dobosz, A.; Soltysek, B. Lemaitre class dark energy model for relaxing cosmological constant. Universe 2017, 3, 39. [Google Scholar] [CrossRef]
- Deng, X.-M. A Modified Generalized Chaplygin Gas as the Unified Dark Matter—Dark Energy Revisited. Braz. J. Phys. 2011, 41, 333–348. [Google Scholar] [CrossRef]
- Bhadra, J.; Debnath, U. Dynamical system analysis of interacting variable modified Chaplygin gas model in FRW universe. Eur. Phys. J. Plus 2012, 127, 30. [Google Scholar] [CrossRef][Green Version]
- Pourhassan, B. Viscous modified cosmic Chaplygin gas cosmology. Int. J. Mod. Phys. 2013, 22, 1350061. [Google Scholar] [CrossRef]
- Cui, J.L.; Yin, L.; Wang, L.F.; Li, Y.H.; Zhang, X. A closer look at interacting dark energy with statefinder hierarchy and growth rate of structure. JCAP 2015, 09, 024. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, S.; Li, X.; Zhang, X.; Li, M. Revisit of the Interaction between Holographic Dark Energy and Dark Matter. JCAP 2012, 06, 009. [Google Scholar] [CrossRef]
- Wang, B.; Gong, Y.; Abdalla, E. Transition of the dark energy equation of state in an interacting holographic dark energy model. Phys. Lett. B 2005, 624, 141–146. [Google Scholar] [CrossRef]
- Hu, B.; Ling, Y. Interacting dark energy, holographic principle and coincidence problem. Phys. Rev. D 2006, 73, 123510. [Google Scholar] [CrossRef]
- Setare, M.R.; Vagenas, E.C. The cosmological dynamics of interacting holograhic dark energy model. Int. J. Mod. Phys. 2009, 18, 147–157. [Google Scholar] [CrossRef]
- Cao, S.; Liang, N. Interacting between dark energy and dark matter: Observational conditions from OHD, BAO, CMB AND SNe Ia. Int. J. Mod. Phys. D 2013, 22, 1350082. [Google Scholar] [CrossRef]
- Wang, J.S.; Wang, F.Y. Cosmological model of the interaction between dark matter and dark energy. A&A 2014, 564, A137. [Google Scholar]
- He, J.-H.; Wang, B. The interaction between dark energy and dark matter. J. Phys. Conf. Ser. 2010, 222, 012029. [Google Scholar] [CrossRef]
- Tamanini, N. On phenomenological models of dark energy interacting with dark matter. Phys. Rev. D 2015, 92, 043524. [Google Scholar] [CrossRef]
- Wei, H.; Cai, R.-G. Statefinder Diagnostic and w-w’ Analysis for the Agegraphic Dark Energy Models without and with Interaction. Phys. Lett. B 2007, 655, 1–6. [Google Scholar] [CrossRef]
- Arabsalmani, M.; Sahni, V. The Statefinder hierarchy: An extended null diagnostic for concordance cosmology. Phys. Rev. D 2011, 83, 043501. [Google Scholar] [CrossRef]
- Zhang, J.-F.; Cui, J.-L.; Zhang, X. Diagnosing holographic dark energy models with statefinder hierarchy. Eur. Phys. J. C 2014, 74, 3100. [Google Scholar] [CrossRef]
- Yu, F.; Cui, J.-L.; Zhang, J.-F.; Zhang, X. Statefinder hierarchy exploration of the extended Ricci dark energy. Eur. Phys. J. C 2015, 75, 274. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, S. Diagnosing holographic type dark energy models with the Statefinder hierarchy, composite null diagnostic and w-w′ pair. Sci. China Phys. Mech. Astron. 2018, 61, 039811. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, S. Diagnosing ΛHDE model with statefinder hierarchy and fractional growth parameter. Sci. China Phys. Mech. Astron. 2016, 59, 670411. [Google Scholar] [CrossRef][Green Version]
- Li, S.; Ma, Y.; Chen, Y. Dynamical Evolution of Interacting Modified Chaplygin Gas. Int. J. Mod. Phys. D 2009, 18, 1785–1800. [Google Scholar] [CrossRef]
- Khurshudyan, M.Z.; Makarenko, A.N. On a phenomenology of the accelerated expansion with a varying ghost dark energy. Astrophys. Space Sci. 2016, 361, 187. [Google Scholar] [CrossRef]
- Chang, B.; Liu, H.; Xu, L.; Zhang, C. Statefinder Parameters for Five-Dimensional Cosmology. Mod. Phys. Lett. A 2008, 23, 269–279. [Google Scholar] [CrossRef]
- Alam, U.; Sahni, V.; Saini, T.D.; Starobinsky, A.A. Exploring the Expanding Universe and Dark Energy using the Statefinder Diagnostic. Mon. Not. R. Astron. Soc. 2003, 344, 1057–1074. [Google Scholar] [CrossRef]
- Sahni, V.; Shafieloo, A.; Starobinsky, A.A. Two new diagnostics of dark energy. Phys. Rev. D 2008, 78, 103502. [Google Scholar] [CrossRef]
- Shafieloo, A.; Sahni, V.; Starobinsky, A.A. A new null diagnostic customized for reconstructing the properties of dark energy from BAO data. Phys. Rev. D 2012, 86, 103527. [Google Scholar] [CrossRef]
- Sahni, V.; Shafieloo, A.; Starobinsky, A.A. Model independent evidence for dark energy evolution from Baryon Acoustic Oscillations. Astrophys. J. 2014, 793, 40. [Google Scholar] [CrossRef]
- Malekjani, M.; Khodam-Mohammadi, A.; Nazari-pooya, N. Cosmological evolution and statefinder diagnostic for new holographic dark energy model in non flat universe. Astrophys. Space Sci. 2011, 332, 515–524. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).