Stable Wormholes in the Background of an Exponential f(R) Gravity
Abstract
1. Introduction
2. The Modified Theory of Gravity
3. Wormhole Solutions
Traceless Fluid for Model
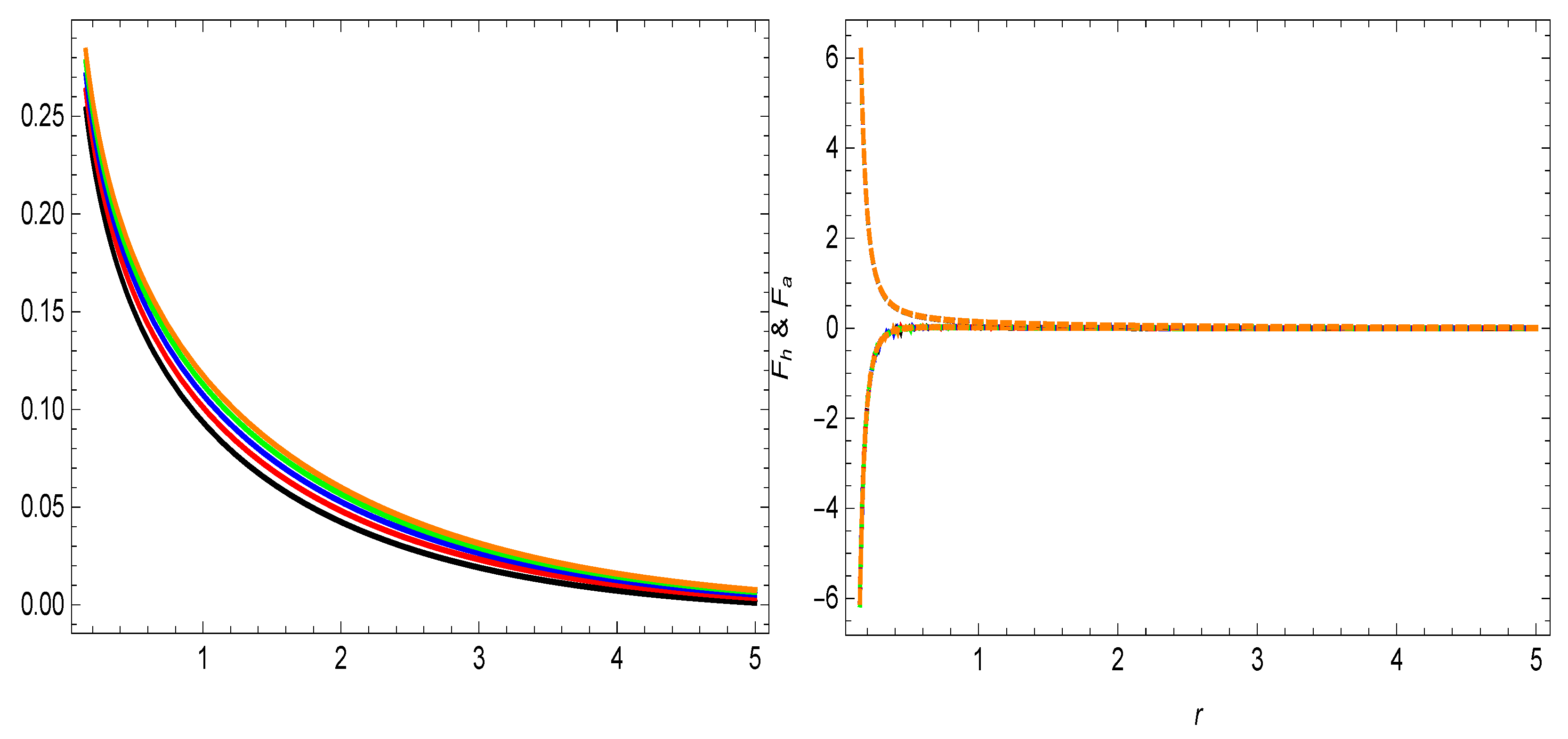
4. Equilibrium Conditions
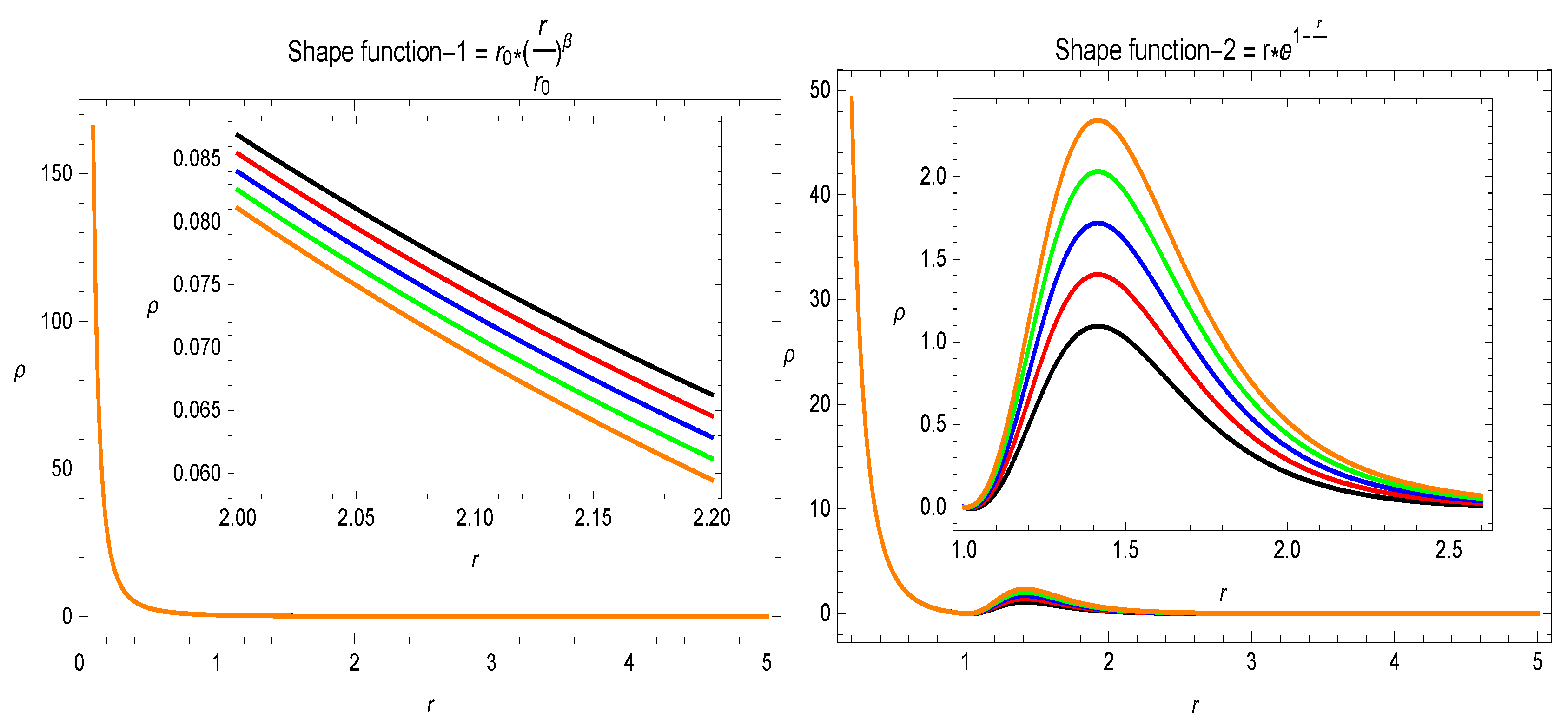
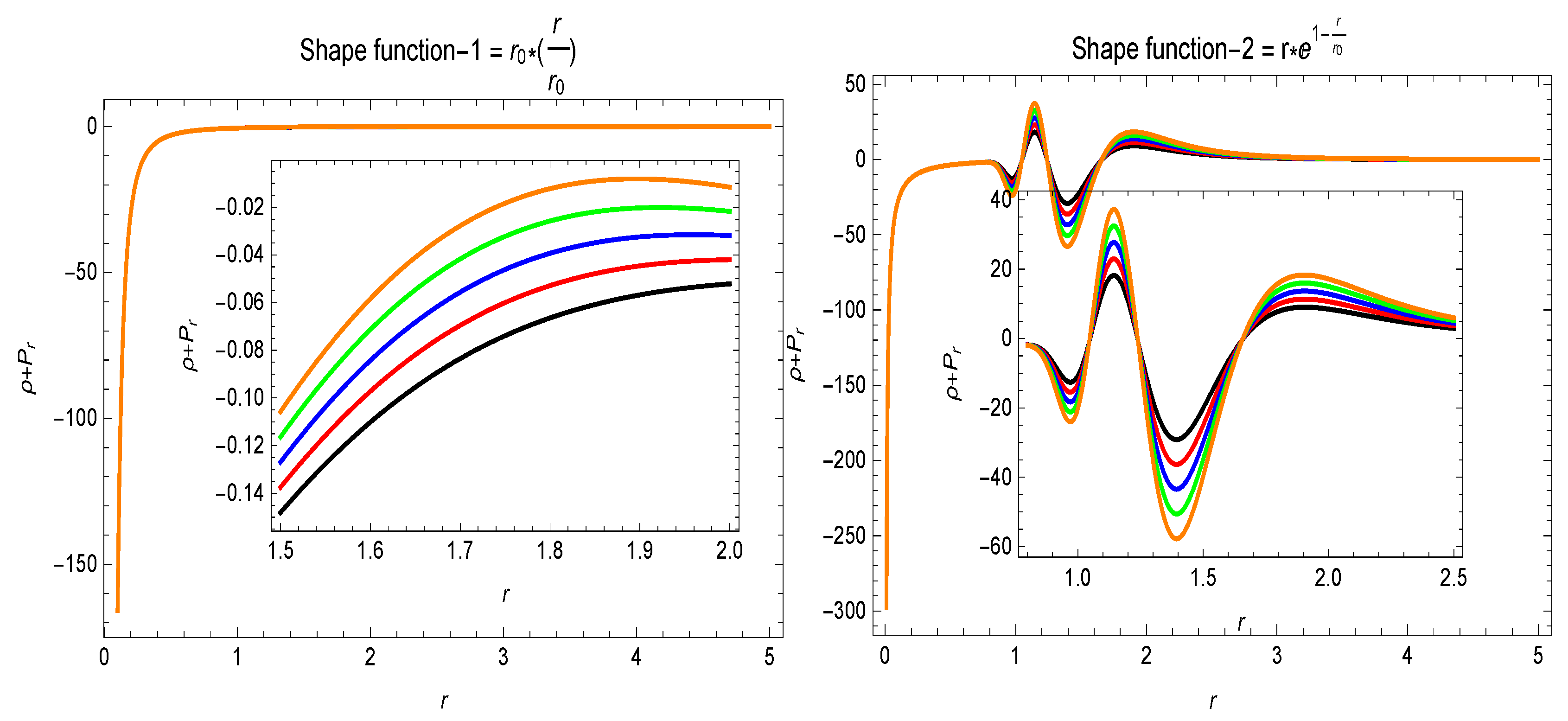
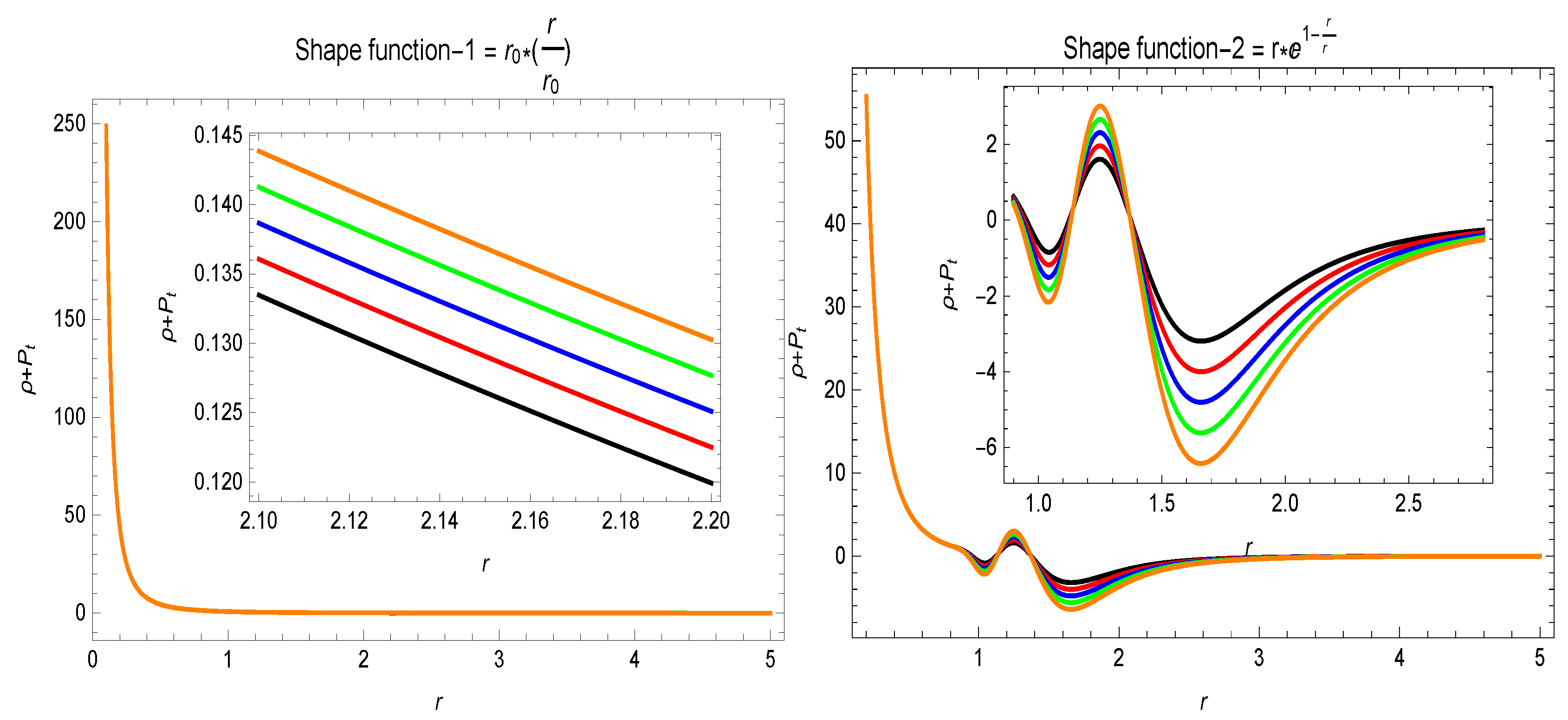
5. WEC and NEC for Two Specific Shape-Functions
6. Summary
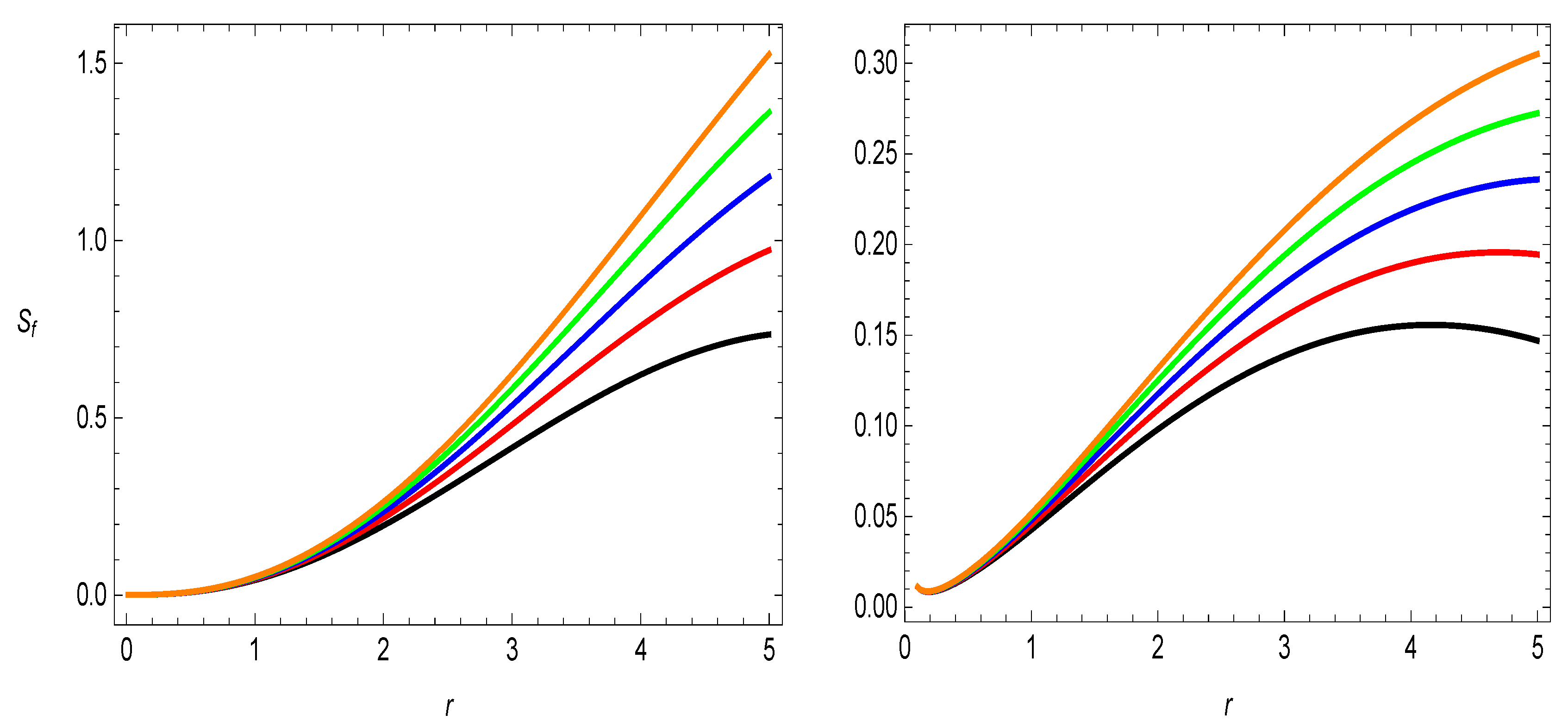
- In Figure 1, the behavior of the shape-function, i.e., , is regularly increasing with positive nature for the five different values of the parameter .
- The ratio, i.e., , does not go to zero as the radial coordinate becomes larger and larger and thus the flatness condition is not satisfied here in this model of gravity and this behavior of is depicted in Figure 1 and Table 1. This behavior of non-flatness is also reported in the literature for some other models in modified theories of gravity [18,20,36].
- It is evident from the left panel of the Figure 2 that the difference of the shape-function with radial coordinate, i.e., , provides the wormholes throat locations for the different values of the parameter , which are approximately observed at , and , for , , , , and , respectively.
- The flaring out condition, i.e., , of the shape-function can be seen in the right plot of Figure 2, which is satisfied, i.e., , , , , and for the five different values of the parameter .
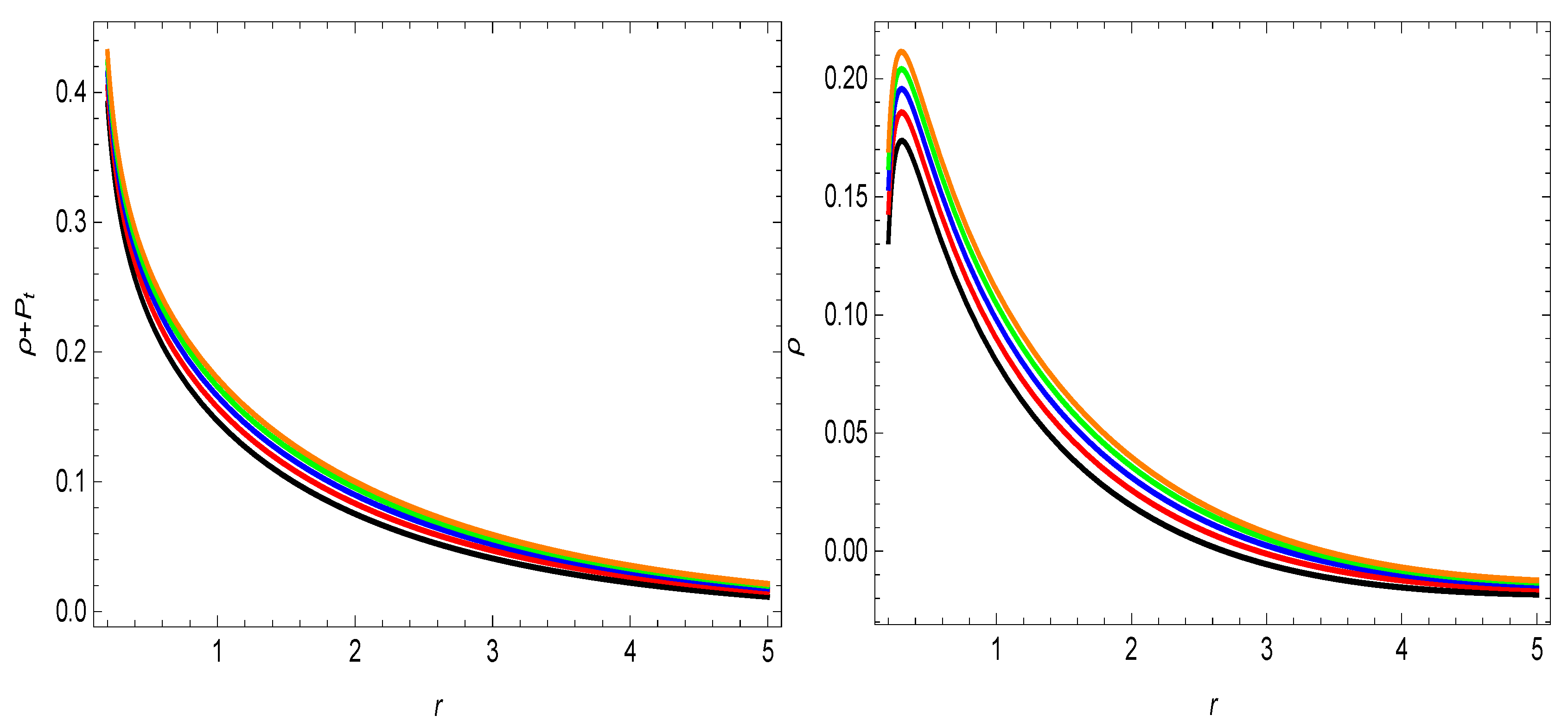
- In the Figure 5, Figure 6 and Figure 7, the behavior for the two specific shape-functions given in Section 5 is given. is violated and the energy density is positive for different values of the parameter . This violation of indicates the presence of some exotic matter, which is a requirement for a traversable wormhole solution.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Flamm, L. Comments on Einstein’s Theory of Gravity. Phys. Z. 1916, 17, 448. [Google Scholar]
- Einstein, A.; Rosen, N. The particle problem in the general theory of relativity. Phys. Rev. 1935, 48, 73. [Google Scholar] [CrossRef]
- Morris, M.S.; Thorne, K.S. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395–412. [Google Scholar] [CrossRef]
- Morris, M.S.; Thorne, K.S.; Yurtsever, U. Wormholes, time machines, and the weak energy condition. Phys. Rev. Lett. 1988, 61, 1446. [Google Scholar] [CrossRef] [PubMed]
- Nojiri, S.; Odintsov, S.D. Dark energy, inflation and dark matter from modified F (R) gravity. arXiv 2008, arXiv:0807.0685. [Google Scholar]
- Nojiri, S.I.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Meth. Mod. Phys. 2007, 4, 115–145. [Google Scholar] [CrossRef]
- Perlmutter, S.; Gabi, S.; Goldhaber, G.; Goobar, A.; Groom, D.E.; Hook, I.M.; Kim, A.G.; Kim, M.Y.; Lee, J.C.; Pain, R.; et al. Measurements of the Cosmological Parameters O and ? from the First Seven Supernovae at z >= 0.35. Astrophys. J. 1997, 483, 565. [Google Scholar] [CrossRef]
- Riess, A.G.; Nugent, P.E.; Gilliland, R.L.; Schmidt, B.P.; Tonry, J.; Dickinson, M.; Thompson, R.I.; Budavári, T.; Casertano, S.; Evans, A.S.; et al. The farthest known supernova: Support for an accelerating universe and a glimpse of the epoch of deceleration. Astrophys. J. 2002, 560, 49. [Google Scholar] [CrossRef]
- Tegmark, M.; Strauss, M.A.; Blanton, M.R.; Abazajian, K.; Dodelson, S.; Sandvik, H. Cosmological parameters from SDSS and WMAP. Phys. Rev. D 2004, 69, 103501. [Google Scholar] [CrossRef]
- Larson, D.; Dunkley, J.; Hinshaw, G.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Kogut, A. Seven-year wilkinson microwave anisotropy probe (WMAP*) observations: power spectra and WMAP-derived parameters. Astrophys. J. Suppl. 2011, 192, 16. [Google Scholar] [CrossRef]
- Komatsu, E.; Smith, K.M.; Dunkley, J.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Spergel, D.N. Seven-year wilkinson microwave anisotropy probe (WMAP*) observations: cosmological interpretation. Astrophys. J. Suppl. 2011, 192, 18. [Google Scholar] [CrossRef]
- Hu, J.W.; Cai, R.G.; Guo, Z.K.; Hu, B. Cosmological parameter estimation from CMB and X-ray cluster after Planck. J. Cosmol. Astropart. Phys. 2014, 1405, 20. [Google Scholar] [CrossRef][Green Version]
- Masi, S.; De Bernardis, P.; De Troia, G.; Giacometti, M.; Iacoangeli, A.; Piacentini, F.; Bond, J.R. The BOOMERanG experiment and the curvature of the universe. Prog. Part. Nucl. Phys. 2002, 48, 243–261. [Google Scholar] [CrossRef]
- Zubair, M.; Waheed, S.; Ahmad, Y. Static spherically symmetric wormholes in f (R, T) gravity. Eur. Phys. J. C 2016, 76, 444. [Google Scholar] [CrossRef]
- Zubair, M.; Mustafa, G.; Waheed, S.; Abbas, G. Existence of stable wormholes on a non-commutative-geometric background in modified gravity. Eur. Phys. J. C 2017, 77, 680. [Google Scholar] [CrossRef]
- Zubair, M.; Waheed, S.; Mustafa, G.; Ur Rehman, H. Noncommutative inspired wormholes admitting conformal motion involving minimal coupling. Int. J. Mod. Phys. D 2019, 28, 1950067. [Google Scholar] [CrossRef]
- Jawad, A.; Rani, S. Lorentz distributed noncommutative wormhole solutions in extended teleparallel gravity. Eur. Phys. J. C 2015, 75, 173. [Google Scholar] [CrossRef]
- Rahaman, F.; Karmakar, S.; Karar, I.; Ray, S. Wormhole inspired by non-commutative geometry. Phys. Lett. B 2015, 746, 73–78. [Google Scholar] [CrossRef]
- Rahaman, F.; Banerjee, A.; Jamil, M.; Yadav, A.K.; Idris, H. Noncommutative wormholes in f(R) gravity with lorentzian distribution. Int. J. Theor. Phys. 2014, 53, 1910–1919. [Google Scholar] [CrossRef]
- Sharif, M.; Nazir, K. Noncommutative wormhole solutions in F(T, TG) gravity. Mod. Phys. lett. A 2017, 32, 1750083. [Google Scholar]
- Sharif, M.; Nazir, K. Lorentz Distributed Noncommutative Wormhole Solutions. Adv. Hig. Ener. Phys. 2018, 2018, 7517634. [Google Scholar]
- Sharif, M.; Rani, S. Charged noncommutative wormhole solutions in f (T) gravity. Eur. Phy. J. Plus 2014, 129, 237. [Google Scholar] [CrossRef]
- Jusufi, K.; Övgün, A. Gravitational lensing by rotating wormholes. Phys. Rev. D 2018, 97, 024042. [Google Scholar] [CrossRef]
- Halilsoy, M.; Ovgun, A.; Mazharimousavi, S.H. Thin-shell wormholes from the regular Hayward black hole. Euro. Phys. J. C 2014, 74. [Google Scholar] [CrossRef]
- Mustafa, G.; Abbas, G.; Xia, T. Wormhole solutions in F (T, TG) gravity under Gaussian and Lorentzian non-commutative distributions with conformal motions. Chin. J. Phys. 2019, 60, 362–378. [Google Scholar] [CrossRef]
- Mustafa, G.; Waheed, S.; Zubair, M.; Xia, T. Gaussian distributed wormholes exhibiting conformal motion in f (T) gravity. Int. J. Geo. Methods. Mod. Phys. 2019, 16, 1950143. [Google Scholar] [CrossRef]
- Mustafa, G.; Waheed, S.; Zubair, M.; Xia, T. Non-commutative Wormholes Exhibiting Conformal Motion in Rastall Gravity. Chin. J. Phys. 2020, 33, 2050035. [Google Scholar] [CrossRef]
- Samanta, G.C.; Godani, N. Validation of energy conditions in wormhole geometry within viable f (R) gravity. Eur. Phys. J. C 2019, 79, 623. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Class of viable modified f (R) gravities describing inflation and the onset of accelerated expansion. Phys. Rev. D 2008, 77, 046009. [Google Scholar] [CrossRef]
- Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Nonsingular exponential gravity: A simple theory for early-and late-time accelerated expansion. Phys. Rev. D 2011, 83, 086006. [Google Scholar] [CrossRef]
- Lobo, F.S.; Oliveira, M.A. Wormhole geometries in f (R) modified theories of gravity. Phys. Rev. D 2009, 80, 104012. [Google Scholar] [CrossRef]
- Garcia, N.M.; Lobo, F.S. Exact solutions of brans–dicke wormholes in the presence of matter. Mod. Phys. Lett. A 2011, 26, 3067–3076. [Google Scholar] [CrossRef]
- DeBenedictis, A.; Horvat, D. On wormhole throats in f (R) gravity theory. Gen. Relat. Gravit. 2012, 44, 2711–2744. [Google Scholar] [CrossRef]
- Azizi, T. Traversable wormhole solutions in the generalized modified gravity model. J. Theor. Phys. 2012, 1, 120–128. [Google Scholar]
- Rahaman, F.; Islam, S.; Kuhfittig, P.K.F.; Ray, S. Searching for higher-dimensional wormholes with noncommutative geometry. Phys. Rev. D 2012, 86, 106010. [Google Scholar] [CrossRef]
- Sharif, M.; Rani, S. f (T) gravity and static wormhole solutions. Phys. Lett. A 2014, 29, 1450137. [Google Scholar] [CrossRef]
- Sharif, M.; Rani, S. Wormhole solutions in f (T) gravity with noncommutative geometry. Phys. Rev. D 2013, 88, 123501. [Google Scholar] [CrossRef]
- Bengochea, G.R.; Ferraro, R. Dark torsion as the cosmic speed-up. Phys. Rev. D 2009, 79, 124019. [Google Scholar] [CrossRef]
- Linder, E.V. Einstein’s Other Gravity and the Acceleration of the Universe. Phys. Rev. D 2010, 81, 127301. [Google Scholar] [CrossRef]
- Ferraro, R.; Fiorini, F. Non-trivial frames for f (T) theories of gravity and beyond. Phys. Lett. B 2011, 702, 75–80. [Google Scholar] [CrossRef]
- Daouda, M.H.; Rodrigues, M.E.; Houndjo, M.J.S. Static anisotropic solutions in f (T) theory. Eur. Phys. J. C 2012, 72, 1890. [Google Scholar] [CrossRef]
- Khufittig, P.K.F. Gravitational lensing of wormholes in the galactic halo region. Eur. Phys. J. C 2014, 74, 2818. [Google Scholar] [CrossRef]
- Quach, J.Q. Gravitational casimir effect. Phys. Rev. Lett. 2015, 114, 081104. [Google Scholar] [CrossRef] [PubMed]
- Godani, N.; Samanta, G.C. Traversable wormholes and energy conditions with two different shape functions in f (R) gravity. Int. J. Mod. Phys. D 2018, 28, 1950039. [Google Scholar] [CrossRef]
- Samanta, G.C.; Godani, N.; Bamba, K. Traversable Wormholes with Exponential Shape Function in Modified Gravity and in General Relativity: A Comparative Study. arXiv 2018, arXiv:1811.06834. [Google Scholar]
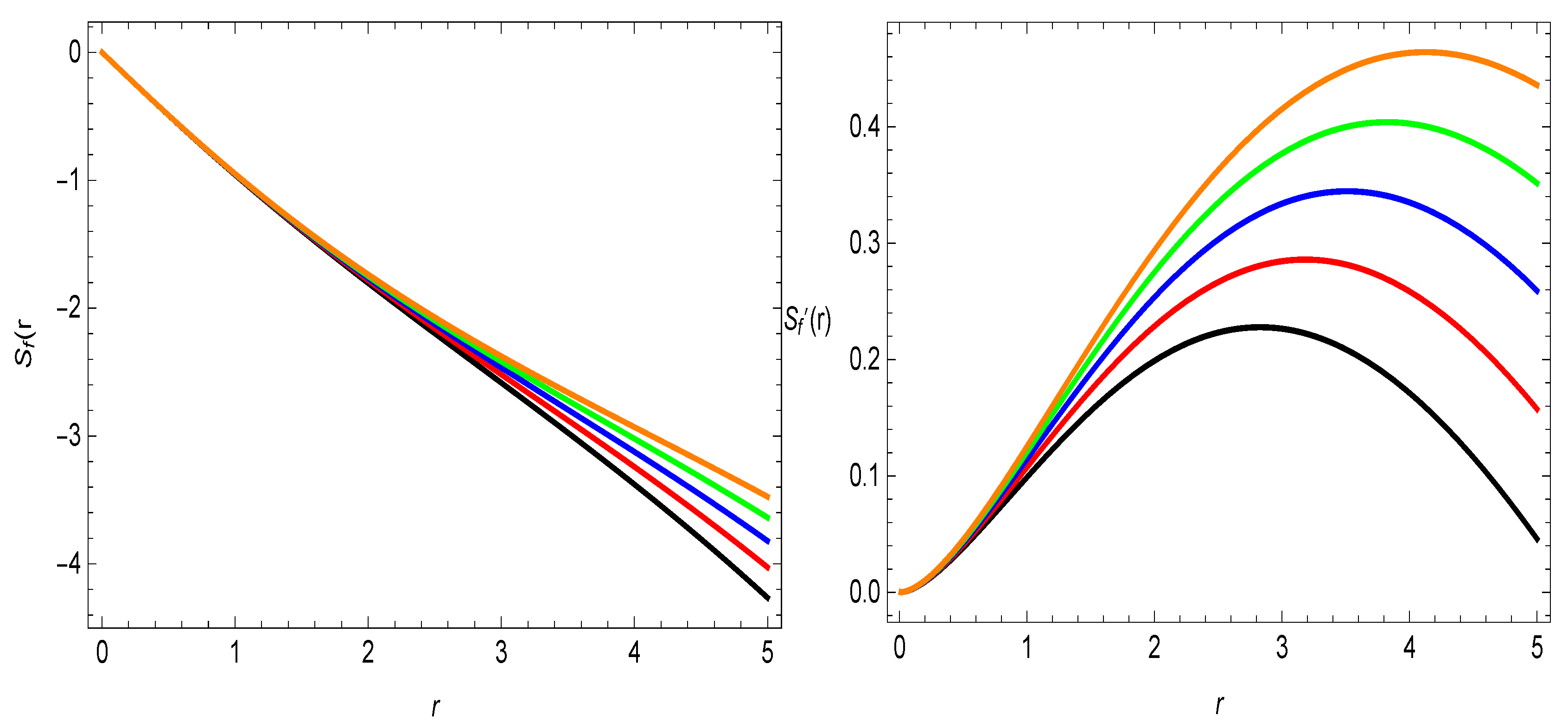
| Properties of shape-function for | |||||
| expressions | (★) | (★) | (★) | (★) | (★) |
| Energy conditions for | |||||
| Forces, i.e., , and for | |||||
| & | Balanced | Balanced | Balanced | Balanced | Balanced |
| Energy conditions for model with and | |||||
| expressions | (★) | (★) | (★) | (★) | (★) |
| Energy conditions for model with and | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mustafa, G.; Hussain, I.; Shamir, M.F. Stable Wormholes in the Background of an Exponential f(R) Gravity. Universe 2020, 6, 48. https://doi.org/10.3390/universe6040048
Mustafa G, Hussain I, Shamir MF. Stable Wormholes in the Background of an Exponential f(R) Gravity. Universe. 2020; 6(4):48. https://doi.org/10.3390/universe6040048
Chicago/Turabian StyleMustafa, Ghulam, Ibrar Hussain, and M. Farasat Shamir. 2020. "Stable Wormholes in the Background of an Exponential f(R) Gravity" Universe 6, no. 4: 48. https://doi.org/10.3390/universe6040048
APA StyleMustafa, G., Hussain, I., & Shamir, M. F. (2020). Stable Wormholes in the Background of an Exponential f(R) Gravity. Universe, 6(4), 48. https://doi.org/10.3390/universe6040048





