Phantom Dark Energy Behavior in Weyl Type f(Q,T) Gravity Models with Observational Constraints

Abstract

This study explores the behavior of phantom dark energy within the framework of Weyl-type $f(Q,T)$ gravity, considering a spatially flat FLRW universe under observational constraints. The field equations are analytically solved for a dust-like fluid source. To determine the present values of the model parameters, we utilize observational data from the Hubble parameter measurements via cosmic chronometers (CC) and the apparent magnitude data from the Pantheon compilation of Type Ia supernovae (SNe Ia). With these obtained parameter values, we analyze the model’s physical characteristics by evaluating the effective and dark energy equation of state parameters ${\omega }_{eff}$ and ${\omega }_{de}$, the deceleration parameter $q\left(z\right)$, and energy conditions. Additionally, we conduct the $O_m$ diagnostic test for the model. We estimate the transition redshift $z_t\le 0.5342, 0.6334$ and the present age of the universe $t_0=13.46, 13.49$ Gyrs with $H_0=67.4\pm 3.6, 68.8\pm 1.9$ Km/s/Mpc, ${\mathsf{\Omega }}_{m0}={0.41}_{-0.24}^{+0.13}, {0.299}_{-0.077}^{+0.042}$, and ${\omega }_{eff}=-0.6447,-0.696$, ${\omega }_{de}=-1.0347,-1.0284$. We find a transit phase accelerating and physically acceptable phantom dark energy model of the universe.

1. Introduction

Recent observational studies in [1,2,3,4,5,6,7] confirmed that the universe entered into an accelerating expansion phase six giga-years ago. This behavior of the universe suggests that it has some unknown components having high negative pressure and in a huge amount, approximately $95\%$, which are so-called dark energy (DE) and dark matter (DM). To understand the unknown parts of the universe, researchers have suggested different theories of gravity over the past few decades. These theories add to general relativity (GR), which is the most successful theory used to study the universe. Some updated theories of gravity, like $f\left(R\right)$ gravity (first introduced in [8]) and its extension called $f(R,T)$ gravity [9], are based on linking the trace T of the energy-momentum tensor to $f\left(R\right)$. There are many other similar theories in Riemannian geometry.

Alternatively, in non-Riemannian geometry, the teleparallel gravity ($f\left(T\right)$) [10,11,12,13] and the symmetric teleparallel gravity ($f\left(Q\right)$) [14,15] are developed in the same way as the Riemannian gravity theory ($f\left(R\right)$). Here, the torsion scalar T and the non-metricity scalar Q, respectively, replace R. A new paper [16] describes the $f(Q,T)$ gravity theory, which adds to the $f\left(Q\right)$ gravity theory by connecting it to the trace T of the energy momentum tensor in a way that is not minimal. They examined the cosmological implications of three distinct models inside the $f(Q,T)$ theory. Their results, together with the solution, delineated both the speeding and decelerating evolutionary phases of the universe. Several studies have shown that $f(Q,T)$ gravity is a reasonable way to explain how fast the universe is currently expanding and provide a logical answer to the dark energy puzzle [17,18,19].

Weyl gravity extends General Relativity (GR) by incorporating non-metricity within the affine connection, aiming to unify gravity and electromagnetism. Recent studies, such as [20], have explored its implications for dark matter and dark energy. In particular, ref. [21] investigates a non-minimal coupling between the trace T and the non-metricity scalar Q within the framework of Weyl gravity. This concept was further refined by [22], introducing Weyl-type $f(Q,T)$ gravity, where non-metricity is entirely determined by the magnitude of the vector field ${\omega }_{\mu }$. In Weyl geometry, gravitational field equations emerge by varying the action with respect to the metric tensor, with the vector field $w_{\mu }$ playing a crucial role in describing gravitational interactions. Despite being a relatively new approach, Weyl-type $f(Q,T)$ gravity has been extensively applied in various cosmological contexts. Works such as [23,24,25] examine its impact on cosmic acceleration, the Newtonian limit, geodesic and Raychaudhuri equations, tidal forces, and power-law solutions, shedding light on the broader implications of this modified gravity theory.

Recently, ref. [26] created a space model in a type of gravity called Weyl-type $f(Q,T)$ by using a specific way to express the Hubble parameter. Meanwhile, ref. [27] looked into a model with friction in this same gravity theory. A cosmological model has been created using a method that does not rely on specific assumptions, along with observational evidence, as mentioned in references [28,29]. Additionally, an interaction related to a deceleration parameter that does not change over time is explored in [30], focusing on a type of gravity called Weyl-type $f(Q,T)$. We use model-independent techniques to construct most of the previously discussed models in Weyl-type $f(Q,T)$ gravity. In the present paper, we develop a cosmological model based on the exact solutions to the cosmological field equations. We build a $\mathsf{\Lambda }$CDM model with a perfect fluid source in the Weyl-type $f(Q,T)$ gravity theory. We use Hubble data from cosmic chronometer (CC) observations and apparent magnitude from the Pantheon sample of SNe Ia to put limits on our model.

Weyl-type gravity $f(Q,T)$ is a modified theory of gravity that connects the non-metricity scalar Q with the trace of the energy-momentum tensor, T, which is derived from Weyl geometry. This idea is used in cosmology to represent the Universe’s late-time evolution, which includes accelerated expansion and dark energy. Bhagat et al. [31] studied the history of the Universe during different cosmological epochs using the exponential Weyl-type $f(Q,T)$ gravity model. In the second approach, the authors [31,32] validated the theoretical predictions using observational data from Cosmic Chronometers (CC) and Pantheon+ databases, obtaining the age of the Universe $13.81$ Gyr and $13.96$ Gyr, respectively. Some more research on Weyl-type $f(Q,T)$ gravity can be seen in [33,34,35].

The paper is organized into the following sections. Section 1 contains a brief introduction to the development of cosmological models. Section 2 provides a brief overview of Weyl-type $f(Q,T)$ gravity, while Section 3 mentions the cosmological field equations. We obtain an analytical solution to the field equations in Section 4; Section 5 contains some observational constraints on solutions. We discuss the results in Section 6, and finally, we present our conclusions in Section 7.

2. Brief Concept of Weyl Type $\mathit{f}(\mathit{Q},\mathit{T})$ Gravity

We consider the following action to derive the field equations in the Weyl-type $f(Q,T)$-gravity [22]:

$$S=\int d^{4}x\sqrt{-g}\left[{\kappa }^{2}f(Q,T)-{\displaystyle \frac{1}{4}}{W}_{ij}{W}^{ij}-{\displaystyle \frac{1}{2}}{m}^2{w}_i{w}^i+\lambda \tilde{R}+{\mathcal{L}}_m\right]$$

(1)

in which we impose the constraint of the vanishing of the total curvature of the Weyl space $\tilde{R}=0$ by adding a Lagrange multiplier in the gravitational action, where $w^i$ is an intrinsic vector field with a semi-metric connection ${\tilde{\mathsf{\Gamma }}}_{ij}^{\lambda }$, introduced by Weyl to generalize the Riemannian geometry in order to describe the simultaneous change of direction and length. The semi-metric connection ${\tilde{\mathsf{\Gamma }}}_{ij}^{\lambda }$ is given by

$${\overline{\mathsf{\Gamma }}}_{ij}^{\lambda }\equiv {\mathsf{\Gamma }}_{ij}^{\lambda }+g_{ij}{w}^{\lambda }-{\delta }_i^{\lambda }{w}_j-{\delta }_j^{\lambda }{w}_i,$$

(2)

where ${\mathsf{\Gamma }}_{ij}^{\lambda }$ is the Christoffel symbol constructed with respect to the metric $g_{ij}$. The $W_{ij}$ is the Weyl length curvature tensor defined by

$$W_{ij}={\nabla }_j{w}_i-{\nabla }_i{w}_j$$

(3)

and $\tilde{R}=(R+6{\nabla }_{\mu }{w}^{\mu }-6w_{\mu }{w}^{\mu })$, where R denotes the Ricci scalar curvature associated with the Levi–Civita connection. ${\mathsf{\Gamma }}_{ij}^{\lambda }$, ${\kappa }^2={\displaystyle \frac{1}{16\pi G}}$. The mass of the particle is denoted as m, while ${\mathcal{L}}_m$ represents the ordinary matter Lagrangian. Moreover, f denotes a general function of the non-metricity scalar. Q and T correspond to the trace of the energy-momentum tensor $T_{ij}$ linked to matter. The second and third terms in the action describe the standard kinetic term and the mass term related to the vector field, respectively. The non-metricity scalar Q is given by

$$Q\equiv -g^{ij}\left(L_{\nu j}^{\mu }{L}_{i\mu }^{\nu }-L_{\nu \mu }^{\mu }{L}_{ij}^{\nu }\right),$$

(4)

where the deformation tensor $L_{ij}^{\lambda }$ is defined as

$$L_{ij}^{\lambda }=-{\displaystyle \frac{1}{2}}{g}^{\lambda \rho }\left(Q_{i\rho j}+Q_{j\rho i}-Q_{\rho ij}\right).$$

(5)

In Riemannian geometry ${\nabla }_{\mu }{g}_{ij}=0$ i.e., the Levi–Civita connection is metric compatible, while in the case of semi-metric connection ${\overline{\mathsf{\Gamma }}}_{ij}^{\lambda }$ in Weyl geometry, we have

$$Q_{\mu ij}\equiv {\tilde{\nabla }}_{\mu }{g}_{ij}={\partial }_{\mu }{g}_{ij}-{\tilde{\mathsf{\Gamma }}}_{\mu i}^{\rho }{g}_{\rho j}-{\tilde{\mathsf{\Gamma }}}_{\mu j}^{\rho }{g}_{\rho i}=2w_{\mu }{g}_{ij},$$

(6)

which are not vanishing at all.

Plugging Equations (5) and (6) in (4), we obtain the relation

$$Q=-6w^2.$$

(7)

By differentiating the variation of action (1) with respect to the vector field $w^i$, we derive the generalized Proca equation that describes the evolution of the field.

$${\nabla }^j{W}_{ij}-\left(m^2+12{\kappa }^2{f}_Q+12\lambda \right)w_i=6{\nabla }_i\lambda .$$

(8)

Through a comparison of Equation (8) with the standard Proca equation, we can derive the effective dynamical mass of the vector field $w^i$ as

$$m_{eff}^2=m^2+12{\kappa }^2{f}_Q+12\lambda .$$

(9)

Once more, the variation of the action (1) concerning the metric field yields the subsequent modified field equations:

$$\begin{array}{c}{\displaystyle \frac{1}{2}}\left(T_{ij}+S_{ij}\right)-{\kappa }^2{f}_T\left(T_{ij}+{\mathsf{\Theta }}_{ij}\right)=-{\displaystyle \frac{{\kappa }^2}{2}}{g}_{ij}f-6k^2{f}_Q{w}_i{w}_j+\lambda \left(R_{ij}-6w_i{w}_j+3g_{ij}{\nabla }_{\rho }{w}^{\rho }\right)\hfill \\ \hfill +3g_{ij}{w}^{\rho }{\nabla }_{\rho }\lambda -6w_{(i}{\nabla }_{j)}\lambda +g_{ij}\square \lambda -{\nabla }_i{\nabla }_j\lambda ,\end{array}$$

(10)

where the energy-momentum tensor for matter is given by

$$T_{ij}\equiv -{\displaystyle \frac{2}{\sqrt{-g}}}{\displaystyle \frac{\delta \left(\sqrt{-g}{L}_m\right)}{\delta g^{ij}}},$$

(11)

and

$$f_T\equiv {\displaystyle \frac{\partial f(Q,T)}{\partial T}},f_Q\equiv {\displaystyle \frac{\partial f(Q,T)}{\partial Q}},$$

(12)

The terms represent the partial derivatives of the arbitrary function $f(Q,T)$ with respect to T and Q, respectively. Additionally, the expression ${\mathsf{\Theta }}_{ij}$ is defined as follows.

$${\mathsf{\Theta }}_{ij}=g^{\mu \nu }{\displaystyle \frac{\delta T_{\mu \nu }}{\delta g_{ij}}}=g_{ij}{L}_m-2T_{ij}-2g^{\mu \nu }{\displaystyle \frac{{\delta }^2{L}_m}{\delta g^{ij}\delta g^{\mu \nu }}}.$$

(13)

Here, $S_{ij}$ is the re-scaled energy momentum tensor of the free Proca field,

$$S_{ij}=-{\displaystyle \frac{1}{4}}{g}_{ij}{W}_{\rho \sigma }{W}^{\rho \sigma }+W_{i\rho }{W}_j^{\rho }-{\displaystyle \frac{1}{2}}{m}^2{g}_{ij}{w}_{\rho }{w}^{\rho }+m^2{w}_i{w}_j,$$

(14)

3. Cosmological Field Equations

For the investigation of an isotropic, homogeneous, and spatially flat universe in the context of Weyl-type $f(Q,T)$ theory, we consider the Friedmann–Robertson–Walker metric given by

$$d{s}^2=-d{t}^2+a{\left(t\right)}^2(d{x}^2+d{y}^2+d{z}^2)$$

(15)

where $a\left(t\right)$ is the scale factor depending upon t only. In a spatially symmetric spacetime, we take the vector field $w_i$ of the form

$$w_i=[\psi \left(t\right),0,0,0].$$

(16)

Hence, $w^2=w_i{w}^i=-{\psi }^2\left(t\right)$, which implies that

$$Q=-6w^2=6{\psi }^2\left(t\right)$$

(17)

Now, we define the stress-energy-momentum tensor $T_{ij}$ corresponding to metric (15) as

$$T_{ij}=(\rho +p)u_i{u}_j+p{g}_{ij}$$

(18)

where $u^i=(-1,0,0,0)$ is the four-velocity vector in a comoving coordinate system with $u^i{\nabla }_i=d/dt$ and $H=\dot{a}/a$ as the Hubble parameter. We also consider the corresponding Lagrangian of the perfect fluid source ${\mathcal{L}}_m=p$.

The constraints of flat space and the generalized Proca equation in the context of cosmology can be expressed as

$$\begin{array}{cc}\hfill \dot{\psi }& =\dot{H}+2H^2+{\psi }^2-3H\psi ,\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill \dot{\lambda }& =\left(-{\displaystyle \frac{1}{6}}{m}^2-2{\kappa }^2{f}_Q-2\lambda \right)\psi =-{\displaystyle \frac{1}{6}}{m}_{\mathrm{eff}}^2\psi ,\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\partial }_i\lambda & =0.\hfill \end{array}$$

(21)

Using (15) to (18) in Equation (10), we can obtain the generalized Friedmann equations as

$${\kappa }^2{f}_T(\rho +p)+{\displaystyle \frac{1}{2}}\rho ={\displaystyle \frac{{\kappa }^2}{2}}f-\left(6{\kappa }^2{f}_Q+{\displaystyle \frac{1}{4}}{m}^2\right){\psi }^2-3\lambda ({\psi }^2-H^2)-3\dot{\lambda }(\psi -H),$$

(22)

$$-{\displaystyle \frac{1}{2}}p={\displaystyle \frac{{\kappa }^2}{2}}f+{\displaystyle \frac{m^2{\psi }^2}{4}}+\lambda (3{\psi }^2+3H^2+2\dot{H})+(3\psi +2H)\dot{\lambda }+\ddot{\lambda }.$$

(23)

By eliminating all the derivatives of $\lambda$ using Equations (20) and (21), we obtain the set of cosmological field Equations (22) and (23) in the form

$${\displaystyle \frac{1}{2}}\left(1+2{\kappa }^2{f}_T\right)\rho +{\kappa }^2{f}_{T}p={\displaystyle \frac{{\kappa }^2}{2}}f+{\displaystyle \frac{m^2{\psi }^2}{4}}+3\lambda \left(H^2+{\psi }^2\right)-{\displaystyle \frac{1}{2}}{m}_{eff}^{2}H\psi ,$$

(24)

$${\displaystyle \frac{1}{2}}\left(1+2{\kappa }^2{f}_T\right)\left(\rho +p\right)={\displaystyle \frac{m_{eff}^2}{6}}\left(\dot{\psi }+{\psi }^2-H\psi \right)+2{\kappa }^2\dot{f_Q}\psi -2\lambda \dot{H}.$$

(25)

The equation of continuity for the model is obtained as

$$\dot{\rho }+3H(\rho +p)={\displaystyle \frac{1}{1+2{\kappa }^2{f}_T}}\left[2{\kappa }^2(\rho +p){\dot{f}}_T-f_T(\dot{\rho }-\dot{p})\right].$$

(26)

Now, we can rewrite the generalized Friedmann Equations (24) and (25) as

$$3H^2={\displaystyle \frac{1}{2\lambda }}\left(\rho +{\rho }_{de}\right),$$

(27)

$$2\dot{H}+3H^2=-{\displaystyle \frac{1}{2\lambda }}\left(\rho +{\rho }_{de}+p+p_{de}\right),$$

(28)

where

$${\rho }_{de}=m_{\mathrm{eff}}^{2}H\psi +2{\kappa }^2{f}_T\left(\rho +p\right)-{\kappa }^{2}f-{\displaystyle \frac{m^2{\psi }^2}{2}}-6\lambda {\psi }^2,$$

(29)

and

$$p_{de}={\displaystyle \frac{m_{\mathrm{eff}}^2}{3}}\left(\dot{\psi }+{\psi }^2-4H\psi \right)+{\kappa }^{2}f+4{\kappa }^2{\dot{f}}_Q\psi +{\displaystyle \frac{m^2{\psi }^2}{2}}+6\lambda {\psi }^2,$$

(30)

respectively.

By considering the limiting case where $f=0$, $\psi =0$, and $\lambda ={\kappa }^2$, the gravitational action given in Equation (1) simplifies to the conventional Hilbert–Einstein form. Under these conditions, the dark energy density and pressure vanish (${\rho }_{de}=0$, $p_{de}=0$), leading Equations (27) and (28) to reduce to the standard Friedmann equations in general relativity: $3H^2={\displaystyle \frac{1}{2}}{\kappa }^2\rho$ and $2\dot{H}=-{\displaystyle \frac{1}{2}}{\kappa }^2(\rho +p)$.

4. Cosmological Solutions

We investigate the linear form of the Lagrangian function $f(Q,T)$ suggested in [22], given by

$$f(Q,T)=\alpha Q+{\displaystyle \frac{\beta }{6{\kappa }^2}}T$$

(31)

where $\alpha$ and $\beta$ are coupling constants.

Hence, we have

$$f_Q=\alpha ,f_T={\displaystyle \frac{\beta }{6{\kappa }^2}}$$

(32)

From Equation (26), we can see that in general, the matter energy-momentum tensor is not conserved in Weyl-type $f(Q,T)$-gravity, but for the particular choice of $f(Q,T)$ expression, energy conservation law is satisfied. For the linear form of $f(Q,T)$ function, one can obtain the matter conserved-like equation. Hence, for a dusty universe ($p=0$) with $\kappa =1$ and using Equations (31) and (32) in (26), we obtain a reduced form of Equation (26) as follows:

$${\displaystyle \frac{\beta +2}{2(\beta +3)}}\dot{\rho }+3H\rho =0,\beta <-3$$

(33)

Integrating Equation (33), we obtain the matter energy density $\rho$ as

$$\rho \left(a\right)={\rho }_0{\left({\displaystyle \frac{a_0}{a}}\right)}^{{\displaystyle \frac{2(\beta +3)}{\beta +2}}},\beta <-3$$

(34)

Now, for simplicity, we take a solution of Equation (20) as $\psi =H$, and using in Equation (25), we have

$$\dot{H}-{\displaystyle \frac{3(m^2+12\alpha )}{2(m_{eff}^2+12\lambda )}}{H}^2={\displaystyle \frac{\beta }{2(m_{eff}^2+12\lambda )}}\rho$$

(35)

Using Equation (34) with the relation $a_0{a}^{-1}=1+z$, [36] in Equation (35), we have

$$H^{\prime }+{\displaystyle \frac{3(m^2+12\alpha )}{2(m_{eff}^2+12\lambda )}}{\displaystyle \frac{H}{1+z}}=-{\displaystyle \frac{3\beta {\mathsf{\Omega }}_{m0}{H}_0^2}{2(m_{eff}^2+12\lambda )H}}{(1+z)}^{{\displaystyle \frac{\beta +4}{\beta +2}}}$$

(36)

where $H_0=H(z=0)$ and ${\mathsf{\Omega }}_{m0}={\displaystyle \frac{{\rho }_0}{3H_0^2}}$. Integrating (36), we obtain

$$H\left(z\right)=H_0\sqrt{{\mathsf{\Omega }}_{m0}{(1+z)}^{{\displaystyle \frac{3(m^2+12\alpha -\beta )}{m^2+12\alpha +24\lambda }}}+(1-{\mathsf{\Omega }}_{m0}){(1+z)}^{{\displaystyle \frac{3(m^2+12\alpha )}{m^2+12\alpha +24\lambda }}}}$$

(37)

where $1-{\mathsf{\Omega }}_{m0}={\mathsf{\Omega }}_{de0}$, and hence, at present

$${\mathsf{\Omega }}_{m0}+{\mathsf{\Omega }}_{de0}=1$$

(38)

Now, we calculate the deceleration parameter $q\left(z\right)=-1+(1+z){\displaystyle \frac{1}{H}}{\displaystyle \frac{dH}{dz}}$ using Equation (37), we obtain

$$q\left(z\right)=-1+{\displaystyle \frac{3}{2}}{\displaystyle \frac{\frac{(m^2+12\alpha -\beta )}{m^2+12\alpha +24\lambda }{\mathsf{\Omega }}_{m0}{(1+z)}^{\frac{-3\beta }{m^2+12\alpha +24\lambda }}+\frac{(m^2+12\alpha )}{m^2+12\alpha +24\lambda }(1-{\mathsf{\Omega }}_{m0})}{{\mathsf{\Omega }}_{m0}{(1+z)}^{\frac{-3\beta }{m^2+12\alpha +24\lambda }}+(1-{\mathsf{\Omega }}_{m0})}}$$

(39)

$${\rho }_{de}={\displaystyle \frac{1}{2}}{m}_{eff}^2{H}_0^2\left[{\mathsf{\Omega }}_{m0}{(1+z)}^{{\displaystyle \frac{3(m^2+12\alpha -\beta )}{m^2+12\alpha +24\lambda }}}+(1-{\mathsf{\Omega }}_{m0}){(1+z)}^{{\displaystyle \frac{3(m^2+12\alpha )}{m^2+12\alpha +24\lambda }}}\right]+{\displaystyle \frac{3}{2}}\beta H_0^2{\mathsf{\Omega }}_{m0}{(1+z)}^{{\displaystyle \frac{2(\beta +3)}{\beta +2}}}$$

(40)

$$\begin{array}{c}{p}_{de}=-{\displaystyle \frac{1}{2}}{m}_{eff}^2{H}_0^2\left[{\displaystyle \frac{(2m^2+24\alpha +24\lambda -\beta )}{m^2+12\alpha +24\lambda }}{\mathsf{\Omega }}_{m0}{(1+z)}^{{\displaystyle \frac{3(m^2+12\alpha -\beta )}{m^2+12\alpha +24\lambda }}}\right.\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\left.+{\displaystyle \frac{(2m^2+24\alpha +24\lambda )}{m^2+12\alpha +24\lambda }}{\mathsf{\Omega }}_{de0}{(1+z)}^{{\displaystyle \frac{3(m^2+12\alpha )}{m^2+12\alpha +24\lambda }}}\right]-{\displaystyle \frac{1}{2}}\beta H_0^2{\mathsf{\Omega }}_{m0}{(1+z)}^{{\displaystyle \frac{2(\beta +3)}{\beta +2}}}\end{array}$$

(41)

$${\omega }_{de}=-1-{\displaystyle \frac{m_{eff}^2\left[\frac{(m^2+12\alpha -\beta )}{m^2+12\alpha +24\lambda }{\mathsf{\Omega }}_{m0}{(1+z)}^{\frac{3(m^2+12\alpha -\beta )}{m^2+12\alpha +24\lambda }}+\frac{(m^2+12\alpha )}{m^2+12\alpha +24\lambda }{\mathsf{\Omega }}_{de0}{(1+z)}^{\frac{3(m^2+12\alpha )}{m^2+12\alpha +24\lambda }}\right]}{m_{eff}^2\left[{\mathsf{\Omega }}_{m0}{(1+z)}^{\frac{3(m^2+12\alpha -\beta )}{m^2+12\alpha +24\lambda }}+(1-{\mathsf{\Omega }}_{m0}){(1+z)}^{\frac{3(m^2+12\alpha )}{m^2+12\alpha +24\lambda }}\right]+3\beta {\mathsf{\Omega }}_{m0}{(1+z)}^{\frac{2(\beta +3)}{\beta +2}}}}$$

(42)

The effective equation of state parameter ${\omega }_{eff}$ is defined as

$${\omega }_{eff}={\displaystyle \frac{p_{eff}}{{\rho }_{eff}}}={\displaystyle \frac{p+p_{de}}{\rho +{\rho }_{de}}}$$

(43)

5. Cosmological Constraints

The expansion rate of the universe can be easily understood by the analysis of Hubble data points from cosmic chronometer (CC) observations [37,38] and apparent magnitudes from the Pantheon sample of SNe Ia observations [39]. To analyze different cosmological measures and study the expansion phase, we use the emcee software to conduct MCMC analysis on CC and Pantheon datasets. This involves minimizing the ${\chi }^2$ function and maximizing the likelihood function, which is related to ${\chi }^2$ by the formula $\mathcal{L}\propto e^{-{\chi }^2}$, while applying appropriate prior information.

5.1. Hubble Data

In this section, we use 31 data points of H(z) from redshift values between 0.07 and 1.965. These measurements were taken using the differential age method and do not affect one another. Hence, we use the following ${\chi }^2$ formula:

$${\chi }_{CC}^2=\sum _{i=1}^{i=31}{\displaystyle \frac{{[H_{ob}\left(z_i\right)-H_{th}(H_0,{\mathsf{\Omega }}_{m0},\beta ,z_i)]}^2}{{\sigma }_{H\left(z_i\right)}^2}}.$$

(44)

where $H_0,{\mathsf{\Omega }}_{m0},\beta$ are the cosmological parameters which we have to estimated, and $H_{ob}$, $H_{th}$ are the observational and theoretical values of $H\left(z\right)$ at $z=z_i$, respectively. The ${\sigma }_{H\left(z_i\right)}$ denotes the standard deviations associated with observed values $H_{ob}$.

5.2. Apparent Magnitude

SNe Ia data is used to illustrate the measurement of the expansion rate of the cosmic evolution of the universe in the form of apparent magnitude $m\left(z\right)$. We analyzed the theoretical notion of apparent magnitude, as outlined in [39,40,41,42].

$$m\left(z\right)=M+5{log}_{10}\left({\displaystyle \frac{D_L}{Mpc}}\right)+25.$$

(45)

Here, M represents the absolute magnitude, while the luminosity distance $D_L$ is expressed in length units and defined as follows.

$$D_L=c(1+z){\int }_0^z{\displaystyle \frac{d{z}^{\prime }}{H\left(z^{\prime }\right)}}.$$

(46)

The Hubble-independent luminosity distance $d_L$ is expressed as $d_L\equiv {\displaystyle \frac{H_0}{c}}{D}_L$, making it a dimensionless parameter. Consequently, the apparent magnitude $m\left(z\right)$ is given by

$$m\left(z\right)=M+5{log}_{10}{d}_L+5{log}_{10}\left({\displaystyle \frac{c/H_0}{Mpc}}\right)+25.$$

(47)

We identified a correlation between $H_0$ and M in the previously discussed equation, which remains unchanged within the $\mathsf{\Lambda }$CDM framework [39,42]. To address this degeneracy, we redefine these parameters as follows:

$$\mathcal{M}\equiv M+5{log}_{10}\left({\displaystyle \frac{c/H_0}{Mpc}}\right)+25.$$

(48)

In this context, the parameter $\mathcal{M}$ is a dimensionless quantity defined by the relation $\mathcal{M}=M-5{log}_{10}\left(h\right)+42.39$, where the Hubble constant is expressed as $H_0=h\times 100$ km/s/Mpc. It is noteworthy that, in most studies [43,44], this degenerate combination is often marginalized. However, recent investigations [45,46,47,48,49] suggest that such an approach might result in the omission of crucial physical insights. Specifically, a cosmological model featuring an abrupt transition in the absolute magnitude M at a low redshift $z_t$ has the potential to simultaneously address both the $H_0$ and growth tensions [50,51,52,53,54,55]. Consequently, we opt to retain this degenerate parameter in our estimation procedure.

Within the $\mathsf{\Lambda }$CDM framework, $\mathcal{M}$ has been calibrated to a value of $23.809\pm 0.011$, as reported in [39]. The parameter $\mathcal{M}$ exhibits variation across different cosmological models (see [39,45,46,47,48,49,50,51,52,53,54,55]). For analyzing the Pantheon dataset, we employ the following ${\chi }^2$ formulation, as outlined in [39].

$${\chi }_P^2=V_P^i{C}_{ij}^{-1}{V}_P^j$$

(49)

The formula $V_P^i$ shows the difference between the observed value $m_{ob}\left(z_i\right)$ and the expected value $m({\mathsf{\Omega }}_{m0},\beta ,\mathcal{M},z_i)$ found in Equation (47). The notation $C_{ij}^{-1}$ represents the inverse of the covariance matrix derived from the Pantheon sample.

To estimate the model parameters jointly, we use 31 cosmic chronometer (CC) data points for the Hubble parameter along with 1048 data points from the Pantheon dataset. By applying the ${\chi }_{CC+P}^2$ formula, we perform a combined Markov Chain Monte Carlo (MCMC) analysis, integrating both Pantheon and CC data. This approach allows us to derive unified constraints on the parameters across all considered models.

$${\chi }_{CC+P}^2={\chi }_{CC}^2+{\chi }_P^2$$

(50)

The Hubble function (37) contains six parameters, and to estimate them independently, we remove the degeneracy between them. For this, we choose $m=\sqrt{12}$, $\alpha =-1$, and $\lambda =0.5$, as suggested in [22], and the Hubble function $H\left(z\right)$ is thus reduced in terms of three independent parameters: $H_0,{\mathsf{\Omega }}_{m0}$, and $\beta$. Table 1 shows the estimated values of these parameters using the CC and CC+Pantheon datasets with MCMC analysis and their contour plots are shown in Figure 1 and Figure 2, respectively, along with two datasets at $\sigma 1$ and $\sigma 2$ confidence level.

Table 1. The MCMC estimates.

Model	Parameter	Prior	CC	CC+Pantheon
	$H_0$	$(50,100)$	$67.4\pm 3.6$	$68.8\pm 1.9$
	${\mathsf{\Omega }}_{m0}$	$(0,1)$	$0.{41}_{-0.24}^{+0.13}$	$0.{299}_{-0.077}^{+0.042}$
$f(Q,T)$	$\beta$	$(-20,-5)$	$-11.4_{-1.6}^{+2.0}$	$-12.2_{-1.4}^{+1.2}$
	$\mathcal{M}$	$(23,24)$	-	$23.810\pm 0.012$
	${\chi }_{CC+P}^2$	-	$14.4946$	$1041.0659$
$\mathsf{\Lambda }$CDM	$H_0$	$(50,100)$	$67.7\pm 3.1$	$68.9\pm 1.8$
	${\mathsf{\Omega }}_{m0}$	$(0,1)$	$0.{333}_{-0.070}^{+0.049}$	$0.303\pm 0.020$
	$\mathcal{M}$	-	-	$23.811\pm 0.010$
	${\chi }^2$	-	$14.4936$	$1041.2708$

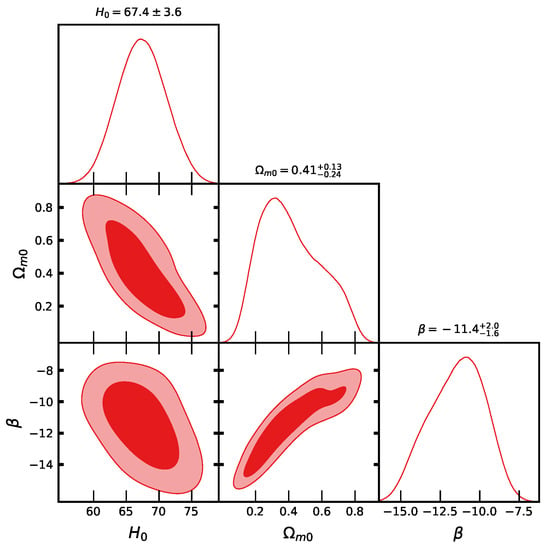
Figure 1. The contour plots of $H_0,{\mathsf{\Omega }}_{m0},\beta$ at $\sigma 1$, $\sigma 2$ confidence levels for the CC dataset.

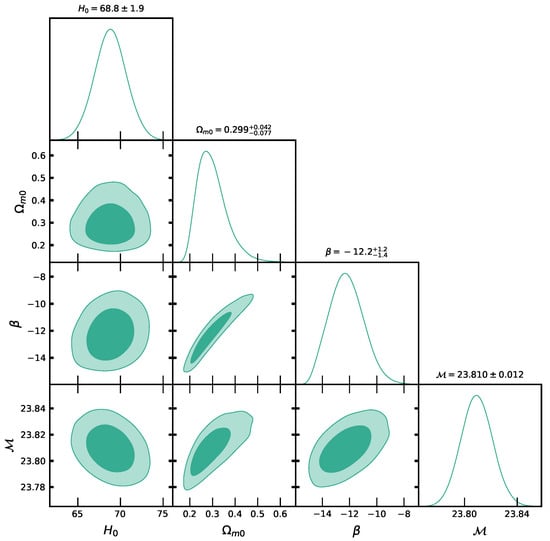
Figure 2. The contour plots of $H_0,{\mathsf{\Omega }}_{m0},\beta$, and $\mathcal{M}$ at $\sigma 1$, $\sigma 2$ confidence levels for CC+Pantheon datasets.

5.3. Information Criteria

In this section, we utilize the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC) as criteria for model selection to statistically evaluate our derived models against the classic cosmological $\mathsf{\Lambda }$CDM model. The AIC criteria can be calculated using the formula provided in references [56,57], assuming Gaussian errors.

$$AIC={\chi }_{min.}^2+{\displaystyle \frac{2Nn}{N-n-1}},$$

(51)

The symbol ${\mathcal{L}}_{max}$ indicates the maximum likelihood associated with the datasets under examination. The variable N denotes the total count of data points employed in the analysis, while n signifies the number of parameters that have been adjusted in a specific model. Reducing the ${\chi }^2$-value is analogous to enhancing the likelihood function $\mathcal{L}$. The computation of the BIC can be carried out using the formula outlined in references [56,57,58].

$$BIC={\chi }_{min.}^2+nlnN$$

(52)

The aim is to classify the models according to their ability to accurately align with the given data, taking into account various scenarios that illustrate the same category of event. In the assessment of a set of models, we identify bias in the information criteria (IC) value. In this process, we employ two particular integrated circuits: AIC and BIC. The expression $\Delta I{C}_{model}=I{C}_{model}-I{C}_{min}$ denotes the difference between the IC value of the derived model ($I{C}_{model}$) and the minimal IC value associated with the standard model ($I{C}_{min}$). We utilize Jeffrey’s scale [59] to assess the appropriateness of each model. If the value of $\Delta$IC is less than or equal to 2, this suggests that the data provides strong support for the conventional model. A disparity value, $\Delta$IC, that lies between 2 and 6 indicates a significant degree of disagreement between the two models. In conclusion, when the disparities are at or above 10, it indicates a moderate degree of tension between the two models [60].

The model parameters were determined by fitting them to the CC Hubble data points and the CC+Pantheon datasets in order to achieve the minimum ${\chi }^2$ value. The minimum ${\chi }^2$ value corresponding to each model is presented in Table 1. The CC dataset comprises $N=31$ datasets, whereas the CC+Pantheon datasets consist of $N=1079$ datasets. The number of fitted parameters for the CC dataset is $n=3$, in contrast to $n=4$ for the CC+Pantheon dataset. For the standard $\mathsf{\Lambda }$CDM model, the value of n is 2 for the CC dataset and 3 for the CC+Pantheon datasets. By applying the specified values in the Formulas (51) and (52), we have calculated the values of AIC, BIC, $\Delta$AIC, and $\Delta$BIC. These results are detailed in Table 2 and Table 3 for the two datasets analyzed.

Table 2. The information criteria for the CC dataset.

Model	AIC	$\mathsf{\Delta }$AIC	BIC	$\mathsf{\Delta }$BIC
$f(Q,T)$	$21.3834$	$2.4613$	$24.7965$	$3.4350$
$\mathsf{\Lambda }$CDM	$18.9221$	$0.0000$	$21.3615$	$0.0000$

Table 3. The information criteria for CC+Pantheon datasets.

Model	AIC	$\mathsf{\Delta }$AIC	BIC	$\mathsf{\Delta }$BIC
$f(Q,T)$	$1049.1031$	$1.8100$	$1069.0010$	$6.7789$
$\mathsf{\Lambda }$CDM	$1047.2931$	$0.0000$	$1062.2221$	$0.0000$

6. Discussion

In this section, we discuss the output of our derived universe model in Weyl-type $f(Q,T)$ gravity. We found a precise solution to the updated field equations that involve a dust-like fluid. We also created a relationship between the model’s parameters and the Hubble function $H\left(z\right)$. Next, we estimate the values of the model parameters $H_0$, ${\mathsf{\Omega }}_{m0}$, and $\beta$ by analyzing data from 31 CC datasets and 1048 Pantheon datasets using a method called MCMC. We do this at two confidence levels, $\sigma 1$ and $\sigma 2$. We obtain the estimated values of the Hubble constant $H_0=67.4\pm 3.6$ Km/s/Mpc, along with CC data, and $H_0=68.8\pm 1.9$ Km/s/Mpc along with joint data CC+Pantheon. We obtain the values of baryonic matter density parameter ${\mathsf{\Omega }}_{m0}={0.41}_{-0.24}^{+0.13}, {0.299}_{-0.077}^{+0.042}$, and dimensionless model parameter $\beta =-{11.4}_{-1.6}^{+2.0}, -{12.2}_{-1.4}^{+1.2}$, along two observational datasets, respectively. The estimated values of the Hubble constant $H_0$ and matter density parameter ${\mathsf{\Omega }}_{m0}$ are in good agreement with recent estimated values in [61,62,63,64,65,66,67,68]. We have non-vanishing dimensionless parameters $\alpha$, $\beta$, $\lambda$, and m in the relation $m^2=-12\alpha$ with $\alpha <0$. If we take $\lambda =0.5$, and $\alpha =-1$, then vector field mass $m=\sqrt{12}$.

From Table 2 and Table 3, we observe that the values of $\Delta$AIC and $\mathbf{\Delta }$BIC corresponding to the CC dataset lie in the range $(2,6)$, which indicates that our derived Weyl-type $f(Q,T)$ model deviates less from the $\mathsf{\Lambda }$CDM standard model, while for the CC+Pantheon dataset, the value of $\Delta$AIC is less than 2, which depicts the consistency of our model with the standard $\mathsf{\Lambda }$CDM, but the value of $\Delta$BIC lies in the range $(2,6)$, which represents a moderate tension between these two models. As a result, we can say that our derived model is close to the $\mathsf{\Lambda }$CDM model.

The change in the effective equation of state parameter, ${\omega }_{eff}$, shows the matter phase. Its formula is found in Equation (43). The geometrical behavior of ${\omega }_{eff}$ over z is shown in Figure 3a. From Figure 3a, one can observe that ${\omega }_{eff}$ is an increasing function of z, and it tends to the $\mathsf{\Lambda }$CDM value when $z\to -1$. We have calculated the current values of the effective equation of state parameters, which are ${\omega }_{eff}=-0.6447$ and ${\omega }_{eff}=-0.696$, based on observational data. These values are in excellent agreement with recent observations. Figure 3b depicts the evolution of the dark energy EoS parameter ${\omega }_{de}$ versus z. In Figure 3b, you can see that the value of ${\omega }_{de}$ crosses -1 (which is the value for the $\mathsf{\Lambda }$CDM model) and approaches this value again in the far future. We estimated the current value of the dark energy EoS parameter as ${\omega }_{de}=-1.0347$ along the CC data and ${\omega }_{de}=-1.0284$ along the CC+Pantheon data. These values of ${\omega }_{de}$ indicate the phantom dark energy behavior of the derived model.

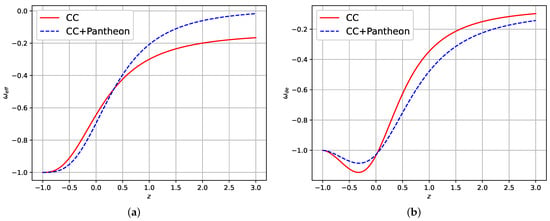
Figure 3. Variation of (a) effective EoS parameter and (b) dark energy EoS parameter over z.

The expansion phase of the universe can be explained with the evolution of the deceleration parameter $q\left(z\right)$, and its expression is given in (39). Figure 4 shows how $q\left(z\right)$ changes with z. It demonstrates that $q\left(z\right)$ increases as z increases, but there is a point where its trend changes direction. This point is known as the transition (decelerating to accelerating) point, and the value of z for which $q\left(z\right)=0$ is called the transition redshift, denoted by $z_t$. We can obtain a decelerating universe phase for $z>z_t$ and an accelerating universe phase for $z<z_t$ while $z=z_t$ represents the transition line. We have obtained the transition redshift value as $z_t=0.5342, 0.6334$, along the CC and CC+Pantheon datasets. The current value of the deceleration parameter is $q_0=-0.4158$ according to the CC data, and $q_0=-0.5441$ based on the joint data from CC and Pantheon. Both values are negative, showing that the universe is currently in an accelerating phase. In Figure 4, one can find $q\to -1$ as $z\to -1$ and $q\to 0.5$, for $z\to \infty$. For the current accelerating universe, the value of $\beta$ should be greater than $\beta >-19.5$. Thus, the estimated value of $\beta =-{11.4}_{-1.6}^{+2.0}, -{12.2}_{-1.4}^{+1.2}$ reveals the transit phase accelerating characteristics of our derived universe model. The transition redshift value $z_t$ was recently estimated in [69] as $z_t=0.{8596}_{-0.2722}^{+0.2886}$ along the SNIa dataset, and along the Hubble dataset, they found $z_t=0.{6320}_{-0.1403}^{+0.1605}$ in $f\left(R\right)$ theory. In an $f\left(T\right)$ gravity framework, it is found as $z_t=0.{643}_{-0.030}^{+0.034}$ [70]. This transition value is estimated as $z_t=0.{646}_{-0.158}^{+0.020}$ in [71], $z_t=0.{702}_{-0.044}^{+0.094}$ in [72], and $z_t=0.{684}_{-0.092}^{+0.136}$ in [73,74]. Thus, our estimation of the value of $z_t$ is acceptable.

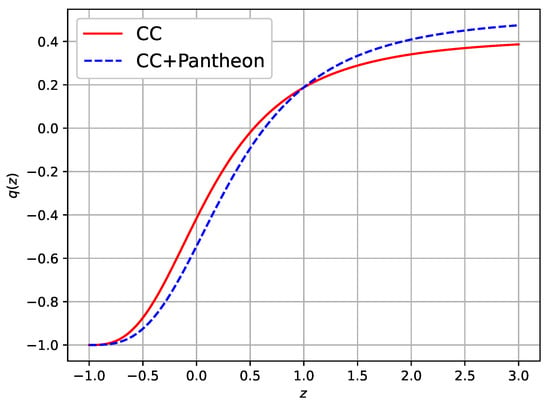
Figure 4. Evolution of deceleration parameter $q\left(z\right)$ versus z.

6.1. Energy Conditions

The Raychaudhuri equations provide insights into energy conditions, illustrating that gravity not only attracts but also implies a requirement for a positive energy density. There are four principal energy conditions: the null energy condition (NEC), the weak energy condition (WEC), the dominant energy condition (DEC), and the strong energy condition (SEC). Further details on these conditions can be found in relevant sources [75,76,77].

In a homogeneous spacetime filled with a perfect fluid, the constraints governing the energy conditions are expressed as follows:

• Null Energy Condition (NEC): ${\rho }_{eff}+p_{eff}\ge 0$
• Weak Energy Condition (WEC): ${\rho }_{eff}\ge 0$, ${\rho }_{eff}+p_{eff}\ge 0$
• Dominant Energy Condition (DEC): ${\rho }_{eff}\ge \left|p_{eff}\right|$, meaning ${\rho }_{eff}\pm p_{eff}\ge 0$
• Strong Energy Condition (SEC): ${\rho }_{eff}+p_{eff}\ge 0$, ${\rho }_{eff}+3p_{eff}\ge 0$

These conditions play a crucial role in defining the viability of cosmological models and their alignment with general relativity.

Figure 5a and Figure 5b illustrate the progression of energy conditions as a function of z for the CC and CC+Pantheon datasets, respectively. It is evident that all energy conditions hold, except for the strong energy condition (SEC) when $z<z_t$. The breakdown of SEC in this range is responsible for the accelerated expansion of the universe.

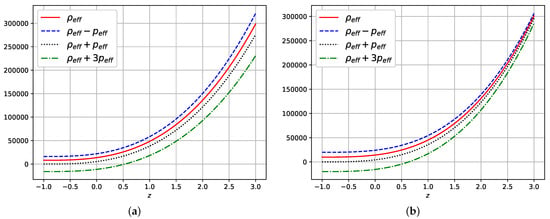
Figure 5. Evolution of energy conditions over z for (a) CC and (b) CC+Pantheon datasets, respectively.

6.2. Om Diagnostic

The Om diagnostic function helps us classify theories about cosmic dark energy based on their behavior [78]. We define the Om diagnostic function for a spatially homogeneous universe.

$$Om\left(z\right)={\displaystyle \frac{{\left(\frac{H\left(z\right)}{H_0}\right)}^2-1}{{(1+z)}^3-1}},$$

(53)

In this context, $H_0$ represents the present-day Hubble parameter, while $H\left(z\right)$ corresponds to the Hubble parameter as defined in Equation (37). When the function $Om\left(z\right)$ exhibits a positive slope, it indicates phantom-like behavior, whereas a negative slope signifies quintessence-like motion. The LambdaCDM model is characterized by a constant $Om\left(z\right)$.

Equation (53) shows the $Om\left(z\right)$ function for the model we developed, and Figure 6 illustrates its geometric meaning. Figure 6 shows that $Om\left(z\right)$ increases as z increases, indicating a positive slope. This suggests that our universe model behaves similarly to a phantom dark energy model. Also, we can see that as $z\to -1$ at late-time future, the value of $Om\left(z\right)$ is constant, which represents the tendency of our derived model to the $\mathsf{\Lambda }$CDM model in the far future.

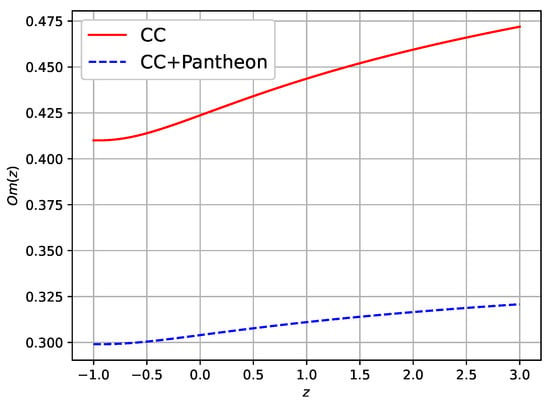
Figure 6. Behaviour of the $Om\left(z\right)$ over z.

6.3. Statefinder Analysis

Researchers have formulated various dark energy cosmological models to examine and define the cosmic evolution of the expanding universe. These models necessitate a precise and reliable diagnostic for accurate classification. As a result, Sahni et al. developed a diagnostic methodology utilizing the parameter pair $(r,s)$, known as the “statefinder” [79]. The statefinder represents a systematic progression from H and q, analyzing the dynamics of the universe’s expansion through higher derivatives of the scale factor. The definitions of these parameters are as follows [79,80,81]:

$$r={\displaystyle \frac{\stackrel{⃛}{a}}{a{H}^3}}s={\displaystyle \frac{r-1}{3(q-\frac{1}{2})}}$$

(54)

The statefinder diagnostic effectively distinguishes between dark energy theories, as various cosmological models, including those involving dark energy, exhibit markedly different evolutionary trajectories in the $r-s$ plane. The statefinder parameters for the spatially flat $\mathsf{\Lambda }$CDM model are identified as $(r,s)=(1,0)$. Additionally, the quintessence model is characterized by the conditions $r<1$ and $s>0$, while the Chaplygin gas model is defined by $r>1$ and $s<0$. The holographic dark energy model is represented by the specific values of $(r,s)=(1,{\displaystyle \frac{2}{3}})$. Another diagnostic pair is $(q,r)$, with the fixed points identified as $(r,q)=(1,-1)$ for the $\mathsf{\Lambda }$CDM model. We derive the statefinder parameters for the model as follows:

$$r\left(z\right)=1-2(1+z){\displaystyle \frac{H^{\prime }}{H}}+{(1+z)}^2{\left({\displaystyle \frac{H^{\prime }}{H}}\right)}^2+{(1+z)}^2{\displaystyle \frac{H^{\prime \prime }}{H}}.$$

(55)

$$s\left(z\right)={\displaystyle \frac{-2(1+z)\frac{H^{\prime }}{H}+{(1+z)}^2{\left(\frac{H^{\prime }}{H}\right)}^2+{(1+z)}^2\frac{H^{\prime \prime }}{H}}{3\left((1+z)\frac{H^{\prime }}{H}-\frac{3}{2}\right)}}$$

(56)

Figure 7a and Figure 7b illustrate the progression of statefinder parameters $r\left(z\right)$ and $s\left(z\right)$ in relation to z, respectively. As the cosmic redshift z nears -1, it is evident that the statefinder parameter r converges to 1, while the parameter s tends toward 0 in the late-time universe. Figure 8a illustrates the relationship between statefinder $s\left(z\right)$ and $r\left(z\right)$. By analyzing Equations (55) and (56), it is evident that as cosmic redshift z approaches −1, the values of $(r,s)$ converge to $(1,0)$. Figure 8a clearly shows that $r>1$ and $s<0$ throughout its evolution, indicating that the derived model exhibits characteristics of a Chaplygin gas model. Figure 8b illustrates the relationship between $r\left(z\right)$ and the deceleration parameter $q\left(z\right)$. Figure 8b indicates that the derived model converges to the $\mathsf{\Lambda }$CDM model as $(r,q)$ approaches $(1,-1)$ in the late-time universe. The current values of the statefinder parameters are determined to be $r_0=0.7868, 1.0227$ and $s_0=0.0734, -0.0072$ across two datasets, respectively, which align with the characteristics of a Chaplygin gas model.

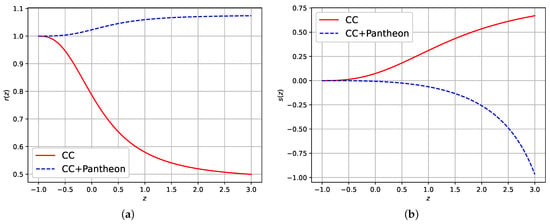
Figure 7. Evolution of statefinder parameters (a) $r\left(z\right)$ and (b) $s\left(z\right)$ versus z for the CC and CC+Pantheon datasets, respectively.

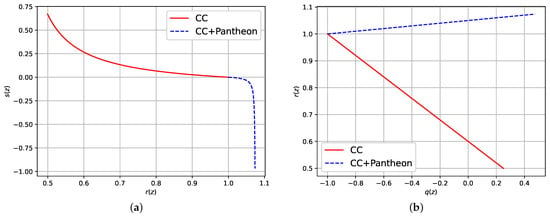
Figure 8. Evolution of (a) $s\left(z\right)$ versus $r\left(z\right)$ and (b) $r\left(z\right)$ versus $q\left(z\right)$ for the CC and CC+Pantheon datasets, respectively.

7. Age of the Universe

We use the following formula to calculate the age of the universe as given below:

$$t_0-t={\int }_0^z{\displaystyle \frac{d{z}^{\prime }}{H\left(z^{\prime }\right)(z^{\prime }+1)}}$$

(57)

We denote ${\displaystyle \frac{H\left(z^{\prime }\right)}{H_0}}=h\left(z^{\prime }\right)$ in Equation (57), we can rewrite (57) as

$$(t_0-t)H_0={\int }_0^z{\displaystyle \frac{d{z}^{\prime }}{h\left(z^{\prime }\right)(z^{\prime }+1)}}$$

(58)

$$t_0{H}_0=\underset{t\to 0}{lim}(t_0-t)H_0=\underset{z\to \infty }{lim}{\int }_0^z{\displaystyle \frac{d{z}^{\prime }}{h\left(z^{\prime }\right)(z^{\prime }+1)}}$$

(59)

From Equation (59), one can see that if $t\to 0$, $z\to \infty$, then $(t_0-t)H_0\to t_0{H}_0$, which gives the present age of the universe. For the CC dataset, we estimate the age of the universe at $t_0=13.{46}_{-0.71}^{+0.52}$ Gyrs, and for the CC+Pantheon dataset, we obtain the age of the universe at $t_0=13.{49}_{-0.50}^{+0.73}$ Gyrs.

8. Conclusions

This paper presents the development of dark energy models within the framework of Weyl-type $f(Q,T)$ gravity, utilizing a dust fluid as the background source and taking into account relevant observational constraints. An analytical solution is derived for the field equations. The current values of the model parameters $H_0$, ${\mathsf{\Omega }}_{m0}$, ${\mathsf{\Omega }}_{de0}$, $\alpha$, $\beta$, m, and $\lambda$ are determined through an analysis of data on the Hubble parameter sourced from cosmic chronometers, alongside brightness measurements obtained from the Pantheon sample of type Ia supernovae. The model’s physical properties are analyzed through the application of estimated values for its parameters, particularly focusing on the effective equation of state, ${\omega }_{eff}$, and the deceleration parameter, $q\left(z\right)$. The primary characteristics of the derived universe model are outlined as follows:

• We identified a transit phase characterized by deceleration in the past and acceleration in the late time, exhibiting phantom behavior in the dark energy model, which aligns well with recent observations.
• We found the Hubble constant value as $H_0=67.4\pm 3.6$ Km/s/Mpc, along with CC data, and $H_0=68.8\pm 1.9$ Km/s/Mpc along with joint data CC+Pantheon. The Hubble tension is the difference between the conclusions of two approaches for calculating the cosmic expansion rate. The $H_0$ observations can be inferred using the cosmological model and early universe data, or directly measured in the local universe. Interestingly, the $H_0$ values measured by these two approaches differ. The disparity between $H_0$ values estimated from the local distance ladder and the CMB poses the most significant challenge to the mainstream $\mathsf{\Lambda }$CDM model. This $H_0$ discrepancy is also known as “Hubble Tension” [82,83,84]. SNIa data in combination with CMB and BAO observations, Giostri et al. [85] investigated the Hubble constant plus deceleration parameter as $H_0=73.8$ and $q_0=-0.54$, respectively. Recently, Aydiner et al. [86] found that the scale factor behaves as $a\left(t\right)\propto {(t/t_0)}^{2/3}$ below $t/t_0\le t_c$, and as $a\left(t\right)\propto e^{h(t/t_0)}$ within the interval of around $H_0=69.5$ and $H_0=73.5$ km/s/Mpc, which shows the dependence on the weak and strong interaction between dark components above $t/t_0>t_c$, respectively. In 2013, Bennett et al. [87] provided $H_0=70.00\pm 2.20$ km/s/Mpc through analyzing the nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations. The first data release of the Planck space observatory, which was operated by the European Space Agency (ESA), gave a precise result $H_0=67.40\pm 1.40$ km/s/Mpc [82]. After that, a more accurate $H_0=67.40\pm 0.50$ km/s/Mpc yielded by the Planck final data release is also in line with the Planck2013 results [88]. Researchers also consider adding the other observational data to constrain $H_0$, Planck2018+lensing $67.36\pm 0.54$ km/s/Mpc and Planck2018+lensing+BAO $67.66\pm 0.42$ km/s/Mpc [88]. Thus, we observe that our finding of $H_0$ is consistent with recent observations [82,87,88].
• We found the matter energy density parameter value as ${\mathsf{\Omega }}_{m0}=0.{41}_{-0.24}^{+0.13},0.{299}_{-0.077}^{+0.042}$, and effective EoS parameter ${\omega }_{eff}=-0.6447,-0.696$ with dark energy EoS parameter as ${\omega }_{de}=-1.0347$ along the CC data and ${\omega }_{de}=-1.0284$ along the CC+Pantheon data, which are in good agreement with recent observations.
• We looked into the model parameters $\alpha$, $\beta$, m, and $\lambda$ that are non-vanishing. These show how different factors affect the Weyl-type $f(Q,T)$ gravity theory.
• We found that the current value of the deceleration parameter is $q_0=-0.4158$ along the CC data and $q_0=-0.5441$ along the CC+Pantheon data. Both of these values are negative $q_0<0$, which means that the universe model is currently accelerating.
• We found the transition redshift value as $z_t=0.5342, 0.6334$, along with the CC and CC+Pantheon datasets, respectively, which are in good agreement with [69,70,71,73,74].
• The current age of the universe is determined to be $t_0=13.{46}_{-0.71}^{+0.52}$ billion years based on the CC dataset. When incorporating both the CC and Pantheon datasets, the estimated age is refined to $t_0=13.{49}_{-0.50}^{+0.73}$ billion years.
• We found that our derived model satisfied all energy conditions except SEC, which produces an accelerating phase of the expanding universe.
• The Om diagnostic analysis reveals the phantom dark energy behavior of the model.
• The analysis of AIC and BIC criterion shows less tension between the model and $\lambda$CDM.
• The statefinder analysis of the model reveals the late-time tendency to the $\lambda$CDM model.

We see that the Weyl-type $f(Q,T)$ gravity theory could explain both the universe’s recent acceleration and its earlier slowing down without needing to add the cosmological constant $\mathsf{\Lambda }$. Therefore, the Weyl-type $f(Q,T)$ gravity needs more investigation to explore the properties of universe evolution.