Abstract
We discuss the large N expansion in backgrounds of extended states with a focus on the implementation of Goldstone symmetries and the construction of the associated Hilbert space. The formulation is given in the general framework of collective field theory. The case of translational symmetry is described first as a basic example. The large N thermofield represents the main topics, with the emergent dynamics of left–right bulk fields and collective symmetry coordinates. These give the basis for a expansion.
1. Introduction
Large N represents the basic non-perturbative scheme for implementing AdS/CFT and more generally gauge/gravity duality. With representing Newton’s constant G, the main confirmations of the duality are most easily seen in a comparison of correlation functions. Beyond that, of even greater interest are non-perturbative extended states, especially at finite temperatures. In particular, the thermofield double (TFD) state conjectured to be dual to a two-sided black hole [1] is of central interest, as is the structure of the emergent Hilbert space and of the associated expansion.
Recently, investigations [2,3] into the Hilbert space were seen in the gravitational setting with discussions of observables (and of propagation) inside the horizon. Furthermore, a general discussion of a possible large N Hilbert space structure of the thermal state was presented in [4,5].
Three-dimensional O(N) invariant quantum field theories with Higher Spin Gravity duality [6,7,8] offer a framework for concrete investigations. Here, an explicit construction of the TFD state at large N was given in [9,10]. Furthermore, a dynamical symmetry representing rotations (in the doubled thermofield space) was identified.
In the present work, we concentrate on the construction of the Hilbert space with the implementation of symmetries. Much like in the case of extended (soliton-type) states in ordinary QFT [11], central to the understanding of perturbation expansion is the implementation of broken (Goldstone) symmetries. These are characterized by large O(N) expectation values and fluctuations involving zero modes. The implementation of these symmetries is carried out through collective coordinates with an associated extended Hilbert space. We discuss this in the large N context and describe a formulation of the nonlinear theory.
The simple case of translations (relevant to large N soliton states) will be presented first. Our main focus is the thermofield case. Here, the question of the appropriate gauge and global symmetries already requires some analysis. Regarding gauging (of U(N) and O(N) groups), we follow the proposal introduced in [9], which gave arguments for diagonal gauging of the doubled large N Hilbert space. It was argued that this is required in the high-temperature phase while the low-temperature phase can be described by direct product gauging. Fluctuations and the zero mode structure of the large N TFD were further studied in [9,10], and a relation with a dynamical symmetry was identified. Both of the above features will play a central role in developing the structure of the Hilbert space and of the expansion. We comment that, even though we find our results through the O(N) vector model, the emergent structure and the method of implementing symmetries (through collective coordinates) are general. One can also expect these to be relevant to issues of sub-region duality and entanglement wedge construction, which have been recently considered in vector models [12,13,14].
The content of the paper is as follows: Section 2 gives a summary of Hamiltonian at large N. The case of translations is then discussed first in Section 3, giving a basic example. Section 4 concentrates on the TFD state and the corresponding degeneracy and symmetry structure. Section 5 describes the associated Hilbert space and the general implementation of Goldstone symmetry in the thermal case. We conclude in Section 6 and outline directions for future study.
2. The Large N Hamiltonian
A large N QFT in the canonical formalism can be completely described through the dynamics of collective fields (single trace operators). These dynamics are governed by a collective Hamiltonian, which is generally of the form
with , the canonical conjugate of . is a function(al) of , whose explicit form depends on the theory. Consider the example of two-matrix quantum mechanics [15]. Let and denote two Hermitian matrices of size , and the corresponding Hamiltonian is invariant under U(N) transformations. In this case, the collective fields are U(N) singlets termed as loop variables, where denoting matrix products . In this case, represents the joining of two loops and thus admits a geometric representation [15]. Also, one has representing the splitting of one loop into two loops [15]. The collective potential has the general form
with the original potential represented by ’s. For a recent numerical study of large N multi-matrix systems, one may refer to [15,16].
In this paper, we follow the O(N) vector model as an analytically solvable theory. In dimensional Minkowski space-time, one has the bi-local collective field
where are scalar fields transforming as with . In this case, we have as
We also have as
Substituting these relations into the above formulae, we have the collective Hamiltonian
where . In three-dimensional Minkowski spacetime, the O(N) vector model has two fixed points, the UV fixed point and the Wilson–Fisher IR fixed point, at which it possesses conformal symmetry and is dual to higher spin theory in AdS4 [6,7,8,17,18]. There is an exact map from the bi-local field in O(N) CFT to higher spin fields in AdS. For example, in AdS4/CFT3 we have [19]
with the kernel representing a canonical transformation of the momenta. Here, is a coordinate in which packages all spin variables.
3. Translations: The Large N Soliton
Generally, the vacuum (ground state) solution is manifestly translational invariant, namely for an arbitrary translational parameter a, with x describing position at . However, in general, one can also have other non-translationally symmetric solutions, such as large N coherent states and solitons. Concrete examples were constructed in the nonlinear sigma model representing large N solitons. Denoting such solution as , one has that the translational symmetry is broken:
since the solution does not commute with the momentum operator:
In this case, problems arise when performing expansions around the backgrounds. In the naive expansion
The collective Hamiltonian becomes
The leading term is the mass of the soliton, and it is of order . The term is quadratic:
In this equation, and . In particular, we shall define the soliton state for the small fluctuations as
with G the static two-point function
The notion for the state indicates that the center of mass of the soliton is located at .
We would like to implement translations:
with the momentum operator that is expanded as:
where we use the shorthand notation . We note the leading term in this expansion: is of order while is of order 1. Due to this N dependence of P, one cannot manifestly see translations in the naive large N expansion scheme. For example, an infinite series re-summation is needed to evaluate
with . Due to the of the leading operator , terms of different orders in become mixed up. As a concrete ingredient in this transformation, let us consider . Since is of order and is of order , this gives an order 1 term. As a result, it contributes to transformations of the background term instead of . In matrix models, the leading term is of order N, and the situation becomes even worse. We will see in subsequent sections that a similar issue also arises in large N expansion around thermofield double states.
In addition, the presence of the zero mode frequency implies that the static two-point function G is divergent and the propagator is ill defined. The appearance of the zero mode is related to the breaking of (translational) symmetry: is the Goldstone mode. In particular, consider the symmetry condition ; in the large N limit of the soliton sector, this condition reduces to , and yields
This results in infrared divergences, in the sense that G is singular, due to the zero mode for ; hence, perturbation in terms of is not possible.
In QFT, the canonical way to project out the zero modes and to develop a systematic perturbation expansion in terms of the coupling constant is the collective coordinate method [11,20,21]. In that case, the soliton background with g as the coupling constant. In the case of the large N nonlinear sigma model, the role of g is played by . The collective coordinate is identified with the position of the center of mass of the soliton, denoted by , which is now promoted to a degree of freedom. We are led to work in the extended Hilbert space: in addition to and , we would also have and its conjugate , with . These new variables obey constraints and gauge conditions
The gauge condition Equation (23) can actually be arbitrary. Here, denotes an arbitrary functional of and , and . To project out the zero mode in the simplest way, we choose the linear gauge condition
On the other hand, one can also choose the canonical gauge condition [21]
where is the collective Hamiltonian density. One can verify that the solutions for these equations indeed obey the canonical commutation relation. Since this gauge is solved by , where K is the boost operator, using Poincaré algebra, we see that the canonical commutation relation is guaranteed
With this collective coordinate, we are able to make a change to the coordinate system through a unitary transformation. We can perform a translation to the soliton frame
and similarly for all field degrees of freedom, including their expansions. The inverse transformations are
In particular, we can apply a translation to the soliton state , such that in coordinate space, the new state becomes
with the zero mode projected out in :
Then, can be translated easily via
We also have momentum eigenstates
As illustrated above, the collective coordinate enables one to implement translations on states and fields without expansion of the momentum operator P. On the extended Hilbert space, translation symmetric forms directly follow. For example, we have for the form factor (one-point function):
Or, in the example of the two-point correlation function, we have
Generally, the coordinate is treated as a dynamical variable. The transformation of shifting to and represents a change in frame. The constraint and the gauge condition Equations (22) and (24) then become
In particular, the gauge condition implies that the zero mode is now projected out, and a systematic expansion can be developed. Writing
we see that the constraint becomes
and with the requirement
one solves for to have
Similarly, we can expand the gauge condition, and find at leading order
Thus, the zero mode is projected out from the linear fluctuation fields. Correspondingly, the wave functional for the small fluctuations around the soliton background is
with as the (equal-time) two-point correlators with the zero mode excluded.
The Hamiltonian becomes
where
and can be systematically expanded in as
providing the basis for the expansion.
4. Thermofield Double State at Large N
We follow the Hamiltonian formalism for the Thermofield double (TFD) [22]. The TFD state is introduced to completely reproduce the thermal averages of various operators:
This is achieved through purification by doubling the Hilbert space. Let denote the energy eigenstates in the doubled Hilbert space with ,
In the context of AdS/CFT correspondence, such states involve two identical copies of large N CFTs at two causally disconnected boundaries and are dual to two-sided eternal black holes in the bulk [1]. The Hamiltonian that governs the dynamics is
Obviously, it annihilates the TFD state for all , i.e., . The thermofield Hamiltonian describes the real-time portion of the Schwinger–Keldysh contour, and the TFD state can be referred to as the thermal vacuum state.
Evolution along the imaginary portion of the Schwinger–Keldysh contour is governed by the Hamiltonian
and we have
where
denotes the maximally entangled state. This relates with the infinite temperature state through a non-unitary transformation. Most importantly, one has that the two Hamiltonians commute (representing a symmetry):
A further dynamical symmetry has been argued at the semiclassical level (in the sense of large N) in [10]. In the free O(N) model case, we have
with
representing a Bogoliubov transformation. In [10], a construction of to first order in the coupling is shown. Generally, this appears to be an on-shell symmetry, which, however, will play a role at the level of fluctuations (in ).
We continue with the O(N) model
which at UV and IR critical points represents the CFT. At finite temperature, the model has a phase transition [23] with free energy for and for . For the TFD scheme, we also have with and , such that the theory generally has an symmetry. The following structure regarding gauging of the O(N) symmetry was seen in [9].
For the lower temperature (the AdS-phase), one imposes the singlet constraint on the original and the doubled Hilbert spaces, namely
where and are O(N) generators of and . This implies that we have two invariant bi-local (only in space) fields in the spectrum
representing a direct product Hilbert spaces of .
For the high-temperature phase, it was proposed in [9] that one needs to relax the above constraints and has diagonal gauging of O(N)
Now, in addition to Equation (59), we have two more bi-local fields (cross modes) in the Hilbert space
The diagonal gauging [9] was seen to allow an order N free energy at the leading classical (in the sense of ) level. At the level of fluctuations [9], the cross modes were seen to be responsible for the presence of evanescent modes and for generating a complete spectrum in the bulk. The presence of cross modes implies that one cannot have a direct product of two CFTs, since they interact here through these mixed modes. We note that at the gravity level, various issues have been discussed for the duality scheme between CFTL × CFTR and two-sided black hole, in particular in [24,25,26]. Also, regarding gauging in CFT, there are recent gravitational studies (for two-sided wormhole space-times) with diagonal implementation of constraint symmetries [27,28,29].
Consequently, we use the bi-local collective fields1
and their canonical conjugates , to represent the thermofield Hamiltonian as , namely as [9,10]
with as the Pauli third matrix, and . To obtain the large N thermal background, we vary with respect to :
which gives the equation determining the large N thermal background. Several important features of this (classical) large N equation were identified in [9,10], foremost being the appearance of a symmetry (mentioned above). Namely, the equation allows for
a one-parameter family of solutions, with f representing the parameter. The classical solution corresponds to the thermal two-point function at equal time, namely and one then identifies , with in Equation (55). The solution is manifestly translational invariant, as in the zero-temperature case. The dispersion relation obeys a thermal gap Equation [10]. It was understood in the previous work [10] that this degeneracy can be attributed to symmetry, and the large N thermal background is related to the zero temperature background via (note that the signs are opposite to those in Equation (56))
In general, appears to be an on-shell symmetry, in particular in the general interacting case. Consequently, it manifests itself in the semi-classical approximation (in the sense of 1/N) as above. It will also manifest itself at the level of fluctuations.
We emphasize that this property is not limited to the O(N) vector model, but also applies to more complicated theories, such as matrix quantum mechanics at finite temperature (to be presented in future works).
For simplicity, in the following, we will consider the free massless theory case. One performs a shift around the thermal background
We will write and its conjugate as vectors whose components are bi-local fields in momentum space:
The collective Hamiltonian has a systematic expansion:
This implies that
The first equality states that in the strict large N limit, must annihilate the TFD state. The second one states that thermal backgrounds correspond to the saddle point solutions of Equation (64). At order 1 (i.e., ), we have a quadratic form (the trace is taken in the bi-local momentum space).
The kinetic matrix K is given by
where
The potential matrix is V is given by
We now turn to the TFD wave functional , which is an eigenstate of :
Based on our previous results [10], we have:
where one has the equal-time two-point functions of ’s at finite temperature
Explicitly (at ),
However, it should be stressed that the solution for is not unique. As discussed in [10], the non-uniqueness is related to the singular structure of , i.e., its zero modes. This singular structure and the zero modes appear to be related to the symmetry pointed out above.
Normal Modes and Bulk Fields
In general, there exists a basis (normal modes) such that the quadratic Hamiltonian is diagonalized. In particular, continuing with the case both K and V can be simultaneously diagonalized through a linear transformation ()
Let
is a matrix given by
The M matrix preserves the canonical commutation relations and generates a two-(functional)-parameter group. Its inverse thus is given by . It is also a symmetric matrix so that . Thus, the canonical conjugate transforms as
For a comprehensive summary, we refer the reader to Appendix B.
The importance of M is that it diagonalizes the matrices K (72) and V (74) simultaneously. For K, we have
with
For V we have
with
With this simultaneous diagonalization, we can represent the free thermofield Hamiltonian Equation (71) in terms of and . Both K and V have zero modes, as we will see in the following section. To illustrate the singular behaviors, it is necessary to separate
The non-singular part is
and the singular part is
Both terms are diagonal. We see that , and their canonical conjugates with are completely absent from .
One also has the corresponding decomposition of the TFD wave functional (76):
where and are Gaussian forms associated with and , respectively. is the wave functional of the missing modes with . They are the zero modes of and will be seen to be associated with symmetry operators. For notational simplicity we will denote and . Since we have that is not determined by Equation (75). A full understanding of it will be seen in the framework of Section 5. Details of the decomposition are given for completeness in Appendix A.
The normal modes of the linearized thermofield Hamiltonian are closely related to bulk-free fields. In the following, we discuss in detail the construction of these bulk fields and . We emphasize that these bulk fields are found to be in one-to-one correspondence with the collective fields. As such, they should not be confused with the often-used notion of ‘generalized free fields’, which are boundary CFT operators. The collective field degrees of freedom provide both the bulk wave functions and the creation-annihilation operators in the bulk. To be more explicit, consists of bi-local annihilation operators and (to be seen in below), while consists of bi-local annihilation operators and . We would like to emphasize that these bulk fields and cannot be simply interpreted as boundary operators purely from either the left or the right CFT, because the bi-local operator (cross modes) involves both of the left and the right CFT boundary operators. To avoid notation clutters, we will restrict our attention to 3D CFT, but higher dimensional CFTs follow similarly.
Let us introduce mode expansions for bi-local fields and as follows
To avoid over-counting the degrees of freedom, we should not integrate over the entire which is spanned by and . Instead, for a given , the integration region for is with a radius and an antipodally identified boundary, which is homeomorphic to . More explicitly,
For simplicity, we will abuse our notations and denote this integration region by .
Then, the quadratic Hamiltonian can be rewritten as
With the mass-shell condition
and the Jacobian
the bulk fields are defined by
Notice that the integration region guarantees that the energy E is bounded from below by 0. We would like to emphasize that and are time-like or light-like operators, while and are space-like operators. It is the latter that corresponds to evanescent modes and consists of soft modes with zero energy and non-zero momentum. Collectively, we denote both and as
and similarly for . Here, we have the extensive field with energy E ranging in . Notice that the zero modes and in the boundary exactly correspond to the soft modes in the bulk. The bulk free fields satisfy the regular commutation relations
which implies that the spectrum is complete. In terms of the bulk free fields, the quadratic Hamiltonian can be recast into the form
Furthermore, let us denote and the inverse Bogoliubov transformation of and induced by :
with
They satisfy the canonical commutation relations
As before, these operators annihilate the ground state instead of the thermal state . Their thermal expectation values are
and similarly for .
For we can expand it in the :
Here, is linear in the bi-local fields, and will be eliminated by the collective coordinate method in Section 5. can be expressed in terms of bulk fields as
such that it gives the correct Bogoliubov transformation on
and similarly for . Therefore at the quadratic order, in (103) and (110) and can be replaced by and
To summarize, from collective fluctuations, we see a complete spectrum of left and right bulk-free fields and satisfying commutation relations (106). These are extensive, with , and reflect bulk spectra in the presence of a horizon. The Hilbert space is a product of the left and right commuting sub-algebras
We have also seen that the symmetry has re-emerged at the level of quadratic fluctuations, taking the form of bulk-level Bogoliubov transformations. Note also that the zero modes (with ) are actually not present in the Hamiltonian . These will be replaced by collective coordinates in the full treatment in Section 5.
5. 1/N Expansions and Collective Coordinates
Quantization around the thermal and extended soliton cases share similarities. In both cases, quadratic fluctuations are characterized by zero modes which are related to the associated symmetries. In the TFD we have two operators and that commute with the Hamiltonian . These symmetry operators, respectively, give two classes of zero modes, and (to be revealed below). These operators when expanded at large N again start with a linear term of order . The leading term of is a c-number of order N, representing the thermal energy, which we subtract. These ‘large operators’ therefore also present problems in the naive expansions: the symmetry transformations are only implemented after an infinite re-summation. We will implement them through collective coordinates. There is a difference, however, between the two symmetries and , with the latter acting through a unitary transformation. In particular, the counterpart for the center of mass of the soliton is the hyperbolic angle , and the state corresponds to the zero temperature state . Also, the analog of the zero modes is (zero modes of the potential matrix V) in TFD. To implement the collective coordinate method, we should impose the gauge condition
The gauge condition can be chosen arbitrarily, and we will require
with the canonical conjugate of .
5.1. Zero Modes and Large Operators
Let us first briefly discuss the relation between symmetry operators and zero modes. Here, we will be schematic, and the complete expressions of the formulae will be presented in detail in the following subsections. Consider the quadratic Hamiltonian that we established in the previous section:
The kinetic matrix K (72) and the potential matrix V (74) were both seen to posses zero modes [10]:
and
with representing a label of the zero modes. These zero modes are associated with the order terms of the symmetry operators. We have2
with and , some functions of (see the following for their precise expressions). We will see that these zero modes arise from the symmetry conditions when expanded order by order in . Especially, at order we have
Detailed calculations of these will be presented in the following.
These results are not limited to vector models. In matrix models, these zero modes will appear in order N in terms of the symmetry operators. In particular, for large N matrix quantum mechanics, we will have one u and one v, and
with denoting a complete set of single trace operators and its canonical conjugate. We stress that the symmetries and explain zero modes of the kinetic and potential term in the quadratic . We also note that (in this vector case) the space (of zero modes) induced by is larger than the space induced by . In the quantum mechanical matrix model case, these sets are the same as both generate a one-parameter symmetry.
5.2.
We will first give the expansion properties of and also give its collective coordinate version. The full Hamiltonian , when written in terms of collective fields, reads:
Expanding it around the thermal background generates a expansion series
The leading order (i.e., ), however, is non-zero, and gives (twice) the average energy at inverse temperature :
At the same time, the sub-leading term (i.e., ) does not vanish and is given by
Within the trace, we have
and we are integrating . They are zero modes of K [9,10] given in Equation (129):
which appear as the consistency condition that and must commute with each other:
In the large N limit, this gives a set of consistency equations at each order of :
Taking , we have
which explicitly shows that u must be the zero mode of K.
In principle, we can treat as a collective coordinate. To apply the collective coordinate method, we demand the constraint equation to be
We consider the critical point for simplicity, such that we can use conformal symmetry. Then, we can choose the canonical gauge condition
where is the dilatation operator, such that
One can shift the appearance of to by redefining the states and operators in the following way
so that the oscillators are factorized into three commuting sets
5.3. as a Collective Coordinate
Let us then demonstrate the implementation of the collective coordinate method with in TFD. First, we reveal the zero mode problems and the issues of -transformation at large N. For simplicity, we will again consider the free theory case. In this case, the potential matrix V (86) has zero modes [10] (we omit the normalization factors):
They obey
The appearance of these modes has been understood well in [10]: they are the Goldstone modes and thus can be computed directly via
up to some coefficients, with the Fourier transform of the thermal background solution. We note that and obey the orthogonality condition
This relation implies that a class of degrees of freedom is completely missing in , as we have seen above. In addition, it also reveals that and are not unrelated.
In the soliton problem, the zero mode can be derived from the symmetry condition . We can also show that the zero modes can be derived from . Let us give a brief demonstration, again using the free theory to simplify calculations. Since itself is invariant under the Bogoliubov transformation, we can write it as (see Equation (55))
In the last step, we use Bogoliubov transformation to write . Here, , with the integrand the zero mode of . Then, we compute the commutator to obtain
which indicates that v must be zero modes of V.
Due to the dependence on N, issues arise when performing -transformations. We perform a expansion for :
with
Due to the appearance of this order term in , we have a similar problem when transforming fields as in the soliton case. Again, let us illustrate this in an analogous pattern. We consider the following transformation of the bi-local field , before which each field is expanded in :
Here, . In the first step in Equation (149), we expand both and in . Note that is the large N background at zero temperature. We expect the results would be Equation (151). However, we see from Equation (150) that this computation cannot be carried out unless we know the full series of the expansions: different orders in become mixed. For example, considering the commutator , we see that the result gives an order 1 term, and hence contributes to the background, and shifts .
Next, to decouple variables in the gauge condition, we can make a change to the reference frame. Since only depends on the magnitude , we will write instead. In O(N) vector TFD, we have the operator as
Define
Then, the bi-local collective field representation of is given by
where
To introduce the collective coordinate, we need to extract the function . This can be carried out by introducing
such that
The operator then can be written as
where we write the integral in spherical coordinates, and ‘’ denotes the matrix trace. We then introduce the collective coordinate to define
This is the analog of in the one-soliton case. There, we only have one zero mode, and hence we have one collective coordinate . Here, we have infinitely many zero modes, each labeled by k, and thus we introduce . One can redefine the states and collective operators in the following way
For bi-local field, we can write down the explicit transformation
We then introduce the constraint and the gauge condition
Here, is the canonical conjugate of . The oscillators are factorized into three commuting sets
The gauge condition is chosen to be of this form so that the -transformation can be undone and the -dependence can be eliminated by switching to the center frame of reference. To be more explicit, we make a transformation
Consequently, the constraint and the gauge condition become
We then perform a expansion of the fields
One can check that the zero modes are given by
Using these relations, the constraint is expanded to be
We have the exact solution of :
This solution can be expanded in ,
At the same time, the zero modes v are projected out from :
The gauge condition can be arbitrary. We choose the simplest gauge
such that with Equation (175) the zero modes are projected out from the fluctuations (they are replaced by the collective coordinates ). For these, one has the subsidiary conditions:
explained in Appendix C, which leads to the center part of the wave functional
Therefore the total wave function of the TFD state reads
As a result, the thermofield Hamiltonian becomes
Comparing with the translational case, the collective coordinates and their canonical conjugates are completely absent from the thermofield Hamiltonian, which is consistent with the fact that
One now has that both and are expanded in
with the large being put to zero (due to the gauge condition). They together with the well-defined propagator allow for a systematic expansion. At the quadratic level (and therefore the Hilbert space), the structure is similar to the one predicted by Witten [4] on very general grounds. However, in regard to perturbation, expansion issues have been brought up in [4], which might be solved in the present treatment.
6. Conclusions
In the present work, we have addressed the structure of the Hilbert space and the expansion in perturbation around large N extended states. Fluctuations around these states are singular and are characterized by zero modes associated with broken symmetries. This is generally addressed by the introduction of quantum mechanical collective coordinates with a Hilbert space containing these in addition to the fluctuating bulk fields. In the TFD state case, the diagonal gauging of O(N) was emphasized, which as it was seen appears appropriate for a two-sided ER bridge space-time. Even though in the vector theory that was used in this study the dual higher spin (HS) theory involves all spins, one still expects that in the thermal case, the appropriate linearized fluctuations are to be in gravitational two-sided backgrounds with a horizon. Clearly, this is to be understood from an analogous study at the HS level. Also, gauging in CFT, one has a parallel in recent gravitational studies (in two-sided wormhole space-times) [24,25,26] with the diagonal implementation of constraint symmetries. Finally, the structure of the large N Hilbert space and implementation of Goldstone symmetries that we have exhibited with explicit evaluations in the large N vector case applies more generally, in particular in matrix type models [15], string theory [30] and cosmology [31]. This follows from the general structure of the Hamiltonian collective field theory.
Author Contributions
All authors contribute the same to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the U.S. Department of Energy under contract DE-SC0010010.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
We would like to acknowledge useful discussions with Sumit Das, Robert de Mello Koch, Samir Mathur, Sanjaye Ramgoolam and Junggi Yoon on topics related to this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. TFD State Decomposition
We now turn to the discussion of the TFD state. To illustrate the TFD wave functional, it is more illustrative to work in the normal modes basis. We have already seen that M diagonalizes the matrices K (72) and V (74) simultaneously. In addition, it also diagonalizes :
This simple relation reveals that the TFD wave function is diagonalized in terms of the normal modes:
In particular, in terms of the normal modes , we can decompose the TFD wave functional into three pieces:
corresponds to the non-singular part of the thermofield Hamiltonian (88):
Similarly corresponds to the singular part of the thermofield Hamiltonian (89):
Lastly, the central sector of the TFD wave functional corresponds to the central part, and cannot be determined from . To obtain , we may add a regulator the of the form (in the following we take and similarly for its canonical conjugate)
with the functions and only depending on the norm of the momentum, and obeying
This regulator commutes with both and (and also ), since we take the limit . It’s useful to the zero mode as
where we denote and as the solid angle variables in momentum space, the thermofield Hamiltonian then has information for this zero mode, from which we can easily obtain :
The normalization factors satisfy . Another way to see this is that the TFD wave functional is related to the equal-time thermal two-point functions of bi-local fields, as indicated in Equation (77). Using the non-vanishing two-point functions (cf. Equation (77))
we immediately recover the central part of the wave function .
Notice that the density fields for and are given by
we may write as
We would like to compare our result with Witten’s [4]. Here, we briefly review Witten’s treatment. In the thermofield double state, we have two copies of algebra and , with respect to the left and right systems, with non-trivial commutators. Consider the regularized left and right Hamiltonian
subtracted by the thermal expectation value. They do not have a well-defined large N limits, but their difference does exist as an operator acting on the thermofield double Hilbert space , which implies that is not a simple tensor product of left and right Hilbert spaces acted on by the algebras and . In fact, Witten pursuits an asymmetric treatment and identifies an operator U only from the regularized right Hamiltonian
which becomes central and commutes with in the limit. This is analogous to our , a.k.a. the first order term of the collective Hamiltonian density in the symmetric setting. Then, one can define an extended algebra as a tensor product
where is the abelian algebra of bounded functions of U. Since has a well-defined large N limit, vanishes at , so also commutes with , in precise agreement of what we found in TFD state decomposition. Furthermore, acts on the extended thermofield double Hilbert space
where is the space of square-integrable functions of U. Note that the connected k-point functions vanish in the large N limit for , together with its variance
the central wavefunction must be Gaussian of the form
which is analogous to our central wavefunction (A13).
Appendix B. Symmetry Transformations
We summarize various Bogoliubov transformation of the thermofield dynamics in free O(N) vector model. In TFD formalism, for an operator , its Bogoliubov transformation is given through the operator by
which satisfies
Thus, the -transformation preserves symplectic structures. Recall that in free theory (55) is given by
O(N) vector fields.
Let , by a direct calculation one can show
with the Bogoliubov transformation matrix U as
The U matrices obey , such that they form a one-(functional)-parameter group. Furthermore, we have , implying that it induces a canonical transformation.
We can also study the Bogoliubov transformations of the fields , and their canonical conjugates. Let , the -transformation can be written as
The new Bogoliubov transformation matrix is now block-diagonal:
One can check that still obeys the properties listed above. At the same time, The S matrices also form a one-(functional)-parameter group, and .
Bi-local collective fields.
Let us consider the Bogoliubov transformations induced by of the bi-local fields :
We find ()
Let
is the tensor product of and Equation (A26), and can be written as:
We have two important properties of M:
- M is a two-(functional)-parameter group:so that its inverse is
- . Let , then we have
Collective oscillators.
It is convenient to define matrices of the bi-local operators as in [9]:
and
The definition and the algebra of these composite operators A, B, C and D are summarized in Appendix A of [10]. Here, we will discuss their Bogoliubov transformations, and also the counterpart for their expansions.
In the large N limit, these operator have expansions. To linear order we have3
and similarly for its hermitian conjugates . On the other hand, does not have linear terms. From the Bogoliubov transformation for bulk fields (104), we can read off the corresponding transformation for large N bi-local oscillators
and similarly for and . They annihilate the zero temperature vacuum state and obey the regular commutation relations
and similarly for and . As a byproduct, the bulk fields can be expressed in terms of large N bi-local oscillators in the same way as (97), except that the subscripts are dropped on both hand-sides of the equation.
transformations.
Let us now study in detail the total Hamiltonian . It induces a non-unitary transformation, under which some certain combinations of operators annihilate the TFD state. According to Equation (52), we find
These simple relations are the basics of the work [32] for building the TFD states. One can of course insert other oscillators , and to make transformations of other collective fields. These transformations are easily computed in free theory, but not in interacting theories, in which case is quite involved. Nevertheless it is in principle calculable. To study the large N limit, two procedures are involved: (1) transformation, and (2) the expansion in collective representation. The process (1) → (2) is well defined and one can in principle perform it. On the other hand, as we will see below, the problem is much harder if we perform (2) → (1), which resembles the translational issues in the soliton case. In the latter procedure, the expansion loses its power since we will need to taking the whole series of the expansion into account. This represents similar issues as in the soliton case.
The presence of this order operator (i.e., ) reveals that thermal backgrounds are not saddle point solutions of . Indeed, has only one stationary point, which is also the minimum: the ground state. It meanwhile causes severe issues when applying to transformations of operators: it gives shifts of order which is not defined in the large N limit. As illustrated above, commutes with the thermofield Hamiltonian , so it becomes central in the large N limit, as discussed by Witten [4]. Let us now take as a collective operator which under the transformation of annihilates the TFD state, e.g., as in Equation (A41). In the collective representation can be expanded in :
However, to compute its transformation
one has to carry out an infinite computation. This is because terms of order and order get mixed, so the evaluation can be carried out by expanding:
with denoting the adjoint transformation, and
Here, to make simplification, we only expand to its order term. The transformation thus reorganizes the all higher order terms expansion series into lower order ones. This is a universal property that does not only arise in the O vector model, but in TFD states for all large N theories. This is illustrated in the diagram below: the process (1) → (2) is calculable and gives a systematic expansion of the transformation of . The other process (2) → (1) is much more involved, and one needs to take the whole expansion series of into account.
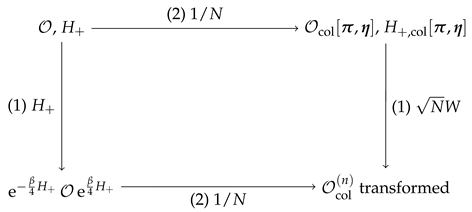
Appendix C. Constraint of Thermofield Double State
To recover the central part wave functional, using the bi-local operators
we can write (158) as
Recall that the vacuum state is annihilated by C:
we can write such that . Thus,
where is defined similarly as . We therefore have
We note that the first two terms can be written in terms of the collective coordinate
Using the constraint we can also write the last term as . Thus, we have
Note that is of order , and thus is of order .
Notes
| 1 | A bit explanation of the notations: Here, with and . In the context of AdS/CFT, one also denotes and . |
| 2 | Here, inside the traces one has one bi-local field and some c-numbers, and the notation means , and similarly in the following discussions. |
| 3 | Here, to emphasize the Bogoliubov transformation of fields, we put a subscript for the fields. Comparing with the notations in [9], we have , and similarly for other bi-local oscillators. |
References
- Maldacena, J.M. Eternal black holes in anti-de Sitter. J. High Energy Phys. 2003, 2003, 021. [Google Scholar] [CrossRef]
- Leutheusser, S.; Liu, H. Causal connectability between quantum systems and the black hole interior in holographic duality. Phys. Rev. D 2023, 108, 086019. [Google Scholar] [CrossRef]
- Leutheusser, S.A.W. Emergent Times in Holographic Duality. Phys. Rev. D 2023, 108, 086020. [Google Scholar] [CrossRef]
- Witten, E. Gravity and the crossed product. J. High Energy Phys. 2022, 10, 008. [Google Scholar] [CrossRef]
- Chandrasekaran, V.; Penington, G.; Witten, E. Large N algebras and generalized entropy. J. High Energy Phys. 2023, 2023, 9. [Google Scholar] [CrossRef]
- Klebanov, I.R.; Polyakov, A.M. AdS dual of the critical O(N) vector model. Phys. Lett. B 2002, 550, 213–219. [Google Scholar] [CrossRef]
- Giombi, S.; Yin, X. Higher Spin Gauge Theory and Holography: The Three-Point Functions. J. High Energy Phys. 2010, 9, 115. [Google Scholar] [CrossRef]
- Das, S.R.; Jevicki, A. Large N collective fields and holography. Phys. Rev. D 2003, 68, 044011. [Google Scholar] [CrossRef]
- Jevicki, A.; Yoon, J. Bulk from Bi-locals in Thermo Field CFT. J. High Energy Phys. 2016, 02, 090. [Google Scholar] [CrossRef]
- Jevicki, A.; Liu, X.; Yoon, J.; Zheng, J. Dynamical Symmetry and the Thermofield State at Large N. Universe 2022, 8, 114. [Google Scholar] [CrossRef]
- Gervais, J.L.; Jevicki, A.; Sakita, B. Perturbation Expansion Around Extended Particle States in Quantum Field Theory. Phys. Rev. D 1975, 12, 1038. [Google Scholar] [CrossRef]
- de Mello Koch, R.; Kemp, G. Holography of information in AdS/CFT. J. High Energy Phys. 2022, 12, 95. [Google Scholar] [CrossRef]
- de Mello Koch, R. Microscopic entanglement wedges. J. High Energy Phys. 2023, 08, 056. [Google Scholar] [CrossRef]
- de Mello Koch, R. Gravitational dynamics from collective field theory. J. High Energy Phys. 2023, 10, 151. [Google Scholar] [CrossRef]
- Koch, R.D.M.; Jevicki, A.; Liu, X.; Mathaba, K.; Rodrigues, J.A.P. Large N optimization for multi-matrix systems. J. High Energy Phys. 2022, 1, 168. [Google Scholar] [CrossRef]
- Mathaba, K.; Mulokwe, M.; Rodrigues, J.A.P. Large N Master Field Optimization: The Quantum Mechanics of two Yang–Mills coupled Matrices. arXiv 2023, arXiv:2306.00935. [Google Scholar] [CrossRef]
- Vasiliev, M.A. Higher Spin Gauge Theories: Star Product and AdS Space; World Scientific: Singapore, 1999; pp. 533–610. [Google Scholar] [CrossRef]
- Didenko, V.E.; Skvortsov, E.D. Elements of Vasiliev theory. arXiv 2014, arXiv:1401.2975. [Google Scholar]
- de Mello Koch, R.; Jevicki, A.; Rodrigues, J.a.P.; Yoon, J. Canonical Formulation of O(N) Vector/Higher Spin Correspondence. J. Phys. A 2015, 48, 105403. [Google Scholar] [CrossRef][Green Version]
- Christ, N.H.; Lee, T.D. Quantum Expansion of Soliton Solutions. Phys. Rev. D 1975, 12, 1606. [Google Scholar] [CrossRef]
- Korepin, V.E.; Faddeev, L.D. Quantization of Solitons. Theor. Math. Phys. 1975, 25, 1039–1049. [Google Scholar] [CrossRef]
- Takahasi, Y.; Umezawa, H. Thermo field dynamics. Collect. Phenom. 1975, 2, 55–80. [Google Scholar]
- Shenker, S.H.; Yin, X. Vector Models in the Singlet Sector at Finite Temperature. arXiv 2011, arXiv:1109.3519. [Google Scholar]
- Mathur, S.D. Black holes and holography. J. Phys. Conf. Ser. 2012, 405, 012005. [Google Scholar] [CrossRef]
- Marolf, D.; Wall, A.C. Eternal Black Holes and Superselection in AdS/CFT. Class. Quant. Grav. 2013, 30, 025001. [Google Scholar] [CrossRef]
- Jensen, K.; Sonner, J. Wormholes and entanglement in holography. Int. J. Mod. Phys. D 2014, 23, 1442003. [Google Scholar] [CrossRef]
- Jafferis, D.L.; Kolchmeyer, D.K. Entanglement Entropy in Jackiw-Teitelboim Gravity. arXiv 2019, arXiv:1911.10663. [Google Scholar]
- Penington, G.; Witten, E. Algebras and States in JT Gravity. arXiv 2023, arXiv:2301.07257. [Google Scholar]
- Engelhardt, N.; Folkestad, R. Canonical purification of evaporating black holes. Phys. Rev. D 2022, 105, 086010. [Google Scholar] [CrossRef]
- Dabholkar, A. Quantum Entanglement in String Theory. arXiv 2022, arXiv:2207.03624. [Google Scholar]
- Gomez, C. Cosmology as a Crossed Product. arXiv 2022, arXiv:2207.06704. [Google Scholar]
- Cottrell, W.; Freivogel, B.; Hofman, D.M.; Lokhande, S.F. How to Build the Thermofield Double State. J. High Energy Phys. 2019, 2019, 58. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
