A Systematic Study of Two-Neutrino Double Electron Capture
Abstract
1. Introduction
2. Formalism for the Two-Neutrino Double Electron Capture
2.1. Energetics
2.2. Half-Life
2.3. Electron Bound States Description
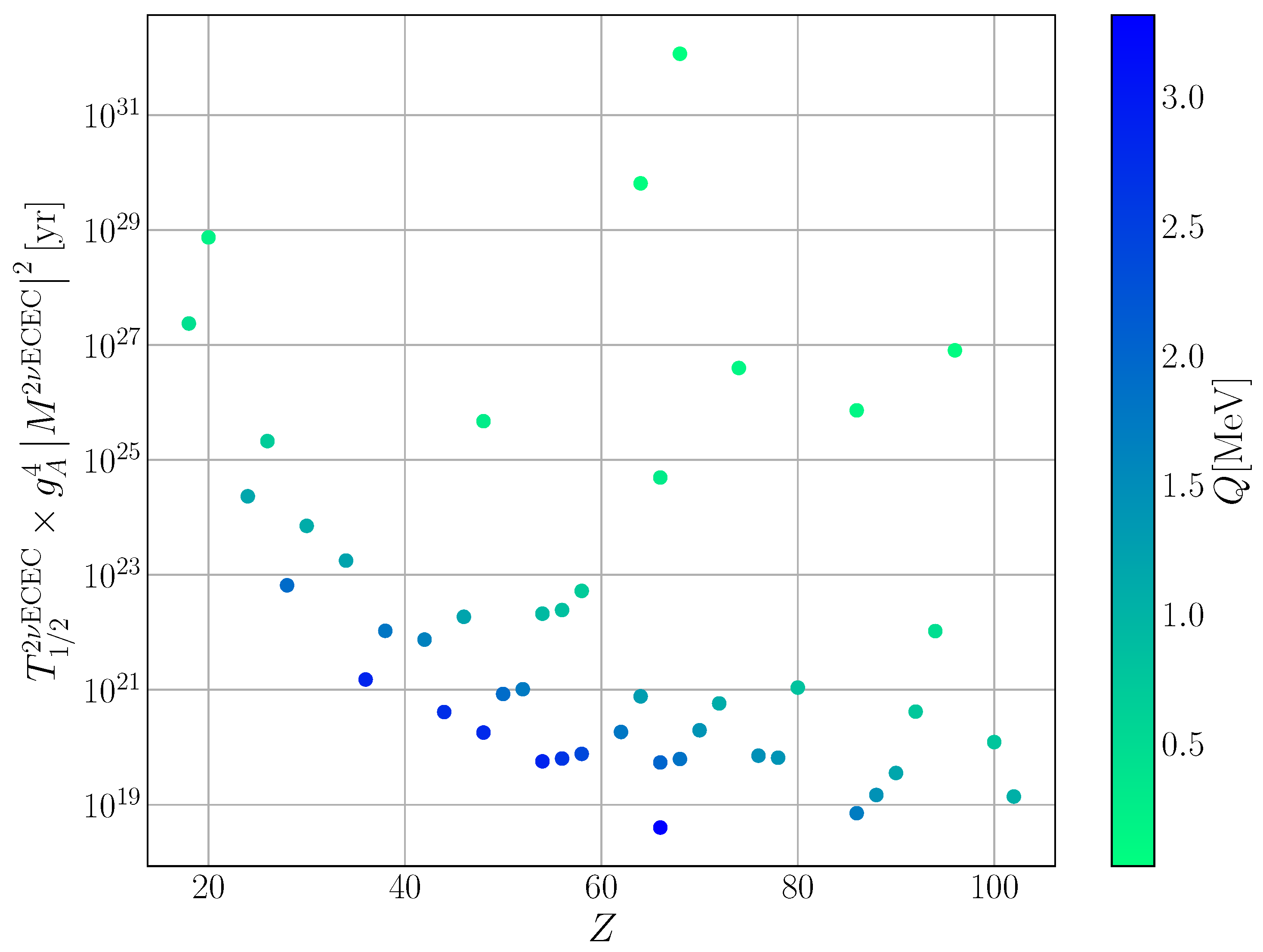
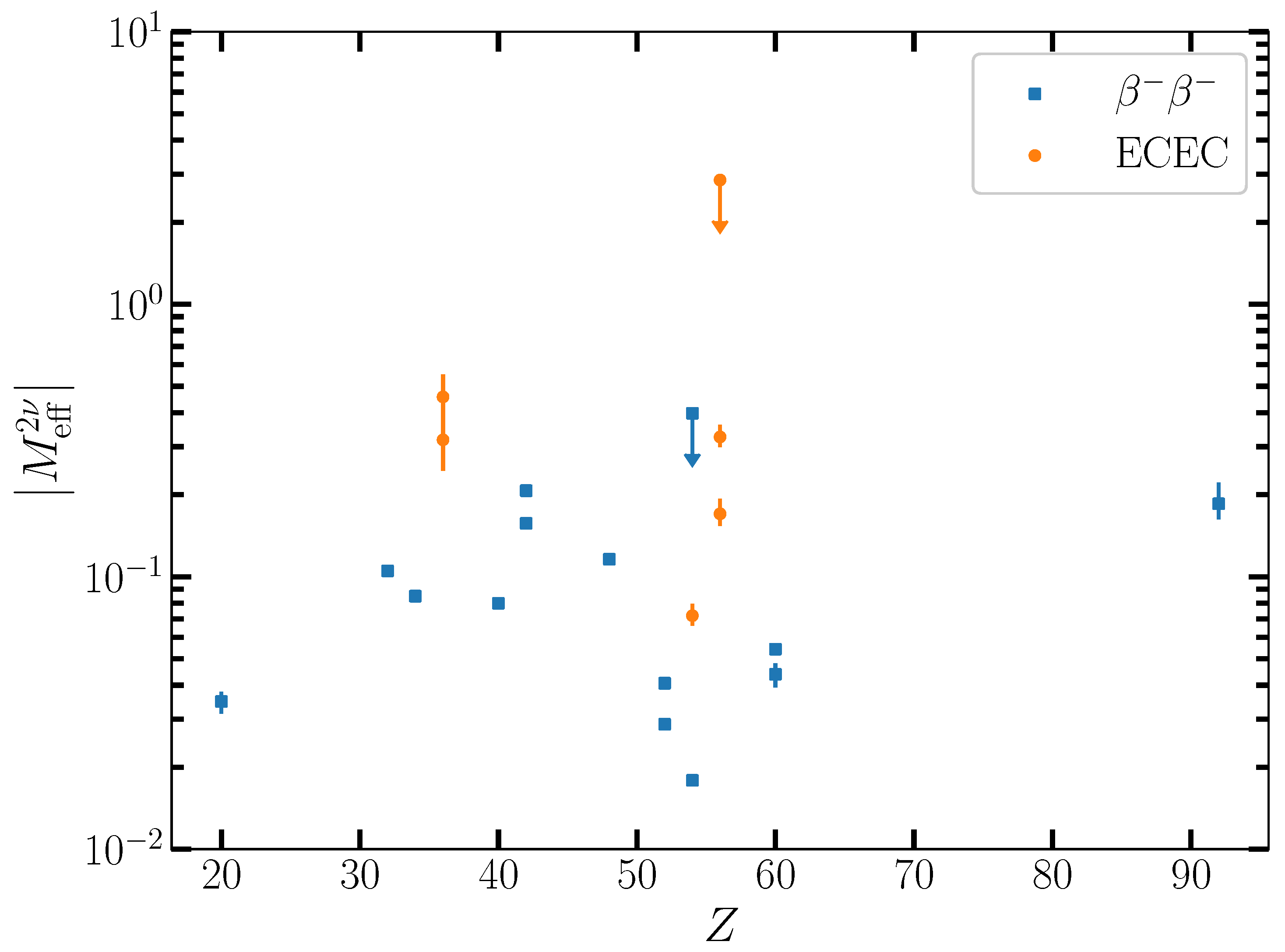
3. Results and Discussions
4. Uncertainties and Further Improvements
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Majorana, E. Teoria simmetrica dell’elettrone e del positrone. II Nuovo C. 1937, 14, 171–184. [Google Scholar] [CrossRef]
- Schechter, J.; Valle, J.W.F. Neutrino decay and spontaneous violation of lepton number. Phys. Rev. D 1982, 25, 774–783. [Google Scholar] [CrossRef]
- Sujkowski, Z.; Wycech, S. Neutrinoless double electron capture: A tool to search for Majorana neutrinos. Phys. Rev. C 2004, 70, 052501. [Google Scholar] [CrossRef]
- Pascoli, S.; Petcov, S.; Schwetz, T. The absolute neutrino mass scale, neutrino mass spectrum, Majorana CP-violation and neutrinoless double-beta decay. Nucl. Phys. B 2006, 734, 24–49. [Google Scholar] [CrossRef]
- Bilenky, S.M.; Giunti, C. Neutrinoless double-beta decay: A probe of physics beyond the Standard Model. Int. J. Mod. Phys. A 2015, 30, 1530001. [Google Scholar] [CrossRef]
- Vergados, J.D.; Ejiri, H.; Šimkovic, F. Neutrinoless double beta decay and neutrino mass. Int. J. Mod. Phys. E 2016, 25, 1630007. [Google Scholar] [CrossRef]
- Girardi, I.; Petcov, S.; Titov, A. Predictions for the Majorana CP violation phases in the neutrino mixing matrix and neutrinoless double beta decay. Nucl. Phys. B 2016, 911, 754–804. [Google Scholar] [CrossRef]
- Šimkovic, F. Neutrino masses and interactions and neutrino experiments in the laboratory. Physics-Uspekhi 2021, 64, 1238. [Google Scholar] [CrossRef]
- Fukugita, M.; Yanagida, T. Barygenesis without grand unification. Phys. Lett. B 1986, 174, 45–47. [Google Scholar] [CrossRef]
- Buchmüller, W.; Peccei, R.; Yanagida, T. Leptogenesis as the origin of matter. Annu. Rev. Nucl. Part. Sci. 2005, 55, 311–355. [Google Scholar] [CrossRef]
- Ebert, J.; Fritts, M.; Gehre, D.; Gößling, C.; Hagner, C.; Heidrich, N.; Klingenberg, R.; Kröninger, K.; Nitsch, C.; Oldorf, C.; et al. Results of a search for neutrinoless double-β decay using the COBRA demonstrator. Phys. Rev. C 2016, 94, 024603. [Google Scholar] [CrossRef]
- Barabash, A.S.; Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; d’Angelo, S.; Incicchitti, A.; et al. Final results of the Aurora experiment to study 2β decay of 116Cd with enriched 116CdWO4 crystal scintillators. Phys. Rev. D 2018, 98, 092007. [Google Scholar] [CrossRef]
- Anton, G.; Badhrees, I.; Barbeau, P.S.; Beck, D.; Belov, V.; Bhatta, T.; Breidenbach, M.; Brunner, T.; Cao, G.F.; Cen, W.R.; et al. Search for Neutrinoless Double-β Decay with the Complete EXO-200 Dataset. Phys. Rev. Lett. 2019, 123, 161802. [Google Scholar] [CrossRef] [PubMed]
- Agostini, M. et al. [GERDA Collaboration] Final Results of GERDA on the Search for Neutrinoless Double-β Decay. Phys. Rev. Lett. 2020, 125, 252502. [Google Scholar] [CrossRef] [PubMed]
- Azzolini, O.; Beeman, J.W.; Bellini, F.; Beretta, M.; Biassoni, M.; Brofferio, C.; Bucci, C.; Capelli, S.; Caracciolo, V.; Cardani, L.; et al. Final Result on the Neutrinoless Double Beta Decay of 82Se with CUPID-0. Phys. Rev. Lett. 2022, 129, 111801. [Google Scholar] [CrossRef]
- Adams, D.Q. et al. [CUORE Collaboration] New Direct Limit on Neutrinoless Double Beta Decay Half-Life of 128Te with CUORE. Phys. Rev. Lett. 2022, 129, 222501. [Google Scholar] [CrossRef] [PubMed]
- Abe, S. et al. [KamLAND-Zen Collaboration] Search for the Majorana Nature of Neutrinos in the Inverted Mass Ordering Region with KamLAND-Zen. Phys. Rev. Lett. 2023, 130, 051801. [Google Scholar] [CrossRef]
- Arnquist, I.J. et al. [Majorana Collaboration] Final Result of the Majorana Demonstrator’s Search for Neutrinoless Double-β Decay in 76Ge. Phys. Rev. Lett. 2023, 130, 062501. [Google Scholar] [CrossRef]
- Saakyan, R. Two-Neutrino Double-Beta Decay. Annu. Rev. Nucl. Part. Sci. 2013, 63, 503–529. [Google Scholar] [CrossRef]
- Barabash, A. Precise Half-Life Values for Two-Neutrino Double-β Decay: 2020 Review. Universe 2020, 6, 159. [Google Scholar] [CrossRef]
- Barabash, A. Double Beta Decay Experiments: Recent Achievements and Future Prospects. Universe 2023, 9, 290. [Google Scholar] [CrossRef]
- Deppisch, F.F.; Graf, L.; Rodejohann, W.; Xu, X.J. Neutrino self-interactions and double beta decay. Phys. Rev. D 2020, 102, 051701. [Google Scholar] [CrossRef]
- Deppisch, F.F.; Graf, L.; Šimkovic, F. Searching for New Physics in Two-Neutrino Double Beta Decay. Phys. Rev. Lett. 2020, 125, 171801. [Google Scholar] [CrossRef]
- Barabash, A.; Dolgov, A.; Dvornický, R.; Šimkovic, F.; Smirnov, A. Statistics of neutrinos and the double beta decay. Nucl. Phys. B 2007, 783, 90–111. [Google Scholar] [CrossRef]
- Bolton, P.D.; Deppisch, F.F.; Gráf, L.; Šimkovic, F. Two-neutrino double beta decay with sterile neutrinos. Phys. Rev. D 2021, 103, 055019. [Google Scholar] [CrossRef]
- Agostini, M.; Bossio, E.; Ibarra, A.; Marcano, X. Search for light exotic fermions in double-beta decays. Phys. Lett. B 2021, 815, 136127. [Google Scholar] [CrossRef]
- Díaz, J.S. Limits on Lorentz and CPT violation from double beta decay. Phys. Rev. D 2014, 89, 036002. [Google Scholar] [CrossRef]
- Niţescu, O.; Ghinescu, S.; Stoica, S. Lorentz violation effects in 2νββ decay. J. Phys. G Nucl. Part. Phys. 2020, 47, 055112. [Google Scholar] [CrossRef]
- Ghinescu, S.A.; Niţescu, O.; Stoica, S. Investigation of the Lorentz invariance violation in two-neutrino double-beta decay. Phys. Rev. D 2022, 105, 055032. [Google Scholar] [CrossRef]
- Arnold, R. et al. [NEMO Collaboration] Limits on different majoron decay modes of 100Mo and 82Se for neutrinoless double beta decays in the NEMO-3 experiment. Nucl. Phys. A 2006, 765, 483–494. [Google Scholar] [CrossRef][Green Version]
- Arnold, R.; Augier, C.; Barabash, A.S.; Basharina-Freshville, A.; Blondel, S.; Blot, S.; Bongrand, M.; Boursette, D.; Brudanin, V.; Busto, J.; et al. Detailed studies of 100Mo two-neutrino double beta decay in NEMO-3. Eur. Phys. J. C 2019, 79, 440. [Google Scholar] [CrossRef]
- Arnold, R. et al. [NEMO-3 Collaboration] Search for Neutrinoless Quadruple-β Decay of 150Nd with the NEMO-3 Detector. Phys. Rev. Lett. 2017, 119, 041801. [Google Scholar] [CrossRef] [PubMed]
- Bossio, E.; Agostini, M. Probing beyond the standard model physics with double-beta decays. J. Phys. G Nucl. Part. Phys. 2023, 51, 023001. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Caracciolo, V. Status and Perspectives of 2ϵ, ϵβ+ and 2β Decays. Particles 2021, 4, 241–274. [Google Scholar] [CrossRef]
- Doi, M.; Kotani, T. Neutrino Emitting Modes of Double Beta Decay. Prog. Theor. Phys. 1992, 87, 1207–1231. [Google Scholar] [CrossRef]
- Doi, M.; Kotani, T. Neutrinoless Modes of Double Beta Decay. Prog. Theor. Phys. 1993, 89, 139–159. [Google Scholar] [CrossRef]
- Barabash, A.S.; Saakyan, R.R. Experimental limits on 2β+, Kβ+, and 2K processes for 130Ba and on 2K capture for 132Ba. Phys. At. Nucl. 1996, 59, 179–184. [Google Scholar]
- Meshik, A.P.; Hohenberg, C.M.; Pravdivtseva, O.V.; Kapusta, Y.S. Weak decay of 130Ba and 132Ba: Geochemical measurements. Phys. Rev. C 2001, 64, 035205. [Google Scholar] [CrossRef]
- Pujol, M.; Marty, B.; Burnard, P.; Philippot, P. Xenon in Archean barite: Weak decay of 130Ba, mass-dependent isotopic fractionation and implication for barite formation. Geochim. Cosmochim. Acta 2009, 73, 6834–6846. [Google Scholar] [CrossRef]
- Gavrilyuk, Y.M.; Gangapshev, A.M.; Kazalov, V.V.; Kuzminov, V.V.; Panasenko, S.I.; Ratkevich, S.S. Indications of 2ν2K capture in 78Kr. Phys. Rev. C 2013, 87, 035501. [Google Scholar] [CrossRef]
- Ratkevich, S.S.; Gangapshev, A.M.; Gavrilyuk, Y.M.; Karpeshin, F.F.; Kazalov, V.V.; Kuzminov, V.V.; Panasenko, S.I.; Trzhaskovskaya, M.B.; Yakimenko, S.P. Comparative study of the double-K-shell-vacancy production in single- and double-electron-capture decay. Phys. Rev. C 2017, 96, 065502. [Google Scholar] [CrossRef]
- Aprile, E. et al. [XENON Collaboration] Observation of two-neutrino double electron capture in 124Xe with XENON1T. Nature 2019, 568, 532–535. [Google Scholar] [CrossRef] [PubMed]
- Aprile, E. et al. [XENON Collaboration] Double-weak decays of 124Xe and 136Xe in the XENON1T and XENONnT experiments. Phys. Rev. C 2022, 106, 024328. [Google Scholar] [CrossRef]
- Primakoff, H.; Rosen, S.P. Double beta decay. Rep. Prog. Phys. 1959, 22, 121. [Google Scholar] [CrossRef]
- Primakoff, H.; Rosen, S.P. A Corrigendum to the Article ‘Double Beta Decay’ by H. Primakoff and S. P. Rosen in Reports on Progress in Physics. Proc. Phys. Soc. 1961, 78, 464. [Google Scholar] [CrossRef]
- Vergados, J. Lepton-violating β−β−, β+β+ decays, (e−, e+) conversion and double electron capture in gauge theories. Nucl. Phys. B 1983, 218, 109–144. [Google Scholar] [CrossRef]
- Kim, C.W.; Kubodera, K. Double-positron decay, positron-emitting K capture, and double K capture. Phys. Rev. D 1983, 27, 2765–2768. [Google Scholar] [CrossRef]
- Boehm, F.; Vogel, P. Physics of Massive Neutrinos; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Kotila, J.; Iachello, F. Phase space factors for β+β+ decay and competing modes of double-β decay. Phys. Rev. C 2013, 87, 024313. [Google Scholar] [CrossRef]
- Mirea, M.; Pahomi, T.; Stoica, S. Values of the phase space factors involved in double beta decay. Rom. Rep. Phys. 2015, 67, 872–889. [Google Scholar]
- Stoica, S.; Mirea, M. Phase Space Factors for Double-Beta Decays. Front. Phys. 2019, 7, 12. [Google Scholar] [CrossRef]
- Martínez-Lema, G. et al. [NEXT Collaboration] Sensitivity of the NEXT experiment to Xe-124 double electron capture. J. High Energy Phys. 2021, 2021, 1029–8479. [Google Scholar] [CrossRef]
- Haxton, W.; Stephenson, G. Double beta decay. Prog. Part. Nucl. Phys. 1984, 12, 409–479. [Google Scholar] [CrossRef]
- Suhonen, J. Double beta decays of 124Xe investigated in the QRPA framework. J. Phys. G Nucl. Part. Phys. 2013, 40, 075102. [Google Scholar] [CrossRef]
- Pirinen, P.; Suhonen, J. Systematic approach to β and 2νββ decays of mass A = 100 − 136 nuclei. Phys. Rev. C 2015, 91, 054309. [Google Scholar] [CrossRef]
- Coello Pérez, E.; Menéndez, J.; Schwenk, A. Two-neutrino double electron capture on 124Xe based on an effective theory and the nuclear shell model. Phys. Lett. B 2019, 797, 134885. [Google Scholar] [CrossRef]
- Niţescu, O.; Stoica, S.; Šimkovic, F. Exchange correction for allowed β decay. Phys. Rev. C 2023, 107, 025501. [Google Scholar] [CrossRef]
- Sevestrean, V.A.; Niţescu, O.; Ghinescu, S.; Stoica, S. Self-consistent calculations for atomic electron capture. Phys. Rev. A 2023, 108, 012810. [Google Scholar] [CrossRef]
- Salvat, F.; Fernández-Varea, J.M. RADIAL: A Fortran subroutine package for the solution of the radial Schrödinger and Dirac wave equations. Comput. Phys. Commun. 2019, 240, 165–177. [Google Scholar] [CrossRef]
- Lotz, W. Electron Binding Energies in Free Atoms*. J. Opt. Soc. Am. 1970, 60, 206–210. [Google Scholar] [CrossRef]
- Wang, M.; Huang, W.; Kondev, F.; Audi, G.; Naimi, S. The AME 2020 atomic mass evaluation (II). Tables, graphs and references*. Chin. Phys. C 2021, 45, 030003. [Google Scholar] [CrossRef]
- Barabash, A.S. Does the weak interaction constant depend on time? J. Exp. Theor. Phys. Lett. 1998, 68, 1–6. [Google Scholar] [CrossRef]
- Barabash, A.S. Possible evidence for a time variation of the weak-interaction constant from double-beta-decay experiments. Phys. At. Nucl. 2000, 63, 1210–1213. [Google Scholar] [CrossRef]
- Barabash, A.S. Possible Evidence of Time Variation of Weak Interaction Constant from Double Beta Decay Experiments. Astrophys. Space Sci. 2003, 283, 607–612. [Google Scholar] [CrossRef]
- Kotila, J.; Iachello, F. Phase-space factors for double-β decay. Phys. Rev. C 2012, 85, 034316. [Google Scholar] [CrossRef]
- Yan, X.; Cheng, Z.; Abdukerim, A.; Bo, Z.; Chen, W.; Chen, X.; Cheng, C.; Cui, X.; Fan, Y.; Fang, D.; et al. Searching for Two-Neutrino and Neutrinoless Double Beta Decay of 134Xe with the PandaX-4T Experiment. arXiv 2023, arXiv:2312.15632. [Google Scholar]
- Eliseev, S.; Roux, C.; Blaum, K.; Block, M.; Droese, C.; Herfurth, F.; Kluge, H.J.; Krivoruchenko, M.I.; Novikov, Y.N.; Minaya Ramirez, E.; et al. Resonant Enhancement of Neutrinoless Double-Electron Capture in 152Gd. Phys. Rev. Lett. 2011, 106, 052504. [Google Scholar] [CrossRef] [PubMed]
- Krivoruchenko, M.; Šimkovic, F.; Frekers, D.; Faessler, A. Resonance enhancement of neutrinoless double electron capture. Nucl. Phys. A 2011, 859, 140–171. [Google Scholar] [CrossRef]
- Blaum, K.; Eliseev, S.; Danevich, F.A.; Tretyak, V.I.; Kovalenko, S.; Krivoruchenko, M.I.; Novikov, Y.N.; Suhonen, J. Neutrinoless double-electron capture. Rev. Mod. Phys. 2020, 92, 045007. [Google Scholar] [CrossRef]
- Šimkovic, F.; Dvornický, R.; Vogel, P. Muon capture rates: Evaluation within the quasiparticle random phase approximation. Phys. Rev. C 2020, 102, 034301. [Google Scholar] [CrossRef]
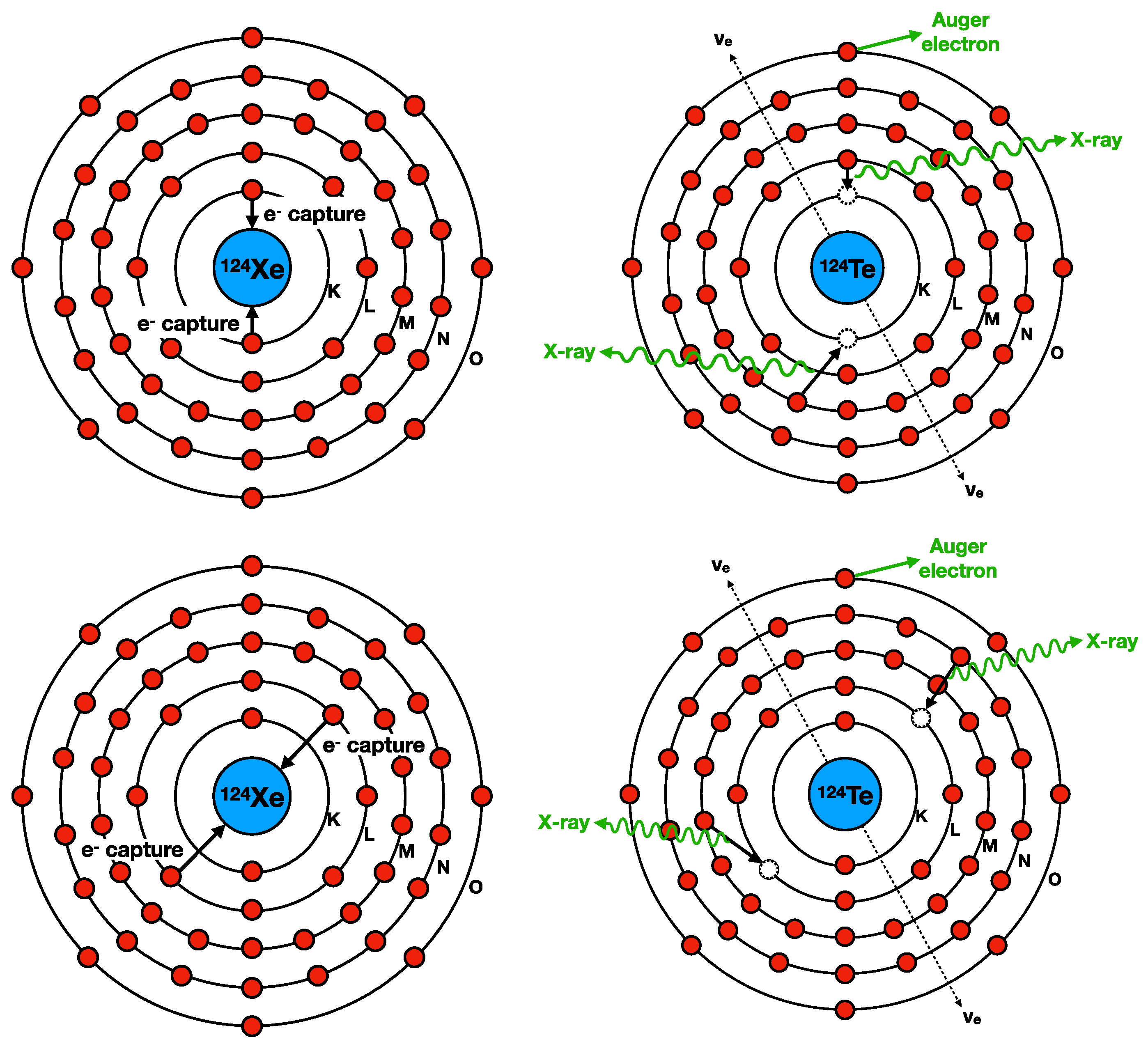
| Shell | [35] | [50,51] | [This Work] | [Experiment] [60] |
|---|---|---|---|---|
| (eV) | (eV) | (eV) | (eV) | |
| Kr | ||||
| – | – | |||
| – | – | |||
| Xe | ||||
| – | – | |||
| – | – | |||
| – | – | |||
| Ba | ||||
| – | – | |||
| – | – | |||
| – | – | |||
| – | – | |||
| Nucleus | Q | [35] | [49] | [50,51] | [This Work] |
|---|---|---|---|---|---|
| (MeV) | |||||
| Ar | 0.43259 | – | – | ||
| Ca | 0.19351 | – | |||
| Cr | 1.1688 | – | |||
| Fe | 0.6798 | – | |||
| Ni | 1.9263 | 17.00 | 15.30 | 9.900 | 14.79 |
| Zn | 1.0948 | – | 1.410 | 1.030 | 1.364 |
| Se | 1.209169 | – | 5.656 | 3.410 | 5.454 |
| Kr | 2.8463 | 774.0 | 660.0 | 410.0 | 637.0 |
| Sr | 1.79 | – | 93.60 | 64.62 | 90.58 |
| Mo | 1.651 | – | 208.0 | 82.32 | 128.2 |
| Ru | 2.71451 | ||||
| Pd | 1.1727 | – | 46.00 | 42.09 | 44.64 |
| Cd | 2.77539 | ||||
| Cd | 0.27204 | – | |||
| Sn | 1.91982 | – | 869.7 | ||
| Te | 1.71481 | – | 888.0 | 840.3 | 866.3 |
| Xe | 2.8654 | ||||
| Xe | 0.92 | – | 46.10 | 60.59 | 44.98 |
| Ba | 2.619 | ||||
| Ba | 0.844 | – | 39.10 | 61.98 | 38.12 |
| Ce | 2.37853 | ||||
| Ce | 0.698 | – | 18.40 | 34.47 | 17.92 |
| Sm | 1.78259 | – | |||
| Gd | 0.0557 | – | – | ||
| Dy | 2.012 | – | |||
| Dy | 0.284 | – | 3.191 | ||
| Er | 1.844 | ||||
| Er | 0.02507 | – | – | ||
| Yb | 1.40927 | – | |||
| Hf | 1.0988 | – | |||
| W | 0.1432 | – | 1.478 | ||
| Os | 1.453 | – | |||
| Pt | 1.384 | – | |||
| Hg | 0.82 | – | 821.0 | 815.8 |
| Nucleus | Q | ||||||
|---|---|---|---|---|---|---|---|
| (MeV) | (%) | (%) | (%) | (%) | (%) | ||
| Ar | 0.4326 | 83.40 | 14.23 | 1.62 | – | 0.61 | |
| Ca | 0.1935 | 81.38 | 15.44 | 2.07 | 0.16 | 0.73 | |
| Cr | 1.1705 | 81.35 | 15.39 | 2.18 | 0.12 | 0.73 | |
| Fe | 0.68076 | 80.41 | 16.01 | 2.35 | 0.16 | 0.80 | |
| Ni | 1.9264 | 15.22 | 80.45 | 15.97 | 2.37 | 0.15 | 0.79 |
| Zn | 1.09502 | 1.407 | 79.73 | 16.50 | 2.48 | 0.14 | 0.85 |
| Se | 1.20924 | 5.648 | 78.64 | 17.03 | 2.74 | 0.30 | 0.92 |
| Kr | 2.84767 | 661.9 | 78.64 | 16.92 | 2.81 | 0.35 | 0.91 |
| Sr | 1.78977 | 94.16 | 77.83 | 17.33 | 2.98 | 0.44 | 0.96 |
| Mo | 1.65044 | 133.8 | 76.69 | 17.89 | 3.25 | 0.56 | 1.04 |
| Ru | 2.7145 | 76.64 | 17.85 | 3.31 | 0.60 | 1.04 | |
| Pd | 1.20347 | 53.70 | 75.16 | 18.77 | 3.59 | 0.68 | 1.17 |
| Cd | 2.77539 | 75.71 | 18.31 | 3.55 | 0.69 | 1.11 | |
| Cd | 0.27179 | 65.39 | 24.87 | 5.12 | 1.01 | 2.26 | |
| Sn | 1.91981 | 74.78 | 18.82 | 3.72 | 0.76 | 1.18 | |
| Te | 1.73558 | 975.8 | 74.06 | 19.20 | 3.87 | 0.83 | 1.24 |
| Xe | 2.85674 | 74.22 | 19.00 | 3.88 | 0.86 | 1.22 | |
| Xe | 0.91778 | 47.36 | 71.66 | 20.62 | 4.28 | 0.95 | 1.48 |
| Ba | 2.6237 | 73.57 | 19.31 | 4.00 | 0.92 | 1.27 | |
| Ba | 0.84407 | 40.87 | 70.45 | 21.26 | 4.50 | 1.03 | 1.59 |
| Ce | 2.37853 | 72.88 | 19.67 | 4.14 | 0.97 | 1.33 | |
| Ce | 0.69594 | 19.03 | 68.37 | 22.43 | 4.86 | 1.14 | 1.82 |
| Sm | 1.7824 | 71.11 | 20.67 | 4.49 | 1.07 | 1.50 | |
| Gd | 1.28728 | 69.29 | 21.72 | 4.81 | 1.16 | 1.69 | |
| Gd | 0.05567 | – | – | 38.56 | |||
| Dy | 3.31234 | 71.29 | 20.48 | 4.51 | 1.09 | 1.47 | |
| Dy | 2.00595 | 70.19 | 21.14 | 4.69 | 1.14 | 1.59 | |
| Dy | 0.28282 | 42.31 | 35.46 | 9.04 | 2.26 | 6.01 | |
| Er | 1.84696 | 69.29 | 21.64 | 4.87 | 1.19 | 1.68 | |
| Er | 0.02508 | – | – | – | – | 0.87 | |
| Yb | 1.40936 | 67.42 | 22.71 | 5.20 | 1.27 | 1.90 | |
| Hf | 1.09994 | 64.94 | 24.06 | 5.62 | 1.39 | 2.20 | |
| W | 0.14323 | 17.72 | 8.08 | 2.34 | 34.73 | ||
| Os | 1.45289 | 65.02 | 23.90 | 5.64 | 1.43 | 2.17 | |
| Pt | 1.40132 | 63.83 | 24.50 | 5.84 | 1.50 | 2.32 | |
| Hg | 0.81859 | 916.2 | 56.49 | 28.25 | 7.04 | 1.84 | 3.38 |
| Rn | 1.71019 | 61.36 | 25.58 | 6.27 | 1.68 | 2.63 | |
| Rn | 0.15031 | – | 1.07 | 1.38 | 0.52 | 39.52 | |
| Ra | 1.42814 | 58.58 | 26.92 | 6.72 | 1.83 | 3.03 | |
| Th | 1.16975 | 54.68 | 28.74 | 7.34 | 2.03 | 3.64 | |
| U | 0.75251 | 42.80 | 33.66 | 9.16 | 2.59 | 5.87 | |
| Pu | 0.45693 | 95.16 | 16.51 | 39.25 | 12.33 | 3.64 | 13.66 |
| Cm | 0.08682 | – | – | – | – | 9.66 | |
| Fm | 0.782 | 34.11 | 36.07 | 10.34 | 3.05 | 7.96 | |
| No | 1.051 | 41.77 | 33.61 | 9.28 | 2.73 | 6.14 |
| Nucleus | Q | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (MeV) | (%) | (%) | (%) | (%) | (%) | (%) | (%) | (%) | (%) | ||
| Gd | 0.05567 | 38.56 | 35.94 | 10.12 | 1.84 | 7.56 | 4.17 | 0.75 | 0.57 | 0.21 | |
| Er | 0.02508 | 0.87 | 26.59 | 12.06 | 2.33 | 28.11 | 20.49 | 3.79 | 3.62 | 1.33 | |
| Cm | 0.08682 | 9.66 | 33.49 | 13.91 | 4.16 | 16.55 | 12.49 | 3.65 | 2.32 | 1.35 |
| Nucleus | ||
|---|---|---|
| (yr) | ||
| Kr | [40] | |
| [41] | ||
| Xe | [43] | |
| Ba | [38] | |
| [39] | ||
| Ba | ≥ [37] | ≤3.335 |
| Nucleus | ||
| (yr) | ||
| Xe | ≥ [66] | ≤0.398 |
| Source | |
|---|---|
| Q-value | (5–7) |
| 0.07 | |
| Nuclear radius | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niţescu, O.; Ghinescu, S.; Stoica, S.; Šimkovic, F. A Systematic Study of Two-Neutrino Double Electron Capture. Universe 2024, 10, 98. https://doi.org/10.3390/universe10020098
Niţescu O, Ghinescu S, Stoica S, Šimkovic F. A Systematic Study of Two-Neutrino Double Electron Capture. Universe. 2024; 10(2):98. https://doi.org/10.3390/universe10020098
Chicago/Turabian StyleNiţescu, Ovidiu, Stefan Ghinescu, Sabin Stoica, and Fedor Šimkovic. 2024. "A Systematic Study of Two-Neutrino Double Electron Capture" Universe 10, no. 2: 98. https://doi.org/10.3390/universe10020098
APA StyleNiţescu, O., Ghinescu, S., Stoica, S., & Šimkovic, F. (2024). A Systematic Study of Two-Neutrino Double Electron Capture. Universe, 10(2), 98. https://doi.org/10.3390/universe10020098







