Abstract
A high efficiency architecture for ring learning with errors (ring-LWE) cryptoprocessor using shared arithmetic components is presented in this paper. By applying a novel approach for sharing number theoretic transform (NTT) polynomial multiplier and polynomial adder in encryption and decryption operations, the total number of polynomial multipliers and polynomial adders used in the proposed ring-LWE cryptoprocessor are reduced. In addition, the processing time of NTT polynomial multiplier is speeded up by employing multiple-path delay feedback (MDF) architecture and deploying pipelined technique between all stages of NTT processes. As a result, the proposed architecture offers a great reduction in terms of the hardware complexity and computation latency compared with existing works. The implementation result for the proposed ring-LWE cryptoprocessor on Virtex-7 FPGA board using Xilinx VIVADO shows a significant decrease in the number of slices and LUTs compared with previous works. Moreover, the proposed ring-LWE cryptoprocessor offers higher throughput and efficiency than its predecessors.
1. Introduction
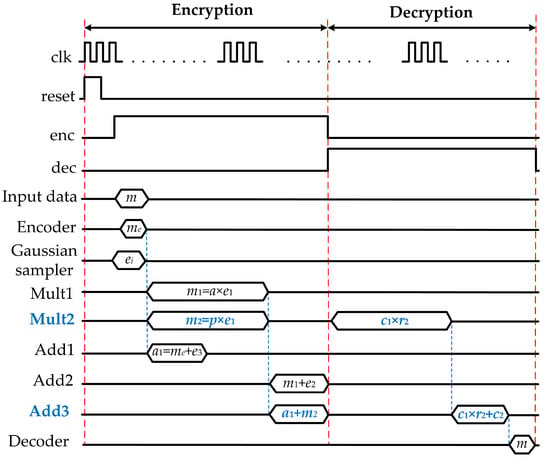
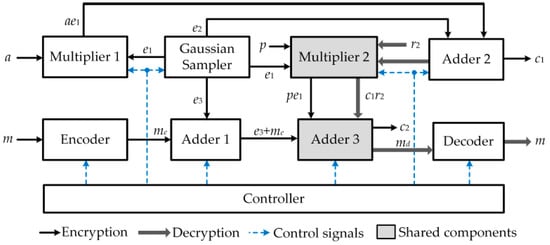
Cryptographic algorithms are grouped into two categories named symmetric algorithms and public key (or asymmetric) algorithms. The former uses a single key between two parties to enable a secure communication, where the key is kept private from all other parties. Symmetric algorithms are widely used because of its simplicity. However, a symmetric key algorithm requires an agreement between sender and receiver on the secret key. Asymmetric, or public key cryptosystems use two different keys called private keys and public keys. Whereas the private key is kept secret for the decryption process, the public key is used for encryption and can be revealed to all other parties. The encryption operation is conducted using a public key, and the encrypted message can only be decrypted using the corresponding private key. The security of Rivest, Shamir, and Adleman (RSA) cryptosystems [1] and elliptic curve cryptosystems (ECC) [2,3] are based on the difficulty of solving some number theoretic problems and the difficulty of solving the elliptic curve discrete logarithm problems, respectively. However, these problems can be solved by the algorithm proposed by Shor [4] in polynomial time with quantum computers. Therefore, stronger security systems or post-quantum cryptosystems have been proposed, and the National Institute of Standards and Technology (NIST) is standardizing them. Among lattice-based cryptosystems for the post-quantum era, ring learning with errors (LWE) is a promising candidate because its security proofs are based on the worst-case hardness of lattice problems that there is no known quantum algorithm can efficiently solve [5]. A typical block diagram of a typical ring-LWE cryptoprocessor is shown in Figure 1. Input message m is encrypted into ciphertext (, ) using arithmetic computation on public key (a, p) and error polynomials , , and . Original message m can be recovered from ciphertext (, ) and private key using the decryption operation.
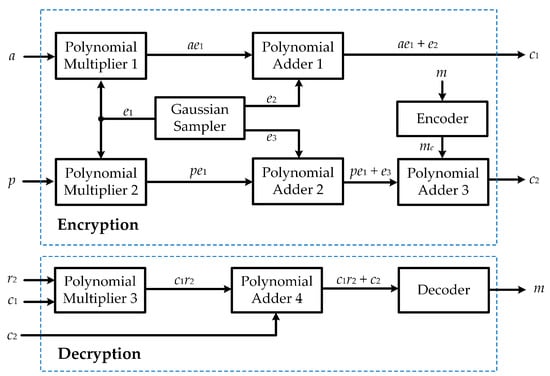
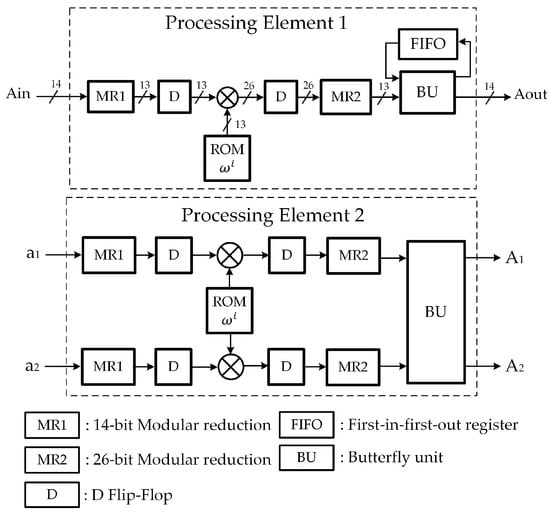
Figure 1.
Block diagram of a typical ring-LWE cryptoprocessor [6].
The ring-LWE problem has been discussed in recent studies, both in software and hardware [5,7,8,9]. In Reference [5], high-throughput ring-LWE cryptoprocessors are designed to perform ring-LWE encryption and decryption operations. In Reference [7], an approach of integrating ring-LWE cryptography into existing fingerprint authentication systems to fully protect the fingerprint data are introduced. Authors in [9] present the implementation of ring-LWE encryption on IoT processors.
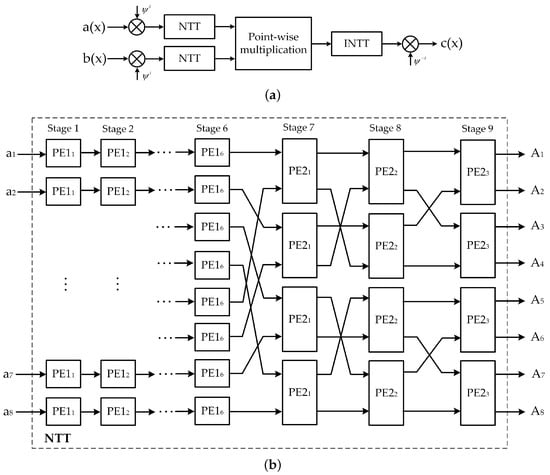
In the ring-LWE cryptosystem, lattices with an algebraic structure like polynomial multiplication and addition are performed over a polynomial ring, typically . Among these operations, polynomial multiplication is the most complex one that can be efficiently performed using number theoretic transform (NTT)-based polynomial multiplication [5]. NTT multiplier is a modified version of fast Fourier transform (FFT) to work in a finite field without inaccurate floating point or complex arithmetic to compute polynomial multiplication efficiently [10]. There are several NTT multiplier architectures that deploy single-path delay feedback (SDF) or multiple path delay commutator (MDC) structures in literature. For example, a high throughput multiplier using NTT cores with radix-2 SDF architecture is presented in [11]. In Reference [5], authors introduce radix-2 and radix-8 MDC architecture-based NTT cores for ring-LWE cryptoprocessors to obtain the encryption throughput of gigabits per seconds and decryption throughput of megabits per second. However, these architectures require large hardware resources and high computation time since the NTT polynomial multipliers work separately and NTT operations are not fully optimized.
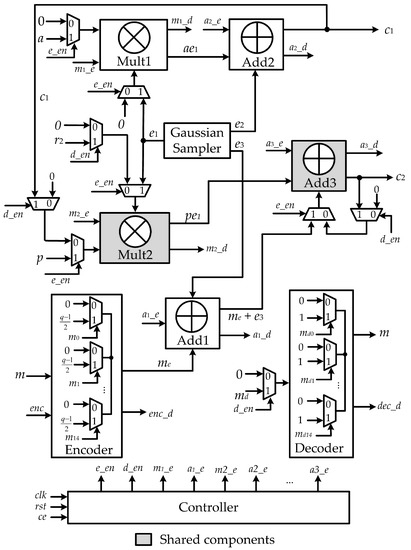
In this paper, a novel approach to efficiently use arithmetic components in ring-LWE cryptoprocessors to achieve a high efficiency is presented. Specifically, the polynomial multiplier and polynomial adder that participate in the ring-LWE encryption operation are reused in decryption phase to reduce hardware complexity. Additionally, the NTT polynomial multiplier is designed using MDF architecture and deploying pipeline technique among all stages of NTT and INTT transforms to mitigate hardware complexity and speed up multiplication operations. Our contributions of this article are summarized as follows:
- We propose a ring-LWE cryptoprocessor architecture in which the same arithmetic components, including one polynomial multiplier and one polynomial adder, are used in both encryption and decryption operations to reduce hardware complexity. As a result, the proposed ring-LWE cryptoprocessor requires less hardware resource than existing architectures to perform encryption and decryption operation.
- We deploy the polynomial multiplier using NTT multiplier with parallel based MDF architecture to enhance the polynomial multiplication. Furthermore, the pipeline technique is applied in the proposed design to reduce the system latency.
- We implement the proposed ring-LWE cryptoprocessor architecture on Xilinx Virtex-7 FPGA board and compare the obtained results with its predecessors. Performance evaluation results show that the proposed architecture offers a higher throughput and a better efficiency than others.
The remaining of this paper is structured as follows. In Section 2, brief discussions on the ring-LWE cryptosystems are carried out. Section 3 presents the proposed algorithm and architecture for ring-LWE cryptoprocessor. Section 4 provides the results of implementation and comparison, and Section 5 includes conclusions.
2. Background
2.1. Ring-LWE Cryptosystem
The ring-LWE problem introduced by Regev [12] in 2005 is a machine learning problem that is equivalent to the worst-case lattice problems. The ring-LWE cryptosystem operates over a ring , where is the irreducible polynomial of degree n, n is a power-of-two number, and q is a prime number such that . The common case of irreducible polynomial is that is presented in [11].
Polynomial multiplication and polynomial addition are employed to carry out the cryptographic primitives of the ring-LWE cryptosystem. The procedures for key generation, encryption, and decryption of ring-LWE cryptosystem are described as follows:
Key generation: This process generates the public key and the private key . Polynomial a is chosen uniformly and two polynomials and are selected from the discrete Gaussian distribution to compute the public key polynomial:
Encryption: The input message m is encoded to get the polynomial . If the coefficient of m is 1, it is mapped to ; otherwise, it is converted to 0. The cipher-text and are computed from the given polynomials and three error polynomials , , and that sampled from the Gaussian distribution:
Decryption: The input message m is recovered from the pre-decoded polynomial :
Depending on the value of each coefficient of the message , the decoder maps it to a corresponding binary bit to recover the original message m.
2.2. Arithmetic Operations over Ring
The arithmetic operations over the ring include modulo reduction, polynomial addition, and polynomial multiplication. Given coefficients and in , two polynomials and over the ring can be defined as follows:
As mentioned previously, the polynomial multiplication requires the most processing time, and the NTT-based algorithm is an efficient algorithm for performing this multiplication. Assume that is a primitive root of unity, the NTT of each coefficient of is defined as:
The inverse NTT (INTT) is calculated as:
Let and be extended vectors of and by filling n zero elements. The multiplication of two polynomials and can be computed based on NTT and INTT:
where ⊙ is the point-wise multiplication.
To avoid zero padding in NTT polynomial multiplication, the negative wrapped convolution is used. Assume that c is the negative convolution of and , the negative wrapped convolution can be expressed as:
Define , , and , where , the NTT polynomial multiplication becomes
By using the negative wrapped convolution, the NTT multiplication can be calculated using only n-coefficients.
The polynomial addition of two polynomials and is simply adding corresponding coefficients of two polynomials and then doing modulo reduction (MR). In MR operation, the coefficients of the resulting polynomial are reduced by modulus q. To execute this operation, a few MR algorithms are presented in [5,13]. Since the parameters used in this paper are and , the SAMS2 algorithm for that is presented in [5] is selected.
2.3. Discrete Gaussian Sampler
In ring-LWE cryptography, error polynomials sampled from a discrete Gaussian distribution with a standard deviation are required. This distribution uses the probability function described as follows:
where E is the random variable on , S is the normalization factor, and i is an integer. By approximating S to the probability density function can also be described using
In References [5,14,15], authors present several methods for performing discrete Gaussian sampling. Among these methods, rejection sampling and inversion sampling are the popular ones [14]. In practice, rejection sampling for a discrete Gaussian distribution is slow due to the high rejection rate for the sampled values, which are far from the center of the distribution. The inversion method first generates a random probability and then selects a sample value such that the cumulative distribution up to that sample point is just larger than the randomly generated probability. Since the random probability should be of high precision, this method also requires a large number of random bits. The Knuth–Yao algorithm [14,15] uses a random walk model for sampling from any non-uniform distribution. However, the output of Knuth–Yao algorithm is generated in an unpredictable time; then, it is not a reliable sampler [5]. In this work, we deploy the linear feedback shift registers (LFSRs) approach that was proposed in [16]. This approach offers a low-complexity with an approximated uniform pseudo-random distribution; hence, it can be exploited to generate an accurate approximation of a Gaussian distribution with low maximum auto-correlation.
4. Implementation Results and Comparison
The proposed architecture for ring-LWE cryptoprocessor is modeled in Verilog HDL, synthesized, and implemented using Xilinx VIVADO 2017.4 on a Virtex-7 FPGA platform. The implementation results of ring-LWE cryptoprocessor are summarized in Table 1.

Table 1.
Performance comparison of different ring-LWE cryptoprocessors.
As can be seen from Table 1, the proposed architecture requires less hardware resources, calculated in number of slices and LUTs, to conduct a completed ring-LWE encryption–decryption operation compared with similar parallel multiplier-based ring-LWE architectures presented in [5,6]. Specifically, to perform ring-LWE encryption and decryption operations, the proposed architecture uses only 23,707 slices and 61,258 LUTs, which is about 42% and 67.83% of that in [5], respectively. Additionally, the encryption and decryption throughput of the proposed architecture are higher than that of architecture in [6] and R8M architecture in [5]. The architectures in [18,19] require a small number of slices and LUTs to perform encryption and decryption; however, these architectures require high latency to complete ring-LWE encryption and decryption operations. Therefore, the values of throughput offered by these architectures are smaller than 150 Mbps, as described in Table 1.
Efficiency presented in [20] can be used as a parameter to evaluate the performance of different designs on various FPGA platforms. In detail, the efficiency parameter represents the throughput value that one hardware unit (LUT) of an architecture can offer. As can be seen from Table 1, the proposed ring-LWE cryptoprocessor architecture can offer a better value of efficiency compared with that of other architectures. Specifically, the obtained efficiency value of the proposed architecture is about two and seven times larger than that of architectures in [5,18], respectively. Comparison in encryption time, decryption time, and efficiency is described in Figure 7.
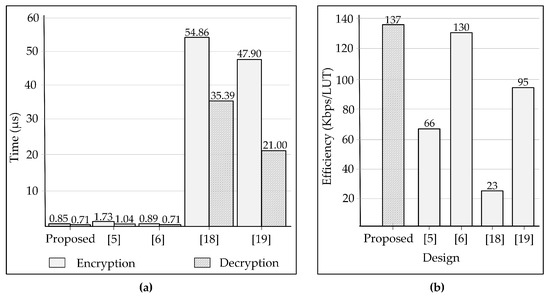
Figure 7.
(a) comparison in encryption and decryption time, and (b) comparison in system efficiency.
5. Conclusions
A novel approach to improve encryption and decryption operation of ring-LWE cryptoprocessors has been presented in this paper. By sharing the hardware resources, including polynomial multiplier and polynomial adder, in both encryption and decryption phases, the hardware complexity of the proposed architecture can be significantly reduced. Furthermore, the polynomial multiplication is greatly enhanced by deploying an efficient NTT multipliers using MDF architecture and the pipeline technique between all stages of NTT multipliers. As a result, the proposed ring-LWE cryptoprocessor offers higher throughput and efficiency compared with that of existing works. Therefore, it can be applied in hardware resource-limited systems that require high throughput and low latency.
Author Contributions
T.N.T. conceptualized the idea of this research, conducted experiments, collected data, and prepared the original version. T.T.B.N. reviewed, analyzed data, and updated the manuscript. H.L. supervised, validated, reviewed, and supported the research with funding. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Basic Science Research Program (2019R1F1A1061926) through the NRF funded by the MSIT and by Inha University, Incheon, Korea.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ochoa-Jiménez, E.; Rivera-Zamarripa, L.; Cruz-Cortés, N.; Rodríguez-Henríquez, F. Implementation of RSA Signatures on GPU and CPU Architectures. IEEE Access 2020, 8, 9928–9941. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Lee, H. Efficient Algorithm and Architecture for Elliptic Curve Cryptographic Processor. J. Semicond. Technol. Sci. 2016, 16, 118–125. [Google Scholar] [CrossRef]
- Basu Roy, D.; Mukhopadhyay, D. High-Speed Implementation of ECC Scalar Multiplication in GF(p) for Generic Montgomery Curves. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2019, 27, 1587–1600. [Google Scholar] [CrossRef]
- Shor, P.W. Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput. 1997, 26, 1484–1509. [Google Scholar] [CrossRef]
- Rentería-Mejía, C.P.; Velasco-Medina, J. High-Throughput Ring-LWE Cryptoprocessors. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2017, 25, 2332–2345. [Google Scholar] [CrossRef]
- Nguyen Tan, T.; Lee, H. Efficient-Scheduling Parallel Multiplier-Based Ring-LWE Cryptoprocessors. Electronics 2019, 8, 413. [Google Scholar] [CrossRef]
- Nguyen Tan, T.; Lee, H. High-Secure Fingerprint Authentication System Using Ring-LWE Cryptography. IEEE Access 2019, 7, 23379–23387. [Google Scholar] [CrossRef]
- Nguyen Tan, T.; Lee, H. High-Performance Ring-LWE Cryptography Scheme for Biometric Data Security. IEIE Trans. Smart Process. Comput. 2018, 7, 97–106. [Google Scholar] [CrossRef]
- Liu, Z.; Azarderakhsh, R.; Kim, H.; Seo, H. Efficient Software Implementation of Ring-LWE Encryption on IoT Processors. IEEE Trans. Comput. 2017. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, C.; Lin, H.; Chen, Y.; Zhang, M. Resource-Efficient and Side-Channel Secure Hardware Implementation of Ring-LWE Cryptographic Processor. IEEE Trans. Circuits Syst. I Reg. Pap. 2019, 66, 1474–1483. [Google Scholar] [CrossRef]
- Rentería-Mejía, C.P.; Velasco-Medina, J. Hardware Design of an NTT-Based Polynomial Multiplier. In Proceedings of the 2014 Southern Conference on Programmable Logic (SPL), Buenos Aires, Argentina, 5–7 November 2014; pp. 1–5. [Google Scholar]
- Regev, O. On Lattices, Learning with Errors, Random Linear Codes, and Cryptography. In Proceedings of the ACM symposium on Theory of Computing, Baltimore, MD, USA, 22–24 May 2005; pp. 84–93. [Google Scholar]
- Cao, Z.; Wu, X. An Improvement of the Barrett Modular Reduction Algorithm. Int. J. Computer Mathematics 2014, 91, 1874–1879. [Google Scholar] [CrossRef]
- Roy, S.S.; Vercauteren, F.; Verbauwhede, I. High Precision Discrete Gaussian Sampling on FPGAs. In Proceedings of the Selected Areas in Cryptography, Burnaby, BC, Canada, 14–16 August 2013; pp. 383–401. [Google Scholar]
- Du, C.; Bai, G. Towards Efficient Discrete Gaussian Sampling for Lattice-Based Cryptography. In Proceedings of the 2015 International Conference on Field Programmable Logic and Applications (FPL), London, UK, 2–4 September 2015; pp. 1–6. [Google Scholar]
- Condo, C.; Gross, W.J. Pseudo-Random Gaussian Distribution Through Optimised LFSR Permutations. Electron. Lett. 2015, 51, 2098–2100. [Google Scholar] [CrossRef]
- Cooley, J.W.; Tukey, J.W. An Algorithm for the Machine Calculation of Complex Fourier Series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Roy, S.S.; Vercauteren, F.; Mentens, N.; Chen, D.D.; Verbauwhede, I. Compact Ring-LWE Cryptoprocessor. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems (CHES), Busan, South Korea, 23–26 September 2014; pp. 371–391. [Google Scholar]
- Pöppelmann, T.; Güneysu, T. Towards Practical Lattice-Based Public-Key Encryption on Reconfigurable Hardware. In Proceedings of the International Conference on Selected Areas in Cryptography, Burnaby, BC, Canada, 14–16 August 2013; pp. 68–85. [Google Scholar]
- Mahdizadeh, H.; Masoumi, M. Novel Architecture for Efficient FPGA Implementation of Elliptic Curve Cryptographic Processor over GF(2163). IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2013, 21, 2330–2333. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).