Abstract
Owing to the destructive impacts of harmonic currents, the topic of reducing their impacts on power system has attracted tremendous research interests. In this regard, a shunt active power filter (SAPF) is recognized to be the most reliable instrument. It performs by first detecting the harmonic currents that are present in a harmonic-contaminated power system, and subsequently generates and injects corrective mitigation current back into the power system to cancel out all the detected harmonic currents. This means that other than the ability to generate corrective mitigation current itself, it is actually more important to make sure that the SAPF is able to operate in phase with the operating power system, so that the mitigation current can correctly be injected. Hence, proper synchronization technique needs to be integrated when designing the control algorithms of SAPF. This paper critically discusses and analyzes various types of existing phase synchronization techniques which have been applied to manage operation of SAPF; in terms of features, working principle, implementation and performance. The analysis provided can potentially serve as a guideline and provision of information on selecting the most suitable technique for synchronizing SAPF with the connected power system.
1. Introduction
Broad utilizations of nonlinear loads have caused alarming power quality issues, notably current harmonic contamination to the electrical power system. Generally, the injected harmonic currents deteriorate power quality by increasing total harmonic distortion (THD) of a power system. Moreover, they are also the main culprit to reduction of overall power system efficiency (indicated by low power factor), overheating of equipment, failure of sensitive devices, and even blown capacitor [1,2,3]. As a result, it is obligatory to limit harmonic contents in power system and maintain it within an acceptable level.
In conjunction with the mitigation efforts, IEEE standard 512-1992 has been formulated (presently revised as IEEE standard 519-2014 [4]) to strictly limit level of harmonic distortion within 5% THD and also harmonic filters are installed in the polluted power system to minimize power quality issues due to harmonic currents. Conventionally, the harmonic filters are developed based on passive elements such as inductors and capacitors to deal with specific harmonic issues (i.e., they only have fixed mitigation ability) [5]. However, due to their inherent weaknesses of inflexibility, instability, and large size, they are soon replaced by active power filters (APFs) which offer versatile solution to harmonic problems [6,7,8].
Owing to their superior mitigation capabilities, technology of APF continues to advance. Presently, APFs are available in a number of forms which can be classified into several distinct categories. As reported in [6,7,8], APF can be classified according to (1) the ways it is connected to the power system (i.e., series or shunt), (2) power rating (i.e., low-power, medium-power or high-power), (3) types of power converter employed (i.e., current-source or voltage-source converters), (4) circuit topology of the power converter employed (such as inverter, switch-capacitor, or hybrid-topology), (5) power system characteristic (i.e., two-wire for single-phase system, three-wire or four-wire for three-phase system), and (6) the targeted mitigation variables (such as current/voltage harmonics, reactive power, power factor, balancing of three-phase system, or any combinations of them). Nevertheless, as can be concluded from the literature [6], to deal with harmonic currents issues, shunt-typed active power filter (SAPF) is revealed to be most reliable.
A typical SAPF is able to measure degree of harmonic current contamination of a power system and based on that measured data, it generates and injects corrective mitigation currents back into the polluted power system to directly cancel out harmonic currents, thus minimizing severity of harmonic current contamination. This is attainable when all the control techniques applied in its control system are functioning as desired. Nonetheless, many technical issues and challenges remained to be addressed for effective installation of SAPF into the polluted power system. One of the most critical issues is synchronization of the SAPF, where its generated output voltage needs to be properly synchronized with the grid voltage to achieve stable and continuous mitigation operation. The problems will be increasingly difficult when the grid voltage is subjected to faults such as harmonic contamination and unbalanced faults. Failure to synchronize leads to incorrect mitigation and may eventually worsen the harmonic issues which are supposed to be reduced.
Phase synchronization in this aspect can be regarded as a process to minimize phase differences between the output voltage of SAPF and the connected grid voltage and at the same time matching their operating frequency. This process has to be achieved before connecting the SAPF to the designated power system, thereby allowing the power system and the synchronized SAPF to work together. As reported in [9,10], an effective synchronization technique should be able to track phase angle of the grid voltage, detect frequency variations, filter out higher order harmonics, and respond to variations in the grid voltage.
In regard to the difficulties and problems in phase synchronization, various techniques with unique merits have been proposed for synchronizing grid-tied converters. As reported in [10,11], grid-tied devices that are required to be precisely synchronized with the grid voltage can distinctively be classified into four groups based on their intended applications: (1) Renewable energy system (RES); (2) flexible ac transmission system (FACTS); (3) custom power system (CUPS); and (4) loads. It is worth noting that SAPF falls under the group of CUPS. Published literature reviews on synchronization techniques exist but most of them focus on the application of RES, such as in [9,10]. Meanwhile, specifically on the topic of SAPF, published reviews on its control techniques are also available such as in [12,13,14,15]. However, the trend has thus far focused on the three main control processes of its control system, i.e., reference current generation, voltage regulation, and current control. The methodology and behavior of its synchronization process have not yet been thoroughly discussed. Hence, it clearly indicates that there is a lack of published material that provides details regarded to the implementation of synchronization techniques for SAPF application. This study will bridge such research gap.
In this study, a comprehensive review focusing on features, working principle, performance, and implementation of phase synchronization technique in the controller of SAPF, is presented. The findings of this study should be able to help researchers in selecting the most suitable synchronization technique for their respective SAPF and may eventually inspire them to generate fresh ideas in enhancing the synchronization process of SAPF. The organization of this manuscript is as follow: Section 2 presents working principle of a typical SAPF and its control system; Section 3 provides and critically discusses the details of various synchronization techniques proposed to date for grid synchronization of SAPF; Section 4 provides comparisons and analyses of the discussed techniques; and Section 5 concludes the review.
2. Shunt Active Power Filter: Working Principle and Control Scheme
Figure 1 shows the overall circuit configuration of a typical voltage source inverter (VSI)-based SAPF (used as main example in this manuscript) and illustrates the four main control algorithms that constituted its control system. Generally, SAPF is connected to a harmonic-polluted power system at point of common coupling (PCC), between voltage supply and harmonic-producing load (or more commonly known as nonlinear load). In the literature, the harmonic-producing load is commonly developed by using an uncontrolled bridge rectifier which is further connected to a combination of resistor (R), inductor (L), and capacitor (C) elements [16,17].
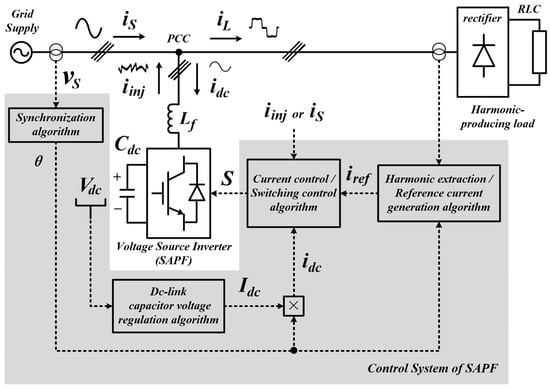
Figure 1.
Typical power circuits connection of voltage source inverter (VSI)-based shunt active power filter (SAPF) and the associated control algorithms in its control system.
The structure of SAPF can distinctively be separated into two parts: power circuits which comprises of power semiconductor switches, capacitors, inductors, power diodes (in some SAPF topologies); and a control system that is designed to control switching operation of the switches.
The operation of SAPF is rather simple. One can easily grasp the basic idea by looking at the current flow in a SAPF-installed power system. Referring to Figure 1 and by applying Kirchhoff’s current law (KCL) at PCC, current flow in a harmonic-polluted power system before connecting a SAPF can be written as
where indicates the source current, and is the load current which potentially contained (fundamental current) and (harmonic current existed due to connection of harmonic-producing loads). It is worth noting that at this moment is distorted and not working in-phase with the source voltage due to the impact of . Hence, the main purpose of installing a SAPF is to eliminate .
After installing SAPF at PCC, two additional current flows are introduced into the power system (as illustrated in Figure 1). First, to cancel out , mitigation current (named as injection current in this manuscript) is injected by the SAPF into the power system via PCC. The injected mitigation current has magnitude which is equal and phase which is opposite to that of . Second, a small amount of current (named as dc-link charging current ) is utilized by the SAPF to maintain a constant dc-link voltage (voltage across its dc-link capacitor ) at desired level. In this manner, its switching losses are regulated and thus ensuring continuous and stable operation of SAPF. In terms of mathematical expression, Equation (1) can be re-written according to KCL as
Theoretically, the magnitude of the generated is influenced by the voltage level across the dc-link capacitor. When voltage across the dc-link capacitor has been reached and is continuously maintained at the desired level, the generated will be exactly equal to where they will cancel out each other. As a result, Equation (2) can further be simplified as
At this moment, with removal of , regained its sinusoidal characteristic with fundamental frequency and work in-phase with .
To better demonstrate operation of SAPF, Figure 2 is provided to show an example waveform consisting of source voltage , load current , injection current , and source current , that can be observed in a harmonic-polluted power system with a SAPF installed. Note that the example provided is considering a balanced-sinusoidal source voltage and an inductive-typed nonlinear load (comprises of a three-phase uncontrolled bridge rectifier feeding a RL element). The use of other scenarios of source voltage and types of nonlinear loads may result in different shape of waveforms.
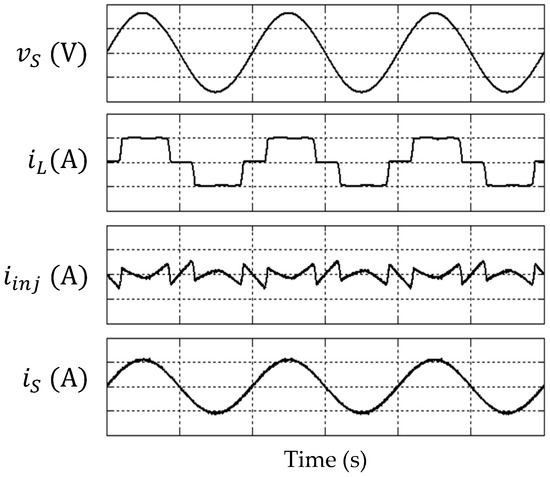
Figure 2.
Theoretical voltage and current waveforms showing the condition of power system with a SAPF installed.
To effectively control the operation of SAPF, its control system must be designed with four types of control algorithms, each with a specific function listed as follows:
- (1)
- Harmonic Extraction Algorithm.The main function of this algorithm is to extract harmonic information from a harmonic-polluted power system and applied the extracted information to form a reference current signal . In this aspect, the distorted load current signal is processed in a way that allows its harmonic and fundamental elements to be separated.After separating the elements, can be derived by using either the harmonic or fundamental elements, each having its own derivation setting. Note that quality of the reference current signal will mainly determine how well the SAPF is going to work, thus it must be generated in a quick and accurate manner. This algorithm is also referred as reference current generation algorithm in some literature, such as in [18,19] due to the reason that reference current is being generated as the final output of this algorithm. Few examples of commonly applied techniques for this algorithm include synchronous reference frame (SRF) or theory [20,21,22], instantaneous power theory [23,24,25], fast Fourier transform (FFT) [26,27], discrete Fourier transform (DFT) [28,29] and artificial neural network (ANN) [30,31,32].
- (2)
- Synchronization Algorithm.The main function of this algorithm is to track angular position of source voltage signal and subsequently generate a phase synchronization angle to match the phase of the generated with the phase of the operating power system. Many harmonic extraction algorithms do not possess a phase tracking feature and are fully dependent on an explicit synchronization algorithm to provide them with an effective synchronization angle. Nevertheless, there are some harmonic extraction algorithms that are inherited with phase tracking ability, for example, the algorithm designed based on instantaneous power theory technique [25,33]. In this case, an explicit synchronization algorithm can be omitted. Further details on the available techniques for this algorithm are presented in the next section.
- (3)
- DC-link Capacitor Voltage Regulation Algorithm.The main function of this algorithm is to estimate the amount of dc-link charging current needed by the SAPF to constantly maintain dc-link voltage at a desired level. This algorithm continuously compares the measured with a predetermined set-point value and minimizes the resulted error by using either proportional-integral (PI) [34,35,36] or fuzzy logic control (FLC) [37,38,39] techniques, via a voltage control loop. When the error between the measured and the predetermined set-point value has been minimized, the effective magnitude of will be generated. Subsequently, by utilizing the phase synchronization angle , can be coordinated in-phase with the operating power system.
- (4)
- Current Control Algorithm.The main function of this algorithm is to convert delivered by harmonic extraction algorithm and delivered by dc-link capacitor voltage regulation algorithm into gate switching pulses via a pulse-width modulation process, while ensuring that the feedback signal or is able to track via a current control loop. This algorithm is also commonly referred as switching algorithm due to its function in generating gate switching pulses. Few examples of commonly applied techniques for this algorithm include hysteresis control [40,41,42,43], sinusoidal pulse-width modulation (SPWM) [44,45,46] and space vector PWM (SVPWM) [47,48,49,50].
The four control algorithms are linked to one another systematically, and they perform in a closed-loop manner in which the actual output (it could be either or ) is monitored and fed back to be compared with the desired until the monitored output achieve its desired response. Even if subjected to disturbances such as dynamic conditions, the algorithms have been practically proven to be able to respond quickly to once again bring the monitored output back to its desired form.
3. Phase Synchronization Techniques
This section discusses about the phase synchronization techniques which have so far been integrated in the control system of SAPF. It includes the two common techniques in the literature namely zero-crossing detection (ZCD) [19,51,52] and phase-locked loop (PLL) [53,54,55], and the more recent techniques such as artificial neural-network (ANN) or adaptive linear neuron (ADALINE) [56,57,58], fundamental component extraction [59,60], and unit vector generation [61,62,63]. In this manuscript, the synchronization techniques are classified according to the intended application of SAPF, i.e., either for single-phase or three-phase power system, as illustrated in Figure 3. Over the years, works on SAPF for three-phase system are more popular compared to single-phase system particularly due to wider applications of power electronics devices and nonlinear loads in three-phase environment [64,65,66]. However, to avoid redundancy, this manuscript will examine the synchronization technique itself and subsequently, suitability of each technique for single-phase and three-phase system applications will be highlighted.
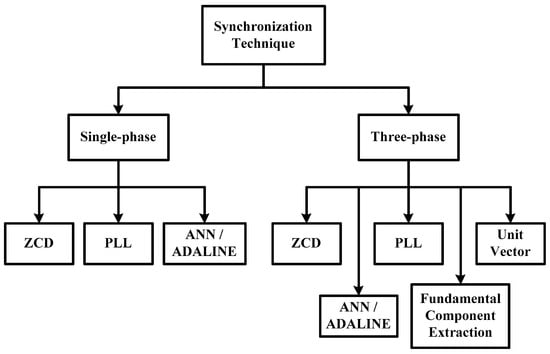
Figure 3.
Overview of synchronization techniques applied to SAPF. ZCD: zero-crossing detection; PLL: phase-locked loop; ANN: artificial neural network; ADALINE: adaptive linear neuron.
3.1. Zero-Crossing Detection (ZCD) Technique
Zero-crossing detection (ZCD) technique is the simplest and one of the early approaches proposed for synchronization purposes [19,51,52]. According to ZCD technique, a circuit is designed to detect zero-crossing point of ac voltage and generate a pulse accordingly [51]. It offers the best advantage in terms of implementation requirements, but poor performances are reported in is application especially when the source voltage is subjected to noises and harmonics [67]. In such cases, multiple zero crossings can occur and this makes difficult for the zero-crossing detector to detect the original zero crossing, thus increases the possibility of inaccurate detection. Nonetheless, some form of filtering can be applied to reduce the distortion before feeding it to the zero-crossing detector [68]. However, pre-filtering may introduce phase lead or lag into the filtered waveform, and this issue is quite difficult to avoid as ZCD is an analog-based technique. Hence, once again its accuracy is degraded. Moreover, zero crossing point can only be detected at every half-cycle of utility fundamental frequency, thus causes poor dynamic performance [69]. Furthermore, this technique requires development of additional hardware circuit (one for each operating phase) which increases the size and cost. For instance, in [51], a ZCD hardware circuit is built to generate an initiating pulse to the controller of SAPF (developed on a digital signal processor (DSP) board) when a zero-crossing voltage is detected at the PCC. The initiating pulse serves as a switch that initiates operation of the controller. This technique is applicable for both single-phase [51] and three-phase system [19]. Nevertheless, owing to its weaknesses, this technique is still the least preferred to be implemented for SAPF’s applications, as compared to the others available techniques.
3.2. Phase-Locked Loop (PLL) Technique
Among the five techniques presented in this manuscript, phase-locked loop (PLL) technique is the most recognized and commonly applied approach, due to its uncomplicated control structure, and effectiveness in handling various grid conditions. PLL is actually an old technology which appeared in the literature in the 1930s, and it has successfully been applied over the past decades in various areas, such as in communication, control systems, and instrumentation [70,71]. The basic concept of PLL has been revealed in [72]. Its structure contains three basic functional blocks known as phase detector (PD), loop filter (LF), and voltage-controlled oscillator (VCO), as illustrated in Figure 4. In a closed-loop control operation, PD will first compare the two input signals (a reference phase signal and a feedback signal ) and generate a phase error signal . The generated error is then filtered by LF (typically a low-pass filter (LPF)) which suppresses noise and other high-frequency elements from PD. The filtered signal is subsequently processed by VCO to generate an updated output phase which is then feedback to the PD. As the looping process continues, the error generated will continuously be reduced and when it reaches zero value, the output phase will be locked and matches the desired reference phase signal .
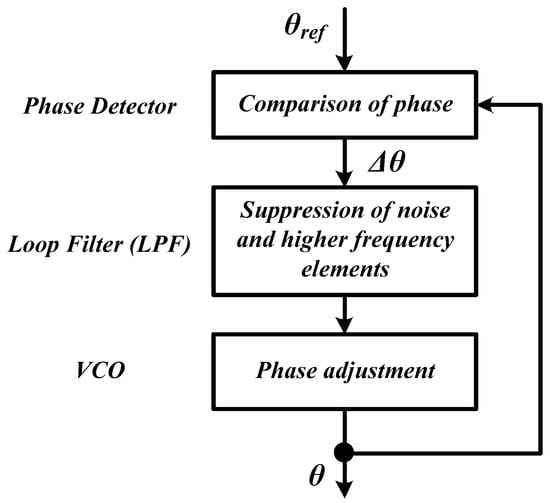
Figure 4.
Control structure of a basic phase-locked loop (PLL) technique [72]. VCO: voltage-controlled oscillator.
Subsequently, for the application of SAPF, the basic PLL has further been enhanced as synchronous reference frame (SRF)-based PLL (or simply SRF-PLL) [53,54,55]. SRF-PLL technique has successfully been applied in both single-phase [55,73,74] and three-phase systems [10,53,54,73]. Figure 5 shows the basic control structure of SRF-PLL technique. As can be seen from Figure 4 and Figure 5, the obvious difference between SRF-PLL and the basic PLL techniques is on the implementation approach for the PD block. As its name implies, SRF-PLL is a technique that utilizes SRF theory for the implementation of its PD block, in which three-phase voltage in natural reference frame is first transformed into two-phase stationary frame (by means of Clarke-transformation) and then into rotating reference frame (by means of Park-transformation), as shown in Equations (4) and (5), respectively. Note that constant refers to sampling rate. A proportional-integral (PI) is then applied to manipulate the resulting variable and eventually the angular frequency of the utility will be generated as the output. The utility phase angle can be obtained by integrating the angular frequency, and the looping process continues by feeding the phase angle back to the transformation block until the phase angle is locked at a fixed value.
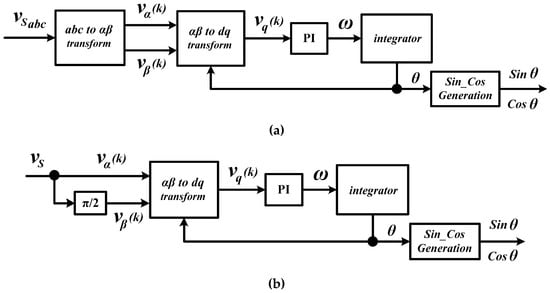
Figure 5.
Control structure of synchronous reference frame (SRF)-PLL technique for (a) three-phase [10,53,54,73] and (b) single-phase [55,73,74] applications.
SRF-PLL technique is initially developed for the application in three-phase system. However, with a little modification on the initial signal processing approach, it can also be used in single-phase system. For single-phase application, there is a need to transform single-phase signal to stationary frame by means of other approach due to the facts that Clarke-transformation (the usual transformation approach) is not applicable in single-phase system. One interesting approach is revealed in [55,73,74] where the single-phase signal is directly treated as frame signal and meanwhile frame signal is created by introducing a phase delay of to the actual single-phase signal (as illustrated in Figure 5b). The subsequent phase locking processes for single-phase SRF-PLL is basically similar to that of three-phase SRF-PLL.
The main advantage of SRF-PLL technique is that it allows accurate and quick tracking of utility frequency and phase angle for the case when the source voltage is free from any distortions and unbalances. Unfortunately, it fails to work appropriately when the source voltage is unbalanced (for a three-phase system) and/or distorted due to presence of harmonics. One good way to alleviate this inherent issue is by applying additional low-pass filter (LPF) in the control loop after the transformation block [75]. However, there is a need to carefully match the order and cutting frequency of the LPF via heuristic manner, to provide satisfactory compromise between its distortion rejection performance and speed. The good news is that the traditional SRF-PLL has been improved as self-tuning filter (STF)-based PLL (or simply STF-PLL) [55] and decoupled double (DD) SRF-PLL (or simply DDSRF-PLL) [53] to ensure its effectiveness when it is required to work under unbalanced and/or distorted utility grid.
Basically, STF-PLL works in a similar manner to that of a traditional SRF-PLL. However, its input signal in frame will be pre-filtered by a STF which suppresses noise and other high-frequency elements before transforming into rotating reference frame. This approach allows distortion-free signal to be processed in the phase-locking loop, thus ensuring accurate detection of utility phase angle and frequency. The basic structure of a STF is shown in Figure 6 and meanwhile its working principle can be summarized as the following approach:
where is the extracted distortion-free (fundamental) element of input signal in frame, is the actual input signal in frame, is a constant gain parameter and is the cutting frequency. Despite its strong points, this technique has one disadvantage where capability of the applied STF is dependent on the selection of its gain parameter. An analysis to study the effect of the gain parameter on the performance of STF has been reported in [59,76]. From the analysis, as an overall, a smaller gain value improves accuracy of STF but at the same time reduces its dynamic responses. The opposite effect holds if a higher gain value is applied. Hence, for a balance between accuracy and speed, the gain value should carefully be selected.
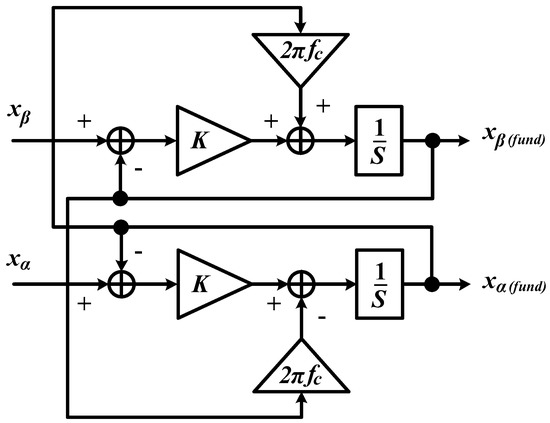
Figure 6.
Basic structure of self-tuning filter tuned at specific [76,77].
On the other hand, in DDSRF-PLL, instead of applying a STF to suppress high-frequency elements contained in the distorted input signal, the positive-sequence and negative-sequence elements existed due to unbalanced and distorted source voltage conditions are distinctively separated and transformed into double SRF loop, and a decoupling network is then integrated to extract the positive-sequence element with fundamental-frequency before applying it in the phase-locking loop. A block diagram of the decoupling network applied in DDSRF-PLL technique is shown in Figure 7 to illustrate the aforementioned process.
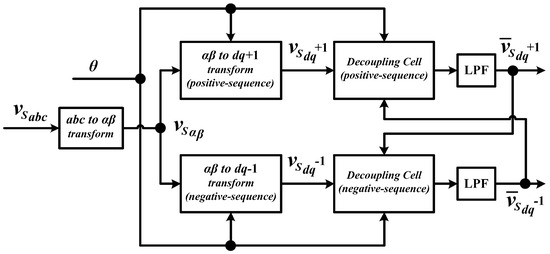
Figure 7.
Block diagram of decoupling network in decoupled double SRF (DDSRF)-PLL [53].
As presented in Figure 7, the initial processing stage of this technique is similar to the conventional PLL technique shown in Figure 5 where it involves signal transformation of three-phase voltage in natural reference frame into two-phase stationary frame and then into rotating reference frame. However, in rotating reference frame, the positive-sequence and negative-sequence elements are separated. Subsequently, fundamental-frequency elements (positive-sequence and negative-sequence ) are extracted from each decoupling cell. The extracted positive-sequence element with fundamental-frequency will then be applied in phase-locking loop until the desired phase angle is generated. Although this enhanced technique is revealed to completely eliminate detection error of the traditional SRF-PLL and precisely worked even under the influence of unbalanced and distorted utility conditions, its detection process is rather complex due to the necessity of an additional SRF loop.
Other than different modifications of conventional PLL techniques, another phase-tracking technique which can provide comparable performance to a robust PLL has been reported in [78,79,80]. The method is named as D-estimation method. It is not based on a conventional PLL approach, but instead it works based on a simple filtering approach named D-filter [78]. It can actually provide instant estimation of phase and frequency similar to that of a PLL. Note that this method is not yet applied in SAPF applications. However, it has been experimentally verified to be stable and robust even operating under the influence of harmonics distortion and contaminated noise [78,79,80]. This is an important feature of phase-tracking/synchronization technique that make it suitable for SAPF applications. Hence, study on the adaptability of D-estimation method in SAPF applications can be a potential research for future work.
3.3. Adaptive Linear Neuron (ADALINE) Technique
One recent synchronization technique is developed based on adaptive linear neuron (ADALINE) concept. Originally, the ADALINE technique is introduced for the purpose of harmonic extraction or generating reference current [30,81,82]. However, with appropriate consideration, the same ADALINE technique for harmonic extraction has been reported to be applied for synchronizing purposes as well. In this regard, a technique that combined both the ADALINEs function which is named as unified ADALINEs is proposed [58]. Figure 8 shows control structure of ADALINE-based synchronization technique.
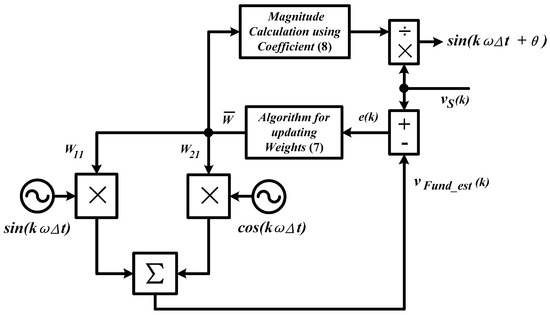
Figure 8.
Control structure of adaptive linear neuron (ADALINE)-based synchronization technique [58].
In operation, the source voltage is first measured and compared with an estimated voltage . Note that constant refers to the sampling rate, for digital implementation. The resulting error is processed by a weight updating algorithm as shown in Equation (7) to update the weight or the amplitude (coefficient) and of sine and cosine vectors.
where,
- is the weight factor,
- is the fundamental sine and cosine components,
- is the error between the measured and estimated voltage signal, and is the learning rate.
At the same time, and will be utilized to compute instantaneous magnitude of according to the following approach.
The iteration is repeated until = . At this moment, the effective magnitude of is produced and eventually being divided from the measured , thus generating the desired synchronization signal . It is worth noting that the desired synchronization signal generated in this manner is unity representation of the instantaneous source voltage.
This synchronization technique has been verified to work effectively for both single-phase [56,57] and three-phase system [58], provided that the source voltage applied is balanced and sinusoidal. It is worth noting that a single unit of ADALINE-based synchronization technique (as illustrated in Figure 8) is only capable of generating synchronization signal for one single operating phase. Hence, for a three-phase system, it would obviously require three similar units (one for each operating phase). One main disadvantage of this technique is that it cannot work appropriately when the source voltage is subjected to harmonic distortion and/or unbalance condition. Another inherent weakness of this technique is that its effectiveness is strictly dependent on its learning rate value, which is normally obtained via heuristic approach.
3.4. Fundamental Component Extraction Technique
Another recent alternative technique to grid-synchronization of SAPF is the fundamental component extraction technique where the target is to extract fundamental component (sinusoidal characteristic) of the source voltage with unity magnitude. In other words, the end product of this technique is actually similar to the ADALINE-based technique discussed previously in Section 3.3. However, in comparison to the ADALINE-based technique, this technique is designed with one important advantage where it is effective even when the source voltage is distorted and/or unbalanced, as reported in [59,60]. This is simply because the technique is integrated with a self-tuning filter (STF) [76,77,83] which has the ability to effectively filter out any distortion from a distorted signal. Figure 9 shows the control structure of fundamental component extraction technique with an integrated STF.
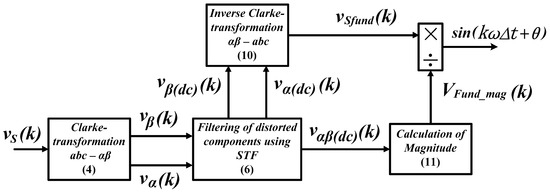
Figure 9.
Control structure of fundamental component extraction technique with an integrated self-tuning filter (STF) [59,60].
In operation, the desired synchronization signal is generated according to three consecutive processes listed as follow:
- Extraction of fundamental (sinusoidal characteristic) source voltage from the measured source voltage . In the first stage, the extraction process is conducted in -domain where a Clarke-transformation ( transformation) is applied according to Equation (4). In -domain, source voltage which is subjected to distortion can be expressed aswhere is the fundamental component and is distorted component of source voltage in α domain, respectively. Similar relation valid for source voltage in β domain, and .Here, a STF (as in Equation (6)) is applied to extract and which is subsequently converted into a pure sinusoidal signal by means of inverse Clarke-transformation ( transformation), as in Equation (10). Note that, the application of STF is only needed when the source voltage is subjected to any distortion. In the case where the source voltage is ideal (balanced-sinusoidal), STF can actually be omitted to reduce structure complexity.
- Magnitude calculation by using the extracted fundamental voltage component ( and ). In this stage, the fundamental magnitude of source voltage is computed as follow
- Direct magnitude division from to obtain its unity form. In the final stage, the desired synchronization signal is obtained as follow
This technique has only been implemented in three-phase system [59,60]. Hence, further researches to study about its adaptability in single-phase system can be interesting. Despite its strong points, this technique has one disadvantage where capability of the applied STF is dependent on the selection of its gain parameter, as clearly been mentioned in Section 3.2. To date, there is still no exact procedure to optimally tune the gain value, and it is mostly performed heuristically which can be time-consuming.
3.5. Unit Vector Generation Technique
Another interesting synchronization technique is unit vector generation technique. As its name indicates, its working principle involves generation of unit vectors (consisting of sine and cosine functions) from the measured source voltage. The control structure of unit vector synchronization technique is illustrated in Figure 10. Similar to fundamental component extraction technique (as described in Section 3.4), the main operation of this technique occurred in domain which requires a domain transformation from three-phase domain to two-phase domain by using a Clarke-transformation (as shown in Equation (4)).
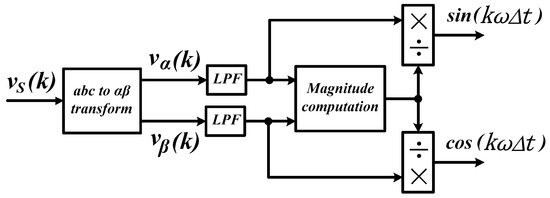
Figure 10.
Control structure of unit vector synchronization technique [61,62,63].
In domain, the signal in coordinate represents a sine function and meanwhile the signal in coordinate represents a cosine function. Note that a low-pass filter (LPF) with cutting frequency of 50 Hz (equal to fundamental frequency of the measured source voltage) is applied to filter out higher order harmonics which are normally present in the source voltage [61]. Subsequently, the desired sine and cosine function for synchronization purposes ( and ) are generated according to the following approach:
and
where is the computed magnitude of and .
This technique has only been applied in three-phase system which is supplied by a balanced and sinusoidal source voltage, where it has practically been proven to perform effectively [61,62]. In theory, LPF actually has the ability to filter out higher order harmonics, thus should be able to work appropriately when the source voltage is subjected to harmonic distortion. However, there is a lack of relevant simulation and experimental materials to justify this matter. Hence, further work regarding this matter can provide useful knowledge to the literature. One advantage of this technique is that its control structure is direct and straightforward without involving any complex computational process. Nonetheless, the use of LPF introduces delay and phase lag to the unit vector generation process which renders this technique less popular compared to the others.
4. Comparative Highlights on Phase Synchronization Techniques and Possible Future Works
Generally, the effectiveness of the applied phase synchronization techniques depend on their performance in distorted and unbalanced grid conditions, phase tracking accuracy, dynamic performance, noise immunity, and compatibility with other algorithms in the control system of SAPF. Besides that, control structure complexity and computational burden are also important criteria to be considered in selecting the most suitable phase synchronization techniques. To provide better understanding on the discussed topic and to ease the reading process, important features of each phase synchronization technique presented previously in Section 3 are highlighted in Table 1 including their strengths and weaknesses.

Table 1.
Feature comparison of the synchronization techniques discussed in this manuscript.
Regardless of evolution and advancement of synchronization techniques, synchronization issue remains a key issue in achieving effective and uninterrupted operation of SAPF in abnormal grid voltage conditions. One existing issue to be addressed is the lack of studies or works that report on the utilization of artificial intelligence (AI) technique for synchronization purposes. Most of the existing synchronization techniques are time-domain based which provides the common benefit of simplicity. Meanwhile, one most recent AI technique which applies the principle of neural network (ADALINE technique as discussed in Section 3.3), has yet been verified to be effective in distorted and unbalanced grid conditions. Moreover, the upcoming smart grid systems will definitely require intelligent technique for effective power flow management. Hence, there is a need for further studies to justify its capability in adverse grid conditions. Other than using AI technique by itself, studies can also be initiated for a hybrid of this technique with the other time-domain based techniques, and the studies should be supported with practical evaluation involving various adverse and dynamic grid conditions.
In most of the existing synchronization techniques discussed in this manuscript, whenever tuning process is involved, the tuning is performed heuristically. Although the synchronization techniques are able to perform satisfactorily by using heuristic tuning approaches, it is actually difficult to know whether their performances are optimal or not. Optimization approaches such as genetic algorithm (GA), particle swarm optimization (PSO), and ant colony optimization (ACO) are well-developed in the literature but none of them have been applied to optimize synchronization processes. Therefore, synchronization scheme with integration of optimization approaches should also be given attention in future studies.
5. Conclusions
This manuscript has thoroughly reviewed and discussed the state-of-the-art phase synchronization techniques for synchronizing SAPF with the power grid. A conceptual diagram which illustrate general working principle of SAPF and how synchronization algorithm interacts with other algorithms in the control system of SAPF, have been presented in Section 2. The need of a synchronization algorithm is dependent on the characteristics of the applied harmonic extraction algorithm. Generally, an explicit synchronization algorithm can be omitted when operation of the applied harmonic extraction algorithm involves voltage processing stage such as the algorithm developed based on theory. The features, suitability, and strengths and weaknesses of the synchronization techniques have been analyzed and discussed in Section 3. From the literature, some recently proposed techniques have been revealed to perform better than the traditional SRF-PLL technique. However, SRF-PLL technique is still well-accepted due to its uncomplicated control structure. Hence, further enhancements have been performed to improve capability of SRF-PLL which enables it to cope with distorted and unbalanced grid conditions. Lastly, it is recommended that hybrid, intelligent and optimized techniques for effective and stable synchronization especially in adverse and dynamic grid conditions should be given more attention in the future studies.
Author Contributions
Y.H. was mainly responsible for preparing the initial draft of the manuscript. M.A.M.R. has actively participated in selecting and analyzing the important works presented in this manuscript. M.A.A.M.Z. and M.A.M.Z. contributed in reviewing and improving the drafted manuscript.
Funding
This research was funded by Universiti Sains Malaysia (USM) short term grants (Grant number: USM 304/PELECT/6315283 and USM 304/PELECT/60313047).
Acknowledgments
The authors are grateful to the Research Creativity and Management Office (RCMO) of Universiti Sains Malaysia (USM) for supporting this manuscript especially regarding research fundings.
Conflicts of Interest
The authors declare no potential conflict of interest.
References
- Kale, M.; Ozdemir, E. An adaptive hysteresis band current controller for shunt active power filter. Electr. Power Syst. Res. 2005, 73, 113–119. [Google Scholar] [CrossRef]
- Soni, M.K.; Soni, N. Review of causes and effect of harmonics on power system. Int. J. Sci. Eng. Technol. Res. 2014, 3, 214–220. [Google Scholar]
- Henderson, R.D.; Rose, P.J. Harmonics: The effects on power quality and transformers. IEEE Trans. Ind. Appl. 1994, 30, 528–532. [Google Scholar] [CrossRef]
- IEEE Standard 519. IEEE recommended practice and requirement for harmonic control in electric power systems. In IEEE Std 519-2014 (Revision of IEEE Std 519-1992); IEEE: Piscataway, NJ, USA, 2014; pp. 1–29. [Google Scholar]
- Das, J.C. Passive filters—Potentialities and limitations. IEEE Trans. Ind. Appl. 2004, 40, 232–241. [Google Scholar] [CrossRef]
- Akagi, H. Active harmonic filters. Proc. IEEE 2005, 93, 2128–2141. [Google Scholar] [CrossRef]
- El-Habrouk, M.; Darwish, M.K.; Mehta, P. Active power filters: A review. IEEE Proc. Electr. Power Appl. 2000, 147, 403–413. [Google Scholar] [CrossRef]
- Singh, B.; Al-Haddad, K.; Chandra, A. A review of active filters for power quality improvement. IEEE Trans. Ind. Electron. 1999, 46, 960–971. [Google Scholar] [CrossRef]
- Jain, B.; Jain, S.; Nema, R.K. Control strategies of grid interfaced wind energy conversion system: An overview. Renew. Sustain. Energy Rev. 2015, 47, 983–996. [Google Scholar] [CrossRef]
- Jaalam, N.; Rahim, N.A.; Bakar, A.H.A.; Tan, C.K.; Haidar, A.M.A. A comprehensive review of synchronization methods for grid-connected converters of renewable energy source. Renew. Sustain. Energy Rev. 2016, 59, 1471–1481. [Google Scholar] [CrossRef]
- Bobrowska-Rafal, M.; Rafal, K.; Jasinski, M.; Kazmierkowski, M.P. Grid synchronization and symmetrical components extraction with pll algorithm for grid connected power electronic converters—A review. Bull. Pol. Acad. Sci. Tech. Sci. 2011, 59, 485–497. [Google Scholar] [CrossRef]
- Green, T.C.; Marks, J.H. Control techniques for active power filters. IEEE Proc. Electr. Power Appl. 2005, 152, 369–381. [Google Scholar] [CrossRef]
- Hoon, Y.; Radzi, M.A.M.; Hassan, M.K.; Mailah, N.F. Control algorithms of shunt active power filter for harmonics mitigation: A review. Energies 2017, 10, 2038. [Google Scholar] [CrossRef]
- Schwanz, D.; Bagheri, A.; Bollen, M.; Larsson, A. Active harmonic filters: Control techniques review. In Proceedings of the 17th International Conference on Harmonics and Quality of Power (ICHQP), Belo Horizonte, Brazil, 16–19 October 2016; pp. 36–41. [Google Scholar]
- Steela, K.; Rajpurohit, B.S. A survey on active power filters control strategies. In Proceedings of the IEEE 6th India International Conference on Power Electronics (IICPE), Kurukshetra, India, 8–10 December 2014; pp. 1–6. [Google Scholar]
- Rahmani, S.; Hamadi, A.; Al-Haddad, K.; Dessaint, L.A. A combination of shunt hybrid power filter and thyristor-controlled reactor for power quality. IEEE Trans. Ind. Electron. 2014, 61, 2152–2164. [Google Scholar] [CrossRef]
- Trinh, Q.-N.; Lee, H.-H. An advanced current control strategy for three-phase shunt active power filters. IEEE Trans. Ind. Electron. 2013, 60, 5400–5410. [Google Scholar] [CrossRef]
- Terriche, Y.; Golestan, S.; Guerrero, J.M.; Kerdoune, D.; Vasquez, J.C. Matrix pencil method-based reference current generation for shunt active power filters. IET Power Electron. 2018, 11, 772–780. [Google Scholar] [CrossRef]
- Chauhan, S.K.; Shah, M.C.; Tiwari, R.R.; Tekwani, P.N. Analysis, design and digital implementation of a shunt active power filter with different schemes of reference current generation. IET Power Electron. 2014, 7, 627–639. [Google Scholar] [CrossRef]
- Monfared, M.; Golestan, S.; Guerrero, J.M. A new synchronous reference frame-based method for single-phase shunt active power filters. J. Power Electron. 2013, 13, 692–700. [Google Scholar] [CrossRef]
- Hoon, Y.; Radzi, M.A.M.; Hassan, M.K.; Mailah, N.F.; Wahab, N.I.A. A simplified synchronous reference frame for indirect current controlled three-level inverter-based shunt active power filters. J. Power Electron. 2016, 16, 1964–1980. [Google Scholar] [CrossRef]
- Jain, N.; Gupta, A. Comparison between two compensation current control methods of shunt active power filter. Int. J. Eng. Res. Gen. Sci. 2014, 2, 603–615. [Google Scholar]
- Eskandarian, N.; Beromi, Y.A.; Farhangi, S. Improvement of dynamic behavior of shunt active power filter using fuzzy instantaneous power theory. J. Power Electron. 2014, 14, 1303–1313. [Google Scholar] [CrossRef]
- Hoon, Y.; Radzi, M.A.M.; Hassan, M.K.; Mailah, N.F. Enhanced instantaneous power theory with average algorithm for indirect current controlled three-level inverter-based shunt active power filter under dynamic state conditions. Math. Probl. Eng. 2016, 2016, 9682512. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Chakraborty, C.; Bhattacharya, S. Shunt compensation—Reviewing traditional methods of reference current generation. IEEE Ind. Electron. Mag. 2009, 3, 38–49. [Google Scholar] [CrossRef]
- Vodyakho, O.; Mi, C.C. Three-level inverter-based shunt active power filter in three-phase three-wire and four-wire systems. IEEE Trans. Power Electron. 2009, 24, 1350–1363. [Google Scholar] [CrossRef]
- Chen, K.F.; Mei, S.L. Composite interpolated fast fourier transform with the hanning window. IEEE Trans. Instrum. Meas. 2010, 59, 1571–1579. [Google Scholar] [CrossRef]
- Mattavelli, P.; Marafao, F.P. Repetitive-based control for selective harmonic compensation in active power filters. IEEE Trans. Ind. Electron. 2004, 51, 1018–1024. [Google Scholar] [CrossRef]
- Maza-Ortega, J.M.; Rosendo-Macías, J.A.; Gómez-Expósito, A.; Ceballos-Mannozzi, S.; Barragán-Villarejo, M. Reference current computation for active power filters by running dft techniques. IEEE Trans. Power Deliv. 2010, 25, 1986–1995. [Google Scholar] [CrossRef]
- Abdeslam, D.O.; Wira, P.; Merckle, J.; Flieller, D.; Chapuis, Y.-A. A unified artificial neural network architecture for active power filters. IEEE Trans. Ind. Electron. 2007, 54, 61–76. [Google Scholar] [CrossRef]
- Saribulut, L.; Teke, A.; Tümay, M. Artificial neural network based discrete-fuzzy logic controlled active power filter. IET Power Electron. 2014, 7, 1536–1546. [Google Scholar] [CrossRef]
- Qasim, M.; Khadkikar, V. Application of artificial neural networks for shunt active power filter control. IEEE Trans. Ind. Inform. 2014, 10, 1765–1774. [Google Scholar] [CrossRef]
- Asiminoaei, L.; Blaabjerg, F.; Hansen, S. Detection is key—Harmonic detection methods for active power filter applications. IEEE Ind. Appl. Mag. 2007, 13, 22–33. [Google Scholar] [CrossRef]
- De Araujo Ribeiro, R.L.; Rocha, T.D.O.A.; de Sousa, R.M.; dos Santos, E.C.; Lima, A.M.N. A robust dc-link voltage control strategy to enhance the performance of shunt active power filters without harmonic detection schemes. IEEE Trans. Ind. Electron. 2015, 62, 803–813. [Google Scholar] [CrossRef]
- Afghoul, H.; Krim, F. Comparison between pi and fuzzy dpc control of a shunt active power filter. In Proceedings of the IEEE International Energy Conference and Exhibition (ENERGYCON), Florence, Italy, 9–12 September 2012; pp. 146–151. [Google Scholar]
- Mahanty, R. Indirect current controlled shunt active power filter for power quality improvement. Int. J. Electr. Power Energy Syst. 2014, 62, 441–449. [Google Scholar] [CrossRef]
- Jain, S.K.; Agrawal, P.; Gupta, H.O. Fuzzy logic controlled shunt active power filter for power quality improvement. IEEE Proc. Electr. Power Appl. 2002, 149, 317–328. [Google Scholar] [CrossRef]
- Mekri, F.; Mazari, B.; Machmoum, M. Control and optimization of shunt active power filter parameters by fuzzy logic. Can. J. Electr. Comput. Eng. 2006, 31, 127–134. [Google Scholar] [CrossRef]
- Mikkili, S.; Panda, A.K. Simulation and real-time implementation of shunt active filter id-iq control strategy for mitigation of harmonics with different fuzzy membership functions. IET Power Electron. 2012, 5, 1856–1872. [Google Scholar] [CrossRef]
- Suresh, Y.; Panda, A.K.; Suresh, M. Real-time implementation of adaptive fuzzy hysteresis-band current control technique for shunt active power filter. IET Power Electron. 2012, 5, 1188–1195. [Google Scholar] [CrossRef]
- Vahedi, H.; Sheikholeslami, A.; Bina, M.T.; Vahedi, M. Review and simulation of fixed and adaptive hysteresis current control considering switching losses and high-frequency harmonics. Adv. Power Electron. 2011, 2011, 397872. [Google Scholar] [CrossRef]
- Doǧan, H.; Akkaya, R. A control scheme employing an adaptive hysteresis current controller and an uncomplicated reference current generator for a single-phase shunt active power filter. Turk. J. Electr. Eng. Comput. Sci. 2014, 22, 1085–1097. [Google Scholar] [CrossRef]
- Suul, J.A.; Ljøkelsøy, K.; Midtsund, T.; Undeland, T. Synchronous reference frame hysteresis current control for grid converter applications. IEEE Trans. Ind. Appl. 2011, 47, 2183–2194. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Q.; Zhao, Y.; Li, D.; Xiong, Y. A novel active power filter for high-voltage power distribution systems application. IEEE Trans. Power Deliv. 2007, 22, 911–918. [Google Scholar] [CrossRef]
- Wu, L.; Zhuo, F.; Zhang, P.; Li, H.; Wang, Z. Study on the influence of supply-voltage fluctuation on shunt active power filter. IEEE Trans. Power Deliv. 2007, 22, 1743–1746. [Google Scholar] [CrossRef]
- Rahmani, S.; Al-Haddad, K.; Kanaan, H.Y. Two pwm techniques for single-phase shunt active power filters employing a direct current control strategy. IET Power Electron. 2008, 1, 376–385. [Google Scholar] [CrossRef]
- Gupta, A.K.; Khambadkone, A.M. A space vector pwm scheme for multilevel inverters based on two-level space vector pwm. IEEE Trans. Ind. Electron. 2006, 53, 1631–1639. [Google Scholar] [CrossRef]
- Choi, U.-M.; Lee, K.-B. Space vector modulation strategy for neutral-point voltage balancing in three-level inverter systems. IET Power Electron. 2013, 6, 1390–1398. [Google Scholar] [CrossRef]
- Zhang, Z.; Xie, Y.-X.; Huang, W.-P.; Le, J.-Y.; Chen, L. A new svpwm method for single-phase three-level npc inverter and the control method of neutral point voltage balance. In Proceedings of the International Conference on Electrical Machines and Systems, 2008 (ICEMS 2008), Tokyo, Japan, 15–18 November 2009; pp. 1–4. [Google Scholar]
- Raj, P.H.; Maswood, A.I.; Ooi, G.H.P.; Lim, Z. Voltage balancing technique in a space vector modulated 5-level multiple-pole multilevel diode clamped inverter. IET Power Electron. 2015, 8, 1263–1272. [Google Scholar] [CrossRef]
- Radzi, M.A.M.; Rahim, N.A. Neural network and bandless hysteresis approach to control switched capacitor active power filter for reduction of harmonics. IEEE Trans. Ind. Electron. 2009, 56, 1477–1484. [Google Scholar] [CrossRef]
- Vainio, O.; Ovaska, S.J.; Polla, M. Adaptive filtering using multiplicative general parameters for zero-crossing detection. IEEE Trans. Ind. Electron. 2003, 50, 1340–1342. [Google Scholar] [CrossRef]
- Rodriguez, P.; Pou, J.; Bergas, J.; Candela, J.I.; Burgos, R.P.; Boroyevich, D. Decoupled double synchronous reference frame pll for power converters control. IEEE Trans. Power Electron. 2007, 22, 584–592. [Google Scholar] [CrossRef]
- Golestan, S.; Monfared, M.; Freijedo, F.D. Design-oriented study of advanced synchronous reference frame phase-locked loops. IEEE Trans. Power Electron. 2013, 28, 765–778. [Google Scholar] [CrossRef]
- Campanhol, L.B.G.; Silva, S.A.O.; Goedtel, A. Application of shunt active power filter for harmonic reduction and reactive power compensation in three-phase four-wire systems. IET Power Electron. 2014, 7, 2825–2836. [Google Scholar] [CrossRef]
- Zainuri, M.A.A.M.; Radzi, M.A.M.; Soh, A.C.; Mariun, N.; Rahim, N.A.; Hajighorbani, S. Fundamental active current adaptive linear neural networks for photovoltaic shunt active power filters. Energies 2016, 9, 397. [Google Scholar] [CrossRef]
- Zainuri, M.A.A.M.; Radzi, M.A.M.; Soh, A.C.; Mariun, N.; Rahim, N.A. Simplified adaptive linear neuron harmonics extraction algorithm for dynamic performance of shunt active power filter. Int. Rev. Model. Simul. 2016, 9, 144–154. [Google Scholar]
- Rahman, N.F.A.; Radzi, M.A.M.; Soh, A.C.; Mariun, N.; Rahim, N.A. Dual function of unified adaptive linear neurons based fundamental component extraction algorithm for shunt active power filter operation. Int. Rev. Electr. Eng. 2015, 10, 544–552. [Google Scholar]
- Hoon, Y.; Radzi, M.A.M.; Hassan, M.K.; Mailah, N.F. Operation of three-level inverter-based shunt active power filter under nonideal grid voltage conditions with dual fundamental component extraction. IEEE Trans. Power Electron. 2018, 33, 7558–7570. [Google Scholar] [CrossRef]
- Hoon, Y.; Radzi, M.A.M.; Hassan, M.K.; Mailah, N.F. A self-tuning filter-based adaptive linear neuron approach for operation of three-level inverter-based shunt active power filters under non-ideal source voltage conditions. Energies 2017, 10, 667. [Google Scholar] [CrossRef]
- Elangovan, S.; Thanushkodi, K.; Neelakantan, P.N. A two level shunt active power filter without pll for industrial loads. Aust. J. Basic Appl. Sci. 2014, 8, 71–77. [Google Scholar]
- Musa, S.; Radzi, M.A.M.; Hizam, H.; Wahab, N.I.A.; Hoon, Y.; Zainuri, M.A.A.M. Modified synchronous reference frame based shunt active power filter with fuzzy logic control pulse width modulation inverter. Energies 2017, 10, 758. [Google Scholar] [CrossRef]
- Marques, G.D.; Pires, V.F.; Malinowski, M.; Kazmierkowski, M. An improved synchronous reference frame method for active filters. In Proceedings of the EUROCON 2007—The International Conference on “Computer as a Tool”, Warsaw, Poland, 9–12 September 2007; pp. 2564–2569. [Google Scholar]
- Kanjiya, P.; Khadkikar, V.; Zeineldin, H.H. A noniterative optimized algorithm for shunt active power filter under distorted and unbalanced supply voltages. IEEE Trans. Ind. Electron. 2013, 60, 5376–5390. [Google Scholar] [CrossRef]
- Tarisciotti, L.; Formentini, A.; Gaeta, A.; Degano, M.; Zanchetta, P.; Rabbeni, R.; Pucci, M. Model predictive control for shunt active filters with fixed switching frequency. IEEE Trans. Ind. Appl. 2017, 53, 296–304. [Google Scholar] [CrossRef]
- Tareen, W.U.K.; Mekhilef, S. Three-phase transformerless shunt active power filter with reduced switch count for harmonic compensation in grid-connected applications. IEEE Trans. Power Electron. 2018, 33, 4868–4881. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef]
- McGrath, B.P.; Holmes, D.G.; Galloway, J.J.H. Power converter line synchronization using a discrete fourier transform (dft) based on a variable sample rate. IEEE Trans. Power Electron. 2005, 20, 877–884. [Google Scholar] [CrossRef]
- Timbus, A.; Liserre, M.; Teodorescu, R.; Blaabjerg, F. Synchronization methods for three phase distributed power generation systems—An overview and evaluation. In Proceedings of the IEEE 36th Power Electronics Specialists Conference, Recife, Brazil, 16 June 2005; pp. 2474–2481. [Google Scholar]
- Chen, L.-R. Pll-based battery charge circuit topology. IEEE Trans. Ind. Electron. 2004, 51, 1344–1346. [Google Scholar] [CrossRef]
- Lai, M.-F.; Nakano, M. Special section on phase-locked loop techniques. IEEE Trans. Ind. Electron. 1996, 43, 607–608. [Google Scholar]
- Hsieh, G.-C.; Hung, J.C. Phase-locked loop techniques—A survey. IEEE Trans. Ind. Electron. 1996, 43, 609–615. [Google Scholar] [CrossRef]
- Bacon, V.D.; Souza, V.D.; Padim, E.T.; Silva, S.A.O.D. Influence of the pll phase-angle quality on the static and dynamic performance of grid-connected systems. In Proceedings of the 2017 Brazilian Power Electronics Conference (COBEP), Juiz de Fora, Brazil, 19–22 November 2017; pp. 1–6. [Google Scholar]
- Silva, S.A.O.D.; Bacon, V.D.; Campanhol, L.B.G.; Angelico, B.A. An adaptive phase-locked loop algorithm for single-phase utility connected system. In Proceedings of the 15th European Conference on Power Electronics and Applications (EPE), Lille, France, 2–6 September 2013; pp. 1–10. [Google Scholar]
- Han, Y.; Xu, L.; Khan, M.M.; Yao, G.; Zhou, L.-D.; Chen, C. A novel synchronization scheme for grid-connected converters by using adaptive linear optimal filter based pll (alof-pll). Simul. Model. Pract. Theory 2009, 17, 1299–1345. [Google Scholar] [CrossRef]
- Abdulsalam, M.; Poure, P.; Karimi, S.; Saadate, S. New digital reference current generation for shunt active power filter under distorted voltage conditions. Electr. Power Syst. Res. 2009, 79, 759–765. [Google Scholar] [CrossRef]
- Djazia, K.; Krim, F.; Chaoui, A.; Sarra, M. Active power filtering using the zdpc method under unbalanced and distorted grid voltage conditions. Energies 2015, 8, 1584–1605. [Google Scholar] [CrossRef]
- Shinnaka, S. A novel fast-tracking d-estimation method for single-phase signals. IEEE Trans. Power Electron. 2011, 26, 1081–1088. [Google Scholar] [CrossRef]
- Shinnaka, S. A robust single-phase pll system with stable and fast tracking. IEEE Trans. Ind. Appl. 2008, 44, 624–633. [Google Scholar] [CrossRef]
- Shinnaka, S. A new characteristics-variable two-input/output filter in d-module-designs, realizations, and equivalence. IEEE Trans. Ind. Appl. 2002, 38, 1290–1296. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Chakraborty, C. A shunt active power filter with enhanced performance using ann-based predictive and adaptive controllers. IEEE Trans. Ind. Electron. 2011, 58, 421–428. [Google Scholar] [CrossRef]
- Tey, L.H.; So, P.L.; Chu, Y.C. Improvement of power quality using adaptive shunt active filter. IEEE Trans. Power Deliv. 2005, 20, 1558–1568. [Google Scholar] [CrossRef]
- Biricik, S.; Redif, S.; Özerdem, Ö.C.; Khadem, S.K.; Basu, M. Real-time control of shunt active power filter under distorted grid voltage and unbalanced load condition using self-tuning filter. IET Power Electron. 2014, 7, 1895–1905. [Google Scholar] [CrossRef]
- Zainuri, M.A.A.M.; Radzi, M.A.M.; Soh, A.C.; Mariun, N.; Rahim, N.A. Dc-link capacitor voltage control for single-phase shunt active power filter with step size error cancellation in self-charging algorithm. IET Power Electron. 2016, 9, 323–335. [Google Scholar] [CrossRef]
- Ng, C.H.; Busawon, K.; Putrus, G.A.; Ran, L. Fast-individual-harmonic-extraction technique. IEEE Proc. Gener. Transm. Distrib. 2005, 152, 556–562. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).