Exponential Synchronization in Inertial Neural Networks with Time Delays

Abstract

In this paper, exponential synchronization for inertial neural networks with time delays is investigated. First, by introducing a directive Lyapunov functional, a sufficient condition is derived to ascertain the global exponential synchronization of the drive and response systems based on feedback control. Second, by introducing a variable substitution, the second-order differential equation is transformed into a first-order differential equation. As such, a new Lyapunov functional is constructed to formulate a novel global exponential synchronization for the systems under study. The two obtained sufficient conditions complement each other and are suitable to be applied in different cases. Finally, two numerical examples are given to illustrated the effectiveness of the proposed theoretical results.

1. Introduction

One of the main problems in the field of motion control is that the motion of multiple mechanisms should be controlled in a synchronous manner [1,2,3], such as position synchronization of two robot systems [4], speed synchronization of multiple induction motors [5], synchronous control for forging machines [6,7] and motion synchronization for dual-cylinder electro hydraulic lift systems [8]. Thus far, various kinds of synchronization control methods have been proposed, including feedback control [9,10,11], adaptive control [12,13], impulse control [14], pinning control [15], and sliding mode control [16,17,18,19].

When the inertia exceeds a critical value and the state of each neuron becomes under-damped, properties of the networks will change qualitatively [20,21]. On the other hand, due to the finite switching speed of amplifiers, time delays usually occur in a neural network [22,23,24,25]. Time delays are commonly regarded as an important factor to degrade system performance [26,27,28]. Thus, it is practically significant to study inertial neural networks with time-delays. For this reason, Ke and Miao [29,30,31,32] investigated stability and periodic solutions in inertial BAM neural networks and inertial Cohen–Grossberg-type neural networks, respectively. Asymptotical synchronization of a delayed inertial neural networks is considered in [33] by using the Lyapunov functional method and the Barbalat Lemma. Cao and Wana [34] presented some matrix measure strategies for stability and synchronization of inertial BAM neural network with time delays. Different from the methods in [35], the direct Lyapunov functional method is successfully applied to study stability and synchronization for a delayed inertial neural networks. However, the above synchronization results cannot reflect how fast the synchronization can be achieved [36,37,38]. As a fundamental issue, exponential synchronization should be paid more attention if fast synchronization is expected. Nevertheless, to the best of the authors’ knowledge, few results have been reported on exponential synchronization of inertial delayed neural networks, which motivates this work.

In this paper, we focus on the problem of exponential synchronization for inertial neural networks with time delays. Two sufficient conditions are formulated on the global exponential synchronization of the drive and response inertial delayed neural networks. The first one is based on a normal Lyapunov functional. The second one is based on a variable transformation. As a result, the second-order differential equation is transformed into a first-order differential equation, which allows us to construct a new Lyapunov functional. The two sufficient conditions can be applied in different cases. Finally, two illustrative examples are provided to show the effectiveness of the obtained theoretical results.

2. Problem Formulation

We consider the following inertial neural networks with time delay

$${\ddot{x}}_i\left(t\right)=-{\beta }_i{\dot{x}}_i\left(t\right)-{\alpha }_i{x}_i\left(t\right)+{\displaystyle \sum _{j=1}^n}{a}_{ij}{f}_j\left(x_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^n}{b}_{ij}{f}_j\left(x_j(t-{\tau }_{ij})\right)+I_i\left(t\right),$$

(1)

for $i=1,2,\dots ,n,$ where ${\alpha }_i$ and ${\beta }_i>0$ are constants. $x_i\left(t\right)$ denotes the states variable; $a_{ij}$ and $b_{ij}$ are connection weights of the system; $f_j$ denotes the activation functions; ${\tau }_{ij}$ is time delay and satisfies $0\le {\tau }_{ij}\le \tau$; and $I_i\left(t\right)$ denotes the external inputs. The initial values of the system in Equation (1) are

$$x_i\left(s\right)={\phi }_{xi}\left(s\right),{\dot{x}}_i\left(s\right)={\psi }_{xi}\left(s\right),-\tau \le s\le 0,$$

(2)

where $i=1,2,\dots ,n,{\phi }_{xi}\left(s\right),{\psi }_{xi}\left(s\right)$ are bounded and continuous functions.

In special cases, the system in Equation (1) contains mathematical models in mechanical fields. For example, if $n=1,$ swing equation is given by

$$m\ddot{\theta }\left(t\right)+c\dot{\theta }\left(t\right)+q\theta (t-\tau )+k\theta \left(t\right)=g\left(t\right).$$

If $n=2,$ the system in Equation (1) contains the torque balance equation for two inertial bodies of isolated

$$\left\{\begin{array}{c}{J}_1\ddot{{\theta }_1}=-B_1\dot{{\theta }_1}+K({\theta }_2-{\theta }_1)-T_1,\hfill \\ J_2\ddot{{\theta }_2}=-B_2\dot{{\theta }_2}-K({\theta }_2-{\theta }_1)+T_2.\hfill \end{array}\right.$$

which has strong application background.

Let the system in Equation (1) be a drive system. Then, the corresponding response system of Equation (1) can be represented as

$${\ddot{y}}_i\left(t\right)=-{\beta }_i{\dot{y}}_i\left(t\right)-{\alpha }_i{y}_i\left(t\right)+{\displaystyle \sum _{j=1}^n}{a}_{ij}{f}_j\left(y_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^n}{b}_{ij}{f}_j\left(y_j(t-{\tau }_{ij})\right)+I_i\left(t\right)+u_i\left(t\right),$$

(3)

where $u_i\left(t\right)$ is the feedback controller, $i=1,2,\dots ,n.$ The initial values of the system in Equation (3) are

$$y_i\left(s\right)={\phi }_{yi}\left(s\right),{\dot{y}}_i\left(t\right)={\psi }_{yi}\left(s\right),-\tau \le s\le 0,$$

(4)

where $i=1,2,\dots ,n$ and ${\phi }_{yi}\left(s\right),{\psi }_{yi}\left(s\right)$ are continuous and bounded functions.

Let $e_i\left(t\right)=y_i\left(t\right)-x_i\left(t\right),$ from Equations (1) and (3), we obtain the following error system

$${\ddot{e}}_i\left(t\right)=-{\beta }_i{\dot{e}}_i\left(t\right)-{\alpha }_i{e}_i\left(t\right)+{\displaystyle \sum _{j=1}^n}{a}_{ij}{\overline{f}}_j\left(e_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^n}{b}_{ij}{\overline{f}}_j\left(e_j(t-{\tau }_{ij})\right)+u_i\left(t\right),$$

(5)

where $\overline{f_j}\left(e_j\left(t\right)\right)=f_j\left(y_i\left(t\right)\right)-f_j\left(x_i\left(t\right)\right),i=1,2,\dots ,n.$

Throughout this paper, the following assumption is needed.

$\left(H\right):$ The functions $f_j(j=1,2,\cdots ,n)$ are assumed to satisfy the Lipschitz condition. That is, there exist constants $l_j>0$, such that

$$|f_j\left(v_1\right)-f_j\left(v_2\right))|\le l_j|v_1-v_2|,v_1,v_2\in \mathbb{R},j=1,2,\dots ,n.$$

In this paper, we focus on exponential synchronization of the systems in Equations (1) and (3), whose definition is given as follows.

Definition 1.

The systems in Equations (1) and (3) are said to be exponentially synchronized if there exist constants $M>0$ and $\sigma >0$ such that

$${\displaystyle \sum _{i=1}^n}|x_i\left(t\right)-y_i{\left(t\right)|}^2\le M{e}^{-\sigma t}{\parallel {\phi }_x-{\phi }_y\parallel }^2,t>0,$$

where

$$\parallel {\phi }_x-{\phi }_y{\parallel }^2=\underset{-\tau \le t\le 0}{sup}{\displaystyle \sum _{i=1}^n}{|{\phi }_{xi}\left(t\right)-{\phi }_{yi}\left(t\right)|}^2.$$

3. Main Results

In this section, two sufficient conditions are given to ascertain the exponentially synchronizing of the systems in Equations (1) and (3).

Theorem 1.

Assume $\left(H\right)$ holds. For the following feedback controller

$$u_i\left(t\right)={\lambda }_i(y_i\left(t\right)-x_i\left(t\right)),i=1,2,\cdots ,n,$$

where ${\lambda }_i$ is a positive constant, if the inequalities

$$-2{\alpha }_i+2{\lambda }_i+|2-{\alpha }_i-{\beta }_i+{\lambda }_i|+{\displaystyle \sum _{j=1}^n}(|a_{ij}|l_j+2|a_{ji}|l_i)+{\displaystyle \sum _{j=1}^n}{l}_j|b_{ij}|<0,$$

$$2-2{\beta }_i+|2-{\alpha }_i-{\beta }_i+{\lambda }_i|+{\displaystyle \sum _{j=1}^n}|a_{ij}|l_j+{\displaystyle \sum _{j=1}^n}{l}_j|b_{ij}|<0,$$

are satisfied for $i=1,2\dots ,n$, then the systems in Equations (1) and (3) are globally exponentially synchronized.

Proof. 

For the feedback controller

$$u_i\left(t\right)={\lambda }_i(y_i\left(t\right)-x_i\left(t\right)),i=1,2,\cdots ,n$$

from Equation (5), we can obtain

$${\ddot{e}}_i\left(t\right)=-{\beta }_i{\dot{e}}_i\left(t\right)-({\alpha }_i-{\lambda }_i)e_i\left(t\right)+{\displaystyle \sum _{j=1}^n}{a}_{ij}{\overline{f}}_j\left(e_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^n}{b}_{ij}{\overline{f}}_j\left(e_j(t-{\tau }_{ij})\right),$$

(6)

where $i=1,2,\dots ,n.$ Now, we consider the Lyapunov functional as

$$V\left(t\right)={\displaystyle \sum _{i=1}^n}[e_i^2\left(t\right)+{(e_i\left(t\right)+{\dot{e}}_i\left(t\right))}^2]e^{\epsilon t}+2{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}|b_{ij}|l_j{\int }_{t-{\tau }_{ij}}^t{e}^{\epsilon (s+{\tau }_{ij})}{e}_j^2\left(s\right)ds,$$

(7)

where $\epsilon$ is a small positive constant.

From Equations (6) and (7), we have

$$\begin{array}{ll}\hfill D^{+}V\left(t\right)& ={\displaystyle \sum _{i=1}^n}\{\epsilon [e_i^2\left(t\right)+{(e_i\left(t\right)+{\dot{e}}_i\left(t\right))}^2]e^{\epsilon t}+2[e_i\left(t\right){\dot{e}}_i\left(t\right)+(e_i\left(t\right)+{\dot{e}}_i\left(t\right))({\dot{e}}_i\left(t\right)+{\ddot{e}}_i\left(t\right)]e^{\epsilon t}\hfill \\ & +2{\displaystyle \sum _{j=1}^n}|b_{ij}|l_j[e_j^2\left(t\right)e^{\epsilon (t+{\tau }_{ij})}-e_j^2(t-{\tau }_{ij})e^{\epsilon t}]\}\hfill \\ & =e^{\epsilon t}{\displaystyle \sum _{i=1}^n}\{\epsilon [e_i^2\left(t\right)+{(e_i\left(t\right)+{\dot{e}}_i\left(t\right))}^2]+2e_i\left(t\right){\dot{e}}_i\left(t\right)+2\left((e_i\left(t\right)+{\dot{e}}_i\left(t\right))\right[(1-{\beta }_i){\dot{e}}_i\left(t\right)\hfill \\ & -({\alpha }_i-{\lambda }_i)e\left(t\right)+{\displaystyle \sum _{j=1}^n}{a}_{ij}{\overline{f}}_j\left(e_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^n}{b}_{ij}{\overline{f}}_j\left(e_j(t-{\tau }_{ij})\right)]+2{\displaystyle \sum _{j=1}^n}|b_{ij}|l_j[e_j^2\left(t\right)e^{\epsilon {\tau }_{ij}}-e_j^2(t-{\tau }_{ij})]\}\hfill \\ & \le e^{\epsilon t}{\displaystyle \sum _{i=1}^n}\{(2\epsilon -2{\alpha }_i+2{\lambda }_i)e_i^2\left(t\right)+(\epsilon +2-2{\beta }_i){\dot{e}}_i^2\left(t\right)+2(\epsilon +2-{\beta }_i-{\alpha }_i+{\lambda }_i)e_i\left(t\right){\dot{e}}_i\left(t\right)\hfill \\ & +2[|e_i\left(t\right)|+|{\dot{e}}_i\left(t\right)|]({\displaystyle \sum _{j=1}^n}|a_{ij}|l_j|e_j\left(t\right)|+{\displaystyle \sum _{j=1}^n}|b_{ij}|l_j|e_j(t-{\tau }_{ij}|)\hfill \\ & +2{\displaystyle \sum _{j=1}^n}|b_{ij}|l_j[e_j^2\left(t\right)e^{\epsilon {\tau }_{ij}}-e_j^2(t-{\tau }_{ij})]\}\hfill \\ & \le e^{\epsilon t}{\displaystyle \sum _{i=1}^n}\{[2\epsilon -2{\alpha }_i+2{\lambda }_i+|\epsilon +2-{\beta }_i-{\alpha }_i+{\lambda }_i|+{\displaystyle \sum _{j=1}^n}(|a_{ij}|l_j|+2|a_{ji}|l_i|)+{\displaystyle \sum _{j=1}^n}(|b_{ij}|l_j\hfill \\ & +2|b_{ji}|l_i{e}^{\epsilon {\tau }_{ij}}\left)\right]e_i^2\left(t\right)+[\epsilon +2-2{\beta }_i+|\epsilon +2-{\beta }_i-{\alpha }_i+{\lambda }_i|+{\displaystyle \sum _{j=1}^n}(|a_{ij}|+|b_{ij}|)l_j]{\dot{e}}_i^2\left(t\right)\}.\hfill \end{array}$$

(8)

By the condition of Theorem 1, we can choose a small $\epsilon >0$ such that

$$2\epsilon -2{\alpha }_i+2{\lambda }_i+|\epsilon +2-{\alpha }_i-{\beta }_i+{\lambda }_i|+{\displaystyle \sum _{j=1}^n}(|a_{ij}|l_j+2|a_{ji}|l_i)+{\displaystyle \sum _{j=1}^n}(|b_{ij}|l_j+2|b_{ji}|l_i{e}^{\epsilon {\tau }_{ij}})\le 0,$$

$$\epsilon +2-2{\beta }_i+|\epsilon +2-{\alpha }_i-{\beta }_i+{\lambda }_i|+{\displaystyle \sum _{j=1}^n}|a_{ij}|l_j+{\displaystyle \sum _{j=1}^n}{l}_j|b_{ij}|\le 0,$$

for $i=1,2\dots ,n$. From Equation (8), we get $D^{+}V\left(t\right)\le 0$, and thus $V\left(t\right)\le V\left(0\right)$, for all $t\ge 0$.

From Equation (7), we have

$$V\left(t\right)\ge {\displaystyle \sum _{i=1}^n}{e}_i^2\left(t\right)e^{\epsilon t}.$$

(9)

$$\begin{array}{cc}\hfill V\left(0\right)& ={\displaystyle \sum _{i=1}^n}[e_i^2\left(0\right)+{(e_i\left(0\right)+{\dot{e}}_i\left(0\right))}^2]+2{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}|b_{ij}|l_j{\int }_{-{\tau }_{ij}}^0{e}^{\epsilon (s+{\tau }_{ij})}{e}_j^2\left(s\right)ds\hfill \\ & ={\displaystyle \sum _{i=1}^n}[e_i^2\left(0\right)+{(e_i\left(0\right)+{\dot{e}}_i\left(0\right))}^2]+2{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}|b_{ij}|l_j{\int }_{-{\tau }_{ij}}^0{e}^{\epsilon (s+{\tau }_{ij})}{({\phi }_{yj}\left(s\right)-{\phi }_{xj})}^2\left(s\right)ds\hfill \\ & \le 3\parallel {\phi }_y-{\phi }_x{\parallel }^2+2(\parallel {\psi }_y-{\psi }_x{\parallel }^2)+2\tau {\displaystyle \sum _{i=1}^n}\underset{1\le j\le n}{max}\{|b_{ij}|l_j\}{e}^{\epsilon \tau }{\parallel {\phi }_y-{\phi }_x\parallel }^2\hfill \\ & \le [3+2\tau {\displaystyle \sum _{i=1}^n}\underset{1\le j\le n}{max}\{|b_{ij}|L_j\}{e}^{\epsilon \tau }]\parallel {\phi }_y-{\phi }_x{\parallel }^2+2{\parallel {\psi }_y-{\psi }_x\parallel }^2.\hfill \end{array}$$

(10)

where $\parallel {\psi }_x-{\psi }_y{\parallel }^2=\underset{-\tau \le t\le 0}{sup}{\displaystyle \sum _{i=1}^n}{|{\psi }_{xi}\left(t\right)-{\psi }_{yi}\left(t\right)|}^2.$

Since $V\left(0\right)\ge V\left(t\right)$, from Equations (9) and (10), we obtain

$${\displaystyle \sum _{i=1}^n}{e}_i^2\left(t\right)e^{\epsilon t}\le [3+2\tau {\displaystyle \sum _{i=1}^n}\underset{1\le j\le n}{max}\{|b_{ij}|L_j\}{e}^{\epsilon \tau }]\parallel {\phi }_y-{\phi }_x{\parallel }^2+2{\parallel {\psi }_y-{\psi }_x\parallel }^2.$$

(11)

By multiplying both sides of Equation (11) with $e^{-\epsilon t}$, we get

$${\displaystyle \sum _{i=1}^n}{e}_i^2\left(t\right)\le M{e}^{-\epsilon t}{\parallel {\phi }_y-{\phi }_x\parallel }^2,t\ge 0,$$

(12)

where $M=[3+2\tau {\displaystyle \sum _{i=1}^n}\underset{1\le j\le n}{max}\{|b_{ij}|L_j\}{e}^{\epsilon \tau }+\frac{2\parallel {\psi }_y-{\psi }_x{\parallel }^2}{\parallel {\phi }_y-{\phi }_x{\parallel }^2}].$

From Equation (12), we have

$${\displaystyle \sum _{i=1}^n}{(x_i\left(t\right)-y_i\left(t\right))}^2\le M{e}^{-\epsilon t}{\parallel {\phi }_y-{\phi }_x\parallel }^2,t>0.$$

By Definition 1, the systems in Equations (1) and (3) are globally exponentially synchronized. □

In the following, we will introduce some variable transformation and construct a new suitable Lyapunov functional to realize the global exponential synchronization between the drive system in Equation (1) and the responsive system in Equation (3).

By the variable transformation:

$$z_i\left(t\right)={\dot{x}}_i\left(t\right)+{\eta }_i{x}_i\left(t\right),w_i\left(t\right)={\dot{y}}_i\left(t\right)+{\eta }_i{y}_i\left(t\right),{\eta }_i>0,i=1,2,\dots ,n,$$

then Equations (1)–(4) can be rewritten as

$$\left\{\begin{array}{c}{\dot{x}}_i\left(t\right)=-{\eta }_i{x}_i\left(t\right)+z_i\left(t\right),\hfill \\ {\dot{z}}_i\left(t\right)=-({\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i)x_i\left(t\right)-({\beta }_i-{\eta }_i)z_i\left(t\right)+{\displaystyle \sum _{j=1}^n}{a}_{ij}{f}_j\left(x_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^n}{b}_{ij}{f}_j\left(x_j(t-{\tau }_{ij})\right)+I_i\left(t\right).\hfill \end{array}\right.$$

(13)

$$\left\{\begin{array}{c}{x}_i\left(s\right)={\phi }_{xi}\left(s\right),{\dot{x}}_i\left(t\right)={\psi }_{xi}\left(s\right),\hfill \\ z_i\left(s\right)={\phi }_{xi}\left(s\right)+{\psi }_{xi}\left(s\right)\doteq {\overline{\phi }}_i\left(s\right).\hfill \end{array}\right.$$

(14)

$$\left\{\begin{array}{c}{\dot{y}}_i\left(t\right)=-{\eta }_i{y}_i\left(t\right)+w_i\left(t\right),\hfill \\ {\dot{w}}_i\left(t\right)=-({\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i)y_i\left(t\right)-({\beta }_i-{\eta }_i)w_i\left(t\right)+{\displaystyle \sum _{j=1}^n}{a}_{ij}{f}_j\left(y_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^n}{b}_{ij}{f}_j\left(y_j(t-{\tau }_{ij})\right)\hfill \\ +I_i\left(t\right)+u_i\left(t\right).\hfill \end{array}\right.$$

(15)

and

$$\left\{\begin{array}{c}{y}_i\left(s\right)={\phi }_{yi}\left(s\right),{\dot{y}}_i\left(s\right)={\psi }_{yi}\left(s\right),\hfill \\ w_i\left(s\right)={\phi }_{yi}\left(s\right)+{\psi }_{yi}\left(s\right)\doteq {\overline{\phi }}_i\left(s\right).\hfill \end{array}\right.$$

(16)

Let the error

$$e_{1i}\left(t\right)=y_i\left(t\right)-x_i\left(t\right),e_{2i}\left(t\right)=w_i\left(t\right)-z_i\left(t\right),i=1,2\dots ,n.$$

From Equations (13) and (15), we can obtain

$$\left\{\begin{array}{c}{\dot{e}}_{1i}\left(t\right)=-{\eta }_i{e}_{1i}\left(t\right)+e_{2i}\left(t\right),\hfill \\ {\dot{e}}_{2i}\left(t\right)=-({\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i)e_{1i}\left(t\right)-({\beta }_i-{\eta }_i)e_{2i}\left(t\right)+{\displaystyle \sum _{j=1}^n}{a}_{ij}\overline{f_j}\left(e_{1j}\left(t\right)\right)+{\displaystyle \sum _{j=1}^n}{b}_{ij}\overline{f_j}\left(e_{1j}(t-{\tau }_{ij})\right)+u_i\left(t\right),\hfill \end{array}\right.$$

(17)

where $\overline{f_j}\left(e_{1i}\left(t\right)\right)=f_j\left(y_i\left(t\right)\right)-f_j\left(x_i\left(t\right)\right).$

Based on the above analysis, we have the following results.

Theorem 2.

Assume $\left(H\right)$ holds. For the following feedback controller

$$u_i\left(t\right)=-{\lambda }_i{e}_{1i}\left(t\right)-{\mu }_i{e}_{2i}\left(t\right),$$

where ${\lambda }_i$ and ${\mu }_i$ are positive constant, if the inequalities

$$-2{\eta }_i+|{\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1|+{\displaystyle \sum _{j=1}^n}|a_{ji}|l_i+{\displaystyle \sum _{j=1}^n}{l}_i|b_{ji}|e^{{\tau }_{ji}}<0,$$

$$-2{\beta }_i+2{\eta }_i-2{\mu }_i+|{\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1+{\displaystyle \sum _{j=1}^n}|a_{ji}|l_i+{\displaystyle \sum _{j=1}^n}{l}_j|b_{ij}|<0,$$

hold for $i=1,2\dots ,n$, then the systems in Equations (1) and (3) are globally exponentially synchronized.

Proof. 

Consider the following feedback controller

$$u_i\left(t\right)=-{\lambda }_i{e}_{1i}\left(t\right)-{\mu }_i{e}_{2i}\left(t\right),i=1,2\dots ,n.$$

From Equation (17), we can obtain

$$\left\{\begin{array}{c}{\dot{e}}_{1i}\left(t\right)=-{\eta }_i{e}_{1i}\left(t\right)+e_{2i}\left(t\right),\hfill \\ {\dot{e}}_{2i}\left(t\right)=-({\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i)e_{1i}\left(t\right)-({\beta }_i-{\eta }_i+{\mu }_i)e_{2i}\left(t\right)+{\displaystyle \sum _{j=1}^n}{a}_{ij}\overline{f_j}\left(e_{1j}\left(t\right)\right)\hfill \\ +{\displaystyle \sum _{j=1}^n}{b}_{ij}\overline{f_j}\left(e_{1j}(t-{\tau }_{ij})\right)\hfill \end{array}\right.$$

(18)

which follows that

$$\begin{array}{cc}\hfill \frac{1}{2}\frac{d(e_{1i}^2\left(t\right)+e_{2i}^2\left(t\right))}{dt}& =-{\eta }_i{e}_{1i}^2\left(t\right)+e_{1i}\left(t\right)e_{2i}\left(t\right)-({\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i)e_{1i}\left(t\right)e_{2i}\left(t\right)-({\beta }_i-{\eta }_i+{\mu }_i)e_{2i}^2\left(t\right)\hfill \\ & +{\displaystyle \sum _{j=1}^n}{a}_{ij}{e}_{2i}\left(t\right)\overline{f_j}\left(e_{1j}\left(t\right)\right)+{\displaystyle \sum _{j=1}^n}{b}_{ij}{e}_{2i}\left(t\right)\overline{f_j}\left(e_{1j}(t-{\tau }_{ij})\right)\hfill \\ & \le -{\eta }_i{e}_{1i}^2\left(t\right)-({\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1)e_{1i}\left(t\right)e_{2i}\left(t\right)-({\beta }_i-{\eta }_i+{\mu }_i)e_{2i}^2\left(t\right)\hfill \\ & +{\displaystyle \sum _{j=1}^n}|a_{ij}|l_j|e_{2i}\left(t\right)||e_{1j}\left(t\right)|+{\displaystyle \sum _{j=1}^n}{l}_j|b_{ij}||e_{2i}\left(t\right)||e_{1j}(t-{\tau }_{ij})|\hfill \\ & \le -{\eta }_i{e}_{1i}^2\left(t\right)-({\beta }_i-{\eta }_i+{\mu }_i)e_{2i}^2\left(t\right)+(|{\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1|\hfill \\ & +{\displaystyle \sum _{j=1}^n}|a_{ji}|l_i)|e_{1i}\left(t\right)||e_{2i}\left(t\right)|+{\displaystyle \sum _{j=1}^n}{l}_j|b_{ij}||e_{2i}\left(t\right)||e_{1j}(t-{\tau }_{ij})|\hfill \\ & \le -{\eta }_i{e}_{1i}^2\left(t\right)-({\beta }_i-{\eta }_i+{\mu }_i)e_{2i}^2\left(t\right)+(|{\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1|\hfill \\ & +{\displaystyle \sum _{j=1}^n}|a_{ji}|l_i)\frac{e_{1i}^2\left(t\right)+e_{2i}^2\left(t\right)}{2}+{\displaystyle \sum _{j=1}^n}{l}_j|b_{ij}|\frac{e_{1j}^2(t-{\tau }_{ij})+e_{2i}^2\left(t\right)}{2}\hfill \\ & =-[{\eta }_i-\frac{1}{2}(|{\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1|\hfill \\ & +{\displaystyle \sum _{j=1}^n}|a_{ji}|l_i\left)\right]e_{1i}^2\left(t\right)-[{\beta }_i-{\eta }_i+{\mu }_i-\frac{1}{2}(|{\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1|\hfill \\ & +{\displaystyle \sum _{j=1}^n}|a_{ji}|l_i+{\displaystyle \sum _{j=1}^n}{l}_j|b_{ij}|)]e_{2i}^2\left(t\right)+{\displaystyle \sum _{j=1}^n}{l}_j|b_{ij}|\frac{e_{1j}^2(t-{\tau }_{ij})}{2},\hfill \end{array}$$

(19)

where $i=1,2\dots ,n.$

We now construct the following Lyapunov functional

$$V\left(t\right)={\displaystyle \sum _{i=1}^n}\{\frac{e_{1i}^2\left(t\right)+e_{2i}^2\left(t\right)}{2}{e}^{\epsilon t}+{\displaystyle \sum _{j=1}^n}\frac{|b_{ij}|}{2}{l}_j{\int }_{t-{\tau }_{ij}}^t{e}^{\epsilon (s+{\tau }_{ij})}{e}_{1j}^2\left(s\right)ds\},$$

(20)

$\epsilon >0$ is a small number. By Equations (18) and (20), we obtain

$$\begin{array}{cc}\hfill D^{+}V\left(t\right)& ={\displaystyle \sum _{i=1}^n}\{\epsilon \frac{e_{1i}^2\left(t\right)+e_{2i}^2\left(t\right)}{2}{e}^{\epsilon t}+\frac{1}{2}\frac{d}{dt}(e_{1i}^2\left(t\right)+e_{2i}^2\left(t\right))e^{\epsilon t}+{\displaystyle \sum _{j=1}^n}\frac{|b_{ij}|}{2}{l}_j[e_{1j}^2\left(t\right)e^{\epsilon (t+{\tau }_{ij})}-e_{1j}^2(t-{\tau }_{ij})e^{\epsilon t}]\}\hfill \\ & \le e^{\epsilon t}{\displaystyle \sum _{i=1}^n}\{\epsilon \frac{e_{1i}^2\left(t\right)+e_{2i}^2\left(t\right)}{2}-[{\eta }_i-\frac{1}{2}(|{\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1|+{\displaystyle \sum _{j=1}^n}|a_{ji}|l_i\left)\right]e_{1i}^2\left(t\right)\hfill \\ & -[{\beta }_i-{\eta }_i+{\mu }_i-\frac{1}{2}(|{\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1|+{\displaystyle \sum _{j=1}^n}|a_{ji}|l_i\hfill \\ & +{\displaystyle \sum _{j=1}^n}{l}_j|b_{ij}|)]e_{2i}^2\left(t\right)+{\displaystyle \sum _{j=1}^n}{l}_j|b_{ij}|\frac{e_{1j}^2(t-{\tau }_{ij})}{2}+{\displaystyle \sum _{j=1}^n}\frac{|b_{ij}|}{2}{l}_j[e_{1j}^2\left(t\right)e^{{\tau }_{ij}}-e_{1j}^2(t-{\tau }_{ij})]\}\hfill \\ & =e^{\epsilon t}{\displaystyle \sum _{i=1}^n}\{\epsilon \frac{e_{1i}^2\left(t\right)+e_{2i}^2\left(t\right)}{2}-[{\eta }_i-\frac{1}{2}(|{\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1|\hfill \\ & +{\displaystyle \sum _{j=1}^n}|a_{ji}|l_i+{\displaystyle \sum _{j=1}^n}{l}_i|b_{ji}|e^{{\tau }_{ji}}\left)\right]e_{1i}^2\left(t\right)-[{\beta }_i-{\eta }_i+{\mu }_i-\frac{1}{2}(|{\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1|\hfill \\ & +{\displaystyle \sum _{j=1}^n}|a_{ji}|l_i+{\displaystyle \sum _{j=1}^n}{l}_j|b_{ij}|)]e_{2i}^2\left(t\right)\hfill \\ & =\frac{1}{2}{e}^{\epsilon t}{\displaystyle \sum _{i=1}^n}\{[\epsilon -2{\eta }_i+(|{\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1|+{\displaystyle \sum _{j=1}^n}|a_{ji}|l_i\hfill \\ & +{\displaystyle \sum _{j=1}^n}{l}_i|b_{ji}|e^{{\tau }_{ji}}\left)\right]e_{1i}^2\left(t\right)+[\epsilon -2{\beta }_i+2{\eta }_i-2{\mu }_i+(|{\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1|\hfill \\ & +{\displaystyle \sum _{j=1}^n}|a_{ji}|l_i+{\displaystyle \sum _{j=1}^n}{l}_j|b_{ij}|)]e_{2i}^2\left(t\right).\hfill \end{array}$$

(21)

By condition of Theorem 2, we can choose a small $\epsilon >0$ such that

$$\epsilon -2{\eta }_i+(|{\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1|+{\displaystyle \sum _{j=1}^n}|a_{ji}|l_i+{\displaystyle \sum _{j=1}^n}{l}_i|b_{ji}|e^{{\tau }_{ji}})\le 0,$$

$$\epsilon -2{\beta }_i+2{\eta }_i-2{\mu }_i+(|{\alpha }_i+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1|+{\displaystyle \sum _{j=1}^n}|a_{ji}|l_i+{\displaystyle \sum _{j=1}^n}{l}_j|b_{ij}|)\le 0,$$

for $i=1,2\dots ,n$. From (21), we get $D^{+}V\left(t\right)\le 0$, for all $t\ge 0$. On the other hand, from Equation (20), we have

$$\begin{array}{cc}\hfill V\left(t\right)& \ge {\displaystyle \sum _{i=1}^n}\frac{e_{1i}^2\left(t\right)+e_{2i}^2\left(t\right)}{2}{e}^{\epsilon t}={\displaystyle \sum _{i=1}^n}\frac{e^{\epsilon t}}{2}[{(y_i\left(t\right)-x_i\left(t\right))}^2+{(w_i\left(t\right)-z_i\left(t\right))}^2]\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill V\left(0\right)& ={\displaystyle \sum _{i=1}^n}\{\frac{e_{1i}^2\left(0\right)+e_{2i}^2\left(0\right)}{2}+{\displaystyle \sum _{j=1}^n}\frac{|b_{ij}|}{2}{l}_j{\int }_{-{\tau }_{ij}}^0{e}_{1j}^2\left(s\right)e^{\epsilon (s+{\tau }_{ij})}ds\}\hfill \\ & ={\displaystyle \sum _{i=1}^n}\{\frac{{({\phi }_{yi}\left(0\right)-{\phi }_{xi}\left(0\right))}^2}{2}+\frac{{({\phi }_{yi}\left(0\right)-{\phi }_{xi}\left(0\right)-{\psi }_{yi}\left(0\right)+{\psi }_{xi}\left(0\right))}^2}{2}\hfill \\ & +{\displaystyle \sum _{j=1}^n}\frac{|b_{ij}|}{2}{l}_j{\int }_{-{\tau }_{ij}}^0{({\phi }_{yj}\left(s\right)-{\phi }_{xj}\left(s\right))}^2{e}^{\epsilon (s+{\tau }_{ij})}ds\}\hfill \\ & \le \frac{3\parallel {\phi }_y-{\phi }_x{\parallel }^2}{2}+\parallel {\psi }_y-{\psi }_x{\parallel }^2+\tau {\displaystyle \sum _{i=1}^n}\underset{1\le j\le n}{max}\{\frac{|b_{ij}}{2}|l_i\}{e}^{\epsilon \tau }{\parallel {\phi }_y-{\phi }_x\parallel }^2\hfill \\ & \le \frac{1}{2}[3+\tau {\displaystyle \sum _{i=1}^n}\underset{1\le j\le n}{max}\{|b_{ij}|l_j\}{e}^{\epsilon \tau }]\parallel {\phi }_y-{\phi }_x{\parallel }^2+{\parallel {\psi }_y-{\psi }_x\parallel }^2,\hfill \end{array}$$

(23)

where $\parallel {\psi }_x-{\psi }_y{\parallel }^2=\underset{-\tau \le t\le 0}{sup}{\displaystyle \sum _{i=1}^n}{|{\psi }_{xi}\left(t\right)-{\psi }_{yi}\left(t\right)|}^2.$

Since $V\left(0\right)\ge V\left(t\right)$, from Equations (22) and (23), we obtain

$${\displaystyle \sum _{i=1}^n}\frac{e^{\epsilon t}}{2}[{(y_i\left(t\right)-x_i\left(t\right))}^2+{(w_i\left(t\right)-z_i\left(t\right))}^2]\le \frac{1}{2}[3+\tau {\displaystyle \sum _{i=1}^n}\underset{1\le j\le n}{max}\{|b_{ij}|l_j\}{e}^{\epsilon \tau }]\parallel {\phi }_y-{\phi }_x{\parallel }^2+{\parallel {\psi }_y-{\psi }_x\parallel }^2.$$

(24)

Multiplying both sides of Equation (24) with $2e^{-\epsilon t}$ yields

$${\displaystyle \sum _{i=1}^n}{[{(x_i\left(t\right)-y_i\left(t\right))}^2+(w_i\left(t\right)-z_{(}t))}^2]\le M{e}^{-\epsilon t}{\parallel {\phi }_y-{\phi }_x\parallel }^2,$$

(25)

where $M=\frac{1}{2}[3+\tau {\displaystyle \sum _{i=1}^n}\underset{1\le j\le n}{max}\{|b_{ij}|l_j\}{e}^{2\epsilon \tau }+\frac{2\parallel {\psi }_y-{\psi }_x{\parallel }^2}{\parallel {\phi }_y-{\phi }_x{\parallel }^2}].$

From Equation (16), we have

$${\displaystyle \sum _{i=1}^n}{(x_i\left(t\right)-y_i\left(t\right))}^2\le M{e}^{-\epsilon t}{\parallel {\phi }_y-{\phi }_x\parallel }^2,t>0.$$

By Definition 1, the systems in Equations (1) and (3) are globally exponentially synchronized. □

If $n=1,f\left(x\right(t\left)\right)=x\left(t\right)$, then the system in Equation (1) becomes the swing equation of ship with time delays

$$\ddot{x}\left(t\right)+{\beta }_1\dot{x}\left(t\right)-b_{11}x(t-{\tau }_{11})+({\alpha }_1-a_{11})x\left(t\right)=I\left(t\right).$$

(26)

The response system is given as follows

$$\ddot{y}\left(t\right)+{\beta }_1\dot{y}\left(t\right)-b_{11}y(t-{\tau }_{11})+({\alpha }_1-a_{11})y\left(t\right)+u_1\left(t\right)=I\left(t\right).$$

(27)

By Theorem 1, we obtain the following corollary.

Corollary 1.

Assume $\left(H\right)$ holds. For the following feedback controller $u_1\left(t\right)={\lambda }_1(y_1\left(t\right)-x_1\left(t\right)),$ if

$$-2{\alpha }_1+2{\lambda }_1+|2-{\alpha }_1-{\beta }_1+{\lambda }_1|+3|a_{11}|+|b_{11}|<0,$$

$$2-2{\beta }_1+|2-{\alpha }_1-{\beta }_1+{\lambda }_1|+|a_{11}|+|b_{11}|<0,$$

then the driven system in Equation (26) and the response system in Equation (27) are globally exponentially synchronized.

If $n=2,{\alpha }_1={\alpha }_2=a_{12}=a_{21},a_{11}=a_{22}=0,f_i\left(x_i\left(t\right)\right)=x_i\left(t\right),b_{ij}=0,I_i\left(t\right)=T_i,i,j=1,2$, then the system in Equation (1) become the torque balance equation for two inertial bodies of isolation

$$\left\{\begin{array}{c}{\ddot{x}}_1\left(t\right)=-{\beta }_1{\dot{x}}_1\left(t\right)+{\alpha }_1(x_2\left(t\right)-x_1\left(t\right))+T_1,\hfill \\ {\ddot{x}}_2\left(t\right)=-{\beta }_2{\dot{x}}_2\left(t\right)-{\alpha }_1(x_2\left(t\right)-x_1\left(t\right))+T_2\hfill \end{array}\right.$$

(28)

The response system that is driven by Equation (28) reads as

$$\left\{\begin{array}{c}{\ddot{y}}_1\left(t\right)=-{\beta }_1{\dot{y}}_1\left(t\right)+{\alpha }_1(y_2\left(t\right)-y_1\left(t\right))+T_1+u_1\left(t\right),\hfill \\ {\ddot{y}}_2\left(t\right)=-{\beta }_2{\dot{y}}_2\left(t\right)-{\alpha }_1(y_2\left(t\right)-y_1\left(t\right))+T_2+u_2\left(t\right)\hfill \end{array}\right.$$

(29)

By Theorem 2, we obtain:

Corollary 2.

Assume $\left(H\right)$ holds. For the following feedback controller

$$u_i\left(t\right)=-{\lambda }_i{e}_{1i}\left(t\right)-{\mu }_i{e}_{2i}\left(t\right),{\lambda }_i>0,{\mu }_i>0,i=1,2,$$

if

$$-2{\eta }_i+|{\alpha }_1+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1|+{\alpha }_1<0,i=1,2,$$

$$-2{\beta }_i+2{\eta }_i-2{\mu }_i+|{\alpha }_1+{\eta }_i^2-{\beta }_i{\eta }_i+{\lambda }_i-1|+{\alpha }_1<0,i=1,2,$$

then the system in Equation (28) exponentially synchronizes.

Remark 1.

In Theorem 1, a Lyapunov function is directly constructed based on the error system in Equation (6) to realize the global exponential synchronization between the the system in Equation (1) and the the system in Equation (3).

Remark 2.

In Theorem 2, we introduce some variable transformation and construct a new suitable Lyapunov functional to realize the global exponential synchronization between the drive system in Equation (1) and the responsive system in Equation (3).

Remark 3.

Theorems 1 and 2 give two sufficient conditions to ensure the global exponential synchronization between the drive system in Equation (1) and the responsive system in Equation (3), respectively. For the purpose of applications, we can select one of them according to the actual requirements. For example, the parameters given in the systems in Equations (28) and (29) satisfy all the conditions of Theorem 2, but cannot satisfy the conditions of Theorem 1. In this situation, we can draw a conclusion on the global exponential synchronization of Equations (1) and (3) by Theorem 2 and not by Theorem 1.

4. Numerical Examples

In this section, we give two numerical examples to illustrate our results.

Example 1.

Consider the following inertial neural networks with time delay ($n=2$)

$${\ddot{x}}_i\left(t\right)=-{\beta }_i{\dot{x}}_i\left(t\right)-{\alpha }_i{x}_i\left(t\right)+{\displaystyle \sum _{j=1}^2}{a}_{ij}{f}_j\left(x_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^2}{b}_{ij}{f}_j\left(x_j(t-{\tau }_{ij})\right)+I_i\left(t\right).$$

(30)

The response system that is driven by Equation (30) is given as follows

$${\ddot{y}}_i\left(t\right)=-{\beta }_i{\dot{y}}_i\left(t\right)-{\alpha }_i{y}_i\left(t\right)+{\displaystyle \sum _{j=1}^2}{a}_{ij}{f}_j\left(y_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^2}{b}_{ij}{f}_j\left(y_j(t-{\tau }_{ij})\right)+I_i\left(t\right)+u_i\left(t\right),$$

(31)

where $u_i\left(t\right)={\lambda }_i(y_i\left(t\right)-x_i\left(t\right)),{\lambda }_i>0,i=1,2.$ Set ${\alpha }_1=1.2,{\alpha }_2=1.5,{\beta }_1=2,{\beta }_2=2.5,$ $a_{11}=\frac{1}{32},a_{12}=-\frac{1}{32},a_{21}=-\frac{1}{64},a_{22}=-\frac{1}{64},$ $b_{11}=-\frac{1}{32},b_{12}=\frac{1}{64},b_{21}=\frac{1}{32},b_{22}=-\frac{1}{64},$ $f_i\left(x\right)=\frac{1}{8}sin\left(8x\right),I_i\left(t\right)=\frac{1}{16}exp(-t),{\tau }_{ij}=ln2,i,j=1,2.$ ${\lambda }_1=0.2,{\lambda }_2=0.4.$ Obviously, $|f_i\left(x\right)-f_i\left(y\right)|\le |x-y|,l_i=1,i=1,2.$

For numerical simulation, the initial condition is supposed to be $[{\phi }_{x1}\left(0\right),{\phi }_{x2}\left(0\right),{\psi }_{x1}\left(0\right)$, ${\psi }_{x2}\left(0\right),{\phi }_{y1}\left(0\right),{\phi }_{y2}\left(0\right),{\psi }_{y1}\left(0\right),{\psi }_{y2}\left(0\right)]=[0.1;0.2;0.1;0.1;0.13;0.12;0.25;0.3]$.

The simulation results are shown in Figure 1, Figure 2 and Figure 3.

Figure 1. The synchronization trajectories between the state $x_1\left(t\right)$ of the drive system in Equation (30) and the state $y_1\left(t\right)$ of the response system in Equation (31) in Example 1.

Figure 2. The synchronization trajectories between the state $x_2\left(t\right)$ of the drive system in Equation (30) and the state $y_2\left(t\right)$ of the response system in Equation (31) in Example 1.

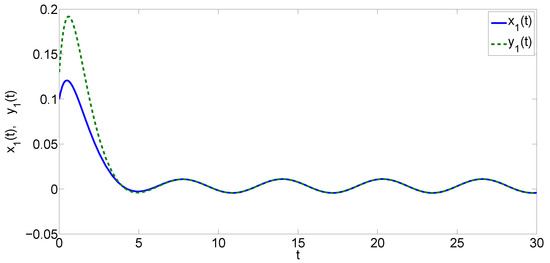
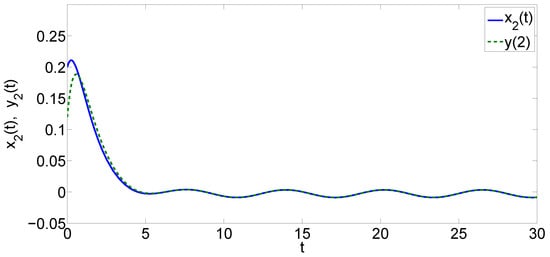
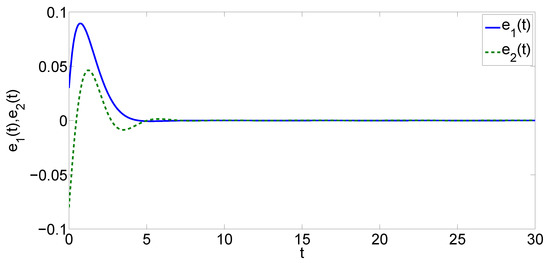
Figure 3. Evolution of synchronization errors $e_1\left(t\right),e_2\left(t\right)$ in Example 1.

Through simple calculation, we get the following results

$$-2{\alpha }_1+2{\lambda }_1+|2-{\alpha }_1-{\beta }_1+{\lambda }_1|+{\displaystyle \sum _{j=1}^2}(|a_{1j}|l_j+2|a_{j1}|l_1)+{\displaystyle \sum _{j=1}^2}{l}_1|b_{j1}|<-0.79<0,$$

$$2-2{\beta }_1+|2-{\alpha }_1-{\beta }_1+{\lambda }_1|+{\displaystyle \sum _{j=1}^2}|a_{1j}|l_j+{\displaystyle \sum _{j=1}^2}{l}_j|b_{1j}|<-0.89<0,$$

$$-2{\alpha }_2+2{\lambda }_2+|2-{\alpha }_2-{\beta }_2+{\lambda }_2|+{\displaystyle \sum _{j=1}^2}(|a_{2j}|l_j+2|a_{j2}|l_2)+{\displaystyle \sum _{j=1}^2}{l}_2|b_{j2}|<-0.38<0,$$

$$2-2{\beta }_2+|1-{\alpha }_2-{\beta }_2+{\lambda }_2|+{\displaystyle \sum _{j=1}^2}|a_{2j}|l_j+{\displaystyle \sum _{j=1}^2}{l}_j|b_{2j}|<-1.29<0.$$

By Theorem 1, the systems in Equations (30) and (31) are globally exponentially synchronized. Clearly, this consequence is coincident with the results of numerical simulation.

Example 2.

We consider the following inertial neural networks with time delay ($n=2$)

$${\ddot{x}}_i\left(t\right)=-{\beta }_i{\dot{x}}_i\left(t\right)-{\alpha }_i{x}_i\left(t\right)+{\displaystyle \sum _{j=1}^2}{a}_{ij}{f}_j\left(x_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^2}{b}_{ij}{f}_j\left(x_j(t-{\tau }_{ij})\right)+I_i\left(t\right).$$

(32)

The response system that is driven by Equation (32) is given as follows

$${\ddot{y}}_i\left(t\right)=-{\beta }_i{\dot{y}}_i\left(t\right)-{\alpha }_i{y}_i\left(t\right)+{\displaystyle \sum _{j=1}^2}{a}_{ij}{f}_j\left(y_j\left(t\right)\right)+{\displaystyle \sum _{j=1}^2}{b}_{ij}{f}_j\left(y_j(t-{\tau }_{ij})\right)+I_i\left(t\right)+u_i\left(t\right),$$

(33)

where$u_i\left(t\right)=-{\lambda }_i(y_i\left(t\right)-x_i\left(t\right))-{\mu }_i(w_i\left(t\right)-z_i\left(t\right)),z_i\left(t\right)=\frac{d{x}_i\left(t\right)}{dt}+{\eta }_i{x}_i\left(t\right),$

$w_i\left(t\right)=\frac{d{y}_i\left(t\right)}{dt}+{\eta }_i{y}_i\left(t\right),i=1,2.$

${\alpha }_1=1,{\alpha }_2=2,{\beta }_1=3,{\beta }_2=2.5,$$a_{11}=\frac{1}{32},a_{12}=-\frac{1}{32},a_{21}=-\frac{1}{64},a_{22}=-\frac{1}{64},$

$b_{11}=-\frac{1}{32},b_{12}=\frac{1}{64},b_{21}=\frac{1}{32},b_{22}=-\frac{1}{64},$$f_i\left(x\right)=\frac{1}{8}sin\left(8x\right),I_i\left(t\right)=\frac{1}{16}exp(-t),$

${\tau }_{ij}=ln2,i,j=1,2.$${\eta }_1=0.6,{\eta }_2=0.8,{\mu }_1=1,{\mu }_2=2,{\lambda }_1=0.5,{\lambda }_2=0.4$

Obviously, $|f_i\left(x\right)-f_i\left(y\right)|\le |x-y|,i=1,2.$ We select $l_i=1.$ The initial condition is set to be $[{\phi }_{x1}\left(0\right),{\phi }_{x2}\left(0\right),{\psi }_{x1}\left(0\right),{\psi }_{x2}\left(0\right),{\phi }_{y1}\left(0\right),{\phi }_{y2}\left(0\right),{\psi }_{y1}\left(0\right),{\psi }_{y2}\left(0\right)]=[0.1;0.2;0.1;0.3;0.02;0.06;0.5;0.3]$. The simulation results of Example 2 are shown in Figure 4, Figure 5 and Figure 6.

Figure 4. The synchronization trajectories between the state $x_1\left(t\right)$ of the drive system in Equation (32) and the state $y_1\left(t\right)$ of the response system in Equation (33) in Example 2.

Figure 5. The synchronization trajectories between the state $x_2\left(t\right)$ of the drive system in Equation (32) and the state $y_2\left(t\right)$ of the response system in Equation (33) in Example 2.

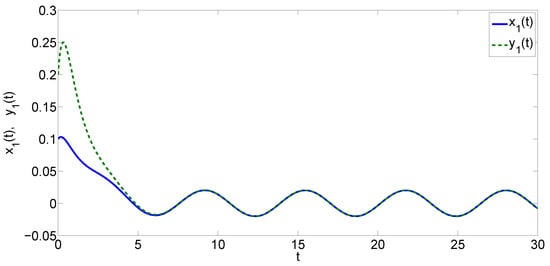
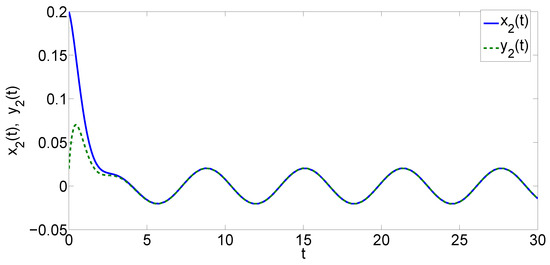
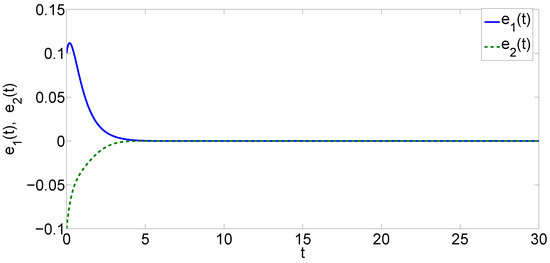
Figure 6. Evolution of synchronization errors $e_1\left(t\right),e_2\left(t\right)$ in Example 2.

We obtain the following results by calculation,

$$-2{\eta }_1+|{\alpha }_1+{\eta }_1^2-{\beta }_1{\eta }_1+{\lambda }_1-1|+{\displaystyle \sum _{j=1}^2}|a_{j1}|l_1+{\displaystyle \sum _{j=1}^1}{l}_1|b_{j1}|<-0.25<0,$$

$$-2{\beta }_1+2{\eta }_1-2{\mu }_1+|{\alpha }_1+{\eta }_1^2-{\beta }_1{\eta }_1+{\lambda }_1-1|+{\displaystyle \sum _{j=1}^2}|a_{j1}|l_1+{\displaystyle \sum _{j=1}^2}{l}_j|b_{1j}|e^{{\tau }_{1j}}<-4.55<0,$$

$$-2{\eta }_2+|{\alpha }_2+{\eta }_2^2-{\beta }_2{\eta }_2+{\lambda }_2-1|+{\displaystyle \sum _{j=1}^2}|a_{j2}|l_2+{\displaystyle \sum _{j=1}^2}{l}_i|b_{j2}|<-1.4<0,$$

$$-2{\beta }_2+2{\eta }_2-2{\mu }_2+|{\alpha }_2+{\eta }_2^2-{\beta }_2{\eta }_2+{\lambda }_2-1|+{\displaystyle \sum _{j=1}^2}|a_{j2}|l_2+{\displaystyle \sum _{j=1}^2}{l}_j|b_{2j}|e^{{\tau }_{2j}}<-7.2<0.$$

Thus, the conditions in Theorem 2 are satisfied. Then, the system in Equation (33) globally exponentially synchronizes with the system in Equation (32). Obviously, the conclusion from Theorem 2 is consistent with the numerical simulation results.

5. Conclusions

In this paper, we study the inertial neural networks with time delays, where ${\beta }_i$ is the damping coefficient. By employing the Lyapunov functional method, two exponential synchronization have been derived for the drive and response systems, which are useful in practice. These two sufficient conditions complement each other to be applied in different cases. Two examples have shown their effectiveness.