Grid Reconfiguration Method for Off-Grid DOA Estimation

Abstract

Off-grid algorithms for direction of arrival (DOA) estimation have become attractive because of their advantages in resolution and efficiency over conventional ones. In this paper, we propose a grid reconfiguration direction of arrival (GRDOA) estimation method based on sparse Bayesian learning. Unlike other off-grid methods, the grid points of GRDOA are treated as dynamic parameters. The number and position of the grid points are varied iteratively via a root method and a fission process. Then, the grid gets reconfigured through some criteria. By iteratively updating the reconfigured grid, DOAs are estimated completely. Since GRDOA has fewer grid points, it has better computational efficiency than the previous methods. Moreover, GRDOA can achieve better resolution and relatively higher accuracy. Numerical simulation results validate the effectiveness of GRDOA.

1. Introduction

Direction of arrival (DOA) estimation is a popular research topic in array signal processing and has been widely used in various fields, such as antenna [1], radar [2], and vehicle localization [3]. For example, driverless vehicle technologies are now quickly emerging with the development of artificial intelligence (AI) and Internet of Things (IoT). DOA can offer a robust and accurate solution for driverless vehicle localization, which has shown many advantages over the conventional global positioning system (GPS) [4]. DOA can also be applied in patient tracking which is a crucial part of the elderly healthcare systems, playing a significant role in today’s aging era [5]. Among the conventional DOA estimation techniques, MUSIC (multiple signal classification ) [6] and ESPRIT (estimation of parameters by rotational invariant techniques ) [7] have become mainstreams due to their super-resolution. However, prior knowledge of source number and a sufficient number of snapshots are required for these subspace-based algorithms. Moreover, the performance of these methods deteriorates seriously when the sources are correlated.

In recent years, the rapid development of compressed sensing (CS) [8] and its application in array antenna and array signal processing [9,10,11,12,13,14,15,16,17,18,19], has provided a new solution for DOA estimation. A great deal of research has emerged, identifying the DOAs by formulating the problem as a sparse signal recovery problem. Assuming the sparsity of the signal in the spatial domain, we can process the array output directly instead of estimating a sensor covariance matrix. Therefore, sparse signal recovery algorithms can address the limitations of subspace-based algorithms and can be applied in several demanding scenarios with no prior knowledge of the source number, correlated sources, and a limited number of snapshots.

Many sparse signal recovery algorithms have been proposed in CS literature, which can be applied to estimate the DOAs by exploiting the spatial sparsity [20,21,22,23,24]. FOCUSS (FOcal Underdetermined System Solver) [25] uses an iterative method which is based on weighted norm minimization. However, it cannot guarantee global optimal. $l_1$-SVD [26] enforces sparsity by imposing penalties based on the $l_1$-norm, which can achieve high accuracy, but has the difficulty of choosing regularized parameters. SPICE [27] is obtained by the minimization of a covariance matrix fitting criterion and is useful in both many-snapshot cases and single-snapshot situations. SBL [28] uses an empirical Bayesian prior to estimate a convenient posterior distribution over candidate basis vectors, which has superior performance because of their use of data adaptive priors and capability of automatic regularization parameter selection.

For these CS methods mentioned above, which are called on-grid methods, true DOAs are assumed as lying on a set of fixed grid points. Therefore, the existing sparse representation techniques can be directly applied. However, in practice, the true DOAs may not be exactly on the fixed grid. The off-grid gap, which is the gap between true DOAs and its nearest grid point, always exists. Besides, the grid interval should be determined empirically. On the one hand, small grid interval brings not only a high computational workload but also a strong correlation with adjacent steering vectors. On the other hand, large grid interval leads to large model error.

To address the off-grid gap, many off-grid methods, in which a sampling grid is still required but true DOAs are not restricted to be on the grid, are proposed. Sparse total least-squares (STLS) [29] approach can yield a MAP optimal estimate if the matrix perturbation caused by the basis mismatch is Gaussian. OGSBI [30] takes a Bayesian perspective on off-grid methods. The model of OGSBI is based on a first-order Taylor series expansion, and a Laplace prior is assumed to exploit the spatial sparsity of signals. PSBL [31] takes an off-grid model based on a perturbed sparse Bayesian learning, in which a linear interpolation between two adjacent grid points is adopted. However, these off-grid methods mentioned above are still faced with the trade-off between accuracy and computational complexity. A dense sampling grid is needed to achieve high accuracy, which, however, will slow its speed. On the contrary, a coarser grid can greatly reduce the computational workload but will introduce more model errors. Root SBL (RSBL) [32] decreases computational workload by using a root method. It also maintains high accuracy with a coarse grid. However, if more than one DOA exists in the same grid interval, RSBL may fail to discriminate these DOAs in the case of coarse grid. GEDOA [33] combines off-grid methods and grid refinement to make the grid nonuniformly evolve from coarse to dense, which can discriminate closely spaced DOAs as well as achieve higher efficiency than RSBL. However, its performance will get worse in the low SNR condition.

Both on-grid and off-grid methods are grid-based methods. Another kind of methods to handle the off-grid gap is gridless methods [34,35,36,37]. They operate in the continuous domain directly so that they can avoid the grid mismatch problem. They are convex and have strong theoretical guarantees as well. However, this kind of methods is only applied to the uniform or sparse linear arrays.

In this paper, an off-grid method named grid reconfiguration direction of arrival (GRDOA) based on sparse Bayesian learning is proposed. Unlike most off-grid methods, in which uniformly sampling and fixed number of grid points are used, the grid number of GRDOA is varied during the reconfiguration process, and the final grid is nonuniform. It has two integral parts: the initial estimation and the fine estimation. Compared with $l_1$-SVD, OGSBI, and RSBL, GRDOA has the advantages of less computational complexity and remains sufficiently accurate. Besides, it can successfully discriminate DOAs that are in the same grid interval. Furthermore, GRDOA has better robustness than GEDOA, especially in low SNR condition.

The rest of this paper is organized as follows. In Section 2, we examine the off-grid DOA model. In Section 3, we introduce the proposed GRDOA algorithm. In Section 4, we present our simulation results. In Section 5, we conclude this paper.

2. Data Model

Assume that K narrow-band and far-field source signals with DOAs (${\theta }_1,{\theta }_2,\dots ,{\theta }_K$) impinge on a ULA with M sensors, where $K<M$. The signal received at the output of the array can be written as

$$\mathbf{y}\left(t\right)=\mathbf{A}\mathbf{s}\left(t\right)+\mathbf{e}\left(t\right),t\in (t_1,t_2,\dots ,t_T),$$

(1)

where $\mathbf{y}\left(t\right)={[y_1\left(t\right),y_2\left(t\right),\dots ,y_M\left(t\right)]}^T$, $\mathbf{s}\left(t\right)={[s_1\left(t\right),s_2\left(t\right),\dots ,s_K\left(t\right)]}^T$, ${(·)}^T$ is the transpose, T is the number of snapshots, $\mathbf{A}=[\mathbf{a}\left({\theta }_1\right),\mathbf{a}\left({\theta }_2\right),\dots ,\mathbf{a}\left({\theta }_K\right)]$ is an $M\times K$ matrix of steering vectors with $\mathbf{a}\left({\theta }_k\right)=[1,v_{{\theta }_k},\dots ,v_{{\theta }_k}^{M-1}{]}^T$, $v_{{\theta }_k}=e^{-j2\pi d/\lambda sin\left({\theta }_k\right)}$, d is the distance between adjacent sensors, $\lambda$ is the wavelength of the source, and $\mathbf{e}\left(t\right)={[e_1\left(t\right),e_2\left(t\right),\dots ,e_M\left(t\right)]}^T$ is an unknown noise vector. For simplicity, Equation (1) can be written as

$$\mathbf{Y}=\mathbf{A}\mathbf{S}+\mathbf{E},$$

(2)

with the definitions of $\mathbf{Y}=[\mathbf{y}\left(t_1\right),\mathbf{y}\left(t_2\right),\dots ,\mathbf{y}\left(t_T\right)]$, $\mathbf{S}=[\mathbf{s}\left(t_1\right),\mathbf{s}\left(t_2\right),\dots ,\mathbf{s}\left(t_T\right)]$, and $\mathbf{E}=[\mathbf{e}\left(t_1\right),\mathbf{e}\left(t_2\right),\dots ,\mathbf{e}\left(t_T\right)]$.

To cast the DOA estimation as a sparse representation problem, the sparse signal model is constructed. Uniform sampling over DOA range is used in the conventional grid-based methods. Let $\tilde{\mathit{\theta }}=[{\tilde{\theta }}_1,{\tilde{\theta }}_2,\dots ,{\tilde{\theta }}_N]$ be a fixed sampling grid in the range $[-\frac{\pi }{2},\frac{\pi }{2}]$, where N denotes the grid number $(N\gg M)$ and $r={\tilde{\theta }}_2-{\tilde{\theta }}_1$ denotes the grid interval. If the grid is fine enough, the true DOAs will lie on (or, practically, close to) the grid. Then, the data model can be written as

$$\mathbf{Y}=\tilde{\mathbf{A}}\mathbf{X}+\mathbf{E},$$

(3)

where $\tilde{\mathbf{A}}=[\mathbf{a}({\tilde{\theta }}_1),\mathbf{a}({\tilde{\theta }}_2),\dots ,\mathbf{a}({\tilde{\theta }}_N)]$, $\mathbf{X}$ is set as a zero-padded extension of $\mathbf{S}$ whose non-zero rows correspond to the true DOAs at ${\theta }_k,k=1,2,\dots ,K$.

Usually, the DOAs cannot be right on the grid, which leads to the off-grid gap problem, as shown in Figure 1 [38]. To handle this problem, there are two kinds of off-grid methods: one is based on a fixed grid with a joint estimation of the sparse signal and the grid offset, and the other relies on a dynamic grid. For the former, a linear approximation is usually used to model the off-grid problem [30]. Dynamic grid methods [32,33,39] were proposed in which the grid is considered as the adjustable parameters. For this kind of methods, the computational complexity is significantly reduced, and the modeling error can be almost eliminated. In this paper, we give a novel dynamic grid method to eliminate the off-grid gap.

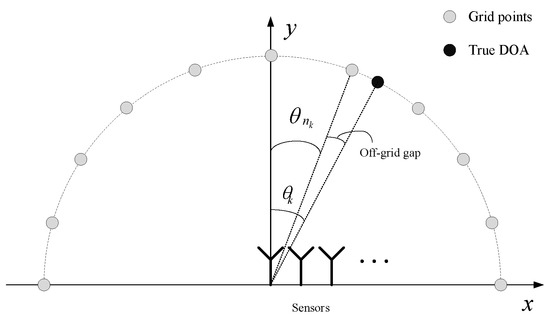
Figure 1. The sparse signal model of off-grid methods.

3. The GRDOA Algorithm

The proposed GRDOA method is divided into two parts, i.e., the initial estimation and the fine estimation. In the initial estimation, the grid update process is implemented to iteratively update the grid points, and the grid fission process is used to generate new grid points. At the end of the initial estimation, the grid will get reconfigured through grid selection. In the fine estimation, the reconfigured grid gets updated iteratively via the grid update process, and DOAs will be estimated finally. The flow chart of GRDOA is shown in Figure 2.

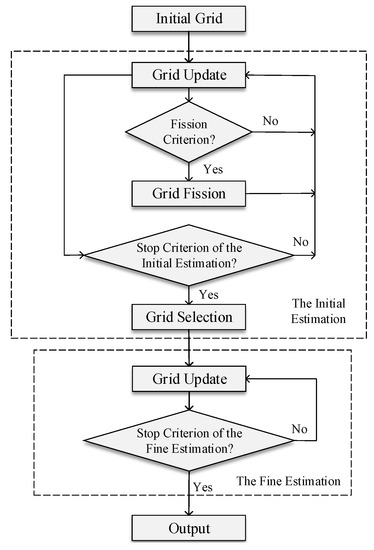
Figure 2. The flow chart of the proposed method.

3.1. Sparse Bayesian Formulation

Follow the sparse Bayesian model that is commonly used in SBL [30], where the noises are regarded as circular symmetric complex Gaussian noises, we have

$$p(\mathbf{Y}\mid \mathbf{X};{\alpha }_0)={\mathsf{\Pi }}_{t=1}^T\mathcal{CN}(\mathbf{y}\left(t\right)\mid \mathbf{x}\left(t\right);{\alpha }_0^{-1}),$$

(4)

where ${\alpha }_0$ denotes the noise precision with a Gamma hyperprior

$$p\left({\alpha }_0\right)=\mathsf{\Gamma }({\alpha }_0\mid a,b),$$

(5)

where the variables a and b are set to small values following [30,40] to obtain a broad hyperprior.

The signals are assumed to be independent among snapshots with two-stage hierarchical prior [30]. Let $\mathit{\alpha }={\left[{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_N\right]}^T$, where the variable ${\alpha }_i$ stands for the inverse variance, and $\mathsf{\Lambda }=diag\left(\mathit{\alpha }\right)$. We have

$$p(\mathbf{X}\mid \mathit{\alpha })={\mathsf{\Pi }}_{t=1}^T\mathcal{CN}(\mathbf{x}\left(t\right)\mid 0,\mathsf{\Lambda }),$$

(6)

$$p\left(\alpha \right)={\mathsf{\Pi }}_{i=1}^N\mathsf{\Gamma }({\alpha }_i\mid 1,\rho ),$$

(7)

where $\rho$ is a small positive constraint (e.g., $\rho =0.01$ [40]).

By combining the stages of the hierarchical Bayesian model, the joint PDF is

$$p(\mathbf{X},\mathbf{Y},{\alpha }_0,\mathit{\alpha })=p(\mathbf{Y}\mid \mathbf{X};{\alpha }_0)p(\mathbf{X}\mid \mathit{\alpha })p\left(\mathit{\alpha }\right)p\left({\alpha }_0\right),$$

(8)

with the distributions on the right-hand side defined by Equations (4), (6), (7) and (5), respectively.

3.2. Grid Update

The expectation maximum algorithm [41] is adopted to perform the Bayesian inference. It is easy to know that the posterior distribution of $\mathbf{X}$ is also a complex Gaussian:

$$p(\mathbf{X}\mid \mathbf{Y},{\alpha }_0,\mathit{\alpha })={\mathsf{\Pi }}_{t=1}^T\mathcal{CN}(\mathbf{x}\left(t\right)\mid \mathit{\mu }\left(t\right),\mathsf{\Sigma }),$$

(9)

with

$$\mathit{\mu }\left(t\right)={\alpha }_0\mathsf{\Sigma }{\tilde{\mathbf{A}}}^H\mathbf{y}\left(t\right),t=1,2,\cdots ,T,$$

(10)

$$\mathsf{\Sigma }={({\alpha }_0{\tilde{\mathbf{A}}}^H\tilde{\mathbf{A}}+{\mathsf{\Lambda }}^{-1})}^{-1},$$

(11)

where $\mathit{\mu }\left(t\right)$ and $\mathsf{\Sigma }$ are the estimations of expectation and variance of $\mathbf{X}$, respectively. The hyperparameters $\mathit{\alpha }$ and ${\alpha }_0$ are needed to calculate $\mathit{\mu }\left(t\right)$ and $\mathsf{\Sigma }$. The updates of $\mathit{\alpha }$ and ${\alpha }_0$ can be obtained by a similar procedure in [30]:

$${\alpha }_i^{new}=\frac{-T+\sqrt{T^2+4\rho {\sum }_{t=1}^T{\left[{\mathsf{\Xi }}_t\right]}_{ii}}}{2\rho },$$

(12)

$${\alpha }_0^{new}=\frac{TM+(a-1)}{b+{\sum }_{t=1}^T{∥\mathbf{y}\left(t\right)-\tilde{\mathbf{A}}\mathit{\mu }\left(t\right)∥}_2^2+Ttr(\tilde{\mathbf{A}}\mathsf{\Sigma }{\tilde{\mathbf{A}}}^H)},$$

(13)

where ${\mathsf{\Xi }}_t\triangleq \mathit{\mu }\left(t\right){\left(\mathit{\mu }\left(t\right)\right)}^H+\mathsf{\Sigma }$.

As a dynamic parameter, $\tilde{\mathit{\theta }}$ gets updated through a root method [32], where the maximization problem is converted to a root seeking problem:

$$[{\upsilon }_{{\tilde{\theta }}_i},1,{\upsilon }_{{\tilde{\theta }}_i}^{-1},...,{\upsilon }_{{\tilde{\theta }}_i}^{-(M-2)}]\left[\begin{array}{c}\frac{M(M-1)}{2}{\varphi }^{\left(i\right)}\\ {\phi }_2^{\left(i\right)}\\ 2{\phi }_3^{\left(i\right)}\\ ⋮\\ (M-1){\phi }_M^{\left(i\right)}\end{array}\right]=0,$$

(14)

with

$${\varphi }^{\left(i\right)}\triangleq \sum _{t=1}^T\left(\right|{\mu }_{ti}{|}^2+{\gamma }_{ii}),$$

(15)

$${\mathit{\phi }}^{\left(i\right)}\triangleq T\sum _{j\ne i}{\gamma }_{ji}{\mathbf{a}}_j-\sum _{t=1}^T{\mu }_{ti}^H{\mathbf{y}}_{t-i},$$

(16)

where ${\upsilon }_{{\tilde{\theta }}_i}\triangleq e^{-j2\pi d/\lambda sin({\tilde{\theta }}_i)}$, ${\mathbf{a}}_i$, ${\mathit{\mu }}_{ti}$, and ${\gamma }_{ij}$ denote the ith column, the ith element, and the $(i,j)$th element of $\tilde{\mathbf{A}}$, $\mathit{\mu }\left(t\right)$, and $\mathsf{\Sigma }$, respectively. ${\mathbf{y}}_{t-i}\triangleq \mathbf{y}\left(t\right)-{\sum }_{j\ne i}{\mu }_{tj}{\mathbf{a}}_j$.

We note that Equation (14) has $M-1$ roots in the complex plane since its order is $M-1$. Practically, the closest root to the unit circle is selected (which is denoted by $z_{i^{\ast }}$) in the noisy environment. Then, the candidate point for grid updating is

$${\tilde{\theta }}_{i^{\ast }}^{new}=arcsin(-\frac{\lambda }{2\pi d}angle\left(z_{i^{\ast }}\right)),$$

(17)

and ${\tilde{\theta }}_{i^{\ast }}^{new}$ will be accepted for grid updating if it falls into the set of $[\frac{{\tilde{\theta }}_{i^{\ast }-1}+{\tilde{\theta }}_{i^{\ast }}}{2},\frac{{\tilde{\theta }}_{i^{\ast }}+{\tilde{\theta }}_{i^{\ast }+1}}{2}]$. As suggested in [32], we update some active grids rather than all grids in each iteration. The $\eta$ largest mean power of rows of $\mathbf{X}$ are regarded as the active grids, where $1⩽\eta ⩽M$. The mean power estimation of $\mathbf{X}$ can be written as $\mathbf{P}=[P_1,P_2,\dots ,P_N],P_i=\sqrt{{\sum }_{t=1}^T{\left|{\mu }_{ti}\right|}^2},i=1,2,...,N$, where ${\mu }_{ti}$ is estimated by Equation (10) in each iteration. If the number of sources K is available, we set $\eta ⩾K$; otherwise, $\eta =M$ is recommended.

3.3. Grid Fission

As we know, a coarse grid can bring great efficiency yet poor resolution. The grid fission process is designed to improve resolution, at the same time maintaining high efficiency. The idea of grid fission is first proposed in [33]. However, the grid fission process in this paper is different from that of [33]. The grid point corresponding to the largest element of $\mathbf{P}$, supposed as ${\tilde{\theta }}_p$, is selected as the one to get fission. A new grid point will be generated as follows:

If ${\tilde{\theta }}_p<{\tilde{\theta }}_p^{last}$

$${\tilde{\theta }}^{new}={\tilde{\theta }}_p-D,$$

(18)

otherwise,

$${\tilde{\theta }}^{new}={\tilde{\theta }}_p+D,$$

(19)

with

$$D=\frac{D^{last}}{step},$$

(20)

where the superscript $last$ denotes the value in the last iteration. At the first iteration, D is set as a half of the initial grid interval, and ${\tilde{\theta }}_p^{last}$ is the closest initial grid point to ${\tilde{\theta }}_p$. $step$ is a parameter with $step>1$. The variable $step$ is a parameter, and the influence of different values of $step$ on the proposed algorithm is discussed in the next section.

The prior distributions of $\tilde{\mathbf{A}}$, $\mathbf{X}$ and $\mathbf{E}$ are needed at the beginning of each iteration. Therefore, when a new grid point is generated, a new row or column corresponding to this grid point should be added for $\tilde{\mathbf{A}}$, $\mathbf{X}$ and $\mathbf{E}$.

The new column of $\tilde{\mathbf{A}}$ can be calculated as

$$\mathbf{a}({\tilde{\theta }}^{new})=[1,v_{{\tilde{\theta }}^{new}},\dots ,v_{{\tilde{\theta }}^{new}}^{M-1}){]}^T,v_{{\tilde{\theta }}^{new}}=e^{-j2\pi d/\lambda sin({\tilde{\theta }}^{new})},$$

(21)

where ${\tilde{\theta }}^{new}$ is the new grid point.

As for $\mathbf{X}$, according to the definition of $\mathbf{X}$, i.e., Equations (6) and (7), $\mathit{\alpha }$ is related to the prior assumption of $\mathbf{X}$, and the problem can be transformed into designing a new $\mathit{\alpha }$. Two elements of $\mathit{\alpha }$ need to be updated. The first is ${\alpha }^{new}$, the new element of $\mathit{\alpha }$, corresponding to ${\tilde{\theta }}^{new}$. The second is ${\alpha }_p$, corresponding to ${\tilde{\theta }}_p$. To keep the distribution of $\mathbf{X}$ invariant after fission, we have

$$p\left({\alpha }^{new}\right)p\left({\alpha }_p\right)=p\left({\alpha }_p^{last}\right),$$

(22)

where ${\alpha }_p^{last}$ is the element of ${\mathit{\alpha }}^{last}$ corresponding to ${\tilde{\theta }}_p^{last}$ in the last iteration.

According to Equation (7), $p\left({\alpha }^{new}\right)p\left({\alpha }_p\right)=\mathsf{\Gamma }({\alpha }^{new}\mid 1,\rho )\mathsf{\Gamma }({\alpha }_p\mid 1,\rho )=e^{-\rho ({\alpha }^{new}+{\alpha }_p)}$, $p\left({\alpha }_p^{last}\right)=\mathsf{\Gamma }({\alpha }_p^{last}\mid 1,\rho )=e^{-\rho \left({\alpha }_p^{last}\right)}$. Thus, we get ${\alpha }^{new}+{\alpha }_p={\alpha }_p^{last}$. Without loss of generality, we have

$${\alpha }^{new}={\alpha }_p=\frac{{\alpha }_p^{last}}{2},$$

(23)

if there is no further information for ${\alpha }^{new}$ and ${\alpha }_p$.

As for $\mathbf{E}$, it will be extended to have one more row and $\mathbf{e}\left(t\right)$ will have one more element according to its definition, i.e., Equations (3) and (4). The noise is with original variance after fission. Thus, ${\alpha }_0$ can be seen as having little change and still be used. The true ${\alpha }_0$ can be estimated along with the iteration by Equation (13).

As mentioned above, a large number of grid points will increase the computational workload. It will also bring more difficulty in selecting useful grid points. To avoid lots of useless grid points being generated, we set a minimal fission distance $D_{min}$. Only if $D⩾D_{min}$, the fission process will be conducted. The choice of $D_{min}$ relates to the resolution we want.

3.4. Criteria of GRDOA

3.4.1. Grid Selection Criterion in the Initial Estimation

As we know, $M-1$ sources can be estimated at the most through an M-element ULA. The larger element of $\mathbf{P}$ means higher possibility of the DOA at the corresponding direction. Therefore, the grid points corresponding to $M-1$ largest elements of $\mathbf{P}$ are selected for the fine estimation. However, if a source has high power, its side lobe may be larger than those sources with low power. Thus, the local maximum value should also be selected. Grid points corresponding to $M-1$ largest value and local maximum value are selected as the reconfigured grid. Note that if the selected grid points in current iteration may miss some true DOAs, as $\mathbf{P}$ will vary with the iteration, the missing DOAs might be activated in the next iterations. Let ${\tilde{\mathit{\theta }}}^{fine}$ be the reconfigured grid after the initial estimation.

3.4.2. The Stop Criterion of the Initial Estimation

Suppose a true DOA is between two adjacent initial grid points, and r denotes the initial grid interval. To generate a grid point that is closest to this DOA, the maximum fission time is $\frac{r}{2D_{min}}$ under ideal conditions. Therefore, the maximum fission time is $\frac{r·K}{2D_{min}}$ for K sources. We set $\frac{r·K}{2D_{min}}$ as the maximum iteration time of the initial estimation. If the number of sources K is not available, $\frac{r·M}{2D_{min}}$ is recommended.

3.4.3. The Stop Criterion of the Fine Estimation

The reconfigured grid ${\tilde{\mathit{\theta }}}^{fine}$ gets updated via the grid update process in the fine estimation. The stop criterion of the fine estimation is: $\frac{{∥{\alpha }^{i+1}-{\alpha }^i∥}_2}{{∥{\alpha }^i∥}_2}<\tau$ or the iteration reaches the maximum time, where superscript i represents iteration time and $\tau$ is a settled tolerance.

3.5. Operating Instruction of GRDOA

The operating instruction of GRDOA can be summarized as Table 1.

Table 1. Operating instruction of GRDOA.

The Proposed GRDOA Algorithm
(1) Input: $\mathbf{Y}$ and $\tilde{\mathbf{A}}$;
(2) Conduct the initial estimation:
(a) Initialize: $\mathit{\alpha }$ and ${\sigma }^2$, D is set as a half of the grid interval.
(b) Conduct the grid update process as follows:
Compute the posterior moments $\mathit{\mu }\left(t\right)$ and $\mathsf{\Sigma }$ using Equations (10) and (11).
Update $\mathit{\alpha }$ and ${\alpha }_0$ using Equations (12) and (13), refine $\tilde{\theta }$ using (17).
(c) If $D⩾D_{min}$, conduct the grid fission process:
Generate new grid point ${\tilde{\theta }}^{new}$ using Equation (18) or Equation (19).
Update $\tilde{\mathbf{A}}$ and $\mathit{\alpha }$ according to Equation (21) and (23).
(d) Iterate (b)–(c) until reaching the stop criterion of the initial estimation.
(e) Form a new grid ${\tilde{\mathit{\theta }}}^{fine}$ according to the grid selection criterion.
(3) Conduct the fine estimation
(a) Input ${\tilde{\mathbf{A}}}^{fine}$ according to the reconfigured grid ${\tilde{\mathit{\theta }}}^{fine}$.
(b) Initialize $\mathit{\alpha }$ and ${\sigma }^2$.
(c) Conduct the grid update process (presented above) until reaching the stop
criterion of the fine estimation.
(4) Output: $\mathbf{X}$ and the final grid;
(5) Achieve off-grid DOA estimation through 1D spectrum search on the final grid.

4. Simulation

We conducted several simulations to investigate the performance of GRDOA. The estimated spectrum of GRDOA is shown and compared with RSBL firstly. Then, we compare GRDOA with $l_1$-SVD [26], OGSBI [30], RSBL [32], and GEDOA [33] on accuracy and computational complexity. All the numerical simulations were carried out by MATLAB on a PC with an Inter i$3-7350$k CPU and 8GB of RAM.

In the following simulations, a standard ULA composed of $M=10$ sensors with $d=\lambda /2$ was used to receive $K=2$ signals. The number of snapshot was $T=50$. The convergence parameter was set the same as settings in [30]: $\rho =0.01, c=d={10}^{-4}$. ${\alpha }_0$ and all the elements of $\mathit{\alpha }$ were set to be 1. The tolerance was $\tau ={10}^{-3}$ and the maximum iteration time was 1000. In addition, we set $\eta =2$ and $D_{min}=2^{\circ }$ as a default.

4.1. Spatial Spectrum

To illustrate the spatial spectrum as well as the resolution of GRDOA, we considered two narrowband uncorrelated signals in far field impinging from directions of ${14}^{\circ }$ and ${17}^{\circ }$ with $SNR=10$ dB. $step$ was set as 2. The initial grid interval was set to be $8^{\circ }$, so that the two sources would be in the same grid interval.

Figure 3 shows the spatial spectrum of GRDOA at the first and second iteration before grid fission process. In Figure 3a, we can see that ${\tilde{\theta }}_p$ is ${14.02}^{\circ }$ at the first iteration. It is easy to know that the initial grid point ${\tilde{\theta }}_p^{last}$ is ${14}^{\circ }$. Since ${\tilde{\theta }}_p>{\tilde{\theta }}_p^{last}$, the new grid ise added at the location of ${18.02}^{\circ }$ (${17.99}^{\circ }$ after grid updating at the second iteration), as showing in Figure 3b.

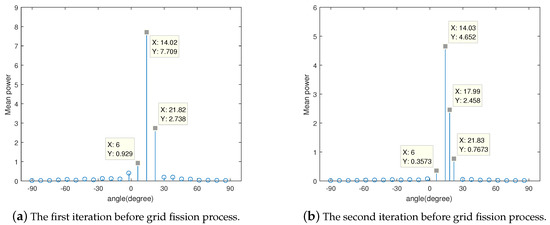
Figure 3. The spatial spectrum at the first and second iteration in the initial estimation. Sources are from ${14}^{\circ }$ and ${17}^{\circ }$ with $SNR=10$ dB.

One new grid point is generated at each iteration. From the fourth iteration, there are no new grids produced since $D<D_{min}$, but the grid continues to get updated. After the eighth iteration, as reaching the stop criterion of the initial estimation, some grid points are selected according to the grid selection criterion. The spatial spectrum at the end of the initial estimation is shown in Figure 4. It can be seen that 12 grid points are selected for the fine estimation, among which ${12.05}^{\circ }$, ${16.97}^{\circ }$ and ${17.97}^{\circ }$ are the new grid points generated by the grid fission process.

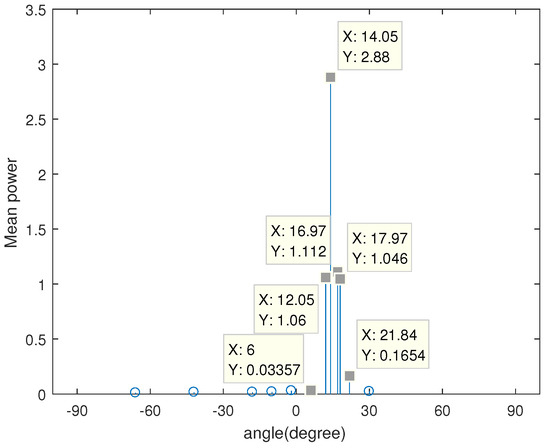
Figure 4. The spatial spectrum of GRDOA at the end of the initial estimation. Sources are from ${14}^{\circ }$ and ${17}^{\circ }$ with $SNR=10$ dB.

Figure 5 shows the spatial spectrum of GRDOA, which is compared with RSBL. Note that the y-axis is the normalized mean power. The blue circled line is for GRDOA and the red asterisk for RSBL. The estimation result of RSBL is ${14.38}^{\circ }$, meaning that RSBL fails to discriminate the two sources due to its assumption that only one source is in a grid interval. However, GRDOA solves this problem and performs well in discriminating two closest sources, with the estimation result of ${13.93}^{\circ }$ and ${17.64}^{\circ }$. For RSBL, a dense enough grid is needed to guarantee closest sources being discriminated, however, it causes massive computational workload. On the contrary, GRDOA can work in coarse grid conditions to achieve low complexity, at the same time maintaining high resolution.

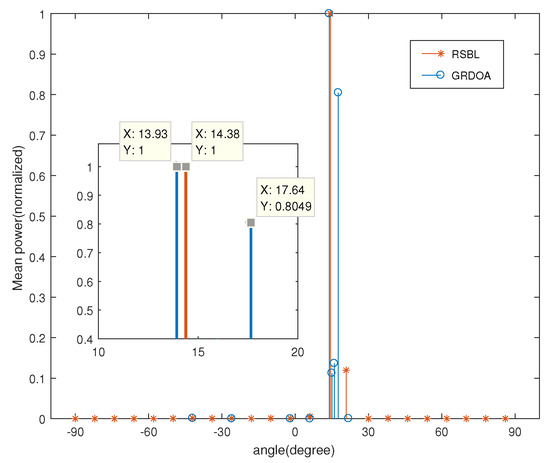
Figure 5. The spatial spectrum of GRDOA and RSBL. Sources are from ${14}^{\circ }$ and ${17}^{\circ }$ with $SNR=10$ dB.

4.2. Performance Analysis

Assume that two sources uniformly come from intervals of $[-{30}^{\circ },-{20}^{\circ }]$ and $[0^{\circ },{10}^{\circ }]$, respectively. The estimation errors are investigated by mean square error (MSE), which is defined as

$$MSE=\frac{1}{K\xi }\sum _{k=1}^K\sum _{i=1}^{\xi }{({\widehat{\theta }}_{i,k}-{\theta }_k)}^2,$$

(24)

where $\xi =200$ is the total number of Monte Carlo trials and ${\widehat{\theta }}_{i,k}$ is the estimated result of ${\theta }_k$ in the ith Monte Carlo simulation.

First, we verify the performance improvement of GRDOA in terms of the MSE and the computational time. Figure 6 shows the MSE of DOA estimation versus grid interval $r=2^{\circ },4^{\circ },6^{\circ },8^{\circ }$ and ${10}^{\circ }$, with $SNR=10$ dB and 0 dB. $step$ is set as 2. It can be seen clearly that GRDOA outperforms the other two methods. Especially, when the grid becomes coarser, GRDOA and RSBL still maintain high accuracy, whereas OGSBI performs worse. That is because the linear approximation used by OGSBI brings large model error in coarse grid conditions, while the grid refining method adopted by RSBL and GRDOA effectively alleviates the off-grid gap. Compared with RSBL, GRDOA can achieve higher accuracy. The performance of RSBL is seriously affected by the location of grid points and DOAs. If a DOA is right at the middle of two adjacent grid points, RSBL performs worst. On the contrary, if a DOA is close to a grid point, the MSE decreases nearly to a noise level. However, for GRDOA, the process of grid reconfiguration is an adaptive one. Therefore, the influence of the initial grid of GRDOA is much less than that of RSBL.

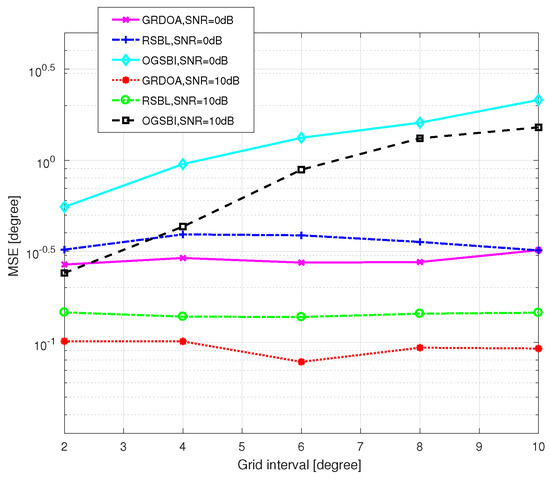
Figure 6. MSE of DOA estimation versus grid interval.

Figure 7 shows the total CPU time of the three methods versus grid interval $r=2^{\circ },4^{\circ },6^{\circ },8^{\circ }$ and ${10}^{\circ }$, with $SNR=10$ dB. $step$ is set as 2. It can be seen clearly that GRDOA is the fastest of all. When the grid interval becomes smaller, the time consuming of GRDOA almost keeps constant while other methods increase. For OGSBI and RSBL, dense grid brings large computational workload. However, for GRDOA, the initial grid has little effect on its computational complexity. This is because that the computational workload of GRDOA mainly comes from the fine estimation, which is related to the number of reconfigured grid points. Since the number of reconfigured grid points is mainly related to the number of array antennas, the total consumed time of GRDOA remains almost unvaried.

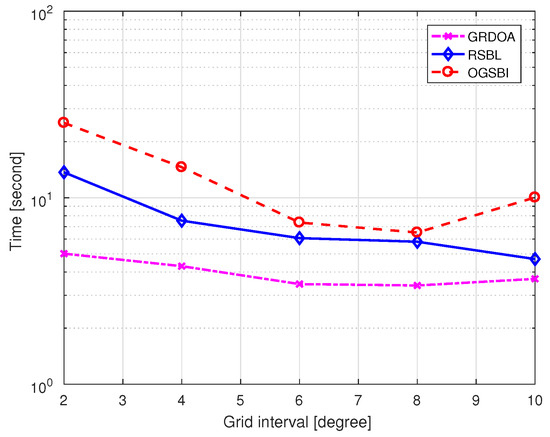
Figure 7. Computational time versus grid interval with $SNR=10$ dB.

Next, we investigate the effect of the parameter $step$ on the DOA estimation performance of GRDOA. Figure 8 shows the MSE of DOA estimation versus $step$. The choice of $step$ mainly affects the location of the new fission points. If the value of $step$ is too large, the fission process cannot be conducted sufficiently. Therefore, the value of $step$ is varied from $1.1$ to $2.9$. As the value of $step$ gets larger, it can be seen that the MSE decreases when $step<1.7$, and keeps almost unvaried when $step>1.7$. It is because, if the value of $step$ is closer to 1, the performance of GRDOA is more susceptible to the location of the initial grid points and DOAs, just like RSBL. Figure 9 shows the total CPU time versus $step$. It is shown that the choice of $step$ does not affect the computational complexity much because the choice of $step$ mainly affects the initial estimation, but the computational workload of GRDOA mainly comes from the fine estimation. Based on the results in Figure 8 and Figure 9, we recommend $1.7<step<2.9$.

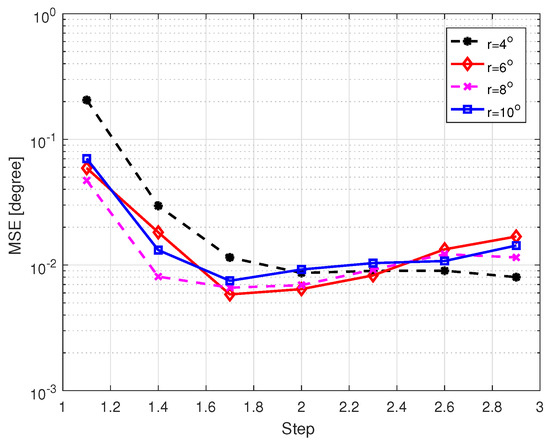
Figure 8. MSE of DOA estimation versus $step$ with $SNR=10$ dB.

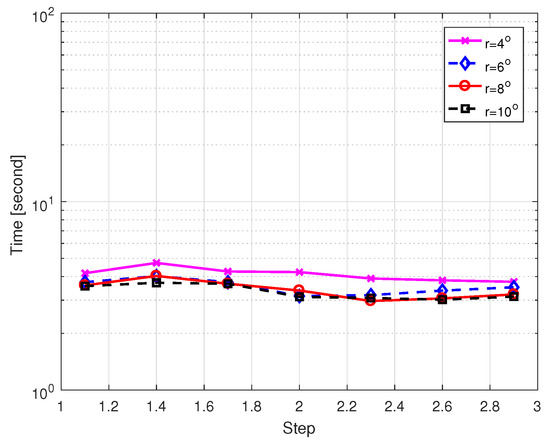
Figure 9. Computational time versus $step$ with $SNR=10$ dB.

4.3. Compared with GEDOA

As the idea of grid fission is first proposed by GEDOA [33], GRDOA is compared with GEDOA on accuracy and computational cost. $l_1$-SVD [26], RSBL [32] and Bayesian Cramer-Rao bound (BCRB) [31] are also compared here. Following the settings in [33], the initial grid interval for RSBL is set as $r=2^{\circ }$. For GEDOA, $r={20}^{\circ }$, and the minimal fission interval is $2^{\circ }$. The BCRB deduced in [31] is 10lg$(\frac{r_0^2}{2M})-$ SNR (dB), where $r_0=1^{\circ }$ is used here. Assume that two sources uniformly come from intervals of $[-{30}^{\circ },-{20}^{\circ }]$ and $[0^{\circ },{10}^{\circ }]$, respectively. Simulations were based on 200 Monte Carlo runs.

Figure 10 shows the MSE of DOA estimation versus SNR, with two uncorrelated sources. Figure 11 shows the MSE with two correlated sources. For GRDOA, $r=6^{\circ }$, $D_{min}=2^{\circ }$, and $step=2$. SNR varies from $-10$ dB to 10 dB. It was found that all methods can be well conducted in both uncorrelated and correlated conditions. GRDOA and GEDOA have better performance than RSBL in high SNR conditions. However, the reverse is true when SNR is low. As mentioned above, the performance of RSBL is seriously affected by the location of grid points and DOAs. For GRDOA and GEDOA, the final grid is a result of the adaptive processes of reconfiguration and evolution, respectively. Therefore, the influence of the initial grid of GRDOA and GEDOA is much less than that of RSBL. However, both the reconfiguration process and evolution process are affected by SNR. It is difficult to properly reconfigure or evolve grid in very poor conditions. Furthermore, GRDOA has better robustness than GEDOA, especially in low SNR conditions. It is because that the initial grid of GEDOA is too coarse, and almost a half grid points of the final grid are generated by the fission process. For GRDOA, much fewer grid points are generated by the fission process. Since SNR is the most significant factor which affects the fission process, GRDOA has been less influenced by SNR than GEDOA.

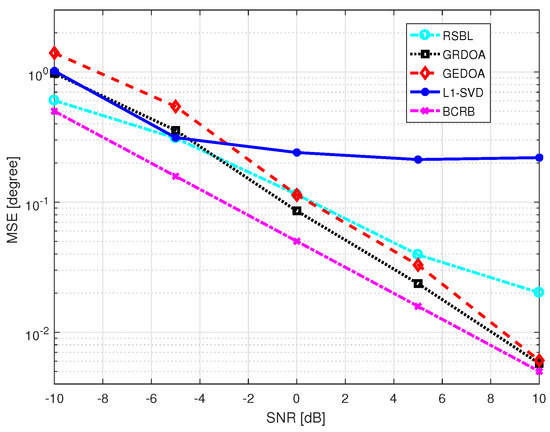
Figure 10. MSE of DOA estimation versus SNR. Two uncorrelated sources uniformly come from intervals of $[-{30}^{\circ },-{20}^{\circ }]$ and $[0^{\circ },{10}^{\circ }]$.

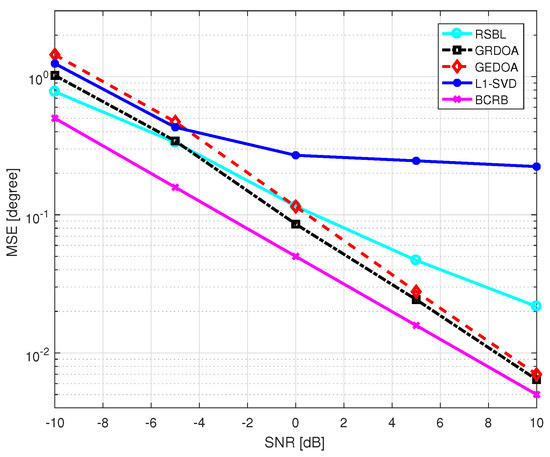
Figure 11. MSE of DOA estimation versus SNR. Two correlated sources uniformly come from intervals of $[-{30}^{\circ },-{20}^{\circ }]$ and $[0^{\circ },{10}^{\circ }]$.

Table 2 shows the total CPU time versus the initial grid interval based on 200 Monte Carlo runs. Simulations were carried out by MATLAB on a PC with an Inter i$3-7350$k CPU and 8GB of RAM. The convergent and initial parameters of RSBL, GRDOA and GEDOA were set as the same: $\rho =0.01$, $c=d={10}^{-4}$, ${\alpha }_0=1$, all the elements of $\mathit{\alpha }$ were 1, $\tau ={10}^{-3}$, and the maximum iteration time was 1000. The initial grid interval of RSBL and GRDOA was set as $r=2^{\circ },4^{\circ },6^{\circ },8^{\circ }$ and ${10}^{\circ }$, for GEDOA $r={20}^{\circ }$, and for $l_1$-SVD $r=2^{\circ }$. For GRDOA, $D_{min}$ was set as $2^{\circ }$, and $step$ was set as 2. The minimal fission interval of GEDOA was $2^{\circ }$. SNR is 10 dB. Note that different hardware environments and parameter settings may influence the experimental data, but the patterns of the data are quite consistent. As shown in Table 2, RSBL and $l_1$-SVD are more time consuming than GEDOA and GRDOA, because they have more grid points to update. Furthermore, GRDOA is faster than GEDOA. Even though GEDOA has a coarser initial grid than GRDOA, GRDOA has a smaller grid number in the final grid than GEDOA, which further enhances efficiency.

Table 2. Time Comparison versus the Initial Grid Interval (IGI).

IGI [${}^{\circ }$]	2	4	6	8	10
CPU time of RSBL [s]	13	7.18	6.19	5.15	4.38
CPU time of GRDOA [s]	4.72	4.49	3.22	3.37	3.67
CPU time of GEDOA [s]	5.19 (IGI = ${20}^{\circ }$)
CPU time of $l_1$-SVD [s]	24.9 (IGI = $2^{\circ }$)

5. Conclusions

In this paper, we propose an efficient off-grid method named GRDOA based on sparse Bayesian learning. We combine the ideas of grid refinement and grid fission to make the grid adaptively reconfigured to a nonuniform grid. GRDOA contains two parts, i.e., the initial estimation and the fine estimation. In the initial estimation, the grid update process and grid fission process are implemented iteratively. The grid gets reconfigured at the end of the initial estimation. In the fine estimation, DOAs are estimated based on the reconfigured grid. Simulation results show that GRDOA achieves lower complexity while maintaining reasonable accuracy. The reconfiguration method of GRDOA is more robust and has greater efficiency than the evolution method of GEDOA. However, how to achieve higher accuracy in the circumstance of strong noise is still an opening question.