Abstract
The work presents the kinematic and dynamic control of a mobile robotic manipulator system based on numerical methods. The proposal also presents the curvature analysis of a path not parameterized in time, for the optimization of energy consumption. The energy optimization considers two aspects: the velocity of execution in curves and the amount of movements generated by the robotic system. When a curve occurs on the predefined path, the execution velocity is analyzed throughout the system in a unified method to prevent skid effects from affecting the mobile manipulator, while the number of movements is limited by the redundancy presented by the robotic system to optimize energy use. The experimental results are shown to validate the mechanical and electronic construction of the system, the proposed controllers, and the saving of energy consumption.
1. Introduction
At present, it is usual to find industries using robots instead of human personnel. In fact, more than 1.4 million new industrial robots are estimated to be installed in factories around the world by 2019, where more than seventy percent of them are placed in automotive, electrical, electronics, and metal industry segments, as stated Gonzalez, et al. [1]. In this aspect, the robots’ configuration depends on the application field where they work as states Magyar et al. in [2]. The most common robotic configuration in production areas is that of manipulators, which can perform tasks similar to those of a human upper limb, supplying the operator in repetitive or tedious tasks, or being a support for loading materials or moving heavy objects, and others, as you can read in Ding, et al. [3]. However, it has a severe limitation, which is to be embedded on a stationary base (often in a structured environment), this makes the robotic manipulator have restrictions in the field of application. To overcome motion limitation, a base that moves the manipulator can be included to achieve the characteristics of locomotion and manipulation, thus increasing the resulting range of applications, García, et al. in [4] show an example. This base can only be a semi-inert mobile base or a mobile robot with minimal or very high intelligence. The mobile manipulators unify the ability to hold objects and freedom of movement of the operating end in space (given by the robotic arm) with the displacement of the entire robotic system (given by the mobile platform). Some tasks, like Mori, et al. shows in [5] such as welding, assembly, paint spraying, accurate positioning systems, placement of elements, surgery, and so on can be deployed by this sort of robot. In this type of application, the precision of work has a decisive role due to the consequences that would generate the error in the execution of tasks, negligence that in the pursuit of roads or trajectories cannot be considered as a normal factor.
The proper design of a controller that will govern the actions of each of the robot’s effectors can ensure optimal execution of the scheduled task. In this respect, Su, et al. in [6] and Prada-Jimenez, et al. in [7] propose different ways of controlling mobile manipulators considering their kinematic model as a single robot. In a different way, Hamner, et al. in [8] works in the hybridization of locomotion and manipulation, joining a mobile platform and a manipulator in several modes of operation, but treating the mobile part and the arm as different robots. Considering the dynamics of the mobile manipulator, Li, et al. in [9] presents an adaptive control strategy for trajectory tracking, Liu, et al. in [10] proposes a diffuse control scheme based on integrated dynamic modelling considering nonholonomic constraints and interactive motions, and Eslamy, et al. in [11] investigates the dynamics resulting from placing a suspension system on the mobile part of a mobile manipulator in order to analyze the effect of vibration-absorbing systems. These works are mainly based on nonlinear control algorithms, given the nature of robotic systems. The nonlinearity of robotic assemblies implies the use of appropriate control methods for this type of system, with techniques based on passivity, slide mode, Lyapunov, and so on. For instance, Abou-Samah, et al. in [12] presents an adaptive sliding mode backstepping control algorithm for a wheeled mobile manipulator, integrating the sliding mode control strategy and adaptive backstepping methodology. The proposed algorithm possesses many characteristics in order to drive the wheeled mobile manipulator tracking error to converge to zero in the short period and be applied to the robotic system considering nonholonomic constrains, uncertainties, and disturbances. In the same way, Tchoń, et al. in [13] shows a three-dimensional (3D) passivity-based visual controller for mobile manipulator with eye-in-hand configuration. This work considers the redundancy of the mobile manipulator system to comply with objectives of obstacle avoidance, where the design of the robotic system is split into two cascaded subsystems: kinematics and dynamics-based controller. Simulated and experimental results are presented, in addition to the stability proof which is based on its passivity properties. Furthermore, Deepak, et al. in [14] presents the simulation of a mobile manipulator considering kinematics and dynamics. The control law is based on a combination of Lyapunov stability theory and an adaptive fuzzy control in order to track a trajectory. The fuzzy compensator is developed given the modelling uncertainties such as friction and external disturbances. For its part, the Lyapunov-based law control is used to reduce approximation errors and ensure system stability.
In addition to plan and control the operating end, features such as the force necessary to maintain an object lifted up continuously must be considered. In contrast to work on optimizing the energy consumption of an air vehicle (which must be kept in flight continuously) Rossi, et al. in [15], power consumption in land vehicles is often not carefully analyzed. However, power consumption optimization can result in a significant aid to the maintenance of the storage elements as well as extending the vehicle’s autonomy. In this respect, Hua, et al. in [16] and Motlagh, et al. in [17] and Lin C, et al. in [18] propose solutions that involve the energy saving of terrestrial robots considering different approaches such as manipulating velocities in certain parts of the trajectory or minimizing functional costs from the torque produced by the actuators. In these works, energy savings are focused on avoiding skidding or reducing velocity at critical points in vehicles whose control actions are executed on a plane, without considering movements over the space of an embedded robotic arm.
In a robotic arm, the manipulator’s redundancy increases its flexibility, versatility, and manipulability capabilities. In order to reach the desired point, redundancy is often exploited without considering undesirable configurations or energy expenditure. However, works such as Abbaspour, et al. in [19] propose the manipulation of redundancy in order to prevent controller solutions from greatly altering the velocities injected into the controllers. Also, within the analysis of energy optimization, redundancy can assist in reducing the movement of degrees of freedom of high consumption and increasing others low to optimize power expenditure.
In this paper, features such as redundancy and motion velocity of the mobile robotic manipulator system are analyzed through numerical methods to pose energy optimizers, a feature shows Li, et al. in [20]. In order to achieve energy-saving objectives and avoid unnecessary power consumption, the analysis of the radius of curvature of a road not parameterized in time is developed, considering the calculation of appropriate velocities for certain periods of time. Likewise, the consideration of reducing the movement of the mobile platform in comparison with the movement of the robotic arm is taken into account and analyzed. A dynamic model for the mobile manipulator is developed which, unlike previous works, accepts velocity inputs as it is usual in commercial robots, where the stability for both the kinematic proposal and the dynamic controller is tested through linear algebra properties. To validate the proposed control algorithms and the proposed energy cost optimization, experimental results are included and discussed. In addition, and as an alternative to the acquisition of a commercial robotic prototype, this work proposes the mechanical and electronic construction of a six-degree arm mounted on a unicycle-type mobile platform, which has an embedded computer for the execution of the kinematic and dynamic controller, together with the energy-saving proposal.
This article is organized as follows: Section 2 proposes energy saving, Section 3 presents the kinematic and dynamic modelling of the mobile manipulator, while Section 4 proposes the design of the static and dynamic control elements. Finally, Section 5 shows the experimental results obtained in this work.
2. Energy Save Proposal
The robot’s energy consumption is rarely taken into account when reaching the desired points of a trajectory. The manipulation of the displacement velocity of a robot allows a most effective use of energy, an example shows in Minitti, et al. [21]; likewise, in robotic systems composed of several robots (wheeled mobile manipulator, present it Park, et al. in [22], aerial manipulator, Thapa, et al. in [23], hexapod robot, humanoid robots, and so on Lunghi, et al. in [24]) it is also possible to optimize energy consumption through control schemes which allow achieving the desired objective with a smaller number of movements, attaining this optimization through restrictions in the control, it says Wu, et al. in [25] of system redundancy.
The velocity of displacement in the execution of path following is directly related to energy consumption. Analyzing the problem as an execution with constant velocity on a road that includes curves, the loss of energy could be produced mainly by skid effects and correction of centrifugal- and centripedics-resulting forces, according to the configuration of the robot that is executing a specific task. In addition, it should be noted that the power consumption of the entire system is equivalent to the sum of the powers consumed in each of the robot actuators.
Thus, in the case of a manipulator robot made up of a mobile platform with actuators () and a robotic arm with actuators (), the total power of the robotic system is defined as , the same that is equivalent to the consumption of the whole system in a defined period of time. As described above, the power expenditure can be determined by:
where and are the start and end time of the execution of the task of the robotic system.
Remark 1.
According to the configuration of the robotic arm, the power of each one of the actuators will depend on the mass and the size of the link or links to be displaced; while the power consumed by the actuators of the mobile platform is equal between both actuators, given that the power necessary to displace a load is distributed among each one of the actuators.
Remark 2.
The power required to move the entire robotic system requires higher consumption in the mobile platform motors compared with the arm actuators.
The power consumption dimensioning estimates that the cost of consumption of each one of the actuators of the mobile platform is up to four times higher than the consumption of the first two articulations of the robotic arm (considering that the first two motors of the robotic arm are the most powerful, compared with the rest of the actuators of the manipulator). Therefore, the energy saving of a mobile manipulator when executing a specific task is directly proportional to the number of movements performed by the platform and the arm simultaneously as stated Li, et al. in [26].
Based on the above, this work proposes a control scheme that optimizes the energy consumption of a mobile manipulator robot when executing a specific task. As an energy optimization criterion, it is considered: i) manipulation of the desired velocity to execute the task; and ii) reduction in the number of movements of the mobile manipulator, giving greater importance to the movement of the arm with respect to that of the mobile platform.
3. Mobile Manipulator Modeling
The mobile manipulator configuration is defined by a vector of independent coordinates called generalized coordinates of the mobile manipulator with , where represents the generalized coordinates of the arm and the generalized coordinates of the mobile platform. It is noticed that , where and are respectively the dimensions of the generalized spaces associated to the robotic arm and to the mobile platform.
The configuration is an element of the mobile manipulator configuration space; denoted by . The location of the end-effector of the mobile manipulator is given by the –dimensional vector , where defines the position and the orientation of the end-effector of the mobile manipulator in . Its coordinates are the operational coordinates of the mobile manipulator. The set of all locations constitutes the mobile manipulator operational space, denoted by .
3.1. Kinematic Modeling
The kinematic model of a mobile manipulator gives the location of the end-effector as a function of the robotic arm configuration and the platform location (or its operational coordinates as functions of the robotic arm’s generalized coordinates and the mobile platform’s operational coordinates).
where, is the configuration space of the robotic arm, is the operational space of the platform.
The instantaneous kinematic model of a mobile manipulator gives the derivative of its end-effector location as a function of the derivatives of both the robotic arm configuration and the location of the mobile platform. Now, after analyzing the above statements, we can represent the end-effector velocity as follow:
where, is the Jacobian matrix that defines a linear mapping between the vector of the mobile manipulator velocities and the vector of the end-effector velocity . The Jacobian matrix is, in general, a function of the configuration . Those configurations where is rank-deficient are termed singular kinematic configurations. Finding the manipulator singularities is of great interest due to the following main reasons: a) Singularities represent configurations where the mobility of the structure is reduced (i.e., it is not possible to impose an arbitrary motion to the end-effector); b) In the neighborhood of a singularity, small velocities in the operational space may cause large velocities in the space.
Remark 3.
In general, the dimension of the operational spaceis smaller than the degree of mobilityof the mobile manipulator. Therefore, there is a redundancy problem to be solved in controlling the mobile manipulator robot tasks.
3.2. Dynamic Modeling
The mathematic model which represents the dynamics of a mobile manipulator can be obtained from Lagrange’s dynamic equations, which are based on the difference between the kinetic and potential energy of each of the joints of the robot (energy balance) based in Sciavicco, et al. [27]. Most of the commercially available robots have low-level PID controllers in order to follow the reference velocity inputs, thus not allowing controlling the motors directly. Therefore, it becomes useful to express more appropriately the dynamic model of the mobile manipulator by considering the rotational and longitudinal reference velocities as the input signals. To do so, the velocity controllers are included in the model.
where,
Thus, is a positive definite matrix representing the system’s inertia, represents centripetal and Coriolis forces, is the gravitational vector, denotes bounded unknown disturbances including unmodeled dynamics and is the vector of velocity control signals, , and are positive definite constant diagonal matrices containing the physical parameters of the mobile manipulator, motors, and velocity controllers of both the mobile platform and the manipulator at state as Andaluz, et al. in [28].
It´s important to notice that the dynamic model of the mobile manipulator can be represented by:
where, and is the vector of unknown parameters of the mobile manipulator (i.e., mass of the mobile robot, mass of the robotic arm, physical parameters of the mobile manipulator, motors, velocity, etc.).
The full mathematical model of the mobile manipulator robot is represented by: (1) the instantaneous kinematic model and (2) the dynamic model, taking the reference velocities of the system as input signals.
4. Controllers Design
The design criteria of the proposed control considers the manipulation of the desired velocity for road tracking, as well as the redundancy control of the mobile manipulator system. The control proposal is applied to follow paths not parameterized in time, because the desired velocity can be modified depending on the task to be executed by the robotic system. The proposed control scheme to solve the motion control problem is shown in Figure 1, where the controller design is based on two cascading subsystems:
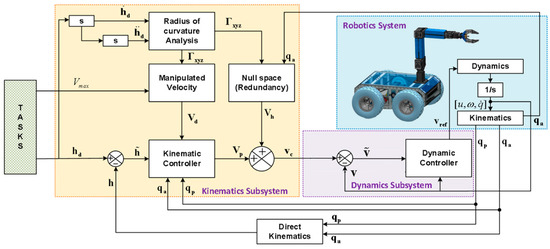
Figure 1.
Block diagram of the motion control problems of mobile manipulators.
i) A minimum norm kinematic controller with saturation of velocity commands, where its inputs are and , which describe the desired location and velocity of the end-effector of the mobile manipulator. The control error is given by the location error of the end-effector defined as . Therefore, the control aim is expressed as
ii) Dynamic compensation controller, of which the main objective is to compensate the dynamics of the mobile manipulator, thus reducing the velocity tracking error. This controller receives as inputs the desired velocities calculated by the kinematic controller, and generates velocity references for the mobile manipulator robot. The velocity control error is defined as . Hence, the control aim is to ensure that
Remark 4.
Both controllers are based on numerical methods.
4.1. Kinematic Controller
The kinematic controller evaluates the control errors in each sampling period, so that the actual velocity obtained from the mobile manipulator can be used as a reference for maneuvering the entire system, thus reducing errors. This section presents road tracking considering the manipulation of a desired velocity with the aim of reducing energy consumption, where the task to be executed will be a function of the road followed and a desired velocity.
4.1.1. Specification of the Path
Figure 2 shows the path-tracking problem represented by , where ; represents the current desired point of the mobile manipulator robot which is considered to be the closest point to the robotic system, this is defined as , where is the defined curvilinear abscissa of the point ; the representation of errors in direction is given by ; the representation of errors in direction is given by ; the representation of errors in direction is given by .
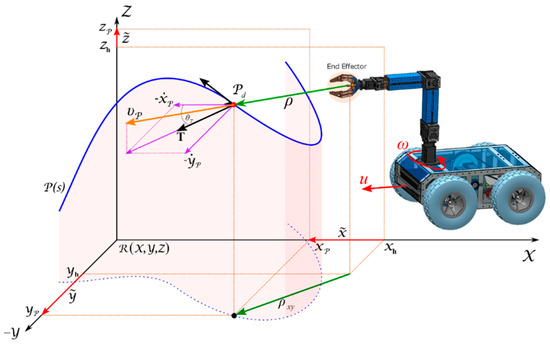
Figure 2.
Path Tracking.
Based on the graphical representation, control errors are calculated by the difference in position between the operating end and the desired point , where the distance between the current position of the robot and the reference point is zero ; is the orientation error of the final effect defined as , where is the orientation of the unit vector tangent to the trajectory of the point with respect to the reference system
Remark 5.
The orientation of the final effector depends directly on the application, so it is not studied in this paper, because the algorithm aim is that the effector reaches the point of interest with a lower power consumption. For example, the application can be take a bottle (vertically oriented), pull a sheet of paper (horizontal orientation), or any other orientation of the clamp. This does not really affect the algorithm, since it will be the same for any application.
4.1.2. Definition of Desired Speed
The consideration of energy saving proposes as a first instance the reduction of velocity in curves when executing the follow-up of a road, therefore, the desired velocity can be manipulated. For path tracking, the desired velocity can depend on different parameters, for example, the task to be executed, control errors, road curvature, optimization criteria, among others.
In order to optimize energy consumption when executing a desired task, the control scheme proposed in this paper considers that the reference velocity on the road to be followed is a function of its radius of curvature.
where represents the radius of curvature and is a dimensionless constant. By considering the required path as a set of points, the value of curvature is defined as:
Remark 6.
The values of the radius curvature in each instant of time of (3) can be found only if one has the analytical expression of the path. This limits to a great extent the use of this type of consideration, since for real applications there is not always the path to follow in the form of derivable mathematical equations.
In order to resolve the limitation of not having the analytical expression, it is proposed to use the next and previous points of the sampling period, in this way , is defined as follows:
and the value is calculated by
The analysis of the radius of curvature can be developed separately since the mobile platform moves on the plane , while the arm on the space .
4.1.3. Design of the Control Law
The design of the kinematic and dynamic controllers proposed in this work are based on numerical method tools. Specifically, for the solution of systems of equations, these systems can be represented in matrix form, for which theorems and axioms of linear algebra are applied.
Considering the first order differential equation
where represents the output of the system to be controller; is the first derivative with respect to time; is the control action; represents different criteria of the task to be executed. The values of in the discrete time are called , where represents the sampling time and . In addition, the use of numerical methods for the calculus of the system evolution is based mainly on the possibility to approximate the state system at the instant time , if the state and the control action on the time instant are known, this approximation is called Euler method [24].
The design of the kinematic controller is based on the kinematic model of mobile manipulator robot. In order to design the kinematic controller, the model of robot (1) can be approximated as (4).
It should be noted that path tracking consists of keeping the operating end of the mobile manipulator within a predefined route without time parameterization. In this way, the control objective is to position the point of interest at the nearest point on the road at a desired velocity . To achieve this objective, the following expression is considered:
where, is the desired path, is a diagonal matrix that control error weights, defined as:
where represents the operational coordinates of the mobile manipulator robot.
Now, to generate the system equations consider (5) and (6), and the system can be rewritten as
Remark 7.
Considering that the configuration of the robotic system is redundant (7), the Jacobian matrixhas more unknowns than equations (), with rangefor each, then (7) represents a subdetermined linear system with general solution.
whereit is a particular solution andis a homogeneous system solution. This result is of fundamental importance for the resolution of redundant systems.
A viable solution method is to formulate the problem as a constrained linear optimization problem.
Then yields the particular solution:
On the other hand, the null space of in is the set of joint velocities and mobile platform velocities that do not produce any end-effector velocity of the mobile manipulator.
In that case, it is necessary to consider a new cost functional in the form:
Then yields the homogeneous solution
Therefore, this work proposes the inclusion of the two types of solutions, the particular solution to optimize the road tracking velocities of the entire robotic system and the homogeneous solution to reduce the amount of movements of the mobile platform with respect to the robotic arm.
This is how, inserting the expression (9) and (10) into (8) yields the solution rather than represents the proposed law of control.
where the first term on the left-hand side is the particular solution , and the second term of this equation belongs to the null space .
The second term in (11) represents the projection on the null space of the mobile manipulator, where is an arbitrary vector which contains the velocities associated to the mobile manipulator. Therefore, any value given to will affect the internal structure of the manipulator only, but not the final control of the end-effector at all, as is shown in Figure 3. By using this term, different control objectives can be achieved, for example, maximum manipulability, energy saving, obstacle avoidance, distance from mechanical joint limits, and so on, it can be read at Paul, et al. in [29] and Li, G., et al. in [30]. This work considers as a secondary objective that the mobile robotic manipulator system must execute the task with a configuration of maximum manipulability and at the same time with a criterion of energy optimization.
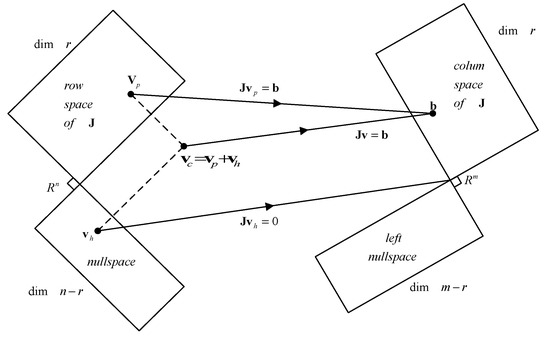
Figure 3.
Orthogonal Projection.
4.1.4. Secondary Objectives
We can observe that one of the main requirements for an accurate task execution by the robot is a good manipulability, defined as the robot configuration which maximizes its ability to manipulate a target object. Therefore, one of the secondary objectives of the control is to maintain maximum manipulability of the mobile manipulator during task execution. Manipulability is a concept introduced by Yoshikawa (1985) to measure the ability of a fixed manipulator to move in certain directions. Bayle and Fourquet (2001) present a similar analysis for the manipulability of mobile manipulators and extends the concept of manipulability ellipsoid as the set of all end-effector velocities reachable by robot velocities satisfying in the Euclidean space. A global representative measure of manipulation ability can be obtained by considering the volume of this ellipsoid which is proportional to the quantity , called the manipulability measure,
This work considers the maximum manipulability of the robotic system in order to avoid unwanted configurations (i.e., ), in addition, the redundancy of the system is used for energy optimization purposes. In order to meet these secondary objectives, it is considered that the arbitrary vector is a function of the robot’s manipulability, the desired velocity, and the radius and direction of curvature of the road.
Therefore, must allow the robotic arm to perform the greatest number of movements in relation to the mobile platform, without the robotic arm ever having a unique configuration, that is, when the road does not contain curves, the robotic system is positioned in the configuration of maximum manipulability, while when there are curves, the arm has greater freedom to move in order to maintain the desired path. Therefore, the arbitrary vector is defined as,
The velocities affecting the mobile platform affect the position of the operating end of the robotic system in the plane of the reference system , therefore,
where is the cross product resulting from the velocity and acceleration in the curvatures projected on the planes (both velocities and accelerations of the third component are annulled) and it is defined as:
is the direction of curvature in the plane; and , , , are gain constants that weigh the incidence of curvature of the road as a function of the movement of the robotic platform.
In difference, the components consider the internal configuration of the robotic arm and the displacement of the operating end in the space of the reference system , thus:
where is the cross product resulting from the velocity and acceleration in the curvatures projected on the space and is defined as:
is the direction of curvature in space ; and , with are constants of gain that weigh the incidence of the curvature of the path as a function of the movement of each of the articulations of the robotic arm.
4.1.5. Stability Analysis
Considering by now the perfect velocity tracking (i.e., ), Equation (11) can be substituted into the kinematic model Equation (5) to obtain the following closed-loop equation:
where the equation (16) is reduced
through the properties of an identity matrix is achieved
Now, defining difference signal between and , then
Defining the control error
at the instant of time
for the analysis the transformed Z
where the poles of the system (19) are:
In order for the poles of the system to be within the unitary radius , it must be defined . Therefore, it is concluded that control errors when , and it has asymptotic stability.
4.2. Dynamic Compensation Controller
The objective of the dynamic compensation controller is to compensate for the dynamics of the mobile manipulator robot, thus reducing the velocity-tracking error. The correction of the velocity error generates energy optimization of the robotic system as it avoids unnecessary movements to generate large decompensations.
4.2.1. Design of the Control Law
Figure 4 shows the proposed control scheme, the dynamic compensation controller receives as inputs the desired velocities calculated by the kinematic controller, and generates velocity references for the mobile manipulator robot. Hence, if there is no perfect velocity tracking, the velocity error is defined as,
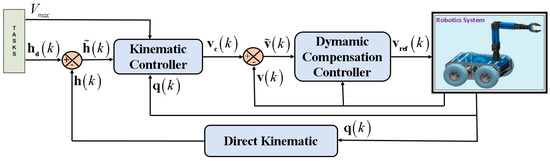
Figure 4.
Proposed control scheme.
This velocity error motivates the dynamic compensation process, which will be performed based on the inverse dynamics of the mobile manipulator. With this aim, we consider the exact model of the mobile manipulator without including disturbances.
Similar to (4), the acceleration of the maneuverability velocities of the mobile manipulator can be defined through the Euler method as
Now, considering the discretized acceleration (22) in (21) one has
For Markov’s property:
In order for errors to tend to zero, it is defined that the velocity of the robotic system is
Therefore, the following control law is proposed:
where, represents a constant diagonal matrix that velocities error weights.
4.2.2. Stability Analysis
To ensure the stability of the proposed dynamic compensator, Equation (23) with (24)
reducing terms and grouping, we have that the error in the current state depends only on the previous error multiplied by a gain matrix , that is,
Considering that ;
and ; Equation (25) can be represented by,
Now, if you analyze the errors when and considering , you have:
Hence, if , it can be concluded that the velocity error of the robotic system mobile manipulator tends asymptotically to zero when .
Finally, the proposed control scheme to solve the motion control problem of the mobile manipulator robot is shown in Figure 1 and Figure 4, where the controller design was based on two cascading subsystems: i) Kinematic controller, for this controller is proposed (11), which solves the motion control problem of the robotic system considering the desired position and velocity of the end-effector of the mobile manipulator robot to the execute the desired task; ii) Dynamic compensation controller, in order to compensate the dynamics of the mobile manipulator, thus reducing the velocity tracking error, the control law is proposed (24), where represents the output of the dynamic compensation controller, that is, is the vector of input velocities to the mobile manipulator robotic system.
5. Experimental Results
The results are presented in two parts: the mechanical–electronic construction and the experimental tests developed to validate the proposed controllers. The construction presents a brief summary of the prototype created to execute the experiments, subdivided into mechanical and electronic construction, while the experimental tests are supported by various graphs showing the effectiveness of the proposed controllers, in addition to validating energy optimization.
5.1. Mechanical–Electronic Construction
For mechanical construction, two parts are analyzed separately: the mobile platform and the robotic arm. The mobile platform is unicycle type, which consists of two motors that generate the movement for each pair of side wheels with a system based on chains. All mechanical elements are strategically distributed so that the control and power components fit inside the mobile platform casing, as shown in Figure 5.

Figure 5.
Configuration of the Mobile Robotic Platform.
For the robotic arm, different components (motors, joints, frames, links) are unified to provide flexibility in the range of positions of the operating end. Figure 6 shows the simulation prior to the construction of the mobile manipulator.
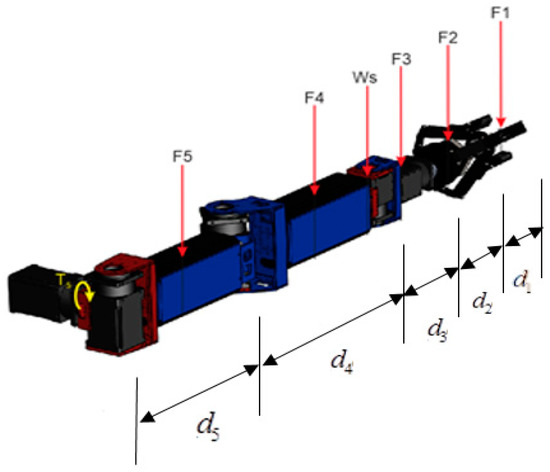
Figure 6.
Built-in robotic arm.
Since the construction of each mechanical part is designed to fit together, the result of mass center analysis and appropriate weight distribution allows the platform and arm to be unified into a single robotic system, as shown in Figure 7.

Figure 7.
Mobile robotic manipulator system.
The electronic components of the mobile manipulator robot are designed to interconnect all the control, power, and power supply equipment and elements. The design consists of eight Dynamixel motors, a computer, an electronic control board, overcurrent prevention elements, a peripheral extender, and a Lithium Polymer (LiPo) battery bank. The distribution of the elements is shown in Figure 8, additionally denoting the communication between them.
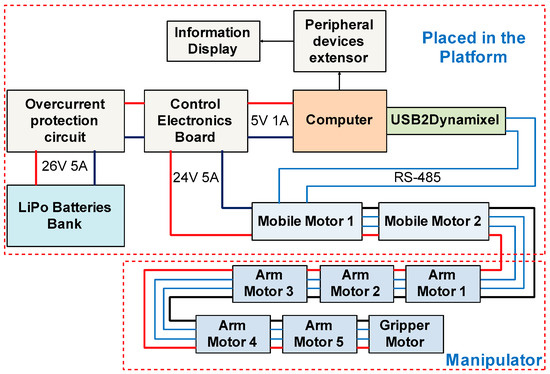
Figure 8.
Electronic design of the components of the robotic system.
(i) Dynamixel motors, unlike frequency-controlled motors, can modify their characteristics by means of a serial communication frame. Communication with the computer is facilitated by the inclusion of a USB2Dynamixel device, which weaves the information to optimize communication and avoid saturation of the serial network. The velocity of communication between the computer and the entire engine network is optimized with the creation of libraries that allow you to invoke functions programmed in C through Mex files. With orientation to this work, information of current, velocity, position, and torque are acquired by the serial frame. The current information allows to know the precise magnitude of power consumed by the robotic system; therefore, it is not necessary to include additional measurement equipment to the information provided by the actuators. (ii) The computer has sufficient resources to run high-level processing programs. In the computer, the calculations necessary for the controllers are carried out in mathematical software. (iii) The electronic control board regulates and distributes power voltages to the entire motor and computer system. The board incorporates elements of current and voltage measurement for the emission of warning signals in possible discharges or disconnection of elements. In addition, a state of charge and connection display is embedded in the electronic control board. (iv) A peripheral ports extensor is included to provide communication between external devices (cameras, memory sticks, and so on) and the internal computer. Finally, (v) a LiPo battery bank provides the necessary power to the system, which delivers up to 15 A/h with peak current support of up to 25 A.
5.2. Experimental Evidence
In order to evaluate the performance of the energy-saving proposal, three experiments were developed, differentiated by the geometric shape of the path to follow: chair, flower, and the sine function. Each one of the experiments was executed with different purposes: to measure the consumption of absorbed current, number of meters traveled, or time of execution. It should be clarified that experiments are considered executions on different roads, while tests are considered executions on the same road but with the use of different controllers (considering or not the analysis of radius of curvature, ROC).
The first experiment considers a desired path described by means , where: , , .
The selection of this particular road was because it seeks to demonstrate directly the action of velocity reduction when finding a curve. To demonstrate energy savings through contrasting results, two types of executions were proposed, both considering the Lyapunov-based controller with redundancy in the robotic arm, but only one with the inclusion of velocity saturation by curvature radius analysis. The path tracking for both configurations was evaluated over the same distance traveled, in this case, 100 m.
The result considering only the control with redundancy presented major errors in each of the axes (Figure 9); and therefore, a greater total error compared with the result considering the analysis of radius of curvature, as shown in Figure 10. Emphasize from now on, ROC will be defined as the radius of curvature.
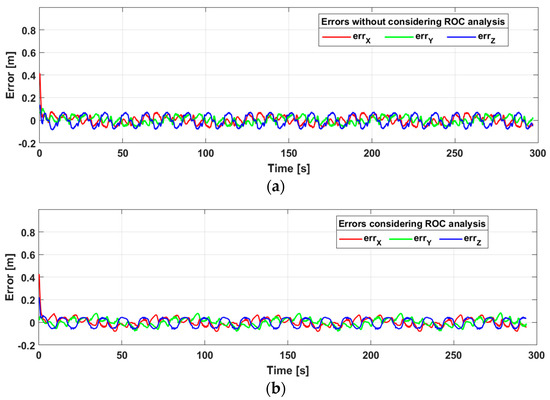
Figure 9.
Errors in each of the axes (a) without considering ROC (radius of curvature) analysis, (b) considering ROC analysis.
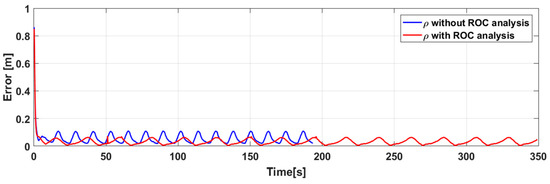
Figure 10.
Quadratic control errors.
This reduction in errors in each of the axes was due to the fact that the mobile platform reduces the control velocities when approaching a curve, as shown in the comparison of linear and angular velocities in Figure 11.
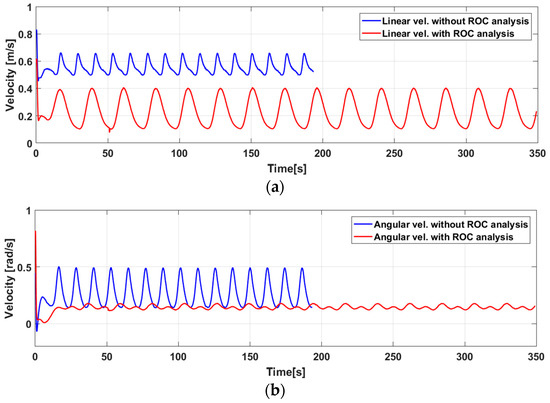
Figure 11.
Control actions of the platform for the execution of follow-up without ROC analysis consideration and with consideration of ROC analysis. (a) robotic arm, (b) mobile robot.
In addition to reducing the velocity of execution in front of curves, the proposed algorithm gives more weight to the corrective actions of the robotic arm, significantly reducing the movements of the mobile platform and therefore, the power consumption. The control actions applied to the robotic arm for both tests (with and without consideration of ROC analysis) are shown in Figure 11.
The strobe movement of the robotic system makes it possible to determine the resulting execution by applying both controllers. Through an upper view, Figure 12 shows the comparison between the strobe movement of the robotic system without consideration of the curvature radius analysis and with the consideration of the curvature radius analysis, differentiating the path of the platform and the movements executed by the robotic arm. The Figure 13 also presents a stroboscopic view of the movements executed by the robot in space.
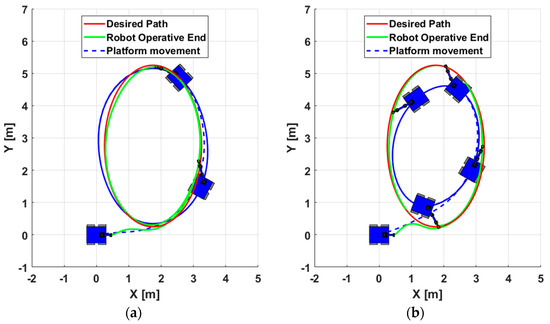
Figure 12.
Upper view of the strobe movement of the path following (a) without consideration of curvature radius analysis and (b) with consideration of curvature radius analysis.

Figure 13.
Strobe movement in the space of the robotic system for the first experiment considering ROC analysis.
The energy consumption of the actuators of the robotic system was measured through one of the properties of the motor network. The measurement of the consumed current is shown in Figure 14, where the contrast between the power consumption is appreciated considering the radius of curvature analysis and without its consideration. As can be seen, given the reduction in velocity of the robotic system, the execution time increased to fulfill the given task. However, after fully executing the task, the proposed controller resulted in an 8.76% energy saving, as shown in the Table 1.
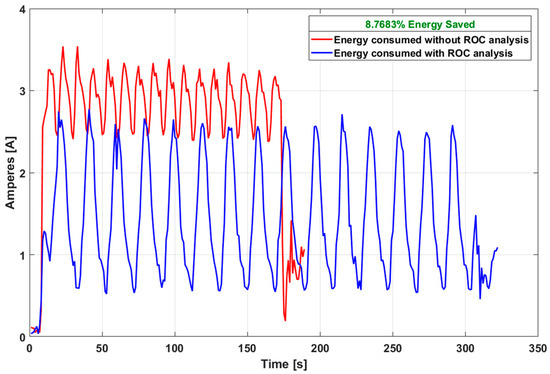
Figure 14.
Measurement of consumed currents.

Table 1.
The Table 1 shows the 8.76% energy saving caused by the controller.
The path considered in the second experiment is described by for values of: , and .
Unlike the first experiment, the established path indicated the efficiency of the controller by establishing a path that contained pronounced curves on all components (Figure 15). This experiment proposed to determine the total distance traveled considering the same amount of energy consumed with and without curvature radius analysis, thus assuming the similarity between the control errors of both tests. This consideration required finding the maximum velocities for the controller with and without radius of curvature analysis that satisfy the equality of errors, in order to make the comparison between the two energy consumptions more equitable. Figure 16 shows the errors in each of the axes, while Figure 17 shows the mean quadratic errors of both tests with maximum velocities of 0.25 m/s in the controller without ROC analysis and with a maximum velocity of 0.45 m/s for the controller with ROC analysis.

Figure 15.
Path considered for the second experiment.
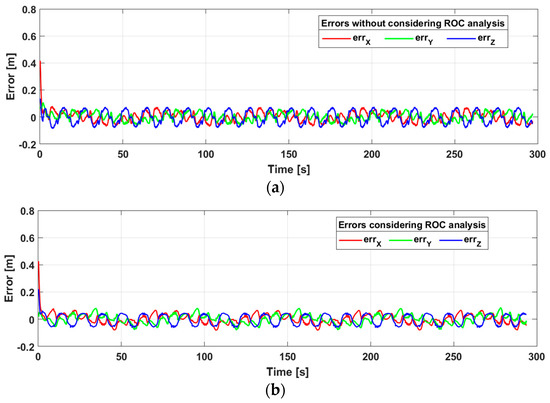
Figure 16.
Errors in each of the axes of the second experiment: (a) without considering ROC analysis and (b) considering ROC analysis.
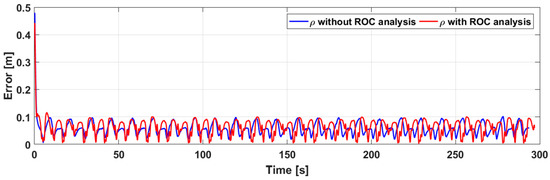
Figure 17.
Total quadratic errors of the second experiment.
Figure 18 shows the comparison from a superior view of the platform route without the inclusion of the curvature analysis and with the inclusion of the same, where the displacement in meters of the second is less in comparison with the execution of the first. This result is given because, in addition to the inclusion of the curvature analysis, the redundancy weights in the robotic arm were greater than those of the mobile platform, considerably reducing the movements of the motors that allowed displacement in the plane.
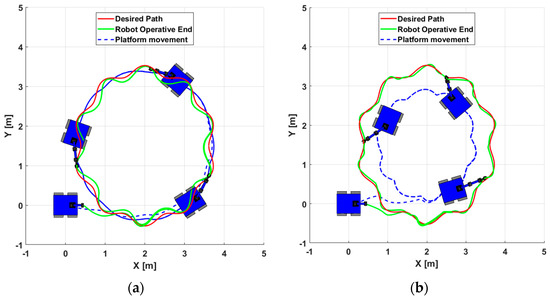
Figure 18.
Top view of robotic system travel without consideration of curvature analysis and with consideration of curvature analysis. (a) without ROC analysis, (b) With ROC analysis.
The current consumed by both tests over the duration of the run (at a total distance of 70 m) is shown in Figure 19 The total energy consumption of the test without considering the radius curvature analysis was 302,464 Joules, while with the consideration of ROC analysis was 208,102 Joules. From these results, it can be determined that the consumption of the robotic system when the curvature analysis was not considered was 4321 J/m (0.23 m/J), while the consumption when the ROC analysis was considered was 4001 J/m (0.25 m/J). Assuming a consumption of 500 Joules as a ceiling for both tests, the distance traveled for the controller without curvature analysis was 115 m, while for the controller with optimization was 125 m.
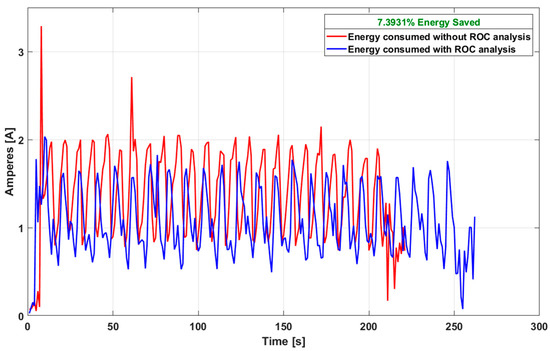
Figure 19.
Power consumption in both tests: without ROC analysis and with ROC analysis.
As shown in the control velocities (Figure 20), the consideration of radius of curvature analysis caused the input values to the robotic platform to be reduced in the presence of a curve, extending the execution time but at the same time optimizing energy consumption.
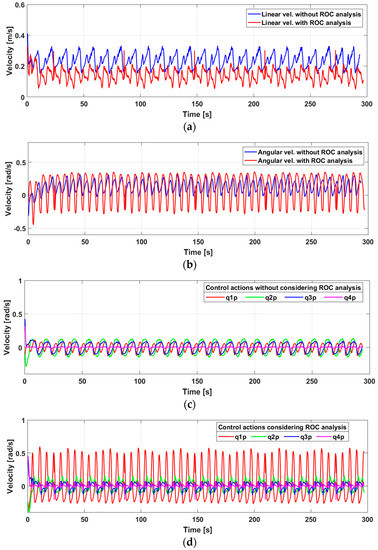
Figure 20.
Control velocities for the entire robotic system. (a) reduced linear velocity, (b) reduced angular velocity, (c) reduced linear control actions, (d) reduced angular control actions.
Finally, the third experiment presents the execution of four tests considering a controller based on Lyapunov for the tracking of roads, but with different characteristics: i) control over the robotic system without consideration of manipulability, ii) control of the mobile platform by analysis of radius of curvature but without consideration of manipulability, iii) control of the robotic system considering manipulability, iv) control of the mobile manipulator considering manipulability and application of velocity saturation for the whole robotic system. To compare all the tests, the selected trajectory is shown in Figure 21, in addition to showing the strobe movements executed by the robotic system considering manipulability and application of velocity saturation given by the curvature radius analysis in Figure 22.
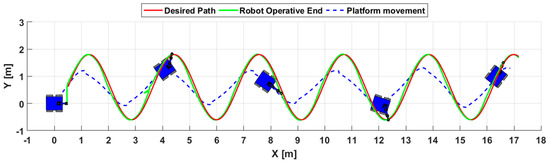
Figure 21.
Path selected for the third experiment considering ROC analysis and manipulability.
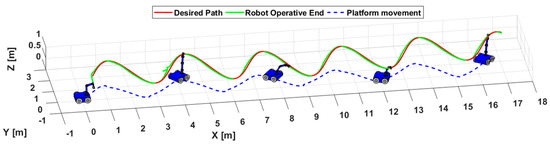
Figure 22.
Strobe movement of the execution of the third experiment considering ROC analysis and manipulability.
The power consumption of all cases was higher in relation to the energy expenditure of the proposed controller for energy optimization. This is verified through the analysis of the graphical representation of the power consumption shown in Figure 23, as well as by Table 2. Table 2 summarizes the results obtained by subjecting the robotic system to the various controller configurations, comparing the energy savings of each with the savings obtained by the proposed controller.
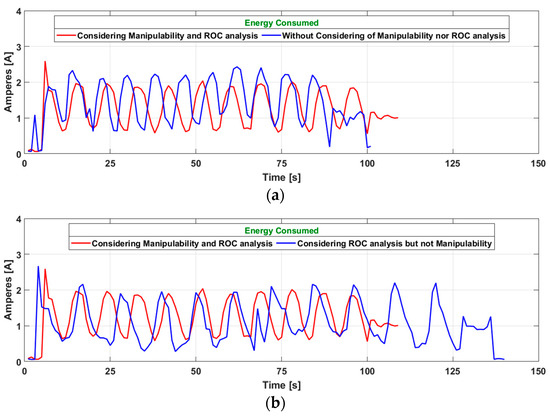
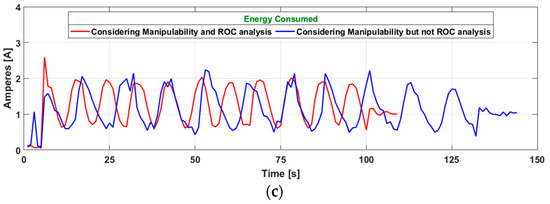
Figure 23.
Power consumption in each of the tests vs. controller considering ROC analysis (red). (a) proposed controller 1, (b) proposed controller 2, (c) proposed controller 3.

Table 2.
Results of the third experiment.
Remark 8.
1st Configuration: Without manipulability nor ROC analysis; 2nd Configuration: Considering ROC analysis but not manipulability; 3rd Configuration: Considering manipulability but not ROC analysis; 4th Configuration: Considering manipulability and ROC analysis.
6. Conclusions
In this work, an embedded robotic system has been presented, which obtains the best characteristics of two important and efficient robotic systems: mobile manipulators and unicycle mobile robots.
The proposal integrates in a single mathematical analysis the two systems in such a way that it takes advantage of their efficient characteristics in the search for the reduction of energy consumption in the tasks it performs. Sophisticated mathematical elements have been added to evaluate its action in the controller, and it has been demonstrated in experimental tests by a reduction of 8.76% of energy consumption in the tasks.
This has been based on a complex mechanical and electronic design that integrates intelligent control and communications systems and an efficient mechanical platform that facilitates maximum versatility in movements, and thus does not introduce energy losses due to mechanical design.
Author Contributions
Conceptualization, J.F.A.N.; Data curation, G.G.-d.-R.P. and J.G.S.; Formal analysis, J.F.A.N., G.G.-d.-R.P. and V.H.A.O.; Funding acquisition, G.G.-d.-R.P., V.H.A.O. and J.G.S.; Investigation, J.F.A.N.; Methodology, J.G.S.; Project administration, V.H.A.O. and J.G.S.; Resources, J.F.A.N., G.G.-d.-R.P., V.H.A.O. and J.G.S.; Software, J.F.A.N. and V.H.A.O.; Supervision, G.G.-d.-R.P., V.H.A.O. and J.G.S.; Validation, J.F.A.N., G.G.-d.-R.P., V.H.A.O. and J.G.S.; Writing–original draft, J.F.A.N.
Funding
This research was funded by Corporación Ecuatoriana para el Desarrollo de la Investigación y Academia–CEDIA.
Acknowledgments
The authors would like to thanks to the Corporación Ecuatoriana para el Desarrollo de la Investigación y Academia–CEDIA for the financing given to research, development, and innovation, through the CEPRA projects, especially the project CEPRA XIII-2019-08; Sistema Colaborativo de Robots Aéreos para Manipular Cargas con Óptimo Consumo de Recursos; also to Grupo de Investigación ARSI, for the support to develop this work.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Gonzalez, A.G.C.; Alves, M.V.S.; Viana, G.S.; Carvalho, L.K.; Basilio, J.C. Supervisory Control-Based Navigation Architecture: A New Framework for Autonomous Robots in Industry 4.0 Environments. IEEE Trans. Ind. Inform. 2018, 14, 1732–1743. [Google Scholar] [CrossRef]
- Magyar, B.; Tsiogkas, N.; Deray, J.; Pfeiffer, S.; Lane, D. Timed-Elastic Bands for Manipulation Motion Planning. IEEE Robot. Autom. Lett. 2019, 4, 3513–3520. [Google Scholar] [CrossRef]
- Ding, X.; Liu, Y.; Hou, J.; Ma, Q. Online Dynamic Tip-Over Avoidance for a Wheeled Mobile Manipulator with an Improved Tip-Over Moment Stability Criterion. IEEE Access 2019, 7, 67632–67645. [Google Scholar] [CrossRef]
- Garcia, M.A.R.; Rojas, R.A.; Pirri, F. Object-Centered Teleoperation of Mobile Manipulators with Remote Center of Motion Constraint. IEEE Robot. Autom. Lett. 2019, 4, 1745–1752. [Google Scholar] [CrossRef]
- Mori, S.; Tanaka, K.; Nishikawa, S.; Niiyama, R.; Kuniyoshi, Y. High-Speed Humanoid Robot Arm for Badminton Using Pneumatic-Electric Hybrid Actuators. IEEE Robot. Autom. Lett. 2019, 4, 3601–3608. [Google Scholar] [CrossRef]
- Su, H.; Qi, W.; Yang, C.; Aliverti, A.; Ferrigno, G.; de Momi, E. Deep Neural Network Approach in Human-Like Redundancy Optimization for Anthropomorphic Manipulators. IEEE Access 2019, 7, 124207–124216. [Google Scholar] [CrossRef]
- Prada-Jiménez, V.; Niáo-Suaréz, P.A.; Portilla-Flores, E.A.; Mauledoux-Monroy, M.F. Tuning a PD+ Controller by Means of Dynamic Optimization in a Mobile Manipulator with Coupled Dynamics. IEEE Access 2019, 7, 124712–124726. [Google Scholar] [CrossRef]
- Hamner, B.; Koterba, S.; Simmons, J.S.; Singh, S. An autonomous mobile manipulator for assembly tasks. Auton. Robot. 2010, 28, 131–149. [Google Scholar] [CrossRef]
- Li, Z.; Ge, S.S.; Adams, M.; Wijesoma, W.S. Robust adaptive control of uncertain force/motion constrained nonholonomic mobile manipulators. Automatica 2008, 44, 776–784. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y. Dynamic Modeling and Adaptive Neural-Fuzzy Control for Nonholonomic Mobile Manipulators Moving on a Slope. Int. J. Control Autom. Syst. 2006, 4, 197–203. [Google Scholar]
- Eslamy, M.; Moosavian, S.A.A. Dynamics and Cooperative Object Manipulation Control of Suspended Mobile Manipulators. J. Intell. Robot. Syst. 2010, 60, 181–199. [Google Scholar] [CrossRef]
- Abou-Samah, M.; Tang, C.P.; Bhatt, R.M.; Krovi, V. A kinematically compatible framework for cooperative payload transport by nonholonomic mobile manipulators. Auton. Robot. 2006, 21, 227–242. [Google Scholar] [CrossRef]
- Tchoń, K.; Jakubiak, J. Endogenous configuration space approach to mobile manipulators: A derivation and performance assessment of Jacobian inverse kinematics algorithms. Int. J. Control 2010, 76, 1387–1419. [Google Scholar] [CrossRef]
- Deepak, B.; Parhi, D.R. Control of an automated mobile manipulator using artificial immune system. J. Exp. Theor. Artif. Intell. 2016, 28, 417–439. [Google Scholar] [CrossRef]
- Rossi, E.; Tognon, M.; Carli, R.; Schenato, L.; Cortés, J.; Franchi, A. Cooperative Aerial Load Transportation via Sampled Communication. IEEE Control Syst. Lett. 2019, 4, 277–282. [Google Scholar] [CrossRef]
- Hua, M.; Wang, Y.; Wu, Q.; Dai, H.; Huang, Y.; Yang, L. Energy-Efficient Cooperative Secure Transmission in Multi-UAV-Enabled Wireless Networks. IEEE Trans. Veh. Technol. 2019, 68, 7761–7775. [Google Scholar] [CrossRef]
- Motlagh, N.H.; Bagaa, M.; Taleb, T. Energy and Delay Aware Task Assignment Mechanism for UAV-Based IoT Platform. IEEE Internet Things J. 2019, 6, 6523–6536. [Google Scholar] [CrossRef]
- Lin, C.; Wang, W.; Liu, S.; Hsu, C.; Chien, C. Heterogeneous Implementation of a Novel Indirect Visual Odometry System. IEEE Access 2019, 7, 34631–34644. [Google Scholar] [CrossRef]
- Abbaspour, A.; Jafari, H.Z.; Hemmat, M.A.A.; Alipour, K. Redundancy Resolution for Singularity Avoidance of Wheeled Mobile Manipulators. In Proceedings of the ASME 2014 International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014; p. V04AT04A036. [Google Scholar]
- Li, T.S.; Kuo, P.; Ho, Y.; Liou, G. Intelligent Control Strategy for Robotic Arm by Using Adaptive Inertia Weight and Acceleration Coefficients Particle Swarm Optimization. IEEE Access 2019, 7, 126929–126940. [Google Scholar] [CrossRef]
- Minniti, M.V.; Farshidian, F.; Grandia, R.; Hutter, M. Whole-Body MPC for a Dynamically Stable Mobile Manipulator. IEEE Robot. Autom. Lett. 2019, 4, 3687–3694. [Google Scholar] [CrossRef]
- Park, D.I.; Kim, H.; Park, C. Design and analysis of the dual arm manipulator for rescue robot. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017. [Google Scholar]
- Thapa, S.; Self, R.V.; Kamalapurkar, R.; Bai, H. Cooperative Manipulation of an Unknown Payload with Concurrent Mass and Drag Force Estimation. IEEE Control Syst. Lett. 2019, 3, 907–912. [Google Scholar] [CrossRef]
- Lunghi, G.; Marin, R.; di Castro, M.; Masi, A.; Sanz, P.J. Multimodal Human-Robot Interface for Accessible Remote Robotic Interventions in Hazardous Environments. IEEE Access 2019, 7, 127290–127319. [Google Scholar] [CrossRef]
- Wu, Y.; Balatti, P.; Lorenzini, M.; Zhao, F.; Kim, W.; Ajoudani, A. A Teleoperation Interface for Loco-Manipulation Control of Mobile Collaborative Robotic Assistant. IEEE Robot. Autom. Lett. 2019, 4, 3593–3600. [Google Scholar] [CrossRef]
- Li, W.; Xiong, R. Dynamical Obstacle Avoidance of Task- Constrained Mobile Manipulation Using Model Predictive Control. IEEE Access 2019, 7, 88301–88311. [Google Scholar] [CrossRef]
- Sciavicco, L.; Siciliano, B. Modeling and Control of Robot Manipulators; Springer: London, UK, 2000. [Google Scholar]
- Andaluz, V.; Roberti, F.; MarcosToibero, J.; Carelli, R. Adaptive unified motion control of mobile manipulators. Control Eng. Pract. 2012, 20, 1337–1352. [Google Scholar] [CrossRef]
- Paul, R.P. Robot Manipulators: Mathematics, Programming, and Control; MIT Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Li, G.; Song, D.; Xu, S.; Sun, L.; Liu, J. A Hybrid Model and Model-Free Position Control for a Reconfigurable Manipulator. IEEE ASME Trans. Mechatron. 2019, 24, 785–795. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).