A Joint Approach for Low-Complexity Channel Estimation in 5G Massive MIMO Systems

Abstract

Traditional Minimum Mean Square Error (MMSE) detection is widely used in wireless communications, however, it introduces matrix inversion and has a higher computational complexity. For massive Multiple-input Multiple-output (MIMO) systems, this detection complexity is very high due to its huge channel matrix dimension. Therefore, low-complexity detection technology has become a hot topic in the industry. Aiming at the problem of high computational complexity of the massive MIMO channel estimation, this paper presents a low-complexity algorithm for efficient channel estimation. The proposed algorithm is based on joint Singular Value Decomposition (SVD) and Iterative Least Square with Projection (SVD-ILSP) which overcomes the drawback of finite sample data assumption of the covariance matrix in the existing SVD-based semi-blind channel estimation scheme. Simulation results show that the proposed scheme can effectively reduce the deviation, improve the channel estimation accuracy, mitigate the impact of pilot contamination and obtain accurate CSI with low overhead and computational complexity.

1. Introduction

Massive MIMO is a very novel communication technology that uses large-scale antenna arrays to replace multiple antennas in 4G networks in existing base station, thus forming a large-scale MIMO communication environment [1,2,3]. In 2010, it was proposed by Bell Labs Scientist Marzetta, which is considered by the industry to be one of the key technologies for future 5G communication systems. The advantages of massive MIMO technology mainly include: spatial resolution is significantly enhanced compared to existing MIMO technology, and it can deeply exploit spatial dimensional resources [4], which can reflect the good stability of large-scale MIMO systems [5,6,7]; Massive MIMO can significantly reduce transmit power [8], thereby improving power efficiency; when the number of base station antennas is large enough, the simplest linear precoding and linear detectors will tend to be optimal, and noise and interference is negligible.

In massive MIMO systems, where base stations number of antennas is greatly increased, and the channels are asymptotically orthogonal [9]. The traditional Minimum Mean Square Error (MMSE) detection scheme can be used in massive MIMO systems and obtain better detection performance. However, the MMSE detection algorithm introduces complex matrix inversion operations, and its computational complexity increases with the number of transmitting antennas, which is difficult to implement quickly and efficiently in large-scale MIMO.

The large number theorem states that when the antennas installed at both ends of the transceiver are large, mutually independent channel vectors appear as large random vectors and appear orthogonal when the channel environment is ideal. The advantage brought by this feature is that when the receiving end obtains accurate channel state information (CSI), a simple recovery algorithm can eliminate the interference of other users and effectively improve the spectrum utilization of the channel [10]. Therefore, accurate CSI has an important role in the Massive MIMO system.

The study found that the performance of massive MIMO technology relies mainly on accurate channel state information (CSI), but existing research indicates that pilot contamination [11] is the main interference problem in channel estimation. Pilot contamination restricts the performance of massive MIMO systems, it is an urgent problem to be solved. In [12], a channel estimation algorithm based on eigenvalue decomposition (EVD) is proposed. Compared with the pilot-based channel estimation algorithm, this algorithm has better channel estimation performance. The precondition is that each channel vector is approximately orthogonal, but the actual situation is that the channel vector is not completely orthogonal, so there is a certain deviation in the method. In [13], a semi-blind channel estimation algorithm based on Singular Value Decomposition (SVD) is proposed for massive MIMO system. Compared to the EVD estimation performance, the performance of the SVD algorithm is significantly improved. However, since the covariance matrix used in the algorithm is obtained by replacing the real data with limited sample data, the channel estimation value must be biased.

In order to improve the accuracy of channel estimation in a massive MIMO system, an improved semi-blind channel estimation algorithm based on SVD (SVD-ILSP) is proposed to overcome the shortcomings in [13]. As the existing SVD algorithm in [13] is based on the assumption that the covariance matrix is obtained by using limited sample data instead of real data. This assumption limits the performance of [13] which motivates the proposed research work in which the novel contribution is to overcome the limitations of [13] and propose an improved SVD-ILSP algorithm to efficiently estimate the channel with high accuracy than [13]. The performance of channel estimation is compared with existing algorithms [12,13] by simulation. It shows that the channel estimation performance of the proposed algorithm is better.

The rest of the paper is organized as follows. Section 2 presents the related work. Section 3 provides the system model. Section 4 discusses the SVD based semi-blind channel estimation algorithm. Section 5 gives the proposed SVD-ILSP joint channel estimation algorithm. Section 6 gives the simulation results and analysis while Section 7 concludes the paper.

2. Related Work

Massive MIMO Technology utilizes a large number of antenna arrays deployed in base stations to achieve many different characteristics compared to traditional MIMO system, especially spectral efficiency, energy efficiency, transmit/receive power linearization operation, spatial beam resolution, significant performance improvements have been achieved in air interface latency and physical layer control signaling overhead [14,15,16]. Because of this, the industry generally believes that the realization of key performance indicators of 5G mobile communication systems in the future depends on the breakthrough of massive MIMO, a key technology of the physical layer [17,18,19]. However, the superior performance of massive MIMO technology is based on the premise that the base station obtains reliable and effective CSI, and the accuracy of CSI also directly determines the downlink spatial beam multiplexing, resource allocation, detection and reception of system, etc. [20,21,22]. For the current dominant Frequency Division Duplex (FDD) cellular system (the global 4G LTE FDD license place exceeds 300, and the Time Division Duplex (TDD) license plate only has more than 40 [22]), due to the upper and lower FDD standards the line channel does not satisfy the reciprocity. The downlink pilot signal must be sent by the base station, and the channel estimation is performed on the user side, and then fed back to the base station for corresponding pre-compilation code or beamforming scheme design [15]. Since the base station is configured with a large-scale antenna array, when the downlink orthogonal pilot sequence is used, the pilot length will increase exponentially as the number of antennas increases, resulting in the consumption of larger system resources which affect the spectrum utilization of the entire system [20]. At the same time, the industry considers the smooth transition from 4G FDD system to 5G system and the backward compatibility of the 5G system, we must focus on the pilot overhead and pilot design problem in FDD massive MIMO system, which is large for FDD system. The application and promotion of MIMO technology have important practical significance [22].

In [23], the pilot design problem under non-orthogonal conditions is studied, and the pilot sequence is used to iteratively optimize the channel sequence. The authors in [24] jointly consider the space-time two-dimensional correlation of the channel and perform channel prediction by means of the temporal coherence of the channel, and then designs a low-overhead pilot and channel estimation scheme under open-loop and closed-loop conditions. In [25], the spatial coherence of the channel is exploited, and the classical channel estimation Mean Square Error (MSE) is minimized as the target, and the pilot signal is optimized. In [26], a low-overhead periodic training sequence transmission scheme is designed by using the channel time correlation and Kalman filter, and considering the limited Radio Frequency (RF) link precoding scheme with low implementation complexity. The above research considers the pilot design in a single-user scenario. This is because the channel space-time correlation of users in different multi-user scenarios is different, and the downlink pilots transmitted by the base station are consistent, and therefore cannot be single. The pilot matrix matches the channel characteristics of all users. As described in [27], the pilot design problem for multi-user ubiquitous scenarios in FDD massive MIMO systems is still an open hot issue. Therefore, most of the existing research is based on single-user scenarios or has some kind of multi-user scenario with characteristic channel conditions. In [28], by grouping, multiple users with the same channel spatial correlation matrix, a two-stage precoding scheme based on block zero-forcing is proposed in a special multi-user scenario. By assuming the orthogonality of the covariance matrix of the users between the groups, the first-stage precoding is used to suppress the inter-group interference, thereby reducing the effective channel dimension of the users in the group, thereby reducing possible pilot overhead and simplify precoding design. However, the focus of [28] is on the design of the two-stage precoding scheme, and the corresponding pilot optimization design scheme is not given.

It is also worth noting that the above pilot design scheme for FDD massive MIMO system is still based on the accuracy of channel estimation, that is, the channel estimation MSE, thereby designing a low-overhead pilot scheme. However, in addition to affecting channel estimation accuracy, the pilot signal will indirectly affect the design of the downlink beam vector of the bases station and the channel matching problem, which in turn affects the transmission rate of the system. At the same time, the duration resource consumed by the pilot signal affects the subsequent effective data transmission duration, which also affects the effective transmission rate of the system. The transmission rate is an important indicator of the communication system, and it also directly reflects the performance of the system. Therefore, using the system effective transmission rate as a criterion to optimize the design of the pilot signal has more practical meaning.

In order to overcome the shortcomings of the above algorithms, especially [13], we proposed an improved joint SVD and ILSP algorithm to effectively improve the detection performance and reduce the computational complexity of the channel estimation in massive MIMO system. Moreover, the proposed scheme will be compared with the existing techniques to provide a clear indication of the relative advantages of the proposed algorithm over the existing algorithms.

3. System Model

Considering a multi-cell massive MIMO system with $L$ cells, each cell has $K$ single-antenna terminals, the base station of each cell is equipped with $M$ antennas, and $M\gg K$ is assumed, and the system works in TDD mode as shown in Figure 1. At this time, the base station estimates the CSI through the reverse link, and the forward link obtains its channel information through the reciprocity principle in the TDD mode. It is assumed that the channel matrix from all terminals of the $L$th cell to the $j$th cell base station is $G_{jl}\in {\mathsf{ℂ}}^{M\times K}$ can be expressed as:

$$G_{jl}=H_{jl}{D}_{jl}$$

(1)

where $H_{jl}\in {\mathsf{ℂ}}^{M\times K}$ is a matrix composed of small-scale fading coefficients. $D_{jl}\in R^{k\times k}$ is a diagonal matrix composed of the large-scale fading coefficient. Specifically, the channel information of the$k$th antenna of the first cell to the $m$th antenna of the $j$th cell base station can be expressed by:

$${\mathrm{g}}_{jlmk}={\left[G_{jl}\right]}_{mk}=h_{jlmk}{\beta }_{jlk}^{\frac{1}{2}}$$

(2)

where $h_{jlmk}={\left[H_{jl}\right]}_{mk}$, ${\beta }_{jlk}^{\frac{1}{2}}={\left[D_{jl}\right]}_{mk}$, ${\beta }_{jlk}$ is a large-scale fading coefficient composed of path loss and shadowing fading, and assuming that ${\beta }_{jlk}$ is a constant and a priori known information, since the path loss condition decreases exponentially with distance, it is considered that in most cases user $k_1$ and $k_2$ are not at the cell boundary, so ${\beta }_{jj{k}_1}\gg {\beta }_{jl{k}_2}$, $\forall l\ne j$. $h_{jlmk}$ are independent and identically distributed (i.i.d) and satisfy $CN\left(0,1\right)$. Therefore, the received signal matrix can be expressed as:

$$Y_j= \left[Y_j^p,Y_j^d\right]={\displaystyle \sum }_{l=1}^L{G}_j{S}_l^T+N_j\in {\mathsf{ℂ}}^{M\times \left(N_p+N_d\right)}$$

(3)

where $Y_j^p\in {\mathsf{ℂ}}^{M\times N_p}$ represents the received pilot matrix, $Y_j^d\in {\mathsf{ℂ}}^{M\times N_d}$ represents the data matrix of the received signal. $S_l$ denotes the symbol matrix transmitted by the terminal in the first cell which can be expressed as:

$$S_l=\sqrt{p_u} \left[\sqrt{N_p} {\phi }_l;X_l \right]\in {\mathsf{ℂ}}^{\left(N_p+N_d\right)\times k}$$

(4)

Figure 1. Massive MIMO system model.

Among them, $p_u$ is the average transmission power of the symbol, ${\phi }_l$ and $X_l$ represent pilot and data symbol information, respectively. $N_j=\left[N_j^p,N_j^d\right]$, is a noise matrix, where $N_j^p$ and, $N_j^d$ both satisfy $CN\left(0,1\right)$ and follow i.i.d distribution. It is assumed here that the channel response is a constant reference channel during the transmission of $N_p+N_d$ time. The purpose is to use the received $Y_j$ information for channel estimation of $G_{jl}$.

The received pilot matrix and data matrix can be expressed by:

$$Y_j^p=\sqrt{p_u{N}_p} {\displaystyle \sum }_{l=1}^L{G}_{jl}{\phi }_j^T+N_j^p$$

(5)

$$Y_j^d=\sqrt{p_u} {\displaystyle \sum }_{l=1}^L{G}_{jl}{X}_j^T+N_j^d$$

(6)

Assuming that the elements in $X_l$ are follow i.i.d distribution with $CN\left(0,1\right)$. In addition, it is assumed that a set of pilot sequences $\phi \in {\mathsf{ℂ}}^{N_p\times k}$ is shared among $L$ cells, where ${\phi }^H\phi =I_k$, $N_p\ge k_0$.

4. SVD Decomposition Based Semi-Blind Channel Estimation

Since the channel estimation algorithm based on eigenvalue decomposition cannot completely solve the problem of the fuzzy matrix, the proposed channel estimation algorithm based on SVD decomposition is more powerful in dealing with fuzzy matrix than the channel estimation algorithm based on EVD decomposition. This paper introduces a channel estimation algorithm based on SVD decomposition.

4.1. Theoretical Properties of Massive MIMO Channel Matrices

In a massive MIMO system, when the number of antennas $M$ tends to infinity, it satisfies:

$$\frac{1}{M}{H}_{j{l}_1}^H{H}_{j{l}_2}\to \delta \left(l_1-l_2\right)I_k$$

(7)

Since the number of base station antennas $M$ is finite, the channel vectors are approximately orthogonal, so $H_{jj}={\tilde{H}}_{jj}{\mathsf{\Xi }}_j$, where ${\tilde{H}}_{jj}\in {\mathsf{ℂ}}^{M\times k}$ satisfies $\frac{1}{M}{\tilde{H}}_{jj}^H{\tilde{H}}_{jj}=I_k$, ${\mathsf{\Xi }}_i\in {\mathsf{ℂ}}^{k\times k}$ can be expressed as ${\mathsf{\Xi }}_i=I_k+{\mathsf{\Gamma }}_i$, the absolute value of the element in ${\mathsf{\Gamma }}_i$ is much smaller than 1, and the covariance matrix of $Y_i^d$ can be expressed as:

$$R_{Y_j^d}=E\left\{Y_j^d{\left(Y_j^d\right)}^H\right\}=p_u{\displaystyle \sum }_{l=1}^L{H}_{jl}{D}_{jl}^2{H}_{jl}^H+I_M\in {\mathsf{ℂ}}^{M\times M}$$

(8)

In the semi-blind channel estimation, the covariance matrix of the received signal is necessary, and the covariance matrix is usually obtained by using the limited sample data, and then the channel estimation is performed. Therefore, the $R_{Y_j^d}$ is approximated by the finite sample data, and the form is:

$${\tilde{R}}_{Y_j^d}=\frac{1}{N}{\displaystyle \sum }_{n=1}^N{\left[Y_j^d\right]}_n{\left[Y_j^d\right]}_n^H$$

(9)

Only when $N\to \infty$, ${\tilde{R}}_{Y_j^d}$ converge to $R_{Y_j^d}$. Since ${\tilde{R}}_{Y_j^d}$ is a Hermite matrix, its SVD is decomposed into:

$${\tilde{R}}_{Y_j^d}=U_j{\displaystyle \sum }_j{U}_j^H$$

(10)

where $U_j\in {\mathsf{ℂ}}^{M\times M}$ is composed of $M$ left singular vectors. ${{\displaystyle \sum }}_j$ is a diagonal matrix, which consists of $M$ singular values, and these singular values are arranged in descending order from the upper left corner, so that $U_j=\left[U_j^s, U_j^n\right]$, where $U_j^s\in {\mathsf{ℂ}}^{M\times \left(M-K\right)}$, $U_j^n\in {\mathsf{ℂ}}^{M\times \left(M-K\right)}$, according to [13], $U_j^s$ can also be expressed as:

$$U_j^s=\frac{1}{\sqrt{M}}\left({\tilde{H}}_{jj}+F_j\right)E_j$$

(11)

where $F_j$ defines interference between cells and within the cell, and the column of $F_j$ can be represented as a linear function of each term of $H_{jl}$. $E_j$ is unknown unitary maan trix, and $\frac{1}{M}{\tilde{H}}_{jj}^H{\tilde{H}}_{jj}=I_k$, $H_{jj}={\tilde{H}}_{jj}{\mathsf{\Xi }}_j$, ${\mathsf{\Xi }}_i\in {\mathsf{ℂ}}^{k\times k}$ can be expressed as ${\mathsf{\Xi }}_i=I_k+{\mathsf{\Gamma }}_i$. Ignore $F_j$, $U_j^s$ determines the matrix $H_{jj}$, ${\tilde{E}}_j={\mathsf{\Xi }}_j^{-1}{E}_j\approx E_j\in {\mathsf{ℂ}}^{k\times k}$, ${\tilde{E}}_j$ is called a fuzzy matrix, and the fuzzy matrix is processed by pilot-based channel estimation.

4.2. Solution of Fuzzy Factor

According to the Equation (5), the pilot-based estimation expression of the $j$th cell channel matrix $H_{jj}$ can be obtained by using the pilot signal transmitted by the user uplink:

$${\tilde{H}}_{jj}^p=\frac{1}{\sqrt{p_u{N}_p}}{Y}_j^p{\phi }^{*}{D}_{jj}^{-1}=H_{jj}+{\Delta }_j$$

(12)

where, ${\Delta }_j={{\displaystyle \sum }}_{l\ne j}\left(H_{jl}{D}_{jl}+\frac{1}{\sqrt{p_u{N}_p}}{Y}_j^p{\phi }^{*}\right)D_{jj}^{-1}\in {\mathsf{ℂ}}^{M\times K}$ represents interference and noise between cells. From Equations (11) and (12) we can get:

$$\frac{1}{\sqrt{M}}{\left(U_j^s\right)}^H{\tilde{H}}_{jj}^p=E_j^H{\mathsf{\Xi }}_{jj}+E_j^H{\gamma }_j^H={\tilde{E}}_j^{-1}+E_j^H{\gamma }_j^H$$

(13)

where ${\gamma }_j=\frac{1}{M}{\Delta }_j^H\left({\tilde{H}}_{jj}+F_j\right)+\frac{1}{M}{H}_j^H{F}_j\in {\mathsf{ℂ}}^{k\times k}$ indicates the sum of noise and interference at the receiving end. Using Equation (13) to eliminate the fuzzy matrix to get:

$$\sqrt{M}{U}_j^s\left(\frac{1}{\sqrt{M}}{\left(U_j^s\right)}^H{\tilde{H}}_{jj}^p\right)=H_{jj}+\frac{1}{M}{\tilde{H}}_{jj}{\tilde{H}}_{jj}^H{\Delta }_j+{\tilde{F}}_j$$

(14)

$${\tilde{F}}_j=\frac{1}{M}\left[\left({\tilde{H}}_{jj}+F_j\right)F_j^H\left(H_{jj}+{\Delta }_j\right)\right]+F_j\left(\frac{1}{M}{\tilde{H}}_{jj}{\Delta }_j+{\mathsf{\Xi }}_j\right)$$

(15)

where ${\tilde{F}}_j$ represents interference. Simplifying Equation (14) we get:

$${\tilde{H}}_{jj}^s=U_j^s{\left(U_j^s\right)}^H{\tilde{H}}_{jj}^p$$

(16)

5. SVD-ILSP Based Channel Estimation Algorithm

Since the covariance matrix used in SVD-based channel estimation replaces the real data with limited sample data, there is an error in the channel estimation value. To reduce the error, the ILSP signal detection algorithm [29] and the SVD algorithm are combinedly used in this paper. The signal detection needs to have the estimated channel information as the basis, and the detected transmission data can continue to re-estimate the channel as a known signal, which is the main idea of joint estimation of SVD and ILSP scheme.

The data signals transmitted by the $k$ users of the first cell to the target cell base station are ma atrix $X_l$ of $K\times N$ dimension, and $H_{li}$ is the $M\times K$ dimension matrix, indicating the channel between the $i$th cell user and the $l$th cell target base station. The received signal in the $l$th cell of the $M\times N$ dimension received by the base station is:

$$Y_l=\sqrt{p_u}{H}_{ll}{X}_l+\sqrt{p_u}{\displaystyle \sum }_{i=l}^L{H}_{li}{X}_i+N_l$$

(17)

The elements of Equation (16) are expressed as:

$$\{\begin{array}{l}{X}_i=\left[x_i\left(1\right)x_i\left(2\right)\dots x_i\left(N\right)\right], i=1,2, \dots , L\\ Y_l=\left[y_l\left(1\right)y_l\left(2\right)\dots y_l\left(N\right)\right]\\ N_l=\left[n_l\left(1\right)n_l\left(2\right)\dots n_l\left(N\right)\right]\end{array}$$

(18)

The last two terms on the right side of Equation (18) are interference signals and noise interference from other cell users. The basic principle of the ILSP signal detection algorithm is to first use the SVD channel estimation algorithm to find the initial channel value ${\tilde{H}}_{\mathrm{ori}}$ as a known condition, and use this initial value instead of the real channel value for signal detection, and then use the detected signal as a known receiving data and re-estimating the channel [29].

Signal detection is performed by a simple least squares method, and the signal detection results are:

$${\tilde{X}}_l= \stackrel{\arg \min }{S_l\in \chi }\Vert \frac{1}{p_u}{H}_{ll}^H{Y}_l-X_l{\Vert }_F^2$$

(19)

where $\chi$ indicates a set of possible values of the transmitted signa, and re-evaluates the channel by using the LS algorithm for the detected signal, thereby obtaining:

$${\tilde{H}}_{ll}=\frac{1}{\sqrt{p_u}}{Y}_l{\tilde{X}}_l^H{\left({\tilde{X}}_l{\tilde{X}}_l^H\right)}^{-1}$$

(20)

5.1. Computational Complexity Analysis

The EVD-based semi-blind channel estimation and the SVD-based semi-blind channel estimation algorithm require $N{M}^2$ complex multiplication when receiving the signal sample autocorrelation matrix. For a known $M\times M$ matrix, calculate the exact EVD algorithm or SVD algorithm. The number of complex multiplications [30] required are $\frac{4}{3}{M}^3$ and $11M^3$ respectively. The semi-blind channel estimation algorithm based on EVD in [12] requires $8M{K}^2\tau +\left(4\tau +1\right)MK+\mathcal{O}\left(K^3\right)$ times complex multiplications to complete the calculation of the fuzzy matrix.

The fuzzy matrix assumed by the algorithm is a diagonal matrix and the final estimation result of $H_{jj}\left(n\right)$ also requires $MK$ complex multiplication. The SVD-based semi blind channel estimation [13] algorithm requires $MK\tau +MK$ complex multiplications to complete the calculation of pilot-based channel estimation. At the same time, $2M{K}^2$complex multiplication is needed to obtain the final estimate of $H_{jj}\left(n\right)$. The complexity of the proposed channel estimation algorithm is mainly related to the LS algorithm, the SVD algorithm and the number of iterations $N_{\mathrm{ite}}$. Table 1 shows the computational complexity of the three channel estimation algorithms. It can be seen that the complexity of the proposed algorithm has been improved due to the introduction of iterative ideas. The proposed algorithm improves the accuracy of the channel estimation algorithm by adding a certain complexity.

Table 1. Computational complexity comparison.

Channel Estimation Algorithm	Computational Complexity
Semi-blind based channel estimation based on EVD	$\frac{4}{3}{M}^3+N{M}^2+8M{K}^2\tau +\left(4\tau +2\right)MK+\mathcal{O}\left(K^3\right)$
Semi-blind channel estimation based on SVD	$11M^3+ N{M}^2+2M{K}^2+ MK\tau +MK$
Proposed Seimi-blind channel estimation	$N_{\mathrm{ite}}\left(MK\left(\tau +1\right)\right)+11M^3+N{M}^2+2M{K}^2+MK\tau +MK$

5.2. Improved Algorithm Flowchart

The algorithm flow chart of the proposed improved algorithm is shown in Figure 2.

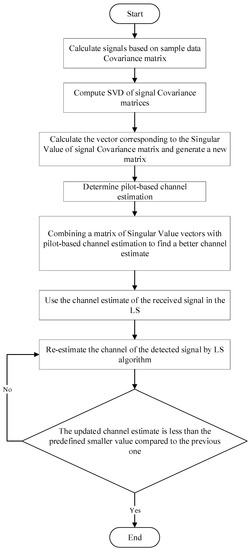
Figure 2. Improved Singular Value Decomposition (SVD) algorithm processing flow.

6. Simulation Results and Analysis

We used MATLAB (R2017a, Mathworks, MA, USA) simulator for experimentations. The configuration of the main simulation parameters in the massive MIMO system is shown in Table 2. In order to better analyze and compare the performance of each algorithm in channel estimation, this paper measures the Mean Square Error (MSE) and compares the channel estimation performance under different SNR with a different number of antennas. Consider a scenario of massive MIMO system with $L=3$ cells. Regardless of shadow fading, the base station of each cell simultaneously serves 3 single antenna terminals, these terminals are evenly distributed in the cell, and the pilot signal length sent by each terminal is $\tau =k$. In order to simplify the channel model, let $D_{jj}=I_k$, $D_{ji}=\lambda I_k \left(i\ne j\right)$, where $\lambda \in \left[0,1\right]$ is the interference factor between cells [6], adopt BPSK modulation, and define each MSE as the average MSE of all elements in the channel matrix, where the MSE is defined as:

$$MSE=\frac{\Vert {\tilde{H}}_{ll-}{H}_{ll}\Vert {}_F}{MK}$$

(21)

Table 2. Simulation Parameters.

Parameter	Setting
$\mathrm{Cell}\mathrm{radius}\left(m\right)$	1000
Path fading index	3.8
Number of terminals per cell	3
Modulation	BPSK
User location	Evenly distributed
Number of iterations	5
Signal detection method	LS
Antenna spacing	$\lambda /2$

With $M=100$, $N=100$, $\lambda =0.3$, with SNR variation, LS estimation, SVD-based semi-blind channel estimation, EVD-based semi-blind channel estimation, and the MSE performance of the semi-blind channel estimation proposed in this paper are simulated. The results are shown in Figure 3. It can be seen from the Figure 3 that LS channel estimation, SVD-based semi-blind channel estimation the MSE of the proposed semi-blind channel estimation decreases with the increase of SNR. The EVD-based semi-blind channel estimation algorithm has the same MSE value as the SNR increases, which is mainly because it is in the actual application scenario. Since the number of antennas is limited and the channels have correlations, the condition that the column vectors of the channel matrix are completely orthogonal is not true, that is, the column vectors cannot guarantee good orthogonality, so the semi-blind channel estimation based on EVD is not established. The inference of the fuzzy matrix as a diagonal matrix in the algorithm does not hold, so the fuzzy matrix problem cannot be properly solved. Under different SNR conditions, the proposed algorithm and SVD-based semi-blind channel estimation algorithm are superior to LS channel estimation algorithm in MSE performance. With the increase of SNR, the proposed joint algorithm can achieve a lower MSE than the SVD-based semi-blind channel estimation algorithm. It can also be seen from Figure 4 that as the SNR increases, the SVD estimation and the proposed algorithm reduce the MSE. It tends to be slow, which means that increasing the user’s transmit power does not improve the system performance. It is necessary to increase the performance of the base station by increasing the number of antennas of the base station. This reflects the significance of studying the configuration of large-scale array antennas at the base station.

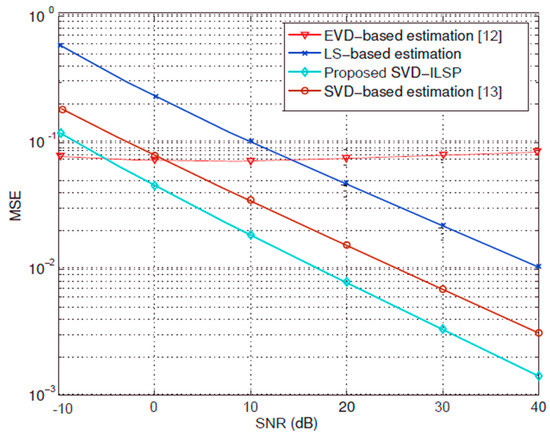
Figure 3. Mean Square Error (MSE) comparison of algorithms under different SNR conditions.

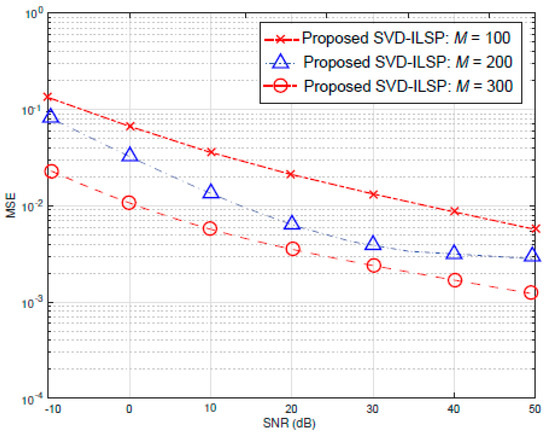
Figure 4. MSE comparison of the proposed joint channel estimation algorithm under different number of base station antennas.

Figure 5 shows the trend graph of the MSE corresponding to the four channel estimation algorithms under a different number of antennas, taking $N=100$, $SNR=10 \mathrm{dB}$. As can be seen from Figure 5, with the increasing number of base station antennas, the performance of the LS channel estimation remains basically unchanged. This is mainly because the LS channel estimation algorithm is seriously polluted by the pilot. As the number of antennas increases, the MSE of the EVD-based semi-blind channel estimation algorithm is significantly reduced. This is because as $M$ increases, the progressive orthogonality between the column vectors of the channel matrix gradually increases, so the interference between users is gradually weakened. In the case of pilot contamination, the channel estimation performance of the SVD algorithm is better than that of the EVD algorithm and the LS channel estimation algorithm as the number of antennas increases, and the SVD algorithm combined with the ILSP is better than the single SVD when the number of antennas increases. This is mainly because the proposed improved algorithm utilizes the iterative idea to better optimize the channel estimation value, thereby improving the accuracy of channel estimation. It can also be seen from the Figure 5 that as the number of base station antennas increases, the MSE slightly decreases, which is mainly due to the large-scale fading coefficient of the user in the system, that is, the position of the mobile terminal in the cell.

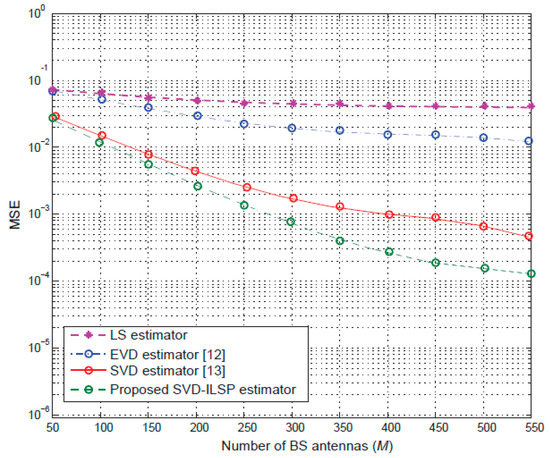
Figure 5. MSE comparison of algorithms under a different number of base station antennas.

Figure 6 compares the spectral efficiency (SE) of the proposed joint SVD-ILSP algorithm with EVD and SVD-based semi-blind channel estimation algorithms under different SNR conditions. As can be seen from Figure 6 when the SNR increases, the SE of all the algorithms increases. The LS scheme shows poor SE and it has a slight variation with SNR. The EVD estimator shows better SE than the LS while the SVD has improved SE than both LS and EVD but lower than the proposed SVD-ILSP algorithm. Furthermore, the rate gap between the proposed SVD-ILSP algorithm and other algorithms gets larger which clearly indicates that the proposed algorithm shows superior SE performance under high SNR conditions as well as low SNR values which makes it attractive candidate from a practical perspective.

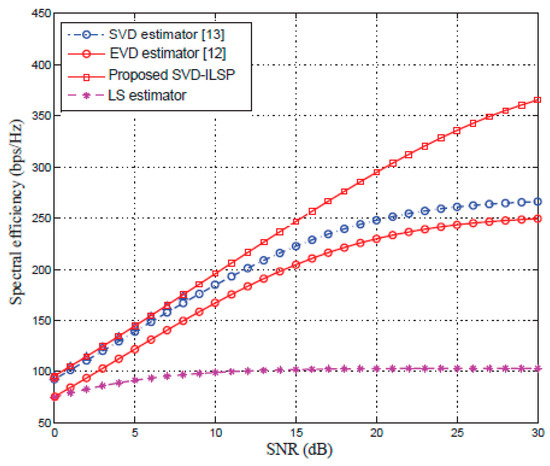
Figure 6. Spectral efficiency comparison of algorithms under different SNR conditions.

Figure 7 compares the spectral efficiency versus the number of base station antennas for the proposed algorithm and the other state-of-the-art algorithms. It is already known that the SE increases with increasing number of base antennas and so, the SE of all the algorithms increases accordingly. As can be seen from Figure 7, the proposed channel estimation scheme outperforms the SVD and EVD-based channel estimators. Moreover, the SE of the proposed scheme rises more quickly than the SE of SVD and EVD which has a slow variation with the number of base station antennas. Therefore, the results indicate that the proposed channel estimation algorithm effectively improves the SE performance of the massive MIMO system.

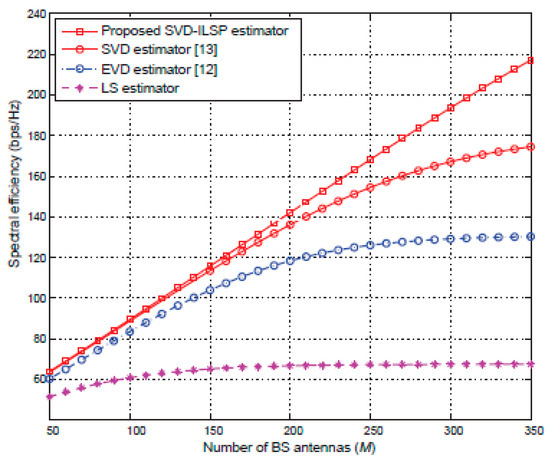
Figure 7. Spectral efficiency comparison of algorithms under a different number of base station antennas.

7. Conclusions

In this paper, the SVD-based semi-blind channel estimation algorithm is studied in a multi-cell massive MIMO TDD system, and the optimization is based on the inadequacies of the algorithm. The optimization method is to combine the SVD algorithm and the ILSP algorithm through the idea of iteration. The reduction of finite sample data instead of covariance exists. The simulation results show that the proposed algorithm has better channel estimation performance than traditional pilot-based LS channel estimation algorithm and EVD-based semi-blind channel estimation. The SVD semi-blind channel estimation algorithm can improve the channel estimation performance of the system and improve the accuracy of CSI estimation in the presence of pilot contamination, thereby effectively reduce the impact of pilot contamination problems on the performance of massive MIMO systems. Therefore, it is conducive to improving the performance of massive MIMO systems. Future work is to consider FDD scenarios and determine the NMSE of channel estimation and compare it with other state-of-the-art channel estimation schemes. Moreover, the next aspect of this research that will be considered is to integrate it with mmWave technology which has plenty of unused spectrum and, therefore, massive MIMO will utilize it.