Pipelined Divider with Precomputed Multiples of Divisor

Abstract

Division remains one of the most computationally demanding operations in digital arithmetic. Traditional algorithms, such as restoring, non-restoring, and SRT (Sweeney–Robertson–Tocher) division, are limited by sequential dependencies that reduce throughput in hardware implementations. To overcome these constraints, this work proposes a pipelined integer divider architecture that employs precomputed divisor multiples and comparator-based logic to eliminate the need for full binary adders in the quotient selection stages. The proposed design consists of a three-stage pipeline, where each stage compares the shifted partial remainder with stored multiples of the divisor (B, 2B, 3B) to generate two quotient bits per clock cycle. This approach achieves a 2× reduction in the number of computation stages compared with conventional radix-2 dividers and ensures continuous operation after an initial pipeline latency. The architecture was described in Verilog hardware description language (HDL) and implemented on a Xilinx Artix-7 (XC7A100T-1CSG324C) field-programmable gate array (FPGA) using the Xilinx ISE Design Suite 14.4. Post-synthesis simulation confirmed correct quotient and remainder generation with a maximum operating frequency of 208 MHz. The implementation occupied less than 0.3% the look-up table (LUT) resources, achieving over a twofold performance improvement compared with a non-pipelined baseline. These results demonstrate that the proposed divider provides an efficient trade-off between speed and hardware cost, making it suitable for digital signal processing and embedded computation systems.

1. Introduction

Division remains one of the most fundamental yet computationally demanding operations in digital arithmetic. Unlike addition and multiplication, which exploit parallel structures such as carry-propagate or carry-save adders, division is inherently sequential because each quotient digit depends on the previous remainder. This dependency creates latency bottlenecks in arithmetic logic units (ALUs), digital signal processors, and embedded systems. As real-time numerical processing becomes increasingly important, high-speed division units are now essential components of modern hardware architectures [1,2].

Classical division algorithms are traditionally classified into three main families: restoring, non-restoring and Sweeney–Robertson–Tocher (SRT) [2,3,4]. Restoring division recalculates the partial remainder by conditional subtraction and restoration, whereas the non-restoring variant removes the restoration step at the cost of additional correction logic. The SRT algorithm, introduced in the 1950s, significantly improved performance by allowing signed quotient digits ($-1$, 0, $+1$) and was later extended to higher radices such as 4, 8, and 16 [5,6]. By selecting multiple quotient digits per iteration, high-radix SRT dividers reduce the number of cycles by up to four times compared with radix-2 approaches.

Despite algorithmic progress, the hardware implementation of division remains challenging, especially on Field-Programmable Gate Arrays (FPGAs). Efficient designs must balance several conflicting parameters: latency, logic utilisation, critical-path delay, and power consumption [7,8]. Conventional SRT dividers rely on look-up tables (LUTs) or small memories for quotient-digit selection. As the radix increases, these tables grow exponentially, inflating hardware complexity and routing delay [9]. Iterative designs without pipelining further suffer from low throughput because each division must finish before the next can start.

To overcome these limitations, researchers have proposed pipelined division architectures that decompose the process into sequential stages, each performing part of the computation [10,11,12,13]. Pipelining enables the overlap of operations across multiple input operands, increasing throughput in proportion to the number of stages. However, most existing pipelined SRT and non-restoring dividers still depend on adders and subtractors in every stage, resulting in considerable area overhead and signal delay. Achieving an optimal balance between hardware cost and operational speed, therefore, remains an open problem.

Recent advances in FPGA technology-including fine-grained logic blocks, embedded DSP slices, and high-speed interconnects - have significantly improved computational capability. These features allow the flexible implementation of custom arithmetic units such as multipliers, dividers, and floating-point operators. However, division units are rarely optimised for pipelined operation, particularly for integer arithmetic. Most available FPGA dividers are generic iterative designs synthesised from high-level descriptions, providing correctness but not efficiency [12,14,15].

This work addresses the above limitations by proposing a pipelined integer division architecture with precomputed divisor multiples, explicitly tailored for FPGA implementation. The central idea is to replace traditional adder-based remainder updates with comparator-driven logic. At each pipeline stage, the partial remainder is compared against precomputed multiples of the divisor (B, 2B, 3B) and their inverted forms to generate a new remainder and two quotient bits simultaneously. This dual-bit-per-stage operation effectively halves the number of pipeline stages compared to conventional approaches.

The proposed architecture introduces a Block for Generating and Storing Divisor Multiples (BGSDM), which precomputes B, 2B, 3B, and their inversions before feeding them to the successive pipeline stages. Each stage is implemented by a Partial Remainder and Quotient Digit Formation Unit (PRU–QDSL), which includes sub-blocks for comparator logic, remainder reconstruction, and quotient bit generation. By employing parallel comparisons instead of serial arithmetic operations, the design minimises combinational delay and enables a higher operating frequency.

Unlike existing high-radix dividers that require complex look-up tables for quotient digit selection [6,9], the proposed design determines quotient bits directly through combinational comparisons, avoiding large memory structures. Furthermore, the modular nature of each stage simplifies scalability: increasing operand bit width or number of pipeline stages can be achieved without redesigning the core logic.

The main objective of this work is to design and validate a pipelined divider architecture that offers improved latency and hardware efficiency by leveraging precomputed divisor multiples and comparator-based remainder logic.

The main contributions of this work can be summarised as follows:

• A novel pipelined division architecture for integer arithmetic with precomputed divisor multiples and dual-bit-per-stage quotient generation.
• A comparator-based remainder formation logic that avoids the use of wide carry-propagate binary adders in the pipeline stages, thereby reducing hardware area.
• A complete FPGA implementation and validation of the proposed architecture, showing minimal resource utilisation and scalable performance.
• A systematic performance evaluation, comparing the proposed design against existing SRT and non-restoring dividers in terms of latency, throughput, and area efficiency.

The remainder of this paper is structured as follows. Section 2 provides an overview of related works and high-radix division techniques. Section 3 describes the proposed pipelined architecture in detail, including block-level design and algorithmic flow. Section 4 discusses FPGA implementation results, timing analysis, and performance comparisons. Section 5 concludes the paper with a discussion of potential extensions, including signed arithmetic and floating-point division support.

2. Analysis of Dividers Implementation in Hardware

The problem of efficient division in digital arithmetic has been studied for more than half a century, yet it remains one of the least optimised operations compared to addition or multiplication. The historical evolution of division algorithms can be divided into several main categories: restoring, non-restoring, SRT-based, digit-recurrence, and multiplicative approximation methods. Each of these approaches offers different trade-offs in terms of latency, hardware complexity, and numerical precision. The following section reviews key works that have shaped the design of hardware dividers and highlights the limitations that motivate the development of a new pipelined architecture.

The earliest digital dividers, introduced in the 1950s, employed restoring division, where each iteration subtracts the divisor from the partial remainder and restores the previous value if the result becomes negative [2,4]. While conceptually simple, this approach is inefficient because it requires a conditional restoration step at every iteration, effectively doubling the average number of arithmetic operations.

To address this inefficiency, the non-restoring algorithm was proposed [2]. In this scheme, the system avoids immediate restoration: if the intermediate result is negative, the next iteration performs an addition instead of subtraction. This modification reduces the total number of arithmetic steps by roughly 50%, improving throughput for both fixed-point and floating-point arithmetic units. Non-restoring division became widely adopted in early microprocessors and continues to be used in many low-power FPGA implementations [7,12,16]. However, its inherently sequential nature still limits performance, as each quotient bit must be derived from the previous partial remainder.

A major breakthrough occurred with the development of the Sweeney–Robertson–Tocher (SRT) algorithm [4,16]. Unlike binary methods, SRT allows the quotient digit to take signed values such as $-1$, 0, and $+1$, reducing the dependency on the exact remainder value. This generalisation enables high-radix division, where multiple bits of the quotient are determined per iteration. For example, radix-4 division produces two quotient bits per step, and radix-8 or radix-16 extends this to three or four bits respectively [17,18].

The SRT approach can be summarised as follows: the partial remainder is shifted by $lo{g}_2\left(R\right)$ bits, where R is the radix, and a suitable multiple of the divisor is subtracted based on the remainder interval. Quotient digits are then determined using look-up tables (LUTs) or decision logic. Despite reducing the iteration count, high-radix implementations demand extensive table-based quotient selection logic, which grows rapidly with radix. For instance, a radix-16 divider must discriminate among 32 or more overlapping remainder intervals, each requiring a unique control pattern [5].

Modern FPGA and ASIC studies, such as those by Nannarelli and Lang [17] and Sutter et al. [9], show that radix-4 and radix-8 implementations achieve better performance–area trade-offs than higher-radix designs (e.g., radix-16), primarily due to the exponential growth of LUT/MEM complexity. Consequently, many current works have shifted toward hybrid architectures that combine moderate radix with pipeline parallelism.

Parallel to SRT research, digit-recurrence division has evolved as a practical method for embedded processors. The digit-recurrence algorithm uses an iterative refinement strategy where each new remainder depends on the previous remainder and quotient digit [16]. When implemented in hardware, it provides moderate speed with limited area overhead, but its latency still scales linearly with operand width.

With the emergence of reconfigurable computing, numerous researchers have explored FPGA-specific optimisations for division. Early designs relied on serial or sequential division units that consumed minimal logic but exhibited large latency. To improve throughput, parallel and pipelined architectures were proposed [10,14].

For instance, recent FPGA-based divider studies such as those by Mehta [19] and Matthews et al. [20] have shown that SRT and data-dependent designs can deliver significant latency reductions and resource-throughput improvements. These works highlight the importance of deep pipelining and parallel operand processing for high-performance arithmetic units.

Parandeh-Afshar et al. [13] analysed the performance of carry-save arithmetic structures and proposed design principles to improve FPGA performance by reducing the critical-path delay inherent in conventional adder chains. Their findings confirmed that incorporating carry-save adders into arithmetic pipelines yields notable timing improvements without significant logic overhead.

The concept of pipelined division has been applied in different contexts to increase throughput while maintaining acceptable area usage. In a pipelined divider, operands move through multiple hardware stages, with each stage computing a partial quotient and remainder. After an initial latency period, new results appear every clock cycle, making the design suitable for continuous data streams and digital signal processors [21,22].

One direction of research focuses on parallel comparison-based quotient selection, where several possible multiples of the divisor (e.g., B, 2B, 3B) are precomputed and compared with the shifted remainder in parallel [23]. This approach replaces arithmetic subtraction with a set of logical comparisons between the shifted remainder and several pre-computed multiples of the divisor. As demonstrated by Nikmehr et al. [24], implementing comparison-based quotient digit selection in a Radix-4 divider significantly reduces propagation delay and hardware complexity, leading to higher operating frequency and more efficient resource utilisation.

Another related method is the precomputation of divisor multiples, which avoids repetitive arithmetic operations. For example, in [18], a hardware block generated B, 2B, and 3B at the start of the division process, storing them in registers for reuse across pipeline stages. Such preprocessing enables parallelism between quotient selection and remainder update, but still requires separate adder structures for remainder correction.

The performed analysis reveals that although many division algorithms exist, there is still no consensus on an optimal FPGA architecture that simultaneously achieves low latency, small area, and high throughput:

• High-radix SRT dividers reduce iteration count but demand large LUT tables.
• Restoring and non-restoring algorithms are simple but slow.
• Newton–Raphson and Goldschmidt methods are fast but resource-intensive.
• Existing pipelined dividers still depend heavily on binary adders, limiting scalability.

Hence, the main motivation for this study is to design a lightweight pipelined integer divider that uses comparator-based remainder formation and precomputed divisor multiples to minimise arithmetic operations. The novelty lies in the integration of these two techniques within a fully pipelined structure, enabling the computation of two quotient bits per stage with negligible area overhead.

Table 1 provides a summary comparison of representative division architectures reported in the literature, highlighting their key characteristics and hardware performance.

Table 1. Comparative analysis of existing and proposed division architectures.

Approach	Type + Bits/Iter.	Pipeline	Complexity	FPGA Util.	Remarks
Restoring Divider [4]	Restoring, 1 Bit/Iter.	No	Low	Very low	Simple but slow
Non-Restoring [2]	Non-Restoring, 1 Bit/Iter.	No	Low	Low	Removes restoration step
SRT Radix-4 [6]	SRT, 2 Bits/Iter.	Partial	Medium	Medium	Needs LUT; limited pipelining
SRT Radix-8 [17]	SRT, 3 Bits/Iter.	Partial	High	High	Large LUT; area intensive
Newton–Raphson [10]	Multiplicative Iterative	Yes	Very High	High	Requires multipliers
Predicted Restoring [24]	Restoring, 1 Bit/Iter.	Yes	Medium	Medium	Prediction reduces latency
Comparator-Based [7]	SRT, 2 Bits/Iter.	Partial	Medium	Low	Uses comparison logic
Proposed Work	Pipelined Integer, 2 Bits/Stage	Full	Low	<0.3% LUTs	Precomputed multiples; fast and scalable

In summary, prior studies have achieved remarkable progress in accelerating division operations through high-radix, redundant digit, and pipelined schemes. Nevertheless, most designs face either exponential growth in selection logic or heavy reliance on arithmetic units. The proposed architecture bridges this gap by combining parallel comparison logic with pipeline synchronization, resulting in a compact and high-throughput solution suitable for FPGA realization.

By precomputing divisor multiples and employing comparator-driven logic instead of conventional adders, the design eliminates long arithmetic chains, thereby shortening the critical path. This innovation provides a balanced trade-off between speed, area, and scalability, positioning it as a practical alternative for real-time embedded systems, digital signal processors, and arithmetic co-processors.

3. Proposed Architecture and Operational Principle

3.1. Overall Structure and Concept

The proposed pipelined integer divider is designed for FPGA implementation and aims to increase computational throughput while maintaining minimal hardware utilisation. The core principle is the precomputation of divisor multiples—specifically B, 2B, and 3B, along with their bitwise inversions. These values are generated once and stored in dedicated registers to be reused at each pipeline stage.

At every stage, the current partial remainder is compared against these precomputed multiples to determine which value should be subtracted. This approach allows the formation of two quotient bits and one updated remainder per clock cycle, effectively halving the number of iterations compared to conventional one-bit dividers.

The overall structure of the divider (Figure 1) consists of three main functional blocks:

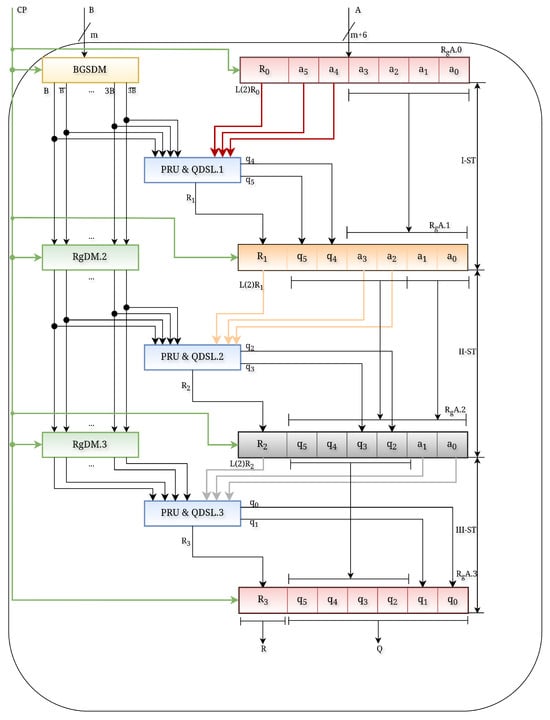
Figure 1. General structural diagram of the three-stage pipelined divider with a divisor multiple generation block.

• BGSDM (Block for Generating and Storing Divisor Multiples): Generates B, 2B, 3B, and their inverted forms at the start of each division operation and supplies them to all pipeline stages;
• PRU–QDSL (Partial Remainder and Quotient Digit Selection Logic): Performs comparison-based selection of divisor multiples, remainder correction, and generation of two quotient bits per cycle;
• Register Arrays (RgDM and RgA): Provide synchronisation and data transfer between pipeline stages and accumulate partial results to form the final quotient and remainder.

3.2. Pipeline Algorithm Description

In the proposed architecture, the division process is organised according to a pipeline principle, in which the computation is decomposed into a sequence of completed stages. Each stage is executed by the PRU–QDSL logic blocks operating in parallel. This structure enables the simultaneous processing of multiple operand pairs $(A_i,B_i)$ and significantly increases the overall throughput of the divider.

The division process follows a synchronous pipeline model where each stage performs a fixed portion of the computation defined by the digit-recurrence relation. At the beginning of every clock cycle, the partial remainder obtained at stage $(i-1)$, denoted as $R_{i-1}$, is shifted left by two bit positions $(R_{i-1}\ll 2)$ and compared with the precomputed multiples of the divisor. Based on this comparison, the quotient-digit selection logic generates the coefficient

$$k_i\in \{0,1,2,3\},$$

which determines the multiple of the divisor to be subtracted. The new remainder is then computed as:

$$R_i=(R_{i-1}\ll 2)-k_i·B.$$

(1)

Subtraction is implemented using bitwise inversion and an increment operation (two’s-complement form), eliminating the need for a full binary adder and reducing hardware complexity.

In radix-4 digit-recurrence division, the recurrence in (1) inherently maintains the intermediate remainder within the bounded interval

$$R_i\in [-4B,4B],$$

which guarantees that the remainder never exceeds the allowable range. This property follows directly from the quotient-digit selection mechanism: the chosen coefficient $k_i$ always ensures that the updated remainder stays within the prescribed limits. Consequently, overflow of $R_i$ is theoretically impossible, and no additional corrective procedures such as normalisation or scaling are required.

Simultaneously, the quotient-bit pair $(q_{i+1},q_i)$ corresponding to the value of $k_i$ is generated and stored in the accumulator register $RgA$. All stages of the pipeline operate in parallel. For example, while the first stage processes new input operands $(A_3,B_3)$, the second and third stages continue the computations for $(A_2,B_2)$ and $(A_1,B_1)$, respectively. After the pipeline is filled, one complete quotient–remainder pair is produced on every rising clock edge.

3.2.1. Synchronization and Data Transfer

At every clock cycle, the results produced at the i-th stage—the remainder $R_i$ and the corresponding quotient-bit pair $(q_{i+1},q_i)$—are transferred to the $(i+1)$-th stage through pipeline buffer registers. This mechanism ensures continuous operation of the divider: while the first stage begins processing a new operand pair, the remaining stages continue processing the previously supplied data. Synchronous operation of all stages is maintained by clock signals distributed simultaneously across the entire pipeline.

3.2.2. Functional Structure and Computational Stages

The functional diagram of the pipeline (Figure 1) consists of three PRU–QDSL units (PRU–QDSL.1–PRU–QDSL.3), as well as the block responsible for generating and storing the divisor multiples (BGSDM). In the BGSDM block, the required multiples $3B$ and $\overline{3B}$, $2B$ and $\overline{2B}$, B and $\overline{B}$ are precomputed and then transferred to the registers RgDM.1–RgDM.3. The pipeline supports division of a sequence of $(m+6)$-bit numbers $A_1,A_2,A_3,\dots ,A_L$ by m-bit divisors $B_1,B_2,B_3,\dots ,B_L$. At the output, the divider produces remainder–quotient pairs $(R_1,Q_1),(R_2,Q_2),\dots ,(R_L,Q_L)$.

3.2.3. Operation of Pipeline Stages

To initialize the pipeline, the intermediate remainder $R_0$ is formed using the most significant bits of the dividend. In the presented example, the upper six bits of A constitute the initial remainder ($R_0=A[11:6]$), while the remaining lower bits are stored in the RgA register. During each pipeline stage, the remainder is shifted left by two positions ($R\ll 2$), and the next two bits of the dividend are supplied from the RgA register ($a_5{a}_4$, then $a_3{a}_2$, and finally $a_1{a}_0$), ensuring correct bit-aligned reconstruction of the remainder.

This mechanism corresponds to the structure depicted in Figure 8, where the four-bit RgA sub-register is preloaded with the lower dividend bits and provides them sequentially during the pipeline operation. This clarification makes explicit how the missing lower bits of the dividend are incorporated during each left-shift step of the remainder generation process. The comparison of these values with the precomputed divisor multiples produces the next remainder $R_1$ and the corresponding quotient bits $q_5{q}_4$. At the first stage, the shifted remainder $(R_0\ll 2)$ is compared with the stored multiples. For instance, for $(A_1,B_1)$ with $R_0^1=22$, the comparison selects $2B_1=70$, resulting in a new remainder $R_1^1=19$ and two quotient bits $(q_5^1,q_4^1)=(1,0)$. It should also be noted that the initial remainder, formed from the most significant bits of the dividend, naturally satisfies the condition. This ensures that the division process starts within the valid operational range defined for radix-4 remainder recurrence.

At the second stage (PRU–QDSL.2), the new remainder $R_2$ and the quotient bits $q_3{q}_2$ are computed based on $R_1\ll 2$ and the bits $a_3{a}_2$.

At the third stage (PRU–QDSL.3), the remainder $R_2\ll 2$ together with the bits $a_1{a}_0$ from the register RgA.2 forms the final remainder $R_3$ and the quotient bits $q_1{q}_0$.

3.2.4. Clocking Organization

The operation of the divider is controlled by clock signals $C_1,C_2,C_3$, and so on. On the rising edge of each clock pulse, the comparison and subtraction operations are executed, while on the falling edge the data are transferred between registers.

At clock $C_1$, the pair $(A_1,B_1)$ is processed; at $C_2$, the pair $(A_2,B_2)$ is processed while $(A_1,B_1)$ advances to the next pipeline stage. At $C_3$, each stage of the pipeline performs its corresponding operation: the first stage processes $(A_3,B_3)$, the second—$(A_2,B_2)$, and the third—$(A_1,B_1)$. After the pipeline is fully filled, a new remainder–quotient pair $(R_i,Q_i)$ is generated on every clock cycle, ensuring a continuous flow of results.

Thus, the proposed pipelined divider achieves efficient parallel data processing through precomputation of divisor multiples, synchronous data transfer between stages, and a modular computational structure. This organization increases performance while maintaining minimal hardware overhead and high computational accuracy.

Figure 1 illustrates the overall structural diagram of the three-stage pipelined divider, which includes three PRU–QDSL blocks connected to the BGSDM block and synchronized through register arrays.

3.2.5. Illustrative Example

Let us consider an example illustrating the execution of division operations in the three-stage pipeline for the operand pairs $(A_1,B_1)$, $(A_2,B_2)$, and $(A_3,B_3)$.

Let

$$A_1={1439}_{10},A_2={2139}_{10},A_3={2289}_{10},$$

For each divisor, the corresponding multiples are computed:

$$B_1={\mathrm{100,011}}_2={35}_{10},2B_1={70}_{10},3B_1={105}_{10};$$

$$B_2={\mathrm{110,001}}_2={49}_{10},2B_2={98}_{10},3B_2={147}_{10};$$

$$B_3={\mathrm{100,111}}_2={39}_{10},2B_3={78}_{10},3B_3={117}_{10}.$$

The initial remainders are formed from the most significant bits of the dividends:

$$R_0^{\left(1\right)}={22}_{10},R_0^{\left(2\right)}={33}_{10},R_0^{\left(3\right)}={35}_{10}.$$

For clarity, all computations are presented in decimal notation.

These results confirm the correctness of the remainder reconstruction and the quotient-digit generation.

The detailed step-by-step computation for this illustrative example is summarised in Table 2, and these results confirm the correctness of the remainder reconstruction and quotient-digit generation.

Table 2. Step-by-step computation for three-stage pipeline divider.

CP Stage	(A1, B1)	(A2, B2)	(A3, B3)
CP1	$\begin{array}{cc}\hfill C_0^1& =L\left(2\right)R_{10}+a_5^1{a}_4^1=89\hfill \\ \hfill R_1^1& =89-2B_1=19\hfill \\ \hfill q_5^1& =1,q_4^1=0\hfill \end{array}$	–	–
CP2	$\begin{array}{cc}\hfill C_1^1& =4R_1^1+a_3^1{a}_2^1=79\hfill \\ \hfill R_2^1& =79-2B=9\hfill \\ \hfill q_3^1& =1,q_2^1=0\hfill \end{array}$	$\begin{array}{cc}\hfill C_0^2& =4R_0^2+a_6^2{a}_6^2=133\hfill \\ \hfill R_1^2& =133-2B_2=35\hfill \\ \hfill q_5^2& =1,q_4^2=0\hfill \end{array}$	–
CP3	$\begin{array}{cc}\hfill C_2^1& =4R_2^1+a_1^1{a}_0^1=39\hfill \\ \hfill R_3^1& =39-B_1=4\hfill \\ \hfill q_1^1& =0,q_0^1=1\hfill \end{array}$	$\begin{array}{cc}\hfill C_1^2& =4R_1^2+a_3^2{a}_2^2=140\hfill \\ \hfill R_2^2& =140-2B_2=42\hfill \\ \hfill q_3^2& =1,q_2^2=0\hfill \end{array}$	$\begin{array}{cc}\hfill C_0^3& =4R_0^3+a_5^3{a}_4^3=143\hfill \\ \hfill R_1^3& =143-3B_3=26\hfill \\ \hfill q_5^3& =1,q_4^3=1\hfill \end{array}$
CP4	–	$\begin{array}{cc}\hfill C_2^2& =4R_2^2+a_1^2{a}_0^2=169\hfill \\ \hfill R_3^2& =169-3B_2=22\hfill \\ \hfill q_1^2& =1,q_0^2=0\hfill \end{array}$	$\begin{array}{cc}\hfill C_1^3& =4R_1^3+a_3^3{a}_2^3=104\hfill \\ \hfill R_2^3& =104-2B_3=27\hfill \\ \hfill q_3^3& =1,q_2^3=1\hfill \end{array}$
CP5	–	–	$\begin{array}{cc}\hfill C_2^3& =4R_2^3+a_1^3{a}_0^3=105\hfill \\ \hfill R_3^3& =105-2B_3=27\hfill \\ \hfill q_1^3& =1,q_0^3=0\hfill \end{array}$
CP6	–	–	–

From Figure 1 it is straightforward to observe that the propagation delay of the PRU–QDSL block can be expressed as:

$$t_{\mathrm{PRU}-\mathrm{QDSL}}=t_{\mathrm{comp}}+5t_{\mathrm{LE}}+t_{\mathrm{add}},$$

(2)

where

• $t_{\mathrm{comp}}$ is the delay of the comparison logic;
• $t_{\mathrm{LE}}$ is the propagation delay of a logic element;
• $t_{\mathrm{add}}$ is the time required for the code summation (increment–inversion).

Implementation and Verification The architecture was described in Verilog HDL and synthesized using the Xilinx ISE Design Suite 14.4 (Xilinx, Inc., San Jose, CA, USA) for a Xilinx Artix-7 (XC7A100T-1CSG324C) FPGA. The synthesized RTL schematic confirmed correct interaction among all logical modules—from multiple generation in the BGSDM block to partial remainder and quotient formation in PRU–QDSL units, synchronized by the register arrays RgDM and RgA.

Post-synthesis functional simulation validated the timing and logical correctness of the divider. The pipeline produced stable outputs after three clock cycles, matching the theoretical results demonstrated in the example above. This confirms that the proposed comparator-based pipeline architecture correctly performs integer division with continuous throughput and minimal hardware overhead.

3.3. Generation of Divisor Multiples (BGSDM)

One of the key elements of the proposed architecture is the BGSDM (Block for Generating and Storing Divisor Multiples). The operation of the divider begins with the generation of the divisor multiples. The BGSDM module computes and stores the following values:

• $B_1$ = B;
• $B_2$ = 2B (obtained by a one-bit left shift);
• $B_3$ = 3B = 2B + B;
• $\overline{B_1},\overline{B_2},\overline{B_3}$–inverted forms.

All calculated values are stored in registers and passed to the subsequent pipeline stages through the $RgDM$ register block. Thus, the multiples of the divisor are generated only once—at the initial stage of division—which eliminates redundant arithmetic operations during each clock cycle.

The BGSDM block was implemented in the Xilinx ISE Design Suite 14.4 using the Verilog HDL. At the RTL level, it represents a combination of three cascaded modules that generate both the divisor multiples and their inverted values. The resulting schematic reflects both the arithmetic part (shifts and additions) and the bit inversion logic.

Figure 2 illustrates the structural diagram of the BGSDM block obtained after HDL synthesis.

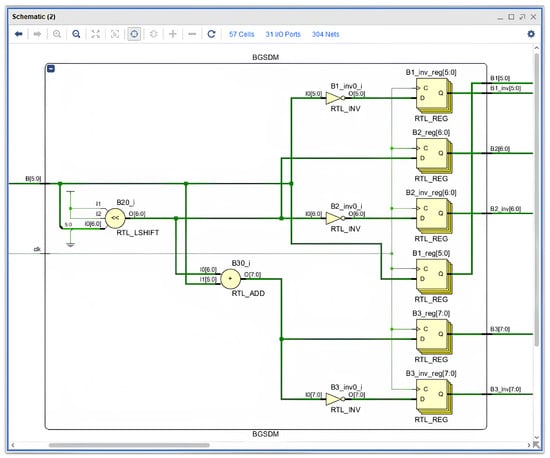
Figure 2. Internal structure of the BGSDM block: generation of the multiples B, 2B, 3B and their inverted forms using shift, addition, and inversion operations.

The BGSDM block operates synchronously with the overall pipeline clock frequency. All generated values $B_1$, $B_2$, $B_3$ and their inverted forms are stored in the RgDM registers and distributed to all stages of the divider. Thus, at each clock cycle, the PRU–QDSL unit receives precomputed data for comparison, eliminating the need for repetitive calculations and ensuring a constant response time.

A key feature of this implementation is the absence of critical arithmetic chains. Since shift and inversion operations introduce minimal delay, the BGSDM block does not increase the critical path of the device, there by maintaining a high operating frequency for the entire divider.

3.4. Partial Remainder Unit and Quotient Digit Selection Logic (PRU–QDSL)

After the preliminary generation of divisor multiples in the BGSDM block, the computational part of the divider is executed within the PRU–QDSL (Partial Remainder Unit and Quotient Digit Selection Logic) module. This block serves as the main computational unit of the pipelined divider, performing a comparison of the current partial remainder with the divisor multiples and generating two quotient bits per clock cycle.

Each PRU–QDSL module operates as an independent pipeline stage and consists of three interconnected sub-blocks:

• BQC (Block of Quotient Comparison)—performs parallel comparison of the remainder with the multiples B, 2B, 3B;
• BRG (Block of Remainder Generation)—generates a new partial remainder based on the selected multiple;
• QDGB (Quotient Digit Generation Block)—determines two quotient bits ($q_1$, $q_0$) depending on the comparison result.

Thus, each PRU–QDSL block implements one iteration of the division algorithm, in which two quotient bits and an updated remainder are computed per clock cycle.

Figure 3 shows the implementation of the PRU–QDSL module developed in the Xilinx ISE Design Suite 14.4 after HDL synthesis. As illustrated, the module includes three main branches: the comparison block (BQC), the remainder correction block (BRG), and the logic section for quotient digit generation (QDGB).

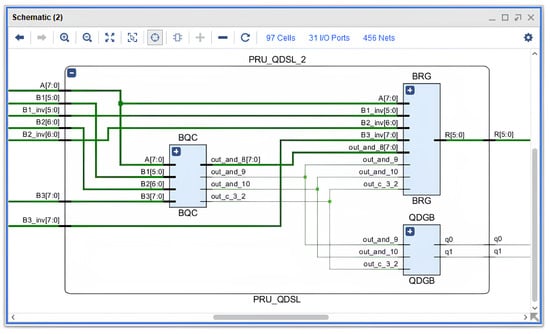
Figure 3. Functional structure of the PRU–QDSL block, consisting of three components: BQC (comparison), BRG (remainder reconstruction), and QDGB (quotient bit generation).

The main computational part of the divider is implemented in the PRU–QDSL block, which simultaneously performs the following operations:

• Comparison of the current partial remainder with the divisor multiples $(B,2B,3B)$;
• Determination of two quotient bits $(q_1,q_0)$ depending on the range in which the remainder falls;
• Updating of the current remainder through logical correction.

Mathematically, the process at the i-th step can be expressed as follows:

$$R_i=(R_{i-1}\ll 2)-k_i·B,$$

(3)

$$Q_i=f\left(k_i\right),$$

(4)

where $k_i\in \{0,1,2,3\}$ is the selected divisor multiple determined by the comparison logic. Thus, each pipeline stage generates two quotient bits per clock cycle, reducing the total number of computation stages.

In the Verilog implementation, the PRU–QDSL logic is built using a combination of simple comparison modules and multiplexers. Each sub-block is designed as an independent HDL module with clearly defined input and output interfaces, ensuring modularity and reusability when scaling the architecture.

A distinctive feature of the architecture is the absence of classical adders within the pipeline stages—instead, logical comparison and inversion operations are employed. This approach reduces the critical path length and increases the overall clock frequency of the device.

The PRU–QDSL module was simulated using Xilinx ISim, confirming the correct generation of two quotient bits and a new remainder at each clock cycle. Furthermore, synthesis on a Xilinx Artix-7 FPGA demonstrated low resource utilization—fewer than 60 LUTs and 45 flip-flops per pipeline stage.

3.5. Block of Quotient Comparison (BQC)

The BQC (Block of Quotient Comparison) is a key element of the computational logic in each pipeline stage of the divider. Its primary function is to determine the range in which the current partial remainder lies and, consequently, to select the multiplier coefficient $k_i$ used to compute the next remainder and quotient digits.

Once the BGSDM block has generated the divisor multiples B, $2B$, and $3B$, and the PRU–QDSL module has received the current partial remainder $R_{(i-1)}$, the BQC block performs a parallel comparison of the value $(R_{(i-1)}\ll 2)$ with these multiples.

The comparison results define the value of coefficient $k_i$, which can take one of four possible values in the range from 0 to 3.

The operation logic of the block is described by the following set of conditions:

$$k_i=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}(R_{(i-1)}\ll 2)<B,\hfill \\ 1,\hfill & \mathrm{if}B\le (R_{(i-1)}\ll 2)<2B,\hfill \\ 2,\hfill & \mathrm{if}2B\le (R_{(i-1)}\ll 2)<3B,\hfill \\ 3,\hfill & \mathrm{if}(R_{(i-1)}\ll 2)\ge 3B.\hfill \end{array}\right.$$

(5)

As a result, four state signals $S_0$, $S_1$, $S_2$, and $S_3$ are generated at the output, representing one-bit flags (one-hot encoding), each corresponding to a specific comparison range. These signals are subsequently used by the BRG and QDGB blocks to select the appropriate inverted multiple and to generate the quotient digits.

The BQC module was implemented in Verilog HDL using a combination of logical if–else operators and comparison expressions (≥, ≤). The design was synthesised in the Xilinx ISE Design Suite 14.4, and RTL analysis results showed that the block primarily consists of comparator cells and multiplexers, without any arithmetic adders (Figure 4). This approach ensures minimal signal propagation delay, which is particularly important for high-frequency pipelined systems.

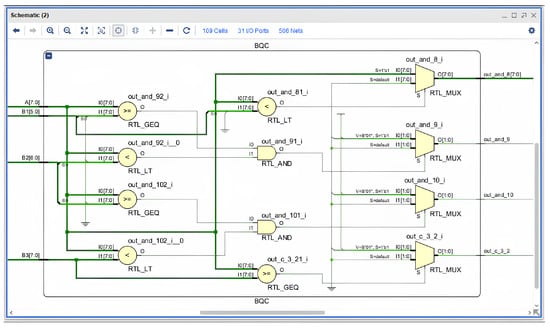
Figure 4. Implemented structural diagram of the BQC (Block of Quotient Comparison) in the Xilinx ISE Design Suite environment.

During simulation, it was confirmed that the block correctly determines the multiplier coefficient $k_i$ for all possible ranges of partial remainders. The circuit’s response time to a change in the input remainder does not exceed 4.8 ns, allowing the module to operate at clock frequencies above 200 MHz. Due to its low hardware complexity (approximately 20 LUTs and 10 flip-flops), the BQC block can be efficiently scaled with an increase in the divisor bit width.

Furthermore, the block’s structure supports modular composition of multiple comparators, enabling transition to dividers with higher radices (radix-8 or radix-16) without modifying the core division logic. This property represents one of the key advantages of the proposed architecture compared to conventional SRT implementations, where increasing the radix typically requires redesigning the quotient-digit selection table.

After determining the remainder range and selecting the coefficient $k_i$, the corresponding signals $S_0$ − $S_3$ are transmitted to the BRG block, where the new partial remainder is generated.

3.6. Block of Remainder Generation (BRG)

The BRG (Block of Remainder Generation) performs the computation of a new partial remainder at each pipeline stage using the comparison results obtained from the BQC block.

The main function of the BRG is to carry out the subtraction of the selected divisor multiple $(k_i·B)$ from the current shifted remainder $(R_{i-1}\ll 2)$. To avoid the use of full adders and subtractors, the design employs two’s complement arithmetic, which allows subtraction to be implemented through logical inversion followed by the addition of one.

Formally, the process can be described by the following equation:

$$R_i=(R_{i-1}\ll 2)+k_i·B=(R_{i-1}\ll 2)+{(k_i·\overline{B})}_{\mathrm{inv}}+1,$$

(6)

where ${(k_i·\overline{B})}_{\mathrm{inv}}$ represents the bitwise inversion of the selected multiple, and the addition of 1 implements the two’s complement operation.

This method of remainder formation provides two key advantages:

• Minimization of the critical path. The inversion and increment operations are executed in parallel and exhibit low logical depth.
• Absence of complex adders. The design avoids carry-chain structures typical of conventional subtraction circuits, which allows for a higher operating frequency.

Figure 5 presents the structural diagram of the BRG block implemented in the Xilinx ISE Design Suite 14.4, synthesized from the Verilog description.

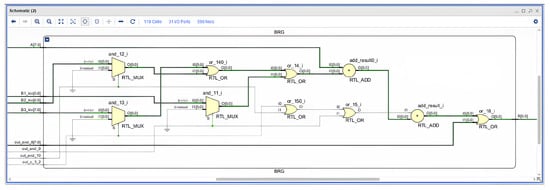
Figure 5. Structural diagram of the BRG block: selection and addition of the inverted multiple for generating the new remainder.

The operating algorithm of the block is as follows:

• The partial remainder $R_{i-1}$, pre-shifted two bits to the left $(R_{i-1}\ll 2)$, is applied to the input.
• Based on the signals $S_0$−$S_3$ received from the BQC block, the corresponding inverted multiple $(k_i·\overline{B})$ is selected from the set generated by the BGSDM block.
• The bitwise addition of $(R_{i-1}\ll 2)$ and $(k_i·\overline{B})$ is performed with the addition of 1.
• The result is passed to the RgA register and used in the next pipeline stage as the new partial remainder $R_i$.

This solution is fully compatible with pipelined data processing: at each clock cycle, a new remainder is generated, and the process does not require feedback loops or additional iterations. Since all operations are completed within a single clock cycle, the total delay of the BRG block is limited to the delay of the multiplexer and the small increment logic network.

The Verilog HDL implementation of the module features a compact structure-approximately 25 LUTs and 15 registers for a 6-bit word length. Testing on a Xilinx Artix-7 FPGA showed that the signal propagation time within the block does not exceed 6 ns, allowing its use in high-speed pipelined systems operating at frequencies up to 160–170 MHz.

Thus, the BRG block is a critical component of the entire architecture. It can ensure accurate remainder restoration with minimal hardware overhead while maintaining data consistency across pipeline stages. The output $R_i$ of the BRG is passed to the QDGB block, where two quotient bits are determined based on the coefficient $k_i$.

3.7. Quotient Digit Generation Block (QDGB)

The QDGB (Quotient Digit Generation Block) completes the computational cycle of each pipeline stage. Its primary function is to convert the comparison results received from the BQC block into the corresponding two quotient bits $(q_1,q_0)$, which are then passed to the RgA register for accumulation of the full quotient value Q.

As described earlier, the BQC block generates four state signals $S_0,S_1,S_2,S_3$, each activated when the current remainder $(R_{i-1}\ll 2)$ falls within a specific range between the divisor multiples (B, 2B, 3B). These signals serve as one-bit range indicators and determine which multiplicative coefficient $k_i$ is used during the given iteration.

The operation logic of the QDGB module consists of converting the signals $S_0-S_3$ into the binary value of coefficient $k_i$, which allows for two quotient bits to be obtained. The functional correspondence can be expressed in the following Table 3:

Table 3. Mapping from active signal to ratio $k_i$ and quotient bits $(q_1,q_0)$.

Active Signal	Ratio ${\mathit{k}}_{\mathit{i}}$	Quotient Bits $({\mathit{q}}_1,{\mathit{q}}_0)$
$S_0=1$	0	$(0,0)$
$S_1=1$	1	$(0,1)$
$S_2=1$	2	$(1,0)$
$S_3=1$	3	$(1,1)$

Thus, each set of comparison signals is directly converted into a pair of quotient bits, without intermediate computations or lookup tables typical of classical SRT dividers.

This approach ensures high performance and low utilization of logic resources. The QDGB block was implemented in Verilog HDL as a purely combinational logic circuit, using a minimal set of assign statements and logical OR expressions. Synthesis in the Xilinx ISE Design Suite 14.4 showed that the block structure includes approximately 8 LUTs and contains no flip-flops, since the block is entirely combinational.

This makes it one of the simplest elements in terms of hardware complexity within the entire divider architecture. Figure 6 presents the structural diagram of the QDGB block obtained after HDL synthesis in the Xilinx ISE environment.

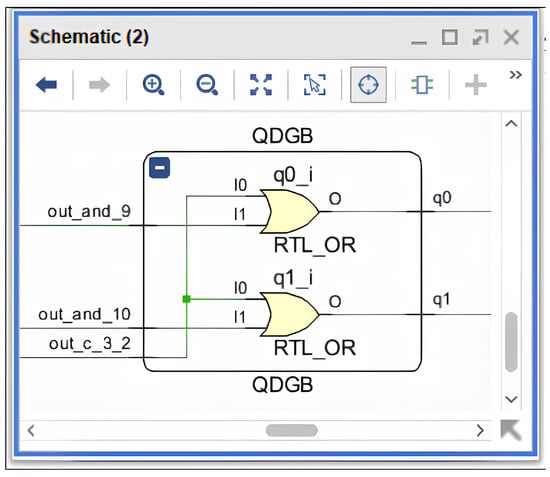
Figure 6. Logical structure of the QDGB block implementing direct mapping of comparison signals into two quotient bits.

The output signals ($q_1,q_0$) from the QDGB block are sent to the RgA register, where they are combined with the previous results to form the complete binary quotient code. Since each pipeline stage generates two bits per clock cycle, the divider begins producing valid division results for new input data every cycle after the pipeline is filled.

Timing diagrams confirmed the correct formation of the ($q_1,q_0$) combinations across different remainder ranges, as well as synchronous output updates with the other PRU–QDSL blocks. Post-synthesis simulation showed that the maximum signal propagation delay is approximately 1.2 ns, making the QDGB block practically negligible in the overall critical path of the divider.

Thus, the QDGB module completes the computational cycle of each pipeline stage, providing fast and accurate quotient-bit generation with minimal hardware cost.

In the next section, we will examine the organization of the RgDM and RgA registers, which ensure data synchronization between stages and the formation of the pipelined data flow.

3.8. Organization of Pipeline Registers (RgDM and RgA)

The operation of the proposed divider is achieved not only through the parallel generation of multiples and simplified computation logic, but also through the well-designed organisation of the pipeline registers. The RgDM and RgA register blocks ensure data transfer between the divider stages, synchronisation of intermediate results, and the formation of a stable pipelined data flow. Each pipeline stage utilises two types of registers:

• RgDM (Remainder and Divisor Multiples Register)—stores the current partial remainder and the set of divisor multiples (B, 2B, 3B) along with their inverted forms. These registers prevent data corruption during interstage transfers and synchronise the operation of all PRU–QDSL modules.
• RgA (Accumulator Register)—accumulates partial results, ensuring sequential formation of the final quotient. At each clock cycle, the two new quotient bits ($q_1,q_0$) generated by the QDGB block are written into the RgA register, shifting toward the lower bits.

Figure 7 shows the structural organisation of the register blocks, illustrating the interaction of PRU–QDSL modules between pipeline stages.

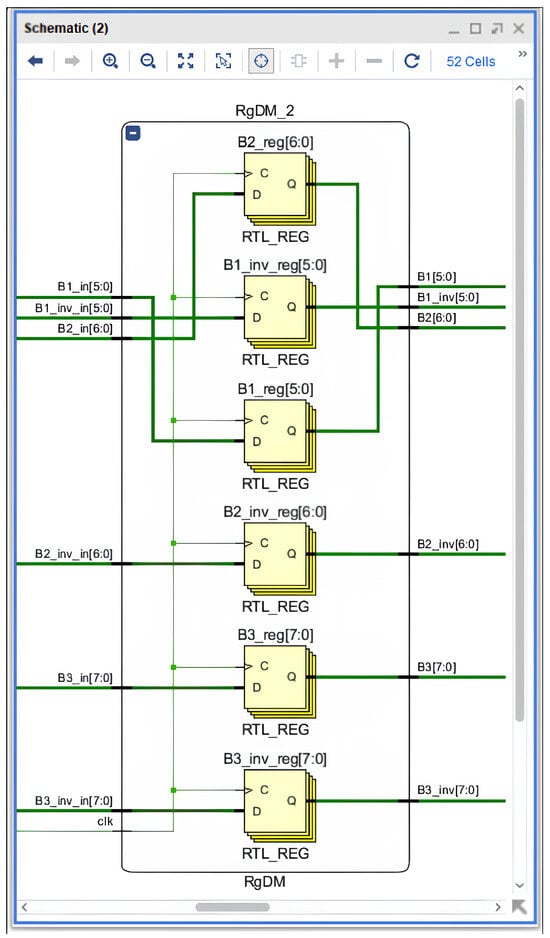
Figure 7. Structure of the RgDM register block in the three-stage pipelined divider.

Each register is synchronised with the common clock signal clk and includes an active reset signal that initialises all values upon device startup. Data transfer between pipeline stages occurs strictly synchronously: at the moment of the clock pulse $t_i$, all output values of the current stage (remainder $R_i$, quotient bits $q_1,q_0$) are written into the corresponding registers and become inputs for the next stage.

Quotient accumulation cascades: $Rg{A}_1,Rg{A}_2,Rg{A}_3$ After synchronisation of the divisor multiples in the RgDM register block, the partial computation results from each PRU–QDSL module are passed into the quotient accumulation cascade RgA. These cascades collect and organise the pairs of bits ($q_1,q_0$) generated at each pipeline stage. Each block ($Rg{A}_1,Rg{A}_2,Rg{A}_3$) operates synchronously with the clock signal clk, performing local accumulation of two quotient bits and adding them to the previously obtained result. To illustrate the internal structure of a single accumulation stage, Figure 8 presents a general RTL-level schematic of the RgA block. This schematic demonstrates how the incoming pair of quotient bits is combined with the partial accumulated value using the RTL-level adder, after which synchronous registers capture the updated result. The same architectural template is reused in all three cascade blocks—$Rg{A}_1$, $Rg{A}_2$, $Rg{A}_3$—with differences only in the specific pair of quotient bits being processed and the position within the pipeline.

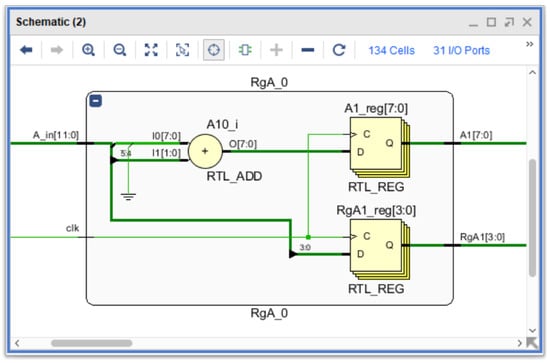
Figure 8. General structural diagram of a single RgA accumulation stage (Xilinx ISE, RTL).

The $Rg{A}_1$ block (Figure 9) implements the first stage of accumulation and receives the higher-order pair of quotient bits, denoted as ($q_4,q_5$). Within the circuit, an RTL_ADD adder is used to combine the incoming quotient bits with the partial result from the previous iteration. The result is stored in two synchronous registers, A2_reg and RgA2_reg, ensuring data capture at every clock edge. This approach eliminates cumulative errors during multi-cycle division and guarantees stable phase synchronisation.

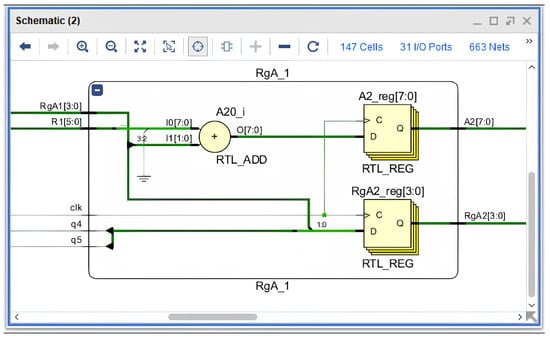
Figure 9. Structural diagram of the $Rg{A}_1$ block implementing the first stage of quotient-bit accumulation (Xilinx ISE, RTL).

$Rg{A}_2$ block. The $Rg{A}_2$ block (Figure 10) serves as an intermediate stage and processes the next pair of bits ($q_2,q_3$) received from the second PRU–QDSL stage. Functionally, it replicates the architecture of $Rg{A}_2$, but operates with data arriving after one pipeline iteration. At the rising edge of the clk signal, the registers capture the new data, and the adder performs a shift and insertion of the lower bits into the accumulator. Thus, the output of $Rg{A}_2$ represents the combined four higher-order bits of the quotient ($q_5,q_4,q_3,q_2$).

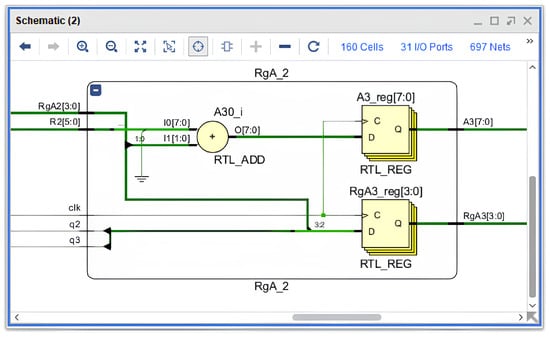
Figure 10. Structural diagram of the $Rg{A}_2$ block (Xilinx ISE, RTL).

$Rg{A}_3$—third accumulation stage (Figure 11). The final cascade $Rg{A}_3$ completes the formation of the full binary quotient word. The schematic clearly shows two registers—Q_reg and R_reg, both synchronised with the clock signal clk. The input receives the lower pair of bits ($q_0,q_1$) and the partial remainder $R_3$. The registers capture the final values Q[5:0] and R[5:0], which represent the quotient and remainder results, respectively.

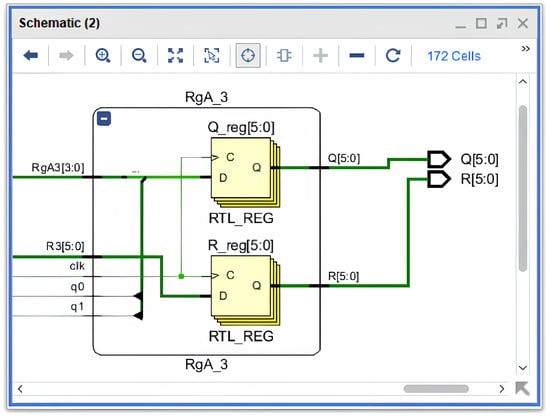
Figure 11. Structural diagram of the $Rg{A}_3$ block implementing the final accumulation of quotient bits and remainder registration (Xilinx ISE Design Suite, RTL).

Synthesis of the RgDM and RgA blocks on the Xilinx Artix-7 FPGA demonstrated the use of fewer than 80 flip-flops and approximately 40 LUTs for the entire register cascade, confirming their low hardware cost. Thus, the register organisation ensures stable pipeline operation and guarantees that new data pairs can be fed into the device input at every clock pulse without synchronisation conflicts. This property enables the implementation of a fully continuous computation flow while maintaining the high operating frequency of the divider.

4. Results and Discussion

4.1. Complete Structural Implementation of the Device

After the design and verification of individual modules (BGSDM, PRU–QDSL, RgDM, $Rg{A}_{1–3}$), all components were integrated into a unified pipelined architecture. Figure 12 shows the final structural diagram of the device implemented in the Xilinx ISE Design Suite environment.

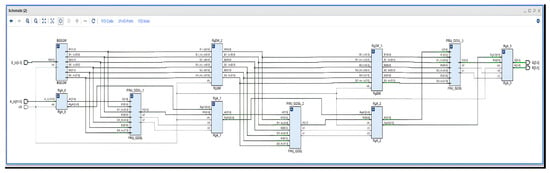
Figure 12. Final structural diagram of the three-stage pipelined divider implemented in the Xilinx ISE Design Suite environment.

As shown, three sequentially connected PRU–QDSL stages generate two-bit quotient segments at each clock cycle. Between them, the RgDM and RgA register blocks provide temporal synchronisation and intermediate data transfer. The BGSDM block generates and stores the divisor multiples (B, 2B, 3B) and their inverses, which are required for comparison operations at each pipeline level.

This structure enables division to be completed within three clock cycles after pipeline filling, with each subsequent result produced on every clock pulse, confirming the efficiency of the implemented design.

4.2. Timing Characteristics

To evaluate the dynamic parameters, a post-synthesis simulation of the device was performed. The timing diagram (Figure 13) shows the characteristic signals of the dividend A, divisor B, intermediate remainders $R_i$, and the output quotient Q. It can be observed that after three clock cycles required for pipeline filling, the device begins producing correct results at every clock cycle, ensuring continuous throughput and high performance.

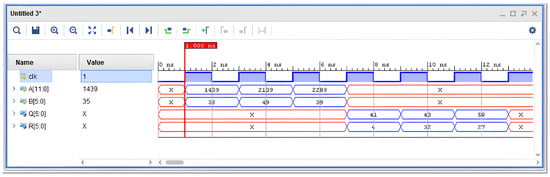
Figure 13. Timing diagram of remainder and quotient-bit propagation through the three pipeline stages.

In the initial phase of the simulation (the first three clock cycles), the RgDM and RgA registers undergo initialisation and pipeline filling. During this period, the values of Q and R remain undefined (X), corresponding to the absence of a valid output result. Starting from the fourth clock cycle, the device stabilises and begins producing correct quotient and remainder values at each clock pulse. This confirms the proper functioning of the pipelining mechanism: each stage simultaneously processes its own data set, ensuring a continuous stream of results without idle cycles.

The timing diagram shows that when a sequence of input values A = 1439, 2139, 2289 and B = 35, 49, 39 is applied, the device generates the corresponding outputs Q = 41, 43, 58 and R = 4, 32, 27. Each new result appears one clock cycle after the previous one, which corresponds to a three-stage pipeline with two-bit quotient processing per cycle.

Thus, after an initial latency of three clock cycles, the device reaches a steady-state operating mode in which a complete pair of output values (Q, R) is produced at every clock pulse. This demonstrates the high throughput of the circuit and confirms the efficiency of the proposed architecture.

4.3. Synthesis Results and Performance Analysis

The project synthesis was carried out in Xilinx ISE 14.7 for a device from the Artix-7 family (XC7A35T). The synthesis results of the proposed divider obtained in the Xilinx ISE environment are summarised in Table 4.

Table 4. Synthesis results of the proposed divider in the Xilinx ISE environment.

Resource	Used	Available	Utilization, %
LUT	144	63,400	0.23
LUTRAM	2	19,000	0.01
FF	122	126,800	0.10

As can be seen from the presented results, the proposed division unit demonstrates an extremely low level of hardware resource utilisation, indicating a high degree of architectural optimisation. To evaluate the relative efficiency of the proposed solution, it is reasonable to compare the obtained parameters with the results of other known implementations of similar divider architectures. A comprehensive analysis of the obtained synthesis results shows that the proposed pipelined divider achieves a strong balance between performance and hardware efficiency when compared to existing FPGA-based implementations. The design operates at approximately 208 MHz, which is slightly below the 736 MHz reported by Wei [25], yet remains comparable to Patankar’s architecture [26] (285 MHz) while requiring significantly fewer hardware resources—around 144 LUTs versus the 266–800 LUT range in prior designs.

The Area–Delay Product (ADP) of the proposed architecture is about $6.9\times {10}^2$ LUT·T_clk, placing it close to the efficiency levels demonstrated by Wei’s ($1.37\times {10}^2$ LUT·T_clk) and Patankar’s ($0.93\times {10}^3$ LUT·T_clk) implementations and confirming the resource-efficient nature of our approach.

The pipeline structure ensures a latency of only three cycles and provides a steady-state throughput of one result per clock period, demonstrating that high-performance division can be achieved without excessive architectural overhead.

Furthermore, the internal submodules responsible for generating quotient digits—BQC and QDGB—exhibit propagation delays of just 4.8 ns and 1.2 ns, respectively. These delays have a negligible impact on the overall critical path, confirming the suitability of the architecture for high-speed FPGA operation.

Overall, the proposed divider achieves an effective compromise between hardware complexity and computational speed, offering a competitive and efficient solution for modern FPGA-based arithmetic systems.

4.4. Discussion

The proposed divider architecture demonstrates several notable advantages arising from the combined use of precomputed multiples of the divisor, comparator-based remainder generation, and a fully pipelined multi-stage structure. These design choices significantly minimise arithmetic complexity inside the pipeline, resulting in reduced use of LUT resources and allowing the architecture to sustain a high operational frequency.

A key observation is that the elimination of full binary adders from each iteration stage does not negatively affect precision or convergence of the division process. Instead, the remainder selection logic based on simple comparators provides a lightweight yet reliable mechanism for quotient-digit determination. This sharply contrasts with SRT dividers and non-restoring architectures, which typically rely on multi-operand adders, lookup tables, or correction steps that increase latency and hardware footprint.

The two-bit-per-cycle quotient generation scheme further enhances throughput without introducing substantial control overhead. When combined with deep pipelining, the architecture achieves a favourable trade-off between speed, latency, and resource efficiency—making it particularly suitable for FPGA families where LUT counts and routing delays impose strict design limitations.

Another important aspect is scalability. Since each pipeline stage uses structurally identical remainder and selection blocks, the divider can be extended to larger bit-widths with predictable synthesis behaviour. This modularity enables straightforward adaptation for domain-specific accelerators, signal-processing blocks, and embedded systems requiring frequent integer division operations.

In addition, the architectural principles introduced in this work open the possibility of exploring higher-radix configurations. Notably, extending the quotient-digit selection to generate three bits per iteration(radix-8 division) represents a promising research direction. Such an enhancement would require an expanded set of precomputed multiples and more sophisticated decision logic, but has the potential to further reduce the number of pipeline stages and increase throughput. Investigating these trade-offs will be an important aspect of future work.

5. Conclusions

This paper presents a novel pipelined architecture for integer division that leverages precomputed multiples of the divisor and comparator-based remainder generation, eliminating the need for full binary adders at every stage. The architecture is optimised for Field-Programmable Gate Arrays (FPGAs) and is built on a three-stage pipeline that generates two quotient bits per clock cycle.

Compared to traditional non-pipelined and partially pipelined approaches, the proposed design demonstrates a more than twofold performance improvement, while also achieving notable savings in hardware resources—occupying less than 0.3% of LUTs on Artix-7 FPGA and maintaining an operational frequency of 208 MHz. The elimination of complex arithmetic units and the use of simple comparators in the remainder logic contribute significantly to this area of efficiency.

In addition to the synthesis results, the architectural innovation lies in its scalable structure, where full pipelining, dual-bit quotient generation, and reduced logic complexity work synergistically to improve both latency and throughput. These features clearly differentiate the proposed work from prior art, including SRT and non-restoring dividers.

The proposed divider is well-suited for digital signal processing, coprocessor designs, and embedded systems that require high-speed and low-footprint division operations. Future work will focus on extending this architecture to support signed and floating-point division, as well as adaptation to high-performance FPGA families operating above 100 MHz.