Unveiling Tank-Liquid Sloshing Effect on Joint Boom Stability of a Field Sprayer Under Different Running Process

Abstract

The strong vibration excited by the tank-liquid sloshing of the field sprayer can result in uneven spraying, vehicle-body cartwheel, and the break of the boom during running process. So, it is crucial to investigate the stability of a field-sprayer boom under hazardous operating conditions on a specified ground surface, focusing on the coupled effects of tank-liquid sloshing, boom-connection stiffness, and nozzle jetting-force characteristics. A fluid–structure interaction framework combining volume of fluid (VOF)-based sloshing simulation, finite element modeling, and full-scale experiments is developed. It is shown that high liquid-filling ratios significantly amplify transient sloshing forces during braking and swerving, inducing strong direction-dependent boom vibrations and a distinct resonance band near 50–60 Hz. Increasing connection stiffness raises natural frequencies and reduces damping, thereby enlarging vibration amplitudes. The jetting-force amplitude attenuates X-direction vibration, while frequency variation produces notable resonance excitation aligned with the harmonics of the boom. Simulation and experimental results demonstrate strong consistency, validating the proposed model. The findings reveal key coupling mechanisms governing boom stability and provide practical guidance for structural optimization and vibration suppression in field sprayers.

1. Introduction

Boom-type field sprayers are essential for modern crop protection due to their high efficiency and large working width, yet ensuring stable spray performance under real operating conditions remains a major engineering challenge. During high-speed travel, braking, turning, and uneven-terrain operations, the boom is subjected to complex coupled excitations arising from vehicle dynamics, ground–structure interactions, liquid sloshing in the chemical tank, and the pulsating jetting force of the nozzles. Liquid sloshing, driven by acceleration, deceleration, and directional changes, generates strong transient impact forces and moments that are transferred to the boom structure, amplifying low-frequency vibrations and degrading droplet deposition uniformity. Meanwhile, the boom itself is a lightweight, low-stiffness, multi-joint structure with inherently low damping and natural frequencies, making it highly susceptible to resonance. The periodic jetting force from the nozzles further introduces frequency-dependent excitation that may coincide with the natural frequencies of the booms, intensifying structural vibration. Existing studies have examined sloshing dynamics, boom flexibility, and nozzle-induced pulsation separately, yet few have simultaneously considered their coupled effects or the influence of joint stiffness on overall dynamic stability. These vibrations not only compromise spray uniformity but also accelerate structural fatigue, joint wear, and potential failure [1,2,3].

The dynamics of liquids with free surfaces have been studied extensively in naval architecture, aerospace engineering, and automotive fuel-tank design. An actual method to calculate the maximum sloshing force has been proposed by Zheng [4] through experiments on the sloshing force moments of liquid in a rectangular tank subjected to harmonic excitation. However, the method is obtained through approximate calculation and the accuracy of the calculations requires improvement. The pressure changes in droplets have been investigated by Yu and Surico [5,6] during the sloshing process of the inner walls of cylindrical and U-shaped tanks. A numerical work on the liquid sloshing behavior of flexible tanks has been conducted by Kim [7] under external loads. However, it is only applied to limited shapes of tanks. Meanwhile, versatility is low. The static and dynamic characteristics of field sprayers have been analyzed by Wang [8] under four typical running conditions. A device known as an elastically constrained floating plate has been proposed by Li [9] to suppress liquid sloshing, but a detailed analysis of the device’s performance is not provided under extreme conditions. The mechanical characteristics of the tank-liquid sloshing under external excitation has been studied by Wang [10] through experimental methods, but the tank internal excitation generated is neglected. The forces in three directions have been measured and analyzed by Zhang [11] under identical running conditions. The force on the tank has been calculated by Lu [12] under acceleration excitation at various liquid-filling ratios. It has been established that there is an equivalent mechanical model of the liquid under tank translation excitation by the Galerkin method. Li [13] has simulated both the low-order sloshing mode and high-order local vibration of the liquid. However, the potential effects of the acquired forces on the boom have not been investigated in these studies thoroughly.

The dynamic behavior of boom structures has been widely investigated due to their inherent flexibility. Researchers have employed finite element (FE) models, modal testing, and reduced-order dynamic modeling to identify natural frequencies, mode shapes, and frequency-response functions of boom assemblies. A work on three commonly used boom nozzles has been conducted by Lipiński [14]. At the same time, the impact of the unstable boom on spray quality has been evaluated. The effects of the nozzle type and the number of nozzles on the boom on the spray quality were studied by Zaffar [15]. However, the work mainly focuses on the nozzle of the boom. Exploring the vibration characteristics of the boom and establishing the vibration model of the boom are also considered the main research approaches. The effectiveness of active boom suspension has been examined by Jeon [16] in stabilizing boom motion. A system for measuring displacements related to the stability of booms has been proposed by Kaliniewicz [17]. In order to determine the dynamic characteristics of the bolted boom, the reduced order model of the bolted boom with a four-parameter Iwan model has been established by Yang [18]. A model for real-time evaluation of boom stability was proposed by Kaliniewicz [19]. The vertical sprayer boom movements have been studied with experimental modal analysis by Langenakens [20]. A hybrid model of spray booms has been developed by Deprez [21] for the development of a stable boom roll suspension. The discrete element method and finite element method of agricultural spray boom modeling have been compared by Anthonis [22,23]. The boom motion of a sprayer with a working width of 12 m has been simulated by Kennes [24] through a nonlinear finite element method. In the work of the boom model, the boom is used as the main research object. However, the influence factors of the stability of the vehicle with the field sprayer to the boom have not been considered in the actual agricultural operation. The operation stability of the field sprayer is greatly affected by these factors. There is a lack of more comprehensive research on the stability of the boom. In a survey of field spraying operations, it has been found that the rotational motion of the field sprayer is one of the important factors causing the tip motion of the vertical and horizontal booms. In this regard, the influence of the rapid rolling motion of the field sprayer on the stability of the boom has been studied by Nation [25]. At the same time, it has been concluded that the influence of the rolling can be reduced in the separation of the boom from the rolling motion. In order to realize the isolation between the boom and the rolling motion, a mathematical model of the active tilting linkage boom suspension has been proposed by Frost [26].

In the field of fluid–solid coupling, there are three mainstream methods. The first is the finite element method [27,28], referred to as FE. These are effectively accommodated and include the deformation of solid structures and the interactions with fluids. In order to yield results for stress–strain and temperature distributions, the ability to accurately simulate complex geometric shapes and boundary conditions is considered its primary advantages. The second method is the finite volume method [29,30], referred to as FV. It is notable for its adeptness in managing boundary conditions and grid irregularities. Additionally, the implementation of parallel computations is facilitated, therefore computational efficiency is enhanced. The third method is smooth particle hydrodynamics [31,32,33], referred to as SPH. It is considered as a particle-based approach for simulating the behavior of fluids and other continuous media. It excels in addressing free surface and large deformation challenges, making it particularly suitable for applications such as tank sloshing. The FE, FV, and SPH methods are employed comprehensively within the established numerical model of the tank-liquid sloshing to ensure an accurate simulation of the intricate interactions between the fluid and solid components. Yan [34] comprehensively considers the effects of the vehicle of the field sprayer and boom suspension on the elastic vibrations by the Euler-Bernoulli beam theory. Subsequently, a geometric continuous model of boom vibration is established and the resulting yaw vibration changes in the boom are analyzed grounded by multi-body vibration theory.

The pulsating force generated by spray nozzles, although periodically small in magnitude, can act as a broadband excitation due to the multi-frequency components of pump-driven flow. Researchers have reported correlations between pulsation frequency and boom vibration modes, but only a few studies incorporate both amplitude and frequency effects into structural dynamics simulations [35,36,37]. Despite these advancements, most studies model the external excitation as chassis-induced or ground-induced vibrations, neglecting the contribution of dynamic loads originating from liquid sloshing or nozzle jetting forces. In addition, existing works primarily analyze chassis motion, while the dynamic stability of the boom structure under sloshing excitation remains insufficiently explored. Furthermore, the nonlinear interaction between joint stiffness and fluid-induced excitation has not been adequately quantified, particularly under emergency braking where transient loads are highest. Therefore, a comprehensive multi-physics investigation integrating structural dynamics and fluid–structure interaction is required to fully understand and mitigate the coupled mechanisms governing boom vibration, with the goal of enhancing spraying precision, operational safety, and long-term durability of field sprayers.

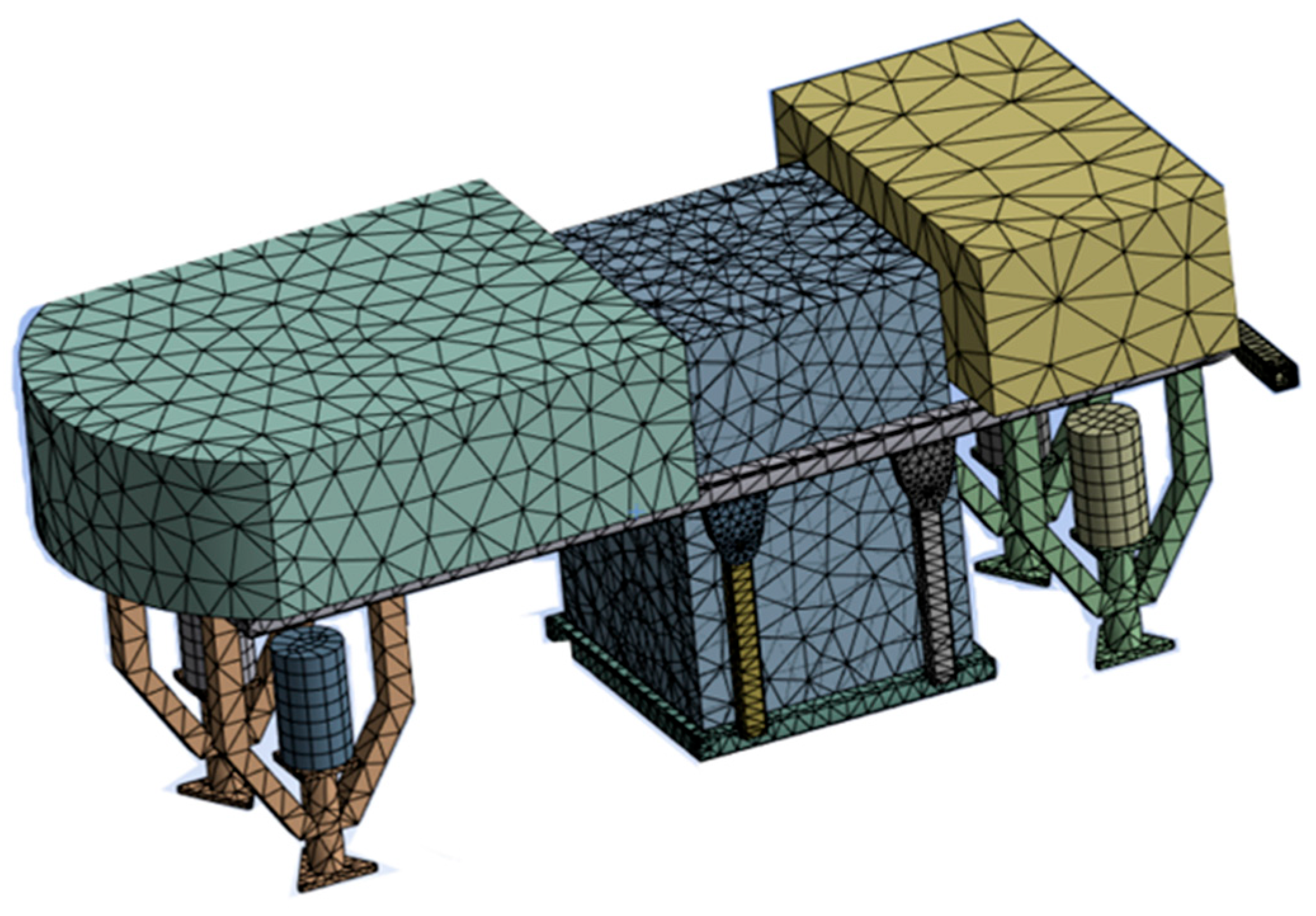
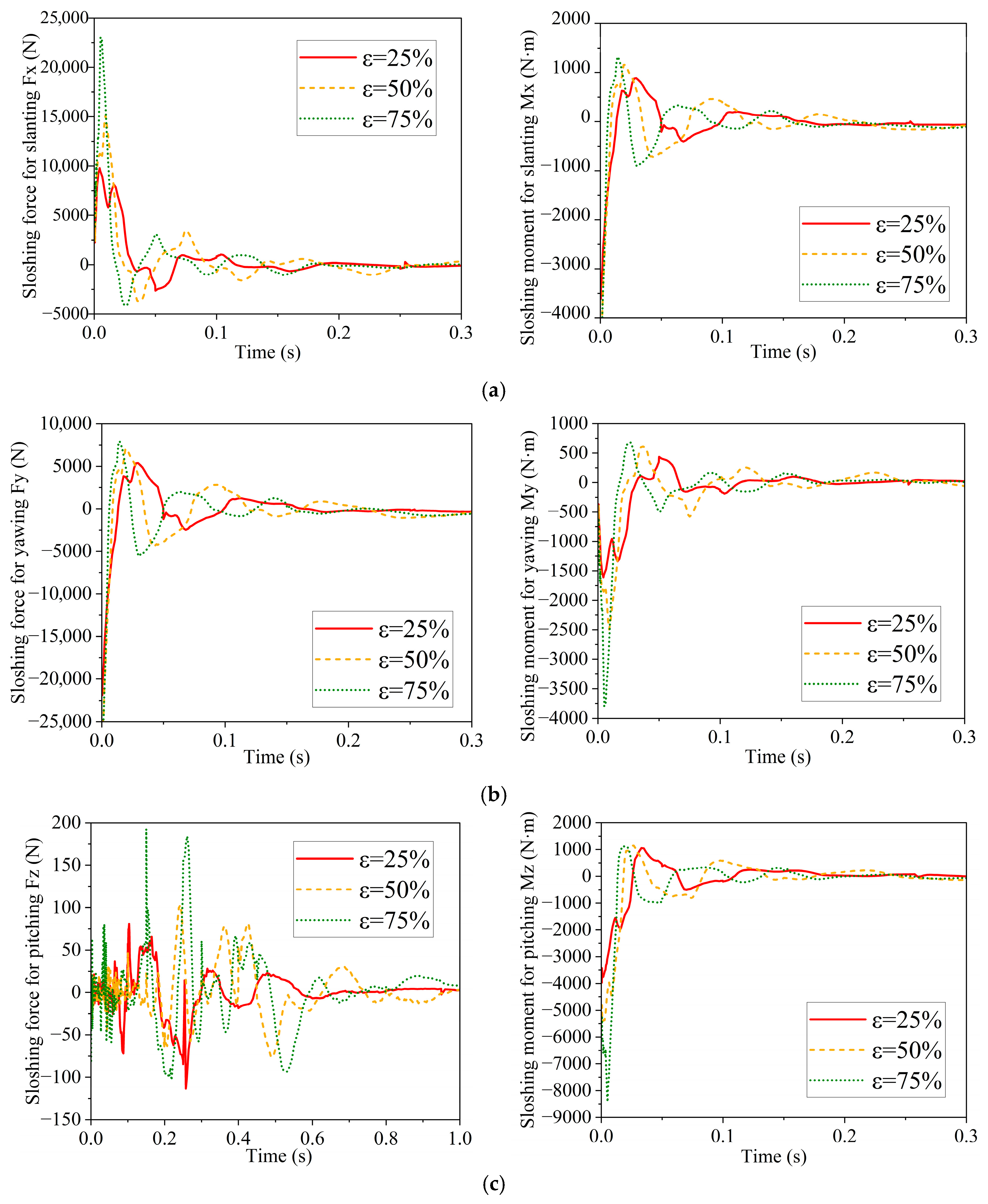
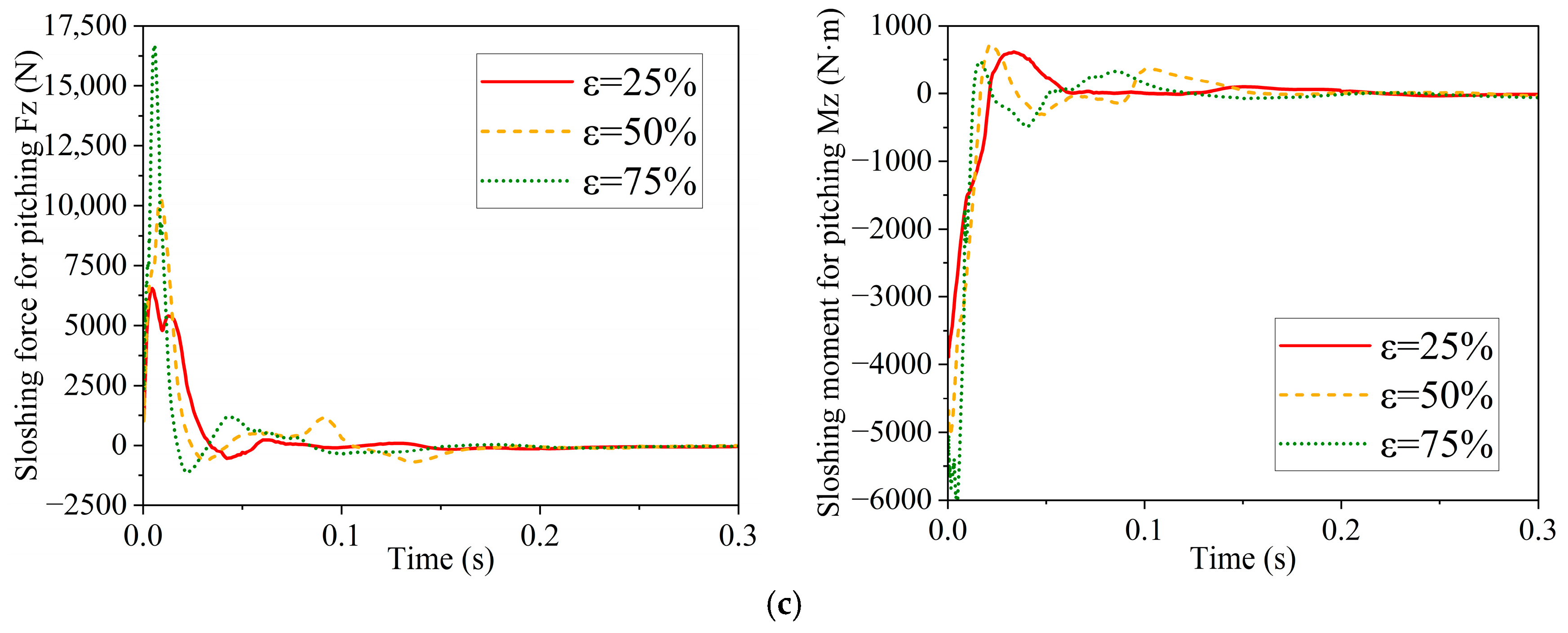
In order to investigate the effect of the tank-liquid sloshing on the stability of the field sprayer, the dynamic characteristics of tank-liquid sloshing, boom-connection stiffness, ground-induced excitation, and nozzle jetting-force characteristics are determined when the field sprayer is braking from 5.4 km/h and swerving at 45°. It should be noted that, although the vibration arising from the wheel–ground interaction has pronounced influences on the dynamic characteristics of the field sprayer, the present study is primarily focused on the analysis of its dynamic characteristics under different running conditions, i.e., braking and swerving, on a specified ground surface. Firstly, based on the experimental test and simulation analysis, the modal parameters of the joint boom are compared and analyzed to determine the most practical connection parameters of the boom so as to establish the finite element model of the vehicle and the joint boom of the field sprayer. Secondly, for the tank with the liquid-filling ratios of 25%, 50%, and 75%, a numerical model of liquid sloshing is developed with the output of the sloshing forces and moments in three directions. Thirdly, considering the tank-liquid sloshing effect, wheel vibration, and the connection characteristics of the joint boom, the tank-liquid sloshing effect on the joint boom is studied through static and dynamic analysis. Fourthly, the brute-force dynamic simulation is carried out to illustrate the influences of connection stiffness, frequencies, and amplitude of the jetting force of the medicinal liquid on the stability of the joint boom. Finally, the conclusions of the work are drawn.

2. Finite Element Model of a Field Sprayer

2.1. Physical Model

The field sprayer studied in this paper consists of a body, a tank, four motors, four wheels, two booms, and six spray nozzles, as shown in Figure 1a. The trussed body of the field sprayer is driven by two back motors and two front motors, which can also be applied to control steering. The four toothed wheels are all solid and suitable for running in paddy fields. As the medicinal liquid filled in the tank flows through the two booms and six spray nozzles, the field sprayer can run and spray. Each boom with three spray nozzles is symmetrically arranged in the bilateral direction of the body. The three-dimensional model of the field sprayer is built by evenly distributing the weight of the accessory controllers into the body. For convenience, the physical directions of the longitudinal driving direction, vertical direction, and lateral direction are, respectively, labeled as the X-, Y-, and Z-axes, as shown in Figure 1a. The forward running direction of the field sprayer is in accordance with the positive direction of the X-axis. During the running process, the booms stretch for spraying, as shown in Figure 1b. While, during non-running process, the booms shrink back to the body, as shown in Figure 1c. The dynamic characteristics of the field sprayer with the stretched booms under the running process are studied in the work.

The polythene tank of the field sprayer is connected to the body using a suspension type mechanism, which is simplified to a cuboid, as shown in Figure 2. The volume V of the tank is calculated by the height H, length L, and width W. Then, the liquid-filling ratio $\epsilon$ can be employed as

$$\epsilon ={\displaystyle \frac{V_l}{V}}={\displaystyle \frac{V_l}{LWH}}$$

(1)

where V_l is the volume of the medicinal liquid.

Then, the finite element model of the body with the tank is established, as shown in Figure 3. The trade-off is that for a fixed choice of the grid cell size decreasing, the size increases the computational expense of the convergent solutions for the dynamic simulation of the large-sized body of the field sprayer. Through an evaluation of mesh sizes, it is indicated that the difference in total deformation between the cases with mesh sizes of 80 mm and 60 mm is less than 0.1%. The results show that the solution becomes insensitive to further mesh refinement beyond a mesh size of 80 mm, while computational cost increases significantly. Accordingly, the grid cells with the size of 80 mm are proved to be an optimal compromise between numerical accuracy and computational efficiency. Therefore, the optimized meshes with 65,413 nodes and 30,681 elements are built by local mesh refinement. In addition, the wheel that received forces during running can be tested under typical road conditions and used as an exciting resource of the body. Importantly, the tank-liquid sloshing effect and the connection characteristics of the boom can also vitally affect the stability of the body of the field sprayer.

The joint boom is composed of a short, blue, square rod and a long, white, round rod jointed by two bolts, as shown in Figure 4a. The square rod is made of structural steel with one end fixed on the body. The round rod is made of aluminum with three spray nozzles. In the running process of the field sprayer, the medicinal liquid is transmitted to the spray nozzles through the tubes along the rods and introduces impact forces. Through the multi-segment local meshing method, the finite element model of the boom is established with 56,925 nodes and 9830 elements, as shown in Figure 4b. For simplification, the details of the bolts between the round rod and the square rod are not accurately modeled, such as the nuts and threads. Instead of the bolt connection, an elastic connection area is established with connection stiffness and damping. Considering the tightness of the support structure, the connection between the square rod and the vehicle body is considered as fixed, forming the fixed end. In practice, it should be noticed that the stiffness characteristics of the bolted connection between the square rod and the round rod are crucial for the stability of the boom.

Taking into account the smaller modulus of elasticity of the aluminum rod relative to that of the steel rod, a rigid connection can induce fatigue fracture in the aluminum boom due to the occurrence of local stress concentration. In practice, the flexible connection, which can provide the requisite support stiffness, is employed to enable minor displacement of the boom during vibrations, shock or thermal deformation. So, the stiffness of the bolted connection of the rods should be determined through experimental test of the field sprayer.

2.2. Identification of the Connection Parameters of the Joint Boom

In order to optimize the connection parameters of the boom, the comparison of the modal parameters from the experimental test and simulation are carried out. An impact test is conducted to obtain the modal parameters of the boom in the field sprayer. The testing system is constructed and built as shown in Figure 5. Two ICP@ (PCB piezoelectric, Buffalo, NY, USA) three-dimensional accelerometers are fixed near the end of the cantilever boom for the measurement of the responses during the running of the field sprayer. The testing data is manipulated by the data acquisition system, which is composed of the computer and the tester of LMS Test. Lab (Siemens, Munich, Germany). The impact force is produced by the impact hammer of PCB 086C04, and the vibration responses are measured by the acceleration sensor of PCB 333B. With the aid of LMS Test. Lab., the modal experiments of the boom are performed by ergodic impact testing of the hammer. Then, a sparse matrix solver with the chunked Lanczos method is applied for modal calculation to accurately obtain the individual modal data and vibration shapes.

Through a large number of the experimental tests and simulations, the modal shapes of the first six modes of the boom with the connection stiffness of 1520 N/m are shown in Figure 6. A comparative analysis of the modal vibration characteristics indicates that the Modal Assurance Criterion (MAC) values between the simulated and experimentally identified mode shapes exceed 90% for the first six modes of the joint boom. This result demonstrates a strong correlation between numerical and experimental mode shapes, thereby confirming the reliability of the proposed modeling and simulation approach. It is concluded that the modal shapes from the simulation with the connection stiffness of 1500 N/m are almost agreed with experimental results.

From the modal frequencies of the first six modes of the boom in

Table 1. Modal frequencies of the boom.

Order	Simulation Frequencies	Experimental Frequencies	Relative Error
1	11.1 Hz	11.2 Hz	0.9%
2	62.0 Hz	61.9 Hz	0.2%
3	101.3 Hz	101.5 Hz	0.2%
4	212.7 Hz	212.8 Hz	0.05%
5	287.2 Hz	286.9 Hz	0.1%
6	313.3 Hz	315.9 Hz	0.8%

, it is seen that the modal frequencies from the simulation present a very good approximation to those from the experiment with the relative error less than 1%. Following common practice, the simulation results provide quite satisfactory modal characteristics of the bolted boom with the connection stiffness of 1520 N/m in the field sprayer.

Then, the connection stiffness is determined as 1520 N/m. Based on the mechanism size of the field sprayer, the parameter values are listed in

Table 2. Parameters of the field sprayer.

Description	Value	Description	Value
Wheelbase	890 mm	Size of the square rod	30 × 30 × 500 mm
Tread	380 mm	Size of the round rod	$\varphi 24 \mathrm{mm}\times 1400 \mathrm{mm}$
Tank capacity	50 L	Spacing of sprayer nozzles	600 mm
Tank length L	330 mm	Connection stiffness of boom	1520 N/m
Tank width W	330 mm	Weight of the field sprayer	237 kg
Tank height H	510 mm	Medicinal liquid density ρ	1.0 × 103 kg/m3

.

2.3. Determination of the Excitation of Wheels

The running performance of the wheels acting on the testing ground can significantly affect the stability of the vehicle body and the boom, due to the bumpiness of the wheels. In order to accurately characterize the vibration behavior of the irregular wheels of a field sprayer, the vibration response is experimentally measured on a leveled test surface with the roughness grade of R10, according to ISO 10545-17 criterion [38]. Then, the acceleration data of the wheels are acquired using an LMS Test. Lab. testing system at a sampling frequency of 10 kHz. The accelerometers are mounted on the vehicle frame that is directly connected to the wheels, ensuring the accurate measurement of the wheel–ground interaction. For the experimental test, a Cartesian coordinate system is defined according to the deformation directions of the boom, i.e., X direction for slanting, Y direction for pitching, and Z direction for yawing. Through the experimental test, the acceleration spectra of the wheels in X, Y, and Z directions are obtained, as shown in Figure 7.

Because the field sprayer investigated in this study is intended for paddy field operations, for which no unified or standardized ground surface spectrum data are currently available, the acceleration spectrum of the interaction between the toothed wheels and the ground is obtained through experimental measurements. The development and application of representative or standardized farmland road surface spectra will be considered as an important direction for future research. In addition, the suspension system of the field sprayer is integrated with the wheel hub, as shown in Figure 1. In the present study, dynamic characteristics of the suspension system are embodied in the vibration signals generated by the interaction between the wheels and the ground through experimental measurements.

Then, the acceleration spectra of the toothed wheels can be added to the bottom of the body as the external excitation for dynamic simulation. Under different running processes, the stability of the joint boom can be affected by different dynamic characteristics of the field sprayer. In order to comprehensively study the dynamic characteristics of the joint boom, the dynamic simulation is carried out for the field sprayers under braking from 5.4 km/h and swerving with 45° in the work.

Taking into account the vibration from the toothed wheels and ground, the sloshing effect of the tank, and the stiffness of the bolted connection of the rod, the stability of the joint boom is comprehensively studied through dynamic simulation and experimental testing in the work. The analysis flow and method for the dynamic analysis of the stability of the joint boom in different running processes are illustrated in Figure 8. When the data of the vibration of the toothed wheels and the connection stiffness of the joint boom are, respectively, acquired by experimental testing and modal analysis, the dynamic characteristics of the tank-liquid sloshing are obtained by dynamic simulation in the volume of fluid (VOF) model. All the characteristics of the wheels, boom, and tank are embedded into the simulation model of the stability analysis of the slender boom in the field sprayer. Then, through the comparison of the results of the dynamic simulation and the experimental testing, the model and the corresponding method of the dynamic simulation are validated. Subsequently, the influences of the connection stiffness of the joint rod, the jetting force of the sprayer nozzle, and the straining forces of the boom on the stability of the joint boom are studied through dynamic simulation. These results can contribute to the optimal design of the field sprayer.

Based on the finite element model and the dynamic characteristics of the field sprayer under braking from 5.4 km/h and swerving with 45°, the sloshing effect of the tank with the liquid-filling ratios of $\epsilon =25\%$, $\epsilon =50\%$, and $\epsilon =75\%$ are studied through dynamic simulation. Therefore, six scenarios, i.e., braking or swerving with $\epsilon =25\%$, $\epsilon =50\%$, and $\epsilon =75\%$, are explored for the field sprayer. Then, the response characteristics and their influences on the joint boom are unveiled for the field sprayer.

In the experimental investigation, uncertainties in acceleration measurements mainly arise from sensor resolution, calibration accuracy, mounting conditions, and signal acquisition and processing, with the overall measurement uncertainty estimated to be within ±3–5% based on system specifications and repeatability tests. In the numerical simulations, uncertainties are primarily associated with modeling assumptions and numerical discretization, where the liquid tank is treated as rigid and excitation inputs are derived from experimentally measured wheel–ground interaction signals. A mesh-independence study confirmed numerical convergence, indicating that variations in key response quantities due to mesh refinement are negligible and that the uncertainty in sloshing-force estimation is dominated by model simplifications rather than numerical instability. As the present study focuses on identifying dominant dynamic trends and coupling mechanisms rather than exact force magnitudes, the associated uncertainty levels are considered acceptable for engineering analysis, with more rigorous uncertainty quantification to be addressed in future work.

3. Tank-Liquid Sloshing Effect

3.1. Volume of Fluid Method

Taking into account the representativeness of typical running conditions and their relevance to liquid-sloshing effects, the late stage of spraying with a low liquid-filling rate of 25%, the most critical condition with a medium liquid-filling rate of 50%, and the early stage of operation with a high liquid-filling rate of 75%, are most relevant to sprayer boom stability during normal agricultural operations. The tank-liquid sloshing behaviors of the field sprayer with different liquid-filling ratios of $\epsilon =25\%$, $\epsilon =50\%$, and $\epsilon =75\%$ are investigated based on a volume of fluid (VOF) model. The governing Navier–Stokes equations are derived as

$${\displaystyle \frac{\partial \rho v_l}{\partial t}}+\nabla \cdot (\rho v_l\otimes v_l)=-\nabla p+{\zeta }_l{\nabla }^2{v}_l+\rho g+f_t$$

(2)

where $v_l$ represents the velocity of the medicinal liquid with p the static pressure, ${\zeta }_l$ the dynamic viscosity, g the gravitational acceleration, and f_t the inertial forces caused by tank motion. $\nabla$ is the gradient operator with $\nabla \cdot v_l=0$ reflecting the incompressibility condition of the medicinal liquid.

Based on the conservation of the liquid-phase volume fractions, the liquid–gas interface is tracked as

$${\displaystyle \frac{\partial \alpha }{\partial t}}+\nabla \cdot (\alpha v_l)+\nabla \cdot [\alpha (1-\alpha )v_{com}]=0$$

(3)

where $\alpha$ represents the volume fraction with $v_{com}$ representing the compression velocity.

The sloshing forces and moments acting on the tank walls are computed by integrating pressure and viscous stresses over the wetted surface S. The formulations of force $f_l$ and moment $M_l$ are derived as

$$\left\{\begin{array}{l}{f}_l={\displaystyle {\int }_S[-p+{\zeta }_l(\nabla v_l+\nabla {v_l}^T)]dS}\hfill \\ M_l={\displaystyle {\int }_{S}r\times [-p+{\zeta }_l(\nabla v_l+\nabla {v_l}^T)]dS}\hfill \end{array}\right.$$

(4)

where $f_l$ is defined as the resultant force that is calculated by integrating both pressure and viscous effects over the wetted surface S. $M_l$ is the resultant moment relative to a reference point. $\tau$ is viscous stress tensor that is expressed as a function of dynamic viscosity ${\zeta }_l$ and the symmetric velocity gradient tensor of $(\nabla v_l+\nabla {v_l}^T)$. r is position from the reference point to the differential surface element of dS.

Then a seven-degree-of-freedom dynamic model including slanting in X direction, pitching in Y direction, yaw in Z direction, and rotational dynamics of four wheels is adopted to analyze the coupled response between body motion and liquid sloshing. Then, it yields

$$\left\{\begin{array}{l}{m}_{total}\ddot{x}+f_{sx}+f_r-f_d=0\hfill \\ I_{xx}\ddot{\varphi }+k_{\varphi }\varphi -M_{sy}-M_{boomz}=0\hfill \\ I_{yy}\ddot{\theta }-M_{sx}-M_{inertia}=0\hfill \\ {\ddot{Q}}_{sus}+C_{sus}{\dot{Q}}_{sus}+K_{sus}{Q}_{sus}+Z_{wheel}=0\hfill \end{array}\right.$$

(5)

where $m_{total}$ denotes total mass of the vehicle and the liquid with x being the slanting displacement, $f_d$ the driving force, $f_{sx}$ the slanting force during sloshing, and $f_r$ the rolling force. $I_{xx}$ and $I_{yy}$ are, respectively, the moments of inertia in X- and Y-axes. $\varphi$ and $\theta$, respectively, represent roll and pitch angles. $M_{sx}$, $M_{sy}$, and $M_{boomz}$ denote the sloshing moments in X- and Y-axes and the moments generated by boom. $k_{\varphi }$ is the rolling stiffness. $Q_{sus}$ is the suspension displacement with $K_{sus}$ being the suspension stiffness, $C_{sus}$ the suspension damping, and $Z_{wheel}$ the irregularity excitation from the unevenness of the wheels and the road.

When the medicinal liquid is forced to slosh, it exerts a sloshing impact on the inner wall of the tank. In order to analyze the tank-liquid sloshing effect, the volume of fluid (VOF) model of the medicinal liquid is discretized into 12,056 tetrahedral fluid grids and 2976 fluid domain boundary grids by the aid of the global grid method. Specifically, the rigid tank assumption is employed to reduce computational cost and is considered reasonable due to the significantly higher stiffness of the tank compared to the liquid and joint booms. Taking into account the fluid–structure interaction between the medicinal liquid and the tank wall, the dynamic simulations of the tanks with the liquid-filling ratios of $\epsilon =25\%$, $\epsilon =50\%$, and $\epsilon =75\%$ are carried out with the volume of fluid method.

To ensure experimental safety and the reliability of the results, water is consistently employed as an equivalent substitute for the medicinal liquid throughout the analysis of the tank-liquid sloshing effect.

3.2. Dynamic Characteristics of the Tank-Liquid Sloshing

When the parameters of the field sprayer are set, as listed in Table 2, with the environmental pressure of 101,325 Pa, the dynamic characteristics of the tank-liquid sloshing with the liquid-filling ratios of $\epsilon =25\%$, $\epsilon =50\%$, and $\epsilon =75\%$ can be obtained by dynamic simulation under a running process with braking from 5.4 km/h and with swerving with 45°. The measured acceleration responses of the vehicle body and sprayer boom indicated that, at a forward speed of approximately 5.4 km/h during normal agriculture operations, both braking and swerving maneuvers result in relatively large dynamic responses. Thus, these two running processes are regarded as the most hazardous conditions for a field sprayer. The sloshing force and the corresponding moments of the simulation model are shown in Figure 9, where Fx, Fz, and Fy are, respectively, the slanting force, the pitching force, and the yawing force, as well as Mx, Mz, and My are, respectively, the corresponding slanting moment, the pitching moment and the yawing moment of the tank around the center of the tank bottom.

In order to facilitate the computing efficiency and the accuracy, the liquid surface waveform is recorded over a period of 5 s under different running conditions. Taking the tank with the liquid-filling ratio of $\epsilon =50\%$ as an example, the time-dependent performance of the liquid surface waveform is obtained under the running processes with braking from 5.4 km/h and with swerving with 45°, as illustrated in Figure 10. From the liquid surface waveform for braking in Figure 10a and for swerving in Figure 10b, intense sloshing is initiated at approximately 0.27 s under both braking and swerving conditions, followed by a gradual decay of the free-surface motion with time. In addition, the liquid exhibits significant fluctuations, characterized by a phenomenon known as breaking waves, characterized by wave flipping and breaking. Such breaking wave behavior leads to partial dissipation of the liquid momentum and kinetic energy as the fluid climbs the tank walls, where gravitational effects and energy redistribution contribute to the attenuation of the impact loads acting on the tank structure. On the other hand, distinct free-surface waveform patterns are observed under different initial excitation conditions, reflecting the sensitivity of liquid sloshing behavior to the imposed vehicle maneuvers. It is presented that the liquid surface waveform is consistent with the sloshing characteristics exhibited by the fluid in the real environment. Through comparison with experimental results in other tanks [3,32], it is also seen from Figure 10 that the evolution trends and qualitative features of the liquid surface waveform closely align with those from experiments. Therefore, the accuracy of the adopted fluid–solid coupling dynamic simulation is validated under the running processes of braking from 5.4 km/h and swerving with 45°.

Subsequently, the dynamic responses of sloshing forces and moments can also be acquired for the tanks filled with the medicinal liquid with the definite liquid-filling ratio $\epsilon$, during the running process of the field sprayer with braking from 5.4 km/h and swerving with 45°.

Case 1: Running process with braking from 5.4 km/h

During the running process with braking from 5.4 km/h, the field sprayer is initially accelerated to 5.4 km/h, and subsequently decelerated to standstill. The sloshing forces and moments for slanting, yawing and pitching of the liquid are, respectively, shown in Figure 11, corresponding to the behavior of the liquid surface waveform in Figure 10a.

Tank-liquid sloshing of the field sprayer is a dynamic process where the centroid of the liquid and the forces/moments due to sloshing require some time to stabilize in new positions. It is illustrated in Figure 11 that during braking from 5.4 km/h, the force and moment changes along the X and Y axes exhibit similar trends, in contrast to those in the Z axis. In the X direction, a low liquid-filling ratio of $\epsilon =25\%$ results in noticeable bimodal fluctuations in sloshing, indicating easier excitation of higher-order sloshing modes. For medium and high liquid-filling ratios of $\epsilon =50\%$ and $\epsilon =75\%$, the sloshing patterns are similar, with minor peaks following the braking impact, indicating the significance of rebound impacts. Moreover, the medium liquid-filling ratio of $\epsilon =50\%$ exhibits a more pronounced delay in sloshing compared to the high liquid-filling ratio. This phenomenon is ascribed to the inertial behavior of the liquid within the tank. The explanation concerning the inertial causes of the effect is consistent with the experimentation in [3] on liquid sloshing. In the Y direction, a delay in sloshing is clear at a low liquid-filling ratio. In the Z direction, sloshing force variations are less significant, with more intense sloshing occurring at the high liquid-filling ratio of $\epsilon =75\%$. The reason is that the side of the tank aligned with the Z axis is perpendicular to the movement direction of the field sprayer, resulting in reduced impact force of the liquid sloshing. So, it is concluded from the simulation results that the peak value of the curve is correlated with the filling rate. Additionally, the sloshing force diagrams obtained in Case 1 align closely with the simulation results presented by Lu [32] using finite element software. Moreover, it displays some consistency in the simulation results concerning the sloshing force moment diagrams from Case 1.

Case 2: Running process with swerving with 45°

During the running process with swerving with 45°, the field sprayer initially maintains a standard speed of 5.4 km/h, subsequently changing direction at an angle of 45°. The sloshing forces and moments for slanting, yawing, and pitching of the liquid are, respectively, shown in Figure 12, corresponding to the behavior of the liquid surface waveform in Figure 10b.

According to Figure 12, it is observed that an increase in the liquid-filling ratio of the tank leads to more vigorous liquid sloshing, resulting in the higher slanting forces and moments in the X axis. Along the Y axis, the amplitudes of the yawing forces are almost invariant across various liquid-filling ratios. In the Z axis, the pitching moments are basically the same as the yawing moments in the Y axis, and a lower liquid-filling ratio causes a more pronounced delay.

It is demonstrated from Case 1 and Case 2 that the medicinal liquid with different volumes can induce different sloshing effects for the tank, leading to changes in the vibration responses of the field sprayer. The tank with a high liquid-filling ratio of $\epsilon =75\%$ can generate greater sloshing forces and moments, more and less. During the running process with braking from 5.4 km/h, violent sloshing occurs in the Z axis resulting in the maximum force moment. Furthermore, the sloshing force moments which are observed in this case align closely with the results obtained by Lu [32] through finite element simulation.

4. Sloshing Effect on the Joint Boom

The slender joint boom in the field sprayer is the weakest component, which is highly susceptible to vehicle vibration and is likely to cause significant swinging of the joint boom. Therefore, the stability of the joint boom is of paramount importance in the dynamic analysis of the field sprayer. Considering the tank-liquid sloshing effect, wheel vibration, and the connection characteristics of the joint boom, the tank-liquid sloshing effect on the joint boom is studied through static and dynamic analysis.

4.1. Static Characteristics

The stress–strain characteristics of the joint boom are obtained through nonlinear simulation. It is indicated that the critical point is forced to occur at the free end of the boom. When the field sprayer is braking from 5.4 km/h, the stress and strain curves of the free end of the joint boom are shown in Figure 13a. It is indicated that the manifestations of both stress and strain show multimodal oscillation, highlighting the intensity of the impact caused by braking. When the field sprayer is swerving with 45°, the stress and strain curves of the free end of the joint boom are shown in Figure 13b. It is shown that the stress and strain of the joint boom in the field sprayer with different liquid-filling ratios exhibit different attenuation trends. The variations in stress and strain properties of the joint boom in a field sprayer with varying liquid filling ratios of $\epsilon =25\%$, $\epsilon =50\%$, and $\epsilon =75\%$ indicate that the stress and strain of the joint boom during braking are significantly influenced by tank-liquid sloshing. Notably, the maximum stress which is experienced by the joint boom is significantly lower than the allowable one of 158 MPa, which is defined as the standard allowable bending stress of Q235 steel under static loading conditions according to GB/T700-2006 [39].

4.2. Dynamic Characteristics

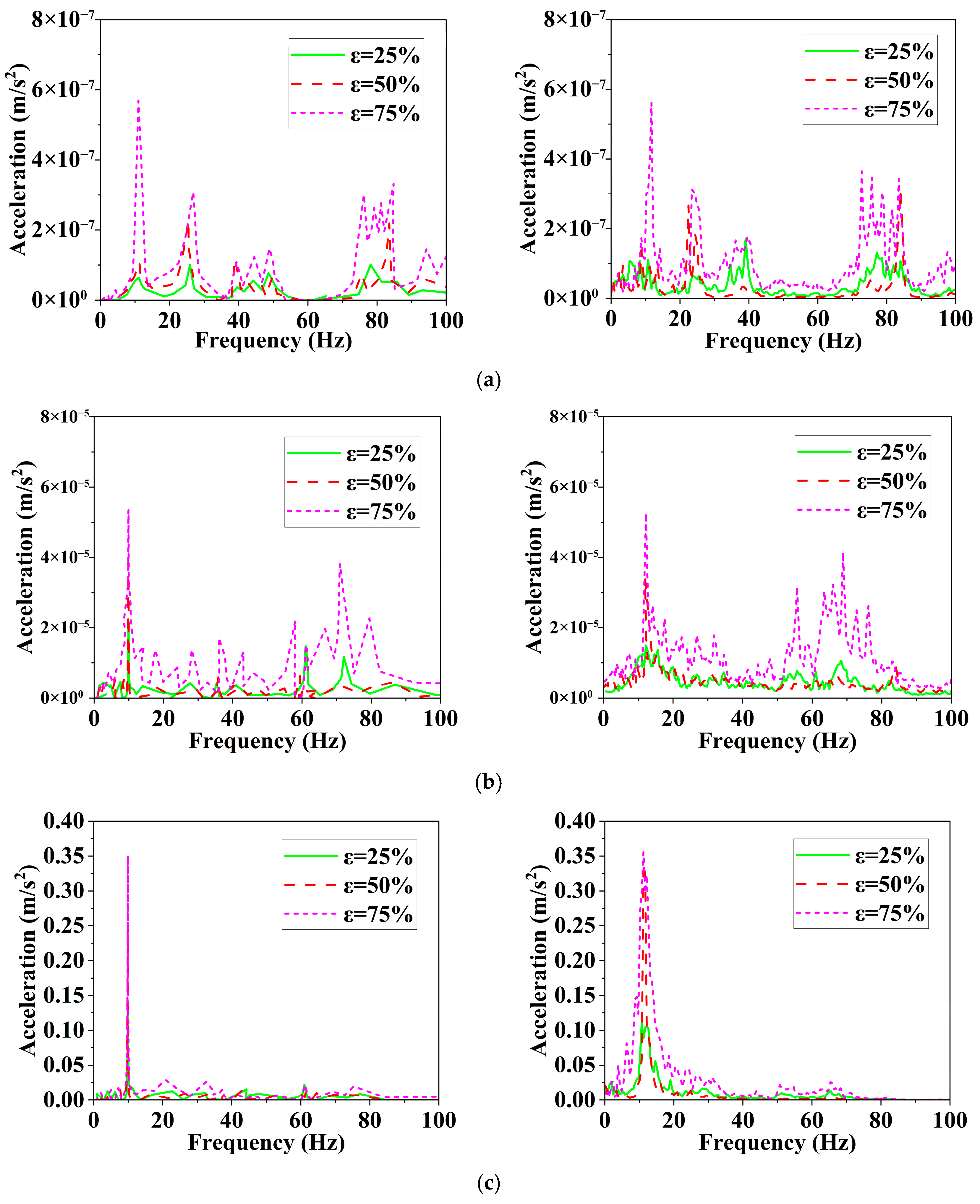
In order to obtain the dynamic characteristics of the wide-amplitude vibration of the joint boom, which is triggered due to its slenderness of the cantilever, the tank-liquid sloshing behaviors of the joint boom in the field sprayer are studied through the stochastic vibration analysis. For the accuracy of comparative analysis, the responses of the free end of the joint boom are obtained by dynamic simulation and experimental testing.

Initially, the vibration behaviors of the joint boom are explained using the principles of structural dynamics. This approach allows for a systematic examination of the random vibrations of the boom by constructing dynamic equations, evaluating frequency response characteristics, and assessing energy allocation. Experiments on the stochastic vibrations of the boom are performed to thoroughly study the impact of tank-liquid sloshing on vibrational mode shapes and energy distribution across varying operational conditions. Frequency-domain cross-validation with a finite element model is carried out, yielding statistically significant profiles of accelerometric amplitude-frequency joint distribution. These profiles are depicted in Figure 14 and Figure 15.

In the X direction, it is indicated from the response results in Figure 14a that at low frequencies, the response amplitude is minimal, escalating sharply at a specific frequency where a clear resonance peak emerges. This suggests the presence of a first-order natural frequency in the X direction. The resonance peaks for both the simulation and experiment occur at nearly identical frequencies, showing that the simulation model accurately represents the dynamic properties. Nonetheless, the experimental peak amplitude is slightly lower, implying additional damping effects in the actual structure.

In the Y direction, the amplitude-frequency responses in Figure 14b display more notable variations. The simulation results depict a sharper and more ideal resonance peak, whereas the experimental peak is slightly shifted and reduced in amplitude. This discrepancy can be attributed to structural characteristics and material nonlinearity in the real machine, which lead to a less sensitive actual response compared to the simulation prediction. In the Z direction, the simulation and experimental results in Figure 14c exhibit consistent overall trends, but the vibration amplitude is smaller than that in the X and Y directions, suggesting higher vertical stiffness of the boom. The simulated peak appears sharper, while the experimental curve is smoother, reflecting the impact of higher damping and complex vibration coupling effects in the real system.

Overall, the simulation and experimental amplitude-frequency responses align well concerning the main characteristic frequencies, validating the reliability of the simulation model. The experimental curves are smoother and less pronounced, highlighting that damping and non-ideal boundary conditions in the real machine lessen the vibration response, particularly in the high-frequency domain.

In Figure 15, both the simulated and experimental results reveal a distinct resonance peak, signifying the primary natural frequency of the joint boom. The resonance frequency observed in the experimental data closely matches that of the simulation, affirming the accuracy of the dynamic model developed. In the Y direction, the response amplitude in Figure 15b exhibits more significant fluctuations with frequency. The simulation predicts a more pronounced resonance peak, whereas the experimental results show a broader and slightly offset peak, suggesting that nonlinear factors, such as connection looseness, impact the real dynamic behavior of the joint boom during operation. In the Z direction, the overall response amplitude is considerably lower compared to the X and Y directions, indicating that the boom has greater stiffness and improved vibration resistance vertically. Both simulation and experimental data demonstrate similar patterns, although the experimental curve is smoother and less responsive to high-frequency excitation, which further confirms the effects of damping and multi-directional coupling in the actual system. Overall, the comparison between simulation and experimental findings suggests that the developed dynamic model effectively captures the principal vibration characteristics of the joint boom of the field sprayer in all three directions. The minor differences between the two results stem mainly from unmodeled damping and real-world structural complexities, attesting to both the reliability and practical utility of the simulation method.

In addition, the response amplitude of the joint boom caused by tank-liquid sloshing can be magnified as the liquid-filling ratio increases. However, the tank-liquid sloshing has little effect on the vibration frequency of the joint boom, only that the larger the liquid filling ratio, the more frequency components of the vibration responses. It is also indicated that the dynamic responses of the joint boom exhibit strong nonlinearity under the influence of connection characteristics. Furthermore, the comparison of results indicates that the numerical model aligns well with the real measurement in lateral, vertical, and longitudinal direction, although the simulated frequency is about 10 Hz and slightly lower than the testing one of about 12 Hz. The observed discrepancies are mainly attributed to factors such as the flexibility of the rear suspension and the compliance of the modification platform, which are not fully represented in the numerical model. These factors may induce variations in the posture and inertial position of the tank, thereby leading to deviations between the idealized simulation inputs and the actual operating conditions. In addition, variables like sensor accuracy, noise, and external disturbances may combine and intensify during the conversion of liquid sloshing forces and moments, leading to divergence between the converted measurement results and the actual sloshing forces and moments.

In this study, the stability of the sprayer boom refers to its dynamic stability, with motions primarily considered in the vertical plane relative to the vehicle body. The dynamic responses of the sprayer boom under different operating conditions, such as braking and swerving, are analyzed with a focus on the effects induced by liquid sloshing within the tank. Other potential sources of excitation, including motor and pump vibrations and ground-induced vibrations during vehicle movement, are acknowledged but are not explicitly modeled in the present analysis. Based on both numerical simulations and experimental measurements, it is found that the oscillatory movement of the liquid constitutes the dominant factor affecting the dynamic characteristics of the sprayer boom under the considered conditions. The contributions from other sources are comparatively smaller and are considered secondary for the scope of this study.

5. Influences of System Parameters on the Dynamic Responses of the Joint Boom

Based on the validated model and the corresponding method, the brute-force dynamic simulation is carried out to illustrate the influences of connection stiffness, frequencies, and amplitude of the jetting force of the medicinal liquid on the stability of the joint boom. In view of the pronounced vibration of the joint boom during braking, the response amplitude of the joint boom under braking conditions is examined in this study.

The influence of connection stiffness between the joint boom and the vehicle body is analyzed for its impact on the stability of joint boom. The vibrational response amplitudes of the joint boom along three orthogonal directions, i.e., X axis, Y axis, and Z axis, under varying connection stiffness are shown in Figure 16. It is found that high connection stiffness is demonstrated to increase the response amplitude of the joint boom when the connection stiffness varies from 500 to 3000 N/m. However, excessive stiffness is identified to risk mechanical resonance, which compromises dynamic performance. In addition, an increase in connection stiffness reduces the energy dissipation capacity of the flexible joint connections. Consequently, a larger portion of the vibrational energy is transmitted along the joint boom and accumulates within its structure, leading to an increase in the overall vibration amplitude.

During pesticide spraying, the field sprayer can be significantly impacted by the amplitude and frequency of the jetting force of the medicinal liquid from the dynamic properties of the joint boom. The vibrational response amplitudes of the joint boom along the X axis, Y axis, and Z axis under varying amplitudes of the jetting forces are shown in Figure 17. As the amplitude of the jetting force ranges from 0 to 1000 N, the vibration responses of the joint boom display distinct directional patterns. In the X direction, the response amplitude decreases almost linearly with increased jetting force, indicating effective suppression of lateral vibration by the jetting force. In contrast, the response amplitude in the Y direction is nearly constant, suggesting the jetting force has little effect on lateral sway. In the Z direction, the vibration amplitude decreases nonlinearly with increased jetting force and stabilizes around 500 N, implying a stabilization of the boom motion beyond this point.

Generally, as the amplitude of the jetting force grows, the overall response of the joint boom declines, with the most notable effect in the vertical direction, i.e., in the Z axis. This observation suggests that the dynamic load generated by liquid-spraying influences both the steady-state control and dynamic characteristics of the joint boom through nonlinear coupling effects. Increasing the amplitude of the jetting force appropriately can enhance the stability of the joint boom. However, excessively high jetting forces might negatively impact damping performance and structural connection stability. Therefore, achieving an optimal balance between the amplitude of the jetting force and the dynamic behavior of the joint boom is crucial in the design of a field sprayer.

The vibrational response amplitudes of the joint boom along the X axis, Y axis, and Z axis under varying frequencies of the jetting forces are shown in Figure 18. As the frequency of the jetting force rises from 0 to 70 Hz, there are notable differences in the amplitude-frequency responses of the joint boom depending on the directions. In the X direction, the response amplitude decreases steadily from 0 to 45 Hz, with peaks noticeably around 50 Hz, stays relatively elevated between 50 and 60 Hz, and then drops again. This pattern highlights a resonance phenomenon occurring near the third harmonic of the natural frequency, i.e., around 55 Hz, which can be attributed to the interaction between the external excitation frequency components and the inherent modal characteristics of the joint boom. When the frequency content of the applied excitation approaches the natural frequency or its higher-order harmonics, the corresponding vibration mode is preferentially activated, leading to a significant amplification of the vibration response. In the Y direction, the vibration amplitude remains roughly unchanged with varying jetting frequencies, suggesting that the structural damping and joint constraints play a more significant role. In the Z direction, the variation in the response amplitude with frequency is generally similar to that in the X direction but with less fluctuation, indicating some dynamic coupling between the two directions in their vibration responses.

Overall, the effect of the frequency of the jetting force on the dynamic response of the joint boom shows clear frequency-dependent and directional coupling characteristics. The response amplitude decreases in the low-frequency range but shows a noticeable resonance response in the mid-frequency range, i.e., around 50–60 Hz, identified as the most sensitive area for dynamic excitation. The frequency of the jetting force should be appropriately adjusted to avoid resonance zones, effectively lowering the vibration amplitude and improving spraying stability and operational accuracy. These insights are crucial for optimizing the boom structural design and developing vibration control strategies in a field sprayer.

The parametric variations in the jetting force reveal that both its amplitude and frequency govern the vibration response of the joint boom through direction-dependent and frequency-sensitive dynamic coupling mechanisms. An increase in jetting force amplitude generally suppresses boom vibrations by altering the load distribution and enhancing dynamic stabilization, whereas specific excitation frequencies, particularly near higher-order natural harmonics, induce resonance and amplify vibration responses. These trends indicate that the dynamic behavior of the joint boom is controlled by the interplay between external fluid-induced excitation and inherent structural characteristics, providing a physical basis for optimizing jetting parameters to improve operational stability.

6. Conclusions

In the study, a comprehensive fluid–solid coupling framework, combining volume of fluid (VOF) simulation, finite element modeling, and full-scale experimental validation, is developed to investigate the dynamic stability of a field sprayer and its joint boom under the most hazardous operating conditions. The influences of tank-liquid sloshing, connection stiffness, and the jetting force characteristics of the joint boom are systematically quantified. The major conclusions are summarized as follows:

(1) Tank-liquid sloshing significantly affects the dynamic load transmission within the field sprayer. The conditions of braking from 5.4 km/h and swerving with 45° are identified as the most critical operating scenarios. Higher liquid filling ratios produce markedly larger sloshing forces and moments, especially in the X and Z directions, resulting in intensified excitation of both the vehicle body and the joint boom. The simulated liquid surface behavior, including wave flipping and breaking, agrees well with experimentally observed phenomena reported in the literature, confirming the reliability of the adopted fluid–structure interaction model.

(2) The joint boom exhibits strong direction-dependent vibration behavior under fluid-induced and structural excitation. Both simulation and experimental results show good agreement in resonance frequencies and overall amplitude-frequency characteristics. The joint boom demonstrates its highest sensitivity in the X direction, moderate sensitivity in the Y direction, and minimal vibration in the Z direction due to higher vertical stiffness. With increasing liquid filling ratio, nonlinear and multi-frequency components in the vibration response become more prominent, highlighting the complexity of the coupled dynamic behavior.

(3) Connection stiffness plays a crucial role in the dynamic stability of the joint boom. Increasing the stiffness from 500 N/m to 3000 N/m raises the vibration amplitudes in all directions. Excessive stiffness elevates the natural frequencies of the boom and reduces the damping effect of the flexible joints, thereby increasing the likelihood of resonance during braking. This stiffness-induced amplification mechanism indicates that an appropriate stiffness range, rather than maximum stiffness, is critical for vibration mitigation.

(4) The amplitude and frequency of the jetting force strongly influence the dynamics of the joint boom. As the amplitude of the jetting force increases from 0 to 1000 N, the vibration amplitude in the X direction decreases nearly linearly, remains almost unchanged in the Y direction, and decreases nonlinearly in the Z direction, stabilizing beyond approximately 500 N. The jetting frequency produces a pronounced resonance peak near 50–60 Hz in the X and Y directions, consistent with the third harmonic of the natural frequency of the boom. These results demonstrate that jetting force parameters can function as either stabilizing or destabilizing factors, depending on their magnitude and frequency.

(5) The integrated dynamic model provides an accurate prediction of boom vibration and offers guidance for structural optimization. The consistency between simulation and experimental results confirms the effectiveness of the modeling approach, while minor discrepancies are attributed to suspension flexibility, structural deformation of the test platform, and measurement uncertainties.

Overall, this work reveals the complex coupled dynamics governing the stability of a field sprayer and provides a quantitative basis for improving boom design, optimizing connection stiffness, selecting appropriate jetting parameters, and mitigating the adverse effects of tank-liquid sloshing. The findings offer practical engineering guidance for enhancing the operational safety and structural longevity of field sprayers. The potential influences on sprayer uniformity through the reduction in boom vibrations are suggested as a possible implication, to be investigated in future work. It should be noted that, in the present study, water is employed as a surrogate for the medicinal liquid. Consequently, physicochemical properties such as viscosity and surface tension of the actual medicinal liquid are not considered in the analysis of the sloshing effect. In future work, the sloshing dynamics will be investigated with explicit consideration of the physicochemical properties of the medicinal liquid.