On Deep Learning Hybrid Architectures for MIMO-OFDM Channel Estimation

Abstract

Traditional estimation methods face challenges in adverse conditions in systems such as Multiple Input Multiple Output (MIMO) with Orthogonal Frequency Division Multiplexing (OFDM). To overcome those challenges, Deep Learning (DL) approaches have been proposed as an interesting alternative, thanks to their ability to capture channel features without much complexity. This paper presents a hybrid approach that combines DL with traditional estimation methods such as Least Squares (LS) and Minimum Mean Square Error (MMSE), which we designate as DL-Enhanced. Our main innovation is a phase-preserving mechanism that maintains critical phase information frequently degraded in purely data-driven approaches. We evaluate the proposed technique considering MIMO-OFDM systems considering 3GPP Clustered Delay Line Model C (CDL-C) channels. Simulation results demonstrate that our method outperforms conventional techniques at high-SNR levels, thanks to neural network-based feature extraction and adaptive processing.

1. Introduction

1.1. Motivation and Related Work

In MIMO-OFDM systems, channel estimation is indispensable for coherent detection and diversity combining. Among the traditional techniques, methods based on the channel frequency response (CFR), such as LS and Linear Minimum Mean Square Error (LMMSE), stand out and can be applied using pilots or detected symbols [1,2]. More advanced approaches include parametric models, suitable for sparse channels, and iterative estimation inspired by turbo and Low-Density-Parity-Check (LDPC) codes, which exploit feedback information from the decoder [3]. When applied to MIMO-OFDM systems, these methods face the additional challenge of overlapping signals from multiple antennas, requiring more robust algorithms [4].

Decision-directed (DD) methods, which use already detected data symbols to refine the estimation, can mitigate this issue as they reduce the need for extra pilots [5]. However, high-mobility scenarios impose additional challenges, demanding adaptive algorithms or Doppler models that track rapid channel variations. For sparse channels, Compressive Sensing (CS)-inspired methods exploit the channel structure, reducing pilot overhead. Finally, in the case of MIMO-OFDM, channel estimation assumes a multidimensional nature, requiring algorithms capable of simultaneously handling selectivity in time, frequency, and space, while maintaining robustness against inter-antenna interference [4,6].

In addition to these techniques, estimation methods based on superimposed pilots stand out, improving spectral efficiency by inserting pilots directly on data symbols, albeit at the cost of power penalties [7]. Transformation-domain techniques have also been explored to reduce computational complexity and mitigate noise in selective channels [7]. Another relevant advance is the use of iterative estimation in turbo and factor graph receivers, which leverage soft information from the decoder to successively improve channel estimation, achieving significant gains over classical methods [7]. Finally, the literature identifies open research directions such as optimal pilot design in high-mobility scenarios, the trade-off between spectral efficiency and complexity in MIMO-OFDM, and the application of CS and machine learning methods to exploit channel sparsity or correlations [7].

There are also joint time–frequency estimation techniques, based on structured CS, which exploit the property of sparse common support in MIMO channels by combining a pseudo-random preamble in the time domain, identical across all transmit antennas, with a reduced set of orthogonal pilots in the frequency domain [8]. This approach enables accurate and spectrally efficient channel recovery, substantially reducing overhead compared with traditional preamble- or pilot-based methods. Moreover, the partial common support information obtained can be used to lower algorithmic complexity and improve robustness in low-SNR scenarios [8].

Beyond the time–frequency combination, the scheme proposed in [8] employs the SA-SOMP algorithm, an adaptive version of the classical SOMP, which integrates partial common support information to reduce complexity and accelerate convergence. Simulation results show that this method achieves a higher probability of successful channel recovery with fewer pilots, providing gains of up to 7 dB in terms of MSE compared with traditional preamble- or pilot-based techniques, while ensuring significantly higher spectral efficiency.

In addition to the approaches already mentioned, there has also been recent research exploring DL architectures for channel estimation in massive MIMO systems. One example is the PACE-Net network, based on polarized self-attention, which transforms the channel estimation problem into a denoising task in the image domain. This approach demonstrated improvements in terms of lower Normalized Mean Square Error (NMSE) and computational complexity compared with conventional methods such as MMSE, particularly in large-scale scenarios [9].

More recently, low-complexity neural network-based channel estimation approaches have emerged, suitable for New Radio (NR) systems. For example, in [10], the authors propose a machine learning estimator that exploits the equivalence between the channel impulse response (CIR) and the channel frequency response (CFR), using a neural network architecture with only one hidden layer and weight quantization techniques. This method significantly reduces memory overhead and computational complexity compared with conventional ML estimators, while maintaining performance close to MMSE and achieving SNR gains in practical scenarios with Sounding Reference Signal (SRS) pilots.

In beam-space front-ends, analog spatial compression precedes baseband processing and therefore reshapes the effective channel seen by any digital estimator. Two recent examples are a cylindrical dielectric lens with hybrid mechanical/electrical two-dimensional scanning [11] and electronically reconfigurable periodic arrays whose steering law is set by the tunable phase constant of a guided/leaky mode [12]. Both achieve wide angular coverage but induce scan state dependent magnitude and, critically, heightened phase sensitivity at the baseband. Unlike these works—which focus on hardware design and radiation patterns—our contribution is a baseband estimator that explicitly preserves phase (by anchoring to the LS angle) while adaptively fusing LS/MMSE magnitudes under a simplex constraint. This phase-preserving fusion mitigates drift and scan-linked gain bias without any RF changes and integrates per beam immediately after the analog combiner. In practice, it complements such beam-scanning architectures by maintaining coherent detection with negligible added complexity.

Complementarily, in the context of Reconfigurable Intelligent Surfaces (RISs), several architectures and algorithms have been proposed to reduce training overhead and enable explicit estimation of cascaded channels. One line relies on hardware with few active elements to allow sampling/reception at the RIS itself and thus explicit estimation [13]. Algorithmically, notable studies include two-phase approaches that exploit the low angular dimensionality in mmWave and formulate estimation as high-resolution Direction of Arrival (DOA) problems (e.g., TRICE) [14], as well as hybrid schemes combining DL and CS for flat and frequency-selective channels, reducing the number of pilots by exploiting common sparsity [15]. For massive MIMO-OFDM channels, tensor-based methods leverage the multilinear space–time–frequency structure to perform joint estimation with gains over LS/LMMSE approaches [16]. In the generative learning domain, both GAN-based models for wideband estimation with few pilots at a low SNR [17] and deep generative networks that impose low-dimensional priors in high-dimensional problems [18] have shown effectiveness. More recently, score-based/diffusion models achieved performance gains and out-of-distribution robustness in MIMO by sampling from the posterior distribution of the channel [19]. In time-selective channels, DL-based estimators are able to track fast variations without prior model knowledge [20]. Massive grant-free access scenarios benefit from turbo receivers that jointly integrate activity detection, channel estimation, and data decoding (BiG-AMP), exploiting common sparsity and extrinsic information [21]. Systematic mapping studies highlight persistent challenges in antenna design and estimation (e.g., pilot contamination and Channel State Information (CSI) overhead) for mMIMO [22]. More broadly, the integration of communication and sensing imposes fundamental trade-offs between the data rate and detection-error exponent of channel states [23], and physical-layer security perspectives show how CSI accuracy constrains proactive eavesdropping strategies based on DRL [24]. Finally, channel customization through multiple RIS in hybrid Tx RISRx architectures demonstrates that joint beamforming design and CSI acquisition are interdependent, with direct implications for the pilot budget [25].

1.2. Objectives, Contributions, and Organization

This paper investigates a hybrid approach to channel estimation in MIMO-OFDM systems, employing a simulated 2 × 2, 4 × 2, 8 × 4 MIMO configuration with Quadrature Phase Shift Keying (QPSK) modulation and a CDL-C channel model. The proposed method integrates conventional estimation techniques with DL models to enhance accuracy under realistic channel conditions.

To address the degradation of phase information often observed in purely data-driven models, we introduce a dedicated phase-preserving mechanism. This mechanism ensures the retention of essential phase components, which is particularly crucial for phase-modulated schemes such as QPSK, where precise phase estimation directly influences demodulation performance.

This system dynamically adjusts the contribution of each estimator according to varying channel conditions and the signal-to-noise ratio (SNR), thereby enhancing overall estimation robustness and accuracy. In addition, because our method uses a Multilayer Perceptron (MLP) with explicit in-phase (I)/quadrature (Q) separation in the symbol domain, it is aligned with the recent literature that adopts similar MLP-based I/Q processing blocks for interference cancellation [26].

The remainder of this paper is organized as follows. Section 2 describes the system and channel model considered in the simulations. Section 3 reviews classical channel estimation methods such as LS and MMSE. Section 4 introduces the proposed DL-Enhanced hybrid architecture, detailing both the fusion strategy and the I/Q refinement stage. Section 5 presents the simulation setup and discusses the numerical results under different MIMO configurations. Finally, Section 6 concludes the paper and outlines directions for future work.

2. System Characterization

2.1. Channel Characterization

We consider a frequency-selective MIMO-OFDM system with T transmit antennas and R receive antennas, where the channel is decomposed into $N=64$ parallel flat-fading subchannels. For the k-th subcarrier, the channel matrix is given by

$$\mathbf{H}\left(k\right)=\left[\begin{array}{cccc}H{\left(k\right)}_{1,1}& H{\left(k\right)}_{1,2}& \dots & H{\left(k\right)}_{1,T}\\ H{\left(k\right)}_{2,1}& H{\left(k\right)}_{2,2}& \dots & H{\left(k\right)}_{2,T}\\ ⋮& ⋮& \ddots & ⋮\\ H{\left(k\right)}_{R,1}& H{\left(k\right)}_{R,2}& \dots & H{\left(k\right)}_{R,T}\end{array}\right].$$

(1)

Here, $H{\left(k\right)}_{r,t}$ represents the frequency-domain channel coefficient between the t-th transmit antenna and r-th receive antenna for subcarrier $k\in \{1,\dots ,N\}$. The channel is normalized to unit average power $\mathbb{E}\left[\right|H{\left(k\right)}_{r,t}{|}^2]=1$. The channel impulse response is modeled using a multipath profile inspired by the 3GPP CDL-C characteristics, representing urban macro-cellular scenarios with non-line-of-sight conditions. The channel impulse response is modeled with a maximum delay spread of $L=16$ taps.

2.2. Transmitted Signals

The transmitted symbols are selected from a QPSK constellation with unit average symbol energy. For each transmit antenna t, the frequency-domain signal vector across all subcarriers is

$${\mathbf{X}}_t={[X_{t,1},X_{t,2},\dots ,X_{t,N}]}^T.$$

(2)

The complete transmitted signal matrix $\mathbf{X}$ has dimensions $T\times N$. For the k-th subcarrier, the transmitted signal vector is

$$\mathbf{X}\left(k\right)={[X_{1,k},X_{2,k},\dots ,X_{T,k}]}^T.$$

(3)

In the $2\times 2$ simulation setup, we have $N_P=7$ scattered pilots with indices $I_p=\{8,16,24,32,40,48,56\}$. For larger arrays, pilots are generated per-transmitter with 16-subcarrier spacing (4 pilots per T), so $N_P=4N_t$ and $N_U=N-N_P$. The resulting subcarrier layout is illustrated in Figure 1.

Figure 1. OFDM subcarrier structure of scattered pilots and data subcarriers across the total bandwidth of subcarriers.

Each pilot on a given antenna is $X_{t,p}=1+j$. The OFDM modulation transforms frequency-domain symbols into time-domain signals through the IDFT, where $\mathbf{F}$ is the DFT matrix:

$${\mathbf{x}}_t={\mathbf{F}}^{-1}{\mathbf{X}}_t,$$

(4)

A cyclic prefix longer than the overall channel impulse response is appended to each time-domain block. The additive white Gaussian noise is modeled as $\mathbf{N}\left(k\right)\sim \mathcal{CN}(\mathbf{0},{\sigma }_n^2\mathbf{I})$.

2.3. Received Signals

For the k-th subcarrier, the received signal vector is

$$\mathbf{Y}\left(k\right)=\mathbf{H}\left(k\right)\mathbf{X}\left(k\right)+\mathbf{N}\left(k\right).$$

(5)

The equalized symbol vector is obtained with the MMSE linear equalizer:

$${\mathbf{X}}_{\mathrm{eq}}\left(k\right)={\mathbf{W}}_{\mathrm{MMSE}}\left(k\right)\mathbf{Y}\left(k\right).$$

(6)

Figure 2 represents the transmission/reception chain equivalent to the subcarrier considered in this work.

Figure 2. Subcarrier-level model for the considered OFDM transmission.

3. Traditional Channel Estimation Methods

The classical estimators considered here are LS and MMSE, which only use the known pilots placed at indices $I_p$. Figure 3 summarizes this baseline pilot-aided stage, and the pilot observations are processed by LS and MMSE blocks to produce the hypotheses ${\widehat{\mathbf{H}}}_{\mathrm{LS}}$ and ${\widehat{\mathbf{H}}}_{\mathrm{MMSE}}$.

Figure 3. Channel estimation using LS and MMSE methods.

Using the received signal at each antenna and the scattered pilot configuration at indices $I_p$, the LS estimate at the r-th receive antenna for pilot position p is

$${\widehat{H}}_{\mathrm{L}\mathrm{S}r,t}\left(p\right)={\displaystyle \frac{Y_{r,p}}{X_{t,p}}},p\in I_p,$$

(7)

To obtain estimates for all N subcarriers, linear interpolation across frequency is applied. For each data subcarrier $k\in I_d$, the estimated channel is

$${\widehat{H}}_{\mathrm{L}\mathrm{S}r,t}\left(k\right)={\widehat{H}}_{\mathrm{L}\mathrm{S}r,t}\left(p_{\mathrm{left}}\right)+{\displaystyle \frac{k-p_{\mathrm{left}}}{p_{\mathrm{right}}-p_{\mathrm{left}}}}\left[{\widehat{H}}_{\mathrm{L}\mathrm{S}r,t}\left(p_{\mathrm{right}}\right)-{\widehat{H}}_{\mathrm{L}\mathrm{S}r,t}\left(p_{\mathrm{left}}\right)\right].$$

(8)

In addition to the LS method, we adopt the MMSE estimator starting from the LS estimate ${\widehat{\mathbf{H}}}_{\mathrm{LS}}$ and a channel correlation model ${\mathbf{R}}_{HH}$; the MMSE estimator yields the minimum mean-square-error estimate under Gaussian noise:

$${\widehat{\mathbf{H}}}_{\mathrm{MMSE}}={\mathbf{R}}_{HH}{\left({\mathbf{R}}_{HH}+{\sigma }_n^2\mathbf{I}+\alpha \mathbf{I}\right)}^{-1}{\widehat{\mathbf{H}}}_{\mathrm{LS}}.$$

(9)

where ${\mathbf{R}}_{HH}$ is the channel correlation matrix, ${\sigma }_n^2=1/{\mathrm{SNR}}_{\mathrm{linear}}$, and $\alpha$ is a regularization term.

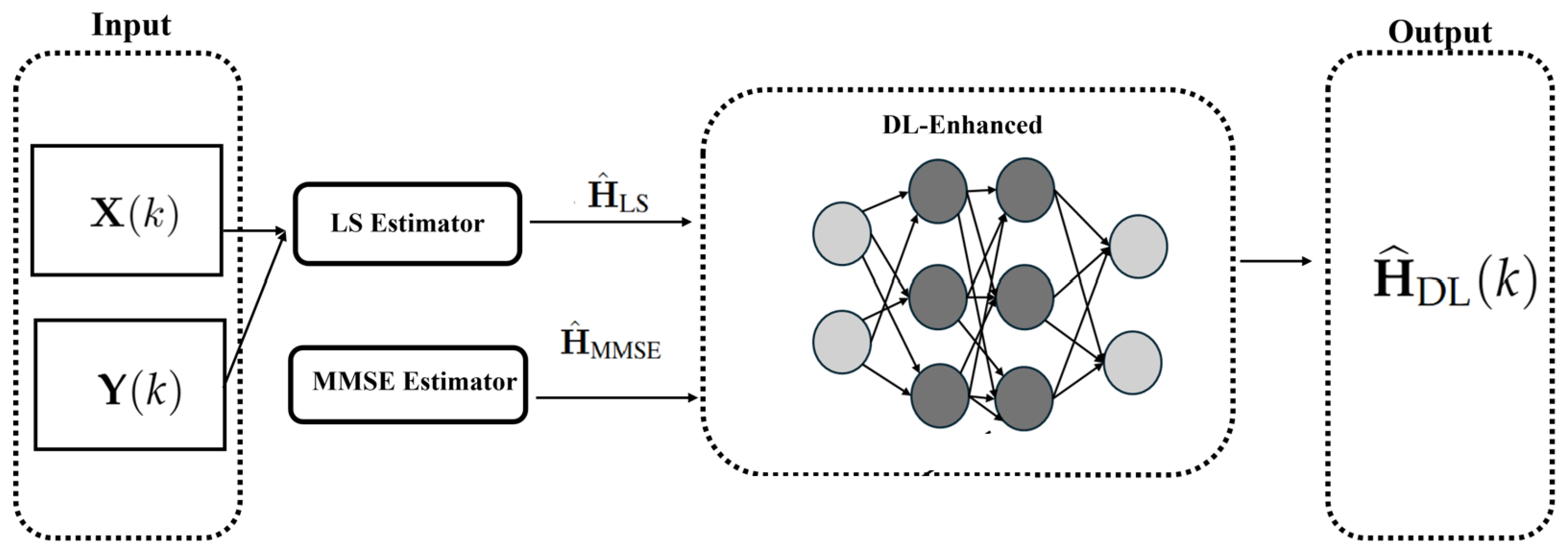
4. Proposed Hybrid DL-Enhanced

The proposed DL-Enhanced has two lightweight learning phases integrated with classical processing: a channel-level fusion that performs a convex magnitude combination of ${\widehat{\mathbf{H}}}_{\mathrm{LS}}$ and ${\widehat{\mathbf{H}}}_{\mathrm{MMSE}}$ under a simplex constraint while restoring the LS phase, and a symbol-level I/Q denoiser applied after linear MMSE equalization. A single decision-directed iteration refines the channel estimate using reliable hard decisions, and final detection uses MMSE equalization. At the channel estimation level, a compact fusion MLP consumes physics-inspired features distilled from the LS and MMSE estimates. At the symbol-processing level, a per-transmitter I/Q denoiser MLP is applied after linear MMSE equalization to refine the in-phase and quadrature components. This combination reduces the structural channel-estimation error while preserving the phase and mitigates residual post-equalization noise at negligible additional complexity.

In combination, the channel-level fusion reduces structural estimation errors while explicitly preserving the phase, whereas the symbol-level denoiser mitigates residual noise and mild distortions at the detector output. Both blocks add negligible complexity relative to standard equalization and are compatible with a single DD polishing step. Figure 4 provides a block-level view of the two-phase DL-Enhanced receiver and its integration with classical methods.

Figure 4. Block diagram of DL-Enhanced method.

4.1. Architecture

The DL fusion component uses self-supervised training. An MLP takes features extracted from ${\mathbf{H}}_{\mathrm{LS}}$ and ${\mathbf{H}}_{\mathrm{MMSE}}$ as input and outputs fusion weights $\mathit{\alpha }$ for

$${\mathbf{H}}_{\mathrm{fusion}}={\alpha }_1{\mathbf{H}}_{\mathrm{LS}}+{\alpha }_2{\mathbf{H}}_{\mathrm{MMSE}},$$

(10)

with ${\alpha }_1,{\alpha }_2\ge 0$ and ${\alpha }_1+{\alpha }_2=1$. The fused magnitude is combined with the LS phase to avoid angle drift:

$${\mathbf{H}}_{\mathrm{DL}}=\left|{\mathbf{H}}_{\mathrm{fusion}}\right|\odot e^{j\angle \left({\mathbf{H}}_{\mathrm{LS}}\right)}.$$

(11)

A second DL component implements per-transmitter I/Q denoisers. After MMSE equalization, each denoiser refines the real and imaginary parts of the equalized symbols, reducing residual noise and mild distortions.

A single decision-directed iteration uses reliable hard decisions to update the channel estimate prior to the final MMSE detection. Final equalization on each subcarrier uses

$$\mathbf{W}={\left({\mathbf{H}}^H\mathbf{H}+{\sigma }^2\mathbf{I}\right)}^{-1}{\mathbf{H}}^H\mathrm{or}{\mathbf{H}}^H{\left(\mathbf{H}{\mathbf{H}}^H+{\sigma }^2\mathbf{I}\right)}^{-1},{\mathbf{X}}_{\mathrm{eq}}=\mathbf{W}\mathbf{Y}.$$

(12)

4.2. Theoretical Rationale for Phase-Preserving Fusion

For a fixed subcarrier, let $H\in \mathbb{C}$ be the true coefficient and let ${\widehat{H}}_{\mathrm{LS}}=H+{\epsilon }_{\mathrm{LS}}$ and ${\widehat{H}}_{\mathrm{MMSE}}=H+{\epsilon }_{\mathrm{M}}$ be the pilot-aided hypotheses produced by LS and MMSE, respectively. We assume the standard small-error regime at moderate/high SNRs, where ${\epsilon }_{\mathrm{LS}}, {\epsilon }_{\mathrm{M}}$ are zero-mean circular complex random variables with finite second moments, possibly correlated (because the MMSE smoothing is built on the LS seed). Denote magnitudes $R_{\mathrm{LS}}\triangleq \left|{\widehat{H}}_{\mathrm{LS}}\right|$, $R_{\mathrm{M}}\triangleq \left|{\widehat{H}}_{\mathrm{MMSE}}\right|$ and the LS-phase error ${\varphi }_{\mathrm{LS}}\triangleq \angle ({\widehat{H}}_{\mathrm{LS}})-\angle \left(H\right)$.

$${\widehat{H}}_{\mathrm{DL}}=\left(\alpha R_{\mathrm{LS}}+(1-\alpha )R_{\mathrm{M}}\right)e^{j\angle \left({\widehat{H}}_{\mathrm{LS}}\right)},\alpha \in [0,1].$$

Rationale for preserving phase. Write $H=\left|H\right|e^{j\theta }$ and ${\widehat{H}}_{\mathrm{LS}}=R_{\mathrm{LS}}{e}^{j(\theta +{\varphi }_{\mathrm{LS}})}$. For small complex perturbations and circular noise, ${\varphi }_{\mathrm{LS}}\approx \mathrm{Im}\{{\epsilon }_{\mathrm{LS}}/H\}$, hence $\mathbb{E}\left[{\varphi }_{\mathrm{LS}}\right]=0$ and $\mathrm{Var}\left({\varphi }_{\mathrm{LS}}\right)\approx {\sigma }_{\varphi }^2={\displaystyle \frac{\mathbb{E}\left[\right|{\epsilon }_{\mathrm{LS}}{|}^2]}{{2\left|H\right|}^2}}$. Unconstrained complex regressors that average phases can introduce a bias $b_{\varphi }\ne 0$ and inflate $\mathrm{Var}\left(\varphi \right)$ by angle wrapping. For phase-modulated constellations, the effective SNR degrades as ${\gamma }_{\mathrm{eff}}\approx \gamma {cos}^2\varphi$ (QPSK) or, more generally, $\mathrm{BER}\approx \mathcal{Q}\left(\sqrt{2\kappa \gamma }cos\varphi \right)$ with modulation-dependent $\kappa$. Enforcing $\angle \left({\widehat{H}}_{\mathrm{DL}}\right)=\angle \left({\widehat{H}}_{\mathrm{LS}}\right)$ guarantees $\mathbb{E}\left[{\varphi }_{\mathrm{DL}}\right]=0$ and $\mathrm{Var}\left({\varphi }_{\mathrm{DL}}\right)={\sigma }_{\varphi }^2$ to first order; the fusion then acts only on the magnitude, where convex gains are attainable.

Magnitude-risk dominance under convex fusion. Define the magnitude risk $E\left(\alpha \right)\triangleq {\left(\alpha R_{\mathrm{LS}}+(1-\alpha )R_{\mathrm{M}}-\left|H\right|\right)}^2$. Since $E\left(\alpha \right)$ is a convex quadratic on $[0,1]$, its minimum on the simplex never exceeds the endpoint risks:

$$\underset{\alpha \in [0,1]}{min}E\left(\alpha \right)\le min\left\{(R_{\mathrm{LS}}-{\left|H\right|)}^2,(R_{\mathrm{M}}-{\left|H\right|)}^2\right\}.$$

Taking expectations and using Jensen,

$$\mathbb{E}\left[\underset{\alpha \in [0,1]}{min}E\left(\alpha \right)\right]\le min\left\{\mathbb{E}\left[(R_{\mathrm{LS}}-{\left|H\right|)}^2\right],\mathbb{E}\left[(R_{\mathrm{M}}-{\left|H\right|)}^2\right]\right\}.$$

Thus, an oracle ${\alpha }^{★}$ that selects the best convex combination per realization strictly dominates both LS and MMSE magnitudes in expected squared error. The learned weight $\widehat{\alpha }$ obeys the non-expansive simplex projection; if the MLP output is L-Lipschitz in the features, the excess magnitude risk satisfies

$$\mathbb{E}\left[E\left(\widehat{\alpha }\right)-E\left({\alpha }^{★}\right)\right]\le C\mathbb{E}\left[|\widehat{\alpha }-{\alpha }^{★}|\right]\le CL\mathbb{E}\left[\parallel \widehat{\mathbf{f}}-{\mathbf{f}}^{★}\parallel \right],$$

for a constant C that depends only on bounded magnitudes. With well-conditioned features, the learned fusion is stable and near-oracle.

MSE decomposition and scaling with the SNR. Let ${\widehat{H}}_{\mathrm{DL}}=\left(\left|H\right|+{\mathrm{\Delta }}_R\right)e^{j(\theta +{\varphi }_{\mathrm{LS}})}$ with ${\mathrm{\Delta }}_R$ being the fused magnitude error. For small ${\varphi }_{\mathrm{LS}}$,

$$\mathbb{E}\left[||{\widehat{H}}_{\mathrm{DL}}{-H|}^2\right]\approx \underset{\mathrm{magnitude}\mathrm{term}}{\underbrace{\mathbb{E}\left[{\mathrm{\Delta }}_R^2\right]}}+\underset{\mathrm{phase}\mathrm{term}}{\underbrace{{\left|H\right|}^2\mathbb{E}\left[{\varphi }_{\mathrm{LS}}^2\right]}}.$$

MMSE magnitude errors obey $\mathbb{E}\left[\right(R_{\mathrm{M}}-{\left|H\right|)}^2]=\mathcal{O}\left({\sigma }^2\right)$, and LS has the same order with a larger constant due to interpolation noise amplification. By the dominance bound above, the fused magnitude term matches the better of the two to first order. The phase term is exactly that of LS (by construction) and scales as $\mathcal{O}\left({\sigma }^2\right)$. Therefore, the NMSE slope of the proposed estimator equals the best magnitude slope among {LS,MMSE} while inheriting the unbiased LS phase, which is the regime where BER gaps open at a medium/high SNR.

Impact on coherent detection (QPSK, first-order). With linear MMSE equalization and residual phase $\varphi$ at the channel estimate, the decision SNR degrades as ${\gamma }_{\mathrm{eq}}\approx \gamma {cos}^2\varphi$. Using $\varphi \sim \mathcal{N}(0,{\sigma }_{\varphi }^2)$ and ${cos}^2\varphi \approx 1-{\varphi }^2$,

$$\mathrm{\Delta }{\mathrm{SNR}}_{\mathrm{dB}}\approx 10{log}_{10}\left(1-{\sigma }_{\varphi }^2\right)\approx -\frac{10}{ln10}{\sigma }_{\varphi }^2=-4.343{\sigma }_{\varphi }^2\mathrm{dB}.$$

Byanchoring the phase to LS, we keep ${\sigma }_{\varphi }^2$ at its unbiased LS value; the fusion then reduces $\mathbb{E}\left[{\mathrm{\Delta }}_R^2\right]$ toward MMSE, yielding a strictly better (or equal) BER than either hypothesis alone. The empirical gaps reported in Section 5 at 10–15 dB are consistent with this expression for the measured ${\sigma }_{\varphi }^2$.

Decision-directed single iteration and variance reduction. Let $\eta$ be the fraction of subcarriers promoted to “virtual pilots” by the reliability mask and $\rho$ be their average decision reliability ($\rho \in [0,1]$). In the LS update with $N_P$ true pilots, the effective sample size becomes $N_P(1+\rho \eta N/N_P)$ and the variance in the LS seed scales approximately as

$${\mathrm{Var}}_{\mathrm{post}\text{-}\mathrm{DD}}\approx {\displaystyle \frac{1}{1+\rho \eta N/N_P}}{\mathrm{Var}}_{\mathrm{pre}\text{-}\mathrm{DD}}.$$

For the pilot layouts used here, typical $(\eta ,\rho )$ in the 10–15 dB range yields a 3–4 dB NMSE improvement.

Stability and robustness. Simplex projection is 1-Lipschitz, so the fusion weights are robust to feature noise. Phase restitution prevents angle wrapping and ensures BIBO stability in the phase channel. Cross-SNR generalization follows from the continuity of the feature-to-weight map; empirically, the held-out SNR experiments in Section 5 show negligible degradation, which is consistent with the excess-risk bound above.

Summary of quantitative takeaways. (i) The fused magnitude matches or improves LS/MMSE in expectation via convex dominance; (ii) the phase term equals the unbiased LS phase to first order, avoiding BER loss from phase drift; (iii) a single DD iteration shrinks variance roughly as ${\left(1+\rho \eta N/N_P\right)}^{-1}$, explaining the observed 3–4 dB NMSE gains over fusion-only.

4.3. Training

Training is fully self-supervised and does not use the true channel as labels. Each sample is generated by drawing a random MIMO channel and building an OFDM frame with pilots and QPSK data, which is then transmitted to obtain $\mathbf{Y}$.

From $(\mathbf{X},\mathbf{Y})$, the receiver first computes two classical channel estimates per link, Least Squares and MMSE-smoothed. Physics-inspired features $\mathbf{f}\in {\mathbb{R}}^6$ are extracted from these hypotheses (normalized SNR, LS and MMSE variability, relative LS–MMSE gap, temporal dispersion from the power delay profile, and a bias term).

Each feature is normalized to the interval [0.01, 0.99] to keep inputs well-conditioned and to avoid outlier saturation. Specifically, the SNR is linearly mapped from the value in dB to a number proportional to the SNR in dB divided by 50 and then clipped to the [0.01, 0.99] range. LS and MMSE variability are expressed as dimensionless coefficients of variation in the magnitudes. The LS–MMSE discrepancy is a normalized mean absolute gap, temporal dispersion is the second central moment of the aggregate power-delay profile normalized by the subcarrier span. We kept exactly six inputs to cover noise level, within-estimator variability, cross-estimator discrepancy, and delay spread with minimal dimensionality, which empirically reduced overfitting and yielded stable validation loss.

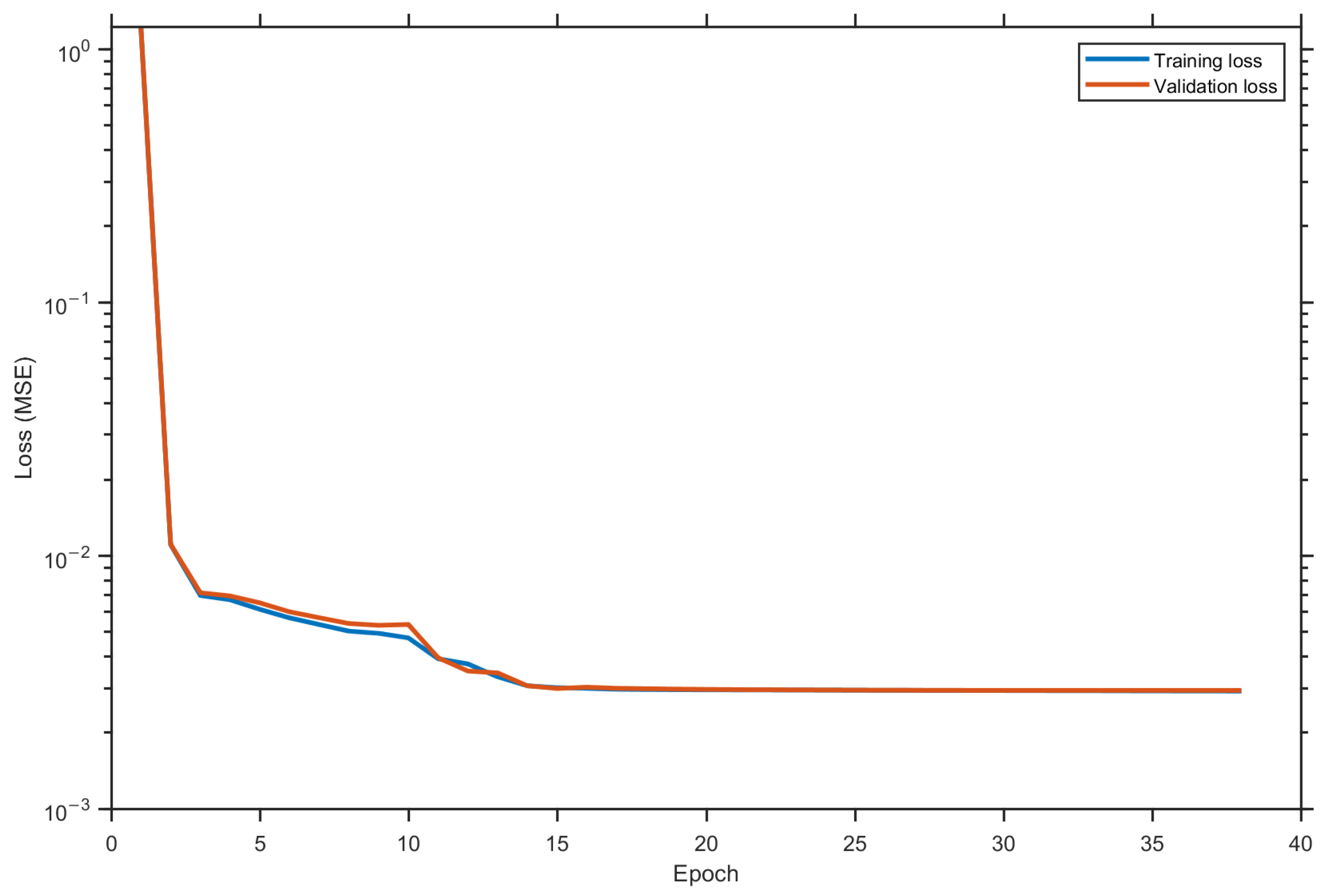
Figure 5 summarizes the learning dynamics of the self-supervised fusion network; the training and validation curves almost overlap over the epochs and reach a common plateau, indicating stable convergence with no signs of overfitting. This behavior suggests that the model constraints and training are sufficient to prevent the network from fitting noise patterns.

Figure 5. Training and validation loss (80/20 split).

To ensure stable convergence without access to true channels, we combine model-based constraints with conservative training. The fusion network outputs are projected onto the probability simplex, enforcing non-negative weights that sum to one. The fused magnitude is always combined with the LS phase, which prevents angle drift in the receiver. For the symbol domain denoiser, we only use high-confidence hard decisions selected by a reliability mask, reducing target noise. Validation uses an 80/20 split by channel with no overlap across SNRs between training and validation, and the final model is selected by early stopping at the best validation epoch. The training and validation losses decrease together and flatten at the same level, indicating convergence without overfitting.

For each sample, optimal fusion weights are obtained without access to the true channel by matching the received vector through a real-valued Least-Squares problem that linearly combines the LS- and MMSE-predicted receive signals; the solution is projected onto the probability simplex to enforce non-negativity and unit sum, yielding the target weights. An MLP with topology $6\to 16\to 8\to 2$ maps $\mathbf{f}$ to the predicted weights, trained with a mean-squared error between the simplex-projected output and the target.

A second self-supervised dataset is formed for symbol denoising. Equalization produces ${\mathbf{X}}_{\mathrm{eq}}$, hard QPSK decisions yield clean targets, and a confidence mask selects reliable samples. Inputs are the real and imaginary parts of ${\mathbf{X}}_{\mathrm{eq}}$. Targets are the corresponding parts of the reliable hard decisions. One MLP per transmit antenna with topology $2\to 16\to 8\to 2$ is trained with mean-squared error and later applied to refine the equalized symbols for all baselines.

The fusion MLP is trained with 1000 channel realizations on an SNR grid from 0 to 15 dB in 2 dB steps (9 points), producing 9000 samples. Data are split 80/20 by channel with no SNR overlap between training and validation. Optimization uses Levenberg–Marquardt (full-batch) with 200 maximum epochs and early stopping based on validation loss. The per-transmitter I/Q denoiser uses 1000 channels and the same 9-point SNR grid, and it is trained with Adam (initial learning rate 1 × 10⁻³, mini-batch 1024, 40 epochs) using reliability-filtered hard decisions as targets. For the auxiliary 4 × 2 and 8 × 4 results, the fusion MLP is trained with 300 channels on the same SNR grid (2700 samples) per configuration.

5. Simulation Setup and Results

In this section, we evaluate the proposed hybrid channel estimation on a QPSK MIMO–OFDM system with three MIMO configurations using the $R\times T$ convention $2\times 2$, $4\times 2$, and $8\times 4$. We evaluate BER and effective throughput, where effective throughput is defined as the number of information bits successfully delivered per channel use computed by multiplying the fraction of subcarriers that carry data excluding pilots by the number of transmit antennas and the QPSK bits per symbol and scaling by one minus the measured Bit Error Rate (BER).The SNR is swept from 0 to 15 dB in 2 dB steps.

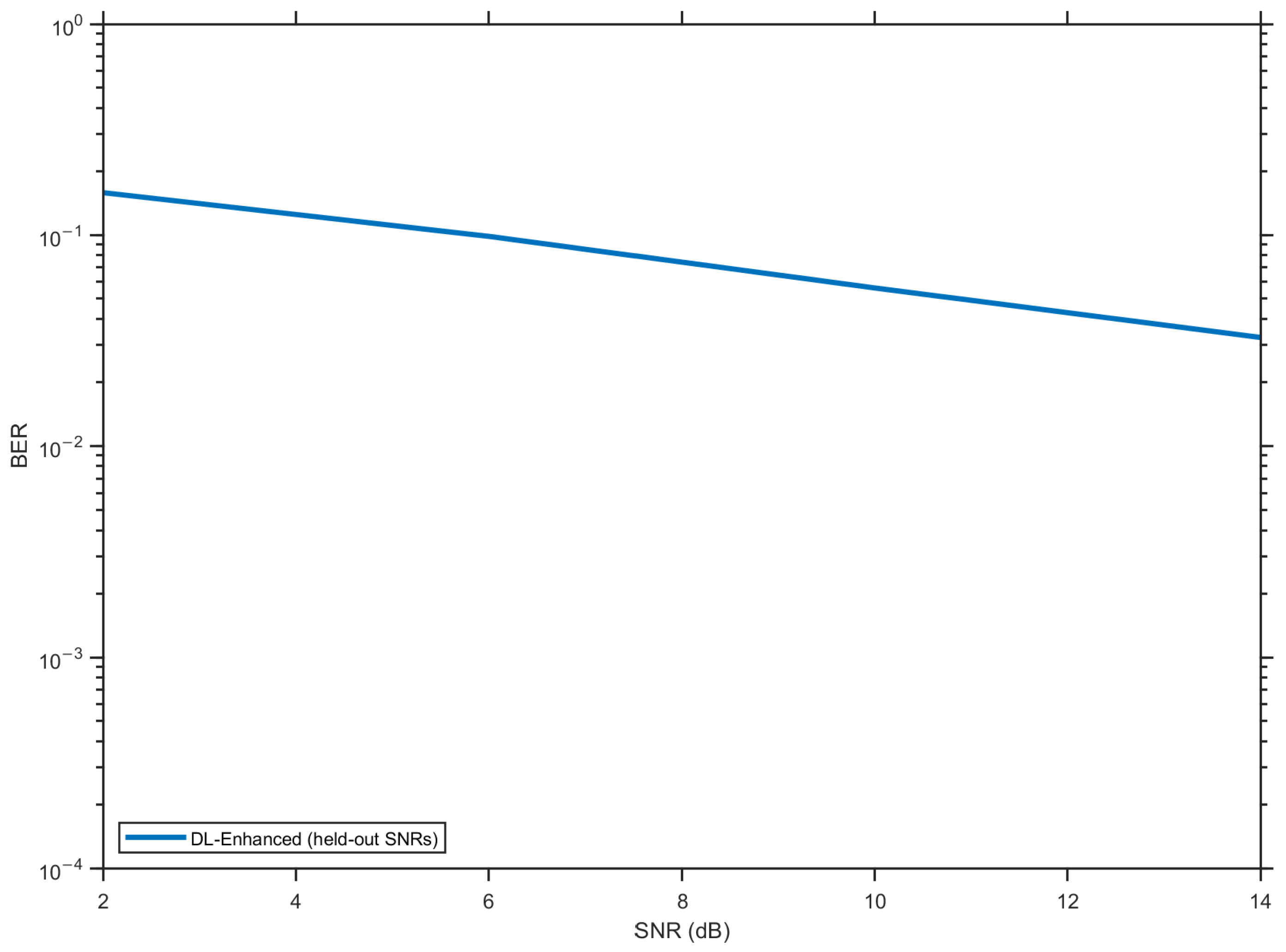
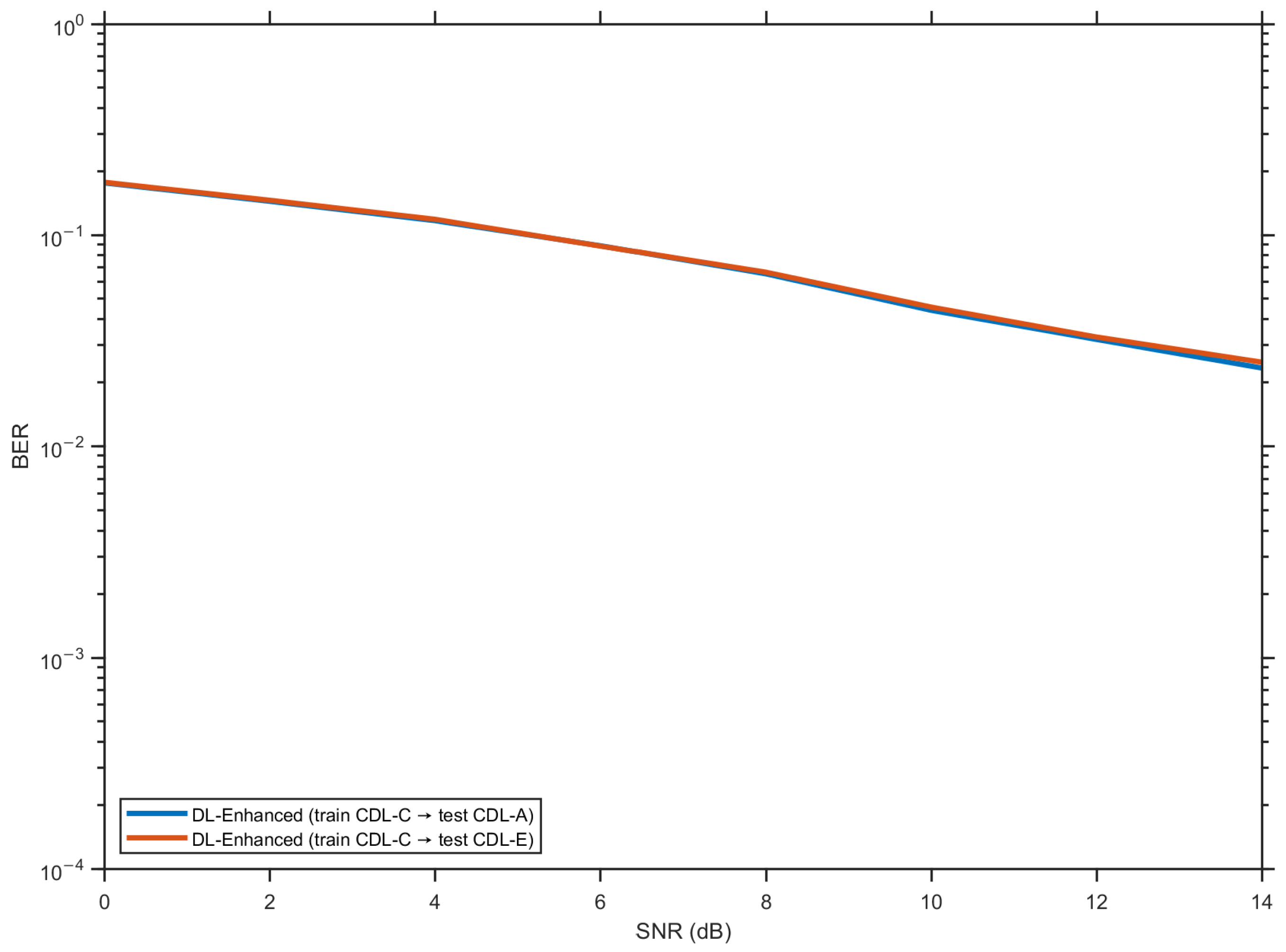
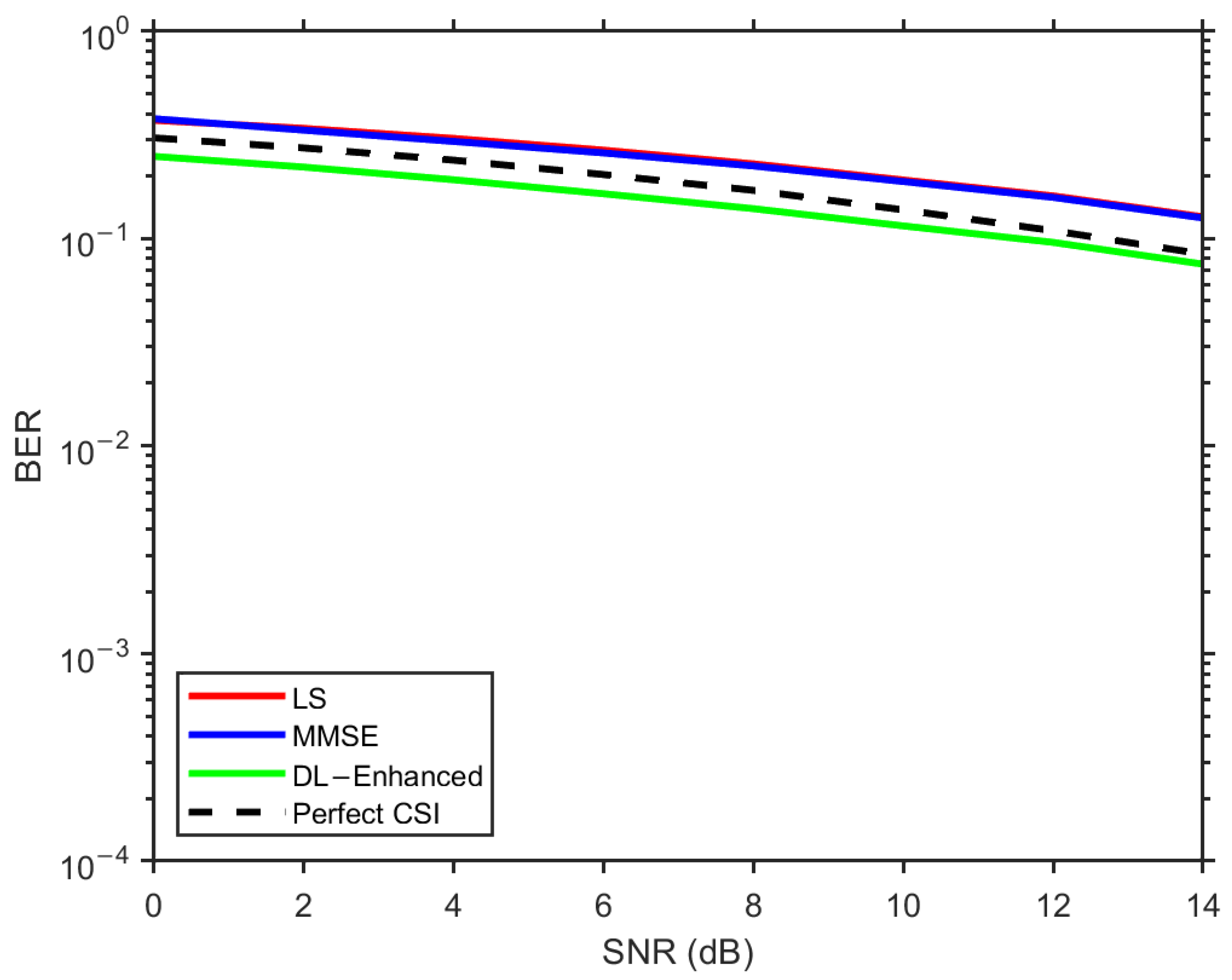
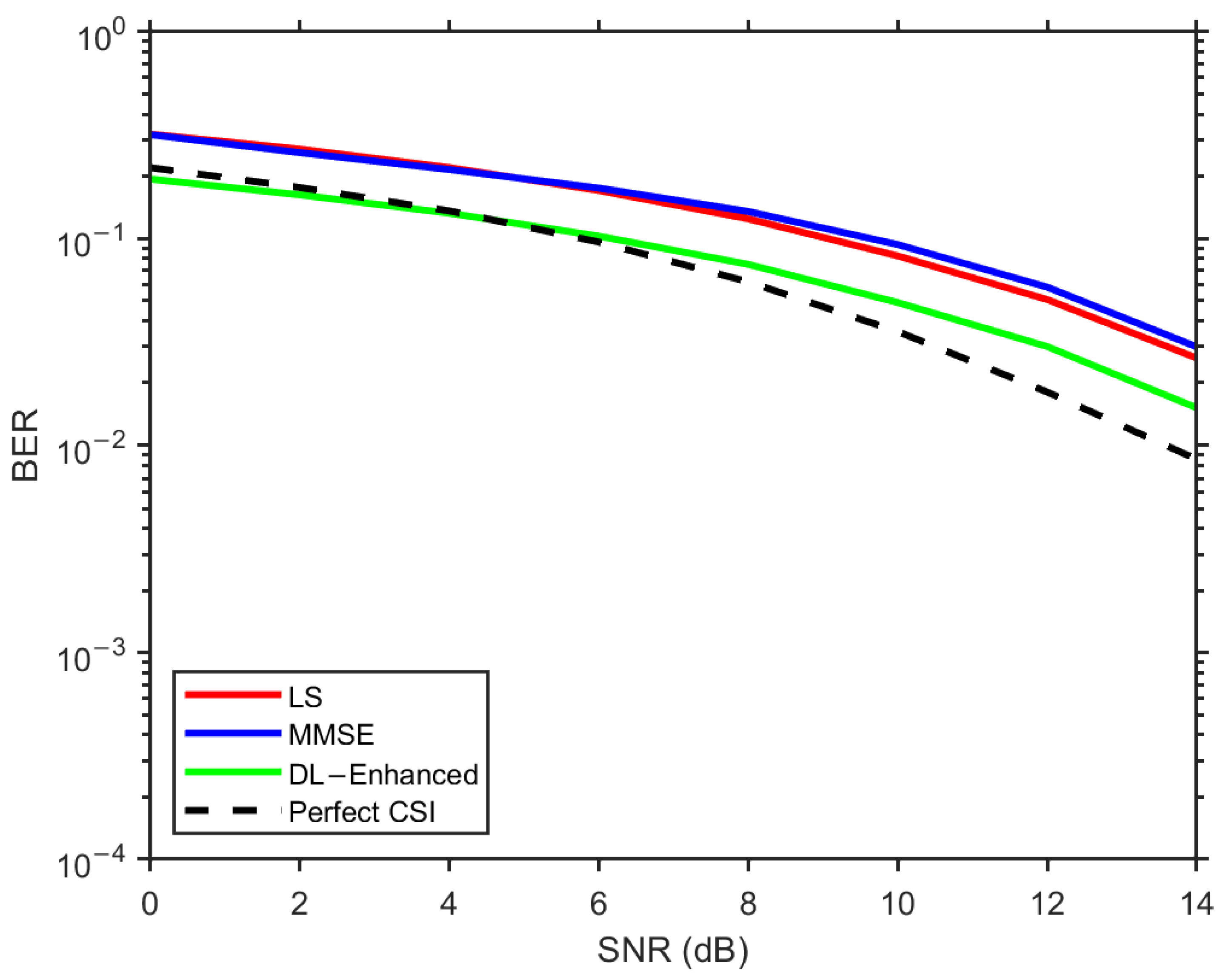
Beyond the main setup, we explicitly assess generalization along three axes. First, we test on unseen SNR points via an SNR hold-out, training on alternating SNRs (e.g., {0,4,8,12,15} dB) and evaluating on the interleaved set ({2,6,10,14} dB). Second, we examine scalability across antenna configurations by reporting results for 2 × 2, 4 × 2, and 8 × 4 arrays (the compact fusion MLP is retrained per array size, and no architectural changes are needed). Third, we evaluate zero-shot channel-profile transfer by training on CDL-C and testing, without retraining, on CDL-A and CDL-E. In all cases, the DL-Enhanced estimator preserves its margin over MMSE in both BER and NMSE. The two plots in Figure 6 and Figure 7 illustrate the hold-out SNR and the CDL-C→A/E transfers, respectively.

Figure 6. SNR hold-out generalization for the $2\times 2$ configuration.

Figure 7. Zero-shot profile transfer for the $2\times 2$ configuration.

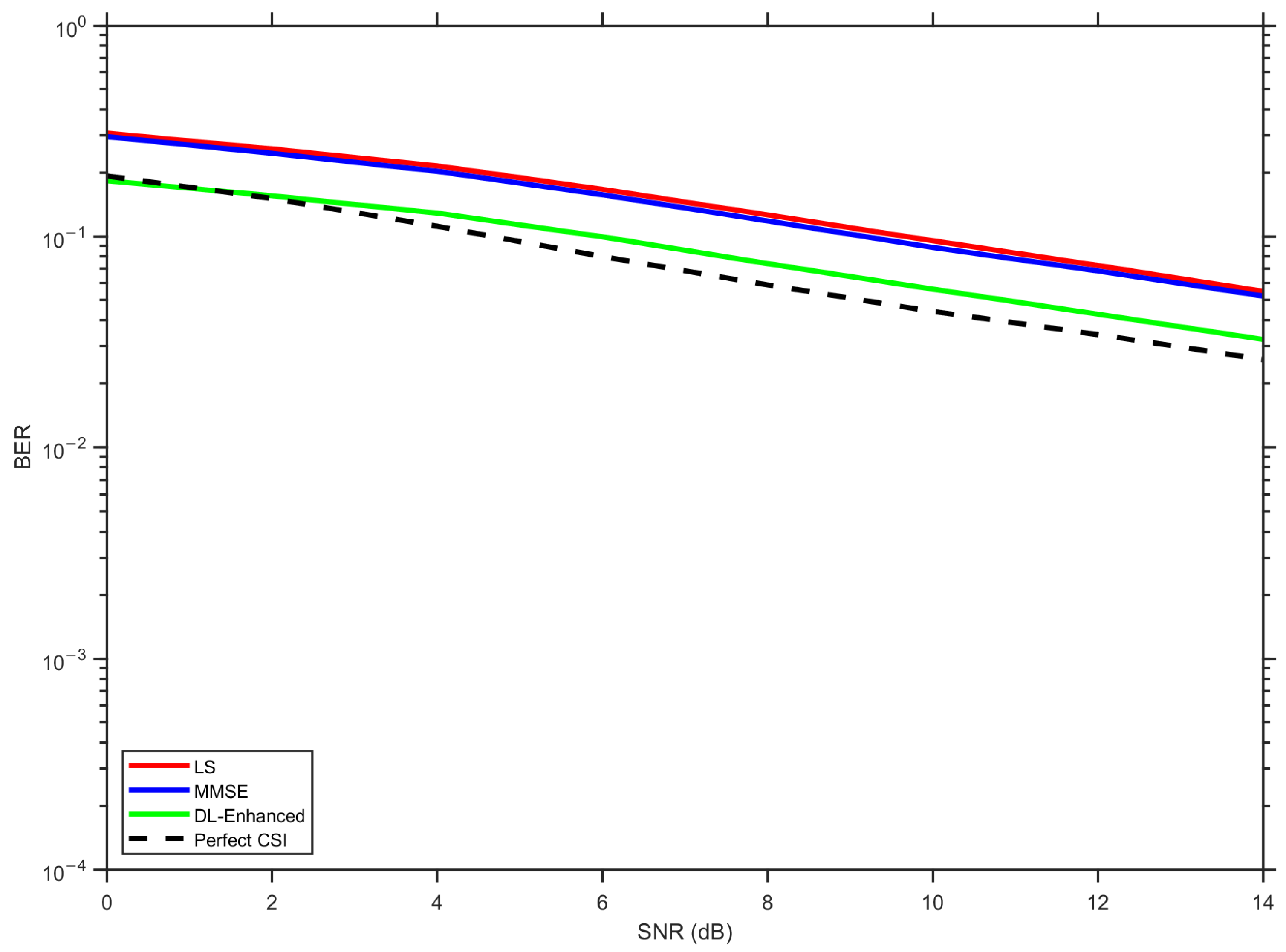
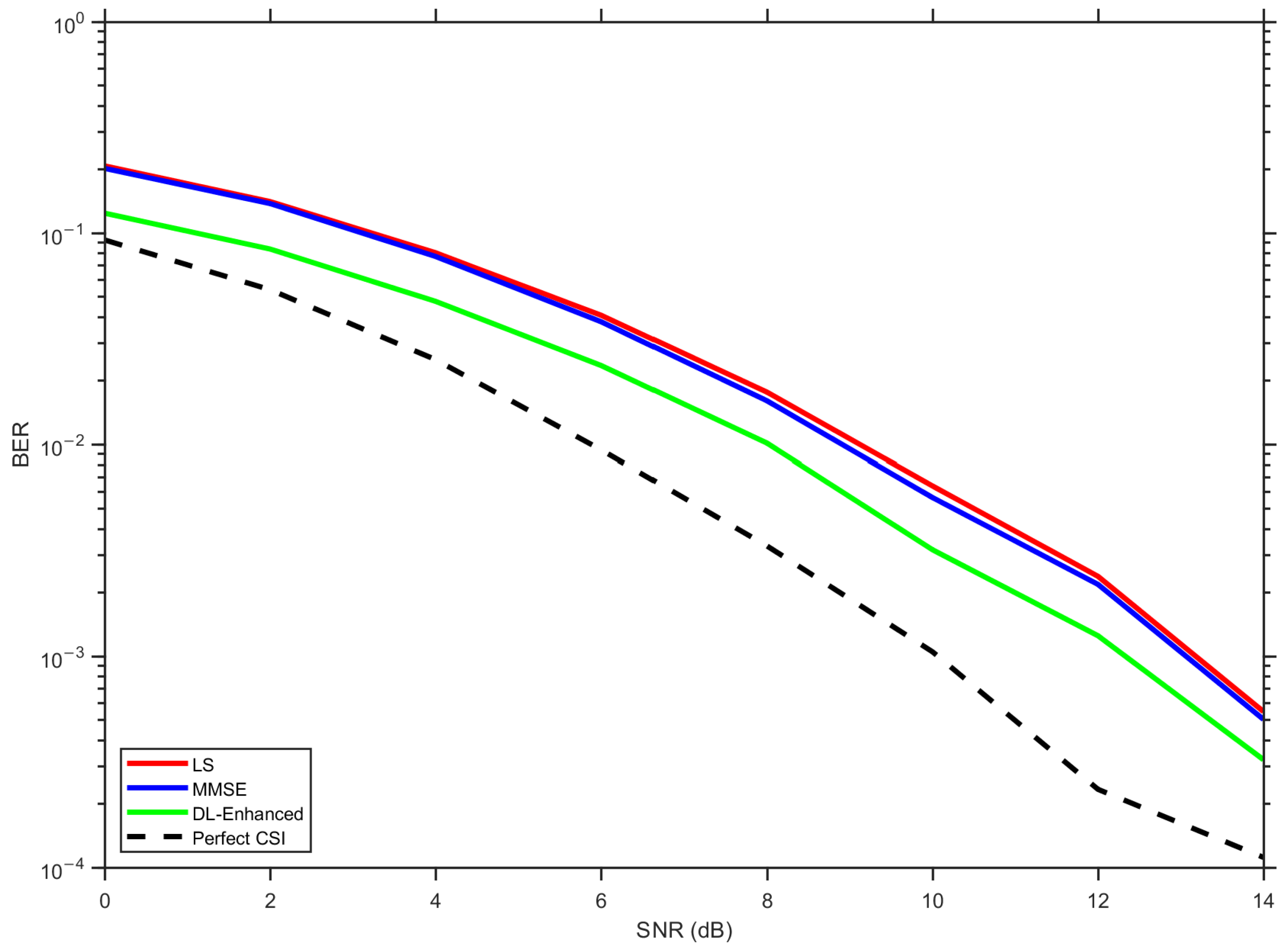
Figure 8 shows the BER obtained with a $2\times 2$ MIMO configuration.

Figure 8. BER for the $2\times 2$ configuration.

As can be observed from the figure, LS and MMSE estimators follow the expected trend, and LS exhibits the largest error floor due to noise amplification and interpolation errors, while MMSE improves on LS by incorporating prior delay-domain statistics but still departs from the perfect CSI bound at a moderate-to-high SNR. The proposed DL-Enhanced fusion remains consistently below MMSE for the entire SNR range, with visible gains, especially as the SNR increases. At low-SNR values between 0 and 5 dB, the curves are close because detection is fundamentally noise-limited and none of the estimators can fully overcome the random perturbations. In this regime, the fusion network assigns relatively balanced weights to both hypotheses, effectively averaging their contributions. As the SNR increases to the range of 10–15 dB, the performance gap becomes more evident. The convex fusion mechanism shifts emphasis toward the higher-quality hypothesis, which allows the magnitude estimate to remain accurate even when the individual methods diverge. At the same time, LS-phase anchoring prevents the angle drift that typically arises in purely data-driven complex regression, ensuring that the fused channel maintains consistent phase information for coherent detection. The optional DD update also contributes in this region. With more reliable symbol estimates available at higher SNRs, a single DD iteration can reinforce the pilot set with additional subcarriers while keeping the computational overhead low. This further stabilizes the equalizer without the cost of multiple feedback loops. The combined effect is a performance that lies significantly closer to the perfect CSI reference than MMSE and is well-separated from LS. These results confirm that the proposed hybrid architecture not only generalizes well in training but also translates into tangible performance gains under practical operating conditions.

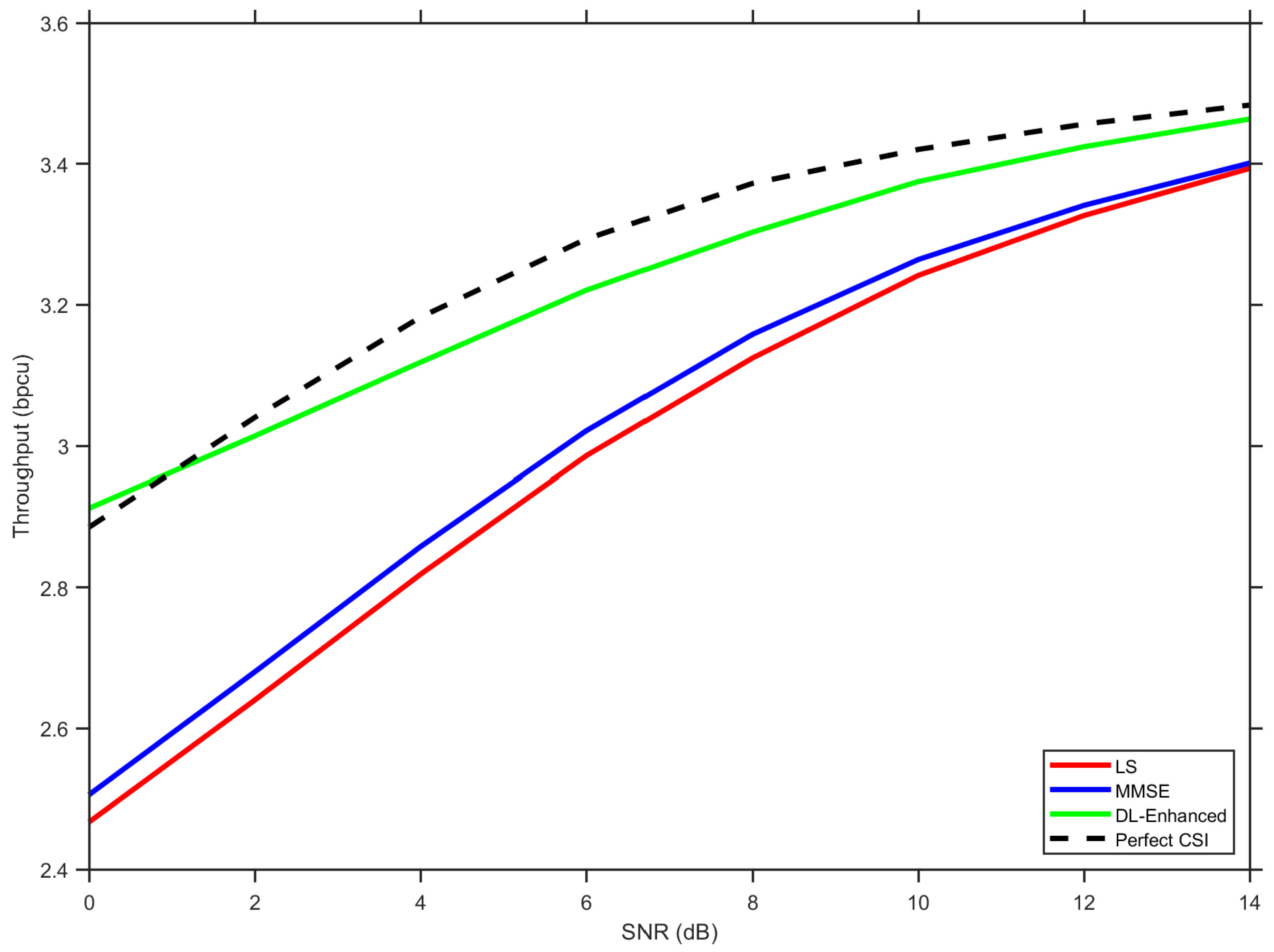
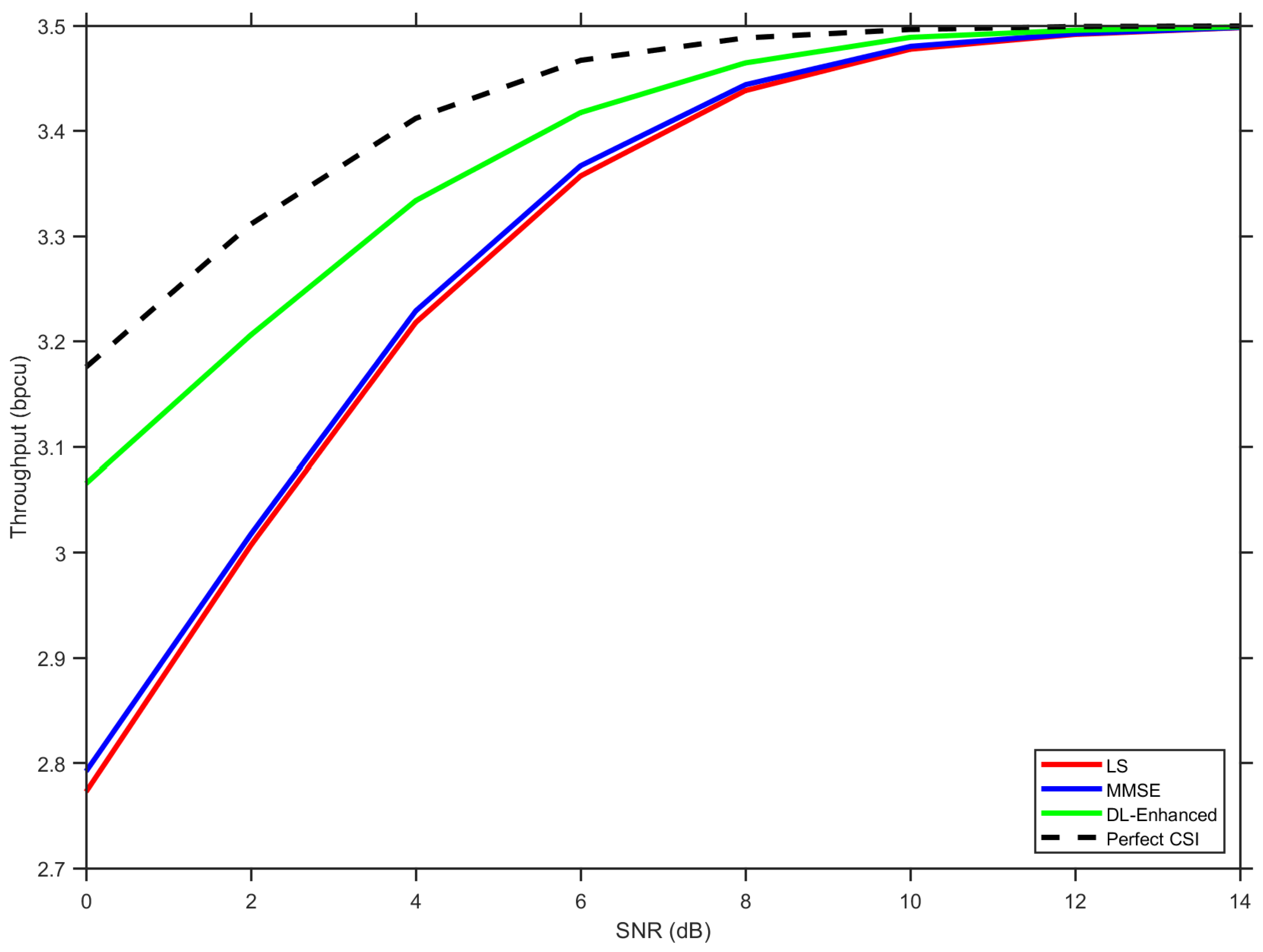
Figure 9 illustrates the throughput performance across the considered SNR range. At a low SNR (0–5 dB), all methods suffer from significant BER-induced capacity loss, with LS performing worst due to its higher error floor. The DL-Enhanced approach maintains a consistent advantage over both baselines, approaching the perfect CSI bound more closely as the SNR increases.

Figure 9. Throughput for the $2\times 2$ configuration.

The throughput gap becomes particularly pronounced at higher SNR values. At 15 dB, DL-Enhanced achieves approximately 3.46 bpcu compared to 3.41 bpcu for MMSE and 3.40 bpcu for LS, representing relative improvements of 1.5% and 1.8%, respectively. While these gains may appear modest in absolute terms, they translate to meaningful capacity increases in bandwidth-limited scenarios. The consistent separation from the baselines across the entire SNR range demonstrates the robustness of the hybrid fusion approach.

The throughput analysis confirms that the proposed method not only reduces BER but also translates these gains into practical system-level improvements. The convex fusion mechanism effectively leverages the complementary strengths of LS and MMSE estimation, while the phase anchoring and DD refinement maintain reliable performance without significant computational overhead.

Figure 10 illustrates the impact of increasing the number of receive antennas from $R=2$ to $R=4$ while keeping $T=2$. As expected, receive diversity shifts all curves downward, since additional spatial observations improve estimation quality and detection robustness.

Figure 10. BER for the $4\times 2$ configuration.

The relative ordering of the methods is preserved, with LS showing the highest BER, MMSE offering a moderate improvement, and the proposed DL-Enhanced approach producing the best performance among the practical estimators. The performance gap between DL-Enhanced and MMSE becomes more pronounced in the medium-to-high SNR range. Above about an SNR of 10 dB, the fusion network benefits from richer statistics discrepancies between the LS and MMSE, and hypotheses become more informative, allowing the MLP to assign weights more decisively depending on channel conditions. The simplex projection guarantees that the learned weights remain stable and non-negative, while LS-based phase anchoring prevents phase slips that can otherwise impair coherent detection at high SNRs when magnitudes are already nearly noise-free. These mechanisms yield a BER curve that tracks the perfect CSI bound more closely than MMSE, especially as the SNR grows. The results confirm that the proposed hybrid retains its generalization ability when scaling to larger antenna configurations and that its benefits increase with receive diversity. This demonstrates that the architecture is not only robust in small arrays but also scalable to larger and richer MIMO scenarios, preserving the balance between data-driven adaptation and physically grounded constraints.

Figure 11 demonstrates the benefit of additional receive antennas on the throughput performance. The four receive antennas provide enhanced spatial diversity, allowing all estimation methods to achieve higher effective capacity at lower SNR values compared to the $2\times 2$ case. At an SNR of 0 dB, the system achieves approximately 2.77 bpcu across all methods, representing improved noise resilience.

Figure 11. Throughput for the $4\times 2$ configuration.

The DL-Enhanced approach maintains its performance advantage throughout the SNR range, with the gap becoming particularly evident in the transition region between 2 and 8 dB. The fusion network’s ability to exploit the complementary characteristics of LS and MMSE estimates becomes more pronounced with increased receive diversity, as the additional spatial observations provide richer statistical information for the adaptive weighting mechanism. In the high-SNR regime above 10 dB, all curves approach the theoretical limit more closely than in the $2\times 2$ configuration. At 15 dB, DL-Enhanced achieves approximately 3.49 bpcu, virtually identical to the perfect CSI bound, while MMSE reaches 3.48 bpcu and LS attains 3.47 bpcu. The relative improvements remain consistent with the $2\times 2$ case but occur at more favorable operating SNRs due to the diversity gain.

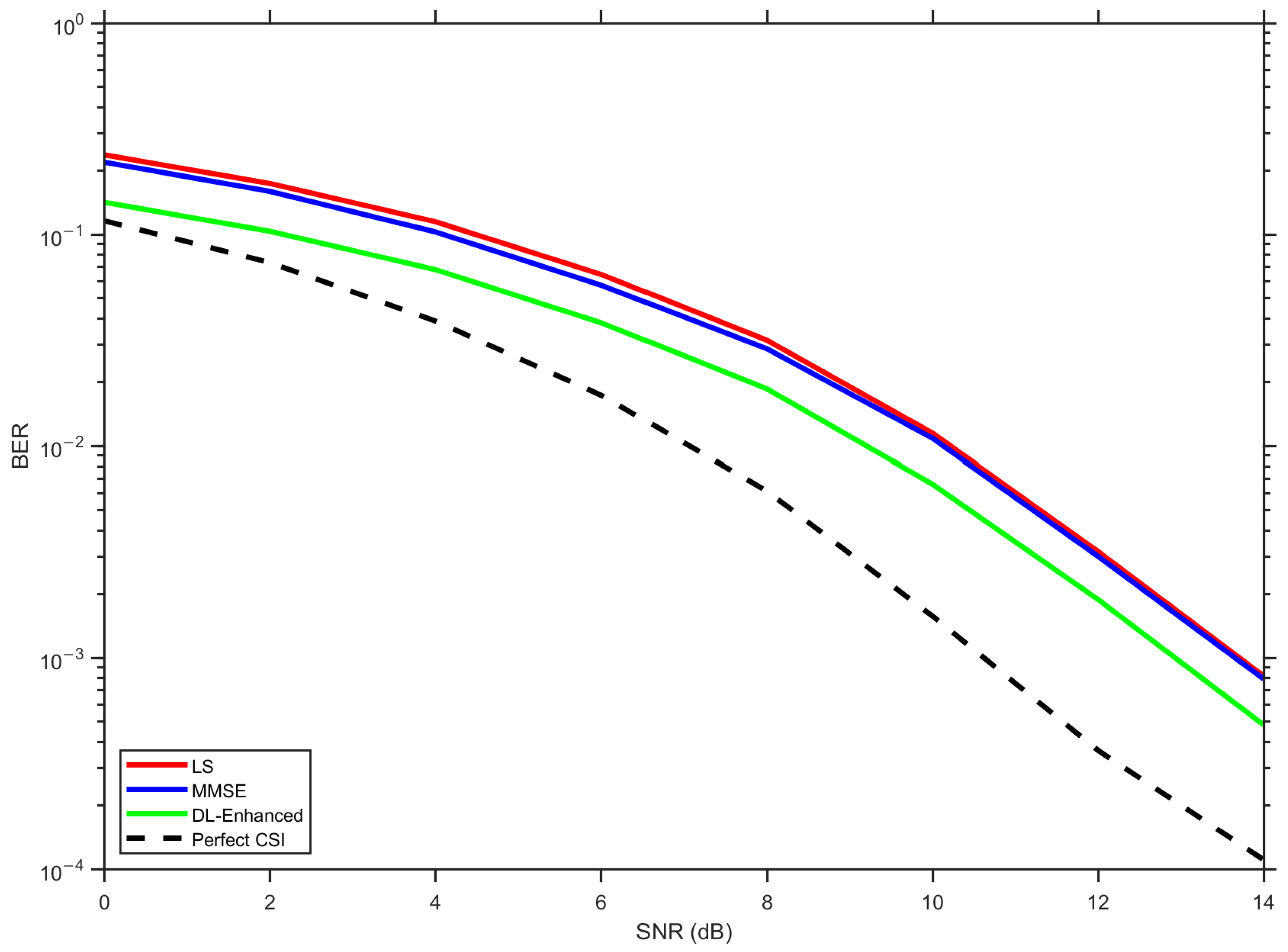
The $8\times 4$ case in Figure 12 further reduces absolute BER thanks to higher spatial diversity and multiplexing. Importantly, the DL-Enhanced approach remains the most accurate non-genie estimator at all tested SNRs and the closest to perfect CSI, which indicates that the two main ingredients of the architecture—simplex-constrained fusion and LS-phase preservation with one DD refinement—generalize beyond small arrays. As the arrays become larger, the gap to perfect CSI shrinks, especially at medium–high SNRs, suggesting that the residual error of the hybrid is dominated by small magnitude mismatches, since phase errors have been effectively suppressed. The $8\times 4$ configuration demonstrates the scalability of the proposed method, achieving BER values approaching ${10}^{-4}$ at a 15 dB SNR while maintaining consistent gains over traditional methods.

Figure 12. BER for the $8\times 4$ configuration.

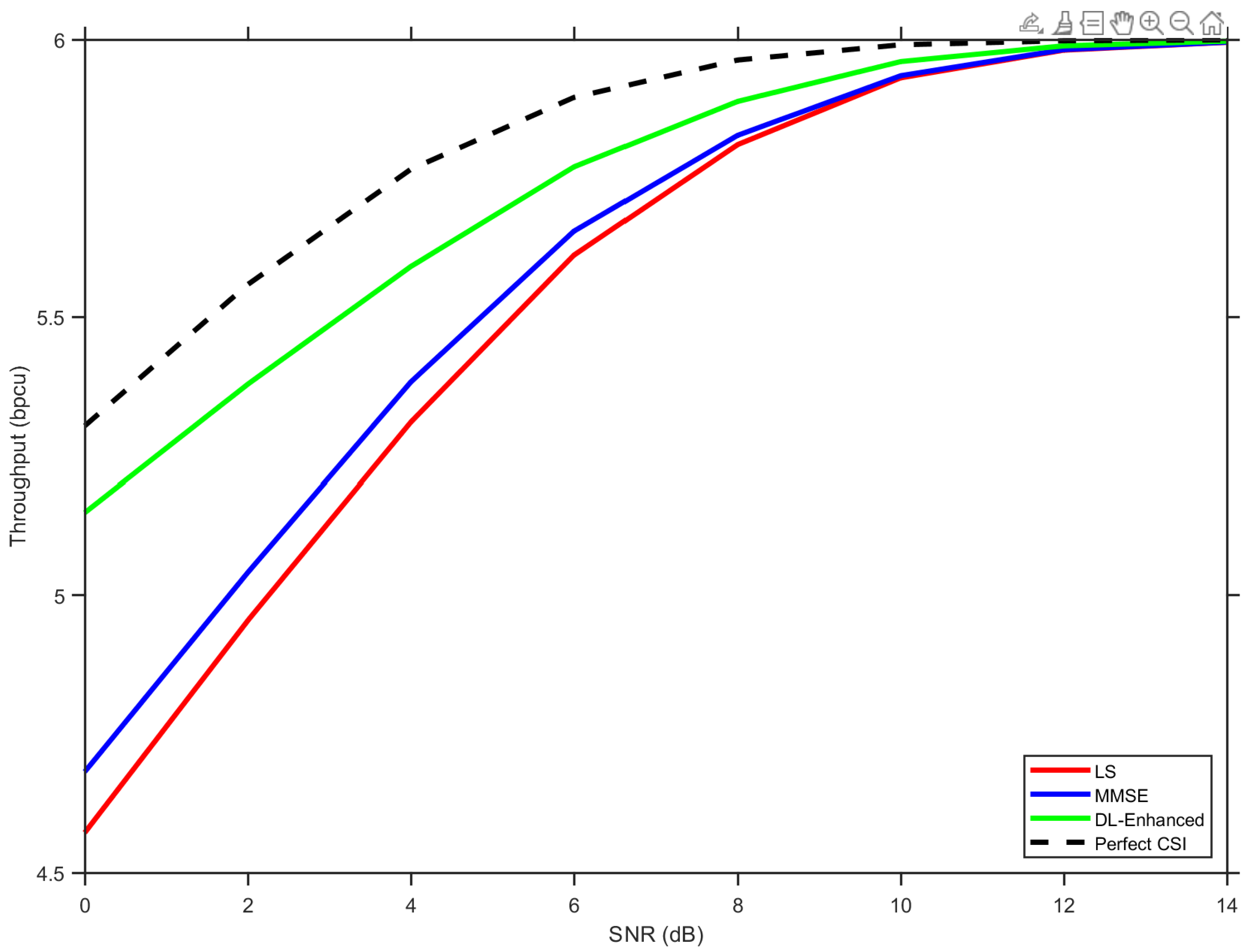
Figure 13 demonstrates the substantial capacity benefits of the larger array. At an SNR of 0 dB, all methods achieve approximately 4.6–4.7 bpcu, representing a significant improvement in noise-limited performance compared to the smaller configurations. This reflects the powerful combination of receive diversity (reducing estimation noise) and spatial multiplexing (increasing data rate).

Figure 13. Throughput for the $8\times 4$ configuration.

The DL-Enhanced approach maintains its consistent advantage across the entire SNR range, with particularly notable gains in the critical transition region between 2 and 8 dB. The adaptive weighting mechanism of the fusion network becomes increasingly effective as the spatial richness of the $8\times 4$ channel provides more diverse statistical information for the MLP to exploit. At a high SNR (15 dB), the throughput hierarchy converges near the theoretical maximum, with DL-Enhanced achieving approximately 5.98 bpcu, closely followed by MMSE at 5.96 bpcu and LS at 5.94 bpcu. The perfect CSI bound reaches the full 6.0 bpcu, demonstrating that even with the sophisticated hybrid approach, small residual estimation errors still impose a modest capacity penalty. The $8\times 4$ results confirm the scalability of the proposed architecture to high-capacity MIMO scenarios. The consistent performance gains across all three MIMO configurations (2 × 2, 4 × 2, 8 × 4) demonstrate that the simplex-constrained fusion and LS-phase anchoring principles retain their effectiveness as the system complexity increases, making the approach suitable for next-generation MIMO deployments requiring both high spectral efficiency and robust channel estimation.

To further assess the impact of phase sensitivity and higher-order constellations, we extended the analysis to 16-QAM while keeping the same pilot pattern and channel models used in the QPSK experiments.

Figure 14 and Figure 15 show the resulting BER curves for the $2\times 2$ and $4\times 2$ configurations, respectively. As expected, moving from QPSK to 16-QAM increases the absolute BER level across all estimators, since the smaller decision regions make the detector more vulnerable to both amplitude errors and residual phase rotations. Still, the relative behavior of the estimators remains consistent with the QPSK case.

Figure 14. BER for the $2\times 2$ configuration with 16-QAM modulation.

Figure 15. BER for the $4\times 2$ configuration with 16-QAM modulation.

In Figure 14, corresponding to the $2\times 2$ configuration, LS exhibits the highest BER over the entire SNR range, MMSE provides a clear improvement owing to its use of delay-domain statistics, and the proposed DL-Enhanced estimator yields the best performance among the practical schemes. The gap between DL-Enhanced and MMSE becomes more pronounced at medium-to-high SNRs (around 10–14 dB), where the effect of phase errors is more critical for 16-QAM. In this regime, the magnitude-domain fusion of LS and MMSE, combined with LS-based phase anchoring and a single DD refinement, effectively limits phase sensitivity and prevents additional error floors, allowing the hybrid curve to track the perfect CSI reference more closely.

Figure 15 reports the 16-QAM results for the $8\times 4$ configuration. Increasing the number of receive antennas from $R=8$ to $R=4$ introduces additional spatial diversity and shifts all curves downward, reducing the BER required to support a given SNR. The ordering of the estimators is again preserved: LS performs worst, MMSE yields a consistent gain, and DL-Enhanced remains the most accurate non-genie estimator. The advantage of the hybrid approach is particularly visible from about 8 dB onwards, where the richer spatial observations accentuate the differences between LS and MMSE and provide more informative features for the fusion MLP. The learned simplex-constrained weights adapt to these conditions, producing a fused estimate whose BER stays closer to the perfect CSI bound while retaining robustness under 16-QAM. Overall, these results confirm that the proposed architecture remains effective and phase-robust when moving to higher-order modulations and when scaling from $2\times 2$ to $8\times 4$ arrays.

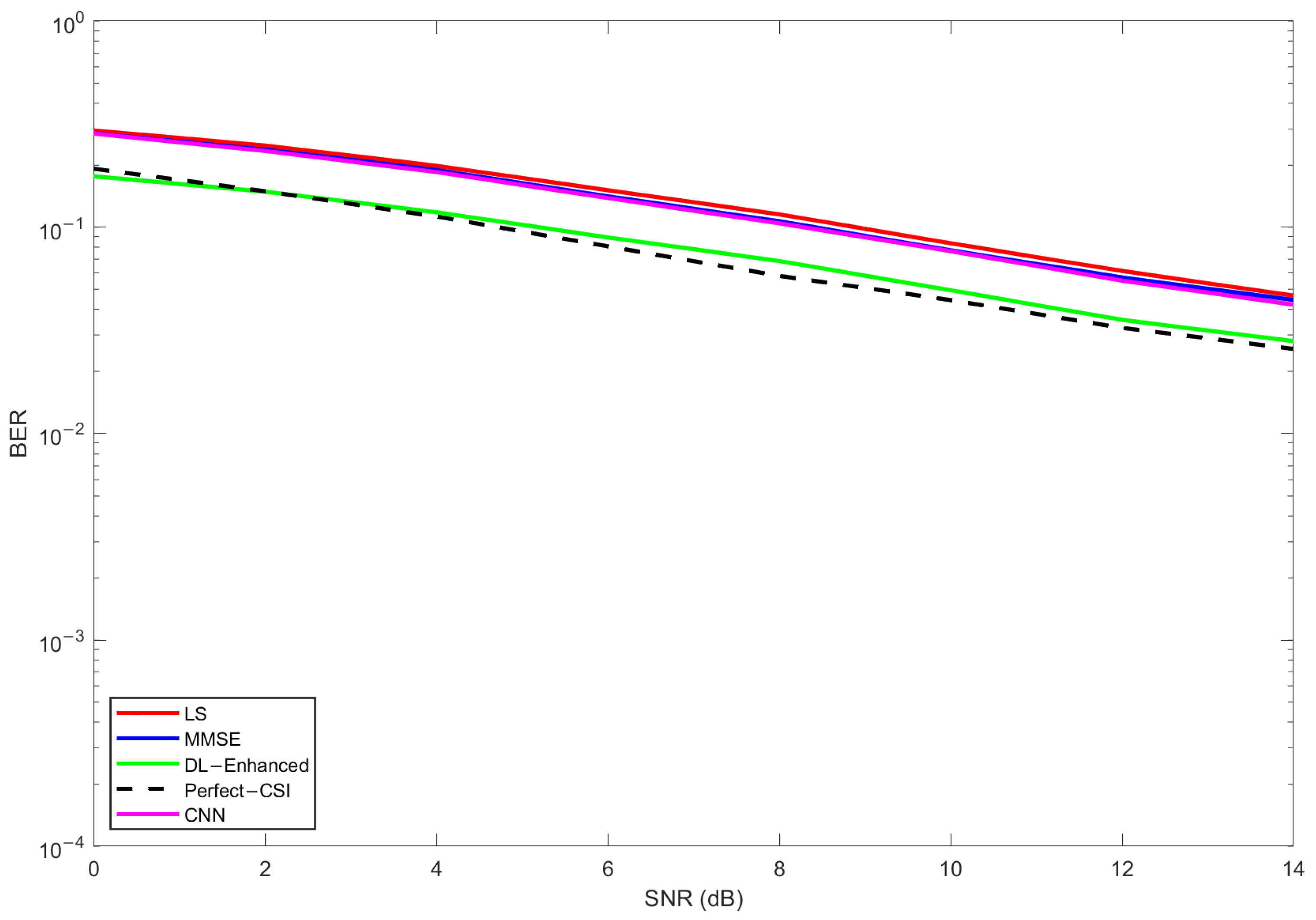
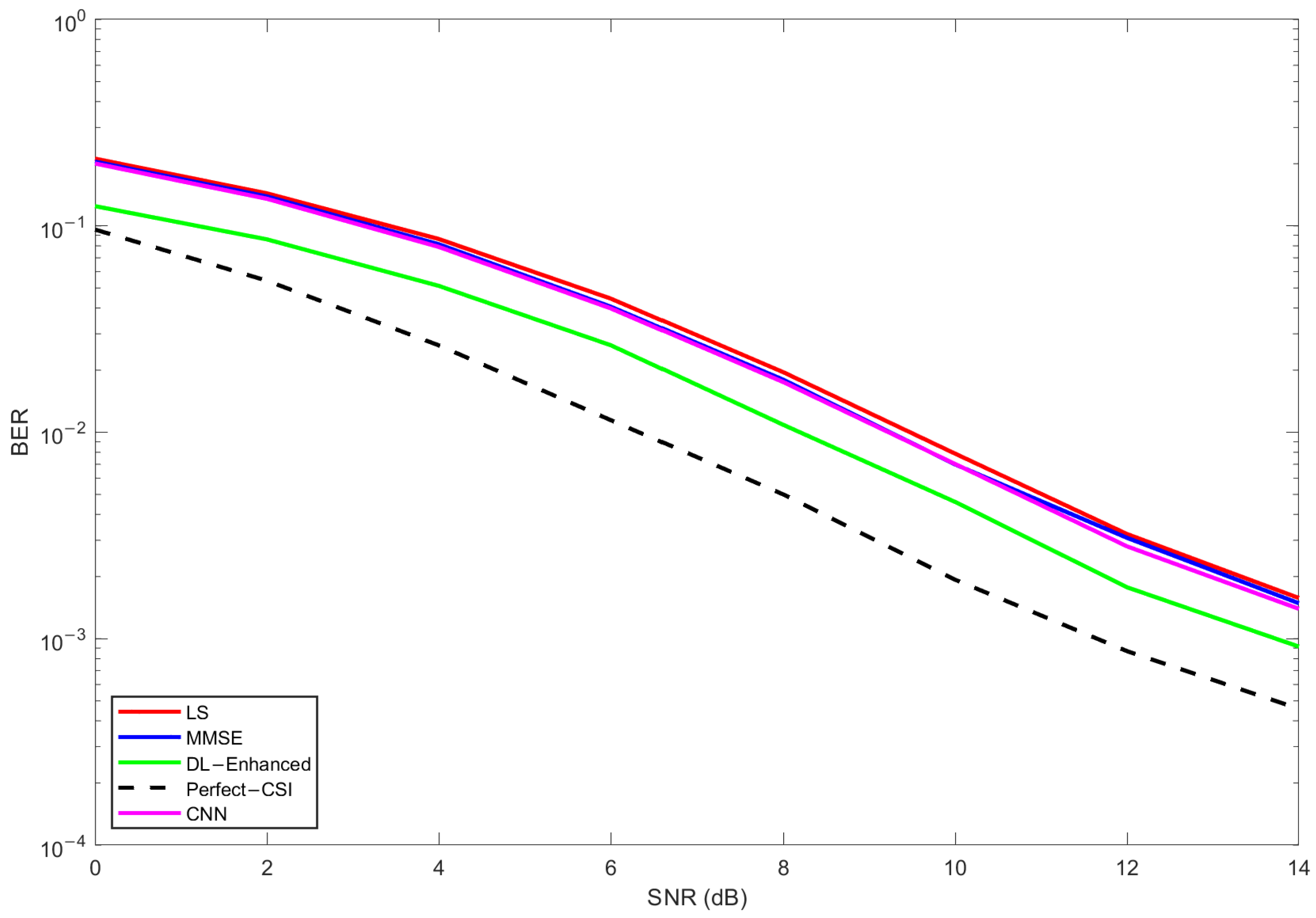
5.1. Comparison with a One-Dimensional CNN Baseline

To contextualize the gains of the proposed hybrid estimator, we include a lightweight 1D-CNN baseline that maps the LS hypothesis to an MMSE-like estimate by processing the $(\Re ,\Im )$ stacks of ${\widehat{\mathbf{H}}}_{\mathrm{LS}}$ with short convolutional blocks and a 1 × 1 head. To avoid phase wrapping, the CNN output is used only in magnitude while the phase is taken from LS, i.e., ${\widehat{\mathbf{H}}}_{\mathrm{CNN}}=\left|{\widehat{\mathbf{H}}}_{\mathrm{CNN}}\right|e^{j\angle \left({\widehat{\mathbf{H}}}_{\mathrm{LS}}\right)}$. 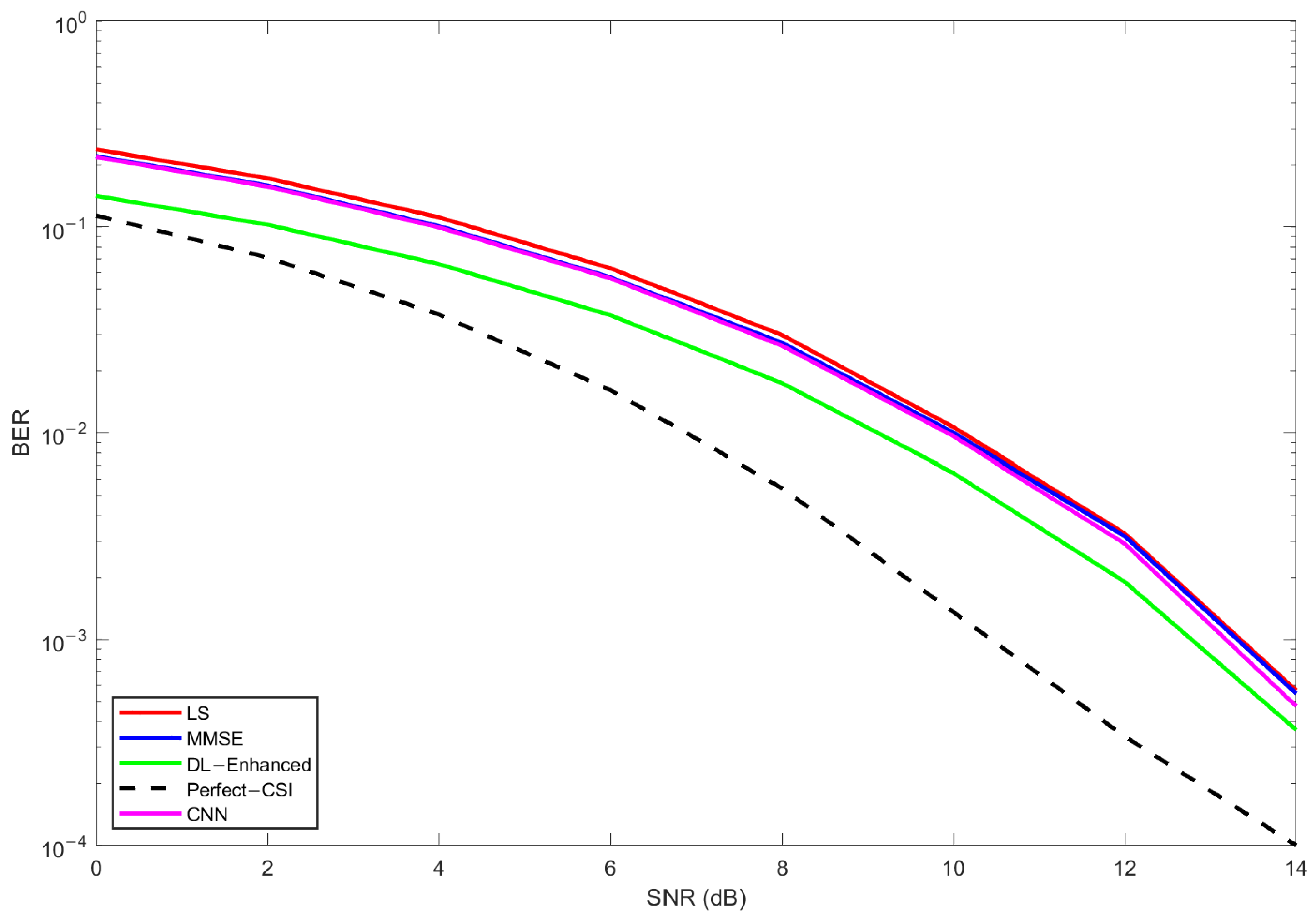Figure 16, Figure 17 and Figure 18 report BER for the three MIMO configurations, comparing LS (red), MMSE (blue), DL-Enhanced (green), perfect CSI (black dashed), and CNN-1D (magenta).

Figure 16. BER for the $2\times 2$ configuration with the CNN-1D baseline.

Figure 17. BER for the $4\times 2$ configuration with the CNN-1D baseline.

Figure 18. BER for the $8\times 4$ configuration with the CNN-1D baseline.

Across all antenna settings, the CNN-1D curve closely tracks the MMSE reference and consistently lies above the DL-Enhanced estimator. This behavior indicates that the CNN largely behaves as a learned frequency-smoothing operator seeded by LS and therefore inherits the MMSE performance ceiling. In the $2\times 2$ case, the five curves are tightly grouped at low SNRs since detection is noise-limited, but differences emerge from about 8–10 dB onward. The CNN remains essentially coincident with MMSE, while DL-Enhanced bends earlier toward the perfect CSI slope, producing a visible BER reduction in the 10–14 dB region where reliable decisions allow the single decision-directed pass to act as virtual pilots and where preserving the LS phase prevents the small-phase biases that penalize coherent detection under QPSK.

The $4\times 2$ results reinforce the same trend under higher receive diversity. Additional observations per subcarrier reduce the absolute BER for all methods, yet the ordering is preserved: LS shows the highest error floor, CNN and MMSE are nearly indistinguishable over the whole sweep, and DL-Enhanced remains the most accurate non-genie estimator. The gap between DL-Enhanced and the CNN/MMSE pair widens in the mid-to-high SNR regime. In this region, the physics-inspired features make the magnitude fusion more decisive, selecting the better hypothesis per realization under a simplex constraint, while the LS-anchored phase keeps the equalizer unbiased as magnitudes become nearly noise-free. The outcome is a curve that approaches the genie bound faster than the CNN baseline without incurring iterative complexity.

In the $8\times 4$ configuration, spatial richness further suppresses absolute error rates and brings all practical estimators closer to perfect CSI. Even in this favorable regime, the CNN remains essentially locked to the MMSE trajectory, whereas DL-Enhanced continues to be the closest practical curve to the genie bound at all tested SNRs. The residual gap at a high SNR is small and mainly attributable to tiny magnitude mismatches, as phase errors have been effectively neutralized by design. This confirms that the two ingredients of the proposed architecture—convex magnitude fusion and explicit LS-phase preservation with a single decision-directed refinement—scale cleanly with array size and remain beneficial when the operating point is dominated by subtle estimation biases rather than gross noise.

Overall, the CNN-1D baseline is a strong learned smoother that reliably reproduces MMSE-like behavior, but it does not overcome MMSE because it lacks a per-tone convex dominance mechanism and does not couple learning with decision-directed polishing. The hybrid DL-Enhanced estimator combines model-based priors and lightweight learning to reduce magnitude risk relative to either LS or MMSE while guaranteeing phase fidelity, which explains its consistent advantage over both MMSE and the CNN across $2\times 2$, $4\times 2$, and $8\times 4$ configuration.

5.2. Complexity, Ablation, and Sensitivity Analysis

Following the implementation used in our simulations, we count complex multiply–accumulate (MAC) operations per OFDM frame with $N=64$ subcarriers and assume a $1\mathrm{GMAC}/\mathrm{s}$ baseband processor and an OFDM symbol duration of $T_{\mathrm{sym}}\approx 71\mathsf{\mu }\mathrm{s}$. For the main $2\times 2$ configuration, LS and MMSE channel estimation require about $4.27\times {10}^2$ MACs/frame (approximately $8.53\times {10}^2$ FLOPs), corresponding to a latency of $0.427\mathsf{\mu }\mathrm{s}$ (about $0.6\%$ of $T_{\mathrm{sym}}$). The proposed DL-Enhanced estimator (fusion MLP + LS/MMSE magnitude-domain combination + one decision-directed refinement) requires about $2.17\times {10}^3$ MACs/frame (approximately $4.35\times {10}^3$ FLOPs), which translates into a latency of $2.17\mathsf{\mu }\mathrm{s}$, i.e., only about $3\%$ of the OFDM symbol duration.

Similar trends are observed for the larger arrays. For a $4\times 2$ system, LS/MMSE require approximately $6.83\times {10}^2$ MACs/frame, while DL-Enhanced requires approximately $4.01\times {10}^3$ MACs/frame (latencies of $0.683\mathsf{\mu }\mathrm{s}$ and $4.01\mathsf{\mu }\mathrm{s}$, respectively). For an $8\times 4$ configuration, LS/MMSE require approximately $3.41\times {10}^3$ MACs/frame versus approximately $1.74\times {10}^4$ MACs/frame for DL-Enhanced, corresponding to latencies of $3.41\mathsf{\mu }\mathrm{s}$ and $17.4\mathsf{\mu }\mathrm{s}$ (about $4.8\%$ and $24.4\%$ of $T_{\mathrm{sym}}$, respectively). Overall, the hybrid estimator is about $5–6\times$ more expensive in MACs than LS/MMSE, but its absolute latency remains well below the OFDM symbol duration for all considered MIMO sizes. In terms of power consumption, the overhead scales roughly linearly with the MAC count, so on modern baseband SoCs with tens to hundreds of GMAC/s capability, the additional energy cost of the hybrid estimator is expected to be modest, a full hardware-in-the-loop characterization is left for future work.

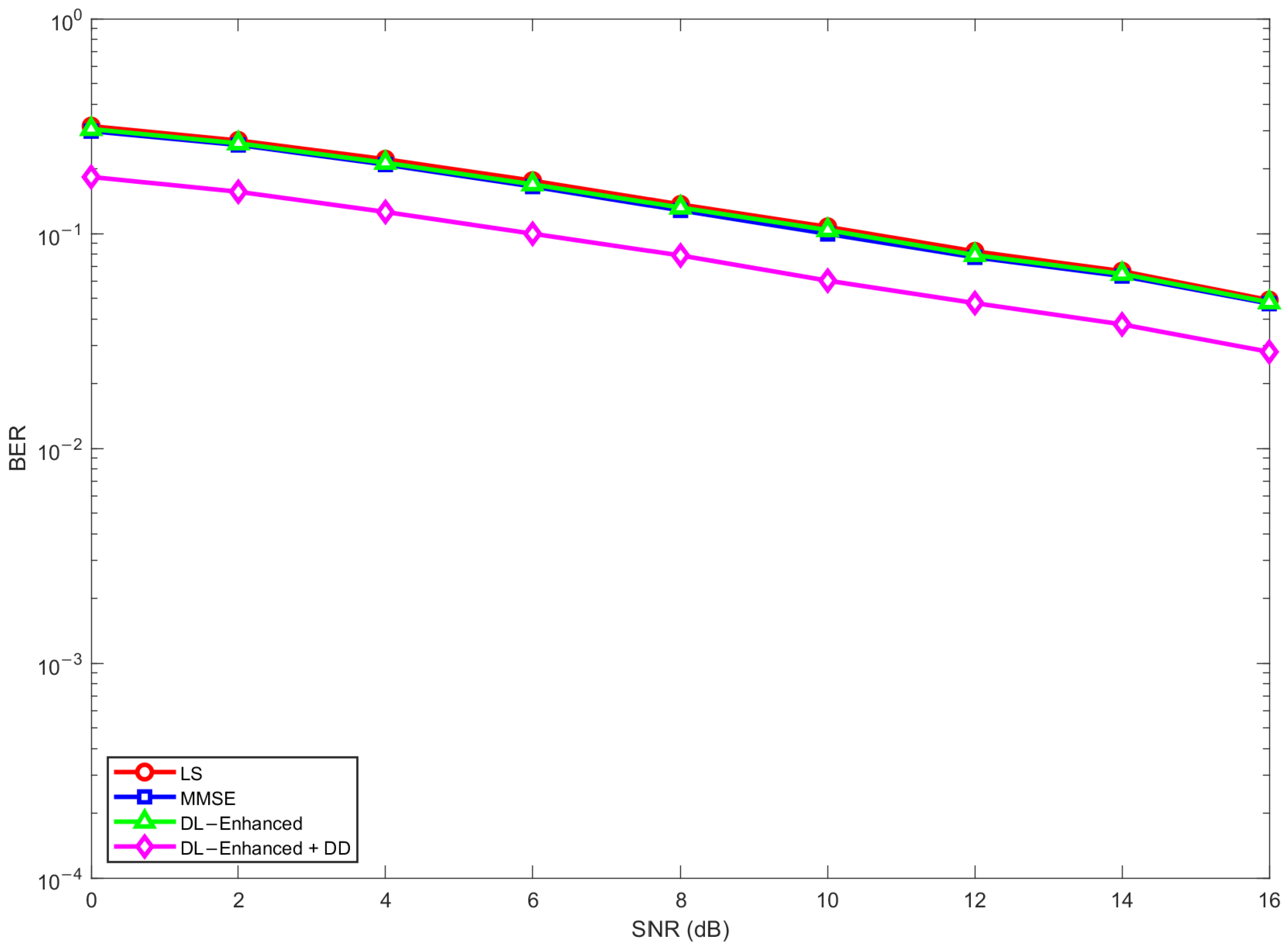
To quantify the contribution of each module, we perform an ablation study for the $2\times 2$ QPSK CDL-C scenario, comparing (i) LS, (ii) MMSE, (iii) LS/MMSE fusion without decision-directed refinement (“DL-Enhanced”), and (iv) the full hybrid estimator with one decision-directed iteration (“DL-Enhanced + DD”), see Figure 19. The fusion-only variant yields BER curves that closely track the MMSE baseline across the SNR range, indicating that the LS/MMSE combination is essentially lossless and provides only a modest gain over MMSE. In contrast, adding the decision-directed refinement produces a consistent BER reduction, typically on the order of 3–4 dB at BER levels between ${10}^{-1}$ and ${10}^{-2}$. This confirms that the decision-directed refinement is the main driver of the performance gains of the proposed hybrid estimator.

Figure 19. Ablation of the proposed DL-Enhanced estimator in the $2\times 2$ QPSK modulation.

We also evaluate the robustness of the DL-Enhanced estimator to the SNR and channel-profile mismatch. First, in an SNR hold-out experiment, the fusion network is trained only on alternating SNR points, while evaluation is carried out on the interleaved, unseen SNR values. The resulting BER/NMSE curves remain very close to those obtained when training on the full SNR grid, showing that the learned fusion generalizes smoothly in the SNR. Second, in a cross-profile experiment, the fusion is trained on CDL-C channels and tested zero-shot on CDL-A and CDL-E profiles. Although a small degradation (typically $1–2\mathrm{dB}$ in NMSE and BER) is observed relative to the matched-profile case, the DL-Enhanced estimator still outperforms LS and closely tracks (or slightly improves on) MMSE over the whole SNR range. These ablation and sensitivity results support the necessity of both the fusion and decision-directed blocks and demonstrate that the proposed hybrid architecture is robust to moderate changes in the SNR and channel statistics.

6. Conclusions

This paper proposed a hybrid DL-Enhanced channel estimator for MIMO–OFDM that combines classical estimation techniques (LS/MMSE) through a lightweight MLP whose outputs are projected onto the probability simplex, followed by an explicit phase restitution using the LS phase and a single DD refinement. Across CDL-C scenarios with QPSK and $N=64$ subcarriers, the method consistently outperformed MMSE, with the largest benefits observed at a medium-to-high SNR where the phase-preserving fusion and the polishing step become reliable, and the BER curve approaches the perfect CSI bound.

In the $2\times 2$ setting, the hybrid estimator achieved BER reductions around roughly 35%. The gains scale favorably with spatial diversity: enlarging the array to $4\times 2$ and $8\times 4$ lowers the error floor uniformly and increases the margin over MMSE, confirming that the convex fusion can capitalize on additional receive/transmit dimensions without destabilizing the estimator.

A practical advantage of the approach is its very low computational overhead. The cost of equalization dominates per frame, whereas the MLP and the convex combination add only a small number of operations compared with what a standard receiver already performs. This makes the method attractive for embedded implementations and permits deployment without altering the base detection chain.

Future work will focus on per-tone or banded weight adaptation with smoothness regularization, lightweight temporal models to exploit coherence across frames, explicit handling of CFO and phase noise, online self-supervised updates to track channel drift, and extensions to higher-order constellations with soft-information integration. Overall, embedding model-based priors inside a compact learned adaptor proved to be a robust and efficient path to close the gap to perfect CSI with negligible additional complexity, offering a practical upgrade for next-generation receivers.