Conception of a Low-Cost Location System for an Unmanned Ground Vehicle
Abstract
1. Introduction
A Literature Review on Sensors for a Low-Cost UGV Location System
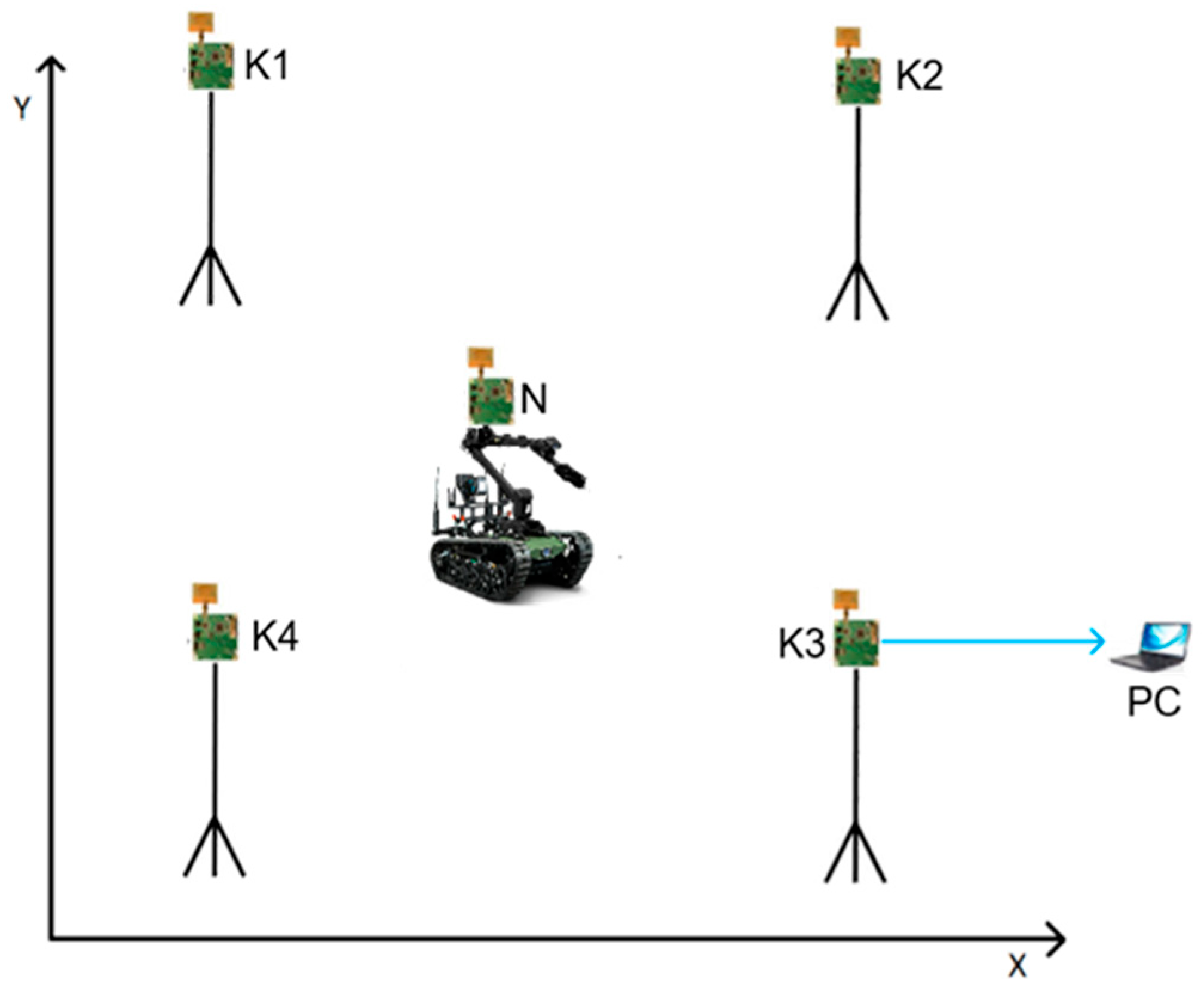
2. Description of the Concept of the Location System
- Application: Low-cost 2D relative localization of UGVs in limited indoor and outdoor environments that may pose threats to human operators.
- Technology: Ultra-Wideband.
- Number of modules: Min. four receivers, one transmitter.
- Configuration: Area min. 20 m × 20 m.
- Accuracy: Max. error 0.3 m under LOS (Line Of Sight) conditions.
- Frequency of location determination: 1 Hz.
- Architecture: TOF/TDOA.
- Data processing: Computationally efficient positioning algorithm and signal filtering methods assuming no UGV kinematics model.
3. Materials and Methods
- K1 (x1 = 0 m, y1 = 25 m),
- K2 (x2 = 25 m, y2 = 25 m),
- K3 (x3 = 25 m, y3 = 0 m),
- K4 (x4 = 0 m, y4 = 0 m).
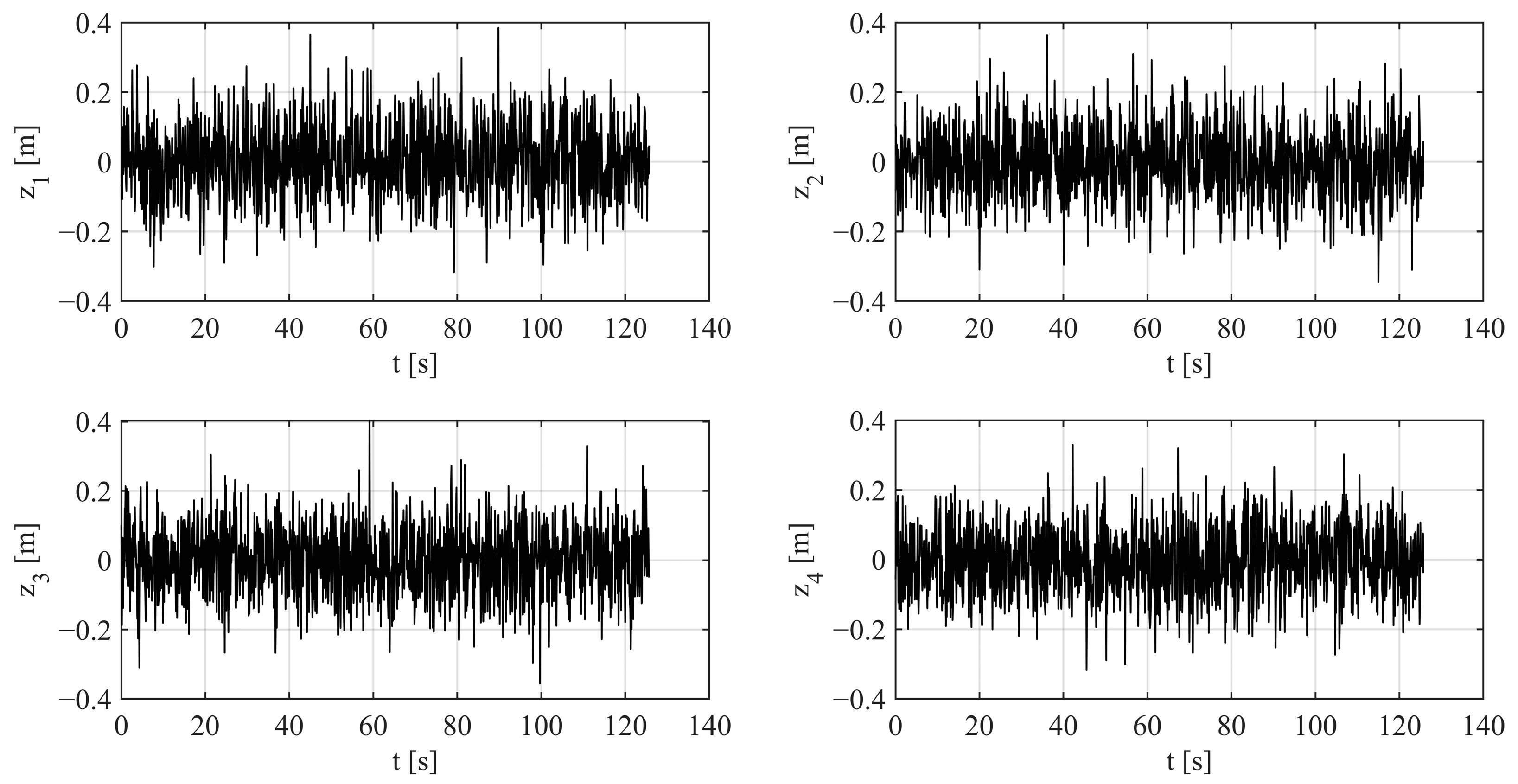
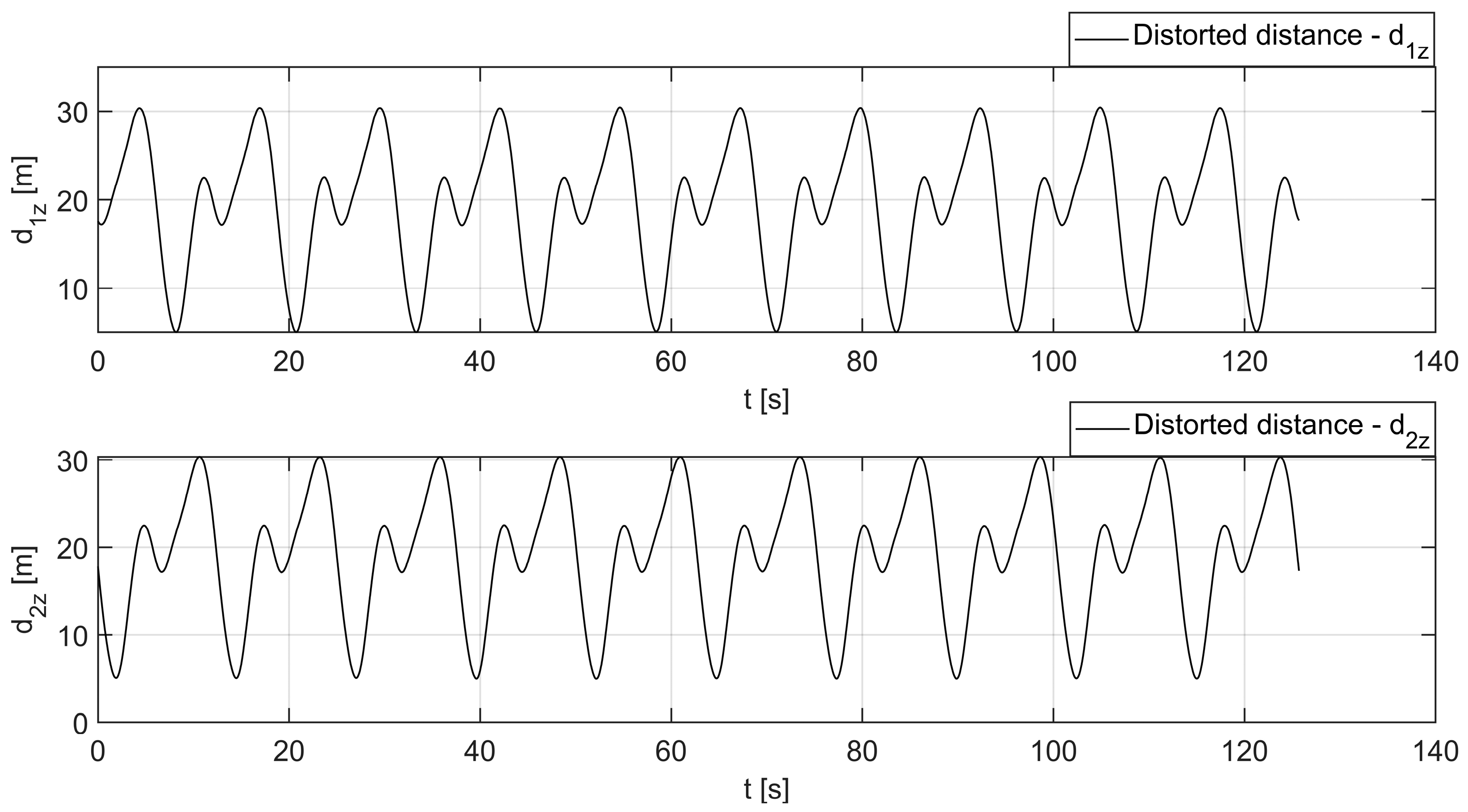
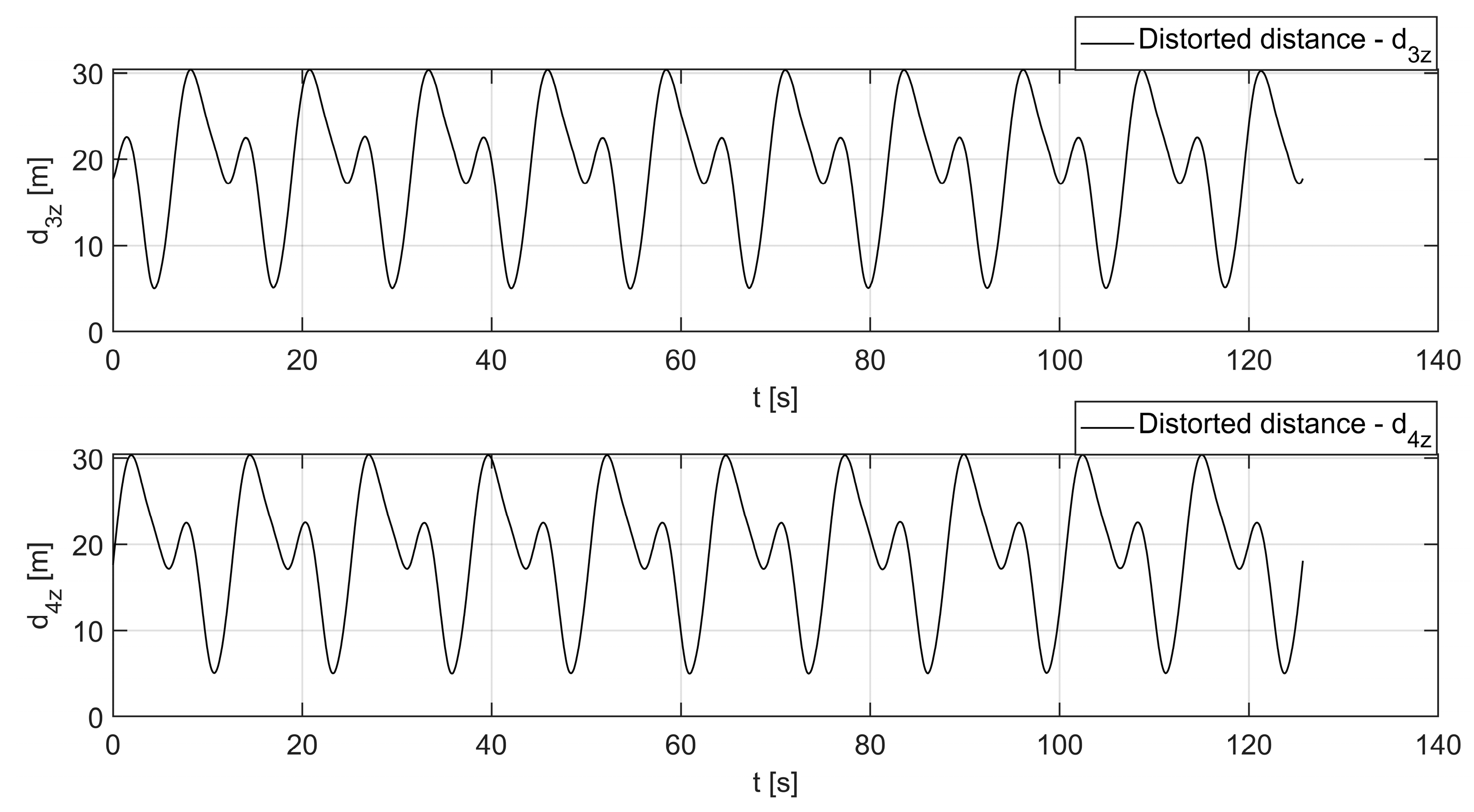
3.1. Distance Measurement
3.2. Initial Filtering
- Moving mean;
- Hampel;
- Median Filter.
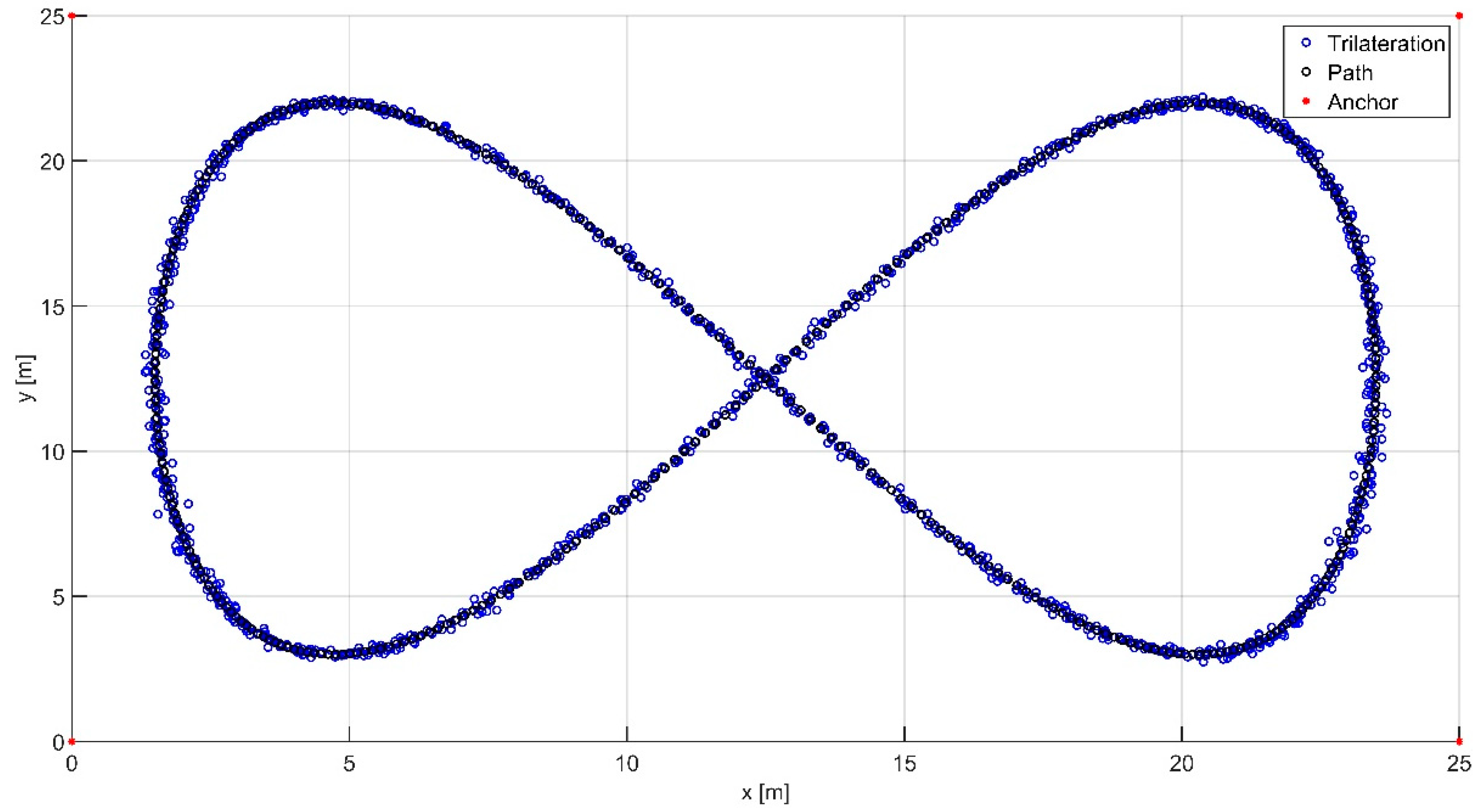
3.3. Trilateration
3.4. Final Filtering
- Moving mean;
- LOESS;
- RLOESS;
- Savitzky–Golay;
- Hampel;
- Median Filter.
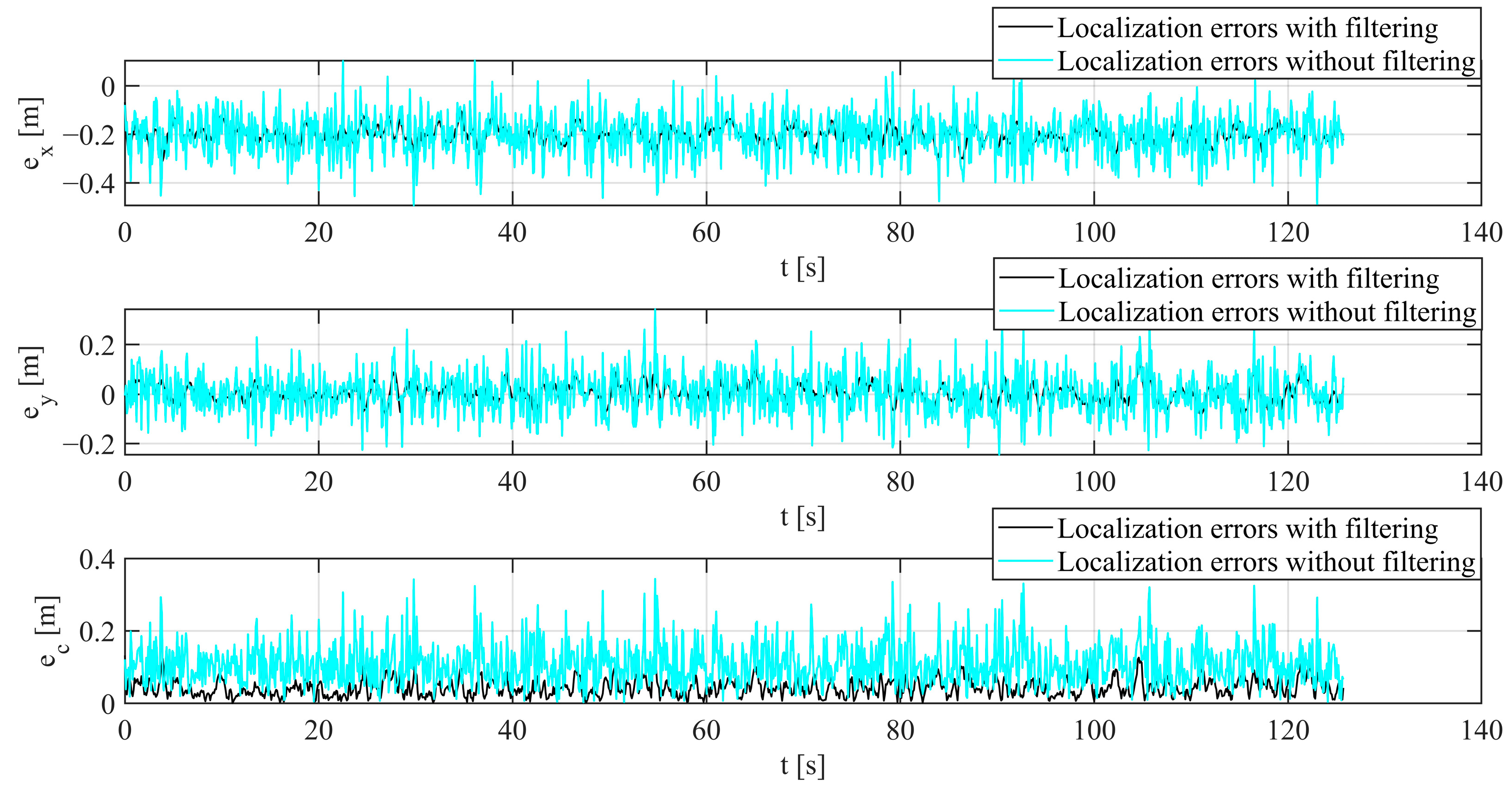
3.5. Quality Indicators
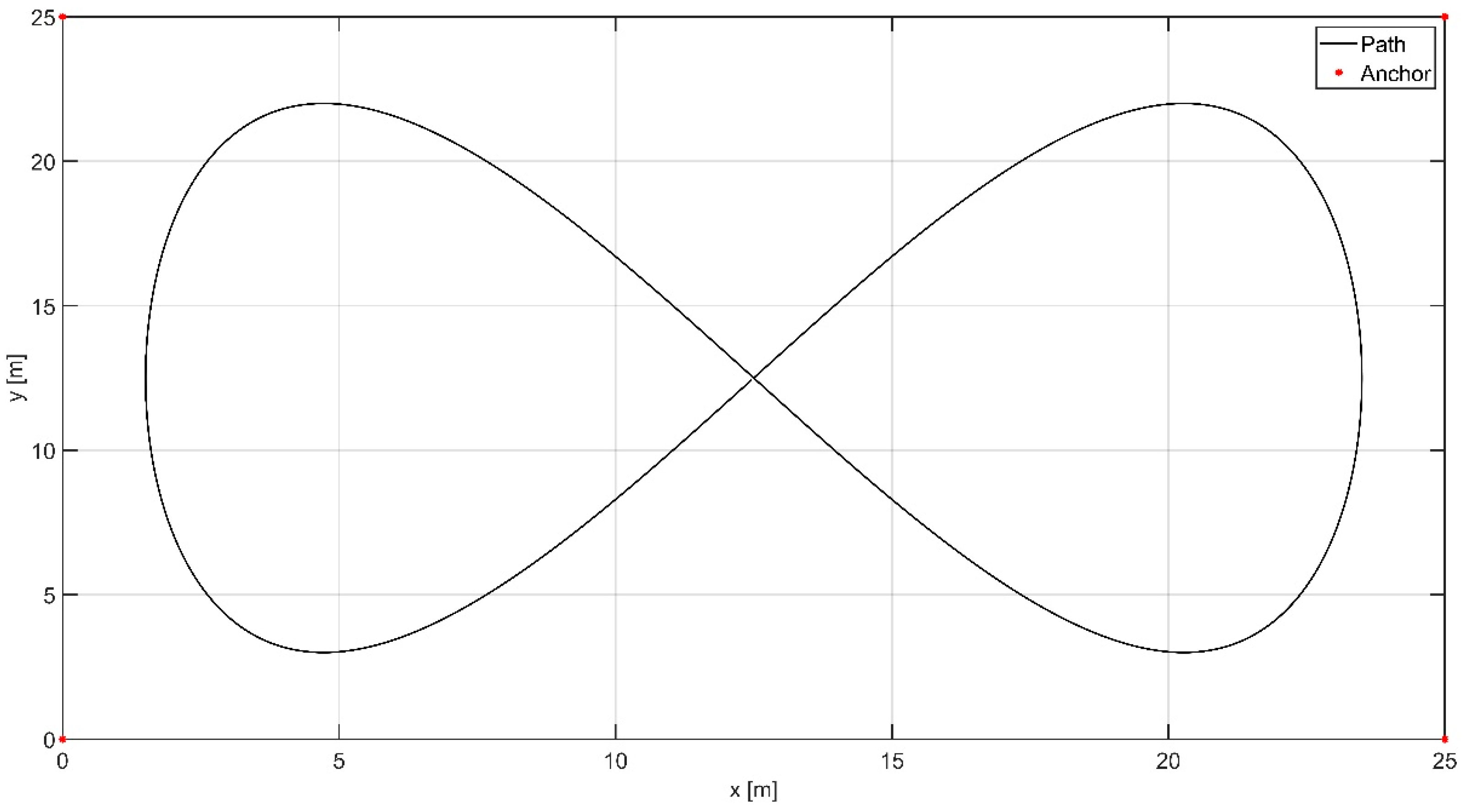
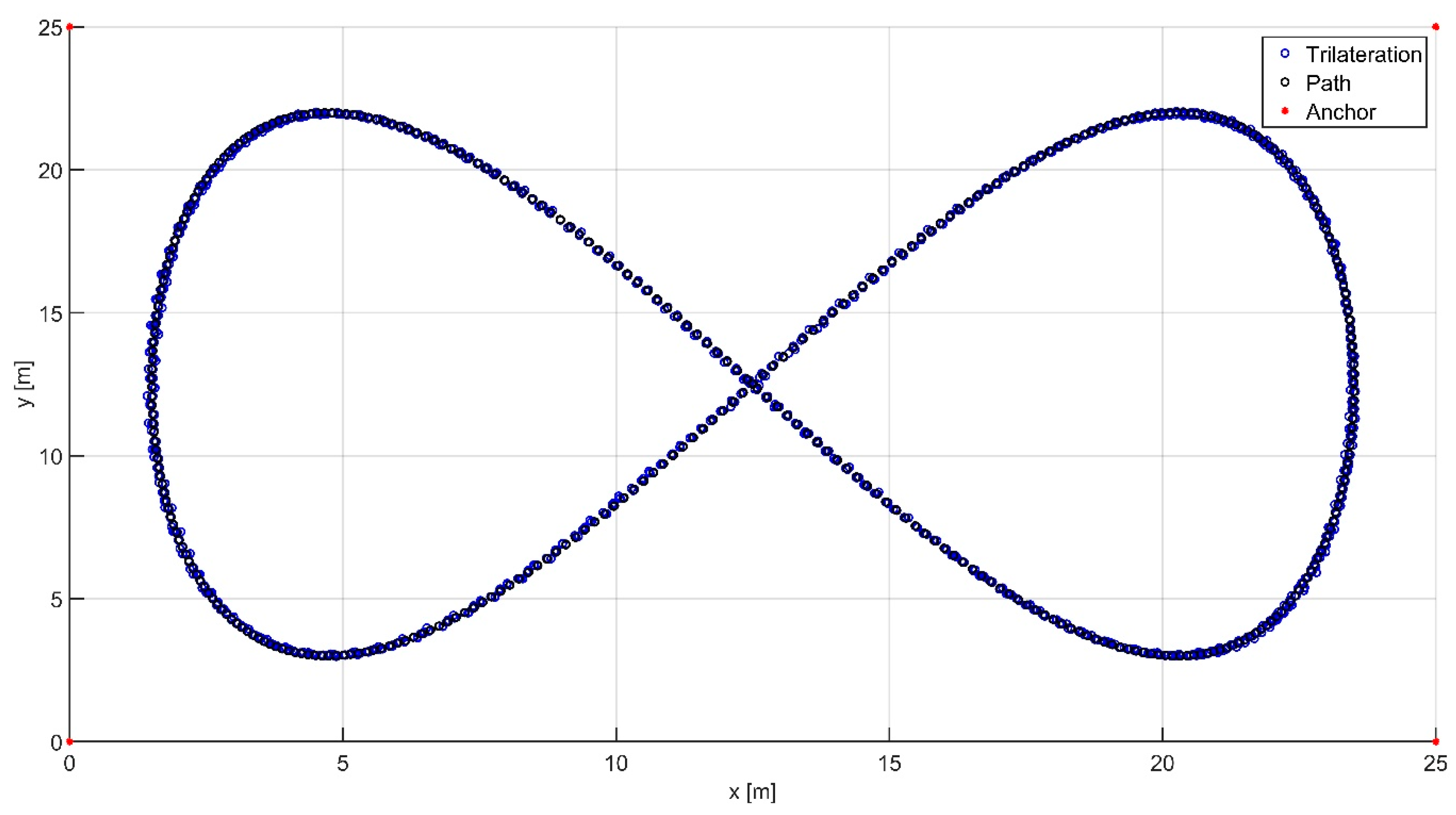
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DMC | Deterministic Multipath Component |
| EGNOS | European Geostationary Navigation Overlay Service |
| EKF | Extended Kalman Filter |
| FIR | Finite Impulse Response |
| GNSS | Global Navigation Satellite Systems |
| IIR | Infinite Impulse Response |
| IMU | Inertial Measurement Unit |
| LIDAR | Light Detection and Ranging |
| LOESS | Locally Estimated Scatterplot Smoothing |
| LOS | Line of Sight |
| MAD | Median Absolute Deviation |
| MAE | Mean Absolute Error |
| MSE | Mean Squared Error |
| NLOS | Non-Line of Sight |
| RGB-D | Red Green Blue—Depth |
| RLOESS | Robust Locally Estimated Scatterplot Smoothing |
| RMS | Root Mean Square |
| RSSI | Received Signal Strength Indicator |
| RTK | Real-Time Kinematic |
| SBAS | Satellite-Based Augmentation System |
| SSE | Sum Of Squares Error |
| TDOA | Time Difference of Arrival |
| TOA | Time of Arrival |
| TOF | Time of Flight |
| TWR | Two-Way Ranging |
| UGV | Unmanned Ground Vehicle |
| UKF | Unscented Kalman Filter |
| UWB | Ultra-Wideband |
| VBAKF | Variational Bayesian Adaptive Kalman Filter |
References
- Rykała, Ł.; Typiak, A.; Typiak, R. Research on Developing an Outdoor Location System Based on the Ultra-Wideband Technology. Sensors 2020, 20, 6171. [Google Scholar] [CrossRef] [PubMed]
- Bartnicki, A. Demand for remote control station of unmanned platform in terms of conducting missions aiming at reducing threat caused by uncontrolled leak of dangerous substances. Logistyka 2012, 3, 61–68. (In Polish) [Google Scholar]
- Typiak, A.; Typiak, R. Researching different control strategies for a manipulator arm in a teleoperated configuration. Logistyka 2010, 2, 1–14. (In Polish) [Google Scholar]
- Typiak, A. Sterowanie Mobilnymi Maszynami Inżynieryjnymi w Układzie Teleoperacji; Wojskowa Akademia Techniczna: Warsaw, Poland, 2013. (In Polish) [Google Scholar]
- Januszewski, J. GPS Satellite Systems, Galileo and Others; PWN: Warsaw, Poland, 2007. [Google Scholar]
- Narkiewicz, J. GPS and Other Satellite Navigation Systems; WKiŁ: Warsaw, Poland, 2007. [Google Scholar]
- Blesing, C.; Finke, J.; Hoose, S.; Schweigert, A.; Stenzel, J. Accuracy evaluation of a low-cost differential global positioning system for mobile robotics. In Proceedings of the 2023 IEEE SENSORS, Vienna, Austria, 29 October–1 November 2023; pp. 1–4. [Google Scholar]
- Takanose, A.; Kondo, K.; Hoda, Y.; Meguro, J.; Takeda, K. Localization system for vehicle navigation based on GNSS/IMU using time-series optimization with road gradient constraint. J. Robot. Mechatron. 2023, 35, 387–397. [Google Scholar] [CrossRef]
- Xuan, J.; Zhu, T.; Peng, G.; Sun, F.; Dong, D. A Review on the Inertial Measurement Unit Array of Microelectromechanical Systems. Sensors 2024, 24, 7140. [Google Scholar] [CrossRef]
- Cramer, M.; Cramer, J.; De Schepper, D.; Aerts, P.; Kellens, K.; Demeester, E. Benchmarking low-cost inertial measurement units for indoor localisation and navigation of AGVs. Procedia CIRP 2019, 86, 204–209. [Google Scholar] [CrossRef]
- Vilau, R.; Voicu, D.; Stoica, R.M.; Ciobotaru, T.; Rykała, M.; Rykała, Ł. Investigating Vibration Transmission in Cargo Containers During Heavy-Duty Off-Road Transport. Adv. Sci. Technol. Res. J. 2024, 18, 312–328. [Google Scholar] [CrossRef]
- Min, K.I.; Jeong, J.B.; Oh, J.S.; Kim, J.H. Research of vision system for perception in UGV. In Proceedings of the 2013 13th International Conference on Control, Automation and Systems (ICCAS 2013), Gwangju, Republic of Korea, 20–23 October 2023; pp. 1351–1355. [Google Scholar]
- Nowakowski, M. Operational Environment Impact on Sensor Capabilities in Special Purpose Unmanned Ground Vehicles. In Proceedings of the 2024 21st International Conference on Mechatronics-Mechatronika (ME), Brno, Czech Republic, 4–6 December 2024; IEEE: New York, NY, USA, 2024; pp. 1–5. [Google Scholar]
- Kiczek, B.; Batsch, M. Exploration of Unsupervised Deep Learning-Based Gear Fault Detection for Wind Turbine Gearboxes. Energies 2025, 18, 3630. [Google Scholar] [CrossRef]
- Icagic, S.D.; Kvascev, G.S. A Smart Alcoholmeter Sensor Based on Deep Learning Visual Perception. Sensors 2022, 22, 7394. [Google Scholar] [CrossRef]
- Batsch, M.; Nowak, D.; Wydrzyński, D.; Kochmański, Ł. Vision-based control of small educational parallel selective compliance assembly robot arm robot. Adv. Sci. Technol. Res. J. 2025, 19, 440–457. [Google Scholar] [CrossRef]
- Kim, T.; Lim, S.; Shin, G.; Sim, G.; Yun, D. An open-source low-cost mobile robot system with an RGB-D camera and efficient real-time navigation algorithm. IEEE Access 2022, 10, 127871–127881. [Google Scholar] [CrossRef]
- Będkowski, J.; Pełka, M. Affordable Robotic Mobile Mapping System Based on Lidar with Additional Rotating Planar Reflector. Sensors 2023, 23, 1551. [Google Scholar] [CrossRef] [PubMed]
- Nowakowski, M.; Kurylo, J.; Dang, P.H. Camera Based AI Models Used with LiDAR Data for Improvement of Detected Object Parameters. In Modelling and Simulation for Autonomous Systems; Springer Nature: Cham, Switzerland, 2023; pp. 287–301. [Google Scholar]
- Liu, Y.; Wang, C.; Wu, H.; Wei, Y.; Ren, M.; Zhao, C. Improved LiDAR Localization Method for Mobile Robots Based on Multi-Sensing. Remote Sens. 2022, 14, 6133. [Google Scholar] [CrossRef]
- Kim, J.; Park, B.-j.; Kim, J. Empirical Analysis of Autonomous Vehicle’s LiDAR Detection Performance Degradation for Actual Road Driving in Rain and Fog. Sensors 2023, 23, 2972. [Google Scholar] [CrossRef]
- Chen, P.; Zhao, X.; Zeng, L.; Liu, L.; Liu, S.; Sun, L.; Li, Z.; Chen, H.; Liu, G.; Qiao, Z.; et al. A Review of Research on SLAM Technology Based on the Fusion of LiDAR and Vision. Sensors 2025, 25, 1447. [Google Scholar] [CrossRef]
- Sukop, M.; Grytsiv, M.; Jánoš, R.; Semjon, J. Simple Ultrasonic-Based Localization System for Mobile Robots. Appl. Sci. 2024, 14, 3625. [Google Scholar] [CrossRef]
- Juan, C.-W.; Hu, J.-S. Object Localization and Tracking System Using Multiple Ultrasonic Sensors with Newton–Raphson Optimization and Kalman Filtering Techniques. Appl. Sci. 2021, 11, 11243. [Google Scholar] [CrossRef]
- Tzafestas, S.G. Introduction to Mobile Robot Control; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Leitch, S.G.; Ahmed, Q.Z.; Abbas, W.B.; Hafeez, M.; Laziridis, P.I.; Sureephong, P.; Alade, T. On Indoor Localization Using WiFi, BLE, UWB, and IMU Technologies. Sensors 2023, 23, 8598. [Google Scholar] [CrossRef] [PubMed]
- Rykała, Ł.; Typiak, A.; Typiak, R.; Rykała, M. Application of Smoothing Spline in Determining the Unmanned Ground Vehicles Route Based on Ultra-Wideband Distance Measurements. Sensors 2022, 22, 8334. [Google Scholar] [CrossRef]
- UWB VS Bluetooth: Which Offers Better Indoor Positioning Accuracy. Available online: https://www.mokosmart.com/uwb-vs-bluetooth-indoor-positioning-guide/ (accessed on 8 November 2025).
- Alarifi, A.; Al-Salman, A.; Alsaleh, M.; Alnafessah, A.; Al-Hadhrami, S.; Al-Ammar, M.A.; Al-Khalifa, H.S. Ultra Wideband Indoor Positioning Technologies: Analysis and Recent Advances. Sensors 2016, 16, 707. [Google Scholar] [CrossRef]
- Dong, M.; Qi, Y.; Wang, X.; Liu, Y. A non-line-of-sight mitigation method for indoor ultra-wideband localization with multiple walls. IEEE Trans. Ind. Inform. 2022, 19, 8183–8195. [Google Scholar] [CrossRef]
- Che, F.; Ahmed, Q.Z.; Khan, F.A.; Lazaridis, P.I. Anomaly detection based on generalized Gaussian distribution approach for ultra-wideband (uwb) indoor positioning system. In Proceedings of the 2021 26th International Conference on Automation and Computing (ICAC), Portsmouth, UK, 2–4 September 2021; IEEE: New York, NY, USA, 2021; pp. 1–5. [Google Scholar]
- Majeed, A.F.; Arsat, R.; Baharudin, M.A.; Latiff, N.M.A.A.; Albaidhani, A. Accurate multiclass NLOS channels identification in UWB indoor positioning system-based deep neural network. IEEE Access 2024, 12, 179431–179448. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, R.; Zhang, H.; Zhu, W.; Jia, P.; Li, C.; Ma, Y. Variable-Weighted Error Propagation Model of a Ultra-Wide-Band Indoor Positioning System in an Intelligent Manufacturing Lab. Appl. Sci. 2023, 13, 8400. [Google Scholar] [CrossRef]
- Sidorenko, J.; Schatz, V.; Scherer-Negenborn, N.; Arens, M.; Hugentobler, U. Decawave UWB Clock Drift Correction and Power Self-Calibration. Sensors 2019, 19, 2942. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Y.; Seow, C.K.; Li, Z.; Sun, M.; De Cock, C.; Plets, D. NLOS Identification and Ranging Trustworthiness for Indoor Positioning with LLM-based UWB-IMU Fusion. IEEE Trans. Instrum. Meas. 2025, 74, 8509417. [Google Scholar] [CrossRef]
- Ali, R.; Liu, R.; Nayyar, A.; Qureshi, B.; Cao, Z. Tightly coupling fusion of UWB ranging and IMU pedestrian dead reckoning for indoor localization. IEEE Access 2021, 9, 164206–164222. [Google Scholar] [CrossRef]
- Jiang, P.; Hu, C.; Wang, T.; Lv, K.; Guo, T.; Jiang, J.; Hu, W. Research on a Visual/Ultra-Wideband Tightly Coupled Fusion Localization Algorithm. Sensors 2024, 24, 1710. [Google Scholar] [CrossRef]
- Huang, Y.; Cao, B.; Wang, A. Design a novel algorithm for enhancing UWB positioning accuracy in GPS denied environments. Sci. Rep. 2024, 14, 23895. [Google Scholar] [CrossRef]
- Vitanov, R.I.; Nikolov, D.N. A state-of-the-art review of ultra-wideband localization. In Proceedings of the 2022 57th International Scientific Conference on Information, Communication and Energy Systems and Technologies (ICEST), Ohrid, North Macedonia, 16–18 June 2022; pp. 1–4. [Google Scholar]
- Trek1000 User Manual. (n.d.). Available online: https://datasheet.octopart.com/TREK1000-Decawave-datasheet-98959800.pdf (accessed on 13 October 2025).
- Malon, K.; Łopatka, J.; Rykała, Ł.; Łopatka, M. Accuracy Analysis of UWB Based Tracking System for Unmanned Ground Vehicles. In Proceedings of the 2018 New Trends in Signal Processing (NTSP), Demänovská Dolina, Slovakia, 10–12 October 2018; pp. 1–7. [Google Scholar]
- PIAP Patrol. Available online: https://piap.lukasiewicz.gov.pl/2020/05/19/nowy-robot-mobilny-piap-patrol/ (accessed on 13 October 2025).
- IEEE Std 802.15.4a-2011; Standard for Local and Metropolitan Area Networks—Part 15.4: Low-Rate Wireless Personal Area Networks (LR-WPANs). IEEE: New York, NY, USA, 2011.
- Lian Sang, C.; Adams, M.; Hörmann, T.; Hesse, M.; Porrmann, M.; Rückert, U. Numerical and Experimental Evaluation of Error Estimation for Two-Way Ranging Methods. Sensors 2019, 19, 616. [Google Scholar] [CrossRef]
- MATLAB and Simulink. (n.d.). MATLAB and Simulink Documentation. Available online: https://www.mathworks.com/ (accessed on 13 October 2025).
- Rykała, Ł.; Przybysz, M.; Cieślik, K.; Krogul, P.; Typiak, R.; Typiak, A. Research on selected location algorithms for the UGV operating in a follow-me scenario based on ultra-wideband positioning system. Adv. Sci. Technol. Res. J. 2025, 19, 1–14. [Google Scholar] [CrossRef]
- Gnaś, D.; Majerek, D.; Styła, M.; Adamkiewicz, P.; Skowron, S.; Sak-Skowron, M.; Ivashko, O.; Stokłosa, J.; Pietrzyk, R. Enhanced Indoor Positioning System Using Ultra-Wideband Technology and Machine Learning Algorithms for Energy-Efficient Warehouse Management. Energies 2024, 17, 4125. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, Z.; Zhang, S.; Kuang, Z.; Zhang, L. UWB Positioning Algorithm Based on Fuzzy Inference and Adaptive Anti-NLOS Kalman Filtering. Appl. Sci. 2022, 12, 6183. [Google Scholar] [CrossRef]
- Xie, C.; Fang, X.; Yang, X. Improved Kalman Filtering Algorithm Based on Levenberg–Marquardt Algorithm in Ultra-Wideband Indoor Positioning. Sensors 2024, 24, 7213. [Google Scholar] [CrossRef] [PubMed]
- Lyandres, V.; Briskin, S. On an approach to moving-average filtering. Signal Process. 1993, 34, 163–178. [Google Scholar] [CrossRef]
- Gijbels, I.; Prosdocimi, I. Loess. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 590–599. [Google Scholar] [CrossRef]
- Eubank, R.L. Nonparametric Regression and Spline Smoothing; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Dombi, J.; Dineva, A. Adaptive Savitzky-Golay filtering and its applications. Int. J. Adv. Intell. Paradig. 2020, 16, 145–156. [Google Scholar] [CrossRef]
- Kordestani, H.; Zhang, C. Direct Use of the Savitzky–Golay Filter to Develop an Output-Only Trend Line-Based Damage Detection Method. Sensors 2020, 20, 1983. [Google Scholar] [CrossRef]
- Borhan, N.; Saleh, I.; Rahiman, W. Comparative Analysis of Filtering Techniques for AGV Indoor Localization with Ultra-Wideband Technology. Pertanika J. Sci. Technol. 2024, 32, 2151–2164. [Google Scholar] [CrossRef]
- Roos-Hoefgeest Toribio, M.; Garnung Menéndez, A.; Roos-Hoefgeest Toribio, S.; Álvarez García, I. A Novel Approach to Speed Up Hampel Filter for Outlier Detection. Sensors 2025, 25, 3319. [Google Scholar] [CrossRef]
- Osowski, S. Metody i Narzędzia Eksploracji Danych; Wydawnictwo BTC: Warsaw, Poland, 2013. (In Polish) [Google Scholar]


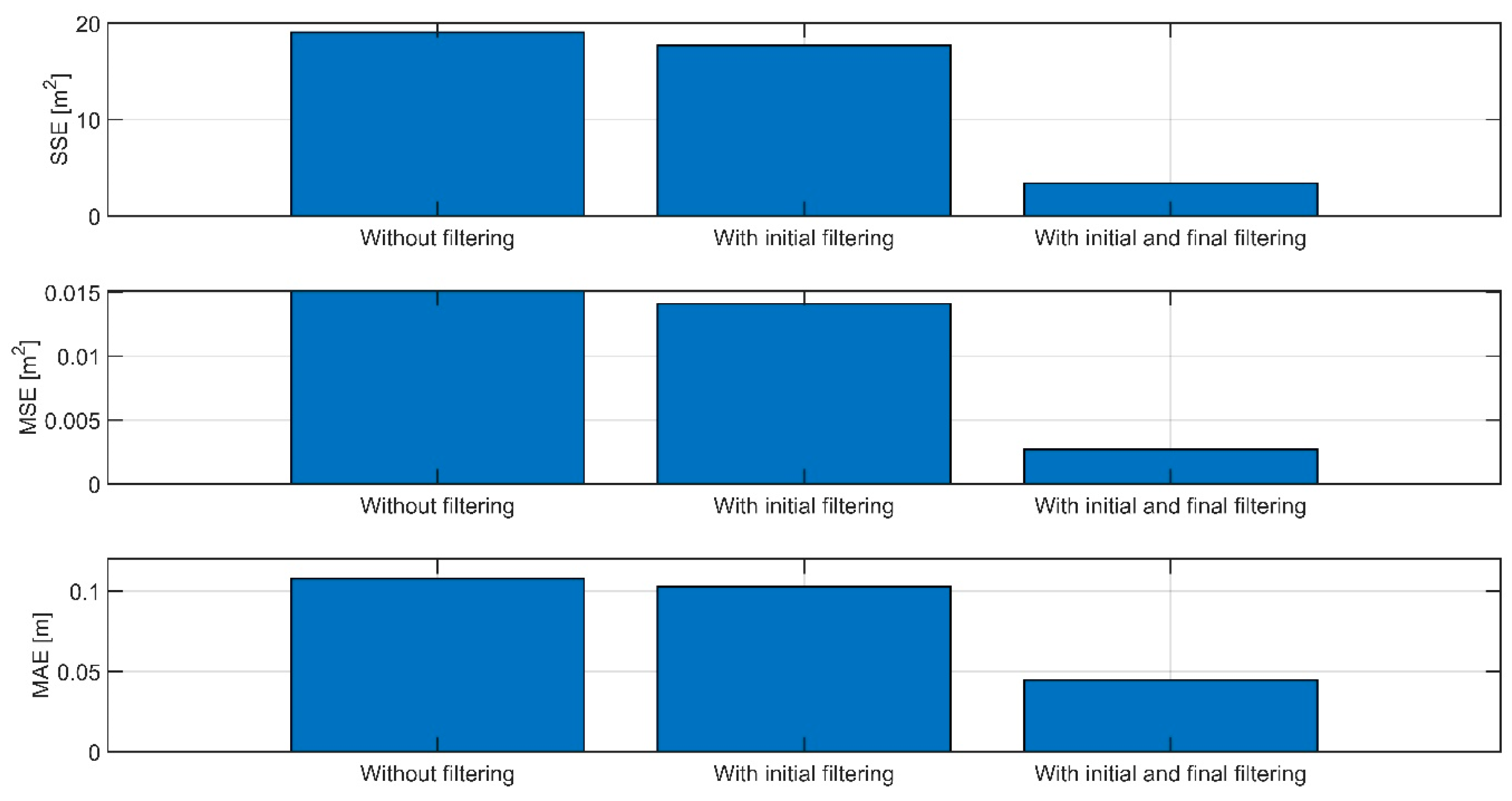
| SSE | MSE | MAE |
|---|---|---|
| 19.041 | 0.015 | 0.108 |
| No | Methods | Parameters | SSE | MSE | MAE |
|---|---|---|---|---|---|
| 1 | Median filter | window size = 3 | 17.679 | 0.014 | 0.103 |
| 3 | Median filter | window size = 5 | 20.151 | 0.016 | 0.105 |
| 5 | Median filter | window size = 7 | 25.767 | 0.020 | 0.113 |
| 7 | Median filter | window size = 9 | 38.185 | 0.030 | 0.129 |
| 9 | Hampel | window size = 3 | 19.068 | 0.015 | 0.108 |
| 17 | Moving mean | window size = 3 | 7.620 | 0.006 | 0.067 |
| 19 | Moving mean | window size = 5 | 12.642 | 0.010 | 0.081 |
| 21 | Moving mean | window size = 7 | 34.501 | 0.027 | 0.136 |
| 23 | Moving mean | window size = 9 | 84.620 | 0.067 | 0.219 |
| No | Methods | Parameters | SSE | MSE | MAE |
|---|---|---|---|---|---|
| 1 | Moving mean | window size = 3 | 8.580 | 0.007 | 0.069 |
| 3 | Moving mean | window size = 5 | 14.778 | 0.012 | 0.086 |
| 5 | LOESS | span = 0.01 | 4.992 | 0.004 | 0.055 |
| 6 | LOESS | span = 0.02 | 3.475 | 0.003 | 0.045 |
| 7 | LOESS | span = 0.03 | 15.203 | 0.012 | 0.097 |
| 8 | RLOESS | span = 0.01 | 5.097 | 0.004 | 0.057 |
| 9 | RLOESS | span = 0.02 | 5.485 | 0.004 | 0.054 |
| 10 | RLOESS | span = 0.03 | 20.593 | 0.016 | 0.115 |
| 11 | Savitzky–Golay | degree = 3, window size = 5 | 9.647 | 0.008 | 0.076 |
| 12 | Savitzky–Golay | degree = 3, window size = 7 | 6.946 | 0.006 | 0.064 |
| 13 | Savitzky–Golay | degree = 3, window size = 9 | 5.449 | 0.004 | 0.057 |
| 14 | Savitzky–Golay | degree = 3, window size = 11 | 4.467 | 0.004 | 0.051 |
| 15 | Savitzky–Golay | degree = 3, window size = 13 | 3.841 | 0.003 | 0.047 |
| 16 | Savitzky–Golay | degree = 3, window size = 15 | 3.398 | 0.003 | 0.045 |
| 17 | Savitzky–Golay | degree = 4, window size = 5 | 17.679 | 0.014 | 0.103 |
| 18 | Savitzky–Golay | degree = 4, window size = 7 | 11.014 | 0.009 | 0.081 |
| 19 | Savitzky–Golay | degree = 4, window size = 9 | 8.521 | 0.007 | 0.071 |
| 20 | Savitzky–Golay | degree = 4, window size = 11 | 6.973 | 0.006 | 0.064 |
| 21 | Savitzky–Golay | degree = 4, window size = 13 | 5.925 | 0.005 | 0.059 |
| 22 | Savitzky–Golay | degree = 4, window size = 15 | 5.146 | 0.004 | 0.055 |
| 23 | Savitzky–Golay | degree = 5, window size = 7 | 11.033 | 0.009 | 0.081 |
| 24 | Savitzky–Golay | degree = 5, window size = 9 | 8.544 | 0.007 | 0.071 |
| 25 | Savitzky–Golay | degree = 5, window size = 11 | 7.032 | 0.006 | 0.064 |
| 26 | Savitzky–Golay | degree = 5, window size = 13 | 5.985 | 0.005 | 0.059 |
| 27 | Savitzky–Golay | degree = 5, window size = 15 | 5.203 | 0.004 | 0.055 |
| 28 | Hampel | window size = 3 | 17.589 | 0.014 | 0.102 |
| 29 | Median filter | window size = 3 | 16.906 | 0.013 | 0.099 |
| 30 | Median filter | window size = 4 | 272.790 | 0.217 | 0.382 |
| 31 | Median filter | window size = 5 | 22.079 | 0.018 | 0.101 |
| 32 | Median filter | window size = 6 | 280.842 | 0.223 | 0.386 |
| 33 | Median filter | window size = 7 | 34.228 | 0.027 | 0.109 |
| 34 | Median filter | window size = 8 | 297.237 | 0.236 | 0.392 |
| 35 | Median filter | window size = 9 | 56.476 | 0.045 | 0.120 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rykała, Ł.; Przybysz, M.; Cieślik, K.; Muszyński, T. Conception of a Low-Cost Location System for an Unmanned Ground Vehicle. Electronics 2025, 14, 4636. https://doi.org/10.3390/electronics14234636
Rykała Ł, Przybysz M, Cieślik K, Muszyński T. Conception of a Low-Cost Location System for an Unmanned Ground Vehicle. Electronics. 2025; 14(23):4636. https://doi.org/10.3390/electronics14234636
Chicago/Turabian StyleRykała, Łukasz, Mirosław Przybysz, Karol Cieślik, and Tomasz Muszyński. 2025. "Conception of a Low-Cost Location System for an Unmanned Ground Vehicle" Electronics 14, no. 23: 4636. https://doi.org/10.3390/electronics14234636
APA StyleRykała, Ł., Przybysz, M., Cieślik, K., & Muszyński, T. (2025). Conception of a Low-Cost Location System for an Unmanned Ground Vehicle. Electronics, 14(23), 4636. https://doi.org/10.3390/electronics14234636







