Unified Performance Analysis of Free-Space Optical Systems over Dust-Induced Fading Channels

Abstract

Free-space optical (FSO) communication systems offer fiber-like bandwidth, high security, and rapid deployment; however, their performance is highly susceptible to atmospheric impairments, such as dust storms, which can cause fading that degrades link reliability. In this study, we analyze the performance of FSO links under a dust-induced fading channel modeled as a Beta distribution channel. We derive an expression for the instantaneous signal-to-noise ratio (SNR) distribution. Using the SNR expression, we construct a general framework that yields closed-form formulas for fundamental performance measures such as outage probability, average bit-error rate (BER), and ergodic capacity. The analysis considers both intensity modulation/direct detection (IM/DD) and coherent detection techniques, encompassing typical modulation schemes including modulation formats such as on–off keying (OOK), M-ary phase-shift keying (M-PSK), and M-ary quadrature amplitude modulation (M-QAM). The results show that dust-induced fading penalizes all modulations, though coherent detection achieves better error performance than IM/DD at equivalent SNR. For example, a coherent receiver requires approximately 4.4 dB lower average SNR than an IM/DD system to achieve the same outage probability. Overall, the proposed unified framework shows that dust-induced fading can severely degrade the performance of FSO links, while also quantifying how network operators can trade off complexity and performance when choosing between coherent and IM/DD detection under realistic dust-storm conditions.

1. Introduction

Free-space optical (FSO) communication is increasingly viewed as a strong candidate for realizing high data rate wireless links that utilizes modulated optical beams to transmit data through the atmosphere, eliminating the need for physical cables or radio spectrum licenses. FSO systems offer several key advantages, including ultra-high bandwidth comparable to optical fiber, enhanced data security due to narrow beamwidths, immunity to electromagnetic interference (EMI), and rapid deployment with minimal infrastructure [1,2]. These benefits make FSO highly attractive for a variety of applications, ranging from metropolitan backhaul links and disaster recovery networks to satellite and unmanned aerial vehicle (UAV) communications. In telecommunications, it serves as a high-capacity backhaul solution for 5G/6G networks [3], particularly in urban areas where laying fiber is impractical. In emergency response scenarios, FSO links can be rapidly deployed to restore connectivity in disaster-struck regions [4]. In defense operations, the inherent directionality and security of FSO links make them ideal for secure tactical communications [5,6]. FSO is also proposed for data-center communications [7], satellite communications [8], and emerging UAV-based wireless networks [9]. The compactness, high data rate, and low latency of FSO make it a strong candidate for next-generation wireless infrastructure across terrestrial and non-terrestrial networks.

However, the performance and availability of FSO systems are strongly affected by atmospheric conditions and alignment precision [10,11]. Since FSO communication requires a clear line of sight between transceivers, factors such as building sway, pointing errors, and environmental disturbances can severely degrade system performance. Among these, weather-induced attenuation is particularly critical. Atmospheric phenomena, such as fog, haze, rain, snow, and dust storms, lead to signal degradation through scattering and absorption mechanisms. While fog attenuation is mainly governed by scattering from water droplets and haze is dominated by scattering from aerosol particles and droplets [12], dust storms combine strong scattering with additional absorption due to mineral dust particles, leading to different attenuation characteristics and motivating a dedicated dust-induced fading model [13]. Moreover, turbulence has a profound impact on beam propagation by inducing random refractive index fluctuations that cause beam wander, beam spreading, and intensity scintillation, which in turn lead to deep fading, increased bit-error rate (BER), and reduced link availability.

There is a rich body of literature that addresses channel modeling and performance analysis of FSO links under atmospheric turbulence. In terms of channel modeling, several statistical models were proposed in the literature. For weak turbulence, the log-normal distribution [14] has been widely adopted. In contrast, moderate-to-strong turbulence conditions are better described by the Gamma–Gamma distribution [15], and negative exponential fading [16] is used in strong saturation regimes. Other statistical models used to characterize turbulence-induced fading in FSO channels include the Málaga model [17], F-distribution model [18], I-K model [19], inverse Gaussian model [20], and exponentiated Weibull model [21]. These channel turbulence models are exploited to derive analytical expressions for metrics such as BER, outage probability, and capacity [22]. For example, BER under Gamma–Gamma fading was expressed using Meijer-G or hypergeometric functions, enabling tractable evaluation of performance under diverse conditions [23,24]. Similarly, ergodic capacity bounds under both log-normal and Gamma–Gamma fading were obtained using statistical averaging over the fading distribution [14,23]. The Gamma–Gamma model is widely regarded as especially flexible, as it can simultaneously represent optical turbulence effects arising from both small-scale and large-scale variations and has been used in numerous analytical studies of FSO links with or without pointing errors. These models specifically address turbulence-induced signal distortions and fading, enabling detailed evaluations of link performance under varying fluctuations in the atmospheric refractive index.

On the other hand, fog has been studied widely and is known to cause severe attenuation of optical signals under heavy fog conditions [25]. Empirical models based on meteorological visibility have long been used to quantify fog-induced attenuation [26]. At the same time, more recent approaches have explored statistical modeling using distributions such as Kumaraswamy [27], Johnson-SB [25], and Gamma [25] to better capture the stochastic nature of atmospheric conditions. Moreover, the authors in [28] analyzed the impact of fog-induced attenuation using a Gamma-distributed channel and derived expressions for outage probability.

In contrast to turbulence and fog, the impact of dust and sandstorms on FSO performance has received comparatively less attention in the literature in terms of channel modeling and performance evaluation, despite being a significant concern for systems deployed in arid and semi-arid environments. Dust storms can drastically reduce visibility and cause severe attenuation of the optical signal. Experimental results have shown that under similar visibility levels, dust-induced attenuation can be significantly higher than that caused by fog [29]. This highlights the need for accurate modeling of dust-induced fading to enable reliable system design and operation.

To address this need, several controlled-chamber studies have demonstrated that dust and sand can degrade FSO links. The authors in [30] used a custom sandstorm chamber with controlled airflow and particle loading to quantify sand-induced attenuation and scintillation on FSO links. In [31], the authors compared co-propagating terahertz (THz) (625 GHz) and infrared (IR) (1.5 $\mathsf{\mu }$m) links in dust clouds and found that dust causes severe additional loss on the IR channel but has a negligible effect on the THz signal. Investigation of dust–turbulence using a chamber at 670 nm and 830 nm was reported in [32], showing that attenuation and Q-factor penalties depend on wavelength, airflow (particle velocity), turbulence strength, and particle type, with ash generally more detrimental than sand. Extending the studies to include 5G backhaul, the authors in [33] showed that all-optical coherent 16-QAM FSO links suffer pronounced BER degradation at low visibility, whereas a parallel 28-GHz RF path remains largely unaffected, enabling robust hybrid FSO/RF designs in dusty conditions. A dedicated dust-storm chamber was used in [29] to derive an empirical visibility–attenuation model, confirming that dust can induce several-fold higher loss than fog but still allows FSO operation over hundreds of meters under light to moderate dust. In [34], a chamber-based study with controllable airflow, turbulence, and particle loading has shown that increasing sand/dust density and wind speed leads to pronounced penalties in Q-factor and BER. An investigation of the performance of an FSO communication system under dust-storm conditions that exploits self-injection-locked lasers was reported in [35]. The results showed multi-Gbps transmission over hybrid single-mode fiber (SMF)–FSO–millimeter-wave (MMW) channels under dusty conditions with improved visibility-limited reach.

In parallel with these experimental efforts, FSO performance under dust conditions has also been explored using simulation tools; for example, through hybrid wavelength-division multiplexing–mode-division multiplexing (WDM–MDM) radio-over-FSO systems [36], dust and rain attenuation impacts on FSO links [37], and mode-division multiplexing (MDM)–FSO simulations [38]. These studies complement the chamber measurements by enabling systematic parameter sweeps and performance prediction under a wide range of environmental scenarios.

Building on both experimental and simulation-based insights, recent studies have begun to fill the modeling gap by introducing a very limited set of empirical and statistical approaches to describe dust-induced fading in FSO links. To the best of our knowledge, only one visibility-based attenuation model has been reported, developed from laboratory experiments and offering practical estimates of signal loss [29]. Similarly, only a small number of statistical models have been proposed for dusty channels: the Johnson SB [39] and negative-exponential [40] distributions, which model FSO signal attenuation, and the more recent Beta distribution [41], which models the normalized received intensity during dust storms and offers a flexible and analytically tractable framework for performance analysis, while [39,40] model FSO signal attenuation, the Beta distribution models the normalized received intensity with only two parameters, enabling compact, closed-form expressions for performance analysis. By contrast, the Johnson SB model in [39] is a four-parameter bounded family that often hampers tractable performance mapping, and the negative-exponential model in [40] depends on dust optical constants and particle size-distribution parameters that are seldom available at the FSO link installation site. Together, these few models play a crucial role in capturing the stochastic behavior of dusty channels and supporting the design of resilient FSO systems in harsh environments.

Consequently, the scarcity of dust-specific statistical models has also limited the number of works that push these descriptions through to full numerical performance evaluation of FSO links. In this context, the authors in [41] used the Beta-based intensity model to investigate the performance of an FSO link employing on–off keying (OOK) modulation under dust storm conditions, providing new insights into how stochastic dust-induced attenuation affects link reliability. Therefore, these probability models offer a foundation for future studies to investigate FSO system performance under dust across a wider range of deployment scenarios and modulation formats, including the incorporation of spatial, temporal, or hybrid diversity techniques as additional mitigation strategies.

This paper presents a comprehensive analysis of FSO communication performance over dust-induced fading channels, modeled using the Beta distribution defined in [41], and evaluates several key performance metrics. Unlike [41], which analyzes intensity modulation/direct detection (IM/DD) On-Off keying (OOK) only, we provide a unified analytical framework for both detection types (IM/DD and coherent) and for multiple modulation formats including OOK, M-PSK, and M-QAM. The main contributions are summarized as follows:

• Derive the distribution of the instantaneous electrical signal-to-noise ratio (SNR) under the Beta fading model.
• Using this SNR model as a foundation, we obtain unified closed-form formulations for fundamental performance measures—outage probability, average BER, and ergodic capacity—applicable to various modulation formats.
• Assess the analytical results using numerical simulations and analyze the influence of dust-induced fading on system performance under both coherent and IM/DD detection schemes.

The remainder of the paper is structured as follows: Section 2 introduces the system model and provides the derivation of the unified SNR expression. Section 3 presents the analytical formulation of outage probability, BER, and capacity. Section 4 discusses the numerical results. Finally, Section 5 wraps up the work and outlines potential avenues for further investigation.

2. FSO Channel Modeling and SNR Characterization

2.1. System Model

In dry and desert-like environments, dust-induced fading alters the received FSO signal by affecting the corresponding irradiance level. In this work, we adopt the Beta dust-induced irradiance model previously inferred from controlled measurements reported in [41]. In that study, an FSO link at 1550 nm was established through a $90\times 40\times 40$ cm³ dust chamber, where dust samples collected from a real dust storm (average particle diameter of approximately 17.3 $\mathsf{\mu }$m) were uniformly dispersed by internal fans, and the received optical power was recorded with a photodetector and data-acquisition system. A time series of $1.6\times {10}^5$ irradiance samples was collected and normalized by the transmitted power; fitting a Beta distribution to these normalized measurements yielded $\alpha =7.34$ and $\beta =0.71$, which are used here as representative parameters for the considered dust-storm conditions.

The normalized irradiance I that is modeled by the Beta distribution with parameters $\alpha ,\beta >0$ is given as [41]

$$f_I\left(I\right)={\displaystyle \frac{I^{\alpha -1}{(1-I)}^{\beta -1}}{B(\alpha ,\beta )}},0<I<1,$$

(1)

where the beta function, $B(\alpha ,\beta )$, is defined by [42] (Equation (5.12.1)),

$$B(\alpha ,\beta )={\int }_0^1{t}^{\alpha -1}{(1-t)}^{\beta -1}\mathrm{d}t.$$

(2)

The beta distribution directly models normalized irradiance and enables closed-form performance derivations, making it suitable for the performance analysis of FSO systems under dust fading channels. Considering that the FSO signal propagates through a dust-induced fading channel, the electrical received signal is defined as [14]

$$y=\eta Ix+n.$$

(3)

Here, $x\in \{0,1\}$ denotes the binary symbol being transmitted, $\eta$ is the conversion gain that maps the optical signal to the electrical domain, and $n\sim \mathcal{N}(0,N_0/2)$ represents the additive white Gaussian noise (AWGN), modeled as a zero-mean Gaussian variable with variance $N_0/2$. To keep the scope focused on dust-induced fading and maintain analytical tractability, atmospheric turbulence and pointing-error effects are omitted; their joint inclusion greatly complicates closed-form BER/capacity derivations and is deferred to future work. The resulting instantaneous electrical SNR at the receiver can be expressed as

$$\gamma ={\displaystyle \frac{{\left(\eta I\right)}^r}{N_0}}=a{I}^r,$$

(4)

where $a={\eta }^r/N_0$ is a scaling parameter, with $r=1$ corresponding to coherent detection and $r=2$ used in the case of IM/DD. Note that, for coherent detection, phase recovery and local-oscillator processing are absorbed into the SNR constants rather than appearing explicitly in the fading coefficient [43,44,45,46]. The average electrical SNR is expressed as

$$\overline{\gamma }=a\mathbb{E}\left[I^r\right]=a{\displaystyle \frac{B(\alpha +r,\beta )}{B(\alpha ,\beta )}}.$$

(5)

Equivalently, in terms of gamma functions, the average electrical SNR is defined as

$$\overline{\gamma }=a{\displaystyle \frac{\mathsf{\Gamma }(\alpha +r)\mathsf{\Gamma }(\alpha +\beta )}{\mathsf{\Gamma }\left(\alpha \right)\mathsf{\Gamma }(\alpha +\beta +r)}},$$

(6)

where $\mathsf{\Gamma }(.)$ is the Gamma function defined as

$$\mathsf{\Gamma }\left(x\right)={\int }_0^{\infty }{t}^{x-1}{e}^{-t}\mathrm{d}t.$$

(7)

2.2. SNR Probability Density Function

To find the distribution of $\gamma$, we apply the transformation of random variables method. From the instantaneous SNR relation in (4):

$$I={\left(\gamma /a\right)}^{1/r}.$$

(8)

By the change-of-variables theorem, the densities satisfy [47]

$$f_{\gamma }\left(\gamma \right)=f_I\left(I\left(\gamma \right)\right)\left|\frac{dI}{d\gamma }\right|.$$

(9)

Differentiating (8) with respect to $\gamma$ yields

$${\displaystyle \frac{dI}{d\gamma }}={\displaystyle \frac{1}{r}}{a}^{-1/r}{\gamma }^{{\displaystyle \frac{1}{r}}-1}.$$

(10)

Substituting (1) and (10) into (9) yields:

$$f_{\gamma }\left(\gamma \right)=f_I\left({(\gamma /a)}^{1/r}\right){\displaystyle \frac{1}{r}}{a}^{-1/r}{\gamma }^{{\displaystyle \frac{1}{r}}-1},0<\gamma <a.$$

(11)

Finally, substituting (1) into (11) produces the SNR distribution as

$$\begin{array}{cc}\hfill f_{\gamma }\left(\gamma \right)& ={\displaystyle \frac{1}{r·a^{\alpha /r}·B(\alpha ,\beta )}}·{\gamma }^{{\displaystyle \frac{\alpha -r}{r}}}{\left(1-{\left({\displaystyle \frac{\gamma }{a}}\right)}^{1/r}\right)}^{\beta -1},0<\gamma <a.\hfill \end{array}$$

(12)

For the special case of coherent detection ($r=1$), the expression simplifies to a scaled beta distribution:

$$\begin{array}{cc}\hfill f_{\gamma }\left(\gamma \right)& ={\displaystyle \frac{1}{a^{\alpha }B(\alpha ,\beta )}}·{\gamma }^{\alpha -1}{\left(1-{\displaystyle \frac{\gamma }{a}}\right)}^{\beta -1},0<\gamma <a.\hfill \end{array}$$

(13)

In the case of IM/DD detection ($r=2$), the SNR follows a generalized beta-like distribution:

$$\begin{array}{cc}\hfill f_{\gamma }\left(\gamma \right)& ={\displaystyle \frac{1}{2a^{\alpha /2}B(\alpha ,\beta )}}·{\gamma }^{{\displaystyle \frac{\alpha }{2}}-1}{\left(1-{\left({\displaystyle \frac{\gamma }{a}}\right)}^{1/2}\right)}^{\beta -1},0<\gamma <a.\hfill \end{array}$$

(14)

2.3. SNR Cumulative Distribution Function

The cumulative distribution function (CDF) of the instantaneous SNR is defined as

$$F_{\gamma }\left(\gamma \right)={\int }_0^{\gamma }{f}_{\gamma }\left({\gamma }^{\prime }\right)d{\gamma }^{\prime },$$

(15)

where $f_{\gamma }\left(\gamma \right)$ is the SNR probability density function derived previously. Since the irradiance I follows a beta distribution and the SNR is given by the transformation $\gamma =a{I}^r$, the CDF of SNR can be obtained using a change in the variable technique. Let $u={\left({\displaystyle \frac{{\gamma }^{\prime }}{a}}\right)}^{1/r}$. Applying this substitution in (15), and using the SNR PDF from (12), transforms the integral into

$$F_{\gamma }\left(\gamma \right)={\int }_0^{{\left({\displaystyle \frac{\gamma }{a}}\right)}^{1/r}}{\displaystyle \frac{1}{B(\alpha ,\beta )}}{u}^{\alpha -1}{(1-u)}^{\beta -1}du,$$

(16)

which corresponds to the regularized incomplete beta function $I_z(\alpha ,\beta )$ [42] (Equation (8.17.2)). Therefore, the CDF of the SNR $\gamma$ is given by

$$F_{\gamma }\left(\gamma \right)=I_{{(\gamma /a)}^{1/r}}(\alpha ,\beta ),0\le \gamma \le a,$$

(17)

2.4. Moments

The moments of the instantaneous SNR, denoted by $\mathbb{E}\left[{\gamma }^n\right]$, are defined as

$$\mathbb{E}\left[{\gamma }^n\right]={\int }_0^a{\gamma }^n{f}_{\gamma }\left(\gamma \right)d\gamma .$$

(18)

By applying the transformation $\gamma =a{I}^r$ and using the change in the variable $I={(\gamma /a)}^{1/r}$, the moments can be obtained in closed-form as

$$\mathbb{E}\left[{\gamma }^n\right]=a^n\mathbb{E}\left[I^{rn}\right]=a^n·{\displaystyle \frac{B(\alpha +rn,\beta )}{B(\alpha ,\beta )}}.$$

(19)

3. Performance Metrics

In this section, we present the derivation of analytical expressions for core performance indicators, namely the outage probability, ergodic channel capacity, and average BER, considering a dust-induced fading environment. The focus is on obtaining mathematically tractable results that can be efficiently evaluated. Although the forthcoming expressions may involve special functions such as hypergeometric functions, they are chosen to ensure computational feasibility using standard scientific tools (e.g., MATLAB, Mathematica, or Python’s SciPy). This makes the proposed analytical framework suitable for both theoretical studies and practical design of FSO systems.

3.1. Outage Probability

Outage probability refers to the likelihood that the instantaneous SNR drops below a specified threshold ${\gamma }_{\mathrm{th}}$, resulting in unreliable communication. This can be expressed mathematically as

$$P_{\mathrm{out}}\left({\gamma }_{\mathrm{th}}\right)=Pr[\gamma <{\gamma }_{\mathrm{th}}]=F_{\gamma }\left({\gamma }_{\mathrm{th}}\right),$$

(20)

Using (17), the outage probability can be expressed in closed-form as

$$F_{\gamma }\left({\gamma }_{th}\right)=I_{{({\gamma }_{th}/a)}^{1/r}}(\alpha ,\beta ),$$

(21)

3.2. Average Bit Error Rate

The average BER is a fundamental metric that characterizes the average probability of bit error in the presence of fading and noise. For a broad class of modulation schemes, the average BER as a function of the instantaneous SNR can be expressed in a unified form as [45]

$${\overline{P}}_b=\delta \sum _{k=1}^n{\displaystyle \frac{1}{2\mathsf{\Gamma }\left(p\right)}}{\int }_0^a\mathsf{\Gamma }(p,q_k\gamma )f_{\gamma }\left(\gamma \right)d\gamma .$$

(22)

where $\mathsf{\Gamma }(p,·)$ denotes the upper incomplete gamma function, and $\delta ,p,q_k,n$ are modulation-specific parameters defined in Table 1. Note that coherent modulation schemes such as BPSK, M-PSK, and M-QAM are assumed to use their standard complex-valued baseband constellations. In the considered system model, the dust channel affects the signal only through the real, non-negative irradiance fading and the corresponding instantaneous SNR.

Table 1. Parameters for Different Modulation Formats [45].

Modulation	$\mathit{\delta }$	p	${\mathit{q}}_{\mathit{k}}$	n	Detection
OOK	1	$\frac{1}{2}$	$\frac{1}{4}$	1	IM/DD
BPSK	1	$\frac{1}{2}$	1	1	coherent
M-PSK	${\displaystyle \frac{2}{max({log}_{2}M,2)}}$	$\frac{1}{2}$	${sin}^2\left({\displaystyle \frac{(2k-1)\pi }{M}}\right)$	$max\left(\frac{M}{4},1\right)$	coherent
M-QAM	${\displaystyle \frac{4}{{log}_{2}M}}\left(1-{\displaystyle \frac{1}{\sqrt{M}}}\right)$	$\frac{1}{2}$	${\displaystyle \frac{3{(2k-1)}^2}{2(M-1)}}$	${\displaystyle \frac{\sqrt{M}}{2}}$	coherent

Using the identity $\mathsf{\Gamma }(p,x)=\mathsf{\Gamma }\left(p\right)-\gamma (p,x)$ [42] (Equation (8.2.3)), the expression in (22) is rewritten as

$$\begin{array}{cc}\hfill {\overline{P}}_b& ={\displaystyle \frac{\delta }{2}}\sum _{k=1}^n\left[1-{\displaystyle \frac{1}{\mathsf{\Gamma }\left(p\right)}}{J}_k\right],\hfill \end{array}$$

(23)

where

$$J_k={\int }_0^a\gamma \left(p,q_k\gamma \right)f_{\gamma }\left(\gamma \right)d\gamma .$$

Let $\gamma =a{u}^r$, and substituting (12) into the expression $J_k$ and simplifying yields the following:

$$\begin{array}{cc}\hfill J_k& ={\displaystyle \frac{1}{B(\alpha ,\beta )}}{\int }_0^1\gamma \left(p,c_k{u}^r\right)u^{\alpha -1}{(1-u)}^{\beta -1}du,\hfill \end{array}$$

(24)

where $c_k=q_{k}a$. Applying the binomial-coefficient identity [42] (Equation (4.6.7)), with $z=-u$ and $a=\beta -1$, the term ${(1-u)}^{(\beta -1)}$ can be expressed as

$${(1-u)}^{\beta -1}=\sum _{m=0}^{\infty }\left({\displaystyle \genfrac{}{}{0pt}{}{\beta -1}{m}}\right){(-u)}^m,u\in [0,1).$$

(25)

Then, using the Binomial theorem [42] (Equation (1.2.6)), we can rewrite (25) as

$${(1-u)}^{\beta -1}=\sum _{m=0}^{\infty }{\displaystyle \frac{{(1-\beta )}_m}{m!}}{u}^m,u\in [0,1),$$

(26)

where ${(\beta -1)}_m=(\beta -1)\left(\beta \right)(\beta +1)\dots (\beta +m-2)$ is the Pochhammer symbol. Substituting (26) in (24) and reordering the terms yields

$$J_k={\displaystyle \frac{1}{B(\alpha ,\beta )}}\sum _{m=0}^{\infty }{\displaystyle \frac{{(1-\beta )}_m}{m!}}{\int }_0^1\gamma \left(p,c_k{u}^r\right)u^{\alpha +m-1}du.$$

(27)

The integration in (27) does not admit a closed form in its original variables, so we first rewrite it in a standard form. To this end, we first define $s=(\alpha +m)/r$ so that the exponent $\alpha +m-1$ can be written as $rs-1$, and then apply the change in the variables $x=c_k{u}^r$. With this choice, we obtain

$${\int }_0^1\gamma \left(p,c_k{u}^r\right)u^{\alpha +m-1}du={\displaystyle \frac{1}{r}}{c}_k^{-s}{\int }_0^{c_k}\gamma (p,x)x^{s-1}dx.$$

(28)

which matches the standard form required to apply the lemma stated in the next step. Next, we use the following lemma (proved by a Fubini-Tonelli swap and an inner elementary integral).

Lemma 1. 

For $p>0$, $s>0$, $c>0$,

$${\int }_0^c\gamma (p,x)x^{s-1}dx={\displaystyle \frac{c^s}{s}}\gamma (p,c)-{\displaystyle \frac{1}{s}}\gamma (p+s,c).$$

(29)

Proof. 

Using the defining integral of the lower incomplete gamma $\gamma (p,x)={\int }_0^x{t}^{p-1}{e}^{-t}dt$ [42] (Equation (8.2.1)), and interchange the order over $0\le t\le x\le c$:

$$\begin{array}{cc}\hfill {\int }_0^c\gamma (p,x)x^{s-1}dx& ={\int }_0^c{\int }_0^x{t}^{p-1}{e}^{-t}{x}^{s-1}dtdx={\int }_0^c{\int }_t^c{t}^{p-1}{e}^{-t}{x}^{s-1}dxdt\hfill \\ \hfill & ={\int }_0^c{t}^{p-1}{e}^{-t}{\displaystyle \frac{c^s-t^s}{s}}dt={\displaystyle \frac{c^s}{s}}\gamma (p,c)-{\displaystyle \frac{1}{s}}\gamma (p+s,c).\hfill \end{array}$$

(30)

□

Substituting (29) into (28) and using $s=(\alpha +m)/r$, we get

$$\begin{array}{cc}\hfill {\int }_0^1\gamma \left(p,c_k{u}^r\right)u^{\alpha +m-1}du& ={\displaystyle \frac{1}{\alpha +m}}\left[\gamma \left(p,c_k\right)-c_k^{-s}\gamma \left(p+s,c_k\right)\right].\hfill \end{array}$$

(31)

Then, substituting (31) into (27) yields

$$\begin{array}{c}\hfill J_k={\displaystyle \frac{1}{B(\alpha ,\beta )}}\sum _{m=0}^{\infty }{\displaystyle \frac{{(1-\beta )}_m}{m!(\alpha +m)}}\left[\gamma \left(p,c_k\right)-c_k^{-{\displaystyle \frac{\alpha +m}{r}}}\gamma \left(p+{\displaystyle \frac{\alpha +m}{r}},c_k\right)\right].\end{array}$$

(32)

Next, substituting (32) into (23) yields

$$\begin{array}{cc}\hfill {\overline{P}}_b& ={\displaystyle \frac{\delta }{2}}\sum _{k=1}^n\left[1-{\displaystyle \frac{1}{\mathsf{\Gamma }\left(p\right)B(\alpha ,\beta )}}\sum _{m=0}^{\infty }{\displaystyle \frac{{(1-\beta )}_m}{m!(\alpha +m)}}\left(\gamma (p,c_k)-c_k^{-{\displaystyle \frac{\alpha +m}{r}}}\gamma \left(p+{\displaystyle \frac{\alpha +m}{r}},c_k\right)\right)\right].\hfill \end{array}$$

(33)

Using ${\displaystyle \frac{1}{\alpha +m}={\int }_0^1{t}^{\alpha +m-1}dt}$, interchanging sum and integral, and using the generalized binomial series identity [42] (Equation (4.6.7)), the summation term in (33) can be simplified as

$$\begin{array}{cc}\hfill \sum _{m=0}^{\infty }{\displaystyle \frac{{(1-\beta )}_m}{m!(\alpha +m)}}& ={\int }_0^1{t}^{\alpha -1}\left(\sum _{m=0}^{\infty }{\displaystyle \frac{{(1-\beta )}_m}{m!}}{t}^m\right)dt\hfill \\ \hfill & ={\int }_0^1{t}^{\alpha -1}{(1-t)}^{\beta -1}dt=B(\alpha ,\beta ).\hfill \end{array}$$

(34)

Finally, substituting (34) into (33) and simplifying, we obtain the final expression of the average BER as

$$\begin{array}{cc}\hfill {\overline{P}}_b& ={\displaystyle \frac{\delta }{2}}\sum _{k=1}^n\left[Q\left(p,c_k\right)+{\displaystyle \frac{1}{\mathsf{\Gamma }\left(p\right)B(\alpha ,\beta )}}\times \sum _{m=0}^{\infty }{\displaystyle \frac{{(1-\beta )}_m}{m!(\alpha +m)}}{c}_k^{-\frac{\alpha +m}{r}}\gamma \left(p+\frac{\alpha +m}{r},c_k\right)\right],\hfill \end{array}$$

(35)

where $Q(p,c_k)=\mathsf{\Gamma }(p,c_k)/\mathsf{\Gamma }\left(p\right)=1-\gamma (p,c_k)/\mathsf{\Gamma }\left(p\right)$ is the regularized upper incomplete gamma function [42] (Equation (8.2.4)).

3.3. Ergodic Capacity

The ergodic capacity quantifies the average achievable rate under ideal channel conditions and is defined as [46]

$$C_{\mathrm{erg}}={\displaystyle \frac{1}{ln2}}{\int }_0^{\infty }{\displaystyle \frac{1-F_{\gamma }\left(\gamma \right)}{1+\gamma }}d\gamma .$$

(36)

Substituting (17) into (36) yields

$$C_{\mathrm{erg}}={\displaystyle \frac{1}{ln2}}{\int }_0^a{\displaystyle \frac{1-I_{{(\gamma /a)}^{1/r}}(\alpha ,\beta )}{1+\gamma }}d\gamma .$$

(37)

Let $u={(\gamma /a)}^{1/r}$. Then

$$C_{\mathrm{erg}}={\displaystyle \frac{ar}{ln2}}{\int }_0^1{\displaystyle \frac{1-I_u(\alpha ,\beta )}{1+a{u}^r}}{u}^{r-1}du.$$

(38)

Using the generalized binomial expansion [42] (Equation (4.6.7)) together with Euler’s beta integral in (2) and integrating the binomial series term-by-term gives the standard expansion of the regularized incomplete beta function. Then, the numerator of (38) can be expressed as

$$1-I_u(\alpha ,\beta )={\displaystyle \frac{1}{B(\alpha ,\beta )}}\sum _{m=0}^{\infty }{\displaystyle \frac{{(1-\beta )}_m}{m!(\alpha +m)}}\left(1-u^{\alpha +m}\right).$$

(39)

Substitute (39) into (38) and swap sum–integral, justified by dominated convergence for $\alpha >0,\beta >0$ on $u\in [0,1]$, yields

$$\begin{array}{cc}\hfill C_{\mathrm{erg}}& ={\displaystyle \frac{ar}{ln2}}{\displaystyle \frac{1}{B(\alpha ,\beta )}}\sum _{m=0}^{\infty }{\displaystyle \frac{{(1-\beta )}_m}{m!(\alpha +m)}}\left[{\int }_0^1{\displaystyle \frac{u^{r-1}}{1+a{u}^r}}du-{\int }_0^1{\displaystyle \frac{u^{\alpha +m+r-1}}{1+a{u}^r}}du\right].\hfill \end{array}$$

(40)

The integration terms in (40) can be represented in terms of the Gauss hypergeometric function [48] (Equation (3.197.3)). The first integration term can be represented as:

$${\int }_0^1{\displaystyle \frac{u^{r-1}}{1+a{u}^r}}du={\displaystyle \frac{1}{r}}{}_{2}F_1\left(1,1;2;-a\right)={\displaystyle \frac{ln(1+a)}{ra}}$$

(41)

where the identity ${}_{2}F_1\left(1,1;2;z\right)=-z^{-1}ln(1-z)$ [42] (Equation (15.4.1)), is used with $z=-a$. The second integration term is represented as

$$\begin{array}{cc}\hfill & {\int }_0^1{\displaystyle \frac{u^{\alpha +m+r-1}}{1+a{u}^r}}du={\displaystyle \frac{1}{\alpha +m+r}}{}_{2}F_1\left(1,1+{\displaystyle \frac{\alpha +m}{r}};2+{\displaystyle \frac{\alpha +m}{r}};-a\right)\hfill \end{array}$$

(42)

Finally, substituting (41) and (42) into (40) and applying (34) yields

$$\begin{array}{cc}\hfill C_{\mathrm{erg}}(\overline{\gamma };\alpha ,\beta ,r)& ={\displaystyle \frac{1}{ln2}}ln(1+a)-{\displaystyle \frac{ar}{ln2}}{\displaystyle \frac{1}{B(\alpha ,\beta )}}\sum _{m=0}^{\infty }{\displaystyle \frac{{(1-\beta )}_m}{m!(\alpha +m)(\alpha +m+r)}}\hfill \\ \hfill & \times {}_{2}F_1\left(1,1+{\displaystyle \frac{\alpha +m}{r}};2+{\displaystyle \frac{\alpha +m}{r}};-a\right).\hfill \end{array}$$

(43)

4. Results Discussion

4.1. Outage Probability Analysis

Figure 1 shows the outage probability versus the normalized average SNR, $\overline{\gamma }/{\gamma }_{\mathrm{th}}$, for both coherent and IM/DD detection techniques. The analysis is based on the closed-form expression in (21). The results of the Monte Carlo simulations show closely match with the closed-form expression, validating the derived formula. As expected, the outage probability decreases monotonically with increasing normalized SNR, reflecting improved link reliability at higher average SNR levels.

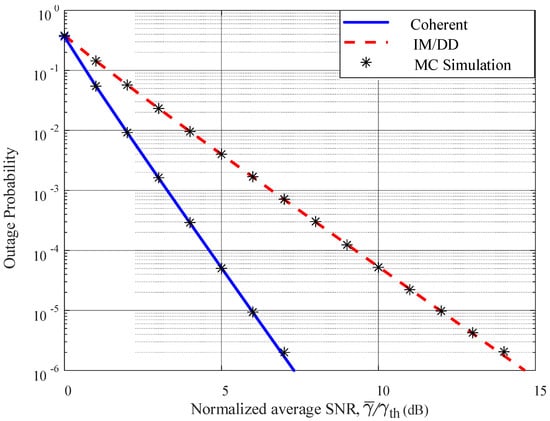
Figure 1. Outage probability versus normalized average SNR, $\overline{\gamma }/{\gamma }_{\mathrm{th}}$ for IM/DD and coherent detection under dust-induced fading.

At low normalized SNR values, both detection schemes experience high outage due to the pronounced effect of dust-induced fading, which severely attenuates the received signal power. However, IM/DD consistently exhibits a higher outage probability compared to coherent detection. This performance gap becomes increasingly significant as the target SNR threshold rises.

The better performance of coherent detection is primarily attributed to its higher receiver sensitivity and enhanced noise suppression. As a result, it can achieve reliable communication at lower SNR values than IM/DD under the same fading conditions. This advantage is evident in Figure 1, where for a target outage probability of ${10}^{-4}$, the required normalized SNR for coherent detection is approximately 4.8 dB. In comparison, IM/DD requires around 9.2 dB—a difference of 4.4 dB in favor of coherent detection.

Moreover, in the high-SNR regime, the outage probability of coherent detection drops more steeply, approaching zero faster than that of IM/DD. This rapid decay illustrates its greater robustness and suitability for FSO links operating in dust-prone environments, where maintaining low outage rates is critical for service continuity.

Figure 2 shows the outage probability versus the average SNR for different SNR threshold values. As the target SNR threshold increases, the outage curves shift to the right for both detection schemes, indicating that higher average SNR is required to achieve the same reliability level. In practical terms, this acts as a nearly one-for-one penalty in dB; for example, at an outage level around ${10}^{-3}$, raising the threshold from 0 dB to 10 dB typically demands about 10 dB more average SNR, and moving from 10 dB to 20 dB adds roughly another 10 dB.

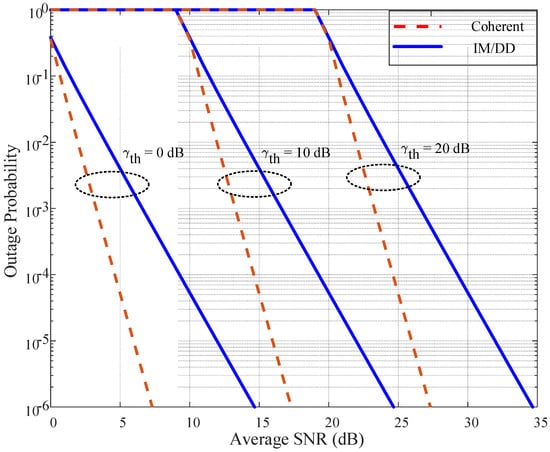
Figure 2. Outage probability versus average SNR for different SNR thresholds: ${\gamma }_{\mathrm{th}}\in \{0,10,20\}\mathrm{dB}$.

4.2. Average BER Analysis

Figure 3 depicts the variation in the average BER with respect to the average SNR for various modulation schemes under a dust-induced fading channel. The theoretical BER results, computed using numerical integration of the exact expression in (22), are compared with the proposed closed-form expression given in (35). The results show that the exact and closed-form expressions agree closely across the entire SNR range, and the Monte Carlo results align with them, confirming the accuracy of the derived closed-form expression.

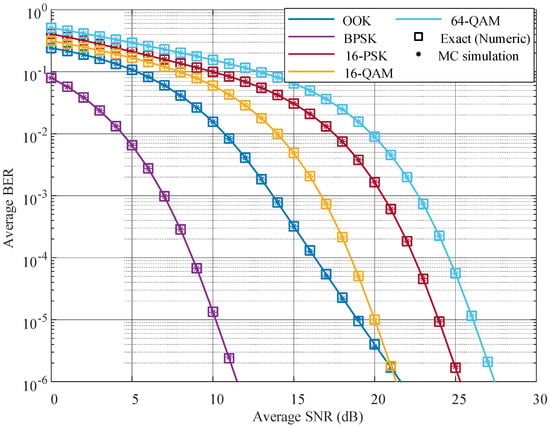
Figure 3. Average BER versus average SNR for different modulation formats under dust-induced fading.

As shown in Figure 3, systems employing higher-order modulation formats such as 16-QAM, 16-PSK, and 64-QAM exhibit significantly improved error performance over OOK at high SNR values, while OOK consistently underperforms BPSK across the entire SNR range, it achieves lower BER than higher-order formats in the low-to-moderate SNR regime. However, as the SNR increases, more spectrally efficient modulation schemes surpass OOK in performance. Specifically, OOK is outperformed by 16-QAM beyond approximately 21 dB.

Moreover, Figure 3 shows that the system using 16-QAM modulation format performs better when using 16-PSK modulation format. In contrast to 16-PSK, which places all constellation points on a circle with constant amplitude, 16-QAM employs a rectangular grid constellation that varies in both amplitude and phase. This structure leads to a greater minimum Euclidean distance between adjacent symbols for the same average energy per bit, thereby enhancing the modulation’s resilience to additive noise. Moreover, 16-QAM benefits from energy diversity within its constellation: inner symbols have lower amplitude and are consequently less affected by amplitude fading. This inherent diversity provides improved robustness in fading channels, allowing 16-QAM to achieve superior BER performance compared to 16-PSK under the same channel conditions.

At a target BER of ${10}^{-4}$, the modulation schemes exhibit varying performance levels in terms of the required average SNR. BPSK offers the best performance, achieving this BER at only 8.9 dB, owing to its strong resilience to noise through binary phase modulation. OOK follows with a requirement of 16.4 dB, reflecting the limitations of intensity-only modulation under fading conditions. 16-QAM outperforms 16-PSK, needing only 18.6 dB compared to the 22.4 dB required by 16-PSK. Finally, 64-QAM, despite its higher spectral efficiency, demands a higher SNR of 24.6 dB to maintain the same BER due to its denser constellation structure, which makes it more vulnerable to noise and fading distortions. These results highlight that among higher-order formats, 16-QAM provides an optimal trade-off between performance and complexity at moderate SNRs.

Figure 4 examines the effect of series truncation in the closed-form average BER for OOK modulation format. We compare the exact integral (Equation (22)) against three approximations: (i) removing the series and retaining only the $Q(p,c_k)$ term, (ii) keeping a single series term ($m=0$), and (iii) truncating after $M=1000$ terms. By visual inspection, the $M=1000$ curve lies essentially on top of the exact result across the plotted SNR range, indicating practical equivalence between the series and integral forms. The single-term approximation already tracks the exact curve closely especially beyond moderate SNR—while the “Q-only” curve departs noticeably at moderate/high SNR and exhibits an incorrect asymptotic slope.

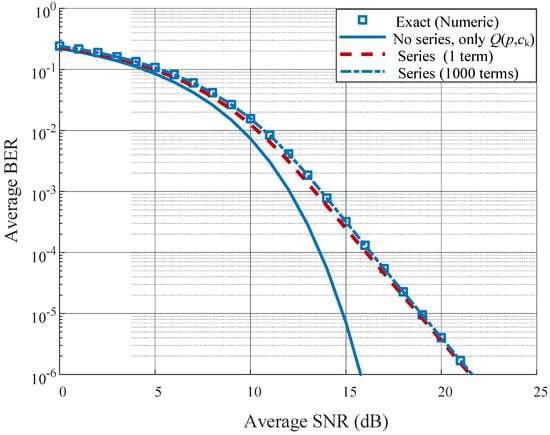
Figure 4. Impact of series truncation on the average BER of the OOK modulation format. Shown are the exact integral (numeric) and three closed-form variants: $Q(p,c_k)$ only, one-term series ($m=0$), and a $M=1000$-term truncation.

4.3. Ergodic Capacity Analysis

Figure 5 illustrates the ergodic capacity of an FSO system under dust-induced fading for two cases: IM/DD modulation ($r=2$) and coherent modulation ($r=1$). Both the exact capacity, computed numerically using the definition in (36), and the closed-form expression obtained in (43), are plotted against the average SNR in dB.

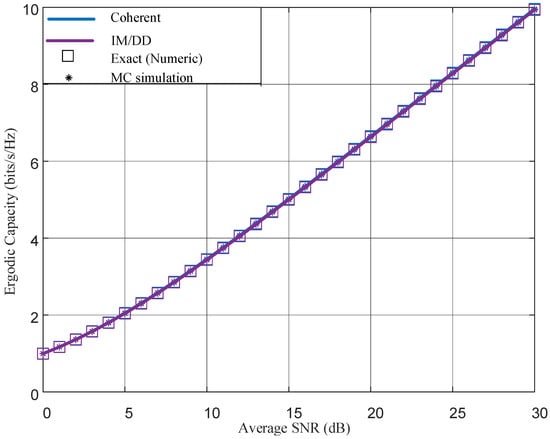
Figure 5. Ergodic capacity versus average SNR for coherent detection system $r=1$ and IM/DD system $r=2$ under dust-induced fading channel. In this figure, the coherent detection curve coincides with the corresponding IM/DD curve over the considered SNR range and is therefore not visually distinguishable.

As shown, the capacity increases monotonically with SNR, which is expected due to improved link reliability at higher signal levels. The curves also confirm that the closed-form expression closely matches the exact (integral) capacity, and the Monte Carlo points coincide with both—thus validating the derived closed-form expression across the entire SNR range.

Moreover, in Figure 5, both IM/DD and coherent detection show almost the same performance. This near overlap arises because, under our shot-noise–limited, equal-power/equal-bandwidth setting, both receivers operate with essentially the same photon budget; in addition, the capacity expression in (36) averages ${log}_2(1+\gamma )$ over a scalar SNR (amplitude-only) and therefore does not exploit coherent phase/I–Q degrees of freedom.

5. Conclusions

This paper presents a comprehensive analytical study of FSO communication systems operating under dust-induced fading, modeled using a Beta distribution. Using this statistical model, we derive closed-form expressions for the instantaneous SNR distribution, outage probability, average BER, and ergodic capacity. The analysis was conducted for both IM/DD and coherent detection schemes. Numerical evaluations confirms that coherent detection consistently outperforms IM/DD in terms of outage and BER performance under dust fading, with the performance gap widening at higher SNR thresholds. Among the modulation schemes analyzed, higher-order formats such as 16-QAM offered improved BER at high SNRs, though at the cost of increased implementation complexity. The closed-form approximations also demonstrated good agreement with exact numerical results in the moderate-to-high SNR regimes. Future work may extend this framework to include pointing errors and consider hybrid FSO/RF architectures to further enhance link reliability in desert and urban environments. Throughout this work, dust-induced fading is modeled using its marginal distribution of normalized irradiance under the slow-fading assumption, i.e., the channel remains quasi-static over many symbol intervals, as is standard for FSO links. We do not explicitly characterize the temporal dynamics of dust (e.g., coherence time with and without dust) nor its joint interaction with atmospheric turbulence and pointing errors. A rigorous experimental study of these aspects would require a more elaborate measurement setup and composite channel model, and is therefore left as an important direction for future work.