Abstract
This study presents a digitally controlled, combined pulse-width and pulse-density modulator (PWDM) that leverages the inherent pulse-width modulation associated with natural binary counting. The proposed approach involves combining the individual bit-counting pulses to synthesize a modulated signal where the mean voltage is directly proportional to the input digital code. A circuit design, based on general-purpose components, is proposed for an 8-bit digital-to-analog converter. The architectural concept is scalable, supporting resolutions that can accommodate any number of bits. The paper describes the simulations conducted to verify the proper functioning of the circuit and to evaluate its performance. Tests were performed to determine the static characteristic of the converter, measure its nonlinearity, and observe its step response. The circuit combines the benefits of both PWMs and PDMs, offering a blend of energy efficiency with simplicity and better smoothing.
1. Introduction
Pulse-width modulation (PWM) and pulse-density modulation (PDM) are two distinct digital-to-analog conversion techniques used to represent an analog signal using a series of pulses. While both methods utilize a binary signal to encode an analog value, their fundamental principles and applications differ significantly (see Figure 1).
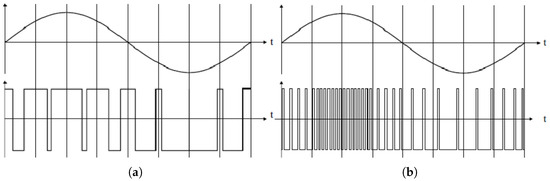
Figure 1.
Pulse-width versus pulse-density modulations: (a) PWM. (b) PDM.
Pulse-width modulation is a digital signaling technique that varies the width of a square wave pulse to encode a specific analog value. The core principle of PWM is to maintain a constant frequency while adjusting the duty cycle. By rapidly switching the digital signal on and off at a high frequency, the average voltage across a load can be controlled, effectively simulating an analog output.
In contrast, pulse-density modulation encodes the analog signal by varying the density of pulses over a fixed time interval. Unlike PWM, where the pulse-width changes, PDM keeps the pulse-width constant but adjusts the number of pulses within a given period. A higher analog value is represented by a higher density of pulses, whereas a lower value is represented by a sparser distribution of pulses. The average value of the signal is proportional to the number of pulses in the time window.
PWM is a cornerstone of power electronics and motor control. Its primary significance lies in its high efficiency, making it ideal to precisely control the average power delivered to a load (e.g., a motor or LED) with minimal switching losses in the power transistors [1,2]. This makes it indispensable for applications like Class-D audio amplifiers, DC-DC converters, and variable-speed drives. Conversely, PDM is paramount in high-resolution signal acquisition, particularly in digital audio. Its significance is its ability to represent a high-fidelity analog signal as a simple 1-bit data stream, achieving high resolution by oversampling and shaping the quantization noise out of the desired signal band [3,4]. This allows for robust, low-cost implementation in devices like MEMS microphones and high-fidelity digital-to-analog converters. In summary, PWM is generally more energy-efficient, as it typically involves fewer on/off transitions over the same time interval, while PDM offers advantages in terms of signal smoothing, as its spectral energy is spread across a wider frequency range.
The most common method for implementing a digital PWM signal is based on the direct digital emulation of a ramp waveform using a binary counter [5]. As depicted in Figure 2a, the counter’s ramp output is compared with the digital input code to establish the output signal’s duty cycle. A new modulation cycle begins when the counter wraps around. The counter’s full cycle, which has a duration of clock periods, determines the frequency of the modulated signal. This method provides excellent linearity; however, for applications requiring high sampling rates and high resolutions, the need for a very high-frequency clock becomes the primary limitation of this approach.
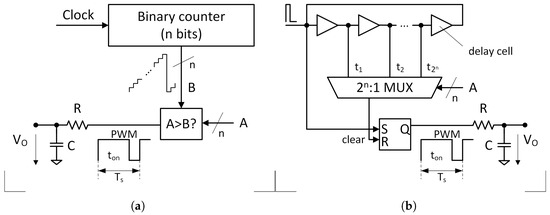
Figure 2.
Digital PWM generators: (a) Comparison with a ramp waveform. (b) Tapped delay line approach.
A faster alternative, based on a tapped delay line, is presented in [6]. As illustrated in Figure 2b, a brief pulse is injected into the delay line and propagates through its cells at a constant speed. The propagation ceases when the pulse reaches a selected tap, which in turn resets the output signal. The selection of the tap is made by a multiplex controlled by the digital input code, making the output signal’s duty cycle proportional to this code. A new modulation cycle begins when the traveling pulse loops around the entire line. The time required for the pulse to traverse the complete delay line determines the frequency of the modulated signal. While this method offers superior speed, its linearity is often compromised, as it is challenging to ensure a constant speed across a delay line with elements.
A critical aspect of PWM is its spectral content, which is composed by the fundamental component located at the sampling frequency, followed by the corresponding high-frequency harmonics [7].
Regarding digital PDM modulators, the delta-sigma () structure [5,8] has gained popularity in recent years. It employs oversampling techniques to achieve high resolution, albeit at the expense of increased latency and reduced bandwidth. Figure 3 shows the working diagram of a delta-sigma () structure. In the discrete-time domain, the relationship in a first-order modulator can be described by the following difference equations. The integrator output, , is given by:
where is the discrete-time input signal (normalized to be between −1 and +1), and is the feedback signal, which is the previous output of the quantizer. The single-bit quantizer output, , which is the PDM stream, is a bipolar signal determined by:
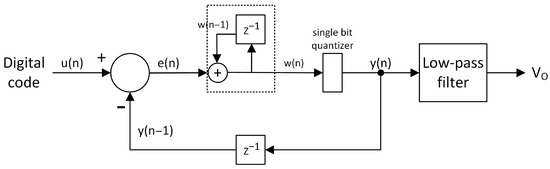
Figure 3.
structure.
The key function of the architecture is noise shaping [9,10,11,12]. The output spectrum, , is defined by the relationship , where is the input signal, is the modeled quantization error (often approximated as additive white Gaussian noise), is the signal transfer function, and is the noise transfer function. The , implemented via the modulator’s loop filter (e.g., an integrator or cascaded integrators), exhibits a high-pass characteristic that ensures the bulk of the quantization noise power is attenuated within the narrow baseband region, and is instead pushed to the higher frequency decades, extending up to the oversampled Nyquist frequency. Consequently, the resultant PDM bitstream spectrum displays a remarkably low noise floor in the baseband, which then rises rapidly at higher frequencies with a slope proportional to the order of the modulator (e.g., a 1st-order modulator provides a 20 dB/decade noise suppression). This spectral arrangement allows for the straightforward retrieval of the high-fidelity signal by applying a low-pass filter, effectively discarding the shaped high-frequency noise.
There are alternatives to the delta-sigma structure, although they are only used in more specific scenarios. It is the case, for example, of the work published by Usui et al. [13], which proposes a DPDM modulator to drive organic light-emitting diode (AMOLED) displays based on a random dither matrix. The modulated signal, responsible for the dithering, is built by comparing the input digital code with a random number generated by a pseudo-uniform random source.
The digital PWDM modulation is a compromise between the PWMs and PDMs that attempts to combine the advantages of both [14,15]. On the one hand, it leads to less transitions than PDM to not compromise energy efficiency, particularly in power applications; and on the other hand, it spreads the spectral content of the PWM signal allowing for better filtering of the DC component.
The digital PWDM modulation splits the PWM signal into multiple, narrower pulses while maintaining its fundamental period and mean value. This approach yields a significant effect on both the time and frequency domains. In the time domain, the output filter’s smoothing element (the capacitor in Figure 2) charges and discharges more frequently and over shorter intervals, leading to a substantial reduction in the ripple of the output signal. Concurrently, in the frequency domain, the fundamental component is spread across higher frequencies, which increases the separation between the DC component and the spectral harmonics, thereby simplifying the smoothing process and relaxing the design requirements of the low-pass filter.
A good example of pulse manipulation while maintaining the mean value is the work of Crovetti et al. [16,17]. The author distributes the pulses evenly over the signal period according to a predefined schedule based on dyadic sequences. The resulting PWDM signal is analyzed in both the time and frequency domains to conclude that the high-frequency spectral components are indeed attenuated and spread. This characteristic allows for a relaxation in the design requirements of the smoothing low-pass filter.
Another example of schedule-based PWDM is the work of Sheng et al. [18], where the authors rearrange the switching pulses over time to reduce current transients on a 20 kW inductively coupled power transfer system.
This paper introduces a novel PWDM that leverages the principles of binary counting for the temporal distribution of pulses. This methodology effectively disperses the high-frequency spectral content of the modulated signal while rigorously preserving its mean value. Furthermore, this technique offers demonstrably greater simplicity and scalability when compared to schedule-based methods.
The paper is organized as follows: Section 2 presents the new PWDM and explains how it can be used as a digital-to-analog (DA) converter; Section 3 describes the experimental tests conducted to validate the circuit; Section 4 discusses the results obtained; and Section 5 summarizes the main conclusions of the work.
Main contributions:
- The proposed PWDM is a new way to mix PWMs and PDMs.
- The proposed PWDM is simpler and easier to understand than existing alternatives, especially schedule-based PWDMs.
- The proposed PWDM is highly scalable. If the number of bits increases, the circuit’s propagation delay remains the same, and the hardware needs increase moderately, in a linear rather than exponential manner.
2. Materials and Methods
The proposed circuit, shown in Figure 4, takes advantage of the pulse-width created naturally by the binary counting sequence. Examining the binary counting sequence shown in Figure 5, we observe that the width of the pulses varies according to the bit’s weight. All bits generally have a pulse width of 50%, but this value is achieved through narrower pulses for the least significant bits and wider pulses for the more significant bits. The idea is to extract the first pulse of each bit—only the first occurrence—and combine them into a single signal. The result will be a width-/density-modulated, binary-weighted pulse that can be used for DA conversion.
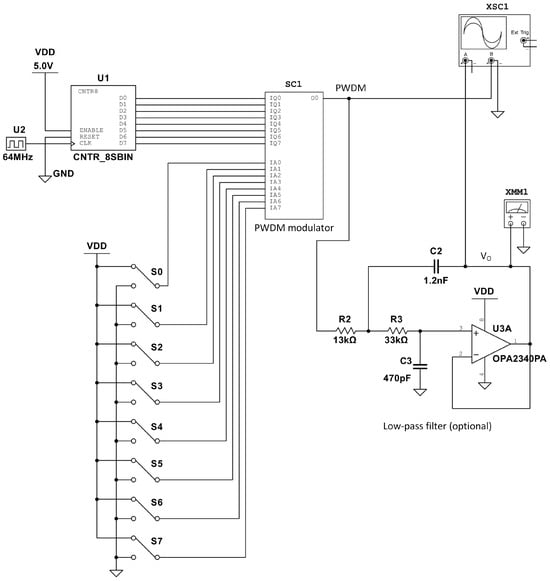
Figure 4.
8-bit DA converter based on PWDM modulation. The input digital code is ∼, with being the most significant bit (MSB) and the least significant bit (LSB). The output is provided as a pulse-width/-density-modulated signal (signal PWDM) or as an analog voltage (signal ).
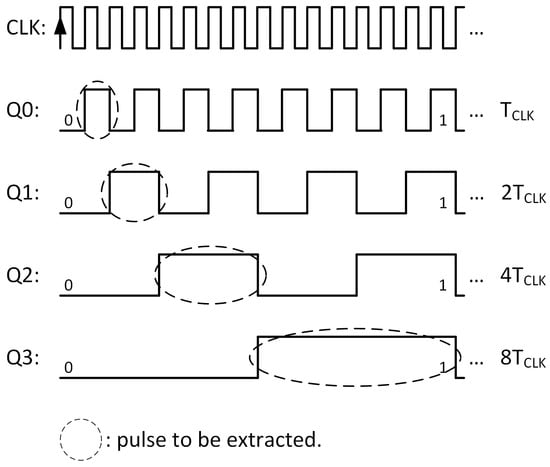
Figure 5.
Output of the binary counter. The width of the pulses increases as a power of 2.
The extraction can be done by a simple logic circuit. For example, the narrower pulse, corresponding to the LSB, shall be collected if the input bit is true AND the output of the binary counter is . This leads to the top AND block shown in Figure 6, where the signal pulses with a width of if (where is the clock period of the binary counter). The same applies to the remaining bits:
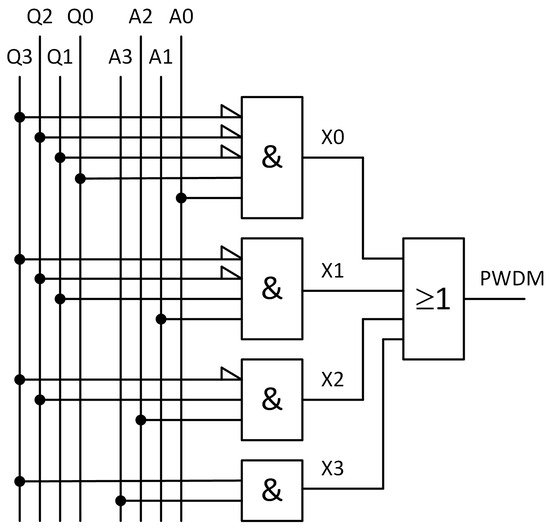
Figure 6.
Pulse extraction from the LSB () to the MSB () followed an OR gate.
- The pulse shall be collected if the corresponding input bit is true AND the output of the binary counter is , leading to signal in Figure 6.
- The pulse shall be collected if is true AND the output of the binary counter is , leading to signal in Figure 6.
- The pulse shall be collected if is true AND the output of the binary counter is , leading to signal in Figure 6.
Finally, all the collected pulses are summed by an OR gate to generate the PWDM output signal shown in Figure 6. The circuit can be optimized to use only negative gates, NAND and NOR, which are universal and faster. By applying De Morgan’s laws, we get:
which leads to the solution shown in Figure 7. This circuit exhibits three distinct processing levels irrespective of the number of bits being processed: a first level consisting of NOR gates, starting with inputs down to two inputs; a second level consisting of n 3-input NAND gates; and a third level composed of one n-input NAND gate, where n is the number of bits of the input code. This is always the case regardless of the number of bits, which makes this circuit very scalable.
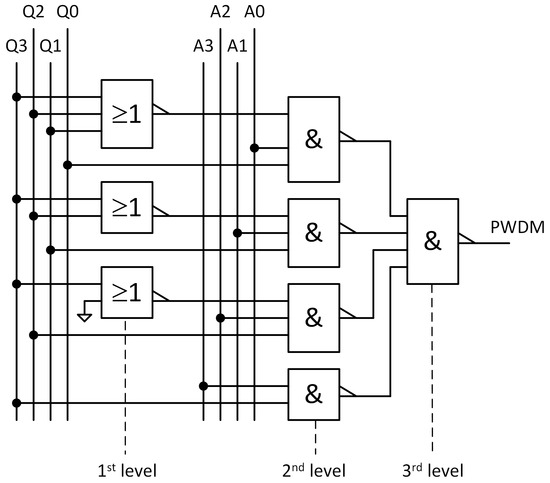
Figure 7.
Optimized pulse extraction using only NAND and NOR gates.
As the number of bits increases, diode resistor logic can be used to implement NOR gates with many inputs. Figure 8 shows a 15-input NOR gate where the delay is mainly determined by the NOT gate. A similar arrangement can be done for the NAND gate at the third level. Looking again at Figure 7, assuming a propagation delay of 15 ns for each of the three processing levels, the cumulative delay in generating the PWDM signal remains consistently at 45 ns, independent of the number of bits processed. The biggest source of delay in the PWDM is not the pulse extraction logic, but the fact that it takes a full binary count to do the conversion, i.e., clock pulses. As n increases, the modulation rate must be relaxed or the clock rate of the binary counter must be increased.
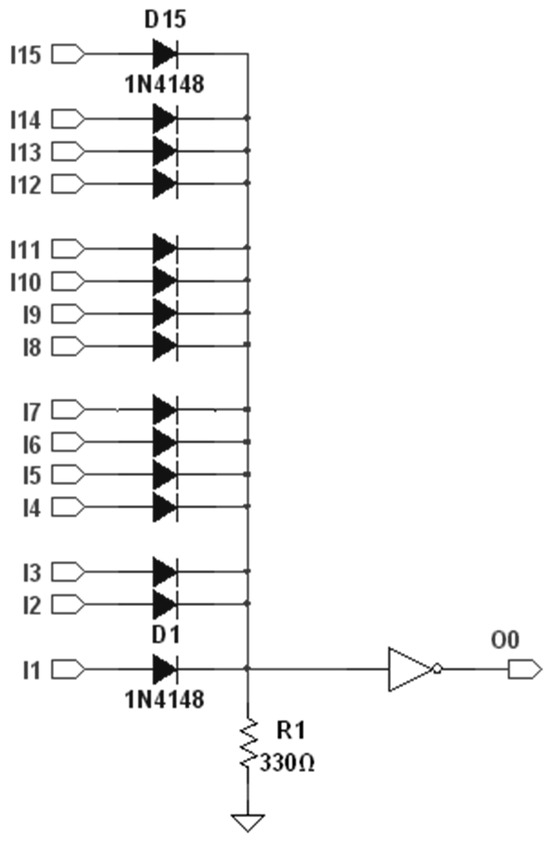
Figure 8.
15-input NOR gate.
To obtain an analog voltage, the PWDM signal must pass through a low-pass filter to recover its mean value. In Figure 4, this is achieved through a Sallen–Key active filter exhibiting Butterworth response. Alternative filter topologies (active or passive) and filter responses (such as Chebyshev or Elliptic) are also viable options for this purpose.
3. Results
This section details the simulations performed to verify the proper functioning of the circuit and to evaluate its performance. The simulations were done using NI Multisim v14.3 running on a computer characterized by Intel(R) Core(TM) i7-8550U CPU @ 1.80 GHz, 16 GB RAM, and Windows 11 64 bits. The simulation protocol encompassed the following tests:
- PWDM operation.
- Static transfer characteristic (output voltage versus input digital code in steady state).
- Differential nonlinearity (DNL).
- Step response.
The discussion will commence with a detailed description of the circuit under test, followed by an individualized explanation of each simulation.
3.1. Circuit Under Test
The circuit under test, shown in Figure 4, is an 8-bit DA converter that includes an 8-bit binary counter, a PWDM, and an optional smoothing filter to provide an analog output voltage. The PWDM’s architecture is analogous to that depicted in Figure 7, with the exception that it has been scaled up to 8 bits. Internally, it is implemented using push–pull CMOS gates that operate at 5 V and exhibit propagation delays of 15 ns for both high-to-low and low-to-high transitions. The clock source and the 8-bit counter were idealized to facilitate a performance evaluation focused exclusively on the custom-designed circuit elements, namely the PWDM and the smoothing filter.
Each conversion takes 256 clock cycles to complete, which corresponds to 4 µs per conversion or 250 k samples per second. Higher conversion rates imply higher clock frequencies.
The smoothing filter works around the OPA2340, which is a general-purpose operational amplifier optimized for low-voltage, rail-to-rail operation. The circuit behaves as a 2nd order Butterworth filter, with a quality factor equal to 0.707, a cutoff frequency equal to 10 kHz, and a stationary gain equal to one. The cutoff frequency is appropriate for a wide range of industrial applications and is substantially lower than the conversion rate (250 kS/s), which is critical for providing a well-smoothed analog output voltage.
The following list describes all the components used, including a brief description of each item, the library to which it belongs, and the model properties that have been edited:
- 8-bit synchronous binary counter (U1):
- –
- Multisim library: Master database/Misc digital/TIL.
- –
- Model properties: None (default settings).
- Digital signal clock source (U2):
- –
- Multisim library: Generic/Digital clock.
- –
- Model properties: Frequency = 64 MHz.
- Single-supply, rail-to-rail operational amplifier OPA2340 (U3A):
- –
- Multisim library: Master database/Analog/OPAMP.
- –
- Model properties: None (default settings).
- Logic gates inside the PWDM sub-circuit (Ux):
- –
- Multisim library: Master database/CMOS/CMOS 5.
- –
- Model properties: Rise delay time = 15 ns; Fall delay time = 15 ns.
- General purpose resistors (Rx):
- –
- Multisim library: IIT/Virtual resistance.
- –
- Model properties: None (default settings).
- General purpose capacitors (Cx):
- –
- Multisim library: IIT/Virtual capacitance.
- –
- Model properties: None (default settings).
3.2. PWDM Operation
The circuit was simulated in transient mode to test the operation of the PWDM. All simulation parameters were set to the default values except for the stop time, which was set to 5 µs in order to cover a complete conversion cycle.
The digital code = 1010 1101 was applied to the input of the PWDM to validate its functionality. This specific sequence was chosen because it generates a wide variety of pulses, allowing for a comprehensive assessment of the modulator’s performance. Figure 9 displays the corresponding output signal. Each 1-bit contributes to an increase in the output’s duty cycle, commencing with the LSB that generates the narrowest pulse and culminating with the MSB responsible for the widest pulse. The signal’s amplitude spans the full rail-to-rail range, from 0 V to 5 V. A complete conversion cycle is executed within 4 µs, as expected. It is important to note that duty cycle never reaches 100% because the PWM line goes down during one clock period when the binary counter returns to zero.
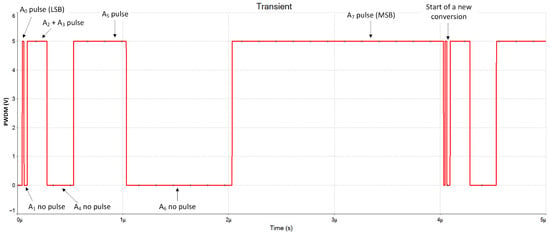
Figure 9.
PWDM signal for the input digital code 1010 1101. The duty cycle is .
It is also important to analyze the spectral signature of the PWDM signal. Figure 10 shows the amplitude spectrum of the PWDM signal shown in Figure 9 (left) and compares it with the amplitude spectrum of an “equivalent” PWM signal with the same duty cycle but only one switching edge (right). As expected, the DC component is the same for both signals (68%), but the first harmonic is significantly lower, 2.17 V versus 2.71 V, which leads to an attenuation equal to dB. These values were also confirmed in the time domain by extending the stop time and measuring the ripple in the steady state: the PWDM signal has a ripple of 6.9 mVpp while the “equivalent” PWM signal has a ripple 8.7 mVpp (after both signals have passed through the same low-pass filter). The attenuation in terms of ripple is dB, the same value as before. This “extra” attenuation adds to that of the smoothing filter and leads to less ripple in the output voltage. The more switching edges the PWDM signal has, the more energy is transferred to the high frequencies. Of course, this improvement depends on the digital sequence at the input, but it exists and is noticeable.
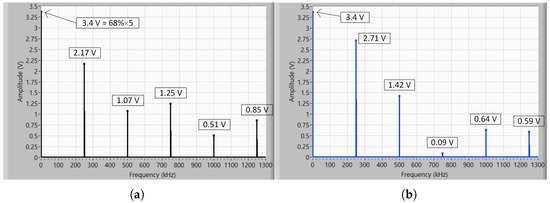
Figure 10.
Spectrum comparison between PWDM and PWM signals: (a) Amplitude spectrum of the PWDM signal shown in Figure 9. (b) Amplitude spectrum of an “equivalent” PWM signal. The spectra were calculated over 400 µs, equivalent to 100 sampling periods, containing a total of 100 k samples acquired with a step size equal to 4 ns. The PWDM signal was generated by the circuit of Figure 4 and the “equivalent” PWM signal was generated by a modulator similar to that of Figure 2a. Both signals were exported to LabVIEW where their spectra were computed with rectangular windowing.
The ripple of both signals—the PWDM signal and the “equivalent” PWM signal—was measured for all input digital codes following the same procedure as before. The results are shown in Figure 11. The performance is similar for the lowest and the highest codes because the switching bits are the least significant ones, which correspond to the shortest pulses (e.g., and ). However, the PWDM is better in the intermediate codes, to the left and to the right of the central value, because there are bits with significant weight that alternate between 0 and 1 (e.g., and ). The mean value of the ripple for the PWDM signal is 5.914 mVpp, while the mean value of the ripple for the “equivalent” PWM signal is 6.242 mVpp, corresponding to an mean attenuation of dB. Again, the improvement depends on the input digital code, but it exists and is noticeable, also in general terms.
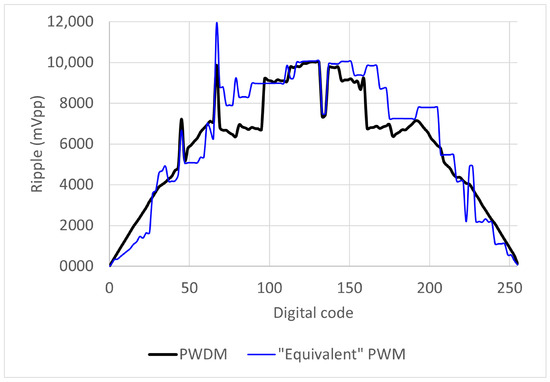
Figure 11.
Comparison of the output ripples for the PWDM signal (black) and the “equivalent” PWM signal (blue).
A final remark to the power consumption of the circuit: the analog part built around the OPA2340 consumes a current of 800 µA; and the digital part, which includes everything else, consumes a current of 400 nA, without significative variations depending on the digital input code. These values are interesting, especially if an analog output is not required.
3.3. Static Transfer Characteristic
The static transfer characteristic of the DA converter was obtained by simulating the circuit in the interactive mode with default values. The complete set of binary input combinations was sequentially applied to the circuit using a digital word generator, and the corresponding output voltages were recorded to a file.
Table 1 presents the output voltage () obtained for a selection of binary input combinations, specifically encompassing the minimum (all zeros), maximum (all ones), and power-of-two codes. The graphical representation of the static transfer characteristic is illustrated in Figure 12, with the abscissa representing the input digital code (expressed as an integer value) and the ordinate representing the corresponding mean output voltage. The observed characteristic exhibits a high degree of linear correlation with a fitted straight line characterized by a slope of 19.547 mV/LSB and an offset of 1.1119 mV. According to [19], these values are the independently based gain and offset of the DA converter, respectively.

Table 1.
Values of the static transfer characteristic of the DA converter.
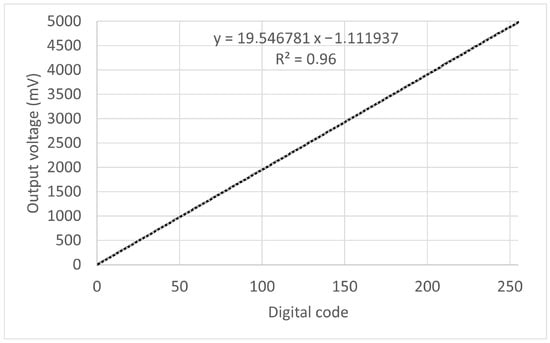
Figure 12.
Static transfer characteristic of the DA converter.
3.4. Differential Nonlinearity (DNL)
The DNL measures the difference between the measured and the ideal output voltages for successive digital codes [20]. It can be expressed as a fraction of the LSB as follows:
where i represents the ith digital code.
The output voltage measurements obtained during the static characterization were applied to Equation (4), leading to the data shown in Figure 13. It is clear that the DNL remains below 1 LSB, thereby confirming the absence of missing codes in the converter’s transfer characteristic. Some performance degradation is also observed for larger digital codes, which is understandable because any deviations in pulse width have a greater impact on the output voltage. Such deviations can be caused by the cumulative effect of minor timing jitters arising from the propagation delay of logic gates.
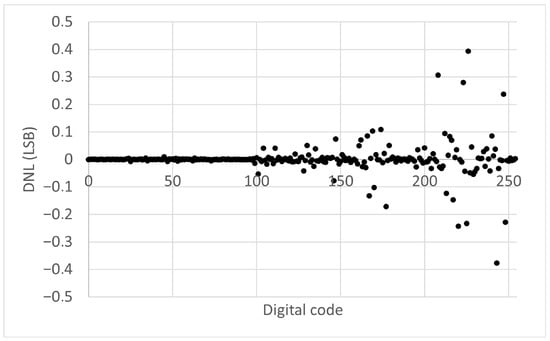
Figure 13.
Differential nonlinearity of the DA converter.
3.5. Step Response
The circuit was simulated in transient mode to see its step response and study its dynamic properties. All simulation parameters were set to the default values except for the stop time, which was set to 200 µs in order to give enough time for the circuit to stabilize.
A sharp transition was made to the input, switching the digital code from 0000 0000 to 1000 0000, and the accompanying output voltage was measured over time. Figure 14 shows the resulting transitory behavior.
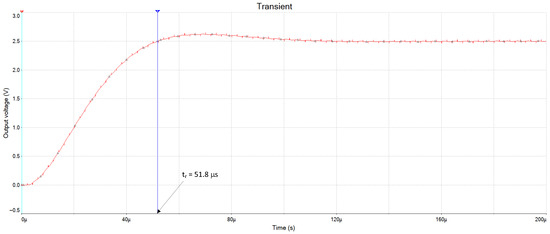
Figure 14.
Step response of the DA converter after switching the MSB from 0 to 1.
Observation of the converter’s dynamic response reveals that it is primarily governed by the second-order low-pass Butterworth filter. The curve is characterized by an overshoot of 4%, a rise time close to 51.8 µs, and a stationary gain equal to one. These values correspond to a damping factor of 0.707 and a natural frequency of 10 kHz, as expected. It should be noted that the Butterworth characteristic is often the preferred choice for smoothing filters due to its optimal balance between overshoot and speed, enabling the fastest transient response without excessive ringing.
4. Discussion
The simulation results confirm that the circuit works as expected, with low power consumption, and that the modulated signal exhibits key characteristics, namely:
- The mean value is proportional to the input digital code.
- The fundamental period is equal to clock cycles .
- Within the fundamental period there are smaller pulses, each one corresponding to a bit equal to 1. The width of these “inner” pulses is related to binary weight of the corresponding bit.
The more switching edges the PWDM signal has, the more energy is transferred to the high frequencies in comparison an “equivalent” PWM signal (with only one switching edge). This leads to less ripple because the output filter’s capacitor has less time to discharge.
The circuit is able to work as a DA converter with negligible gain and offset errors, and no missing codes. The main limitation of the circuit is the time it takes to perform a conversion, which is always equal to . It should be noted that this limitation is also present in other PWDMs, such as the Crovetti modulator [16,17]. Higher conversion rates require higher clock frequencies and, consequently, faster logic gates. The present case, characterized by a sampling rate of 250 kS/s and a resolution of 8 bit, requires a clock frequency of 64 Mhz and logic gates with a propagation delay of 15 ns. A resolution of 12 bits would require a clock frequency 16× higher and logic gates 16× faster.
The main advantage of this modulator over the state of the art is its simplicity and explainability because it is based on straight logic. Another important advantage is its scalability because adding another bit does not require duplicating the hardware. If we look again at the circuit in Figure 7, adding a bit requires only one more OR gate in the first processing level, one more AND gate in the second level, and one more input at the AND gate of the third level. Moreover, the propagation delay remains always the same, i.e., the propagation delay of the three processing levels ( ns in the present case).
5. Conclusions
The paper presented a PWDM that leverages on the inherent pulse-width modulation associated with natural binary counting. The core concept is the combination of individual bit-counting pulses to synthesize a modulated signal where the mean voltage is directly proportional to the input digital code. A low-power circuit, capable of executing this function, was presented using general-purpose components. The circuit design is highly scalable to accommodate any number of bits; however, it is crucial to note that increasing the modulator’s resolution will result in a longer processing time and a reduction in bandwidth.
The PWDM was tested to validate its functionality and to assess its performance as a DA converter. The modulator operated as expected, generating multiple pulses over a sampling period, which translates to a spreading and attenuation of the high-frequency components. As a digital converter, the circuit demonstrated negligible gain and offset errors, no missing codes, and a dynamic performance dominated by a second-order low-pass Butterworth filter with a 10 kHz bandwidth.
As future work, it is planned to implement the circuit on an FPGA in order to evaluate its performance under real conditions. It would also be interesting to go down a level and implement the circuit, not with logic gates, but with CMOS transistors in order to maximize its performance. The migration to transistors would be done in simulation first, and then in silicon, if possible. Future work should be done for a larger number of bits (at least 12).
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Holmes, D.G.; Lipo, T.A. Pulse Width Modulation for Power Converters: Principles and practice; Wiley-IEEE Press: Hoboken, NJ, USA, 2003. [Google Scholar]
- Wojtkowski, W.; Kociszewski, R. Pulse-width modulation approaches for efficient harmonic suppression. Electronics 2025, 14, 2651. [Google Scholar] [CrossRef]
- Reiss, J.D. Understanding sigma-delta modulation: The solved and unsolved issues. J. Audio Eng. Soc. 2008, 56, 49–64. [Google Scholar]
- McKenzie, R.N.; Ng, W.T. A distortion suppression technique for a digital class D audio power amplifier with pulse density modulation. In Proceedings of the 2018 International Conference on Audio, Language and Image Processing (ICALIP), Shanghai, China, 7–10 October 2018; pp. 315–320. [Google Scholar] [CrossRef]
- Adrian, V.; Gwee, B.H.; Chang, J.S. A review of design methods for digital modulators. In Proceedings of the 2007 International Symposium on Integrated Circuits, Singapore, 26–28 September 2007; pp. 85–88. [Google Scholar] [CrossRef]
- Syed, A.; Ahmed, E.; Maksimovic, D.; Alarcón, E. Digital pulse width modulator architecture. In Proceedings of the 35th Power Electronics Specialists Conference (IEEE Cat. No.04CH37551), Aachen, Germany, 20–25 June 2004; pp. 4689–4695. [Google Scholar] [CrossRef]
- Song, Z.; Sarwate, D.V. The frequency spectrum of pulse width modulated signals. Signal Process. 2003, 83, 2227–2258. [Google Scholar] [CrossRef]
- Enuchenko, M.; Korotkov, A. Digital-to-analog converters based on delta-sigma modulators. J. Commun. Technol. Electron. 2022, 67, 1–16. [Google Scholar] [CrossRef]
- Schreier, R.; Temes, G.C. Understanding Delta-Sigma Data Converters; Wiley-IEEE Press: Hoboken, NJ, USA, 2005. [Google Scholar]
- Candy, J.C.; Temes, G.C. Oversampling methods for data conversion. In Proceedings of the IEEE Pacific Rim Conference on Communications, Computers and Signal Processing, Victoria, BC, Canada, 9–10 May 1991; Volume 2, pp. 498–502. [Google Scholar] [CrossRef]
- Hawksford, M.O. A tutorial guide to noise shaping and oversampling in ADC and DAC systems. Proc. Inst. Acoust. 1989, 11, 290–302. [Google Scholar]
- Calleja, H.; Pacheco, J. Power distribution in pulse-density modulated waveforms. In Proceedings of the IEEE Annual Power Electronics Specialists Conference, Galway, Ireland, 23 June 2000; pp. 1457–1462. [Google Scholar] [CrossRef]
- Usui, T.; Nakajima, Y.; Shiga, T. A digital driving method using pulse-density modulation with a random dither matrix for higher motion image quality. J. Soc. Inf. Disp. 2022, 30, 198–208. [Google Scholar] [CrossRef]
- Gerasimov, V.A. FPGA-based implementation of a high resolution and high carrier frequency pulse-width modulator. In Proceedings of the International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Saint-Petersburg, Russia, 16–19 May 2017. [Google Scholar] [CrossRef]
- Lee, H.-S.; Lee, H.-M. A 92.7%-efficiency 6.78-MHz dual-output energy-resuscitating resonant regulating rectifier for wirelessly powered system. In Proceedings of the IEEE Asian Solid-State Circuits Conference (A-SSCC), Haikou, China, 5–8 November 2023. [Google Scholar] [CrossRef]
- Crovetti, P. All-digital high resolution D/A conversion by dyadic digital pulse modulation. IEEE Trans. Circuits Syst. 2017, 64, 573–584. [Google Scholar] [CrossRef]
- Abdullah, A. High-Resolution Digital Pulse Width Modulation Techniques for Digitally Controlled Power Supplies. Ph.D. Thesis, Doctoral Program in Electronics Engineering, Politecnico di Torino, Turin, Italy, 2024. [Google Scholar]
- Sheng, X.; Shi, L.; Fan, M. An improved pulse density modulation of high-frequency inverter in ICPT system. IEEE Trans. Ind. Electron. 2021, 68, 8017–8027. [Google Scholar] [CrossRef]
- IEEE 1057-2017; IEEE Standard for Digitizing Waveform Recorders. IEEE Standards Association: Piscataway, NJ, USA, 2017.
- Understanding Data Converters (Application Report). Available online: www.ti.com/lit/an/slaa013/slaa013.pdf (accessed on 22 September 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).