Abstract
With the rapid advancement of cloud computing, edge computing, and the Internet of Things, traditional routing protocols such as OSPF—which rely solely on network topology and link state while neglecting computing power resource status—struggle to meet the network-computing synergy demands of the Computing Power Network (CPN). Existing reinforcement learning-based routing approaches, despite incorporating deep strategies, still suffer from issues such as resource imbalance. To address this, this study proposes a reinforcement learning-based computing-aware routing path selection method—the Computing-Aware Routing-Reinforcement Learning (CAR-RL) algorithm. This achieves coordination between network and computing power resources through multi-factor joint computation of “computational power + network”. The algorithm constructs a multi-factor weighted Markov Decision Process (MDP) to select the optimal computing-aware routing path by real-time perception of network traffic and computing power status. Experiments conducted on the GN4–3N network topology using Mininet and K8S simulations demonstrate that compared to algorithms such as Q-Learning, DDPG, and CEDRL, the CAR-RL algorithm achieves performance improvements of 24.7%, 35.6%, and 23.1%, respectively, in average packet loss rate, average latency, and average throughput. This research not only provides a reference technical implementation path for computing-aware routing selection and optimisation in computing power networks but also advances the efficient integration of network and computing power resources.
1. Introduction
With the development of new technologies such as edge computing, computing power and networks are continuously evolving and developing towards computing power-network integration [1]. Traditional routing protocols such as OSPF mainly rely on network topology and link status to select the optimal path [2]. However, in the context of computing power networks, ignoring computing resources can easily lead to resource imbalances [3]. To efficiently utilize edge computing resources, Computing Power Networks (CPNs) have emerged [4]. Against this backdrop, Computing-Aware Routing (CAR), one of the key technologies of CPNs, has been proposed. It primarily employs multi-factor joint computing of “computing power + network” to schedule application requests to the optimal computing power node along the optimal path, thereby enhancing network performance [5]. To address the continuous growth of heterogeneous devices in edge computing environments, Software-Defined Networking (SDN) is simultaneously emerging as a research hotspot. SDN enables real-time sensing of network traffic and computing power resource status while supporting global resource scheduling [6]. This complements heterogeneous resource management in edge computing and lends itself well to integration with reinforcement learning. Reinforcement Learning (RL) technology holds immense potential in complex network optimization due to its ability to autonomously explore environments and dynamically optimize decisions [7].
Current research predominantly focuses on unilateral network optimization, lacking studies on dynamic coordination mechanisms between computing power and network coupling. Particularly in computing power node deployment, traditional methods based on static weights or fixed thresholds struggle to adapt to fluctuating service demands, often triggering chain reactions of computing overload and network congestion [8].
To address the above issues, this study introduces an intelligent plane to SDN, a Reinforcement Learning-based Intelligent Optimization Decision Engine, and a Computing-Aware Routing path selection based on the Reinforcement Learning (CAR-RL) algorithm. This algorithm continuously monitors network status data in real time while simultaneously integrating real-time computing power resource data collected from Kubernetes (K8S) clusters to guide decision-making, aligning with digital twin applications in smart manufacturing [9]. Furthermore, within cybersecurity and industrial automation domains, AI and machine learning are increasingly employed to enhance routing optimisation and resource management—such as enabling real-time monitoring in smart manufacturing through digital twins [10], which provides novel perspectives for the deployment of computing power networks in smart manufacturing scenarios. Simulation results based on real traffic show that the CAR-RL algorithm significantly outperforms traditional and partially improved algorithms in terms of link packet loss rate, delay, and throughput. It can effectively address the issues of dynamic adaptation and resource imbalance in computing power networks.
The contributions of this paper are as follows:
- We propose the CAR-RL algorithm, which integrates network and computing power indicators into the reward function through the Markov decision process (MDP) model to achieve dynamic routing path selection from the source node to the optimal computing power node.
- We introduce the Task-Aware Dynamic Principal Component Analysis (TA-DPCA) computing power measurement method to unify computing power indicators into a comprehensive computing power score, providing accurate computing power cost data for CAR-RL and improving the algorithm’s adaptability.
- We construct a four-layer CAR-RL system architecture, relying on SDN and K8S to provide data input for computing-aware routing, and use it to verify the performance of the CAR-RL algorithm. Simulation experiments based on the Mininet platform show that compared to other algorithms such as Q-Learning, the CAR-RL algorithm improves the average packet loss rate, latency, and throughput by approximately 24.7%, 35.6%, and 23.1%, respectively.
2. Related Work
Routing systems are critical components of internet infrastructure, forwarding data packets from source nodes to destination nodes [11], significantly impacting network performance. Existing routing selection methods include traditional routing algorithms and reinforcement learning-based routing algorithms [12]. Conventional routing protocols, such as OSPF, calculate the minimum path through a link-state database and the Dijkstra algorithm. However, in dynamic networks, changes in computing power make it difficult for traditional algorithms to perceive state evolution on time, making it impossible to optimize decisions dynamically [13]. Therefore, it is crucial to study intelligent routing strategies based on network status and computing power resources.
In recent years, reinforcement learning technology has demonstrated significant potential in routing optimization. Its core mechanism is based on MDP modeling, which defines the state space, action space, and reward function. It enables intelligent agents to adaptively learn the dynamic characteristics of the network through interaction with the environment [14]. Early on, FU et al. applied DQL to SDN data centre networks, achieving load balancing and low-latency routing optimisation, though their approach relied on the relatively simplistic fat tree topology [15]. Casas-Velasco et al. proposed DRSIR, an SDN routing method based on deep reinforcement learning, to optimise throughput and resource utilisation. However, the reward function did not incorporate node computing power status information [16]. CHEN et al. utilised SRv6 technology to achieve end-to-end routing in computing power network based on a microservices architecture. Yet, it only supported fixed weights and could not dynamically adjust [17]. Subsequently, YE et al. proposed the hierarchical architectures DRL-M4MR and DHRL-FNMR for efficient multicast traffic scheduling, though hierarchical rewards risk local optima [18,19]. M.A. Gunavathie et al. introduced an SDN routing optimisation method using neural network traffic prediction, yet real-time prediction falters during burst traffic [12]. SUN et al. enhanced the RBDQN algorithm to optimise gate mechanisms, combining it with a greedy algorithm for collaborative routing planning, yet real-time adaptability remained elusive [20]. Jinesh N et al. developed a QoS-aware routing method, but its high computational complexity rendered it unsuitable for resource-constrained environments [21]. Wang et al. proposed an intelligent routing algorithm based on DuelingDQN, though the state space lacked dimensionality reduction, resulting in slow training for large topologies [22]. ZHANG et al. dynamically generated multiple paths using deep reinforcement learning to enhance load balancing and fault tolerance, yet path counts remained non-adaptive [23]. YE et al. proposed a multi-agent reinforcement learning cross-domain routing approach to improve robustness, though coordination mechanisms proved complex [24]. Animesh Giri et al. introduced a multi-objective reward function to optimise latency and bandwidth utilisation, but objective weighting failed to achieve autonomous exploration [25].
In the field of computing-aware routing, Liu et al. proposed a deep reinforcement learning-based intelligent routing method, DDPG, which is one of the algorithms compared in this paper. It primarily achieves low latency and high throughput by dynamically adjusting paths through global network state awareness. However, its experiments employed relatively simple topologies, and its adaptability in complex dynamic environments remains to be improved [26]. Yao et al. proposed a computation-aware routing protocol CARP that treats computational information as a cost to schedule service requests to optimal endpoints and coordinate distributed computational resources. However, the cost weights cannot adapt to load changes [27]. Ye et al. combined network situational awareness with deep reinforcement learning to successively propose single-agent and multi-agent SDWN routing algorithms. Yet, lacking a global computational power view, these failed to adapt well to sudden computing power fluctuations [28,29]. Chen et al. proposed a multi-agent-based computing power network routing strategy optimisation algorithm to enhance exploration efficiency and robustness, but the fixed entropy regularisation coefficient may compromise timeliness [30]. Ma et al. introduced a computing power routing algorithm based on deep reinforcement learning and graph neural networks to achieve intelligent path selection and load balancing, yet graph convolutions may inadequately model affinity for heterogeneous hardware [31]. Yassin et al. proposed a Q-Learning-based intelligent routing model, one of the algorithms compared herein, which enhances bandwidth utilisation while reducing congestion and packet loss. However, it neglects computing power resource states [32]. Tang et al. jointly optimised routing and scheduling, introducing the CaRCS framework—another algorithm compared herein—but its sampling variance surges with increasing topology scale, potentially slowing convergence as nodes multiply [33]. Table 1 presents a comparative overview of various routing algorithms and their respective advantages and disadvantages.

Table 1.
Classification of Relevant Routing Algorithms.
In summary, while computing-aware routing has established a research foundation, significant scope for advancement remains. This study expands on the existing Q-learning algorithm framework, focusing on the dynamic coordination and optimization of network status and computing power resources in the SDN environment, considering real-time performance, global optimality, and low computational complexity. Through simulation experiments, we verify that the CAR-RL algorithm outperforms the other comparison algorithms presented herein.
3. System Design
The essential symbols and related terms used in this section are defined in Table 2.

Table 2.
Important symbols and related term definitions.
This section introduces the CAR-RL system architecture, as shown in Figure 1. The architecture consists of a foundation plane, a control plane, an intelligent plane, and a management plane: the foundation plane collects network status and computing power resource information, the control plane executes routing decisions, the intelligent plane dynamically optimizes the route through reinforcement learning algorithms, and the management plane interacts with other planes through top-down and bottom-up coordination. The system architecture is described in detail below.
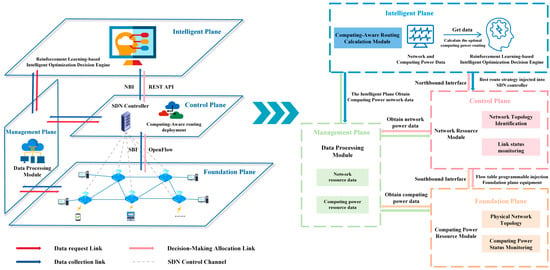
Figure 1.
CAR-RL Overall Architecture.
3.1. CAR-RL System Architecture
In 2017, Mestres et al. proposed the Knowledge-Defined Networking (KDN) framework [34], which supports adaptive routing algorithms by integrating network state awareness and routing decisions. Based on this, the CAR-RL system introduces a reinforcement learning intelligent plane to integrate network state and computing power resources. Compared with RIP, OSPF, and BGP [35], the CAR-RL system relies on SDN global topology awareness. It uses network indicators such as packet loss rate, delay, and throughput, as well as computing power indicators such as CPU utilization, memory utilization, and storage capacity utilization, as core parameters to construct end-to-end routing from the source request node to the optimal computing power node, thereby achieving the selection of the optimal path for computing-aware routing.
The CAR-RL architecture is illustrated in Figure 1. Drawing upon the layered concept of the OSI model and the SDN plane decoupling principle, this research innovatively constructs a collaborative mechanism comprising four functional planes: the intelligent plane, control plane, foundation plane, and management plane. The foundation plane underpins the physical infrastructure. The control plane collects network data via the southbound interface of the SDN controller to construct a global network view. The management plane transmits the gathered computing power and network data to the intelligent plane. Upon receiving the data, the intelligent plane calculates network and computing power costs, executes the CAR-RL algorithm, and disseminates the policy through the control plane to devices within the foundation plane, thereby selecting the computing-aware routing path. The functions of each plane are detailed below.
Foundation Plane—Infrastructure Layer. The foundation plane forms the physical foundation of the CAR-RL architecture, comprising routers, hosts, and links. It integrates computing power resource monitoring modules. In this study, this includes the Mininet-simulated GN4–3N topology and K8S-orchestrated computing power nodes. It continuously collects and processes computing power parameters such as CPU utilisation, memory utilisation, and storage utilisation from computing power nodes, transmitting this data to the management plane. This provides real-time computing power data support for the intelligent plane’s decision-making.
In the foundation plane, the computing power resource module monitors the dynamic distribution status of computing power resources in each computing power node and sends the collected raw monitoring data to the data processing module in the management plane. In this study, the computing power resource module mainly implements computing power resource collection and management through the K8S Master-Node architecture. As the control center of the K8S cluster, the K8S master receives resource status information from the node through the API Server. It uses components such as Scheduler, Api-server, Metrics-server, and Controller Manager to perform task allocation and status maintenance, ensuring efficient resource utilization and high cluster availability. It should be noted that the K8S master obtains the data collected by the nodes by accessing the interface/apis/metrics.k8s.io/v1beta1/nodes of Metrics-server. The K8S node is a working node in the cluster that runs Kubelet and Container Runtime, is responsible for receiving instructions from the master to complete tasks, and regularly reports computing power data to the master so that the master can keep track of the node status in real time.
Control Plane—Resource Management Layer. As the central hub for network resource management, the control plane achieves global oversight and dynamic scheduling of network resources through a centralised controller. It interacts with the underlying plane via southbound interfaces to construct network topology and monitor link status; it coordinates with the intelligent plane via northbound interfaces to obtain optimal routing policies and distribute flow tables to foundation plane devices, thereby enabling efficient utilisation of compute and network resources. In this experiment, the control plane is implemented via an SDN controller, periodically extracting OpenFlow port states and traffic conditions to construct a comprehensive network view.
In the control plane, network resource modules include network topology identification and link status monitoring. Network topology identification relies on the controller periodically sending data packets to devices in the network. Upon receiving the packets, each network device performs neighbor relationship forwarding operations. By collecting neighbor information from all devices, the controller can accurately construct a global topology map of the entire network. Link status monitoring uses the OpenFlow protocol’s PORT_STATS message to periodically collect traffic data and obtain key indicators of the network topology: instantaneous throughput , packet loss rate , and end-to-end delay . Among these, is the total link capacity, is the number of bytes sent and received obtained by the SDN controller periodically sending statistical request messages to each port of the router, is the time difference between data transmission and reception, and are the number of packets lost during transmission and the total number of packets sent, respectively, and are the times when the kth packet is sent and received. N is the total number of packets in the statistics. Based on the instantaneous throughput, we can also obtain the available link bandwidth . The computing-aware routing deployment module obtains the optimal routing strategy from the intelligent plane, converts it into a flow table, and then sends it to the foundation plane devices through the southbound interface.
Management Plane—Computing and Networking Collaboration Layer. As a vertical interaction plane, the management plane aggregates, processes, and coordinates resource data. It obtains network data from the control plane and computing power data from the foundation plane, optimizes and integrates them, and sends them to the intelligent plane to provide quantitative support for subsequent dynamic routing decisions.
In the management plane, the core components of the data processing module include network resource data and computing power resource data, which collaborate to achieve integrated processing and analysis of data resources. Network resource data originates from the network resource module of the control plane and contains key information such as network topology and link status, including packet loss rate, latency, and throughput. Computing power resource data originates from the computing power resource module of the foundation plane, acquiring real-time computing power metrics via the K8S Metrics API and transmitting this data to the intelligence plane.
Intelligent Plane—Algorithm Execution Layer. As the decision-making core of the CAR-RL architecture, the intelligent plane integrates an innovative reinforcement learning algorithm, the CAR-RL algorithm. When a source node in the foundation plane initiates a task request, the intelligent plane acquires network and computing power resource data via the management plane. Computing power measurement is then applied to computing power data to derive individual computing power performance scores. Subsequently, the CAR-RL algorithm is executed to determine the optimal path, with the resulting strategy being dispatched to devices in the foundation plane.
The computing-aware routing calculation module in the intelligent plane mainly comprises a Reinforcement Learning-based Intelligent Optimization Decision Engine. It analyzes the network topology status and computing resource characteristics in real time to construct a dynamic coupling model of task demand and resource supply, thereby completing the optimal path decision for computing-aware routing.
3.2. Markov Decision Process Model—Reinforcement Learning-Based Intelligent Optimization Decision Engine
The Reinforcement Learning-based Intelligent Optimization Decision Engine is based on MDP modeling and uses the CAR-RL algorithm to select dynamic routing paths from the source node to the optimal computing power node. The model is shown in Figure 2. The state space includes network and computing power states; the action space is path selection. The reward function combines network indicators such as packet loss rate, delay, and throughput with computing power indicators such as CPU score, memory score, and storage score obtained through computing power measurement. The optimal routing strategy is solved through state transition and strategy iteration. The following sections elaborate on the CAR-RL architecture and its MDP modelling methodology.
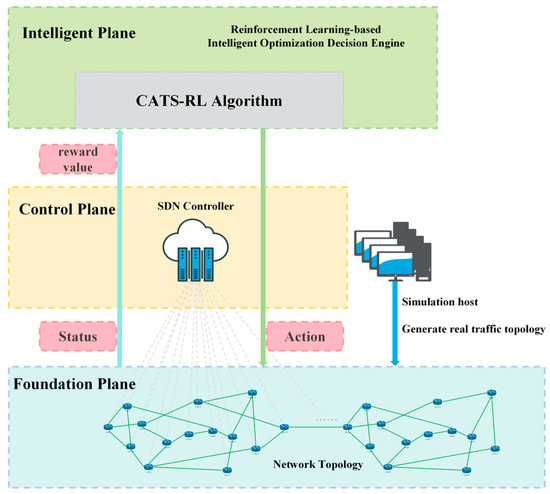
Figure 2.
CAR-RL Architecture and Markov Decision Process.
Reward function: The reward function constitutes the core element of the MDP, quantifying system performance following routing decisions by comprehensively evaluating network performance and computational load. This paper designs the reward function as the total negative link cost, encompassing both network cost and computing power cost. Formula (1) is the network cost, Formula (2) is the computing power cost, and Formula (3) is the total link cost, where ∈ [0,1] are used for weight distribution and are adjustable parameters. The optimal value will be explored in the experiment.
Since the units of measurement in Formulas (1)–(3) are different, and to avoid any single metric dominating the model training due to excessive differences in its numerical range, this paper adopts the minimum-maximum normalisation method to process Formulas (1)–(3); the minimum-maximum normalisation method maps each indicator x to the [0,1] interval using Formula (4), where is the normalised value, and and are the minimum and maximum values observed for the indicator during sampling.
Formulas (5) and (6) represent the normalised reward functions: Within the network cost , latency and packet loss rate are directly treated as positive costs—i.e., higher values indicate poorer performance—while bandwidth operates inversely. Thus, the inverted term is employed to ensure low bandwidth corresponds to high cost, thereby aligning all components with the minimisation objective. Consequently, the normalised reward function is derived as:
To minimise path cost by maximising cumulative reward, we define the reward function as the negative normalised total expenditure, namely:
State space part: The state space S forms the foundation for perception networks and computing power resources. This study uses a state space model to represent the network architecture, where G is the set of nodes and links, and X is the set of computing power node states.
Action space: Action space A defines the routing selection operations that intelligent agents can perform in each state. Action a∈A describes the path selection decision from the source node where the task is initiated to the target computing power node. The action is refined to select the next hop node j from the current node i, forward the data packet through the link (i,j), and gradually construct the routing path. For a given state s, the action space A(s) is:
Optimal Decision-Making Component: Optimal decision-making aims to minimise the reward value of Q-learning and select the action a that maximises the long-term cumulative reward for each state s. Under the CAR-RL framework, the optimal policy is determined by the optimal Q-function , as shown in Formula (11), where represents the expected cumulative reward of executing action a in state s. Through iterative updates, the system progressively approximates optimal decisions to maximise the Q-value, i.e., in Equation (8). This may also be interpreted as minimising cost, thereby achieving optimal computing-aware routing path selection from the current node to the target computing power node.
Exploration method: The exploration mechanism balances the relationship between CAR-RL attempting new actions to discover potentially better strategies and selecting known optimal actions to maximise rewards, ensuring that better routing options are discovered in the accumulated experience. This study adopts the ε-greedy strategy, where, in state s, the agent randomly selects an action with probability ε to explore new paths or selects the current best action with probability 1 − ε:
- ①
- With probability ε, where ε ∈ [0,1], randomly select action a∈A(s) to explore new paths.
- ②
- With probability 1 − ε, select the action with the highest Q-value, i.e., select the optimal path using known experience:
4. Computing-Aware Routing Algorithm
4.1. Computing Power Measurement
In the computing-aware routing algorithm, computing power measurement is the core of the joint optimization of the network and computing power resources. Traditional methods rely on static indicators, which cannot reflect dynamic fluctuations in load and are challenging to meet time-varying demands. This study proposes the TA-DPCA computing power measurement method, which collects CPU utilization, memory utilization, and storage utilization in real time, pre-processes them using minimum-maximum normalization, and then uses TA-DPCA dimension reduction scoring to obtain comprehensive indicator scores and individual indicator scores, providing accurate computing power cost for routing decisions.
Standardization of computing power indicators. Since differences in the dimensions and numerical ranges of CPU, memory, and storage utilization may lead to deviations, this paper uses the minimum-maximum normalization method to standardize the real-time computing power data and map it to the [0,1] interval. This method is consistent with the system design section of the paper. The processed indicators are shown in Formulas (13)–(15), where is the CPU utilization of the computing power node at the sampling time, and and are the minimum and maximum CPU utilization observed in all sampling data, respectively. The same applies to memory and storage. After normalization, all indicators are mapped to the [0,1] interval for subsequent weighting and comprehensive score calculation.
TA-DPCA Dimension Reduction and Comprehensive Score Calculation. Due to correlations among normalized computing power data, simple methods like fixed-weight summation may introduce redundant scores and biases when computing power metrics are interdependent. This can lead to suboptimal routing decisions in dynamic environments. The TA-DPCA method addresses this by extracting principal components that capture most variance, enabling more precise adaptive composite scoring. Specifically, it reduces the dimensionality of high-dimensional metrics and uses the reduced-dimensional data to generate a composite score for each computing power node. After processing, each computing power node has one comprehensive score and three indicator scores. The specific steps are as follows:
First, construct the data matrix. There are n computing power nodes, and the three indicators collected by each node are normalised to form a vector . The data of all nodes is combined to form a data matrix X of n × 3.
Next, calculate the covariance matrix and perform a singular value decomposition. Calculate the covariance matrix of the data matrix X to reflect the correlations between the metrics, as shown in Formula (17).
where is the transpose of matrix X. The result ∑ is a symmetric matrix of size w × w, where each element represents the covariance between the mth and kth indicators. After obtaining the covariance matrix, perform an eigenanalysis, i.e., find the eigenvalues and eigenvectors of the matrix ∑, satisfying:
where are the eigenvalues, reflecting the ability of the corresponding eigenvectors to carry the variance of the original data; are the corresponding eigenvectors, whose directions indicate the main trends of data variation in that dimension. The eigenvalues are sorted in descending order to obtain the principal component directions contributing most to the overall information.
Finally, select the principal components and calculate the scores. Using the results of the feature decomposition, select the top k principal components with the highest contribution rates for dimensionality reduction. Let the first k eigenvectors form the matrix , and then project the normalised vectors of each node onto this low-dimensional principal component space to obtain the score vectors:
Then, the projection scores are weighted and summed according to the contribution rates of each principal component to obtain the comprehensive computing power score of each node:
By extension, the normalised single-item metric scores for each node can be obtained: . These can be converted into computing power cost data via Formula (2), which is then subjected to MDP iterative optimisation to achieve joint decision-making for network and computing power. Building upon this foundation, this paper introduces the computing-aware routing algorithm based on reinforcement learning—the CAR-RL algorithm—to achieve intelligent path selection from the source node to the optimal computing power node.
4.2. Q-Learning-Based Computing-Aware Routing Algorithm
Q-learning is a model-free reinforcement learning algorithm that defines state and action spaces, iteratively updating the Q-value function to approximate optimal routing strategies. The CAR-RL algorithm is an enhancement of the Q-learning algorithm, primarily designed to achieve dynamic routing path selection and optimisation. Its core principle involves utilising Q-learning within a state space composed of network conditions and computing power states, employing path selection as the action space. Through iterative optimisation of routing strategies, it seeks the optimal path from the source node to the target computing power node while balancing network performance and computing power resource equilibrium. As MDP modelling has been detailed previously, it is omitted here. The following describes the operational process of the CAR-RL algorithm.
The CAR-RL algorithm takes network and computing power data as input, namely link latency, packet loss rate, and bandwidth collected by the SDN controller, alongside CPU utilisation, memory utilisation, and storage utilisation of computing power nodes gathered by the K8S Master. Note that computing power node data undergoes normalisation and TA-DPCA dimensionality reduction to compute computing power cost . The output comprises the optimal path, optimal computing power node, and corresponding packet loss rate, latency, and throughput. The algorithm operates across three phases: initialisation, training loop, and path selection. The specific algorithm is shown in Algorithm 1.
| Algorithm 1: CAR-RL | |
| input:SDN topology G(V, E), computing nodes J ⊆ V, | |
| real-time telemetry (D_net, L_net, BW_net, X_j^CPU, X_j^Mem, X_j^Sto) | |
| output:best_path P*, optimal node j*, Packet Loss, Latency, Throughput | |
| initialize Q_table[s, a; θ] | |
| 1: | FOR episode = 1 to MaxEpisodes do |
| 2: | src ← random node; dst ← random node in J |
| 3: | current ← src; path ← [src]; steps ← 0 |
| 4: | WHILE current_node != dst and steps < MaxSteps do |
| 5: | state ← (current_node, global_load_profile) |
| 6: | IF random() < ε THEN |
| 7: | next_node ← random neighbor of current_node |
| 8: | ELSE |
| 9: | next_node ← arg max_a Q(state, a; θ) |
| 10: | END IF |
| 11: | D_net^*(i,j), L_net^*(i,j), BW_net^*(i,j)←Ryu controller |
| 12: | Cost_net^*(i,j) = α*1/BW_net^*(i,j) + β*D_net^*(i,j) + (1 − α − β)*L_net^*(i,j) |
| 13: | IF next_node == dst THEN |
| 14: | S_j^CPU*, S_j^Mem*, S_j^Sto*←TA-DPCA(X_j) |
| 15: | Cost_comp^*(j) = δ*1/S_j^CPU* + η*1/S_j^Mem* + (1 − δ − η)*1/S_j^Sto* |
| 16: | ELSE |
| 17: | Cost_comp^*(j) = 0 |
| 18: | END IF |
| 19: | metric^*_{(i,j)}←w1*Cost_net^*(i,j) + (1 − w1)*Cost_comp^*(j) |
| 20: | R_t =−metric^*_{(i,j)} |
| 21: | IF next_node == dst THEN |
| 22: | target = R_t |
| 23: | ELSE |
| 24: | target = R_t + γ max_{a’} Q(s_{t + 1}, a’; θ) |
| 25: | END IF |
| 26: | Q(state, next_node)←Q(state, next_node) + α [target − Q(state, next_node)] |
| 27: | current_node ← next_node; path.append(next_node);steps←steps + 1 |
| 28: | END WHILE |
| 29: | END FOR |
| 30: | return best_path P*, optimal node j*, Packet Loss, Latency, Throughput |
During the initialisation phase, the algorithm first constructs and initialises the Q-table Q(s, a; θ) to store the value function for state-action pairs. Here, state s is defined as the combination of the current node and the global load profile, while action a represents selecting the next-hop neighbouring node. Concurrently, hyperparameters such as learning rate α, discount factor γ, and exploration rate ε are set.
During the training iteration phase, an iterative training approach is employed. Lines 1–3 randomly select a source node src and a target computing power node dst in each iteration, initialising the path with src as the current node. Lines 4–28 constitute the core path exploration and Q-value update loop, continuing until the destination node is reached or the MaxSteps are exhausted. Line 5 constructs the current state; lines 6–10 employ an ε-greedy strategy to balance exploration and exploitation, selecting the next hop probabilistically with ε or choosing the node with the highest current Q-value. Lines 11–12 retrieve real-time link metrics from the Ryu controller and compute the normalised network cost . Lines 13–18 determine whether the target node has been reached. If reached, the computing power metric is reduced-dimensioned via TA-DPCA to yield , and the normalised computing power cost is computed; otherwise, it is set to zero. Lines 19–20 compute the weighted composite metric and take its negative as the instant reward . Lines 21–25 construct the Bellman objective value: if the target node is reached, the objective value is ; Otherwise, it is plus the discounted maximum Q-value of the next state. Line 26 performs Q-value updates based on the learning rate α. Line 27 updates the current node and path, continuing exploration to the next hop until the loop terminates.
During the path selection and performance evaluation phase, upon training completion, the converged Q-table is utilised to greedily select the next-hop node with the maximum Q-value from any source node, hop by hop. This constructs the optimal path P and identifies the optimal computing power node j, while simultaneously outputting the path’s cumulative packet loss rate, latency, and throughput. This process achieves dynamic joint optimisation of network and computing power cost, ensuring optimal computing-aware routing paths with low latency, low packet loss, and high throughput under high-load and heterogeneous resource scenarios.
The time complexity of the CAR-RL algorithm is an essential indicator for evaluating its feasibility and efficiency in a network environment. The CAR-RL algorithm is based on reinforcement learning, and its time complexity mainly originates from the outer training loop, the inner path search loop, and the Q table management. The following is a detailed analysis.
The total number of training rounds in the outer training loop is E, corresponding to MAX_EPISODES in the pseudocode. In each training round, the algorithm randomly selects a path from the source node to the destination node and performs a complete path search and Q-value update.
In the inner path search loop, the algorithm completes the path search through multiple action selections in each training round. The average degree of the network topology is D, and the number of nodes in the network topology is N. The time complexity of each action selection is O(D). GN4–3N, as a genuine subgraph of the European research backbone network, exhibits typical small-world characteristics. Despite the vast geographical span between its nodes, this topology achieves high connectivity through a small number of hubs. Measurements reveal that Dijkstra paths from any edge node to the most distant computing power node almost invariably fall within 3–5 hops, far fewer than the total number of nodes. This “logarithmic” diameter has been repeatedly validated in GEANT series topology analyses and is widely adopted in SDN routing literature. Consequently, this paper conservatively defines the average path length as . Even when treated under worst-case linear assumptions, the overall complexity remains within an acceptable sub-quadratic range, sufficiently supporting sub-second traffic switching. In the management and updating of the Q table, the Q table stores all possible state-action pairs. According to the state definition, there are states, so the size of the Q table is . Each Q-value update only involves searching for and modifying a single entry in the Q-table, with a time complexity of O(1). Combined with the path length, the total complexity of Q-table updates in a single training run is . The total complexity of Q-table updates throughout the entire training process is . Considering the complexity of action selection, the total time complexity of the CAR-RL algorithm is .
In summary, the total time complexity of the CAR-RL algorithm is primarily determined by the number of training rounds, network scale, and node connection density. In the experiments in this paper, based on the GN4–3N topology and K8S cluster computing power resource monitoring, through reasonable cycle structure design and hyperparameter optimization, the CAR-RL algorithm can efficiently complete training and path selection. Its time complexity fully meets the experimental network scale and performance requirements, and its efficiency is within an acceptable range, providing theoretical and practical support for dynamic routing optimization in computing power networks.
5. Experiments and Results
5.1. Experimental Environment Configuration
This experiment utilised the GN4–3N (GEANT Network 4–Phase 3 Network) [36] logical topology, as shown in Figure 3. This topology represents a typical architecture of European high-performance education networks, comprising 47 nodes and 68 bidirectional links. GN4–3N integrates three representative sub-structures: fat tree, ring-mesh, and hierarchical tree. This enables simulation of real high-performance networks with diverse latency and bandwidth characteristics, while exhibiting wide-area network traits such as long-distance links and variable traffic patterns. This fully demonstrates the algorithm’s effectiveness within typical distributed systems. The experiment utilises a K8S cluster to simulate computing power resources, validating the performance of the CAR-RL algorithm.
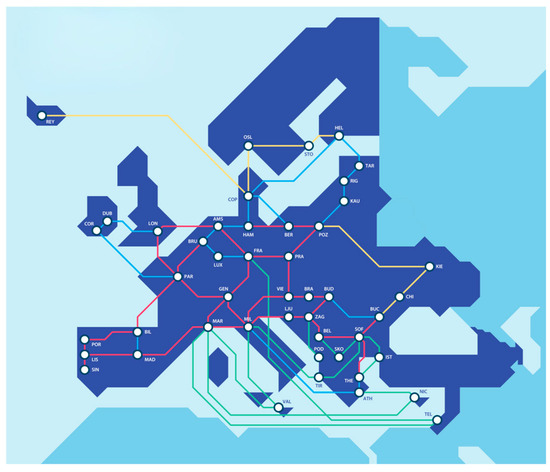
Figure 3.
GN4–3N Network Topology Map (Source: GEANT website).
Based on the above topology, the test environment configuration for this experiment is as follows:
The foundation plane devices use a hardware platform with an Intel Core i9-14900HX24 processor, NVIDIA GeForce RTX 5070 graphics card, and 64 GB DDR5 memory architecture. The operating system is Ubuntu 20.04 LTS. On this platform, the experiment used Mininet 2.3.1b4 to construct the GN4–3N logical topology, with the Ryu controller of K8S 1.19.16 collecting link status data and interacting with the foundation plane through the OpenFlow 1.3 protocol to sense computing power resource data. The network link status data is stored in CSV format, and the optimal route configuration is saved in JSON format. The management plane is based on the Python 3.8 environment and integrates the Pandas 1.3.5 and NumPy 1.21.6 libraries to process network and computing power data. The intelligent plane is also based on Python 3.8 and runs the CAR-RL algorithm to calculate the optimal route by integrating network and computing power data. The specific experimental topology is shown in Figure 4.
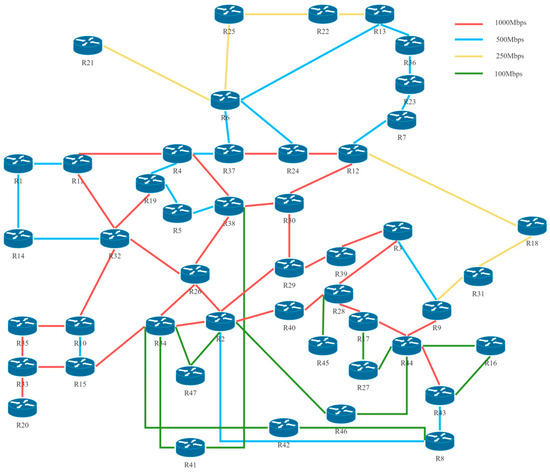
Figure 4.
GN4–3N Topology Diagram.
As shown in Figure 2 above, to accurately reflect the dynamic changes in network status and computing power resources, the experiment employs K8S to deploy computing power node clusters to simulate real-world computing power resource data. To simulate real-world scenarios, each router in the Mininet topology is connected to a host to emulate varying computational demands and network requirements. Concurrently, six virtual machines serve as K8S Master and Nodes, simulating the actual computational resources of routers 8, 15, 18, 36, and 44, as detailed in Table 3. The K8S Master orchestrates cluster state management through components including the API Server, Scheduler, and Controller Manager. The K8S Nodes run Kubelet, configuring CPU, memory, and storage heterogeneously to simulate edge-cloud environments. The Ryu controller monitors link network status for calculating the . Meanwhile, K8S nodes report real-time computing power data to the K8S Master via the Metrics Server. Single computing power metric scores are obtained through TA-DPCA, subsequently calculating the using Formula (2). Given the extensibility of Mininet’s underlying Python code, this research enables compatibility with the OpenFlow 1.3 protocol and facilitates efficient communication with the Ryu controller by customising Mininet’s router module, whilst preserving the native characteristics of the Mininet architecture.

Table 3.
K8S Cluster Information.
5.2. Experimental Results Analysis
To comprehensively evaluate the performance of the CAR-RL algorithm, this experiment simulated uniform and high-load scenarios under a unified testing environment and standardized parameters. Data from eight hourly intervals between 8:00 and 15:00 were selected to compare key performance metrics of the CAR-RL algorithm against Q-Learning [32], CEDRL [33], and DDPG [26]. Specifically, the average packet loss rate, average latency, and average throughput of the optimal computing power path generated by the CAR-RL algorithm after identifying the optimal computing power node were compared with the results from the reinforcement learning-based routing algorithm Q-Learning, the deep reinforcement learning-based deterministic policy gradient DDPG algorithm, and the deep reinforcement learning-based computationally aware CEDRL algorithm. Through these comparisons, this paper verifies the superiority of CAR-RL over traditional and some improved algorithms. The experimental results are shown below.
Figure 5 compares the average packet loss rates of the CAR-RL algorithm and the other three algorithms across eight time intervals. The results show that CAR-RL’s packet loss rate fluctuates between 0.031% and 0.061%, with a mean of 0.046% and a standard deviation of 0.010%. In contrast, the Q-Learning algorithm’s packet loss rate ranged from 0.044% to 0.078%, with a mean of 0.061% and a standard deviation of 0.011%. The DDPG algorithm’s packet loss rate ranged from 0.037% to 0.069%, with a mean of 0.054% and a standard deviation of 0.010%. The packet loss rate for the CEDRL algorithm ranged from 0.035% to 0.063%, with a mean of 0.048% and a standard deviation of 0.009%. The average packet loss rate of the CAR-RL algorithm was approximately 24.7% lower than that of Q-Learning, 14.0% lower than that of DDPG, and 3.7% lower than that of CEDRL.
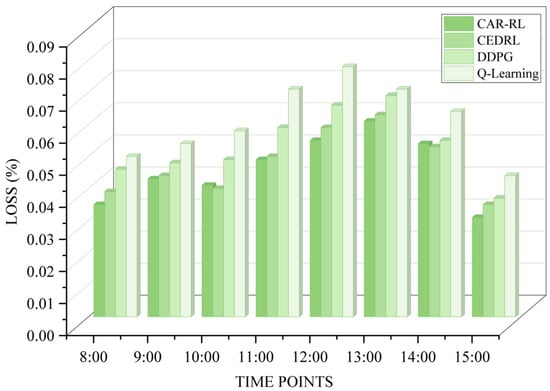
Figure 5.
Average packet loss rate within a fixed period.
Under high-load scenarios, CAR-RL demonstrates superior stability. In the simulated high-load scenario around 12:00, the packet loss rate of the Q-Learning algorithm surged to 0.078%, while CAR-RL remained at 0.055%. This indicates that by dynamically sensing network status and computing power load, CAR-RL effectively avoids selecting congested links. Although DDPG outperforms Q-Learning in packet loss optimization, its neural network architecture remains inadequate in highly dynamic scenarios, failing to fully adapt to traffic fluctuations and the cascading effects of computing power overload. As a computation-aware joint optimization method, CEDRL performs similarly to CAR-RL during low-load periods but experiences a packet loss rate increase to 0.059% during peak periods, exceeding CAR-RL’s performance.
Results demonstrate that CAR-RL comprehensively considers network load and link status. Through iterative optimization of the MDP reward function, it reduces packet loss probability during transmission. This improvement stems from TA-DPCA’s dynamic dimensionality reduction of computing power metrics, which avoids the state explosion issue in multi-factor environments common to traditional RL methods and outperforms DDPG in balancing computing power costs.
Figure 6 compares the average latency of CAR-RL and the other three algorithms across eight time periods. Data indicates CAR-RL’s latency ranged from 7.5 ms to 9.9 ms, with a mean of 8.89 ms and a standard deviation of 0.77 ms. Q-Learning’s latency ranged from 12.5 ms to 15.9 ms, with a mean of 13.8 ms and standard deviation of 1.07 ms; DDPG’s latency ranged from 9.8 ms to 12.8 ms, with a mean of 10.91 ms and standard deviation of 0.90 ms; The CEDRL algorithm’s latency ranged from 8.5 ms to 10.4 ms, with a mean of 9.46 ms and a standard deviation of 0.59 ms. CAR-RL’s average latency was approximately 35.6% lower than Q-Learning’s, about 18.6% lower than DDPG’s, and roughly 6.1% lower than CEDRL’s.
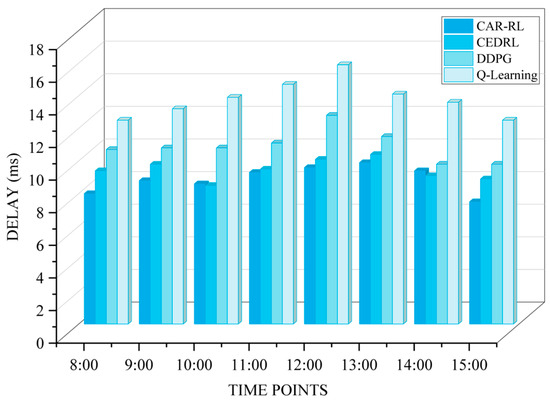
Figure 6.
Average delay over a fixed period.
As shown in the results graph, CAR-RL demonstrates superior latency performance under both uniform traffic and high-load scenarios. This advantage stems from CAR-RL’s integrated consideration of network link latency and computing power node load, where the TA-DPCA computing power measurement method prioritizes resource-rich nodes and low-latency paths. Q-Learning, as a basic reinforcement learning method, experiences significant latency spikes during peak periods. Its reliance on a simple Q-table prevents effective handling of multidimensional state spaces, causing routing decisions to lag behind network changes. DDPG enhances decision robustness by incorporating deep policy gradients but remains constrained by exploration efficiency in continuous action spaces, underperforming during computing power overload. CEDRL approaches CAR-RL performance during low-load periods through joint optimization, yet its peak latency reaches 10.1 ms—significantly exceeding CAR-RL.
The results demonstrate that CAR-RL achieves a balance between latency and computing power in multi-objective optimization through its dynamic learning mechanism, exhibiting excellent equilibrium and high robustness.
Figure 7 compares the average throughput of the CAR-RL algorithm and the other three algorithms across eight time periods. Between 8:00 and 15:00, CAR-RL’s throughput ranged from 320 Mbps to 340 Mbps, with a mean of 333 Mbps and a standard deviation of 6.3 Mbps. The Q-Learning algorithm’s throughput ranged from 256 Mbps to 286 Mbps, with a mean of 270 Mbps and a standard deviation of 11.5 Mbps. The DDPG algorithm’s range was 278 Mbps to 305 Mbps, averaging 293 Mbps with a standard deviation of 9.3 Mbps. The CEDRL algorithm’s range was 297 Mbps to 323 Mbps, with a mean of 314 Mbps and a standard deviation of 8.5 Mbps. CAR-RL’s average throughput exceeded Q-Learning’s by approximately 23.1%, surpassed DDPG’s by about 13.7%, and outperformed CEDRL’s by roughly 6.2%.
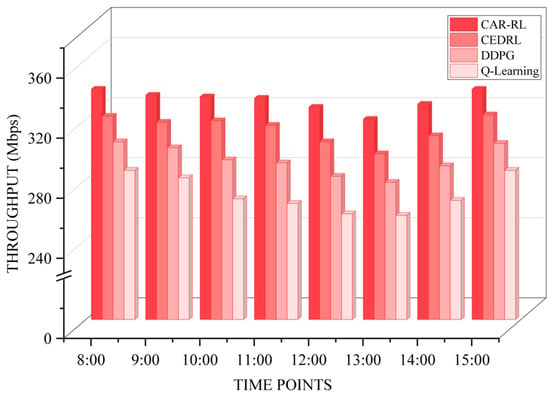
Figure 7.
Average throughput within a fixed period.
Under uniform traffic conditions, CAR-RL demonstrated stable throughput performance, consistently maintaining high levels. For instance, at 10:00, CAR-RL achieved 335 Mbps throughput while Q-Learning reached only 267 Mbps. As an RL variant of static shortest path algorithms, Q-Learning struggles to adapt to fluctuating traffic demands, resulting in suboptimal throughput. DDPG enhances throughput by optimizing bandwidth allocation through deep policy gradient optimization. However, its path selection remains constrained when facing fluctuations in computing power node load. CEDRL, as a heuristic computing power-aware solution, approaches CAR-RL during off-peak periods through multi-objective weighting. Yet, its throughput drops to 305 Mbps during peak periods, indicating room for improvement in its dynamic adjustment strategy. Overall, CAR-RL demonstrates a clear throughput advantage by effectively enhancing bandwidth utilization and data transfer rates through real-time sensing of network bandwidth and computing power states.
Statistical analysis of the three experimental results reveals that CAR-RL achieves packet loss rates, latency, and throughput standard deviations of 0.010%, 0.77 ms, and 6.3 Mbps, respectively—significantly outperforming Q-Learning, DDPG, and CEDRL algorithms. This demonstrates CAR-RL’s capability to accurately select optimal computing-aware routing paths from source nodes to optimal computing power nodes.
6. Conclusions and Outlook
In response to the limitations of routing algorithms in computing power networks, which lack dynamic computing resource awareness, this study proposes an SDN-based computing-aware routing path selection algorithm, CAR-RL, and designs a four-layer collaborative system architecture that includes an intelligent plane, a control plane, a foundation plane, and a management plane, thereby achieving the deep integration of SDN and reinforcement learning. Through MDP modeling, the CAR-RL algorithm combines the TA-DPCA computing power measurement method with network status data and computing power resource data collected in real time by the Ryu controller and K8S cluster to dynamically select the optimal route from the source node to the best computing power node, thereby achieving joint optimization of network performance and computing power resources. The experimental results demonstrate that within the GN4–3N network topology simulated on the Mininet platform, the optimal computing power path generated by the CAR-RL algorithm after locating the optimal computing power node exhibits superior average packet loss rate, average latency, and average throughput compared to other algorithms. This fully validates its superiority in dynamic network environments.
Future research can further explore the application potential of the CAR-RL algorithm in cutting-edge scenarios such as edge computing and 6 G networks, especially by combining the ultra-high bandwidth and large-scale connectivity characteristics of 6 G networks with more advanced multi-agent reinforcement learning to solve multi-user and multi-path coordination problems, thereby providing a broader practical foundation for the development of integrated computing and networking.
Author Contributions
C.L. contributed to the conceptualisation, methodology and software development, as well as writing the original draft. X.C. is responsible for the formal analysis and for reviewing and editing the manuscript. J.L. is responsible for the visualisation and validation of the results. J.W. contributed to the review and editing process and supervised the project. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Datasets are available upon request from the authors.
Acknowledgments
We extend our gratitude to Wang Jian for his excellent technical support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- China Mobile Communications Corporation. White Paper on Computing-Aware Network Technology; China Mobile Communications Corporation: Beijing, China, 2022. [Google Scholar]
- Okonkwo, I.J.; Douglas, I. Comparative study of EIGRP and OSPF protocols based on network convergence. Int. J. Adv. Comput. Sci. Appl. 2020, 11. [Google Scholar] [CrossRef]
- Wumian, W.; Saha, S.; Haque, A.; Sidebottom, G. Intelligent routing algorithm over SDN: Reusable reinforcement learning approach. arXiv 2024, arXiv:2409.15226. [Google Scholar] [CrossRef]
- China Mobile Communications Corporation. Computing-Aware Network White Paper; China Mobile Communications Corporation: Beijing, China, 2021. [Google Scholar]
- China Mobile Research Institute. White Paper on Integrated Network Architecture and Technology System Outlook for Computing-Aware Network; China Mobile Research Institute: Beijing, China, 2022. [Google Scholar]
- Masoudi, R.; Ghaffari, A. Software defined networks: A survey. J. Netw. Comput. Appl. 2016, 67, 1–25. [Google Scholar] [CrossRef]
- Boutaba, R.; Salahuddin, M.A.; Limam, N.; Ayoubi, S.; Shahriar, N.; Estrada-Solano, F.; Caicedo, O.M. A comprehensive survey on machine learning for networking: Evolution, applications and research opportunities. J. Internet Serv. Appl. 2018, 9, 16. [Google Scholar] [CrossRef]
- Mammeri, Z. Reinforcement learning based routing in networks: Review and classification of approaches. IEEE Access 2019, 7, 55916–55950. [Google Scholar] [CrossRef]
- Addula, S.R.; Tyagi, A.K. Future of computer vision and industrial robotics in smart manufacturing. In Artificial Intelligence-Enabled Digital Twin for Smart Manufacturing; Tyagi, A.K., Tiwari, S., Arumugam, S.K., Sharma, A.K., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2024; pp. 505–539. [Google Scholar]
- Tyagi, A.K.; Tiwari, S.; Arumugam, S.K.; Sharma, A.K. (Eds.) Artificial Intelligence-Enabled Digital Twin for Smart Manufacturing; John Wiley & Sons: Hoboken, NJ, USA, 2024. [Google Scholar]
- Prabu, U.; Ch, S.; Panda, S.K.; Geetha, V. An enhanced dynamic multi-path routing algorithm for software defined networks. Procedia Comput. Sci. 2024, 233, 12–21. [Google Scholar] [CrossRef]
- Gunavathie, M.A.; Umamaheswari, S. Traffic-aware optimal routing in software defined networks by predicting traffic using neural network. Expert Syst. Appl. 2024, 239, 122415. [Google Scholar] [CrossRef]
- Wang, Z.H.; Xi, H.L.; Xu, M.Z.; Liu, X.; Pan, N.; Xiao, Z. A review of intra-domain routing algorithms. Radio Eng. 2022, 52, 1755–1764. [Google Scholar]
- He, Q.; Wang, Y.; Wang, X.; Xu, W.; Li, F.; Yang, K.; Ma, L. Routing optimisation with deep reinforcement learning in knowledge-defined networking. IEEE Trans. Mob. Comput. 2023, 23, 1444–1455. [Google Scholar] [CrossRef]
- Fu, Q.; Sun, E.; Meng, K.; Li, M.; Zhang, Y. Deep Q-learning for routing schemes in SDN-based data centre networks. IEEE Access 2020, 8, 103491–103499. [Google Scholar] [CrossRef]
- Casas-Velasco, D.M.; Caicedo Rendon, O.M.; da Fonseca, N.L.S. DRSIR: A deep reinforcement learning approach for routing in software-defined networks. IEEE Trans. Netw. Serv. Manag. 2021, 19, 4807–4820. [Google Scholar] [CrossRef]
- Chen, X.; Huang, G.P. Computing-aware routing technique under microservice architecture. ZTE Technol. 2022, 28, 70–74. [Google Scholar]
- Zhao, C.; Ye, M.; Xue, X.; Lv, J.; Jiang, Q.; Wang, Y. DRL-M4MR: An intelligent multicast routing approach based on DQN deep reinforcement learning in SDN. arXiv 2022, arXiv:2208.00383. [Google Scholar] [CrossRef]
- Ye, M.; Zhao, C.; Wen, P.; Wang, Y.; Wang, X.; Qiu, H. DHRL-FNMR: An Intelligent Multicast Routing Approach Based on Deep Hierarchical Reinforcement Learning in SDN[A/OL]. arXiv 2023, arXiv:2305.19077. [Google Scholar] [CrossRef]
- Sun, G.W.; Xu, F.M.; Zhu, J.Y.; Zhang, H.; Zhao, C. Deterministic scheduling and routing joint intelligent optimisation scheme in computing-aware networks. J. Beijing Univ. Posts Telecommun. 2023, 46, 9–14. [Google Scholar]
- Jinesh, N.; Shinde, S.; Narayan, D.G. Deep reinforcement learning-based QoS aware routing in software defined networks. In Proceedings of the 14th International Conference on Computing Communication and Networking Technologies (ICCCNT), Delhi, India, 6–8 July 2023; IEEE: New York, NY, USA, 2023; pp. 1–6. [Google Scholar]
- Wang, J.; Zhou, T.; Liu, Z.; Zhu, J. An intelligent routing approach for SDN based on improved DuelingDQN algorithm. In Proceedings of the 9th International Conference on Computer and Communications (ICCC), Chengdu, China, 8–11 December 2023; IEEE: New York, NY, USA, 2023; pp. 46–52. [Google Scholar]
- Zhang, Y.; Qiu, L.; Xu, Y.; Wang, X.; Wang, S.; Paul, A.; Wu, Z. Multi-path routing algorithm based on deep reinforcement learning for SDN. Appl. Sci. 2023, 13, 12520. [Google Scholar] [CrossRef]
- Ye, M.; Huang, L.Q.; Wang, X.L.; Wang, Y.; Jiang, Q.X.; Qiu, H.B. A novel intelligent cross-domain routing method in SDN based on a proposed multi-agent reinforcement learning algorithm. arXiv 2023, arXiv:2303.07572. [Google Scholar]
- Giri, A.; Ujwal, C.; Siri, H.V.; Rakish, A. Reinforcement learning employing a multi-objective reward function for SDN routing optimisation. In Proceedings of the International Conference on Evolutionary Algorithms and Soft Computing Techniques (EASCT), Bengaluru, India, 20–21 October 2023; IEEE: New York, NY, USA, 2023; pp. 1–8. [Google Scholar]
- Liu, W.X.; Cai, J.; Chen, Q.C.; Wang, Y. DRL-R: Deep reinforcement learning approach for intelligent routing in software-defined data-centre networks. J. Netw. Comput. Appl. 2021, 177, 102865. [Google Scholar] [CrossRef]
- Yao, H.; Duan, X.; Fu, Y. A computing-aware routing protocol for Computing Force Network. In Proceedings of the 2022 International Conference on Service Science (ICSS), Zhuhai, China, 13–15 May 2022. [Google Scholar]
- Ye, M. An Intelligent SDWN Routing Algorithm Based on Network Situational Awareness and Deep Reinforcement Learning. arXiv 2023, arXiv:2305.10441. [Google Scholar] [CrossRef]
- Ye, M. Intelligent multicast routing method based on multi-agent deep reinforcement learning in SDWN. arXiv 2023, arXiv:2305.10440. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, S.; Tang, Y.; Ye, M.; Huo, W. Optimisation of Computing Power Network Routing Strategies Based on Multi-Agent Soft Actor-Critic; IEEE: New York, NY, USA, 2024. [Google Scholar]
- Ma, G.; Ren, Y.; Qiu, Z.; Wu, J.; Wang, J. A Routing Algorithm for Computing Power Networks Based on Deep Reinforcement Learning and Graph Neural Networks. In Proceedings of the 2024 IEEE International Conference on High Performance Computing and Communications (HPCC), Wuhan, China, 13–15 December 2024. [Google Scholar]
- Yassin, G.F.; Abdulqader, A.H. An Intelligent Q-Learning-Based Routing Model. Int. Res. J. Innov. Eng. Technol. 2025, 9, 58–68. [Google Scholar] [CrossRef]
- Tang, Q.; Zhang, R.; Chen, T.; Huang, T.; Feng, L. CaRCS: Joint Optimisation of Computing-Aware Routing and Collaborative Scheduling in Computing Power Networks. IEEE Netw. 2025. [Google Scholar] [CrossRef]
- Mestres, A.; Rodriguez-Natal, A.; Carner, J.; Barlet-Ros, P.; Alarcón, E.; Solé, M.; Muntés-Mulero, V.; Meyer, D.; Barkai, S.; Hibbett, M.J.; et al. Knowledge-defined networking. ACM SIGCOMM Comput. Commun. Rev. 2017, 47, 2–10. [Google Scholar] [CrossRef]
- Biradar, A.G. A comparative study on routing protocols: RIP, OSPF and EIGRP and their analysis using GNS-3. In Proceedings of the 5th IEEE International Conference on Recent Advances and Innovations in Engineering (ICRAIE), Jaipur, India, 1–3 December 2020; IEEE: New York, NY, USA, 2020; pp. 1–5. [Google Scholar]
- Allochio, C.; Campanella, M.; Chown, T.; Golub, I.; Jeannin, X.; Loui, F.; Myyry, J.; Parniewicz, D.; Savi, R.P.; Szewczyk, T.; et al. Deliverable D6.5: Network Technology Evolution Report; European Commission: Brussels, Belgium, 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).