Abstract
As convolutional neural networks (CNNs) become gradually larger and deeper, their applicability in real-time and resource-constrained environments is significantly limited. Furthermore, while self-attention (SA) mechanisms excel at capturing global dependencies, they often emphasize low-frequency information and struggle to represent fine local details. To overcome these limitations, we propose a multi-scale adaptive modulation network (MAMN) for image super-resolution. The MAMN mainly consists of a series of multi-scale adaptive modulation blocks (MAMBs), each of which incorporates a multi-scale adaptive modulation layer (MAML), a local detail extraction layer (LDEL), and two Swin Transformer Layers (STLs). The MAML is designed to capture multi-scale non-local representations, while the LDEL complements this by extracting high-frequency local features. Additionally, the STLs enhance long-range dependency modeling, effectively expanding the receptive field and integrating global contextual information. Extensive experiments demonstrate that the proposed method achieves an optimal trade-off between computational efficiency and reconstruction performance across five benchmark datasets.
1. Introduction
In the current digital era, images serve as a critical medium for information, whose quality and resolution directly affect the effectiveness of information transmission and analysis. Single-Image Super-Resolution (SISR) aims to reconstruct low-resolution (LR) images as high-resolution (HR) counterparts through algorithmic processing, thereby restoring fine details and enhancing overall image quality. Beyond basic bicubic interpolation [1], more sophisticated classical methods (e.g., overlapping bicubic interpolation [2] and prior-based [3,4,5]) have also been developed, pushing the performance boundaries of non-learning-based approaches. However, due to the inherently ill-posed nature of SISR, traditional super-resolution (SR) methods [1,2,3,4,5] often struggle to effectively model complex non-linear mapping relationships between LR and HR images.
Deep learning-based methods [6,7,8,9,10,11,12] have significantly advanced SR by automatically learning complex details and high-frequency information from large datasets. Among these, convolutional neural network (CNN)-based approaches [6,8,13,14] have been widely adopted. However, due to the inherent locality of convolutional operations, shallow CNN models struggle to capture global contextual information, which often leads to distortions when reconstructing large-scale textures and long-range dependencies. To mitigate these issues and enhance representational capacity, CNN architectures have tended to grow both deeper and larger. For instance, RCAN [9] builds an over 400-layer network and contains more than 15 million parameters. Nevertheless, as CNN-based models grow deeper and more complex, they demand substantially more computational resources and memory than lightweight models, thereby hindering their deployment in real-time applications and on resource-constrained devices.
Recently, Vision Transformers (ViTs) [11,12,15,16,17] effectively capture global dependencies and improve detail recovery in SR through self-attention (SA). However, SA typically requires high computational resources, especially for HR images. While efficient variants like window-based [11], permuted [12], and spatial window [17] models reduce costs, they still face efficiency issues in feature dependency modeling, leading to slow training and inference. Furthermore, recent research has shown that ViTs tend to prioritize low-frequency information, limiting their ability to represent local details [18,19].
To address the above challenges, we propose a multi-scale adaptive modulation network (MAMN), a simple yet efficient architecture that integrates multi-scale adaptive modulation blocks (MAMBs) to achieve a favorable balance between reconstruction quality and computational efficiency. In contrast to merely stacking lightweight convolutional modules, we introduce a Swin Transformer Layer (STL) to better capture long-range dependencies. Specifically, we develop a multi-scale adaptive modulation layer (MAML) that leverages variance-based weighting to dynamically modulate multi-scale non-local representations. Given MAML’s global characteristic, we further design a local detail extraction layer (LDEL) to complement the modulation process with fine-grained local contextual information. Additionally, two Swin Transformer Layers (STLs) are incorporated to enhance the modeling of long-range features. Together, these components form an end-to-end trainable framework that effectively achieves high reconstruction performance with manageable complexity, as demonstrated in Figure 1.
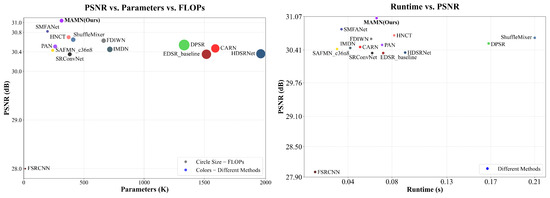
Figure 1.
Model complexity and performance comparison between the proposed method and other lightweight methods on Manga109 [20] for SR. The left subplot illustrates the relationship between PSNR (a measure of image reconstruction quality), parameters, and FLOPs (a measure of computational complexity) for different SR methods. The sizes of circles in the figure denote the models’ FLOPs. The right subplot illustrates the relationship between PSNR and runtime (a measure of computational efficiency) for different SR methods. The proposed MAMN achieves a better trade-off between computational complexity (reflected by parameters, FLOPs, and runtime) and reconstruction performance (reflected by PSNR) compared to other lightweight SR models.
The remainder of this paper is organized as follows: Section 2 provides a comprehensive review of the existing research in SR, including CNN-based, ViT-based, and lightweight approaches, while also highlighting the shortcomings of these methods, which serve as the motivation for the present study. Section 3 details the proposed multi-scale adaptive modulation network (MAMN), including the MAML, LDEL, and STL modules, ensuring the validity of our research. Section 4 presents and discusses experimental results, including quantitative and qualitative comparisons, with supporting data visualized in figures and tables. Finally, Section 5 concludes the paper and suggests directions for future research.
The main contributions of this paper are summarized as follows:
- We propose a novel multi-scale adaptive modulation layer (MAML) that employs multi-scale decomposition and variance-based modulation to effectively extract multi-scale global structural information.
- We design a lightweight local detail extraction layer (LDEL) to capture fine local details, complemented by Swin Transformer Layers (STLs) to efficiently model long-range dependencies.
- Through comprehensive quantitative and qualitative evaluations on five benchmark datasets, we demonstrate that our method achieves a favorable trade-off between computational complexity and reconstruction quality.
2. Related Works
2.1. CNN-Based Super-Resolution
Compared to traditional SR methods, CNN-based approaches can automatically learn complex non-linear mappings from extensive datasets. Owing to this capability, CNN-based models have achieved significant success on SR tasks. For instance, SRCNN [6] pioneered an end-to-end learning framework that directly maps LR inputs to HR outputs. Subsequent models (e.g., FSRCNN [13] and ESPCN [21]) introduced an efficient post-upsampling mechanism that significantly accelerates the inference process while maintaining competitive reconstruction quality. Further advancing the field, VDSR [22] incorporates residual learning to facilitate the training of deeper networks and improve mapping accuracy. However, small networks often struggle to effectively model long-range dependencies due to limited model capacity and small receptive fields, resulting in insufficient image detail and excessive smoothing. To overcome the limitations of smooth results generated by previous CNN-based methods [6,13,21], generative adversarial network (GAN)-based SR approaches (e.g., [23,24]) leverage adversarial learning to reconstruct high-resolution images with more realistic textures and enhanced detail. However, these methods still suffer from challenges (e.g., training instability, occasional illusory textures, and structural inconsistencies) and still face limitations in maintaining pixel-level precision.
To further enhance representational capacity, many CNN-based SR methods have adopted increasingly deep and wide architectures. For example, EDSR [8] scales up to 43 million parameters, resulting in improved reconstruction accuracy and visual quality. Similarly, RCAN [9] employs a very deep structure of over 400 layers and integrates a channel attention mechanism to adaptively extract informative features from different image regions, thereby enhancing both local detail and global consistency. However, these large-scale models require considerable computational resources and exhibit slow inference speeds, rendering them less suitable for real-time or mobile applications.
2.2. ViT-Based Super-Resolution
Owing to the remarkable ability of the Transformer architecture [25] in modeling global contextual information, it has attracted growing interest in the SR field. Vision Transformer (ViT) [26], for instance, employs global self-attention (SA) to capture long-range dependencies, significantly improving the reconstruction of fine details and global consistency. This approach has achieved breakthrough performance in various SR tasks, surpassing traditional convolutional neural networks. IPT [15] utilizes a pre-trained SA mechanism based on the ImageNet dataset to integrate both global and local features, thereby enhancing high-frequency details and structural integrity. Nevertheless, the standard SA mechanism demands the calculation of pair interactions between all image patches, resulting in quadratic growth in computational and memory costs as the image size increases, which severely limits its practicality.
To mitigate these computational challenges, numerous efficient ViT variants have been developed. For instance, SwinIR [11] introduces local window-based SA and cross-layer feature fusion, effectively capturing detailed local structures while maintaining computational efficiency. ELAN [27] incorporates a streamlined long-range attention mechanism that reduces complexity while preserving the ability to model dependencies between distant pixels, thereby improving both detail recovery and structural coherence. Restormer [16] employs adaptive feature fusion strategies to balance local and global information for high-quality image reconstruction. SRFormer [12] achieves efficient large-window SA by transferring computation to the channel dimensions, reducing spatial complexity. Meanwhile, HAT [28] activates a larger proportion of pixels via hybrid attention to enhance representation capacity, and DAT [17] introduces dual aggregation across spatial and channel dimensions (both intra-block and inter-block), significantly improving the model’s expressive capability with a reduced number of channels. Although these methods effectively leverage SA to capture global dependencies and improve long-range feature propagation, they still face growing computational and memory demands as image resolution and network depth increase, ultimately constraining training and inference efficiency and imposing higher hardware requirements.
2.3. Lightweight and Efficient Image Super-Resolution
To balance computational efficiency and resource consumption, numerous lightweight SR methods have been developed. For instance, FSRCNN [13] and ESPCN [21] employ a post-upsampling strategy to accelerate SR processing and alleviate computational overhead from input upscaling. CARN [7] introduces group convolutions and a cascading mechanism to progressively refine image details, thereby enhancing network performance. IMDN [29] leverages multi-stage information distillation to effectively extract and fuse multi-level features, significantly improving SR quality with reducing computational cost. LatticeNet [30] utilizes serial lattice blocks coupled with backward feature fusion to minimize parameters while preserving competitive reconstruction performance. Meanwhile, LCRCA [31] proposes a lightweight yet efficient deep residual block (DRB) capable of generating more accurate residual information. ShuffleMixer [32] integrates channel shuffling and group convolution to optimize feature reorganization and computation, markedly improving efficiency without sacrificing performance. BSRN [33] adopts blueprint separable convolution to reduce model complexity, and HNCT [34] introduces a hybrid architecture that combines local and non-local priors using both CNN and Transformer components for enhanced SR performance. Furthermore, SAFMN [10] implements a spatially adaptive feature modulation mechanism to dynamically select informative representations, while HDSRNet [35] exploits heterogeneous dynamic convolution for efficient SR. SMFANet [36] contributes a self-modulating feature aggregation (SMFA) module to enhance feature expressiveness in spatial dimensions. Despite gaining ground in efficiency-oriented designs, achieving an optimal trade-off between reconstruction accuracy and computational efficiency remains a continuous challenge in lightweight SR tasks.
3. Proposed Method
In this paper, we propose an efficient SR method that integrates a multi-scale adaptive modulation layer (MAML) to capture multi-scale non-local information and a local detail extraction layer (LDEL) to extract fine-grained local details. To further enhance feature refinement and long-range dependency modeling, we introduce a Swin Transformer Layer (STL), which effectively refines the extracted features and facilitates global contextual interaction throughout the network. The proposed method achieves a superior balance between model complexity and reconstruction performance.
As illustrated in Figure 2, the overall architecture of the proposed multi-scale adaptive modulation network (MAMN) comprises three components: a convolution layer, a series of stacked multi-scale adaptive modulation blocks (MAMBs), and an upsampler layer. Given an LR input (), we first adopt a convolution layer to extract shallow features (). These features are then progressively refined through multiple MAMBs to produce more representative deep features. Each MAMB integrates one MAML, one LDEL, and two STLs. To facilitate the reconstruction of high-frequency details, a global residual connection is introduced. Finally, the HR output image () is reconstructed through an upsampler layer, which consists of a convolution followed by a sub-pixel convolution [10]. The entire process can be formulated as follows:
where denotes a convolution operation, represents a series of stacked MAMBs, and refers to an upsampler layer. Following previous studies [10,32], the loss function combines a mean pixel-wise loss and an FFT-based frequency loss to enhance the recovery of high-frequency details. The overall loss function is defined as follows:
where is the ground-truth HR image, refers to the fast Fourier transform, and the parameter represents a weight value (empirically set to 0.05).
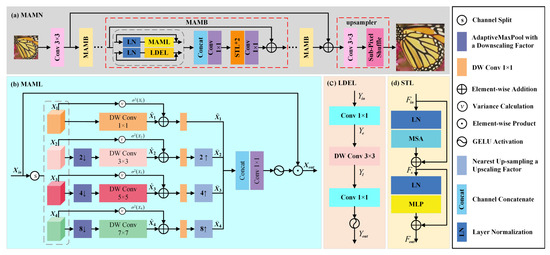
Figure 2.
The upper figure shows the network architecture of the proposed MAMN. The MAMN comprises a convolution layer, multi-scale adaptive modulation blocks (MAMBs), and an upsampler layer. The key component of an MAMB consists of a multi-scale adaptive modulation layer (MAML), a local detail extraction layer (LDEL), and two Swin Transformer Layers (STLs).
3.1. Multi-Scale Adaptive Modulation Layer
Existing methods primarily rely on single-scale features [8,9,34,35], which often fail to capture multi-level details and global information, leading to an incomplete representation of complex image structures. To address this limitation, we propose a multi-scale adaptive modulation module that extracts features at multiple scales and adaptively adjusts the importance of information at each scale. This enables refined integration of global context and enhances the model’s capacity to handle variations in scale. As illustrated in Figure 2b, to reduce model complexity while obtaining multi-scale representations, we first split the input () channel-wise into four components. The first component is processed using a depth-wise convolution, while the remaining three are fed into feature generation units with progressively increased receptive fields to produce multi-scale features. This procedure can be expressed as follows:
where refers to the channel-split operation, and are and depth-wise convolution layers, represents adaptive max pooling for k downsampling, , , and . Here, adaptive max pooling is combined with convolutions of different scales to capture broader contextual information and extract more abstract and global features. Inspired by SMFANet [36], the variance of X is employed as a measure of spatial information variability. To enhance the model’s expressiveness and adaptability, the introduction of the learnable parameters and to weight different feature information (the variance of the convolution processed features and the input features) allows the model to dynamically adjust the importance of this feature information based on the training data. This procedure is expressed as:
where is the variance of , N is the total number of pixels, represents the pixel value, and is the mean value of all pixels.
Subsequently, a depth-wise convolution performs the channel-adaptive nonlinear modulation of multi-scale features and variance statistics-weighted results to enhance feature representation. We then obtain the non-local feature representation by applying a convolution to the concatenated multi-scale features. The process operation is as follows:
where is a convolution operation, and are learnable parameters, denotes k upsampling feature maps to the original resolution through nearest interpolation, are the variance-adjusted features, are the after upsampling features, represents the channel concatenation operation, is the channel concatenating feature.
Finally, we use the concatenating feature to modulate the input feature () to extract the representative feature (), which can be expressed as follows:
where denotes the GELU function [37] and ⊙ is the element-wise product.
3.2. Local Detail Extraction Layer
Local details play a crucial role in enhancing the recovery of fine image structures. While the MAML captures global multi-scale information, we designed a lightweight local detail extraction layer (LDEL) to simultaneously augment local detail representation. As illustrated in Figure 2c, the input () is first projected via a convolution to expand its channel dimensions. The expanded features () are then processed by a depth-wise convolution to encode localized patterns, producing feature set . Finally, a convolution followed by a GELU activation [37] is applied to reduce channel dimensions and generate the refined local feature (). The entire procedure can be formulated as follows:
where and remain the same as the previous definition.
3.3. Swin Transformer Layer
The Transformer architecture [25] effectively captures long-range dependencies and integrates global information through its SA mechanism, thereby enhancing the flexibility and expressiveness of feature representation. However, classic SA approaches [25,26] suffer from high computational complexity, particularly when processing long sequences, leading to a significant burden on memory and computational resources. To mitigate these limitations, we incorporate the Swin Transformer Layer (STL) from SwinIR [11], which maintains the ability to model long-range interactions while significantly improving computational efficiency.
As shown in Figure 2d, the inputs () are first normalized by a LayerNorm layer to stabilize the training process. Subsequently, the normalized feature is fed into a multi-head self-attention (MSA) module to effectively capture long-range dependencies. At the end of the MSA, a residual connection is introduced to add the MSA’s output to the original input feature, thereby preserving original information and enhancing gradient flow. This process can be described as follows:
where represents a LayerNorm operation, and is the intermediate feature. is then processed by the second LayerNorm layer for further normalization. The normalized feature is subsequently fed into a multi-layer perceptron (MLP) to perform non-linear transformation and enhancement. Finally, a residual connection is similarly introduced at the output of the MLP to add its output to the feature preceding the second LayerNorm. This procedure can be formulated as follows:
where is the output of the STL.
3.4. Multi-Scale Adaptive Modulation Block
Based on the complementary function of the MAML, LDEL, and STL, we integrate these modules into a multi-scale adaptive modulation block (MAMB) to extract rich and representative deep features. The input is simultaneously processed through two parallel branches: the MAML, which captures multi-scale non-local contextual information, and the LDEL, which focuses on extracting fine-grained local details. This process can be expressed as follows:
Subsequently, the features extracted from these two branches are concatenated along the channel dimensions to form a comprehensive representation that integrates both multi-scale global information and fine local details. The concatenated features are then processed by a convolutional layer to adjust channel dimensions and compress the feature representation, thereby enhancing computational efficiency and facilitating effective information integration. This process can be formulated as follows:
The processed features are then passed through two consecutive STLs to enable deeper modeling, further enhancing the network’s ability to capture long-range dependencies. Finally, the output of the STLs undergoes refinement via a convolutional layer and is combined with the original input features through a residual connection [38]. This design not only improves the representational capacity of the features but also ensures stability during training.
where , , and represent the intermediate features, while and refer to the input and output of the MAMB.
4. Experimental Results
In this section, we evaluate the performance of the proposed method from both quantitative and qualitative perspectives on five benchmark test datasets.
4.1. Datasets and Implementation Details
Datasets. Similar to previous works [10,11], we employ the DIV2K [8] and Flickr2K [8] datasets for model training. DIV2K provides 800 high-resolution and high-quality images, which can effectively support the model in learning rich textures and details. Flickr2K offers 2650 diverse real-world images, contributing to the improvement of the generalization ability and robustness of the model. LR images are generated by bicubic downscaling from HR images. As for test data, we use five benchmark datasets as test datasets: Set5 [39], Set14 [40], BSD100 [41], Urban100 [42], and Manga109 [20]. Set5 and Set14 are designed to facilitate quick and fair numerical comparisons with other methods. The BSD100 dataset consists of 100 natural scene images that contain natural noise and complex structures. We use PSNR and SSIM as evaluation metrics. Urban100 comprises 100 urban images including numerous regular repeating structures (e.g., building windows, staircases, and floor tiles). Manga109 comprises 109 manga-style images characterized by sharp edges and smooth color regions. These datasets collectively cover diverse image types, enabling fair comparison and objective evaluation of different SR models’ performance. The peak signal-to-noise ratio (PSNR) [43] and structural similarity index measure (SSIM) [44] are calculated on the Y channel after converting the images to the YCbCr color space.
The PSNR is employed to quantitatively assess the reconstruction quality of SR images by measuring the pixel-level similarity between the generated high-resolution image and the corresponding ground truth. It is defined as follows:
where represents the maximum possible pixel value of the image (typically 255 for 8-bit images), denotes the mean squared error between the super-resolved image and the ground-truth high-resolution image. The MSE can be expressed as follows:
where and denote the pixel values at position (i,j) of the ground-truth high-resolution image and the SR image, respectively, while m and n represent the width and height of the images. The SSIM evaluates the perceptual similarity between these two images by comparing brightness, contrast, and structural characteristics. Its calculation is defined as follows:
where and represent the average brightness of the ground-truth high-resolution image and the SR image, respectively; and denote their standard deviations; and is the covariance between the two images. Constants and are introduced to stabilize the division, with and , where = 0.01, = 0.03, and L indicates the pixel value’s dynamic range (e.g., L = 255 for 8-bit image).
Implementation details. During training, low-resolution (LR) input images are randomly cropped into patches with dimensions of and augmented through random horizontal flipping and rotation. A batch size of 16 is used throughout the training process. The MAMN employs 8 MAMBs with a feature channel of 36. We train the proposed model with the Adam optimizer [45], , and . The number of total iterations is set to 1,000,000. The initial learning rate is set to and decayed to a minimum of following a cosine annealing scheme [46]. All experiments are implemented using the PyTorch (torch==2.3.0 + CUDA 11.8) framework and executed on an NVIDIA GeForce RTX 3090 GPU.
4.2. Comparisons with State-of-the-Art Methods
Quantitative comparisons. To evaluate the performance of the proposed model, we perform comprehensive comparisons with state-of-the-art CNN-based and traditional lightweight SR methods, including Bicubic [1], FSRCNN [13], EDSR-baseline [8], CARN [7], IMDN [29], PAN [47], DPSR [48], LatticeNet [30], LCRCA [31], ShuffleMixer [32], HNCT [34], FDIWN [49], and HDSRNet [35]. Table 1 presents the quantitative comparisons of , , and SR using a CNN-based architectureacross five benchmark datasets. Besides the widely adopted PSNR and SSIM metrics, we also provide parameters and FLOPs (three color channels) to assess model complexity with the fvcore1 library (i.e., https://detectron2.readthedocs.io/en/latest/modules/fvcore.html#fvcore.nn.parameter_count (accessed on 25 June 2025)) under an LR image to pixels. Params are linked to the memory footprint, and FLOPs reflect computational consumption. As shown in Table 1, the proposed model achieves the best performance on both and SR tasks. For the , the proposed MAMN attains the second best PSNR/SSIM results (excluding Set5 and Urban100) while using only 40% of the parameters compared with the best model, LatticeNet.

Table 1.
Comparative results of different CNN-based methods. PSNR/SSIM are calculated on the Y channel. The top two methods are labeled and bold in red and blue.
We also compared our approach with attention-based methods, including lightweight dynamic modulation (e.g., SAFMN [10], SMFANet [36], and SRConvNet [50]) and large-scale self-attention (e.g., SwinIR [11], HAT [28], and RGT [51]). As observed in Table 2, compared to similar lightweight models (SAFMN, SMFANet, and SRConvNet), the proposed MAMN consistently achieves the best overall performance while maintaining comparable parameters. At scaling factors of and , MAMN attains the highest metrics across all five test datasets. The most significant improvements are observed on the scale for the Urban100 (28.43/0.8570) and Manga109 (34.20/0.9478) datasets while maintaining reasonable FLOP control (only 21 G at ). Compared to large-scale models (SwinIR, HAT, and RGT) with parameter counts dozens of times greater than ours, MAMN achieves approximately 95% of HAT’s PSNR performance in SR tasks while utilizing less than 3.1% of the parameters (0.31 M vs. 10 M–21 M). In terms of computational efficiency, MAMN requires only 1.4–3.5% of the FLOPs of these large models (e.g., 21 G vs. 592 G–1458 G at scale). Particularly on the Set5 dataset for SR, the proposed method attains about 98% of HAT’s performance with merely 1.5% of its parameters.

Table 2.
Comparative results of different attention-based methods (e.g., SA-based and dynamic modulation methods). PSNR/SSIM are calculated on the Y channel. The top two methods are labeled and bold in red and blue. Our results are displayed in bold.
Qualitative comparisons. Visual comparisons for and SR are presented in Figure 3 and Figure 4, respectively, using images from the Urban100 dataset. The results demonstrate that the proposed method achieves superior reconstructions compared to other approaches, exhibiting enhanced recovery of fine details and improved structural integrity. Specifically, the proposed method preserves original image details more effectively while reducing blurring and visual distortions. Although all compared methods achieve perceptually plausible results, the proposed approach shows notably stronger performance in reconstructing complex textures and sharp edges, indicating its enhanced capability in handling complex scenarios.

Figure 3.
Visual comparisons for SR image061 from the Urban100 dataset.

Figure 4.
Visual comparisons for SR image099 from the Urban100 dataset.
Running time comparisons. To further assess the computational efficiency and practical applicability of various SR methods, we compare the inference times of different methods (including DPSR [48], LatticeNet [30], HNCT [34], ShuffleMixer [32], SAFMN [10], SMFANet [36], and SRConvNet [50]) when performing SR on 50 images with a resolution of pixels. The test platform utilizes an Intel(R) i5-13600KF processor (20 cores @ 3.5 GHz), 32 GB system memory, and an NVIDIA GeForce RTX 4060 Ti GPU running on the Windows operating system. Based on the running time comparisons presented in Table 3, the proposed MAMN achieves an average inference time of 0.066 s. This performance demonstrates highly competitive efficiency among state-of-the-art methods.

Table 3.
Running time comparisons on SR. #Avg.Time is the average running time on 50 LR images with a size of pixels.
As shown in Table 1 and Table 3, MAMN achieves superior reconstruction quality across all five benchmark datasets while being 20.5% faster than HNCT (0.066 s vs. 0.083 s). Compared to the lightweight SMFANet [36], which requires 0.034 s, MAMN maintains a better trade-off between performance and speed, achieving significantly higher accuracy despite a moderate increase in inference time. Furthermore, the proposed method demonstrates substantially greater efficiency than several larger models; for example, DPSR [48] requires 0.169 s (156.1% slower), while LatticeNet [30] takes 0.120 s (81.8% slower) to process the same data. Table 1 and Table 3 indicate that the proposed method balances computational efficiency with high reconstruction quality. Specifically, the overall runtime is displayed in Figure 1 (labeled as “Runtime vs. PSNR”).
LAM comparisons. The Local Attribution Map (LAM) [52] highlights significant correlations between red pixels and rectangular reference patches during the reconstruction process. In Figure 5, we compare the LAM visualizations of the proposed method with other efficient SR approaches [10,29,32] and annotate the corresponding Diffusion Index (DI) value below each subfigure. Higher DI values indicate a broader range of pixel participation in the reconstruction. The results demonstrate that the proposed MAMN effectively integrates information from a wider spatial area, leading to superior reconstruction quality.

Figure 5.
Comparison of local attribution maps (LAMs) [52] and diffusion indices (DIs) [52]. The proposed MAMN can utilize more feature information and reconstruct a more accurate image structure.
4.3. Model Analysis
To thoroughly evaluate the contribution of each component in the proposed MAMN, we conduct comprehensive ablation studies under consistent experimental conditions. All ablation experiments are performed at an upscaling factor of using identical settings to ensure fair comparisons. As summarized in Table 4, the baseline corresponds to the complete MAMN model. The notation “A→B” indicates replacing component A with B, while “None” denotes removing the corresponding operation. The abbreviations represent the following modules: FA (Feature Aggregation), FM (Feature Modulation), MC (Multi-scale Convolution), Down (Downsampling), VM (Variance Modulation), and FFTLoss (Frequency Loss). Performance is evaluated quantitatively on the Set5 [39] and Manga109 [20] datasets.

Table 4.
Performance Analysis of the proposed MAMN and its variants on the Set5 and Manga109 datasets for SR. Parameters and FLOPs computed using an input resolution of pixels. The Baseline’s results are highlighted in bold.
Effectiveness of the multi-scale adaptive modulation layer. We conduct an ablation study to evaluate the impact of the multi-scale adaptive modulation layer (MAML). Experimental results indicate that removing this module causes PSNR decreases of 0.08 dB on the Set5 dataset and 0.17 dB on the Manga109 dataset, underscoring the critical importance of MAML. To further elucidate its underlying mechanism, we perform a depth analysis of this module.
- Feature Modulation. The MAML incorporates a feature modulation mechanism to adaptively adjust feature weights. Ablation results show that removing this operation (“w/o FM”) leads to performance degradation of 0.02 dB on Set5 and 0.03 dB on Manga109 compared to the baseline model.
- Multi-scale representation. To evaluate the effectiveness of multi-scale features in the proposed MAMN, we construct two variant models: “w/o MC” and “w/o Down”. Here, the “w/o MC” configuration replaces the multi-scale depth-wise convolution with a single-scale depth-wise convolution for spatial feature extraction. As shown in Table 4, the use of multi-scale features yields a PSNR improvement of 0.04 dB on the Manga109 dataset. The “w/o Down” variant, which removes the downsampling operation, confirms that incorporating downsampling can bring about superior PSNR performance. These results demonstrate that multi-scale feature extraction enhances the model’s ability to capture information at different levels of detail, thereby improving SR reconstruction. Furthermore, we employ adaptive max pooling to construct multi-scale representations. In comparison to adaptive average pooling and nearest interpolation, adaptive max pooling more effectively identifies salient features, contributing to improved reconstruction quality.
- Variance modulation. To enhance the ability to capture non-local information, the proposed MAMN incorporates variance modulation within the MAML branch. An ablation study is conducted by removing this operation to evaluate its contribution. As summarized in Table 4, the absence of variance modulation results in a consistent performance reduction of 0.06 dB on both the Set5 and Manga109 datasets. Furthermore, replacing variance modulation with standard attention mechanisms improves performance but leads to sharp increases in parameters and computational complexity, rising by 58.6% and 81%, respectively. These findings confirm that variance modulation plays a critical role in improving the representational capacity of the model.
- Feature aggregation. To evaluate the effectiveness of feature aggregation, we construct an ablation model denoted as “w/o FA”, in which the convolutional layer for the integration of multi-scale features along the channel dimensions is removed. Experimental results show that incorporating feature aggregation improves PSNR by 0.06 dB on the Set5 dataset and 0.07 dB on the Manga109 dataset. These results demonstrate the essential role of multi-scale feature aggregation in improving reconstruction performance.
Effectiveness of the local detail extraction layer. To capture local features and fine-grained details, we design a LDEL branch. An ablation study is performed by removing this branch to evaluate its contribution. As presented in Table 4, the absence of the LDEL results in PSNR decreases of 0.13 dB on the Set5 dataset and 0.36 dB on the Manga109 dataset. These results demonstrate the critical role of the LDEL in extracting and preserving locally important features and structural details.
Figure 6 presents the power spectral density (PSD) maps and corresponding feature visualizations, illustrating the complementary interactions between the MAML and LDEL branch. Through periodic spectrum map transformation, the low-frequency components are shifted to the center, where a brighter central region indicates stronger energy concentration in low-frequency components. The MAML exhibits higher energy density, with pronounced brightness at the center, whereas the feature from the LDEL shows more dispersed energy distribution in the peripheral regions compared to the input feature () and the MAML output (). This contrast highlights the distinct yet complementary roles of the two branches in capturing frequency information.
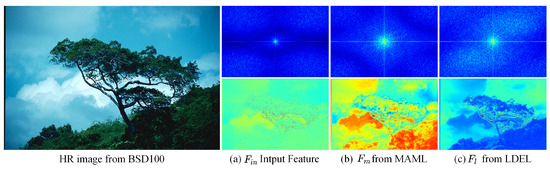
Figure 6.
The power spectral density (PSD) and feature map visualizations. The low-frequency components are shifted to the center via periodic spectrum map transformation, which indicates that the brighter center region of the image represents the stronger energy of the low-frequency component. The MAML activates more low-frequency components for feature , and the LDEL enhances high-frequency representations for feature .
Figure 7 visualizes the high-frequency components within feature maps of the input, MAML, and LDEL across different radial regions. The low-frequency components are extracted through the following procedure: First, a low-frequency mask is generated by computing the squared distance from each pixel to the center coordinates within a given radius (r). Pixels within or on the circle of radius r are assigned a mask value of 1, while all others are set to 0. The high-frequency mask is then obtained by inverting the low-frequency mask using 1-mask such that regions with mask values of 1 correspond to the high-frequency components. Finally, the high frequency mask is inverted by a transform operation to obtain a time-domain image (complex form); then, its absolute value is taken to produce a real-valued image, and its mean value is computed to quantify the high-frequency energy within the current radial region.
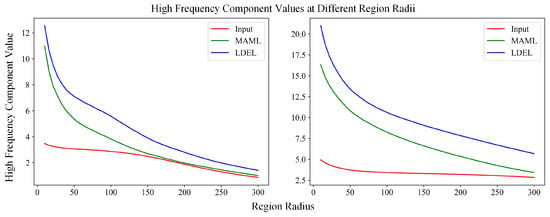
Figure 7.
The high-frequency components are shown on the feature map across different radius areas of input, MAML, and LDEL. The results demonstrate that the LDEL contains more high-frequency components.
As shown in Figure 7, the high-frequency component values of the LDEL are significantly higher than those of the Input and MAML at small region radii, indicating that the LDEL retains richer high-frequency information in its initial state and is more effective at capturing fine textural details. As the radial region expands, the high-frequency responses of the LDEL decrease at a relatively gradual rate. In contrast, the MAML exhibits a more observable decline in high-frequency energy, while the input maintains consistently low values throughout. These results demonstrate that the LDEL can stably preserve high-frequency information across varying scale regions, indicating its superior capability in maintaining high-frequency features when processing images of different sizes.
Effectiveness of the Swin transformer layer. The introduced STL can enhance the global representation capability of MAMN by effectively capturing long-range dependencies. To evaluate the contribution of this module, we remove the STL from the MAMB. As summarized in Table 4, the model without STL achieves PSNR values of only 32.01 dB on the Set5 dataset and 30.30 dB on the Manga109 dataset. These results underscore the critical importance of modeling long-range dependencies for high-quality image SR.
5. Conclusions
In this paper, we propose a lightweight and efficient super-resolution network, termed the multi-scale adaptive modulation network (MAMN), which leverages multi-scale adaptive modulation to enhance reconstruction performance for complex details. The core component, the multi-scale adaptive modulation layer (MAML), effectively captures multi-level information while dynamically adjusting feature contributions at different scales. To further improve the recovery of fine details, a local detail extraction layer (LDEL) is proposed. Moreover, we introduce a Swin Transformer Layer (STL) to strengthen long-range feature dependencies and improve contextual coherence. Extensive experimental results demonstrate that the proposed MAMN achieves a highly favorable balance between computational complexity and reconstruction quality across multiple benchmark datasets. However, the self-attention (SA) mechanism inherent in the STL still imposes high memory and computational demands, particularly when processing high-resolution images. Future work will focus on the development of architectural optimization and acceleration strategies (e.g., exploring low-rank attention mechanisms or adaptive token pruning) to substantially reduce the computational costs of Transformer-based models and enhance operational efficiency in HR applications.
Author Contributions
Z.L.’s main contribution was to propose the methodology of this work and write the paper. G.Z. guided the entire research process, participated in the writing of the paper, and secured funding for the research. J.T. participated in the implementation of the algorithm. R.Q. was responsible for algorithm validation and data analysis. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Xinjiang Uygur Autonomous Region (2022D01C461 and 2022D01C460), the “Tianshan Talents” Famous Teachers in Education and Teaching project of Xinjiang Uygur Autonomous Region (2025), and the “Tianchi Talents Attraction Project” of Xinjiang Uygur Autonomous Region (2024TCLJ04).
Data Availability Statement
The data are openly available in a public repository. The code is available at https://github.com/smilenorth1/MAMN-main (accessed on 30 June 2025).
Conflicts of Interest
The authors declare that they have no competing interests. There are no financial, personal, or professional relationships, affiliations, or circumstances that could be construed as influencing the research reported in this manuscript.
Nomenclature
The following nomenclature is used in this manuscript:
| CNNs | Convolutional neural networks | SA | Self-attention |
| MAMN | Multi-scale adaptive modulation network | LR | Low-resolution |
| MAMB | Multi-scale adaptive modulation block | HR | High-resolution |
| MAML | Multi-scale adaptive modulation layer | ViT | Vision Transformer |
| LDEL | Local detail extraction layer | STL | Swin transformer layer |
| SISR | Single-image super-resolution | Variance | |
| Adaptive max pooling downsampling | N | Total pixels | |
| Nearest interpolation upsampling | GELU activation | ||
| MSA | Multi-head self-attention | MLP | Multi-layer perceptron |
| PSNR | Peak signal-to-noise ratio | Mean squared error | |
| SSIM | Structural similarity index measure | Maximum pixel value | |
| GAN | Generative adversarial network |
References
- Donya, K.; Abdolah, A.; Kian, J.; Mohammad, H.M.; Abolfazl, Z.K.; Najmeh, M. Low-Cost Implementation of Bilinear and Bicubic Image Interpolation for Real-Time Image Super-Resolution. In Proceedings of the GHTC, Online, 29 October–1 November 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Ruangsang, W.; Aramvith, S. Efficient super-resolution algorithm using overlapping bicubic interpolation. In Proceedings of the GCCE, Nagoya, Japan, 24–27 October 2017; pp. 1–2. [Google Scholar] [CrossRef]
- Dai, S.; Han, M.; Xu, W.; Wu, Y.; Gong, Y. Soft Edge Smoothness Prior for Alpha Channel Super Resolution. In Proceedings of the CVPR, Minneapolis, MN, USA, 23–28 June 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Radu, T.; Vincent, D.; Luc, V. A+: Adjusted Anchored Neighborhood Regression for Fast Super-Resolution. In Proceedings of the ACCV, Singapore, 1–5 November 2015; pp. 111–126. [Google Scholar] [CrossRef]
- Yang, J.; Wright, J.; Huang, T.S.; Ma, Y. Image Super-Resolution Via Sparse Representation. IEEE Trans. Image Process. 2010, 19, 2861–2873. [Google Scholar] [CrossRef] [PubMed]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Learning a deep convolutional network for image super-resolution. In Proceedings of the ECCV, Zurich, Switzerland, 6–12 September 2014; pp. 184–199. [Google Scholar] [CrossRef]
- Ahn, N.; Kang, B.; Sohn, K. Fast, accurate, and lightweight super-resolution with cascading residual network. In Proceedings of the ECCV, Munich, Germany, 8–14 September 2018; pp. 252–268. [Google Scholar] [CrossRef]
- Lim, B.; Son, S.; Kim, H.; Nah, S.; Lee, K.M. Enhanced deep residual networks for single image super-resolution. In Proceedings of the CVPRW, Honolulu, HI, USA, 21–26 July 2017; pp. 136–144. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image super-resolution using very deep residual channel attention networks. In Proceedings of the ECCV, Munich, Germany, 8–14 September 2018; pp. 286–301. [Google Scholar] [CrossRef]
- Sun, L.; Dong, J.; Tang, J.; Pan, J. Spatially-adaptive feature modulation for efficient image super-resolution. In Proceedings of the ICCV, Paris, France, 2–6 October 2023; pp. 13190–13199. [Google Scholar] [CrossRef]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Van Gool, L.; Timofte, R. Swinir: Image restoration using swin transformer. In Proceedings of the ICCVW, Montreal, QC, Canada, 11–17 October 2021; pp. 1833–1844. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, Z.; Guo, C.L.; Bai, S.; Cheng, M.M.; Hou, Q. SRFormer: Permuted Self-Attention for Single Image Super-Resolution. In Proceedings of the ICCV, Paris, France, 2–6 October 2023; pp. 12734–12745. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; Tang, X. Accelerating the super-resolution convolutional neural network. In Proceedings of the ECCV, Amsterdam, The Netherlands, 11–14 October 2016; pp. 391–407. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, H.; Zhang, L. Edge-oriented Convolution Block for Real-time Super Resolution on Mobile Devices. In Proceedings of the ACMM, Virtual Event, China, 20–24 October 2021; pp. 4034–4043. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Y.; Guo, T.; Xu, C.; Deng, Y.; Liu, Z.; Ma, S.; Xu, C.; Xu, C.; Gao, W. Pre-trained image processing transformer. In Proceedings of the CVPR, Nashville, TN, USA, 10–25 June 2021; pp. 12299–12310. [Google Scholar] [CrossRef]
- Zamir, S.W.; Arora, A.; Khan, S.; Hayat, M.; Khan, F.S.; Yang, M.H. Restormer: Efficient transformer for high-resolution image restoration. In Proceedings of the CVPR, New Orleans, LA, USA, 18–24 June 2022; pp. 5728–5739. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Y.; Gu, J.; Kong, L.; Yang, X.; Yu, F. Dual aggregation transformer for image super-resolution. In Proceedings of the ICCV, Paris, France, 2–6 October 2023; pp. 12278–12287. [Google Scholar] [CrossRef]
- Dong, J.; Pan, J.; Yang, Z.; Tang, J. Multi-scale residual low-pass filter network for image deblurring. In Proceedings of the ICCV, Paris, France, 2–6 October 2023; pp. 12311–12320. [Google Scholar] [CrossRef]
- Namuk, P.; Songkuk, K. How Do Vision Transformers Work? In Proceedings of the ICLR, Virtual, 25–29 April 2022. [Google Scholar] [CrossRef]
- Matsui, Y.; Ito, K.; Aramaki, Y.; Fujimoto, A.; Ogawa, T.; Yamasaki, T.; Aizawa, K. Sketch-based manga retrieval using manga109 dataset. Multimed. Tools Appl. 2017, 76, 21811–21838. [Google Scholar] [CrossRef]
- Shi, W.; Caballero, J.; Huszár, F.; Totz, J.; Aitken, A.P.; Bishop, R.; Rueckert, D.; Wang, Z. Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network. In Proceedings of the CVPR, Las Vegas, NV, USA, 27–30 June 2016; pp. 1874–1883. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.; Lee, K. Accurate image super-resolution using very deep convolutional networks. In Proceedings of the CVPR, Las Vegas, NV, USA, 27–30 June 2016; pp. 1646–1654. [Google Scholar] [CrossRef]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the CVPR, Honolulu, HI, USA, 21–26 July 2017; pp. 105–114. [Google Scholar] [CrossRef]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Chen, C.L. ESRGAN: Enhanced Super-Resolution Generative Adversarial Networks. In Proceedings of the ECCV, Munich, Germany, 8–14 September 2019; pp. 63–79. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the NeurIPS, Red Hook, NY, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. In Proceedings of the ICLR, Vienna, Austria, 3–7 May 2021. [Google Scholar] [CrossRef]
- Zhang, X.; Zeng, H.; Guo, S.; Zhang, L. Efficient long-range attention network for image super-resolution. In Proceedings of the ECCV, Tel Aviv, Israel, 23–27 October 2022; pp. 649–667. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Zhou, J.; Dong, C. Activating more pixels in image super-resolution transformer. In Proceedings of the CVPR, Vancouver, BC, Canada, 18–22 June 2023; pp. 22367–22377. [Google Scholar] [CrossRef]
- Hui, Z.; Gao, X.; Yang, Y.; Wang, X. Lightweight image super-resolution with information multi-distillation network. In Proceedings of the ACMM, Nice, France, 21–25 October 2019; pp. 2024–2032. [Google Scholar] [CrossRef]
- Luo, X.; Xie, Y.; Zhang, Y.; Qu, Y.; Li, C.; Fu, Y. Latticenet: Towards lightweight image super-resolution with lattice block. In Proceedings of the ECCV, Glasgow, UK, 23–28 August 2020; pp. 272–289. [Google Scholar] [CrossRef]
- Peng, C.; Shu, P.; Huang, X.; Fu, Z.; Li, X. LCRCA: Image super-resolution using lightweight concatenated residual channel attention networks. Appl. Intell. 2022, 52, 10045–10059. [Google Scholar] [CrossRef]
- Sun, L.; Pan, J.; Tang, J. Shufflemixer: An efficient convnet for image super-resolution. In Proceedings of the NeurIPS, New Orleans, LA, USA, 28 November–9 December 2022; pp. 17314–17326. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Y.; Chen, X.; Cai, H.; Gu, J.; Qiao, Y.; Dong, C. Blueprint separable residual network for efficient image super-resolution. In Proceedings of the CVPRW, New Orleans, LA, USA, 19–20 June 2022; pp. 833–843. [Google Scholar] [CrossRef]
- Fang, J.; Lin, H.; Chen, X.; Zeng, K. A hybrid network of cnn and transformer for lightweight image super-resolution. In Proceedings of the CVPRW, New Orleans, LA, USA, 19–20 June 2022; pp. 1102–1111. [Google Scholar] [CrossRef]
- Tian, C.; Zhang, X.; Wang, T.; Zhang, Y.; Zhu, Q.; Chia-Wen, L. A Heterogeneous Dynamic Convolutional Neural Network for Image Super-resolution. Image Video Process. 2024. [Google Scholar] [CrossRef]
- Zheng, M.; Sun, L.; Dong, J.; Jinshan, P. SMFANet: A Lightweight Self-Modulation Feature Aggregation Network for Efficient Image Super-Resolution. In Proceedings of the ECCV, Milan, Italy, 29 September–4 October 2025; pp. 359–375. [Google Scholar] [CrossRef]
- Hendrycks, D.; Gimpel, K. Gaussian error linear units (gelus). arXiv 2016, arXiv:1606.08415. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the CVPR, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Bevilacqua, M.; Roumy, A.; Guillemot, C.; Morel, M.l.A. Low-Complexity Single Image Super-Resolution Based on Nonnegative Neighbor Embedding. In Proceedings of the BMVC, Surrey, UK, 3–7 September 2012; pp. 1–10. [Google Scholar] [CrossRef]
- Zeyde, R.; Elad, M.; Protter, M. On Single Image Scale-Up Using Sparse-Representations. In Proceedings of the Curves and Surfaces, Avignon, France, 24–30 June 2010; pp. 711–730. [Google Scholar] [CrossRef]
- Arbeláez, P.; Maire, M.; Fowlkes, C.; Malik, J. Contour Detection and Hierarchical Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 898–916. [Google Scholar] [CrossRef]
- Huang, J.; Singh, A.; Ahuja, N. Single image super-resolution from transformed self-exemplars. In Proceedings of the CVPR, Boston, MA, USA, 7–12 June 2015; pp. 5197–5206. [Google Scholar] [CrossRef]
- Korhonen, J.; You, J. Peak signal-to-noise ratio revisited: Is simple beautiful? In Proceedings of the QoMEX, Melbourne, Australia, 5–7 July 2012; pp. 37–38. [Google Scholar] [CrossRef]
- Zhou, W.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the ICLR, San Diego, CA, USA, 7–9 May 2015. [Google Scholar] [CrossRef]
- Loshchilov, I.; Hutter, F. Sgdr: Stochastic gradient descent with warm restarts. In Proceedings of the ICLR, Toulon, France, 24–26 April 2017. [Google Scholar] [CrossRef]
- Zhao, H.; Kong, X.; He, J.; Qiao, Y.; Dong, C. Efficient image super-resolution using pixel attention. In Proceedings of the ECCVW, Glasgow, UK, 23–28 August 2020; pp. 56–72. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Zhang, L. Deep Plug-and-Play Super-Resolution for Arbitrary Blur Kernels. In Proceedings of the CVPR, Long Beach, CA, USA, 15–20 June 2019; pp. 1671–1681. [Google Scholar] [CrossRef]
- Gao, G.; Li, W.; Li, J.; Wu, F.; Lu, H.; Yu, Y. Feature distillation interaction weighting network for lightweight image super-resolution. In Proceedings of the AAAI, Virtual, 22 February–1 March 2022; pp. 661–669. [Google Scholar] [CrossRef]
- Li, F.; Cong, R.; Wu, J.; Bai, H.; Wang, M.; Zhao, Y. SRConvNet: A Transformer-Style ConvNet for Lightweight Image Super-Resolution. Int. J. Comput. Vis. 2025, 133, 173–189. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Y.; Gu, J.; Kong, L.; Yang, X. Recursive Generalization Transformer for Image Super-Resolution. In Proceedings of the ICLR, Vienna, Austria, 7–11 May 2024. [Google Scholar] [CrossRef]
- Gu, J.; Dong, C. Interpreting super-resolution networks with local attribution maps. In Proceedings of the CVPR, Nashville, TN, USA, 19–25 June 2021; pp. 9195–9204. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).