A Fast Algorithm for Boundary Point Extraction of Planar Building Components from Point Clouds
Abstract
1. Introduction
2. Related Work
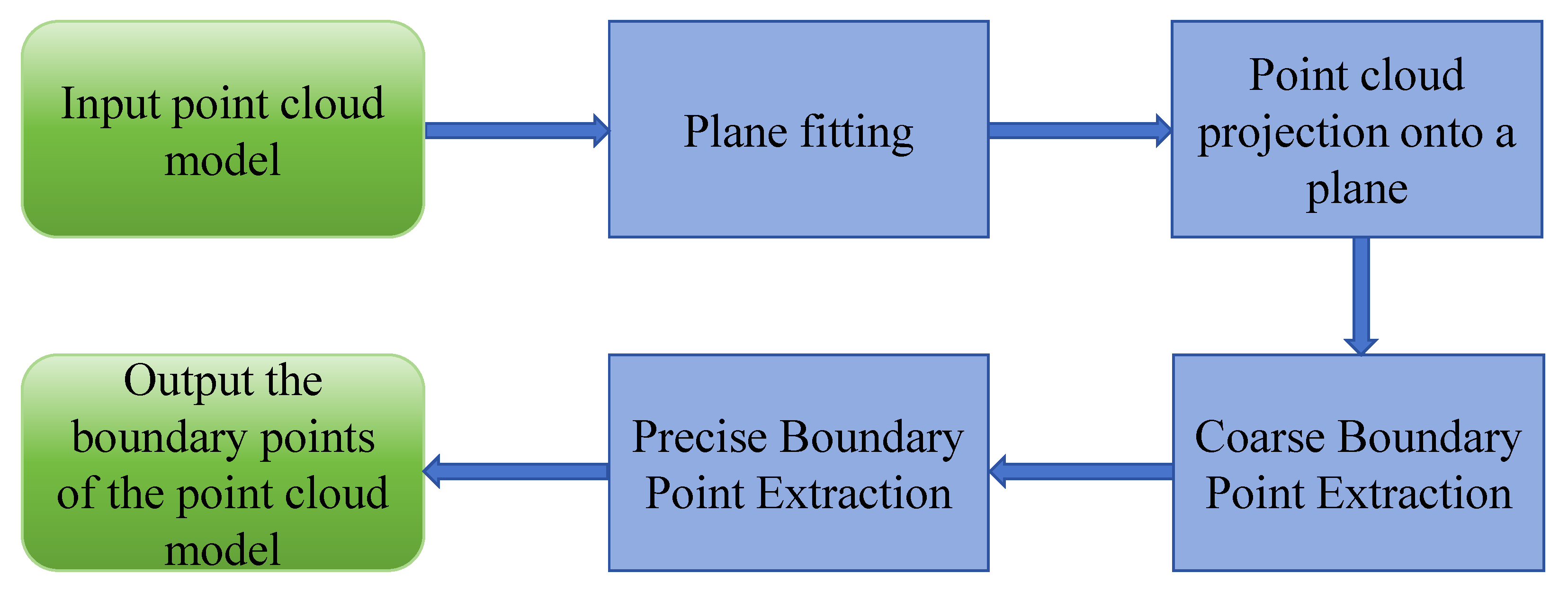
3. Boundary Point Extraction Algorithm
3.1. Point Cloud Plane Fitting and Projection
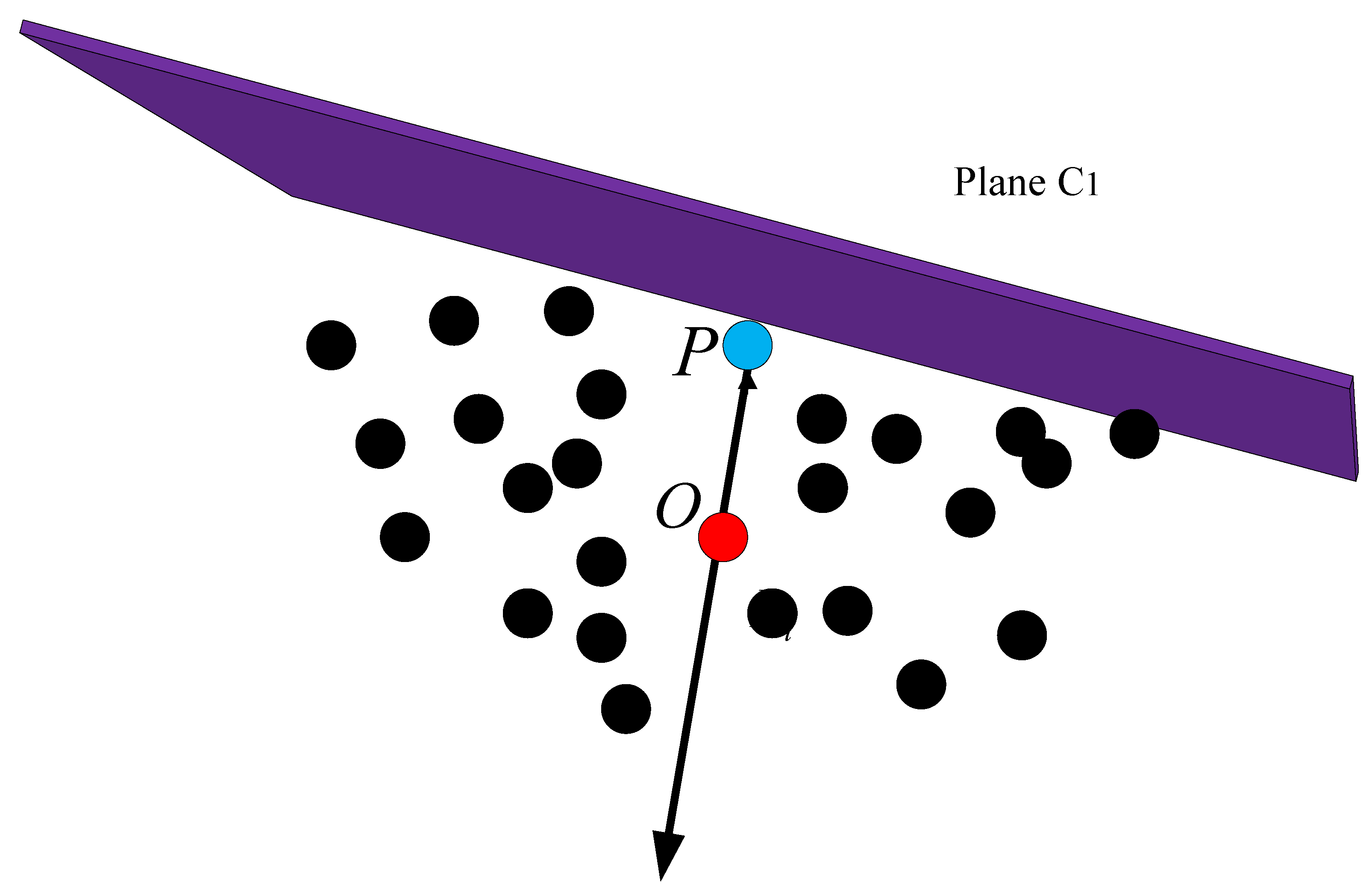
3.2. Extraction of Coarse Boundary Points
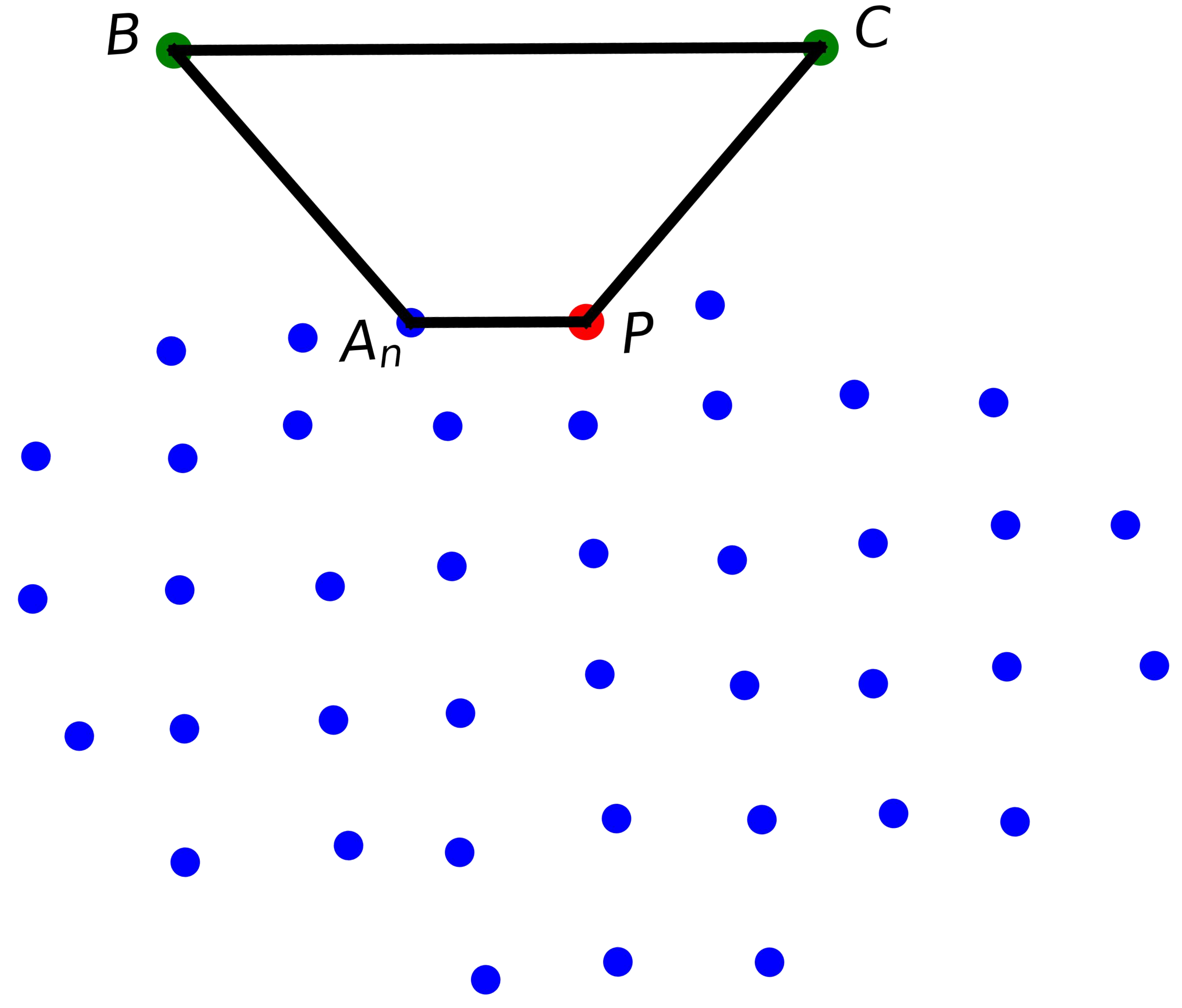
3.3. Extraction of Precise Boundary Points
4. Experimental Results and Analysis
4.1. Experimental Results
4.2. Accuracy Analysis of Boundary Point Extraction
4.3. Noise Resistance Analysis
4.4. Efficiency Analysis of Boundary Point Extraction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, X.; An, Q.; Zhao, B.; Tao, W.; Lu, T.; Zhang, H.; Han, X.; Ozdemir, E. Contour Extraction of UAV Point Cloud Based on Neighborhood Geometric Features of Multi-Level Growth Plane. Drones 2024, 8, 239. [Google Scholar] [CrossRef]
- Su, Z.; Peng, J.; Feng, D.; Li, S.; Yuan, Y.; Zhou, G. A Building Point Cloud Extraction Algorithm in Complex Scenes. Remote Sens. 2024, 16, 1934. [Google Scholar] [CrossRef]
- Awrangjeb, M. Using point cloud data to identify, trace, and regularize the outlines of buildings. Int. J. Remote Sens. 2016, 37, 551–579. [Google Scholar] [CrossRef]
- Zong, W.; Li, M.; Li, G.; Wang, L.; Wang, L.; Zhang, F. Toward efficient and complete line segment extraction for large-scale point clouds via plane segmentation and projection. IEEE Sens. J. 2023, 23, 7217–7232. [Google Scholar] [CrossRef]
- Ni, H.; Lin, X.; Ning, X.; Zhang, J. Edge detection and feature line tracing in 3D-point clouds by analyzing geometric properties of neighborhoods. Remote Sens. 2016, 8, 710. [Google Scholar] [CrossRef]
- Lu, Z.; Baek, S.; Lee, S. Robust 3D line extraction from stereo point clouds. In Proceedings of the 2008 IEEE Conference on Robotics, Automation and Mechatronics, Chengdu, China, 21–24 September 2008; pp. 1–5. [Google Scholar]
- Yang, B.; Wei, Z.; Li, Q.; Li, J. Semiautomated building facade footprint extraction from mobile LiDAR point clouds. IEEE Geosci. Remote Sens. Lett. 2012, 10, 766–770. [Google Scholar] [CrossRef]
- Lu, X.; Liu, Y.; Li, K. Fast 3D line segment detection from unorganized point cloud. arXiv 2019, arXiv:1901.02532. [Google Scholar] [CrossRef]
- Lei, P.; Chen, Z.; Tao, R.; Li, J.; Hao, Y. Boundary recognition of ship planar components from point clouds based on trimmed delaunay triangulation. Comput. Aided Des. 2025, 178, 103808. [Google Scholar] [CrossRef]
- Yang, B.; Wei, Z.; Li, Q.; Li, J. Automated extraction of street-scene objects from mobile lidar point clouds. Int. J. Remote Sens. 2012, 33, 5839–5861. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, C.; Yang, B.; Wang, Z.; Ma, R.; Wu, W.; Sun, W. Geometric feature enhanced line segment extraction from large-scale point clouds with hierarchical topological optimization. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102858. [Google Scholar] [CrossRef]
- Sampath, A.; Shan, J. Building boundary tracing and regularization from airborne LiDAR point clouds. Photogramm. Eng. Remote Sens. 2007, 73, 805–812. [Google Scholar] [CrossRef]
- Pu, S.; Vosselman, G. Knowledge based reconstruction of building models from terrestrial laser scanning data. ISPRS J. Photogramm. Remote Sens. 2009, 64, 575–584. [Google Scholar] [CrossRef]
- Boulaassal, H.; Landes, T.; Grussenmeyer, P. Automatic extraction of planar clusters and their contours on building façades recorded by terrestrial laser scanner. Int. J. Archit. Comput. 2009, 7, 1–20. [Google Scholar] [CrossRef]
- Hackel, T.; Wegner, J.D.; Schindler, K. Contour detection in unstructured 3D point clouds. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1610–1618. [Google Scholar]
- Liu, K.; Ma, H.; Zhang, L.; Gao, L.; Xiang, S.; Chen, D.; Miao, Q. Building outline extraction using adaptive tracing alpha shapes and contextual topological optimization from airborne LiDAR. Autom. Constr. 2024, 160, 105321. [Google Scholar] [CrossRef]
- Lin, Y.; Wang, C.; Chen, B.; Zai, D.; Li, J. Facet segmentation-based line segment extraction for large-scale point clouds. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4839–4854. [Google Scholar] [CrossRef]
- Tian, P.; Hua, X.; Tao, W.; Zhang, M. Robust Extraction of 3D Line Segment Features from Unorganized Building Point Clouds. Remote Sens. 2022, 14, 3279. [Google Scholar] [CrossRef]
- Bendels, G.H.; Schnabel, R.; Klein, R. Detecting Holes in Point Set Surfaces. J. WSCG 2006, 14, 89–96. [Google Scholar]
- Wei, J.; Wu, H.; Yue, H.; Jia, S.; Li, J.; Liu, C. Automatic extraction and reconstruction of a 3D wireframe of an indoor scene from semantic point clouds. Int. J. Digit. Earth 2023, 16, 3239–3267. [Google Scholar] [CrossRef]
- Dos Santos, R.C.; Pessoa, G.G.; Carrilho, A.C.; Galo, M. Automatic Building Boundary Extraction from Airborne LiDAR Data Robust to Density Variation. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Kirkpatrick, D.; Seidel, R. On the shape of a set of points in the plane. IEEE Trans. Inf. Theory 2003, 29, 551–559. [Google Scholar] [CrossRef]
- Liao, Z.; Liu, J.; Shi, G.; Meng, J. Grid partition variable step alpha shapes algorithm. Math. Probl. Eng. 2021, 2021, 9919003. [Google Scholar] [CrossRef]
- dos Santos, R.C.; Galo, M.; Carrilho, A.C. Extraction of building roof boundaries from LiDAR data using an adaptive alpha-shape algorithm. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1289–1293. [Google Scholar] [CrossRef]
- Chen, X.; Yu, K. Feature line generation and regularization from point clouds. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9779–9790. [Google Scholar] [CrossRef]
- Armeni, I.; Sener, O.; Zamir, A.R.; Jiang, H.; Brilakis, I.; Fischer, M.; Savarese, S. 3D semantic parsing of large-scale indoor spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 1534–1543. [Google Scholar]
- Liu, K.; Ma, H.; Zhang, L.; Liang, X.; Chen, D.; Liu, Y. Roof segmentation from airborne LiDAR using octree-based hybrid region growing and boundary neighborhood verification voting. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 2134–2146. [Google Scholar] [CrossRef]
- Awrangjeb, M.; Fraser, C.S. An automatic and threshold-free performance evaluation system for building extraction techniques from airborne LIDAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4184–4198. [Google Scholar] [CrossRef]
- Park, M.K.; Lee, S.J.; Lee, K.H. Multi-scale tensor voting for feature extraction from unstructured point clouds. Graph. Model. 2012, 74, 197–208. [Google Scholar] [CrossRef]
- Zhao, R.; Pang, M.; Zhang, Y. Robust shape extraction for automatically segmenting raw LiDAR data of outdoor scenes. Int. J. Remote Sens. 2018, 39, 9181–9205. [Google Scholar] [CrossRef]


| Model 1 | Model 2 | Model 3 | Model 4 | |
|---|---|---|---|---|
| (%) | 94.6% | 96.6% | 98.3% | 92.8% |
| (%) | 98.9% | 98.7% | 98.7% | 98.9% |
| Q(%) | 93.6% | 95.4% | 97.0% | 92.0% |
| Model 1 | Model 4 | |||||
|---|---|---|---|---|---|---|
| (%) | (%) | (%) | (%) | (%) | (%) | |
| AC | 86.9% | 100% | 86.9% | 85.6% | 99.8% | 85.5% |
| AS | 90.1% | 100% | 90.1% | 86.3% | 99.8% | 86.2% |
| Our | 94.6% | 98.9% | 93.6% | 92.8% | 98.9% | 92.0% |
| Zero Noise | 10% Gaussian Noise | 20% Gaussian Noise | |
|---|---|---|---|
| (%) | 95.1% | 94.8% | 93.1% |
| (%) | 100% | 99.1% | 95.6% |
| Q (%) | 95.1% | 94.0% | 89.3% |
| Model 1 | Model 2 | Model 3 | Model 4 | Total Time | |
|---|---|---|---|---|---|
| T (AC) | 1.054 | 1.632 | 1.413 | 3.083 | 7.182 |
| T (AS) | 1.835 | 3.068 | 2.415 | 5.668 | 12.986 |
| T (ours) | 0.476 | 0.689 | 0.646 | 1.045 | 2.856 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Chen, M.; He, G.; Liu, J. A Fast Algorithm for Boundary Point Extraction of Planar Building Components from Point Clouds. Electronics 2025, 14, 4313. https://doi.org/10.3390/electronics14214313
Huang Y, Chen M, He G, Liu J. A Fast Algorithm for Boundary Point Extraction of Planar Building Components from Point Clouds. Electronics. 2025; 14(21):4313. https://doi.org/10.3390/electronics14214313
Chicago/Turabian StyleHuang, Yongzhong, Ming Chen, Gaoming He, and Jianming Liu. 2025. "A Fast Algorithm for Boundary Point Extraction of Planar Building Components from Point Clouds" Electronics 14, no. 21: 4313. https://doi.org/10.3390/electronics14214313
APA StyleHuang, Y., Chen, M., He, G., & Liu, J. (2025). A Fast Algorithm for Boundary Point Extraction of Planar Building Components from Point Clouds. Electronics, 14(21), 4313. https://doi.org/10.3390/electronics14214313





