Real-Time Speed Measurement of Moving Objects with Continuous Wave Doppler Radar Using Software-Defined Radio: Implementation and Performance Analysis

Abstract

This paper presents a novel continuous-wave Doppler RADAR system for real-time speed measurement of moving objects, implemented using software-defined radio (SDR). Unlike traditional high-cost solutions typically found in research centers or specialized laboratories, this prototype offers a low-cost, compact, and easily deployable platform that lowers the entry barrier for experimentation and research. Operating within the 70 MHz–6 GHz range, SDR enables highly flexible signal processing; in this implementation, a 5.5 GHz carrier is selected to improve the detection precision by exploiting its reduced bandwidth for more accurate observation of frequency shifts. The carrier is modulated with a 2 kHz signal, and Doppler frequency deviations induced by object motion are processed to calculate velocity. Using a Welch spectral estimator, the system effectively reduces noise and extracts the Doppler frequency with high reliability. The prototype achieves speed measurements up to 196.36 km/h with approximately 2% error in the 0–100 km/h range, confirming its suitability for road traffic monitoring. A key innovation of this work is its single-antenna cross-polarized configuration, which simplifies hardware requirements while maintaining measurement accuracy. Furthermore, the system’s portability and open-access design make it ideal for in-vehicle applications, enabling direct deployment for automotive testing, driver-assistance research, and educational demonstrations. All design files and implementation details are openly shared, eliminating patent restrictions and encouraging adoption in low-resource academic and research environments.

1. Introduction

Nowadays, radio detection and ranging (RADAR) technology is widely used in diverse fields, including aircraft detection systems at airports, maritime object tracking, and highway speed enforcement, among others [1]. However, the high implementation cost of these systems often limits access to such technology. In recent years, the emergence of software-defined radio (SDR) technology has significantly simplified the development of radio frequency systems [2]. SDR dramatically reduces the system complexity, enabling deployment in environments lacking specialized infrastructure but requiring access to detection and measurement capabilities.

Motivated by these developments, this paper proposes a cost-effective RADAR prototype capable of real-time speed measurement of moving objects using the ADALM-Pluto SDR platform [3]. The prototype is based on a continuous-wave (CW) RADAR, which transmits a continuous signal while simultaneously receiving the echo reflected from moving targets. Depending on whether the object is stationary or in motion, the frequency of the echo signal remains unchanged or is shifted due to the Doppler effect [1]. The proposed CW RADAR can detect moving targets in a multi-target environment, enabling accurate speed and range estimation. Unlike traditional systems, which often require multiple antennas and complex synchronization, our design uses a single dual-polarization antenna, achieving compactness and portability while maintaining high accuracy [4,5].

The remainder of this paper is organized as follows. Section 2 reviews the related research. Section 3 describes the methodology for CW RADAR design. Section 4 presents the real-time CW Doppler implementation. Section 5 discusses the experimental results under various speed conditions. Finally, Section 6 summarizes the findings and outlines directions for future work.

2. Related Work

In radar technology, various approaches have been explored for object speed measurement and localization. We first provide an overview of the relevant prior work and then highlight the novelty of our approach. In [6], the authors employ three antennas to achieve short-range 3-D localization using CW Doppler RADAR, assuming the target path is orthogonal to the antenna’s pointing vector. Similarly, In ref. [7], the authors describes a commercial CW Doppler RADAR using two sensor modules to estimate relative object speed. In [8], a method for measuring multiple targets’ velocities based on CW Doppler RADAR is presented.

Moving beyond CW Doppler RADAR, pulsed Doppler RADAR has been used to address receiver saturation by separating transmission and reception time slots [9]. However, this comes at the expense of higher system complexity. Frequency-modulated continuous-wave (FMCW) RADAR systems, as demonstrated in [10,11,12], enable simultaneous range and speed estimation but require more sophisticated hardware and signal-processing algorithms [13,14].

In [15], a CW Doppler RADAR at 100 GHz is implemented using a low-IF dual-sideband architecture for mechanical vibration and vital-sign monitoring. In ref. [3], the authors proposed a CW Doppler RADAR based on SDR for offline speed measurement, achieving errors between 0.18 % and 6 %. Building on this work, our study introduces a real-time SDR-based RADAR system distinguished by its simplicity, consisting of a single SDR device, a dual-polarized antenna, and a standard laptop.

Receiver saturation is a well-known challenge in single-antenna CW RADAR systems [9]. Our implementation overcomes this issue by leveraging SDR technology, which facilitates precise signal conditioning, software-based filtering, and flexible debugging, thereby improving the detection performance. Furthermore, as noted in [16], the design of CW Doppler RADAR typically involves significant hardware complexity. In contrast, our approach integrates the necessary RF components into the SDR platform, allowing reconfiguration through software without additional hardware modifications.

Unlike prior studies [4,6,8,17] that require expensive and bulky instruments, our system minimizes hardware requirements and uses computationally efficient algorithms—such as the Welch spectral estimator and peak detection—to extract the Doppler frequency. Additionally, we reduce the system architecture from two antennas to one, resulting in a compact, portable, and cost-effective solution. In [18], the authors explore circularly polarized single-antenna configurations for short-range detection. In contrast, our prototype uses dual polarization and demonstrates that Doppler-induced peak power remains unaffected, achieving comparable accuracy while improving portability.

Software-defined radio (SDR) platforms have become a primary tool for rapid prototyping and experimental validation of automotive radar concepts due to their flexibility to modify waveforms, signal-processing chains, and real-time control without hardware redesign. Recent works demonstrate low-cost SDR + GNU Radio testbeds for Frequency-Modulated Continuous-Wave (FMCW) and alternative waveform families (e.g., PMCW, OFDM) enabling over-the-air hardware-in-the-loop (HWIL) experiments and waveform co-design for integrated sensing-and-communications (ISAC). These efforts show that SDR testbeds can evaluate practical issues such as timing/synchronization, waveform distortion, and real-time performance trade-offs before moving to dedicated RF hardware [19,20].

Joint radar–communication (JRC) and multi-function radar waveform research has used SDRs to implement digital baseband strategies and prototype full-stack JRC platforms. Implementations reported in 2023 demonstrate fully digital MIMO OFDM JRC platforms and real-time JRC experiments using commercially available SDRs (USRP family) and custom mmWave front-ends, illustrating SDRs’ role in validating multifunctional automotive sensing paradigms and exploring spectrum-sharing strategies [21].

Several 2024 studies emphasize real-time radar processing and classification on SDR platforms. For example, SDR implementations combined with GPU acceleration and efficient clustering/classification algorithms enable real-time radar signal classification and parameter extraction at high sampling rates—a capability relevant for in-vehicle processing and edge-AI deployment on automotive platforms. These works highlight processing-chain optimization (e.g., C++ implementations, parallel extraction of PDWs) required to meet real-time constraints on SDR testbeds [22].

The SDR research stream has also been used to study vulnerabilities, interference, and countermeasures in automotive radar. Notably, black-box physical-layer attack frameworks and experimental demonstrations have used SDR prototypes to show spoofing, false-object injection, and other threats against mmWave FMCW automotive radars—underscoring the importance of security testing on reconfigurable SDR platforms prior to field deployment. Parallel work addresses mutual interference mitigation (e.g., PMCW waveform design) and synchronization issues for netted SDR systems, which are both critical for dense automotive deployment scenarios [23,24].

Finally, the open-source ecosystem (GNU Radio, gr-plasma additions, USRP/Adalm-Pluto front-ends) has accelerated reproducible SDR radar research: multiple conference contributions (GRCon, RadarConf, EuRAD) and community modules now provide reusable blocks for FMCW/PMCW generation, real-time processing, and support for newer SDR front-ends—enabling researchers to iterate quickly on automotive radar algorithms and evaluate system-level tradeoffs such as range/velocity resolution, angular processing, and real-time latency [19,20].

3. Methodology for CW Doppler RADAR

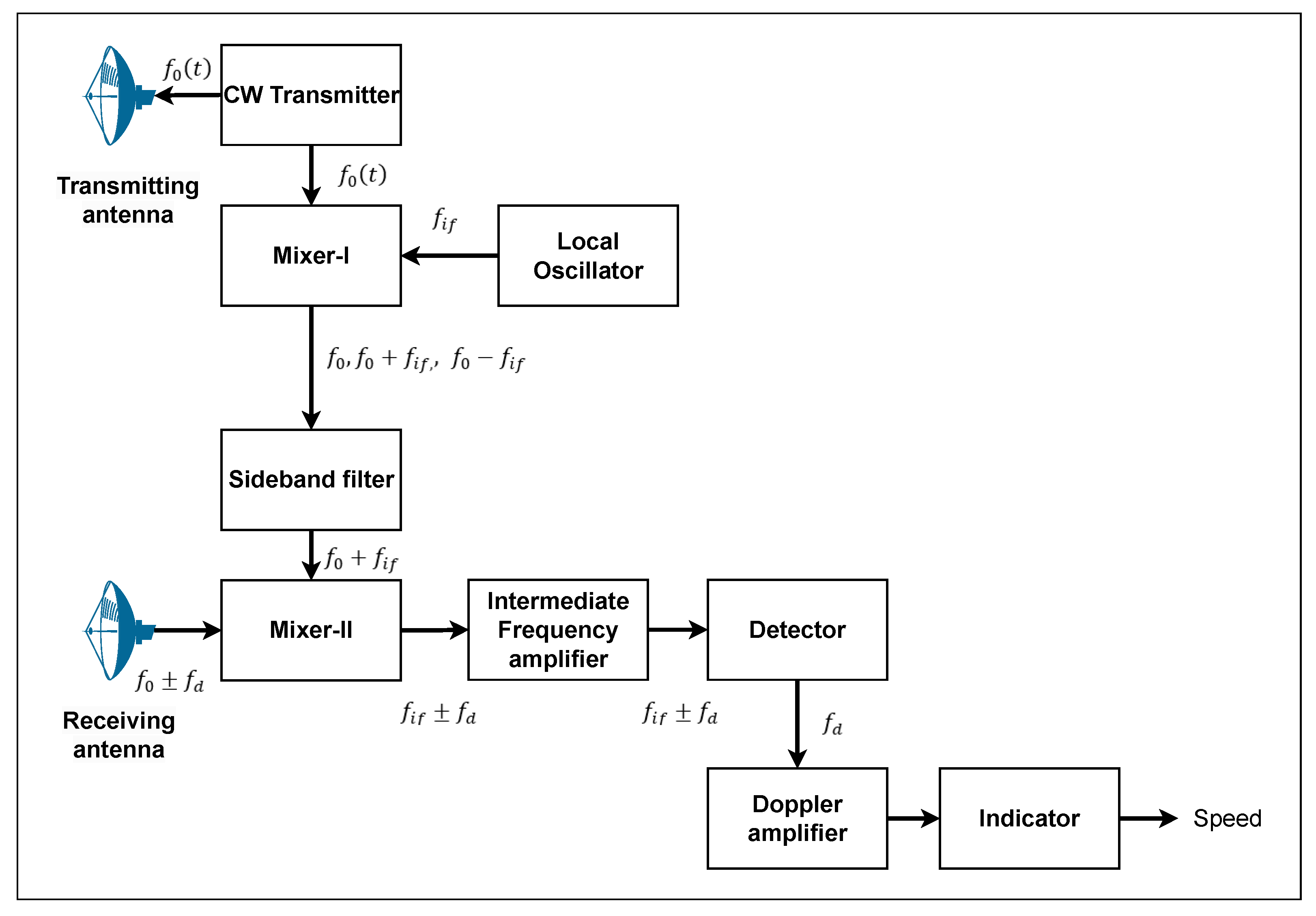
To implement the CW Doppler RADAR design using SDR, as shown in Figure 1, we first analyze the block diagram of a conventional CW RADAR system. This analysis not only guides the replication of each functional stage but also enables us to simplify and optimize the design for SDR implementation, reducing the hardware complexity and enhancing the portability. Each stage is carefully mapped to the corresponding hardware and software elements, resulting in a compact, reconfigurable, and cost-effective prototype.

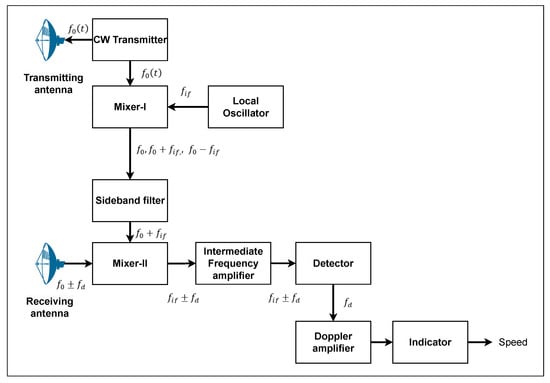
Figure 1. Block diagram RADAR CW doppler [17].

3.1. Operating Principle RADAR CW Doppler

The Doppler RADAR system comprises multiple stages that work together to detect the relative speed of a moving object. The CW transmitter generates a stable analog signal at a fixed frequency $f_0$. This signal is simultaneously routed to both the transmitting antenna and a mixer-I. A local oscillator (LO) produces a separate signal at a frequency $f_{if}$, which is also fed into Mixer-I. Mixer-I performs frequency translation by outputting the sum and difference of the input signals, resulting in three components: $f_0, f_0+f_{if}$, and $f_0-f_{if}$. A sideband filter isolates the desired signal, allowing only the upper sideband frequency $f_0+f_{if}$ to pass through. This filtered signal is then used as a reference for the second mixing stage.

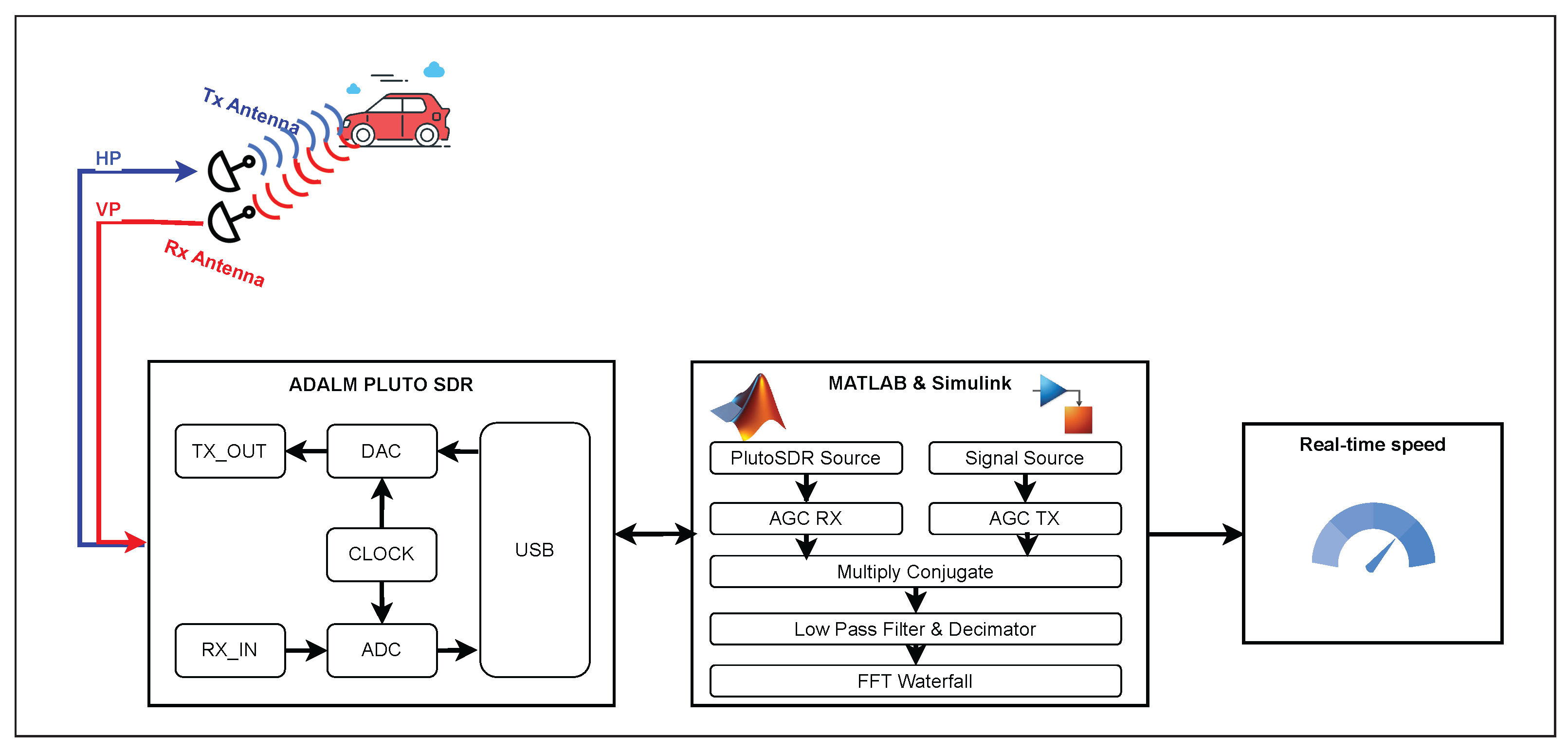
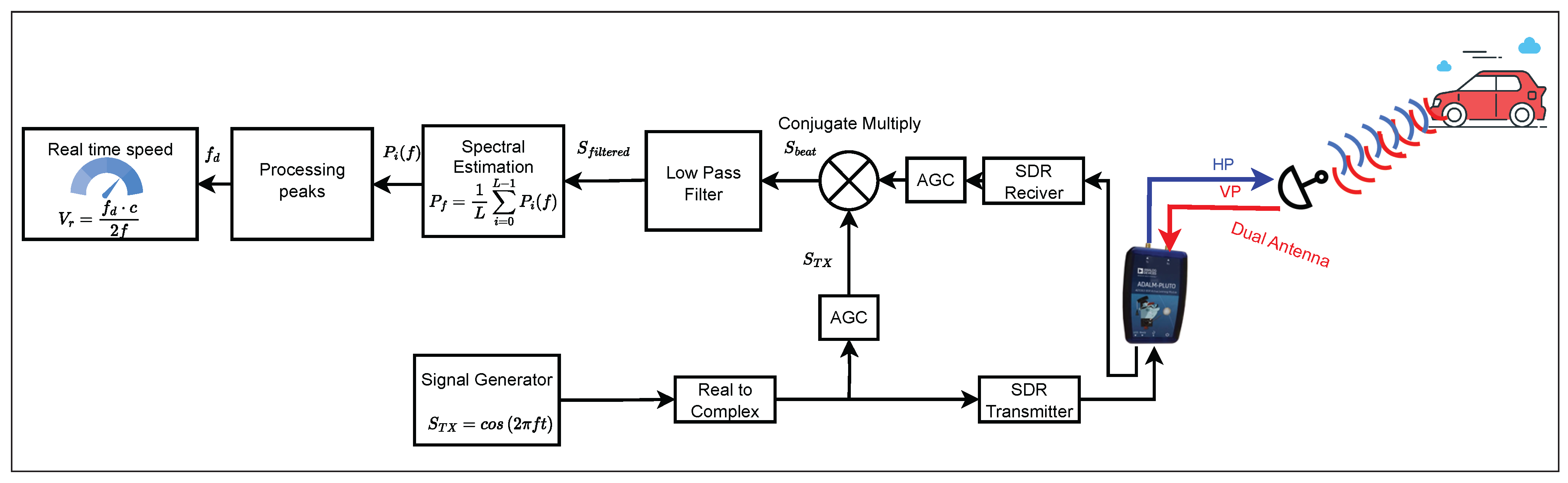
Mixer-II receives signals at $f_0+f_{if}$ or $f_0\pm f_d$, where $f_d$ represents the Doppler frequency change caused by a moving target. The output of Mixer-II includes new frequency components at $f_{if}\pm f_d$. These are passed through an IF amplifier, which selectively amplifies only the desired frequencies, enhancing the Doppler-shifted signal for further processing. The detector stage then extracts the Doppler frequency $f_d$, which is directly related to the relative speed of the target. The Doppler amplifier further amplifies this signal to ensure clarity and readability. Finally, the processed signal reaches the indicator stage, which displays whether the target is approaching or receding, along with its estimated speed. In the prototype presented in this paper, the oscillator modules and the mixers are programmed within the SDR, and the acquisition or processing of the Doppler frequency is carried out using Matlab and Simulink, as shown in Figure 2.

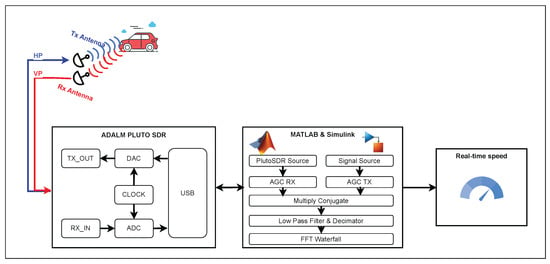
Figure 2. Radar flow diagram with SDR.

3.2. Materials

To implement the CW Doppler RADAR, the operating frequency was set to 5.5 GHz to match the operating range of the external Altelix AD5G23M2-2PK antennas. The SDR was configured with minimum attenuation and maximum gain settings to maximize the amount of data acquired. Although the experiments were conducted at 5.5 GHz, it is recommended to operate at 5.8 GHz in future implementations, as this frequency lies within an unlicensed ISM band, thereby avoiding potential regulatory constraints and simplifying system deployment. Table 1 summarizes the parameters of the SDR and antennas used in this work.

Table 1. SDR, antennas, and PC specifications.

Equipment	Description	Range
Adalm Pluto SDR	Operation Frequency	70–6000 MHz
	Channel Bandwidth	200 kHz–20 MHz
	Tx Power Output	7 dBm
	Rx and Tx Modulation Accuracy	−34 dB (2%)
	ADC and DAC Sample Rate	65.2 kSPS to 61.44 MSPS
	ADC and DAC Resolution	12 bits
	Frequency Accuracy	±25 ppm
	Rx Noise Figure	<3.5 dB
	Core	Single ARM Cortex®-A9
		@ 667 MHz
Altelix antennas	Operation Frequency	4900–6400 MHz
ad5g23m2-2pk	Bandwidth	1500 MHz
	Gain	30 $d{B}_i$
	VSWR	<1.6:1
	Vertical Beamwidth	5.5 Degrees
	Horizontal Beamwidth	5.5 Degrees
	Polarization	Dual Linear
	ETSI Specification	EN 302 326 DN2
PC Laptop	Processor	11th Gen Intel(R)
		Core(TM)i7-1165G7
		@ 2.80 GHz, 1.69 GHz
	RAM	16 GB

The next step for implementing the CW RADAR is configuring the equipment with the parameters of carrier frequency, continuous signal type, sampling time, and bandwidth. Table 2 shows the specifications for the CW RADAR. The software platform used to process data in real-time is Matlab and Simulink.

Table 2. Design specifications for CW Doppler RADAR.

Parameter	Specification
Sampling rate	2 Mbps
Signal frequency	2 kHz
Samples per frame	16,384
Type of wave	Cosine
Carrier frequency	5.5 GHz
Intermediate frequency	2 kHz

4. Implementation of Real-Time CW Doppler RADAR

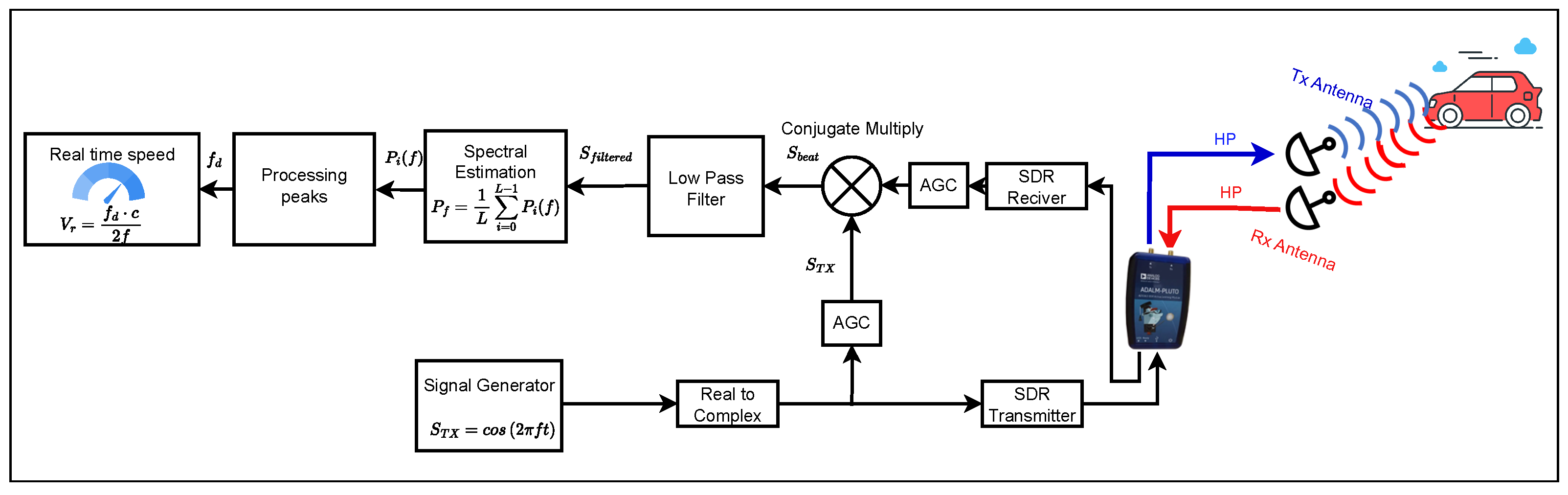
The real-time CW Doppler RADAR diagram implemented is shown in Figure 3; its blocks are described below. In the proposed prototype, the hardware is concentrated in the SDR and sends the signals to the antenna; the return signal is processed in the SDR and then processed by the Simulink computer program. An automatic gain control (AGC) adjusts the gain for the conjugate multiplication process to obtain the baseband signal, which is then filtered to avoid components more significant than 2 kHz. Spectral estimation by the Welch method allows us to improve the processed signal. Peak detection discriminates between the values of stationary and mobile objects to process these detected peaks and transform them into speed.

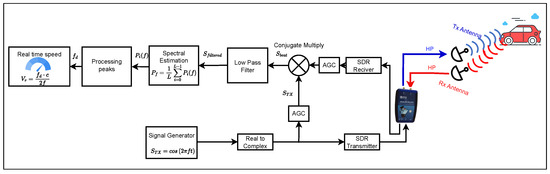
Figure 3. SDR-based real-time CW Doppler RADAR diagram.

4.1. Signal Generator

The transmission and reception blocks of the Adalm-Pluto platform are configured in Simulink. The continuous signal used is a cosine wave at 2 kHz using the signal generator, as shown in Equation (1). By adjusting the frequency to 2 kHz, we can obtain a maximum deviation in the Doppler frequency equivalent to a range of 0 to 196.86 km/h, which is theoretically sufficient to measure vehicle speeds up to this limit. However, due to road safety considerations and current traffic regulations, it was not possible to experimentally validate speeds above 100 km/h, which is the maximum legal speed limit on public roads in our country.

$$S_{TX}=cos\left(2\pi ft\right)$$

(1)

4.2. Transformation to Complex Signal

A binary phase shift modulation block (BPSK) transforms the real signal into a complex signal. The complex signal is then modulated with the 5.5 GHz carrier frequency to transmit the signal $f_t=f_c+2\mathrm{kHz}$. The SDR requires a complex signal as input; so, the modulation above is performed.

4.3. Sending the Signal to the Moving Object

The modulated signal is transmitted by the Altelix antenna, whose operating range is from 4.9 to 6.4 GHz. Stationary objects that the signal encounters in its path cause this wave to be reflected, and a portion of it returns to the CW Doppler RADAR [3,25,26].

4.4. Acquisition of the Signal Reflected on the Moving Object, Including the Doppler Effect

The received signal, which includes the Doppler effect due to the bounce of the wave transmitted on the mobile object, enters the SDR, and a demodulation process is performed by conjugate multiplication. Before this operation, the AGCs ensure that the transmitted and received signals are at equal amplitude levels. Equation (5) indicates two components, one at high frequency and one at low frequency, containing the Doppler frequency information plus the noise input $N\left(t\right)$. To obtain the value of such a Doppler frequency, it is necessary to use a low-pass filter [17,27].

$$S_{beat}=S_{Rx}·S_{Tx}+N\left(t\right)$$

(2)

$$S_{beat}=cos\left(2\pi \left(f\pm f_d\right)t\right)+cos\left(2\pi ft\right)+N\left(t\right)$$

(3)

$$S_{beat}={\displaystyle \frac{1}{2}}[cos\left(2\pi \left(f\pm f_d+f\right)t\right)+cos\left(2\pi \left(f\pm f_d-f\right)t\right)]+N\left(t\right)$$

(4)

$$S_{beat}={\displaystyle \frac{1}{2}}[cos\left(2\pi \left(2f\pm f_d\right)t\right)+cos\left(2\pi \left(\pm f_d\right)t\right)]+N\left(t\right)$$

(5)

$S_{beat}$ appears when two waves with slightly different frequencies interfere; the resulting wave is called a beat.

4.5. Spectral Estimation of the Filtered Signal Including the Doppler Effect

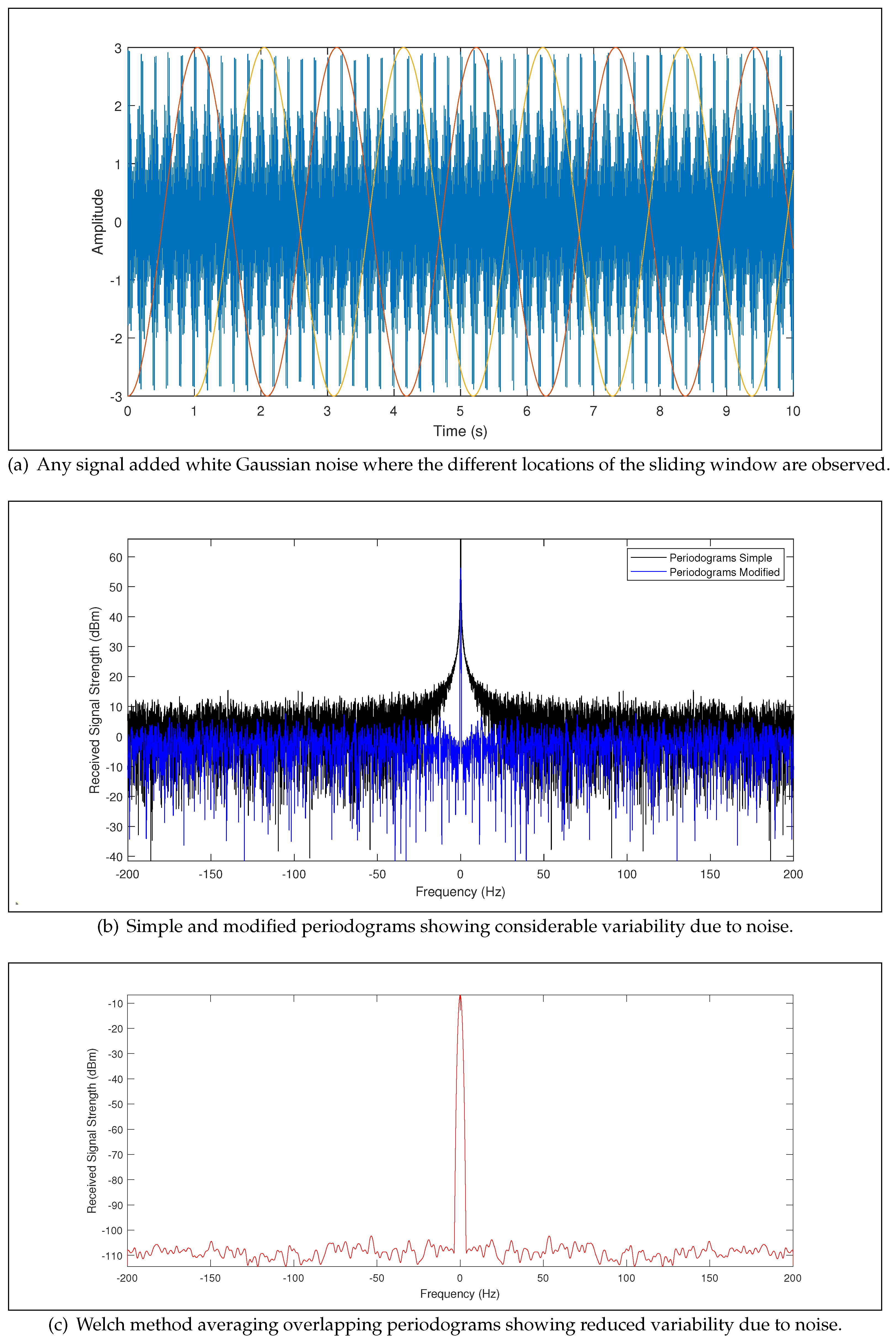
To detect the component due to the Doppler effect more efficiently, it is necessary to reduce the impact of noise. Therefore, the Welch spectral estimation technique was used, which is summarized in the following steps: (i) divide the signal into overlapping segments, (ii) apply a window function to each segment to reduce spectral leakage, (iii) compute the Fourier transform of each segment, and (iv) average the squared magnitudes of the Fourier transforms to obtain the spectral estimate. This technique helps to improve the signal-to-noise ratio and enhances the detection of the Doppler frequency component. The rest of the spectral estimation process is described as follows.

• Divide the signal into L segments using a sliding window, which is overlapped by 50%, as shown in Equation (6).

  $$S_{filtered}i\left[n\right]=S_{filtered}[n+iD],$$

  (6)

  where
  L: number of segments,
  i: 0, 1, …, $L-1$,
  M: the number of signal samples,
  n: 0, 1, …, $M-1$,
  D: sequence i start index number.
• Calculate the modified periodogram of each segment according to Equation (7).

  $$P_i\left(f\right)={\displaystyle \frac{1}{MU}}{\left({\displaystyle \sum _{n=0}^{M-1}}{S}_{filtered}i\left[n\right]·w\left[n\right]·e^{-j2\pi fn}\right)}^2,$$

  (7)

  where
  $S_{filtered}i\left[n\right]$: is the time signal from 0, 1, … to $L-1$,
  $w\left[n\right]$: sliding window,
  $U:{\displaystyle \frac{1}{M}}{\sum }_{n=0}^{M-1}{w}^2\left[n\right]$, normalization factor.
• Reduce noise variability by averaging periodograms of all L segments according to Equation (8) so that only the peak due to the Doppler effect stands out.

  $$P_f={\displaystyle \frac{1}{L}}{\displaystyle \sum _{i=0}^{L-1}}{P}_i\left(f\right)$$

  (8)

To observe the advantages of this method, consider a signal with added white Gaussian noise, as shown in Figure 4a. When using a simple or modified periodogram, as illustrated in Figure 4b, the spectral estimate exhibits high variability due to noise. If this were the received signal, such variability could hinder accurate Doppler peak detection. Welch’s method was therefore selected because it reduces the variance of the spectral estimate compared to the classical periodogram, which is critical for reliable Doppler peak detection under noisy conditions. In our implementation, a Hamming window of 1024 samples (NFFT segment length) with 50% overlap is applied to the signal. This configuration was chosen because it provides an optimal trade-off between spectral resolution and noise smoothing. The resulting partial spectra are computed and averaged, yielding the smoothed spectrum shown in Figure 4c, where noise-induced variability is significantly reduced, and the Doppler peak becomes easier to identify.

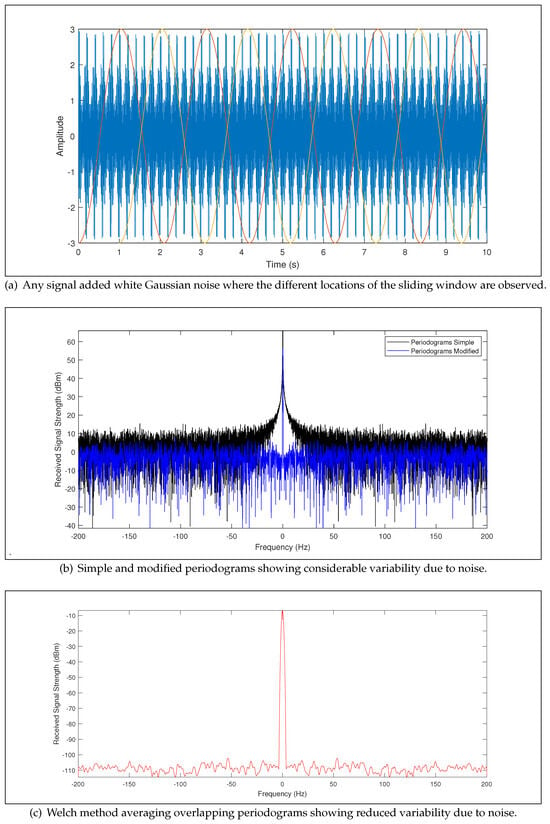
Figure 4. Welch method.

4.6. Determination of the Threshold for Eliminating Noise Peaks

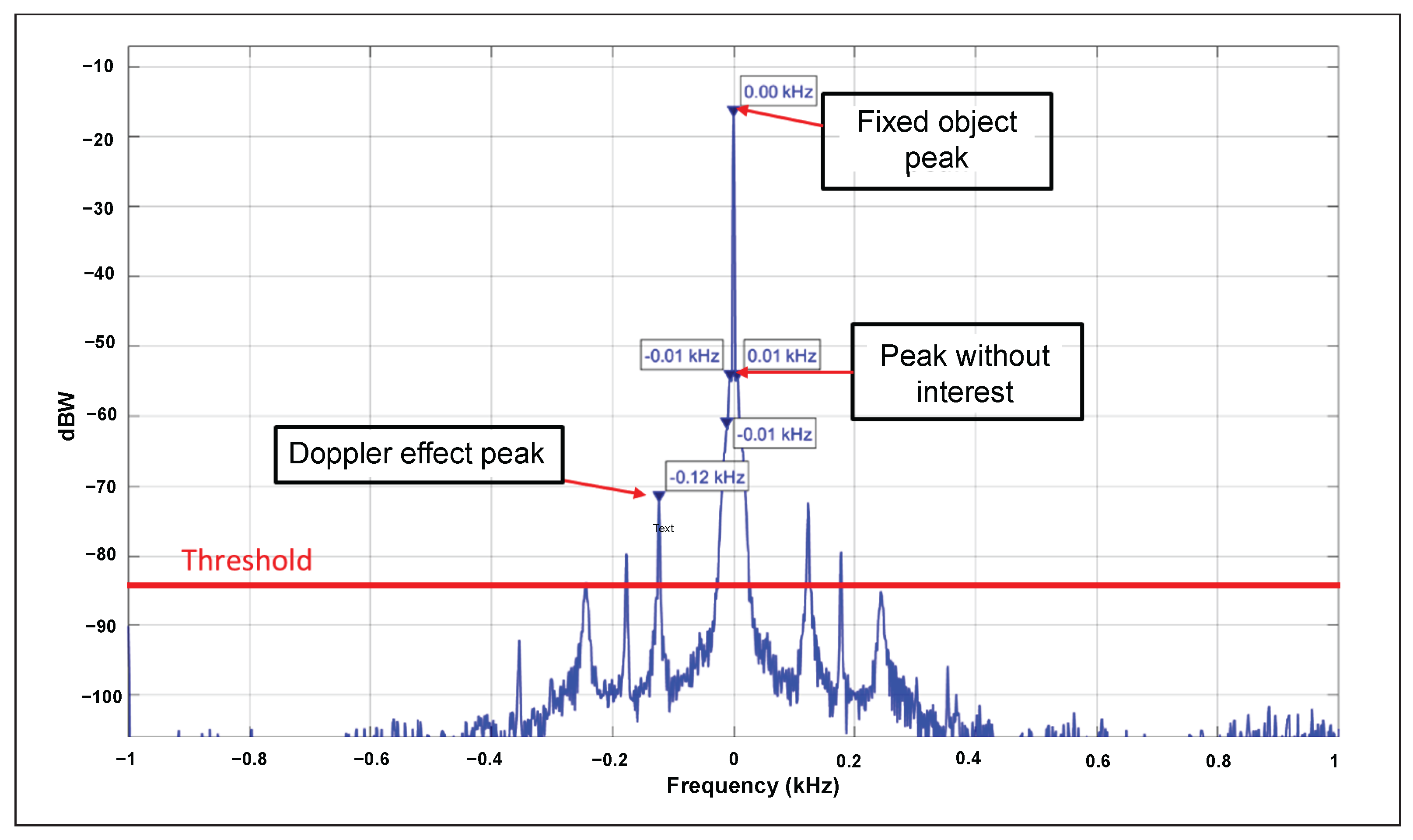
After reducing the noise effect in the previous stage, the noise level was analyzed for urban environments (between −90 and −110 dBW approximately) and rural environments (between −93 and −112 dBW approximately). As can be seen (Figure 5), there are no significant differences between these two scenarios; therefore, we proceeded to set a threshold at −85 dBW, a value established through field testing, where it was identified as the optimal threshold, whereby signals below this limit are discarded in later stages (Figure 5).

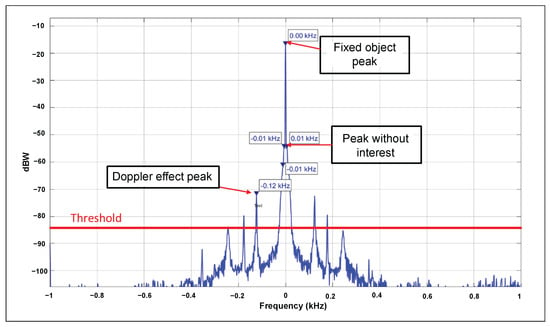
Figure 5. Power spectral density of the received signal, estimated by the Welch method, where the peak can be observed due to the Doppler effect.

4.7. Determination of the Peak Due to the Doppler Effect

As seen in Figure 5, the maximum peak is fixed at the frequency 0 Hz, which corresponds to stationary objects that produce a reflection of the transmitted signal. The second peaks are also fixed; so, they are discarded. The third peak, which moves, is due to the reflection of the transmitted signal on the moving object (Doppler effect), and it reaches its most significant distance from the central frequency. This is the point at which it must be captured to calculate the corresponding speed of the moving object.

4.8. Determining the Speed of the Moving Object in Real Time

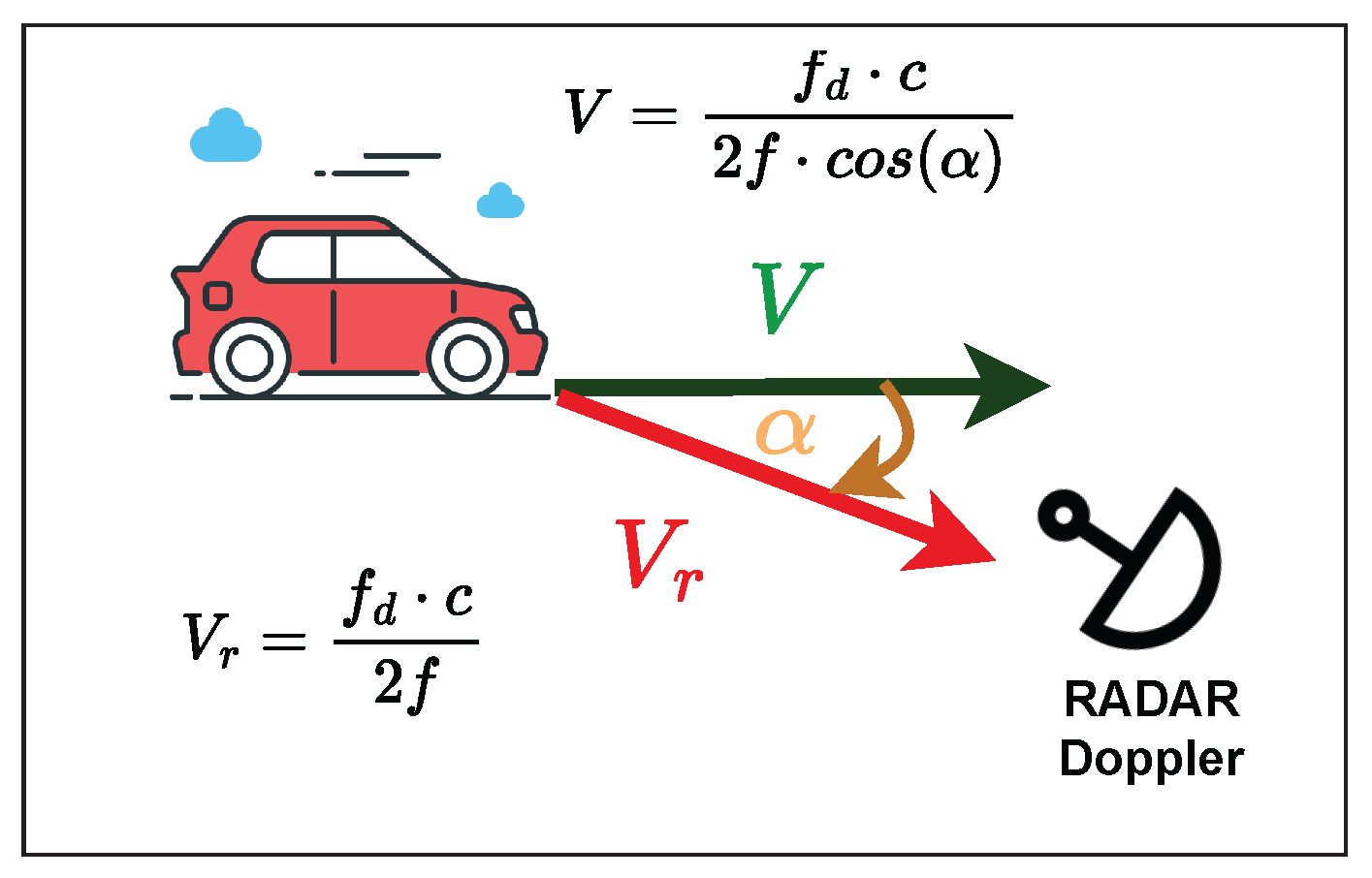
The speed $V_r$ is considered the speed of the moving object relative to the RADAR location, V is the speed in the direction of travel of the moving object, and $\alpha$ is the angle between the direction of propagation of electromagnetic waves and the direction of the speed of the target, as shown in Figure 6.

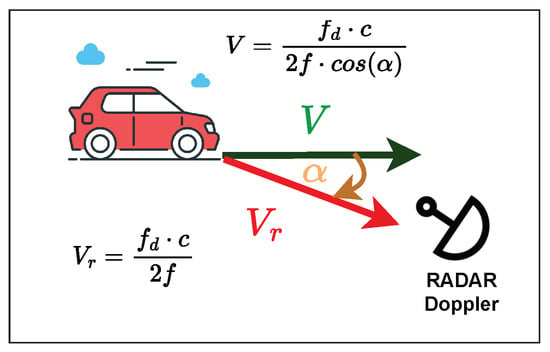
Figure 6. Variables involved in determining speed using a CW Doppler RADAR.

Equation (9) relates the previous velocities to the Doppler frequency $f_d$, where f is the carrier frequency (5.5 GHz), and c is the speed of light with a value of $3\times {10}^8$ m/s, which is the speed concerning RADAR.

$$V_r={\displaystyle \frac{f_d·c}{2f}}$$

(9)

We are interested in measuring the object’s speed relative to the road, for which we include the angle between the location of the radar and the road. In this way, Equation (10) relates this data and determines the object’s speed relative to the road.

$$V={\displaystyle \frac{f_d·c}{2f·cos\left(\alpha \right)}}$$

(10)

Once the implementation phase of the CW RADAR based on the Doppler effect using SDR and following the diagram in Figure 3 is completed, it can be easily transported to research sites due to its modular design, as shown in Figure 7.

Figure 7. CW Doppler RADAR implemented with an SDR, two antennas, and a computer for data processing.

4.9. Reduction to a Single Antenna

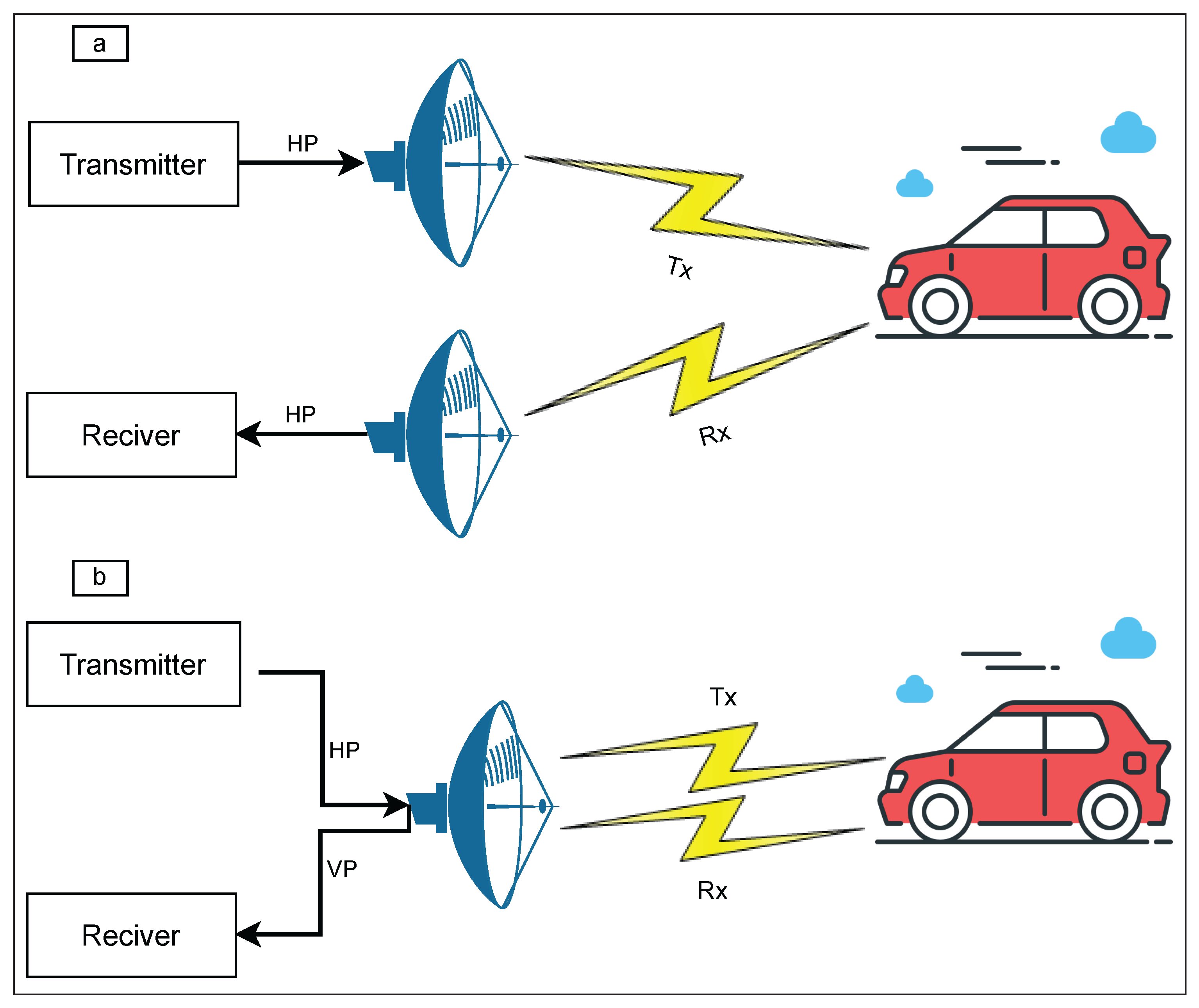
To reduce the complexity and optimize our system, we reduced two antennas to only one, transforming the bistatic RADAR into a monostatic one [28], as shown in Figure 8.

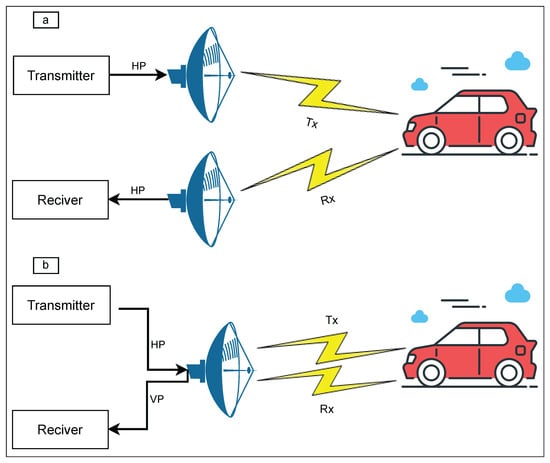
Figure 8. (a) Bistatic and (b) monostatic RADARs.

If a single antenna is used with two connectors, one with horizontal polarization and one with vertical polarization, it should be considered that the maximum polarization information is obtained when measuring the polarization scattering matrix S (PSM) of a target. Equation (11) describes the four components of PSM [17,27]. These terms $\sqrt{\sigma }{e}^{j\theta }$ are called echo backscatter coefficients, expressed as a vector quantity having magnitude and phase. The subscripts indicate polarization: 1 for horizontal polarization (HP) and 2 for vertical polarization (VP). Subscript 11 indicates the transmission and reception HP, index 22 indicates transmission and reception VP, index 21 indicates the transmission HP and reception VP, and finally, index 12 indicates the transmission VP and reception HP.

$$S=\left[\begin{array}{cc}\sqrt{{\sigma }_{11}}{e}^{j{\theta }_{11}}& \sqrt{{\sigma }_{12}}{e}^{j{\theta }_{12}}\\ \sqrt{{\sigma }_{21}}{e}^{j{\theta }_{21}}& \sqrt{{\sigma }_{22}}{e}^{j{\theta }_{22}}\end{array}\right]$$

(11)

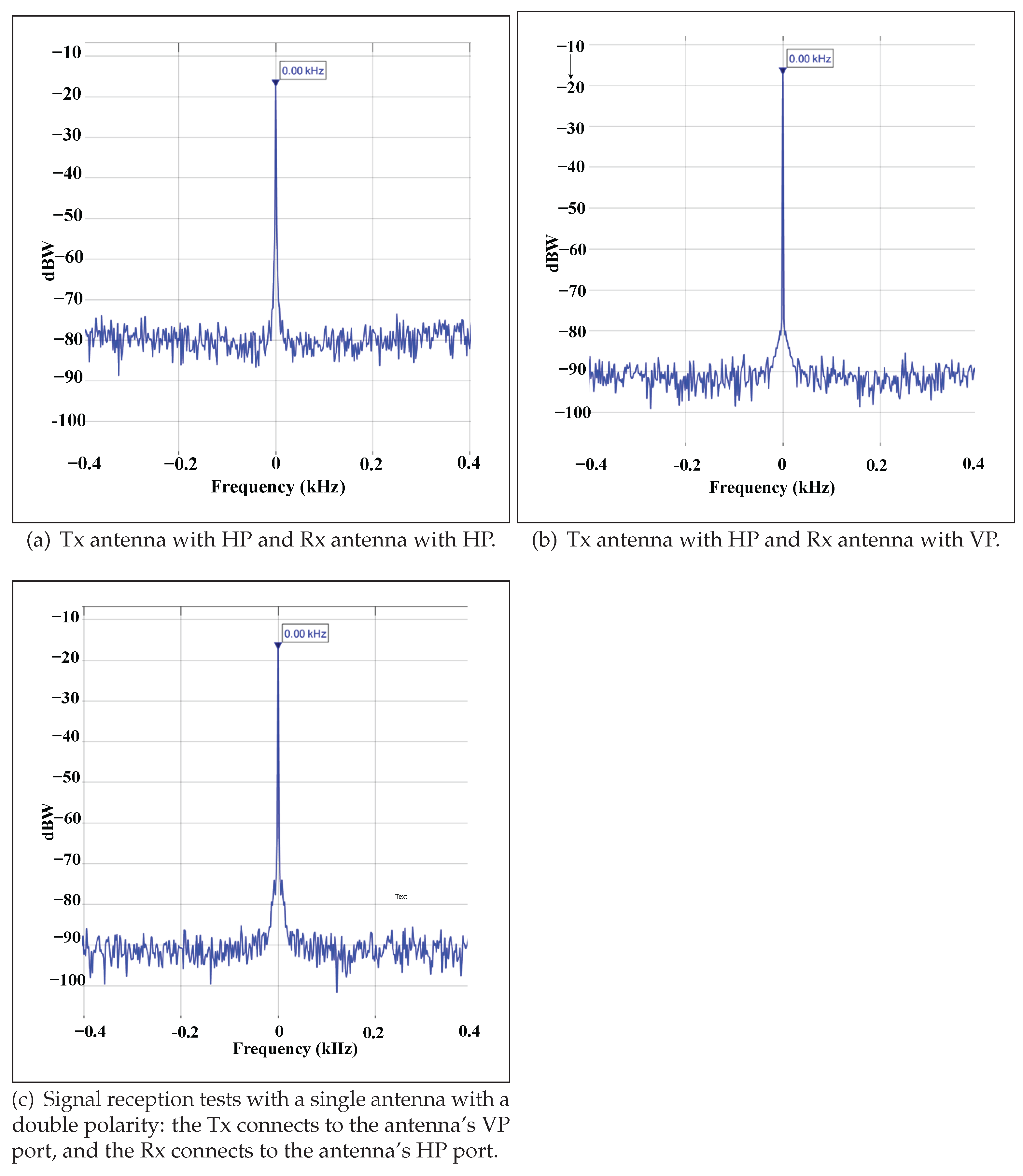
To analyze the effect of using a single antenna with two polarizations, two antennas (one for transmission and one for reception) were initially used as a reference during the experimental phases, both with horizontal polarization, obtaining the spectrum (Figure 9a). At the time of the change in the receiver antenna connector, from horizontal to vertical polarization, it was observed that the levels of received power remained unchanged (Figure 9b). This allowed us to infer that having a single antenna with dual polarization might be enough. Then, by replacing the two antennas with a single one, where the transmitter connects to the horizontal polarization terminal and the receiver to the vertical polarization connector, it was confirmed that the power levels remained similar to the two previous cases (Figure 9c), thus reducing the complexity of the system by using a single antenna as seen in Figure 10. Therefore, thanks to SDR-based technology and a single antenna, the complexity of a Doppler RADAR system used to measure the speed of an object in real time was significantly reduced compared to previously used systems.

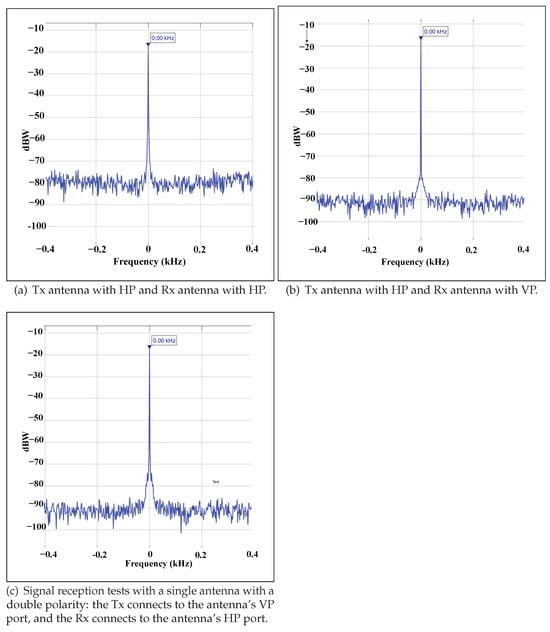
Figure 9. Signal reception tests with two antennas in different polarities.

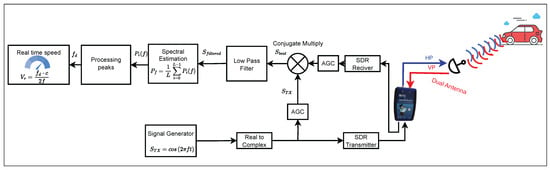
Figure 10. Block diagram of a Doppler RADAR system for measuring the speed of an object in real time, using SDR technology and a single antenna with double polarity.

The final aspect of the CW Doppler RADAR for real-time speed measurement, implemented with a single SDR, a dual-polarization antenna, and a computer, is shown in Figure 11. The use of a dual-polarization antenna is a key requirement that enables the system to operate with a single antenna for both transmission and reception, reducing the hardware complexity and improving the portability. During experimentation, no issues were observed related to cross-polarization interference or signal degradation, confirming the feasibility of this configuration. A dual-polarized antenna provides two independent polarization channels while sharing the same feed point and physical structure, maintaining performance equivalent to two. Furthermore, the ability to measure an object’s speed in real time allows tracking its evolution over time, enabling its use in multiple applications such as traffic monitoring, in-vehicle testing, and dynamic object tracking.

Figure 11. CW Doppler RADAR using SDR and a single antenna in real time.

4.10. Testing and Calibration Site

The testing and calibration of the prototype were carried out on a 500 m road located in a remote area to ensure equipment safety and allow testing at specific speeds, as shown in Figure 12. The system calibration focused on adjusting the frequency-to-speed conversion process implemented in Simulink, using as reference both the vehicle’s speedometer and a commercially available roadside radar.

Figure 12. Testing and calibration site.

The environmental conditions were not considered in the present work and are proposed as part of future research. During the initial tests performed to validate the prototype, no issues were observed related to signal reflections or refractions. Therefore, the system was subsequently validated under controlled test conditions, and the necessary data were collected to perform the analysis.

Unlike commercial roadside radar systems that directly display the measured speed, our prototype implements the underlying radar measurement concept but does not provide real-time speed visualization. This limitation is acknowledged in the manuscript, and future work will consider adding user-friendly visualization features to align more closely with commercial solutions.

5. Experimental and Simulation Results

The first step in acquiring results was determining the noise floor, which, as mentioned above, is at −85 dBW. Tests were performed in rural (outside the city) and urban (inside the town) environments to obtain this data.

5.1. Polarization Isolation

Tests conducted using either a single antenna or a two-antenna configuration showed no evident changes in the measured noise floor, confirming the stability of the system before data acquisition. The second step was determining the effect of using a bistatic or monostatic RADAR. In both cases, the data obtained did not present variations that should be considered significant. Therefore, an analysis was performed by configuring the CW RADAR in monostatic mode. These tests were carried out on a highway where the speeds of vehicles passing through the site were monitored. Although the experiments presented in this work were conducted under clear weather conditions, it is important to acknowledge the potential impact of environmental factors on radar performance. Rainfall, in particular, introduces attenuation of electromagnetic waves due to absorption and scattering. This effect becomes more pronounced at higher operating frequencies: moderate in the X-band (8–12 GHz) and significant in the K/Ka bands (24–77 GHz), often leading to reduced effective detection range. Since our prototype operates at 5.5 GHz, rain-induced attenuation is expected to be less critical; however, future work will explicitly validate the system under rainy conditions to ensure robustness in real-world deployment. Controlled environment tests with constant speeds were also conducted on straight paths, where speeds ranging from 0 to 100 km/h could be safely achieved. The following operating parameters were considered, as described in Table 3.

Table 3. Parameters of the RADAR CW Doppler.

Parameter	Specification
Carrier frequency	5.5 GHz
Speed of light	3$·{10}^8$ m/s
Type of wave	Cosine
Incidence angle $\alpha$	${30}^{\circ }$

Two antennas with identical polarization typically yield maximum received power, but they demand larger physical separation, precise alignment, and higher deployment costs. In contrast, a dual-polarized antenna provides orthogonal channels (horizontal/vertical), which significantly reduce the direct coupling from Tx to Rx and act as a natural filter against self-interference.

In our experiments, the backscattered signal from the target was received with the same power level under cross polarization, demonstrating that the change in polarization does not degrade the useful signal. Furthermore, the computed noise statistics (mean, variance, standard deviation, as well as maximum and minimum values) confirm the stability of the measurement and validate the effectiveness of using cross polarization in this setup, as shown in Table 4.

Table 4. Noise statistics in dual-polarized antenna.

#	Mean	Median	Variance	Std Deviation	Minimum	Maximum
	[dBW]	[dBW]	[dBW2]	[dBW]	[dBW]	[dBW]
1	−88.621	−87.76	30.413	5.5148	−120.55	−78.385
2	−88.663	−87.778	32.407	5.6927	−111.01	−77.725
3	−88.246	−87.393	27.392	5.2337	−118.16	−78.061
4	−88.839	−87.844	32.668	5.7156	−118.57	−76.937
5	−88.512	−87.704	30.835	5.5529	−122.41	−77.354
6	−88.593	−87.655	29.575	5.4383	−122.41	−75.499
7	−88.771	−88.041	29.839	5.4625	−118.73	−76.789
8	−88.748	−87.982	30.316	5.506	−122.23	−77.617
9	−88.802	−87.905	32.701	5.7185	−126.37	−76.833
10	−88.783	−87.813	30.645	5.5358	−120.07	−76.914
11	−88.733	−87.798	32.221	5.6763	−129.78	−77.511
12	−88.373	−87.54	30.002	5.4774	−121.53	−76.914
13	−88.473	−87.777	27.967	5.2884	−116.62	−75.456
14	−88.789	−87.713	34.253	5.8526	−120.62	−77.499
15	−88.601	−87.759	32.604	5.71	−134.15	−77.277
16	−88.55	−87.646	29.295	5.4125	−122.68	−77.747
17	−88.663	−87.757	32.168	5.6717	−124.25	−77.456
18	−88.774	−87.687	32.804	5.7275	−117	−76.371
19	−88.574	−87.554	30.479	5.5208	−124.48	−77.432
20	−88.47	−87.661	30.161	5.4919	−123.32	−77.291

5.2. Performance Analysis

The measured end-to-end latency of the prototype is below 100 ms, which is widely recognized as the threshold for real-time operation in communication and signal processing systems. This value includes both the processing time of the software-defined radio (SDR) and the computational delay introduced by the host CPU. Latencies under this level ensure that the system responds fast enough to be perceived as instantaneous and suitable for time-critical applications. Therefore, the obtained results validate that the proposed prototype operates in real time, as shown in Table 5.

Table 5. Latency measurements.

Metric	Measurement Method	Mean	Standard	Observation
	[timestamp]	[ms]	[ms]
$t_{acq}$ (capture frame)	SDR to host	6.5	1.2	USB3 + buffer
$t_{proc}$ (Welch + peak)	Host processing	23.7	4.5	CPU load avg = 42%
$t_{total}$	$t_{act}+t_{proc}$	32.5		Target < 100 ms

5.3. Statistical Analysis

In the analysis of physical or engineering systems, the results depend not only on the measured or modeled variables but also on the uncertainty associated with them. The propagation of uncertainty describes how the individual uncertainties of input variables affect the uncertainty of the output.

For a function $V=V(f,f_d,\theta )$ that depends on three variables, the combined uncertainty ${\sigma }_V$ Equation (12), can be approximated using an error propagation formula, using the partial derivatives present in Equation (13):

$${\sigma }_V=\sqrt{{\left({\displaystyle \frac{\partial V}{\partial f}}{\sigma }_f\right)}^2+{\left({\displaystyle \frac{\partial V}{\partial f_d}}{\sigma }_{f_d}\right)}^2+{\left({\displaystyle \frac{\partial V}{\partial \theta }}{\sigma }_{\theta }\right)}^2,}$$

(12)

where ${\sigma }_f$, ${\sigma }_{f_d}$, and ${\sigma }_{\theta }$ represent the uncertainties associated with f, $f_d$, and $\theta$, respectively. This approach allows quantifying how variations in each input parameter propagate through the model, providing insight into the reliability and sensitivity of the results.

$${\displaystyle \frac{\partial V}{\partial f}}=-{\displaystyle \frac{f_{d}c}{2f^{2}cos\alpha }},{\displaystyle \frac{\partial V}{\partial f_d}}={\displaystyle \frac{c}{2fcos\alpha }},{\displaystyle \frac{\partial V}{\partial \alpha }}={\displaystyle \frac{f_{d}csin\alpha }{2f{cos}^2\alpha }}$$

(13)

Incorporating uncertainty propagation enhances the rigor of the analysis and provides critical information for decision-making, experimental design, and process optimization.

At lower speeds, the absolute uncertainty decreases (e.g., ±0.30 km/h at 20 km/h). The trend is approximately linear: the uncertainty increases with the speed, since a higher $f_d$ amplifies the effects of ${\sigma }_{\alpha }$. This provides a strong argument for including Table 6 as extended validation and uncertainty analysis.

Table 6. Propagation uncertainty.

Speed	${\mathit{f}}_{\mathit{d}}$	Calculated Speed	Uncertainty
[km/h]	[Hz]	[km/h]	[± km/h]
20	176.34	19.99	0.3
40	352.69	39.98	0.46
60	529.03	59.98	0.65
80	705.58	79.99	0.84
100	881.82	99.97	1.03

5.4. Experimental Results

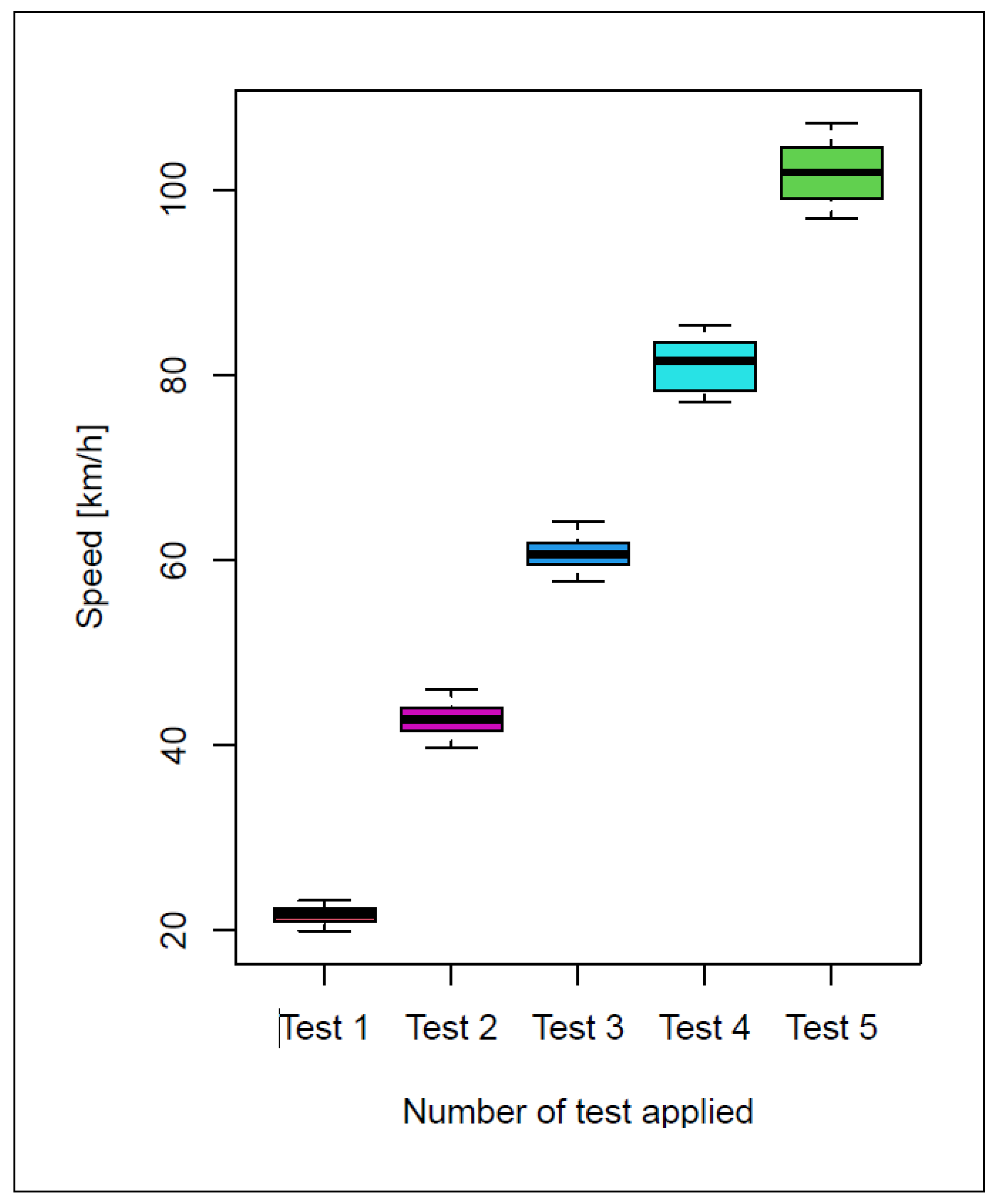
About 50 experiments were performed for each speed test (20, 40, 60, 80, 100 km/h). The data obtained from these experiments are represented by the box diagram presented in Figure 13. The operational parameters and object speed values, the theoretical value of the Doppler frequency, the actual value obtained by the proposed algorithm, and the error committed were processed and are shown in Table 7.

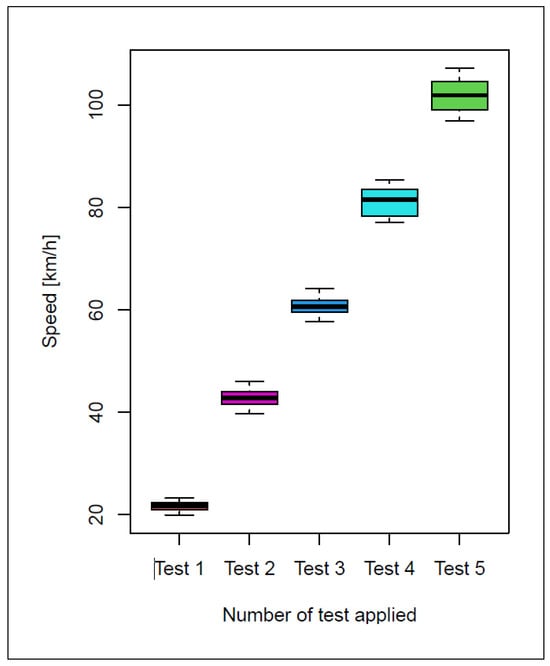
Figure 13. Boxplot test vs. speed.

Table 7. Real values, theoretical values, and those found with the proposed algorithm.

Speed	Theoretical Value	Acquired Value	Relative Error
[km/h]	[Hz]	[Hz]	[%]
20	176.34	180	2.1
40	352.69	360	2.08
60	529.03	540	2.03
80	705.58	720	2
100	881.82	900	2.02

A Student’s t-test was performed on the 50 speed measurements for each of the three test speeds (20, 40, 60, 80, and 100 km/h) obtained with the CW Doppler RADAR prototype, using RStudio V 2025.05.1 for statistical analysis. In all three cases, the resulting p-values were below or close to 0.05, indicating statistical significance at approximately the 95% confidence level. These results validate the accuracy and repeatability of the prototype across different speed conditions, confirming that the measured values are consistent and not due to random variation, as shown in Table 8.

Table 8. One-sample t-test.

Speed	t	p-Value	Confidence Interval	Mean
[km/h]			[km/h]	[km/h]
20	14.325	2.2 × ${10}^{-16}$	21.4254–21.8906	21.658
40	12.526	2.2 × ${10}^{-16}$	42.31385–43.19815	42.756
60	3.0214	0.003992	60.23335–61.16032	60.697
80	3.1184	0.003042	80.39414–81.822697	81.108
100	4.2683	8.993 × ${10}^{-5}$	101.0310–102.8657	101.948

In the following link: https://epnecuador-my.sharepoint.com/:v:/g/personal/luis_flores04_epn_edu_ec/EUlucyoZRcFFvbqM5zY2q-wB0rAm_k5J22dtjpnMwjcKcw?nav=eyJyZWZlcnJhbEluZm8iOnsicmVmZXJyYWxBcHAiOiJPbmVEcml2ZUZvckJ1c2luZXNzIiwicmVmZXJyYWxBcHBQbGF0Zm9ybSI6IldlYiIsInJlZmVycmFsTW9kZSI6InZpZXciLCJyZWZlcnJhbFZpZXciOiJNeUZpbGVzTGlua0NvcHkifX0&e=TbHRbc (accessed on 25 September 2025), we present a video that demonstrates the operation of the real-time device implemented in this research for measuring the speed of an object using CW Doppler RADAR with SDR.

5.5. Economic Analysis

In terms of the cost–benefit analysis, the implemented system demonstrates a clear advantage compared to commercial radar solutions. As summarized in Table 9, the total cost of the developed prototype is approximately USD 910, including all the components required for operation. This value contrasts strongly with commercial traffic radars, whose prices can easily exceed USD 7500 in advanced configurations [29]. The difference of more than one order of magnitude in initial investment makes the proposed system a highly accessible alternative for academic institutions, research centers, and pilot field applications. Moreover, the system is fully autonomous and does not require proprietary software licenses, which substantially reduces the operation and maintenance costs compared to many commercial radars that often depend on licenses, subscriptions, or additional support services. Consequently, the proposed solution not only provides comparable performance in speed estimation and statistical robustness but also democratizes access to this technology by enabling replication and scaling at a low cost.

Table 9. Cost details of the radar with SDR.

Item	Qty	Unit Price (USD)
ADALM-Pluto SDR	1	180
Dual-polarized antenna (Altelix/patch or dish)	1	150
Coaxial cables/connectors	–	50
Laptop	1	500
Metal support	1	30
TOTAL		910

6. Conclusions

This paper presents the detailed implementation of RADAR technology based on a single SDR, a single antenna with vertical and horizontal polarization connectors, and a laptop. This will enable access to RADAR technology at a low cost and with minimal infrastructure requirements. Consequently, research centers and universities with limited resources can now continue investigating various scenarios, such as the material composition of moving objects and the factors influencing their size. Moreover, the system will be open, as all necessary files and equipment are available for implementation without restrictions through patents. A software-defined radar allows full control over maintenance and configuration. All adjustment parameters can be safely managed by the user, reducing the operational costs and increasing the flexibility compared to commercial alternatives.

The Welch method was employed to mitigate the variability resulting from noise, a common issue with traditional spectral estimation methods. This method was prioritized to enhance the detection of the component attributed to the Doppler effect. The noise level remained relatively consistent throughout testing conducted in both rural and urban environments. As a result, a noise threshold was determined to filter out peaks attributed to this background noise, thereby emphasizing the component associated with the Doppler effect.

The experimental tests were carried out at speeds ranging from 20 to 100 km/h, resulting in a remarkably low relative error of 2.03%, calculated as the difference between the measured value and the expected value obtained from the theoretical formula, which served as the calibration of the equipment.

Due to its affordability and ease of implementation, the system described herein will facilitate applications that enhance road safety. While commercial radar systems are proprietary and require complex maintenance, our software-defined radar allows complete control over maintenance and configuration. Users can safely adjust all system parameters, providing operational flexibility and potential cost savings. This offers a practical advantage over commercial alternatives, even though direct quantitative performance comparisons are limited at this stage. For instance, it could detect pedestrians in scenarios with poor visibility. Unlike cameras, CW RADAR operates based on the transmission of electromagnetic waves and is not affected by low-light conditions. This system can generally be deployed at various points around a vehicle, enhancing safety and mitigating potential accidents. The risk of accidents and associated mortality rates can be significantly reduced by integrating it with audible alarms or emergency braking systems.