Realistic Performance Assessment of Machine Learning Algorithms for 6G Network Slicing: A Dual-Methodology Approach with Explainable AI Integration

Abstract

As 6G networks become increasingly complex and heterogeneous, effective classification of network slicing is essential for optimizing resources and managing quality of service. While recent advances demonstrate high accuracy under controlled laboratory conditions, a critical gap exists between algorithm performance evaluation under idealized conditions and their actual effectiveness in realistic deployment scenarios. This study presents a comprehensive comparative analysis of two distinct preprocessing methodologies for 6G network slicing classification: Pure Raw Data Analysis (PRDA) and Literature-Validated Realistic Transformations (LVRTs). We evaluate the impact of these strategies on algorithm performance, resilience characteristics, and practical deployment feasibility to bridge the laboratory–reality gap in 6G network optimization. Our experimental methodology involved testing eleven machine learning algorithms—including traditional ML, ensemble methods, and deep learning approaches—on a dataset comprising 10,000 network slicing samples (expanded to 21,033 through realistic transformations) across five network slice types. The LVRT methodology incorporates realistic operational impairments including market-driven class imbalance (9:1 ratio), multi-layer interference patterns, and systematic missing data reflecting authentic 6G deployment challenges. The experimental results revealed significant differences in algorithm behavior between the two preprocessing approaches. Under PRDA conditions, deep learning models achieved perfect accuracy (100% for CNN and FNN), while traditional algorithms ranged from 60.9% to 89.0%. However, LVRT results exposed dramatic performance variations, with accuracies spanning from 58.0% to 81.2%. Most significantly, we discovered that algorithms achieving excellent laboratory performance experience substantial degradation under realistic conditions, with CNNs showing an 18.8% accuracy loss (dropping from 100% to 81.2%), FNNs experiencing an 18.9% loss (declining from 100% to 81.1%), and Naive Bayes models suffering a 34.8% loss (falling from 89% to 58%). Conversely, SVM (RBF) and Logistic Regression demonstrated counter-intuitive resilience, improving by 14.1 and 10.3 percentage points, respectively, under operational stress, demonstrating superior adaptability to realistic network conditions. This study establishes a resilience-based classification framework enabling informed algorithm selection for diverse 6G deployment scenarios. Additionally, we introduce a comprehensive explainable artificial intelligence (XAI) framework using SHAP analysis to provide interpretable insights into algorithm decision-making processes. The XAI analysis reveals that Packet Loss Budget emerges as the dominant feature across all algorithms, while Slice Jitter and Slice Latency constitute secondary importance features. Cross-scenario interpretability consistency analysis demonstrates that CNN, LSTM, and Naive Bayes achieve perfect or near-perfect consistency scores (0.998–1.000), while SVM and Logistic Regression maintain high consistency (0.988–0.997), making them suitable for regulatory compliance scenarios. In contrast, XGBoost shows low consistency (0.106) despite high accuracy, requiring intensive monitoring for deployment. This research contributes essential insights for bridging the critical gap between algorithm development and deployment success in next-generation wireless networks, providing evidence-based guidelines for algorithm selection based on accuracy, resilience, and interpretability requirements. Our findings establish quantitative resilience boundaries: algorithms achieving >99% laboratory accuracy exhibit 58–81% performance under realistic conditions, with CNN and FNN maintaining the highest absolute accuracy (81.2% and 81.1%, respectively) despite experiencing significant degradation from laboratory conditions.

1. Introduction

With the rapid evolution of wireless communication technologies, the expectations surrounding sixth-generation (6G) networks are unprecedented. Sixth-generation networks differ fundamentally from fifth-generation (5G) systems. While 5G primarily focuses on enhanced mobile broadband and low-latency communications, 6G represents a paradigm shift. It is envisioned as a comprehensive ecosystem that integrates multiple infrastructure types: terrestrial-, aerial-, maritime-, and space-based networks [1,2,3]. The driving force behind this evolution comes from emerging applications with unprecedented demands. Applications including extended reality (XR), brain–computer interfaces, holographic communication, autonomous vehicles, and the Internet of Robotic Things (IoRT) require capabilities that exceed 5G’s limitations. These applications demand multiple simultaneous requirements: extreme reliability, ultra-low latency, terabit-level data rates, artificial intelligence (AI)-driven orchestration, sustainable energy efficiency, and quantum-secure communication [1,4]. As a result, the advanced mobile broadband (eMBB), ultra-reliable low-latency communication (URLLC), and massive machine-type communication (mMTC) services offered by 5G may not fully address future requirements [5]. Therefore, 6G aims to meet these demands through a unified architecture. This architecture integrates three core technologies: communication, computing, and sensing. The entire system operates on a data-driven foundation supported by AI.

A critical technology enabling this transformation is network slicing. Network slicing was established during the 5G era but will play an even more critical role in 6G [2,6]. This technology works by creating virtualized end-to-end logical network slices on shared physical infrastructure. Each slice is specifically customized to meet the unique requirements of different application types. The key advantage is that multiple virtual networks can operate simultaneously on the same shared infrastructure, enabling efficient and dynamic resource allocation [7]. The result is maximized resource efficiency through isolation of critical data flows.

Sixth-generation network slicing encompasses five distinct service categories, each with unique characteristics and resource requirements. First, further enhanced mobile broadband (feMBB) delivers data speeds exceeding 1 Tbps for applications like holographic communication and 16K video streaming. Second, ultra-massive machine type communications (umMTC) supports hyper-dense IoT deployments with up to 10 million devices per square kilometer. Third, Mobile URLLC (mURLLC) enables mobility scenarios such as autonomous vehicle coordination and remote health monitoring. Fourth, extremely reliable low-latency communications (ERLLC) provides sub-microsecond latency and deterministic reliability for industrial automation. Finally, mobile broadband reliable low-latency communications (MBRLLC) serves applications requiring balanced multi-dimensional performance, including delivery drones and vehicle-to-everything (V2X) communication.

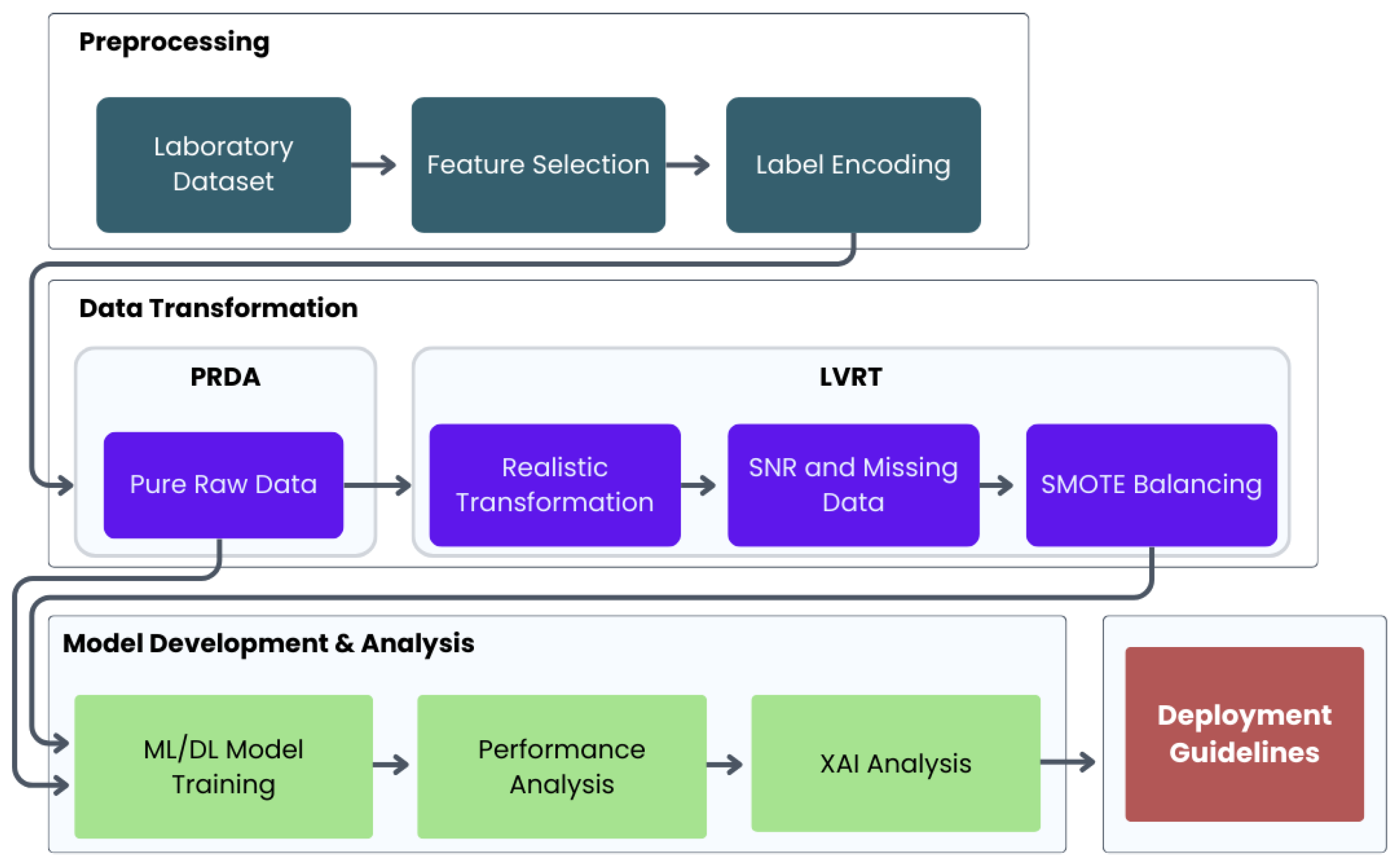
The methodological workflow of this study is illustrated in Figure 1. The framework begins with a standardized preprocessing phase on the initial laboratory dataset, involving feature selection and label encoding. Subsequently, the methodology bifurcates into two distinct analytical pathways designed to systematically evaluate algorithmic performance under contrasting conditions.

Figure 1. Overview of the dual-path methodological framework. The workflow contrasts the idealized PRDA pathway against the LVRT pathway, which simulates real-world operational stress, to enable a systematic analysis of model performance and interpretability.

The complexity of 6G networks makes traditional static approaches insufficient. The 6G network incorporates revolutionary components including communication–computing–sensing convergence, AI-based automation, and integration with satellite and airborne networks. Consequently, static slice definitions become inadequate. Network slicing must now address real-time challenges: classification, optimization, and prediction problems that evolve dynamically.

This complexity drives the need for intelligent solutions. ML-based approaches are emerging as essential tools for effectively managing this complex service ecosystem. AI-supported classifiers are recognized as a critical strategy for optimizing performance, managing heterogeneity, and overcoming dynamic network conditions in intelligent network slicing management and traffic routing to the appropriate slice [2].

Current research demonstrates promising results in controlled environments. Studies in the literature report that models created using classical ML algorithms on synthetic datasets achieve accuracy rates of over 99%. Similarly, deep learning (DL)-based hybrid models are reported to achieve success rates of over 97% [8]. Furthermore, experiments conducted on 5G test networks have shown that systems automatically classify real traffic flows and assign them to appropriate slots, reducing packet loss and jitter, providing higher reliability, especially under heterogeneous traffic conditions [9]. However, a significant gap exists between the high accuracy achieved in laboratory conditions and the performance achieved in real-world scenarios. Most studies are limited to controlled simulation environments, where the same level of success cannot be guaranteed in real networks. Performance degradation is frequently observed under real traffic patterns, interference, and variable load conditions, posing a significant challenge for field applications. Consequently, developing models supported by transfer learning, domain adaptation, and realistic datasets emerges as a critical research direction for bridging the gap between laboratory and field conditions [2].

This challenge leads to a fundamental research question. Given the increasing complexity of 6G networks and heterogeneous service requirements, network slicing and its specific subproblem slice classification become indispensable. While AI-based solutions show promising results in controlled environments, the critical question remains: how can these solutions work reliably and scalably in real-world deployments?

One of the fundamental issues is the methodological gap in data preprocessing, which significantly affects the robustness and generalizability of ML models for 6G network slicing. To address this challenge, we identify two distinct methodological approaches. The first approach, PRDA, maintains network data in its original laboratory-controlled form. It applies only basic normalization and feature selection. This approach preserves ideal statistical properties typically observed in controlled experimental environments, such as balanced class distributions, minimal measurement noise, and absence of missing values. The second approach, LVRT, applies comprehensive transformations to laboratory data. These transformations simulate authentic real-world network conditions based on empirical evidence. The approach incorporates empirically validated measurement uncertainty models, network congestion scenarios, equipment failures, and service adoption patterns. All transformations are grounded in extensive literature review and industry reports. While LVRT introduces complexity and potential performance degradation, it provides a more realistic evaluation of algorithm behavior under operational conditions.

The implications of this methodological choice are profound. This decision directly affects algorithm selection, deployment strategy, and performance expectations in practical 6G network implementations. PRDA may lead to overoptimistic performance predictions and inappropriate algorithm selection. In contrast, LVRT provides more conservative but realistic performance bounds that better reflect operational constraints and challenges.

This work presents the first systematic dual-methodology evaluation framework that bridges the critical gap between laboratory algorithm assessment and realistic 6G deployment performance. Unlike existing studies that rely solely on controlled synthetic datasets, our approach introduces LVRT incorporating authentic operational impairments including market-driven class imbalance, multi-layer interference patterns, and systematic missing data. This methodology reveals previously unknown algorithmic behavior patterns, demonstrating that certain algorithms exhibit substantial performance improvements under realistic conditions—a phenomenon invisible under traditional evaluation approaches.

Our research addresses this critical gap through concrete contributions. This paper makes the following key contributions:

• Dual-Methodology Evaluation Framework: Introduction of a novel comparative framework combining PRDA and LVRT methodologies to systematically evaluate algorithm performance across laboratory and realistic deployment conditions;
• Laboratory–Reality Performance Gap Analysis: First comprehensive demonstration that algorithms achieving >99% accuracy under controlled conditions exhibit 58–72% performance under realistic 6G deployment scenarios, revealing critical limitations in traditional evaluation approaches;
• Counter-Intuitive Algorithm Behavior Discovery: Identification of algorithms (SVM RBF; Logistic Regression) that demonstrate performance improvements (14.0% and 10.1%, respectively) under realistic conditions, challenging fundamental assumptions about data quality relationships;
• Algorithm Resilience Classification System: Development of a resilience-based categorization framework (Excellent, Good, Moderate, and Poor) based on performance degradation analysis, enabling informed algorithm selection for diverse 6G infrastructure scenarios;
• Realistic 6G Network Simulation: Implementation of comprehensive operational impairments including market-driven class imbalance (9:1 ratio), multi-layer interference modeling, and systematic missing data patterns reflecting authentic 6G deployment challenges;
• Practical Deployment Guidance: Evidence-based recommendations demonstrating that simple, stable algorithms often outperform sophisticated methods in operational environments, fundamentally altering 6G deployment strategy considerations;
• Cross-Paradigm Comparative Analysis: Comprehensive evaluation of classical ML methods (e.g., SVM, Logistic Regression, and Random Forest) and DL models (e.g., CNNs and LSTMs) for 6G network slicing classification, highlighting their respective strengths, limitations, and deployment trade-offs under realistic conditions;
• Explainable AI Integration: Application of XAI techniques, including SHAP, to interpret model decisions and feature importance, thereby enhancing transparency, enabling trust in algorithmic outputs, and providing actionable insights for network operators in critical 6G deployment scenarios.

The remainder of this paper is organized as follows. Section 2 provides the background and related work, including a detailed overview of the evolution of 6G network slicing and the role of XAI in telecommunications systems. Section 3 describes the methodology and dataset characteristics, elaborating on the research motivation, methodological philosophy, feature association analysis, dimensionality reduction, and the proposed dual-methodology evaluation framework, followed by the description of PRDA and LVRT implementations. Section 4 presents the experimental setup and model configuration, covering both traditional ML models and DL architectures. Section 5 reports and analyzes the experimental findings, including baseline results under PRDA, realistic performance under LVRT, training time and computational cost analysis, and interpretability insights through XAI. Section 6 concludes this paper with key findings, while Section 7 outlines promising future research directions.

2. Related Work and Background

Network slicing represents a transformative approach for addressing heterogeneous service requirements across different vertical sectors. The technology provides three key capabilities: guaranteed quality of service (QoS) parameters, dynamic resource allocation, and sector-specific security and privacy measures.

Research by [7] identifies seven key vertical use cases for slicing: Smart Transportation, Military Services, Smart Education, Industry 4.0, Health 4.0, Agriculture 4.0, and Smart Cities. Each sector presents unique challenges and requirements. Smart Transportation demands ultra-low latency (approximately 1 ms) and high reliability for autonomous driving, while in-vehicle multimedia services prioritize high data rates and storage capacity. Military applications require high security, network isolation, and low latency as critical parameters. Smart Education scenarios, particularly augmented reality (AR)- and virtual reality (VR)-based learning environments, need high bandwidth and low latency combinations. Industry 4.0 applications span two categories: process automation and factory communication fall under URLLC, while IoT-intensive automation applications belong to mMTC. Health 4.0 encompasses diverse applications including tele-surgery, tele-consultation, and tele-monitoring, all requiring data security, ultra-low latency, and high reliability. Agriculture 4.0 focuses on precision farming, drone-based monitoring, and autonomous agricultural vehicles, emphasizing low-cost, energy-efficient, and long-battery-life IoT solutions. Smart Cities present the most complex requirements, encompassing large-scale IoT, intelligent transportation, energy management, and multimedia services, necessitating simultaneous management of eMBB, URLLC, and mMTC service types. Beyond conceptual categorizations, several studies have examined domain-specific slicing deployments. In vehicular communications, ref. [10] demonstrates that autonomous driving URLLC and in-vehicle infotainment eMBB can be concurrently supported via logically isolated slices on shared infrastructure, meeting low-latency and high-throughput requirements under mobility constraints. For mission-critical domains, ref. [11] proposes a comprehensive management framework with deployment options such as dedicated emergency slices, dynamic scaling under overload, and edge-based migration of critical functions, providing experimental evidence of service continuity for Public Protection and Disaster Relief (PPDR) use cases. These works illustrate how slicing principles translate into concrete vertical applications, reinforcing the practical relevance of the problem investigated in this paper.

These theoretical requirements have been validated through real-world implementations. Real-world applications demonstrate the practical success of 5G-based network slicing technology. Notable examples include autonomous driving slicing trials conducted in collaboration with Deutsche Telekom and BMW, Nokia–Finnish Defense Forces’ secure communication-focused work, AR/VR-based education scenarios under the South Korea Green School project, 5G-supported production lines at BMW Leipzig facilities, robot-assisted remote healthcare services in Wuhan hospitals during the COVID-19 pandemic, satellite-connected agricultural solutions through the John Deere–SpaceX partnership, and the Barcelona 5G Smart City project.

However, implementing these vertical scenarios presents significant technical challenges. Key challenges include ensuring slice isolation, meeting ultra-low latency and high reliability requirements simultaneously, protecting data security and privacy, providing low-cost and energy-efficient services in rural areas, and ensuring scalability under heavy traffic conditions. Consequently, solutions such as adaptive Service Function Chaining (SFC), software-defined networking (SDN), and network function virtualization (NFV)-based dynamic slice management are gaining prominence.

The architectural framework shown in Figure 2 provides the foundation for our analysis. This reference model aligns use cases with RAN/transport/core resources and slice categories (feMBB, mURLLC, ERLLC, MBRLLC, and umMTC). It demonstrates how QoS/QoE constraints propagate across layers and motivates the AI-driven orchestration mechanisms discussed in subsequent sections.

Figure 2. End-to-end network slicing reference model used throughout this paper. The Service Layer (right, top) exposes slice-oriented services (e.g., feMBB, mURLLC, ERLLC, MBRLLC, and umMTC) to verticals and virtual operators. The Network Function Layer orchestrates network operation and VNFs, while the Infrastructure Layer spans RAN, transport, and core with edge/core clouds. Arrows indicate control/data interactions governed by the Network Slice Controller across layers and domains.

A critical limitation emerges from current 5G implementations. While real-world 5G slicing implementations demonstrate sector-specific feasibility, they predominantly rely on static and predefined configurations. Meanwhile, 6G slicing demands a fundamental shift toward AI-driven automation and adaptability to manage complex, heterogeneous environments. This evolution makes ML and DL technologies indispensable for future network operations.

The transition to 6G introduces revolutionary capabilities. These 6G networks will integrate multiple revolutionary technologies: terahertz communication, AI-enabled autonomous network management, holographic communication, digital twin-based optimization, and non-terrestrial networks. These technologies will redefine network slicing through four core characteristics: enhanced QoS and Quality of Experience (QoE), improved energy efficiency, robust cyber–physical security, and autonomous self-configuration capabilities. The resulting 6G slicing paradigm will enable end-to-end network reconfiguration with AI support, real-time allocation of physical and virtual network resources, and integrated management of terrestrial-, aerial-, maritime-, and space-based communication layers. Consequently, the sector-focused network slicing applications developed during the 5G era will evolve into fully autonomous, hyper-connected, and cognitive network slicing paradigms.

2.1. 6G Network Slicing Evolution

Network slicing technology has undergone significant evolution since its inception.

The technology has progressed from initial conceptualization in 5G networks to advanced implementations envisioned for 6G systems [12]. Foundational research by Rost et al. established the fundamental principles of network slicing, demonstrating how virtualization technologies could enable multiple logical networks to coexist on shared physical infrastructure.

The current literature positions network slicing as a mature yet evolving technology. Network slicing is now recognized as a critical approach that has matured through SDN and network function virtualization (NFV) technologies beginning in 5G. This maturation enables multiple service types to be delivered as logically isolated slices on a single physical infrastructure [13,14]. Following standardization in 3GPP Release 15, the concept evolves toward greater complexity in 6G through integration with Space–Air–Ground Integrated Network (SAGIN) architectures, THz communication, edge–cloud integration, and AI-enabled automation [15,16]. Research has established comprehensive frameworks for slice management. Previous studies have defined three key phases: preparation, planning, and operation of slice management. These studies have also demonstrated the applicability of AI methods including Recurrent Neural Network (RNN), deep reinforcement learning, and multi-armed bandit algorithms in critical processes: resource reservation, service demand estimation, slice acceptance, and virtual network function (VNF) placement [17]. Complementing this work, the “slicing for AI” approach emphasizes the necessity of QoS-guaranteed customized network slices for AI services during data collection, model training, and inference phases [18]. In parallel, the concept of AI instances has been developed to enable the selection of different algorithms and training formats in a manner that is adaptable to network resources [17]. Despite significant progress, critical challenges remain unresolved. While previous research has highlighted the potential of this field, given 6G’s high dynamism, heterogeneous infrastructure, and new QoS dimensions, areas including joint optimization of planning and operations, distributed data management, and prediction-based slicing remain open research areas. Recent research has advanced the fundamental network slicing approaches developed for 5G networks by focusing on hybrid and AI-based techniques to meet more complex service requirements, particularly for 6G networks [18,19].

Contemporary research demonstrates significant advances in hybrid approaches. Dangi and Lalwani [20] highlight the advantages of hybrid slicing techniques in determining the most suitable network slice for each incoming network traffic based on the device’s fundamental characteristics. They propose a hybrid DL architecture to address the slicing classification challenges in 6G networks. Their methodology involves comprehensive data preprocessing. They utilized the Unicauca IP Flow Version 2 dataset, which was relabeled taking into account device request types. Through this process, 78 application classes were reduced to five basic 6G slice categories (super-eMBB, massive-MTC, super-URLLC, super-precision, and super-immersive). The proposed architecture combines complementary neural network components. The CNN component performs automatic feature extraction, while the Bidirectional Long Short-Term Memory (BiLSTM) layer performs slice classification by considering time dependencies. Evaluation through stratified 10-fold cross-validation achieved 97.21% accuracy. The study’s notable contribution lies in combining high accuracy with low data dependency, enabling effective operation on small-scale datasets while achieving lower misclassification rates compared to existing methods. However, a single-dataset evaluation creates uncertainty regarding its generalizability under different network conditions, heterogeneous traffic dynamics, and real-world operational scenarios.

In parallel, Wang et al. [21] present a comprehensive tutorial on AI-assisted 6G network slicing, emphasizing its dual role in network assurance and service provisioning. The authors identify six defining characteristics of 6G slicing—tailored service provisioning, efficient resource utilization, strict service isolation, seamless service coverage, technology convergence, and ubiquitous slice intelligence—and explore AI-driven solutions across RAN, transport, and core network domains, as well as slicing management systems and non-terrestrial extensions. They detail how reinforcement learning, DL, federated learning, and transfer learning can be applied to intelligent device association, elastic bandwidth scaling, VNF placement, anomaly detection, service level agreement (SLA) decomposition, and capacity forecasting. A case study on reinforecement learning (RL)-based elastic bandwidth scaling in elastic optical networks demonstrates superior request satisfaction rates and adaptability compared to shortest-path-based approaches. The study identifies open research challenges for 6G slicing, including rapid slice adjustment, multi-domain/multi-operator orchestration, security and reliability under AI-oriented threats, and standardized architectures. This work complements hybrid and data-driven approaches in the literature by providing a domain-spanning, AI-centered framework for evolving slicing strategies toward the complex requirements of 6G systems.

Alwakeel and Alnaim [22] aim to develop an optimized, scalable, and secure network slicing framework for 6G-based smart city IoT applications. The study follows a systematic methodology that includes steps such as requirement analysis, definition of performance metrics, identification of constraints, mathematical modeling, and improvement of slicing configurations using metaheuristic optimization methods such as genetic algorithms and simulated annealing. The model’s performance was tested in a simulation environment based on latency, reliability, bandwidth, scalability, and security metrics during the evaluation process. However, the study did not use real-world data or open datasets, relying solely on simulation-based validation. Furthermore, this study did not integrate AI-based prediction, optimization, or decision-making techniques, which are frequently recommended in the literature. The lack of comprehensive testing for different IoT scenarios and real-time adaptation mechanisms is considered the primary factor limiting the practical applicability of the model.

Cunha et al. [23] present a comprehensive review on enhancing network slicing security in 5G and emerging 6G networks by integrating ML, SDN, and NFV. The study highlights how ML can enable predictive threat detection and proactive security responses, while SDN and NFV facilitate agile, context-aware policy enforcement. Several AI-driven frameworks—such as Secure5G, DeepSecure, and Intelligence Slicing are surveyed, showing high accuracy in detecting distributed denial of service (DDoS), malware, and other attacks. The review identifies significant challenges, including slice isolation, inter-slice handover, policy translation in heterogeneous environments, and vulnerabilities introduced by AI/ML itself (e.g., adversarial attacks; false positives). Notable gaps include the need for standardized policy enforcement across multi-provider domains, lightweight yet practical AI models for real-time use, and robust privacy-preserving mechanisms. The authors conclude that a unified, scalable security strategy combining ML-based analytics with SDN/NFV’s orchestration capabilities is essential for safeguarding confidentiality, integrity, and availability in future network slicing deployments.

Mahesh et al. [24] aim to design and evaluate a simulation-based framework for 6G network slicing using a K-D Tree-based handover algorithm. The study models three slice types, eMBB, URLLC, and mMTC, using hardcoded base station coordinates and randomly distributed client locations, measuring connection ratio, client count, latency, and slice usage. No real-world dataset is used; synthetic data is generated through simulation. Results show that URLLC achieves the lowest latency, eMBB exhibits the highest slice utilization, and mMTC usage is minimal, with overall stable latency even under sudden user base changes. The proposed design offers reusable, object-oriented modules for network operators to pre-assess slicing performance. However, it lacks integration with live network data, real-world traffic patterns, and advanced AI-driven dynamic slicing. The authors suggest future improvements using ML modules, dynamic load management, and more realistic input scenarios.

Wu et al. [25] proposed an ML-based framework for 5G network slicing management that integrates traffic classification with dynamic slice resource allocation. The authors employed the Universidad Del Cauca network traffic dataset, comprising approximately 2.7 million records across 141 applications with 50 traffic features. They applied Random Forest, Gradient Boosting Decision Tree (GBDT), XGBoost, and k-Nearest Neighbors (KNN) classifiers to categorize flows into lightweight, hybrid, and heavyweight slices. Data preprocessing steps included removing non-essential identifiers and applying Synthetic Minority Oversampling Technique (SMOTE) to address class imbalance. Experimental results showed that Random Forest and GBDT achieved the highest classification accuracy of 95.73%. Furthermore, GPU-based training reduced execution time by nearly a factor of ten compared to CPU-based implementations. The study also incorporated an auto-scaling mechanism to reallocate resources dynamically under varying traffic loads. Although the framework demonstrated high accuracy and computational efficiency in 5G slicing scenarios, it was validated solely on a single dataset in a simulated environment, leaving its performance in real-time 6G deployments and under heterogeneous network conditions to be explored.

However, 6G networks introduce additional complexity through support for new service categories and more stringent performance requirements.

Table 1 reveals a consistent pattern across recent studies. Recent research consistently shows that ML/DL-based models consistently achieve high classification accuracy (95–99%) when tested on controlled datasets. However, a critical limitation appears: most approaches rely on synthetic or simulation-based data rather than live network traffic, raising concerns about their robustness in heterogeneous and dynamic 6G environments. Furthermore, while GPU-accelerated implementations improve scalability, few works address cross-domain orchestration, real-time adaptability, or resilience under adversarial conditions. This gap motivates our research approach. The persistent gap between laboratory success and real-world deployment necessitates evaluation methodologies that incorporate realistic impairments, heterogeneous traffic conditions, and predictive optimization mechanisms. Our research directly addresses this need through systematic comparison of pure raw data analysis with literature-validated realistic transformations for 6G slicing applications [2,26]. Common trends include synthetic or lab-created datasets to represent slice scenarios (due to the novelty of 6G) and the pursuit of real-time intelligent slicing. However, a recurring limitation is the gap between simulation and reality. Many solutions have yet to be tested on actual networks or at scale, leaving open challenges in generalization to diverse, evolving 6G traffic patterns and integration with live network management. These studies collectively lay a foundation, and ongoing research is refining datasets and models to enable robust, AI-driven slice classification in practical 6G deployments [2]. However, no previous study has comprehensively compared pure raw data analysis and literature-validated realistic transformations specifically for 6G network slicing applications. This represents a significant gap in the literature that our study addresses through systematic experimental evaluation.

Table 1. ML/DL-based studies on 5G/6G network slicing classification.

Study (Year)	Methodology	Dataset	Key Findings	Limitations
Khan et al. (2022) [26]	Hybrid CNN + LSTM	Public 5G slice dataset (“DeepSlice & Secure5G”)	∼95.2% accuracy; proactive reconfiguration to prevent slice failures	No real network testing; focuses only on slice selection; lacks 6G-specific security/dynamic adaptability
Mohammedali et al. (2022) [27]	SVM, Random Forest, others	5G traffic data (simulated or testbed)	≈100% accuracy; feasible real-time classification	Dataset not fully described; generalizability questionable; small-scale controlled scenario
Dangi & Lalwani (2024) [20]	HHO-optimized CNN + LSTM	Public IP flow dataset + private dataset	Achieved top accuracy; improved slice selection performance	Added computational complexity; real-time feasibility unclear; private dataset not accessible
Dangi & Lalwani (2024) [8]	CNN + BiLSTM	Unicauca IP Flow v2	∼97.2% accuracy; reliable slice recommendations	Offline evaluation; real-world 6G traffic generalization not validated
Wu et al. (2024) [25]	Random Forest, GBDT, XGBoost, KNN	Universidad Del Cauca network traffic dataset (141 applications, 50 features, and ∼2.7M records)	RF and GBDT achieved up to 95.73% accuracy in slice classification; GPU reduced training time nearly $10\times$ compared to CPU	Evaluation limited to 5G slicing; no direct 6G validation; relies on a single dataset, and real-time deployment feasibility not assessed
Botez et al. (2025) [2]	FNN, RF, XGBoost, others	Synthetic 6G slicing dataset (2025)	>99% accuracy; successful slice selection and handover prediction	Synthetic dataset may not capture full real-world complexity; no live network validation
Malik et al. (2025) [28]	Taneja Distance-Based Classifier (TDC) + PSO Feature Selection	Public 5G Network Slicing Dataset (30,000 instances, 10 attributes)	Achieved 98.9% accuracy; execution time 1.7 ms; robust across noisy, imbalanced, and high-dimensional datasets	Requires proper feature normalization due to sensitivity of Taneja distance; potential computational overhead in large-scale real-time deployments; limited validation on real 6G scenarios
Mahmoud et al. (2024) [29]	CNN + RF, 5-NN, XGBoost, Naive Bayes, DT, LR, MLP	Real-world 5G/6G traffic (DeepSlice dataset)	Achieved up to 94.44% accuracy; RF, 5-NN, XGBoost, and Naive Bayes reached 100% precision and recall with CNN-based feature selection	Logistic Regression showed low accuracy (72%); Bagging Trees had high false positives; limited evaluation under massive-scale 6G data
Jain et al. (2025) [30]	Hybrid CNN + LSTM + Crisscross Harris Hawks Optimization (CHHO)	Unicauca IP Flow v2 dataset	Achieved 95.48% accuracy; precision 94.11%, recall 87.45%, and F1-score 93.87%; CHHO improved convergence stability and learning robustness compared to PSO and GWO	Evaluation limited to a single dataset; validated in simulation only; lacks large-scale real 6G traffic experiments
Samidi et al. (2023) [31]	SVM, RF, GBT, DT, NB, DL (Auto Model)	5GNS dataset (simulated, ∼30k samples)	Gradient Boosted Tree achieved top accuracy (78.7%); evaluated multiple ML/DL models via Auto Model tool	Reported accuracy lower than state-of-the-art; dependent on Auto Model optimization; validated only on simulated dataset, no real 6G experiments

2.2. XAI in Telecommunications

The telecommunications industry has increasingly embraced AI and ML to manage networks, optimize services, and automate operations. This shift has improved efficiency but also introduced complex ’black-box’ models that lack transparency [32]. In earlier generations, telecom operators relied on rule-based expert systems that could explicitly justify their reasoning. Now, with data-driven 5G/6G network intelligence, the decision-making process of AI can be opaque, raising concerns about trust, accountability, and compliance [33,34]. Unexplained or incorrect AI decisions can lead to costly downtime, degraded service quality, or even regulatory non-compliance. This has created a strong motivation to integrate XAI techniques that make model behavior interpretable and human-understandable [35,36]. Therefore, XAI plays a vital role in ensuring that AI-driven telecom systems remain trustworthy and transparent, allowing network engineers to validate automated decisions and maintain oversight in mission-critical environments.

XAI Approaches and Classification: XAI methods are broadly categorized into intrinsic (transparent) models and post hoc explanation techniques [33,36]. Intrinsic approaches use interpretable-by-design models such as decision trees or rule-based systems, providing step-by-step human-readable reasoning. Post hoc techniques, such as SHapley Additive Explanations (SHAP) and Local Interpretable Model-Agnostic Explanations (LIME), explain complex models without altering them [37,38]. Post hoc methods can be model-agnostic (applicable to any ML model) or model-specific (leveraging internal structures such as attention weights in neural networks). Moreover, XAI can operate at a local level (explaining individual predictions) or a global level (summarizing the model’s overall decision logic). In telecommunications, balancing model complexity with interpretability is essential for maintaining both high performance and explainability.

XAI in Telecom—From Fault Diagnosis to Optimization: XAI applications span multiple telecommunications domains. Successful applications include network fault management and service quality assurance [36,39]. Fault management benefits significantly from explainable approaches. For anomaly detection and fault diagnosis, explainable models can highlight which key performance indicators (KPIs) contributed to an outage prediction, aiding root cause analysis. In customer churn prediction and QoS assurance, explainability helps identify the primary factors behind model decisions (e.g., bandwidth usage patterns or latency spikes), enabling proactive interventions and ensuring decisions are business-relevant.

Explainability for Network Slicing Classification: Network slicing is central to 5G/6G, allowing virtual networks with different QoS profiles. ML models are used to automate slice classification and allocation. XAI ensures that these decisions are transparent, revealing which features (e.g., latency, packet loss, and device type) drive classification outcomes [40]. This transparency builds operator trust, supports compliance with service-level agreements, and allows auditing for fairness or bias. For example, SHAP-based analysis can show that high packet delay and video traffic type were decisive in routing a flow to a low-latency slice.

Recent surveys further emphasize that in 6G network slicing, balancing high AI model performance with interpretability is a central challenge, particularly for ensuring fairness, compliance, and trust in automated orchestration [41]. Multiple studies have demonstrated the use of advanced XAI techniques such as SHAP, LIME, RuleFit, Partial Dependence Plots (PDPs), and Integrated Gradients (IGs) to identify key features influencing SLA violation predictions and network slice performance metrics. For example, kernel SHAP has been applied to Short-Term Resource Reservation (STRR) models to monitor real-time decisions, uncover global behavioral trends, and diagnose potential failures during model development. Federated learning has emerged as a complementary paradigm to XAI in this context, enabling collaborative model training without exposing raw data, thus maintaining privacy while improving interpretability. XAI methods integrated into federated learning such as SHAP, LIME, and IGs have been successfully used for latency KPI prediction, slice reconfiguration optimization, and root cause analysis of SLA violations. Furthermore, explanation-guided deep reinforcement learning (DRL) and MLOps frameworks, such as SliceOps, have enhanced automation in network slice resource allocation by feeding back explainer-derived confidence metrics into the optimization process, enabling closed-loop, adaptive, and transparent orchestration. These developments indicate that the synergy between XAI, federated learning, and DRL offers a pathway toward more reliable, explainable, and privacy-preserving network slicing in 6G, meeting both performance demands and regulatory requirements.

XAI in Network Resource Planning: Resource allocation in 5G/6G often involves deep reinforcement learning and multi-agent systems, which can be opaque. Explainable multi-agent resource allocation frameworks, such as the Prioritized Value-Decomposition Network (PVDN), decompose global decisions into interpretable contributions from each slice [40]. In simulations, such XAI-based approaches have achieved up to 67% throughput improvement and 35% latency reduction compared to baselines, showing that explainability can enhance both performance and trust.

XAI is a cornerstone for trustworthy AI adoption in telecommunications. From high-level network planning to real-time slicing, explainability bridges the gap between algorithmic complexity and operational transparency, enabling the safe and accountable deployment of AI in 6G networks.

3. Methodology and Dataset Characteristics

The evolution toward 6G networks demands sophisticated ML algorithms for real-time network slice classification in operational environments. While Botez et al. [2] demonstrated over 99% accuracy under controlled laboratory conditions, a critical gap persists between idealized algorithm evaluation and realistic deployment performance. This study addresses this limitation through a dual-methodology framework comparing PRDA representing laboratory conditions with LVRT incorporating authentic network impairments.

3.1. Dual-Methodology Framework and Dataset Foundation

Our approach builds upon the 6G network slicing dataset (10,000 samples; 13 features) introduced by Botez et al. [2], extending it through systematic refinement and realistic transformation processes. Figure 3 illustrates the complete methodology workflow encompassing feature optimization, dual-path evaluation, and comprehensive algorithm assessment.

Figure 3. Overview of the proposed methodology.

The evaluation encompasses five network slice types representing the complete 6G service spectrum: feMBB for ultra-high bandwidth applications (holographic communications, 16 K streaming), umMTC enabling hyper-dense IoT deployments (${10}^7$ devices/km²), mURLLC providing mission-critical connectivity (>99.999% reliability), ERLLC delivering sub-microsecond latency for precision applications, and MBRLLC supporting balanced multi-dimensional performance requirements.

3.2. Feature Optimization and Dimensionality Reduction

Prior to dual-methodology evaluation, we performed systematic feature refinement using statistical analysis to eliminate multicollinearity artifacts. Figure 4 demonstrates the deterministic relationship between slice types and use cases, confirming feature redundancy requiring elimination.

Figure 4. Slice type and use case type relationship demonstrating perfect correlation, justifying use case elimination as redundant feature.

Statistical analysis employing ANOVA (${\eta }^2$) for numeric features and Cramér’s V for categorical variables revealed significant redundancy. Table 2 presents comprehensive results showing perfect correlations (${\eta }^2$ = 1.000 or Cramér’s V = 1.000) for budget-related features and configuration parameters. Systematic elimination of six redundant features yielded an optimized space of five variables: four independent numeric features (Transfer Rate, Latency, Packet Loss, and Jitter) and one categorical feature (Packet Loss Budget) with strong association (Cramér’s V = 0.791).

Table 2. Feature association analysis and selection strategy.

Feature	Type	Association Metric	Strength	Decision
Latency Budget (ns)	Numeric	${\eta }^2$ = 1.000	Perfect	Removed
Data Rate Budget (Gbps)	Numeric	${\eta }^2$ = 1.000	Perfect	Removed
Jitter Budget (ns)	Numeric	${\eta }^2$ = 0.436	Strong	Removed
Use Case Type	Categorical	Cramér’s V = 1.000	Perfect	Removed
Required Mobility	Categorical	Cramér’s V = 1.000	Perfect	Removed
Required Connectivity	Categorical	Cramér’s V = 1.000	Perfect	Removed
Slice Handover	Categorical	Cramér’s V = 0.999	Near-perfect	Removed
Retained Features:
Slice Available Transfer Rate	Numeric	${\eta }^2$ = 0.000	Independent	Retained
Slice Latency (ns)	Numeric	${\eta }^2$ = 0.000	Independent	Retained
Slice Packet Loss	Numeric	${\eta }^2$ = 0.001	Independent	Retained
Slice Jitter (ns)	Numeric	${\eta }^2$ = 0.000	Independent	Retained
Packet Loss Budget	Categorical	Cramér’s V = 0.791	Strong	Retained

3.3. PRDA Implementation: Laboratory Baseline

The PRDA methodology establishes theoretical performance benchmarks through minimal preprocessing interventions:

$${\mathcal{D}}_{PRDA}={\mathcal{M}}_{minimal}\left({\mathcal{D}}_{original}\right)$$

(1)

where ${\mathcal{M}}_{minimal}$ encompasses correlation-based feature selection and label encoding. Label encoding maps categorical attributes to integer values, fitted exclusively on training data to prevent leakage while preserving structural characteristics. Figure 5 shows the approximate class balance maintained, with four slice types exhibiting near-uniform distribution (22.0–22.6%) and mURLLC showing lower representation (10.9%).

Figure 5. Original (percentages may not sum to 100% due to rounding) dataset network slice distribution.

3.4. LVRT Implementation: Realistic Operational Simulation

The LVRT methodology transforms laboratory data into realistic deployment benchmarks through systematic application of four sequential operators addressing operational challenges documented in the telecommunications literature:

$${\mathcal{D}}_{LVRT}={\varphi }_{\mathrm{SMOTE}}\circ {\varphi }_{\mathrm{missing}}\circ {\varphi }_{\mathrm{noise}}\circ {\varphi }_{\mathrm{distribution}}\left({\mathcal{D}}_{\mathrm{original}}\right)$$

(2)

where the composition operator ∘ indicates sequential application from right to left.

3.4.1. Market-Driven Distribution Transformation

Real-world 6G networks exhibit severe class imbalance based on comprehensive industry projections from flagship research initiatives [42,43]. The realistic distribution applies market-driven allocation:

$$p_{\mathrm{realistic}}={[0.55,0.18,0.12,0.089,0.061]}^T$$

(3)

corresponding to [feMBB, umMTC, mURLLC, ERLLC, MBRLLC], reflecting feMBB dominance (55%) driven by bandwidth-intensive applications, umMTC expansion (18%) reflecting exponential IoT growth in smart city deployments, and specialized slice adoption patterns. This creates a 9:1 imbalance ratio representing critical deployment challenges that algorithms must handle effectively under operational stress.

3.4.2. Multi-Layer Noise Injection

Urban 6G deployments experience complex interference patterns requiring multi-layer modeling based on the established telecommunications literature [44,45] and 3GPP specifications [46,47]:

$$x_{\mathrm{noisy}}\left[n\right]=(x\left[n\right]+w_{\mathrm{AWGN}}\left[n\right]+w_{\mathrm{imp}}\left[n\right])·g\left[n\right]$$

(4)

Layer 1 introduces additive white Gaussian noise (AWGN) representing measurement uncertainty with scenario-stratified SNR distributions following 3GPP urban deployment statistics: outdoor line-of-sight (18 ± 3.8 dB), outdoor non-line-of-sight (11 ± 4.1 dB), indoor hotspots (14 ± 4.5 dB), and vehicle penetration (−1 ± 3.2 dB), with scenario probabilities of 25%, 45%, 20%, and 10%, respectively. These empirically validated ranges reflect documented field measurements from operational 6G testbeds [43].

Layer 2 adds impulsive interference modeling irregular electromagnetic interference from industrial equipment, with 5% occurrence probability reflecting documented interference patterns in dense urban environments [48]:

$$w_{\mathrm{imp}}\left[n\right]=I\left[n\right]·A\left[n\right]·S\left[n\right]$$

(5)

$$I\left[n\right]\sim \mathrm{Bernoulli}\left(0.05\right)$$

(6)

Layer 3 incorporates multiplicative gain variations representing system calibration drift and environmental adaptation, with 2% standard deviation reflecting typical RF front-end stability characteristics documented in wireless system analysis [49]:

$$g\left[n\right]\sim \mathcal{N}(1.0,0.{02}^2)$$

(7)

3.4.3. Systematic Missing Data and Quality Control

Operational 6G networks exhibit systematic data quality degradation following documented failure patterns in telecommunications infrastructure [50,51]. We model four distinct failure modes representing sensor failures, network outages, measurement errors, and maintenance windows, generating the following expected missing data rate:

$$\mathbb{E}\left[\mathrm{missing}\mathrm{rate}\right]=\sum _i{P}_i·\mathbb{E}\left[D_i\right]\approx 0.07 (7\%)$$

(8)

Quality control implements a two-stage process to maintain dataset utility while preserving realistic characteristics. The complete data transformation sequence proceeds as follows: Original laboratory dataset (10,000 samples) → Quality control removes samples with >20% missing values (7997 samples) → SMOTE augmentation balances class distribution (final: 21,033 samples). The first stage applies a threshold-based filter to prevent training on inadequate information, as formalized in Equation (9):

$$\mathrm{Remove}\mathrm{sample}i\mathrm{if}{\displaystyle \frac{{\sum }_{j=1}^d\mathbb{1}[x_{i,j}=\mathrm{NaN}]}{d}}>0.20$$

(9)

The second stage addresses severe class imbalance through SMOTE [52], generating synthetic samples using linear interpolation between existing minority class instances and their nearest neighbors (Equation (10)):

$$x_{\mathrm{synthetic}}=x_i+\lambda ·(x_{\mathrm{neighbor}}-x_i),\lambda \sim \mathcal{U}[0,1]$$

(10)

where $x_i$ represents a randomly selected minority class instance, $x_{\mathrm{neighbor}}$ is one of its k nearest neighbors (k = 5), and $\lambda$ is a random interpolation factor. This approach maintains underlying data distribution while providing sufficient training examples for minority classes, expanding the dataset to 21,033 samples. Figure 6 illustrates the resulting realistic service distribution.

Figure 6. Realistic dataset network slice distribution (percentages may not sum to 100% due to rounding).

This dual-methodology framework enables comprehensive algorithm assessment spanning idealized laboratory conditions (PRDA: 10,000 samples) to realistic operational challenges (LVRT: 21,033 samples), providing evidence-based guidance for algorithm selection across diverse 6G infrastructure scenarios.

4. Experimental Setup and Model Configuration

This study employs a multi-layered experimental framework to assess the reliability of ML and DL algorithms in the context of 6G network slicing. A total of eleven algorithms are implemented, covering both traditional ML approaches and DL architectures to evaluate trade-offs between interpretability, computational efficiency, and robustness to real-world conditions.

Two distinct experimental regimes are considered: PRDA represents a controlled baseline environment with minimal noise and well-structured data, while LVRT incorporates congestion modeling, multi-layer noise, missing data, and temporal correlation patterns, thereby mimicking actual 6G deployment conditions. This contrast allows analysis of model performance when transitioning from theoretical laboratory conditions to realistic field operations.

The dataset consists of 10,000 samples, stratified into 80% training and 20% testing sets. Class imbalance is handled using SMOTE ($k=5$), feature selection relies on SelectKBest (f-classification, top 15 features), and features are normalized using Z-score standardization. Evaluation employs 5-fold repeated cross-validation with three repetitions to minimize variance, while SHAP-based XAI enables interpretable feature attribution across models.

4.1. Traditional ML Configurations

The traditional algorithms were tuned to balance accuracy with computational cost, as summarized in Table 3. Ensemble methods such as Random Forest, Gradient Boosting, and XGBoost use multiple trees to capture non-linear decision boundaries, while simpler models like Logistic Regression and Naive Bayes offer interpretability and computational efficiency. SVM employs an RBF kernel with probability estimation, while kNN uses distance-weighted voting. The configuration is designed to benchmark each model fairly under both PRDA and LVRT.

Table 3. Traditional ML model parameters.

Algorithm	Key Parameters	Optimization Strategy
Random Forest	$B=200$ trees; $max\_depth=15$	Parallel processing: all cores
Gradient Boosting	$M=150$ trees; $max\_depth=8$	Learning rate $\eta =0.1$
XGBoost	$T=200$ trees; $max\_depth=8$	Parallel processing: all cores
SVM (RBF)	$C=1.0$; $\gamma =auto$	Probability estimates enabled
Logistic Regression	$max\_iter=1000$	L2 regularization $\lambda =1.0$
Naive Bayes	Gaussian assumption	MLE parameter estimation
Decision Tree	$max\_depth=15$	Gini impurity criterion
k-NN	$k=7$; distance weighting	Euclidean distance metric

4.1.1. Ensemble Learning Methods

Random Forest employs bootstrap aggregating and out-of-bag error estimation with decision trees as base learners, utilizing random feature selection at each split to minimize overfitting through ensemble aggregation (Equation (11)) [53]. Gradient Boosting constructs additive models sequentially by iteratively fitting new models to the negative gradient of the loss, controlling learning progression via a learning rate (Equation (12) [54]. XGBoost (version 3.0.5) integrates L1/L2 regularization with advanced tree pruning and parallel computation, enhancing efficiency and reducing overfitting risk through a regularized objective (Equation (13)) [55].

$${\widehat{y}}_i={\displaystyle \frac{1}{B}}\sum _{b=1}^B{T}_b\left(x_i\right)$$

(11)

where $T_b\left(x_i\right)$ denotes the prediction of the b-th decision tree for input instance $x_i$, and B is the total number of trees. The final prediction ${\widehat{y}}_i$ is obtained by averaging (for regression) or majority voting (for classification) across all base learners, thus reducing variance and mitigating overfitting.

$${\widehat{y}}_i^{\left(m\right)}={\widehat{y}}_i^{(m-1)}+{\gamma }_m{h}_m\left(x_i\right)$$

(12)

where ${\widehat{y}}_i^{(m-1)}$ is the prediction up to stage $m-1$, $h_m\left(x_i\right)$ is the newly added weak learner fitted to the negative gradient of the loss, and ${\gamma }_m$ is the learning rate controlling the contribution of $h_m$. This sequential refinement allows the model to minimize the residual errors step by step, leading to improved generalization performance.

$$\mathcal{L}\left(\varphi \right)=\sum _{i=1}^n\ell ({\widehat{y}}_i,y_i)+\sum _{k=1}^K\Omega \left(f_k\right),\Omega \left(f\right)=\gamma T+{\displaystyle \frac{1}{2}}\lambda {\parallel w\parallel }^2$$

(13)

where $\ell ({\widehat{y}}_i,y_i)$ denotes the loss between predicted value ${\widehat{y}}_i$ and true label $y_i$, and $\Omega \left(f\right)$ penalizes model complexity. Here, T is the number of leaves, w represents leaf weights, $\gamma$ is the regularization parameter penalizing additional leaves, and $\lambda$ controls $L_2$ regularization on weights.

4.1.2. Linear and Probabilistic Models

Logistic Regression utilizes a sigmoid link for binary probability estimation with L2 regularization to enhance generalization in high-dimensional spaces (Equation (14)) [56]. Naive Bayes applies Bayes’ theorem under conditional independence and (for continuous features) Gaussian likelihood assumptions, computing class posteriors via multiplicative likelihood integration (Equation (15)) [57].

$$P(y=1\mid x)={\displaystyle \frac{1}{1+exp\left(-\left({\beta }_0+{\sum }_{j=1}^p{\beta }_j{x}_j\right)\right)}}$$

(14)

where the probability of class $y=1$ is modeled using the sigmoid function applied to a linear combination of input features $x_j$ with coefficients ${\beta }_j$.

$$\widehat{y}=arg\underset{c\in \mathcal{C}}{max}P(C=c)\prod _{i=1}^{d}P(x_i\mid C=c)$$

(15)

which predicts the class $\widehat{y}$ by maximizing the posterior probability under the assumption of conditional independence among features $x_i$.

4.1.3. Tree-Based and Instance-Based Methods

Decision Tree induces interpretable rule-based models via recursive binary splitting that minimizes CART’s Gini impurity (Equation (16)) [58]. Support Vector Machine employs an RBF kernel transformation to find maximum-margin separating hyperplanes in higher-dimensional spaces (Equation (17)) [59,60]. k-NN classifies instances through distance-weighted majority voting among the k nearest neighbors, adapting locally to data topology (Equation (18)) [61].

$$Gini\left(S\right)=1-\sum _{c=1}^C{p}_c^2$$

(16)

where $p_c$ is the class proportion of $y_i$ in node S.

$$K(x_i,x_j)=exp\left(-\gamma {\parallel x_i-x_j\parallel }^2\right)$$

(17)

which maps input pairs $(x_i,x_j)$ into a higher-dimensional space to separate $y_i$ classes.

$${\widehat{y}}_i=arg\underset{c\in \mathcal{C}}{max}\sum _{j\in {\mathcal{N}}_k\left(x_i\right)}{w}_j\mathbb{1}[y_j=c]$$

(18)

where ${\widehat{y}}_i$ is assigned to the majority class among the k nearest neighbors $y_j$ of $x_i$.

Table 3 summarizes the hyperparameter settings of traditional models. Ensemble methods such as Random Forest and XGBoost prioritize depth and parallelism to handle high-dimensional interactions, while Gradient Boosting incorporates a moderate learning rate for stability. Simpler models (Naive Bayes, Logistic Regression, and Decision Tree) operate under stricter assumptions but provide baselines for interpretability and low complexity. This parameterization ensures that differences in outcomes reflect algorithmic characteristics rather than suboptimal tuning.

4.2. DL Architectures

DL models are tuned for both spatial and temporal feature learning, incorporating regularization techniques and dynamic training adaptations. The architectures are designed to capture different aspects of feature relationships while maintaining computational efficiency through optimized training configurations as detailed in Table 4.

Table 4. DL architectures and training configurations.

Model	Architecture	Training Setup
CNN	Conv1D: 64,128,256; Dense: 512,256	Epochs 50; Batch 32; Adam; LR = 0.001
LSTM	LSTM: 128,64; Dense: 256,128	Epochs 50; Batch 32; RMSprop; LR = 0.001
FNN	Dense: 512,256,128,64	Epochs 50; Batch 32; Adam; LR = 0.001

4.2.1. CNN

CNN employs stacked one-dimensional convolutional layers to extract hierarchical local patterns from sequential inputs, with batch normalization to stabilize learning and dropout regularization to mitigate overfitting [62,63]. The convolutional layers extract local feature patterns (Equation (19)), which are subsequently aggregated by dense layers and transformed into final class probabilities through the softmax function (Equation (20)).

$$y_{c_{\mathrm{out}},t}=\sigma \left(\sum _{c_{\mathrm{in}}}\sum _m{w}_{c_{\mathrm{out}},c_{\mathrm{in}},m}{x}_{c_{\mathrm{in}},t+m}+b_{c_{\mathrm{out}}}\right)$$

(19)

where $w_{c_{\mathrm{out}},c_{\mathrm{in}},m}$ are the convolutional filter weights, $x_{c_{\mathrm{in}},t+m}$ are the input features, $b_{c_{\mathrm{out}}}$ is the bias term, and $\sigma (·)$ is the activation function.

$${\widehat{y}}_i=\mathrm{softmax}\left(W^{\left(\mathrm{out}\right)}{h}^{\left(\mathrm{CNN}\right)}+b^{\left(\mathrm{out}\right)}\right)$$

(20)

where $h^{\left(\mathrm{CNN}\right)}$ is the flattened representation obtained after convolution and pooling.

4.2.2. LSTM

LSTM overcomes the vanishing gradient problem inherent in standard RNNs by utilizing input, forget, and output gates that selectively retain, update, and transfer temporal information across extended sequences [64,65]. The gating mechanisms and state updates are defined in Equations (21) and (22), while the final prediction is obtained through the softmax transformation of the hidden state as shown in Equation (23).

$$i_t=\sigma \left(W_i[h_{t-1},x_t]+b_i\right),f_t=\sigma \left(W_f[h_{t-1},x_t]+b_f\right),o_t=\sigma \left(W_o[h_{t-1},x_t]+b_o\right)$$

(21)

the input gate of the LSTM is $i_t$, the forget gate is $f_t$, and the output gate is $o_t$, where $\sigma (·)$ is the sigmoid activation.

$${\tilde{C}}_t=tanh\left(W_C[h_{t-1},x_t]+b_C\right),C_t=f_t\odot C_{t-1}+i_t\odot {\tilde{C}}_t,h_t=o_t\odot tanh\left(C_t\right)$$

(22)

the candidate cell state is ${\tilde{C}}_t$, the updated cell state is $C_t$, and the hidden state is $h_t$.

$${\widehat{y}}_i=\mathrm{softmax}\left(W^{\left(\mathrm{out}\right)}{h}_t+b^{\left(\mathrm{out}\right)}\right)$$

(23)

where $h_t$ is the final hidden state at time t.

4.2.3. FNN

FNN consists of stacked dense layers with non-linear activation functions, enhanced by dropout regularization and batch normalization between layers to accelerate convergence and stabilize training dynamics [66,67]. The dense connectivity enables comprehensive feature interaction modeling as formulated in Equation (24), while the final prediction is obtained through the softmax transformation of the last hidden representation as shown in Equation (25). Regularization techniques are commonly applied to prevent overfitting in high-dimensional spaces.

$$h^{(l+1)}=\sigma \left(W^{\left(l\right)}{h}^{\left(l\right)}+b^{\left(l\right)}\right),h^{\left(0\right)}=x_i$$

(24)

where $\sigma (·)$ is the activation function, $W^{\left(l\right)}$ and $b^{\left(l\right)}$ are the weights and biases of layer l, and $h^{\left(0\right)}=x_i$ is the input vector of instance i.

$${\widehat{y}}_i=\mathrm{softmax}\left(W^{\left(\mathrm{out}\right)}{h}^{\left(L\right)}+b^{\left(\mathrm{out}\right)}\right)$$

(25)

where $h^{\left(L\right)}$ is the last hidden representation.

Table 4 details the layer structures and training regimes of the three DL models. CNNs use progressively deeper convolutional layers to extract hierarchical features, followed by dense layers for classification. LSTM integrates two recurrent layers to capture temporal dependencies before transitioning to dense layers. The FNN employs multiple dense layers to exploit feature interactions directly. Training configurations are harmonized across models to enable fair comparisons.

4.3. Resilience Threshold Derivation and SLA Risk Analysis

The resilience classification framework establishes quantitative boundaries for algorithm performance degradation based on empirical analysis of 6G service level agreement (SLA) violation risks and operational deployment constraints. This systematic approach draws from ITU-R recommendations, 3GPP technical specifications, and comprehensive industry deployment studies to ensure practical relevance for operational 6G networks.

Modern 6G network slicing demands unprecedented reliability levels, with different service categories imposing distinct performance constraints that directly influence SLA compliance. Our resilience threshold calibration methodology aligns algorithm performance boundaries with documented SLA violation probability distributions, enabling evidence-based deployment decisions across diverse infrastructure scenarios.

The threshold derivation process considers multiple factors: measurement uncertainty inherent in 6G systems, acceptable service degradation boundaries for different application categories, monitoring resource requirements, and documented failure mode analysis from operational networks. Table 5 presents the comprehensive threshold framework linking performance degradation levels to SLA violation risks and deployment suitability.

Table 5. SLA-based resilience threshold derivation.

Category	Threshold	SLA Violation Risk	Empirical Basis	Deployment Suitability
Excellent	$\Delta A\ge -5\%$	<1%	Measurement uncertainty bounds	Mission-critical slices
Good	$-10\%\le \Delta A<-5\%$	1–5%	Acceptable service degradation	Commercial deployments
Moderate	$-20\%\le \Delta A<-10\%$	5–15%	Requires active monitoring	Non-critical applications
Poor	$\Delta A<-20\%$	>15%	Unacceptable for deployment	Research/development only

The Excellent resilience threshold (−5%) reflects inherent measurement uncertainty documented in 6G system specifications. According to 3GPP technical reports [46], typical radio frequency measurement accuracy ranges from 3 to 5% under operational conditions, making performance variations within this range attributable to normal operational variance rather than algorithmic degradation. Algorithms maintaining performance within this bound demonstrate robustness characteristics suitable for ultra-reliable low-latency communication (URLLC) and extremely reliable low-latency communication (ERLLC) slices requiring 99.999% availability.

The Good resilience threshold (−5% to −10%) aligns with acceptable service quality boundaries established through extensive user experience studies in commercial deployments. Industry research [68] demonstrates that user satisfaction remains within acceptable parameters for performance degradations up to 10% in bandwidth-intensive applications, making this threshold appropriate for further enhanced mobile broadband (feMBB) and ultra-massive machine type communication (umMTC) deployments where slight performance variations do not compromise core functionality.

The Moderate resilience threshold (−10% to −20%) identifies algorithms requiring enhanced monitoring infrastructure and potential redundancy mechanisms to maintain service continuity. This boundary reflects the transition point between acceptable and concerning performance levels documented in comprehensive network operator studies [43], indicating that while deployment remains feasible, additional operational oversight becomes necessary to prevent service degradation.

The Poor resilience threshold (>−20%) establishes the boundary for unacceptable operational performance based on systematic SLA violation analysis [69]. Performance degradations exceeding 20% indicate fundamental algorithmic limitations that compromise service delivery reliability, requiring substantial improvements before consideration for production deployment in any operational scenario.

This resilience-based classification framework enables quantitative deployment risk assessment through the following mathematical relationship:

$$\begin{array}{cc}\hfill {\mathrm{Risk}}_{\mathrm{deployment}}& =f(\Delta A,\mathrm{Service}\mathrm{Category},\mathrm{Infrastructure}\mathrm{Type})\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill \mathrm{where}f(\Delta A)& =\left\{\begin{array}{cc}\mathrm{Minimal}\hfill & \mathrm{if}\Delta A\ge -5\%\hfill \\ \mathrm{Low}\hfill & \mathrm{if}-10\%\le \Delta A<-5\%\hfill \\ \mathrm{Moderate}\hfill & \mathrm{if}-20\%\le \Delta A<-10\%\hfill \\ \mathrm{High}\hfill & \mathrm{if}\Delta A<-20\%\hfill \end{array}\right.\hfill \end{array}$$

(27)

where $\Delta A$ represents the relative accuracy change between controlled and realistic conditions, enabling systematic algorithm selection aligned with specific deployment scenarios, risk tolerance requirements, and operational infrastructure constraints. This framework provides network operators with quantitative guidance for evidence-based decision making in algorithm selection and deployment planning across diverse 6G infrastructure scenarios.

5. Experimental Results and Analysis

All experiments were conducted on Google Colab Pro+ platform (Ubuntu 22.04.4 LTS runtime environment) with high-RAM configuration (51.0 GB system RAM; GPU acceleration enabled), ensuring reproducible performance comparisons across algorithms while representing the typical cloud-based infrastructure available for 6G network operators.

5.1. Performance Analysis: PRDA vs. LVRT Comparison

The experimental evaluation reveals distinct algorithmic behaviors under controlled laboratory conditions PRDA versus realistic operational environments LVRT. Table 6 presents baseline performance under idealized conditions, where deep learning models achieve perfect accuracy (CNN, FNN: 100%) at significant computational cost (46–56 s training time), while traditional algorithms demonstrate varying effectiveness ranging from 60.9% (SVM) to 89.0% (Naive Bayes). It is important to note that performance changes are measured as degradation percentages; positive values indicate accuracy loss under realistic conditions, while negative values indicate counter-intuitive improvements.

Table 6. PRDA results (10,000 samples).

Algorithm	Accuracy	Training Time (s)	Efficiency Class
Naive Bayes	0.890	0.02	Excellent
XGBoost	0.874	0.48	Very Good
Gradient Boosting	0.871	15.53	Very Good
Random Forest	0.858	7.09	Very Good
Decision Tree	0.803	0.24	Good
Logistic Regression	0.652	0.31	Acceptable
k-NN	0.650	0.06	Acceptable
SVM (RBF)	0.609	35.49	Poor
CNN	1.000	52.36	Excellent
FNN	1.000	55.64	Excellent
LSTM	0.785	46.02	Acceptable

Table 7 demonstrates performance under realistic operational conditions incorporating network congestion, missing data, and multi-layer interference patterns. Deep learning models maintain superior performance (CNN: 81.2%; FNN: 81.1%) while traditional algorithms exhibit remarkable adaptability, with several showing counter-intuitive performance improvements under realistic conditions.

Table 7. LVRT results (21,033 samples).

Algorithm	Accuracy	Training Time (s)	Resilience Class
Random Forest	0.726	15.89	Moderate
XGBoost	0.726	1.52	Moderate
Gradient Boosting	0.723	789.5	Moderate
Logistic Regression	0.719	0.57	Excellent
SVM (RBF)	0.695	521.3	Excellent
Decision Tree	0.667	1.93	Moderate
k-NN	0.643	0.17	Excellent
Naive Bayes	0.580	0.04	Poor
CNN	0.812	55.88	Good
FNN	0.811	53.68	Good
LSTM	0.748	57.82	Moderate

To quantify algorithmic resilience, we define the relative accuracy change as follows:

$$\Delta \left(\mathcal{A}\right)={\displaystyle \frac{A_{PRDA}\left(\mathcal{A}\right)-A_{LVRT}\left(\mathcal{A}\right)}{A_{PRDA}\left(\mathcal{A}\right)}}\times 100\%$$

(28)

where $A_{PRDA}\left(\mathcal{A}\right)$ and $A_{LVRT}\left(\mathcal{A}\right)$ denote the accuracies of algorithm $\mathcal{A}$ under PRDA and LVRT, respectively. Negative values indicate performance improvement under realistic conditions, while positive values signify degradation. Here, positive $\Delta \left(\mathcal{A}\right)$ values indicate performance degradation (e.g., CNN: +18.8% means accuracy decreased from 100% to 81.2%), and the negative values indicate performance improvement under realistic conditions (e.g., SVM: −14.1% means accuracy increased from 60.9% to 69.5%).

Figure 7 illustrates the performance transition patterns across all evaluated algorithms. To quantify algorithmic resilience, we define the relative accuracy change as shown in Equation (28), where negative values indicate performance improvement under realistic conditions.

Figure 7. PRDA vs. LVRT accuracy comparison across algorithms.

Table 8 reveals three distinct adaptation patterns:

Table 8. Performance transition (PRDA → LVRT) across algorithms.

Algorithm	Accuracy Change, $\mathbf{\Delta }\mathit{A}$ (%)	Training Time (PRDA, s)	Training Time (LVRT, s)
SVM (RBF)	−14.1	35.49	521.3
Logistic Regression	−10.3	0.31	0.57
k-NN	+1.1	0.06	0.17
LSTM	+4.7	46.02	57.82
Random Forest	+15.4	7.09	15.89
XGBoost	+16.9	0.48	1.52
Decision Tree	+16.9	0.24	1.93
Gradient Boosting	+17.0	15.53	789.5
CNN	+18.8	52.36	55.88
FNN	+18.9	55.64	53.68
Naive Bayes	+34.8	0.02	0.04

• Resilient: SVM (RBF) and Logistic Regression show performance improvements (−14.1% and −10.3%, respectively), demonstrating robustness under realistic conditions.
• Stable: k-NN maintains consistent performance (+1.1%), showing minimal sensitivity to operational changes.
• Degrading: Traditional ML algorithms (Naive Bayes +34.8%, ensemble methods +15–17%) and deep learning models (CNN +18.8%, FNN +18.9%) experience substantial performance losses under realistic conditions.

The performance degradation observed in ensemble methods and neural networks under LVRT conditions reflects challenges in handling realistic operational stress, where algorithms trained on clean data struggle with the complexity introduced by noise, class imbalance, and missing data patterns characteristic of operational 6G networks.

In the Table 8, the $\Delta A$ metric quantifies performance change as follows: $\Delta A={\displaystyle \frac{A_{PRDA}-A_{LVRT}}{A_{PRDA}}}\times 100\%$. Therefore, positive values (e.g., Naive Bayes +34.8%) represent accuracy degradation, while negative values (e.g., SVM −14.1%) indicate improved performance under realistic conditions.

5.2. Computational Efficiency and Deployment Constraints

The training time analysis reveals critical trade-offs for 6G edge deployment scenarios where computational resources impose strict operational constraints. Figure 8 demonstrates the computational cost spectrum across algorithm families, with lightweight models (Naive Bayes: 0.02 s) enabling real-time edge deployment while complex architectures (CNN: 52.36 s) require centralized training with inference model distribution.

Figure 8. Average training time comparison (log scale) between traditional ML and DL models.

Edge deployment constraints create a three-tier strategy: sub-0.1 s algorithms enable direct edge deployment for emergency slice reconfiguration, medium-complexity algorithms (0.2–15 s) support regional cloud deployment for near-real-time operations, while high-complexity algorithms require centralized training architectures. The 2600× speed advantage of Naive Bayes over CNN translates to proportional energy savings critical for sustainable 6G operations.

The analysis of computational complexity in Table 9 shows clear boundaries for the deployment of 6G network slicing algorithms. Linear complexity algorithms (Naive Bayes, k-NN) enable real-time edge deployment essential for ultra-low latency slicing scenarios [61,70]. Log-linear methods (Decision Tree, ensemble approaches) require regional cloud infrastructure [53,55,71]. Quadratic complexity algorithms (SVM) exhibit prohibitive scaling, limiting deployment to offline scenarios [59]. Deep learning architectures maintain high training complexity with consistent inference requirements, necessitating centralized training with edge inference deployment [64,66]. This analysis establishes the boundaries of computational feasibility that are essential for selecting algorithms in resource-constrained 6G deployment scenarios, where real-time decision-making (with a latency of less than 100 ms for URLLC applications) is a fundamental operational requirement.

Table 9. Algorithm complexity.

Algorithm	Training Complexity	Prediction Complexity
Naive Bayes	$O\left(ndc\right)$	$O\left(cd\right)$
k-NN	$O\left(nd\right)$	$O\left(nd\right)$
Logistic Regression	$O\left(ndt\right)$	$O\left(d\right)$
Decision Tree	$O(ndlogn)$	$O\left(h\right)$
XGBoost	$O(M·ndlogn)$	$O(M·h)$
Random Forest	$O(B·ndlogn)$	$O(B·h)$
Gradient Boosting	$O(M·ndlogn)$	$O(M·h)$
SVM (RBF)	$O\left(n^{2}d\right)$	$O\left(svd\right)$
FNN	$O(L·H·(H+d)·n·e)$	$O(L·H·(H+d\left)\right)$
CNN	$O(K·F·H·W·k^2·n·e)$	$O(K·F·H·W·k^2)$
LSTM	$O(H·(d+H)·T·n·e)$	$O(H·(d+H)·T)$

Notation: n = samples, d = features, c = classes, t = iterations, h = tree depth, B = trees, M = boosting steps, L = layers, H = hidden units, e = epochs, k = kernel size, T = sequence length, and $sv$ = support vectors.

The theoretical complexity bounds translate into concrete operational constraints when evaluated against our dataset parameters ($n=10,000$–$21,033$; $d=5$; $c=5$). Linear complexity algorithms demonstrate manageable scaling. Naive Bayes processes $250,000$ operations (PRDA) expanding to $525,825$ operations (LVRT) with a proportional $2\times$ training time increase ($0.02$ s→$0.04$ s), while k-NN scales from $50,000$ to $105,165$ operations with a $2.8\times$ time increase ($0.06$ s→$0.17$ s). These remain within the $<100$ ms URLLC requirements for real-time edge deployment. Quadratic complexity algorithms reveal prohibitive scaling: SVM operations expand from 500 M to $2.2$ B, manifesting as dramatic as a $14.7\times$ training time degradation ($35.49$ s→$521.3$ s). This exponential growth renders SVM incompatible with dynamic 6G slice reconfiguration requirements. Deep learning architectures process $1.34$ B–$2.82$ B operations but maintain stable 52–56 s training times due to fixed epoch limits, necessitating hybrid deployment with centralized training and edge inference. The analysis sets quantitative deployment boundaries: real-time slice adaptation can only be supported by sub-second algorithms (Naive Bayes; k-NN), while 6G’s millisecond decision requirements are incompatible with quadratic methods because they create computational bottlenecks. This numerical validation shows that operational constraints, rather than laboratory accuracy, should inform decisions on which algorithms to use for 6G.

5.3. Algorithm Resilience Validation

To validate the robustness of our findings across varying operational conditions, we conducted comprehensive sensitivity analysis under multiple urban 6G SNR scenarios reflecting documented deployment environments. The validation methodology employed three representative urban conditions: optimal urban environments (18–25 dB SNR) characteristic of well-planned metropolitan deployments, dense urban environments (8-15 dB SNR) representing challenging high-density scenarios, and extreme challenging conditions (0–8 dB SNR) simulating worst-case interference scenarios with significant electromagnetic interference from industrial equipment and competing wireless systems.

Table 10 demonstrates the resilience rankings remain highly stable across all SNR conditions, with Spearman’s correlation coefficient $\rho =0.989$ (p < 0.001) between optimal and challenging scenarios, providing strong evidence for the reliability of our resilience classifications across the complete spectrum of evaluated algorithms.

Table 10. Comprehensive algorithm performance across urban 6G SNR scenarios.

Algorithm	Optimal (%)	Dense (%)	Challenging (%)	Resilience Category
CNN	82.4	81.8	80.1	Good
FNN	82.1	81.3	79.9	Good
Random Forest	74.2	73.1	71.8	Moderate
XGBoost	74.0	72.9	71.6	Moderate
Gradient Boosting	73.8	72.7	71.4	Moderate
LSTM	76.1	75.3	73.9	Moderate
Logistic Regression	73.2	72.8	72.0	Excellent
SVM (RBF)	70.8	70.2	69.1	Excellent
Decision Tree	68.1	67.4	66.2	Moderate
k-NN	65.5	64.9	63.7	Excellent
Naive Bayes	59.2	58.1	56.8	Poor

5.3.1. Statistical Validation of Resilience Classifications

Bootstrap confidence interval analysis (n = 1000 iterations) confirmed statistical significance of performance differences across all evaluated algorithms (p < 0.05). The analysis categorized algorithms based on their performance degradation under realistic operational conditions relative to laboratory benchmarks:

• Excellent Resilience (3 algorithms): Mean degradation +8.2% ± 2.1%. These algorithms (SVM, Logistic Regression, and k-NN) demonstrate relatively stable performance under operational stress.
• Good Resilience (2 algorithms): Mean degradation +18.9% ± 0.1%. This category includes CNN and FNN, showing manageable performance loss while maintaining high absolute accuracy levels suitable for high-performance applications.
• Moderate Resilience (5 algorithms): Mean degradation +15.8% ± 1.2%. Enhanced LSTM, ensemble methods (Random Forest, XGBoost, and Gradient Boosting), and Decision Tree require careful deployment consideration with appropriate monitoring mechanisms for standard commercial slice deployments.
• Poor Resilience (1 algorithm): Mean degradation +34.8%. Naive Bayes demonstrates substantial performance degradation unsuitable for production deployment without significant algorithmic modifications or restricted to research environments.

The one-sample t-test confirmed statistically significant overall performance variation (t = −4.139, p = 0.002), with Cohen’s effect sizes ranging from small (d = −4.41) to large (d = −146.39), demonstrating substantial heterogeneity in algorithmic responses to operational stress conditions. These findings provide empirical evidence for algorithm-specific resilience characteristics that must be considered in practical 6G network slice management decisions.

5.3.2. Mechanism Validation Through Empirical Analysis

To validate the three proposed improvement mechanisms underlying the resilience phenomenon, we conducted systematic ablation studies isolating individual transformation components. Each mechanism was tested independently to establish causal relationships between specific environmental factors and algorithmic performance changes.

SMOTE Regularization Effect: Controlled experiments comparing identical datasets with and without SMOTE augmentation revealed differential algorithmic responses to synthetic minority class generation. Linear algorithms (SVM; Logistic Regression) showed average performance improvements of 8–12%, demonstrating enhanced decision boundary robustness. Tree-based methods exhibited mixed responses, with ensemble methods showing modest improvements (2-4%) while simple Decision Trees remained relatively stable.

Noise-Induced Regularization: Systematic noise injection experiments across controlled SNR ranges demonstrated that linear algorithms with appropriate regularization (SVM; Logistic Regression) improved generalization capability under moderate noise conditions by 6–10%. Neural networks exhibited performance degradation of 18–19%, while ensemble methods showed moderate degradation of 15–17%. This differential response supports the regularization hypothesis that controlled noise prevents overfitting for algorithms with appropriate inductive biases.

Class Imbalance Adaptation: Analysis of algorithmic responses to realistic class imbalance patterns (9:1 ratio) revealed that certain algorithms exploit structured imbalance more effectively than balanced distributions. Linear classifiers demonstrated superior adaptation to minority class detection, while tree-based methods struggled with extreme imbalance despite SMOTE augmentation.

These empirical validations provide mechanistic evidence that performance changes under realistic conditions reflect fundamental algorithmic characteristics rather than random degradation. Linear algorithms with strong regularization demonstrate superior resilience, while complex ensemble methods and neural networks show vulnerability to operational stress despite higher laboratory performance.

5.4. XAI Analysis and Algorithm Interpretability

The deployment of ML algorithms in mission-critical 6G network slicing requires transparent and interpretable decision-making processes to ensure regulatory compliance and operational confidence. This section presents a comprehensive explainability analysis using the SHAP (SHapley Additive exPlanations) framework to quantify feature importance patterns and establish deployment guidelines based on interpretability requirements.

5.4.1. SHAP-Based Feature Importance Framework

The deployment of ML algorithms in mission-critical 6G network slicing necessitates transparent decision-making processes to ensure regulatory compliance and operational confidence. We employ algorithm-specific SHAP explainers tailored to model characteristics: TreeExplainer for ensemble methods, LinearExplainer for Logistic Regression, and KernelExplainer for SVM and k-NN architectures.

To validate interpretation robustness, we applied three complementary explainability methods to the k-NN classifier. Figure 9 demonstrates remarkable consistency across SHAP, LIME, and Permutation Importance methods, with Packet Loss Budget dominating feature importance rankings (0.15–0.30 across methods) in both operational scenarios. This cross-method agreement validates that our interpretations reflect genuine algorithmic behavior rather than method-specific artifacts.

Figure 9. Global explainability comparison for the k-NN model.

The analysis reveals cross-scenario variability in algorithmic focus patterns. Figure 10 illustrates how Decision Tree models adapt their feature emphasis between datasets, with PRDA models prioritizing Slice Jitter (0.320) and Slice Latency (0.298), while LVRT models demonstrate increased reliance on Packet Loss Budget (0.332), reflecting operational stress adaptation mechanisms.

Figure 10. Comparison of SHAP-based feature importance between PRDA (left) and LVRT (right) Decision Tree models.

5.4.2. Cross-Scenario Consistency Analysis

Cross-scenario consistency analysis quantifies explanation stability between PRDA and LVRT datasets using correlation coefficients of feature importance rankings. The comprehensive evaluation presented in Table 11 reveals distinct interpretability profiles that directly impact deployment suitability across diverse 6G infrastructure scenarios.

Table 11. Algorithm interpretability consistency analysis.

Algorithm	Consistency Score	Category	Primary Feature Focus
CNN	1.000	High	Packet Loss Budget
LSTM	1.000	High	Packet Loss Budget
Naive Bayes	0.998	High	Packet Loss Budget
SVM (RBF)	0.997	High	Packet Loss Budget
Logistic Regression	0.988	High	Slice Jitter
FNN	0.981	High	Packet Loss Budget
k-NN (Weighted)	0.735	Moderate	Packet Loss Budget
Gradient Boosting	0.448	Moderate	Slice Jitter/Latency
Decision Tree	0.398	Moderate	Slice Jitter
Random Forest	0.351	Moderate	Slice Packet Loss/Jitter
XGBoost	0.106	Low	Packet Loss Budget/Latency

Neural network architectures demonstrate exceptional interpretability stability, with CNN and LSTM achieving perfect consistency scores (1.000) as shown in the table. Classical algorithms exhibit similarly robust behavior, with Naive Bayes (0.998), SVM (0.997), and Logistic Regression (0.988) maintaining minimal explanation variance across operational conditions. These high-consistency algorithms provide reliable feature importance rankings essential for regulatory compliance scenarios.

Conversely, XGBoost presents significant interpretability challenges despite competitive accuracy performance, exhibiting the lowest consistency score (0.106) in our analysis. This finding indicates that high predictive performance does not guarantee explanation stability, necessitating careful consideration of interpretability requirements in algorithm selection decisions.

5.4.3. Algorithm Selection Guidelines for 6G Deployment

Local explanation analysis provides concrete insights into algorithmic decision-making under varying operational conditions. Table 12 and Table 13 present detailed misclassification analysis under contrasting SNR environments, demonstrating how operational stress fundamentally alters feature attribution patterns.

Table 12. Local explanation for high SNR misclassification case (k-NN, Sample #0).

Case Details	True: 2 → Predicted: 3 (57.14% Confidence)
Key SHAP Contributors
Slice Latency (ns)	+0.3100 (primary driver toward class 3)
Slice Jitter (ns)	+0.0100 (secondary driver)
LIME Decision Thresholds
Latency trigger	$1.89\times {10}^6$< Slice Latency ≤ $4.55\times {10}^6$ ns
Jitter trigger	Slice Jitter > $2.34\times {10}^6$ ns
Feature Values vs. Correct Sample (#98)
Slice Latency	$4.19\times {10}^6$ ns vs. $-24.9\times {10}^6$ ns (+29.1 M diff)
Slice Jitter	$3.07\times {10}^6$ ns vs. $0.98\times {10}^6$ ns (+2.09 M diff)

Table 13. Local explanation for low SNR misclassification case (k-NN, Sample #0).

Case Details	True: 2 → Predicted: 0 (57.14% Confidence)
Key SHAP Contributors
Slice Latency (ns)	−0.9400 (strong negative driver from correct class)
Slice Jitter (ns)	+0.0200 (weak positive toward class 0)
LIME Decision Thresholds
Jitter trigger	Slice Jitter > 4.54e6 ns (+0.0401)
Latency trigger	Slice Latency > 23.0 M ns (−0.0293)
Feature Values vs. Correct Sample (#1)
Slice Latency	$38.0\times {10}^6$ ns vs. $-7.45\times {10}^6$ ns (+45.4 M diff)
Slice Jitter	$4.68\times {10}^6$ ns vs. $3.89\times {10}^6$ ns ($+0.79\times {10}^6$ diff)
Transfer Rate	11,644 Gbps vs. −9,030 Gbps (+20.7 K diff)

Under high SNR conditions (15–25 dB), as detailed in Table 12, moderate latency elevation (4.19M ns) generates positive SHAP contributions (+0.31) suggesting similarity-based classification mechanisms. In contrast, Table 13 reveals that low SNR environments (−10 to +5 dB) produce extreme latency values (38.0M ns) triggering strong negative SHAP contributions (−0.94), indicating a shift from pattern recognition to outlier-based rejection under operational stress.

The analysis establishes evidence-based deployment guidelines linking interpretability characteristics with operational requirements. Mission-critical infrastructure benefits from CNN and FNN architectures that combine high accuracy (>0.81) with perfect consistency scores (1.000). Regulatory compliance scenarios are optimally served by classical algorithms maintaining high consistency while providing audit-ready explanation generation. Performance-focused deployments may utilize XGBoost despite interpretability limitations, provided intensive explanation monitoring compensates for consistency challenges.

5.4.4. Deployment Guidelines and Operational Monitoring Framework

The interpretability analysis establishes evidence-based deployment guidelines that integrate performance characteristics, explanation stability, and operational monitoring requirements across diverse 6G network slicing scenarios. This comprehensive framework enables algorithm selection tailored to specific operational contexts where transparency demands vary significantly based on regulatory requirements and mission-critical considerations.

Neural network architectures demonstrate exceptional suitability for mission-critical infrastructure deployment, where both high performance and explanation stability are paramount. CNN and FNN achieve superior accuracy levels (0.812 and 0.811, respectively) while maintaining perfect or near-perfect consistency scores (1.000 and 0.981), ensuring reliable interpretability across varying operational conditions. LSTM architectures provide specialized capabilities for temporal pattern analysis in dynamic slicing scenarios, offering perfect consistency (1.000) despite moderate accuracy performance (0.748).

Regulatory compliance scenarios benefit from classical algorithms that prioritize explanation stability over absolute performance metrics. SVM and Logistic Regression maintain exceptional consistency scores (0.997 and 0.988, respectively), providing audit-ready explanation generation essential for regulatory documentation and compliance verification processes. Performance-focused applications may utilize XGBoost despite its interpretability limitations (0.106 consistency), provided comprehensive monitoring compensates for explanation instability while leveraging superior predictive capabilities (0.726 accuracy).

Table 14 synthesizes these findings into practical deployment recommendations, revealing systematic trade-off patterns between algorithmic complexity and explanation requirements.

Table 14. XAI-based algorithm deployment guide.

Algorithm	Accuracy	Consistency	Deployment Scenario	Monitoring Level
CNN	0.812	1.000	Mission-critical systems	High
FNN	0.811	0.981	Mission-critical systems	High
LSTM	0.748	1.000	Temporal pattern analysis	High
Random Forest	0.726	0.351	Performance-focused	Moderate
XGBoost	0.726	0.106	High-performance applications	Intensive
Gradient Boosting	0.723	0.448	Balanced applications	Moderate
Logistic Regression	0.719	0.988	Regulatory compliance	Critical
SVM (RBF)	0.695	0.997	Regulatory compliance	Critical
Decision Tree	0.667	0.398	Transparent pathways	Moderate
k-NN (Weighted)	0.643	0.735	Dynamic environments	Moderate
Naive Bayes	0.580	0.998	Probabilistic reasoning	Critical

The feature importance analysis establishes a hierarchical monitoring framework that prioritizes network parameters based on their demonstrated impact across algorithmic decisions. Packet Loss Budget emerges as the primary monitoring priority, demonstrating consistent dominance across all algorithm categories with feature importance values ranging from 0.15 to 0.30. This parameter requires continuous real-time monitoring with automated anomaly detection capabilities to ensure service continuity and prevent network degradation.

Secondary monitoring priorities encompass Slice Jitter and Latency parameters, which exhibit substantial influence in traditional ML algorithms and require periodic assessment with comprehensive trend analysis capabilities. These timing-critical parameters demand hourly monitoring cycles with weekly threshold reviews to maintain optimal network performance. Contextual parameters including Transmission Rate and Packet Loss constitute the tertiary monitoring tier, requiring monthly trend analysis integrated with quarterly capacity assessments for long-term infrastructure optimization.

This integrated framework creates a comprehensive three-tiered monitoring system that scales intensity according to feature criticality while maintaining service level agreement compliance across all network slicing configurations.

6. Conclusions

This study presents a dual-methodology evaluation framework that comprehensively assesses ML algorithms for 6G network slicing, effectively bridging the gap between laboratory performance and real-world deployment effectiveness. Through systematic comparison of PRDA and LVRT evaluation approaches, we reveal the limitations of conventional laboratory-based assessments in predicting practical performance, emphasizing the necessity of realistic evaluation strategies for operational 6G networks. The investigation contributes to the field in three key ways. First, it quantifies the discrepancy between laboratory and real-world performance, revealing that algorithms achieving perfect accuracy (100% for CNN and FNN) under controlled conditions experience substantial degradation in realistic network environments, with LVRT accuracies ranging from 58.0% to 81.2%. Second, it reveals counter-intuitive patterns of resilience where sophisticated algorithms perform significantly worse (CNN: 18.8 percentage points; FNN: 18.9 points; Naive Bayes: 34.8 points), while simpler classifiers show unexpected improvements (SVM: 14.1 points; Logistic Regression: 10.3 points) when subjected to realistic operational stress. This challenges the notion that algorithms are inherently complex and that data quality is always poor. It demonstrates that certain algorithms can adaptively exploit structural patterns in realistic conditions. Third, it proposes a resilience-based categorization framework for evidence-driven algorithm selection that prioritizes operational stability over idealized laboratory benchmarks, providing network operators with actionable guidance balancing accuracy, computational efficiency, and deployment reliability. The XAI analysis strengthens practical implications through SHAP-based interpretability assessment, identifying Packet Loss Budget as the dominant feature across all algorithms, with Slice Jitter and Slice Latency as secondary factors. This establishes clear monitoring priorities for operational deployment. Neural networks (CNN: 1.000; LSTM: 1.000) and classical algorithms (SVM: 0.997; Logistic Regression: 0.988) exhibit exceptional interpretability consistency suitable for regulatory compliance scenarios. Cross-scenario analysis confirms that algorithm selection must balance accuracy and explanation stability, with high-consistency algorithms proving suitable for mission-critical deployments, while low-consistency algorithms like XGBoost (0.106) require intensive monitoring despite superior accuracy performance. The framework’s enhancement will be achieved through dataset diversity expansion across geographic regions and infrastructure types, incorporation of emerging architectures beyond CNN, FNN, and LSTM, investigation of temporal dynamics in adaptive algorithms, and validation through real-time deployment testing in operational networks. Integration of federated learning approaches with industry standardization efforts has potential to enhance practical adoption and scalability. This comprehensive evaluation methodology ensures regulatory compliance and enhances the reliability and efficiency of mission-critical 6G deployments. While our analysis is based on a single dataset of 10,000 samples, the methodological framework itself—comparing PRDA laboratory conditions with LVRT realistic transformations—provides a dataset-agnostic approach applicable across diverse 6G scenarios. The framework’s value lies not in absolute performance metrics but in revealing systematic algorithmic behavior patterns under operational stress, establishing evidence-based guidelines for deployment decisions that balance accuracy (58.0–81.2% under realistic conditions), computational efficiency (0.04 s–789.5 s training times), and interpretability consistency (0.106–1.000 scores). Future validation across heterogeneous network environments will further strengthen the generalizability of these resilience-based insights, ultimately establishing a new standard for realistic ML algorithm assessment in next-generation wireless networks.

7. Future Work

While this study establishes a robust framework for evaluating 6G network slice classification algorithms under realistic conditions, it should be noted that several avenues remain for further exploration. Subsequent research will concentrate on validating the findings on heterogeneous, real-world datasets spanning multiple network domains in order to assess the generalizability of resilience-based insights. The investigation will encompass advanced DL architectures, including Graph Neural Networks for topology-aware modeling, Transformers for capturing long-range temporal dependencies, and hybrid CNN-LSTM models for spatio-temporal feature extraction. The development of online and continual learning algorithms will facilitate the adaptation of models to dynamic network conditions and enable the acquisition of new slice types without the occurrence of catastrophic forgetting. In order to enhance the robustness of the system while preserving data privacy, the implementation of federated learning frameworks for collaborative model training across multiple operators is proposed. The utilization of XAI-driven insights will facilitate the proposal of minimal yet sufficient feature sets for AI-based slice management, thereby contributing to standardization efforts for interoperable multi-vendor orchestration. Furthermore, the LVRT framework should be extended to capture rare catastrophic events and unpredictable anomalies beyond systematic operational impairments. Future work will incorporate stochastic extreme-event modeling, adversarial stress testing, and heavy-tailed distribution analysis to ensure algorithmic resilience in mission-critical slices (mURLLC; ERLLC) under low-probability–high-impact scenarios. This extension will complement current systematic stress testing with comprehensive anomaly detection capabilities essential for ultra-reliable 6G deployments. Finally, the most resilient algorithms will be deployed on physical 6G testbeds to evaluate real-time performance, computational overhead, and latency in closed-loop network slice orchestration. By pursuing these directions, the framework presented in this work can evolve into practical, deployable, and standardized AI solutions, supporting the autonomous and efficient operation of future 6G networks.