Abstract
Dynamic environments pose significant challenges for visual SLAM, including feature ambiguity, weak textures, and map inconsistencies caused by moving objects. We present a robust SLAM framework integrating image enhancement, a mixed-precision quantized feature detection network, semantic-driven dynamic feature filtering, and NeRF-based static scene reconstruction. The system reliably extracts features under challenging conditions, removes dynamic points using instance segmentation combined with polar geometric constraints, and reconstructs static scenes with enhanced structural fidelity. Extensive experiments on TUM RGB-D, BONN RGB-D, and a custom dataset demonstrate notable improvements in the RMSE, mean, median, and standard deviation. Compared with ORB-SLAM3, our method achieves an average RMSE reduction of 93.4%, demonstrating substantial improvement, and relative to other state-of-the-art dynamic SLAM systems, it improves the average RMSE by 49.6% on TUM and 23.1% on BONN, highlighting its high accuracy, robustness, and adaptability in complex and highly dynamic environments.
1. Introduction
In order to autonomously complete complex tasks in unknown environments, robots need to have an accurate perception of their own state and effective cognition of the surrounding environment. Visual sensors, as a key tool for information acquisition, make Simultaneous Localization and Mapping (SLAM) based on image information one of the core directions of research, and the related technology is called visual SLAM. Among many application scenarios, visual SLAM in indoor environments is highly valued for its wide range of applications in the fields of intelligent robotics, Augmented Reality (AR), indoor navigation and security monitoring, etc., and has received a great deal of attention due to its wide application value [1]. Compared with outdoor environments, indoor scenes tend to be more complex in structure, sparse in texture information, and usually do not have access to auxiliary information from global navigation satellite systems (e.g., GPS or BDS [2]), which puts more stringent requirements on the system’s sensor robustness and algorithmic accuracy. In recent years, benefiting from the rapid development of computer vision and deep learning, a number of high-performance vision SLAM systems such as SVO [3], LSD-SLAM [4], VINS-Fusion [5], and the ORB-SLAM series [6,7,8] have been introduced. Among them, ORB-SLAM3 [8], as one of the most representative feature point methods, is widely recognized as representative of current systems with excellent accuracy and robustness due to its excellent performance in multi-sensor fusion and scene adaptation. However, mainstream visual SLAM methods generally rely on static scene assumptions, which significantly limits their ability to adapt to dynamic environments in the real world, and becomes a key bottleneck that restricts their practical deployment and generalization.
Most other mature vision SLAM schemes deal with dynamic anomalies based on the Random Sampling Consistency Algorithm (RANSAC) [9]. SVO combines the photometric error minimization of the direct method of image blocks with RANSAC to improve the adaptability to dynamic regions, and VINS-Fusion filters out false matches in dynamic scenes by estimating the essentiality matrix via the RANSAC + five-point method. The ORB-SLAM family computes the single responsiveness matrix or the basis matrix, and combines RANSAC to accurately reject abnormal feature points. However, the robustness of RANSAC still has limitations in dynamic feature-intensive scenarios: when the proportion of outlier points is too high, its model fitting ability decreases rapidly [10], which, in turn, affects the tracking stability and map accuracy of the SLAM system. To break through this limitation, some works have started to introduce deep learning methods for explicit modeling of dynamic regions.
Dynamic SLAM methods based on target detection or semantic segmentation (e.g., Detect-SLAM [11], DynaSLAM [12]) improve robustness by recognizing and rejecting dynamic targets, but are prone to misclassifying potentially dynamic objects such as stationary pedestrians or parked vehicles as moving regions, leading to over-filtering of information. In contrast, motion-consistent segmentation methods based on optical flow or scene flow (e.g., STDyn-SLAM [13], DytanVO [14]) can achieve pixel-level dynamic detection; however, they are prone to be limited by the accuracy of the optical flow and perform inconsistently in low-texture, illumination-varying, or slow-motion scenes. In addition, the uncertainty of deep learning methods may also lead to erroneous deletion of valuable information, which makes some dynamic SLAM systems perform poorly in static environments.
Therefore, more accurate detection algorithms and more reasonable processing strategies are urgently needed for dynamic targets. Instance segmentation allows for fine segmentation and instance-level labeling of independent objects in an image, providing a stronger a priori information for modeling potentially dynamic regions. Traditional geometric methods detect dynamic regions using inter-frame consistency, but they often fail under low-texture or changing lighting conditions, increasing uncertainty in tracking and dynamic segmentation. Instance segmentation provides prior information for feature selection, which can be combined with geometric constraints. To address these issues, this paper proposes a visual SLAM framework with image enhancement that handles both potential and explicit dynamic objects. The main contributions are as follows:
- (1)
- We introduce image enhancement in the front-end to balance grayscale distribution and replace traditional ORB features with a mixed-precision quantized feature detection network. This improves robustness and matching accuracy in low-texture, low-light, and jittery environments.
- (2)
- Using YOLO to extract prior information of dynamic objects and polar geometry, we propose a dynamic feature filtering method. It combines instance segmentation masks with geometric constraints to improve SLAM localization accuracy.
- (3)
- To improve map detail and scene integrity, we introduce a NeRF module to model the static scene after removing dynamic objects. This enhances the structural restoration and geometric consistency of the maps.
- (4)
- We evaluated our system on TUM RGB-D, BONN RGB-D, and a home-made dataset. Compared to ORB-SLAM3, it achieves higher localization accuracy in dynamic scenes and outperforms other state-of-the-art dynamic SLAM methods in terms of robustness.
The rest of the paper is organized as follows: Section 2 introduces related research, Section 3 details the theoretical foundation of the proposed framework, Section 4 demonstrates the experimental design and performance evaluation of dynamic SLAM, and Section 5 summarizes the main conclusions of this study.
2. Related Work
To cope with the SLAM problem in dynamic environments, several studies have used geometric information as a basis for detecting and eliminating the interference of dynamic objects by utilizing spatial geometric constraints between features. COEB-SLAM [15] combines target detection and polar geometry. It first marks dynamic regions by detection, then removes dynamic points through spatial consistency checks. Image blurring is also used as a cue. StaticFusion [16] recognizes dynamic objects by clustering depth maps and calculating dynamic probabilities for each cluster based on camera motion. Trifocal SLAM [17] introduces three-view coplanarity constraints. By using three consecutive frames, it achieves more reliable motion consistency and overcomes the limits of traditional binocular geometry in dynamic scenes. CoSLAM [18] identifies dynamic points by computing the matching relationship between images and then triangulating them. DynaVINS [19] uses a keyframe-based global optimization method. It estimates camera position with IMU and applies multiple constraint assumptions to reduce the effect of dynamic objects on loop detection. PPS-SLAM [20] combines optical flow and polar geometry to detect dynamic regions and retain useful static parts for tracking. It also applies probabilistic cross-frame propagation to reduce the impact of missing semantic information.
Among many geometric methods, although most SLAM systems mainly rely on point features, line features and planar features are also gradually introduced into dynamic visual SLAM, e.g., PL-SLAM [21] performs well in the case of sparse or uneven distribution of point features, but it relies only on the RANSAC method, with a limited effect when processing dynamic objects. Joan et al. [22] proposed an RGB-D based MSC-VO algorithm that integrates point and line features. It leverages geometric constraints and a Manhattan coordinate system to optimize camera pose using both Manhattan axes and reprojection errors. Yuan et al. [23] proposed PLDS-SLAM, which achieves the separation of dynamic and static objects by proposing a geometric constraint method for line segment matching combined with an epipolar constraint method for feature points. DynPL-SLAM [24] introduces a dynamic feature detector that integrates point and line features to handle highly dynamic objects. It also incorporates a new spatial line residual error into pose optimization and applies a histogram-based regional similarity model for keyframe selection and loop detection.
In recent years, deep learning methods such as target detection, target tracking, and feature extraction networks have been widely applied to visual SLAM. These methods effectively improve the robustness and accuracy of the system in localization and image building by providing rich semantic information. Typical representatives include YOLO [25], Siamese network [26], and SuperPoint [27]. Visual semantic-based SLAM methods in static scenes, such as SLAM++ [28], QuadricSLAM [29] have shown good results. In dynamic scenes, semantic information can also provide valuable a priori information for SLAM. DYO-SLAM [30] estimates target parameters by combining clustering, weighted PCA, and minimum bounding rectangles. It further designs a multimodal data association strategy that fuses appearance, semantic, and spatial information to improve tracking robustness in complex dynamic scenes. SP-VSLAM [31] uses the SuperPoint network for feature extraction and binary descriptors. With non-maximum suppression, it ensures uniform feature detection and builds robust feature associations. PLD-SLAM [32] utilizes MobileNet [33] with clustering algorithms for object recognition, followed by the use of epipolar geometric relations to enhance the spatial structure information of the feature points, and deep consistency checking to ensure the consistency of the feature points across different viewpoints. DDN-SLAM [34] addresses dynamic interference by segmenting feature points with semantic features and a hybrid Gaussian model. It further applies sparse point cloud sampling with background restoration and builds maps using NeRF. MVS-SLAM [35] uses YOLOv7 [36] to obtain a priori semantic information to eliminate dynamic features. DGM-VINS [37] uses dyadic geometry and DBSCAN [38] clustering to detect dynamic feature points.
Although the above dynamic SLAM system improves the accuracy and robustness to a certain extent, its feature extraction and semantic perception abilities are still limited, which makes it difficult to fully cope with the complex occlusions and changes in highly dynamic scenes. In order to further improve the perception and localization accuracy of the system in dynamic environments, this paper introduces the ZippyPoint feature network to enhance the stability of keypoint extraction and matching, and combines it with the NeRF for high-quality scene mapping, so as to improve the overall robustness and reconstruction effect of the system in dynamic scenes.
3. System Overview
In this paper, a novel SLAM system integrating semantic understanding and neural rendering is constructed on the basis of ORB-SLAM3. By introducing instance segmentation and a priori information extraction threads, as well as NeRF building threads, the recognition and rejection of dynamic objects are realized. At the same time, the system adopts ZippyPoint to replace the original feature extraction and matching method, which improves the robustness and the quality of image construction in dynamic scenes. The improved system structure is shown in Figure 1:
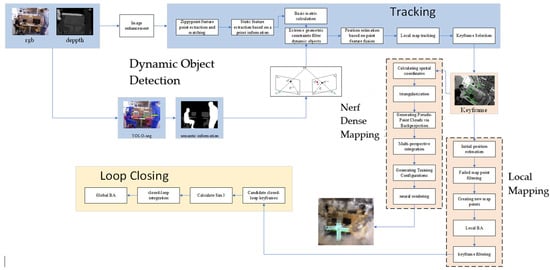
Figure 1.
System module. In addition to the three core threads of ORB-SLAM—tracking, local mapping, and loop closing—the system includes auxiliary threads for instance segmentation, semantic prior extraction, and a dedicated NeRF-based dense mapping process.
In the instance segmentation and semantic information extraction thread, the TensorRT inference-accelerated YOLO instance segmentation network is used to provide accurate instance-level a priori information for the tracking thread; in the tracking thread, ZippyPoint is used for feature extraction, in combination with our proposed MNN matching algorithm, which is designed to improve upon the limitations of ORB features in specific scenarios due to the scarcity of effective feature points. Subsequently, based on the extracted a priori information and polar geometry constraints, dynamic object detection is performed to reject the dynamic features in the current frame. Subsequently, the system completes the inter-frame pose estimation based on static feature points and multi-frame triangulation, and the NeRF mapping module generates a sparse pseudo-point cloud by using the key frame images and the estimated poses to further construct the training data, and then reconstructs the dense, high-fidelity 3D scene through neural rendering, which is an alternative to the traditional point cloud mapping method.
3.1. Image Enhancement Methods for Grayscale Equalization
In this section, an improved image equalization algorithm based on the spatial domain is proposed to extend the idea of traditional grayscale image equalization. The color equalization algorithm calculates the cumulative distribution function by histogram statistics of the input image I and introduces a proportional threshold to remove extreme pixels to precisely define the effective dynamic range. Subsequently, the pixel values are linearly stretched so that they are uniformly distributed over the target range to enhance the overall contrast. The stretched pixel values are calculated as follows:
where denotes restricting the value to the interval [0, 1]. To further improve the local detail performance of the image, a weighted convolution mechanism is introduced, and the weight of the convolution kernel is jointly determined by the local contrast and the local mean:
This weight function is controlled by the moderating coefficient α and the exponentiation factor p. denotes the absolute difference between the current pixel and its local mean, reflecting the local brightness deviation of the image. reflects the local contrast of the image. However, the enhancement based on local statistical features still suffers from poor adaptation to image content and is prone to local over-enhancement or under-enhancement.
For this reason, this paper introduces a meta-heuristic optimization strategy to simulate the process of finding the optimal solution through pheromone propagation by individual butterflies in space. The weights of the convolution kernel are optimized by defining the fitness function, which is shown in Equation (3), and the process of finding the optimal solution is shown in Figure 2.
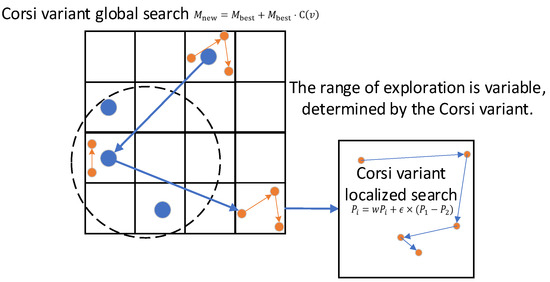
Figure 2.
Weighted search schematic. The (left) panel shows the global search with blue dots and arrows representing solutions updated via Cauchy variation, while the (right) panel illustrates local search refinements using inertia and difference strategies, marked in orange.
The optimization process consists of a global search of the Cauchy variation [39] with local fine-tuning of the difference strategy, which gradually and iteratively updates the population and converges to the optimal solution.
After the optimization of the convolutional kernel is completed, a multi-scale strategy is introduced to improve the efficiency and enhancement effect: the image is first downsampled for initial enhancement at low resolution, then upsampled to the original size and weighted to fuse with the high-resolution results. Finally, CLAHE (see Figure 3) is combined to further enhance the local details, so that the enhanced image has a better hierarchical performance while maintaining the natural sense.
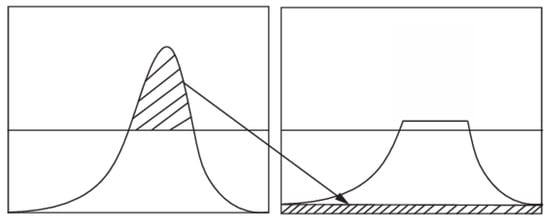
Figure 3.
CLAHE schematic diagram. It processes images in blocks and performs histogram equalization separately on each local region, enhancing local detail contrast while maintaining the natural feel of the image.
3.2. Feature Extraction and Matching
Zippypoint [40] is an advanced keypoint detection and description framework with an encoder of eight convolutional layers and a decoder with three output branches. It employs binary-oriented L2 normalization and a macro block-based mixed-precision quantization scheme to improve efficiency by assigning different numerical precisions to distinct network regions. However, this can cause feature discontinuities and quantization errors, limiting the performance of traditional matching methods. In this work, we modify the Zippypoint architecture (Figure 4) and propose an adaptive feature matching strategy, the MNN method, to overcome these limitations.
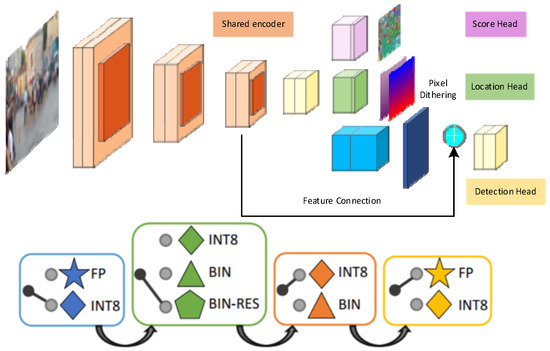
Figure 4.
Improved Zippypoint feature extraction network architecture. The target network is partitioned into macro blocks, each of which is associated with a set of candidate quantization configurations. A traversal process is used to select the optimal configuration for each block.
Feature matching calculates the similarity between different image feature descriptors by means of a distance metric, as indicated by the following equation:
D0, D1 are the sets of feature descriptors of the two images; N0 and N1 denote the number of feature points extracted from the two images; and d denotes the dimension of the descriptor. By combining the inverse values of the feature descriptors with their own inner products, the distance matrix between two descriptors is obtained, where dist[i,j] denotes the distance between the i-th descriptor D0[i] and the j-th descriptor D1[j]. After computing the distance matrix, each descriptor selects its nearest and second-nearest neighbors. A match is accepted if the distance ratio is below threshold and the nearest neighbor’s distance is within threshold . A bidirectional consistency check is then applied to enhance reliability. As shown in Section 4, this method achieves a significantly better matching performance than that of ORB-SLAM3. However, its computational cost grows with the number of features. To reduce complexity, we simplify the distance matrix calculation using squared Euclidean distance.
The improved distance matrix computation reduces computational overhead, where and denote the k-th elements of descriptors from sets and , respectively. Furthermore, the traditional point-wise consistency check limits efficiency. To accelerate matching, we obtain candidate pairs in batches from reverse matching results and verify bidirectional consistency using tensor-based operations.
where represents the reverse match result from to , a bidirectional consistency mask can be constructed based on to obtain the match index of each feature, if and only if
This indicates a bidirectional match. After testing and improvement, the MNN method (referred to as MNN2 in subsequent tests) further improved matching accuracy and speed.
3.3. Dynamic Feature Rejection
3.3.1. Dynamic Feature Filtering via Prior Information and Epipolar Constraints
Traditional dynamic feature filtering methods often rely on dynamic masks, such as removing pixels in regions labeled as highly dynamic (e.g., human bodies). Although computationally efficient, these methods can mistakenly discard static objects labeled as dynamic, such as stationary people, leading to a loss of valid features and reduced localization accuracy. To address this, we propose a dynamic feature filtering algorithm that combines prior semantic information with epipolar geometric constraints. By fusing semantic labels and geometric consistency, the method more accurately distinguishes truly dynamic objects from static background regions misclassified as dynamic. This reduces feature loss due to misclassification while maintaining efficiency, thereby improving overall localization and mapping performance. The algorithm workflow is illustrated in Figure 5.
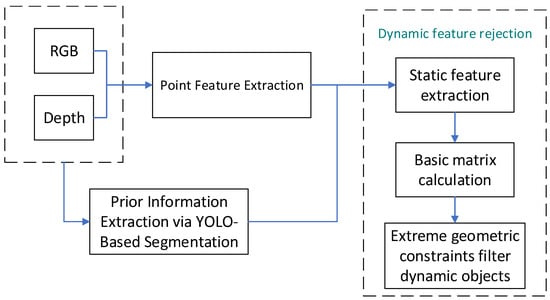
Figure 5.
Dynamic feature filtering algorithm framework. Prior information is obtained through YOLO semantic segmentation, and dynamic objects are filtered out by integrating point features with stringent geometric constraints.
Geometric constraints on polar geometry properties can be used to distinguish whether features are dynamic or static. In multi-view geometry, static features should satisfy the polar surface constraint, whereas dynamic features usually violate this constraint.
For point features, first, it is assumed that all feature points are static. Under this assumption, the polar planes, 3D landmark positions (by least squares solution), camera poses, or projections can be estimated. Then, the error between the estimated and actual measurements is calculated and dynamic features are detected based on a predefined threshold.
Several cases in Figure 6a set thresholds with geometric constraints for static data associations to detect dynamic features.
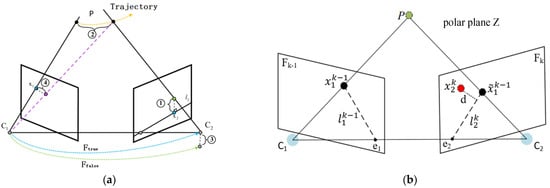
Figure 6.
Point dynamic feature judgment and polar geometry constraints. (a) The violation of geometric constraints for point features in dynamic environments: ① the tracked feature is too far away from the polar line; ② the back-projected rays of the tracked feature are not satisfied; ③ the base matrix is incorrectly estimated when the dynamic feature is included in the attitude estimation; and ④ the distance between the reprojected feature and the observed feature is large. (b) The relationship between corresponding point features in two consecutive frames, showing the epipolar lines, epipoles, and epipolar planes.
After the depth camera captures the k-th frame’s RGB image and corresponding depth data, the YOLO instance segmentation network generates class-specific object masks to extract semantic priors. In parallel, point features are detected in a separate thread. The segmentation-derived priors are then used to define the initial static region , containing point features , which are stored in array for subsequent processing. This step helps suppress dynamic object interference in feature extraction and scene understanding. The initialization arrays are given in (8) and (9).
The correspondence between image point features in two consecutive frames is illustrated in Figure 6b. Let be a static map point whose projections in frames and are denoted as and , respectively, where is the matching point of in .The projection of onto frame is denoted as . Let and denote the camera optical centers. The line connecting them, which is referred to as the baseline, together with the map point , defines the epipolar plane The epipolar plane intersects the image planes of frames and at the epipolar lines and , respectively. The intersection of the baseline with each image plane is called the epipole, denoted as and . This geometric constraint describes the mapping from a point in one image to the corresponding baseline in the other. Let the homogeneous coordinates of and be and , respectively. The mapping can be expressed using the fundamental matrix and homogeneous coordinates as
Based on the transformation relationship between world coordinates and pixel coordinates:
where K is the internal reference matrix of the camera, obtained by couplings (10) and (11):
where is the antisymmetric matrix of the translation vector , such that:
A and B are the linear parameters of obtained by solving according to and . is the distance from to the polar line , as shown in Equation (14):
The value is used to verify dynamic features, where denotes the epipolar threshold parameter. Points with are classified as static, while those with are classified as dynamic. For each instance segmentation mask containing keypoints, we label the mask as dynamic if more than 60% of its points are dynamic—this threshold was determined empirically based on our test results. Finally, points within regions not classified as dynamic, , are added to the array , completing the dynamic feature filtering process based on prior information and epipolar constraints.
3.3.2. NeRF Construction Method
NeRF [41] reconstructs high-quality 3D scenes by learning from sequences of 2D images captured from multiple viewpoints. The framework of our method is shown in Figure 7. After applying the dynamic feature filtering algorithm that integrates prior information with epipolar geometric constraints, a static point set is obtained. To further lift the 2D correspondences in these images into 3D space, linear triangulation is applied to the static point pairs using the known camera poses .
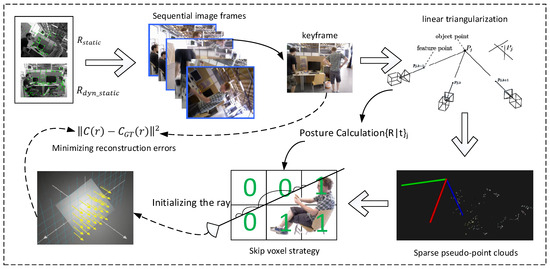
Figure 7.
NeRF mapping framework. The filtered static points are tracked to estimate camera poses, followed by linear triangulation, voxel skipping, and rendering to generate NeRF maps.
Here, and denote the camera poses of the current and reference frames, respectively, and represents the reconstructed 3D points. To ensure triangulation accuracy and stability, reconstruction is performed only when the feature points exhibit favorable covariance. Pseudo-points failing the positive depth constraint or exhibiting large projection errors are discarded to strengthen subsequent geometric constraints. The remaining 3D points from static matches form a sparse pseudo-point cloud for the current frame. Once triangulation is completed, each keyframe and the corresponding camera pose are used as NeRF training inputs, and both the summation and supervised loss functions are constructed.
is the total number of points in the pseudo-point cloud, is the color value of image at pixel coordinates , and represents the color of 3D point . This loss guides the NeRF network to emphasize key 3D geometric structures during training. Rendering colors are obtained by integrating along each ray using the volume-rendering formula:
represents the spatial position of a sampled point along the ray, where is the camera center and is the ray direction. Here, denotes the density function, the color function, and the forward transmittance is defined as
The overall training objective is to minimize both the image reconstruction error and the geometric supervision loss:
where the rendering reconstruction loss is
denotes the color corresponding to ray in the real image, while is the hyperparameter that regulates the geometric supervision weights.
4. Experiments
The experimental platform configuration for this paper is as follows: Ubuntu20.04, The experimental platform configuration for this paper is as follows: Ub-untu20.04, lntel(R) Core(TM) i5-12400F CPU, NVIDIA GeForce RTX 4060Ti GPU, and 8 GB of operating memory. The custom dataset was acquired using an Intel RealSense D435i depth camera (Intel Corporation, Santa Clara, CA, USA), configured at a resolution of 640 × 480, capturing RGB and depth data at 30 FPS.
4.1. Image Enhancement and Feature Extraction
Image enhancement is evaluated on blurred images from the GoPro [42] dataset (see Supplementary Materials) using the deep learning-based Zero-DCE TF [43], CLAHE, and the proposed algorithm. Feature extraction is conducted on custom weak-texture images using ORB, SuperPoint, XFeat [44], and the proposed method. The experimental results are presented in Figure 8.
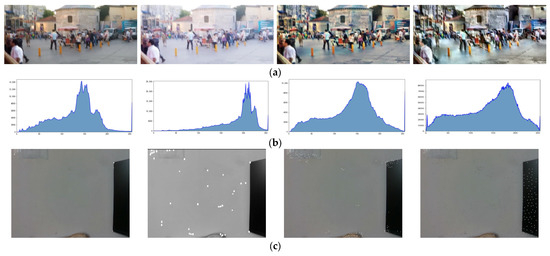
Figure 8.
Image enhancement and feature extraction results. Here, (a) shows the enhanced images; (b) illustrates the corresponding grayscale histograms, where the horizontal axis denotes grayscale levels and the vertical axis indicates pixel counts; and (c) displays the feature extraction results in a weak-texture environment. The algorithm order follows the description above.
In Figure 8a,b, the Zero-DCE TF algorithm improves image brightness but suffers from over-enhancement, with limited adjustment of gray values. CLAHE significantly increases image contrast and yields a more uniform grayscale distribution. In comparison, the proposed algorithm combines the strengths of both, enhancing brightness without over-enhancement and producing a more uniform grayscale distribution. The feature extraction results in Figure 8c are summarized in Table 1, using a confidence threshold of 0.015 and a non-maximum suppression (NMS) window size of 3.

Table 1.
Feature extraction experimental data statistics.
The experimental results show that ORB extracts fewer feature points, while SuperPoint produces more but with significant overlap. XFeat performs well in high-texture regions but is less effective in weak-texture areas. In contrast, the proposed algorithm achieves a more uniform distribution of feature points. Although its total number is lower than SuperPoint, it delivers the best overall performance, with more balanced and effective feature extraction across different regions.
4.2. Feature Point Matching
In SLAM, feature point matching is a core task that identifies identical or similar features in images captured at different times, supporting pose estimation, map updates, and loop closure detection. To evaluate the proposed algorithm, five image sets from HPatches [45], GoPro (see Supplementary Materials), and a custom dataset were tested under varying conditions: illumination change, rotation, viewpoint change, motion blur, and low-texture environments.
In the experiments, 500 feature points were extracted per image pair, and RANSAC was applied to remove false matches. To enhance matching accuracy, the non-maximum suppression (NMS) radius was set to 3, and the matching ratio threshold was set to 0.95. The results are shown in Figure 9.

Figure 9.
Image-matching results. The green line indicates that the match is correct and the wrong match has been eliminated.
The average performance of the four algorithms is summarized in Table 2. The proposed method achieves matching accuracies of 83.10%, 91.63%, 80.95%, 58.66%, and 40.00%, with matching times of 0.245 s, 0.241 s, 0.243 s, 0.256 s, and 0.229 s, respectively. Its average matching accuracy of 70.87% is 52.07%, 26.32%, and 21.25% higher than the other three methods. These results demonstrate that the proposed algorithm effectively reduces localization errors and map drift in SLAM while lowering computational cost, thereby improving overall efficiency and robustness.

Table 2.
Feature matching experimental statistics.
4.3. Posture Estimation
We test our algorithm on the publicly available TUM and BONN datasets (see Supplementary Materials). To evaluate the effectiveness of our SLAM system, we used the EVO [46] tool to measure the absolute trajectory error and compute the root mean square error (RMSE), mean error (Mean), median error (Med), and standard deviation (STD). For reliability, each sequence was tested in ten independent runs, and the median result was reported to minimize the influence of outliers. The results are presented in Table 3.

Table 3.
Absolute trajectory error experimental results (ATE).
Figure 10 shows a comparison of APE trajectory errors for each sequence. The dashed line represents the actual trajectory, while the colored lines represent the trajectories estimated by the SLAM system. The colors indicate the magnitude of the trajectory errors, with colors ranging from blue to red, representing a distribution of errors from low to high.
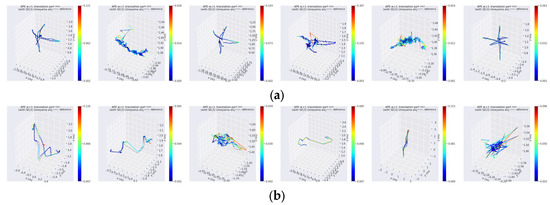
Figure 10.
APE trajectory images. The order of the images is consistent with the order in Table 3. (a) APE trajectories from the TUM dataset. (b) APE trajectories from the BONN dataset.
We further compared the proposed improved algorithm with several state-of-the-art SLAM methods. To objectively assess performance in different dynamic scenarios, the root mean square error (RMSE) was used as a metric to quantify the overall deviation between the estimated and ground-truth trajectories. The results are presented in Table 4 and Table 5.

Table 4.
TUM dataset absolute trajectory error RMSE results.

Table 5.
BONN dataset absolute trajectory error RMSE results.
As shown in the TUM dataset results, the proposed SLAM system consistently achieved the lowest absolute trajectory error across all sequences. It also exhibited superior robustness, avoiding the sudden error spikes observed in LVID-SLAM under rpy rotation and in Dynamic-VINS under xyz vertical translation, even when facing diverse viewpoint trajectories.
According to the BONN dataset results, the proposed SLAM system delivers an outstanding performance in highly dynamic scenarios—such as crowd and synchronous sequences—achieving the lowest absolute trajectory error. For the remaining sequences, its accuracy is generally comparable to, and in some cases surpasses, that of other state-of-the-art methods.
Finally, we conducted ablation studies on three sequences to evaluate the contribution of each module. Specifically, image enhancement is denoted as A, feature extraction and matching as B, and dynamic feature rejection as C. The ablation results are summarized in Table 6.

Table 6.
Melting experiment results.
4.4. NeRF Mapping
This section provides a comprehensive evaluation of the proposed NeRF-based map construction method. The datasets used include the TUM high-dynamic sequences, the BONN moving-camera sequences, and a self-collected dynamic sequence. The point cloud maps without dynamic feature removal are shown in Figure 11.

Figure 11.
Point cloud maps without dynamic feature removal. The results are obtained using the TUM walking_half sequence, the BONN static_close_far sequence, and a self-collected dynamic sequence.
The dense point clouds, octree maps, and NeRF-based maps after dynamic objectremoval are presented in Figure 12.


Figure 12.
Maps after dynamic object removal. From left to right: dense point cloud, octree-based map, and NeRF-based map. (a) TUM walking_halfsphere sequence. (b) BONN static_close_far sequence. (c) Self-collected dynamic sequence.
The dense point clouds, octree maps, and NeRF-based maps after dynamic object removal are shown in Figure 12. In the NeRF-based maps, the red lines represent the camera trajectory. For the self-collected dataset, the trajectory is unavailable due to the lack of ground-truth camera poses, and thus the red trajectory is absent.
4.5. Real-Time Experiments
To further evaluate the operational efficiency of our algorithm, we compared its real-time performance with several leading dynamic SLAM methods, focusing specifically on the average tracking time. The evaluation results are presented in Table 7.

Table 7.
Real-time comparison.
5. Conclusions
In this paper, we present a highly robust visual SLAM system tailored for dynamic scenes. The proposed framework exhibits superior feature extraction and matching performance under challenging conditions, including low-texture regions, weak illumination, and viewpoint jitter. By effectively suppressing the influence of dynamic objects, our method significantly enhances both pose estimation accuracy and the structural completeness of reconstructed maps. Comprehensive evaluations on the TUM RGB-D, BONN RGB-D, and a custom dataset demonstrate substantial gains in key metrics such as RMSE, mean, median, and standard deviation. Compared to ORB-SLAM3, our approach achieves an average RMSE reduction of 93.4%, with notable improvements across all evaluated metrics. Furthermore, while other state-of-the-art dynamic SLAM systems attain average RMSE values of 0.0413 on the TUM dataset and 0.0489 on the BONN dataset, our method achieves 0.0208 and 0.0376, respectively, corresponding to accuracy improvements of 49.6% and 23.1%. These results highlight not only the enhanced precision but also the robustness and adaptability of our system in highly dynamic and complex environments.
However, our current system is primarily evaluated on indoor datasets and may not generalize well to large-scale outdoor environments or scenarios involving rapid motion. To address these limitations, future work could focus on integrating additional geometric features, such as line and planar constraints, to improve map accuracy in structured environments. Incorporating multi-sensor fusion, including LiDAR, IMU, and event cameras, would likely enhance robustness and scalability under challenging outdoor or fast-motion conditions. Furthermore, exploring advanced 3D representations, such as Gaussian or neural implicit models, could enable more detailed and efficient scene reconstruction, balancing high-fidelity mapping with real-time performance. In addition, optimizing NeRF data and developing lightweight neural representations could reduce computational and memory overhead, making high-resolution, real-time scene reconstruction more practical for large-scale or resource-constrained environments.
Supplementary Materials
The following supporting information is available for download: TUM dataset: https://cvg.cit.tum.de/data/datasets/rgbd-dataset/download (accessed on 5 September 2025). BONN dataset: https://www.ipb.uni-bonn.de/data/rgbd-dynamic-dataset/index.html. (accessed on 5 September 2025). HPatches dataset: https://github.com/hpatches/hpatches-dataset. (accessed on 5 September 2025). GoPro Dataset: https://seungjunnah.github.io/Datasets/gopro. (accessed on 5 September 2025). Self-made dataset: Available from the corresponding author upon request.
Author Contributions
Conceptualization, Y.M.; methodology, Y.M. and J.L.; software, J.W.; validation, J.L. and Y.M.; writing—original draft preparation, J.L.; writing—review and editing, J.L.; visualization, J.L. and Y.M.; supervision, J.L.; funding acquisition, Y.M. and J.L.; Y.M. and J.L. contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China (51774235), the Shaanxi Provincial Key R&D General Industrial Project (2021GY-338), and the Xi’an Beilin District Science and Technology Plan Project (GX2333).
Data Availability Statement
Data available on request from the authors. The data that support the findings of this study are available from the corresponding author, Jiahao LV, upon reasonable request.
Conflicts of Interest
Author Jie Wei was employed by Hang Seng Bank Limited, 83 Des Voeux Road Central, Central and Western District, Hong Kong 999077, China. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Sheng, X.; Mao, S.; Yan, Y.; Yang, X. Review on SLAM algorithms for Augmented Reality. Displays 2024, 84, 102806. [Google Scholar] [CrossRef]
- Wang, X.; Li, X.; Yu, H.; Chang, H.; Zhou, Y.; Li, S. GIVL-SLAM: A Robust and High-Precision SLAM System by Tightly Coupled GNSS RTK, Inertial, Vision, and LiDAR. IEEE/ASME Trans. Mechatron. 2024, 30, 1212–1223. [Google Scholar] [CrossRef]
- Forster, C.; Zhang, Z.; Gassner, M.; Werlberger, M.; Scaramuzza, D. SVO: Semidirect visual odometry for monocular and multicamera systems. IEEE Trans. Robot. 2016, 33, 249–265. [Google Scholar] [CrossRef]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-scale direct monocular SLAM. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; Springer International Publishing: Cham, Switzerland, 2014; pp. 834–849. [Google Scholar]
- Qin, T.; Cao, S.; Pan, J.; Shen, S. A general optimization-based framework for global pose estimation with multiple sensors. arXiv 2019, arXiv:1901.03642. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM: A versatile and accurate monocular SLAM system. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Tardos, J.D. ORB-SLAM2: An open-source slam system for monocular, stereo, and RGB-D cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodriguez, J.J.G.; Montiel, J.M.M.; Tardos, J.D. ORB-SLAM3: An accurate open-source library for visual, visual–inertial, and multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- He, W.; Lu, Z.; Liu, X.; Xu, Z.; Zhang, J.; Yang, C.; Geng, L. A real-time and high precision hardware implementation of RANSAC algorithm for visual SLAM achieving mismatched feature point pair elimination. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 5102–5114. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, Y.; Pan, W. Dynamic RGB-D SLAM based on static probability and observation number. IEEE Trans. Instrum. Meas. 2021, 70, 8503411. [Google Scholar] [CrossRef]
- Zhong, F.; Wang, S.; Zhang, Z.; Chen, C.; Wang, Y. Detect-SLAM: Making object detection and SLAM mutually beneficial. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 1001–1010. [Google Scholar]
- Bescos, B.; Facil, J.M.; Civera, J.; Neira, J. DynaSLAM: Tracking, mapping, and inpainting in dynamic scenes. IEEE Robot. Autom. Lett. 2018, 3, 4076–4083. [Google Scholar] [CrossRef]
- Esparza, D.; Flores, G. The STDyn-SLAM: A stereo vision and semantic segmentation approach for VSLAM in dynamic outdoor environments. IEEE Access 2022, 10, 18201–18209. [Google Scholar] [CrossRef]
- Shen, S.; Cai, Y.; Wang, W.; Scherer, S. Dytanvo: Joint refinement of visual odometry and motion segmentation in dynamic environments. arXiv 2022, arXiv:2209.08430. [Google Scholar]
- Min, F.; Wu, Z.; Li, D.; Wang, G.; Liu, N. COEB-SLAM: A robust VSLAM in dynamic environments combined object detection, epipolar geometry constraint, and blur filtering. IEEE Sens. J. 2023, 23, 26279–26291. [Google Scholar] [CrossRef]
- Scona, R.; Jaimez, M.; Petillot, Y.R.; Fallon, M.; Cremers, D. StaticFusion: Background reconstruction for dense RGB-D SLAM in dynamic environments. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 3849–3856. [Google Scholar]
- Dhali, S.; Dasgupta, B. Trifocal SLAM: A dynamic SLAM based on three frame views. Neurocomputing 2025, 625, 130993. [Google Scholar] [CrossRef]
- Zou, D.; Tan, P. CoSLAM: Collaborative visual SLAM in dynamic environments. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 354–366. [Google Scholar] [CrossRef]
- Song, S.; Lim, H.; Lee, A.J.; Myung, H. DynaVINS: A visual-inertial SLAM for dynamic environments. IEEE Robot. Autom. Lett. 2022, 7, 11523–11530. [Google Scholar] [CrossRef]
- Qian, W.; Zhang, H.; Peng, J. PPS-SLAM: Dynamic Visual SLAM with a Precise Pruning Strategy. Comput. Mater. Contin. 2025, 82, 2849–2868. [Google Scholar] [CrossRef]
- Gomez-Ojeda, R.; Moreno, F.; Scaramuzza, D.; Gonzalez-Jimenez, J. Pl-SLAM: A stereo slam system through the combination of points and line segments. IEEE Trans. Robot. 2019, 35, 734–746. [Google Scholar] [CrossRef]
- Company-Corcoles, J.P.; Garcia-Fidalgo, E.; Ortiz, A. MSC-VO: Exploiting Manhattan and structural constraints for visual odometry. IEEE Robot. Autom. Lett. 2022, 7, 2803–2810. [Google Scholar] [CrossRef]
- Yuan, C.; Xu, Y.; Zhou, Q. PLDS-SLAM: Point and line features SLAM in dynamic environment. Remote. Sens. 2023, 15, 1893. [Google Scholar] [CrossRef]
- Zhang, B.; Dong, Y.; Zhao, Y.; Qi, X. Dynpl-slam: A robust stereo visual slam system for dynamic scenes using points and lines. IEEE Trans. Intell. Veh. 2024, early access. [Google Scholar] [CrossRef]
- Jiang, P.; Ergu, D.; Liu, F.; Cai, Y.; Ma, B. A review of yolo algorithm developments. Procedia Comput. Sci. 2022, 199, 1066–1073. [Google Scholar] [CrossRef]
- KS, S.S.; Joo, Y.H.; Jeong, J.H. Keypoint prediction enhanced Siamese networks with attention for accurate visual object tracking. Expert Syst. Appl. 2025, 268, 126237. [Google Scholar]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superpoint: Self-supervised interest point detection and description. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018; pp. 224–236. [Google Scholar]
- Salas-Moreno, R.F.; Newcombe, R.A.; Strasdat, H.; Kelly, P.H.; Davison, A.J. Slam++: Simultaneous localisation and mapping at the level of objects. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 1352–1359. [Google Scholar]
- Nicholson, L.J.; Milford, M.J.; Sunderhauf, N. QuadricSLAM: Dual quadrics from object detections as landmarks in object-oriented SLAM. IEEE Robot. Autom. Lett. 2018, 4, 1–8. [Google Scholar] [CrossRef]
- Hu, X.; Wu, Y.; Zhao, M.; Cao, Z.; Zhang, X.; Ji, X. DYO-SLAM: Visual Localization and Object Mapping in Dynamic Scenes. IEEE Trans. Circuits Syst. Video Technol. 2025, early access. [Google Scholar] [CrossRef]
- Yin, Z.; Feng, D.; Fan, C.; Ju, C.; Zhang, F. SP-VSLAM: Monocular visual-SLAM algorithm based on superpoint network. In Proceedings of the 2023 15th International Conference on Communication Software and Networks (ICCSN), Shenyang, China, 21–23 July 2023; pp. 456–459. [Google Scholar]
- Zhang, C.; Huang, T.; Zhang, R.; Yi, X. PLD-SLAM: A new RGB-D SLAM method with point and line features for indoor dynamic scene. ISPRS Int. J. Geo-Inf. 2021, 10, 163. [Google Scholar] [CrossRef]
- Khan, S.U.R.; Zhao, M.; Li, Y. Detection of MRI brain tumor using residual skip block based modified MobileNet model. Clust. Comput. 2025, 28, 248. [Google Scholar] [CrossRef]
- Li, M.; Guo, Z.; Deng, T.; Zhou, Y.; Ren, Y.; Wang, H. DDN-SLAM: Real time dense dynamic neural implicit SLAM. IEEE Robot. Autom. Lett. 2025, 10, 4300–4307. [Google Scholar] [CrossRef]
- Islam, Q.U.; Ibrahim, H.; Chin, P.K.; Lim, K.; Abdullah, M.Z. MVS-SLAM: Enhanced multiview geometry for improved semantic RGBD SLAM in dynamic environment. J. Field Robot. 2024, 41, 109–130. [Google Scholar] [CrossRef]
- Wang, C.Y.; Bochkovskiy, A.; Liao, H.Y.M. YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 7464–7475. [Google Scholar]
- Song, B.; Yuan, X.; Ying, Z.; Yang, B.; Song, Y.; Zhou, F. DGM-VINS: Visual–inertial SLAM for complex dynamic environments with joint geometry feature extraction and multiple object tracking. IEEE Trans. Instrum. Meas. 2023, 72, 8503711. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J.; Du, K.; Tao, M. Enhanced discontinuity characterization in hard rock pillars using point cloud completion and DBSCAN clustering. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 2025, 186, 106005. [Google Scholar] [CrossRef]
- Patout, F. The Cauchy problem for the infinitesimal model in the regime of small variance. Anal. PDE 2023, 16, 1289–1350. [Google Scholar] [CrossRef]
- Kanakis, M.; Maurer, S.; Spallanzani, M.; Chhatkuli, A.; Van Gool, L. ZippyPoint: Fast interest point detection, description, and matching through mixed precision discretization. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Vancouver, BC, Canada, 17–24 June 2023; pp. 6114–6123. [Google Scholar]
- Chen, T.; Yang, Q.; Chen, Y. Overview of NeRF Technology and Applications. J. Comput. Aided Des. Comput. Graph. 2025, 37, 51–74. [Google Scholar]
- Nah, S.; Kim, T.H.; Lee, K.M. Deep multi-scale convolutional neural network for dynamic scene deblurring. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 3883–3891. [Google Scholar]
- Guo, C.; Li, C.; Guo, J.; Loy, C.C.; Hou, J.; Kwong, S.; Cong, R. Zero-reference deep curve estimation for low-light image enhancement. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1780–1789. [Google Scholar]
- Potje, G.; Cadar, F.; Araujo, A.; Martins, R.; Nascimento, E.R. XFeat: Accelerated Features for Lightweight Image Matching. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 2682–2691. [Google Scholar]
- Balntas, V.; Lenc, K.; Vedaldi, A.; Mikolajczyk, K. HPatches: A benchmark and evaluation of handcrafted and learned local descriptors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5173–5182. [Google Scholar]
- Grupp, M. evo: Python Package for the Evaluation of Odometry and Slam. 2017. Available online: https://github.com/MichaelGrupp/evo (accessed on 5 September 2025).
- Liu, Y.; Miura, J. RDS-SLAM: Real-time dynamic SLAM using semantic segmentation methods. IEEE Access 2021, 9, 23772–23785. [Google Scholar] [CrossRef]
- Liu, J.; Li, X.; Liu, Y.; Chen, H. Dynamic-VINS: RGB-D inertial odometry for a resource-restricted robot in dynamic environments. IEEE Robot. Autom. Lett. 2022, 7, 9573–9580. [Google Scholar] [CrossRef]
- Yu, X.; Zheng, W.; Ou, L. CPR-SLAM: RGB-D SLAM in dynamic environment using sub-point cloud correlations. Robotica 2024, 42, 2367–2387. [Google Scholar] [CrossRef]
- Wang, S.; Hu, Q.; Zhang, X.; Li, W.; Wang, Y.; Zheng, E. LVID-SLAM: A Lightweight Visual-Inertial SLAM for Dynamic Scenes Based on Semantic Information. Sensors 2025, 25, 4117. [Google Scholar] [CrossRef]
- He, J.; Li, M.; Wang, Y.; Wang, H. OVD-SLAM: An online visual SLAM for dynamic environments. IEEE Sens. J. 2023, 23, 13210–13219. [Google Scholar] [CrossRef]
- Ul Islam, Q.; Ibrahim, H.; Chin, P.K.; Lim, K.; Abdullah, M.Z. FADM-SLAM: A fast and accurate dynamic intelligent motion SLAM for autonomous robot exploration involving movable objects. Robot. Intell. Autom. 2023, 43, 254–266. [Google Scholar] [CrossRef]
- He, L.; Li, S.; Qiu, J.; Zhang, C. DIO-SLAM: A dynamic RGB-D SLAM method combining instance segmentation and optical flow. Sensors 2024, 24, 5929. [Google Scholar] [CrossRef]
- Feng, D.; Yin, Z.; Wang, X.; Zhang, F.; Wang, Z. YLS-SLAM: A real-time dynamic visual SLAM based on semantic segmentation. Ind. Robot. Int. J. Robot. Res. Appl. 2025, 52, 106–115. [Google Scholar] [CrossRef]
- Cheng, J.; Wang, Z.; Zhou, H.; Li, L.; Yao, J. DM-SLAM: A feature-based SLAM system for rigid dynamic scenes. ISPRS Int. J. Geo-Inf. 2020, 9, 202. [Google Scholar] [CrossRef]
- Zhu, D.; Liu, P.; Qiu, Q.; Wei, J.; Gong, R. BY-SLAM: Dynamic Visual SLAM System Based on BEBLID and Semantic Information Extraction. Sensors 2024, 24, 4693. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).