Milepost-to-Vehicle Monocular Depth Estimation with Boundary Calibration and Geometric Optimization
Abstract
1. Introduction
2. Related Works
2.1. Monocular Depth Estimation
2.2. Monocular Depth Estimation Scale Recovery Algorithms
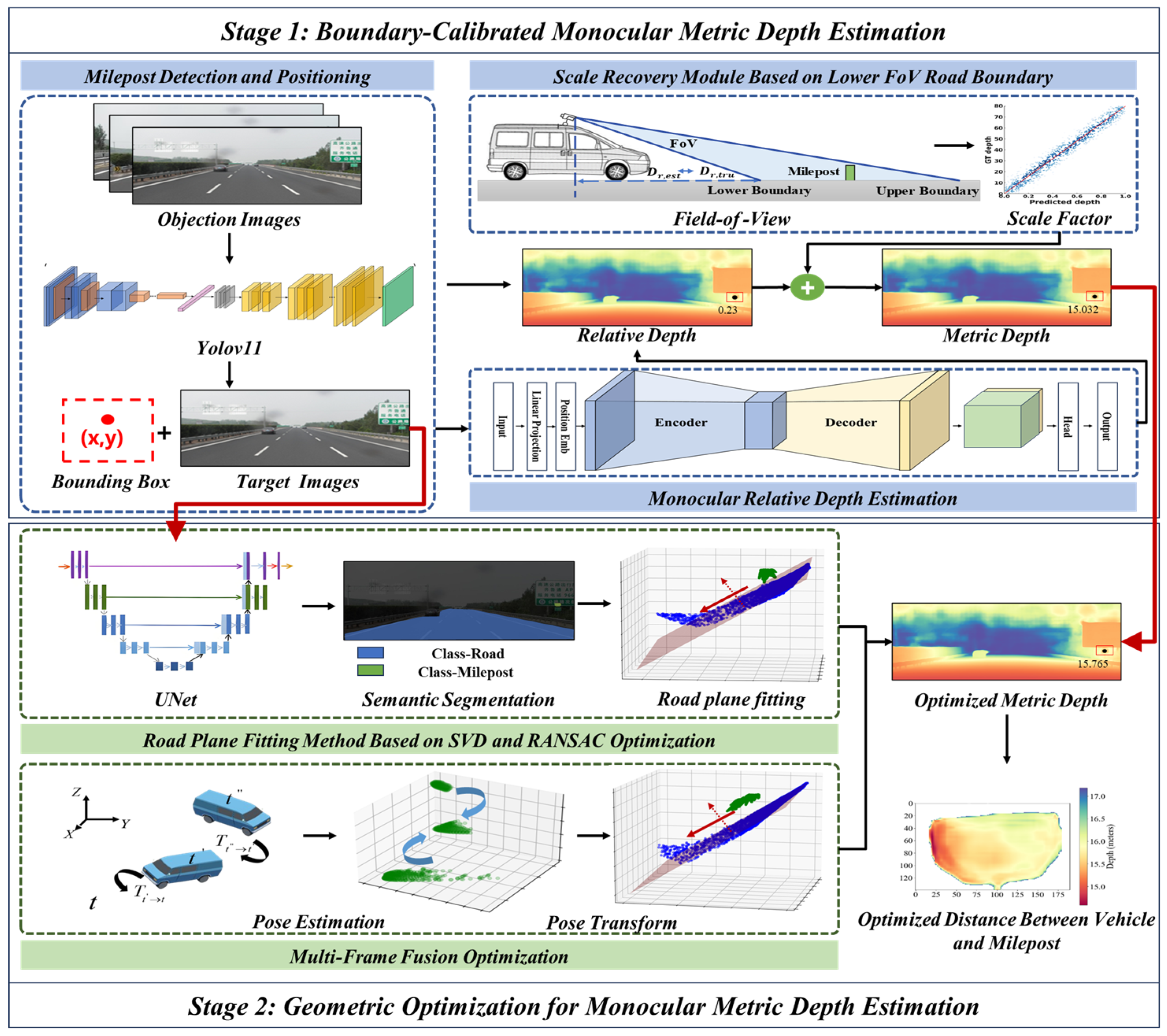
3. Methodology
3.1. Overview
3.2. YOLOv11-Based Milepost Detection and Positioning
3.3. Unsupervised Learning Monocular Relative Depth Estimation Model
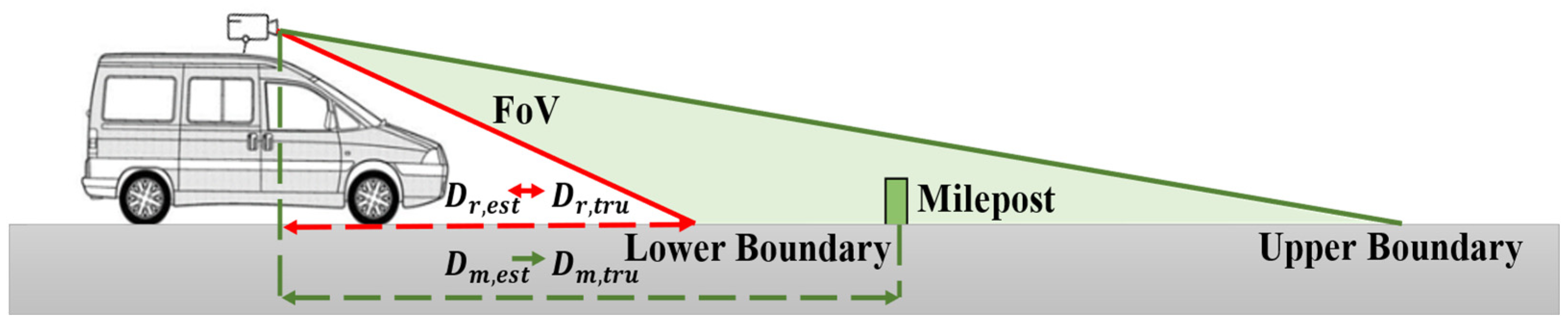
3.4. Scale Recovery Module Based on Lower Field-of-View Road Boundary
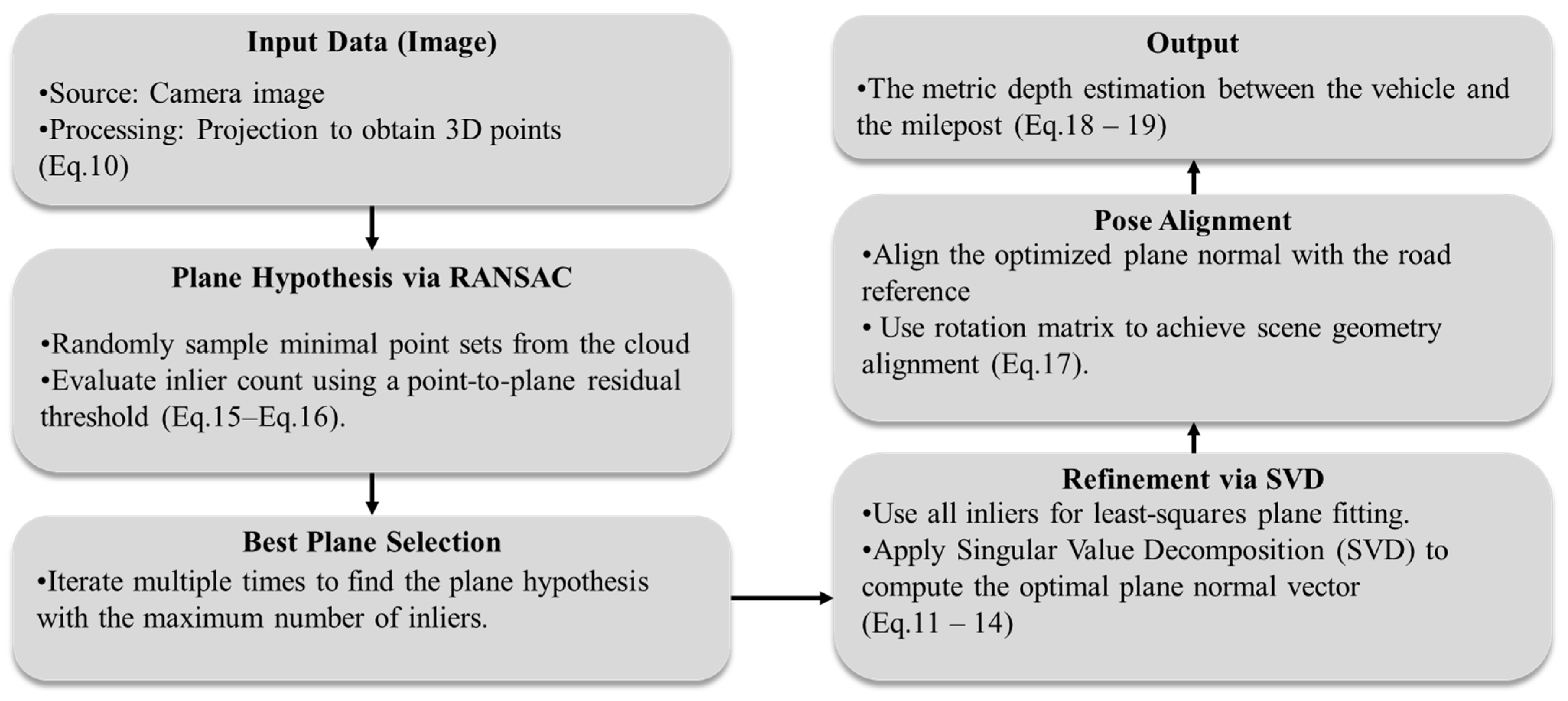
3.5. Road Plane Fitting Method Based on SVD and RANSAC Optimization
3.6. Dynamic Single-Frame Computation and Multi-Frame Fusion Optimization
| Algorithm 1. Geometric optimization for monocular metric depth estimation (GO-MMDE) |
| Input: : Input images K: Camera intrinsic matrix : True depth of lower boundary road points Output: Df: Estimated metric depth of milepost |
 |
4. Results and Discussion
4.1. Implementation Details
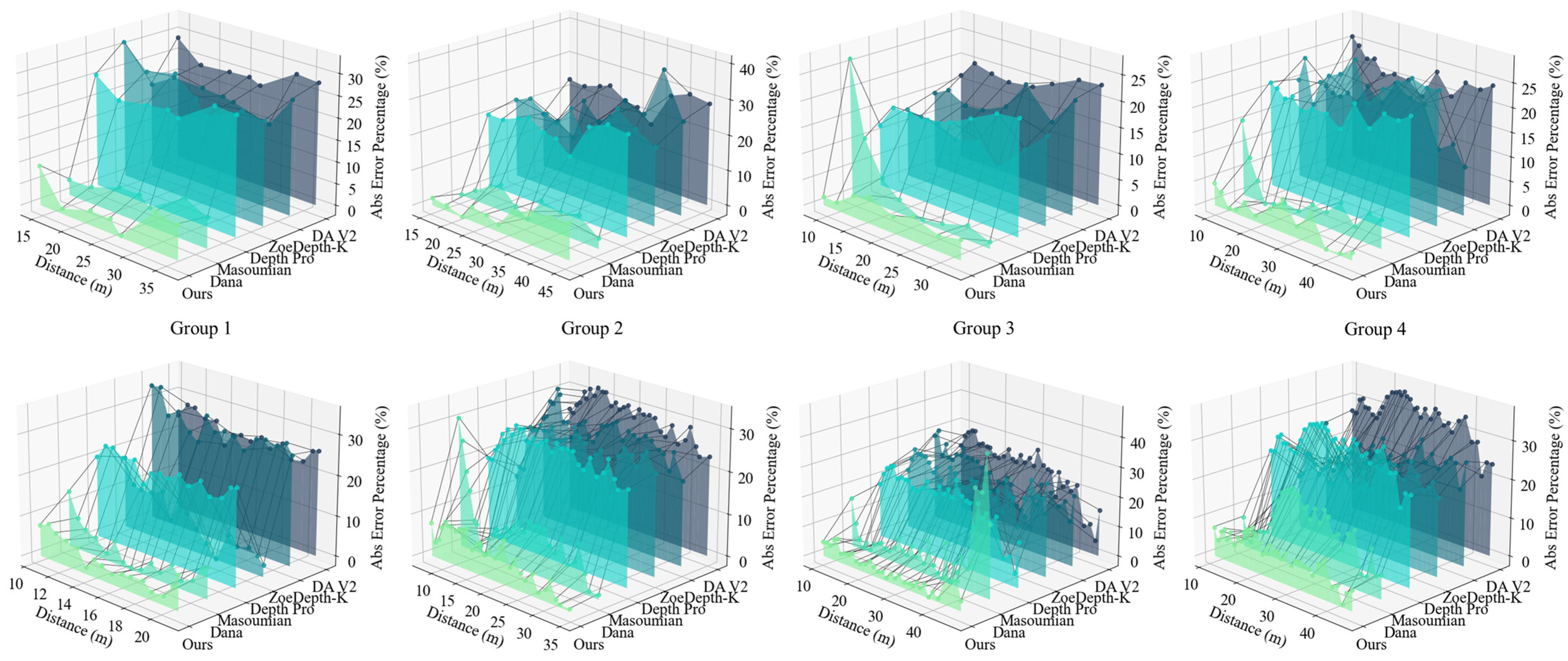
4.2. Comparison with State-of-the-Arts
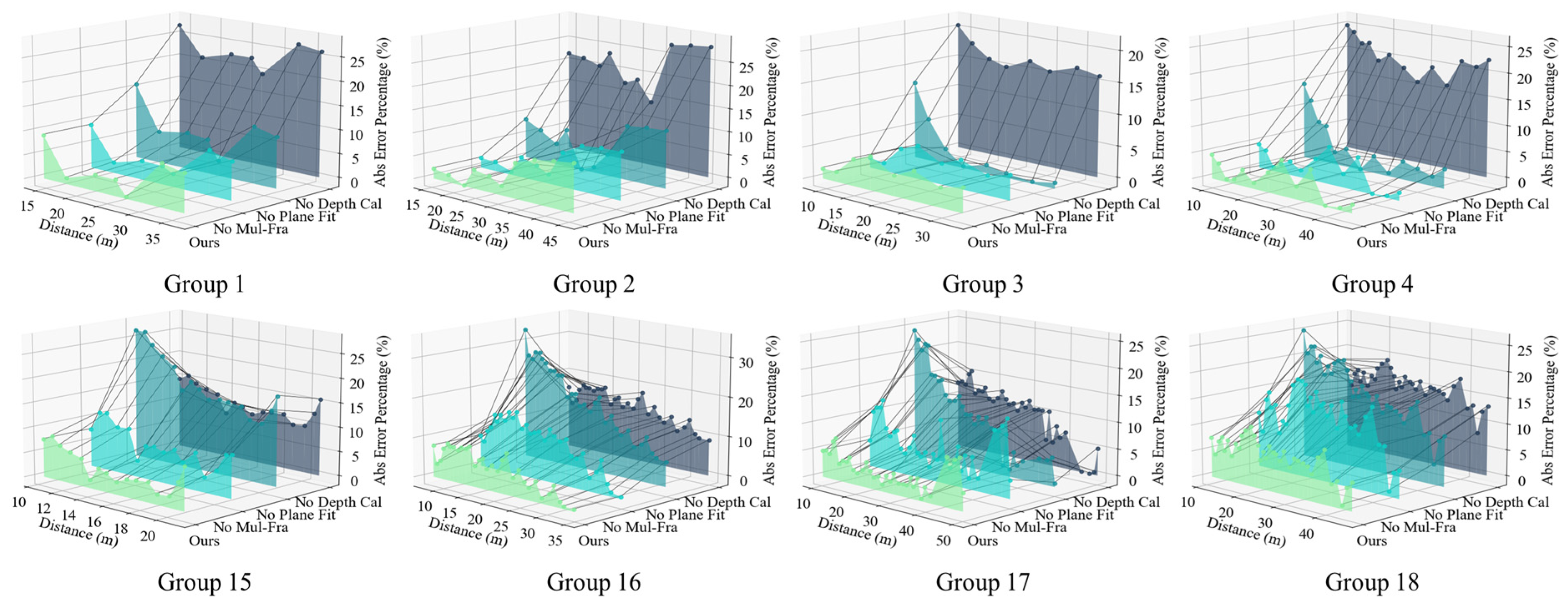
4.3. Ablation Study
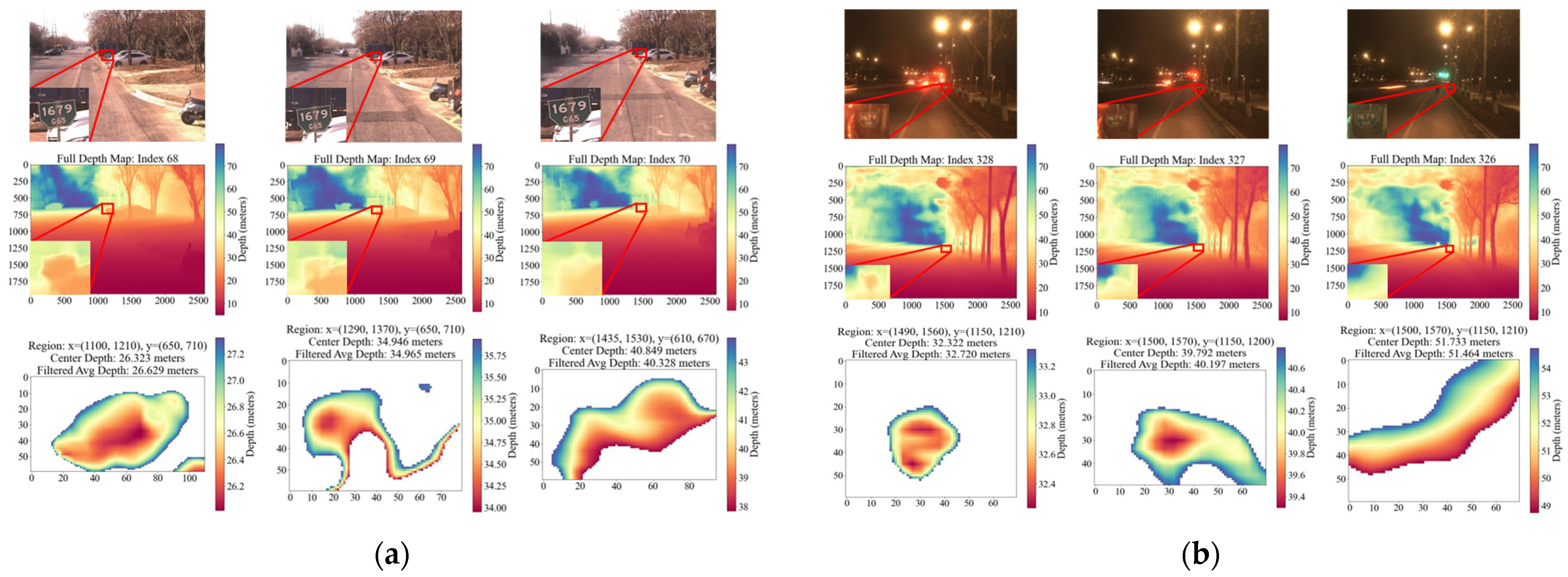
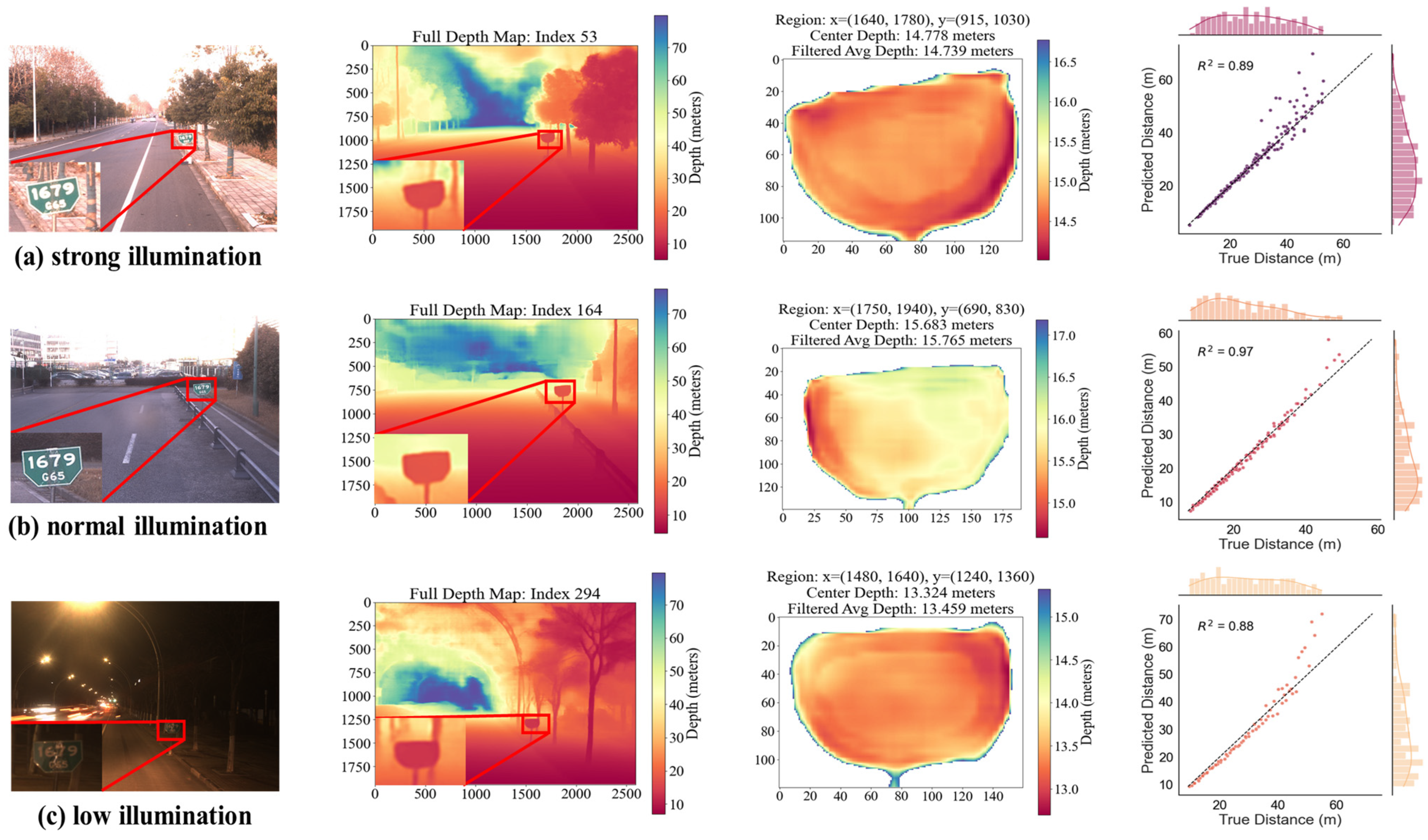
4.4. Stability Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gong, Y.; Zhang, X.; Feng, J.; He, X.; Zhang, D. LiDAR-Based HD Map Localization Using Semantic Generalized ICP with Road Marking Detection. In Proceedings of the 2024 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Abu Dhabi, United Arab Emirates, 14 October 2024; pp. 3379–3386. [Google Scholar]
- Cong, L.; Li, D.; Meng, K.; Zhu, S. Road-Aware Localization With Salient Feature Matching in Heterogeneous Networks. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21 April 2024; pp. 1–6. [Google Scholar]
- Nemec, D.; Šimák, V.; Janota, A.; Hruboš, M.; Bubeníková, E. Precise Localization of the Mobile Wheeled Robot Using Sensor Fusion of Odometry, Visual Artificial Landmarks and Inertial Sensors. Robot. Auton. Syst. 2019, 112, 168–177. [Google Scholar] [CrossRef]
- Wan, G.; Yang, X.; Cai, R.; Li, H.; Zhou, Y.; Wang, H.; Song, S. Robust and Precise Vehicle Localization Based on Multi-Sensor Fusion in Diverse City Scenes. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, QLD, Australia, 21–25 May 2018; pp. 4670–4677. [Google Scholar]
- Zhang, H.; Chen, C.-C.; Vallery, H.; Barfoot, T.D. GNSS/Multisensor Fusion Using Continuous-Time Factor Graph Optimization for Robust Localization. IEEE Trans. Robot. 2024, 40, 4003–4023. [Google Scholar] [CrossRef]
- Liu, H.; Ma, R. Research on Automatic Mileage Pile Positioning Technology Based on Multi-Sensor Fusion. 2023. Available online: https://ssrn.com/abstract=4598722 (accessed on 20 July 2025).
- Liu, H.; Ma, R. An Efficient and Automatic Method Based on Monocular Camera and GNSS for Collecting and Updating Geographical Coordinates of Mileage Pile in Highway Digital Twin Map. Meas. Sci. Technol. 2024, 35, 126011. [Google Scholar] [CrossRef]
- Eigen, D.; Puhrsch, C.; Fergus, R. Depth Map Prediction from a Single Image Using a Multi-Scale Deep Network. In Advances in Neural Information Processing Systems, Proceedings of the 28th International Conference on Neural Information Processing Systems Montreal, QC, Canada, 8–13 December 2014; MIT Press: Cambridge, MA, USA, 2014; Volume 27. [Google Scholar]
- Zhang, G.; Tang, X.; Wang, L.; Cui, H.; Fei, T.; Tang, H.; Jiang, S. Repmono: A Lightweight Self-Supervised Monocular Depth Estimation Architecture for High-Speed Inference. Complex Intell. Syst. 2024, 10, 7927–7941. [Google Scholar] [CrossRef]
- Xi, Y.; Li, S.; Xu, Z.; Zhou, F.; Tian, J. LapUNet: A Novel Approach to Monocular Depth Estimation Using Dynamic Laplacian Residual U-Shape Networks. Sci. Rep. 2024, 14, 23544. [Google Scholar] [CrossRef]
- Sui, X.; Gao, S.; Xu, A.; Zhang, C.; Wang, C.; Shi, Z. Lightweight Monocular Depth Estimation Using a Fusion-Improved Transformer. Sci. Rep. 2024, 14, 22472. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, L.; Xu, G.; Wang, X.; Zhang, Z.; Deng, Y.; Zang, J.; Chen, Y.; Cai, Z.; Yang, X. Monster: Marry Monodepth to Stereo Unleashes Power. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 9–14 June 2025; pp. 6273–6282. [Google Scholar]
- Song, Z.; Wang, Z.; Li, B.; Zhang, H.; Zhu, R.; Liu, L.; Jiang, P.; Zhang, T. DepthMaster: Taming Diffusion Models for Monocular Depth Estimation. arXiv 2025, arXiv:2501.02576. [Google Scholar] [CrossRef]
- Kuznietsov, Y.; Stuckler, J.; Leibe, B. Semi-Supervised Deep Learning for Monocular Depth Map Prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6647–6655. [Google Scholar]
- Zama Ramirez, P.; Poggi, M.; Tosi, F.; Mattoccia, S. Geometry Meets Semantics for Semi-Supervised Monocular Depth Estimation. In Computer Vision—ACCV 2018, Proceedings of the Asian Conference on Computer Vision (ACCV), Perth, Australia, 2–6 December 2018; Springer International Publishing: Cham, Switzerland, 2018; pp. 298–313. [Google Scholar]
- Rahman, M.A.; Fattah, S.A. Semi-Supervised Semantic Depth Estimation Using Symbiotic Transformer and NearFarMix Augmentation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–7 January 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 250–259. [Google Scholar]
- Song, K.; Yoon, K.J. Learning Monocular Depth Estimation via Selective Distillation of Stereo Knowledge. arXiv 2022, arXiv:2205.08668. [Google Scholar] [CrossRef]
- Gurram, A.; Urfalioglu, O.; Halfaoui, I.; Bouzaraa, F.; Lopez, A.M. Semantic monocular depth estimation based on artificial intelligence. IEEE Intell. Transp. Syst. Mag. 2020, 13, 99–103. [Google Scholar] [CrossRef]
- Garg, R.; Bg, V.K.; Carneiro, G.; Reid, I. Unsupervised CNN for Single View Depth Estimation: Geometry to the Rescue. In Computer Vision—ECCV 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; pp. 740–756. [Google Scholar]
- Zhou, T.; Brown, M.; Snavely, N.; Lowe, D.G. Unsupervised learning of depth and ego-motion from video. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Shim, D.; Kim, H.J. SwinDepth: Unsupervised Depth Estimation Using Monocular Sequences via Swin Transformer and Densely Cascaded Network. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May 2023; pp. 4983–4990. [Google Scholar]
- Lian, L.; Qin, Y.; Cao, Z.; Gao, Y.; Bai, J.; Ge, X.; Guo, B. A Continuous Autonomous Train Positioning Method Using Stereo Vision and Object Tracking. IEEE Intell. Transp. Syst. Mag. 2024, 16, 6–62. [Google Scholar] [CrossRef]
- Hui, T.-W. RM-Depth: Unsupervised Learning of Recurrent Monocular Depth in Dynamic Scenes. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 1665–1674. [Google Scholar]
- Chawla, H.; Varma, A.; Arani, E.; Wang, J. Continual Learning of Unsupervised Monocular Depth from Videos. In Proceedings of the 2024 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2024; pp. 8419–8429. [Google Scholar]
- Saunders, K.; Vogiatzis, G.; Manso, L.J. Self-Supervised Monocular Depth Estimation: Let’s Talk about the Weather. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–3 October 2023; pp. 11255–11265. [Google Scholar]
- Fu, H.; Gong, M.; Wang, C.; Batmanghelich, K.; Tao, D. Deep Ordinal Regression Network for Monocular Depth Estimation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2002–2011. [Google Scholar]
- Guizilini, V.; Vasiljevic, I.; Chen, D.; Ambruş, R.; Gaidon, A. Towards Zero-Shot Scale-Aware Monocular Depth Estimation. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–3 October 2023; pp. 9233–9243. [Google Scholar]
- Bhat, S.F.; Birkl, R.; Wofk, D.; Wonka, P.; Esteves, C. ZoeDepth: Zero-Shot Transfer by Combining Relative and Metric Depth. arXiv 2023, arXiv:2302.12288. [Google Scholar]
- Bochkovskii, A.; Delaunoy, A.; Germain, H.; Georgoulis, S.; Proesmans, M.; Van Gool, L. Depth Pro: Sharp Monocular Metric Depth in Less than a Second. arXiv 2024, arXiv:2410.02073. [Google Scholar] [CrossRef]
- Piccinelli, L.; Yang, Y.H.; Sakaridis, C.; Van Gool, L. UniDepth: Universal Monocular Metric Depth Estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 17–21 June 2024; pp. 10106–10116. [Google Scholar]
- Yang, L.; Kang, B.; Huang, Z.; Chen, S.; Wang, S.; Zhao, H.; Feng, J. Depth Anything: Unleashing the Power of Large-Scale Unlabeled Data. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 17–21 June 2024; pp. 10371–10381. [Google Scholar]
- Chawla, H.; Varma, A.; Arani, E.; Zonooz, B. Multimodal Scale Consistency and Awareness for Monocular Self-Supervised Depth Estimation. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May 2021; pp. 5140–5146. [Google Scholar]
- Zhang, S.; Zhang, J.; Tao, D. Towards Scale-Aware, Robust, and Generalizable Unsupervised Monocular Depth Estimation by Integrating IMU Motion Dynamics. In Computer Vision—ECCV 2022, Proceedings of the 17th European Conference, Tel Aviv, Israel, 23–27 October 2022; European Conference on Computer Vision; Springer Nature Switzerland: Cham, Switzerland, 2022; pp. 143–160. [Google Scholar]
- Hu, M.; Yin, W.; Zhang, C.; Cai, Z.; Long, X.; Chen, H.; Wang, K.; Yu, G.; Shen, C.; Shen, S. Metric3D v2: A Versatile Monocular Geometric Foundation Model for Zero-Shot Metric Depth and Surface Normal Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 10579–10596. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Peng, S.; Chen, J.; Peng, S.; Sun, J.; Liu, M.; Bao, H.; Feng, J.; Zhou, X.; Kang, B. Prompting Depth Anything for 4K Resolution Accurate Metric Depth Estimation. In Proceedings of the Computer Vision and Pattern Recognition Conference, Nashville, TN, USA, 11–15 June 2025; pp. 17070–17080. [Google Scholar]
- Cui, X.-Z.; Feng, Q.; Wang, S.-Z.; Zhang, J.-H. Monocular Depth Estimation with Self-Supervised Learning for Vineyard Unmanned Agricultural Vehicle. Sensors 2022, 22, 721. [Google Scholar] [CrossRef]
- Gelso, E.R.; Sjoberg, J. Consistent Threat Assessment in Rear-End Near-Crashes Using BTN and TTB Metrics, Road Information and Naturalistic Traffic Data. IEEE Intell. Transp. Syst. Mag. 2017, 9, 74–89. [Google Scholar] [CrossRef]
- Elazab, G.; Gräber, T.; Unterreiner, M.; Hellwich, O. MonoPP: Metric-Scaled Self-Supervised Monocular Depth Estimation by Planar-Parallax Geometry in Automotive Applications. In Proceedings of the 2025 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Tucson, AZ, USA, 26 February 2025; pp. 2777–2787. [Google Scholar]
- Zheng, C.; Cham, T.J.; Cai, J. T2net: Synthetic-to-Realistic Translation for Solving Single-Image Depth Estimation Tasks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 767–783. [Google Scholar]
- Lo, S.-Y.; Wang, W.; Thomas, J.; Zheng, J.; Patel, V.M.; Kuo, C.-H. Learning Feature Decomposition for Domain Adaptive Monocular Depth Estimation. In Proceedings of the 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 23 October 2022; pp. 8376–8382. [Google Scholar]
- Li, Z.; Bhat, S.F.; Wonka, P. PatchRefiner: Leveraging Synthetic Data for Real-Domain High-Resolution Monocular Metric Depth Estimation. In Computer Vision—ECCV 2024, Proceedings of the European Conference on Computer Vision (ECCV), Cham, Switzerland, 29 September–4 October 2024; Springer Nature Switzerland: Cham, Switzerland, 2024; pp. 250–267. [Google Scholar]
- Zhang, C.; Weng, X.; Cao, Y.; Zhang, M.; Wang, L.; Li, H. Monocular Absolute Depth Estimation from Motion for Small Unmanned Aerial Vehicles by Geometry-Based Scale Recovery. Sensors 2024, 24, 4541. [Google Scholar] [CrossRef]
- Masoumian, A.; Marei, D.G.F.; Abdulwahab, S.; Abualkishik, A.Z. Absolute Distance Prediction Based on Deep Learning Object Detection and Monocular Depth Estimation Models. In Artificial Intelligence Research and Development; IOS Press: Amsterdam, The Netherlands, 2021; pp. 325–334. [Google Scholar]
- Dana, A.; Carmel, N.; Shomer, A.; Zvirin, Y.; Bagon, S.; Dekel, T. Do More with What You Have: Transferring Depth-Scale from Labeled to Unlabeled Domains. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Piscataway, NJ, USA, 16–22 June 2024; pp. 4440–4450. [Google Scholar]
- Zhu, R.; Wang, C.; Song, Z.; Zhang, H.; Sun, J. ScaleDepth: Decomposing Metric Depth Estimation into Scale Prediction and Relative Depth Estimation. arXiv 2024, arXiv:2407.08187. [Google Scholar] [CrossRef]
- McCraith, R.; Neumann, L.; Vedaldi, A. Calibrating Self-Supervised Monocular Depth Estimation. arXiv 2020, arXiv:2009.07714. [Google Scholar]
- Xue, F.; Zhuo, G.; Huang, Z.; Fu, W.; Wu, Z.; Ang, M.H. Toward Hierarchical Self-Supervised Monocular Absolute Depth Estimation for Autonomous Driving Applications. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020; pp. 2330–2337. [Google Scholar]
- Yang, W.; Li, H.; Li, X.; Wang, Z.; Zhang, B. UAV Image Target Localization Method Based on Outlier Filter and Frame Buffer. Chin. J. Aeronaut. 2024, 37, 375–390. [Google Scholar] [CrossRef]
- Khanam, R.; Hussain, M. Yolov11: An Overview of the Key Architectural Enhancements. arXiv 2024, arXiv:2410.17725. [Google Scholar] [CrossRef]
- Yang, L.; Kang, B.; Huang, Z.; Zhao, Z.; Xu, X.; Feng, J.; Zhao, H. Depth Anything v2. Adv. Neural Inf. Process. Syst. 2024, 37, 21875–21911. [Google Scholar]
- National Standard GB 5768.2-2022; Road Traffic Signs and Markings—Part 2: Road Traffic Signs. Standardization Administration of China: Beijing, China, 2022.






| Method | Lower Is Better ↓ | Higher Is Better ↑ | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Latency | FPS | ||||||||
| DA V2 [50] | 0.212 | 0.050 | 5.962 | 0.257 | 36 | 0.449 | 1.000 | 1.000 | 28 |
| ZoeDepth-K [28] | 0.216 | 0.071 | 7.351 | 0.330 | 45 | 0.463 | 0.662 | 1.000 | 22 |
| Depth Pro [29] | 0.238 | 0.067 | 8.046 | 0.318 | 50 | 0.344 | 0.875 | 0.986 | 20 |
| Masoumian [43] | 0.129 | 0.042 | 8.570 | 0.167 | 59 | 0.881 | 0.960 | 0.997 | 17 |
| Dana [44] | 0.195 | 0.042 | 5.684 | 0.234 | 42 | 0.534 | 1.000 | 1.000 | 24 |
| Ours | 0.055 | 0.008 | 3.421 | 0.080 | 30 | 0.972 | 1.000 | 1.000 | 33 |
| Method | Lower Is Better ↓ | Higher Is Better ↑ | |||||
|---|---|---|---|---|---|---|---|
| No Depth Cal | 0.216 | 0.071 | 7.351 | 0.330 | 0.463 | 0.662 | 1.000 |
| No Plane Fit | 0.102 | 0.018 | 3.622 | 0.139 | 0.875 | 1.000 | 1.000 |
| No Mul-Fra | 0.081 | 0.013 | 4.224 | 0.108 | 0.960 | 1.000 | 1.000 |
| Ours | 0.055 | 0.008 | 3.421 | 0.080 | 0.972 | 1.000 | 1.000 |
| Method | Lower Is Better ↓ | Higher Is Better ↑ | |||||
|---|---|---|---|---|---|---|---|
| short-range | 0.046 | 0.003 | 0.667 | 0.058 | 1.000 | 1.000 | 1.000 |
| mid-range | 0.038 | 0.002 | 1.070 | 0.049 | 1.000 | 1.000 | 1.000 |
| long-range | 0.079 | 0.017 | 5.489 | 0.113 | 0.923 | 1.000 | 1.000 |
| Method | Lower Is Better ↓ | Higher Is Better ↑ | |||||
|---|---|---|---|---|---|---|---|
| Strong | 0.052 | 0.010 | 3.891 | 0.087 | 0.958 | 1.000 | 1.000 |
| Normal | 0.044 | 0.003 | 1.618 | 0.055 | 0.992 | 1.000 | 1.000 |
| Low | 0.082 | 0.010 | 4.368 | 0.097 | 0.971 | 1.000 | 1.000 |
| Method | Lower Is Better ↓ | Higher Is Better ↑ | |||||
|---|---|---|---|---|---|---|---|
| Flat road | 0.053 | 0.008 | 3.277 | 0.080 | 0.970 | 1.000 | 1.000 |
| Curved road | 0.062 | 0.008 | 3.827 | 0.082 | 0.957 | 1.000 | 1.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, E.; Ma, T.; Yang, H.; Li, J.; Xie, Z.; Tong, Z. Milepost-to-Vehicle Monocular Depth Estimation with Boundary Calibration and Geometric Optimization. Electronics 2025, 14, 3446. https://doi.org/10.3390/electronics14173446
Zhang E, Ma T, Yang H, Li J, Xie Z, Tong Z. Milepost-to-Vehicle Monocular Depth Estimation with Boundary Calibration and Geometric Optimization. Electronics. 2025; 14(17):3446. https://doi.org/10.3390/electronics14173446
Chicago/Turabian StyleZhang, Enhua, Tao Ma, Handuo Yang, Jiaqi Li, Zhiwei Xie, and Zheng Tong. 2025. "Milepost-to-Vehicle Monocular Depth Estimation with Boundary Calibration and Geometric Optimization" Electronics 14, no. 17: 3446. https://doi.org/10.3390/electronics14173446
APA StyleZhang, E., Ma, T., Yang, H., Li, J., Xie, Z., & Tong, Z. (2025). Milepost-to-Vehicle Monocular Depth Estimation with Boundary Calibration and Geometric Optimization. Electronics, 14(17), 3446. https://doi.org/10.3390/electronics14173446








